Prerpints.org logo
Preprint
Article

Deep Network Optimization Using a Genetic Algorithm for Recognizing Hand Gestures via EMG Signals

Altmetrics

Downloads

263

Views

165

Comments

0

Submitted:

31 December 2022

Posted:

04 January 2023

You are already at the latest version

Alerts
Abstract
Hand gesture recognition has many valuable applications in engineering and health care. This study proposes a novel model which can accurately distinguish hand gestures using forearm muscles' surface electromyogram (sEMG) signals. A deep learning algorithm with hyper parameters impacting the final model’s accuracy and a convolutional neural network (CNN) were employed in the recognition stage. The number of convolutional layers, kernels per layer, and neurons in the dense layer were selected for optimization, while the remaining parameters, such as the learning rate, batch size, and number of epochs, were chosen based on trial and error and prior knowledge. The optimal values for the selected hyperparameters were obtained using a genetic algorithm to achieve maximum recognition accuracy. The UC2018 Dual-Myo database was used for training and testing the model based on EMG signals characterizing the activity of eight different hand gestures. The final structure of the model consisted of two convolutional layers with 131 and 28 kernels, a dense layer with 111 neurons, and a softmax layer with eight neurons. Upon optimizing the hyperparameters using the genetic algorithm, the accuracy of the proposed model increased from 91.86% to 96.4% at best and 95.3% on average in real-time applications and 99.6% in an offline mode. Future work is warranted towards improving the architecture and the computational cost.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Electromyography (EMG), a technique used for capturing the electrical activity of skeletal muscles, has been long considered invaluable in decoding movements of the musculoskeletal system 1. In the last few decades, human motion detection using EMG signals, also known as EMG pattern recognition, was successfully employed in various applications, including powered upper-limb prostheses 2, electric power wheelchairs 3, human-computer interactions (HCI) 4, and diagnostic medicine and rehabilitation 5. Compared to other well-known electrophysiological signals, such as the electrocardiogram (ECG) which records heart signals, the electrooculogram (EOG) which captures eye movement, and galvanic skin response (GSR) which reflects electrodermal activity, the analysis of surface EMG signals is considered more challenging6. These challenges include the dynamic changing characteristics of the signal over time, electrode location shift, muscle fatigue, variations in muscle contraction intensity, limb position changes, and forearm orientation. However, due to its non-invasive nature and overall ease of recording, surface EMG (sEMG) continues to be the main modality employed for non-invasively quantifying skeletal muscle activity 2,7–11. The most common EMG pattern recognition algorithms include support vector machine (SVM), K-nearest neighbor (K-NN), Linear discriminant analysis (LDA), multilayer perceptron (MLP), artificial neural network (ANN), and random forest classifiers. Alkan and Gunay 12 used an SVM algorithm to classify four EMG data classes with 97±1% accuracy. Tkach et al. 13 used an LDA algorithm to classify 13 classes of EMG data with 92% accuracy. Using a boosted random forest classifier, Li et al. 14 performed an RR of 92%, although the novelty detection accuracy was only 20%. This algorithm was consequently refined to enhance the detection accuracy to 80% with an RR in the trained samples of 80%.
Current EMG pattern recognition approaches can be broadly divided into two categories: (1) methods based on feature engineering; and (2) methods based on feature learning. Although so far, feature engineering has been the dominant tool for EMG pattern recognition, feature learning, as exemplified by deep learning, has recently demonstrated enhanced recognition performance as compared to traditional hand-crafted features. Unlike feature engineering and conventional machine learning approaches, deep learning leverages the multiplicity of many samples to extract high-level features from low-level inputs. However, deep learning algorithms require large training datasets to train large deep networks (hidden layers, each with a large number of neurons) and associated numerous parameters (millions of free parameters). On the other hand, in this big data era, with the increasing availability of large shared datasets and advances in processing technology, deep learning algorithms in EMG pattern recognition provide effective means for capturing and describing the complexity and variability of sEMG signals for a wide spectrum of relevant applications 15. Geng et al. 16 evaluated CNN’s performance in recognizing hand and finger movement based on sEMG from three public databases containing data obtained using a single row of electrodes or a 2D high-density electrode array. Without using windowed features, the classification accuracy of an eight motion within-subject problem achieved 89.3% on a single frame (1 ms) of the sEMG image. The accuracy reached 99.0% and 99.5% using 128 channels of the HD-sEMG signals and simple majority voting over 40 and 150 frames (40 and 150 ms), respectively.
Preprints 66887 g001
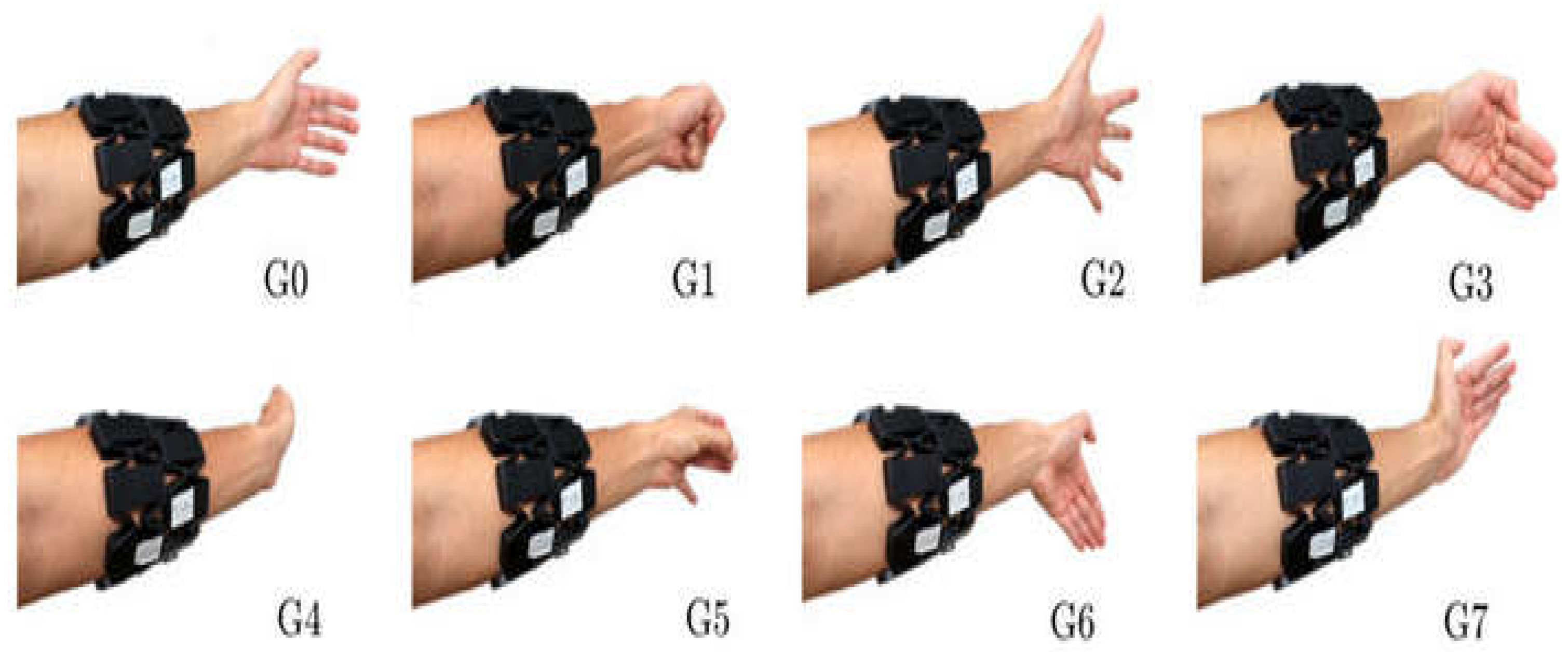
Figure 1. UC2018 DualMyo dataset gestures: (G0) rest, (G1) closed fist, (G2) open hand, (G3) wave in, (G4) wave out, (G5) double-tap, (G6) hand down, (G7) hand up 17.
Figure 1. UC2018 DualMyo dataset gestures: (G0) rest, (G1) closed fist, (G2) open hand, (G3) wave in, (G4) wave out, (G5) double-tap, (G6) hand down, (G7) hand up 17.
Preprints 66887 g001
Cote-Allardet et al. 18,19 demonstrated that CNN is accurate enough to detect complex movements while being robust to short-term muscle fatigue, slight displacement of electrodes, and long-term use without recalibration. Laezza 20 evaluated the performance of three different network models for myoelectric control, including RNN, CNN, and RNN + CNN. RNN provided the best performance with 91.81% classification accuracy as compared to CNN (89.01%) and RNN + CNN (90.4%). This result, however, may be due to RNN and LSTM networks’ advantages in time series processing. Asif et al. 21 investigated the effect of hyperparameters on different hand gestures. They showed that a learning rate set to either 0.0001 or 0.001 significantly outperformed other selections. Ossaba 22 implemented a Recurrent Neural Network (RNN) model using Long-short Term Memory (LSTM) units and dense layers for developing a gesture classifier for hand prosthesis control with the purpose of decreasing the number of EMG channels and the overall model complexity. The presented model was able to recognize five hand gestures with an accuracy of 99% for the training and validation stages, and an accuracy of 87 ± 7% during real-time testing while using only four EMG channels. In another study 23, a feature extraction method in the frequency domain of EEG and EMG signals was successfully used in conjunction with deep learning for enhancing the recognition of amputated wrist and hand movement. Zhao et al. 24 used deep learning for hand gesture recognition based on EMG signals, suggesting a model which recognizes hand gestures with 99.6% accuracy rate and fewer parameters.
This study proposes a novel model which can accurately distinguish hand gestures using forearm muscles' surface electromyogram (sEMG) signals. The UC2018 DualMyo dataset 25 will be used to train a deep CNN, with additional data generated using the windowing technique 26 to enable effective deep network training. A genetic algorithm will be used to optimize the model structure for maximum accuracy 27, and a confusion matrix using the optimal parameters, will be developed representing the model’s performance.

2. Material and Methods

2.1. Preprocessing

The UC2018 DualMyo data set was used 25 for developing our proposed model. This dataset was created by recording EMG signals using an armband while capturing hand movements by a data glove, resulting in a database containing different hand gestures and the corresponding signals 25. The preprocessing phase included filtering, normalizing, removing municipal electricity and heartbeat noise, windowing, labeling, and finally converting the data into three subsets: train, validation, and test 28,29. The UC2018 data set was obtained from two EMG sensors (www.myoware.com) with a subject performing eight distinct hand gestures (Fig. 1). A total of 110 repetitions of each class of gesture was obtained across five recording sessions. Each armband included eight sensors, and the data was recorded at a frequency of 200 Hz. (dimension of 16×400 with a sampling timeframe of 2 seconds). Fig. 1 depicts the eight movements associated with the signals obtained from the database: (G0) rest, (G1) closed fist, (G2) open hand, (G3) wave in, (G4) wave out, (G5) double-tap, (G6) hand down, (G7) hand-up. Although noise filtering was applied to the data set, the data was still not suitable as input to the model due to long signals and insufficient amount of data for training the deep network. To resolve this, the signals were first stacked and then split into shorter signals using the windowing technique. Window sizes of 125 milliseconds and 1 second was used for real-time and offline usage, respectively, without overlap. The last 15 and 50 data samples were used for labeling, and the label with the most repetition was selected as the sample label. A total of 14080 signals (dimensions of 25×16 and 200×16) was finally obtained with a signal range of [−128 to 128]. To increase the speed of convergence, stabilize the network, and prevent gradient explosion, it was necessary to normalize the input data. Using MinMax, the data was divided by the maximum value of 128, resulting in a range of [−1 and +1]. The data was then randomly divided into three groups of train, test, and validation, with ratios of 70%, 15%, and 15%, respectively.

2.2. Model Design

The structure and parameters of any proposed model significantly impact the accuracy of hand gesture recognition. The choice of a model also depends on the dimensions and size of data, as well as their nature. Selecting model parameters typically requires trial and error, making the design process complicated and time-consuming 30. The number of model parameters can also be one of the design variables, although this study’s primary purpose was to maximize the model’s accuracy in EMG pattern recognition.
The proposed model was developed based on supervised learning by using labeled training input data. The deep CNN network, selected as a classifier, extracts high-level data features by convolutional layers. This feature extraction method, referred to as feature learning, has previously demonstrated better performance as compared to traditional hand-crafted features 31. The model consists of a series of convolutional layers, a dense layer, and a SoftMax layer with eight neurons 32. Each convolutional layer contains kernels of specified dimensions which move on the signal with a fixed step and extract the properties. In this work, rectified linear units (Relu) are used as an activation function to prevent the Gradient vanishing phenomenon and improve the training speed 33. The dimension of the kernels is 20×8, with a step size of one. The number of convolutional layers, the number of neurons of dense layer neurons, and the number of kernels in each layer are the parameters for which the optimal values are calculated using a genetic algorithm detailed in the next section. The last layer of the model consists of 8 neurons with the SoftMax activation function.
Typically, a high learning rate value causes training to fluctuate and may lead to nonconvergence, while a low value reduces the convergence rate of the model. The learning rate choice also affects the number of epochs, where the lower the learning rate, the higher the epochs. On the other hand, an increased number of epochs may overfit the model 34. Figure 2 shows that the model converges faster with a higher learning rate, but overfitting occurs at higher epochs. Alternatively, model training with a small learning rate requires higher processing power.
According to the experimental results, the number of epochs in the proposed model is 30, the learning rate is 0.000, and the Batch size is 65. The activation functions in all the layers are Relu and the kernel size is 20×8. These parameters can also be added to the independent variables to be optimized by the genetic algorithm, although computation time increases with the addition of each parameter. Therefore, in this study, only the model structure parameters, including the number of convolutional layers, the number of kernels in each layer, and the number of dense layer neurons, are considered as independent variables. We used the Adaptive moment estimation optimizer to train the coefficients, where the categorical cross-entropy is used as the error function, and the coefficients are initialized by the random uniform method 35,36.

2.3. Model Optimization

In the previous section we proposed a CNN-based model capable of recognizing hand gestures based on sEMG signals. The accuracy of the model was found to be highly dependent on the selected parameters. This challenge was mitigated by formulating an optimization problem, where the cost function is associated with enhancing the model’s accuracy. A genetic algorithm (GA) was chosen for optimization. GA is a robust stochastic algorithm which uses random elements, considers a population of solutions, and recombines different solutions as needed. More specifically, a GA determines the first generation with a specific population size so that each of the chromosomes of this generation is a structure for the convolutional model. The convolutional model, in turn, is based on the chromosomes’ system and provides recognition accuracy, which is used as the algorithm’s objective function. The chromosomes are then randomly integrated to form the next generation. The higher the chromosome scores from the objective function, the better the chance of advancing to the next generation. Chromosome integration is performed by cross-over, mutation, parents portion, and elite portion methods 37. The process continues until the algorithm converges and reaches the best generation. The best chromosome of this generation is consequently selected as the optimal structure of the model.
To improve the results, some of the parameters in the GA were adjusted, including the number of chromosomes in each generation (usually between 2 and 4 times the number of variables). In this case, the number of variables was 4, however, the chromosomes’ population was assumed to be 25 for better results. The maximum number of generation sequences is typically selected as a large number to ensure that the algorithm continues until convergence. In the crossover method, two members of the current population were randomly selected with different weight coefficients. The cross-over probability coefficient was 0.7 and was uniform. Each member of the new generation was generated with a 20% chance of crossing over. The mutation probability coefficient in this study was 0.1. Overall, the more significant is the value of the coefficient, the less likely will the algorithm be confined in a local minimum. Based on the parent portion method, some parents are randomly passed on to the next generation, but with different weight coefficients. The probability of choosing parents is based on their score from the objective function. The parent’s portion coefficient is 0.2. This slightly differs from the elite method which passes some elites of each generation on to future generations. The share of elites from each generation is 0.05. A stop criterion is also defined for stopping the algorithm if it converges before reaching maximum iterations. If there is no increase in the objective function in 6 consecutive generations, the GA is considered to have reached the convergence point.
In this study we defined the objective function of the genetic algorithm as the accuracy of the CNN model. Therefore, for each generation member, the model needed to be trained, and the model's accuracy had to be determined, rendering the computational cost very high. To reduce this cost, a filter was placed in the objective function detecting duplicate inputs. If an input is duplicated, and the model has already been trained within the same structure, the algorithm searches for the corresponding answer among the previous solutions and records it as the objective function’s output. The search algorithm used was custom developed in Python on the Tensorflow framework and the Keras library. The test was run on a computer with a 3.2GHz CPU, 32GB RAM & NVIDIA GeForce GTX 1080 specifications.

3. Results and Discussion

A confusion matrix is a technique for summarizing the performance of a classification algorithm. It represents the model’s performance for each tag and is used to evaluate its performance. Each row of the matrix represents instances in a predicted class, while each column represents the actual class instance. The model's accuracy, precision, and sensitivity are calculated using Table 1 and equations (1-3), respectively.
A c c u r a c y = T P + T N T P + T N + F P + F N
P r e c i s i o n = T P F P + T P
S e n s i t i v i t y = T P T P + F N
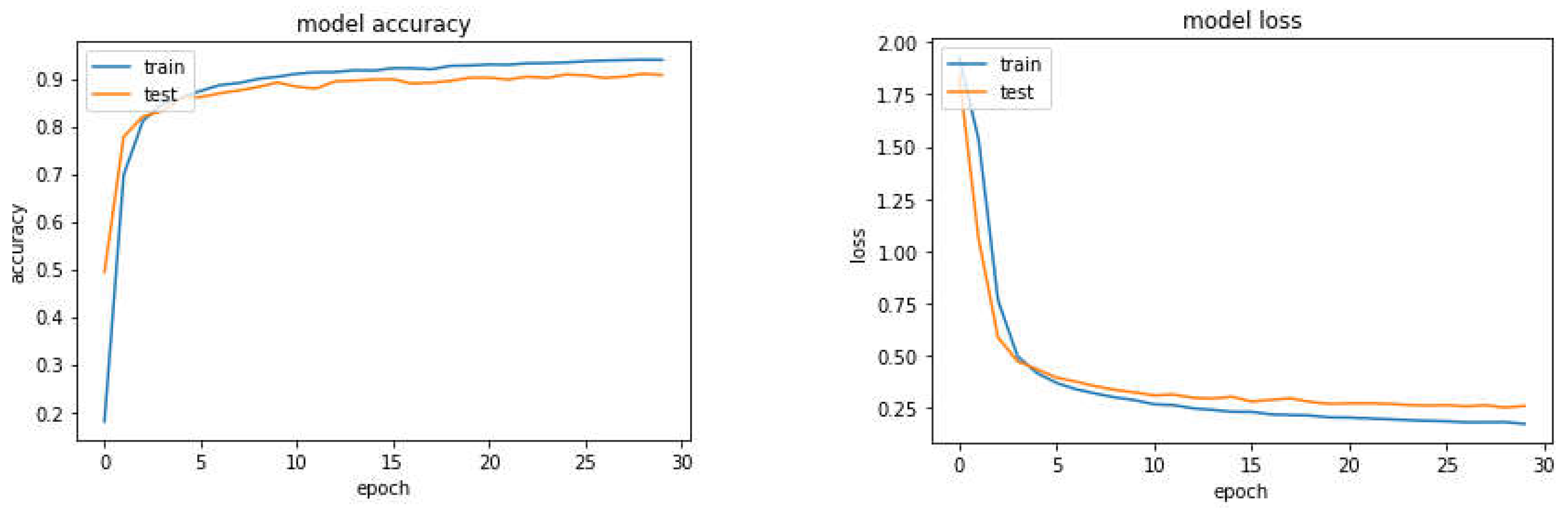
Table 2 shows the confusion matrix of the original model in epoch 30. The structure of this model consists of two convolutional layers and one dense layer. The first convolutional layer has 16 kernels, the second layer has 32 kernels, and the dense layer has 70 neurons. This structure contains 553166 independent parameters. The accuracy of this model in detecting hand movements is 91.86%.
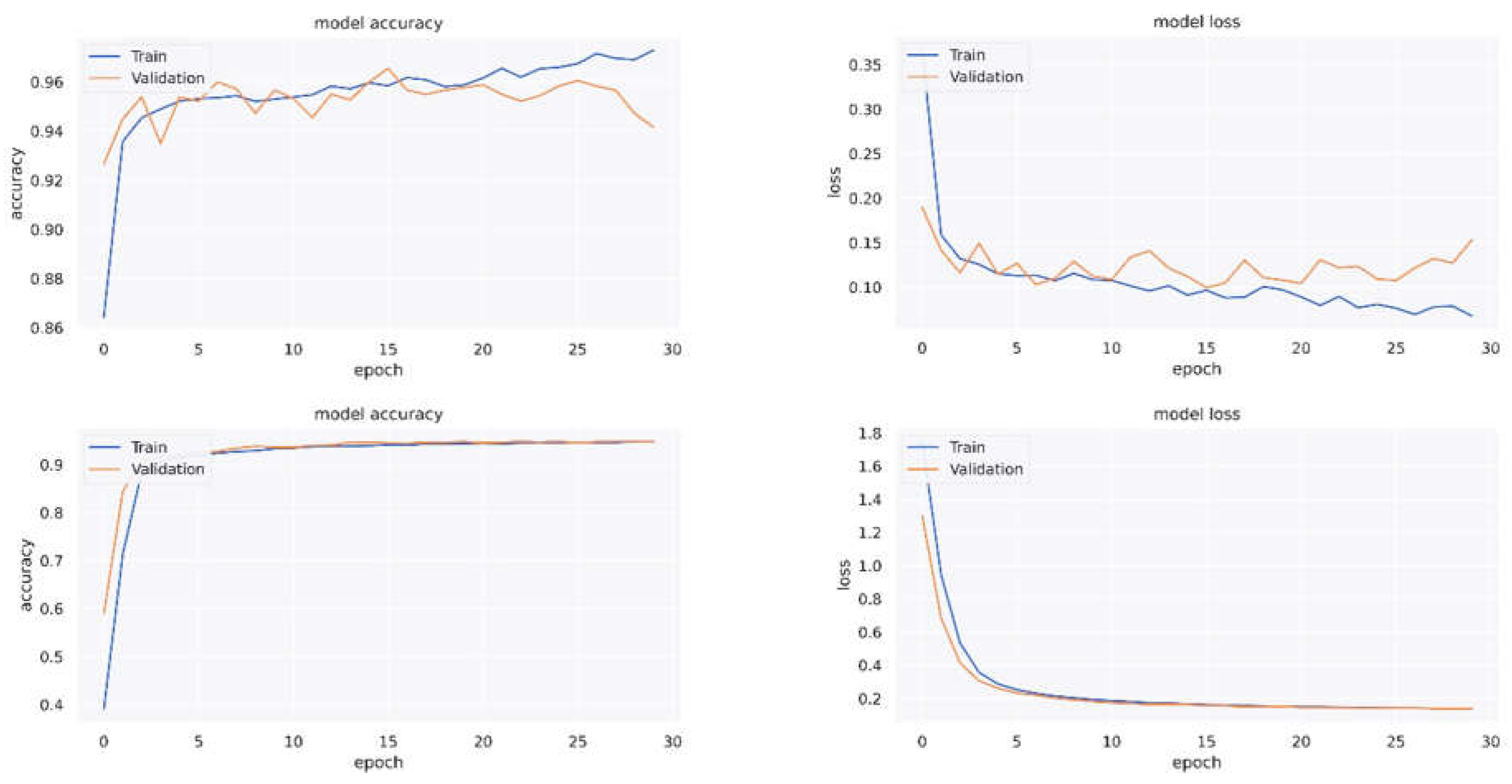
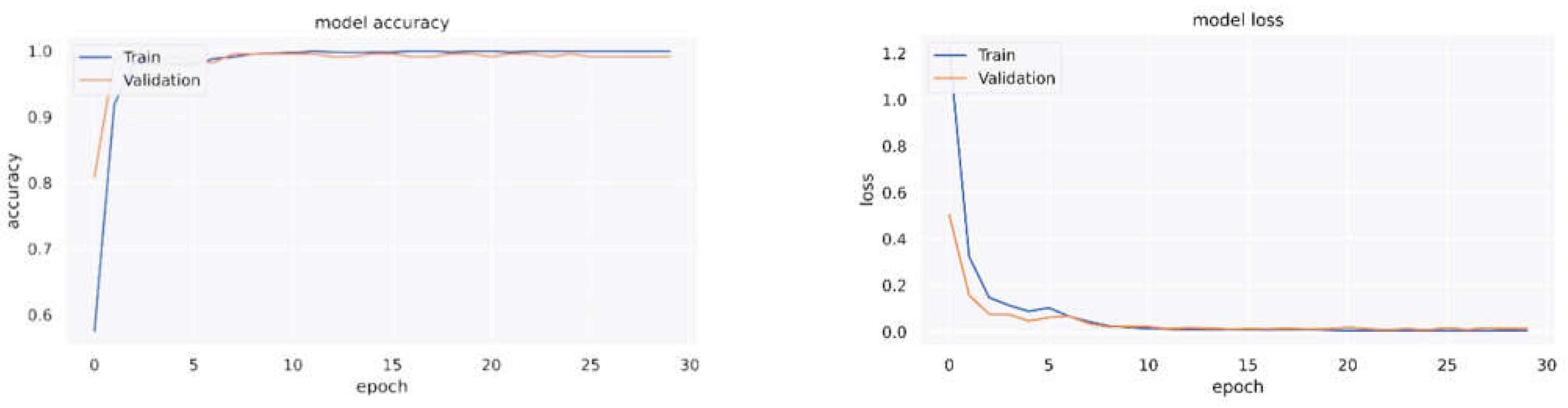
Table 3 demonstrates the model’s precision and sensitivity for each movement. Both Table 2 and Table 3 show that although the model successfully detected most activities, it had more difficulty in distinguishing the G0 and G5 gestures. As a result, the G5’s detection precision is relatively low, and the model’s sensitivity to G0 and G5 movements is not favorable (75.5 and 86.9 respectively). Figure 3 shows the model loss and accuracy in terms of epochs for the test and training data, respectively. According to these diagrams, the original model has converged, and no overfit has occurred. The figure also reveals that the accuracy and error of the model are fixed in the test data and that fluctuation is slight. Moreover, since the curve’s slope is related to the test data’s accuracy and the error is close to zero, the model’s accuracy will not change significantly as the epoch increases. Therefore, 30 epochs seem to be appropriate to achieve convergence. Although the number of epochs is linearly related to the time required to calculate the optimal model, it needs to range between10 and 100 to ensure optimal model convergence.
The proposed model converged to an optimal structure using the genetic algorithm and considering the fixed parameters mentioned earlier. The optimal structure consists of two convolutional layers with 131 and 28 kernels, a dense layer with 111 neurons, and a SoftMax layer with eight neurons. The genetic algorithm converged on this structure after ten generations in approximately 34 hours and 42 minutes. To ensure repeatability, the solution was repeated five times. The results reported here represent the best results.
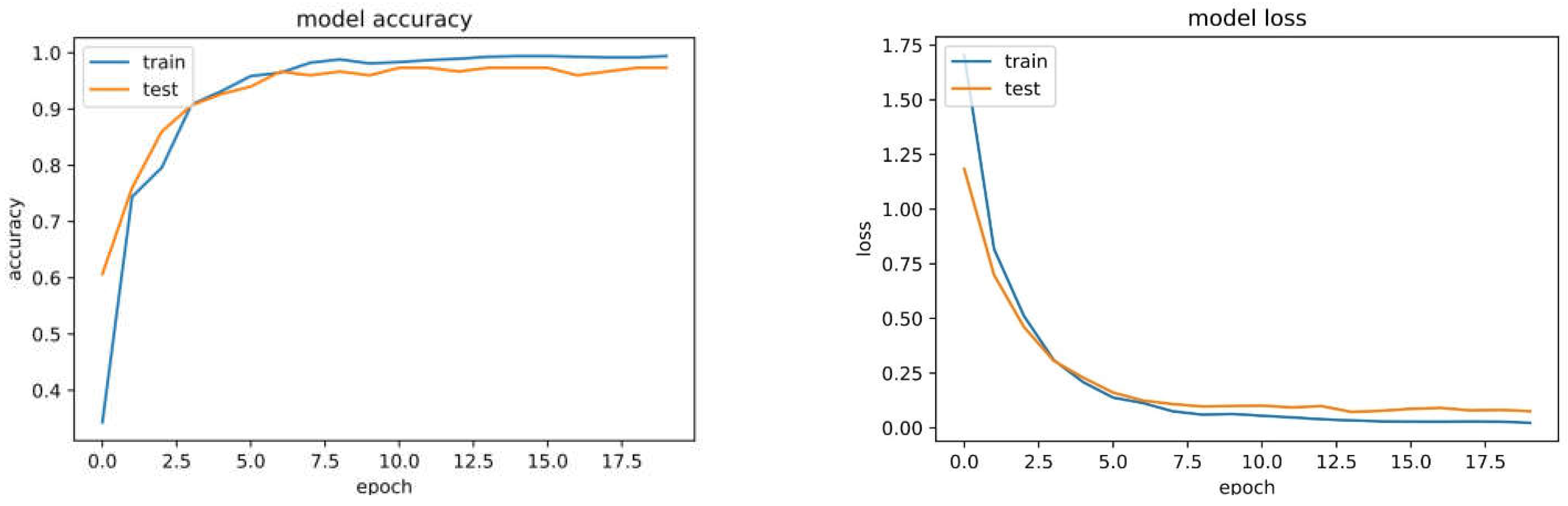
After achieving the optimal structure, the number of epochs was changed to achieve maximum accuracy. Figure 4 reflects the optimal model’s loss and accuracy in terms of epochs. It can be seen from the figure that in epoch 30, the optimal model reached convergence. As the number of epochs increases, the model’s accuracy may improve slightly, but the model could become overfit. Table 4 and Table 5 depict the confusion matrix, precision, and sensitivity for each movement, respectively. The tables demonstrate that the model’s accuracy has increased post optimization and the network’s distinction of the G0 and G5 gestures was enhanced. Since the deep learning algorithm is stochastic, its accuracy may vary during different runs. In this study, the accuracy of the optimal model in detecting hand gesture movements was 96.4, and the average accuracy in 5 runs was 95%. This indicates that the optimization has improved the deep network, and the results are reliable. The model achieved the best performance in G1 motion detection and the weakest in G0 and G5 motion detection. The model’s weakness in separating G0 and G5 is most likely due to the similarity between these positions (Fig. 1: hand’s resting position is relatively similar to open open).
For offline use, the window size was increased to 1 second, and a new dataset was obtained. The deep network with parameters optimized by the genetic algorithm was retrained with the new dataset. According to Figure 5, which depicts the loss and accuracy of the deep network, increasing the signal’s length significantly affects the accuracy of classification. Classification accuracy in the offline mode reached 99.6%.
The offline network confusion matrix presented in Table 6 shows that increasing the signal length has also made it easier for the network to distinguish between the G0 and G5 gestures. Although the accuracy and robustness of the model improve with increasing signal length, a larger window means more latency, making the model unsuitable for real-time use.

3.1. Limitations

There are several limitations in this study that should be delineated. First, we considered a simple base model in order to reduce the time and computational cost of the optimization process. While this model is useful for recognizing simple hand gestures, such as the ones used here, future work should consider enhancing the model. Complicated models with more parameters are needed for classifying and distinguishing sophisticated gestures, as well as gestures with small variations, such as finger movements. Furthermore, in the current work, a small delay occurs in the online mode when we alter the hand gesture. Other types of models, such as recurrent neural networks or transformers, may be more effective towards resolving this. During the EMG signal preprocessing phase, useful data is sometimes lost. It is possible to use brain signal data instead of EMG and translate it to EMG in order to overcome the data loss. Importantly, the model proposed here is used for recognizing static hand gestures, and it is not appropriate for other tasks such as trajectory drawing or sign language recognition. Generating EMG signals from hand gestures by Generative Adversarial Network (GAN) would be valuable for future studies.

4. Conclusions

This study proposed a deep convolutional network model optimized by a genetic algorithm to detect hand movements using forearm surface electromyography signals. Although deep networks have a great potential in identifying EMG patterns, their performance is highly dependent on well-designed architecture, structure, and parameters. In this work, only three parameters (the number of convolutional layers, the number of kernels in each convolutional layer, and the number of dense layer neurons) were optimized. Identifying the optimal values for these parameters increased the model’s accuracy from 91.86% to 96.4% at best and to 95.3% on average in real-time usage. The accuracy of the optimized model in an offline mode is 99.6%. Optimizing the number of epochs and training the model to 100% convergence can significantly affect the model’s accuracy. The objective function of the genetic algorithm used here is associated with the accuracy of the model. Adding the number of independent model variables to the objective function’s output may reduce the computational cost, and hence a compromise should be made between the model’s accuracy and the computational load. Ongoing and future work include overcoming computational constraints, implementing new initiatives in model architecture and optimization, and validation in relevant applications, such as hand gesture recognition (HGR) in robotics and smart healthcare solutions.

References

  1. Liarokapis, M.V.; Artemiadis, P.K.; Kyriakopoulos, K.J.; Manolakos, E.S. A learning scheme for reach to grasp movements: On EMG-based interfaces using task specific motion decoding models. IEEE J. Biomed. Health Inform. 2013, 17, 915–921. [Google Scholar] [CrossRef]
  2. Scheme, E.; Englehart, K. Electromyogram pattern recognition for control of powered upper-limb prostheses: state of the art and challenges for clinical use. J. Rehabil. Res. Dev. 2011, 48. [Google Scholar] [CrossRef]
  3. Moon, I.; Lee, M.; Chu, J.; Mun, M. Wearable EMG-based HCI for electric-powered wheelchair users with motor disabilities. In Proceedings of the Proceedings of the 2005 IEEE International Conference on Robotics and Automation; IEEE, 2005; pp. 2649–2654. [Google Scholar]
  4. Quitadamo, L.R.; Cavrini, F.; Sbernini, L.; Riillo, F.; Bianchi, L.; Seri, S.; Saggio, G. Support vector machines to detect physiological patterns for EEG and EMG-based human–computer interaction: a review. J. Neural Eng. 2017, 14, 011001. [Google Scholar] [CrossRef]
  5. Drost, G.; Stegeman, D.F.; van Engelen, B.G.; Zwarts, M.J. Clinical applications of high-density surface EMG: a systematic review. J. Electromyogr. Kinesiol. 2006, 16, 586–602. [Google Scholar] [CrossRef]
  6. Padmanabhan, P.; Puthusserypady, S. Nonlinear analysis of EMG signals-a chaotic approach. In Proceedings of the the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; IEEE, 2004; Vol. 1, pp. 608–611. [Google Scholar]
  7. Scheme, E.; Englehart, K. Training strategies for mitigating the effect of proportional control on classification in pattern recognition based myoelectric control. J. Prosthet. Orthot. JPO 2013, 25, 76. [Google Scholar] [CrossRef]
  8. Phinyomark, A.; Quaine, F.; Charbonnier, S.; Serviere, C.; Tarpin-Bernard, F.; Laurillau, Y. EMG feature evaluation for improving myoelectric pattern recognition robustness. Expert Syst. Appl. 2013, 40, 4832–4840. [Google Scholar] [CrossRef]
  9. Phinyomark, A.; Quaine, F.; Charbonnier, S.; Serviere, C.; Tarpin-Bernard, F.; Laurillau, Y. A feasibility study on the use of anthropometric variables to make muscle–computer interface more practical. Eng. Appl. Artif. Intell. 2013, 26, 1681–1688. [Google Scholar] [CrossRef]
  10. Tkach, D.; Huang, H.; Kuiken, T.A. Study of stability of time-domain features for electromyographic pattern recognition. J. Neuroengineering Rehabil. 2010, 7, 1–13. [Google Scholar] [CrossRef]
  11. Khushaba, R.N.; Al-Timemy, A.; Kodagoda, S.; Nazarpour, K. Combined influence of forearm orientation and muscular contraction on EMG pattern recognition. Expert Syst. Appl. 2016, 61, 154–161. [Google Scholar] [CrossRef]
  12. Alkan, A.; Günay, M. Identification of EMG signals using discriminant analysis and SVM classifier. Expert Syst. Appl. 2012, 39, 44–47. [Google Scholar] [CrossRef]
  13. Tkach, D.C.; Young, A.J.; Smith, L.H.; Rouse, E.J.; Hargrove, L.J. Real-time and offline performance of pattern recognition myoelectric control using a generic electrode grid with targeted muscle reinnervation patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 727–734. [Google Scholar] [CrossRef] [PubMed]
  14. Li, Z.; Wang, B.; Yang, C.; Xie, Q.; Su, C.-Y. Boosting-based EMG patterns classification scheme for robustness enhancement. IEEE J. Biomed. Health Inform. 2013, 17, 545–552. [Google Scholar] [CrossRef]
  15. Phinyomark, A.; Scheme, E. EMG pattern recognition in the era of big data and deep learning. Big Data Cogn. Comput. 2018, 2, 21. [Google Scholar] [CrossRef]
  16. Geng, W.; Du, Y.; Jin, W.; Wei, W.; Hu, Y.; Li, J. Gesture recognition by instantaneous surface EMG images. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef]
  17. Simão, M.; Neto, P.; Gibaru, O. EMG-based online classification of gestures with recurrent neural networks. Pattern Recognit. Lett. 2019, 128, 45–51. [Google Scholar] [CrossRef]
  18. Allard, U.C.; Nougarou, F.; Fall, C.L.; Giguère, P.; Gosselin, C.; Laviolette, F.; Gosselin, B. A convolutional neural network for robotic arm guidance using sEMG based frequency-features. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); IEEE, 2016; pp. 2464–2470. [Google Scholar]
  19. Gosselin, B.; Gosselin, C.; Campeau-Lecours, A.; Laviolette, F.; Fall, C.L.; Côté Allard, U. Transfer learning for sEMG hand gesture recognition using convolutional neural networks. 2017.
  20. Amado Laezza, R. Deep neural networks for myoelectric pattern recognition-An implementation for multifunctional control. Master’s Thesis, 2018.
  21. Asif, A.R.; Waris, A.; Gilani, S.O.; Jamil, M.; Ashraf, H.; Shafique, M.; Niazi, I.K. Performance evaluation of convolutional neural network for hand gesture recognition using EMG. Sensors 2020, 20, 1642. [Google Scholar] [CrossRef]
  22. Toro-Ossaba, A.; Jaramillo-Tigreros, J.; Tejada, J.C.; Peña, A.; López-González, A.; Castanho, R.A. LSTM Recurrent Neural Network for Hand Gesture Recognition Using EMG Signals. Appl. Sci. 2022, 12, 9700. [Google Scholar] [CrossRef]
  23. Kim, S.; Shin, D.Y.; Kim, T.; Lee, S.; Hyun, J.K.; Park, S.-M. Enhanced Recognition of Amputated Wrist and Hand Movements by Deep Learning Method Using Multimodal Fusion of Electromyography and Electroencephalography. Sensors 2022, 22, 680. [Google Scholar] [CrossRef]
  24. Zhao, H.; Zheng, B.; Wang, L. Deep Learning with Attention on Hand Gesture Recognition Based on sEMG. In Proceedings of the 2022 Prognostics and Health Management Conference (PHM-2022 London); 2022; pp. 316–320. [Google Scholar]
  25. Simao, M.; Neto, P.; Gibaru, O. Uc2018 dualmyo hand gesture dataset. URL Httpsdoi Org105281zenodo 2018, 1320922. [Google Scholar]
  26. Eckstein, A.; Vlachos, P.P. Assessment of advanced windowing techniques for digital particle image velocimetry (DPIV). Meas. Sci. Technol. 2009, 20, 075402. [Google Scholar] [CrossRef]
  27. Davis, L. Handbook of genetic algorithms. 1991.
  28. De Luca, C.J.; Gilmore, L.D.; Kuznetsov, M.; Roy, S.H. Filtering the surface EMG signal: Movement artifact and baseline noise contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef]
  29. Halaki, M.; Ginn, K. Normalization of EMG signals: to normalize or not to normalize and what to normalize to. Comput. Intell. Electromyogr. Anal.- Perspect. Curr. Appl. Future Chall. 2012, 10, 49957. [Google Scholar]
  30. Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
  31. Park, K.-H.; Lee, S.-W. Movement intention decoding based on deep learning for multiuser myoelectric interfaces. In Proceedings of the 2016 4th international winter conference on brain-computer Interface (BCI); IEEE, 2016; pp. 1–2. [Google Scholar]
  32. Dunne, R.A.; Campbell, N.A. On the pairing of the softmax activation and cross-entropy penalty functions and the derivation of the softmax activation function. In Proceedings of the Proc. 8th Aust. Conf. on the Neural Networks, Melbourne; Citeseer, 1997; Vol. 181, p. 185. [Google Scholar]
  33. Ide, H.; Kurita, T. Improvement of learning for CNN with ReLU activation by sparse regularization. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN); IEEE, 2017; pp. 2684–2691. [Google Scholar]
  34. Gupta, S.; Zhang, W.; Wang, F. Model accuracy and runtime tradeoff in distributed deep learning: A systematic study. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM); IEEE, 2016; pp. 171–180. [Google Scholar]
  35. Tato, A.; Nkambou, R. Improving adam optimizer. 2018.
  36. Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
  37. Kumar, M.; Husain, D.; Upreti, N.; Gupta, D. Genetic algorithm: Review and application. Available SSRN 3529843 2010. [Google Scholar] [CrossRef]
Preprints 66887 g002
Figure 2. Comparison of model accuracy and loss for learning rate 0.0001 (top) and 0.00001 (bottom.
Figure 2. Comparison of model accuracy and loss for learning rate 0.0001 (top) and 0.00001 (bottom.
Preprints 66887 g002
Preprints 66887 g003
Figure 3. Original model: loss/accuracy in each epoch.
Figure 3. Original model: loss/accuracy in each epoch.
Preprints 66887 g003
Preprints 66887 g004
Figure 4. Optimized models loss/accuracy in each epoch in real-time mode.
Figure 4. Optimized models loss/accuracy in each epoch in real-time mode.
Preprints 66887 g004
Preprints 66887 g005
Figure 5. optimized models’ loss/accuracy in each epoch in offline mode.
Figure 5. optimized models’ loss/accuracy in each epoch in offline mode.
Preprints 66887 g005
Table 1. Basis for model accuracy, precision, and sensitivity.
Table 1. Basis for model accuracy, precision, and sensitivity.
Actual
Positive Negative
Predicted Positive T P F P
Negative F N T N
Table 2. Confusion matrix of the original model.
Table 2. Confusion matrix of the original model.
Predicted
G0 G1 G2 G3 G4 G5 G6 G7
Actual G0 260 0 0 0 0 12 0 0
G1 0 251 0 1 0 0 0 0
G2 0 0 255 1 16 0 16 1
G3 0 0 0 256 0 4 1 1
G4 1 0 1 0 248 1 1 1
G5 82 0 1 1 0 160 0 14
G6 1 1 4 1 0 0 261 0
G7 0 0 2 0 0 7 0 251
Table 3. Precision, sensitivity of each movement in the original model.
Table 3. Precision, sensitivity of each movement in the original model.
Precision sensitivity
G0 99.6 75.5
G1 99.6 99.6
G2 88.2 96.9
G3 97.7 98.4
G4 98.0 93.9
G5 62.0 86.9
G6 97.3 93.5
G7 96.5 93.6
Table 4. confusion matrix of the optimized model in real-time mode.
Table 4. confusion matrix of the optimized model in real-time mode.
Predicted
G0 G1 G2 G3 G4 G5 G6 G7
Actual G0 215 0 0 0 0 18 0 0
G1 0 264 0 0 0 0 0 0
G2 0 0 252 0 6 0 0 0
G3 0 0 1 275 3 0 0 0
G4 0 0 2 0 258 0 0 0
G5 48 0 0 1 0 220 0 0
G6 0 0 0 0 0 0 281 0
G7 0 0 0 0 3 0 0 267
Table 5. Precision and sensitivity of each movement for the optimized model in the real-time mode.
Table 5. Precision and sensitivity of each movement for the optimized model in the real-time mode.
precision sensitivity
G0 93.99 77.94
G1 100.0 100.0
G2 98.45 95.49
G3 97.85 100
G4 96.15 96.15
G5 76.21 92.76
G6 99.64 100
G7 98.52 98.89
Table 6. Confusion matrix of the optimized model in offline mode.
Table 6. Confusion matrix of the optimized model in offline mode.
Predicted
G0 G1 G2 G3 G4 G5 G6 G7
Actual G0 40 0 0 0 0 0 0 0
G1 0 36 0 0 0 0 0 0
G2 0 0 34 0 0 0 0 0
G3 0 0 0 40 0 0 0 0
G4 0 0 1 0 28 0 0 0
G5 0 0 0 0 0 28 0 0
G6 0 0 0 0 0 0 28 0
G7 0 0 0 0 0 0 0 29
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated