Prerpints.org logo
Preprint
Article

Simple but Powerful: Viroids can Hijack their Host Cells’ Metabolism due to Greater Gibbs Energy Dissipation

This is a preprint, it has not been peer-reviewed.

Submitted:

03 January 2023

Posted:

05 January 2023

You are already at the latest version

Abstract
Viroids represent the simplest, but are also among the most interesting life-like forms. They represent a great problem in agriculture. Moreover, pathogens similar to viroids, such as the hepatitis Delta virus represent a risk for human health. Viroids encode no proteins, but are still able to hijack their host cells’ metabolism to perform multiplication. This paper attempts to reply three questions about viroids. First, how can viroids hijack their host cells’ metabolism, even though they encode no proteins to achieve this? Second, what advantages do viroids have from their simplicity? Third, what can viroids, as the simplest life-like forms, tell us about life as a natural phenomenon? These questions are discussed from the perspective of biothermodynamics. In order to do this, elemental composition, biosynthesis reactions and standard thermodynamic properties of viroids have been determined and analyzed.
Keywords: 
  -  

1. Introduction

Viroids have been discovered in the 1970s. The unique properties of viroids have been recognized by the international committee on taxonomy of viruses [King et al., 2011]. Sanger et al. have shown that viroids consist of single stranded circular RNA molecules [Sanger et al., 1976; Wang, 2021]. The structure of viroids has been confirmed by electron microscopy [Sogo et al., 1973]. Nucleotide sequence of a viroid has been determined in 1978 [Gross et al., 1978].
Viroids are obligate intracellular parasites, like viruses [Riedel et al., 2019]. Viruses have been extensively studied from the perspective of biothermodynamics. Knowing virus genetic and protein sequences has enabled to find the empirical formulas for several viruses, using the atom counting method [Popovic, 2022a]. Based on the empirical formulas, it is possible to formulate growth reactions, representing formation of new live matter from nutrients [Battley, 2013, 1999b, 1998; von Stockar, 2013b].
Organisms and microorganisms represent open thermodynamic systems with the property of growth [von Bertalanffy, 1950, 1971; von Stockar, 2013a, 2013b, Popovic, 2019]. Empirical formulas and thermodynamic properties have been determined for many viruses [Popovic and Minceva, 2020a, 2020b; Popovic, 2022h, 2022i, 2022j, 2022k; Şimşek et al., 2021; Degueldre, 2021]. Biothermodynamic background of virus-host interactions has been under intense research during the last 20 years [Gale, 2021, 2020, 2019, 2018; Lucia et al., 2021, 2020a, 2020b; Mahmoudabadi et al., 2017; Casasnovas and Springer, 1995; Popovic and Minceva, 2021a].
Host organisms of viroids are plants. Thermodynamic properties and empirical formulas of plants can be found in the literature [Popovic and Minceva, 2021b]. Hepatitis Delta virus is a pathogen similar to viroids. It interacts with the human liver tissue. Thermodynamic properties of human tissues can be found in [Popovic and Minceva, 2022c; Popovic, 2022k].
This paper attempts to find a response for three questions about viroids. The first is how can viroids to multiply inside their host cells, even though they encode no proteins to help them achieve this? The second is what advantage do viroids obtain from their simplicity? The third is what can viroids, as the simplest known life-like forms, tell us about life as a natural phenomenon? These questions are discussed from the biothermodynamic perspective, since energy is a key factor determining microorganism-host interactions [Head et al., 2022]. To perform thermodynamic analysis, it is necessary to calculate the empirical formulas, formulate biosynthesis reactions and find biothermodynamic properties of viroids.

2. Methods

2.1. Data sources

Genetic sequences of the analyzed viroids were obtained from the NCBI database [NCBI, 2022; Sayers et al., 2022]. The genetic sequence of the Apple scar skin viroid can be found under the accession number M36646.1. The genetic sequence of the Avocado sunblotch viroid can be found under the accession number M31099.1. The genetic sequence of the Citrus exocortis viroid can be found under the accession number S67442.1. The genetic sequence of the Coconut cadang-cadang viroid can be found under the accession number KM588102.1. The genetic sequence of the Coleus blumei viroid 1 can be found under the accession number MZ326146.1. The genetic sequence of the Potato spindle tuber viroid can be found under the accession number M25199.1. The genetic sequence of the Tomato chlorotic dwarf viroid can be found under the accession number NC_000885.1.
Elemental composition of plant live matter was taken from the literature [Nam & Capareda, 2015; Pineda-Insuasti et al., 2014; Fialho et al, 2019; Titiloye et al, 2013; Latshaw and Miller, 1924; Medic et al., 2012].
Standard Gibbs energies of biosynthesis of cellular organisms (E. coli and human) and viruses (Ebola, SARS-CoV-2 and Herpes simplex virus type 1) have been taken from the literature [Popovic and Minceva, 2020a; Popovic, 2022h, 2022k]. Standard Gibbs energy of biosynthesis of Escherichia coli is -45.25 kJ/C-mol [Popovic and Minceva, 2020a]. Standard Gibbs energy of biosynthesis of human tissues is -23.78 kJ/C-mol [Popovic, 2022k]. Standard Gibbs energy of biosynthesis of the Ebola virus is -151.59 kJ/C-mol [Popovic, 2022k]. Standard Gibbs energy of biosynthesis of SARS-CoV-2 (Hu-1 variant) is -222.2 kJ/C-mol [Popovic, 2022k]. Standard Gibbs energy of biosynthesis of the Herpes simplex virus type 1 is -371.99 kJ/C-mol [Popovic, 2022L].

2.2. Elemental composition of live matter and biosynthesis reactions

Empirical formulas of the viroids were calculated based on their genetic sequences, using the atom counting method [Popovic, 2022a]. The atom counting method is a computational approach, which can find elemental composition of live matter of viroids, based on their genetic sequences [Popovic, 2022a]. It is implemented using a computer program, which goes along the nucleic acid sequences of viroids and adds atoms coming from every residue in the sequence [Popovic, 2022a]. The atom counting method can also be applied to find elemental composition of viruses [Popovic, 2022a].
Empirical formulas of plant live matter were found based on elemental compositions reported in the literature as mass fractions. Mass fraction data can be converted into empirical formulas, using the equation
n J = w J w C M C M J
where nJ is the number of atoms of element J in the empirical formula of live matter, wJ mass fraction of element J in the live matter, wC mass fraction of carbon in the live matter, MC molar mass of carbon and MJ molar mass of element J [Duboc et al., 1999].
The empirical formulas of viroid particles were used to construct biosynthesis reactions, summarizing conversion of nutrients into new live matter [von Stockar, 2013a, 2013b; Battley, 1998]. The biosynthesis reaction has the general form [Popovic, 2022b, 2022g, 2022k]
(Amino acids) + CH2O + O2 + HPO42- + HCO3- + K+ + Mg2+ + Ca2+ + Cl- = (Bio) + SO42- + H2O + HCO3- + H2CO3
where (Bio) represents new live matter, described by an empirical formula given by the atom counting method [Popovic, 2022a]. (Amino acid) represents a mixture of amino acids with the empirical formula CH1.798O0.4831N0.2247S0.022472 (expressed per mole of carbon), representing the source of energy, carbon, nitrogen and sulfur [Popovic, 2022b, 2022g]. CH2O represents carbohydrates, as the additional energy and carbon source [Popovic, 2022k]. O2 is the electron acceptor [Popovic, 2022b, 2022g]. HPO42- is the source of phosphorus [Popovic, 2022b, 2022g]. HCO3- is a part of the bicarbonate buffer that takes excess H+ ions that are generated during biosynthesis [Popovic, 2022b, 2022g]. The ions K+, Mg2+ and Ca2+ and Cl- represent the sources of potassium, magnesium, calcium and chlorine, respectively [Popovic, 2022k]. SO42- is an additional metabolic product that takes excess sulfur atoms [Popovic, 2022b, 2022g]. H2CO3 takes the oxidized carbon atoms and is also a part of the bicarbonate buffer [Popovic, 2022b, 2022g].

2.3. Thermodynamic properties of live matter and biosynthesis

Empirical formulas were used to find thermodynamic properties of live matter for viroids and plants. This was done using predictive biothermodynamic models, such as the Patel-Erickson equation and the Battley equation. The Patel-Erickson equation was used to find enthalpy of live matter. First, empirical formulas of live matter were used to find number of electrons transferred to oxygen, E, during complete combustion
E = 4 n C + n H − 2 n O − 0 n N + 5 n P + 6 n S
where nC, nH, nO, nN, nP and nS, represent the number of C, H, O, N, P and S atoms in the empirical formula of live matter, respectively [Battley, 1998, 1992; Popovic, 2019]. Then, E was used to find standard enthalpy of combustion, ΔCH⁰, of live matter, through the Patel-Erickson equation [Patel and Erickson, 1981; Battley, 1998, 1992; Popovic, 2019].
∆ C H 0 = − 111.14 k J m o l · E
ΔCH⁰ is defined as the enthalpy change for the reaction
CnCHnHOnONnNPnPSnSKnKMgnMgCanCaClnCl + (nC + ¼ nH + 1¼ nP + 1½ nS + ¼ nK + ½ nMg + ½ nCa + ¾ nFe - ½ nO – ¼ nCl) O2 → nC CO2 + ½ nH H2O + ½ nN N2 + ¼ nP P4O10 + nS SO3 + ½ nK K2O + nMg MgO + nCa CaO + nCl HCl
Thus, Hess’s law can be used to find standard enthalpy of formation, ΔfH⁰, of live matter [Battley, 1998, 1992; Popovic, 2019].
∆ f H 0 ( b i o ) = n C ∆ f H 0 ( C O 2 ) + 1 2 n H ∆ f H 0 ( H 2 O ) + 1 4 n P ∆ f H 0 ( P 4 O 10 ) + n S ∆ f H 0 ( S O 3 ) +        1 2 n K ∆ f H 0 ( K 2 O ) + n M g ∆ f H 0 ( M g O ) + n C a ∆ f H 0 ( C a O ) + n C l ∆ f H 0 ( H C l )        − ∆ C H 0
Standard molar entropy of live matter, S⁰m, was found using the Battley equation [Battley, 1999a; Battley and Stone, 2000; Popovic, 2019]. The Battley equation has the form
S m 0 b i o = 0.187   ∑ J S m 0 ( J ) a J n J
where nJ is the number of atoms of element J in the empirical formula of live matter [Battley, 1999; Battley and Stone, 2000; Popovic, 2019]. S⁰m(J) and aJ are standard molar entropy and number of atoms per formula unit of element J in its standard state elemental form [Battley, 1999; Battley and Stone, 2000; Popovic, 2019]. The Battley equation can be modified to give standard entropy of formation, ΔfS⁰, of live matter [Battley, 1999; Battley and Stone, 2000; Popovic, 2019]
S m 0 b i o = − 0.813   ∑ J S m 0 ( J ) a J n J
Finally, ΔfH⁰ and ΔfS⁰ are combined to give standard Gibbs energy of formation of live matter, ΔfG⁰.
∆ f G 0 b i o = ∆ f H 0 b i o − T ∆ f S 0 b i o
Once live matter is characterized by finding its ΔfH⁰, S⁰m and ΔfG⁰, these properties can be combined with biosynthesis reactions to find standard thermodynamic properties of biosynthesis. Standard thermodynamic properties of biosynthesis include standard enthalpy of biosynthesis, ΔbsH⁰, standard entropy of biosynthesis, ΔbsS⁰, and standard Gibbs energy of biosynthesis, ΔbsG⁰. These properties are found by applying the Hess’s law to biosynthesis reactions
∆ b s H 0 = ∑ p r o d u c t s ν   ∆ f H 0 − ∑ r e a c t a n t s ν   ∆ f H 0
∆ b s S 0 = ∑ p r o d u c t s ν   S m o − ∑ r e a c t a n t s ν     S m o
∆ b s G 0 = ∑ p r o d u c t s ν   ∆ f G 0 − ∑ r e a c t a n t s ν   ∆ f G 0
where ν represents a stoichiometric coefficient [Popovic, 2022b; Atkins and de Paula, 2011, 2014; von Stockar, 2013a, 2013b; Battley, 1998]. The most important of these three properties is standard Gibbs energy of biosynthesis, which represents the thermodynamic driving force for growth of all organisms [von Stockar, 2013a, 2013b; von Stockar and Liu, 1999], including viruses [Popovic, 2022b].

2.4. Elemental composition of viroid nucleic acid

The calculation starts from the chemical formulas of the 4 nucleotides that comprise the viroid RNA molecule: Adenosine monophosphate (C10H14O7N5P), Uridine monophosphate (C9H13O9N2P), Guanosine monophosphate (C10H14O8N5P) and Cytidine monophosphate (C9H14O8N3P). First, a water molecule is subtracted to find the formulas of nucleotide residues in the RNA: Adenine (C10H12O6N5P), Uracil (C9H11O8N2P), Guanine (C10H12O7N5P) and Cytosine (C9H12O7N3P). Then the chemical formulas of the nucleotide residues are combined to find chemical formulas of AU (C19H23O14N7P2) and GC (C19H24O14N8P2). Finally, the chemical formulas were converted into empirical formulas, by dividing the number of atoms of all elements with the number of carbon atoms. The empirical formula of the AU is CH1.2105O0.7368N0.3684P0.1053, while that of the GC is CH1.2632O0.7368N0.4211P0.1053. Now we can use these AU and GC empirical formulas to find the influence of AU and GC contents on the empirical formula of the nucleic acid.
If we compare the empirical formulas of the A and U (CH1.2105O0.7368N0.3684P0.1053), and G and C (CH1.2632O0.7368N0.4211P0.1053) nucleotides, we see that both have the same content of C, O and P, while differing in the H and N content. G and C nucleotides has more H and N than A and U bases. Thus, as the GC content of the viroid RNA increases, the H and N content will also increase. If we have an RNA with a GC content of 0%, then it will consist solely of AU basepairs, meaning that it will have the same empirical formula of the AU base (CH1.2105O0.7368N0.3684P0.1053). On the other hand, if the GC content is 100%, the RNA will have an empirical formula of the GC base (CH1.2632O0.7368N0.4211P0.1053). Thus, the H content will increase from 1.2105 to 1.2632 (difference of 0.0526) and the N content from 0.3684 to 0.4211 (difference of 0.0526). Thus, the empirical formula of an RNA with a GC content x is CH(1.2105+0.0526∙x)O0.7368N(0.3684+0.0526∙x)P0.1053. The empirical formulas were then used to find standard thermodynamic properties of viroid live matter and biosynthesis, as described in Section 2.3. These data were then used for discussion in Section 4.2.

3. Results

Based on genetic sequences, elemental composition of viroids was determined using the atom counting method [Popovic, 2022a]. They are reported in the form of empirical formulas in Table 1. The empirical formula of the Apple scar skin viroid is CH1.2474O0.7578N0.3969P0.105550. The empirical formula of the Avocado sunblotch viroid is CH1.2301O0.7826N0.3811P0.105487. The empirical formula of the Citrus exocortis viroid is CH1.2434O0.7621N0.3966P0.105419. The empirical formula of the Coconut cadang-cadang viroid is CH1.2419O0.7547N0.4026P0.105128. The empirical formula of the Coleus blumei viroid 1 is CH1.2416O0.7698N0.3908P0.105553. The empirical formula of the Potato spindle tuber viroid is CH1.2434O0.7648N0.3940P0.105511. The empirical formula of the Tomato chlorotic dwarf viroid is CH1.2416O0.7646N0.3947P0.105417. Finally, the empirical formula of plant live matter was found to be CH1.6329O0.7965N0.0245P0.000521S0.001119K0.001969Mg0.000652Ca0.000597Cl0.001007. The empirical formulas of live matter were used to construct biosynthesis reactions for viroids and plants, which are reported in Table 2.
The empirical formulas from Table 1 were used to find standard thermodynamic properties of live matter of viroids and plants, using predictive biothermodynamic models (Patel-Erickson and Battley). The results are shown in Table 3. These include standard enthalpy of formation, ΔfH⁰, standard molar entropy, S⁰m, and standard Gibbs energy of formation, ΔfG⁰. For the Apple scar skin viroid, standard enthalpy of formation is -177.75 kJ/C-mol, standard molar entropy is 38.73 J/C-mol K, and standard Gibbs energy of formation is -127.55 kJ/C-mol. For the Avocado sunblotch viroid, standard enthalpy of formation is -182.72 kJ/C-mol, standard molar entropy is 38.71 J/C-mol K, and standard Gibbs energy of formation is -132.54 kJ/C-mol. For the Citrus exocortis viroid, standard enthalpy of formation is -178.55 kJ/C-mol, standard molar entropy is 38.76 J/C-mol K, and standard Gibbs energy of formation is -128.31 kJ/C-mol. For the Coconut cadang-cadang viroid, standard enthalpy of formation is -176.81 kJ/C-mol, standard molar entropy is 38.70 J/C-mol K, and standard Gibbs energy of formation is -126.64 kJ/C-mol. For the Coleus blumei viroid 1, standard enthalpy of formation is -180.24 kJ/C-mol, standard molar entropy is 38.78 J/C-mol K, and standard Gibbs energy of formation is -129.97 kJ/C-mol. For the Potato spindle tuber viroid, standard enthalpy of formation is -179.18 kJ/C-mol, standard molar entropy is 38.76 J/C-mol K, and standard Gibbs energy of formation is -128.93 kJ/C-mol. For the Tomato chlorotic dwarf viroid, standard enthalpy of formation is -179.05 kJ/C-mol, standard molar entropy is 38.75 J/C-mol K, and standard Gibbs energy of formation is -128.82 kJ/C-mol. Finally, for plant live matter, standard enthalpy of formation is -178.83 kJ/C-mol, standard molar entropy is 36.76 J/C-mol K, and standard Gibbs energy of formation is -131.18 kJ/C-mol.
Thermodynamic properties of live matter from Table 3 were combined with biosynthesis stoichiometries from Table 2, to find standard thermodynamic properties of biosynthesis for viroids and plants. The results are presented in Table 4, and include standard enthalpy of biosynthesis, ΔbsH⁰, standard entropy of biosynthesis, ΔbsS⁰, and standard Gibbs energy of biosynthesis, ΔbsG⁰. For the Apple scar skin viroid, standard enthalpy of biosynthesis is -513.18 kJ/C-mol, standard entropy of biosynthesis is -104.03 J/C-mol K, and standard Gibbs energy of biosynthesis is -483.41 kJ/C-mol. For the Avocado sunblotch viroid, standard enthalpy of biosynthesis is -480.20 kJ/C-mol, standard entropy of biosynthesis is -99.36 J/C-mol K, and standard Gibbs energy of biosynthesis is -451.82 kJ/C-mol. For the Citrus exocortis viroid, standard enthalpy of biosynthesis is -514.08 kJ/C-mol, standard entropy of biosynthesis is -104.42 J/C-mol K, and standard Gibbs energy of biosynthesis is -484.19 kJ/C-mol. For the Coconut cadang-cadang viroid, standard enthalpy of biosynthesis is -528.07 kJ/C-mol, standard entropy of biosynthesis is -106.64 J/C-mol K, and standard Gibbs energy of biosynthesis is -497.51 kJ/C-mol. For the Coleus blumei viroid 1, standard enthalpy of biosynthesis is -501.04 kJ/C-mol, standard entropy of biosynthesis is -102.43 J/C-mol K, and standard Gibbs energy of biosynthesis is -471.74 kJ/C-mol. For the Potato spindle tuber viroid, standard enthalpy of biosynthesis is -507.98 kJ/C-mol, standard entropy of biosynthesis is -103.44 J/C-mol K, and standard Gibbs energy of biosynthesis is -478.38 kJ/C-mol. For the Tomato chlorotic dwarf viroid, standard enthalpy of biosynthesis is -509.96 kJ/C-mol, standard entropy of biosynthesis is -103.81 J/C-mol K, and standard Gibbs energy of biosynthesis is -480.25 kJ/C-mol. Finally, for plant live matter, standard enthalpy of biosynthesis is -26.79 kJ/C-mol, standard entropy of biosynthesis is 10.88 J/C-mol K, and standard Gibbs energy of biosynthesis is -29.16 kJ/C-mol.

4. Discussion

Viroids are subviral entities, representing the simplest known form of life-like structures [Strauss and Strauss, 2008; Tsagris et al., 2008; Flores et al., 1997; Riedel et al., 2019]. Unlike viruses, viroids do not possess a capsid: they consist of a naked circular RNA molecule, which does not encode any proteins [Strauss and Strauss, 2008; Tsagris et al., 2008; Flores et al., 1997; Riedel et al., 2019]. Thus, they hijack host cell machinery. The metabolism of a viroid is reduced to just one chemical process – biosynthesis of its nucleic acid [Strauss and Strauss, 2008; Tsagris et al., 2008; Flores et al., 1997; Riedel et al., 2019]. Synthesis of the viroid RNA represents a chemical reaction of polymerization of nucleotides [Pinheiro et al., 2008; Dodd et al., 2020; Johansson and Dixon, 2013; Popovic, 2022b, 2022c].
Viroids have a high GC content (guanine-cytosine content) [Adkar-Purushothama et al., 2020; Diener, 1989]. Viruses that in their nucleic acid have a high GC content are characterized by a highly negative Gibbs energy of biosynthesis [Popovic, 2022d]. On the other hand, viruses that have a high AU content, are characterized by a less negative Gibbs energy of biosynthesis [Popovic, 2022d].
Gibbs energy of biosynthesis is the driving force for multiplication of microorganisms [von Stockar, 2013a, 2013b; Popovic and Popovic, 2022; Popovic, 2022b, 2022c, 2022e, 2022f, 2022g]. An organism characterized by a more negative Gibbs energy of biosynthesis, according to the biosynthesis phenomenological equation exhibits a greater multiplication rate [Popovic, 2022h].
The discussion below focuses on three questions about viroids. The first is what enables viroids to hijack the metabolisms of their host cells, even though they encode no proteins and thus have no enzymes of their own to help them. The second question is what kind of advantage does their simplicity offers to viroids over viruses. The third question is what viroids, as the simplest known life-like structures, tell us about life as a phenomenon.

4.1. How do viroids hijack their host cell’s metabolism?

Gibbs energies of biosynthesis of viroids and their host plants are presented in Figure 1 and Table 4. From Figure 1, we can see that Gibbs energies of biosynthesis of viroids are much more negative than those of plants. Gibbs energy of biosynthesis represents the thermodynamic driving force for multiplication of microorganisms [von Stockar, 2013a, 2013b], including viruses [Popovic, 2022d, 2022h]. Biosynthesis reactions of the viroids and their host cells are competitive, since they start from the same building blocks, e.g. nucleotides [Popovic, 2022d, 2022h].
The biosynthesis rate, rbs, is proportional to the Gibbs energy of biosynthesis, ΔbsG, according to the biosynthesis phenomenological equation
r b s = − L b s T ∆ b s G
where Lbs is the biosynthesis phenomenological coefficient and T is temperature [Popovic, 2022d, 2022h]. Gibbs energy of biosynthesis of viroids is much more negative than those of their host plants. Thus, according to the biosynthesis phenomenological equation, the biosynthesis rate of viroid RNA will be much greater than that of their host cells components. Therefore, due to its greater biosynthesis rate, much more viroid RNA will be produced than host cell components. This will allow the viroid to hijack its host cell’s metabolism and use it for its multiplication.
Synthesis of viroid live matter is more energetically favorable than that of the host cell live matter. This is why, according to the phenomenological equation, biosynthesis of viroid live matter is much faster than that of host cell building blocks. Thus, much more viroid live matter will be produced and very little host live matter. This is how viroids multiply and damage plants. Since a lot of energy flows through the viroid biosynthesis pathway, little remains for the host plant, which is thus damaged. Moreover, viroid multiplication uses building blocks that are also required for the host cell. Therefore, in the competition of two chemical processes, the biosynthesis of viroids prevails, due to its much greater thermodynamic driving force.

4.2. Why did viroids evolve to be even simpler then viruses?

There are two dominant theories about the origin of viroids. Diener suggested that viroids represent living relics, a part of the pre-cellular RNA world [Diener, 1989; Moelling and Broecker, 2021; Di Serio et al., 2017]. From this perspective, viroids are viewed as a step from non-living to living matter [Diener, 1989]. However, viroids could have also arisen through evolution from RNA viruses [Di Serio et al., 2017].
Figure 2 shows standard Gibbs energies of biosynthesis of three classes of organisms: cellular organisms, viruses and viroids. Cellular organisms have the least negative Gibbs energies of biosynthesis. More negative Gibbs energies of biosynthesis are characteristic of viruses. The greater thermodynamic driving force for virus multiplication is what allows viruses to hijack their host cells’ metabolisms [Popovic, 2022b, 2022c, 2022d, 2022h]. Viroids are characterized by even more negative Gibbs energies of biosynthesis, meaning that they have an even greater thermodynamic driving force for their multiplication. Some viruses, like the Herpes simplex virus type 1, have highly negative Gibbs energies of biosynthesis close to those of viroids. However, Gibbs energy of biosynthesis of viroids is the most negative among all thermodynamically characterized classes of organisms. The highly negative values can be explained by the lack of protein and lipid components, which are present in viruses. Thus, the simplicity of viroids is what allows them to have the greatest thermodynamic driving force for multiplication.
Viroids have a more negative Gibbs energy of biosynthesis than viruses. The loss of proteins allowed viroids to achieve a more negative Gibbs energy of biosynthesis than viruses. Thus, viruses lost cellular components to make their multiplication easier, although dependent on the host organism. Viroids have proceeded even further down this path, losing even proteins to make their multiplication even faster than that of viruses. Therefore, thermodynamic analysis might provide an explanation for the simplicity of viroids and their lack of proteins.
Viroids could have arisen through evolution from RNA viruses, which lost protein components. The loss of protein components could have made Gibbs energy of biosynthesis of viroids even more negative than that of viruses, enabling them to hijack their host cells more efficiently. On the other hand, viroids could have also arisen very early in evolution during the RNA world as highly efficient parasites. Their highly negative Gibbs energy of biosynthesis would have allowed them to hijack their host cells very efficiently. Due to their high efficiency, there would have been no selective pressure on viroids to evolve further and they remained unchanged as living fossils.
Viroids have a high GC content [Adkar-Purushothama et al., 2020; Diener, 1989]. The high GC content might have been selected during evolution due to the high stability of the GC basepairs [Diener, 1989]. In addition, the high GC content could offer viroids an energetic advantage during multiplication. Figure 2 shows that Gibbs energy of biosynthesis of viroid RNA and its GC content. Gibbs energy of biosynthesis becomes more negative as the GC content of viroid RNA increases. Thus, a greater GC content provides viroids with a greater thermodynamic driving force for multiplication. According to the biosynthesis phenomenological equation (11), this results in a greater multiplication rate and an even greater ability to hijack host cell metabolism. This is also supported by the finding that viruses with a high GC content have a more negative Gibbs energy of biosynthesis and greater multiplication rate [Popovic, 2022d]. Thus, the high GC content could also represent an adaptation that allowed viroids to multiply and hijack host cell metabolism even more efficiently.

4.3. What can viroids tell us about the essence of life itself?

It has been suggested that, in a broad sense, viroids encode for an RNA conformation, which is recognized and replicated by the host cell [Flores et al., 1997]. However, viroid RNA does not encode any proteins [Flores et al., 1997; Tsagris et al., 2008]. Thus, their RNA has no information content for translation into proteins [Flores et al., 1997; Tsagris et al., 2008]. Yet, viroids are able to multiply and evolve like other organisms [Flores et al., 1997; Tsagris et al., 2008]. Moreover, they can enter the host cell, using their RNA as the antigen that fits the host cell receptor. In this respect, viroids might represent the bare essence of life. Their entire metabolism is reduced to just one chemical process of replication. Therefore, it is exactly their simplicity that makes viroids the most energetically efficient life forms. They do not waste energy on any processes except creating new life. Among all organisms, viroids have the greatest thermodynamic driving force for multiplication and exchange of matter with their environment. For a viroid, the environment is its host cell, from which it takes energy and building blocks [Popovic, 2014a, 2014b].
Figure 2 shows that Gibbs energy of biosynthesis of viroids is much more negative than that of their host plants. It is even more negative than Gibbs energy of biosynthesis of viruses. Viroids discovered until now are not pathogenic for humans. However, if viroids in the future evolve and make an interspecies jump to infect humans, they could due to their efficiency represent a great risk for humanity. The human pathogen Hepatitis Delta virus (HDV) is similar to viroids [Alves et al., 2013]. Thus, it might be interesting to consider thermodynamics of multiplication of the Hepatitis Delta virus. HDV cannot multiply alone, but only in coinfection with the Hepatitis B virus, on which it relies for supporting its multiplication [Alves et al., 2013]. Moreover, HDV in coinfection with Hepatitis B virus has a more severe clinical picture than infection with Hepatitis B alone [Alves et al., 2013]. This is in agreement with the finding that viroids have a greater thermodynamic driving force for multiplication than viruses. This leads to faster multiplication and more severe clinical picture. Thermodynamic analysis of human tissues has been made in [Popovic and Minceva, 2020c]. Furthermore, due to their simplicity, viroids are theoretically interesting, since they reveal the bare model of pathogen-host interactions.
The fact that viroids do not possess information in genes for production of proteins might support the metabolism first hypothesis, as the basis for understanding life processes. Viroids represent open thermodynamic systems with the property of growth, characterized by an empirical formula (Table 1) and thermodynamic properties (Table 3 and Table 4), which performs only one metabolic process. It fits into the concept of open systems in biology proposed by von Bertalanffy [von Bertalanffy, 1950, 1971; Popovic, 2018a, 2018b].
Viroids show the importance of metabolism for life. Viroids consist of a nucleic acid molecule, which encodes no proteins, but allows the viroid to perform its sole metabolic process of biosynthesis. Thus, viroids might show that the essence of life is not the information content in the genome, but the metabolism.

5. Conclusions

Viroids can hijack host cell metabolism due to their more negative Gibbs energy of biosynthesis. Viroids have a much more negative Gibbs energy of biosynthesis than their host cells. Thus, according to the biosynthesis phenomenological equation, viroid live matter will be produced much faster than the host cell components. This will allow the viroid to hijack the host cell’s metabolism. Viroids damage host cells by wasting usable energy for their multiplication, leaving less energy for the host cell. The thermodynamically more favorable biosynthesis of viroid live matter takes most of the usable energy produced by the host cell. Thus, less energy remains for the host cell to use. This is how viroids damage host cells.
The simplicity of viroids gives them an advantage in multiplication, in the form of a greater thermodynamic driving force and biosynthesis rate. Viroids do not contain any proteins. This makes their Gibbs energy of biosynthesis even more negative than that of viruses. Thus, the simplicity of viruses has enabled them to multiply very efficiently in their host cells. Viroids are an even more extreme example, with greater simplicity and even more efficient multiplication inside host cells.
Viroids do not have any genetic code with information to be translated into proteins. However, viroids perform one metabolic reaction – biosynthesis. Moreover, viroids possess many properties of life, including multiplication, genetic variability, exchange of matter with their environment and evolution. These facts are in favor of hypothesis that metabolism, rather than information content, forms the essence of life.

References

  1. Adkar-Purushothama, C.R.; Bolduc, F.; Bru, P.; Perreault, J.P. Insights Into Potato Spindle Tuber Viroid Quasi-Species From Infection to Disease. Front. Microbiol. 2020, 11, 1235. [Google Scholar] [CrossRef] [PubMed]
  2. Alves, C.; Branco, C.; Cunha, C. Hepatitis delta virus: a peculiar virus. Adv. Virol. 2013, 2013, 560105. [Google Scholar] [CrossRef] [PubMed]
  3. Atkins, P.W.; de Paula, J. Physical Chemistry for the Life Sciences, 2nd ed.; W. H. Freeman and Company: New York, NY, USA, 2011; ISBN 978-1429231145. [Google Scholar]
  4. Atkins, P.W.; de Paula, J. Physical Chemistry: Thermodynamics, Structure, and Change, 10th ed.; W. H. Freeman and Company: New York, NY, USA, 2014; ISBN 978-1429290197. [Google Scholar]
  5. Battley, E.H. A theoretical study of the thermodynamics of microbial growth using Saccharomyces cerevisiae and a different free energy equation. Q. Rev. Biol. 2013, 88, 69–96. [Google Scholar] [CrossRef] [PubMed]
  6. Battley, E.H.; Stone, J.R. A comparison of values for the entropy and the entropy of formation of selected organic substances of biological importance in the solid state, as determined experimentally or calculated empirically. Thermochim. Acta 2000, 349, 153–161. [Google Scholar] [CrossRef]
  7. Battley, E.H. An empirical method for estimating the entropy of formation and the absolute entropy of dried microbial biomass for use in studies on the thermodynamics of microbial growth. Thermochim. Acta 1999, 326, 7–15. [Google Scholar] [CrossRef]
  8. Battley, E.H. The thermodynamics of microbial growth. In Handbook of Thermal Analysis and Calorimetry, vol. 4: From Macromolecules to Man; Kemp, E.B., Ed.; Elsevier: Amsterdam, The Netherlands, 1999; pp. 219–235. [Google Scholar] [CrossRef]
  9. Battley, E.H. The development of direct and indirect methods for the study of the thermodynamics of microbial growth. Thermochim. Acta 1998, 309, 17–37. [Google Scholar] [CrossRef]
  10. Battley, E.H. On the enthalpy of formation of Escherichia coli K-12 cells. Biotechnol. Bioeng. 1992, 39, 5–12. [Google Scholar] [CrossRef] [PubMed]
  11. Casasnovas, J.M. and Springer, T.A. Kinetics and thermodynamics of virus binding to receptor: Studies with rhinovirus, intercellular adhesion molecule-1 (ICAM-1), and surface plasmon resonance. J. Biol. Chem. 1995, 270, 13216–13224. [Google Scholar] [CrossRef]
  12. Degueldre, C. Single virus inductively coupled plasma mass spectroscopy analysis: A comprehensive study. Talanta 2021, 228, 122211. [Google Scholar] [CrossRef]
  13. Di Serio, F.; Navarro, B.; Flores, R. Origin and Evolution of Viroids. Viroids Satell. 2017, 125–134. [Google Scholar] [CrossRef]
  14. Diener, T.O. Circular RNAs: relics of precellular evolution? Proc. Natl. Acad. Sci. USA 1989, 86, 9370–9374. [Google Scholar] [CrossRef] [PubMed]
  15. Dodd, T.; Botto, M.; Paul, F.; Fernandez-Leiro, R.; Lamers, M.H.; Ivanov, I. Polymerization and editing modes of a high-fidelity DNA polymerase are linked by a well-defined path. Nat. Commun. 2020, 11, 5379. [Google Scholar] [CrossRef] [PubMed]
  16. Duboc, P.; Marison, I.; Von Stockar, U. Quantitative calorimetry and biochemical engineering. In Handbook of Thermal Analysis and Calorimetry; 4(BOOK_CHAP); Elsevier: Amsterdam, The Netherlands, 1999; pp. 267–365. [Google Scholar] [CrossRef]
  17. Fialho, L.D.F.; Carneiro, A.D.C.O.; Carvalho, A.M.M.L.; Figueiró; C. G.; Silva, C.M.S.D.; Magalhães, M.A.; Peres, L.C. Bio-coal production with agroforestry biomasses in Brazil. Maderas. Cienc. Tecnol. 2019, 21. [Google Scholar] [CrossRef]
  18. Flores, R.; Di Serio, F.; Hernández, C. Viroids: The Noncoding Genomes. Semin. Virol. 1997, 8, 65–73. [Google Scholar] [CrossRef]
  19. Gale, P. Using thermodynamic equilibrium models to predict the effect of antiviral agents on infectivity: Theoretical application to SARS-CoV-2 and other viruses. Microb. Risk Risk Anal. 2021, 100198. [Google Scholar] [CrossRef] [PubMed]
  20. Gale, P. How virus size and attachment parameters affect the temperature sensitivity of virus binding to host cells: Predictions of a thermodynamic model for arboviruses and HIV. Microb. Risk Anal. 2020, 15, 100104. [Google Scholar] [CrossRef] [PubMed]
  21. Gale, P. Towards a thermodynamic mechanistic model for the effect of temperature on arthropod vector competence for transmission of arboviruses. Microb. Risk Anal. 2019, 12, 27–43. [Google Scholar] [CrossRef] [PubMed]
  22. Gale, P. Using thermodynamic parameters to calibrate a mechanistic dose-response for infection of a host by a virus. Microb. Risk Anal. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
  23. Gross, H.J.; Domdey, H.; Lossow, C.; Jank, P.; Raba, M.; Alberty, H.; Sänger, H.L. Nucleotide sequence and secondary structure of potato spindle tuber viroid. Nature 1978, 273, 203–208. [Google Scholar] [CrossRef]
  24. Head, R.J.; Lumbers, E.R.; Jarrott, B.; Tretter, F.; Smith, G.; Pringle, K.G.; Islam, S.; Martin, J.H. Systems analysis shows that thermodynamic physiological and pharmacological fundamentals drive COVID-19 and response to treatment. Pharmacol. Res. Perspect. 2022, 10, e00922. [Google Scholar] [CrossRef]
  25. Johansson, E.; Dixon, N. Replicative DNA polymerases. Cold Spring Harb. Perspect. Biol. 2013, 5, a012799. [Google Scholar] [CrossRef]
  26. King, A.M.Q.; Adams, M.J.; Carstens, E.B.; Lefkowitz, E.J. Virus Taxonomy: Ninth Report of the International Committee on Taxonomy of Viruses; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-12-384684-6. [Google Scholar]
  27. Latshaw, W.L.; Miller, E.C. Elemental composition of the corn plant. J. Agric. Res. 1924, 27, 845–861. [Google Scholar]
  28. Lucia, U.; Grisolia, G.; Deisboeck, T.S. Thermodynamics and SARS-CoV-2: neurological effects in post-Covid 19 syndrome. Atti Della Accad. Peloritana Dei Pericolanti 2021, 99, A3. [Google Scholar] [CrossRef]
  29. Lucia, U.; Grisolia, G.; Deisboeck, T.S. Seebeck-like effect in SARS-CoV-2 bio-thermodynamics. Atti Accad. Peloritana Pericolanti-Cl. Sci. Fis. Mat. Nat. 2020, 98, 6. [Google Scholar] [CrossRef]
  30. Lucia, U.; Deisboeck, T.S.; Grisolia, G. Entropy-based pandemics forecasting. Front. Phys. 2020, 8, 274. [Google Scholar] [CrossRef]
  31. Mahmoudabadi, G.; Milo, R.; Phillips, R. Energetic cost of building a virus. Proc. Natl. Acad. Sci. USA 2017, 114, E4324–E4333. [Google Scholar] [CrossRef]
  32. Medic, D.; Darr, M.; Shah, A.; Rahn, S. The Effects of Particle Size, Different Corn Stover Components, and Gas Residence Time on Torrefaction of Corn Stover. Energies 2012, 5, 1199–1214. [Google Scholar] [CrossRef]
  33. Moelling, K.; Broecker, F. Viroids and the Origin of Life. Int. J. Mol. Sci. 2021, 22, 3476. [Google Scholar] [CrossRef]
  34. Nam, H.; Capareda, S. Experimental investigation of torrefaction of two agricultural wastes of different composition using RSM (response surface methodology). Energy 2015, 91, 507–516. [Google Scholar] [CrossRef]
  35. NCBI. National Center for Biotechnology Information (NCBI)[Internet]. Bethesda (MD): National Library of Medicine (US), National Center for Biotechnology Information; [1988]. Available online: https://www.ncbi.nlm.nih.gov/ (accessed on 31 December 2022).
  36. Pineda-Insuasti, J.A.; Soto-Arroyave, C.P.; Ramos-Sánchez, L.B. Stoichiometry equation to describe the growth of the Pleurotus ostreatus ceba-gliie-po-010606 strain. Biotecnol. Apl. 2014, 31, 43–47. [Google Scholar]
  37. Pinheiro, A.V.; Baptista, P.; Lima, J.C. Light activation of transcription: photocaging of nucleotides for control over RNA polymerization. Nucleic Acids Res. 2008, 36, e90. [Google Scholar] [CrossRef] [PubMed]
  38. Popovic, M.; Popovic, M. Strain Wars: Competitive interactions between SARS-CoV-2 strains are explained by Gibbs energy of antigen-receptor binding. Microb. Risk Anal. 2022, 21, 100202. [Google Scholar] [CrossRef] [PubMed]
  39. Popovic, M. Atom counting method for determining elemental composition of viruses and its applications in biothermodynamics and environmental science. Comput. Biol. Chem. 2022, 96, 107621. [Google Scholar] [CrossRef] [PubMed]
  40. Popovic, M. Strain wars 3: Differences in infectivity and pathogenicity between Delta and Omicron strains of SARS-CoV-2 can be explained by thermodynamic and kinetic parameters of binding and growth. Microb. Risk Anal. 2022, 22, 100217. [Google Scholar] [CrossRef] [PubMed]
  41. Popovic, M. Strain wars 4—Darwinian evolution through Gibbs’ glasses: Gibbs energies of binding and growth explain evolution of SARS-CoV-2 from Hu-1 to BA.2. Virology 2022, 575, 36–42. [Google Scholar] [CrossRef] [PubMed]
  42. Popovic, M. Biothermodynamics of Viruses from Absolute Zero (1950) to Virothermodynamics (2022). Vaccines 2022, 10, 2112. [Google Scholar] [CrossRef]
  43. Popovic, M. Strain wars 2: Binding constants, enthalpies, entropies, Gibbs energies and rates of binding of SARS-CoV-2 variants. Virology 2022, 570, 35–44. [Google Scholar] [CrossRef] [PubMed]
  44. Popovic, M. Strain wars 5: Gibbs energies of binding of BA.1 through BA.4 variants of SARS-CoV-2. Microb. Risk Anal. 2022, 22, 100231. [Google Scholar] [CrossRef] [PubMed]
  45. Popovic, M. Beyond COVID-19: Do biothermodynamic properties allow predicting the future evolution of SARS-CoV-2 variants? Microb. Risk Anal. 2022, 22, 100232. [Google Scholar] [CrossRef]
  46. Popovic, M. Omicron BA.2.75 Sublineage (Centaurus) Follows the Expectations of the Evolution Theory: Less Negative Gibbs Energy of Biosynthesis Indicates Decreased Pathogenicity. Microbiol. Res. 2022, 13, 937–952. [Google Scholar] [CrossRef]
  47. Popovic, M. Omicron BA.2.75 Subvariant of SARS-CoV-2 Is Expected to Have the Greatest Infectivity Compared with the Competing BA.2 and BA.5, Due to Most Negative Gibbs Energy of Binding. BioTech 2022, 11, 45. [Google Scholar] [CrossRef]
  48. Popovic, M. Formulas for death and life: Chemical composition and biothermodynamic properties of Monkeypox (MPV, MPXV, HMPXV) and Vaccinia (VACV) viruses. Therm. Sci. 2022, 26, 4855–4868. [Google Scholar] [CrossRef]
  49. Popovic, M. Why doesn’t Ebola virus cause pandemics like SARS-CoV-2? Microb. Risk Anal. 2022, 100236. [Google Scholar] [CrossRef]
  50. Popovic, M. Everything you Always Wanted to Know about the Biothermodynamic Background of Herpes Simplex Virus Type 1—Host Interaction. Preprints 2022, 2022120063. [Google Scholar] [CrossRef]
  51. Popovic, M.; Minceva, M. Coinfection and Interference Phenomena Are the Results of Multiple Thermodynamic Competitive Interactions. Microorganisms 2021, 9, 2060. [Google Scholar] [CrossRef]
  52. Popovic, M.; Minceva, M. Standard Thermodynamic Properties, Biosynthesis Rates, and the Driving Force of Growth of Five Agricultural Plants. Front. Plant Sci. 2021, 12, 671868. [Google Scholar] [CrossRef]
  53. Popovic, M.; Minceva, M. A thermodynamic insight into viral infections: do viruses in a lytic cycle hijack cell metabolism due to their low Gibbs energy? Heliyon 2020, 6, e03933. [Google Scholar] [CrossRef]
  54. Popovic, M.; Minceva, M. Thermodynamic insight into viral infections 2: empirical formulas, molecular compositions and thermodynamic properties of SARS, MERS and SARS-CoV-2 (COVID-19) viruses. Heliyon 2020, 6, e04943. [Google Scholar] [CrossRef]
  55. Popovic, M.; Minceva, M. Thermodynamic properties of human tissues. Therm. Sci. 2020, 24, 4115–4133. [Google Scholar] [CrossRef]
  56. Popovic, M. Thermodynamic properties of microorganisms: determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon 2019, 5, e01950. [Google Scholar] [CrossRef]
  57. Popovic, M. Research in entropy wonterland: A review of the entropy concept. Therm. Sci. 2018, 22, 1163–1178. [Google Scholar] [CrossRef]
  58. Popovic, M. Living organisms from Prigogine’s perspective: an opportunity to introduce students to biological entropy balance. J. Biol. Educ. 2018, 52, 294–300. [Google Scholar] [CrossRef]
  59. Popovic, M. Comparative study of entropy and information change in closed and open thermodynamic systems. Thermochim. Acta 2014, 598, 77–81. [Google Scholar] [CrossRef]
  60. Popovic, M. Entropy change of open thermodynamic systems in self-organizing processes. Therm. Sci. 2014, 18, 1425–1432. [Google Scholar] [CrossRef]
  61. Riedel, S.; Hobden, J.A.; Miller, S.; Morse, S.A.; Mietzner, T.A.; Detrick, B.; Mitchell, T.G.; Sakanari, J.A.; Hotez, P.; Mejia, R. Jawetz, Melnick and Adelberg’s Medical Microbiology, 28th ed.; McGraw-Hill: New York, NY, USA, 2019; ISBN 978-1260012026. [Google Scholar]
  62. Sanger, H.L.; Klotz, G.; Riesner, D.; Gross, H.J.; Kleinschmidt, A.K. Viroids are single-stranded covalently closed circular RNA molecules existing as highly base-paired rod-like structures. Proc. Natl. Acad. Sci. USA 1976, 73, 3852–3856. [Google Scholar] [CrossRef] [PubMed]
  63. Sayers, E.W.; Bolton, E.E.; Brister, J.R.; Canese, K.; Chan, J.; Comeau, D.C.; Connor, R.; Funk, K.; Kelly, C.; Kim, S.; et al. Database resources of the national center for biotechnology information. Nucleic Acids Res. 2022, 50, D20–D26. [Google Scholar] [CrossRef] [PubMed]
  64. Şimşek, B.; Özilgen, M.; Utku, F.Ş. How much energy is stored in SARS-CoV-2 and its structural elements? Energy Storage 2021, e298. [Google Scholar] [CrossRef]
  65. Sogo, J.M.; Koller, T.; Diener, T.O. Potato spindle tuber viroid. X. Visualization and size determination by electron microscopy. Virology 1973, 55, 70–80. [Google Scholar] [CrossRef] [PubMed]
  66. Strauss, J.H.; Strauss, E.G. Subviral Agents. Viruses Hum. Dis. 2008, 345–368. [Google Scholar] [CrossRef]
  67. Titiloye, J.O.; Bakar, M.S.A.; Odetoye, T.E. Thermochemical characterisation of agricultural wastes from West Africa. Ind. Crops Prod. 2013, 47, 199–203. [Google Scholar] [CrossRef]
  68. Tsagris, E.M.; Martínez de Alba, A.E.; Gozmanova, M.; Kalantidis, K. Viroids. Cell. Microbiol. 2008, 10, 2168–2179. [CrossRef] [PubMed]
  69. Von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller Inc.: New York, NY, USA, 1971; ISBN 978-0807604533. [Google Scholar]
  70. Von Bertalanffy, L. The theory of open systems in physics and biology. Science 1950, 111, 23–29. [Google Scholar] [CrossRef] [PubMed]
  71. Von Stockar, U. Live cells as open non-equilibrium systems. In Biothermodynamics: The Role of Thermodynamics in Biochemical Engineering; von Stockar, U., Ed.; EPFL Press: Lausanne, Switzerland, 2013; pp. 475–534. [Google Scholar] [CrossRef]
  72. Von Stockar, U. Biothermodynamics of live cells: energy dissipation and heat generation in cellular structures. In Biothermodynamics: the role of thermodynamics in Biochemical Engineering; von Stockar, U., Ed.; EPFL Press: Lausanne, Switzerland, 2013; pp. 475–534. [Google Scholar] [CrossRef]
  73. Wang, Y. Current view and perspectives in viroid replication. Curr. Opin. Virol. 2021, 47, 32–37. [Google Scholar] [CrossRef] [PubMed]
Preprints 67003 g001
Figure 1. Gibbs energies of biosynthesis of viroids and plants. This graph shows standard Gibbs energies of biosynthesis, ΔbsG⁰, of viroids and plants. The green column (■) represents plants. The blue columns (■) represent viroids.
Figure 1. Gibbs energies of biosynthesis of viroids and plants. This graph shows standard Gibbs energies of biosynthesis, ΔbsG⁰, of viroids and plants. The green column (■) represents plants. The blue columns (■) represent viroids.
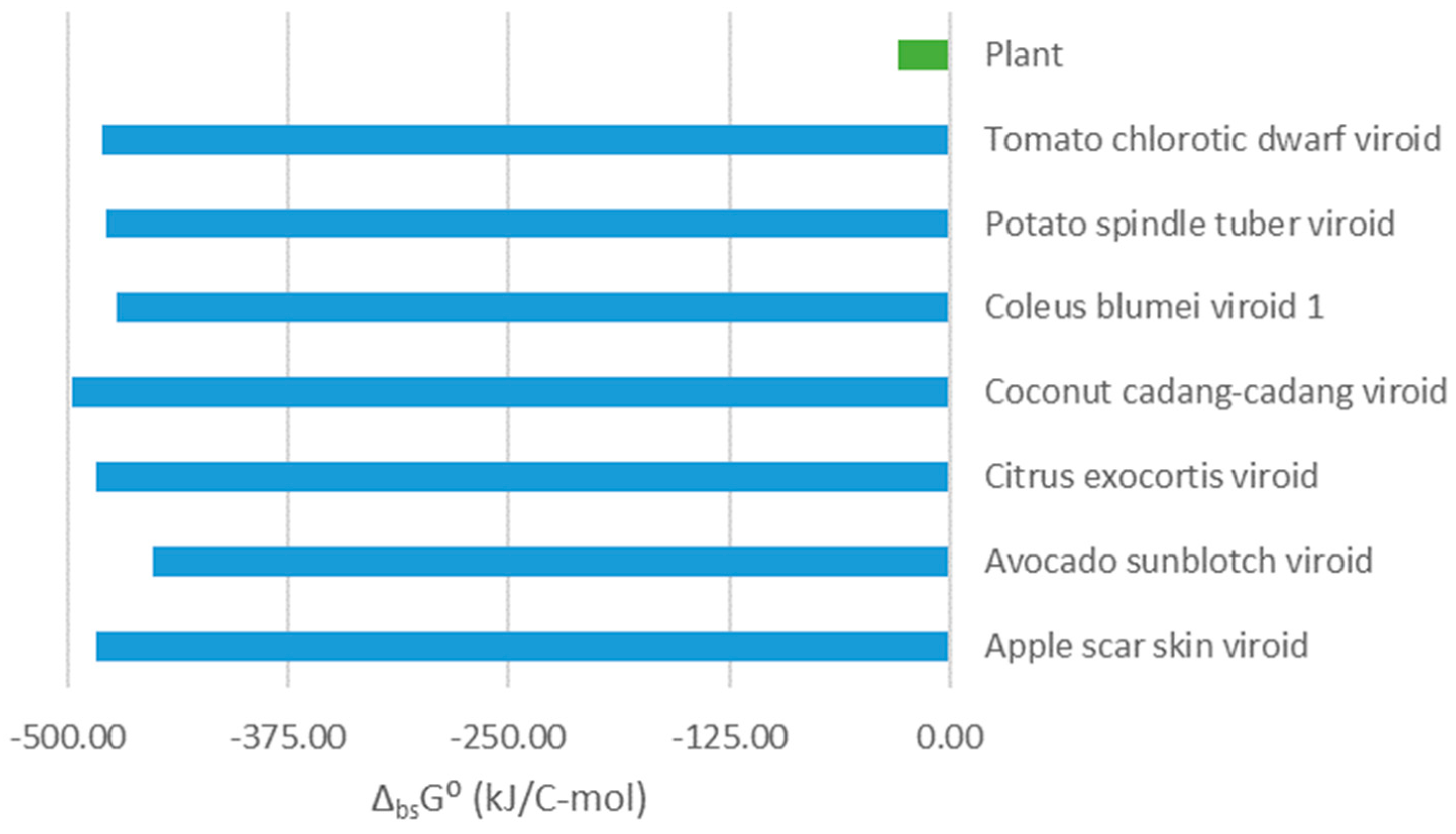
Preprints 67003 g001
Preprints 67003 g002
Figure 2. Gibbs energies of biosynthesis of viroids, viruses and cellular organisms. This graph shows standard Gibbs energies of biosynthesis, ΔbsG⁰, for 3 classes of organisms. The first are cellular organisms, represented by orange columns (■). The second are viruses, represented by blue columns (■). The third are viroids, represented by green columns (■).
Figure 2. Gibbs energies of biosynthesis of viroids, viruses and cellular organisms. This graph shows standard Gibbs energies of biosynthesis, ΔbsG⁰, for 3 classes of organisms. The first are cellular organisms, represented by orange columns (■). The second are viruses, represented by blue columns (■). The third are viroids, represented by green columns (■).
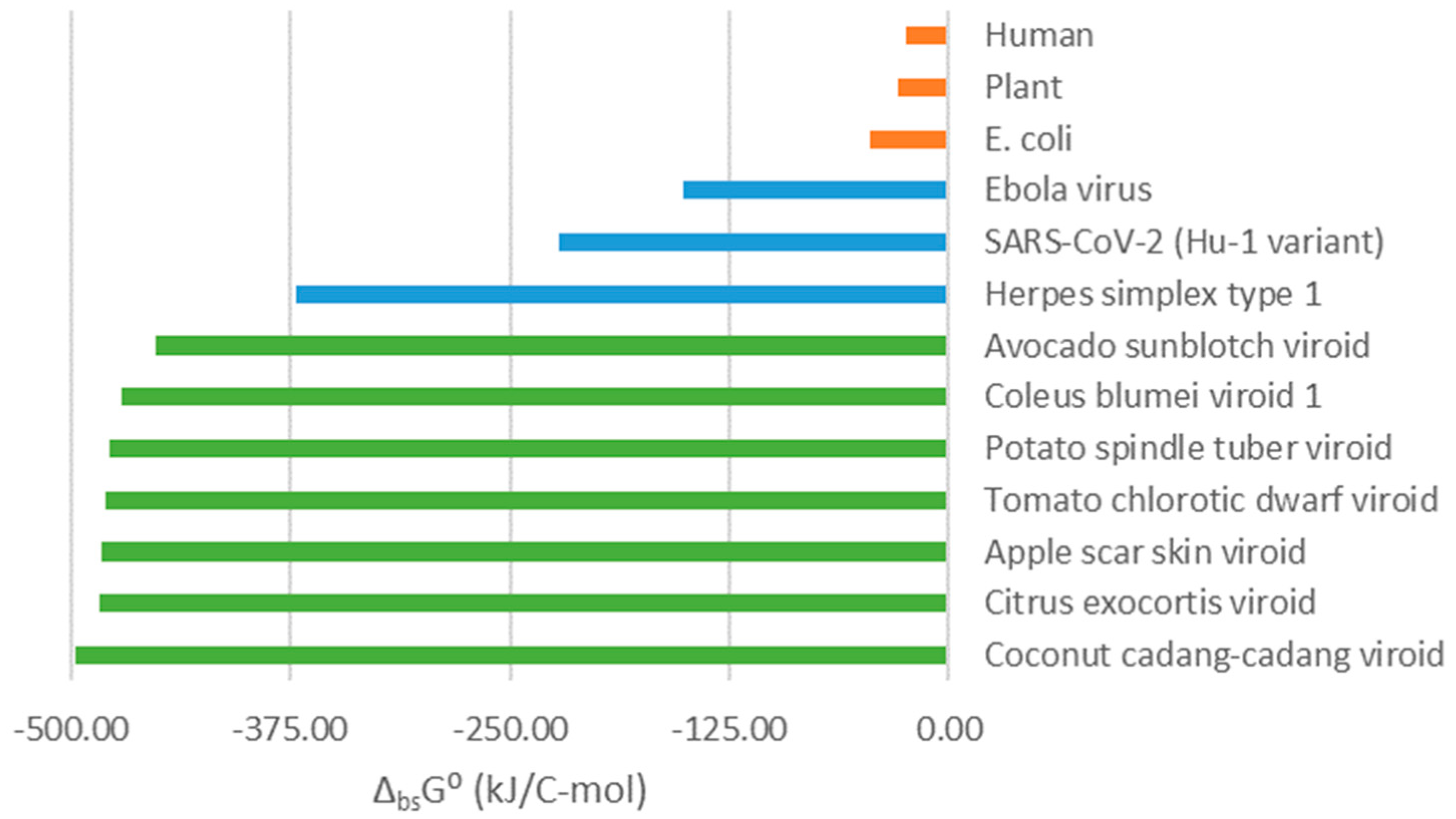
Preprints 67003 g002
Preprints 67003 g003
Figure 3. Gibbs energy of biosynthesis and GC content of viroids. The blue line (―) represents a prediction based on the elemental composition of AU and GC basepairs (Section 2.4). The orange dots (●) represent Gibbs energies of biosynthesis of the viroids analyzed in this research.
Figure 3. Gibbs energy of biosynthesis and GC content of viroids. The blue line (―) represents a prediction based on the elemental composition of AU and GC basepairs (Section 2.4). The orange dots (●) represent Gibbs energies of biosynthesis of the viroids analyzed in this research.
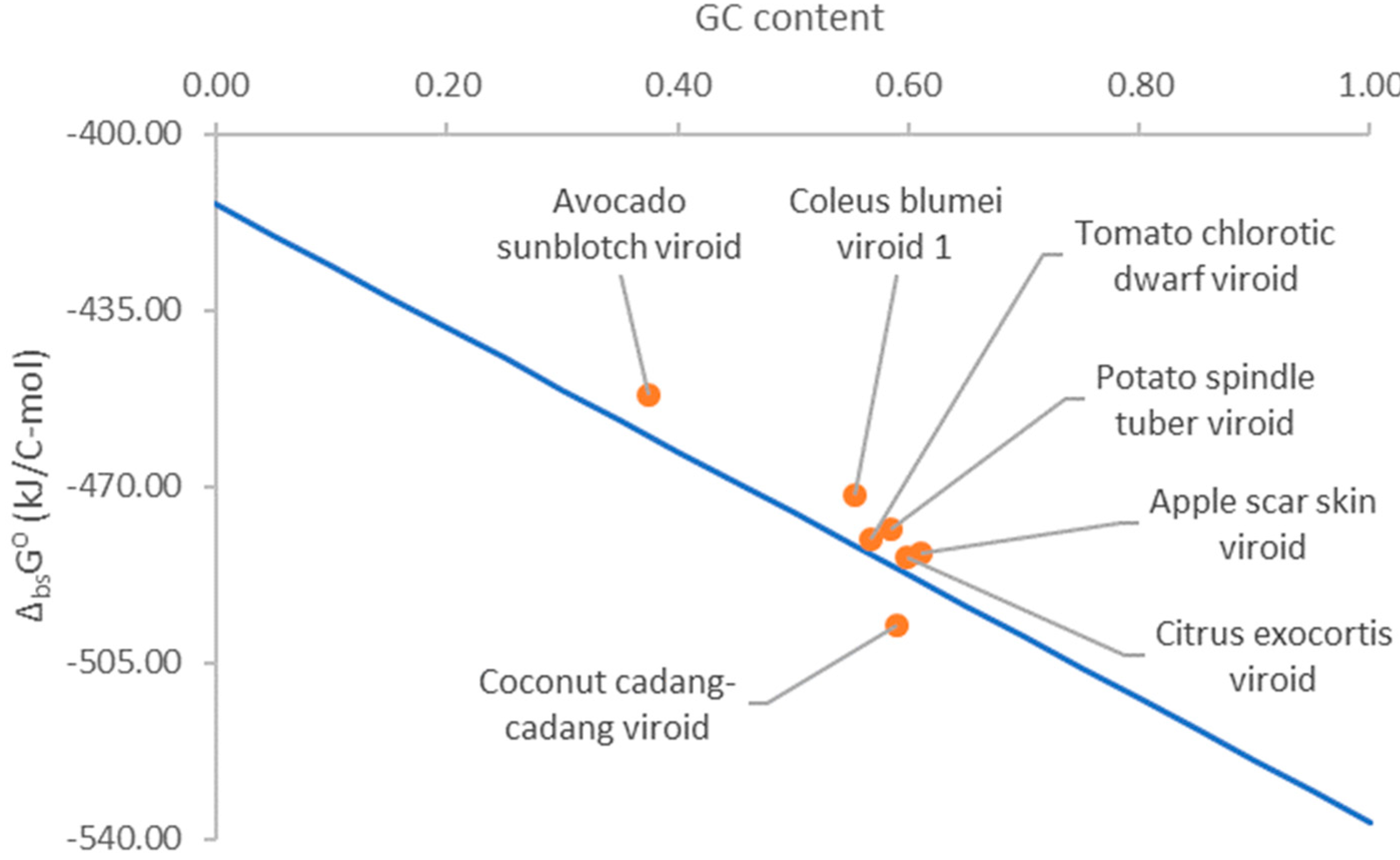
Preprints 67003 g003
Table 1. Empirical formulas of live matter for viroids and plants. This table shows elemental composition in the form of empirical formulas. A general empirical formula has the form CnCHnHOnONnNPnPSnSKnKMgnMgCanCaClnCl.
Table 1. Empirical formulas of live matter for viroids and plants. This table shows elemental composition in the form of empirical formulas. A general empirical formula has the form CnCHnHOnONnNPnPSnSKnKMgnMgCanCaClnCl.
Name C H O N P S K Mg Ca Cl
Apple scar skin viroid 1 1.2474 0.7578 0.3969 0.105550
Avocado sunblotch viroid 1 1.2301 0.7826 0.3811 0.105487
Citrus exocortis viroid 1 1.2434 0.7621 0.3966 0.105419
Coconut cadang-cadang viroid 1 1.2419 0.7547 0.4026 0.105128
Coleus blumei viroid 1 1 1.2416 0.7698 0.3908 0.105553
Potato spindle tuber viroid 1 1.2434 0.7648 0.3940 0.105511
Tomato chlorotic dwarf viroid 1 1.2416 0.7646 0.3947 0.105417
Plant 1 1.6329 0.7965 0.0245 0.000521 0.001119 0.001969 0.000652 0.000597 0.001007
Table 2. Biosynthesis reactions for viroids and plants. A general bionsythesis reaction has the form: (Amino acids) + CH2O + O2 + HPO42- + HCO3- + K+ + Mg2+ + Ca2+ + Cl- = (Bio) + SO42- + H2O + HCO3- + H2CO3, where (Bio) denotes the empirical formula of live matter from Table 1. The stoichiometric coefficients for the biosynthesis reactions are given in this table.
Table 2. Biosynthesis reactions for viroids and plants. A general bionsythesis reaction has the form: (Amino acids) + CH2O + O2 + HPO42- + HCO3- + K+ + Mg2+ + Ca2+ + Cl- = (Bio) + SO42- + H2O + HCO3- + H2CO3, where (Bio) denotes the empirical formula of live matter from Table 1. The stoichiometric coefficients for the biosynthesis reactions are given in this table.
Name Reactants Products
Amino acid CH2O O2 HPO42- HCO3- K+ Mg2+ Ca2+ Cl- → Bio SO42- H2O HCO3- H2CO3
Apple scar skin viroid 1.7660 0.0000 1.1277 0.1056 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0397 0.3164 0.1317 0.6343
Avocado sunblotch viroid 1.6960 0.0000 1.0576 0.1055 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0381 0.3336 0.1348 0.5612
Citrus exocortis viroid 1.7650 0.0000 1.1298 0.1054 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0397 0.3183 0.1315 0.6335
Coconut cadang-cadang viroid 1.7914 0.0000 1.1596 0.1051 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0403 0.3153 0.1297 0.6617
Coleus blumei viroid 1 1.7393 0.0000 1.1020 0.1056 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0391 0.3226 0.1329 0.6063
Potato spindle tuber viroid 1.7535 0.0000 1.1168 0.1055 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0394 0.3198 0.1322 0.6213
Tomato chlorotic dwarf viroid 1.7565 0.0000 1.1210 0.1054 0.0000 0.0000 0.0000 0.0000 0.0000 → 1 0.0395 0.3202 0.1319 0.6247
Plant 0.1091 0.8909 0.0132 0.0005 0.0051 0.0020 0.0007 0.0006 0.0010 → 1 0.0013 0.1703 0.0000 0.0051
Table 3. Standard thermodynamic properties of live matter for viroids and plants. This table gives data on standard enthalpies of formation, ΔfH⁰, standard molar entropies, S⁰m, and standard Gibbs energies of formation, ΔfG⁰.
Table 3. Standard thermodynamic properties of live matter for viroids and plants. This table gives data on standard enthalpies of formation, ΔfH⁰, standard molar entropies, S⁰m, and standard Gibbs energies of formation, ΔfG⁰.
Name ΔfH⁰ (kJ/C-mol) S⁰m (J/C-mol K) ΔfG⁰ (kJ/C-mol)
Apple scar skin viroid -177.75 38.73 -127.55
Avocado sunblotch viroid -182.72 38.71 -132.54
Citrus exocortis viroid -178.55 38.76 -128.31
Coconut cadang-cadang viroid -176.81 38.70 -126.64
Coleus blumei viroid 1 -180.24 38.78 -129.97
Potato spindle tuber viroid -179.18 38.76 -128.93
Tomato chlorotic dwarf viroid -179.05 38.75 -128.82
Plant -178.83 36.76 -131.18
Table 4. Standard thermodynamic properties of biosynthesis for viroids and plants. This table gives data on standard enthalpies of biosynthesis, ΔbsH⁰, standard entropies of biosynthesis, ΔbsS⁰, and standard Gibbs energies of biosynthesis, ΔbsG⁰.
Table 4. Standard thermodynamic properties of biosynthesis for viroids and plants. This table gives data on standard enthalpies of biosynthesis, ΔbsH⁰, standard entropies of biosynthesis, ΔbsS⁰, and standard Gibbs energies of biosynthesis, ΔbsG⁰.
Name ΔbsH⁰ (kJ/C-mol) ΔbsS⁰ (J/C-mol K) ΔbsG⁰ (kJ/C-mol)
Apple scar skin viroid -513.18 -104.03 -483.41
Avocado sunblotch viroid -480.20 -99.36 -451.82
Citrus exocortis viroid -514.08 -104.42 -484.19
Coconut cadang-cadang viroid -528.07 -106.64 -497.51
Coleus blumei viroid 1 -501.04 -102.43 -471.74
Potato spindle tuber viroid -507.98 -103.44 -478.38
Tomato chlorotic dwarf viroid -509.96 -103.81 -480.25
Plant -26.79 10.88 -29.16
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated