Preprint
Article
Neutrosophic Messy-Style SuperHyperGraphs To Form Neutrosophic SuperHyperStable To Act on Cancer's Neutrosophic Recognitions In Special ViewPoints
Altmetrics
Downloads
124
Views
25
Comments
0
This version is not peer-reviewed
Submitted:
03 January 2023
Posted:
05 January 2023
You are already at the latest version
Alerts
Abstract
in this research, new setting is introduced for new SuperHyperNotion, namely, Neutrosophic SuperHyperStable. In this research article, there are some research segments for ``Neutrosophic SuperHyperStable'' about some researches on neutrosophic SuperHyperStable. With researches on the basic properties, the research article starts to make neutrosophic SuperHyperStable theory more understandable. Assume a neutrosophic SuperHyperGraph. Then a ``neutrosophic SuperHyperStable'' $\mathcal{I}_n(NSHG)$ for a neutrosophic SuperHyperGraph $NSHG:(V,E)$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet $S$ of neutrosophic SuperHyperVertices such that there's no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. A basic familiarity with SuperHyperGraph theory and neutrosophic SuperHyperGraph theory are proposed.
Keywords:
Subject: Computer Science and Mathematics - Computer Vision and Graphics
MSC: 05C17; 05C22; 05E45
1. Background
2. Neutrosophic SuperHyperStable
Assume a neutrosophic SuperHyperGraph. Then a “neutrosophic SuperHyperStable” for a neutrosophic SuperHyperGraph is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common.
Example 2.1.
Assume the neutrosophic SuperHyperGraphs in the Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20.
-
On the Figure 1, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. and neutrosophic SuperHyperStable are some empty neutrosophic SuperHyperEdges but is a loop neutrosophic SuperHyperEdge and is an neutrosophic SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, The neutrosophic SuperHyperVertex, is isolated means that there’s no neutrosophic SuperHyperEdge has it as an endpoint. Thus neutrosophic SuperHyperVertex, is contained in every given neutrosophic SuperHyperStable. All the following neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices are the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable.The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, are the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are corresponded to a neutrosophic SuperHyperStable for a neutrosophic SuperHyperGraph is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex. But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, don’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable are up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, are the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are corresponded to a neutrosophic SuperHyperStable for a neutrosophic SuperHyperGraph is the neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and they are corresponded to a neutrosophic SuperHyperStable. Since They’vethe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSets, Thus the non-obvious neutrosophic SuperHyperStable, are up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, are neutrosophic SuperHyperSets, don’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic neutrosophic SuperHyperStable amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, is only
-
On the Figure 2, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. and neutrosophic SuperHyperStable are some empty neutrosophic SuperHyperEdges but is a loop neutrosophic SuperHyperEdge and is an neutrosophic SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, The neutrosophic SuperHyperVertex, is isolated means that there’s no neutrosophic SuperHyperEdge has it as an endpoint. Thus neutrosophic SuperHyperVertex, is contained in every given neutrosophic SuperHyperStable. All the following neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices are the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable.The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, are the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are corresponded to a neutrosophic SuperHyperStable for a neutrosophic SuperHyperGraph is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex. But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, don’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable are up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, are the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are corresponded to a neutrosophic SuperHyperStable for a neutrosophic SuperHyperGraph is the neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and they are corresponded to a neutrosophic SuperHyperStable. Since They’vethe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSets, Thus the non-obvious neutrosophic SuperHyperStable, are up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, are neutrosophic SuperHyperSets, don’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic neutrosophic SuperHyperStable amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, is only
- On the Figure 3, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. and are some empty neutrosophic SuperHyperEdges but is an neutrosophic SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, are the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable aren’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, don’t have more than one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable aren’t up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, aren’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, are corresponded to a neutrosophic SuperHyperStable for a neutrosophic SuperHyperGraph is the neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and they are neutrosophic SuperHyperStable. Since they’vethe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There are only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSets, Thus the non-obvious neutrosophic SuperHyperStable, aren’t up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, are the neutrosophic SuperHyperSets, don’t include only more than one neutrosophic SuperHyperVertex in a connected neutrosophic SuperHyperGraph It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic neutrosophic SuperHyperStable amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic SuperHyperStable, is only
- On the Figure 4, the neutrosophic SuperHyperNotion, namely, an neutrosophic SuperHyperStable, is up. There’s no empty neutrosophic SuperHyperEdge but are a loop neutrosophic SuperHyperEdge on and there are some neutrosophic SuperHyperEdges, namely, on alongside on and on The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex since it doesn’t form any kind of pairs titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 5, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex thus it doesn’t form any kind of pairs titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. and it’s neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph is mentioned as the SuperHyperModel in the Figure 5.
-
On the Figure 6, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,is the maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only only neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’s the maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet,Thus the non-obvious neutrosophic SuperHyperStable,is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable,is a neutrosophic SuperHyperSet,doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph with a illustrated SuperHyperModeling of the Figure 6.
- On the Figure 7, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph of depicted SuperHyperModel as the Figure 7.
- On the Figure 8, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re not only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only two neutrosophic SuperHyperVertices doesn’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph of dense SuperHyperModel as the Figure 8.
-
On the Figure 9, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,is the maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only only neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’s the maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet,Thus the non-obvious neutrosophic SuperHyperStable,is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable,is a neutrosophic SuperHyperSet,doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic neutrosophic SuperHyperGraph with a messy SuperHyperModeling of the Figure 9.
- On the Figure 10, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re not only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only two neutrosophic SuperHyperVertices doesn’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph of highly-embedding-connected SuperHyperModel as the Figure 10.
- On the Figure 11, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 12, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re not only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only two neutrosophic SuperHyperVertices doesn’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and they are neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only more than one neutrosophic SuperHyperVertex in a connected neutrosophic SuperHyperGraph in highly-multiple-connected-style SuperHyperModel On the Figure 12.
- On the Figure 13, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 14, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 15, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph as Linearly-Connected SuperHyperModel On the Figure 15.
- On the Figure 16, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 17, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph as Lnearly-over-packed SuperHyperModel is featured On the Figure 17.
- On the Figure 18, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, does has less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’s only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, does includes only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 19, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
- On the Figure 20, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperStable, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There’re only two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperStable is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet includes only less than two neutrosophic SuperHyperVertices don’t form any kind of pairs are titled to SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, doesn’t have less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable is up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, is the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, is the neutrosophic SuperHyperSet Ss of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common and it’s a neutrosophic SuperHyperStable. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. There aren’t only less than two neutrosophic SuperHyperVertices inside the intended neutrosophic SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, doesn’t include only less than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperGraph
Figure 1.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 1.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 2.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 2.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 3.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 3.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 4.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 4.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 5.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 5.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
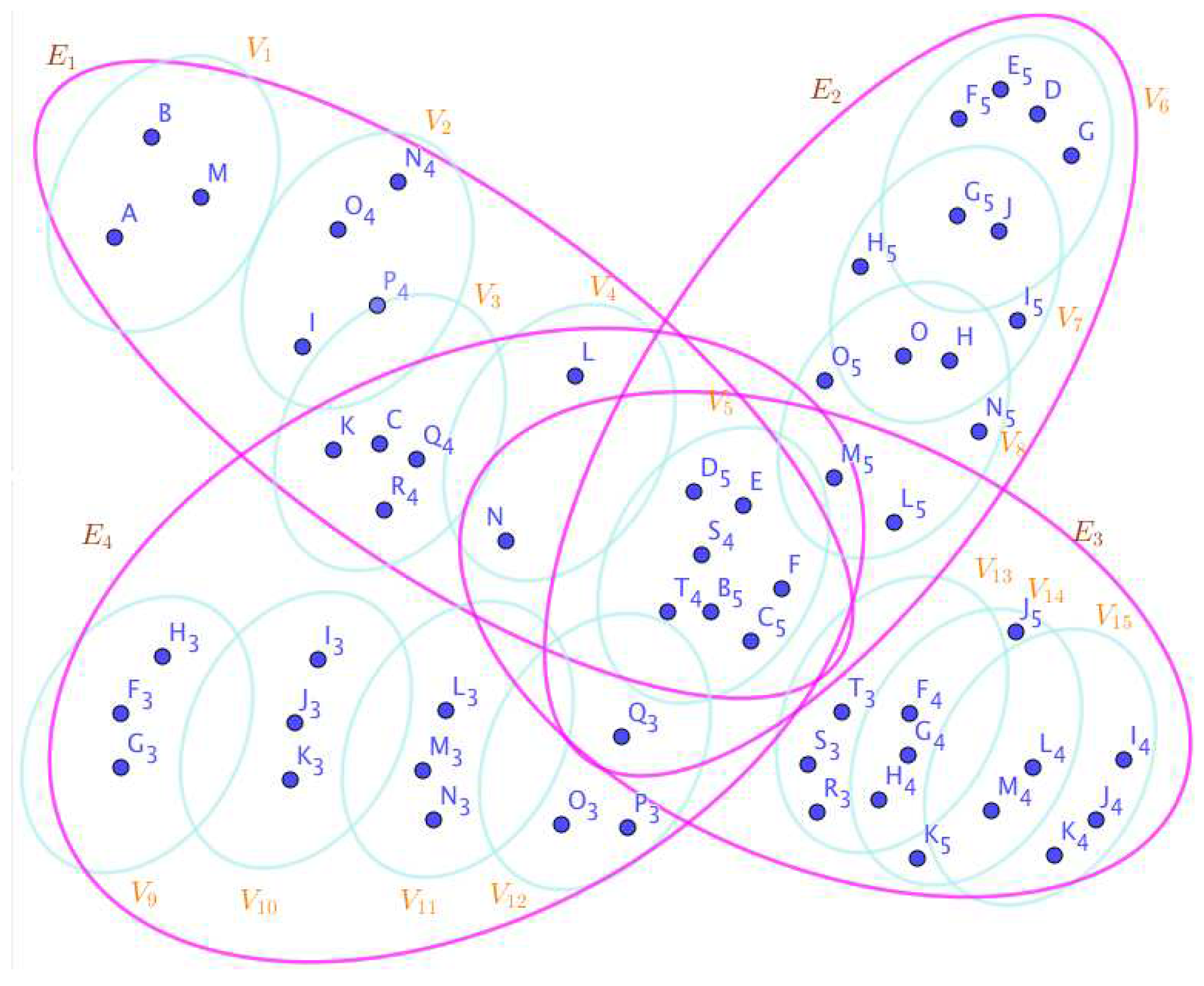
Figure 6.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 6.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 7.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 7.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 8.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 8.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 9.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 9.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
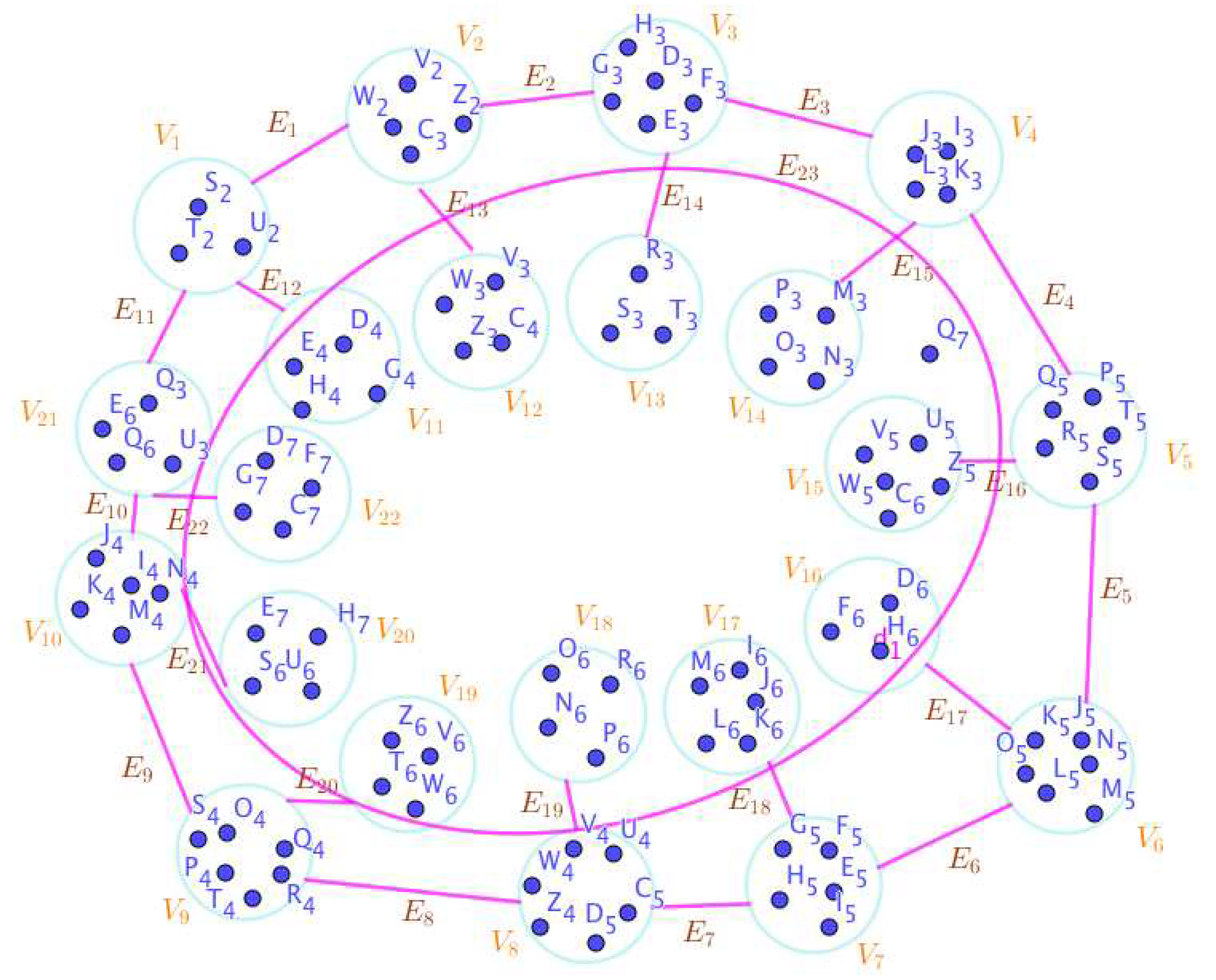
Figure 10.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 10.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
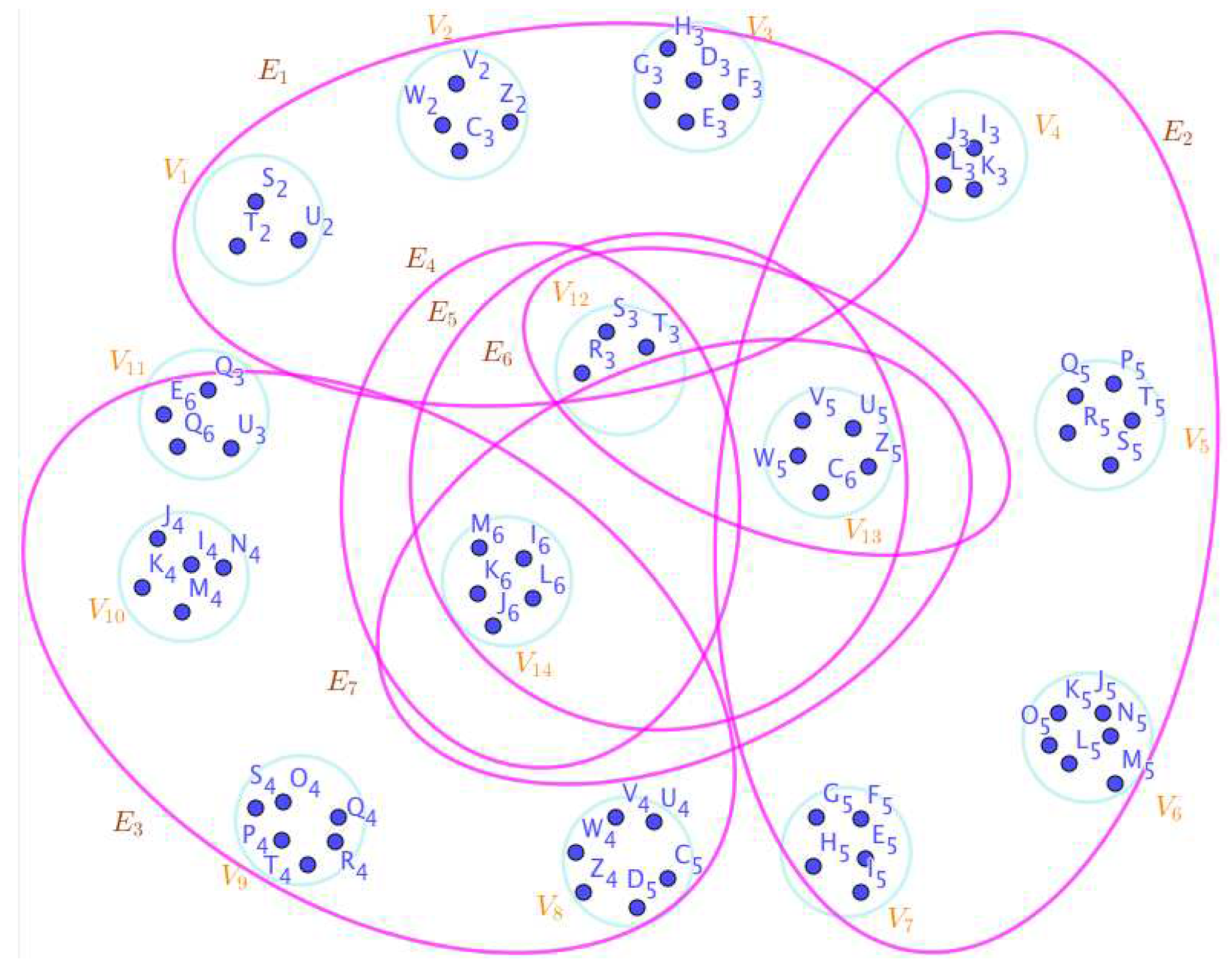
Figure 11.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 11.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.

Figure 12.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 12.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
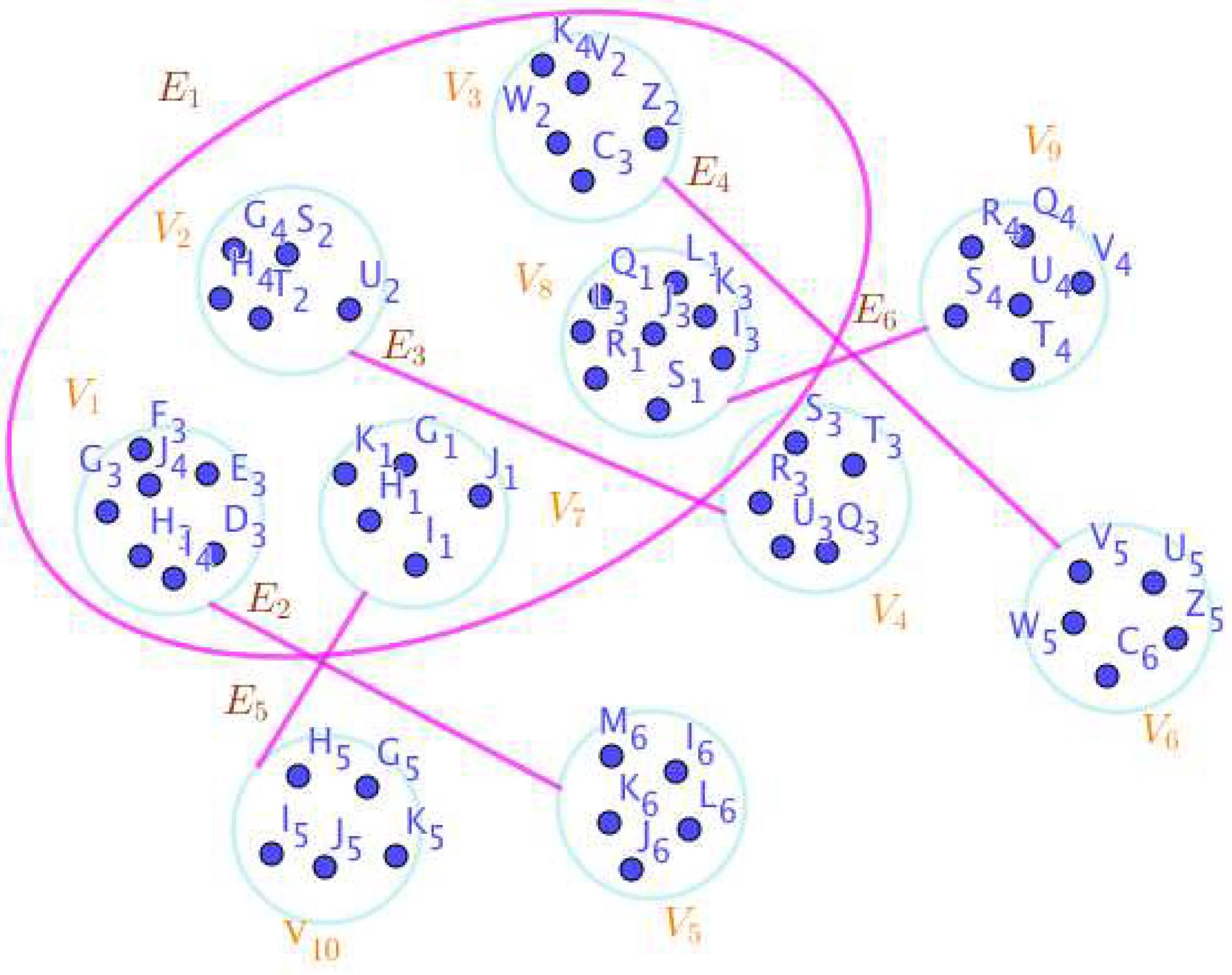
Figure 13.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 13.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
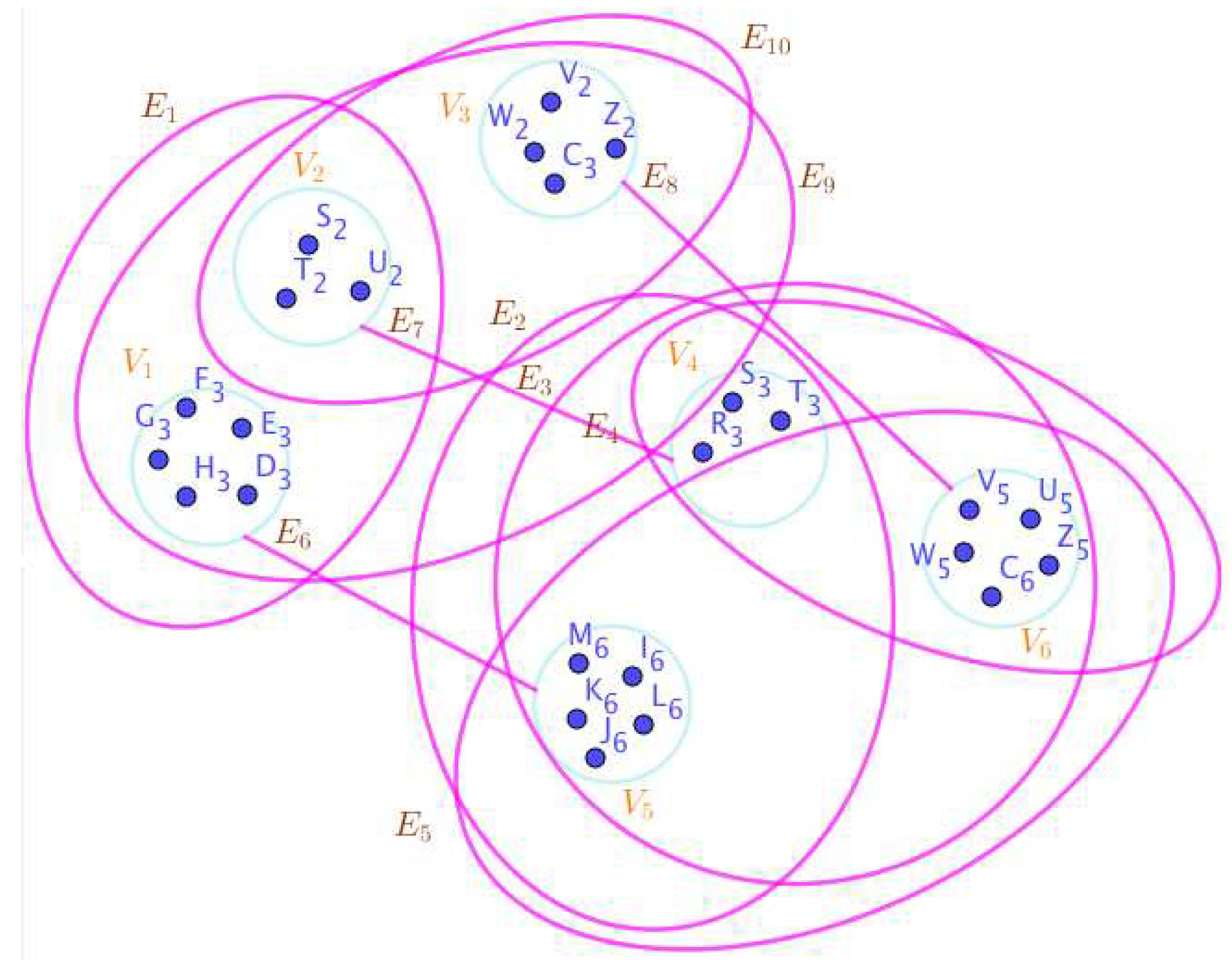
Figure 14.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 14.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
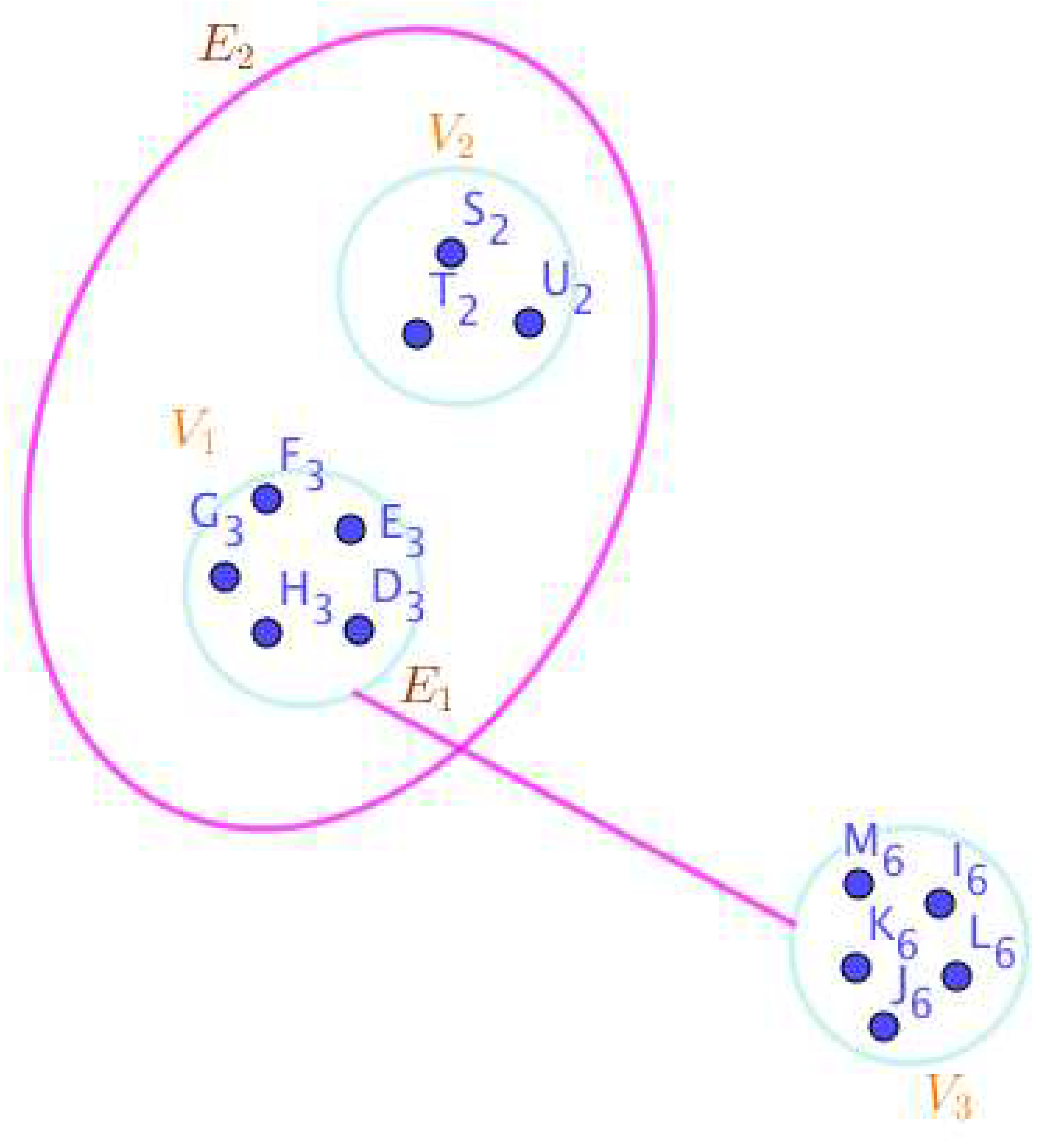
Figure 15.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 15.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
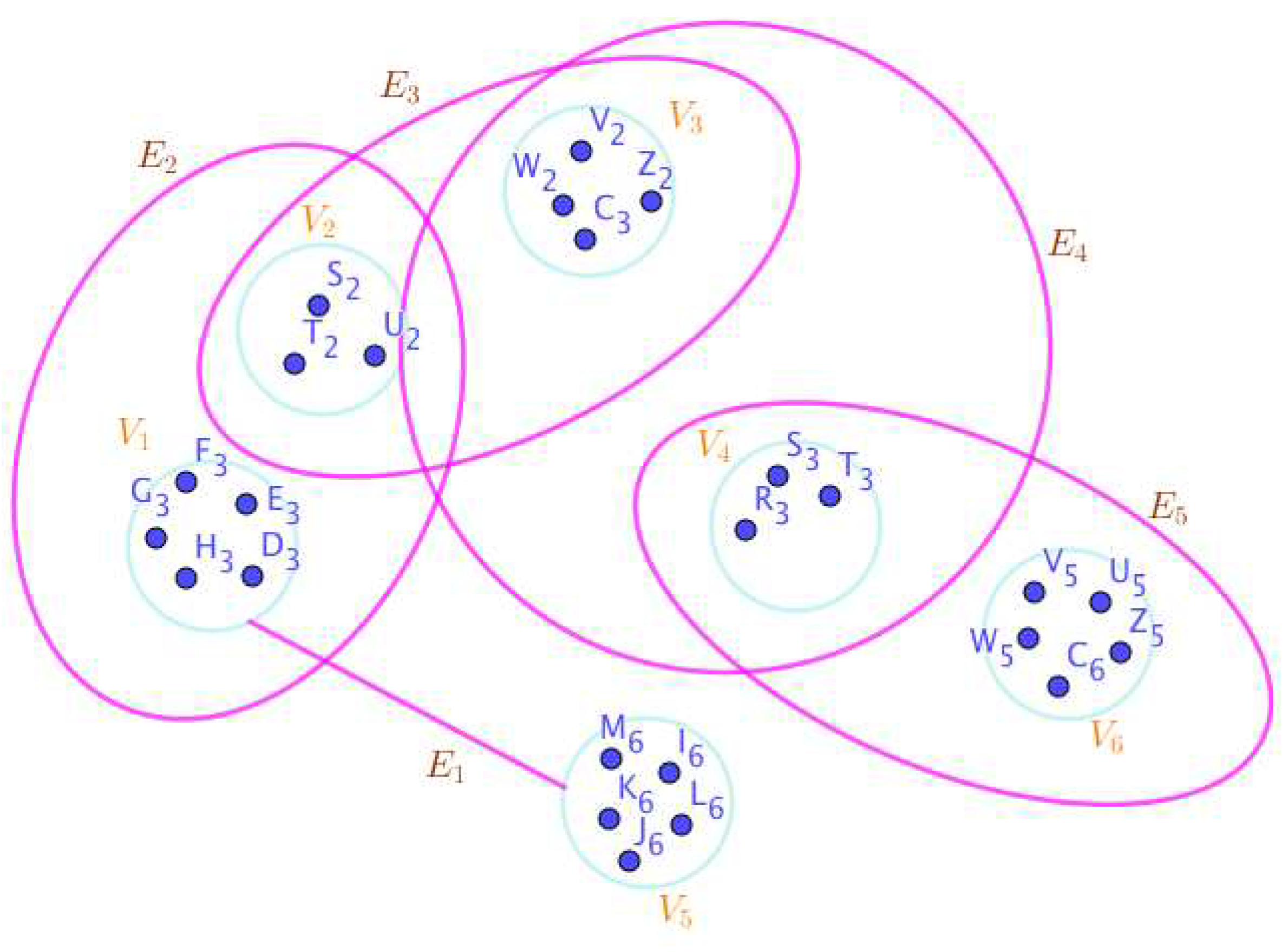
Figure 16.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 16.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 17.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 17.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 18.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 18.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
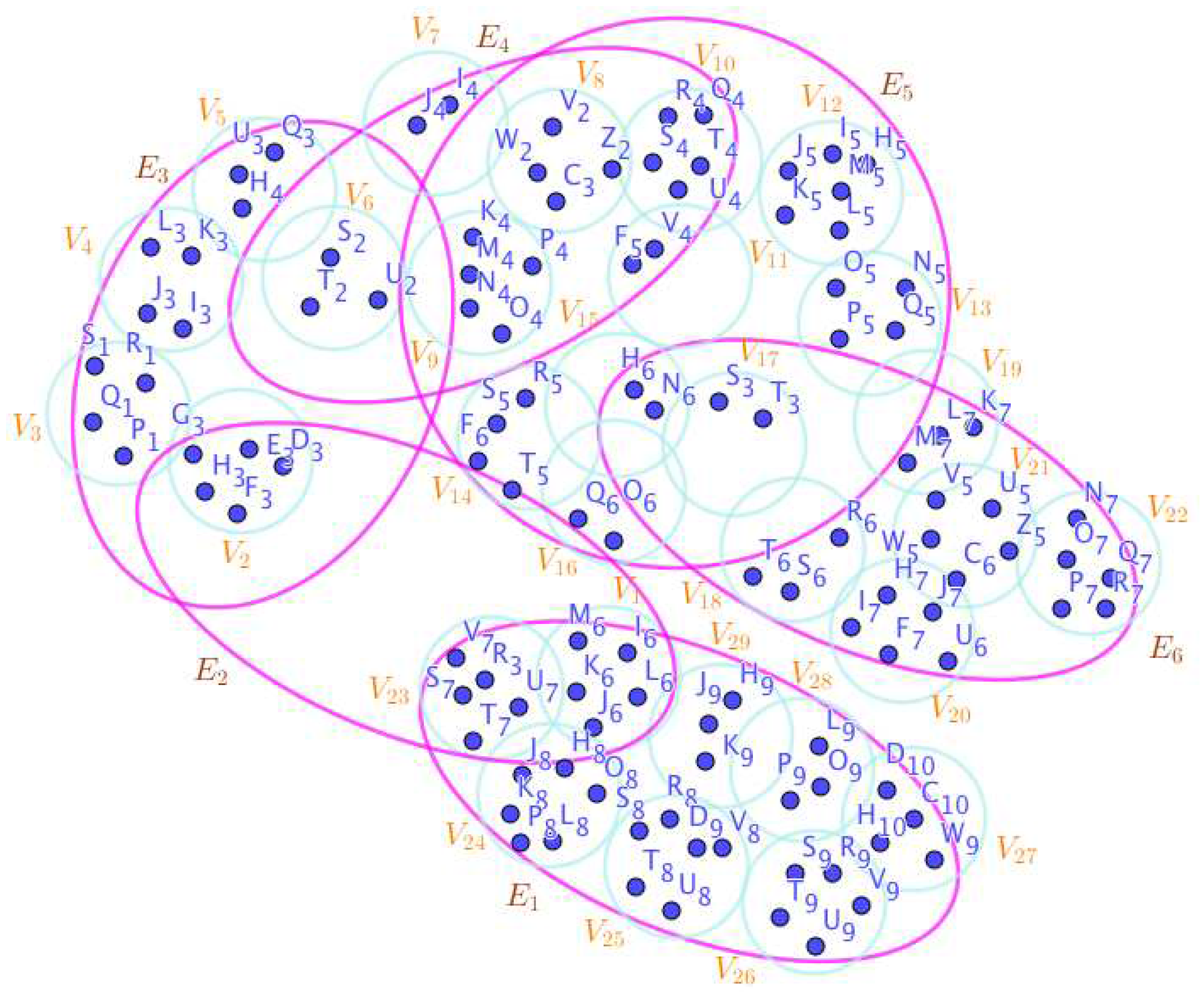
Figure 19.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 19.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 20.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Figure 20.
The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic SuperHyperStable in the Example 2.1.
Proposition 2.2.
Assume a connected neutrosophic SuperHyperGraph Then in the worst case, literally, is a neutrosophic SuperHyperStable. In other words, the least neutrosophic cardinality, the lower sharp bound for the neutrosophic cardinality, of a neutrosophic SuperHyperStable is the neutrosophic cardinality of
Proof.
Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. □
Proposition 2.3.
Assume a connected neutrosophic SuperHyperGraph Then the extreme number of neutrosophic SuperHyperStable has, the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of if there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality.
Proof.
Assume a connected neutrosophic SuperHyperGraph Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Then the extreme number of neutrosophic SuperHyperStable has, the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of if there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. □
Proposition 2.4.
Assume a connected neutrosophic SuperHyperGraph If a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices, then number of those interior neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge exclude to any neutrosophic SuperHyperStable.
Proof.
Assume a connected neutrosophic SuperHyperGraph Let a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices. Consider number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, if a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices, then number of those interior neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge exclude to any neutrosophic SuperHyperStable. □
Proposition 2.5.
Assume a connected neutrosophic SuperHyperGraph There’s not any neutrosophic SuperHyperEdge has only more than one distinct interior neutrosophic SuperHyperVertex inside of any given neutrosophic SuperHyperStable. In other words, there’s not an unique neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices in a neutrosophic SuperHyperStable.
Proof.
Assume a connected neutrosophic SuperHyperGraph Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding more than one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, there’s not any neutrosophic SuperHyperEdge has only more than one distinct interior neutrosophic SuperHyperVertex inside of any given neutrosophic SuperHyperStable. In other words, there’s not an unique neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices in a neutrosophic SuperHyperStable. □
Proposition 2.6.
Assume a connected neutrosophic SuperHyperGraph The all interior neutrosophic SuperHyperVertices belong to any neutrosophic SuperHyperStable if for any of them, there’s no other corresponded neutrosophic SuperHyperVertex such that the two interior neutrosophic SuperHyperVertices are mutually SuperHyperNeighbors.
Proof.
Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, the all interior neutrosophic SuperHyperVertices belong to any neutrosophic SuperHyperStable if for any of them, there’s no other corresponded neutrosophic SuperHyperVertex such that the two interior neutrosophic SuperHyperVertices are mutually SuperHyperNeighbors. □
Proposition 2.7.
Assume a connected neutrosophic SuperHyperGraph The any neutrosophic SuperHyperStable only contains all interior neutrosophic SuperHyperVertices and all exterior neutrosophic SuperHyperVertices where there’s any of them has no SuperHyperNeighbors in and there’s no SuperHyperNeighborhoods in but everything is possible about SuperHyperNeighborhoods and SuperHyperNeighbors out.
Proof.
Assume a connected neutrosophic SuperHyperGraph Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, the any neutrosophic SuperHyperStable only contains all interior neutrosophic SuperHyperVertices and all exterior neutrosophic SuperHyperVertices where there’s any of them has no SuperHyperNeighbors in and there’s no SuperHyperNeighborhoods in but everything is possible about SuperHyperNeighborhoods and SuperHyperNeighbors out. □
Remark 2.8.
The words “ neutrosophic SuperHyperStable” and “SuperHyperDominating” refer to the maximum type-style and the minimum type-style. In other words, they refer to both the maximum[minimum] number and the neutrosophic SuperHyperSet with the maximum[minimum] neutrosophic cardinality.
Proposition 2.9.
Assume a connected neutrosophic SuperHyperGraph Consider a SuperHyperDominating. Then a neutrosophic SuperHyperStable is either in or out.
Proof.
Assume a connected neutrosophic SuperHyperGraph Consider a SuperHyperDominating. By applying the Proposition 2.7, the results are up. Thus on a connected neutrosophic SuperHyperGraph and in a SuperHyperDominating. Then a neutrosophic SuperHyperStable is either in or out. □
3. Results on Neutrosophic SuperHyperClasses
Proposition 3.1.
Assume a connected SuperHyperPath Then a neutrosophic SuperHyperStable-style with the maximum SuperHyperneutrosophic cardinality is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices.
Proposition 3.2.
Assume a connected SuperHyperPath Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices from the common neutrosophic SuperHyperEdges. An neutrosophic SuperHyperStable has the number of all the interior neutrosophic SuperHyperVertices minus their SuperHyperNeighborhoods.
Proof.
Assume a connected SuperHyperPath Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperPath a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices from the common neutrosophic SuperHyperEdges. An neutrosophic SuperHyperStable has the number of all the interior neutrosophic SuperHyperVertices minus their SuperHyperNeighborhoods. □
Example 3.3.
Proposition 3.4.
Assume a connected SuperHyperCycle Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices from the same SuperHyperNeighborhoods. A neutrosophic SuperHyperStable has the number of all the neutrosophic SuperHyperEdges and the lower bound is the half number of all the neutrosophic SuperHyperEdges.
Proof.
Assume a connected SuperHyperCycle Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperCycle a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices from the same SuperHyperNeighborhoods. A neutrosophic SuperHyperStable has the number of all the neutrosophic SuperHyperEdges and the lower bound is the half number of all the neutrosophic SuperHyperEdges. □
Example 3.5.
In the Figure 22, the connected SuperHyperCycle is highlighted and featured. The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected SuperHyperCycle in the SuperHyperModel Figure 22,
is the neutrosophic SuperHyperStable.
Proposition 3.6.
Assume a connected SuperHyperStar Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices, excluding the SuperHyperCenter, with only all exceptions in the form of interior neutrosophic SuperHyperVertices from common neutrosophic SuperHyperEdge. An neutrosophic SuperHyperStable has the number of the neutrosophic cardinality of the second SuperHyperPart.
Proof.
Assume a connected SuperHyperStar Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperStar a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices, excluding the SuperHyperCenter, with only all exceptions in the form of interior neutrosophic SuperHyperVertices from common neutrosophic SuperHyperEdge. An neutrosophic SuperHyperStable has the number of the neutrosophic cardinality of the second SuperHyperPart. □
Example 3.7.
In the Figure 23, the connected SuperHyperStar is highlighted and featured. The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected SuperHyperStar in the SuperHyperModel Figure 23,
is the neutrosophic SuperHyperStable.
Proposition 3.8.
Assume a connected SuperHyperBipartite Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices titled SuperHyperNeighbors. A neutrosophic SuperHyperStable has the number of the neutrosophic cardinality of the first SuperHyperPart multiplies with the neutrosophic cardinality of the second SuperHyperPart.
Proof.
Assume a connected SuperHyperBipartite Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperBipartite a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only all exceptions in the form of interior neutrosophic SuperHyperVertices titled SuperHyperNeighbors. A neutrosophic SuperHyperStable has the number of the neutrosophic cardinality of the first SuperHyperPart multiplies with the neutrosophic cardinality of the second SuperHyperPart. □
Example 3.9.
In the Figure 24, the connected SuperHyperBipartite is highlighted and featured. The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected SuperHyperBipartite in the SuperHyperModel Figure 24,
is the neutrosophic SuperHyperStable.
Proposition 3.10.
Assume a connected SuperHyperMultipartite Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only one exception in the form of interior neutrosophic SuperHyperVertices from a SuperHyperPart and only one exception in the form of interior neutrosophic SuperHyperVertices from another SuperHyperPart titled “SuperHyperNeighbors”. A neutrosophic SuperHyperStable has the number of all the summation on the neutrosophic cardinality of the all SuperHyperParts form distinct neutrosophic SuperHyperEdges.
Proof.
Assume a connected SuperHyperMultipartite Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperMultipartite a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices with only one exception in the form of interior neutrosophic SuperHyperVertices from a SuperHyperPart and only one exception in the form of interior neutrosophic SuperHyperVertices from another SuperHyperPart titled “SuperHyperNeighbors”. A neutrosophic SuperHyperStable has the number of all the summation on the neutrosophic cardinality of the all SuperHyperParts form distinct neutrosophic SuperHyperEdges. □
Example 3.11.
In the Figure 25, the connected SuperHyperMultipartite is highlighted and featured. The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected SuperHyperMultipartite
in the SuperHyperModel Figure 25, is the neutrosophic SuperHyperStable.
Proposition 3.12.
Assume a connected SuperHyperWheel Then a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices, excluding the SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from same neutrosophic SuperHyperEdge. A neutrosophic SuperHyperStable has the number of all the number of all the neutrosophic SuperHyperEdges have no common SuperHyperNeighbors for a neutrosophic SuperHyperVertex.
Proof.
Assume a connected SuperHyperWheel Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider all numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding one distinct neutrosophic SuperHyperVertex, exclude to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic SuperHyperStable with the least neutrosophic cardinality, the lower sharp bound for neutrosophic cardinality. Assume a connected neutrosophic SuperHyperGraph The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common but it isn’t an neutrosophic SuperHyperStable. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices but it isn’t a neutrosophic SuperHyperStable. Since it doesn’t do the procedure such that such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. [there’s at least one neutrosophic SuperHyperVertex inside implying there’s, sometimes in the connected neutrosophic SuperHyperGraph a neutrosophic SuperHyperVertex, titled its SuperHyperNeighbor, to that neutrosophic SuperHyperVertex in the neutrosophic SuperHyperSet S so as S doesn’t do “the procedure”.]. There’s only one neutrosophic SuperHyperVertex inside the intended neutrosophic SuperHyperSet, Thus the obvious neutrosophic SuperHyperStable, is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic SuperHyperStable, is a neutrosophic SuperHyperSet, includes only one neutrosophic SuperHyperVertex doesn’t form any kind of pairs are titled SuperHyperNeighbors in a connected neutrosophic SuperHyperGraph Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices such that there’s no neutrosophic SuperHyperVertex to have a neutrosophic SuperHyperEdge in common. Thus, in a connected SuperHyperWheel a neutrosophic SuperHyperStable is a neutrosophic SuperHyperSet of the interior neutrosophic SuperHyperVertices, excluding the SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from same neutrosophic SuperHyperEdge. A neutrosophic SuperHyperStable has the number of all the number of all the neutrosophic SuperHyperEdges have no common SuperHyperNeighbors for a neutrosophic SuperHyperVertex. □
Example 3.13.
In the Figure 26, the connected SuperHyperWheel is highlighted and featured. The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected SuperHyperWheel
in the SuperHyperModel Figure 26, is the neutrosophic SuperHyperStable.
References
- Henry Garrett, “Properties of SuperHyperGraph and Neutrosophic SuperHyperGraph”, Neutrosophic Sets and Systems 49 (2022) 531-561 (doi: 10.5281/zenodo.6456413). (http://fs.unm.edu/NSS/NeutrosophicSuperHyperGraph34.pdf). (https://digitalrepository.unm.edu/ nss_journal/vol49/iss1/34).
- Henry Garrett, “Neutrosophic Co-degree and Neutrosophic Degree alongside Chromatic Numbers in the Setting of Some Classes Related to Neutrosophic Hypergraphs”, J Curr Trends Comp Sci Res 1(1) (2022) 06-14.
- Henry Garrett, “(Neutrosophic) SuperHyperModeling of Cancer’s Recognitions Featuring (Neutrosophic) SuperHyperDefensive SuperHyperAlliances”, Preprints 2022, 2022120549. [CrossRef]
- Henry Garrett, “(Neutrosophic) SuperHyperAlliances With SuperHyperDefensive and SuperHyperOffensive Type-SuperHyperSet On (Neutrosophic) SuperHyperGraph With (Neutrosophic) SuperHyperModeling of Cancer’s Recognitions And Related (Neutrosophic) SuperHyperClasses”, Preprints 2022, 2022120540. [CrossRef]
- Henry Garrett, “SuperHyperGirth on SuperHyperGraph and Neutrosophic SuperHyperGraph With SuperHyperModeling of Cancer’s Recognitions”, Preprints 2022, 2022120500. [CrossRef]
- Henry Garrett, “Some SuperHyperDegrees and Co-SuperHyperDegrees on Neutrosophic SuperHyperGraphs and SuperHyperGraphs Alongside Applications in Cancer’s Treatments”, Preprints 2022, 2022120324. [CrossRef]
- Henry Garrett, “SuperHyperDominating and SuperHyperResolving on Neutrosophic SuperHyperGraphs And Their Directions in Game Theory and Neutrosophic SuperHyperClasses”, Preprints 2022, 2022110576. [CrossRef]
- Henry Garrett, “Neutrosophic Messy-Style SuperHyperGraphs To Form Neutrosophic SuperHyperStable To Act on Cancer’s Neutrosophic Recognitions In Special ViewPoints”, ResearchGate 2023. [CrossRef]
- Henry Garrett, “(Neutrosophic) SuperHyperStable on Cancer’s Recognition by Well-SuperHyperModelled (Neutrosophic) SuperHyperGraphs”, ResearchGate 2023. [CrossRef]
- Henry Garrett, “Neutrosophic 1-Failed SuperHyperForcing in the SuperHyperFunction To Use Neutrosophic SuperHyperGraphs on Cancer’s Neutrosophic Recognition And Beyond”, ResearchGate 2022. [CrossRef]
- Henry Garrett, “(Neutrosophic) 1-Failed SuperHyperForcing in Cancer’s Recognitions And (Neutrosophic) SuperHyperGraphs”, ResearchGate 2022. [CrossRef]
- Henry Garrett, “Basic Notions on (Neutrosophic) SuperHyperForcing And (Neutrosophic) SuperHyperModeling in Cancer’s Recognitions And (Neutrosophic) SuperHyperGraphs”, ResearchGate 2022. [CrossRef]
- Henry Garrett, “Basic Neutrosophic Notions Concerning SuperHyperDominating and Neutrosophic SuperHyperResolving in SuperHyperGraph”, ResearchGate 2022. [CrossRef]
- Henry Garrett, “Initial Material of Neutrosophic Preliminaries to Study Some Neutrosophic Notions Based on Neutrosophic SuperHyperEdge (NSHE) in Neutrosophic SuperHyperGraph (NSHG)”, ResearchGate 2022. [CrossRef]
- Henry Garrett, (2022). “Beyond Neutrosophic Graphs”, Ohio: E-publishing: Educational Publisher 1091 West 1st Ave Grandview Heights, Ohio 43212 United States. ISBN: 979-1-59973-725-6 (http://fs.unm.edu/BeyondNeutrosophicGraphs.pdf).
- Henry Garrett, (2022). “Neutrosophic Duality”, Florida: GLOBAL KNOWLEDGE - Publishing House 848 Brickell Ave Ste 950 Miami, Florida 33131 United States. ISBN: 978-1-59973-743-0 (http://fs.unm.edu/NeutrosophicDuality.pdf).
- F. Smarandache, “Extension of HyperGraph to n-SuperHyperGraph and to Plithogenic n-SuperHyperGraph, and Extension of HyperAlgebra to n-ary (Classical-/Neutro-/Anti-) HyperAlgebra”, Neutrosophic Sets and Systems 33 (2020) 290-296. [CrossRef]
- M. Akram et al., “Single-valued neutrosophic Hypergraphs”, TWMS J. App. Eng. Math. 8 (1) (2018) 122-135.
- S. Broumi et al., “Single-valued neutrosophic graphs”, Journal of New Theory 10 (2016) 86-101.
- H. Wang et al., “Single-valued neutrosophic sets”, Multispace and Multistructure 4 (2010) 410-413.
- H.T. Nguyen and E.A. Walker, “A First course in fuzzy logic”, CRC Press, 2006.
Figure 21.
A SuperHyperPath Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.3.
Figure 21.
A SuperHyperPath Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.3.
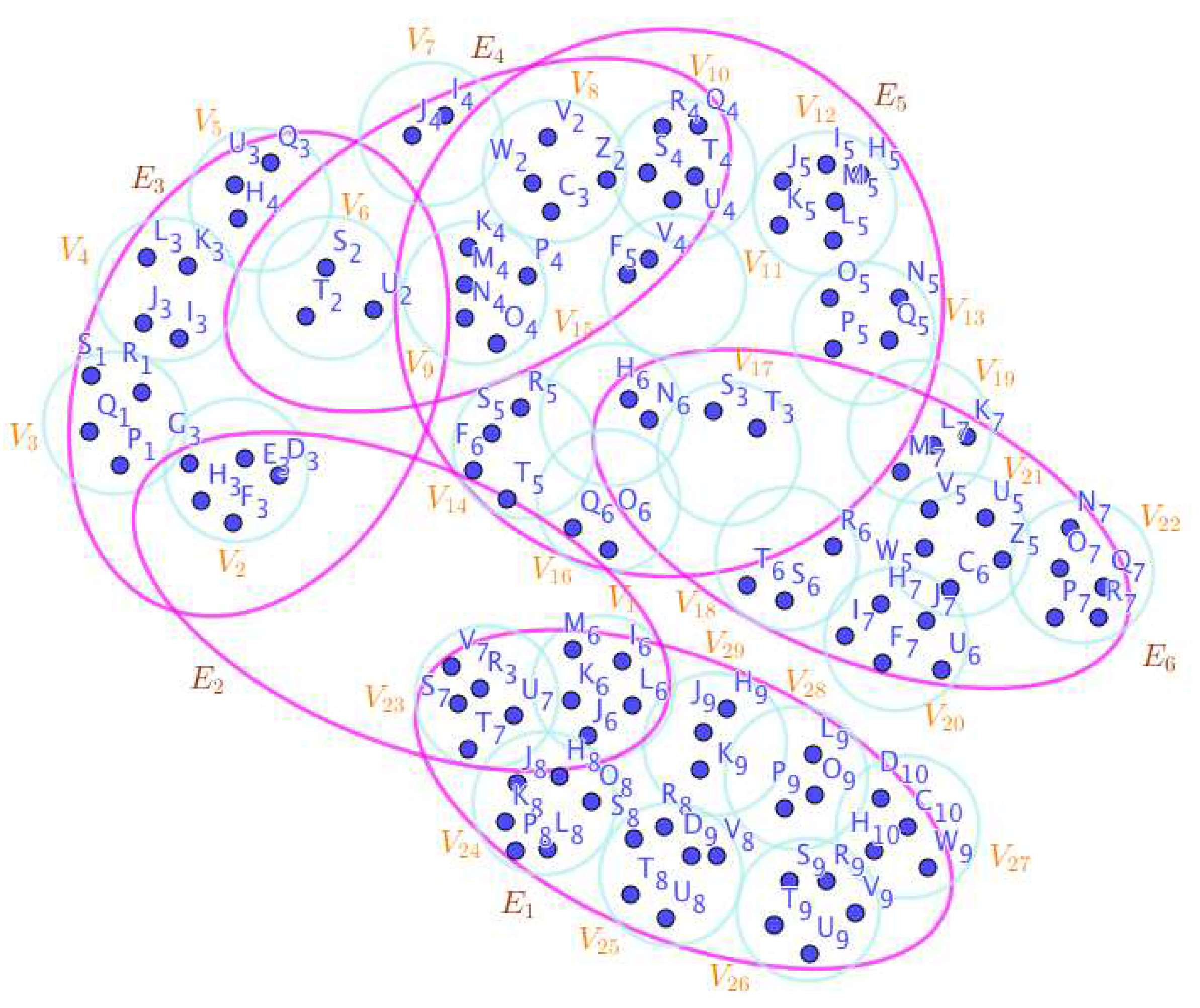
Figure 22.
A SuperHyperCycle Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.5.
Figure 22.
A SuperHyperCycle Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.5.
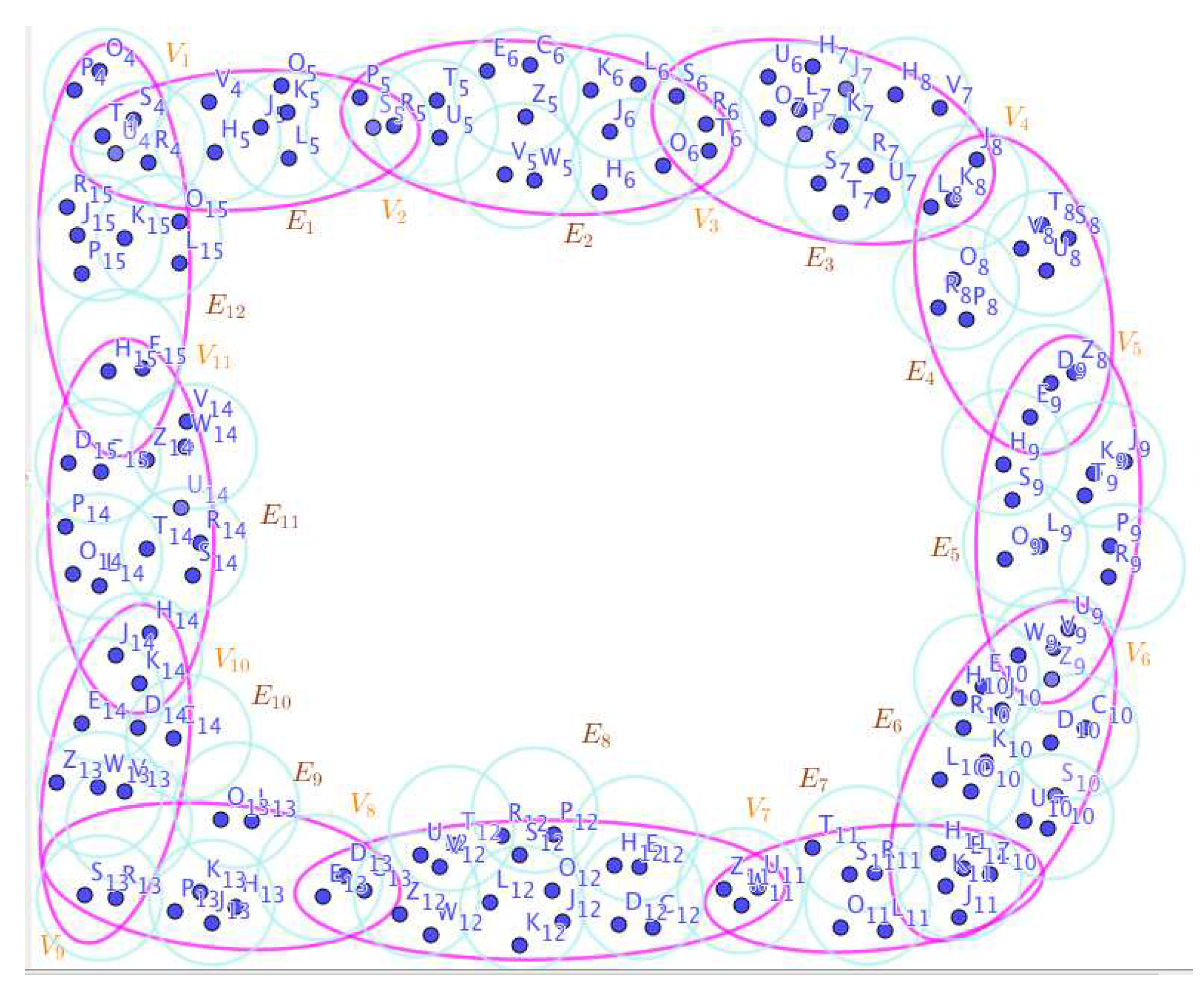
Figure 23.
A SuperHyperStar Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.7.
Figure 23.
A SuperHyperStar Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.7.
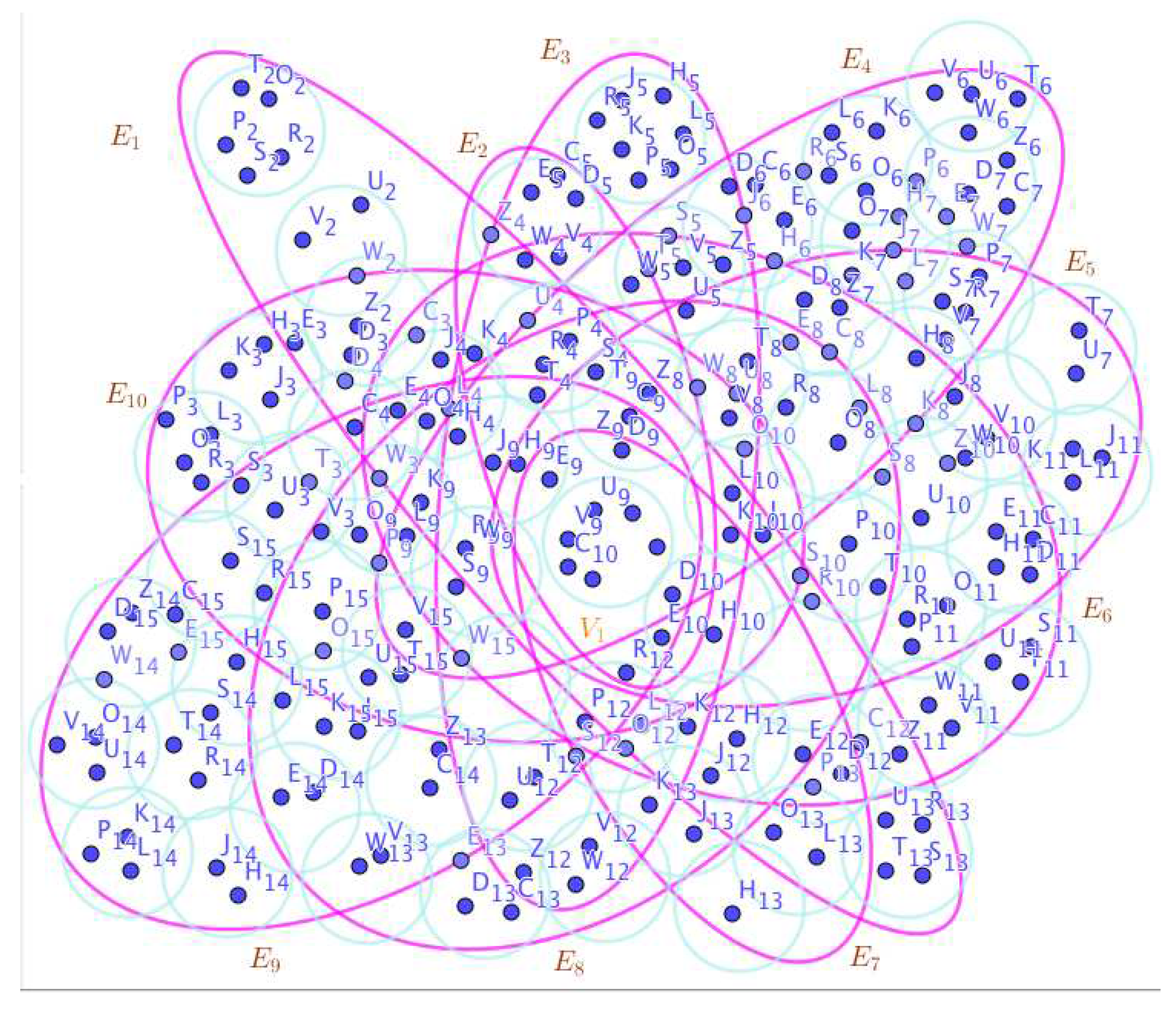
Figure 24.
A SuperHyperBipartite Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.9.
Figure 24.
A SuperHyperBipartite Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.9.
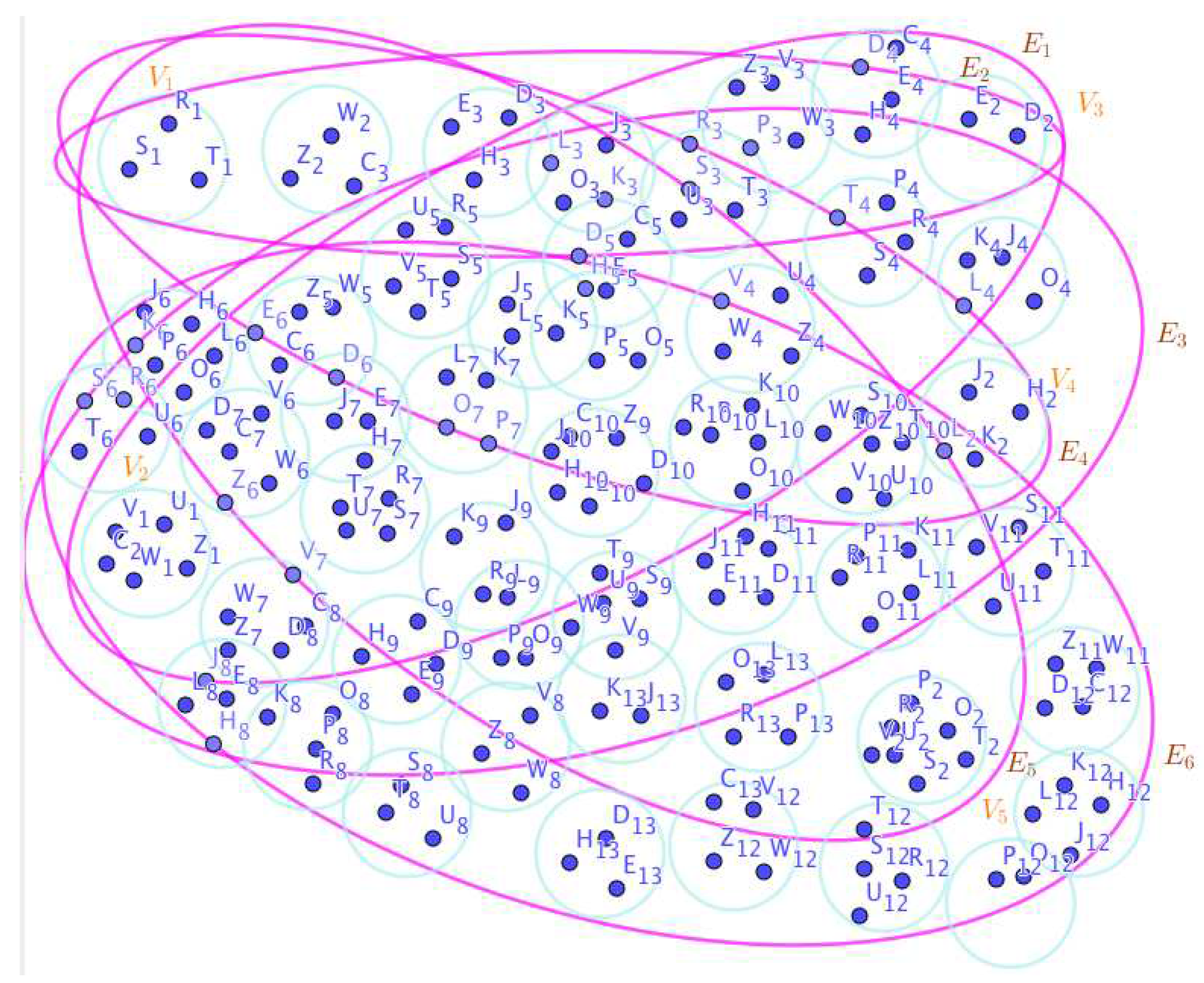
Figure 25.
A SuperHyperMultipartite Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.11.
Figure 25.
A SuperHyperMultipartite Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.11.
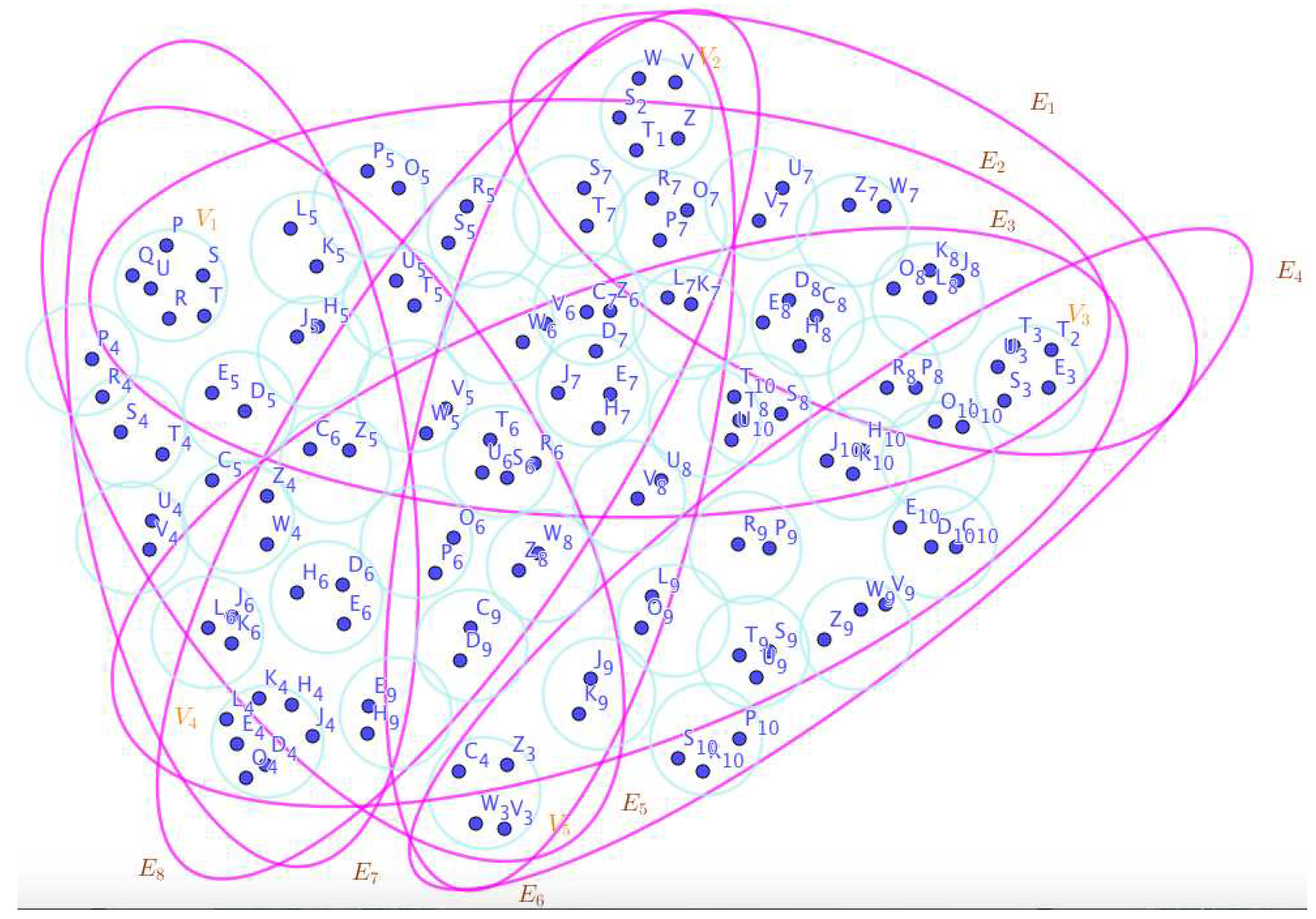
Figure 26.
A SuperHyperWheel Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.13.
Figure 26.
A SuperHyperWheel Associated to the Notions of neutrosophic SuperHyperStable in the Example 3.13.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





