Prerpints.org logo
Preprint
Article

Federated Learning for Education Data Analytics

Altmetrics

Downloads

271

Views

189

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 December 2022

Posted:

05 January 2023

You are already at the latest version

Alerts
Abstract
Federated learning techniques aim to train and build machine learning models based on distributed datasets across multiple devices, avoiding data leakage. The main idea is to perform training on remote devices or isolated data centers without transferring data to centralized repositories, thus mitigating privacy risks. Data analytics in education, in particular learning analytics, is a promising scenario to apply this approach to address the legal and ethical issues related to processing sensitive data. Indeed, given the nature of the data to be studied (personal data, educational outcomes, data concerning minors), it is essential to ensure that the conduct of these studies and the publication of the results provide the necessary guarantees to protect the privacy of the individuals involved and the protection of their data. In addition, the application of quantitative techniques based on the exploitation of data on the use of educational platforms, student performance, use of devices, etc., can account for educational problems such as the determination of user profiles, personalized learning trajectories, or early dropout indicators and alerts, among others. This paper presents the application of federated learning techniques to two learning analytics problems: dropout prediction and unsupervised student classification. The experiments allow us to conclude that the proposed solutions achieve comparable results from the performance point of view with the centralized versions, avoiding centralizing the data for training the models.
Keywords: 
Subject: Computer Science and Mathematics  -   Information Systems

1. Introduction

In its traditional approach, building, training and deploying Machine Learning (ML) models and Artificial Intelligence (AI) techniques involves simple data-sharing models. Data is fused, cleaned and integrated, then used to train and test the models. However, this procedure faces challenges related to the privacy of individuals and the protection of personal data. These privacy and ethical issues are essential in learning analytics (LA), which is the application of quantitative techniques to educational data to help solve problems such as the design of learning trajectories or the development of early dropout alerts. The privacy issues and the ethical use of data in ML activities have been widely documented in the literature [1,2,3].
Two approaches to ensure privacy in the context of LA appear in the literature. On the one hand, the privacy-preserving data publishing approach, which consists of applying data de-identification and anonymization techniques (e.g., satisfying the definition of k-anonymity [4]) and then using conventional ML methods [5,6]. On the other hand, in the approach known as privacy-preserving data mining or statistical disclosure control, the analyst does not directly access the data, but uses a query mechanism that adds statistical noise to the response, implementing differential privacy [7]. The latter strategy may be more robust and scalable, but some authors suggest that it may be difficult to implement in practice [8].
Federated Learning (FL) is a decentralized approach initially proposed by Google [9] to build ML models using distributed datasets across multiple devices. The main goal is to train statistical models on remote devices or isolated data centres without transferring the data to centralised repositories. FL incorporates ideas from multiple areas, including cryptography, ML, heterogeneous computing and distributed systems. In recent years the concept has been growing and consolidating, along lines ranging from improvements in security aspects, the study of statistical problems that arise in the distributed scenario, to the extension of the concept to cover collaborative learning scenarios between organizations [10]. There are two variants of FL: horizontal and vertical [11]. In the horizontal case, it is assumed that all clients participating in the training stages share the same data schema, i.e. the same variables or attributes. At the same time, clients may have different variables in the vertical case (also called cross-silo). This second scenario is usually applied to integrating data from different sources.
This paper presents the application of the horizontal Federated Learning approach to typical Analytical Learning tasks: dropout prediction using neural networks and unsupervised student classification. We assume a scenario in which a global analysis is required without centralizing student data stored in different educational centers. The experiments performed aim to compare whether this approach is feasible. In particular, we compare the performance of different federated versus centralized solutions. This comparison is made in terms of prediction accuracy. Our results are encouraging as they do not show a significant loss of accuracy.
The rest of the document is organized as follows. First, in Section 2 we present relevant related work, while in Section 3 we describe our application scenario. Then, in Section 4 we describe our experiments on federated dropout prediction and federated unsupervised student classification

2. Preliminary Concepts and Related Work

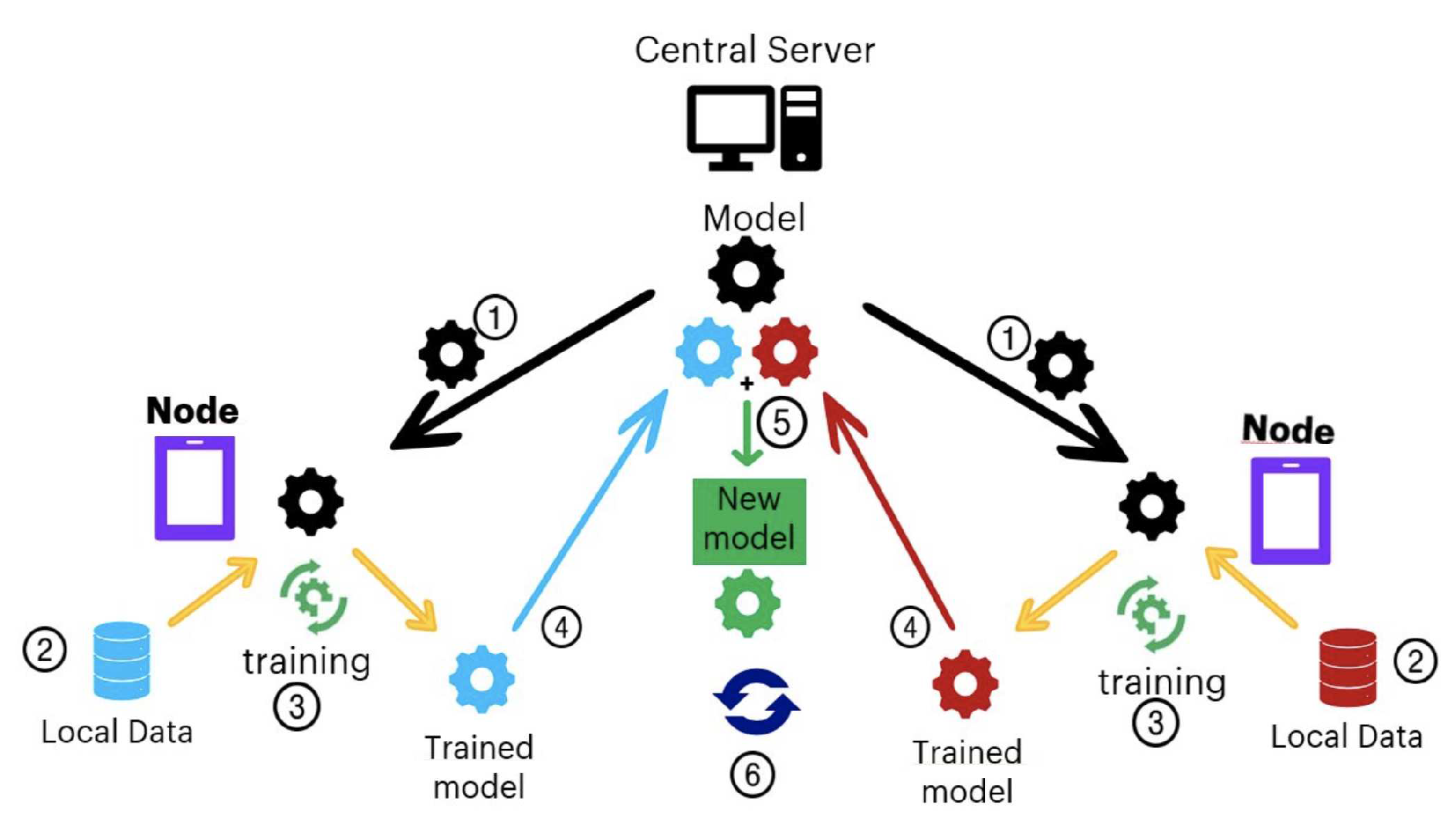
The Federated Learning approach is based on performing AA model training in a distributed manner. In this setting, the participating entities are usually classified as servers and clients, where the server is the one who orchestrates the model training. An iterative process is carried out, where in each iteration (also called round), certain clients are chosen on which several epochs of local training of the model will be performed. In these epochs, each client uses only the data it owns. Finally, the server aggregates all clients’ results to update the model’s state, which will be deployed on new clients in the next iteration, repeating the process [12] .
Figure 1 shows the steps necessary to train a model using the FL scheme. The central server sends the last model parameters to the nodes or initial parameters in case it is the first run (step 1). Then, in step 2, data is selected at each node, and each local model is trained based on the last parameters (step 3). At the end of the local training, each client communicates the updated parameters of the local model to the global model (step 4), where the updates of each model are combined, generating a new model (step 5). Finally, the process is restarted from step 1 (step 6). The model generated in step 5 can then be put into production.
Each deployment, local training on selected clients, and updating the server model cycle constitutes a round. In the case of neural networks, the global model update is typically done by the federated averaging algorithm [14]. This algorithm proposes a method to adjust the weights of the server model from the adjustment that must be made in each client’s weights.
In the federated case for neural networks, one has to consider the parameters that define the behavior of the models on the clients (epochs and batch-size), but also those specific to the federation. Specifically: the number of rounds, the number of clients chosen per round, the total number of clients, and how the data is distributed among them. The parameters mentioned above may influence, a priori, the performance of the models obtained. Therefore, one of our goals is to experiment in this direction to understand the effects of these parameters.
Our work applies horizontal Federated Learning techniques to Analytic Learning problems on data distributed across different educational institutions. This scenario presents specific characteristics. On the one hand, the number of participants is reduced, but they all share the same attributes. Therefore, there are more typical cases of application with tens of thousands of client devices, and in this sense, it is more similar to the cross-silo case where vertical FL is usually applied. On the other hand, the main difference with the vertical case is that all datasets have the same schema in our case. To summarize, the scenario we propose in this paper is a hybrid between these two situations: a low number of very stable clients sharing the same schema (the same attributes) of a potentially disjoint set of entities. A similar scenario has been extensively studied in the context of healthcare applications. [15,16,17]
The Learning Analytics problems we address have been studied before. In particular, the development of dropout prediction systems is a relevant concern in many educational communities, and different proposals have been devised in this regard. In particular, our approach is based on the work presented in [18], where the dropout detection problem is addressed centrally in the context of online learning platforms. Finally, very few papers present the application of FL in the context of LA. A framework for educational data analysis, called FEEDAN, is described in [19]. This work presents a similar approach to ours. However, it does not emphasize the evaluation of the obtained results or the discussion of how different parameters affect the convergence of the solutions.

3. Applying Federated Learning to Educational Data Analysis

Regardless of the governance and organization scheme of the education system in each country, it is widespread for there to be governmental entities above the schools. One of the main tasks carried out by these institutions is the collection and analysis of data from the education system. We see a clear opportunity to capitalize on the benefits of federated learning in this context. Education systems are usually composed of different educational centers (i.e. kindergartens, high schools, etc.). Each center involves students and teachers who interact daily in various learning activities. All the interaction in the learning process generates valuable information, both locally for the individual school and globally for the whole educational system. When these interactions occur through digital educational platforms, a potentially massive volume of data is generated that can be harnessed for various academic and pedagogical purposes.
Our goal is to provide mechanisms that allow us to study the information generated in each school globally but avoid consolidating raw data generated in each school. This scheme improves data management in terms of privacy preservation. We will evaluate the impact this has on the results of the data analysis. The first step to accomplish our goals is to define a suitable federated learning framework that is adequately adapted to the typical relationships between schools and a convenient way to evaluate the results.
As already mentioned, we can differentiate two federated learning schemes: cross-device or horizontal and cross-silo or vertical. The first relates to applications similar to the one that coined federated learning: smartphones’ predictive keyboard. Communication problems play a relevant role in this case, as devices are only sometimes available, hindering machine learning models’ training rounds. The second corresponds to the exchange of information between different institutions, which usually involves data communication between well-established data centers.
Another significant difference between federated learning schemes is the way data is arranged. In the cross-device case, we usually speak of horizontal partitioning since the data structure in the different devices is the same. Each device has its own data set, but all the sets share the same attributes or variables. The records in each data set have the same fields but for different participants. In contrast, vertical partitioning corresponds to the case where different data sets share common identifiers (e.g., information from the same users). However, each data set includes different fields in its records. A typical case of the latter could be a cross-silo scheme in which different government agencies share information on their citizens.
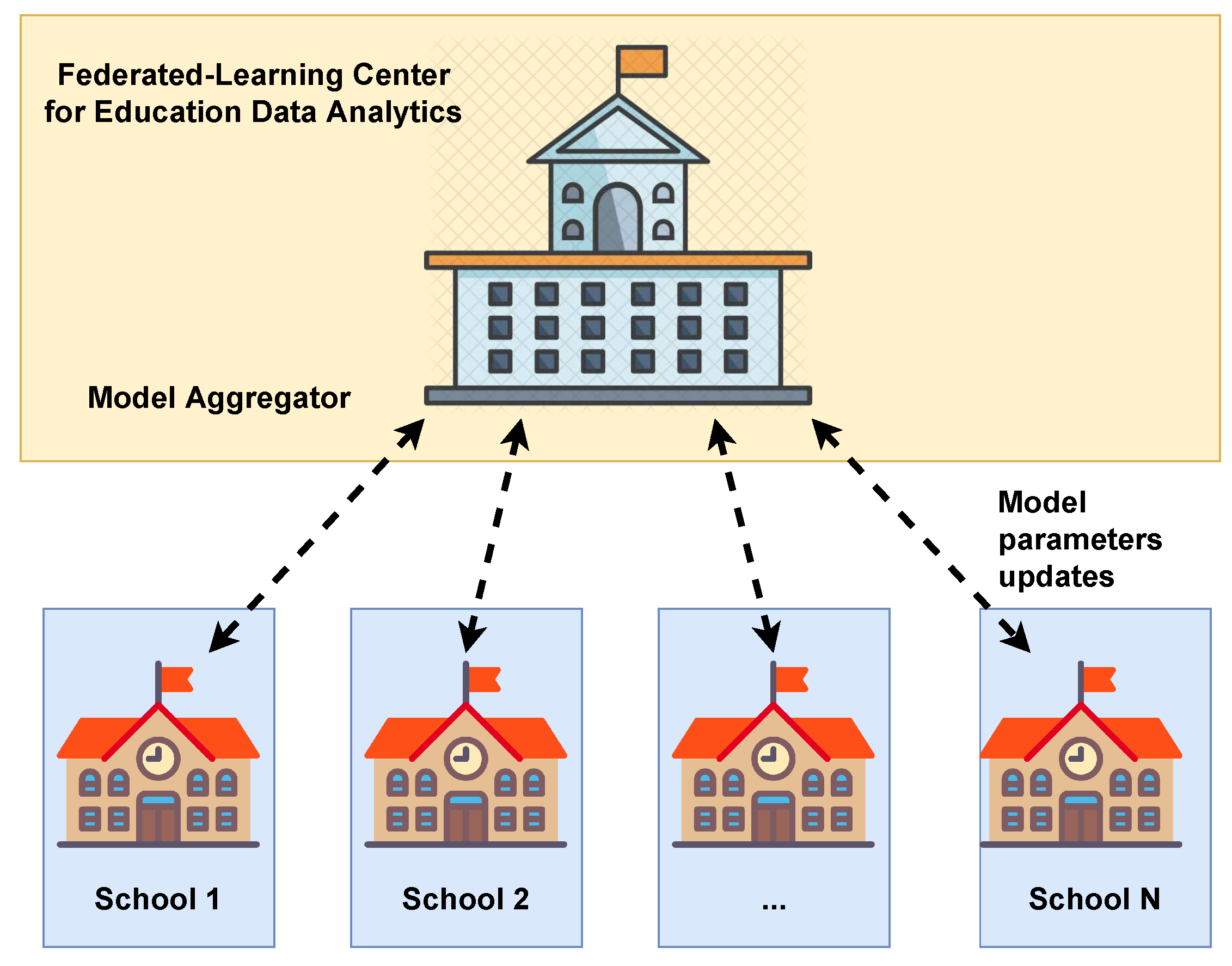
As for the education case we are interested in, it seems clear that it corresponds to a cross-silo scheme. In our proposal, each educational center manages all the information related to its teachers and students. This situation does not necessarily imply that each educational center has its on-premises data center. We could also have educational platforms in the cloud, where data is hosted on third-party servers. However, we assume that each educational center has the administration rights to all data on its teachers and students. Thus, each institution in the educational system corresponds to a silo in the proposed federated scheme.
In Figure 2, we illustrate the proposed cross-silo scheme for the education system. The goal is to take advantage of the federated learning paradigm to enable a centralized analysis of the education system data while avoiding the corresponding raw data centralization. This would enable superior governmental institutions in charge of the educational system to carry out data analysis employing machine learning models while preserving the privacy of teachers and students involved.

4. Experimental Setup and Results

As already mentioned, our work focuses on studying the applicability of Federated Learning to two different tasks: student dropout prediction and unsupervised student classification. This section presents our implementation of each task using Federated Learning frameworks and the experiments carried out in each case using a public dataset from KDDCup 2015[20].

4.1. Dataset Description

KDDCup2015 dataset contains activity logs from XuetangX, a Chinese MOOC (Massive Online Open Course) learning platform. Information is provided about the course and student activity over time. Student information includes a record of participation in assorted aspects of each course (discussion forum, quiz, media usage, etc). There are 21 defined aspects or activities, and their availability varies across courses which are identified by course_id. Also, a student ID is provided and can be used to link records for a given student across courses. This can be used to calculate metrics such as student-level completion rates across courses. The logs have 42M individual entries and have a total size of approximately 2.1GB. There are approximately 77000 distinct students and 247 courses.
Our data preparation tasks transform the individual entries of the raw activity logs, aggregating data for each activity, course_id, and username and counting the number of entries for each group. Final is a 225642 × 21 matrix where each entry corresponds to a distinct pair ( c o u r s e _ i d , u s e r n a m e ) ) , which is also identified by a e n r o l l _ i d number. The features are the number of activities performed by e n r o l l _ i d . Data preparation code is available at our repository [21].

4.2. Task 1: Student Dropout Prediction

As mentioned in Section 2, we use the approach presented in [18] to predict student dropout. For every e n r o l l _ i d on the dataset, it is known whether the student dropped out of the course. We then use these labels to train and test a deep-learning model that predicts dropout. We use a DNN architecture consisting of the input layer, 3 hidden layers of size 100, and an output layer of 1 neuron with a sigmoid as an activation function. We used Adam optimizer [22] and binary cross-entropy as a loss function.
The experiments have two main goals: 1) to assert whether the federated models can reach the accuracy of the centralized setting or not, and 2) to evaluate the influence of the above-mentioned parameters on the accuracy and total training time of the federated models. Firstly, a centralized solution is deployed using Tensorflow, which works as a baseline for the federated models. For federating, we use the Federated Averaging algorithm [14] implemented in Tensorflow Federated. Notice that in addition to the usual local parameters of each client, such as the epochs and the batch size, in the federated version, we need to deal with additional parameters, such as the number of training rounds per client, the number of clients chosen in each round, the total number of clients and how the data is distributed among them.

4.2.1. Experiment Execution

A centralized model is trained for 20 epochs. The number of epochs was chosen empirically; we searched for a number large enough to allow for parameter tuning of the federated approach that also maintained an acceptable level of accuracy without much overfitting. We sample 70% of all student usernames and collect their data to build the training dataset, using the remaining to build the test set. The model is evaluated using 50 different random splits of the students, achieving a mean accuracy of 81.7% and a mean running time of 105 seconds.
In the federated model, each client comprises samples of 1,000 students representing one school, totaling 77 schools (clients). Clients do not share students but could share courses. The training-evaluation process consists of 50 different random splits in a 70/30 proportion. Using 1000 students per client, that 70% of the data turns into 54 different clients. The remaining data is used for testing; this is done in a centralized manner where a model with the same architecture is initialized with weights from the federated model at the end of each round.
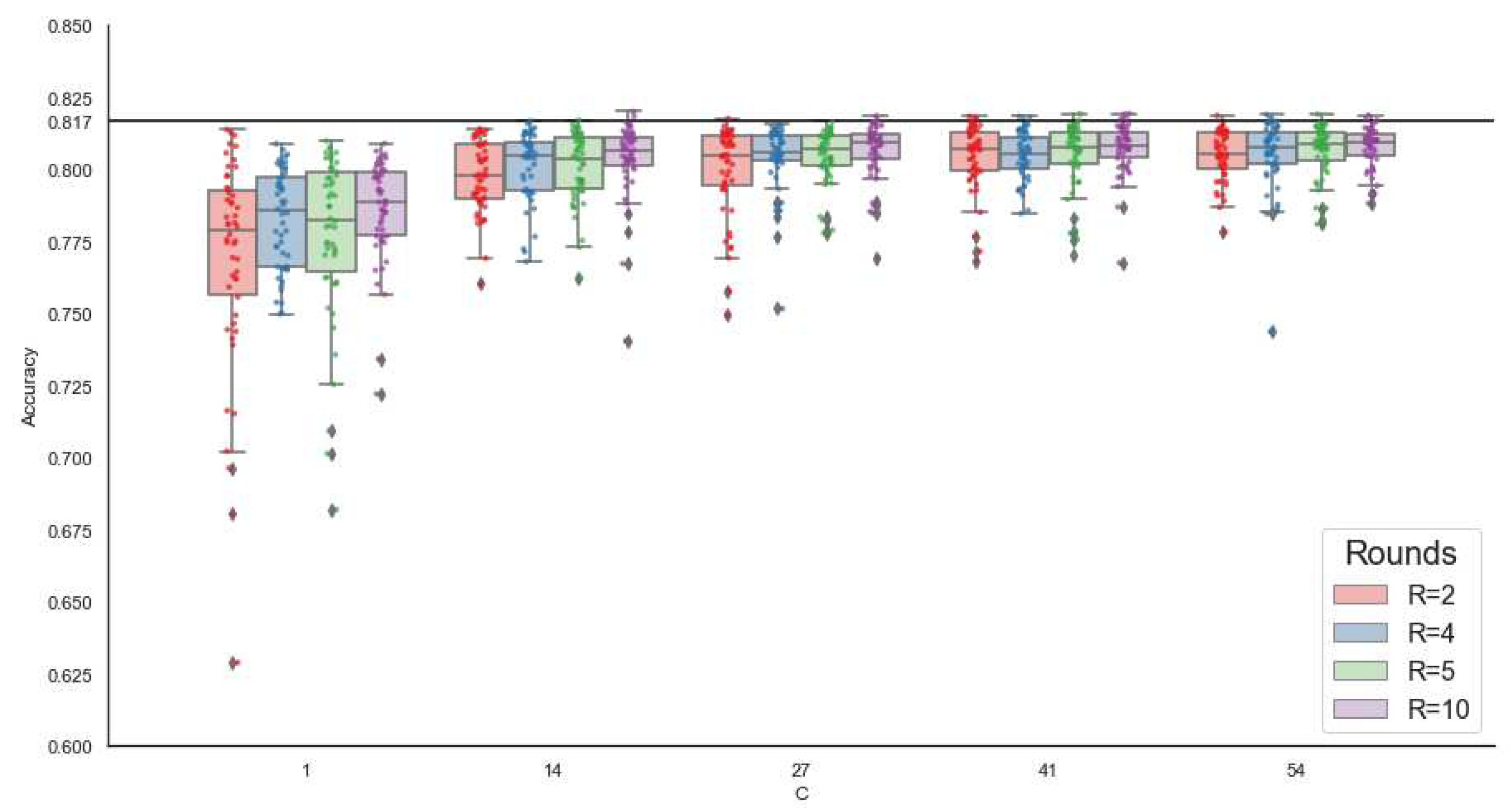
The process is repeated in each of the experiments, where we try different combinations on the number of rounds (R) and local epochs (E), leaving a fixed number of total epochs R × E = 20 , and varying the number of clients per round using: 1 client (minimum availability of clients), 14 clients ( 25% availability), 27 ( 50%), 43 ( 75%) and 54 (maximum availability). The results in terms of accuracy are shown in Figure 3.
Increasing the number of clients from 1 to 14 causes a leap of 2%-3% on the mean accuracy, while additional increments in the number of clients only cause a marginal increase in the mean accuracy but also produce a rise in the execution time (see Figure 3 in Appendix). If the number of clients is fixed, we can see that favoring the number of rounds R over local epochs E tends to yield a better accuracy overall (boxes in each group go up), but again this will cause an increment in time. It is also worth noting that variance decreases as we increase the clients and the rounds.
Performance in this federated setting is close to the one found in the centralized model, with a mean accuracy larger than 76% in every experiment (which goes up to 80% when excluding the experiments with 1 client per round), a top accuracy of 82% (reached on a run with 14 clients and 10 rounds) and with around 63% of all individual runs, across all experiments, having more than 80% accuracy. However, some executions still have relatively low accuracy.
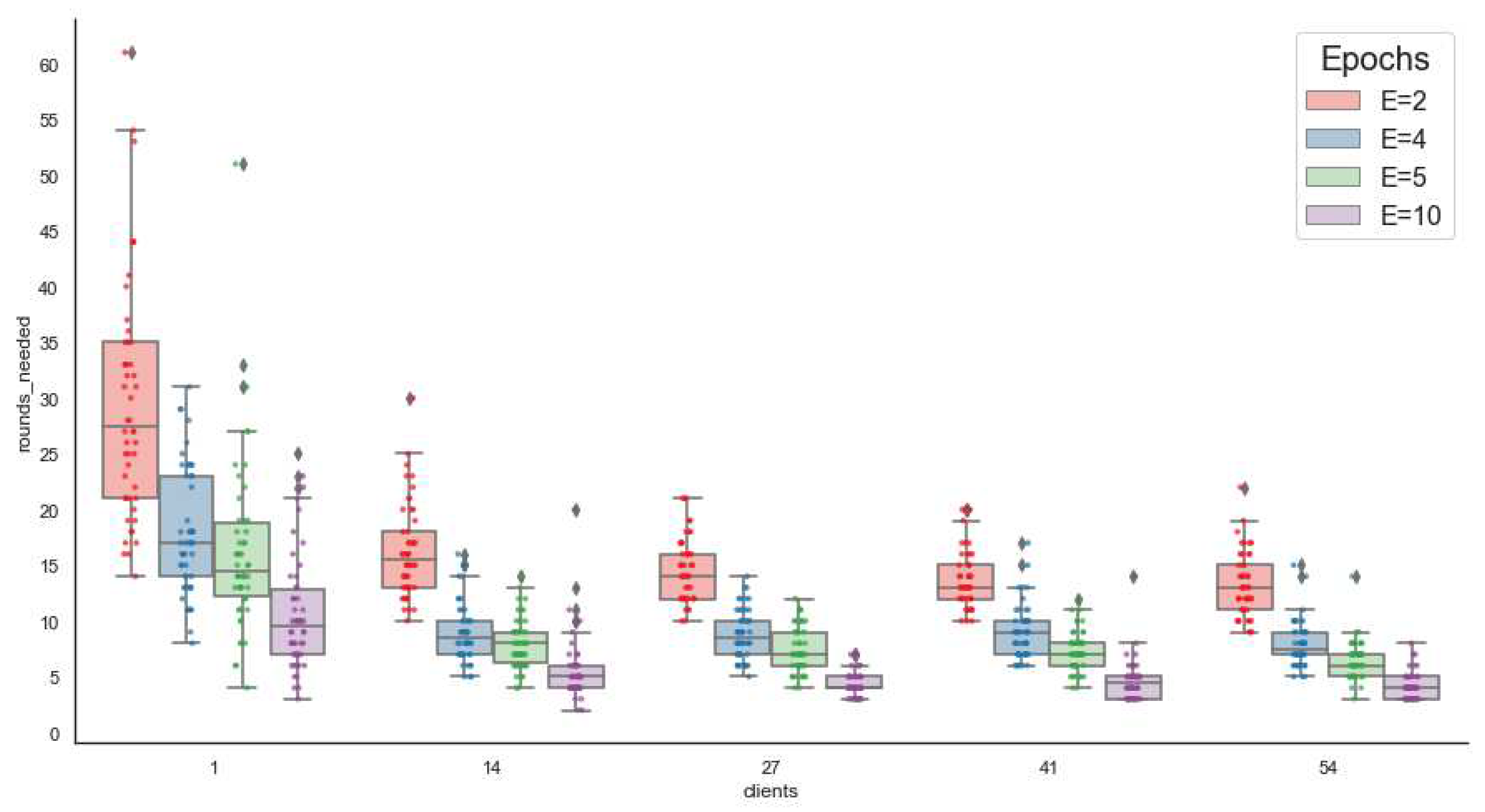
We question whether it is possible to consistently reach the results of the centralized environment. Therefore we repeated the experiments running as many rounds as needed to reach 81.7% accuracy. This evaluation method is inspired by [14]. Figure 4 shows our results; we can see that it is possible to reach the accuracy of the centralized model in every case, with the caveat that many rounds may be needed. The maximum number of rounds is needed when training with one client per round, and the resulting accuracy presents a large variance. From 14 clients onward, the results do not vary significantly; that is to say, increasing the number of clients does not necessarily improve convergence. Increasing E lowers the average R necessary to reach our baseline accuracy (81.7% ) in every case. However, there is no 1:1 inverse relationship: for instance, with 14 clients, if E=2 an average of 16 rounds is needed, but if E=10, we need 6 rounds, that is an x5 increase ratio in E but only an x2.6 decrease ratio on R.

4.2.2. Further Experiments: Homogeneous vs. Heterogeneous Data Distribution

The experiments described in Section 4.2.1 test the interaction between different parameters and how they affect performance, given a fixed experimental setup. In this section, we will select the parameters but vary the setups. Basically, we will compare three training schemes: 1) each institution trains a model using only its local data, 2) a federated setting, and 3) a centralized approach with training taking place on collected data from all institutions. In each case, testing is performed locally on each institution’s held-out test data. We also vary the data distribution hypothesis using (a) a homogeneous data distribution (client data is chosen randomly from the initial dataset) and (b) a heterogenous one where the data distribution criteria is based on the dropout rate.
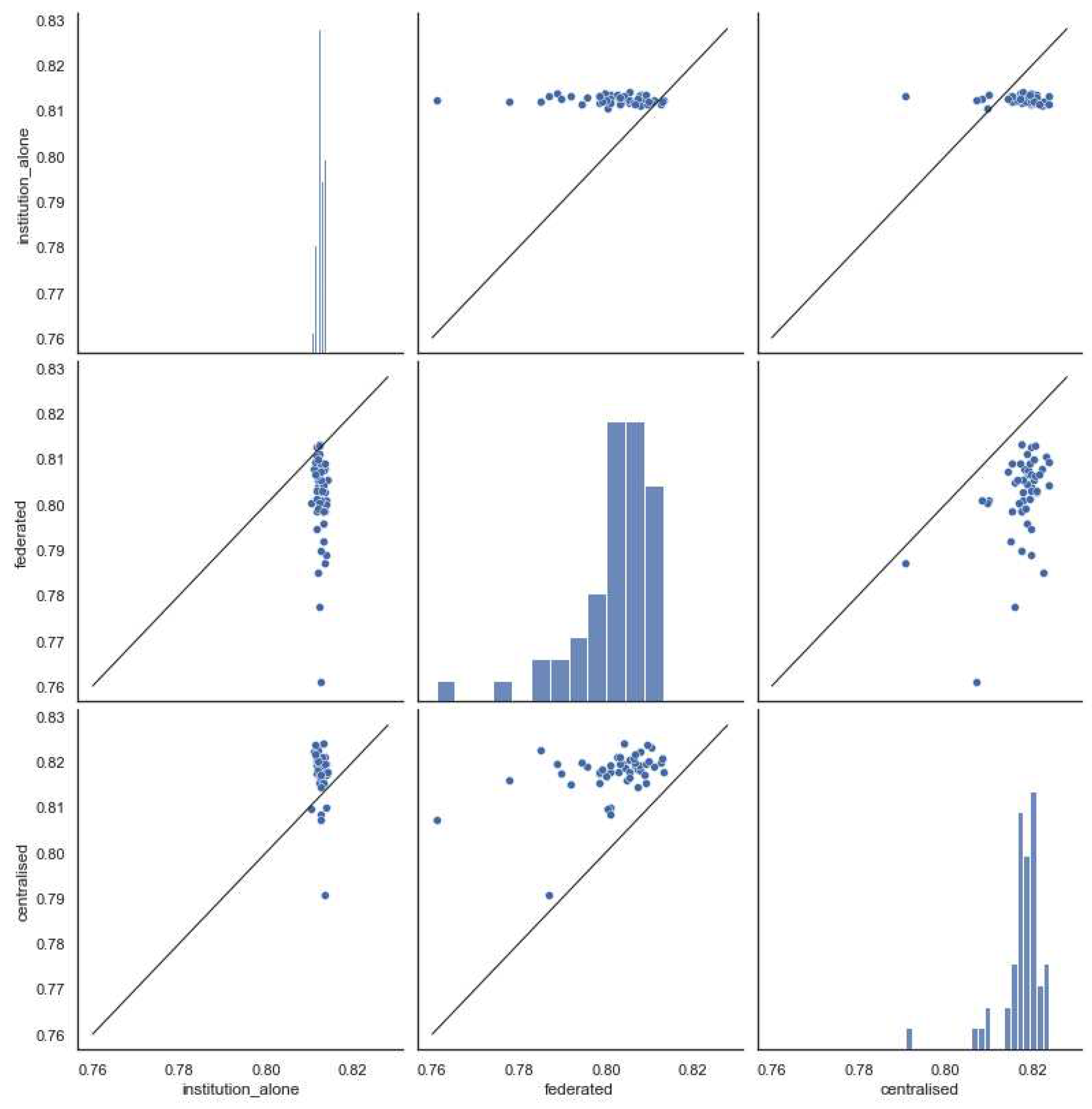
Figure 5 shows the results of 50 independent runs using the homogeneous data distribution assumption where students are randomly distributed across clients. Each point in this figure represents the average accuracy achieved on the test data across all clients.
If we focus on the diagonal of the histograms, we can observe that the results have a higher variance in the federated version than in the other schemes. The cases in which each institution trains separately have better results on average than in the federated version (center-left and top-center). However, they tend to perform worse than in a centralized scheme (bottom-left and top-right). Finally, the federated version performs worse than the centralized model in general (bottom-center and center-right). Under the hypothesis of homogeneous data distribution, federating the training does not increase accuracy.
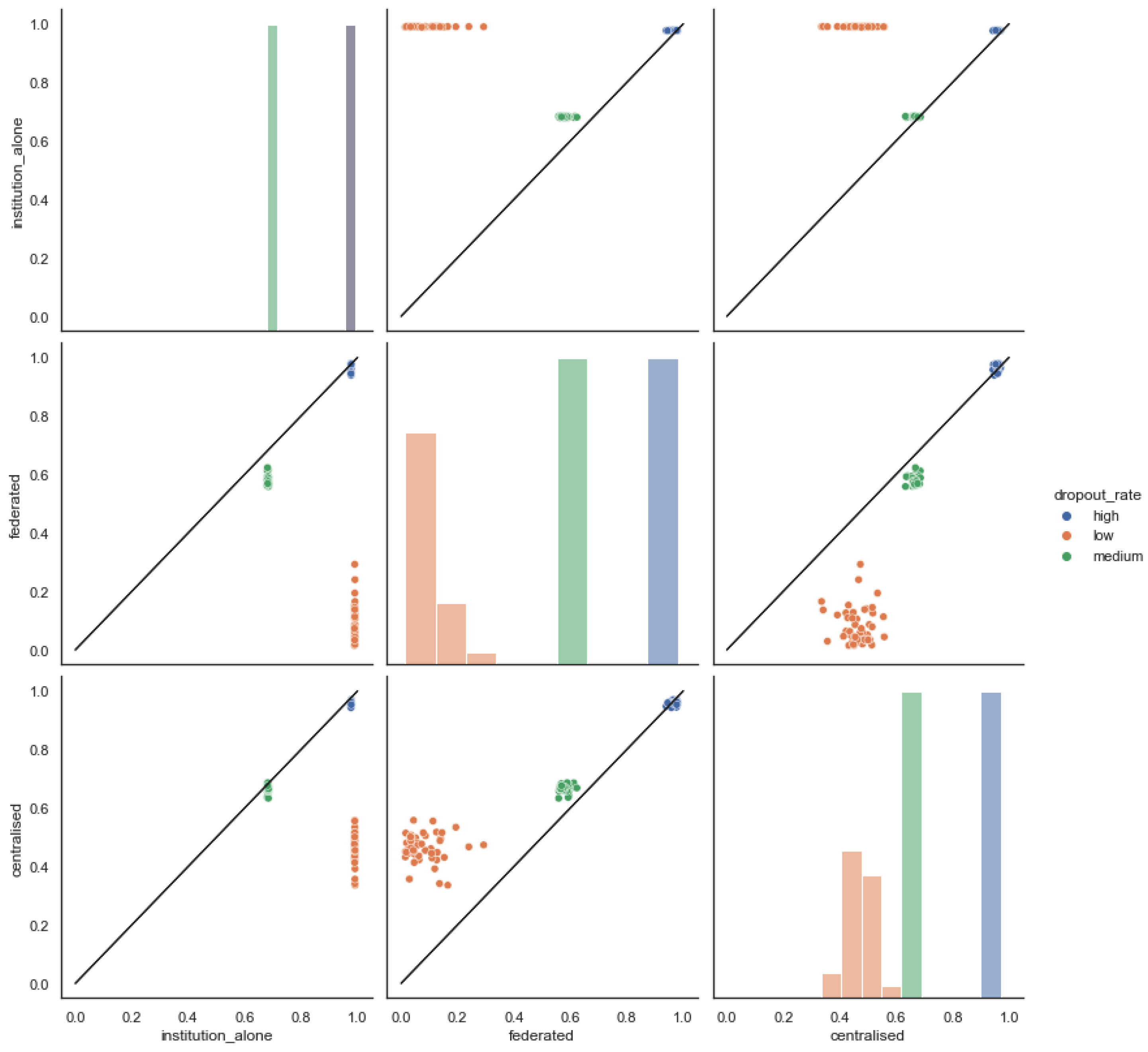
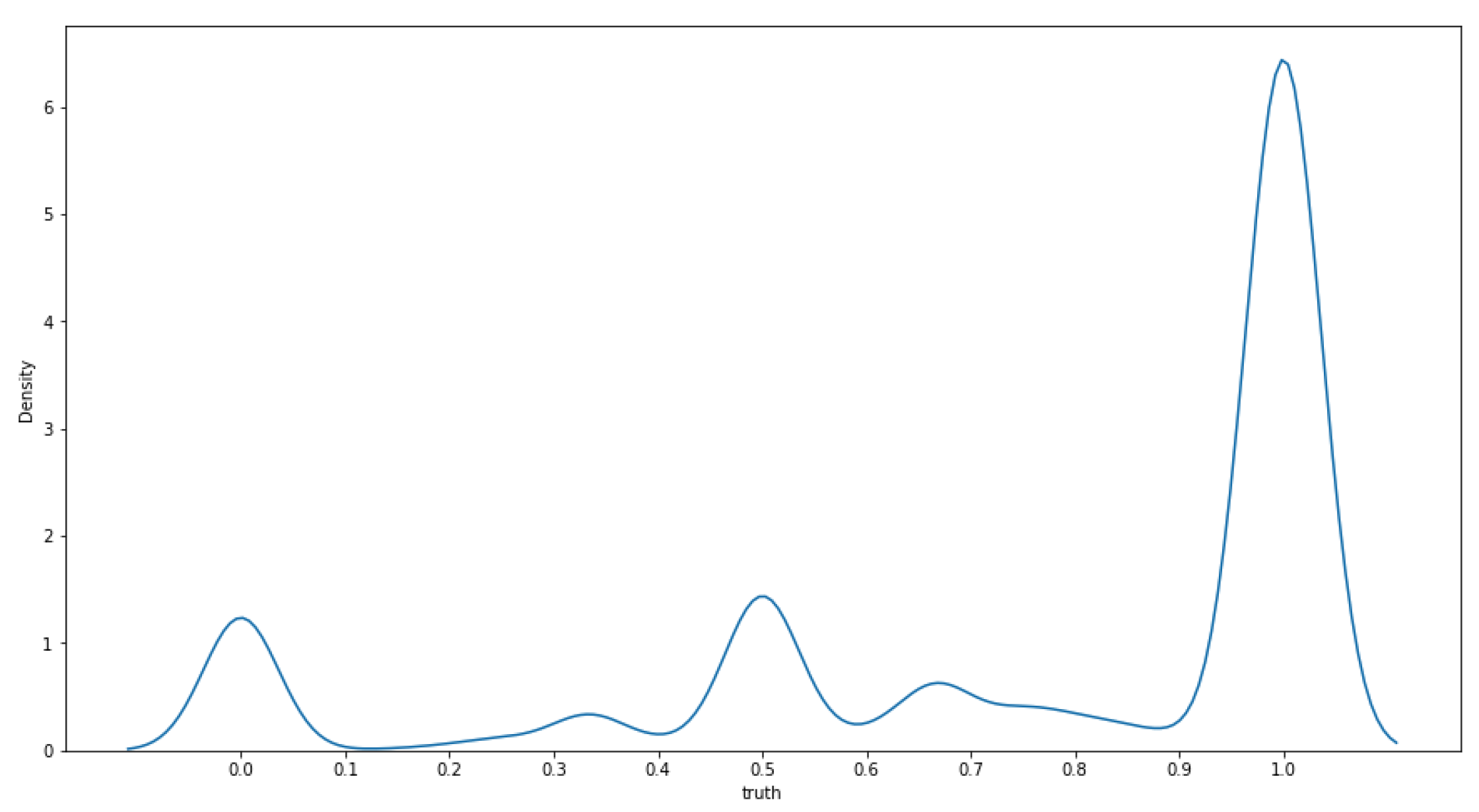
Since it’s interesting to study the effect of data distribution on the model’s performance, we apply other criteria to allocate data across clients. In this case, we study the dropout rate distribution considering the whole dataset (see Figure 6) and use it to split the student population across institutions according to the dropout rate of each student. Table 1 presents the defined categories and the number of students per category.
Preprints 66852 g005
Figure 5. Mean accuracy comparison after 50 independent runs using three training schemes: institutions alone, federated, and centralized.
Figure 5. Mean accuracy comparison after 50 independent runs using three training schemes: institutions alone, federated, and centralized.
Preprints 66852 g005
Figure 7 shows the mean accuracy after 50 independent runs distributing data according to dropout rate (each client institutions have a fixed number of students = 1000). Since fewer students have a low dropout rate (11.32% of the whole population), they are underrepresented in the total dataset, which probably leads to poor performance in the federated training case. Accordingly, notice that few client institutions are formed in this category (only nine). In the case of client institutions with a medium dropout rate, the models trained using the federated and centralized approaches have similar performance. We hypothesize that these institutions benefit from the use of more data. Finally, given that most students have a high dropout rate, good results are obtained for the centralized and federated versions in the cases of client institutions belonging to this dropout category.
We can conclude that if the institution belongs to a "favored class", i.e., those for which there is more data, then there is not much difference between using one scheme or another. If the institution has a random distribution, it is better to use approaches that leverage data from other clients, such as centralized or federated schemes. In this case, there is no evidence of performance loss using federation. To complete this analysis, if the institution belongs to one of the categories with less data, it is more convenient to use a customized model trained only with its data.
Preprints 66852 g007
Figure 7. Mean accuracy comparison after 50 independent runs using three training schemes: institutions alone, federated, and centralized. Dropout rate varies between clients according to the categories defined in Table 1.
Figure 7. Mean accuracy comparison after 50 independent runs using three training schemes: institutions alone, federated, and centralized. Dropout rate varies between clients according to the categories defined in Table 1.
Preprints 66852 g007

4.3. Task 2: Unsupervised Student Classification

Our second task corresponds to unsupervised student classification. This task can be accomplished in a centralized setting using the well-known k-means algorithm. There are also distributed versions of this algorithm. The Federated Learning version of k-means combines ideas from the distributed algorithm with the concept of only using a fraction of the clients on each iteration [23]. Our implementation of federated k-means is an adaptation of the ideas presented in [24].
It is necessary to comment on how we evaluated the experimental results in this case. To compare the performance of clustering algorithms, it is not feasible to follow the same approach presented in Section 4.2, where the accuracy metric was used to compare the performance of different models. Clustering algorithms are used to group data points based on the similarities they share between them. But there is no single criterion for determining what is considered a good result. Different assumptions can be made when defining what makes different points similar, and for each assumption, different clusters will be obtained, each equally valid. Which assumptions and final clusters are used will depend on the interests, and even then, it is usually necessary to analyze the clusters obtained and interpret the results.
Since we can not simply compare accuracies obtained with the centralized and federated clustering algorithms, we will compare the clusters obtained with each approach using the Jaccard Similarity Index. The higher the value, the more similar the results are to each other. Using this index, the similarity between the results obtained is computed without any value judgment on the particular solutions. We assume that if they are sufficiently similar, they will allow us to reach the same conclusions and similarly interpret them, regardless of whether their implementation is centralized or federated.
Thus, the experiment will not focus on the usefulness of the k-means algorithm in general or for this task but on whether centralized and federated k-means can be used interchangeably, providing the same information as the centralized one but with all the privacy-preserving advantages of the federated version.

Experimental Setup

The objective of the experiment is to compare the two approaches. We start from the same initial centroids in each case. Then, in the centralized version, we execute the algorithm until all the centroids move less than a specific value ϵ . For the federated versions, we run some defined number of rounds r, and we calculate the Jaccard index using the final centralized clusters and the federated ones in each round. This way, we get the evolution of the Jaccard score to tell if the clusters are getting similar to the final centralized ones.
The number of clusters k will be fixed at 3 for the experiment. For the centralized version, we use a stop condition of ϵ = 0.001 , and execute 4 federated versions with 5, 10, 20 & 40 clients per round for 100 rounds. Figure 8 shows the results of this experiment. As expected, the versions that used more clients per round tend to have greater scores. Nevertheless, after 10 rounds, all versions of the federated k-means have a Jaccard score greater than 0.96, even the one that used only 5 clients.

5. Discussion

The results show that increasing the number of clients and favoring more rounds results in higher accuracy. Concentrating resources on more rounds than local epochs of clients without network constraints brings better results. If time and connectivity are not an issue, using as many clients as possible per round is also optimal. However, the gain is not substantial and reasonable results could be achieved using much less data (as in our experiment, using 25% and 50% of all clients). FL has the potential to achieve the same results as traditional ML in real-world settings, as it does in our experiments. However, testing in a non-experimental setting is needed to confirm this.
However, it is crucial to remember that this is a simulation, and we have yet to consider the problems involved in transferring information over the network in the real world. For example, when connectivity is an issue (such as in institutions in rural areas), it may only be possible to use some clients simultaneously in the same round. Latency may also be a factor to consider. For example, an increase in communication time could make it prohibitive to run many rounds. In these cases, it would be advisable to favor local epochs, even when the experiment in Figure 2 showed that it is not optimal in terms of accuracy. It is also worth noting that we have yet to consider privacy-preserving schemes (e.x. Differential Privacy [25]) in our experiments.
It is essential to remember that all experiments are based on MOOCs data; this should be kept in mind when extrapolating the results to the context of a physical institution. Some variables have an equivalent (number of courses taken, for example), but others certainly differ.
Finally, we have focused on assessing whether a model can yield similar results in federated and centralized training settings. However, we have yet to explore the extent to which each client benefits from the federation. The question is: does the institution benefit from the patterns learned by the model at other institutions, or would it be better off simply training a centralized model of its own? The answer to this question varies and depends mainly on the amount of data the institution possesses. For example, a model trained on a single institution would work well with previously unseen data from the same location but would not adapt to changes in data distribution. The latter would be when new students with very different and unseen behavior enroll at the institution). In contrast, a federated model enriched with data from several other institutions might be more robust. An experiment that artificially introduces drift into the data could shed light on this issue.

6. Conclusion

In this paper, we evaluate the application of Federated Learning for Learning Analytics, specifically for dropout prediction and student clustering tasks. In both cases, federated solutions were implemented and tested. In addition, the influence of parameters such as the number of clients, data distribution, batch size, and the number of epochs on the results obtained was evaluated. Although more exhaustive evaluations of the approach are still to be carried out, the results are auspicious. Our future work includes using real data and studying the possible repercussions that enabling mechanisms such as Differential Privacy could have. In all cases, interesting conclusions are reached, which demonstrate the feasibility of this approach and allow for envisioning its application at institutional and industrial levels in many scenarios.

Author Contributions

Conceptualization, Paola Bermolen Germán Capdehourat, Lorena Etcheverry, María Inés Fariello ; software, Christian Fachola, Agustín Tornaria; validation, Germán Capdehourat,María Inés Fariello; investigation, Paola Bermolen Germán Capdehourat, Lorena Etcheverry, María Inés Fariello, Christian Fachola, Agustín Tornaria ; writing—original draft preparation, Paola Bermolen Germán Capdehourat, Lorena Etcheverry, María Inés Fariello; writing—review and editing, Lorena Etcheverry; visualization, María Inés Fariello; supervision, Paola Bermolen Germán Capdehourat, Lorena Etcheverry, María Inés Fariello; . All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Agencia Nacional de Innovación e Investigación (ANII) Uruguay, Grant Number FMV_3_2020_1_162910.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Drachsler, H.; Kismihók, G.; Chen, W.; Hoel, T.; Berg, A.; Cooper, A.; Scheffel, M.; Ferguson, R. Ethical and privacy issues in the design of learning analytics applications. ACM International Conference Proceeding Series 2016, 25-29-Apri, 492–493. [CrossRef]
  2. Banihashem, S.K.; Aliabadi, K.; Pourroostaei Ardakani, S.; Delaver, A.; Nili Ahmadabadi, M. Learning Analytics: A Systematic Literature Review. Interdisciplinary Journal of Virtual Learning in Medical Sciences 2018, 9, 63024. [Google Scholar] [CrossRef]
  3. Mangaroska, K.; Giannakos, M. Learning Analytics for Learning Design: A Systematic Literature Review of Analytics-Driven Design to Enhance Learning. IEEE Transactions on Learning Technologies 2019, 12, 516–534. [Google Scholar] [CrossRef]
  4. Sweeney, L. k-anonymity: A model for protecting privacy. International journal of uncertainty, fuzziness and knowledge-based systems 2002, 10, 557–570. [Google Scholar] [CrossRef]
  5. Khalil, M.; Ebner, M. De-Identification in Learning Analytics. Journal of Learning Analytics 2016, 3, 129–138. [Google Scholar] [CrossRef]
  6. Kyritsi, K.H.; Zorkadis, V.; Stavropoulos, E.C.; Verykios, V.S. The pursuit of patterns in educational data mining as a threat to student privacy. Journal of Interactive Media in Education 2019, 2019, 1–10. [Google Scholar] [CrossRef]
  7. Dwork, C. Differential privacy: A survey of results. In Proceedings of the International conference on theory and applications of models of computation. Springer, 2008, pp. 1–19.
  8. Gursoy, M.E.; Inan, A.; Nergiz, M.E.; Saygin, Y. Privacy-Preserving Learning Analytics: Challenges and Techniques. IEEE Transactions on Learning Technologies 2017, 10, 68–81. [Google Scholar] [CrossRef]
  9. Konečný, J.; McMahan, H.B.; Ramage, D.; Richtarik, P. Federated Optimization: Distributed Machine Learning for On-Device Intelligence, 2016.
  10. Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Processing Magazine 2020, 37, 50–60. [Google Scholar] [CrossRef]
  11. Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10. [Google Scholar] [CrossRef]
  12. Kairouz, P.; McMahan, B.; Song, S.; Thakkar, O.; Thakurta, A.; Xu, Z. Practical and Private (Deep) Learning without Sampling or Shuffling 2021. pp. 1–34.
  13. Zaman, F. Instilling Responsible and Reliable AI Development with Federated Learning. https://medium.com/accenture-the-dock/instilling-responsible-and-reliable-ai-development-with-federated-learning-d23c366c5efd, 2020.
  14. McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial intelligence and statistics. PMLR, 2017, pp. 1273–1282.
  15. Hakak, S.; Ray, S.; Khan, W.Z.; Scheme, E. A framework for edge-assisted healthcare data analytics using federated learning. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data). IEEE, 2020, pp. 3423–3427.
  16. Nguyen, D.C.; Pham, Q.V.; Pathirana, P.N.; Ding, M.; Seneviratne, A.; Lin, Z.; Dobre, O.; Hwang, W.J. Federated learning for smart healthcare: A survey. ACM Computing Surveys (CSUR) 2022, 55, 1–37. [Google Scholar] [CrossRef]
  17. Rieke, N.; Hancox, J.; Li, W.; Milletari, F.; Roth, H.R.; Albarqouni, S.; Bakas, S.; Galtier, M.N.; Landman, B.A.; Maier-Hein, K.; et al. The future of digital health with federated learning. NPJ digital medicine 2020, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
  18. Feng, W.; Tang, J.; Liu, T.X. Understanding dropouts in MOOCs. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, 2019, Vol. 33, pp. 517–524.
  19. Guo, S.; Zeng, D. Pedagogical Data Federation toward Education 4.0. In Proceedings of the Proceedings of the 6th International Conference on Frontiers of Educational Technologies; ICFET ’20; Association for Computing Machinery: New York, NY, USA, 2020; pp. 51–55. [Google Scholar] [CrossRef]
  20. KDD. KDDCup. http://moocdata.cn/challenges/kdd-cup-2015, 2015.
  21. FLEA. FLEA project public repository. https://gitlab.fing.edu.uy/flea/flea, 2022.
  22. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014; arXiv:1412.6980. [Google Scholar]
  23. Kumar, H.H.; Karthik, V.; Nair, M.K. Federated k-means clustering: A novel edge AI based approach for privacy preservation. In Proceedings of the 2020 IEEE International Conference on Cloud Computing in Emerging Markets (CCEM). IEEE, 2020, pp. 52–56.
  24. Oskar, J. Triebe, R.R. Federated K-Means:clustering algorithm and proof of concept 2019.
  25. Liu, B.; Ding, M.; Shaham, S.; Rahayu, W.; Farokhi, F.; Lin, Z. When Machine Learning Meets Privacy: A Survey and Outlook. ACM Computing Surveys 2021, 54. [Google Scholar] [CrossRef]
Preprints 66852 g001
Figure 1. Federated Learning Architecture. Source: [13].
Figure 1. Federated Learning Architecture. Source: [13].
Preprints 66852 g001
Preprints 66852 g002
Figure 2. Our proposal for a cross-silo federated learning scheme for centralized data analysis of the educational system.
Figure 2. Our proposal for a cross-silo federated learning scheme for centralized data analysis of the educational system.
Preprints 66852 g002
Preprints 66852 g003
Figure 3. Accuracy results of dropout prediction (Federated version), averaging over 50 random executions with different amount of clients per round (C), number of rounds (R) and local epochs of clients (E) where R × E = 20 . The black line marks accuracy averaged by the centralized model.
Figure 3. Accuracy results of dropout prediction (Federated version), averaging over 50 random executions with different amount of clients per round (C), number of rounds (R) and local epochs of clients (E) where R × E = 20 . The black line marks accuracy averaged by the centralized model.
Preprints 66852 g003
Preprints 66852 g004
Figure 4. Number or rounds R needed to reach the centralized accuracy baseline (81.7%), averaging over 50 random executions with different amounts of clients per round (C) and local epochs at clients (E).
Figure 4. Number or rounds R needed to reach the centralized accuracy baseline (81.7%), averaging over 50 random executions with different amounts of clients per round (C) and local epochs at clients (E).
Preprints 66852 g004
Preprints 66852 g006
Figure 6. Dropout rate distribution over all students.
Figure 6. Dropout rate distribution over all students.
Preprints 66852 g006
Preprints 66852 g008
Figure 8. Jaccard score evolution for federated kmeans with 5, 10, 20 & 40 clients available per round and centralised kmeans clusters for ϵ = 0.001 .
Figure 8. Jaccard score evolution for federated kmeans with 5, 10, 20 & 40 clients available per round and centralised kmeans clusters for ϵ = 0.001 .
Preprints 66852 g008
Table 1. Student distribution categories, according to dropout rate.
Table 1. Student distribution categories, according to dropout rate.
Students with low dropout rate (lower than 0.2): 8723 11.32%
Students with medium dropout rate (between 0.2 and 0.8): 20567 26.68%
Students with high dropout rate (higher than 0.8): 46687 60.57%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated