Benveniste’s Experiments and the So-Called “Water Memory” Phenomenon: an Example of Serendipity?

Preprint

Hypothesis

Benveniste’s Experiments and the So-Called “Water Memory” Phenomenon: an Example of Serendipity?

Altmetrics

Downloads

363

Views

233

Comments

Francis BEAUVAIS^*

This version is not peer-reviewed

Submitted:

06 January 2023

Posted:

09 January 2023

Read the latest preprint version here

Alerts

Abstract

Benveniste’s experiments – known in the lay press as the “water memory” phenomenon – are generally considered to be a closed case. However, the amount of data generated by twenty years of well-conducted experiments prevents closing the file so simply. An issue, which has been little highlighted so far, merits to be emphasized. Indeed, if Benveniste failed to persuade his peers of the value of his experiments, it was mainly because of a stumbling block, namely the difficulty of convincingly proving the causal relationship between the supposed cause (“informed water”) and the experimental outcomes in different biological models. To progress in the understanding of this phenomenon, we abandon the idea of any role of water in these experiments (“water memory” and its avatars). In other words, we assume that “controls” and “tests” that were evaluated were all physically identical; only their respective designations (labels) differentiated them. Since we state that there is no causal link between labels (“controls” vs. “tests”) and corresponding states of the biological system (no change vs. change), these variables are independent. Therefore, the key question is: “Is it possible to observe a correlation between independent variables that mimics a causal relationship but is itself not causal?” In this article, we show how simple considerations based on probability theory lead to describe non-classical correlations involving the experimenter. This probabilistic modelling allows to propose an alternative explanation to Benveniste’s experiments where water plays no role and where the place of the experimenter is central.

Keywords:

Subject: Medicine and Pharmacology - Other

1. Introduction

Serendipity has been defined as “the faculty or phenomenon of finding valuable or agreeable things not sought for” according to Merriam-Webster Dictionary [1]. This word was coined in 1754 by Horace Walpole as a reference to the fairy tale “The three princes of Serendip” from Cristoforo Armeno. The heroes of this story discovered by “chance and sagacity” things they were not looking for. The history of science is full of such chance discoveries as X-rays, radioactivity or penicillin. In this article, we will see why Benveniste’s experiments – also known in the lay press as the “water memory” phenomenon – could be a new example of serendipity.

The purpose of this article is not to tell again the entire story with all the details of the scientific debate and controversies that can be found elsewhere. A complete and systematic account of this case has been published by the author in a freely available text, both in a French version [2] and in its English translation [3]. Other points of views can be found in several books or articles [4–12]. The present article is hoped to be an element to reach a successful conclusion and, more importantly, to open new horizons.

It is important to remember that the experiments we are talking about were spread over almost 20 years (from 1983 to Benveniste’s death in 2003). This saga is too often reduced to the famous controversy with the journal Nature in 1988 [13,14]. Moreover, before this controversy, Benveniste had a position in the scientific community that was far from marginal. His research unit was affiliated with INSERM, the French national medical research institution, and Benveniste himself was recognized internationally. The original idea to test extreme dilutions was not from Benveniste himself who, as a good Cartesian, was rather reluctant initially to test homeopathic medicines, but was nevertheless open to countercurrent ideas. Indeed, homeopathy is an alternative medicine which, to put it mildly, is based on ideas from another time and it has never proven its efficacy. B.

Poitevin, who was a thesis student at that time, was also involved in the practice of homeopathy and proposed to Benveniste collaborations with the homeopathy industry [3,7]. Thus, the famous “Benveniste’s experiments” were initially nothing more than research contracts with homeopathy firms aimed to evaluate some homeopathic medications. These studies were performed in the context of allergy and inflammation which was the area of expertise of Benveniste’s team. It is important to notice that Benveniste’s team was not the first to test homeopathic medications. What was probably new was that a renowned laboratory from a public research institution managed such a research topic and that Benveniste did not hesitate to promote the high-dilution issue into the academic debate.

In the former experiments, high dilutions of various preparations were tested on human basophils which are cells involved in allergic disorders (years 1983–1991). Some of the diluted compounds were used in homeopathic practice, but others were not homeopathic medications (antibodies, for example). The hypothesis behind these first experiments performed in the 1980′ was that a drug or a biologically-active compound could apparently continue to manifest some activity after being highly diluted. Obtaining a specific effect on a biological model with high dilutions was theoretically impossible given physical chemistry laws. To get an idea, less one molecule of antibody was theoretically present in the assay after about fifteen serial ten-fold dilutions of the initial sample. Therefore, the first positive results were received with surprise and skepticism in the laboratory, including Benveniste himself.

However, the basophil model needed fastidious and time-consuming counting under a microscope by trained experimenters and required a number of tricks to avoid pitfalls. In addition, the controversy with the journal Nature prompted Benveniste to consider other biological models. A physiological model already in use in the laboratory, namely the isolated rodent heart, appeared to be promising (years 1992–1998). Changes in the state of this biological model (coronary flow variations) could be followed live by observers and this new model was therefore more convincing and demonstrative than the basophil model. The results with high dilutions of various compounds were confirmed using the isolated rodent heart model [3].

After high dilutions, Benveniste developed from the year 1992 different devices based on electromagnetism and made of electric coils and electronic amplifiers which were supposed to “transfer the activity” of biologically-active molecules directly to water samples without the dilution process [3,15–20]. The “transmission” experiments were also supposed to avoid contaminations that could be responsible for the observed effects. In a further refinement, Benveniste obtained in 1995 experimental data suggesting that the “activity” issued from a biologically-active solution could be captured and stored in a computer memory. The electric current that passed through a coil surrounding a biologically-active sample was supposed to be modulated by an electromagnetic emission from the sample and was digitized before being stored in a computer file. Then the “biological activity” recorded in the file could be diffused via an electric coil to a water sample initially devoid of any “information”. In another variation of this device, the diffusion of the “biological activity” was done directly to the biological system via the electric coil without intermediate water sample. Benveniste coined at this occasion the term of “digital biology”. These new developments and his new ideas about a future breakthrough in biology and medicine thanks to “digital biology” further isolated Benveniste from the scientific community and caused him to lose his early supports.

The isolated heart rodent model, however, appeared to be difficult to export into other laboratories because few teams had the experience to use it routinely. Benveniste then developed experiments based on plasma coagulation that could be easily performed in most laboratories (years 1999–2001). This experimental model also offered the possibility of being completely automated. A robot that performed all steps of an experiment, including the random selection of experimental conditions and processing of biological samples, was thus developed. Again, the successful results obtained with this new device convinced Benveniste that he was on the right track. This robot attracted the attention of the US Defense Advanced Research Projects Agency (DARPA), which commissioned an expertise [21]. We will talk of the results of this expertise later in the text.

However, if these astonishing results were so obvious, why did Benveniste fail to convince his peers? The main reason was that he could not get rid of a strange phenomenon that literally poisoned his experiments, in particularly when he tried to carry out proof-of-concept experiments involving other researchers he wanted to convince. In a next section, we shall see what this stumbling block was and why it systematically and constantly stopped Benveniste in his race to the “decisive experiment”. But first, we need some conventions and definitions to describe these experiments.

2. Causal relationships in experimental biology

Suppose that we are interested in a parameter of a biological experimental system that we study in the laboratory in various experimental conditions. A change of this parameter during an experiment is noted Δ⁺ while no change is noted Δ⁰. Experimental conditions are either control condition (noted C) or test condition (noted T). If we notice that C is always associated to Δ⁰ and that T is always associated to Δ⁺, we conclude that a (strong) relationship exists between the experimental conditions (designated by the labels C and T) and the system states (Δ⁰ and Δ⁺ obtained after measurement). By convention, we name this relationship as “direct”; the “reverse” relationship would associate C with Δ⁺ and T with Δ⁰.

The purpose of experimental biology is precisely to reveal such relationships. Indeed, modern biology is based on causal relationships where X induces Y which in turn induces Z, etc. For example, if we inject a solution of histamine (test T) into the skin, we obtain a local edema at the place of the injection surrounded by a red area indicating that the system state has changed (Δ⁺). If we inject only the carrier solution without the active compound (control C), there is no change of the system state (Δ⁰). Since the experimenter can choose at will the experimental conditions, we conclude that histamine induces a skin response in a causal relationship. Describing the complete chain of events that occurs locally from the initial cause (histamine) to the final effect (edema/skin redness) is a typical research program. In this description, the principle of locality, which states that a physical object is only influenced by its immediate environment, is respected. As a matter of fact, most biologists do not even imagine that other types of relationships could be involved or simply envisioned. In Benveniste’s experiments, the principle of locality was also implicit since the supposed causes (“structured water” or electromagnetic fields) were thought to exert their effects locally. But are local cause-and-effect relationships the only ones possible? A clue is provided by the results of Benveniste’s experiments themselves as we will see in the next section.

3. When the scientific interest is not where it was supposed to be

We must now explain in detail why the field of research based on “water memory” was stopped in its development in spite of well-conducted experiments and seemingly convincing results. In short, the central problem was the impossibility of proving the causal nature of the relationship observed between experimental conditions and states of the biological system. Another reason – which is related to it, as we shall see – was the difficulty of having these experiments replicated by independent teams.

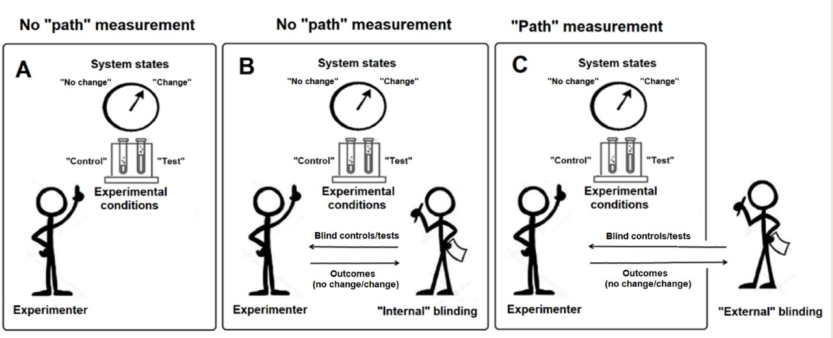
First, we will explain why Benveniste was convinced – with sound arguments – that he had discovered “something”. For this purpose, we will describe three experimental settings: open-label experiments, internal blinding and external blinding (Figure 1).

Figure 1. Configurations for (A) open-label, (B) “internally” blinded and (C) “externally” blinded experiments. The “internal” or “external” supervisor provides the experimenter with “control” and “test” samples whose labels have been masked (blind controls/tests). After the experiment is done, the experimenter returns to the supervisor the outcomes which have been obtained (change or no change of system state noted Δ⁰ and Δ⁺, respectively) for each control or test. The supervisor assesses the rate of “success” of the experiment (i.e., how many direct relationships have been obtained with the masked samples: “control” associated with “no change” or “test” associated with “change”).

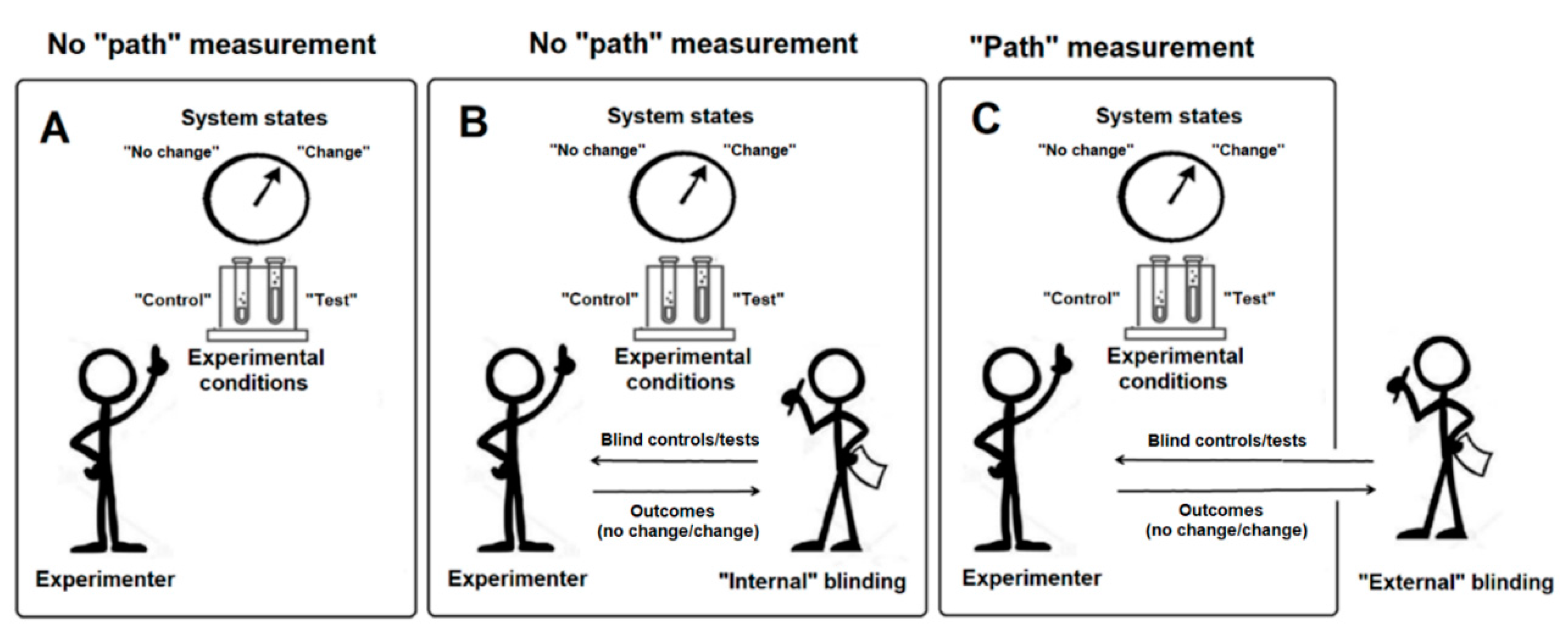
Open-label experiments. Figure 2 reports results on two devices that were used in parallel in 1992–1996. There was no blinding between the two measurements; these duplicate experiments were done in order to consolidate the data. To analyze these results, we do not care of the nature of the samples tested (C or T, high dilutions, electronic transmission, etc.) We only consider the concordance of the outcomes obtained with the two devices. We observe a high correlation of these measurement (the most probable pairs of outcomes are Δ⁰/Δ⁰ and Δ⁺/Δ⁺). The important point is for the pairs Δ⁺/Δ⁺. Indeed, these correlated pairs are a strong argument in favor of Benveniste’s theses. They indicate that there is “something” that occurs in these experiments. Whether one agrees or not with Benveniste’s views on these experiments, the source of correlations needs to be explored. This is precisely the purpose of the present article.

Internal blinding. The data of Table 1 indicate that these correlations persist after an internal blinding. Internal blinding means a blinding of labels of the samples to be tested (controls and tests) by a colleague who interacts with the experimenter in the laboratory (Figure 1). These data show that the pairs C/Δ⁰ and T/Δ⁺ are the most probable, thus strongly suggesting a direct relationship between labels and system states. Again, we understand why Benveniste defended his research with determination and why he could not resign himself to forgetting his results in a drawer as many suggested he should do [3].

External blinding. To share his experimental results and to convince his peers, Benveniste organized “public demonstrations” carried out in the presence of an audience of colleagues and observers who did not belong to the laboratory. These demonstrations were designed in order to give a “definitive” confirmation on the reality of these experiments and to establish their scientific interest. For this purpose, an experimental protocol was written and then a study report with all raw data was shared with participants [3]. During a typical session of demonstration, controls and tests were prepared (either high dilutions for the early demonstrations or computer files later) in another laboratory than Benveniste’s laboratory. These samples were prepared under supervision of all participants. Then, the labels of the control and test samples were replaced by a code by participants not belonging to Benveniste’s laboratory. Some samples were also kept unblinded to check that everything was fine in non-blinded conditions. Then, Benveniste’s team recovered all samples and tested them in its laboratory within the next days. After all measurements had been done, the outcomes (Δ⁰ and Δ⁺) corresponding to all blind samples were sent to the external supervisor who detained the code (Figure 1). This supervisor compared the two lists: list of labels (C vs. T) under a code name and list of outcomes (Δ⁰ vs. Δ⁺) and assessed whether outcomes were as expected (C associated to Δ⁰ and T associated to Δ⁺).

A series of experiments with external blinding is presented in Table 2. It is easy to see that the relationship between labels and system states was lost in the experiments with external blinding. Indeed, in this table, square labels are not superimposed on round labels of the same color, but distributed at random. There was still an “effect”, i.e., the observation of changes of system state (Δ⁺), but not at the place where they were supposed to be.

Figure 2. Open-label experiments made in duplicate on two experimental systems (dates: 1992–1996; experimental model: changes of coronary flow in isolated rodent heart; N=574 pairs of measurements) [22]. (a) In this figure we do not care about the label (control or test), only the concordance of the system states (Δ⁰ or Δ⁺) on the two devices matters. We also do not care of the method used by Benveniste’s team to produce controls and tests (high dilutions, electronic transmission, digital biology, etc.) The data obtained in devices A and B appear to be highly correlated. (b) If the value measured on the device A is <10% (no change; Δ⁰), then the probability of a value <10% on device B is 0.93. (c) If the value measured on the device A is ≥10% (change; Δ⁺), then the probability of a value ≥10% on device B is 0.89. Note that scales are logarithmic.

Table 1. Experiments with internal blinding (dates: 1993–1997; experimental model: changes of coronary flow in isolated rodent heart) [22].

Table 2. “Digital biology” experiments with external blinding (dates: 1996-1997; experimental model: changes of coronary flow in isolated rodent heart) [3]. In these experiments (public demonstrations with external supervisor), system states are distributed at random in contrast with open-label or internal blinding experiments presented in Figure 2 and Table 1). Therefore, no relationship can be established between labels and system states. If a causal relationship existed, one would expect square labels to be superimposed on round labels of the same color. These “mismatches” were considered by Benveniste as experimental failures. In the present analysis, we consider that “successful” and “failed” experiments are the two faces of the same phenomenon. Note that the observation of state changes (noted ●), whatever their place, requires an explanation. Indeed, according to current scientific knowledge, we would expect to observe only no change of system state (○-○-○-○-○-○-○, etc). The scientific context and the experimental details of these experiments can be found in [3].

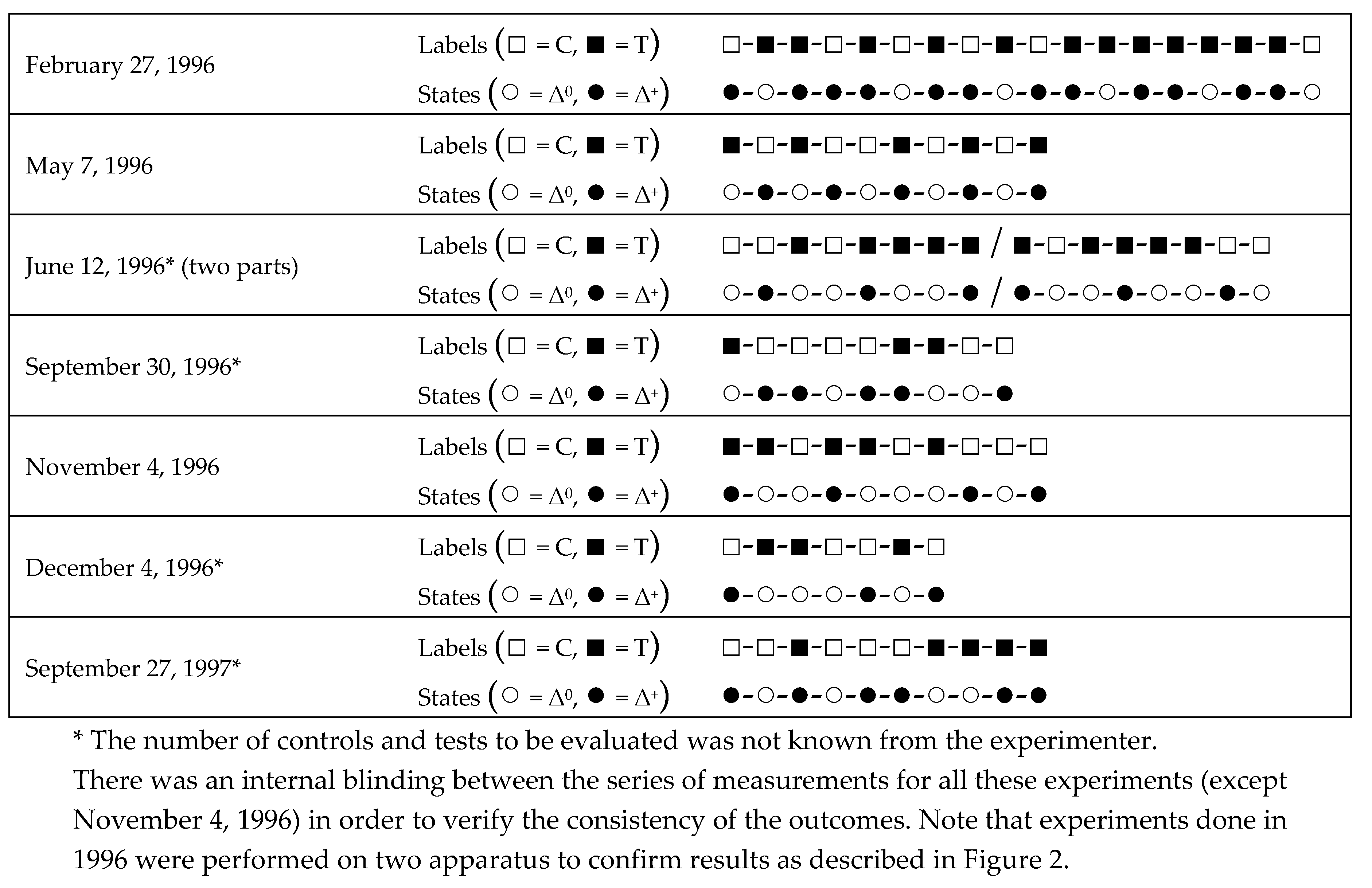
To explain these oddities, Benveniste put forward various hypotheses (human errors for label allocation, water contamination, electromagnetic pollution, “remnant activity” in the apparatus, spontaneous “jumps of activity” from one sample to another, etc.) These mismatches prompted a technological race in which Benveniste engaged to rule out these supposedly disturbing external events. In contrast, in the present analysis, we consider that “successes” with open-label/internal blinding experiments (A and B in Figure 1) and “failures” with external blinding experiments (C in Figure 1) are the two faces of the same phenomenon. Actually, we consider that these disturbing events are the scientific fact of this story. One important point must again be stressed. If Benveniste’s experiments were of no scientific interest, no change of the system state (Δ⁰) should be observed under either control or test conditions.

In order to take into account all these aspects of Benveniste’s experiments – i.e., both “successes” and “failures” – we propose to abandon the idea of any role of water (“water memory” and its avatars) and to begin by revisiting the notion of relationship in experimental biology.

4. Theoretical considerations on correlation in experimental biology

To progress in the understanding of the phenomena reported by Benveniste’s team, we consider that all various procedures for diluting solutions or electronic stuff aimed to “transfer biological activity” make no sense. We state that they have no more value than a ritual or meaningless gesticulations.

We assume that the control and test conditions are physically identical and that their difference lies only in the respective labels (“control” or “test”) that they randomly or subjectively receive. Labels and states of the system are of course not linked by a causal relationship. Since there is no link between these variables, they are independent and, consequently, the occurrence of one does not affect the probability of occurrence of the other. Yet a relationship was observed in Benveniste’s experiments. This is the problem we have to solve. Therefore, the key question is: “Is it possible to observe a correlation between independent variables that mimics a causal relationship but is itself not causal?”

Figure 3. Law of total probability for two sets of independent variables: experimental conditions (control C vs. test T) and system states (no change, Δ⁰ vs. change of system state, Δ⁺). According to the law of total probability, the sum of the probabilities of the four branches is equal to one.

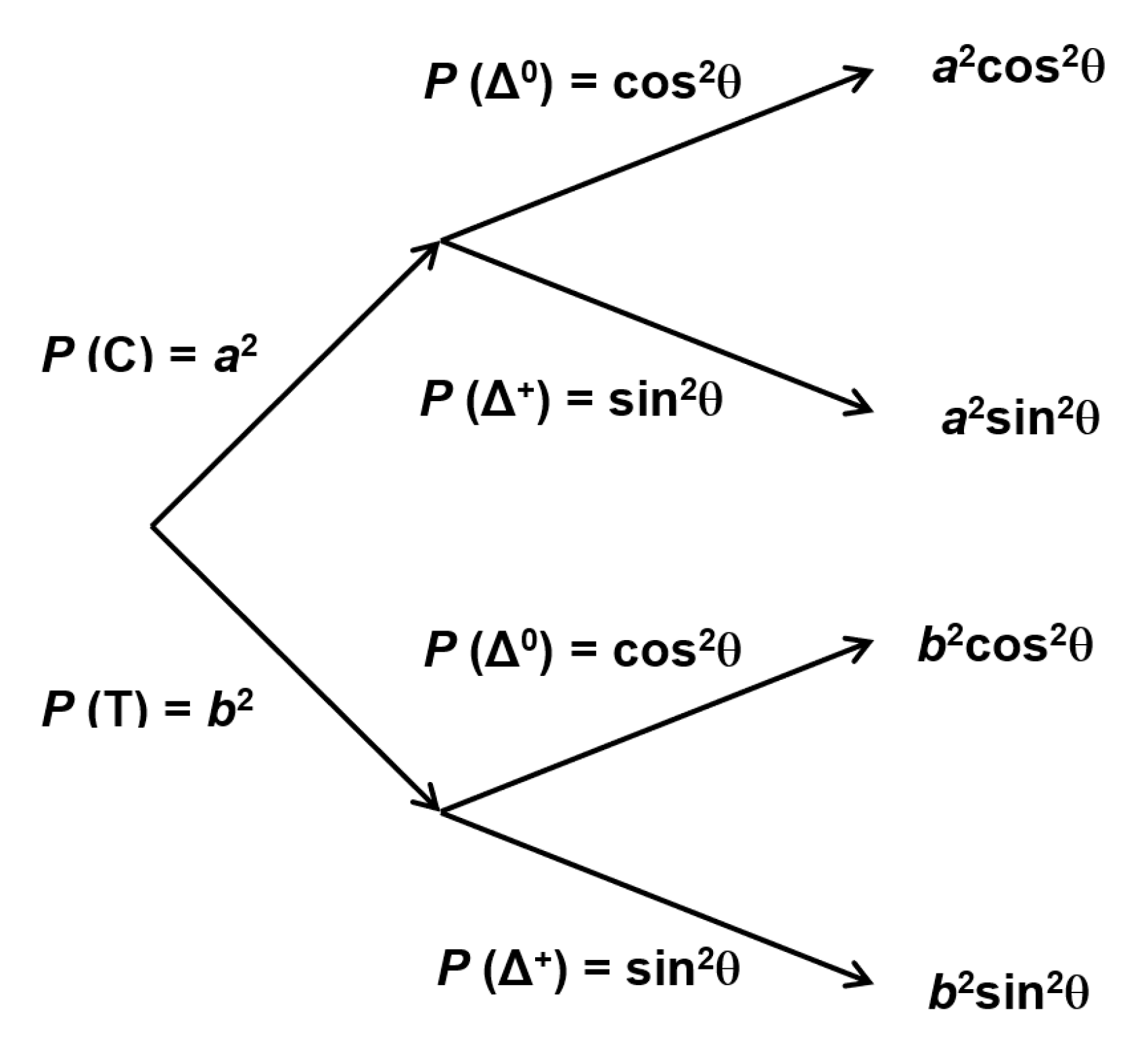
For this purpose, we suppose a simple situation where labels (control, C; test, T) and system states (no change, Δ⁰; change of system state, Δ⁺) are independent variables (Figure 3). In this case, the law of total probability is:

P (C) × P (Δ⁰) + P (C) × P (Δ⁺) + P (T) × P (Δ⁰) + P (T) × P (Δ⁺) = 1 ¹

(1)

with P (C) + P (T) = 1 and P (Δ⁰) + P (Δ⁺) = 1.

For reasons that will appear later, we write:

i.: P (C) = a² and P (T) = b² where a and b are real numbers
ii.: P (Δ⁰) = cos²θ and P(Δ⁺) = sin²θ

With these conventions, the law of total probability described in Equation (1) becomes:

(a.cosθ)² + (b.sinθ)² + (b.cosθ)² + (a.sinθ)² = 1

(2)

We add δ = 2ab.cosθsinθ – 2ab.cosθsinθ = 0 to Equation (2):

[(a.cosθ)² + (b.sinθ)² + 2ab.cosθsinθ] + [(b.cosθ)² + (a.sinθ)² – 2ab.cosθsinθ] = 1

(3)

δ is equal to zero, but its addition allows to reorganize the equation with two remarkable identities:

(a.cosθ + b.sinθ)² + (b.cosθ – a.sinθ)² = (a.cosθ)² + (b.sinθ)² + (b.cosθ)² + (a.sinθ)² = 1

(4)

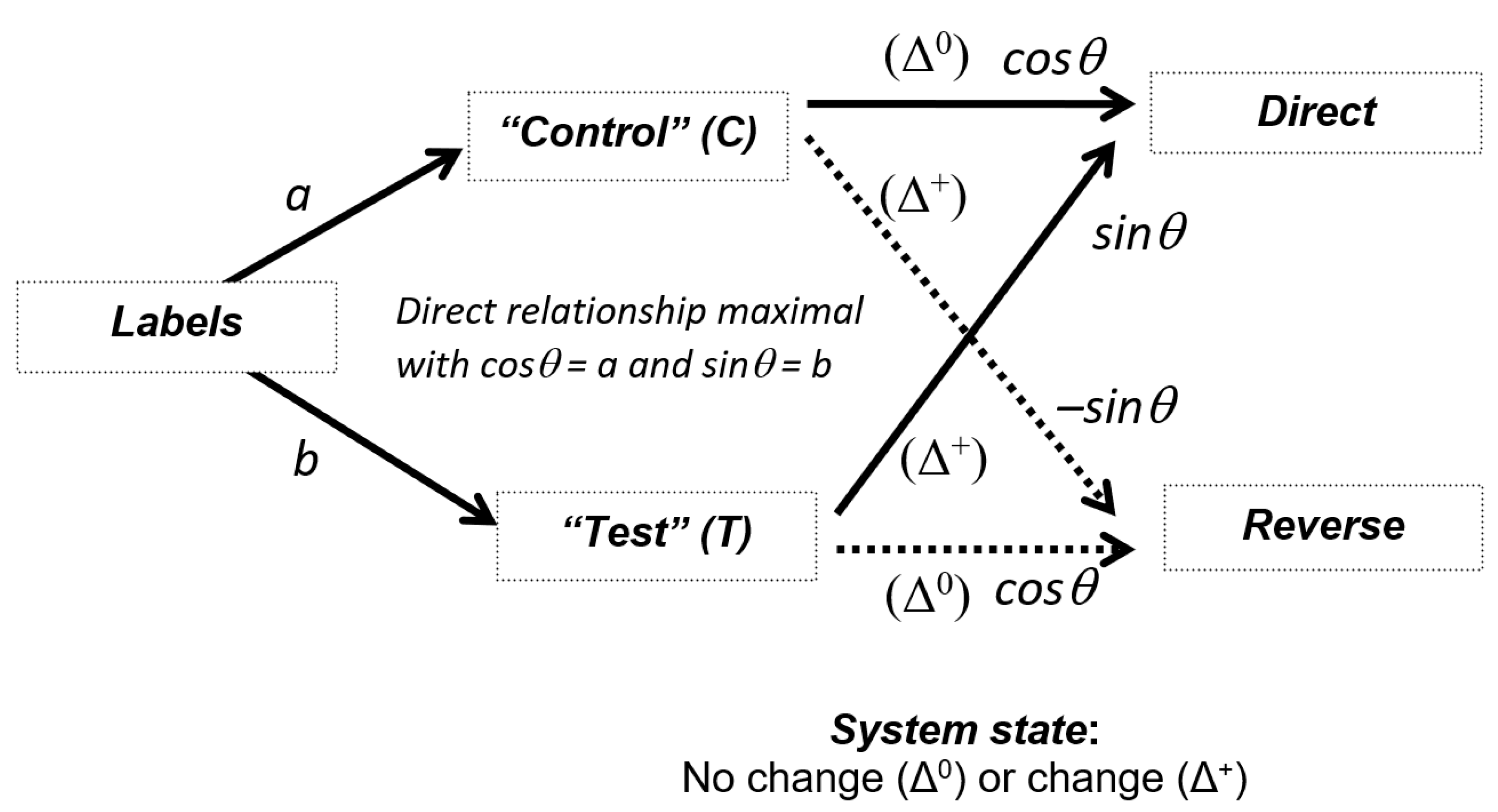
Equation (4) shows that there are two possible writings of the law of total probability for two independent variables. We can also represent this equation graphically (Figure 4). We recognize a logic similar to an experiment where a photon “interferes with itself” such as in a two-slit Young’s experiment or in a Mach-Zehnder interferometer.

Figure 4. Construction of a relationship between two independent sets of dichotomic variables (labels and system states). Probabilities of direct/reverse relationship is calculated as the square of the sum of the probability amplitudes of the two possible paths: P (direct)_I = (a.cosθ + b.sinθ)² and P (reverse)_I = (b.cosθ – a.sinθ)². In contrast, when a path measurement is performed, probabilities are calculated as the sum of the squares of the probability amplitudes of paths: P (direct)_{II =} a²cos²θ + b²sin²θ and P (reverse)_{II =} b²cos²θ + a²sin²θ.

In the same logic as an interference experiment, the left side of Equation (4) corresponds to the absence of path measurement (superposition with interference pattern), while the right side corresponds to path measurement (no interference pattern and random outcomes). The real number a (resp. b) can be assimilated to a “probability amplitude” while a² (resp. b²) is the corresponding probability.

Therefore, there are two possible definitions of P (direct) according to path measurement or not:

P (direct)_I = (a.cosθ + b.sinθ)² if no path measurement

(5)

P (direct)_II = (a.cosθ)² + (b.sinθ)² if path measurement

(6)

Similarly, there are two possible definitions of P (reverse):

P (reverse)_I = (b.cosθ – a.sinθ)² if no path measurement

(7)

P (reverse)_II = (b.cosθ)² + (a.sinθ)² if path measurement

(8)

P (direct)_II can be also written by using conditional probabilities where P (X?Y) means probability of the event X given that the event Y is known:

P (direct)_II = a²cos²θ + b²sin²θ = P (C) × P (Δ⁰?C) + P (T) × P (Δ⁺?T)

(9)

We see clearly with Equation (9) how P (direct)_II is related to the knowledge (or measurement) of the path (from a point of view outside the laboratory). It could be tempting to use conditional probabilities to rewrite Equation (3). However, the difference δ of the “interference terms” is not egal to zero in all cases:

δ = 2 a b \sqrt{P (Δ^{0} ∣ C)} \sqrt{P (Δ^{+} ∣ T)} - 2 a b \sqrt{P (Δ^{0} ∣ T)} \sqrt{P (Δ^{+} ∣ C)}

(10)

Indeed, δ = 0 only if P (Δ⁰?C) = P (Δ⁰?T) = P (Δ⁰) and if P (Δ⁺?T) = P (Δ⁺?C) = P (Δ⁺). In other terms, the two “interference terms” cancel each other only if labels (C or T) and system states (Δ⁰ or Δ⁺) are independent events as initially postulated in Equation (1). The “same randomness” must operate for the selection of system states, regardless of the paths C and T (see Figure 4).

Another important remark is for a particular case of Equation (5) and Equation (7):

If a = cosθ and b = sinθ, then P (direct)_I = 1 and P (reverse)_I = 0

(11)

Equation 11 means that we have answered the initial question: “Is it possible to observe a correlation between independent variables that mimics a causal relationship but is itself not causal?” The answer is positive with the condition that θ is different from zero (maximal correlation is obtained with sinθ = b and cosθ = a). Another important condition is to not try to measure path (for an observer outside the laboratory), otherwise the relationship is broken and system states and labels are randomly associated. For example, if b = sinθ and b² = 1/2, then P (direct)_I = 1 while P (direct)_II is equal to 1/2.

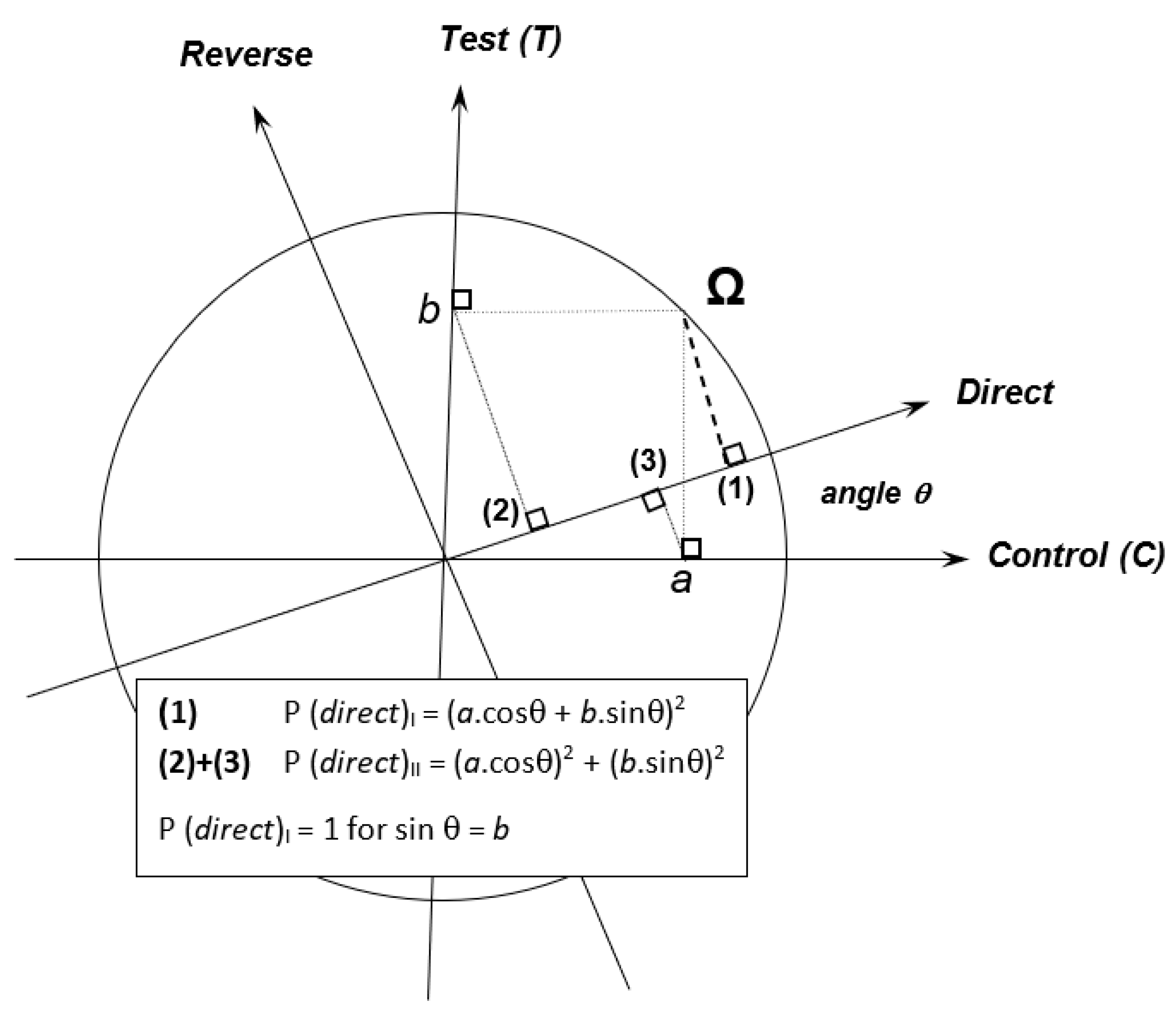
We can also represent Equation (4) geometrically in a Cartesian coordinate system (Figure 5). In this representation, there are two bases, one for the labels (C and T) and the other for the relationships (direct and reverse). Sinθ and cosθ are the “probability amplitudes” of Δ⁰ and Δ⁺, respectively. The two bases are related by a rotation matrix:

(\begin{matrix} a & b \end{matrix}) \times (\begin{matrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{matrix}) = (\begin{matrix} a c o s θ + b s i n θ \\ b c o s θ - a s i n θ \end{matrix})

(12)

Each point can be projected (i.e., expressed) in one basis or the other (C/T or direct/reverse). The projection of a point of the unit circle leads to different results if projected directly to the basis direct/reverse or if projected first on the basis C/T and then on the basis direct/reverse. This last case (projection first on the basis C/T) is equivalent to a which-path measurement. For θ ≠ 0, direct/reverse relationships and control/test labels are said “non-commuting” variables. This geometric representation does not bring anything more than Equation (5) to Equation (9), but it allows a comprehensive visualization of labels, system states and their relationships.

Figure 5. Geometrical representation of the two bases depicting labels and system states. The point Ω with coordinates a and b in basis C/T has coordinate a.cosθ + b.sinθ on the direct relationship axis; the associated probability is therefore (a.cosθ + b.sinθ)². If the relationship is assessed separately for C and T (path measurement), the coordinates on the direct relationship axis are a.cosθ for C and b.sinθ for T, with the corresponding probability for direct relationship equal to (a.cosθ)² + (b.sinθ)². For clarity, projections for reverse relationship are not presented on the figure.

5. What is the origin of the basis “direct/reverse”?

Probabilities make the link between our reality and the theoretical model based on probability amplitudes (which have no correspondence in real world). If we look more attentively P (direct)_{I =} a²cos²θ + b²sin²θ + 2ab.cosθsinθ, there are three terms. The first two terms are clearly identified in the real world: they are combinations of a² = P (C), b² = P (T), cos²θ = P (Δ⁰) and sin²θ = P (Δ⁺). The third term (interference term) combines four probability amplitudes, which concern labels and system states, without element of reality that corresponds to this combination. In other words, labels and system states in the interference term must be considered as a unique entity that cannot be dissociated. If we try to dissociate it (i.e., by path measurement), the interference term disappears and we get P (direct)_II = a²cos²θ + b²sin²θ. Labels, which participate to this unique entity, are not physical objects, but are the result of the experimenter’s decisions or opinions about the properties of the samples to be assessed. They are therefore related to the cognitive states of the experimenter.

We propose that the structuring of the cognitive states of the experimenter and the system states taken as a whole (mathematically described in Equation (5) and Equation (7)) has its origin in the repeated observation of correlations between labels and system states. Such correlated observations can be, for example, the observation by the experimenter of a classical causal experiment with the experimental system. By classical, we mean an experiment with a “classical cause” (e.g., a pharmacological compound at the usual micromolar concentration added to the biological system). Note that this was the case in Benveniste’s laboratory; the experimental systems were routinely used for “classical” experiments and they were also used to verify that the systems used to demonstrate “non-classical” relationships were functioning correctly under “classical” conditions.

In an experiment with a “classical” stimulus, we suppose that the correlation between labels and system states is perfect, i.e., P (direct) = 1. For this causal relationship, we can write:

P (direct)_causal = P (C)×P (Δ⁰?C) + P (T)×P (Δ⁺?T) = 1 with P (Δ⁰?C) = 1 and P (Δ⁺?T) = 1

(13)

We name n₁ the number of trials where the experimenter observes that Δ⁰ is associated to C and n₂ the number of trials where the experimenter observes that Δ⁺ is associated to T (with n₁ + n₂ = N). The experimenter records couples of results that verify P (direct)_causal = 1, for example (C, Δ⁰), (T, Δ⁺), (T, Δ⁺), (C, Δ⁰), (C, Δ⁰), (T, Δ⁺), (T, Δ⁺), etc. When the number of trials N increases, we can state that n₁/N→ a² and n₂/N → b².

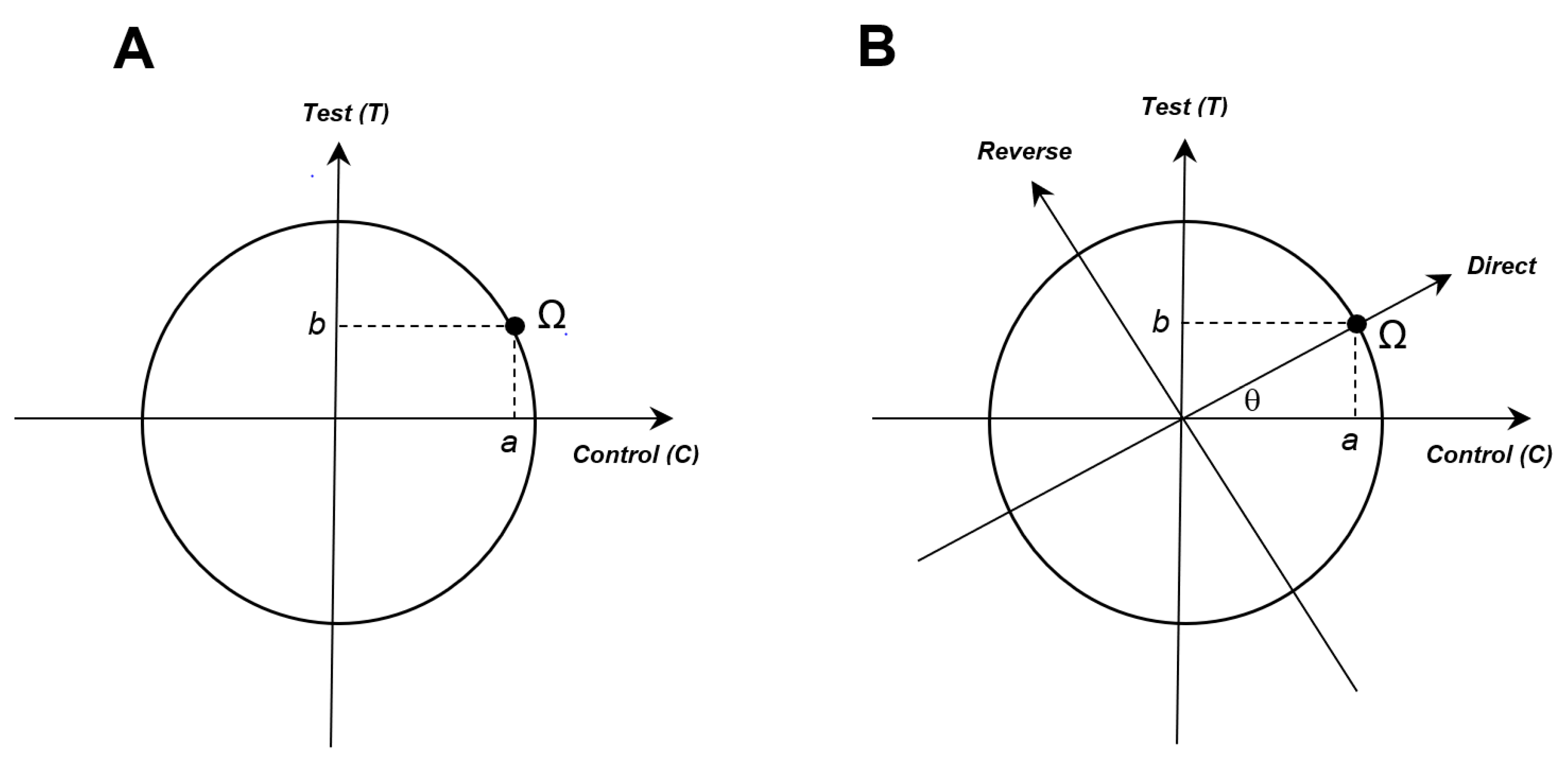
Since a² + b² = 1, the point Ω with coordinates and can be represented on the unit circle of Figure 6. The point Ω, corresponding to P (direct)_causal = P (direct)_I = 1, allows defining the axis for direct relationship and the perpendicular axis for reverse relationship. It defines also the value of θ since sinθ = b.

After this phase, which could be considered as learning or conditioning, we have to explain how is maintained the structuring of the entity made of the experimenter’s cognitive states and the experimental system states. During the “learning” phase, the non-classical relationship is shaped on correlated variables. Note that this structuring does not depend on the underlying nature of the observed correlation between labels and system states (local causality or other types of correlations). In other words, once established, this structuring is self-sustained. This explains why, even if the classical/local cause has been removed, the same relationship continues to be observed between labels and system states.

Figure 6. Construction of the basis direct/reverse. (A) During repeated measurements (e.g., causal relationship with a “classical” biologically-active compound), C is systematically associated to Δ⁰ and T to Δ⁺. Since P (C) = a² and P(T) = b², these correlations can be summarized on the unit circle by the point Ω with coordinates a and b. (B) The point Ω allows defining a “direct relationship” and a new basis (direct/reverse). In this new basis, the direct relationship is recognized as such, independently of the elements (experimental observations) that permitted to define it. The point Ω, which integrates the results of repeated measurements of experimental correlations, is therefore a crossing point between a classical causal relationship and a non-classical correlation.

6. Are all experimental systems suitable?

Until now, we did not impose any condition for the experimental system. We just tried to find a logical structure to describe Benveniste’s experiments. In this model, the experimental conditions (labels) and the states of the system are nothing more than independent random variables to which we can associate probabilities of occurrence. However, one can intuitively think that it is difficult to consider replacing the biological system by any other system producing randomness such as a random draw of black and white balls from a bag or a dice roll.

All experimental systems used in Benveniste’s experiments were biological systems involving cells, isolated organs or enzymatic reactions. We assume that – in the absence of a conditioned experimenter – θ is not strictly equal to zero, but slightly varies around zero due to random tiny fluctuations of the experimental system. Since P (Δ⁺) = sin²θ, the transition from no change to change of system state (Δ⁰ → Δ⁺) is a possible event, even if its probability is low. It means that there is at least one sequence of elementary random events that leads from Δ⁰ to Δ⁺. Therefore, the biological system can undergo a transition from Δ⁰ to Δ⁺ during an experiment done by a conditioned experimenter. The experimental system must obey to P (direct)_I = 1 and it behaves as a dropped apple that moves according to the gravitational field (if there is no obstacle on its way).

In contrast, suppose a bag full of many white balls (Δ⁰) and only a few black balls (Δ⁺). The probability to draw a black ball is low and white balls cannot transform into black balls; indeed, there is here no “sequence of elementary random events” changing white balls into black balls. Since the probability to draw black balls cannot increase, such an experimental system would not allow the establishment of a relationship with another independent variable (e.g., labels), as it is the case in Benveniste’s experiments.

7. Open-label vs. blind experiments explained

Open-label experiments/internal blinding. Both the labels (C or T) and the system states (Δ⁰ or Δ⁺) are random events that are governed by their respective probabilities. The records of these events by the experimenter are measurements: during open-label experiments, the experimenter measures first the label (C or T) and then the system state (Δ⁰ or Δ⁺); during internal blinding, the experimenter measures first the system state and then the label (Figure 1). Internal blinding of labels can be performed by an automatic device or by a colleague present in the neighborhood of the experimenter. In this case, the blinding device (machine or human) is nothing more than a part of the experimental system.

We see in Figure 3 and Equation (1) that there is no imposed order for labels and system states. Thus, in Equation (3), the order of probability amplitudes referring to labels and states of the system does not matter. Even though Figure 3 and Figure 4 suggest that the labels are measured first, we could describe the same situation by exchanging what refers to labels with what refers to system states. Therefore, in our modelling, there is no difference in nature between open-label experiments and experiments with internal blinding.

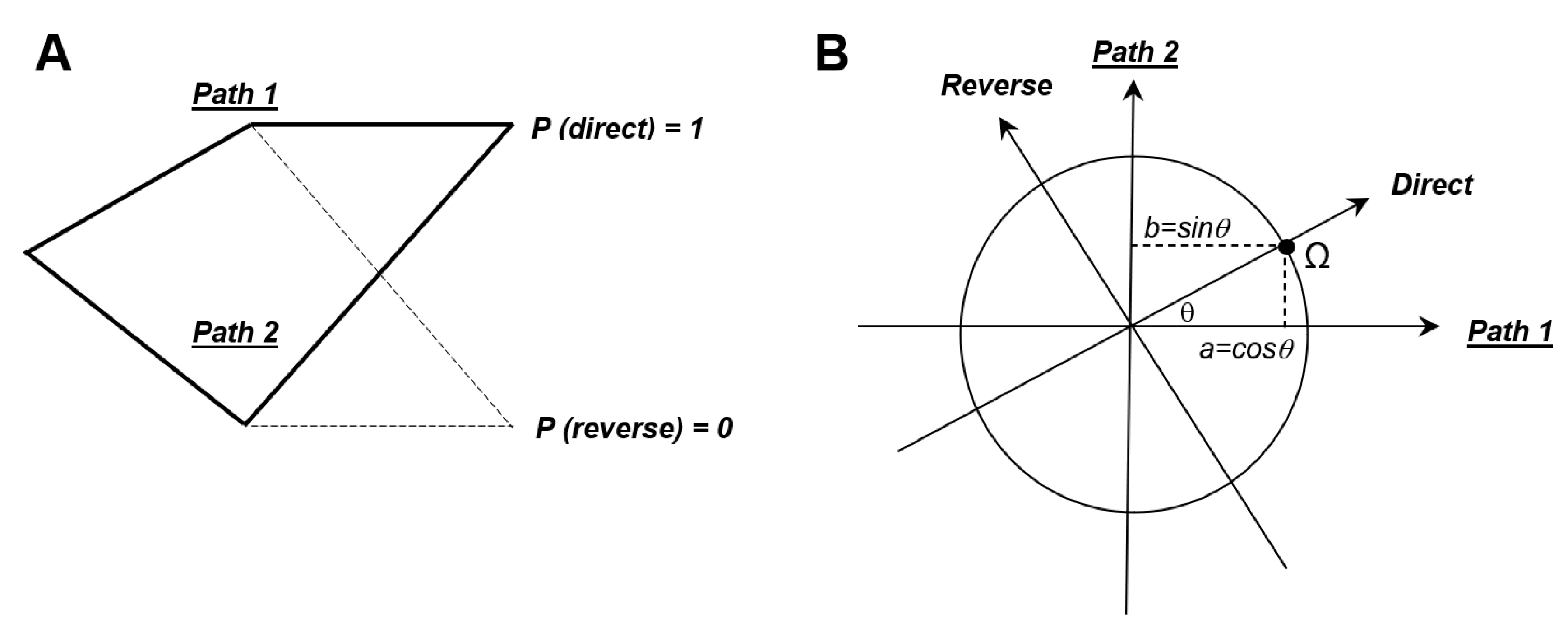
In addition, we have seen that P (direct) = 1 and P (reverse) = 0 for sinθ = b and cosθ = a, thus showing that the probability amplitudes of labels and outcomes are merging when the correlation is maximal. C and Δ⁰ are combined in a single path (Path 1) and T and Δ⁺ are combined in another single path (Path 2) (Figure 7).

The internal blind experiments made always a strong impression on Benveniste’s team because they strongly suggested that the effects of high dilutions or digital biology were a tangible reality (“it works”). It was these experiments that convinced Benveniste that he had to persevere and that one day his theories and discoveries would be recognized. However, we have seen in this article that a logic other than a classical causal relationship is possible. This does not mean that causality is absent of this description, but the causality operates at a higher level, i.e., at the level of the relationship. Internal blinding in Benveniste’s experiments should be no more surprising than internal blinding for a classical causal relationship. We must simply admit that what is at stake is not the physical composition of the sample to be tested – they are all identical – but its designation (label C or T). This label can be “measured” like any other parameter and a probability can be attributed to it.

External blinding. The external blinding – which constituted the “stunning block” described above – is simply explained by a which-path measurement (Figure 7). Everything happens as if the external supervisor is making a measurement of the path from the outside by exchanging data on labels and system states (Figure 1). It is the external supervisor who provides the experimenter with coded samples to be tested; finally, the external supervisor receives the records of the corresponding system states and, after unblinding, establishes whether the experiment is “successful”. This procedure is a which-path measurement, with the laboratory in its ensemble being considered as an “interferometer”. Therefore, we can understand why these experiments were so disturbing for Benveniste’s team. Indeed, even if these experiments were considered as “failures”, they nevertheless indicated that “something” happened because changes of the system were recorded (but randomly associated with C and T). The experiments seemed to be going “crazy”. In the “classical” and local approach of Benveniste’s team, there was no place for such outcomes and external causes of disturbances were searched leading to a technological race for the “perfect” and indisputable experiment.

Figure 7. Maximal correlations between labels and system states and consequences on open-label, “internally” blinded and “externally” blinded experiments. (A) Correlations between labels and system states are maximal with a = cosθ and b = sinθ. In this case, C and Δ⁰ are combined in a single path (Path 1) and T and Δ⁺ are combined in another single path (Path 2). In this case, P(direct)_I = [P(C) + P(T)]² = 1 (no path measurement; open-label experiments or “internal” blinding) and P(direct)_II = [P(C)]² + [P(T)]² (path measurement; external blinding). (B) Geometrical representation on a unit circle of the two bases C/T and Path 1/Path 2.

8. Discussion

In this analysis of Benveniste’s experiments, details on the biological models and the different methods used to “inform” water are left aside. Only the logical structure of the outcomes is analyzed. In order to review these experiments with a renewed perspective, a radical choice has been done by considering that control and test conditions that were evaluated by Benveniste’s team differed only by their name. Indeed, we previously noted that whatever the process used to inform water (high dilutions, direct electromagnetic transmission, record on a computer memory, etc.), the effect size whatever the experimental system was of the same order of magnitude [3,22]. This suggested that an alternative unique explanation – independent of the different methods and devices used – might be at work. This radical choice seems to make any explanation of Benveniste’s experiments even more problematic. Indeed, how could a relationship be observed if the samples tested are all physically comparable to simple controls? Therefore, we asked whether it was possible to construct a relationship between two independent variables that had – up to a certain point –the appearance of a causal relationship, but was not causal.

For this purpose, the mathematical formalism starts from scratch with the definition of the total probability law for two dichotomic independent variables, namely labels (which designate the experimental conditions) and the system states. We easily obtain Equation (4) where the left and right parts can be considered as complementary. They are the two opposite poles of the same reality, but both are necessary to understand the logic of Benveniste’s experiments. The formalism requires a description from the outside where the laboratory and its content behave with the same logic as an “interferometer”. The “causality” of the relationship described by the present formalism is only apparent since measurement of the “path” destroys the correlations: labels (C vs. T) are then randomly associated to system states (no change vs. change). This is precisely the description of the Benveniste’s stumbling block.

Labels (“control” and “test”) in our modelling are not physical objects, but are concepts constructed and manipulated by the cognitive structures of the experimenter. Nevertheless – as for any “physical” variable – these subjective and abstract entities can be measured. In the field of experimental psychology, quantum-like logic has been used with success in a new approach named quantum cognition. Cognitive processes such as decision making, judgment, memory, reasoning, language or perception, not adequately described by “classical” probabilities, are modelled with mathematical quantum-like tools, thus better fitting experimental data [23,24]. However, in quantum cognition, all processes are supposed to be limited to human brain, while our modelling involves not only the experimenter’s cognitive structures, but also an experimental biological system. Cognitive structures are generally considered to be limited to the brain or by the external envelope of the body if the peripheral nervous system and sense organs are also included. The extended mind thesis (EMT) proposes to expand cognitive structures to the physical world outside the body [25]. Thus, devices used for calculating or memorizing could be considered as an extension of cognitive structures. Similarly, measurement devices are nothing more than an extension of sense organs. Such an expanded definition of cognitive structures is implicit in our modelling when labels – inscribed in cognitive structures – and biological system states are considered as a unique entity that cannot be dissociated. However, there is nothing magical since there is no “action” of the mental structures on the experimental system. If one tries to use the correlations in a causal way to perform an action (e.g., giving an order or sending a message), the relationship between the experimenter and the system breaks down.

The source of the non-classical correlations between the experimenter and the experimental system is to be found in the complementarity of local measurements (labels and system states) and global measurement (relationship). A parallel can be drawn with the wave-particle duality, the global measurement corresponding to the detection of “waves” and the local measurements to that of “particles”. “Particles” and “waves” are classical concepts that we can apprehend with our measurement tools, our senses, our language and our usual concepts to describe reality. Depending on the experimental environment, either “wave” or “particle” descriptions are appropriate (they are said complementary). Thus, light behaves as waves when it does not interact with matter and behaves as particles (i.e., photons) when it interacts with matter (for example, with a measurement apparatus). These two descriptions – particles and waves – are incompatible pictures of reality (we cannot think about them simultaneously). Nevertheless, both descriptions are necessary to account for quantum or quantum-like phenomena when we use our usual concepts about reality. In the formalism of this article, experimental “elements” (C, T, Δ⁰ and Δ⁺) are described as “particles” while the relationship between them is described as “wave”. Thus, P (direct)_II = (a.cosθ)² + (b.sinθ)² is a “particle” description of the experimental situation; P (direct)_I = (a.cosθ + b.sinθ)² is a “wave” description which differs from P (direct)_II by the interference term 2ab.cosθsinθ. Interferences are characteristic of wave interactions that can be constructive or destructive according to the values of the amplitudes of the waves that are superposed at a given point. Thus, to calculate P (direct)_I, the two amplitudes a.cosθ and b.sinθ are added (amplitudes can be positive or negative). In quantum or quantum-like formalism, amplitudes are probability amplitudes which have no correspondence in the reality. The connection with reality is done via probabilities, which are obtained after squaring the sum of all probability amplitudes that concur to the outcome (direct or reverse relationship in the present case).

The crucial element of our description of Benveniste’s experiments is how to explain the structuring of the entity made of the combination of the experimenter’s cognitive states and the experimental system states. For this purpose, we propose that the experimenter unconsciously learn to recognize the association between labels and system states after repeated observation of a “classical” relationship with a comparable experimental system. This step could be compared to a Pavlovian conditioning: the cognitive structures associate the label “test” to a change of the system state and the label “control” to no change. It is important to underscore that this combination of a label with the corresponding system state is not a simple addition or juxtaposition. Indeed, during this process, the relationship is recognized as such (i.e., independently of its constitutive elements). This is a more abstract level of description than a simple account of the individual experimental events. These considerations are reminiscent of Gestalt theory. According to this theory, objects are perceived as a whole or as a form (Gestalt) by the human mind and not as the sum of their parts; the whole has therefore its own independent existence [26,27].

The automation of the experimental process is not necessarily the solution to avoid an “experimenter effect”. As previously said, Benveniste’s team set up a robot analyzer (based on fibrinogen coagulation) that required only to push one switch to launch an experiment. The choice of control and test conditions was randomized by a computer and the experimenter was informed of the results when the experiment was finished. An expertise of this apparatus was mandated by the DARPA and was performed in Summer 2001 in a US laboratory at Bethesda [21]. In their report, the multidisciplinary team concluded that they had not observed anything abnormal about the robot analyzer and that the experiments they had observed in the presence of Benveniste’s team seemed to confirm the concepts of “digital biology”. They noted, however, that the presence of the experimenter dedicated to these experiments seemed to be necessary for the expected results to be observed. They also reported that after the departure of Benveniste’s team, no effect at all (i.e., no change of system state whatever the label) could be observed using this robot. The existence of unknown “experimenter factors” was suggested by some members of the supervisory team [21]. The final conclusion was that the alleged phenomenon based on “digital biology” was not replicable. Note that this failure was different from the failures reported above with external blinding. Here, what has been raised as a concern in the DARPA expertise was the requirement of a trained/conditioned experimenter to record a change of the system state. The relationship between conditioned vs. non-conditioned experimenter, on the one hand, and “success” vs. “failure” of the experiment, on the other, appears to be the actual causal relationship that was at work during Benveniste’s experiments. Incidentally, this suggests another interpretation of the present formalism where what is measured is not the state of the biological system but the degree of conditioning of the experimenter by using the biological system as a measurement device.

With this latest episode of DARPA expertise, which concludes the “water memory” saga, it is unreasonable to persist in considering – as Benveniste and his supporters did – that high dilutions, “water memory” or “digital biology” constituted a major breakthrough in biology and medicine. If plain causal relationships were really at work, the existence of “water memory” and its avatars would certainly have been demonstrated without the difficulties we described. It is even possible that such non-classical correlations between labels and biological systems occur in other laboratories unwittingly to the experimenters who think that they have evidenced a “real” (causal) relationship. We can also hypothesize that the lack of replicability of certain experiments could be explained by such a non-classical phenomenon. If this type of phenomenon is suspected, experiments with an external supervisor can help clarify. This modelling could also be useful in the description of the placebo effect or in some alternative medicines.

In conclusion, we have seen in this article how simple considerations based on probability theory lead to describe non-classical correlations involving the experimenter. This probabilistic modelling allows to propose an alternative explanation to Benveniste’s experiments where water plays no role and where the place of the experimenter is central. All aspects of Benveniste’s experiments are taken into account in this modelling, including the weird stumbling block. This obstacle prevented proving the causal relationship between the information supposedly stored in water and the corresponding “effect” observed on the biological system. Nevertheless, because Benveniste persisted in his quest for the definitive experiment that would convince everyone, he has transmitted to us a corpus of well-conducted experiments. For this reason, we must express our gratitude to him. He was pursuing what seems today a chimera, but his experimental data allows us to suggest the possible emergence of non-classical correlations between an experimenter and a biological system. These correlations mimic classical relationships, but are not causal because no local effect is involved. Causality is not absent, however, but the cause of these correlations is at the level of the experimenter’s cognitive states and not at the level of the experimental elements.

Funding

The author received no financial support.

Note

1	Note that P (C) and P (T) are based on the a priori knowledge of the experimenter about the number of controls and tests to be evaluated (this point is important for blind experiments).

References

“Serendipity.” Merriam-Webster.com Dictionary, Merriam-Webster, https://www.merriam-webster.com/dictionary/serendipity.
Beauvais F. L’Âme des Molécules – Une histoire de la “mémoire de l’eau” (2007) Collection Mille Mondes. https://www.researchgate.net/publication/280625214_L’Ame_des_Molecules_-_Une_Histoire_de_la_Memoire_de_l’Eau.
Beauvais F. Ghosts of Molecules – The case of the “memory of water” (2016) Collection Mille Mondes. https://www.researchgate.net/publication/280625430_Ghosts_of_Molecules_-_The_Case_of_the_Memory_of_Water.
Benveniste J. Ma vérité sur la mémoire de l’eau. Paris: Albin Michel; 2005.
de Pracontal M. Les mystères de la mémoire de l’eau. Paris: La Découverte; 1990.
Thomas Y. The history of the Memory of Water. Homeopathy. 2007;96:151-7. [CrossRef]
Poitevin B. The continuing mystery of the Memory of Water. Homeopathy. 2008;97:39-41. [CrossRef]
Schiff M. The Memory of Water: Homoeopathy and the Battle of Ideas in the New Science. London: Thorsons Publishers; 1998.
Alfonsi M. Au nom de la science. Paris: Bernard Barrault; 1992.
Ragouet P. The Scientific Controversies and the Differenciated Nature of Science. Lessons from the Benveniste Affair. L’Année sociologique. 2014;64:47-78. [CrossRef]
Ball P. H2O: A biography of water: Weidenfeld & Nicolson; 1999.
Kaufmann A. The affair of the memory of water. Towards a sociology of scientific communication. Réseaux The French journal of communication. 1994;2:183-204. [CrossRef]
13. Maddox J, Randi J, Stewart WW. “High-dilution” experiments a delusion. Nature. 1988;334:287-91. [CrossRef]
Benveniste J. Benveniste on Nature investigation. Science. 1988;241:1028. [CrossRef]
15. Benveniste J, Aïssa J, Litime MH, et al. Transfer of the molecular signal by electronic amplification. Faseb J. 1994;8:A398.
16. Aïssa J, Jurgens P, Litime MH, et al. Electronic transmission of the cholinergic signal. Faseb J. 1995;9:A683.
17. Benveniste J, Jurgens P, Aïssa J. Digital recording/transmission of the cholinergic signal. Faseb J. 1996;10:A1479.
18. Benveniste J, Jurgens P, Hsueh W, et al. Transatlantic transfer of digitized antigen signal by telephone link. J Allergy Clin Immunol. 1997;99:S175.
19. Benveniste J, Aïssa J, Guillonnet D. Digital biology: specificity of the digitized molecular signal. Faseb J. 1998;12:A412.
20. Benveniste J, Aïssa J, Guillonnet D. The molecular signal is not functional in the absence of “informed” water. Faseb J. 1999;13:A163. [CrossRef]
21. Jonas WB, Ives JA, Rollwagen F, et al. Can specific biological signals be digitized? FASEB J. 2006;20:23-8. [CrossRef]
Beauvais F. Emergence of a signal from background noise in the “memory of water” experiments: how to explain it? Explore (NY). 2012;8:185-96. [CrossRef]
23. Busemeyer J, Bruza P. Quantum models of cognition and decision: Cambridge University Press; 2012.
24. Bruza PD, Wang Z, Busemeyer JR. Quantum cognition: a new theoretical approach to psychology. Trends Cogn Sci. 2015;19:383-93. [CrossRef]
Clark A, Chalmers D. The extended mind. Analysis. 1998;58:7-19.
26. Jakel F, Singh M, Wichmann FA, et al. An overview of quantitative approaches in Gestalt perception. Vision Res. 2016;126:3-8. [CrossRef]
Amann A. The Gestalt problem in quantum theory: generation of molecular shape by the environment. Synthese. 1993;97:125-56. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Benveniste’s Experiments and the So-Called “Water Memory” Phenomenon: an Example of Serendipity?

Abstract

1. Introduction

2. Causal relationships in experimental biology

3. When the scientific interest is not where it was supposed to be

4. Theoretical considerations on correlation in experimental biology

5. What is the origin of the basis “direct/reverse”?

6. Are all experimental systems suitable?

7. Open-label vs. blind experiments explained

8. Discussion

Funding

Note

References

MDPI Initiatives

Important Links

Subscribe