Preprint
Article
Solve the 3x+1 Problem by the Multiplication and Division of Binary Numbers
Altmetrics
Downloads
440
Views
206
Comments
1
This version is not peer-reviewed
Submitted:
14 February 2023
Posted:
20 February 2023
You are already at the latest version
Alerts
Abstract
The 3x+1 problem asks the following: Suppose we start with a positive integer, and if it is odd then multiply it by 3 and add 1, and if it is even, divide it by 2. Then repeat this process as long as you can. Do you eventually reach the integer 1, no matter what you started with? Collatz conjecture (or 3n+1 problem) has been explored for about 85 years. In this paper, we convert an integer number from decimal to binary number, and convert the Collatz function to binary function, which is multiplication and division of two binary numbers. Finally the iternation of the Collatz function, eventually reach the integer 1, thus we solve the 3x+1 problem completely.
Keywords:
Subject: Computer Science and Mathematics - Algebra and Number Theory
1. Introduction
The problem, also known as the Collatz conjecture, mapping, Ulam conjecture, Kakutani’s problem, Thwaites conjecture, Hasse’s algorithm, or Syracuse problem [1], is one of the unsolved problems in mathematics. Paul Erdos (1913-1996) commented on the intractability of the problem [2], stating that "Mathematics is not ready for those problems yet".
The problem states that, for any positive integer x, if x is even, divide it by 2; if x is odd, multiply it by 3 and add 1. Repeating this process continuously leads to the conjecture that no matter which number is initially chosen, the result will always reach 1 eventually.
2. Terminology and notations
We use the notations as in [4,7], and describe a Collatz function as follows:
Let N denote the set of positive integers. For , and and denote n and , respectively. Concerning the behavior of the iteration of the Collatz function, for any integer n, there must exist an integer r so that
2.1. The modified Sarkovskii ordering and integer lattice
We convert the last row of numbers into the first column to get a modified Sarkovskii ordered integer lattice[6] as the following,
In the first row, they are odd numbers from left to right, that are . From the second row, each number is two times the number in its previous row, and so on.
2.2. The algebraic formula and Collatz graph
If we draw a line segment with an arrow between two digits in the lattice of integers in the modified Sarkovskii ordering, one being the original value x and the other being its value of the Collatz function , and then connect to , and so on to , we get a graph which can be called a Collatz graph.
For different integers k and l, if there is a common vertex in their Collatz graphs, their graphs will overlap from that point onwards until they reach the minimum value of 1. Using the Collatz function , we can obtain an algebraic formula of , where r is the number of vertical segments and m is the number of oblique segments in the Collatz graph,
For example, , , the algebraic formula is
and the Collatz graph is Figure 1.
And , , the algebraic formula is
and the Collatz graph is Figure 2.
We observe that there is a property present,
Proposition 1.
For positive integers , and , if , then there is a recurrence relation
where , and
For example, there are
We can get the recurrence formula about the Collatz function,
3. Numerical example
Using the above Collatz graphs of the integer lattice of the modified Sarkovskii ordering, we give the following algebraic formulas,
Example 2.
For the formula
we rewrite it as an integer equation,
Proof.
To calculate the power of 3 and the value of 18 using powers of 2,
substituting these expressions into the left-hand side of the above equation, one obtains,
and get the value which is equal to the right value of the equation. □
4. Convert the integer number from decimal to binary
Be inspired by the above, we use binary to rewrite the Collatz function (1) as the following formulas (2) and (3). We denote a binary number, which is a string of 0s and 1s, as , where × is either 1 or 0, e.g. ,
The result is
Namely, when n is an odd number, we multiply it with (11)2 and add 1 to the end of the binary number. For example, in Figure 3. When n is an even number, the division is equal to deleting the zero at the end in the binary number. We give the iteration of the Collatz function for 97 in binary as the following five tables.
Example 3.
For positive integer 1, we manipulate the iteration of the Collatz function in both decimal and binary numbers,
Example 4.
For positive integer , we manipulate the iteration of the Collatz function in both decimal and binary numbers,
Example 5.
For , we manipulate the iteration of the Collatz function in both decimal and binary numbers.
Example 6.
For , we manipulate the iteration of the Collatz function in both decimal and binary numbers.
Example 7. 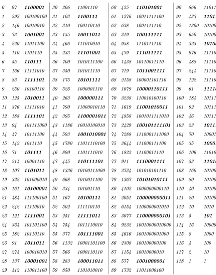
For we manipulate the iteration of the Collatz function in binary as the following table,

Corollary 8.
The Collatz function makes an odd integer number in binary bigger by adding 1 or 2 bits to the left of the sequence of 1s and 0s, and an even integer number in binary smaller by deleting all zeros at the end of the sequence of 1s and 0s. Thus, although in some cases the value of The Collatz function T(x) may be bigger than x in decimal, in general, the iteration of the Collatz function will make an integer number smaller and smaller, eventually reaching the smallest positive integer number 1.
We can rewrite the Collatz conjecture in binary, which makes it an easier problem to solve, thus allowing us to completely solve the Collatz conjecture.
Fact 9.
For any positive integer, under the Collatz function, the sequence of integer numbers in binary will eventually reach 1.
Proof.
For an odd binary integer, we multiply it by (11)2 and add 1 in the last bit, the result number must be an even number in binary which at least one zero at the end. We delete all these zeros, namely it is the division. This is the above corollary 8. Thus, we repeat this process as long as we can, because the bits of the sequence in binary of a positive integer number is finite. Eventually, we must in finitely steps reach the smallest positive integer number 1. □
Remark 10.
We can say that the 3x+1 problem is a converse proposition of "period three implies chaos" [4], and it is also an example of any one positive integer number having a period of 3 in the Collatz function.
5. Conclusions
We rewrite the Collatz function in binary, which makes the problem easier. The multiplications of (11)2 and divisions of (10)2 make the positive integer number smaller and smaller with the iterations of the Collatz function. In some cases, the value of the Collatz function may be bigger than x, thus allowing us to completely solve the Collatz conjecture.
References
- Jeffrey, C. Lagarias. The 3x + 1 Problem and Its Generalizations. American Mathematical Monthly, Vol. 92, No. 1, pp 3-23.(1985).
- Jeffrey, C. Lagarias. The 3x+1 Problem: An Overview, arXiv:2111.02635.
- Stefan, P. A Theorem of Sarkovshii on the existence of periodic orbits of continuous endomorphisms of the real line. Commun. math. Phys. 54,237-248(1977).
- Li, T. , Yorke, J. A. Period three implies chaos. Am. Mat. Monthly, 82, 985–992 (1975).
- TERENCE TAO, Almost all orbits of the Collatz map attain almost bounded values. arXiv:1909.03562v5, 2022,1,15. arXiv:1909.03562v5, 2022,1,15.
- Jishe FENG, Xiaomeng WANG, Xiaolu GAO, Zhuo PAN. The research and progress of the enumeration of lattice paths. Frontiers of Mathematics in China, 2022, 17(5): 747-766.
- Alf Kimms. The structure of the 3x+1 problem, Electronic Journal of Graph Theory and Applications, 9(1)(2021),157–174.
Figure 1.
The Collatz graph of in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.
Figure 1.
The Collatz graph of in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.
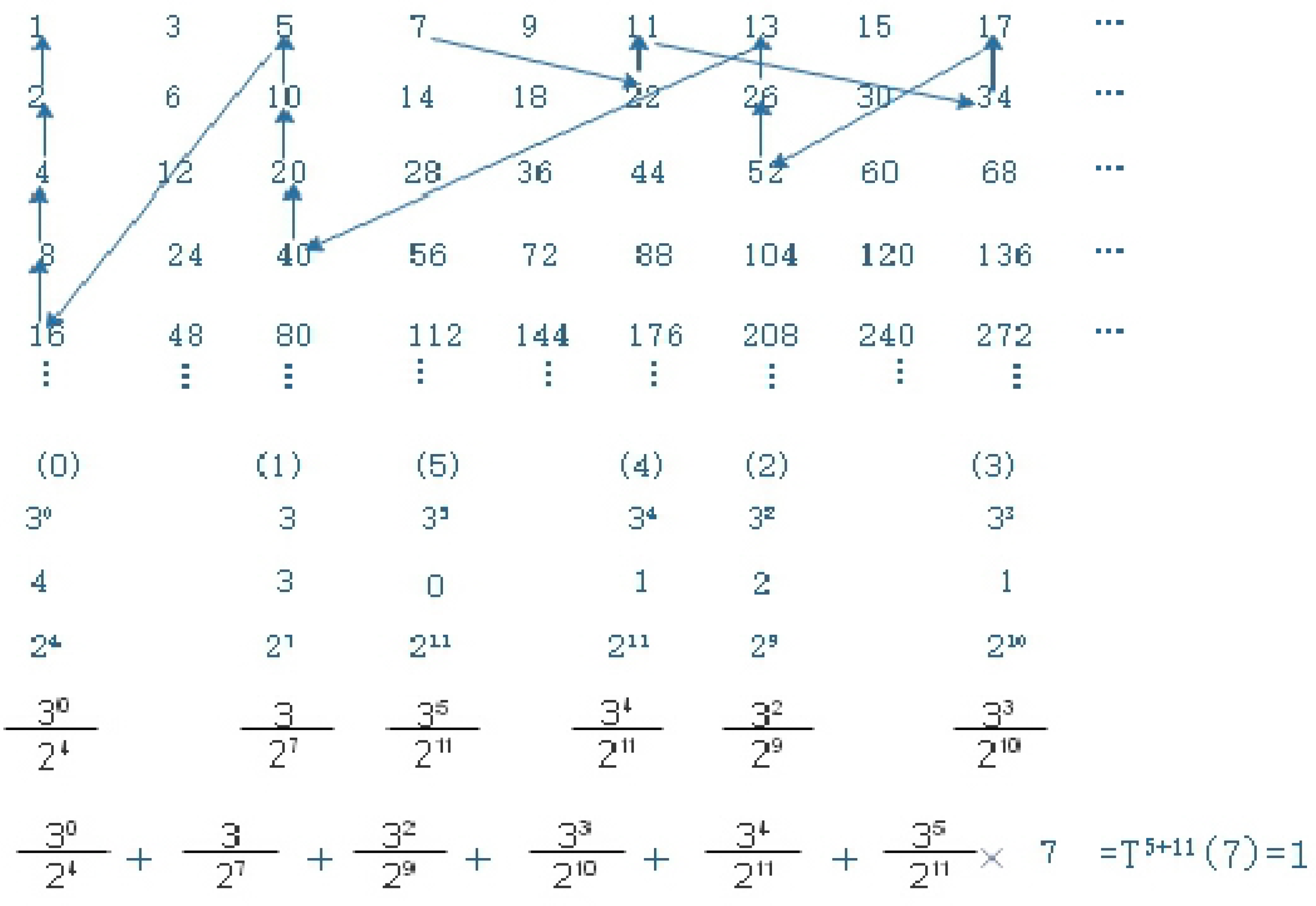
Figure 2.
The Collatz graph of in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.
Figure 2.
The Collatz graph of in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.
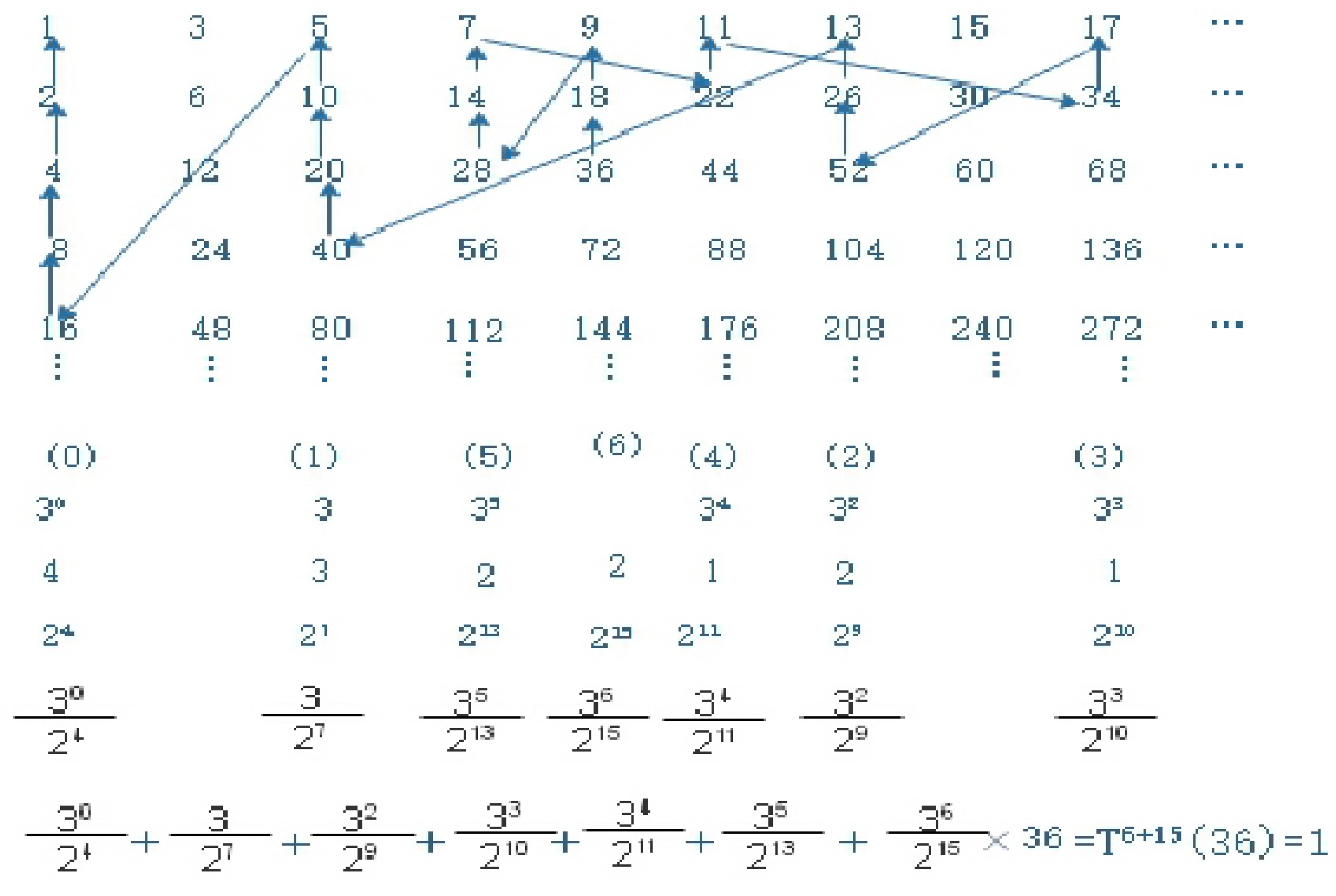
Figure 3.
For the Collatz function in binary, the first step is the multiplication in left, the second step is division in the right bottom.
Figure 3.
For the Collatz function in binary, the first step is the multiplication in left, the second step is division in the right bottom.
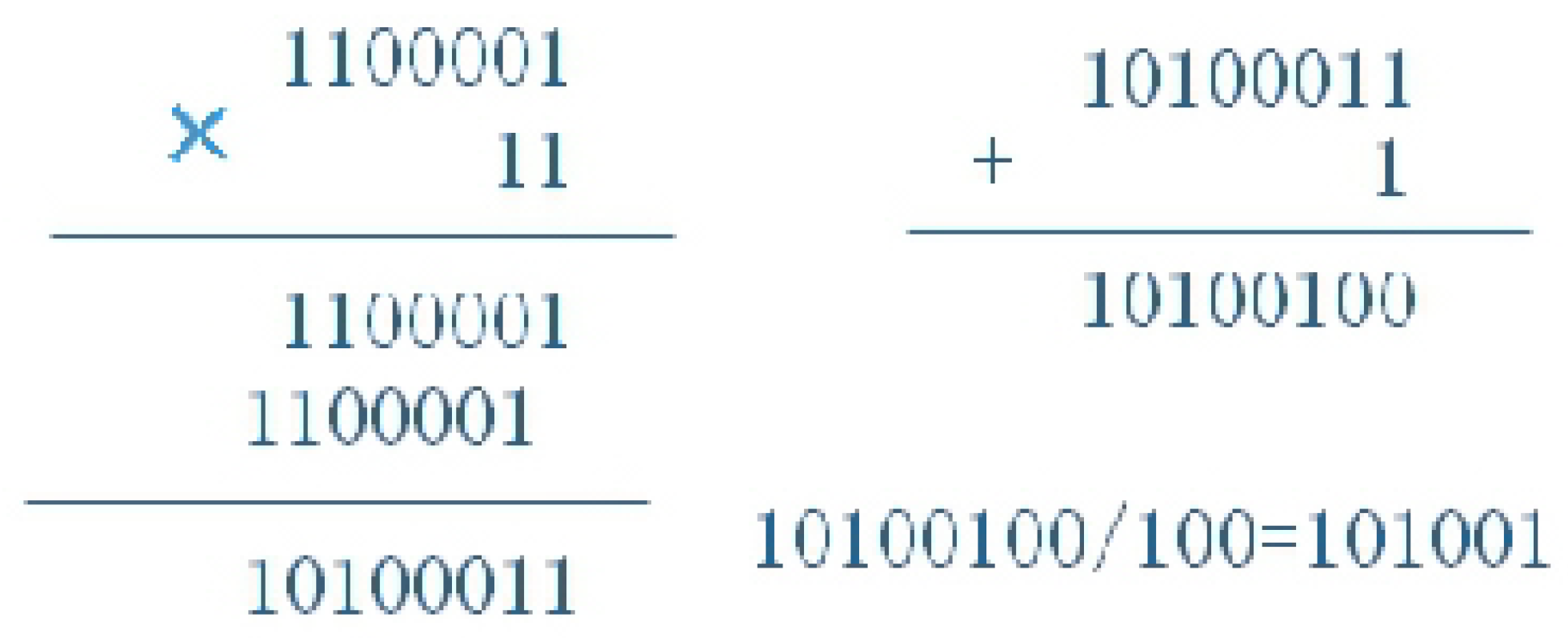
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




