Prerpints.org logo
Preprint
Article

Influence of Morphological Parameters on the Flow Development Within Human Airways

Altmetrics

Downloads

238

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 January 2023

Posted:

10 January 2023

Read the latest preprint version here

Alerts
Abstract
Anatomical airways parameters as length, diameter and angles have a strong effect on the flow dynamics. Aiming to explore the effect of variations of the bifurcation angle (BA) and carina rounding radius (CRR) of lower human airways on the respiratory processes, numerical simulations of airflow during inhalation and exhalation were performed using a synthetic bifurcation models. Geometries for the airways models were parameterized based on a set of different BA’s and several CRR’s. A range of Reynolds numbers (Re) relevant to the human breathing process were selected to analyzed the airflow behaviour. The numerical results show a significant influence of BA and the CRR on the development of the airflow within the airways, and therefore affecting some relevant features of the flow, namely the deformation of velocity profiles, alterations of pressure drop, the secondary flow patterns, and finally enhance or attenuation of wall shear stresses (WSS) appearing during the regular respiratory process. A particular relationship between velocity profiles, vorticity and the secondary flow patterns is also discussed.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

The human airways, as described by [37], are divided in three zones: conducting, transitional, and respiratory zones. The conducting zone is intended to transport the air from upper airways to the gas exchange zone, and is composed by the trachea, main bronchus, lobar bronchus and bronchioles. As explained by [25], the trachea stretches from the lower edge of the cricoid cartilage to the point of bifurcation of the main bronchus, also known as the carina. Some geometrical parameters such as diameters, lengths and angles, among others, make it possible to concretely characterise the types of morphological branches and therefore to establish a hierarchy of generations, as indicated by [31]. The bifurcation angle (BA) is a parameter closely related to lung morphology. Its numerical value depends on a number of factors including chest width ([13]), and gender and age ([2]). Similarly, the choice of techniques and methodologies used to measure the value of the BA has a significant influence on the determination of the BA, with radiography, computed tomography and in-vitro measurements on human cadavers being among the most commonly used ([5]). The values of the bifurcation angle reported in the literature vary widely. In [13] a range of subcarinal angle variation between 55 ∘ and 65 ∘ is shown for all ages, while in [5] a range between 50 ∘ to 130 ∘ was found. Furthermore, [8] reports ranges from 65.04 ∘ to 122.01 ∘ for men and from 69.46 ∘ to 113.94 ∘ for women. On the other hand, the study by [30] showed that this parameter has values ranging from 42 ∘ to 75 ∘ in human fetuses. The widening of the bifurcation angle may also be influenced by some physical pathologies such as pericardial fluid accumulation ([7]), or enlargement of the left atrium ([22,26]). These abnormal conditions cause displacement of the bronchi and thus alteration of the bifurcation angle.
Another relevant morphological parameter is the carina rounding radius (CRR). As pointed out by [16], the rounding radius varies in shape from an almost straight and sharp junction in some cases to a very blunt bifurcation in others. This radius can be related to the diameter of the daughter branch, from which a dimensionless parameter characterising the cross-section as a function of diameter can be estimated. This ratio, although variable, is approximately 0.1 ([16]). From a geometrical perspective, [24] describes four potential configurations for this parameter: blunt, parabolic, saddle, and asymmetric. These configurations affect the airflow patterns and conditions within the human airways. For example, asymmetric and saddle configurations are generally linked to the development of larger regions of instability compared to parabolic and symmetric shapes.
The ventilation process and other related phenomena occurring in the human airways during inhalation and exhalation processes have been extensively studied, both numerically and experimentally. Numerical simulation studies generally require the development of a computational domain from a geometrical configuration of the airways. The most commonly used models are the Weibel model [36] and the Horsfield model [16]. For the characterisation of these models it is necessary to define several morphological parameters, among which are the bifurcation angle and the carina rounding radius mentioned above. As described in several works (see [14,17,19,20,34]), the areas near the bifurcation points are of special attention, as they are, for example, associated with particle accumulation and dispersion. In fact, numerical work performed by [3] to analyze the effect of carina shape on particle behaviour shows how the deposition patterns are quite similar for carina geometries with a straight joint and one with a slight smoothing. Therefore, it is important to characterise the behaviour of fluid flow through the airways, as well as the affectation of flow due to variation of morphological parameters associated with bifurcation, such as BA and CRR. Although a lot of numerical investigations has focused on the analysis of flow through branched systems, the specific effect of BA and CRR on velocity profiles, secondary flow patterns, pressure drops and shear stresses has not been extensively studied.
In order to shed additional light on the effects of morphological parameters on the respiratory cycle, the main objective of the present work was to analyse the effect of variations of the bifurcation angle (BA) and carina rounding radius (CRR) on the respiratory process. The exploration of the effect of BA and CRR was performed by numerical experiments on synthetic models of the human lower airways. Geometric models were used for seven different BA values and three different CRRs. In addition, airflow at different Reynolds numbers was used to explore the influence of these morphological parameters on different flow regimes in the inspiratory and expiratory phases.
The present manuscript is organised as follows. The first section of this paper specifies the methodology and the numerical model used in this work, while the second section presents and discusses the results obtained from the numerical simulations for the inhalation (BA and CRR) and exhalation (BA only) processes. Finally, the last section of this manuscript presents the main conclusions and recommendations arising from this work.

2. Methodology

In this study, the effects of variations of two morphological parameters on the breathing process were explored. Bifurcation angle (BA) and carina rounding radius (CRR) were evaluated using independent geometric models and specific boundary conditions. Both morphological parameters were analysed using computational models implemented in OpenFOAM following the assumptions of incompressible and isothermal air as the working fluid. The details of each of these models and their respective methodological aspects are presented below.

2.1. Bifurcation Angle (BA). Morphological Definition and Flow Conditions

The analysis of the bifurcation angle was carried out using a synthetic Weibel model, which included the first three generations of human morphology (see [36]). Those generations represent the trachea, main bronchus and secondary bronchus. To simplify the analysis, the notation for airways provided by [8] was adopted. The values selected for the geometric parameters of the model are shown in Table 1 and illustrated in Figure 1.
To avoid problems related to flow development in the regions close to the outlets, the length of each of the last generation branches was extended to ensure a minimum length of five times the related outlet diameter. The bifurcation points were considered as straight joints, i.e. the carina rounding radius for these geometries was set equal to zero.
To evaluate the effect of the bifurcation angle (BA), two values of 55.9 ∘ and 63.1 ∘ were selected from experimental measurements of physiologically relevant subcarinal angles reported by [13]. As shown in Table 2, these angles correspond to the average measured for people between 50 and 60 years old, and the average for people 61 years old or older, respectively. In order to extend the analysis, a model with an additional value for BA of 70 ∘ was also explored, according to the mean angle with minimum resistance discussed by [15]. Each selected angle value was prescribed as the bifurcation angle for all model generations in each of the numerical experiments.
The two main breathing processes, i.e. exhalation and inhalation, were simulated numerically. For the simulations of the inhalation process, a uniform pressure boundary condition was prescribed for all outlets. As indicated by [4], this consideration allows the flow to adjust to different pressure gradients across different airway generations. [40] shows that the inflow velocity profile (on inhalation) significantly affects the flow development within the airway model, especially the distribution of mass flow in the branches.
To ensure proper flow development in the inhalation process simulations, a parabolic velocity profile was adopted. This profile was prescribed as symmetrical about the axis of the inlet duct, i.e. the trachea. Human breathing rates range from 0.2 L / s to 2.5 L / s ([23,24]), which corresponds to a range of Reynolds numbers (Re) between 200 and 2800. This range was observed by [1] in an experimental investigation using a pulsatile flow, where a maximum value of Re = 3000 was reached. Different Reynolds number values were explored in the present study, however, for brevity only the results for two values, representative of the extremes of the breathing process and corresponding to Re = 500 and Re = 2000 , are presented. The simulations of the exhalation process were set up using a uniform pressure condition at the outlet, corresponding in these cases to the trachea. In order to ensure fully developed flow before reaching the first bifurcations, parabolic velocity profiles were prescribed at each of the inlets representing the secondary bronchi. The velocity profiles were defined symmetric with respect to the centre lines of each last generation branch, and their maximum value equal to the maximum velocity obtained at the outlets in the respective inhalation cases. A Dirichlet no-slip boundary condition was applied to the velocity field at all airway walls.

2.2. Carina Rounding Radius (CRR). Morphological Definition and Flow Conditions

For the study of the CRR, a synthetic airways model based on the bifurcation geometry proposed by [21] was selected. Parameters and values for the implementation of this model are presented in detail in Table 3 and Figure 2. These generations represent the trachea and main bronchus. As in the BA study, the geometric model was adjusted to ensure a minimum length of the branches of the last generation of at least five times the related outflow diameter. Specifically, the parameters R d and α describe the curvature of the bifurcation. The CRR was non-dimensionalised using the following expression,
r c = C R R r t
where r c is the dimensionless rounding radius and r t the trachea radius.
As reported by [16] and [3], for human airways the average value of r c ranges around 0.1 . In fact, dimensionless rounding radius of 0.07 and 0.14 for symmetric and asymmetric airways, respectively, were used in the lung architecture characterisation work carried out by [21]. Based on the above, three dimensionless carina radii, equivalent to 0, 0.07 and 0.14 , were selected in the present work.
For the evaluation of the effect of the CRR, unlike the methodology followed for the BA analysis, only the inhalation breathing process was numerically simulated. A uniform pressure boundary condition was prescribed at the outlets, and a parabolic velocity profile at the tracheal inlet was adopted as the boundary condition at the flow inlet. As in the BA case, a Dirichlet-type no-slip boundary condition was defined at the airway walls. Likewise, results are also presented for numerical experiments carried out at Re = 500 and Re = 2000 .

2.3. Governing Equations and Computational Model

The ventilation process within human beings takes place at relatively low Reynolds numbers regimes, and at very low Mach numbers, even for agitated breathing situations ([23,24]). Therefore, for both BA and CRR experiments, the fluid flow through the synthetic human airways was assumed to be laminar and incompressible. Additionally, isothermal air was assumed as the working fluid, in line with the predefined flow conditions. The governing equations selected for this fluid flow regime were the conservation of mass equation and the Navier-Stokes (conservation of momentum) equations, which, for incompressible and isothermal flow, can be formulated as,
∇ · v → = 0
∂ u i ∂ t + ∇ · ( u i v → ) = − 1 ρ ∇ p + ∇ · ( ν ∇ u i )
where u i and v → are the i-th velocity component and the velocity vector field, respectively Equally, in Equation (3), p is the fluid pressure and ν = μ / ρ its kinematic viscosity with ρ standing for the density of the fluid. For the purposes of this work, the Reynolds number has been defined as
Re = ρ U a v e D μ
The governing equations were solved numerically using the open source computational fluid dynamics (CFD) suite OpenFOAM, which offers different schemes and numerical methods to solve different fluid flow phenomena. For the selected flow conditions and mathematical model, a finite volume method (FVM) approach was adopted. OpenFOAM (OF) offers a number of the so-called solvers and for the purposes of the present study the pisoFoam solver was selected, which is suitable for unsteady and incompressible laminar flows. Temporal integration was performed by using a backward scheme and the spatial discretisation was solved using second-order interpolation schemes for the gradient and divergence terms. The Geometric Agglomerated Algebraic Multigrid Solver (GAMG) was used to solve the Poisson-pressure equations, whereas the velocity field was obtained using the smoothSolver scheme available in OF. Pressure-velocity coupling was accomplished by using the PISO algorithm. The unstructured mesh generator snappyHexMesh was employed to generate the computational grid for the different geometries covered in this work. The average number of tetrahedral cells in the different computational models was 3.5 × 10 6 for BA’s study and 1.5 × 10 6 for CRR’s study. All the numerical simulations of this study were performed in parallel using a Simple Domain Decomposition.
Our discussion and results for both the effects of BA and CRR variations focus on the analysis of velocity profiles, secondary flow patterns, pressure drops and wall shear stresses (WSS). These indicators are generally analysed in the coronal and sagittal planes. In the present work, these values were explored specifically in the areas and at the points shown in Figure 3.

3. Results I. Effect of Variations of the Bifurcation Angle (BA)

3.1. Velocity Profiles

One of the main features of any flow pattern is the mean velocity profile. For the intended analysis, mean velocity profiles on the coronal plane for the selected BAs were constructed and are shown in Figure 4 for flows at Re = 500 and Re = 2000 . These curves were built using a normalized length d / D which was measured at the centre of each branch (LMB, LUB and LLB). The unit of the magnitude of the mean velocity is [m/s]. As reported by different authors ([6,23,32,38,41]), a narrowing of the velocity profile, as well as a shift of the maximum peak from the outer to the inner walls, are among the main effects of flow through a bifurcation. Observing Figure 4, it can be seen how these alterations of the velocity profiles are affected by changes in the bifurcation angle, especially at high Re numbers. For the Re = 500 regime the velocity profiles measured at the three selected positions (LMB, LUB and LLB) present a similar behavior, with a single velocity peak tending towards the inner wall of the branch, as shown in Figure 4a to Figure 4c. Noteworthy, at the lower Re regime, the BA mildly affects the narrowing of the profile, where there is a slightly increase of the peak value at lower BA values, although this effect is almost imperceptible in the LUB branch. In turn, for Re = 2000 , only in the LMB branch, Figure 4d, the behavior described above is preserved. For the LUB branch, shown in Figure 4e, a two-peaks profile is obtained for the larger angles. In the case of the LLB branch, Figure 4f, a deceleration in the center of the branch leads to the development of an even clearer two-peaks profile, an effect that becomes more noticeable as the BA decreases. It seems clear then that the BA deformation effect on the velocity profiles, at least in comparison with symmetrical profile patterns, is stronger as the Reynolds number increases.
Figure 5 show the velocity profiles taken in the sagittal plane for the selected angles at Re = 500 and Re = 2000 . These profiles show mirror symmetry around the axis of the branches, and a characteristic "M" shape can be identified. This shape was described by [32] and it illustrates how the flow velocity increases near the walls and decreases towards the branch axis. As shown in Figure 5a and Figure 5c for Re = 500 , and Figure 5d and Figure 5f for Re = 2000 , this effect is more noticeable for the LMB and LLB branches as BA increases. In contrast, for the LUB branch, Figure 5b and Figure 5e, it is more pronounced as BA decreases. Again, it is evident that the velocity profiles taken in the sagittal plane are more affected by the BA as the Reynolds number becomes larger.
Results for the exhalation stage, presented in Figure 6, show how the velocity profiles are symmetrical both in coronal and sagittal planes, a result that was previously observed and reported by [9,32]. The existence of a single velocity peak centered in the middle of the branch in the coronal plane is illustrated in Figure 6a. In turn, the velocity profiles in the sagittal plane develop again the M-shape, as shown in Figure 6b, which had been obtained for the branches in the inhalation stage. These effects are observed for Re = 500 and are more noticeable for lower BA values. The velocity profiles in the coronal and sagittal planes for Re = 2000 are shown in Figure 6c and Figure 6d, respectively. These plots show how a higher flow velocity leads to the generation of three peaks located both in the center and near the branch walls. For the profiles taken on the coronal plane this effect is more pronounced for larger BAs, contrary to the sagittal plane where the effect increases with lower BA’s.

3.2. Secondary Flow Patterns

Analysis of the secondary flow patterns (SFPs) was performed using a line integral convolution projection, commonly known as Surface LIC. Using the surface LIC method it is possible to establish visual analogies with temporal stability points, and to identify spatial points that act as orbit centres or as saddle points. In the present work, a correlation between these SFPs and velocity and vorticity profiles was obtained for all the bifurcation angles studied. By performing a juxtaposition of the Surface LIC plots with the velocity and vorticity profiles, a particular relationship between the vortical structures and the profiles was observed. An example of this characteristic link for the inhalation stage is presented in Figure 7 for a model featuring a BA equals to 55.9 ∘ . Examining the secondary flow patterns it seems clear that in all branches dean vortices ([10]) and saddle points are developed. These vortical structures are symmetric with respect to the coronal plane and their quantity and location depend on the Reynolds number. If the velocity and vorticity profiles are superposed to each other using a non-dimensional axis, a composed profile is obtained as those presented in Figure 7. In the present work such profiles are called “V-W" profiles. By examining these profiles, it is possible to observe how the velocity peak coincides with the point of minimum vorticity, and which also consistently coincides with the location of the saddle point on the secondary flow. As illustrated in Figure 7a and Figure 7b, the V-W curves for Re = 500 present a single velocity peak and a vorticity minimum which are aligned with the saddle point. For higher flow velocities two new vortices are generated and the saddle point is relocated. As previously shown in Figure 4f, for Re = 2000 there are two velocity peaks in the LLB branch. By analyzing Figure 7c, it is observed how the peak of higher magnitude is also aligned with a local minimum of vorticity and with the central saddle point. In turn, the secondary velocity peak is also aligned with another local minimum of vorticity and with another not so well defined saddle point.
The secondary flow patters and the V-W profiles at exhalation stage are shown in Figure 8. In line with the velocity profiles exhibit previously in Figure 6, these flow patterns and vorticity profiles are symmetric with respect to the coronal and sagittal planes. Figure 8a evidences the existance of four vortices rotating around the axial axis of the trachea for Re = 500 . The saddle point is located exactly at the center of the branch, as well as the peak velocity and the local minimum vorticity. Similarly, for the LMB branch at Re = 500 the saddle point remains centered on the axial axis and aligned with the peak velocity and minimum vorticity, as illustrates Figure 8c. As described in Figure 6d, the velocity profiles over the sagittal plane for Re = 2000 show three peaks. Figure 8b illustrates how these peaks are coincident with three local minima of vorticity and three saddle points visible through the flow patterns. For this case, eight vortices were clearly identifiable.

3.3. Pressure Behaviour

Pressure drop behaviour, as explained by [28], is directly influenced by changes in kinetic energy and by the dissipation of viscous energy. Geometry configuration and the definition of parameters such as length and cross section impact the pressure behavior in branched systems. In fact, the numerical study in micro-channel networks developed by [35] illustrates how the growth of the bifurcation angle influences the increase of pressure drops for branched systems of rectangular cross section. Plots of Δ P versus a normalizad length along the branches axial axes are presented in Figure 9. The unit of the magnitude of the pressure is [Pa]. In all generations for all the cases explored a local pressure growth at the beginning of the axial line is evidenced. This behavior is a result of the increase of pressure gradients generated by the bifurcation points. As might be expected, a higher magnitude in pressure drop is the result of an increase in BA for all branches. This local growth is slightly noticeable for the LLB branch (Figure 9c and Figure 9f) with respect to the LUB branch (Figure 9b and Figure 9e). This difference is related to the velocity profiles over the coronal and sagittal plane shown in Figure 4 and Figure 5, respectively. For the LLB branch, the velocity magnitudes are slightly larger than for the LUB branch.
The pressure drop profiles in the exhalation state for Re = 500 are shown in Figure 10. these profiles are plotted in the upstream direction, i.e., from the last generation towards the trachea. Contrary to the results obtained in the inhalation state, no particular behavior derived from the bifurcation angles is identified for the exhalation stage.

3.4. Wall Shear Stresses

During inhalation and exhalation stages, the maximum shear stresses developed are located on the inner and externals wall, respectively, as reported by different authors ([11,27,39]). In a similar manner as discussed with the pressure drop, and as it might be expected, this behaviour of the WSS is also strongly related to the specific changes of the velocity profiles reported in this paper. Particularly, the previously discussed tendency of displacement of the peak of the profiles (shown earlier in Figure 4) is always associated to the appearance of regions of maximum wall shear stress.
Wall shear stress was measured along to the inner wall (for inhalation) and in a perpendicular direction of the inner wall (for exhalation) on each of the branches. In the different plots (Figure 11 and Figure 12), the length is presented in normalized form ( x / L , where L is the total length of the branch). In all cases, for the x-label, the value of “0” and “1” refers to the upstream and downstream, respectively. The unit of the magnitude of the WSS is [Pa]. By analysing the effect of the bifurcation angle (BA) on the wall shear stress distribution for the inhalation process, it is possible to determine that, as observed in different studies, the maximum shear stress is located towards the intersection of the bifurcation, that is in the region nearby the joints. It is further observed that for the different branches, as the BA considered is augmented, the magnitude of the maximum WSS decreases, giving as a result that, for instance, the highest figures for WSS are observed for the smallest angle, which in the present study is BA= 55.9 ° . Examining the WSS in each of the branches, along the local axial direction and therefore progressing through the branching line, the WSS seem to collapse reaching an average common value regardless of the BA explored. This trend, however, is sightly disrupted in LLB (Figure 11c and Figure 11f), where it is possible to appreciate a very subtle difference between the Mean values of wall shear stress attained for BA= 63.1 ° in comparison to the other BA explored. Thus, it can be established that the shear forces vary with respect to the bifurcation angle only in the zones or regions near the bifurcation point, but converging to an average value downstream of such a point when considering inhalation.
The results obtained for the exhalation process, and presented in Figure 12, show a complete different picture for the distribution of the wall shear stresses, at least in comparison with the inhalation process described just above. For instance, it is possible to observe that exhalation brings about an increase of the WSS in the first half of each branch, so the maximum values of WSS are present between 0.2 < x / L < 0.5 . In this case x / L is measured from the upstream bifurcation following the downstream direction and, as mentioned previously, using as normalising factor the length of the respective branch L. In any case, for all the branches, there is a reduction of the WSS that seems to have a similar behaviour for the different angles considered in this work. In this exhalation process, however, a converging or collapsing trend to an average value is not clear. Noteworthy, the maximum WSS in each branch is accompanied by strong oscillations, albeit this oscillatory tendency is stronger for LMB than for the TRA. This particular effect may be related to the onset of flow instabilities and eventually some perturbations which grow in the flow direction as a result of the increment of the local flow rate and cross section area. A clear indication of this phenomena is increase of the local Reynolds number as the fluid flows downstream towards the TRA.

4. Results II. Effect of Variations of the Carina Rounding Radius (CRR)

4.1. Velocity Profiles

Mean velocity profiles on the coronal plane for the selected CRRs were constructed and are shown in Figure 13 and Figure 14 for flows at Re = 500 and Re = 2000 . Newly, these curves were built using a normalized length d / D and these were measured in sections at 20% and 50% of the total LMB branch length, with the main intention of analyzing the velocity profiles both at a point close to the carina and in the middle of the branch. Figure 13 shows how the rounding radius has a slight effect on the velocity profiles measured at 20% of the LMB length. The narrowing of the profile toward the inner face of the branch is more noticeable as the CRR is larger. As the flow is transported downstream this behavior becomes almost imperceptible, as can be seen in Figure 14 for velocity profiles measured at 50% of the LMB length.
Figure 15 and Figure 16 show the velocity profiles over the sagittal plane for Re = 500 and Re = 2000 . Theses measurement were taken at 20% and 50% of the LMB branch length. In contrast to the coronal plane profiles, the effect of the CRR variation is clearly noticeable. The flow experiences a greater acceleration as the CRR is larger for both Re = 500 and Re = 2000 , respectively. It is also possible to observe how the profiles near the bifurcation develop the maximum peak at the center of the branch, as illustrated in Figure 15. The profiles take on the characteristic M-shape previously described in the results for the BA as the flow moves downstream, as shown in Figure 16.

4.2. Vorticity Profiles and Secondary Flow Patterns

Vorticity profiles on the coronal plane for different for the selected CRR are shown in Figure 17 for flows at Re = 500 and Re = 2000 . These curves were built using a normalized length d/D and a normalized vorticity ω / ω m a x and were taken at 20% of the total LMB branch length. The vorticity measured at 50% branch length is not shown in this paper since it does not show any singular behavioral pattern concerning the CRR variation. The maximum vorticity intensity is located on the inner wall of the branch for Re = 500 , as shown in Figure 17a. The existence of a local vorticity peak located near the center of the branch is also evidenced. The increase of the magnitude of this local peak is associated with the increase of the CRR. This effect is preserved as the flow accelerates, as seen in Figure 17b for Re = 2000 . This behavior indicates that the rounding radius influences to some extent the rotation that the flow experiences as it passes through the bifurcation.
As well as in the BA study, the secondary flow patterns were performed using the Surface LIC method. Figure 18 shows the juxtaposition of the Surface LIC plots with the velocity and vorticity profiles in the sections at 20% and 50% of the branch length. These plots corresponding to the geometry with r c = 0 at Re = 2000 . Two dean vortices and a saddle point are clearly identified and the relationship of these vortical structures to the V-W curves is again observed. As illustrated in Figure 18a, at 20% of the branch length the vorticity has not reached its global minimum. This value is reached as the flow advances downstream and its location coincides with the peak velocity, as shown in Figure 18b.

4.3. Pressure Behaviour

The pressure drop across the LMB branch for the selected RRCs is shown in Figure 19 for flows at Re = 500 and Re = 2000 . These curves were built using a normalized length x/L which was measured over the branch inner wall. The plots show only 20% of the length since beyond this point the curves do not show any CRR-derived variation. The maximum peak pressure is located exactly at the bifurcation point and is higher as the CRR increases. At the same time it can be observed that the pressure drop is also higher for larger CRRs and smaller for a straight junction. This effect is evident in the two Reynolds numbers analyzed.

4.4. Wall Shear Stresses

As with the pressure drop, the wall shear stress behavior is measured on the internal wall of the branch and expressed using the normalized length x/L. These curves are plotted up to 50% of the length since after this point the effects are negligible. Figure 20a shows how the maximum WSS for Re = 500 is developed by the bifurcation with straight joint r c = 0 . As expected, this point acts as a kind of stress concentrator. The location of the WSS maximum moves away from the carina in the downstream direction as the CRR increases and the joint becomes smoother. This displacement tendency of the maximum WSS is also observed for Re = 2000 , as illustrated in Figure 20b. Although the WSS is still higher for the straight joint at the exact point of the carina, for this case the maximum WSS is developed by the geometry with radius r c = 0.14 . These results are in line with the velocity profiles in the sagittal plane. The increase of the rounding radius generates a higher flow acceleration and therefore a higher accumulation of wall shear stresses.

5. Discussion and Conclusions

The present numerical study aimed to produce an assessment of the effect of bifurcation angle (BA) and the carina rounding radius (CRR) on the behaviour of the flow through synthetic respiratory airway models. The main focus was to detail and quantify the influence of these morphological parameters on the respiratory process examining both the inhalation and exhalation stages. Numerical experiments were performed on airway models set up for three different angles and three rounding radius, using two symmetrical models ([36] for BA analysis and [21] model for CRR). The respiratory mechanisms of human inhalation and exhalation were decoupled and hence considered as independent processes. Analysis of the results derived from the variations of the bifurcation angle indicate a remarkable influence of this morphological parameter on the flow behavior through the airways. For the inhaled state, the narrowing of the velocity profile in the coronal plane with a tendency towards the inner wall of the airway becomes more pronounced as the BA increases. In turn, this variation in BA drives the acceleration near the walls of the branches in the profiles measured in the sagittal plane. A particular relationship between the vortical structures and the velocity an vorticity profiles was identified: the coincidence in the location of the peak velocity profile, the miminum vorticity magnitud and the saddle point seen through the secondary flow patterns. This behavior is observed for the different flow velocities analyzed. Moreover, a local pressure growth is generated by gradients at the bifurcation points. This local growth has a greater magnitude for the larger BAs. At the same time, it is noteworthy that this larger angles impacts on the decrease of wall shear stresses developed near the bifurcation. The variation of the BA also has a noticeable effect on the velocity profiles in the exhalation stage. The mirror symmetry around the branch axis in both the coronal and sagittal planes is the most notable feature in these profiles. As the flow velocity increases from Re = 500 to Re = 2000 an acceleration near the branch walls is evident. This acceleration is greater for the lower BAs in the sagittal plane and for the higher BAs in the coronal plane. Wall shear stress for this stage exhibits a particular increase in the first half of the branch for all cases. This behaviour may be related to the resistance and oscillations produced by the changes in the cross section area as the flow is transported through the branches. The relationship between the V-W profiles and the vortical structures is also observed at exhalation. In fact, this coincidence in the location of the vortical structures is present in all existing velocity peaks. Contrary to the results obtained at inhalation stage, the effect of the BA varations on the behaviour of the pressure flow was almost unnoticeable.
As with the BA, the results obtained in the CRR analysis show a noticeable impact on the flow. The increase in the CRR causes a greater acceleration of the flow observed in the velocity profiles over the sagittal plane. In turn, it also slightly influences the narrowing of the profile toward the inner walls of the airways measured in the coronal plane. The variation of this morphological parameter also has an impact on the flow rotation. As the radius increases, the rotation observed through the vorticity curves on the coronal plane is greater. The relationship of flow patterns to velocity and vorticity profiles is also evidenced by variations in the CRR. The carina is the point of interest for the analysis of pressure drop and wall shear stress. When the bifurcation is considered as a straight junction (with CRR equal to 0) the maximum pressure at the carina decreases and the WSS increases. With the increase of the CRR, i.e. the smoothing of the junction, the pressure drop starts to increase and the location of the maximum WSS moves downstream in the branch.

Author Contributions

Conceptualization, AS Espinosa-Moreno and CA Duque-Daza; Formal analysis, AS Espinosa-Moreno and CA Duque-Daza; Investigation, AS Espinosa-Moreno; Methodology, AS Espinosa-Moreno; Resources, CA Duque-Daza and DA Garzón-Alvarado; Software, AS Espinosa-Moreno; Supervision, CA Duque-Daza and DA Garzón-Alvarado; Validation, AS Espinosa-Moreno and CA Duque-Daza; Writing – original draft, AS Espinosa-Moreno; Writing – review & editing, CA Duque-Daza and DA Garzón-Alvarado.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The work was technical supported by the investigation group GNUM (Grupo de Modelado y Metodos Numericos en Ingenieria) of the Universidad Nacional de Colombia.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CFD Computational Fluids Dynamics
WSS Wall Shear Stress
BA Bifurcation angle
CRR Carina rounding radius
TRA Trachea
RMB Right Main Bronchus
LMB Left Main Bronchus
RUB Right Upper Lobar Bronchus
LUB Left Upper Lobar Bronchus
RIB Right Intermediate Bronchus
LLB Left Lower Lobar Bronchus

References

  1. Adler, K.; Brücker, C. Dynamic flow in a realistic model of the upper human lung airways. Experiments in Fluids 2007, 43, 411. [Google Scholar] [CrossRef]
  2. Alavi, S.M.; Keats, T.E.; O’Brien, W.M. The angle of tracheal bifurcation: its normal mensuration. American Journal of Roentgenology 1970, 108, 546–549. [Google Scholar] [CrossRef] [PubMed]
  3. Balashazy, I.; Heistracher, T.; Hofmann, W. Air flow and particle deposition patterns in bronchial airway bifurcations: the effect of different CFD models and bifurcation geometries. Journal of Aerosol Medicine 1996, 9, 287–301. [Google Scholar] [CrossRef]
  4. Bauer, K.; Brücker, C. The influence of airway tree geometry and ventilation frequency on airflow distribution. Journal of biomechanical engineering 2015, 137, 081001. [Google Scholar] [CrossRef] [PubMed]
  5. Bipinchandra, K.; Waheed, A.R.A.; Yadav, N.; Diwan, C. Study of sub carinal angle of human trachea by computerized tomography. International Journal of Anatomy and Researchy 2016, 4, 2828–2832. [Google Scholar] [CrossRef]
  6. Calay, R.; Kurujareon, J.; Holdø, A.E. Numerical simulation of respiratory flow patterns within human lung. Respiratory physiology & neurobiology 2002, 130, 201–221. [Google Scholar] [CrossRef]
  7. Chen, J.; Putman, C.E.; Hedlund, L.W.; Dahmash, N.; Roberts, L. Widening of the subcarinal angle by pericardial effusion. American Journal of Roentgenology 1982, 139, 883–887. [Google Scholar] [CrossRef]
  8. Christou, S.; Chatziathanasiou, T.; Angeli, S.; Koullapis, P.; Stylianou, F.; Sznitman, J.; Kassinos, S.C. Anatomical variability in the upper tracheobronchial tree: sex-based differences and implications for personalized inhalation therapies. Journal of Applied Physiology, 2021, 130, 678–707. [Google Scholar] [CrossRef]
  9. Corieri, P. Experimental and numerical investigation of flows in bifurcations within lung airways. Doctoral dissertation, Ph. D. thesis, von Karman Institute for Fluid Dynamics, Université Libre de Bruxelles and Rheinisch-Westfälische Technische Hochschule Aachen, 1994.
  10. Dean, W.R. Note on the motion of fluid in a curved pipe. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1927, 4, 208–223. [Google Scholar] [CrossRef]
  11. Green, A.S. Modelling of peak-flow wall shear stress in major airways of the lung. Journal of Biomechanics 2004, 37, 661–667. [Google Scholar] [CrossRef]
  12. Fresconi, F.E.; Prasad, A.K. Secondary velocity fields in the conducting airways of the human lung. Journal of biomechanical engineering 2007, 129, 722–732. [Google Scholar] [CrossRef]
  13. Haskin, P.H.; Goodman, L. Normal tracheal bifurcation angle: a reassessment. American Journal of Roentgenology 1982, 139, 879–882. [Google Scholar] [CrossRef]
  14. Hofmann, W. Modelling inhaled particle deposition in the human lung: a review. Journal of Aerosol Science 2011, 42, 693–724. [Google Scholar] [CrossRef]
  15. Horsfield, K.; Cumming, G. Angles of branching and diameters of branches in the human bronchial tree. The Bulletin of mathematical biophysics 1967, 29, 245–259. [Google Scholar] [CrossRef]
  16. Horsfield, K.; Dart, G.; Olson, D.E.; Filley, G.F.; Cumming, G. Models of the human bronchial tree. Journal of applied physiology 1971, 31, 207–217. [Google Scholar] [CrossRef]
  17. Islam, M.S.; Paul, G.; Ong, H.X.; Young, P.M.; Gu, Y.T.; Saha, S.C. A review of respiratory anatomical development, air flow characterization and particle deposition. International journal of environmental research and public health 2020, 17, 380. [Google Scholar] [CrossRef] [PubMed]
  18. Kang, M.Y.; Hwang, J.; Lee, J.W. Effect of geometric variations on pressure loss for a model bifurcation of the human lung airway. Journal of biomechanics 2011, 44, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
  19. Kim, Y.; Tong, Z.; Chan, H.; Yang, R. CFD modelling of air and particle flows in different airway models. Journal of Aerosol Science 2019, 134, 14–28. [Google Scholar] [CrossRef]
  20. Lai, T.C.; Morsi, Y.S.; Das, S.; Owida, A. Numerical analysis of particle deposition in asymmetrical human upper airways under different inhalation cycles. Journal of Mechanics in Medicine and Biology 2013, 13, 1350068. [Google Scholar] [CrossRef]
  21. Lee, D.; Park, S.S.; Ban-Weiss, G.A.; Fanucchi, M.V.; Plopper, C.G.; Wexler, A.S. Bifurcation model for characterization of pulmonary architecture. The Anatomical Record 2008, 291, 379–389. [Google Scholar] [CrossRef]
  22. Lin, C.; Lee, J.-H.; Hsieh, C.-M. The correlation between subcarinal angle and left atrial volume. Acta Cardiologica Sinica 2012, 28, 332–336. [Google Scholar]
  23. Liu, Y.; So, R.; Zhang, C. Modeling the bifurcating flow in a human lung airway. Journal of biomechanics 2002, 35, 465–473. [Google Scholar] [CrossRef]
  24. Martonen, T.; Yang, Y.; Xue, Z. Effects of carinal ridge shapes on lung airstreams. Aerosol science and technology 1994, 21, 119–136. [Google Scholar] [CrossRef]
  25. Minnich, D.J.; Mathisen, D.J. Anatomy of the trachea, carina, and bronchi. Thoracic surgery clinics 2007, 17.4, 571–585. [Google Scholar] [CrossRef]
  26. Murray, J.; Brown, A.; Anagnostou, E.; Senior, R. Widening of the tracheal bifurcation on chest radiographs: value as a sign of left atrial enlargement. AJR. American journal of roentgenology 1995, 164, 1089–1092. [Google Scholar] [CrossRef]
  27. Nucci, Gianluca; SUKI, Béla; Lutchen, Kenneth. Modeling airflow-related shear stress during heterogeneous constriction and mechanical ventilation. Journal of Applied Physiology 2003, 95, 348–356. [CrossRef] [PubMed]
  28. Pedley, T.; Schroter, R.; Sudlow, M. Energy losses and pressure drop in models of human airways. Respiration physiology 1970, 9, 371–386. [Google Scholar] [CrossRef]
  29. Pedley, T.; Schroter, R.; Sudlow, M. Flow and pressure drop in systems of repeatedly branching tubes. Journal of Fluid Mechanics 1971, 46, 365–383. [Google Scholar] [CrossRef]
  30. Sahni, D.; Batra, Y.K.; Rajeev, S. Anatomical dimensions of trachea, main bronchi, subcarinal and bronchial angles in fetuses measured ex vivo. Pediatric Anesthesia 2006, 18, 1029–1034. [Google Scholar] [CrossRef]
  31. Singhal, S.; Henderson, R.; Horsfield, K.; Harding, K.; Cumming, G. Morphometry of the human pulmonary arterial tree. Circulation Research 1973, 33, 190–197. [Google Scholar] [CrossRef]
  32. Schroter, R.; Sudlow, M. Flow patterns in models of the human bronchial airways. Respiration physiology 1969, 7, 341–355. [Google Scholar] [CrossRef] [PubMed]
  33. Snyder, B.; Olson, D. Flow development in a model airway bronchus. Journal of Fluid Mechanics 1989, 207, 379–392. [Google Scholar] [CrossRef]
  34. Tsega, E.G.; Katiyar, V.K.; Gupta, P. Numerical Simulation of Transport and Deposition of Dust Particles in Human Tracheobronchial Airways. International Journal of Biomedical Science and Engineering 2019, 7, 8. [Google Scholar] [CrossRef]
  35. Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Effect of bifurcation angle in tree-shaped microchannel networks. Journal of Applied Physics 2007, 102, 073530. [Google Scholar] [CrossRef]
  36. Weibel, E.R.; Cournand, A.F.; Richards, D.W. Morphometry of the human lung, 1st ed.; Springer Verlag OHG Berlin Goltigen Heidelberg: Berlin, Germany, 1963. [Google Scholar]
  37. West, J.B. Respiratory physiology: the essentials, 9th ed.; Lippincott Williams & Wilkins: United States, 2012. [Google Scholar]
  38. Van Ertbruggen, C.; Hirsch, C.; Paiva, M. Anatomically based three-dimensional model of airways to simulate flow and particle transport using computational fluid dynamics. Journal of Applied Physiology 2005, 98, 970–980. [Google Scholar] [CrossRef] [PubMed]
  39. Xia, G.; Tawhai, M.H.; Hoffman, E.A.; Lin, C.-L. Airway wall stiffening increases peak wall shear stress: a fluid-structure interaction study in rigid and compliant airways. Annals of biomedical engineering 2010, 38, 1836–1853. [Google Scholar] [CrossRef] [PubMed]
  40. Yang, X.; Liu, Y.; So, R.; Yang, J. The effect of inlet velocity profile on the bifurcation COPD airway flow. Computers in biology and medicine 2006, 36, 181–194. [Google Scholar] [CrossRef]
  41. Zhao, Y.; Lieber, B.B. Steady inspiratory flow in a model symmetric bifurcation. Transactions of the ASME-K-Journal of Biomechanical Engineering 1994, 116, 488–496. [Google Scholar] [CrossRef]
Preprints 67147 g001
Figure 1. Geometric parameters of Weibel model [36].
Figure 1. Geometric parameters of Weibel model [36].
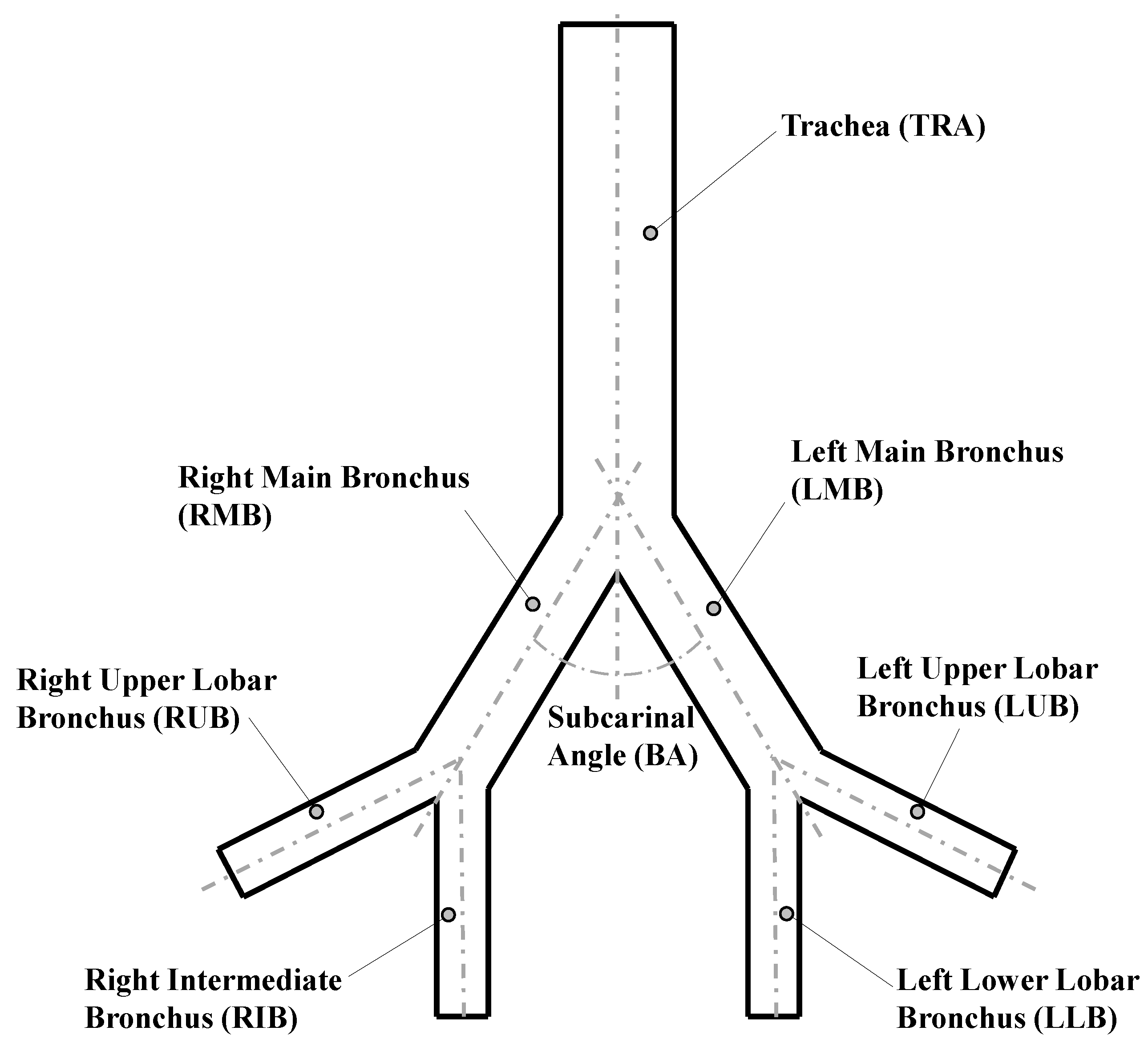
Preprints 67147 g001
Preprints 67147 g002
Figure 2. Bifurcation model geometry.
Figure 2. Bifurcation model geometry.
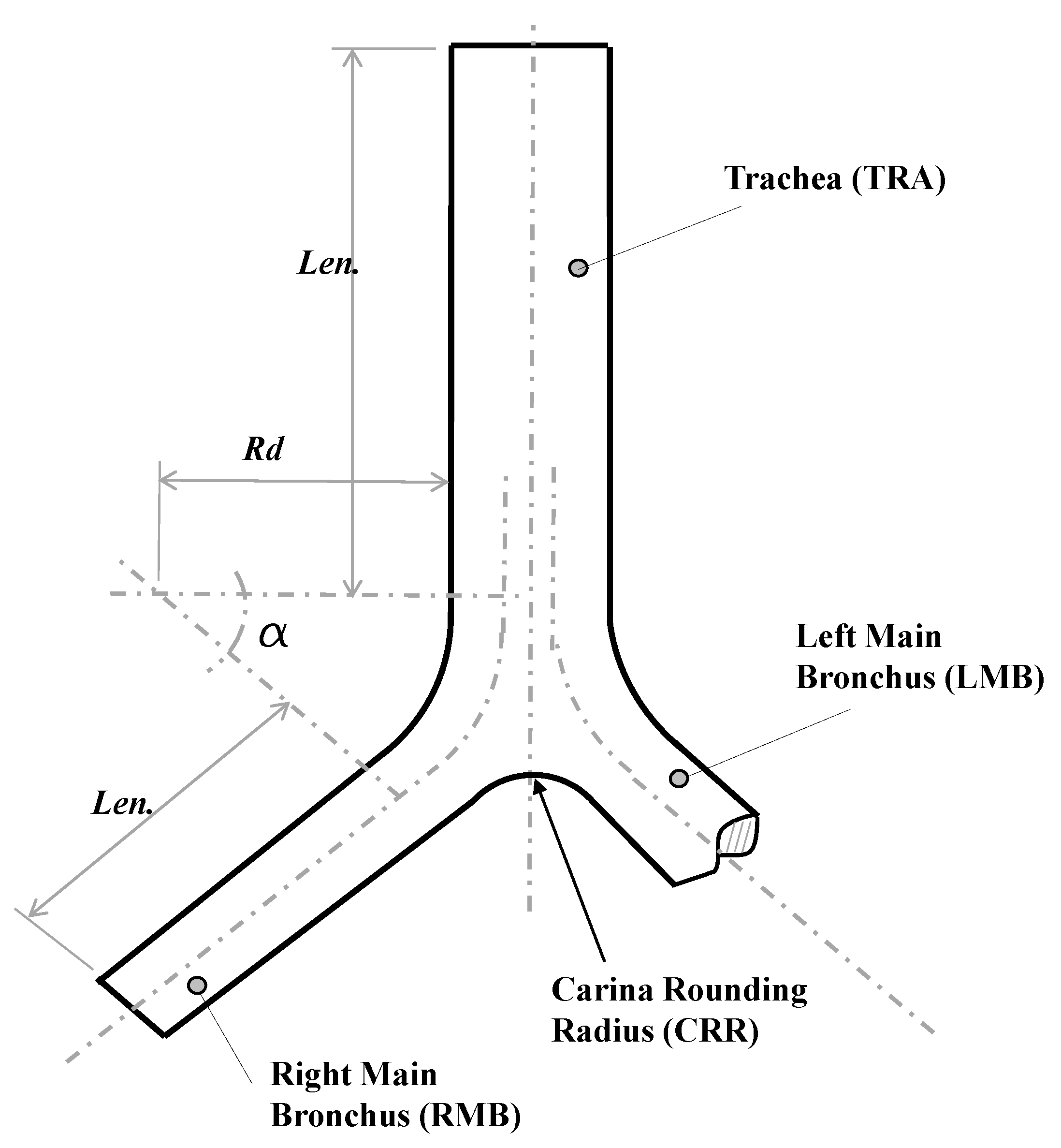
Preprints 67147 g002
Preprints 67147 g003
Figure 3. Indicative scheme of the zones and points where the results are reported.
Figure 3. Indicative scheme of the zones and points where the results are reported.
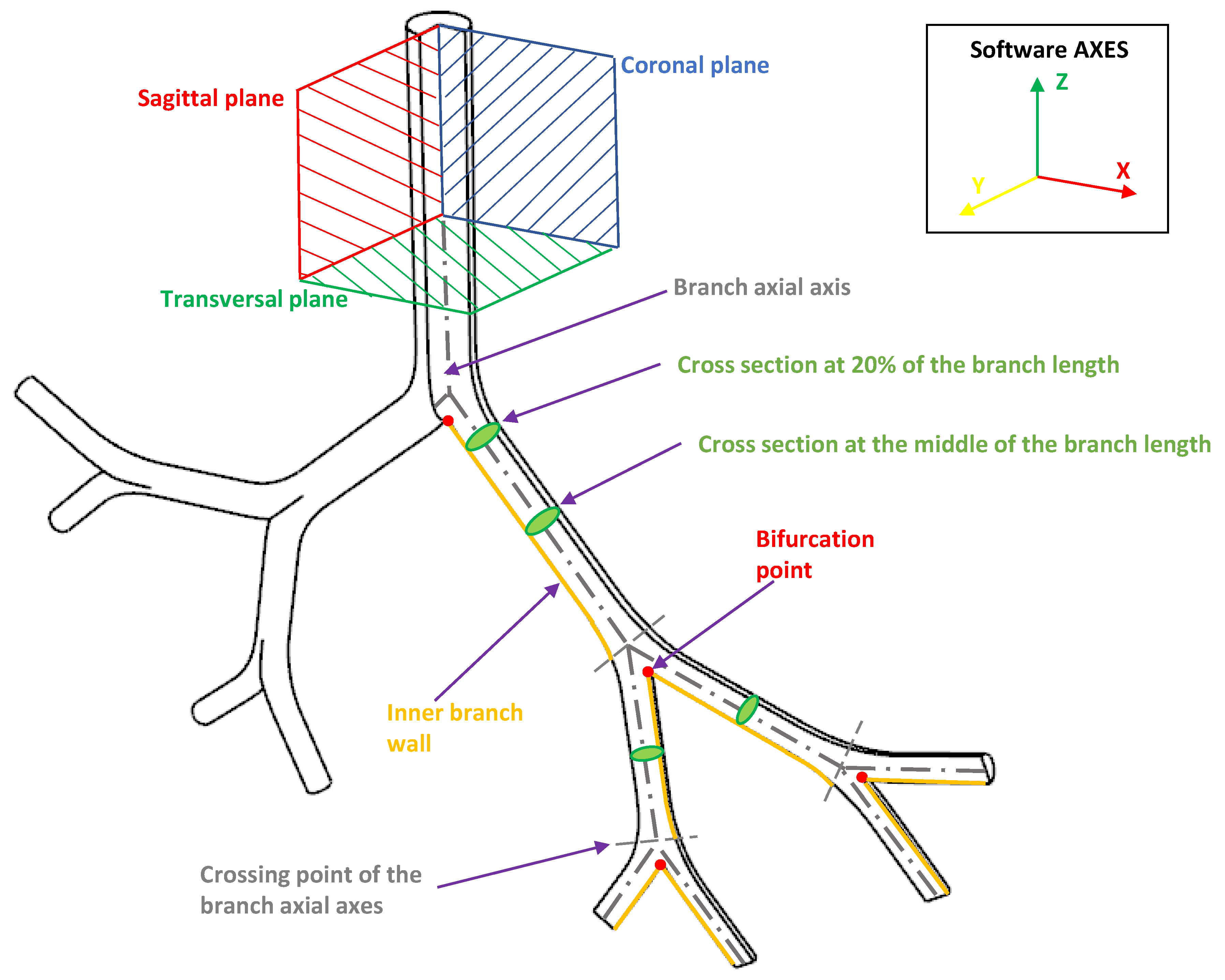
Preprints 67147 g003
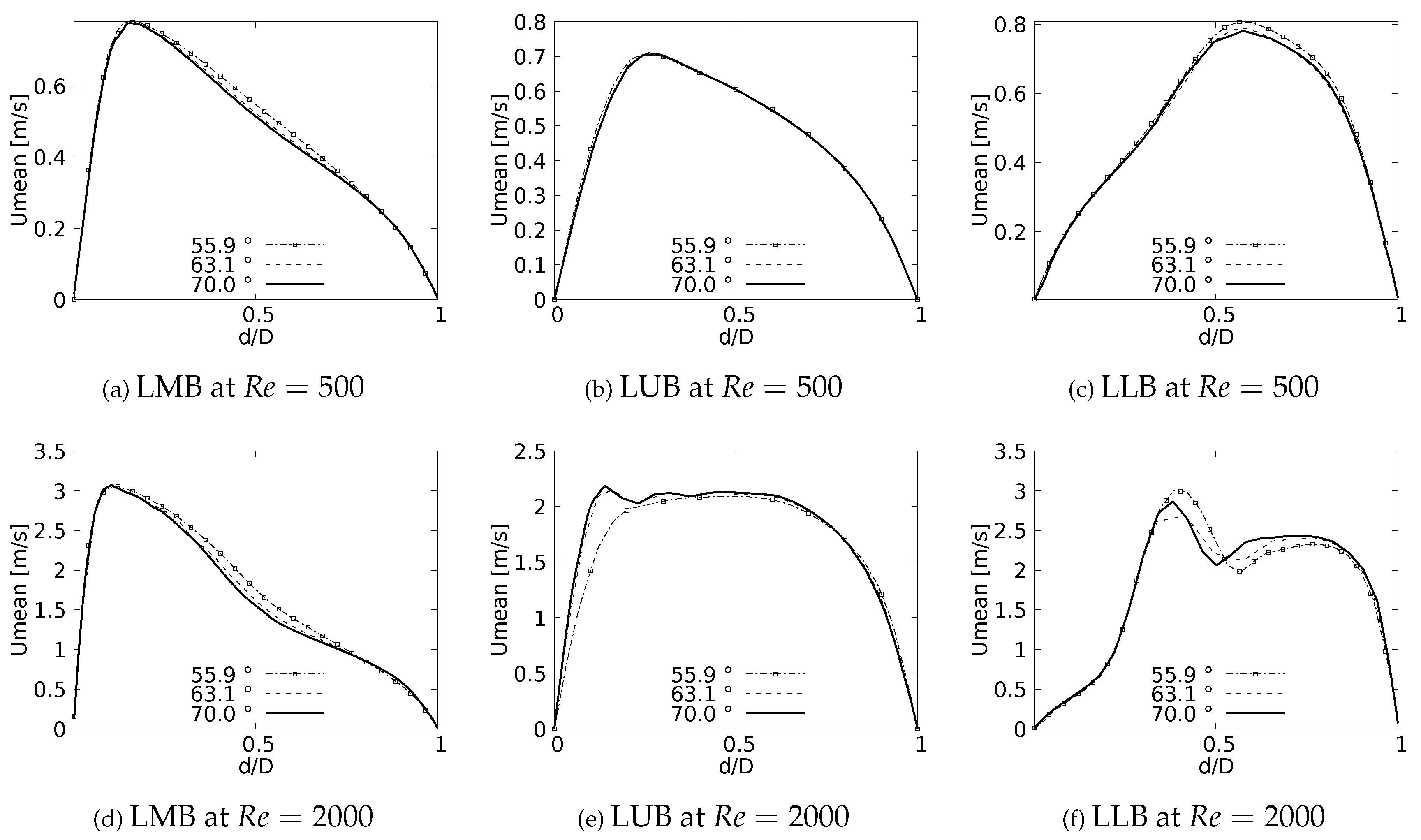
Preprints 67147 g004
Figure 4. Velocity profiles on coronal plane.
Figure 4. Velocity profiles on coronal plane.
Preprints 67147 g004
Preprints 67147 g005
Figure 5. Velocity profiles on sagittal plane.
Figure 5. Velocity profiles on sagittal plane.
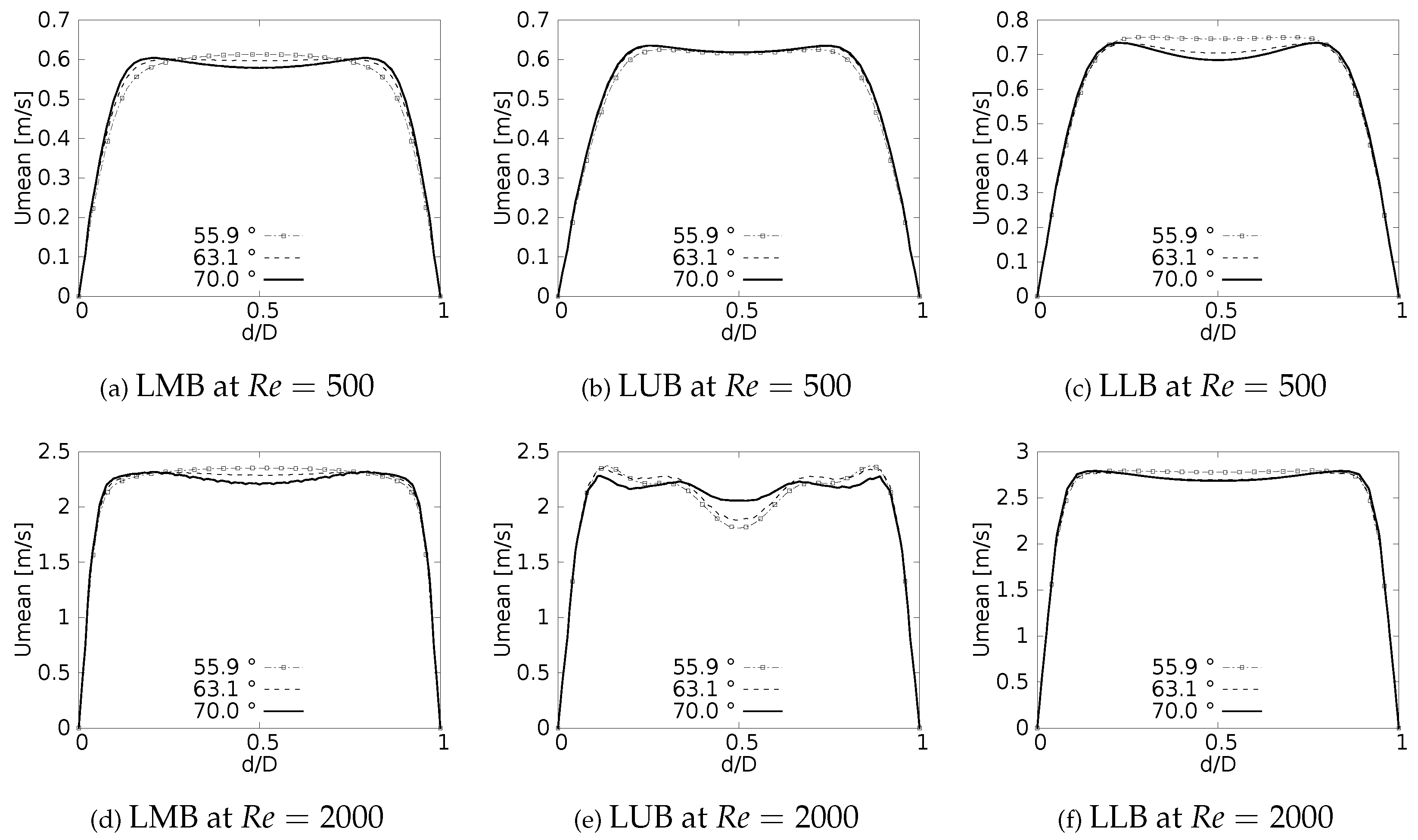
Preprints 67147 g005
Preprints 67147 g006
Figure 6. Velocity profiles at exhalation stage for TRA branch.
Figure 6. Velocity profiles at exhalation stage for TRA branch.
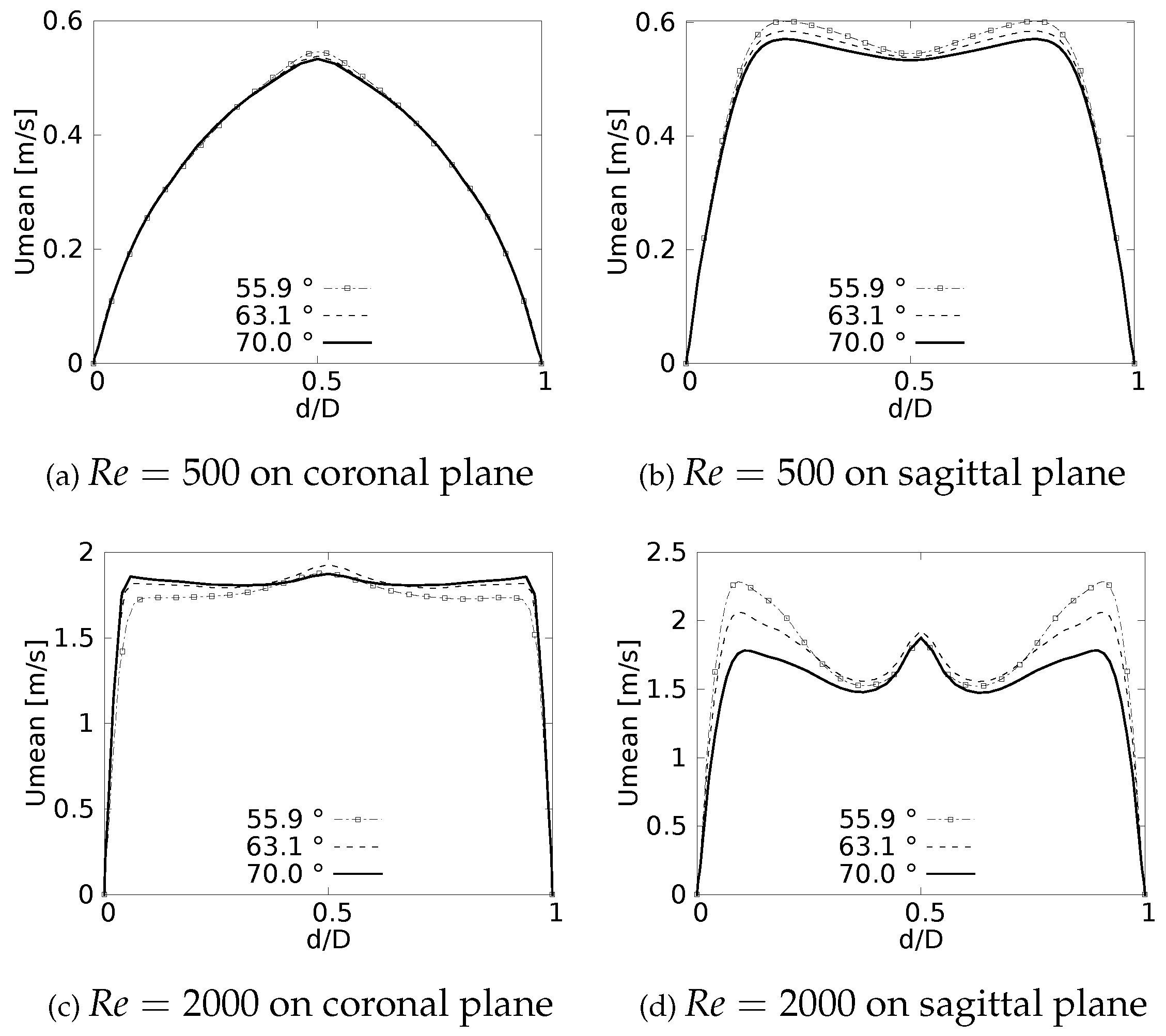
Preprints 67147 g006
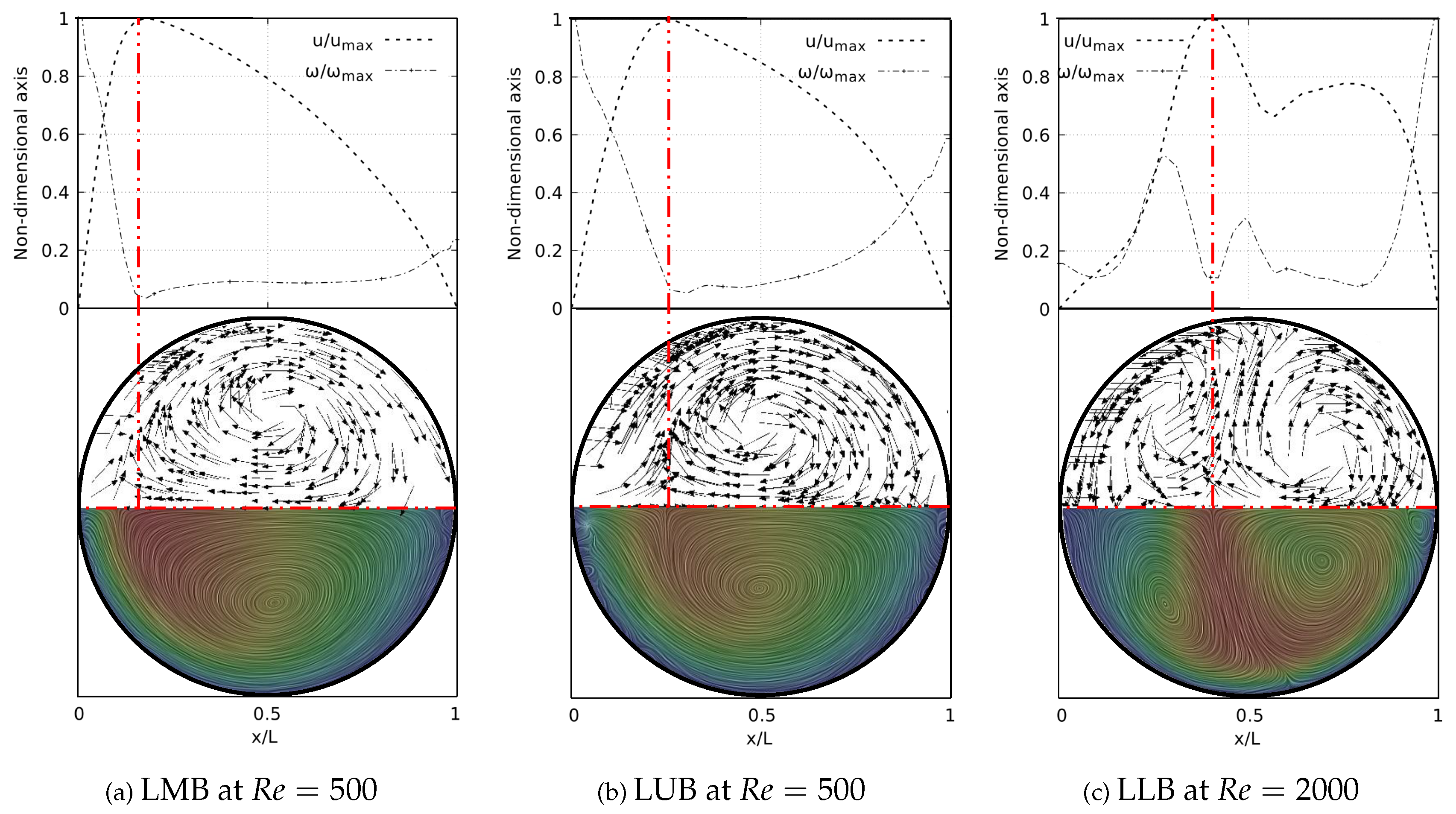
Preprints 67147 g007
Figure 7. V-W profile and secondary flow patterns for inhalation stage.
Figure 7. V-W profile and secondary flow patterns for inhalation stage.
Preprints 67147 g007
Preprints 67147 g008
Figure 8. V-W profile and secondary flow patterns for exhalation stage.
Figure 8. V-W profile and secondary flow patterns for exhalation stage.
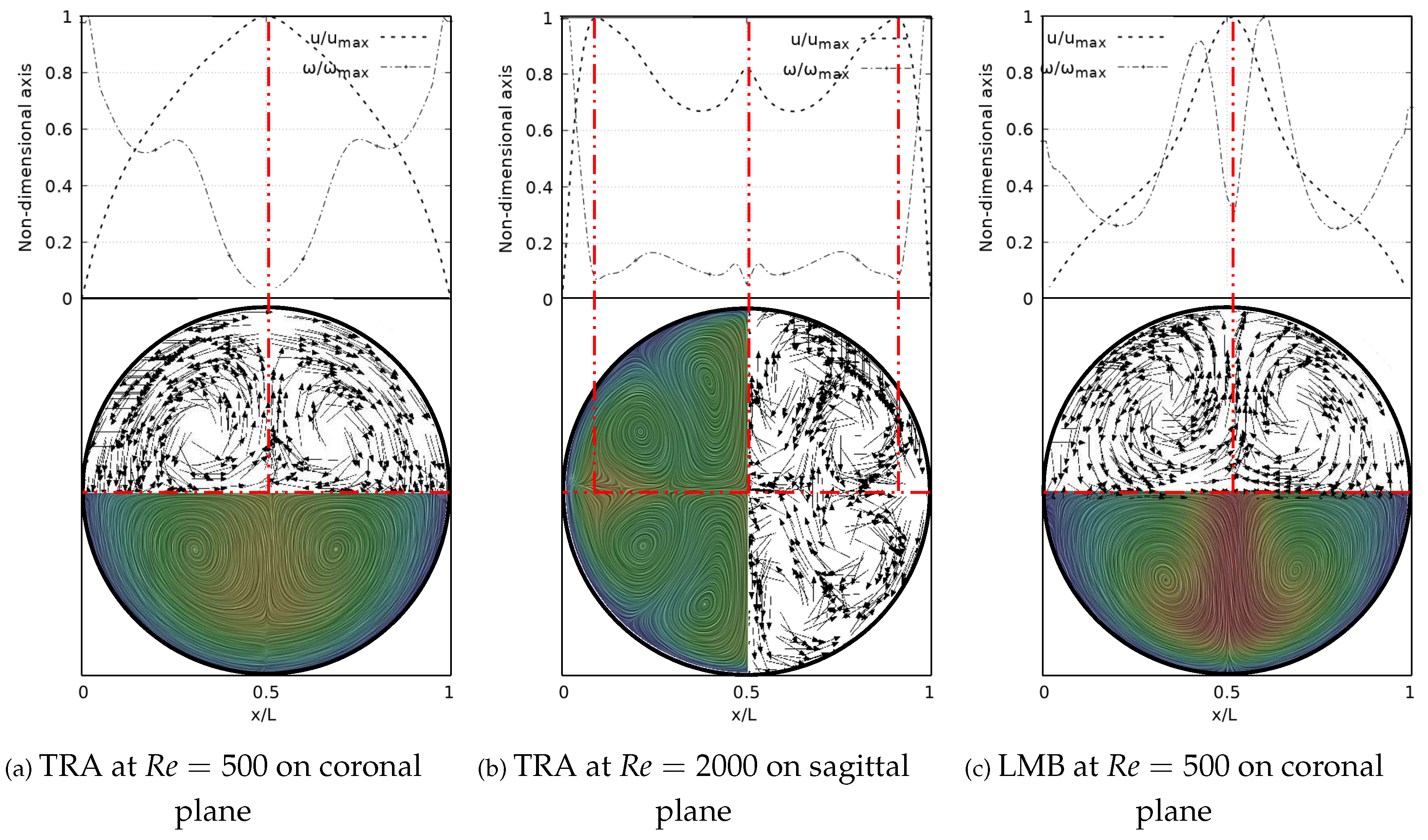
Preprints 67147 g008
Preprints 67147 g009
Figure 9. Pressure drops across the axial axes of the branches.
Figure 9. Pressure drops across the axial axes of the branches.
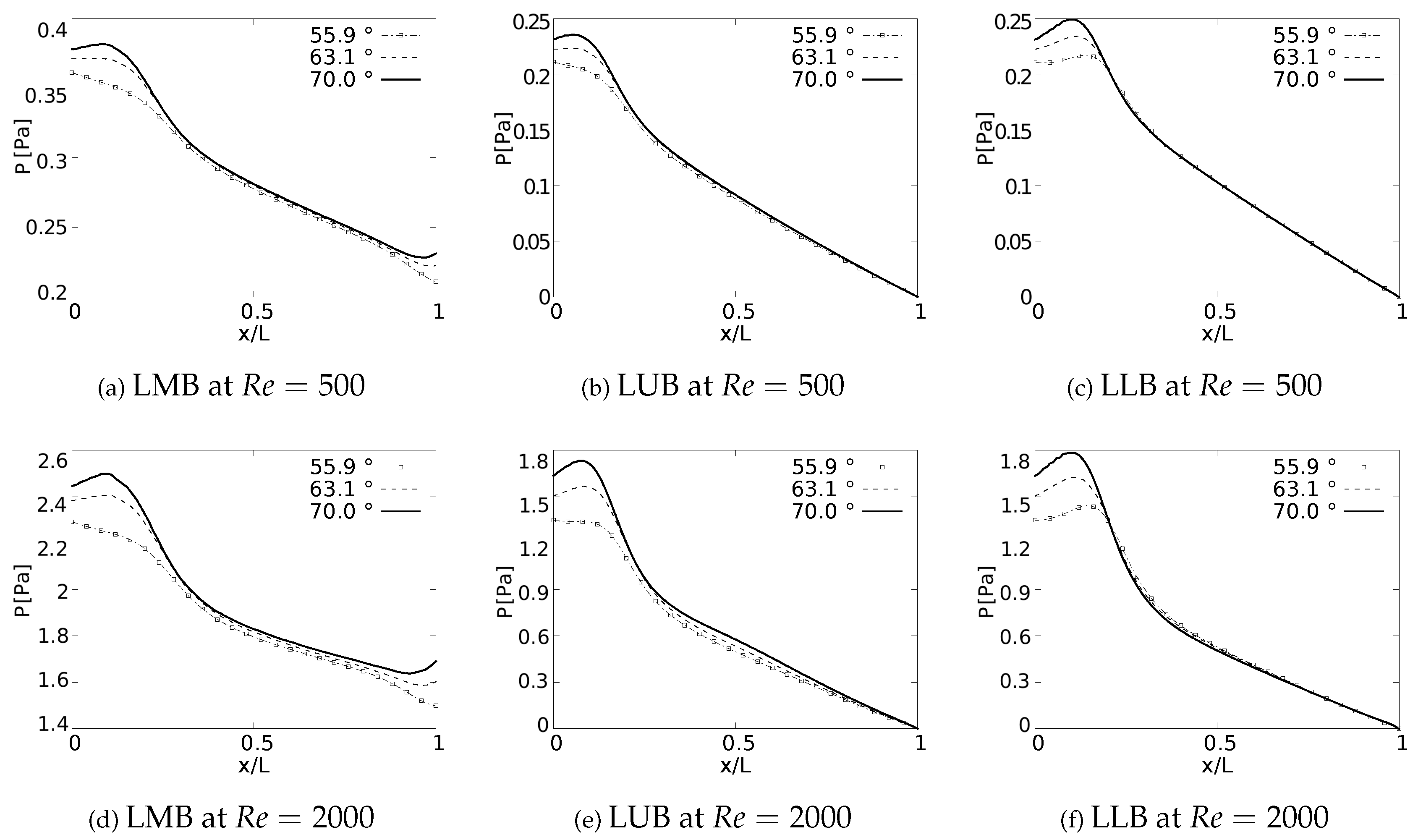
Preprints 67147 g009
Preprints 67147 g010
Figure 10. Pressure drops across the axial axes of the branches at exhalation stage.
Figure 10. Pressure drops across the axial axes of the branches at exhalation stage.
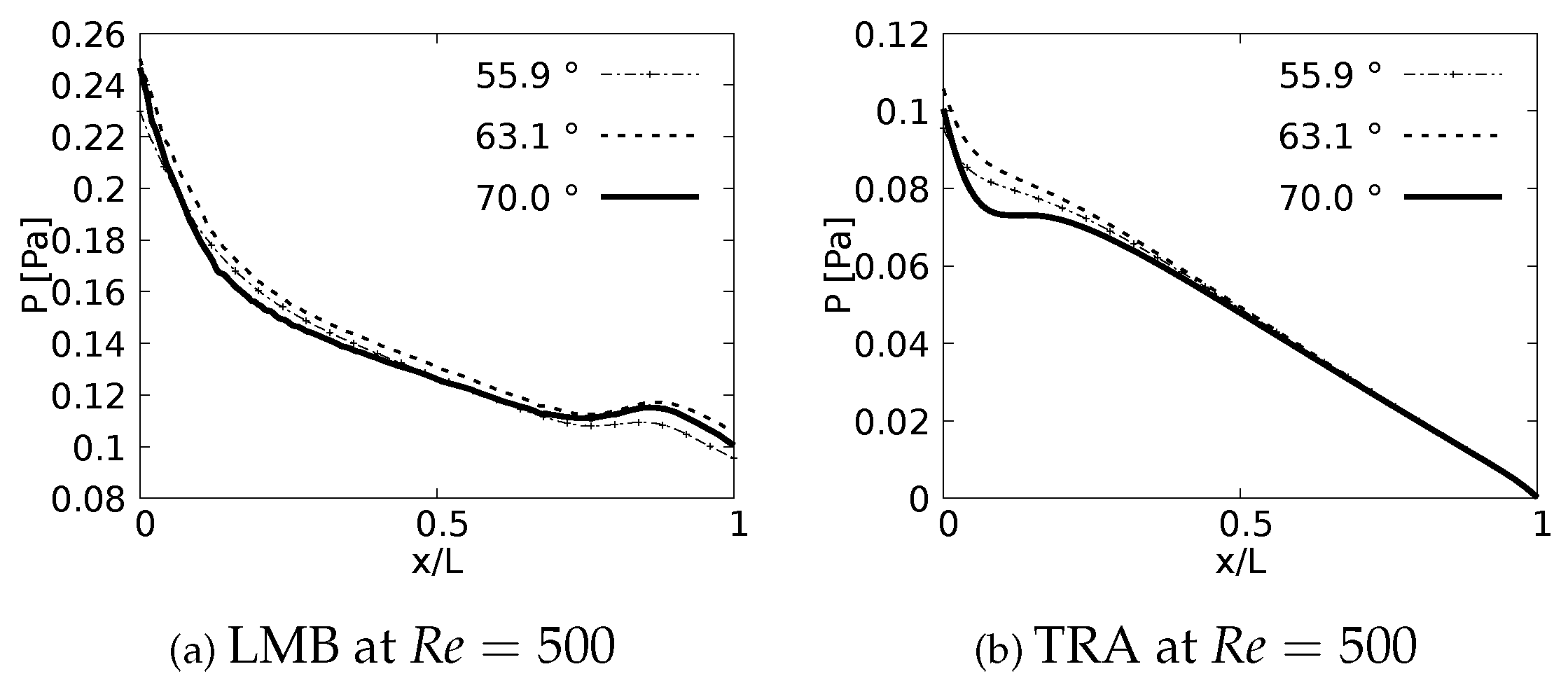
Preprints 67147 g010
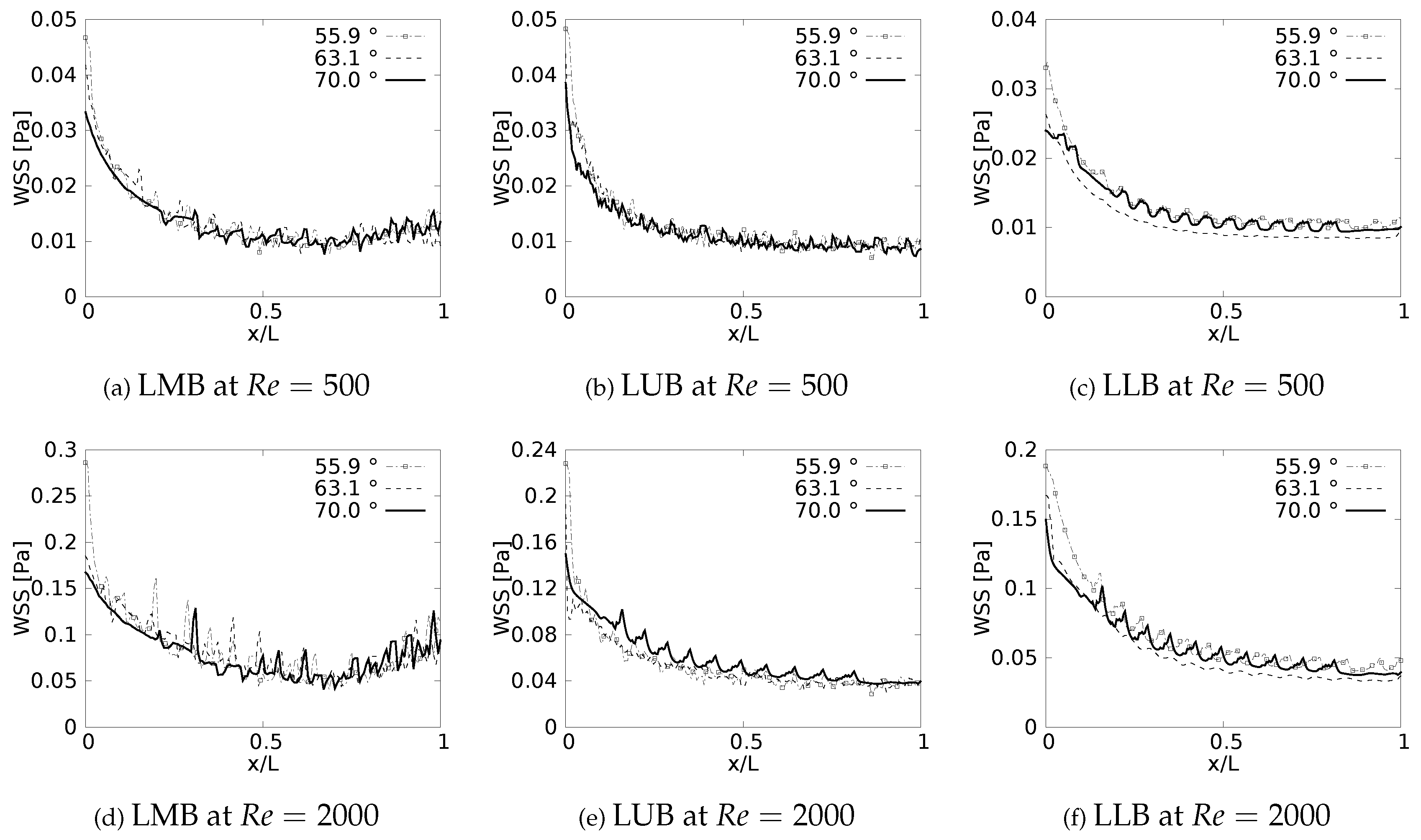
Preprints 67147 g011
Figure 11. Wall Shear Stress on inner wall for inhalation.
Figure 11. Wall Shear Stress on inner wall for inhalation.
Preprints 67147 g011
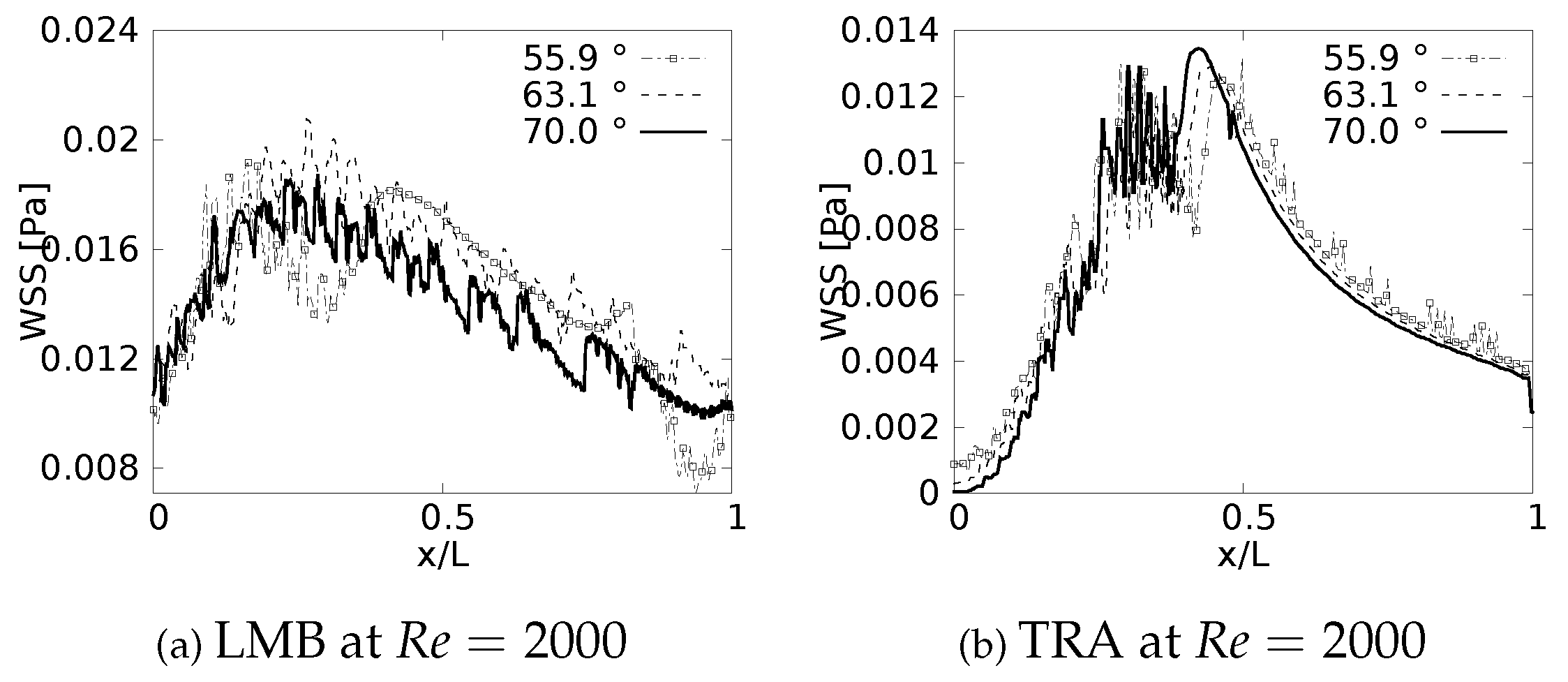
Preprints 67147 g012
Figure 12. Wall Shear Stress on outer wall for exhalation.
Figure 12. Wall Shear Stress on outer wall for exhalation.
Preprints 67147 g012
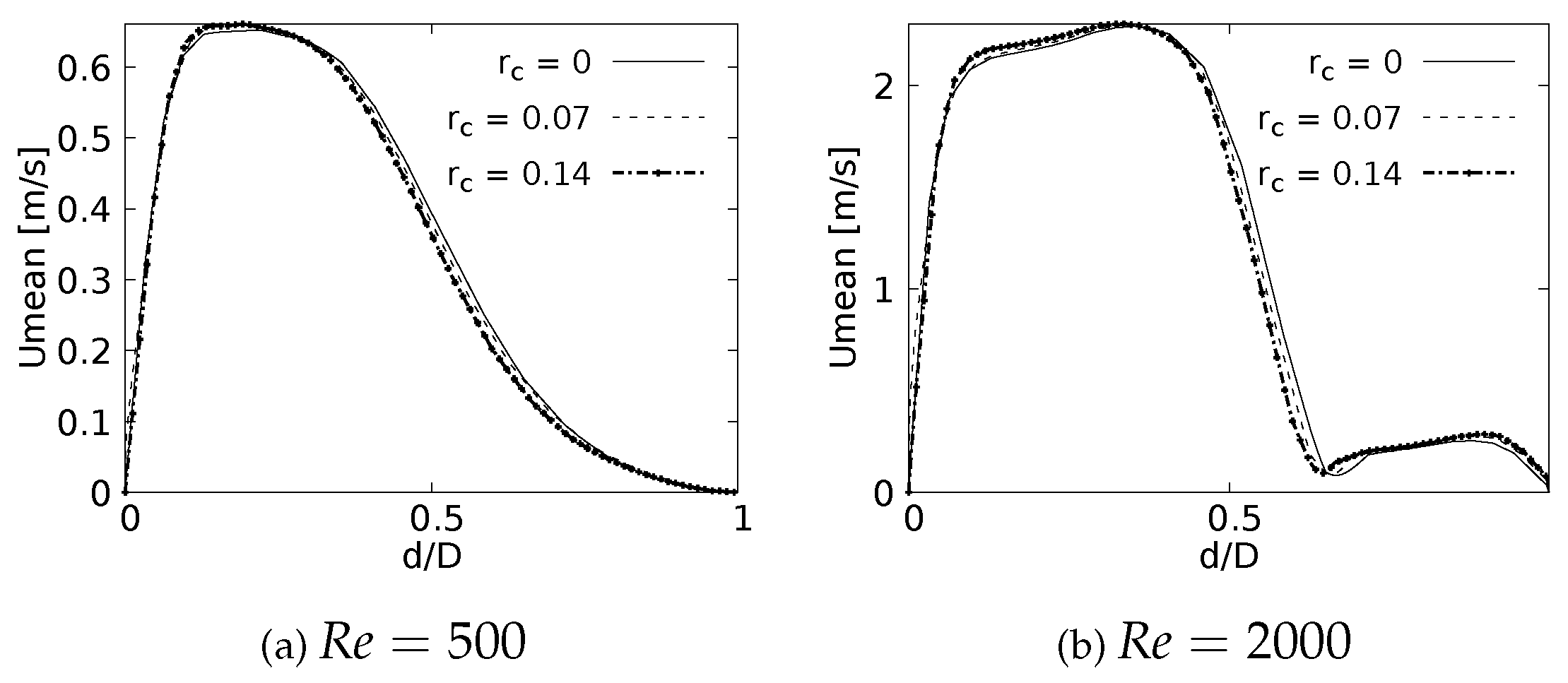
Preprints 67147 g013
Figure 13. Velocity profiles on coronal plane at 20 % of the LMB length.
Figure 13. Velocity profiles on coronal plane at 20 % of the LMB length.
Preprints 67147 g013
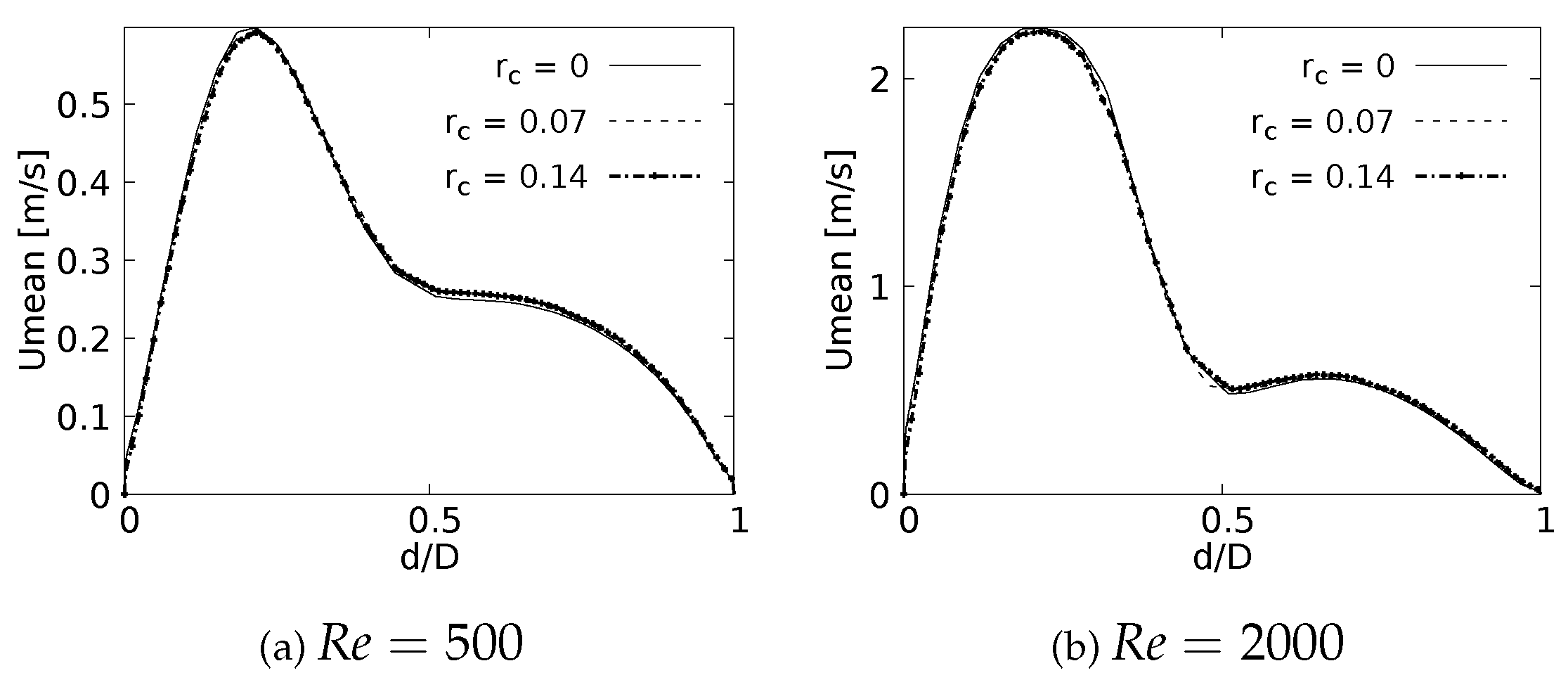
Preprints 67147 g014
Figure 14. Velocity profiles on coronal plane at 50 % of the LMB length.
Figure 14. Velocity profiles on coronal plane at 50 % of the LMB length.
Preprints 67147 g014
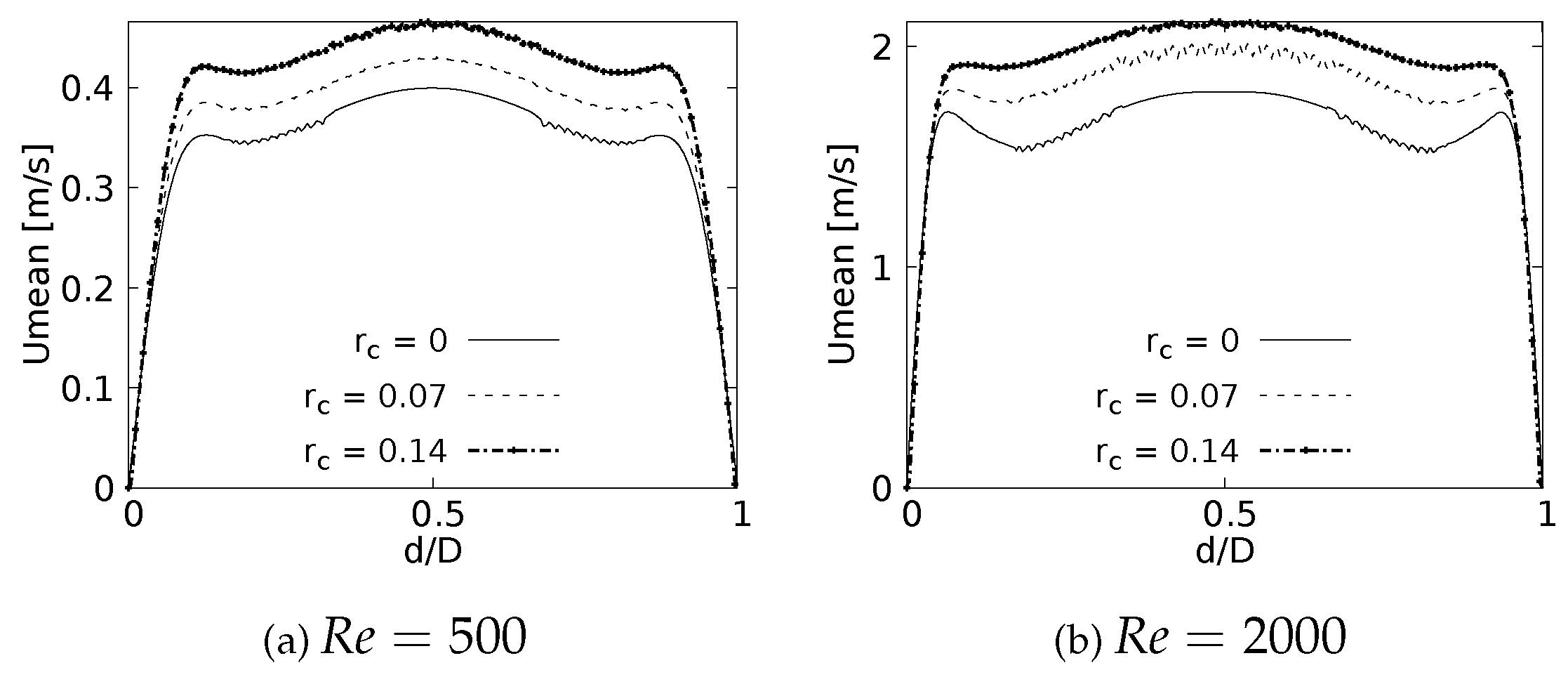
Preprints 67147 g015
Figure 15. Velocity profiles on sagittal plane. Taken at 20 % of the LMB length.
Figure 15. Velocity profiles on sagittal plane. Taken at 20 % of the LMB length.
Preprints 67147 g015
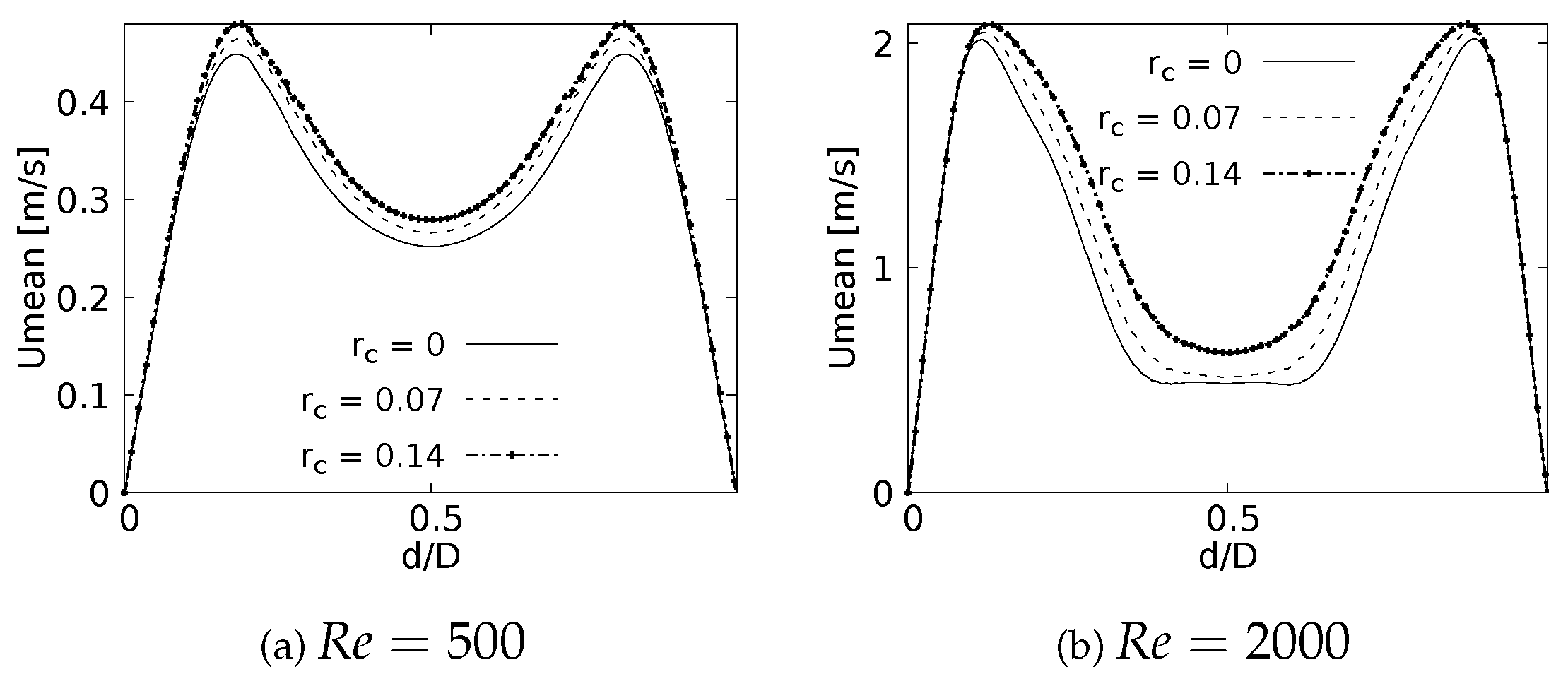
Preprints 67147 g016
Figure 16. Velocity profiles on sagittal plane. Taken at 50 % of the LMB length.
Figure 16. Velocity profiles on sagittal plane. Taken at 50 % of the LMB length.
Preprints 67147 g016
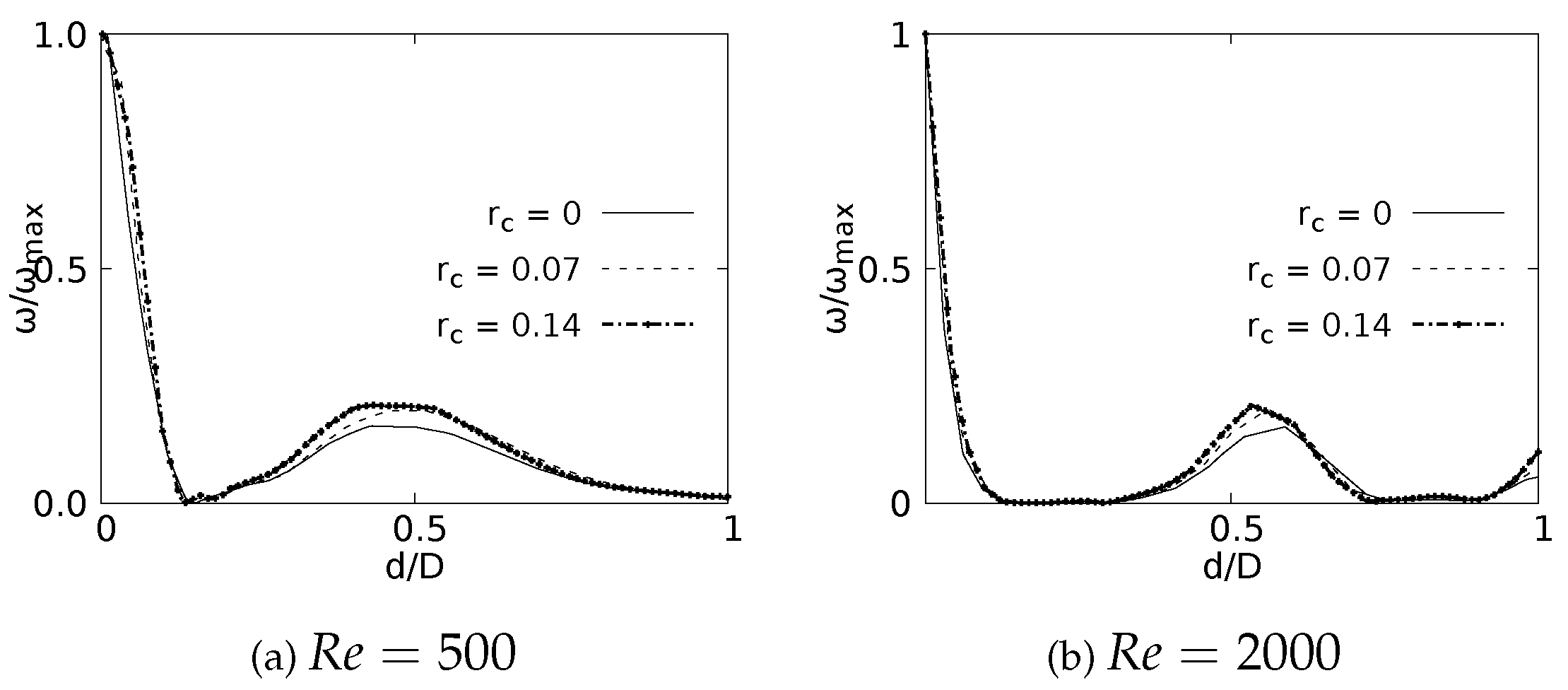
Preprints 67147 g017
Figure 17. Vorticity profile on coronal plane at 20 % of the LMB length
Figure 17. Vorticity profile on coronal plane at 20 % of the LMB length
Preprints 67147 g017
Preprints 67147 g018
Figure 18. V-W profile at coronal plane and secondary flow patterns in LMB airway.
Figure 18. V-W profile at coronal plane and secondary flow patterns in LMB airway.
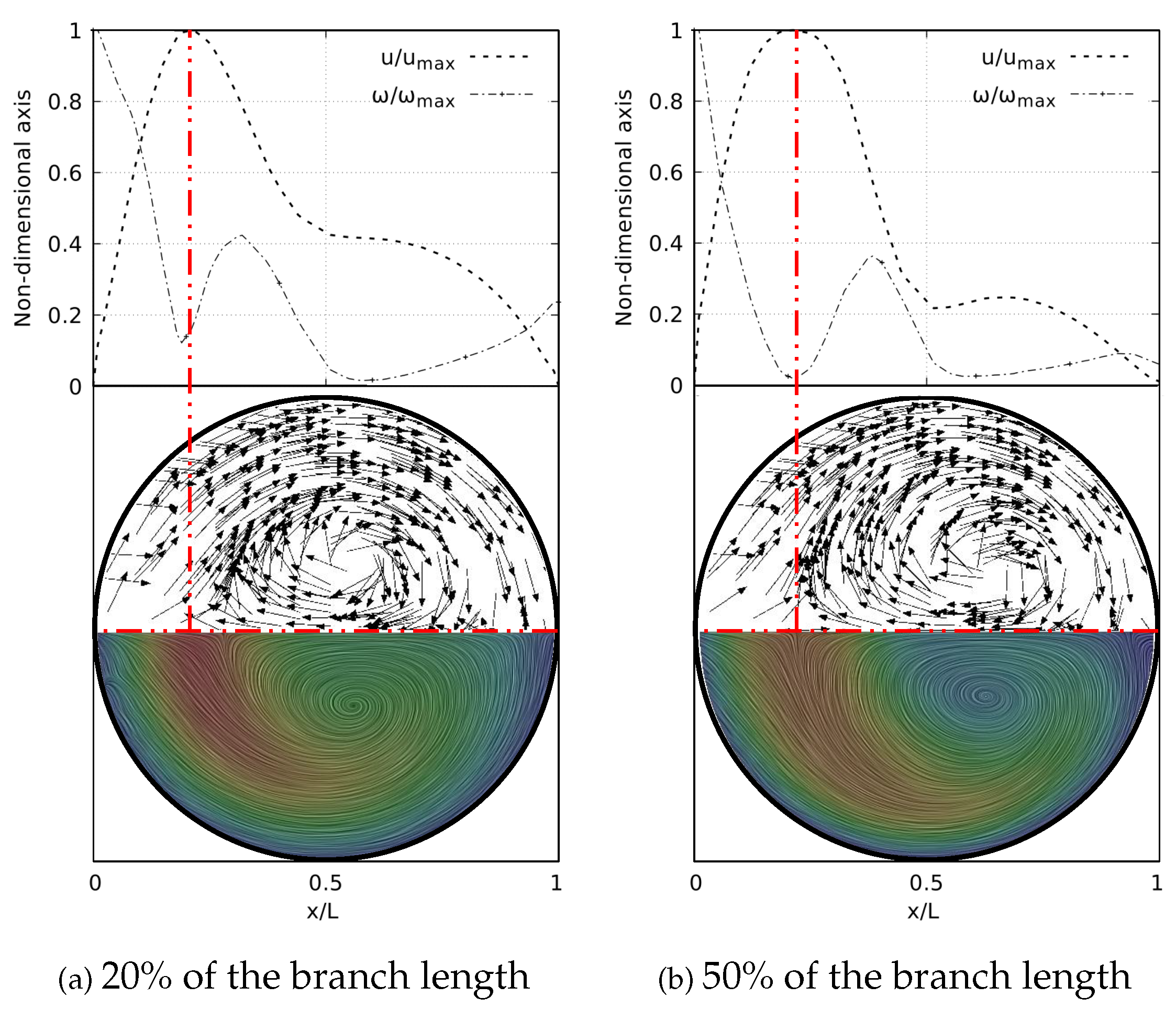
Preprints 67147 g018
Preprints 67147 g019
Figure 19. Pressure drop across the airways axial line.
Figure 19. Pressure drop across the airways axial line.
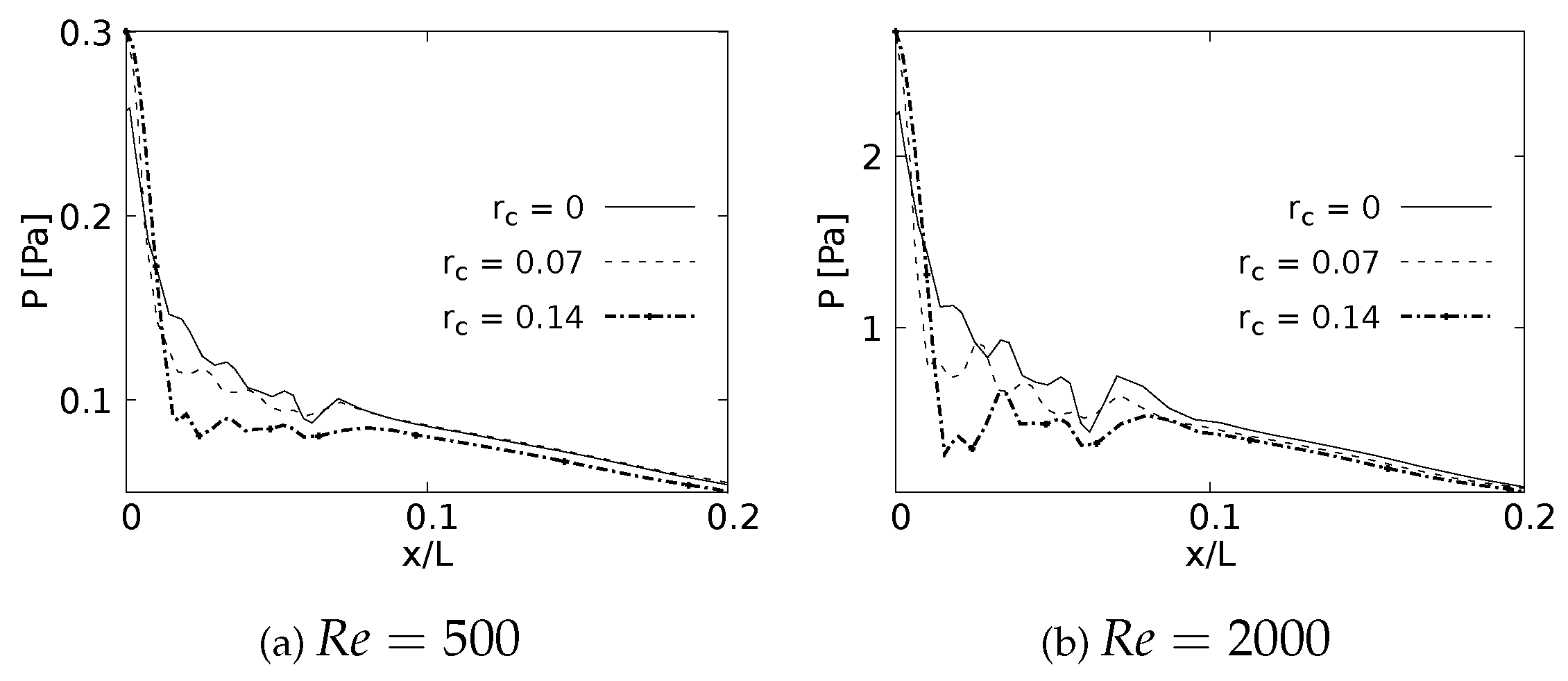
Preprints 67147 g019
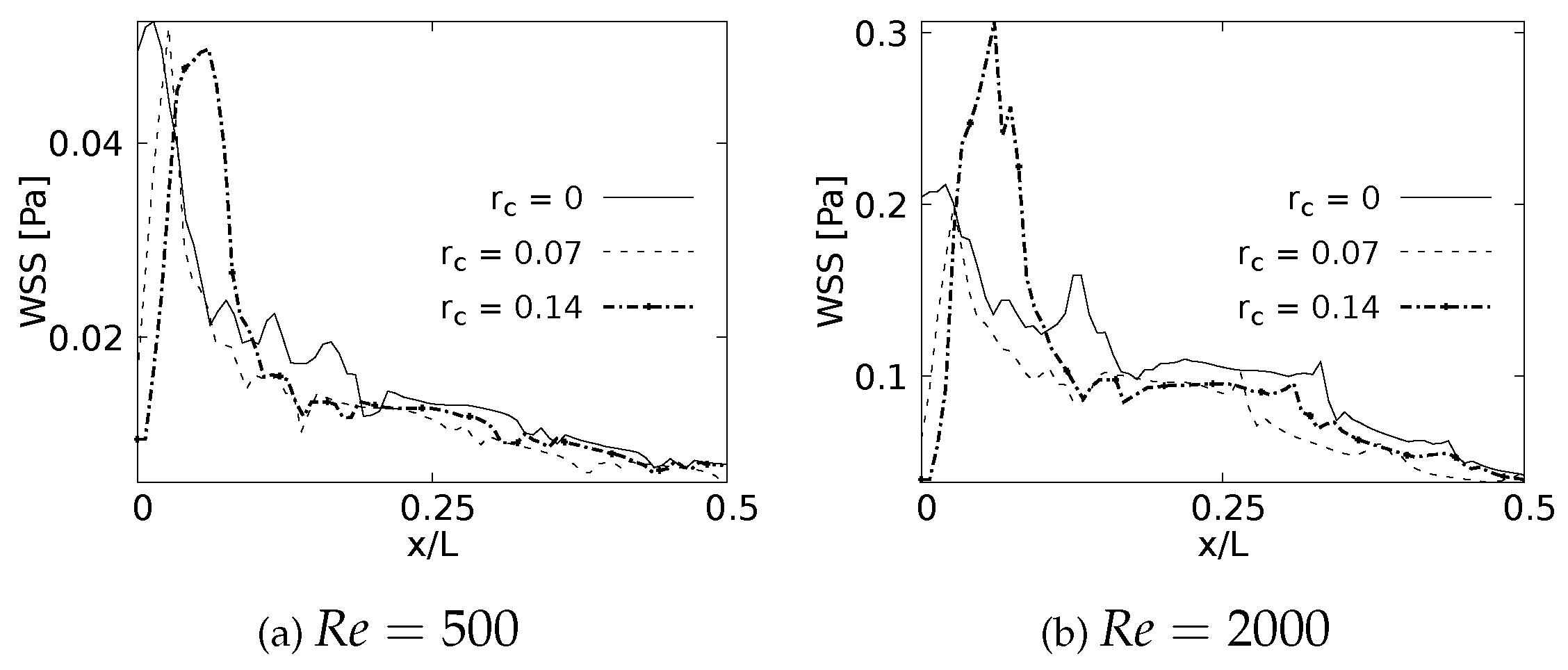
Preprints 67147 g020
Figure 20. Wall Shear Stress on inner wall for inhalation.
Figure 20. Wall Shear Stress on inner wall for inhalation.
Preprints 67147 g020
Table 1. Weibel’s model parameters in the first three generations.
Table 1. Weibel’s model parameters in the first three generations.
AIRWAY D (mm) L (mm)
TRA 18 120
LMB / RMB 12 47.6
LUB / RUB / LLB / RIB 8.3 41.5
Table 2. Subcarinal angles reported by [13].
Table 2. Subcarinal angles reported by [13].
AGE [YEARS] ANGLE [°]
21 - 30 64.2
31 - 40 58.9
41 - 50 61.9
51 - 60 63.1
61 - + 55.9
All ages 60.8
Table 3. Model Parameters values for CRR study.
Table 3. Model Parameters values for CRR study.
Branch D (mm) Len. (mm) α (o) Rd (mm)
TRA 16 80 35 81.5
LMB / RMB 14 70
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated