Prerpints.org logo
Preprint
Article

Sorption of CO2, CH4 and their mixtures in Amorphous Poly(2,6-dimethyl-1,4-phenylene)oxide (PPO)

Altmetrics

Downloads

188

Views

66

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 January 2023

Posted:

16 January 2023

You are already at the latest version

Alerts
Abstract
Sorption of pure CO2 and CH4 and CO2/CH4 binary gas mixtures in amorphous glassy Poly(2,6-dimethyl-1,4-phenylene) oxide (PPO) at 35°C up to 1000 Torr is investigated. Sorption experiments were carried out using an approach that combines barometry with FTIR spectroscopy in the transmission mode to quantify the sorption of pure and mixed gases in polymers. The pressure range is chosen to prevent any variation of the glassy polymer density. The solubility within the polymer of the CO2 present in the gaseous binary mixtures is practically coincident with the solubility of pure gaseous CO2, up to a total pressure of the gaseous mixtures equal to 1000 Torr and for CO2 mole fraction of ~0.5 mol mol-1 and ~0.3 mol mol-1. The Non-Equilibrium Thermodynamics for Glassy Polymers (NET-GP) modelling approach has been applied to the Non-Random Hydrogen Bonding (NRHB) lattice fluid model to fit the solubility data of pure gases. We have assumed here that no specific interactions are occurring between the matrix and the absorbed gas. The same thermodynamic approach has been then used to predict the solubility of CO2/CH4 mixed gases in PPO resulting in a deviation lower than 9.5% from the experimental results for CO2 solubility.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

The use of combustible gases has been increasing in the last few decades and this trend is expected to persist in the next future. Indeed, in 2021, the inland demand of natural gas (NG) in the EU and the US increased by 4.3 % and 0.5% respectively compared with 2020 [1,2]. Glassy polymeric membranes already play an important role in the purification of methane from NG and, usually, cellulose acetate or polyimide membranes are used to remove carbon dioxide [3]. Their CO2/CH4 selectivity is high when measured from pure gas permeation tests but is severely depleted, when field conditions are considered, even by 80% [4]. This behavior is attributed to enhanced ageing phenomena when hydrocarbon or water traces are present in the feed line and to competitive sorption phenomena or induced swelling produced in the case of mixed gases [5]. Conversely, poly(2,6-dimethyl-1,4-phenylene) oxide (PPO) has shown satisfactory separation performances for CO2/CH4 mixtures and a great thermal stability, having a glass transition temperature (Tg) of approximately 210°C. Chenar et al. [6] also demonstrated a good chemical stability of this polymer in the presence of water. In fact, they conducted permeation measurements on hollow fiber modules made of PPO by fixing the pressure of the feed at 7.9 bar and the temperature at 30°C. The authors conducted dry and wet experiments: in the former, the feed gas mixture only consisted of pure methane or a mixture of carbon dioxide and methane while in the latter the same streams were saturated with water vapor. They found a small reduction of the selectivity from 9.0 (dry regime) to 8.0 (wet regime) at a feed CO2 concentration of 5% by volume. When the concentration of CO2 reached 25% by volume, the water content produced no effect on the selectivity being equal to ~8.5 in both regimes.
Previously, Story and Koros measured the solubility of mixed CO2/CH4 in PPO [7]. They observed that the solubility of each gas was reduced in the polymer with respect to that measures for pure gas sorption experiment conducted at pressure values equal to the value of partial pressure of the gas in the mixture. In this contribution, we study the sorption of pure CO2, CH4 and their mixtures in PPO at 35°C up to 1000 Torr and present both experimental results, gathered by combining barometric and spectroscopic approaches, and their interpretation based on a theory rooted in statistical thermodynamics.
The closed volumetric method is commonly used to measure the solubility of mixed gases in polymers [7,8,9]. The measurement of the gas phase composition at sorption equilibrium is conducted ex situ with gas chromatography (GC), the volumes must be precisely calibrated and an accurate Equation of State is required to evaluate the number of moles of each gas species [10]. Recently, we introduced a new experimental technique coupling barometry and FTIR Spectroscopy in the transmission mode to measure the solubility of binary gas mixtures in rubbery polymers [11]. Specifically, we studied the sorption of mixed CO2/CH4 in Polydimethylsiloxane (PDMS) at ambient temperature and were able to evaluate the solubility of CO2 in PDMS up to 9 bar of total pressure and CO2 mole fraction ~0.5 mol mol-1. With this new technique, the classical closed volumetric method can be used by monitoring the concentration depletion of each gas species in situ with the corresponding IR signal. Alternatively, the solubility of each absorbed species can be evaluated directly in the polymer phase by isolating their own IR signals with difference spectroscopy. Hong et al. previously used this second approach with FTIR Spectroscopy in the ATR mode [12]. They studied the sorption of a binary vapor mixture of Methyl Ethyl Ketone and Toluene in Polyisobutylene and, since the gas phase composition could not be measured, it was fixed during the sorption test. The approach we have introduced has the important advantage of being relatively simple to perform thus avoiding the complexity of the experimental techniques currently used to measure the solubility of mixed gases in glassy polymers that hampers the evaluation of the performances and the selection of the best performing material for a specific gas separation application [13].
Regarding the theoretical approaches capable of predicting accurately the transport properties of glassy polymers in contact with multicomponent gas mixture, as pointed out by Minelli and Sarti, they must be still fully developed and a few good results have been obtained so far by applying the Non-Equilibrium Thermodynamics for Glassy Polymers (NET-GP) to extend the use of compressible lattice fluid (LF) models, originally developed to describe the behavior of rubbery polymers, to deal with the case of glassy polymers [14,15,16]. Minelli et al. followed this approach to extend the Sanchez and Lacombe LF (SL) model to predict the sorption uptake at thermodynamic equilibrium of CO2/CH4 in PPO, CO2/C2H4 and CO2/N2O in Poly(methyl methacrylate) (PMMA), after retrieving each polymer – penetrant mean field interaction parameter from the fitting of the pure gas solubility data. Later, we used the same approach to extend the Non-Random Hydrogen Bonding (NRHB) lattice fluid model proposed by Panayiotou et al. [17,18]. This model overcomes some important limitations of the SL theory. In fact, the NRHB model, differently from the SL approach, is thermodynamically consistent if applied to multicomponent fluid mixtures, providing chemical potential expressions that converge, in the ideal gas limit, to the corresponding expressions for ideal gas mixtures. Moreover, the NRHB model accounts for non-randomicity of contacts between the polymer repeat units, the penetrant molecules and the empty sites as well as for possible specific self- and cross-interactions in the penetrant-polymer mixture (e.g., self and cross hydrogen bonding or Lewis acid-base interactions). In the present context, in view of the characteristics of the system under scrutiny, we have not accounted for the presence of specific interactions considering only the non-randomicity of contacts. In the following, the modelling approach, obtained by applying the NET-GP procedure to the NRHB model deprived of the HB contribution, will be referred to as NETGP-NR theory.
To evaluate the efficacy of the NET-GP extension applied to a LF theoretical framework for predicting mixed gas sorption in a polymer, a broad spectrum of thermodynamic conditions and polymer-penetrant systems should be investigated [15]. Indeed, to this aim, the availability in the literature of mixed gas solubility data in polymers is still inadequate.
Moving from these considerations, our goal is multiple. First, we extend the experimental technique coupling Barometry and FTIR Spectroscopy in the transmission mode, applied till now only to the case of rubbery polymers, to the case of glassy polymers by investigating the sorption of pure CO2, CH4 and their mixtures in PPO. Second, we interpret the solubility data of pure CO2 and CH4 in PPO with the NETGP-NR theory. Last, we use the same model to predict the mixed CO2/CH4 solubility in PPO and compare these results with the experimental data on mixture sorption.

2. Theoretical background

2.1. The NETGP-NRHB model

The Non-Equilibrium Thermodynamics of Glassy Polymers – Non Random Hydrogen Bonding (NETGP-NRHB) model has been developed and successfully implemented by our group [16,19,20,21,22,23,24,25,26] to the aim of modelling the two-phase equilibrium, at fixed pressure, P, and temperature, T, established between a polymer-penetrant amorphous mixture “frozen” in a non-equilibrium (glassy) state and a multicomponent penetrant fluid phase mixture of assigned composition, under the assumption that the polymer is not soluble in the penetrant phase. This Pseudo-Equilibrium nature of phase condition refers to the solubility of penetrants within a non-equilibrium glassy polymer at a temperature far below the glass-to-rubber transition temperature, Tg, of the polymer-penetrants mixture so that it can be assumed that the mass density of the polymer within the glassy mixture is kinetically locked at an out-of-equilibrium value that, in the case of light gases at low pressure as is the case of the present investigation, can be identified with the value of the unpenetrated polymer mass density ρ p , 0 , right before the start of the sorption process. This value is a function of the previous thermomechanical history of the unpenetrated polymer sample and, being an out-of-equilibrium value, it cannot be provided by any equation of state (EoS) model, and it is commonly retrieved experimentally so that it represents a key input parameter of the model. Indeed, the NETGP framework, introduced by Sarti et al. [27,28] is a general procedure which allows to extend in principle any equilibrium thermodynamics model to the case of a non-equilibrium “glassy” polymer-penetrant mixtures exposed to an equilibrium penetrant phase, NETGP-NRHB refers to the NETGP implementation for the case of NRHB equilibrium thermodynamics model [17,18]. In particular, the NETGP extension procedure is consistently built in such way that the proper out-of-equilibrium expressions of the chemical potentials in the glassy phase, being related to a first order derivative of the Gibbs energy, G, collapse into the corresponding equilibrium expressions when the glassy state approaches the corresponding equilibrium state at the same P, T and composition, i.e. when the phase volume is dictated by the EoS of the equilibrium thermodynamic model adopted in the NETGP procedure [26]. Since the mass of polymer is constant in the polymer-based phase, the collapse into the equilibrium expressions can be equivalently expressed imposing that the out-of-equilibrium value of ρ p , 0 attains the corresponding equilibrium value dictated by the EoS of the thermodynamics model adopted in the procedure of extension. According to this required internal consistency of the NETGP procedure, the pure component parameters of the general adopted NETGP-EoS model coincide with the corresponding parameters of the associated equilibrium EoS model. Finally, the NETGP procedure assumes that the equilibrium external phase is consistently described by the equilibrium thermodynamics model.
Differently from the more extensively adopted NETGP-Sanchez-Lacombe theory (also known as NELF model [27,28]), the NETGP-NRHB model can account for the intrinsic non-random distribution of “mean-field” contacts and voids and for possible occurrence of strong specific interactions, such as Hydrogen Bonding. In addition, it has been recently shown that NETGP-NRHB model allows to overcome a serious drawback of the NELF model that consists in the thermodynamic inconsistency exhibited by this model in the limit of the ideal gas behavior when dealing with a multicomponent external fluid phase. The latter result is in turn a consequence of the corresponding inconsistency displayed by the SL model when implemented using any of the sets of operative mixing rules proposed in literature [16,19,21,29,30,31].
Since the systems investigated in the present contribution do not exhibit strong specific interactions, as also confirmed by FTIR analysis, in the following we adopt here a simplified version of the general NETGP-NRHB framework, that is the one where any HB term is canceled out in the calculation of the Pseudo-Equilibrium expressions of chemical potentials[19,26]. Here and in the following we refer to this version of the model as NETGP-NR (where NR stands for the corresponding pure “mean-field” version of NRHB model).
Considering the restrictions imposed by the II law of thermodynamics, it can be demonstrated that the described phase Pseudo-Equilibrium conditions are still dictated by an ad hoc equivalence of the chemical potentials, μ i , of each component i present in both the coexisting phases [19,27,28] (the meaning of the symbols of eq. (1) and of all the following equations is reported in the ‘List of symbols’ section at the end of the manuscript):
μ i , p o l N E T , x 1 N E , … , x m − 1 N E , ρ p , 0 = μ i ,     e x t E Q T , P , x 1 , e x t , … , x m − 2 , e x t f o r   i = 1 , … m − 1
In fact, differently from a true phase equilibrium condition, in which both the coexisting phases are in an equilibrium state, in the phase Pseudo-Equilibrium conditions, Eq. 1 requires that for the glassy polymer-penetrant phase each penetrant chemical potential is provided by its proper non-equilibrium expression. In Equation 1, subscript pol and ext stand for polymer-penetrant and external penetrant phase, respectively. Moreover, T and P represent the uniform temperature and pressure fields of the multicomponent biphasic system, respectively (the condition of P uniformity is imposed since the effects of external force fields are disregarded), xi stands for the molar fraction of penetrant species i, m-1 represents the total number of types of penetrants considered in the system, x i N E represents the composition of each component within the polymer phase at the Pseudo-Equilibrium of phase condition, and the superscripts NE and EQ in the expressions of the chemical potential underline that the related terms are referred to non-equilibrium and equilibrium conditions respectively. We recall that the entropy inequality restriction also determines that the non-equilibrium chemical potential is not a function of P. In the specific case of the NETGP-NR model the required non-equilibrium expression of the penetrant chemical potentials is obtained by deriving as a function of the number of moles of the penetrant of interest, a proper non-equilibrium expression of molar Gibbs energy that, in turn, is calculated starting from the general non-equilibrium expression of molar Gibbs energy, G, provided explicitly by the statistics of the NR model. In fact, in its non-equilibrium extension of the (N,P,T) ensemble, the NR model, the generic component Nij of the set   N _   i j represents the total number of moles of Lattice Fluid (i.e. “mean field”) ij contacts within the phase, between a species i and a species j (with j > i), including also the voids (i = 0) considered to be G ( N _ , P , T ,   ρ , N _   i j ) . Moreover, the generic component Ni of the set N, represents the total number of moles of i-th species.
The key assumption of the NETGP-NR model is that, in a kinetically locked in glassy phase, the volume, (or equivalently the polymer mass density, as discussed), is fixed to an out-of-equilibrium time-invariant value (in the time scale of interest), whereas the set of N _   i j , still follows the minimization condition of G towards this set of variables, as required in principle by the equilibrium conditions of the phase of interest. Therefore, the set of LF contacts N _   i j becomes an assigned function of P, T, composition and of the fixed out-of-equilibrium polymer mass density N _   i j ( N _ , P , T ,   ρ ) . On this basis, this function exhibits the same formal expression of the true equilibrium conditions, but it is now calculated in correspondence of the assigned out-of-equilibrium ρ p , 0 instead of the equilibrium polymer mass density dictated by the EoS of the NR model. This condition, referred in literature as “instantaneous equilibrium” (IE) condition, is reasonable if one recognizes that the LF “mean fields” contacts act on an extremely local scale compared to the one involved in the cooperative molecular mobility which is inhibited under Tg. Based on the IE assumption, the proper NETGP expression of the Gibbs energy is in principle obtained by substituting the function N _   i j ( N _ , P , T ,   ρ ) (provided by IE minimization conditions) into the general Gibbs energy expressions G ( N _ , P , T ,   ρ , N _   i j ) (provided by the NR statistics) and by fixing in all the expressions the mass polymer density ρ equal to ρ p , 0 . Finally, according to the NETGP procedure, by deriving this expression of the Gibbs energy, as a function of the total number of moles of penetrant i at fixed T, P and number of moles of the other species, could be obtained by the corresponding NE expressions of the chemical potential to be used in Eq. 1. In practice, the operative determination of these non-equilibrium penetrant chemical potentials, according to the described theoretical procedure, is cumbersome since the minimization conditions can be only solved numerically so that an analytical expression for the N _   i j ( N _ , P , T ,   ρ p , 0 ) function is not available. To obtain a derivation of the analytical expressions of chemical potentials, a specific procedure based upon the chain rules of derivation and the IE conditions can be commonly adopted (see ref. [16,19,21]). The basic result of such procedure is that the NE expressions of the chemical potentials to be used in Equation 1 is provided by deriving the general non-equilibrium expressions of G ( N _ , P , T ,   ρ p , 0 ,   N _   i j ) :
μ i , p o l N E = ∂ G ∂ N i P , T , N j ≠ i , ρ p , 0 , N _ i j ( N _ , P , T , ρ p , 0 )
and coupling Equation 2 with the IE minimization conditions regarding the “mean-field” contacts.
Conversely, the molar equilibrium penetrant chemical potential expression of species i in the external fluid phase, μ i , e x t E Q , is obtained by deriving the expression of G e q ( N _ , P , T ) of the NR model, as a function of the number of moles of species i at fixed P and T and number of moles of the other components of this phase. G e q is obtained in turn by coupling the expression of G provided by NR statistics with both the minimization conditions of G, towards N _   i j and the phase volume (the latter represents the EoS of the NR model). This set of minimization equations thus provide the equilibrium set N _   i j E Q ( N _ , P , T ) and the equilibrium phase density ρ i E Q ( N _ , P , T ) . However, these functions cannot be expressed in an analytical form. Operatively, a well-established procedure based upon derivative chain rules as well on the minimization conditions, is implemented and the equilibrium chemical potential of i-th penetrant species is provided by deriving the general non-equilibrium expressions of G:
μ i , e x t E Q = ∂ G ∂ N i P , T , N j ≠ i , ρ i E Q ( N _ , P , T ) , N _   i j E Q ( N _ , P , T )
and coupling the expression of Eq. 3 with the whole set minimization conditions, i.e., the ones regarding the “mean-field” contacts and EoS of NR model.
For the sake of brevity, in the present section only the operative equations of NETGP-NR model, which dictate the Pseudo-Equilibrium phase conditions, are reported. Full details regarding the development of these equations are reported in ref. [16] and meaning of symbols is recalled in the list of symbols at the end of the manuscript. The following set of dimensionless equations provide the non-equilibrium chemical potential of the i-th penetrant:
μ i , p o l N E R T = ln ⁡ ɸ i δ i   r i + ln ⁡ ρ ~ − r i ln ⁡ 1 − ρ ~ − z 2 r i q i r i − 1 ln ⁡ 1 − ρ ~ + q r ρ ~ + z   q i 2 ln ⁡ Γ i i − r i q i ln ⁡ Γ 00 − q i T ~ i
Γ i j 2 Γ i i   Γ j j = exp ⁡ − ∆ ε i j R T                 f o r   e a c h   i , j = 0 ,   1 , … ,   m   a n d   j > i
∑ j = 0 m Θ j Γ i j = 1                           f o r   e a c h   i = 0 ,   1 , … ,   m
The following set of dimensionless equations provides instead the equilibrium chemical potential of the i-th penetrant:
μ i e q R T = ln ⁡ ɸ i δ i   r i − r i ∑ j = 1 m ɸ j l j r j + ln ⁡ ρ ~ + r i v ~ − 1 ln ⁡ 1 − ρ ~ − z 2 r i v ~ − 1 + q i r i ln ⁡ 1 − ρ ~ + q r ρ ~ + z   q i 2 ln ⁡ Γ i i + r i q i v ~ − 1 ln ⁡ Γ 00 + r i p ~   v ~ T ~ − q i T ~ i
Γ i j 2 Γ i i   Γ j j = exp ⁡ − ∆ ε i j R T           f o r e a c h   i ,   j = 0 ,   1 , … , m a n d j > i
∑ j = 0 m Θ j Γ i j = 1       f o r e a c h i = 0 ,   1 , … , m
P ~ + T ~ ln ⁡ 1 − ρ ~ − ρ ~ ∑ i = 1 m ɸ i ˙ l i ˙ r i ˙ − z 2 ln ⁡ 1 − ρ ~ + q r ρ ~ + z 2 l n Γ 00 = 0
The equations for a pure component phase (in this case m = i = 1 holds) are consistently obtained by setting ɸ 1 = 1 , where ɸ i represents the fraction of mers of species i. The dimensionless form of the NETGP-NR model equations (4)-(10) is obtained by properly scaling the temperature, pressure, and phase density variables in each phase by using the related NR lattice fluid parameters [17,18,19]. To this regard we remark that, in line with the described consistency of NETGP framework required when the out-of-equilibrium phase volume value approaches the equilibrium one, the same kind of reduced variables as well as of scaling parameters and related mixing rules, appear both in the expressions of the NR model and of the NETGP-NR. Consequently, these lattice fluid parameters of NETGP-NR model can be retrieved by non-linear regression of equilibrium thermophysical properties regarding the components the mixture of interest. In fact, in the framework of NR model, each component is characterized by four composition-independent lattice fluid parameters so that they are commonly estimated by non-linear regressions of equilibrium thermophysical properties of the pure components. Vapor-liquid equilibrium data are in general used in the case of low molecular weight compounds while equilibrium dilatometric data are adopted in the case of polymers.
The first two LF parameters are related to the “mean field interaction energy” per molar segment, ε i * that is calculated by combining an “enthalpic contribution” parameter, ε i , h * , and an “entropic contribution” parameter, ε i , s * . A third parameter, v i , s p , 0 * , represents the temperature-independent contribution to the close packed specific volume of the pure component i, v i , s p * . ε i , h * , ε i , s * and v i , s p , 0 * , represent three parameters to be retrieved for any component i by fitting its equilibrium thermophysical properties. Finally, the fourth composition independent LF parameter, associated to component i, is represented by the shape factor, si, defined as the ratio of molar surface to molar volume, si = qi/ri of the i-th component. To reduce the number of optimization parameters involved in the mentioned fitting procedure of equilibrium thermophysical data of component i, si is commonly estimated through the UNIFAC group contribution method and this is also the approach followed in the present investigation [32].
Once the four LF parameters have been determined for each pure component, the scaling parameters of a mixture of these components are univocally evaluated according to the NR model mixing rules, as a function of concentration and of the pure component LF parameters involved [17,18,19].
Regarding the LF scaling energy, the following mixing rule is assumed (each θ i is function of concentration) [17,18,19]:
ε * = ∑ i = 1 m ∑ j = 1 m θ i θ j ε i j *
where:
ε i j * = ε i * ε j *   1 − k i j
Eq. 12 introduces an additional dimensionless parameter, k i j , associated to each couple of components (i,j) involved in the multicomponent mixture. It measures the departure from the geometric mean rule for the corresponding LF (“mean field”) interactional energy, ε i j * . k i j is commonly assumed to be a pure binary parameter only function of the nature of binary interactions of the couple of components i-j. Consequently, it can be obtained by a non-linear regression of equilibrium and/or Pseudo-Equilibrium of phase properties of the corresponding binary system. Indeed, this approach has been followed in the present investigation and the value of k i j for the penetrant binary phase of interest has been retrieved by VLE data of the methane/carbon dioxide system while the values of k i j for the couples PPO-methane and PPO-carbon dioxide are respectively evaluated by non-linear regressions of corresponding Pseudo-of Equilibrium solubility data.
Note that in the equations (5) and (8) the following mixing rule, involving k i j , holds:
Δ ε i j = ε i i + ε j j − 2 ( 1 − k i j ) ε i i ε j j
where ε 00 = 0 (subscript ‘0’ refers to the voids) and the relationship ε i * = z 2 ε i i holds, z being the lattice coordination number (z = 10 is assumed here in the framework of the NR model).
According to the previous discussion, we remark that the reduced density of the out of equilibrium glassy mixture, ρ ~ , is not obtained from the NR equation of state but it is dictated by the out of equilibrium value of ρ p , 0 :
ρ ~ = ρ p , 0 / ω p ρ *
where ω p , is the mass fraction of polymer and ρ * is the closed-packed density of the polymer-penetrant mixture which is dictated by the corresponding mixing rules of the LF model for the numbers of occupied mers for component i [17,18,19].

2.2. Solution Diffusion Model of Small Molecules in Polymers

The transport of low molecular mass species, such as gases or vapors, in dense polymeric membranes is commonly described as a two steps process involving the dissolution of the guest within the host matrix and the subsequent diffusion through it [33]. In a pure gas permeation test through a plane polymeric sheet, if the gas pressure and concentration of gas molecules solubilized within the polymer (P, C) at the upstream side of the membrane are far greater than at the downstream side, the steady state mean permeability ( P e r m ¯ ) of the gas in the material may be expressed as [34,35]:
P e r m ¯ = D ¯ × S
if one assumes that the constitutive equation for mass transport is provided by the Fick’s law [34]. Here S is the apparent solubility coefficient and D ¯ is the effective diffusivity coefficient. S is defined as the ratio of the gas solubility in the polymer corresponding to the upstream pressure of the system. The mutual diffusion coefficient D may be concentration dependent and D ¯ is an estimate of the average diffusivity in the concentration range [ C d , C u p ], where C d and C u p represent, respectively, the concentration within the polymer in contact with the gas at the downstream and upstream side of the membrane, calculated as follows:
D ¯ = 1 C u p − C d ∫ C d C u p D x   d x
S and D take into account the host/guest affinity and the guest mobility within the hostmatrix respectively. The polymer capability of separating two low molecular weight components of a gas mixture (identified here with the subscript ‘i’ and ‘j’) is usually evaluated from the ideal selectivity ( α i d ) equal to:
α i d = P e r m i P e r m j = D ¯ i S i D ¯ j S j = α S i d ⋅ α D i d
where α S i d and α D i d are, respectively, the solubility and diffusivity ideal selectivity provided the diffusivity is invariant in the range [ C d , C u p ]. However, when designing a gas mixture separation apparatus based on permeation through a polymer membrane, the real selectivity should be considered. To this aim, we still consider the case where the upstream partial pressure of each component is significantly higher than the corresponding downstream ones. The solubility coefficient within the polymer phase of the gaseous species i is estimated at the corresponding upstream pressure ( P i u p ), i.e.:
S i m i x = C i u p / P i u p
and, therefore, the solubility selectivity is expressed as [35]:
α m i x = S i m i x / S j m i x
In parallel, the diffusion process occurring in a sorption experiment of a penetrant in a polymer plane sheet can be described in terms of evolution with time of the total mass of absorbed penetrant by integrating the one-dimensional differential mass balance over the thickness of the polymer film. The proper symmetrical boundary conditions that are imposed are that the concentration of the penetrant within the polymer at both surfaces in contact with the external phase at time = 0 are fixed , C i ∞ , as the value dictated by the sorption equilibrium while the initial condition is that the concentration of penetrant is uniform within the polymer, C i 0 (and equal to zero if the penetrant is initially not present within the polymer sample). If the constitutive expression for mass flux is Fickian, with a diffusivity independent from the penetrant concentration, the evolution with time of the mass of the absorbed penetrant (M(t)) in a plane sheet of thickness L, as obtained by solving the differential mass balance, can be expressed [34]:
M t M ∞ = 1 − ∑ n = 0 ∞ 8 2 n + 1 2 π 2 e x p − D 2 n + 1 π 2 t L 2
where M ∞ is the mass of absorbed penetrant when the sorption equilibrium with the external phase has been asymptotically attained. In equation (20), it is assumed that the specimen thickness L and the boundary conditions are invariant during sorption.
In the following, C ¯ i indicates the arithmetic average concentration during a sorption experiment (i.e., determined as ( C i ∞ + C i 0 ) / 2 ) and D ¯ in Eq. 20 is intended as calculated at C = C ¯ i .

3. Materials and Methods

3.1. Materials

Poly(2,6-dimethyl-1,4-phenylene)oxide (PPO) Ultra High P6130 grade (Mw = 350000 g mol−1) was purchased from Sabic (Riyadh, Saudi Arabia). Sigma-Aldrich (Milan, Italy) supplied chloroform (CHCl3, purity ≥ 99.9%) and acetonitrile (ACN). Amorphous PPO films were prepared by solution casting from a 0.5%wt CHCl3 solution at T=60°C. The absorbed CHCl3 was removed from the cast films by ACN guest sorption/desorption at room temperature. The density of amorphous PPO films was measured by flotation in a CaCl3 aqueous solution and is equal to 1.063 g cm-3. Sol Spa (Monza, Italy) supplied carbon dioxide with molar fraction purity 999,950 μmol mol−1. Nippon Gases Industrial Sud S.r.l. (Naples, Italy) supplied methane with molar fraction purity 999,995 μmol mol−1.
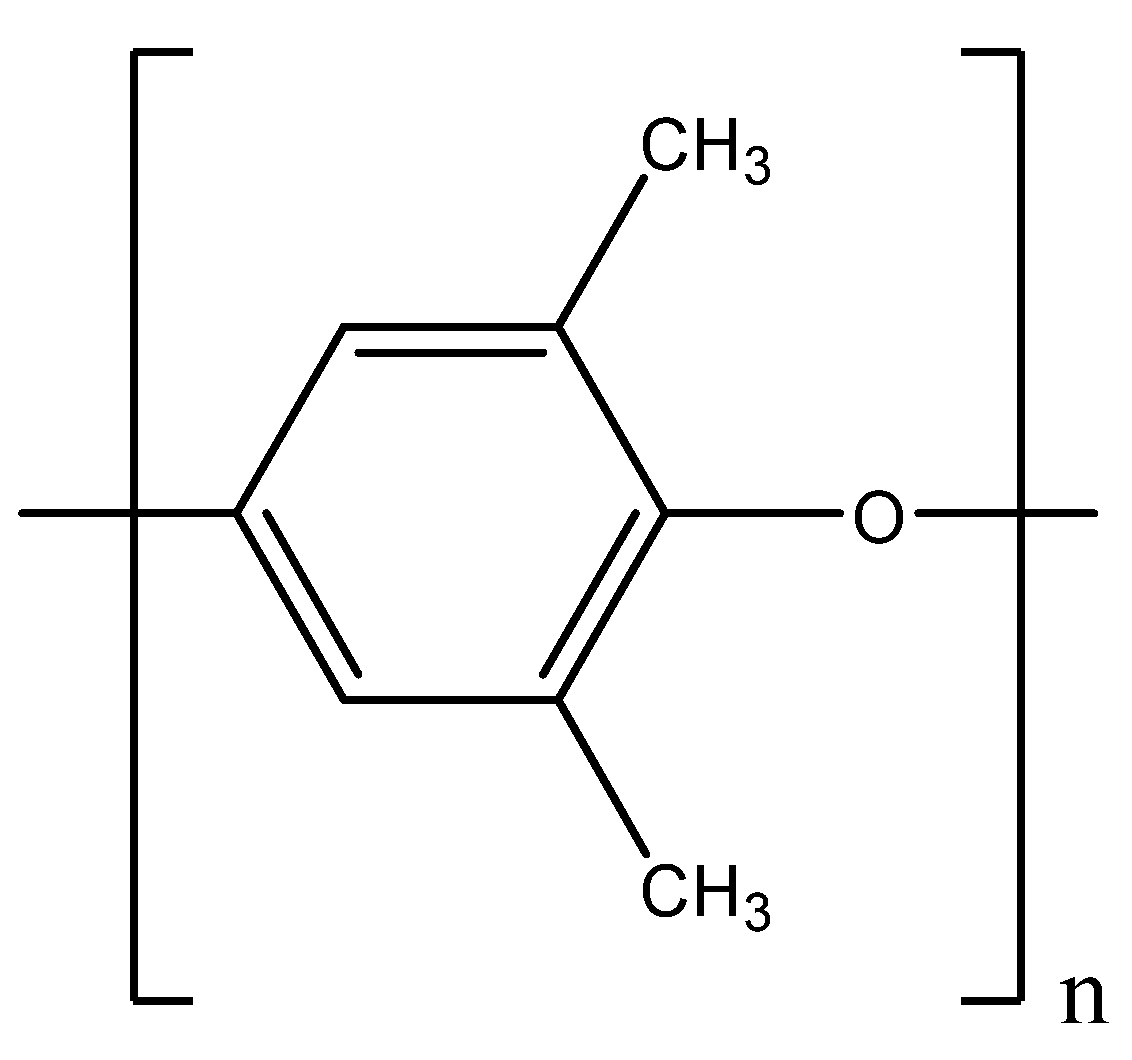
Preprints 67461 g001
Figure 1. Repeating unit of Poly(2,6-dimethyl-1,4-phenylene)oxide.
Figure 1. Repeating unit of Poly(2,6-dimethyl-1,4-phenylene)oxide.
Preprints 67461 g001

3.2. Methods

3.2.1. Closed Volume –Variable Pressure Apparatus

Integral and differential sorption experiments of pure CO2, CH4 and their mixtures in PPO were conducted in a closed volume variable pressure system similar to the one described by Loianno et al. [11]. The apparatus is schematically represented in Figure 2. It consists of three chambers indicated with the symbols V1, V2 and V3, whose volumes were calibrated with the Burnett expansion method and are equal to 15.87 cm3, 35.21 cm3 and 61.13 cm3, respectively. The latter is reduced with stainless steel spheres down to 44.71 cm3. They are separated from each other with shut-off valves type 4H-V-51 from Swagelok (Nordival S.r.l., Bs, Italy). The connections between service lines are obtained with VCR fittings from Swagelok to ensure that the system is leak proof. Chamber 2 is equipped with two Baratron 121A pressure transducers from MKS Instruments (MA, USA) respectively with a full-scale pressure range of 100 Torr and 1000 Torr. Their resolution is equal to 0.01 Torr and 0.1 Torr respectively and both have an accuracy of 0.5% of reading. For temperature control Chamber 3 is jacketed and circulating water is supplied by a HAAKE F6 thermal bath. Chambers 1 and 2 are at ambient temperature. The latter is measured with a HD9215 thermometer from RS (Milan, Italy) coupled with a PT100 temperature transducer (resolution 0.1 ◦C, uncertainty ±0.2 ◦C). Pure gas sorption tests were conducted by excluding chamber 1. Mixed gas sorption tests were conducted by including chamber 1. The gas mixture is prepared using thermal mass controllers type GM50A-013102RMM020 from MKS Instruments (full scale volumetric flow range of N2 100 sccm) following the protocol proposed by Loianno and Mensitieri [36].
To perform a static sorption test, the gas mixture of desired composition is first prepared in chambers 1 and 2 and is subsequently let to expand in chamber 3. Conversely, to perform a dynamic sorption test, the two gases, at the desired molar ratio, are introduced at the same time in the whole system, still using the mass flow controllers, and sorption is occurring while the system is being filled to reach the desired pressure.

3.2.2. FTIR- Spectroscopy in the transmission mode

During the sorption test, both the pressure signal and the IR spectrum are collected simultaneously: the latter is measured in the transmission mode in chamber 3. Two flat and coplanar KBr windows (4 mm thickness each) are aligned with the sample and allow the IR beam to pass through the chamber. The chamber is made leak proof by placing Viton O-rings between the IR windows and their seats. The sample is cut into multiple pieces of the same thickness (63 µm), one of which is placed within the optical path of the IR beam. A spectrometer Spectrum 100 from Perkin Elmer (Norwalk, CT) was used to perform the IR spectrum measurement. It is equipped with a wide band deuterated triglycine sulfate detector working at room temperature and an interferometer including a germanium/KBr beam splitter. The detector has a wavelength response ranging from the near to the far infrared. The IR spectra collected at sorption thermodynamic equilibrium were averages of 32 coadded scans at 2 and 4 cm-1 and with a scan frequency of 5 s per spectrum. During detection of sorption kinetics, IR spectra were collected at 4 cm-1 with a scan frequency of 1 s per spectrum.

4. Results and Discussion

4.1. Sorption of pure CO2 and CH4 in PPO

In a typical pure gas sorption test, chamber 2 is filled up to a specific pressure at ambient temperature and the gas is then expanded into chamber 3 whose temperature is controlled and fixed at 35.00±0.02°C. Chamber 3 is initially either under high vacuum (integral test) or filled with gas at thermodynamic equilibrium with the polymer phase prior to the gas expansion (differential test). The solubility of the gas absorbed within the polymer is retrieved from a mole balance over the gas phase by evaluating the gas concentration depletion with barometry. We assume that the pressure is uniform throughout the apparatus and that the temperature displays a step change at the border between chambers 2 and 3. The concentration of the gas is evaluated from the NIST Standard Reference Database 69: NIST Chemistry WebBook [37]. The same approach has been already adopted to investigate the sorption of CO2 in polydimethylsiloxane [38]. In that case, a single polymer slab was tested while, in the present case, multiple pieces of PPO were inserted into the volume of the measuring chamber to reduce the uncertainty of the solubility measurement. The total mass of PPO sample introduced into the measuring chamber was 0.3491 g.
The concentration of pure carbon dioxide and methane in amorphous PPO absorbed within the polymer measured at equilibrium are reported in Figure 3 as a function of gas pressure and are compared with analogous data available in the literature [7,39]. Our results are in excellent agreement with those from Story and Koros as expected since the sample preparation method was the same and the density of the two amorphous samples were very close (1.068 g cm-3 for our samples vs a value of 1.063 g cm-3 in the case of the samples used by Story and Koros) [7,40]. Conversely, the solubility data reported by Galizia et al. [38] are systematically lower than the ones we obtained and, specifically, in the case of carbon dioxide and methane an average reduction of 20% and 76% of the solubility coefficient is observed, respectively. The reason lies in the different method of preparation of the samples that in [38] were melt at 290°C and then compression molded, thus resulting in a lower film density equal to 1.016 g cm-3.
We first discuss the IR spectra collected at sorption equilibrium for the PPO – CO2 system. In Figure 4, the absorbance spectrum of the polymer under high vacuum and at different pressures of CO2 are reported. Difference Spectroscopy is used to remove the IR contribution of the gas phase from the overall spectrum so that the resulting spectra only consist of the signals related to the polymer and the CO2 absorbed within it. Three frequency regions are identified where carbon dioxide absorbs IR light: the bending vibration at 659 cm-1; the antisymmetric stretching vibration at 2336 cm-1 and two overtones at 3586 and 3692 cm-1. The peak at 659 cm-1 shows the strongest absorptivity and is saturated above 250 Torr. In the range [250, 1000] Torr, the overtone at 3692 cm-1 is the most suitable signal for a quantitative analysis. Indeed, its absorptivity is the greatest among the two identified overtones. Also, the absorbance uncertainty is lower in the range [3400, 3900] cm-1 than in [600, 700] cm-1 due to the greater transparency of the KBr windows.
The bandshape analysis of the signals produced by sorbed CO2 provides information on the interactions of the probe molecule with the surrounding environment (see Figure 5).
The ν3 profile represented in Figure 5A displays a secondary maximum at 2323 cm-1. This feature is due to a non-fundamental transition [a (ν3 + ν2) – ν2 hot-band in Fermi resonance with the neighboring peak] and is to be neglected after proper resolution [41]. The main band, centered at 2336 cm-1 has a complex shape which, according to the theory of vibrational relaxation, can be simulated with high accuracy (R2 = 0.9988) by the sum of a Gaussian and a Lorentzian function, both centered at the peak maximum [42,43]. The composite band shape is originated by the probe dynamics within the molecular environment; in particular, free rotation in the early stages of the relaxation process (0.2−1.0 ps), which produces the Gaussian component, and random rotational diffusion at later stages (the so-called Debye regime), from which the Lorentz component arises. The pronounced Gaussian component (44.6 % of the total band area) demonstrates a significant free-rotation regime, which, in turn, suggests that the probe is interrogating an essentially inert environment. The CO2 bending mode (ν2) is equally informative: this transition is degenerate for an isolated molecule but when an interaction takes place, a distortion of the linear configuration is produced which removes the original D ∞ h symmetry. This effect activates distinct in-plane and out-of-plane modes and the signal splits in two fully or partially resolved components, depending on the degree of distortion. The occurrence of a two component bandshape provides a clear signature of an existing interaction between the probe and active sites on the polymer backbone, and has been detected in numerous matrices including PMMA, poly(butyl methacrylate), poly(vinyl acetate), poly(vinyl fluoride) and, more recently, in an amorphous polyetherimide [26,41]. In the present case, the ν2 bandshape is symmetrical and can be reliably simulated by a single gaussian function (Figure 5B) which confirms the absence of vibrationally detectable interactions. The present band profile is coincident with that observed in an ethylene-propylene copolymer, a fully inert matrix [26].
The calibration of the CO2 IR peaks at 2336 cm-1 and 3692 cm-1 is obtained from each pure gas sorption test by correlating the absorbance intensity with the concentration of CO2 within PPO (Figure 6). A linear trend is observed in both cases resulting in an absorptivity of 58.66 and 0.808 cm3STP cm-3PPO cm-1 respectively. The CO2 IR peaks are symmetrical and well resolved as expected when no specific interactions are occurring with the polymer matrix.
We recently reported that the absorptivity of the IR peak at 4955 cm-1 of CO2 in PDMS is 1.335∙10-2 ±3.4∙10-4 cm3STP cm-3PDMS cm-1 [38]. The solubility coefficient of CO2 in PDMS is equal to 1.9∙10-3 cm3STP cm-3PDMS Torr-1 and is much lower than in PPO (9.2∙10-3 cm3STP cm-3PPO Torr-1). However, no IR signal of CO2 in PPO were identified in the range [4800, 5200] cm-1 where the Fermi triad is located. By following the classical Beer-Lambert relation and by assuming an analogous absorptivity of the peak at 4955 cm-1 of CO2 in PPO, a greater specimen thickness must be chosen to identify it in the case of PPO. On this basis, it follows that a compromise must be found when combining IR Spectroscopy and Barometry to study the diffusion of low MW species in polymers to optimize the diffusion time, the spectral resolution and the uncertainty of the IR peaks of interest. Clearly, such a compromise will be different when studying rubbery or glassy polymers.
In the case of methane in amorphous PPO, the subtraction of the gas phase background spectrum from the overall IR spectrum at sorption equilibrium did not produce any significant result. Conversely, the IR stretching vibration of CH4 absorbed in PPO could be isolated by analyzing the desorption kinetics. This approach should be preferred when the signals to be isolated have low intensity and/or their absorptivity is still unknown. During an integral desorption step, a pressure jump down to 1∙10-3 Torr is produced in chamber 3 in approximately 100 seconds so that, after this time, the IR signals which identify the gas phase disappear and those associated to the absorbed gas are unveiled in the same frequency region. In Figure 7A, the sequence of spectra measured in the range [2850, 3100] cm-1 during an integral desorption step starting from 753.5 Torr is presented along with the variation of the signal at 2973 cm-1 as a function of time. After approximately 1 min from the valve opening the gas phase signal is no more appreciable and the kinetics only represents the desorption of CH4 from PPO. In Figure 7B, the absorbance area evaluated in the frequency region [2969, 3005] cm-1 is reported. The relative uncertainty is lower and the sorption kinetics is better reproduced. At the authors knowledge, this is the first time that methane is observed directly within a polymer phase. Li and Xi investigated the adsorption of methane on Cerium Oxide with FT-IR Spectroscopy at -100°C [44]. Also, Yoshida et al. observed CH4 adsorbed on active carbon at -120°C [45]. The identification of methane physiosorbed on porous materials or absorbed in dense materials is a rather difficult task at ambient temperature with FTIR Spectroscopy. We have conducted further experiments to evaluate the absorptivity of the isolated signal for quantitative analyses. A preliminary result is obtained by extrapolating at t=0 the plot of the values of the absorbance at 2973 cm-1 and of the absorbance area in the range [2969, 3005] cm-1 (see Figure 7) reported as a function of square root of time (Fick’s plot) and by dividing these values by the concentration of methane in PPO (Figure 3). The absorptivity of the signal at 2973 cm-1 has been estimated to be 1.216 cm3PPO cm-3STP cm-1 while the absorptivity of the absorbance area in the range [2969, 3005] cm-1 has been estimated to be 31.65 cm3PPO cm-3STP cm-2.

4.2. Diffusion of Pure CO2 in PPO

The diffusivity of pure CO2 in PPO can be evaluated by fitting Eq. 20 to the sorption kinetics measured with FTIR Spectroscopy. The temperature is not uniform throughout the closed volume so that the procedure outlined in the Section Sorption of Pure CO2 and CH4 in PPO for the solubility of each gas in PPO at equilibrium should be used to evaluate the sorption kinetics with the pressure decay method. Conversely, the sorption kinetics obtained from the time resolved IR spectrum of the gas species absorbed within the polymer is not affected by this constraint, being the IR signal measured at 35°C. In addition, a further source of error in the case of the pressure decay method is the thickness variance among all the samples placed inside the measuring chamber as compared to the IR spectroscopy measurement that is instead performed on a single specimen, thus lowering, in this case, the uncertainty of the estimated value of diffusivity.
Worth mentioning, the concentration depletion of the gas phase during sorption introduces two distinct problems. First, Equation 20 is the analytical solution to the diffusion problem in a plane sheet when the boundary conditions in terms of concentration at the surface of the sheet are kept constant. We have observed a pressure decrease of 4.3% and 0.8% relative to the pressure at sorption equilibrium during the tests at 24.49 and 756.2 Torr respectively. Within this pressure range, the observed pressure variation is low enough to assume the validity of Eq. 20. Second, to retrieve the IR signal of the species absorbed within the polymer during sorption, difference spectroscopy should be used to remove the gas phase contribution (Agas) from the overall spectrum (A). To this aim, one should account for the fact that the IR signal of the gas phase is changing during time so that the subtraction relation can be rewritten as follows:
A g a s t − k t ⋅ A b k g = 0
where Abkg is the gas phase background spectrum measured at the same pressure and temperature reached at sorption equilibrium and corrected for the polymer specimen thickness; k(t) is a time dependent correction factor accounting for the deviation of thermodynamic conditions of the gas phase at a generic time during sorption from those attained at sorption equilibrium (i.e., when k(t→∞) = 1). The time dependent correction is easily calculated from the classical Beer-Lambert law applied to Eq. 21, as follows:
k t = C g t C ∞ g
where C g t and C ∞ g are the gas phase concentration during time and at sorption equilibrium and are retrieved from the barometric measurement. In Figure 8A, are reported the IR integral sorption kinetics of CO2 in PPO at 98.56 Torr respectively obtained applying the gas phase correction (according to Eq. 22) and without any correction (i.e., with k(t) = 1). The two results are very close. Eq. 21 and 22 show the complementarity of barometry and FTIR Spectroscopy to measure the diffusivity of the species in the polymer from the IR signal of the species within the polymer phase but FTIR Spectroscopy can be also used as a standalone technique to evaluate the sorption kinetics and the diffusivity of CO2 in PPO with the present apparatus. Conversely, the combination of the two techniques is essential to calibrate the absolute IR signals. The value of D ¯ estimated from the fitting of the data in red is 9.4·10-8 cm2 s-1.
In Figure 8B, the estimated values of the effective diffusivity ( D ¯ ) of CO2 in PPO is reported as a function of the average CO2 concentration during each sorption test. In the concentration range investigated, the diffusivity is almost constant showing a slight linear increase. The effective diffusivity ( D ¯ ) of CH4 in PPO is measured from the desorption kinetics presented in Figure 7 and has been estimated to be equal to 6∙10-9 cm2 s-1 at an average concentration of 2.11 cm3STP cm-3PPO.

4.3. Modelling sorption of light gases in PPO

Since the analysis of the IR bands of the polymer and the absorbed CO2 has shown that specific interactions are absent in the polymer – penetrant systems investigated, the NETGP-NRHB model by excluding the contribution of specific interactions. Hence, in the following analysis we have interpreted the sorption isotherms using the NETGP-NR model. The four NR composition-independent lattice fluid parameters of PPO, CO2 and CH4 have been taken from the literature and are reported in Table 1. Using the available parameters for pure components, the NETGP-NR model was used to fit the solubility data of pure CO2 and CH4 in PPO and to evaluate the kij binary interaction parameter for each polymer – penetrant system. In Table 2, the kij values are reported and in Figure 9 are shown the results of the fitting procedure.
In a previous publication, we have modelled the binary solubility data at 35°C of CO2 and CH4 in an amorphous PPO which, due to a different thermo-mechanical history, displayed a slightly different value of ρ p , 0 [16]. This set of data spans a higher range of pressure (up to 20 atm) so that a swelling effect, induced by the penetrant, was taken into account according to the phenomenological equation [19,27,28]:
ρ p , 0 s w = ρ p , 0 ⋅ ( 1 − k s w P )
where ρ p , 0 s w represents the actual polymer mass density to be used in the equations regarding the polymeric phase and k s w represents an additional binary adjustable parameter which allows to express the elastic swelling contribution due to the absorbed penetrant in the glassy polymeric matrix.
In that case, extremely low values of ksw for PPO/CO2 and PPO/CH4 systems were determined (respectively, 1.96∙10-6 Torr-1 and 4.48∙10-7 Torr-1). On this basis, we estimated that the swelling induced by the two penetrants in the low range of pressures analyzed here is negligible. This confirms the outcome of the IR investigation that no-swelling takes place in the overall range of pressure investigated. The same assumption has been adopted also in the following analysis of the solubility of CO2/CH4 mixtures within the PPO glassy matrix in view of the low values of pressure of the external phase used in the experimental characterization. In addition, we underline that the values of kij obtained in the present investigation from fitting of the sorption isotherms by fixing ksw = 0, and are in good agreement with those determined in ref. [16] (see Table 2).
The comparison between the two investigations shows the agreement of the kij values for each polymer – penetrant system, confirming that the ksw and kij parameters are independent from each other.

4.4. Mixed gas sorption in PPO

Mixed gas sorption experiments were conducted at 35°C, at several values of total pressure up to 1000 Torr using mixtures of two compositions, i.e., with a CO2 mole fraction of ~0.50 and ~0.37 mol mol-1. In Figure 10, the solubility of each gas absorbed within the polymer is reported as a function of the total pressure (indicated by the symbol P) if the measurement refers to pure gas sorption experiments and as a function of the partial pressure of the gaseous species (indicated by the symbol Pi) if the measurement refers to mixed gas sorption experiments. The partial pressure at sorption equilibrium is calculated based on the total pressure of the system and of the composition of the gas phase. The latter is measured spectroscopically by evaluating the concentration of CO2 and CH4 in the gas phase from the IR peaks located at 4991 and 4218 cm-1, respectively. At these frequencies, no IR bands associated to the polymer or to the absorbed species are present so that the gas phase signals are well isolated and resolved and have been used without any further treatment. The protocol proposed by Loianno et al. is followed to calibrate these signals [11,36].
We measured the concentration of carbon dioxide absorbed within the amorphous PPO (Figure 10A) using the IR signal of absorbed CO2 centered at 3692 cm-1 (calibrated using data in Figure 6B). Its absorptivity is assumed constant and independent of the composition of the polymer phase since no specific interactions are occurring with the polymer or the methane molecules absorbed in PPO. The numerical values are reported in Table S1 (see Supplementary Materials). The solubility of CO2 in PPO is invariant up to a partial pressure equal to 379.0 Torr in the range of gas mixture composition investigated. Story and Koros conducted sorption experiments of CO2/CH4 gas mixtures in amorphous PPO by fixing the partial pressure of one gas and by changing the partial pressure of the other [7]. At a partial pressure of CO2 equal to 5.097 bar and CO2 mole fractions equal to 0.549 and 0.380 mol mol-1, they observed a reduction of the CO2 solubility with respect to pure gas sorption equal to 9.6% and 20%, respectively. Then, a significant deviation from the pure gas sorption isotherm is expected at CO2 partial pressure greater than 2 bar. We did not evaluate the solubility of CH4 in PPO during mixed gas sorption tests since we could not resolve any signal at sorption equilibrium. Work is in progress to reach this goal.
Using the PPO/CO2 and PPO/CH4 binary parameters estimated from pure gas sorption tests and the value of kij = 0.0406 for the system CO2/CH4 taken from the literature we were able to predict, using the NETGP-NR model, the solubility of each gas absorbed in PPO at the same thermodynamic conditions of the mixed gas sorption tests [16]. The predicted solubility of CO2 in PPO deviates at the most by 9.3% from the experimental values. This difference is within the uncertainty of both data sets and confirms the efficacy of the model to predict the behavior of such polymer – penetrant systems. Worth mentioning, we can confirm the complementarity of the model and the experiments since we could not measure the solubility of CH4 in PPO during mixed gas sorption tests.
A comparison between the ideal and real solubility selectivity, both calculated using the NETGP-NR model, is presented in Figure 11 as a function of the partial pressure of CO2 in the case of two gas mixtures of different CO2 composition.
The real solubility selectivity is found to be rather independent from the gas mixture composition within the narrow range of pressure investigated. Conversely, the ideal solubility selectivity is found to decrease as a function of CO2 partial pressure. This is since the use of ideal selectivity implies that no interference occurs between the two absorbed species while the real selectivity accounts for the fact that the more condensable CO2 molecules displace the CH4 molecules form adsorption sites within the glassy polymer.

5. Conclusions

In this contribution, the sorption of carbon dioxide, methane and their mixtures in amorphous PPO was studied both experimentally and theoretically up to 1000 Torr at 35°C. Barometry and FTIR Spectroscopy were combined to evaluate the solubility of each gas in the polymer and to retrieve relevant IR signals in the polymer phase for each penetrant. The results are in excellent agreement with the literature and validate the applicability of the proposed technique to the case of glassy polymers.
We identified several IR bands of carbon dioxide absorbed in PPO which were conveniently calibrated over the penetrant concentration from pure gas barometric sorption tests. These signals were useful to evaluate the concentration of CO2 in PPO during mixed gas sorption tests. Although we identified one IR band for CH4 absorbed in PPO from the pure gas desorption kinetics, this is to be considered a preliminary result which could not be used to quantify methane in PPO during the mixed gas sorption tests. FTIR spectroscopy also allowed us to evaluate the diffusivity of CO2 in amorphous PPO. The main result we obtained is the invariance of the carbon dioxide solubility up to 450 Torr of CO2 partial pressure at 35°C and CO2 mole fraction equal to ~0.37 and ~0.5.
From the theoretical point of view, we adopted the NETGP-NR thermodynamic model to describe the solubility of CO2 and CH4 in PPO. Once the model binary parameters have been determined, we tested the capability of the model to predict the solubility in the PPO in it in the case of the corresponding binary gas mixture. The model only includes one parameter for each couple of components and only accounts for “mean field” energy interaction since we could exclude from the IR analysis the occurrence of specific interactions between the polymer chains and the absorbed molecules. The model prediction of carbon dioxide solubility negligibly deviates from the experimental data set (<9.3%) and shows that, in contrast with decreasing ideal selectivity, the real solubility selectivity is constant as a function of CO2 partial pressure and mole fraction.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: CO2 sorption kinetics measured with the IR peak at 2336 cm-1; Table S1: Mixed gas sorption experiments: solubility of CO2 (component #1) in amorphous PPO.

Author Contributions

Conceptualization, Valerio Loianno, Pellegrino Musto and Giuseppe Mensitieri; Data curation, Valerio Loianno and Antonio Baldanza; Formal analysis, Valerio Loianno, Antonio Baldanza and Giuseppe Scherillo; Investigation, Valerio Loianno, Antonio Baldanza and Giuseppe Scherillo; Methodology, Valerio Loianno; Software, Antonio Baldanza and Giuseppe Scherillo; Supervision, Pellegrino Musto and Giuseppe Mensitieri; Validation, Valerio Loianno, Antonio Baldanza and Giuseppe Scherillo; Writing – original draft, Valerio Loianno and Giuseppe Scherillo; Writing – review & editing, Pellegrino Musto and Giuseppe Mensitieri. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

New data generated in this investigation are reported in Table S1 of the Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

List of symbols

A g a s ( t ) gas phase contribution to the overall absorbance spectrum at time t
A b k g gas phase contribution to the overall absorbance spectrum at sorption equilibrium state
C molar concentration of the pure penetrant
C d molar concentration of the pure penetrant in the polymer phase at downstream side in a permeation experiment
C u p molar concentration of the pure penetrant in the polymer phase at upstream side in a permeation experiment
C i concentration of component i within the polymer phase in a sorption experiment
C ¯ i average concentration of component i within the polymer phase in a sorption experiment
C i 0 initial uniform concentration of component i within the polymer phase in a sorption experiment
C i ∞ equilibrium concentration of component i within the polymer phase in a sorption experiment
C g t molar gas phase concentration at time t
C ∞ g molar gas phase concentration at sorption equilibrium state
D mutual diffusion coefficient
Di mutual diffusion coefficient of the component i
D ¯ effective diffusivity coefficient
G non-equilibrium expression of molar Gibbs energy
G e q equilibrium expression of molar Gibbs energy
k t defined in equation (21) and calculated from equation (22)
k i j mean field lattice fluid binary interactional parameter between the species i and j
k s w the swelling factor associated to the polymer-penetrant couple
l i is defined as z 2 r i − q i − ( r i − 1 ) L membrane thickness
m number of components
M t mass of absorbed penetrant at time t in a sorption experiment
M ∞ equilibrium mass of absorbed penetrant in a sorption experiment
Ni moles of species i
N total moles
N vector of moles of the components
N i j moles of i component and j-component pairs
N _ i j vector of moles of each i-component and j-component pairs
N _   i j E Q equilibrium vector of moles of each i-component and j-component pairs
P i u p partial pressure of the component i at upstream side
P pressure
P ~ scaled pressure of the pure component or of the mixture
P e r m ¯ mean steady-state permeability
P e r m i steady-state permeability of component i
q average number of lattice contacts per molecule in the mixture and it is equal to ∑ i = 0 m x i q i qi number of external contacts made by one molecule of species i
R universal gas constant
r average number of sites occupied by one molecule in the mixture and it is equal to ∑ i = 0 m x i r i ri number of sites occupied by one molecule of species i
S apparent solubility coefficient
S i m i x solubility coefficient of component i in the polymer-penetrant mixture
t time
T temperature
Tg glass-to-rubber transition temperature
T ~ scaled temperature of the pure component or of the mixture
T ~ i scaled temperature of the pure component i in the mixture
v i , s p , 0 * the temperature-independent contribution to the close packed specific volume of the pure component i
v i , s p * close packed specific volume of the pure component i
v ~ scaled lattice fluid volume of the pure components or of the mixture and it is equal to 1 / ρ ~ s i the ratio of molar surface to molar volume of component i
xi molar fraction of species i
x i N E molar fraction of species i at Pseudo-Equilibrium of phase condition
z coordination number
Greek letters
α m i x solubility selectivity defined by equation (19)
aid ideal selectivity
α S i d solubility contribution to the ideal selectivity
α D i d diffusivity contribution to the ideal selectivity
Γ i j non-random factor
Δ ε i j defined by equation (13)
δ i flexibility factor of species i
ε * mean field interaction energy within the mixture
ε i * mean field interaction energy per molar segment
ε i j * defined by equation (12)
ε i , h * mean interaction energy per molar segment, enthalpic contribution
ε i , s * mean interaction energy per molar segment, entropic contribution
ε i i defined as ε i i = 2 z ε i * θ i = x i q i q Θ i surface fraction of component i
μ i molar chemical potential of the species i
μ i , e x t E Q equilibrium molar chemical potential of the species i
μ i , p o l N E non-equilibrium molar chemical potential of the species i within the glassy polymer-penetrant phase
ρ non-equilibrium polymer mass density within the mixture
ρ * closed-packed density of the polymer-penetrant mixture
ρ p , 0 s w polymer mass density induced by elastic instantaneous swelling
ρ i E Q equilibrium mass density of the species i
ρ p , 0 the value of the unpenetrated polymer mass density right before the start of the sorption process
ρ ~ scaled lattice fluid density of a pure component or of the mixture
ɸ i “close-packed” volumetric fraction of component i
ω p polymer mass fraction

References

  1. Eurostat. Available Online: HTTPS://Ec.Europa.Eu/Eurostat/.
  2. Short-Term Energy Outlook, september 2022. Available Online: HTTPS://Www.Eia.Gov/Todayinenergy/Detail.Php?Id=53839.
  3. Baker, R.W.; Lokhandwala, A. Natural Gas Processing with Membranes:  An Overview. Ind. Eng. Chem. 2008, 47, 2109–2121. [CrossRef]
  4. White, L.S. Effect of Operating Environment on Membrane Performance. Current Opinion in Chemical Engineering 2020, 28, 105–111. [CrossRef]
  5. Genduso, G.; Ghanem, B.S.; Pinnau, I. Experimental Mixed-Gas Permeability, Sorption and Diffusion of CO2-CH4 Mixtures in 6FDA-MPDA Polyimide Membrane: Unveiling the Effect of Competitive Sorption on Permeability Selectivity. Membranes 2019, 9. [CrossRef] [PubMed]
  6. Pourafshari Chenar, M.; Soltanieh, M.; Matsuura, T.; Tabe-Mohammadi, A.; Khulbe, K.C. The Effect of Water Vapor on the Performance of Commercial Polyphenylene Oxide and Cardo-Type Polyimide Hollow Fiber Membranes in CO2/CH4 Separation Applications. Journal of Membrane Science 2006, 285, 265–271. [CrossRef]
  7. Story, B.J.; Koros, W.J. Sorption of CO2/CH4 Mixtures in Poly(Phenylene Oxide) and a Carboxylated Derivative. Journal of Applied Polymer Science 1991, 42, 2613–2626. [CrossRef]
  8. Sanders, E.S.; Koros, W.J.; Hopfenberg, H.B.; Stannett, V.T. Mixed Gas Sorption in Glassy Polymers: Equipment Design Considerations and Preliminary Results. Journal of Membrane Science 1983, 13, 161–174. [CrossRef]
  9. Ricci, E.; Benedetti, F.M.; Noto, A.; Merkel, T.C.; Jin, J.; De Angelis, M.G. Enabling Experimental Characterization and Prediction of Ternary Mixed-Gas Sorption in Polymers: C2H6/CO2/CH4 in PIM-1. Chemical Engineering Journal 2021, 426, 130715. [CrossRef]
  10. Genduso, G.; Litwiller, E.; Ma, X.; Zampini, S.; Pinnau, I. Mixed-Gas Sorption in Polymers via a New Barometric Test System: Sorption and Diffusion of CO2-CH4 Mixtures in Polydimethylsiloxane (PDMS). Journal of Membrane Science 2019, 577, 195–204. [CrossRef]
  11. Loianno, V.; Mensitieri, G.; Baldanza, A.; Scherillo, G.; Musto, P. Combining FTIR Spectroscopy and Pressure-Decay Techniques to Analyze Sorption Isotherms and Sorption Kinetics of Pure Gases and Their Mixtures in Polymers: The Case of CO2 and CH4 Sorption in Polydimethylsiloxane. Journal of Membrane Science 2022, 652, 120445. [CrossRef]
  12. Hong, S.U.; Barbari, T.A.; Sloan, J.M. Multicomponent Diffusion of Methyl Ethyl Ketone and Toluene in Polyisobutylene from Vapor Sorption FTIR-ATR Spectroscopy. Journal of Polymer Science Part B: Polymer Physics 1998, 36, 337–344. [CrossRef]
  13. Shade, D.; Bout, B.W.S.; Sholl, D.S.; Walton, K.S. Opening the Toolbox: 18 Experimental Techniques for Measurement of Mixed Gas Adsorption. Ind. Eng. Chem. Res. 2022, 61, 2367–2391. [CrossRef]
  14. Minelli, M.; Campagnoli, S.; De Angelis, M.G.; Doghieri, F.; Sarti, G.C. Predictive Model for the Solubility of Fluid Mixtures in Glassy Polymers. Macromolecules 2011, 44, 4852–4862. [CrossRef]
  15. Minelli, M.; Sarti, G.C. Modeling Mass Transport in Dense Polymer Membranes: Cooperative Synergy among Multiple Scale Approaches. Current Opinion in Chemical Engineering 2020, 28, 43–50. [CrossRef]
  16. Baldanza, A.; Loianno, V.; Mensitieri, G.; Scherillo, G. Predictive Approach for the Solubility and Permeability of Binary Gas Mixtures in Glassy Polymers Based on an NETGP-NRHB Model. Ind. Eng. Chem. Res. 2022, 61, 3439–3456. [CrossRef]
  17. Panayiotou, C.; Pantoula, M.; Stefanis, E.; Tsivintzelis, I.; Economou, I.G. Nonrandom Hydrogen-Bonding Model of Fluids and Their Mixtures. 1. Pure Fluids. Ind. Eng. Chem. Res. 2004, 43, 6592–6606. [CrossRef]
  18. Panayiotou, C.; Tsivintzelis, I.; Economou, I.G. Nonrandom Hydrogen-Bonding Model of Fluids and Their Mixtures. 2. Multicomponent Mixtures. Ind. Eng. Chem. Res. 2007, 46, 2628–2636. [CrossRef]
  19. Mensitieri, G.; Scherillo, G.; Panayiotou, C.; Musto, P. Towards a Predictive Thermodynamic Description of Sorption Processes in Polymers: The Synergy between Theoretical EoS Models and Vibrational Spectroscopy. Materials Science and Engineering: R: Reports 2020, 140, 100525. [CrossRef]
  20. Scherillo, G.; Galizia, M.; Musto, P.; Mensitieri, G. Water Sorption Thermodynamics in Glassy and Rubbery Polymers: Modeling the Interactional Issues Emerging from FTIR Spectroscopy. Ind. Eng. Chem. Res. 2013, 52, 8674–8691. [CrossRef]
  21. Scherillo, G.; Sanguigno, L.; Galizia, M.; Lavorgna, M.; Musto, P.; Mensitieri, G. Non-Equilibrium Compressible Lattice Theories Accounting for Hydrogen Bonding Interactions: Modelling Water Sorption Thermodynamics in Fluorinated Polyimides. Fluid Phase Equilibria 2012, 334, 166–188. [CrossRef]
  22. Scherillo, G.; Petretta, M.; Galizia, M.; La Manna, P.; Musto, P.; Mensitieri, G. Thermodynamics of Water Sorption in High Performance Glassy Thermoplastic Polymers. Frontiers in Chemistry 2014, 2. [CrossRef]
  23. de Nicola, A.; Correa, A.; Milano, G.; La Manna, P.; Musto, P.; Mensitieri, G.; Scherillo, G. Local Structure and Dynamics of Water Absorbed in Poly(Ether Imide): A Hydrogen Bonding Anatomy. J. Phys. Chem. B 2017, 121, 3162–3176. [CrossRef] [PubMed]
  24. Correa, A.; De Nicola, A.; Scherillo, G.; Loianno, V.; Mallamace, D.; Mallamace, F.; Ito, H.; Musto, P.; Mensitieri, G. A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide. International Journal of Molecular Sciences 2021, 22. [CrossRef]
  25. Mensitieri, G.; Scherillo, G.; La Manna, P.; Musto, P. Sorption Thermodynamics of CO2, H2O, and CH3OH in a Glassy Polyetherimide: A Molecular Perspective. Membranes 2019, 9. [CrossRef] [PubMed]
  26. Scherillo, G.; Mensitieri, G.; Baldanza, A.; Loianno, V.; Musto, P.; Pannico, M.; Correa, A.; De Nicola, A.; Milano, G. Weak Interactions between Poly(Ether Imide) and Carbon Dioxide: A Multiscale Investigation Combining Experiments, Theory, and Simulations. Macromolecules 2022. [CrossRef]
  27. Doghieri, F.; Sarti, G.C. Nonequilibrium Lattice Fluids:  A Predictive Model for the Solubility in Glassy Polymers. Macromolecules 1996, 29, 7885–7896. [CrossRef]
  28. Sarti, G.C.; Doghieri, F. Predictions of the Solubility of Gases in Glassy Polymers Based on the NELF Model. Chemical Engineering Science 1998, 53, 3435–3447. [CrossRef]
  29. von Konigslow, K.; Park, C.B.; Thompson, R.B. Application of a Constant Hole Volume Sanchez–Lacombe Equation of State to Mixtures Relevant to Polymeric Foaming. Soft Matter 2018, 14, 4603–4614. [CrossRef]
  30. Neau, E. A Consistent Method for Phase Equilibrium Calculation Using the Sanchez–Lacombe Lattice–Fluid Equation-of-State. Fluid Phase Equilibria 2002, 203, 133–140. [CrossRef]
  31. Baldanza, A.; Loianno, V.; Mensitieri, G.; Panayiotou, C.; Scherillo, G. On the Thermodynamic Consistency of Non-Random Hydrogen Bonding Lattice-Fluid Model for Multicomponent Mixtures. Fluid Phase Equilibria 2022, 553, 113302. [CrossRef]
  32. Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures. AIChE Journal 1975, 21, 1086–1099. [CrossRef]
  33. Graham, T. LV. On the Absorption and Dialytic Separation of Gases by Colloid Septa. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1866, 32, 401–420. [CrossRef]
  34. J. Crank The Mathematics of Diffusion; second edition.; Oxford University Press: Clarendon Press Oxford, 1975.
  35. Loianno, V.; Luo, S.; Zhang, Q.; Guo, R.; Galizia, M. Gas and Water Vapor Sorption and Diffusion in a Triptycene-Based Polybenzoxazole: Effect of Temperature and Pressure and Predicting of Mixed Gas Sorption. Journal of Membrane Science 2019, 574, 100–111. [CrossRef]
  36. Loianno, V.; Mensitieri, G. A Novel Dynamic Method for the Storage of Calibration Gas Mixtures Based on Thermal Mass Flow Controllers. Measurement Science and Technology 2022, 33, 065017. [CrossRef]
  37. NIST Chemistry WebBook, SRD 69. Available Online: HTTPS://Webbook.Nist.Gov/Chemistry/Fluid/.
  38. Loianno, V.; Baldanza, A.; Scherillo, G.; Jamaledin, R.; Musto, P.; Mensitieri, G. A Hyphenated Approach Combining Pressure-Decay and In Situ FT-NIR Spectroscopy to Monitor Penetrant Sorption and Concurrent Swelling in Polymers. Ind. Eng. Chem. Res. 2021, 60, 5494–5503. [CrossRef]
  39. Galizia, M.; Daniel, C.; Fasano, G.; Guerra, G.; Mensitieri, G. Gas Sorption and Diffusion in Amorphous and Semicrystalline Nanoporous Poly(2,6-Dimethyl-1,4-Phenylene)Oxide. Macromolecules 2012, 45, 3604–3615. [CrossRef]
  40. Story, B.J.; Koros, W.J. Sorption and Transport of CO2 and CH4 in Chemically Modified Poly(Phenylene Oxide). Journal of Membrane Science 1992, 67, 191–210. [CrossRef]
  41. Kazarian, S.G.; Vincent, M.F.; Bright, F.V.; Liotta, C.L.; Eckert, C.A. Specific Intermolecular Interaction of Carbon Dioxide with Polymers. J. Am. Chem. Soc. 1996, 118, 1729–1736. [CrossRef]
  42. Turner, J.J. Bandwidths. In Handbook of Vibrational Spectroscopy; J.M. Chalmers and P.R. Griffiths, John Wiley & Son: Chichester, UK, 2002; Vol. 1, pp. 101–127.
  43. Clarke, J.H.R. Band Shapes and Molecular Dynamics in Liquids. In Advances in Infrared and Raman Spectroscopy; Clarke, J. H.R. and Hester, R. E., Heyden: London, UK, 1978; Vol. 4, p. 109−193.
  44. Li, C.; Xin, Q. FT-IR Spectroscopic Investigation of Methane Adsorption on Cerium Oxide. J. Phys. Chem. 1992, 96, 7714–7718. [CrossRef]
  45. Yoshida, H.; Yamazaki, T.; Ozawa, S. IR Spectra of CH4 Physisorbed on an Active Carbon at Low Temperature. Journal of Colloid and Interface Science 2000, 224, 261–264. [CrossRef]
  46. Tsivintzelis, I.; Spyriouni, T.; Economou, I.G. Modeling of Fluid Phase Equilibria with Two Thermodynamic Theories: Non-Random Hydrogen Bonding (NRHB) and Statistical Associating Fluid Theory (SAFT). Fluid Phase Equilibria 2007, 253, 19–28. [CrossRef]
  47. Musto, P.; Loianno, V.; Scherillo, G.; La Manna, P.; Galizia, M.; Guerra, G.; Mensitieri, G. Benzene-Induced Crystallization of PPO: A Combined Thermodynamic and Vibrational Spectroscopy Study. Ind. Eng. Chem. Res. 2020, 59, 5402–5411. [CrossRef]
Preprints 67461 g002
Figure 2. Schematic diagram of the apparatus to conduct pure and mixed gas sorption experiments. The symbols V1, V2 and V3 identify the three closed volumes of the apparatus.
Figure 2. Schematic diagram of the apparatus to conduct pure and mixed gas sorption experiments. The symbols V1, V2 and V3 identify the three closed volumes of the apparatus.
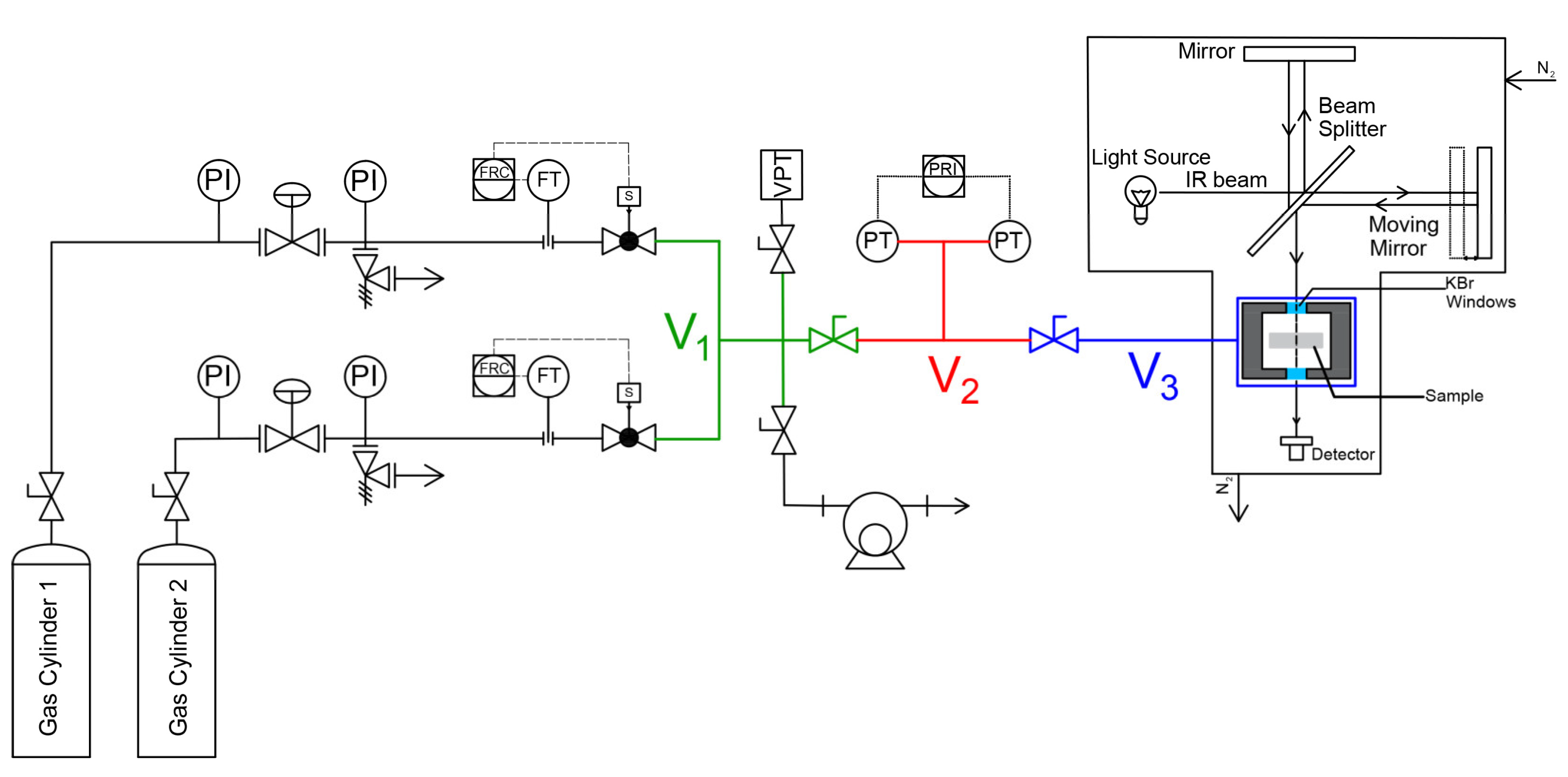
Preprints 67461 g002
Preprints 67461 g003
Figure 3. Sorption isotherms of pure CO2 and CH4 in amorphous PPO from the present investigation compared with literature data [7,39].
Figure 3. Sorption isotherms of pure CO2 and CH4 in amorphous PPO from the present investigation compared with literature data [7,39].
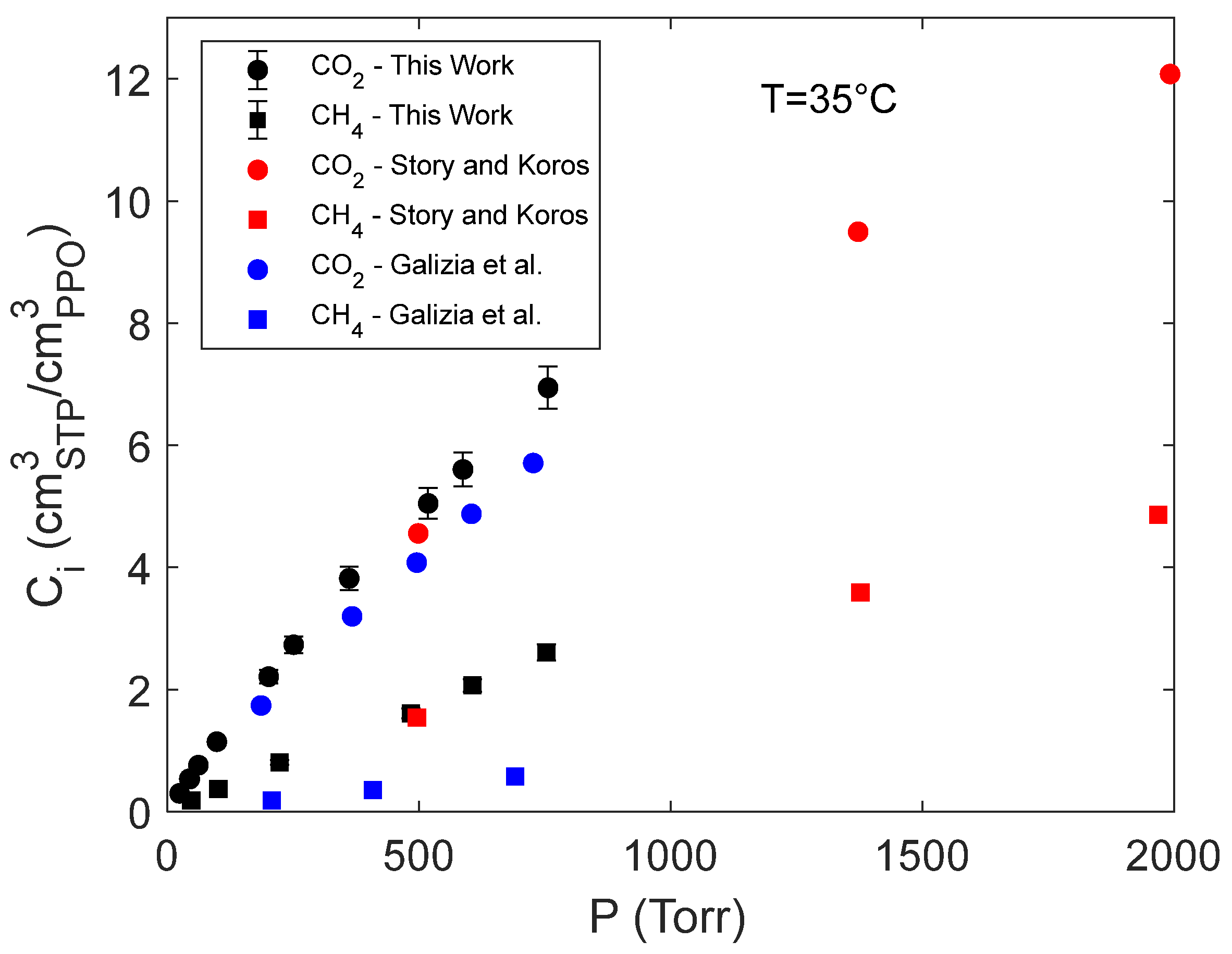
Preprints 67461 g003
Preprints 67461 g004
Figure 4. Absorbance spectra at 35°C and sorption equilibrium after removal of the gas phase spectrum at 2 cm-1 resolution. The insets show the frequency regions in which carbon dioxide absorbs IR light within the polymer phase. In the range [2200, 2450] cm-1, the spectrum at 518.2 Torr is saturated and is not reported for the sake of clarity.
Figure 4. Absorbance spectra at 35°C and sorption equilibrium after removal of the gas phase spectrum at 2 cm-1 resolution. The insets show the frequency regions in which carbon dioxide absorbs IR light within the polymer phase. In the range [2200, 2450] cm-1, the spectrum at 518.2 Torr is saturated and is not reported for the sake of clarity.
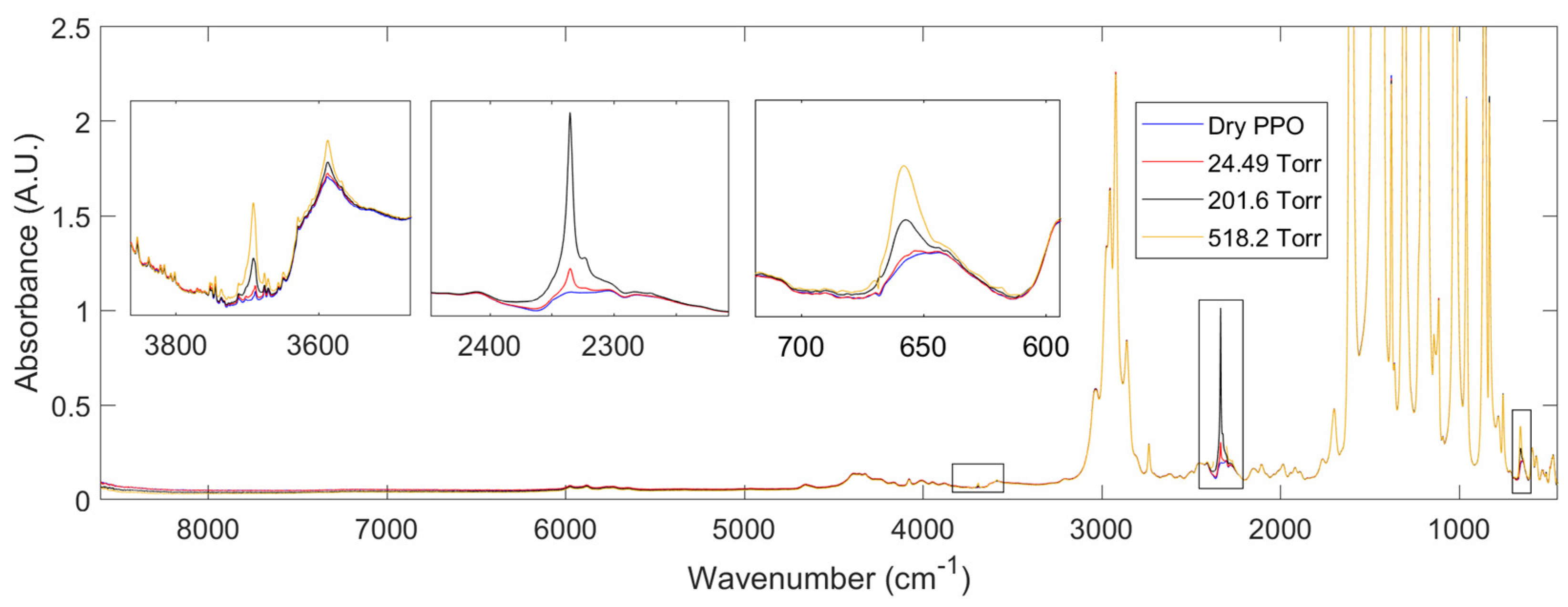
Preprints 67461 g004
Preprints 67461 g005
Figure 5. Bandshape analysis of the ν3 (A) and ν2 (B) modes of CO2 sorbed in PPO. The spectrum, obtained by Difference Spectroscopy, refers to the test at 201.6 Torr. Blue dots: experimental data. Red line: simulated profile. Black lines: resolved components.
Figure 5. Bandshape analysis of the ν3 (A) and ν2 (B) modes of CO2 sorbed in PPO. The spectrum, obtained by Difference Spectroscopy, refers to the test at 201.6 Torr. Blue dots: experimental data. Red line: simulated profile. Black lines: resolved components.
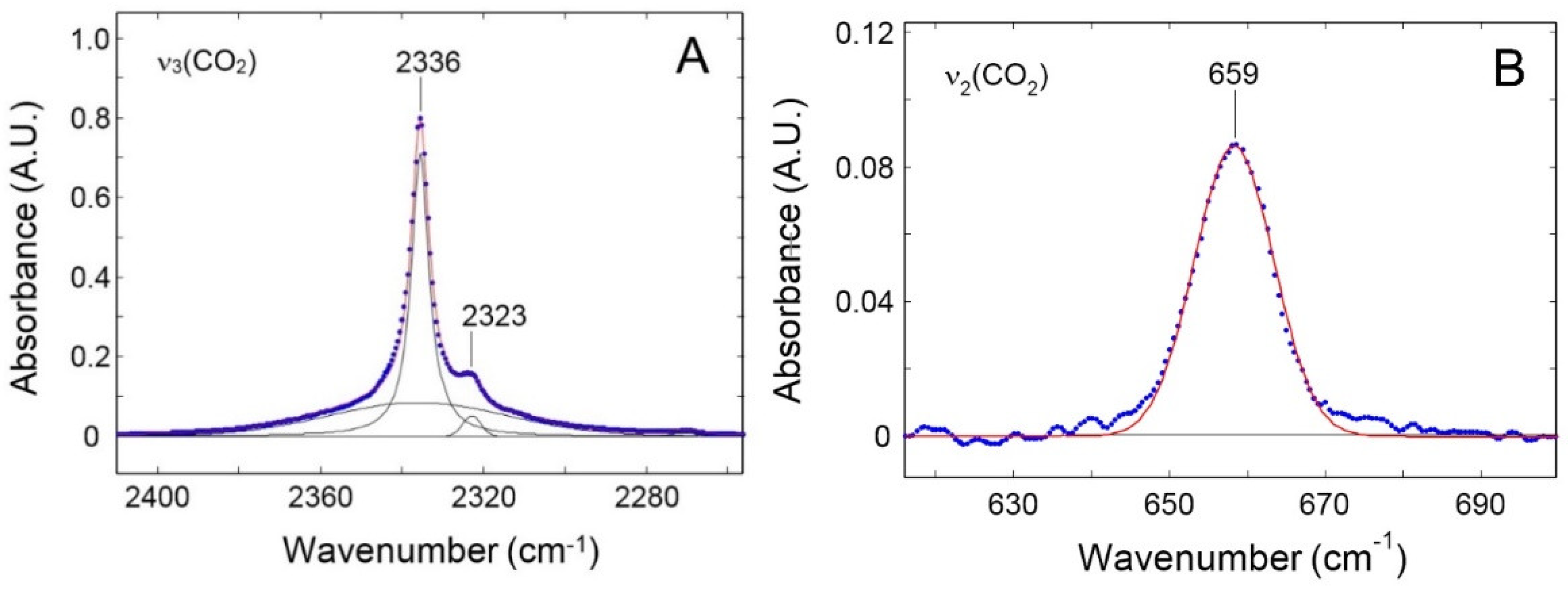
Preprints 67461 g005
Preprints 67461 g006
Figure 6. Correlation between the absorbance measured at 2 cm-1 frequency resolution and the concentration of carbon dioxide in PPO. A: IR peak centered at 2336 cm-1; B: IR peak centered at 3692 cm-1.
Figure 6. Correlation between the absorbance measured at 2 cm-1 frequency resolution and the concentration of carbon dioxide in PPO. A: IR peak centered at 2336 cm-1; B: IR peak centered at 3692 cm-1.
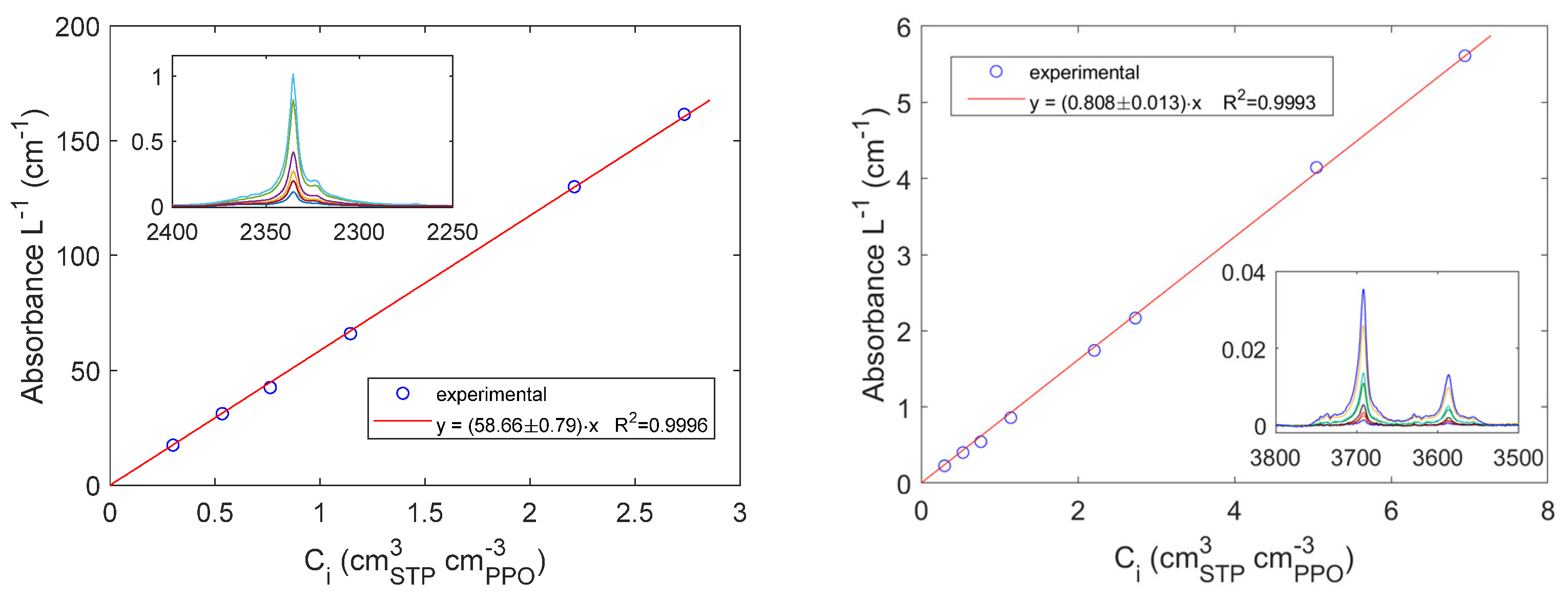
Preprints 67461 g006
Preprints 67461 g007
Figure 7. Integral desorption kinetics of CH4 from PPO. The initial pressure is equal to 753.5 Torr. A: Absorbance at 2973 cm-1; B: Absorbance Area in the range [2969, 3005] cm-1.
Figure 7. Integral desorption kinetics of CH4 from PPO. The initial pressure is equal to 753.5 Torr. A: Absorbance at 2973 cm-1; B: Absorbance Area in the range [2969, 3005] cm-1.
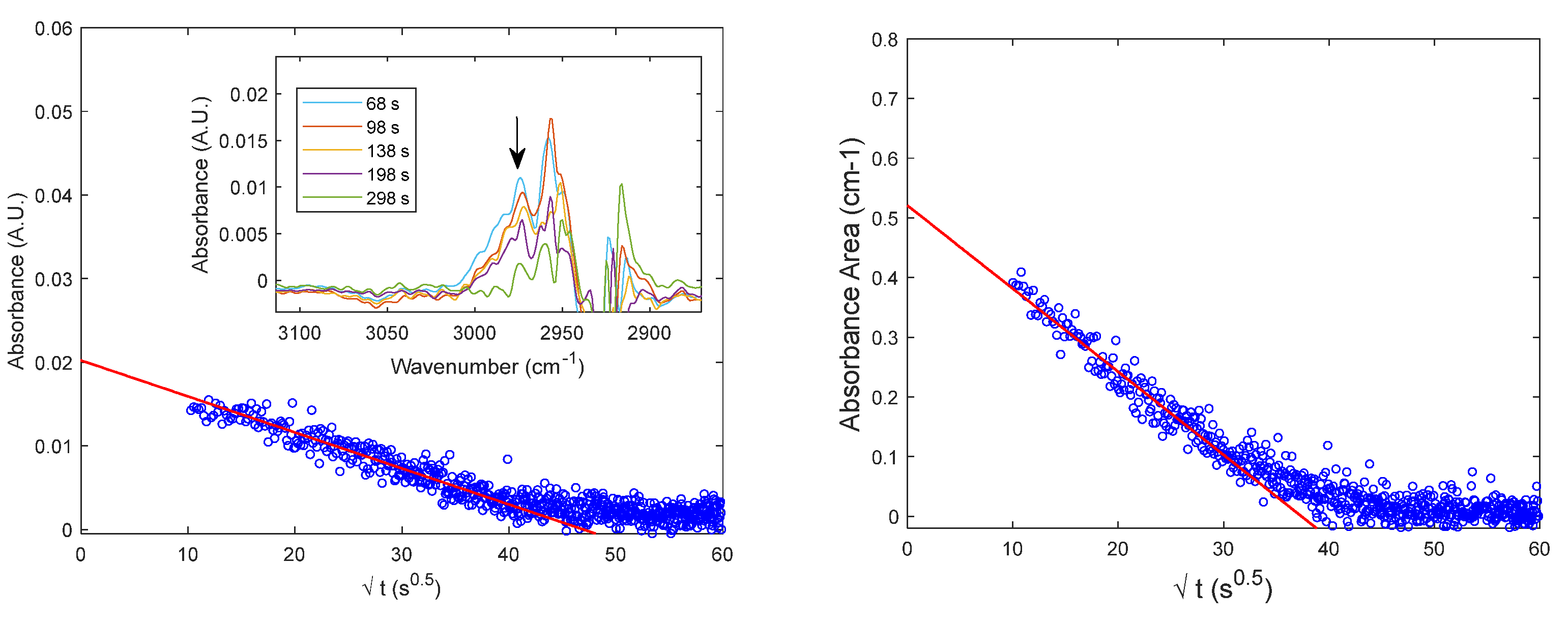
Preprints 67461 g007
Preprints 67461 g008
Figure 8. Sorption kinetics of CO2 in amorphous PPO. A: IR integral sorption kinetics up to 98.56 Torr at 35°C with and without the gas phase correction reported in Eq. 22. The black continuous line is the fitting from Eq. 20; B: Estimated values of effective diffusivity of carbon dioxide in amorphous PPO as a function of average CO2 concentration during each sorption step.
Figure 8. Sorption kinetics of CO2 in amorphous PPO. A: IR integral sorption kinetics up to 98.56 Torr at 35°C with and without the gas phase correction reported in Eq. 22. The black continuous line is the fitting from Eq. 20; B: Estimated values of effective diffusivity of carbon dioxide in amorphous PPO as a function of average CO2 concentration during each sorption step.
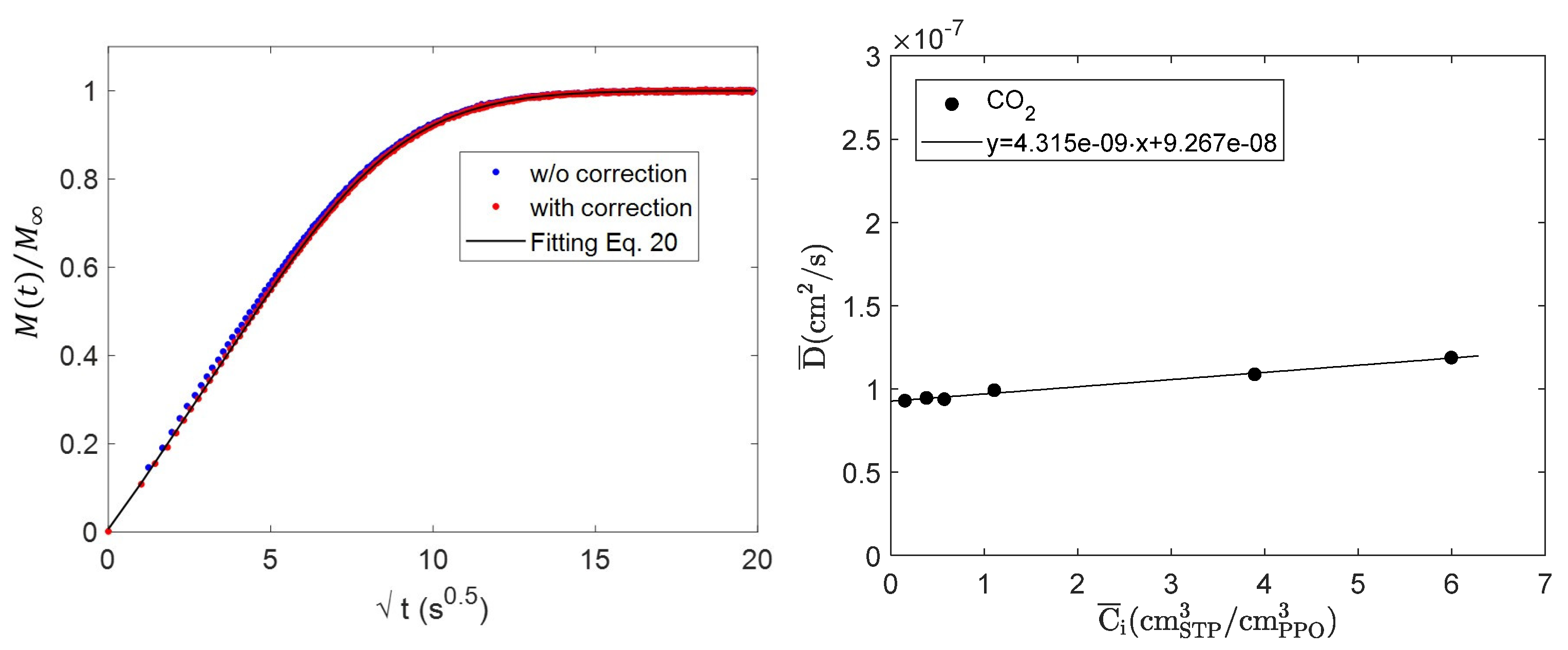
Preprints 67461 g008
Preprints 67461 g009
Figure 9. NETGP-NR model fitting of pure gas sorption in PPO (ksw = 0).
Figure 9. NETGP-NR model fitting of pure gas sorption in PPO (ksw = 0).
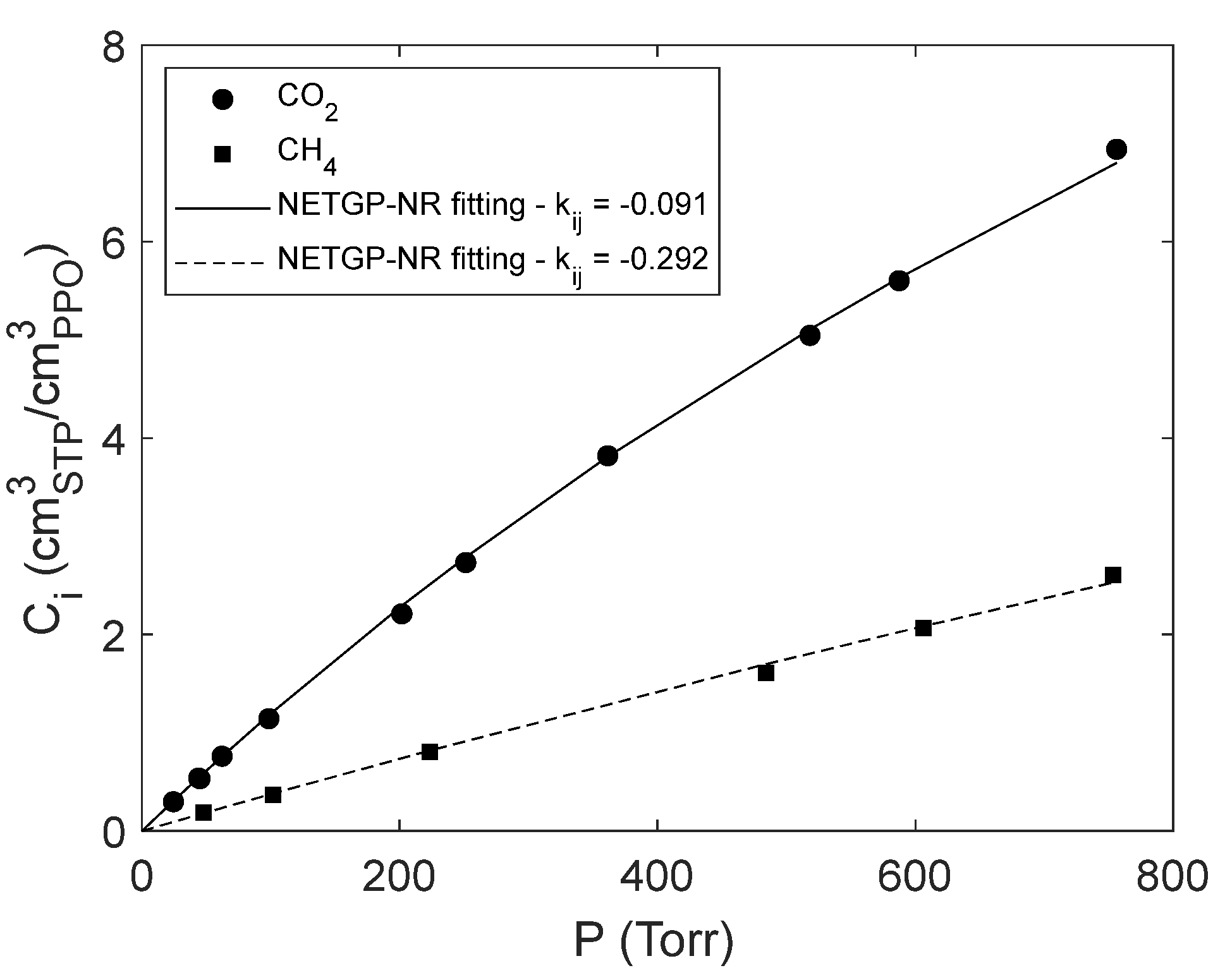
Preprints 67461 g009
Preprints 67461 g010
Figure 10. Pure and mixed gas solubility of CO2 and CH4 in amorphous PPO. Predicted values are obtained with the NETGP-NR model. A: CO2; B: CH4.
Figure 10. Pure and mixed gas solubility of CO2 and CH4 in amorphous PPO. Predicted values are obtained with the NETGP-NR model. A: CO2; B: CH4.
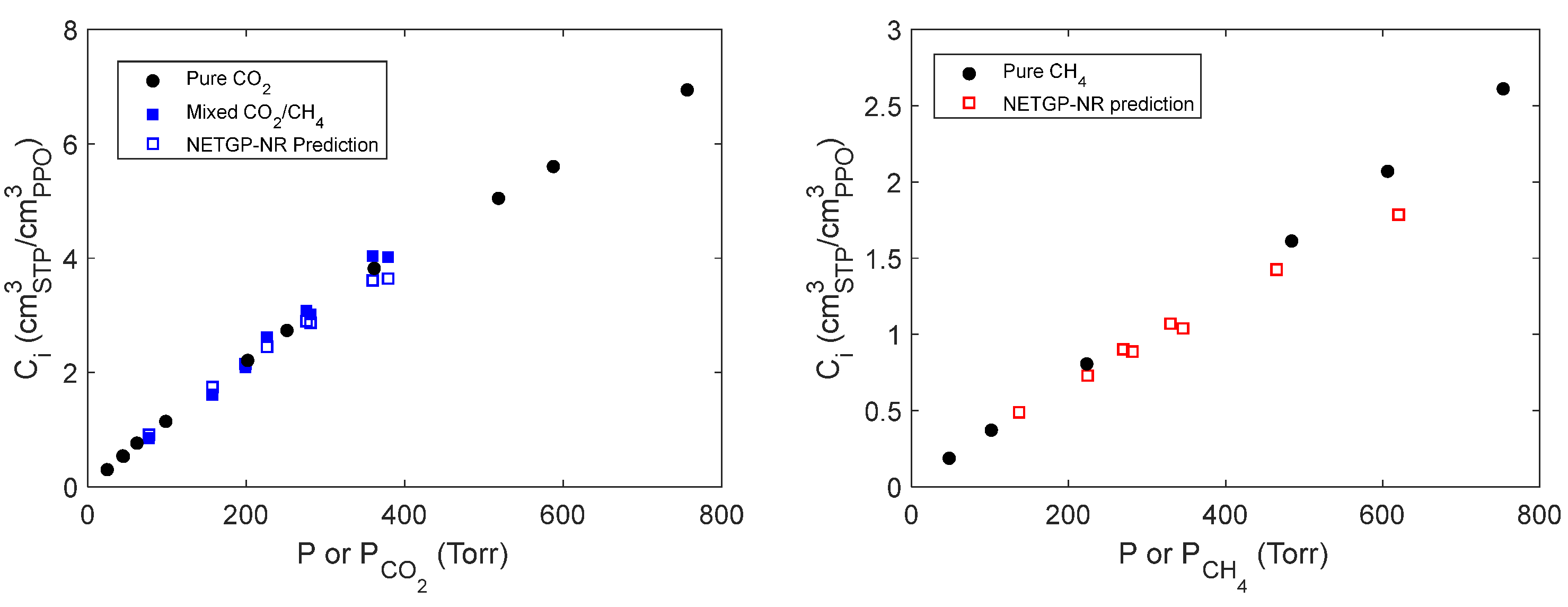
Preprints 67461 g010
Preprints 67461 g011
Figure 11. Comparison between ideal and real solubility selectivity as a function of carbon dioxide partial pressure and mole fraction. The solubility selectivity is calculated with the NETGP-NR model.
Figure 11. Comparison between ideal and real solubility selectivity as a function of carbon dioxide partial pressure and mole fraction. The solubility selectivity is calculated with the NETGP-NR model.
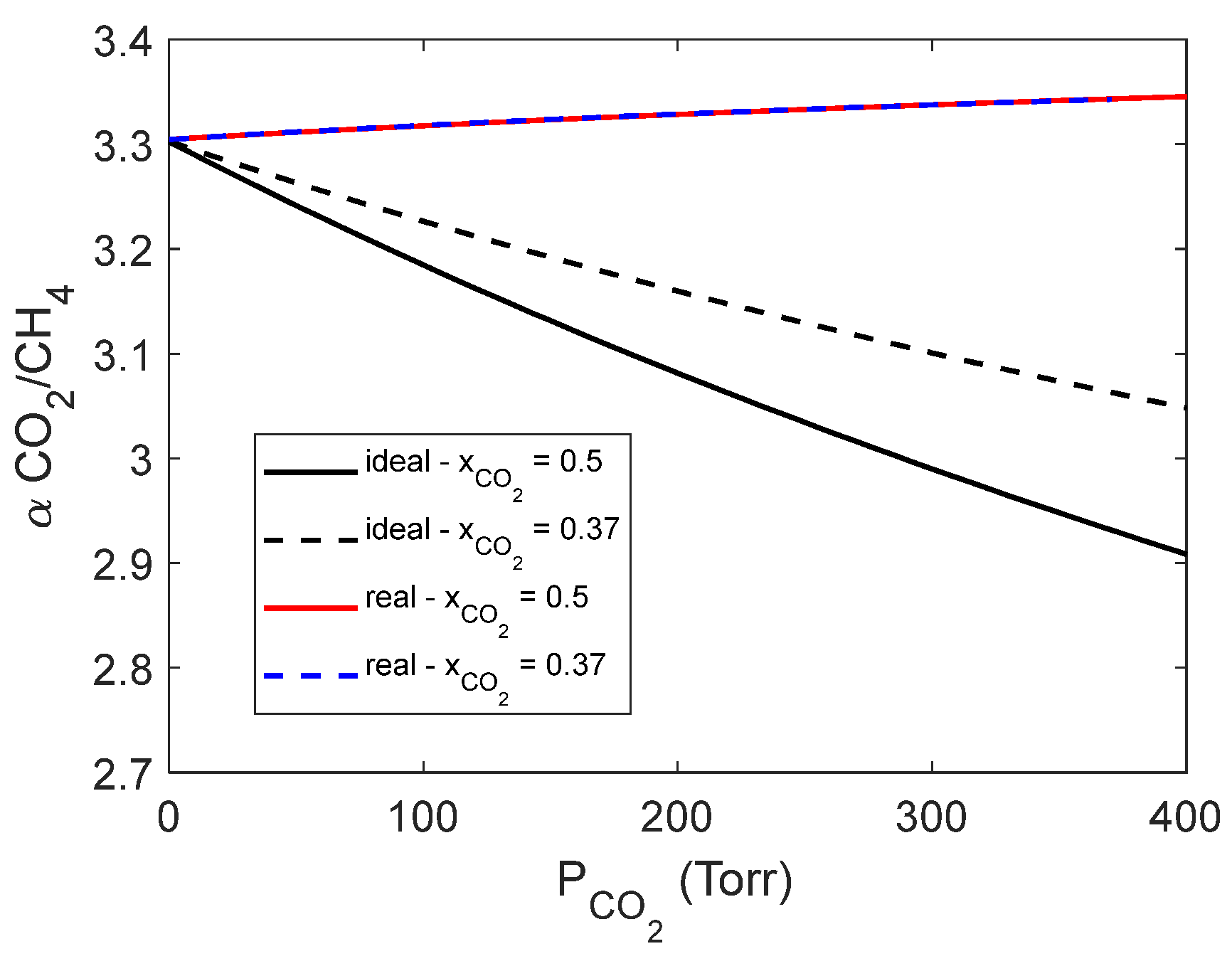
Preprints 67461 g011
Table 1. NR Lattice fluid parameters.
Table 1. NR Lattice fluid parameters.
ε i , h *
(Jmol-1)		 ε i , s *
(Jmol-1K-1)		 v i , s p , 0 *
(cm3g-1)		 s i Ref.
CO2 3468.4 -4.5855 0.79641 0.909 [46]
CH4 1956.2 -0.9181 2.12519 0.961 [46]
PPO 5320 3.440 0.862 0.748 [47]
Table 2. kij mean-field interaction parameter of pure CO2 and CH4 in PPO.
Table 2. kij mean-field interaction parameter of pure CO2 and CH4 in PPO.
CO2 CH4 Ref.
-0.091 -0.292 This Work
−0.087 −0.278 [16]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated