Symbolic Parametric Representation of the Area and the Second Moments of Area of Periodic B-Spline Cross-Sections

Preprint

Article

Symbolic Parametric Representation of the Area and the Second Moments of Area of Periodic B-Spline Cross-Sections

Altmetrics

Downloads

116

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 January 2023

Posted:

17 January 2023

You are already at the latest version

Alerts

Abstract

The calculation of moments of area is one of the most fundamental aspects of engineering mechanics for calculating the properties of beams or for the determination of invariants in different kind of geometries. While a variety of shapes such as circles, rectangles, ellipses or their combinations can be described symbolically, such symbolic expressions are missing for freeform cross-sections. In particular, periodic B-spline cross-sections are suitable for an alternative beam cross-section, e.g. for the representation of topology optimization results. In this work, therefore, a symbolic description of the moments of area of various parametric representations of such B-splines is computed. The expressions found are then compared with alternative computational methods and checked for validity. The resulting equations show a simple way for fast conceptual computation of such moments of area of periodic B-splines.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

In engineering mechanics, there are idealized 1D models such as rods or beams as well as 2D models such as shells and plates. In particular, the beam represents a high abstraction of a 3D body consisting of a curve and a cross-section. These cross-sections usually consist of the composition of different 2D geometric objects such as circles, ellipses, rectangles or triangles [1], leading for example to cross-sections such as for example, U, T, H, I, or tube sections. Structural optimization for such wireframe structures can be applied to the element stiffness matrix of a beam by changing the moments of area [2,3], or accounting parameters for specific types of cross-sections [4,5]. While such cross-sections are typically found in frame structures such as cars, buses, or bridges, the results of a topology optimization tend to result in root-shaped geometric freeform bodies [2]. Visually, the results provided by topology optimization considering plate or volumetric elements lead often to organic shapes [6], which can be interpreted as beams with circular or elliptical cross-sections [7,8]. Alternatively, freeform surfaces can be selected manually [9,10] or estimated automatically [11,12] for such optimization results.

Freeform curves in particular offer the advantage of high shape variation and are especially well suited for the reconstruction of organic models. Such a free-form cross-section consists of a so-called control polygon [13], with which the spline can be adjusted and controlled. A significant advantage is that such cross-sections can be used to derive a frame structure consisting of several beams to a closed freeform surface model. These control polygons of the individual beams can be linked to form a comprehensive control mesh [14]. In contrast to the unification of cylinders or spheres by means of constructive solid geometry, this results in a continuous surface. Furthermore such control polygon can be parametrized and further applied for shape reconstruction and wireframe optimization [14]. So, it is highly desirable to investigate the geometric properties of such B-splines defined by a parametric representation.

1.1. Motivation

The advantage of CSG derived from circular and elliptical cross-sections is the parametric representation of the curve as well as the moments of area, which are necessary for the evaluation of the bending stiffness as well as for FE simulations. For free-form cross-sections, the calculation of the moments is usually done in a large number of numerically treated point coordinates, where they are determined via a boundary integral. In a recent publication [14], instead of a numerical calculation approach, a parametric formula was derived analytically, e.g. for the area of a triangle and rectangle control polygon. 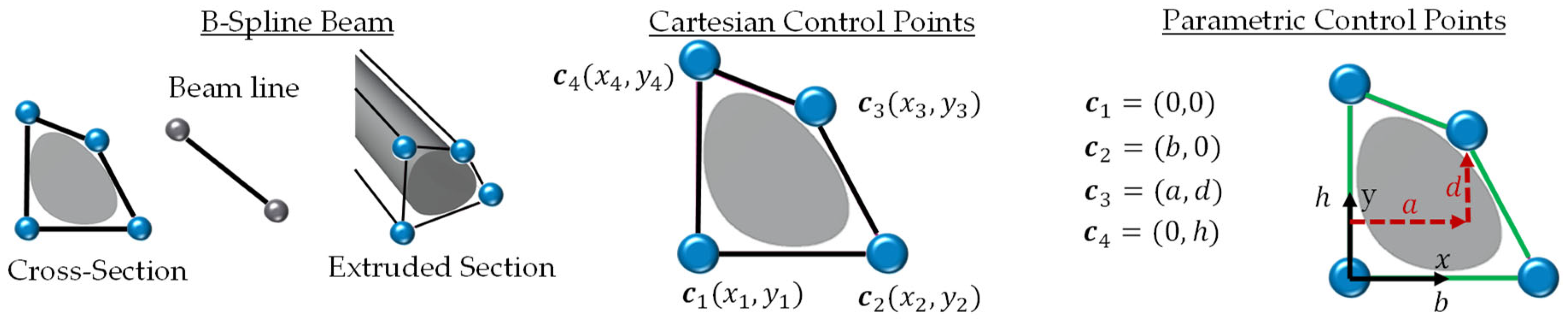Figure 1 shows the example of a bar with Cartesian coordinates and with a parametric of the control polygon of a B-spline.

However, since in [14] only a triangle and a rectangle and a numerical estimation of the coefficients of the second moments of area is carried out, a parametric description of the moments of area is analyzed in the context of this work. On the one hand, the zero- and second-order moments of area are determined analytically, and on the other hand, in addition to the triangle and rectangle, various control polygons such as the moments of area of a parallelogram, a trapeze, a symmetric pentagon and a symmetric hexagon control polygon are derived.

In addition to the determination of the equations for the moments, an extensive validation strategy is presented. First, the formulas are checked against correlations of valid cross-sections, so that, for example, the cross-sectional area must always be greater than 0. Then, the free-form curves are converted into polygons by an appropriate choice of control points and compared with results from the literature using a triangle and a rectangle as examples. Finally, a numerical comparison of the moments of area is performed with alternative calculation methods of moments of polygons as well as 2D binary images. This validation can be used to ensure the validity of the automatically calculated formulas.

In the following, properties and the methods for the determination of the moments of area of periodic splines are described. Then, alternative methods for calculating moments of polygons and images are explained. Finally, essential parameters of moments are described.

1.2. State of the Art

There are several different kinds of splines such as Overhauser spline [15,16] or alternatively called Catmull-Rom-spline [17], B-splines [18] or Bezier-splines [19]. These different spline types may differ in properties such as the convex hull criterion or the type of continuity [20]. The convex hull criterion describes the property that, given a convex control polygon, the resulting spline lies within that control polygon. While B-splines provide

C^{2}

continuity and the convex hull criterion, Bezier curves only guarantee

C^{1}

continuity and the convex hull criterion [20]. Catmull-Rom-splines are only

C^{1}

continuous and violate the convex hull criterion [20]. The Catmull-Rom-spline and Bezier-spline offer in contrast to B-splines the advantage that the control points are located on the curve. Due to the convex criterion and the

C^{2}

continiuty this article focuses on B-splines.

The calculation of moments of freeform curves has been treated in several of publications [21,22,23]. The calculation is carried out via the boundary integral along the spline using Greens Theorem in order to be able to calculate the moments of area directly [21,22]. This boundary integral can be traced back to a summation of the individual points including weighting factors. The authors of [21] compared their equations using the several B-splines to approximate to the ellipse against the exact moments of area. While the authors of [21,22] considered the calculation on 2D shapes, the authors of [24] calculated the moment of inertia for 3D shapes of freeform surfaces instead. Such moments of area particular for splines are often used for shape matching [25,26] due to the invariant properties.

However, since this summation has a large number of coefficients, a more compact parametric description is often desirable. The authors of [14] were able to find an exact parametric description of triangles and rectangles for the value of the cross-sectional area in whose formula was subsequently used for the truss optimization as well as the 3D reconstruction. In this work, analogous to [14], such a compact description shall be found for different control polygons, but also for different types of splines. In contrast to [14], a complete analytical description of the second order of moments area as well as the transfer to control polygons consisting of a parallelogram, a trapeze, a symmetric pentagon and a symmetric hexagon is guaranteed.

In addition to the numerical calculation of spline cross-sections, alternative geometric representations such as a polygon or an image can also be used. The moments of binary images were investigated several article such as [27,28]. By summing up the single pixels to a rectangle, the area can be calculated and considering Steiner's theorem and the center of area, the second moments of area can be calculated with

A_{I m g} = \sum_{i \in B} 1; S_{x_{I m g}} = \sum_{i \in B} y_{i} 1 ²; S_{y_{I m g}} = \sum_{i \in B} x_{i} 1 ² I_{x_{I m g}} = \sum_{i \in B} (\frac{1}{12} + {(y_{s} - y_{i})}^{2}); I_{y_{I m g}} = \sum_{i \in B} \frac{1}{12} + {(x_{s} - x_{i})}^{2}; I_{{x y}_{I m g}} = - \sum_{i \in B} (y_{s} - y_{i}) (x_{s} - x_{i}) .

(1)

[27]. For polygonal cross-sections, the moments of area with respect to the center of area can be determined with

I_{x_{P o l y}} = \frac{1}{12} \sum_{i}^{n} (y_{i}^{2} + y_{i} y_{i + 1} + y_{i + 1}^{2}) a_{i} I_{y_{P o l y}} = \frac{1}{12} \sum_{i}^{n} (x_{i}^{2} + x_{i} x_{i + 1} + x_{i + 1}^{2}) a_{i} I_{{x y}_{P o l y}} = - \frac{1}{24} \sum_{i}^{n} (x_{i} y_{i + 1} + 2 x_{i} y_{i} + 2 x_{i + 1} y_{i + 1} + x_{i + 1} y_{i}) a_{i} a_{i} = x_{i} y_{i + 1} - x_{i + 1} y_{i}

(2)

[29,30]. Typically, cross-sections can be converted from algebraic curves to images or polygons directly. Therefore, it is reasonable to cross-validate the new equations to the alternative representations using equation (1) and equation (2). While the equations of the polygon cross-section are determined by a boundary integration, the equations for the binary image were determined by an area integration. While these numerical approximation of the moments of area can be computed quite fast, the main advantage of parametric cross-sections is their interpretability and direct use in algebraic equations. For example, the beam stiffness matrix can be constructed directly using the parametric spline description, which can be further optimized [14].

2. Materials and Methods

In order to determine the formulas for the moments, the description of a periodic B-spline is first explained in more detail. Then, based on the publication [21], the approach to derive the formulas for the analytical moments is presented. Finally, a suitable experimental setup is presented to automatically test the formulas numerically against alternative calculation methods as well as against general correlations of valid cross-sections. A tensor product spline describes a family of curves that can be represented with

P (t) = T M C,

(3)

[20,31], where

P (t)

describes the curve,

T

the monomial basis,

C

the control points of the spline, and

M

the geometry matrix [20]. In the case of a cubic B-spline, the relationship for a segment can be described as follows

P_{i} (t) = (\begin{matrix} x (t) \\ y (t) \end{matrix}) = [t^{3} t^{2} t 1] \frac{1}{6} [\begin{matrix} - 1 & 3 & - 3 & 1 \\ 3 & - 6 & 3 & 0 \\ - 3 & 0 & 3 & 0 \\ 1 & 4 & 1 & 0 \end{matrix}] {[c_{i - 1} c_{i} c_{i + 1} c_{i + 2}]}^{T}

(4)

where

c_{i}

is the individual control points and

t

is the parameterization along the spline of the monomial basis. Figure 2 shows for a triangular control polygon the computation of the B-spline using different sequences of control points. A periodic B-spline can be obtained by repeating the first two control points. If the individual control points are repeated in the sequence itself, a sharper spline is obtained. Repeating twice gives the control polygon as a contour

In this work, we restrict ourselves to periodic splines since they only lead to a closed cross-section. For the first validation, the moments of area of the control polygon by repeating the control points must match with the moments of area of a directly computed polygon in equation (2). Therefore, the moment formulas of a rectangle or triangle must match those from the approach with the B-spline.

2.1. Moments of Area of a Periodic B-Spline

Different control polygons can be parameterized for the calculation of the moments of area. Figure 3 shows a variation of different control polygons with the parameters used in each case.

For the moments of splines, the authors [21,22] used a boundary integral along the tensor product spline with

N

control points and the respective coordinates

X_{n}, Y_{n}

to calculate the area of such a spline with

A = \sum_{i = 0}^{N} \sum_{l}^{4} \sum_{m}^{4} C_{l m} X_{i + l - 2} Y_{i + m - 2}

(5)

where the coefficients

C_{l m}

can be calculated by summing the geometry matrix with

C_{l m} = \sum_{j = 1}^{4} \sum_{k = 1}^{3} \frac{M_{j l} M_{k m} (4 - k)}{8 - j - k} .

(6)

[21]. Analogously, the first and second order moments were determined in [21] with

S_{x} = \frac{- 1}{2} \sum_{i = 0}^{N} \sum_{l = 1}^{4} \sum_{m = 1}^{4} \sum_{n = 1}^{4} C_{l m n} Y_{i + l - 2} Y_{i + m - 2} X_{i + o - 2}

(7)

S_{y} = \frac{1}{2} \sum_{i = 0}^{N} \sum_{l = 1}^{4} \sum_{m = 1}^{4} \sum_{n = 1}^{4} C_{l m n} X_{i + l - 2} X_{i + m - 2} X_{i + n - 2} Y_{i + o - 2}

(8)

I_{x} = \frac{- 1}{3} \sum_{i = 0}^{N} \sum_{l = 1}^{4} \sum_{m = 1}^{4} \sum_{n = 1}^{4} \sum_{o = 1}^{4} C_{l m n o} Y_{i + l - 2} Y_{i + m - 2} Y_{i + n - 2} X_{i + o - 2}

(9)

I_{y} = \frac{1}{3} \sum_{i = 0}^{N} \sum_{l = 1}^{4} \sum_{m = 1}^{4} \sum_{n = 1}^{4} \sum_{o = 1}^{4} C_{l m n o} X_{i + l - 2} X_{i + m - 2} X_{i + n - 2} Y_{i + o - 2}

(10)

I_{y z} = - \frac{1}{2} \sum_{i = 0}^{N} \sum_{l = 1}^{4} \sum_{m = 1}^{4} \sum_{n = 1}^{4} \sum_{o = 1}^{4} C_{l m n o} X_{i + l - 2} X_{i + m - 2} Y_{i + n - 2} Y_{i + o - 2}

(11)

with the coefficients

C_{l m n}

and

C_{l m n o}

C_{l m n} = \sum_{j = 1}^{4} \sum_{k = 1}^{4} \sum_{r = 1}^{3} \frac{M_{j l} M_{k m} M_{r n} (4 - r)}{12 - j - k - r}

(12)

C_{l m n o} = \sum_{j = 1}^{4} \sum_{k = 1}^{4} \sum_{r = 1}^{4} \sum_{s = 1}^{3} \frac{M_{j l} M_{k m} M_{r n} M_{s o} (4 - s)}{16 - j - k - r - s}

(13)

[21]. With the help of these equations’ parametric descriptions of the control polygons can be generated. In the following, the parametrization is determined schematically for a triangular control polygon.

2.2. Parametric Representation of the B-Spline of a Triangle

Based on the parametric in Figure 3, the area can now be determined. For a B-spline the area can be calculated as follows

A = \frac{1}{36} [- \frac{9}{20} c h - \frac{15}{2} h p - \frac{9}{10} c h - \frac{1}{2} h p + \frac{1}{20} h p - \frac{19}{10} c h + \frac{71}{20} c h - \frac{1}{20} h p + \frac{1}{2} h p + \frac{183}{20} c h + \frac{15}{2} h p]

resulting in the expression similar to [14] to

A = 21 c \frac{h}{80} .

(14)

Analogously, the first and second order moments of area with respect to the coordinate origin can be calculated with

S_{x}^{(0,0)} = 7 c \frac{h^{2}}{80}

S_{y}^{(0,0)} = 7 \frac{c^{2} h}{80} + 7 c h \frac{p}{80}

I_{x x}^{(0,0)} = 15769 c \frac{h^{3}}{443520}

I_{y y}^{(0,0)} = 15769 \frac{c^{3} h}{443520} + 23039 c^{2} h \frac{p}{443520} + 15769 c h \frac{p^{2}}{443520}

I_{x y}^{(0,0)} = - 23039 \frac{c^{2} h^{2}}{887040} - 15769 c \frac{h^{2} p}{443520} .

From the first moments of area, the center of area of the spline cross-section can now be calculated with

x_{s} = \frac{S_{y}}{A} = \frac{c}{3} + \frac{p}{3}

y_{s} = \frac{S_{x}}{A} = h / 3 .

Using the center of area, the second order moments can now be referenced to the center of area with

I_{B, x x} = I_{B, x x}^{(0,0)} - y_{s}^{2} A = \frac{2833}{443520} c h^{3}

(15)

I_{B} = I_{B, y y}^{(0,0)} - x_{s}^{2} A = \frac{2833}{443520} c h (c^{2} - c p + p^{2})

(16)

I_{B, x y} = I_{B, x y}^{(0,0)} + x_{s} y_{s} A = 2833 c \frac{h^{2} (c - 2 p)}{887040} .

(17)

It is noticeable that the structure of the moments of the B-spline differs from that of a triangle only in the coefficients (see also Table 1). To check the validity of the formulas found for the moments, it is necessary to compare them with alternative calculation methods and to check valid cross-section properties.

2.3. Comparision of with Polygon Cross-Sections

By repeating the control points, the B-spline formula can be used to accurately reproduce the shape of a polygon. If the parametric formula is derived from this, the moment of area formula of for example a rectangle or a triangle is obtained in Table 1. The following Table shows the determination of the moments via the B-spline formula, the use of the polygon directly via equation (2) and the formula from [1].

The comparison with the Table shows an agreement of the calculation methods with the literature. Thus, it can be seen that at least if the control points (polygon) are repeated twice, the results from the literature can be determined directly.

2.4. Numerical Comparision Framework

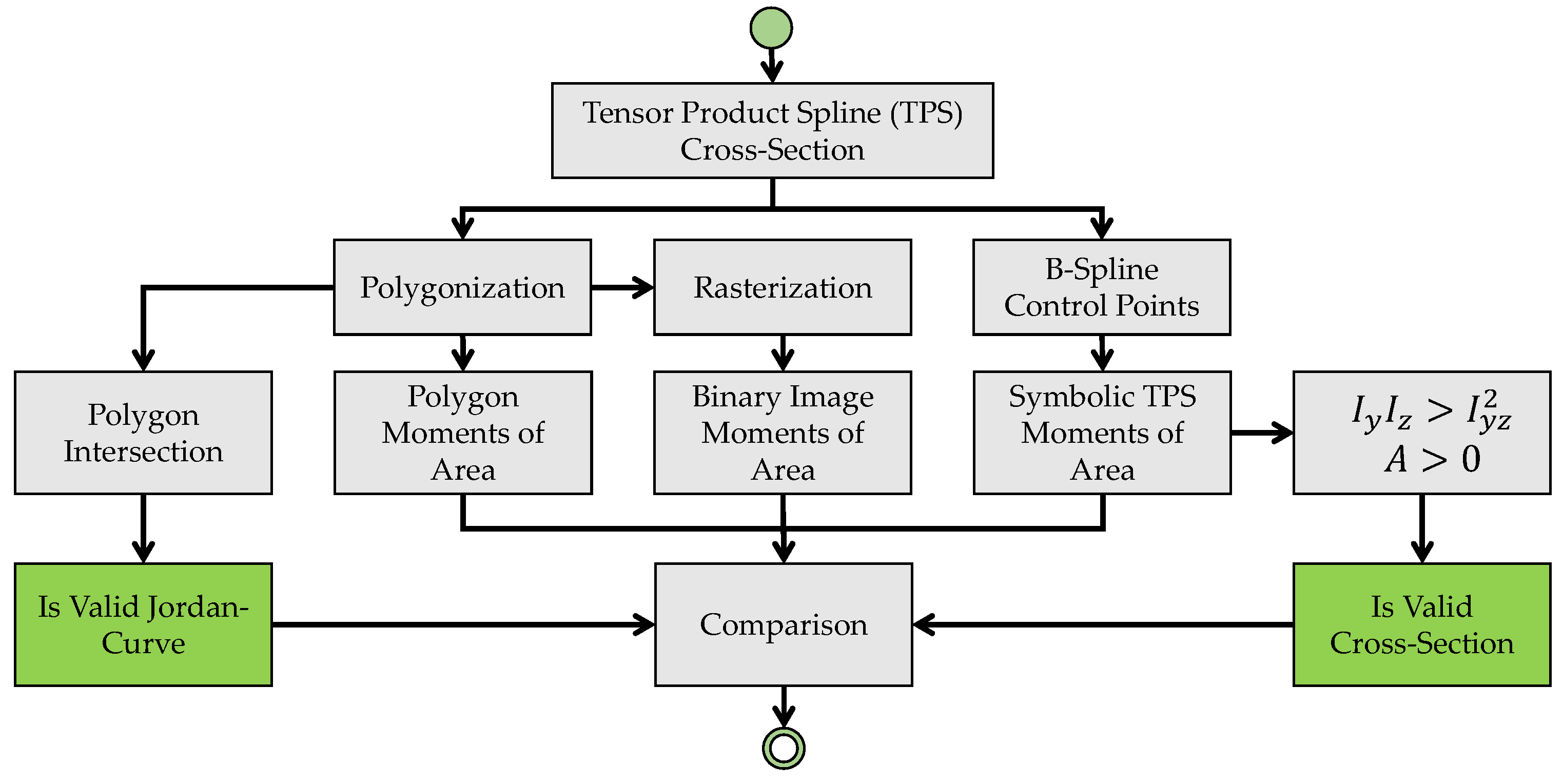
To ensure the validity of the formulas with a high degree of accuracy, they must be validated with alternative calculation methods and by checking the Jordan curve theorem and valid cross-section properties. Figure 4 now shows the steps involved in the automatic validation of the equations for the cross-sections. First, a tensor product spline is defined. This curve is then converted into a discrete polygon and the control polygon points. From the control polygon points, the parametric equation is derived and the numerical results of the moments are then compared to the moments of the polygon as well as the moments from a binary image.

In addition, for each formula it is checked whether it is a valid cross-section or a curve in terms of a Jordan curve.

2.4.1. Spline Cross-Section with Valid Cross-Section Property

A valid cross-section has a positive cross-sectional area and positive principal axis moments (eigenvalues), so that all combinations of parameters must fulfill

A > 0 \land I_{1} > 0 \land I_{2} > 0 .

(18)

Principal moments can be computed with

I_{1,2} = \frac{I_{y} + I_{z}}{2} \pm \sqrt{{(\frac{I_{y} - I_{z}}{2})}^{2} + I_{y z}^{2}} > 0 .

However, since this expression can be very complex, it is first necessary to find a simplified criterion for valid cross-sections. It is sufficient to state that the smaller principal moment of area given by

I_{2} = \frac{I_{y} + I_{z}}{2} - \sqrt{{(\frac{I_{y} - I_{z}}{2})}^{2} + I_{y z}^{2}} > 0

has to be greater than zero. This leads to

\frac{I_{y} + I_{z}}{2} > \sqrt{{(\frac{I_{y} - I_{z}}{2})}^{2} + I_{y z}^{2}}

I_{y}^{2} + 2 I_{y} I_{z} + I_{z}^{2} > I_{y}^{2} - 2 I_{y} I_{z} + I_{z} ² + 4 I_{y z}^{2}

I_{y} I_{z} > I_{y z}^{2} .

Therefore, for all parameter combinations a valid cross-section has to fulfill

A > 0 \land I_{y} I_{z} - I_{y z}^{2} > 0 .

(19)

In addition to the relationship between the moments of area for valid cross-sections, it is also necessary to compare the formula found with various alternative calculation methods.

2.4.2. Spline Cross-Section as Valid Jordan-Curve

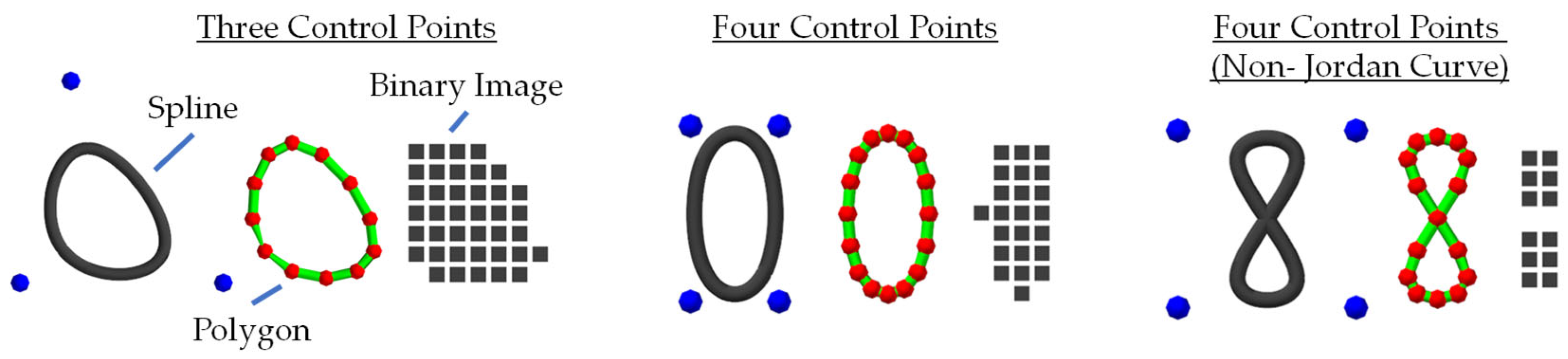
For validation, the spline is converted into a polygon and into a 2D binary image. Then the moments can be calculated in different ways for the particular spline. Figure 4 shows three different B-splines, their polygon (red-green) and a binary image of the cross-section.

The Comparison of the equation (1) and equation (2) is used to check the accuracy and validity. As the number of segments along the polygon line is increased, the accuracy of the moments of area estimate also increases. The comparison with the formula of the binary image serves to ensure the validity of the curve found, so that no Jordan curves are detected. Figure 5 shows a non-Jordan curve by swapping the order of the nodes. While such a cross-section can be estimated with some accuracy using the binary image, the boundary integration approach using the polygon approach as well as the chosen formula derived for the B-spline leads to incorrect results (e.g. area=0 here).

To achieve a high degree of coverage, it is necessary to compare the approach with a large number of possible polygon and binary image cross-sections. For each parameterization, a Latin hypercube sampling is chosen by generating a large number of cross-sections. Then, the mean error and the variance of the error are chosen as evaluation criteria in comparison to the alternative computational methods. For this purpose, the respective relative errors are determined as follows.

2.4.3. Spline Cross-Section Numerically Compared to Polygon and Image Cross-Section

To validate each formula, the moments from the derived polygon cross-section and the image

A_{I m g, P o l y}

{I_{x}}_{I m g, P o l y}

{I_{y}}_{I m g, P o l y}

{I_{x y}}_{I m g, P o l y}

are compared with the moments of the B-spline formula

A_{T P S},

{I_{x}}_{T P S},

{I_{y}}_{T P S}

{I_{x y}}_{T P S}

. Thereby the relative errors

ϵ_{A} = |\frac{A_{I m g, P o l y} - A_{T P S}}{A_{T P S}}|

(20)

ϵ_{I_{x}} = |\frac{{I_{x}}_{I m g, P o l y} - {I_{x}}_{T P S}}{A_{T P S}}|

(21)

ϵ_{I_{y}} = |\frac{{I_{y}}_{I m g, P o l y} - {I_{y}}_{T P S}}{{I_{y}}_{T P S}}|

(22)

ϵ_{I_{x y}} = |\frac{{I_{x y}}_{I m g, P o l y} - {I_{x y}}_{T P S}}{{I_{x y}}_{T P S}}|

(23)

of a large number of combinations of the control polygons can be compared. Possible geometric values can be selected in the range of the geometric space, for example for a triangle between

c \in [0, \infty [, h \in [0, \infty [, p \in [0, \infty [.

Thus, each individual geometric variable and its influence can be checked directly. However, since an evaluation up to ∞ is not possible, a limiting parameter of the respective geometric variable of 100.0 is chosen. For each case, 100 samples are generated using Latin Hypercube Sampling.

3. Results

Based on the described strategy for the parameterization as well as for the evaluation of the found formulas, it is necessary in the following to design different parametric control points for the tensor product splines. From these parametric control point coordinates the respective moments are then calculated automatically and analytically. In this work, the moments of a general triangle, a rectangle, a trapeze, a parallelogram, an isosceles pentagon and an isosceles hexagonal honeycomb are considered, since for these parametric quantities a suitable simple expression, which can still be presented on a few lines.

For the evaluation of these moments of area, the approach from 2.4 is chosen. To ensure Jordan curve theorem, the parametric is restricted so that only valid Jordan curves as cross-section results.

3.1. Moments of Area Parametrization of a Triangle Control Polygon

Figure 6 shows three examples of different B-spline curves based on the variation of control points over a triangle. For the polygon

P_{3}

, three points are evaluated for each curve segment via equation (4). For the gridded cross-section

I_{8}

, the underlying polygon was rasterized with 8x8 pixels. Since the triangle itself is always a convex polygon, the curve also lies within the selected polygon. The value of the area must therefore be smaller than that of the triangle itself.

Table 2 shows the formulas for calculating the moments of area and relative errors compared to a polygon with 100 segments, a polygon with 10 segments per spline segment, an image

I_{128}

with a grid size of 128x128 pixels, and an image

I_{16}

with a grid size of 16x16 pixels.

Equation (19) shows always values greater than zero for the geometric parameters of

c, h

. Thus, the essential properties for a valid cross-section are guaranteed for positive geometric parameters. The relative error from the calculation shows an average relative error of 0.015% for

P_{100}

. This error increases when fewer segments per spline

P_{10}

are used. The errors for binary images are significantly higher compared to the polygon approach. Furthermore, if a 16x16 pixel grid is chosen, an error of 25.7% can occur for the second order moment of area.

The relative errors show good agreement between the different calculation methods, so that the formulas from Table 1 can be assumed to be correct. In particular, the small error for a high resolution of the spline as polygon

P_{100}

shows good agreement.

3.2. Moments of Area Parametrization of a Quadrilateral Control Polygon Area

For a quadrangular control polygon, the cross-sectional area of the B-spline can be generally expressed as follows

A = - 61 a \frac{h}{180} + 61 b \frac{h}{180} + 61 c \frac{d}{180}

(24)

according to the parametrization covered in Figure 3. However, the parameterization of the general quadrilateral can lead to the violation of the Jordan curve theorem, so that the curve can intersects itself. This can lead to a negative cross-sectional area, so that more appropriate boundary conditions for the dependencies of the parameters of the control polygon has to be considered for a robust application. In the following, the quadrilateral is constructed as a rectangle, trapeze and parallelogram.

3.2.1. Moments of Area Parametrization of a Rectangle Control Polygon

Figure 7 shows the variation of a rectangular control polygon, a derived polygonal cross-section and a binary image. Due to the chosen parameterization, only positive and valid cross-sections can be realized compared to the general quadrilateral.

Table 3 shows the equations for the moments of area of the rectangular control polygon as well as the numerical errors. Analogous to the triangle, a high accuracy of the relative errors is again shown in comparison to the polygonal approach. Likewise, it can be seen that equation (19) leads exclusively to positive values. The moment of area of

I_{x y}

leads to a value of 0, due to the symmetric shape of the control polygon.

3.2.2. Moments of Area Parametrization of a Parallelogram Control Polygon

Figure 8 shows the variation of a B-spline using a parallelogram control polygon, its derived polygon cross-section and a rasterized image cross-section. Due to the chosen parameterization, only positive and valid cross-sections can be realized compared to the general quadrilateral.

Table 4 shows the results for the moments of area of the control polygon as a parallelogram as well as the numerical errors. Analogous to the triangle, a high accuracy of the relative errors is also shown here in comparison to the polygonal approach. Likewise, it can be seen that equation (19) leads exclusively to positive values. The moment of area

I_{x y}

is 0 for the parallelogram with

p = 0,

which represents a rectangle. Otherwise, this leads to values unequal to 0 due to the asymmetry of the cross-section.

3.2.3. Moments of Area Parametrization of a Trapeze Control Polygon

Figure 9 shows the variation of a trapeze control polygon for a B-spline cross-section, a derived polygon cross-section and its binary image cross-section. Due to the chosen parameterization, only positive and valid cross-sections can be realized compared to the general quadrilateral.

For the validity of the trapezoids according to equation (19) the following relation is positive and therefore valid

I_{x} I_{y} - I_{x y}^{2} = \frac{h^{4} (75371706005 b^{4} + 564591208444 b^{3} p)}{820077802790400} + \frac{h^{4} (1525810647880 b^{2} p^{2} + 2258364833776 b p^{3} + 1205947296080 p^{4})}{820077802790400}

(25)

for each possible parameter combination. Table 5 shows the results for the moments of area of the control polygon as a trapeze as well as the numerical errors. Analogous to the triangle, a high accuracy of the relative errors is also shown in comparison to the polygonal approach. The moment

I_{x y}

is consistently zero due to the symmetry. For the parameter

p = \frac{b}{2}

the relation of the rectangle is obtained

In an analogous way, further quadrilaterals can now be parameterized and their formulas for the moments of area can be derived. In the following, the calculation of the moments of area of a parametric pentagon as well as a hexagon is performed.

3.3. Moments of Area Parametrization of a Symmetric Pentagon Control Polygon

Figure 10 shows the variation of a symmetrical, pentagonal control polygon for a B-spline cross-section, its polygonal representation and its rasterized image.

For the validity of the pentagon according to equation (19) the following relation

I_{x} I_{y} - I_{x y}^{2} = \frac{h^{4} (82305438169 b^{2} + 212310520756 b p + 120438027736 p^{2})}{(169 b + 218 p)} \cdot \frac{(1527254 b^{3} + 5667223 b^{2} p + 7684452 b p^{2} + 3712596 p^{3})}{963658637770752000}

(26)

leads to only positive values. Table 6 shows the results for the moments of area of the control polygon as a symmetric pentagon as well as the numerical errors. Analogous to the triangle, the relative errors also show a high accuracy compared to the polygonal approach. The moment

I_{x y}

is consistently zero due to the symmetry.

Finally, the parameterization for a hexagon can now be specified analogously.

3.4. Moments of Area Parametrization of a Symmetric Hexagonal Control Polygon

Figure 11 shows the variation of a symmetrical, pentagonal, control polygon for a B-spline cross-section, its polygon cross-section and its binary image cross-section.

I_{x} I_{y} - I_{x y}^{2} = \frac{h^{4} (1267299 b + 927031 p)}{143401583001600} \cdot (354311 b^{3} + 1131397 b^{2} p + 1267299 b p^{2} + 490213 p^{3})

(27)

4. Discussion

The final formulas show a very good suitability for the design and determination of beams with free-form cross-sections. In particular, the comparison of the formulas with alternative calculation methods suggests a high validity.

One point of criticism could be the chosen parameterization of the control polygons. While the triangle was still covered for arbitrary shapes, there are already restrictions for the moment of area for a quadrilateral due to the complexity of the perpetual expressions. The same is true for pentagons and hexagons. Only a restriction of the parametric allows simpler expressions e.g. for a parallelogram as well as a trapeze. However, this simplification can be improved to achieve high shape coverage with a suitable set of variables. For example, the parametric of the positive lengths of the symmetric hexagon yields exclusively convex polygons, so this unfavorable choice implicitly excludes a large number of alternative symmetric hexagons.

While the numerical formula for determining the moments of area is easy to implement and universally applicable, the symbolic expressions lead to the restriction of the cross-sectional geometry. However, due to the numerical accuracy of such formulas, erroneous moments of area cannot be absolutely guaranteed, unlike the analytical formula. The symbolic expressions can be used completely up to the limit ranges, so that also a consideration of the convergence behavior towards infinity is possible. Especially in the case of optimization, cross-section values close to zero can occur, where a numerical approximation can lead do misleading results.

The validation framework exhibits high robustness and reliability, so that symbolic formulas can be tested directly. However, for future work, estimation over a polygon consisting of many segments is usually sufficient. Unlike the polygon and the B-spline, the binary image and evaluation step is based on an area integral rather than a boundary integral and is therefore not directly comparable.

In summary, however, a large number of expressions are shown which can be used to determine moments of area of such freeform curves in the simplest way. These can now be used for aspects of structural optimization, but also for reconstruction analogous to [14]. In contrast to [14], however, a fully analytical function of the beam stiffness matrix can be realized, so that geometric values close to zero can be accurately captured.

5. Conclusions

This work has dealt with the derivation of analytical formulas for the moments of area of periodic B-splines. The position of the control points was mapped parametrically and then embedded in the boundary integral for the calculation of the moments of area of splines. In contrast to common methods for numerical determination of such moments of area, a symbolic calculation with integer numerator and denominator was considered. This integer calculation leads to an exact determination of the cross-sectional area and the second moments of area of such periodic B-spline cross-sections.

While in [14] only the cross-sectional area was determined analytically, in this work mainly a symbolic description for the second moments of area could be obtained. Especially in structural optimization, cross-section parameters close to zero can be determined, for which an exact calculation of the moments is necessary.

The obtained expressions can now be used for various applications in the field of reconstruction, design as well as verification calculations. Likewise, further control polygons can be parameterized using the approach described above.

Author Contributions

Software, conceptualization, methodology, visualization, validation, investigation, resources, data curation writing–original draft preparation M.D.; investigation, writing—review, resources M.J.; project administration, funding question, supervision S.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

D. Gross, W. Hauger, J. Schröder, and W. A. Wall, ‘Balkenbiegung’, in Technische Mechanik 2: Elastostatik, D. Gross, W. Hauger, J. Schröder, and W. A. Wall, Eds. Berlin, Heidelberg: Springer, 2017, pp. 81–165. [CrossRef]
M. P. Bendsoe and O. Sigmund, Topology Optimization: Theory, Methods, and Applications, 2nd ed. Berlin Heidelberg: Springer-Verlag, 2004. [CrossRef]
N. Changizi and G. P. Warn, ‘Topology optimization of structural systems based on a nonlinear beam finite element model’, Struct Multidisc Optim, Jul. 2020. [CrossRef]
H. Fredricson, T. Johansen, A. Klarbring, and J. Petersson, ‘Topology optimization of frame structures with flexible joints’, Structural and Multidisciplinary Optimization, vol. 25, no. 3, pp. 199–214, Aug. 2003. [CrossRef]
J. Lim, C. You, and I. Dayyani, ‘Multi-objective topology optimization and structural analysis of periodic spaceframe structures’, Materials & Design, vol. 190, p. 108552, May 2020. [CrossRef]
M. Denk, K. Rother, and K. Paetzold, ‘Multi-Objective Topology Optimization of Heat Conduction and Linear Elastostatic using Weighted Global Criteria Method’, in Proceedings of the 31st Symposium Design for X (DFX2020), Bamberg, Sep. 2020, vol. 31, pp. 91–100. [CrossRef]
T. Stangl and S. Wartzack, ‘Feature based interpretation and reconstruction of structural topology optimization results’, in Proceedings of the 20th International Conference on Engineering Design (ICED15), Jul. 2015, p. Vol. 6, 235-245.
A. Nana, J.-C. Cuillière, and V. Francois, ‘Automatic reconstruction of beam structures from 3D topology optimization results’, Computers & Structures, vol. 189, pp. 62–82, Sep. 2017. [CrossRef]
P.-S. Tang and K.-H. Chang, ‘Integration of topology and shape optimization for design of structural components’, Struct Multidisc Optim, vol. 22, no. 1, pp. 65–82, Aug. 2001. [CrossRef]
M. Denk, R. Klemens, and K. Paetzold, ‘Beam-colored Sketch and Image-based 3D Continuous Wireframe Reconstruction with different Materials and Cross-Sections’, in Entwerfen Entwickeln Erleben in Produktentwicklung und Design 2021, Dresden, Jun. 2021, pp. 345–354. [CrossRef]
M. Denk, K. Rother, and K. Paetzold, ‘Fully Automated Subdivision Surface Parametrization for Topology Optimized Structures and Frame Structures Using Euclidean Distance Transformation and Homotopic Thinning’, in Proceedings of the Munich Symposium on Lightweight Design 2020, Berlin, Heidelberg, 2021, pp. 18–27. [CrossRef]
A. Amroune, J.-C. Cuillière, and V. François, ‘Automated Lofting-Based Reconstruction of CAD Models from 3D Topology Optimization Results’, Computer-Aided Design, vol. 145, p. 103183, Apr. 2022. [CrossRef]
L. Piegl and W. Tiller, The NURBS Book. Berlin, Heidelberg: Springer, 1995. [CrossRef]
M. Denk, ‘Curve Skeleton and Moments of Area Supported Beam Parametrization in Multi-Objective Compliance Structural Optimization’, Dissertation, Nov. 2022, [Online]. Available: https://nbn-resolving.org/urn:nbn:de:bsz:14-qucosa2-822020.
A.W. Overhauser, ‘Analytic Definition of Curves and Surfaces by Parabolic Blending’, arXiv:cs/0503054, vol. Technical Report SL 68-40, no. Scientific Laboratory, Ford Motor Company, Dearborn, Michigan, May 1968.
N. El-Abbasi, S. A. Meguid, and A. Czekanski, ‘On the modelling of smooth contact surfaces using cubic splines’, International Journal for Numerical Methods in Engineering, vol. 50, no. 4, pp. 953–967, 2001. [CrossRef]
E. Catmull and R. Rom, ‘A CLASS OF LOCAL INTERPOLATING SPLINES’, in Computer Aided Geometric Design, R. E. Barnhill and R. F. Riesenfeld, Eds. Academic Press, 1974, pp. 317–326. [CrossRef]
H. B. Curry and I. J. Schoenberg, ‘On Pólya frequency functions IV: The fundamental spline functions and their limits’, J. Anal. Math., vol. 17, no. 1, pp. 71–107, Dec. 1966. [CrossRef]
V. V. Borisenko, ‘Construction of Optimal Bézier Splines’, J Math Sci, vol. 237, no. 3, pp. 375–386, Mar. 2019. [CrossRef]
J. H. Clark, ‘Parametric curves, surfaces and volumes in computer graphics and computer-aided geometric design’, Technical Report 221, Nov. 1981.
P. Rozenthal and M. Gattass, ‘Geometrical properties in the B-spline representation of arbitrary domains’, Communications in Applied Numerical Methods, vol. 3, no. 4, pp. 345–349, 1987. [CrossRef]
S. Sheynin and A. Tuzikov, ‘Moment computation for objects with spline curve boundary’, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 10, pp. 1317–1322, Oct. 2003. [CrossRef]
S. Sheynin and A. Tuzikov, ‘Area and Moment Computation for Objects with a Closed Spline Boundary’, in Computer Analysis of Images and Patterns, Berlin, Heidelberg, 2003, pp. 33–40. [CrossRef]
Soldea, G. Elber, and E. Rivlin, ‘Exact and efficient computation of moments of free-form surface and trivariate based geometry’, Computer-Aided Design, vol. 34, no. 7, pp. 529–539, Jun. 2002. [CrossRef]
Z. Huang and F. S. Cohen, ‘Affine-invariant B-spline moments for curve matching’, IEEE Transactions on Image Processing, vol. 5, no. 10, pp. 1473–1480, Oct. 1996. [CrossRef]
M. Jacob, T. Blu, and M. Unser, ‘An exact method for computing the area moments of wavelet and spline curves’, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 23, no. 6, pp. 633–642, Jun. 2001. [CrossRef]
M. Denk, K. Rother, T. Höfer, J. Mehlstäubl, and K. Paetzold, ‘Euclidian Distance Transformation, Main Axis Rotation and Noisy Dilitation Supported Cross-Section Classification with Convolutional Neural Networks’, Proceedings of the Design Society, vol. 1, pp. 1401–1410, Aug. 2021. [CrossRef]
J. Flusser and T. Suk, ‘On the Calculation of Image Moments’. 1999.
R. Soerjadi, On the Computation of the Moments of a Polygon, with some Applications, Heron 15., vol. 5. Stevin Laboratory, 1968.
D. Hally, ‘Calculation of the Moments of Polygons.’, Technical Report ADA183444, Jun. 1987.
M. Botsch, L. Kobbelt, M. Pauly, P. Alliez, and B. Lévy, Polygon Mesh Processing. AK Peters / CRC Press, 2010.

Figure 1. B-spline beam: cross-section and centerline beam, Cartesian coordinates of control points, parametric coordinates of contour points.

Figure 2. Variation of the number of control points: B-spline segment, two segments, periodic B-spline, sharped B-spline, polygon.

Figure 3. Parametrization of the control polygon: triangle, rectangle, parallelogram, quadrilateral, trapeze, symmetric pentagon, symmetric hexagon.

Figure 4. Framework for the validation of the symbolic equations of the moments of area.

Figure 5. Tensor product spline cross-section (B-spline) and its polygon and binary image.

Figure 6. Triangle B-spline cross-section and its polygon and binary image.

Figure 7. Rectangle B-spline cross-section and its polygon and binary image.

Figure 8. B-spline cross-section and its polygon and binary image representation.

Figure 9. Trapeze B-spline cross-section and its polygon and binary image.

Figure 10. Pentagon B-spline cross-section and its polygon and binary image.

Figure 11. Hexagonal B-spline cross-section and its polygon and binary image.

Table 1. Comparison of the moments of area equation of the control polygon using equation the equations for the B-spline, the equations of a polygon (2) and equations from the literature.

	B-Spline Triangle Poly	Polygon Triangle	Literature [1]
$A$	$c \frac{h}{2}$	$c \frac{h}{2}$	$c \frac{h}{2}$
$I_{x}$	$c \frac{h^{3}}{36}$	$c \frac{h^{3}}{36}$	$c \frac{h^{3}}{36}$
$I_{y}$	$c h \frac{c^{2} - c p + p^{2}}{36}$	$c h \frac{c^{2} - c p + p^{2}}{36}$	$c h \frac{c^{2} - c p + p^{2}}{36}$
$I_{x y}$	$c \frac{h^{2} (c - 2 p)}{72}$	$c \frac{h^{2} (c - 2 p)}{72}$	$c \frac{h^{2} (c - 2 p)}{72}$
$x_{s}, y_{s}$	$(\frac{c}{3} + \frac{p}{3}, \frac{h}{3})$	$(\frac{c}{3} + \frac{p}{3}, \frac{h}{3})$	$(\frac{c}{3} + \frac{p}{3}, \frac{h}{3})$
	B-Spline Rectangle Poly	Polygon Rectangle	Literature [1]
$A$	$b h$	$b h$	$b h$
$I_{x}$	$b \frac{h^{3}}{12}$	$b \frac{h^{3}}{12}$	$b \frac{h^{3}}{12}$
$I_{y}$	$\frac{b^{3} h}{12}$	$\frac{b^{3} h}{12}$	$\frac{b^{3} h}{12}$
$I_{x y}$	$0$	$0$	$0$
$x_{s}, y_{s}$	$(\frac{b}{2}, \frac{h}{2})$	$(\frac{b}{2}, \frac{h}{2})$	$(\frac{b}{2}, \frac{h}{2})$

Table 2. Equations for the parametric control polygon for the triangle and its numerical error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$21 c \frac{h}{80}$	$\bar{ϵ_{A}}$	0,007	0,879	1,922	11,951
$I_{x}$	$2833 c \frac{h^{3}}{443520}$	$σ ² (ϵ_{A})$	0,000	0,000	0,168	4,990
$I_{y}$	$2833 c h \frac{c^{2} - c p + p^{2}}{443520}$	$\bar{ϵ_{I_{x}}}$	0,015	1,776	4,299	19,075
$I_{x y}$	$2833 c \frac{h^{2} (c - 2 p)}{887040}$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	0,810	5,377
$x_{s}, y_{s}$	$(\frac{c}{3} + \frac{p}{3}, \frac{h}{3})$	$\bar{ϵ_{I_{y}}}$	0,015	1,776	3,247	18,471
$I_{x} I_{y} - I_{x y}^{2}$	$8025889 \frac{c^{4} h^{4}}{262279987200}$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	0,291	5,914
		$\bar{ϵ_{I_{x y}}}$	0,015	1,776	5,046	25,759
		$σ ² (ϵ_{I_{x y}})$	0,000	0,000	1,575	6,264

Table 3. Equations for the parametric control polygon for the rectangle and its relative error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$61 b \frac{h}{90}$	$\bar{ϵ_{A}}$	0,004	0,505	2,674	13,488
$I_{x}$	$27371 b \frac{h^{3}}{748440}$	$σ ² (ϵ_{A})$	0,000	0,000	1,110	5,877
$I_{y}$	$27371 \frac{b^{3} h}{748440}$	$\bar{ϵ_{I_{x}}}$	0,008	1,009	3,858	16,736
$I_{x y}$	$0$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	1,473	6,440
$x_{s}, y_{s}$	$(\frac{b}{2}, \frac{h}{2})$	$\bar{ϵ_{I_{y}}}$	0,008	1,009	3,687	17,262
$I_{x} I_{y} - I_{x y}^{2}$	$749171641 \frac{b^{4} h^{4}}{560162433600}$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	1,248	5,963

Table 4. Equations for the parametric control polygon for the triangle and its numerical error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$61 a \frac{h}{90}$	$\bar{ϵ_{A}}$	0,004	0,505	2,218	12,118
$I_{x}$	$27371 b \frac{h^{3}}{748440}$	$σ ² (ϵ_{A})$	0,000	0,000	1,075	4,609
$I_{y}$	$27371 b h \frac{b^{2} + p^{2}}{748440}$	$\bar{ϵ_{I_{x}}}$	0,008	1,009	3,831	19,453
$I_{x y}$	$- 27371 b \frac{h^{2} p}{748440}$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	1,489	5,294
$x_{s}, y_{s}$	$(\frac{b}{2} + \frac{p}{2}, \frac{h}{2})$	$\bar{ϵ_{I_{y}}}$	0,008	1,009	3,463	20,586
$I_{x} I_{y} - I_{x y}^{2}$	$749171641 \frac{b^{4} h^{4}}{560162433600}$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	1,298	5,750
		$\bar{ϵ_{I_{x y}}}$	0,008	1,009	4,474	30,458
		$σ ² (ϵ_{I_{x y}})$	0,000	0,000	1,920	9,431

Table 5. Equations for the parametric control polygon for the rectangle and its relative error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$61 h \frac{b + 2 p}{180}$	$\bar{ϵ_{A}}$	0,004	0,505	0,915	9,991
$I_{x}$	$\frac{h^{3} (4412605 b^{2} + 22420724 b p + 17650420 p^{2})}{273929040 (b + 2 p)}$	$σ ² (ϵ_{A})$	0,000	0,000	0,013	3,937
$I_{y}$	$h \frac{17081 b^{3} + 75322 b^{2} p + 150644 b p^{2} + 136648 p^{3}}{2993760}$	$\bar{ϵ_{I_{x}}}$	0,008	0,961	2,180	15,232
$I_{x y}$	$0$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	0,132	4,967
$x_{s}, y_{s}$	$(\frac{b}{2}; h \frac{461 b + 1274 p}{1098 (b + 2 p)})$	$\bar{ϵ_{I_{y}}}$	0,009	1,097	1,385	13,110
$I_{x} I_{y} - I_{x y}^{2}$	$(25)$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	0,002	4,336

Table 6. Equations for the parametric control polygon for the rectangle and its relative error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$h \frac{169 b + 218 p}{288}$	$\bar{ϵ_{A}}$	0,003	0,332	2,438	14,852
$I_{x}$	$\frac{h^{3} (82305438169 b^{2} + 212310520756 b p + 120438027736 p^{2})}{20118067200 (169 b + 218 p)}$	$σ ² (ϵ_{A})$	0,000	0,000	1,298	6,766
$I_{y}$	$h \frac{1527254 b^{3} + 5667223 b^{2} p + 7684452 b p^{2} + 3712596 p^{3}}{47900160}$	$\bar{ϵ_{I_{x}}}$	0,005	0,643	4,220	19,337
$I_{x y}$	$0$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	1,454	7,039
$x_{s}, y_{s}$	$(\frac{b}{2}; h \frac{167189 b + 254368 p}{2520 (169 b + 218 p)})$	$\bar{ϵ_{I_{y}}}$	0,006	0,690	2,291	17,653
$I_{x} I_{y} - I_{x y}^{2}$	$(26)$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	1,276	7,541

Table 7. Equations for the parametric control polygon for the rectangle and its relative error.

	Equation	Error [%]	$P_{100}$	$P_{10}$	$I_{128}$	$I_{16}$
$A$	$301 h \frac{b + p}{360}$	$\bar{ϵ_{A}}$	0,002	0,225	1,128	15,193
$I_{x}$	$\frac{h^{3} (1267299 b + 927031 p)}{23950080}$	$σ ² (ϵ_{A})$	0,000	0,000	0,081	7,610
$I_{y}$	$h \frac{354311 b^{3} + 1131397 b^{2} p + 1267299 b p^{2} + 490213 p^{3}}{5987520}$	$\bar{ϵ_{I_{x}}}$	0,003	0,398	2,405	20,943
$I_{x y}$	$0$	$σ ² (ϵ_{I_{x}})$	0,000	0,000	0,419	8,302
$x_{s}, y_{s}$	$(\frac{b}{2}, \frac{h}{2})$	$\bar{ϵ_{I_{y}}}$	0,004	0,511	1,037	15,814
$I_{x} I_{y} - I_{x y}^{2}$	$(27)$	$σ ² (ϵ_{I_{y}})$	0,000	0,000	0,037	7,627

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Symbolic Parametric Representation of the Area and the Second Moments of Area of Periodic B-Spline Cross-Sections

Abstract

1. Introduction

1.1. Motivation

1.2. State of the Art

2. Materials and Methods

2.1. Moments of Area of a Periodic B-Spline

2.2. Parametric Representation of the B-Spline of a Triangle

2.3. Comparision of with Polygon Cross-Sections

2.4. Numerical Comparision Framework

2.4.1. Spline Cross-Section with Valid Cross-Section Property

2.4.2. Spline Cross-Section as Valid Jordan-Curve

2.4.3. Spline Cross-Section Numerically Compared to Polygon and Image Cross-Section

3. Results

3.1. Moments of Area Parametrization of a Triangle Control Polygon

3.2. Moments of Area Parametrization of a Quadrilateral Control Polygon Area

3.2.1. Moments of Area Parametrization of a Rectangle Control Polygon

3.2.2. Moments of Area Parametrization of a Parallelogram Control Polygon

3.2.3. Moments of Area Parametrization of a Trapeze Control Polygon

3.3. Moments of Area Parametrization of a Symmetric Pentagon Control Polygon

3.4. Moments of Area Parametrization of a Symmetric Hexagonal Control Polygon

4. Discussion

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe