Preprint
Article
A Mechanical Newton-Einstein Hybrid Gravity based on Matter-vacuum Equilibrium Mediated by Gravitons
Altmetrics
Downloads
207
Views
174
Comments
2
This version is not peer-reviewed
Submitted:
26 January 2023
Posted:
28 January 2023
You are already at the latest version
Alerts
Abstract
There has been a disconnect between our understanding of the universe's working at the micro and macro scale - that is, disagreement between quantum mechanics (QM) and general relativity (GR). A theory of vacuum-matter equilibrium is presented from scratch to bridge this gap. It is proposed that gravitons are both quanta of matter and gravitation, as every matter entity is believed to interact with gravitation. The vacuum has an energy density that gives rise to virtual-graviton pairs. Upon collision, a virtual-graviton may get stuck to the matter while a graviton from the matter gets ejected. It is possible as all gravitons are identical in mass and size. Equilibrium is thus established where matter erodes in the vacuum, and the vacuum condenses as matter. The probability of graviton exchange depends on the relative energies of the virtual-graviton and matter entity, as calculated in the inertial frame of reference (IFoR) decided by the state motion of vacuum energy at that place. If the rate of matter-vacuum equilibrium is taken as a constant, it leads to the notion of time and time dilation. The force appearing on a matter entity through collision with virtual-gravitons is calculated, and the expression is a hybrid of Newton's and Einstein's equation. It further helps to answer the queries related to phenomena like the flatness of galaxy rotation curves, misconceptions about relativistic mass and length contraction, the relation between time, gravity, and quantum entanglement (QE), and the composite nature of the universal gravitational constant.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
Introduction
Several theories have been proposed that attempt to explain the working of the universe. Together, GR and QM are very successful theoretical frameworks describing the universe’s workings. However, when viewed together, QM and GR do not align completely. For one, the vacuum of space is treated as smooth in GR, while it is a ‘chunky’ sea composed of virtual particle pairs in QM. Most research to further understand the universe either starts with treating both theories as valid or aims to satisfy both views. The result is that any unexplained phenomenon in QM/GR remains an outlier in the new theory.
One major problem reconciling QM and GR is gravity [1,2,3,4]. Gravity is formulated in the framework of GR, while QM describes the other three fundamental forces. A quantum theory of gravity is needed to formulate a unified theory describing all four fundamental forces.
Additionally, QM/GR have a few problems in their regimes. For example, there is a debate over the length contraction [5,6] and relativistic mass [7,8,9,10] in special relativity (SR). GR fails to explain the flatness of galaxy rotation curves [11,12], and QM faces the challenge of correctly estimating and measuring the vacuum energy density [13]. There is also an increasing interest in connecting time with quantum entanglement and gravity [14,15,16]. Further, concerns are raised over if the fundamental understanding of gravitation and the universal gravitational constant is accurate [17,18,19,20,21,22,23,24,25].
For any progress to be made, it is essential to recognize that either or both theories are inaccurate (which does not mean incorrect). Guided by it, this article will take the liberty of borrowing concepts from either theory while also introducing other ideas that may conflict with QM/GR. It is shown that Newton’s gravitational formula results from considering graviton interaction with matter. The force expression will be a Newton-Einstein hybrid as it will follow mass proportionality and inverse square law but also result from a gradient in vacuum energy density - analogous to space-time curving around a mass. Several unresolved queries in QM/SR/GR will also be addressed.
1. Model of the universe
1.1. Vacuum model
The vacuum in the universe is modeled as a sea of particle-antiparticle pairs. Previous work on similar lines [26,27,28,29,30,31] assumed a superfluid of fermion pairs. This article proposes that the superfluid consists of graviton pairs with non-zero mass.
Graviton with non-zero mass is not a radically new idea [32,33,34]. However, attention is drawn to the implications of a massive graviton. If it is assumed that gravitation affects all kinds of matter, then it is argued that every type of matter is ultimately composed of graviton. Since graviton also has a mass, this makes the graviton not only quanta for gravity but quanta for matter as well.
Further, graviton pairs are assumed to be formed from vacuum energy fluctuations. For this to occur, the vacuum is assumed to have an (initially) isotropic uniform energy density denoted by . As with usual virtual particle pairs, gravitons are produced in pairs of equal and opposite velocities, making the net momentum at any point in vacuum zero. Graviton pairs also carry equal and opposite charges or be neutral.
In short, the vacuum is filled with an arbitrary yet finite isotropic energy density which fluctuates to form graviton pairs. The sea of virtual-graviton pairs is assumed to have net zero momentum and charge. The net-zero momentum of the vacuum is a crucial property and will be utilized to form the basis of reference frames.
1.2. Probability distribution of kinetic energy (KE) of virtual graviton
Since net charge and momentum of vacuum are assumed null, the only quantity of interest is the energy of graviton pairs. Further, spin (either mechanical or quantum) is also assumed to be zero or net zero. Therefore, the only contribution to the energy of graviton is kinetic energy.
The kinetic energy of a single graviton can take any value from zero to some upper-velocity limit determined by the local energy density of the vacuum. The following observation is made about the probability density function (PDF) of the kinetic energy of the gravitons. For a finite energy density of the vacuum, many low kinetic energy pairs are produced than the pairs with high kinetic energy. For a simplistic case, let the probability of finding a graviton with given kinetic energy decreases with the increase in kinetic energy. Divergence at zero kinetic energy is avoided by adding a constant to the energy of graviton, which results in the following equation.
Here the total energy of graviton is E, mass of graviton is , velocity is , and is the constant energy required to produce a graviton irrespective of kinetic energy. The coefficient of the above equation is doubled for a pair of the graviton.
A representative PDF based on the discussion is shown in Figure 1. As usual with PDFs, the area under the curve is unity. Further, a function is introduced with the following property:
That is, gives the area under PDF for graviton with KE greater than or equal to of the maximum KE.
1.3. Inertial frame of reference (IFoR)
So far, it has been stated that vacuum energy gives rise to a graviton super-fluid. Vacuum energy and particle-antiparticle super-fluid have been treated as one, and the same thing in previous works [28,29,30,31]. However, it must be recognized that vacuum energy is the background on which virtual-graviton pairs are formed. Therefore, virtual-graviton pairs are expected to exist in the same state of motion that the local vacuum energy exhibits. Hence, a virtual-graviton’s net velocity is the sum of its “birth" velocity and the velocity of the local vacuum energy in which it is drifting.
If an observer is at rest with the local vacuum energy, the velocities of virtual-gravitons in the immediate vicinity of the observer will add up to zero. It is because the “birth" velocities are oriented randomly with equal probabilities. However, if the local vacuum energy has a velocity with respect to the observer, the velocity of a virtual-graviton with respect to the observer is
Here, is the velocity of a virtual-graviton with respect to the observer. Therefore, the average velocity of graviton pairs will not be null, i.e., , and the observer will experience a fictitious force in the direction of .
For any reference frame to qualify as an IFoR, the fictitious forces must be absent. Therefore, an IFoR is a frame of reference in which local vacuum energy is at rest.
1.4. Matter-vacuum equilibrium
1.4.1. Mass proportionality
The porosity of gross matter is a central concept in mechanical gravity theories [35,36]. It is essential to ensure mass proportionality while deriving the expression for force. The concept is borrowed and applied here. Speculation has been presented in the appendix section. The speculation presented is merely an argument for mass proportionality, and the theory of matter-vacuum equilibrium is not affected if the speculation is incorrect as long as mass proportionality is ensured through some other view.
To summarise, every matter entity is composed of gravitons and each graviton in the matter can interact with the vacuum-superfluid.
1.4.2. Nature of observer virtual-graviton interaction
Maxwell [37], and Poincaré [38] argued that virtual-gravitons interaction with matter can not be perfectly elastic, but a non-elastic collision leads to a heat problem. A re-analysis shows that an elastic collision is possible and that the heat problem is solvable [36]. However, there exists some merit to inelastic collisions proposed by Maxwell and Poincaré.
The observer is a stable structure of charged gravitons in a sea of the short-lived virtual-gravitons. As such, the observer polarizes the virtual-graviton pairs, providing sites for the oppositely charged virtual-gravitons to attach. It leads to a change in the charge and mass of the observer. It continues until any further increase in mass makes the observer structure unstable. Henceforth, a virtual-graviton interacts with the observer in two distinct manners.
- The incoming virtual-graviton collides with the observer with some kinetic energy. The force of the collision is transferred across the observer to the last observer-graviton on the opposite side. The last observer-graviton is expelled out of the observer, while the former virtual-graviton becomes a part of the observer. It is similar to the working of Newton’s pendulum.
- The incoming virtual-graviton strikes the observer, but the collision force is distributed between the observer-gravitons because of multiple contacts. The former virtual-graviton comes to a rest, attaches to the observer, and makes it unstable. A random observer-graviton is ejected from the observer to maintain stability.
A virtual-graviton will replace an observer-graviton as all gravitons are similar in size and mass. Any charge instability of the observer that arises from graviton exchange promotes observer-graviton exchange. Due to electrical charge interaction, a virtual-graviton’s change in kinetic energy as it approaches the observer is assumed negligible when averaged for attraction and repulsion.
The modeling of observer and virtual-gravitons interaction can be perfectly elastic, but in reality, it is perfectly inelastic. The outgoing graviton is expelled randomly and carries some energy with it, similar to results obtained in [36].
As a final comment, the interaction between the observer and virtual-gravitons leads to an equilibrium. Virtual-gravitons are continuously condensing into the observer while, at the same time, the observer is evaporating into the vacuum.
1.4.3. Energetics of observer-virtual graviton interaction
Mechanical gravity theories, for example, Fatio’s theory of gravitation [35], explain gravity as force caused by the collision of particles. In these theories, every collision is believed to produce a force. Such a viewpoint is carried over from collision observation at the macro-world level, where every contact leads to a contact force. But, since the gravitons are the carrier of gravitational force, the only interaction that results in any force involves the exchange of gravitons.
Consider that photovoltaic and photoelectric effects, nuclear fission [39], and chemical reactions demonstrate strong dependence on the energy state of the participants. It is similarly argued that a graviton exchange is influenced by the energy levels of virtual and observer-gravitons.
In the local IFoR, let the observer has a velocity , and a virtual-graviton has a velocity . Further, assume that the binding energy of each observer-graviton is identical and constant. Then the only quantities that are variable and influence the interaction are the kinetic energies of participants. For a simplistic case, it is assumed that any virtual-graviton with kinetic energy equal to or greater than the observer-graviton will lead to a graviton exchange.
Further, the outgoing graviton carries away some energy from the observer. The magnitude of energy carried away by the outgoing graviton is always less than the energy of the incoming graviton. To correctly assess the momentum transfer to the observer, it is essential to know the difference in energies of incoming and outgoing gravitons. The fraction of energy carried away by outgoing graviton for observers of varying masses is given in [36]. For a high mass observer, the outgoing graviton has nearly identical energy as the incoming graviton. For calculation sake, it is assumed that incoming and outgoing gravitons have the same energy.
1.4.4. Graviton exchange frequency and clock time
In the local IFoR, the observer has a velocity . The probability of finding a virtual-graviton with a velocity equal to or greater than is calculated from the Figure 1 using Eq. (2). The probability is expressed as
Here the means the function is calculated for observer . Since it is assumed that every virtual-graviton with required energy will lead to graviton exchange, the frequency f of graviton exchange is expressed as
Therefore, the time duration between two consecutive graviton exchanges is expressed as
The time duration between graviton exchange is when .
Graviton exchange or matter-vacuum equilibrium is the most fundamental and universal interaction between matter and its surrounding. If the equilibrium rate is taken as a universal constant, it gives a sense of the flow of time. The higher the equilibrium rate, the faster the time flows. Following it, the clock time for an observer is
Where t is the clock time when .
1.5. Vacuum energy flux caused by an observer
1.5.1. Flux caused by vacuum energy diffusion
Initially, the vacuum energy density has an isotropic constant value of . An observer is introduced in the vacuum that creates an equilibrium through graviton exchange. The vacuum energy density reduces near and inside the observer. However, since the quantity of interest lies outside the observer, let the vacuum energy density inside the space occupied by the observer be some averaged constant. Therefore, the vacuum energy density decreases from the value of at infinity to some reduced value at the observer’s location.
The gradient in the vacuum energy density causes a flow of vacuum energy toward the observer. The flux of vacuum energy is expressed according to the first law of diffusion as
The diffusion constant D is assumed constant and taken outside the spatial derivative operator ∇.
1.5.2. Flux caused by graviton exchange
Since the observer is the epicenter of vacuum energy flux, every segment of the observer is in motion in its local IFoR. The vacuum energy density enclosing the observer is approximated as a constant; similarly, the observer is considered to have some averaged constant velocity in its local IFoR. Thus, the vacuum energy flux caused by the graviton exchange rate is dependent on the following factors:
- The total vacuum energy available to the observer, which is a product of vacuum energy density enclosing the observer and the volume of the observer, i.e.,
- The frequency of graviton exchange corresponding to the available vacuum energy. It is obtained by multiplying total vacuum energy with the graviton exchange frequency .
- The number of gravitons that are available for exchange in the observer. Following the arguments for mass proportionality in mechanical gravity theories, the number of gravitons inside the observer that are available for exchange is , where is the mass of the observer.
Therefore, the vacuum energy flow towards the observer in the form of gravitons per unit time is
The flux of vacuum energy toward the observer is
Here the distance is measured radially outwards from the center of the observer. Equation (8) and Eq. (10) are combined to eliminate and rearranged to obtain
Further, the vacuum behaves as a super-fluid, the energy density gives a measure of pressure. Equation (11) is rewritten in the pressure term as
1.6. Force acting on a test mass
1.6.1. Case I : Force acting on a test particle (object) placed on the surface of observer (Earth)
Figure 2.
Representation of virtual-graviton flux lines passing through an object (test particle) placed on the surface of Earth (observer).
Figure 2.
Representation of virtual-graviton flux lines passing through an object (test particle) placed on the surface of Earth (observer).
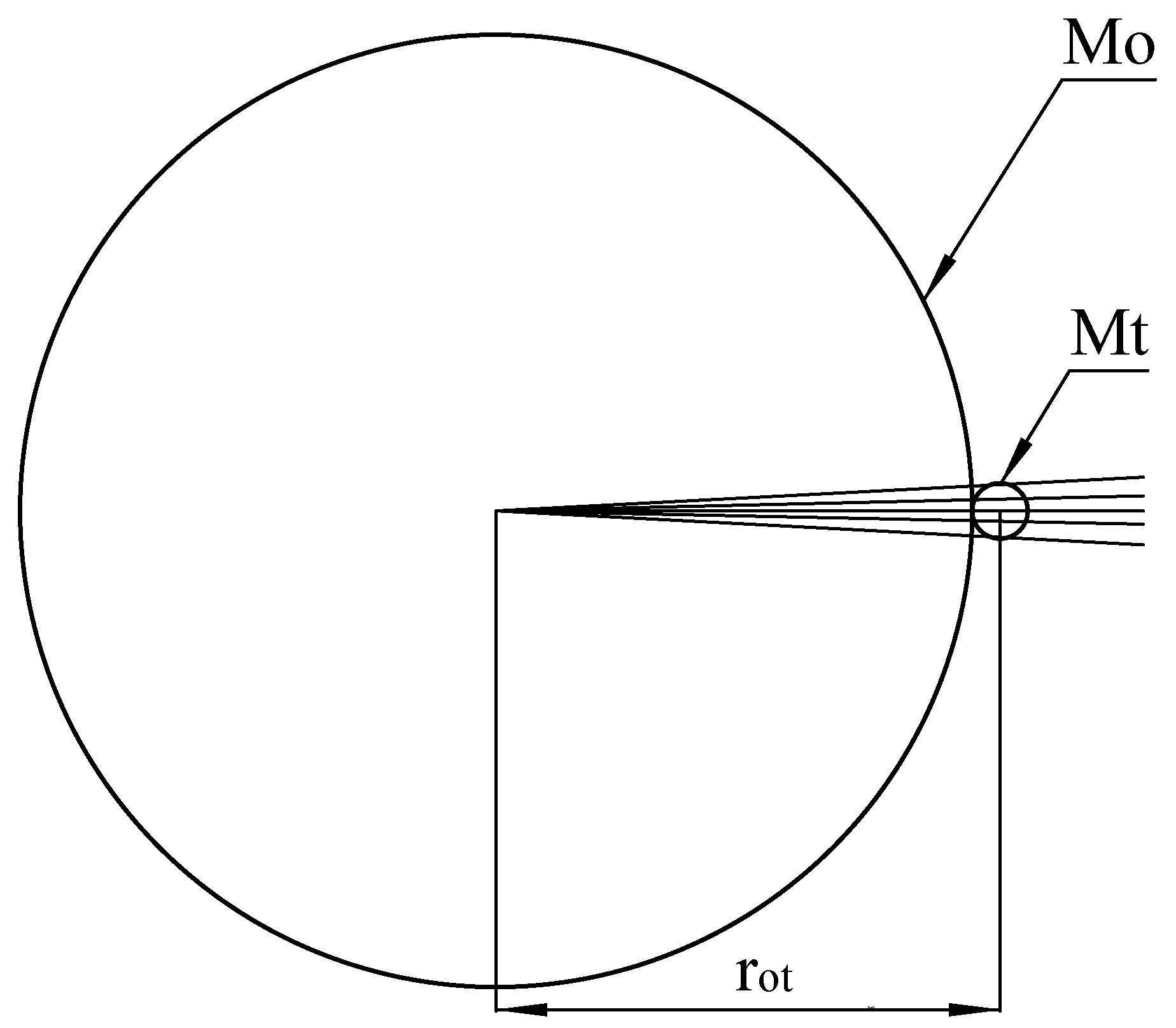
The following assumptions are made for an object resting on the surface of the Earth:
- The size of the object is negligible compared to the Earth.
- The virtual-graviton flux generated by the object is negligible compared to the flux generated by the Earth.
- The flux lines are collimated at the object.
The vacuum energy density at the object is obtained by integrating Eq. (11) and taking the energy density at infinity, i.e., as the datum.
The influence of the test particle on the energy density is negligible compared to the Earth. Therefore, the energy density inside the test particle is assumed to be given by Eq. (13).
Although the test particle is at rest on the Earth, the vacuum is not. The equilibrium between the test particle and the vacuum is governed by . The variation of flux over the volume of the test particle is also ignored.
The test particle interacts with the vacuum through graviton exchange. Coupling with the virtual-graviton flux is also the only pathway through which the Earth affects the test particle, if the physical contact is ignored. Therefore, as before, the vacuum energy flux, energy density gradient, and pressure gradient are calculated for the test particle as
In this case, is measured radially outward from the center of the test particle.
The net pressure gradient at any point is space is . The combined action of the Earth and test particle accelerates the vacuum super-fluid. But, as pointed out earlier, the influence of the test particle on the vacuum is ignored compared to the Earth. Therefore, the vacuum super-fluid is approximated as accelerated under the influence of the Earth alone. Thus, the pressure at the test particle is obtained by integrating the net pressure gradient with the Earth as the source. The pressure at infinity is taken as the datum, so the pressure at the test particle is
The velocity of the virtual-graviton super-fluid at the test particle is calculated using Bernoulli’s principle.
Here, is the density of vacuum super-fluid and is taken constant at every point in space. The velocity of the vacuum at infinity is taken as zero.
The momentum carried by a virtual-graviton near the test particle is . As before, is oriented in random directions with equal probabilities. Therefore, the average value of equals zero, i.e., the average momentum carried by a virtual-graviton is . Similarly, the outgoing observer-graviton carries a momentum . But the outgoing observer-graviton is ejected in a random direction with equal probability. Therefore, the net momentum carried by the outgoing observer-graviton is also zero. It is concluded that the average momentum transferred to the observer in interaction with one virtual-graviton is .
The force transferred on the test particle is
Here, . From Eq. (6), the equilibrium rate is not the same for the observer and the test particle. Equation (19) gives the force acting on the test particle, in an ideal case when . To calculate the force on the test particle, in its own time frame, Eq. (7) is used:
Here, is the graviton mass flow rate at test particle, and is the cross-sectional area of test particle normal to graviton flow.
Substitute the value of from Eq. (18) in Eq. (22) to obtain the expression of force
The first term in the parenthesis of Eq. (23) has no coupling with the test particle. It represents the uncoupled graviton flux that can couple with another test particle, as will be shown in subsequent sections. As such, this term will be ignored from the expression of force.1
The final expression of force between observer and the test particle is
Here, .
1.6.2. Case II: Force acting on a planet orbiting a star
Figure 3.
(a) Representation of virtual-graviton flux lines between the planet (test particle) and star (observer) (b) Approximation of flux lines passing through the planet and converging at some point between the planet and the star.
Figure 3.
(a) Representation of virtual-graviton flux lines between the planet (test particle) and star (observer) (b) Approximation of flux lines passing through the planet and converging at some point between the planet and the star.
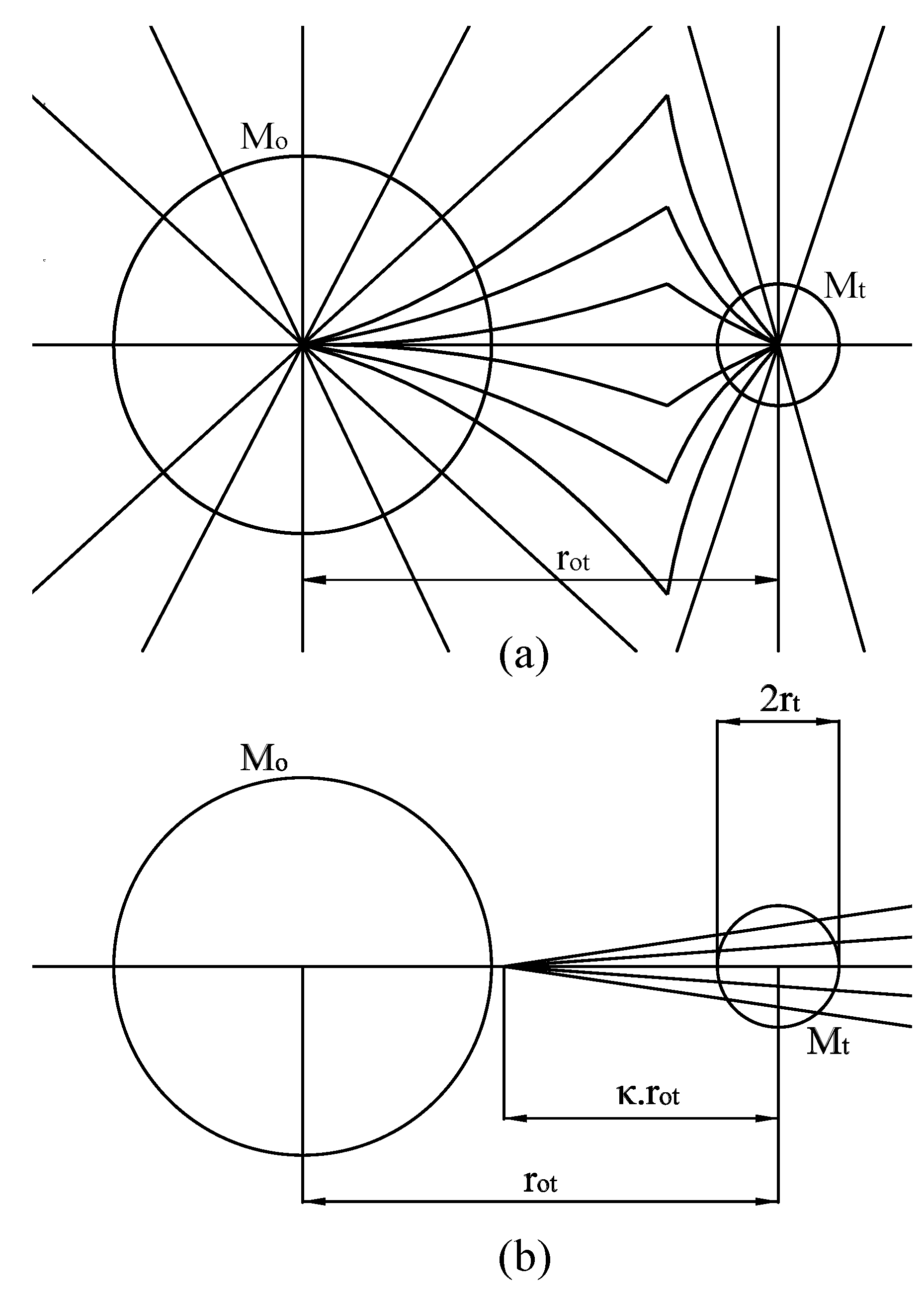
The following assumptions are made:
- The energy density at the location of the planet is determined by the energy gradient set by the star.
- The flux generated by the star is greater than the planet.
- .
Since the flux generated by the planet is not ignored, the net flux at any point inside the planet is a vector sum given by . Therefore, th virtual-gravitons’ velocity is a vector along the net flux direction. Thus, the flux lines are not collimated about , which makes the force calculation difficult.
An approximation is made based on the following argument. In the previous case, the flux of the test particle is ignored in favor of the Earth, and flux lines converge on Earth’s center. In an extreme case where the flux generated by the Earth is ignored in favor of the test particle, the situation will reverse, and flux lines will converge at the center of the test particle. Therefore, in between the two extremes, the flux lines converge at some point between the Earth and the test particle..
In the present case, where the star’s flux is greater than the planet, the flux lines may be assumed to converge at a distance from the planet. Since the planet’s size is much smaller than the distance , it is further assumed that flux lines are collimated at the planet. Following the above argument, the force between the planet and the sun is similar to the Eq. (24):
Where .
2. Implications
The expression for force derived in Eq. (24) and Eq. (25) is similar to classical Newton’s gravitational formula. It contains new terms, and the term may look like the Gravitational constant, but it is only valid for a binary system. The expressions are analyzed in the following sections, and the significance of new terms is suggested. Correlation to the known physical phenomenon is established, some far-fetched suggestions are made, and the expression of is expanded to a large-scale system to derive .
2.1. Relativity of time, length and mass
Equation (7) gives the time dilation for clock time. The expression of force in Eq. (24) is re-written in the following forms:
Or
Since the force is expressed in the frame of the test particle, the RHS of the Eq. (26) and (27) denotes the length and mass as measured in the frame of the test particle. In the SR, the RHS in the above equations denotes quantities measured in the moving frame.
A comparison of SR relativistic relations and relations obtained through matter-vacuum equilibrium are given in Table 1. The relations for time and length are similar if . Also, note that although the equation for mass relativity is not similar, the mass-energy equivalence expression remains unchanged if .
Additionally, the following queries are answered:
-
Issue with the relativistic mass and length contraction: The idea of relativistic mass created in special relativity is not fundamental to the theory [7]. In a 1948 letter to Lincoln Barnett, Einstein wrote, "It is not good to introduce the concept of the mass of a body for which no clear definition can be given. It is better to introduce no other mass than the rest mass." Einstein never derived an equation for relativistic mass. Different definitions of masses are confusing, and Einstein never mentioned them again after August 1906 [8].Similarly, experiments presented as proofs of relativistic length contraction can be interpreted as manifestations of dynamical interactions taking place in the experiments [5].The relations for mass and length obtained in the matter-vacuum equilibrium hypothesis are an apparent effect and not a real one. Further, mass and length relations are not correct simultaneously as can be grouped with only one term at a time.
-
Problem of time: The first problem with time is that GR and QM treat time differently [40]. Time is treated as absolute in QM, whereas it is dynamic in GR. It has been described as the significant issue in the unification of GR and QM [41,42].The second issue concerns the arrow of time [43,44,45]. Relativity suggests that time can be reversed at super-luminal velocities and most fundamental laws are time-symmetrical.In the matter-vacuum hypothesis, time is an emergent, dynamical property. Time is not a fixed background parameter but the flow of time emerges as an observer’s interaction rate with its surroundings at the graviton level. As such, the flow of time can not be in the negative direction as graviton exchange denote a whole number that can be zero but never negative.
2.2. Interconnected time, QE and gravity
Several theoretical papers have discussed if time is an emergent property deriving from quantum correlations [14]. It has also been conjectured that total the QE of matter and vacuum in the universe increases with time. A gravity like force is associated with the increase in QE [15]. More recent proposals assume gravity as the mediator of quantum correlations and are based on the fact that QE between otherwise non-interacting objects can only increase via a quantum mediator [16].
It has been shown that matter-vacuum equilibrium through graviton exchange leads to a force with the same expression as the classical Newton’s gravitational force. Further, the rate of equilibrium influences the clock time of the observer as per Eq. (7).
Suppose two observers and are void of any physical contact. A pair of virtual-gravitons is produced with the following entangled state:
absorbs virtual-graviton A while absorbs the graviton B. Since the macroscopic properties of a system depend on the average properties of its microscopic constituents, it is inferred that properties of depend on virtual-graviton A. In the same way, properties of are influenced by the virtual-graviton B. Therefore, the properties of and will show some correspondence or entanglement.
The entanglement mediated by graviton need not be limited to a binary system. Say, is entangled with through a graviton pair while and are entangled through another graviton pair, say . It forms a chain of entanglement where systems are pair-wise entangled or entangled with many other systems through gravitons shared from the same pair.
2.3. Gravity at different scales
2.3.1. Gravity at galactic scale
As per Newton and Einstein, the force of gravity is a monotonously decreasing force with distance. It is not so with the matter-vacuum equilibrium hypothesis. Consider two identical planet and at a radial distance of and from a star S such that . It is considered that graviton flux created by S at is and at is such that . Let the size of the planets is negligible compared to the distance from the star.
As before, the net flux is approximated to converge at some epicenter between the S and the planets. Since the flux of star is weaker at , while the flux generated by and is identical, the epicenter shifts towards the planet for , i.e., . Also, since the flux velocity of virtual-graviton is smaller at , it gives .
2.3.2. Gravity at micro-scale
For a massive object like a planet or a star, the flux created is massive and, in turn, far-reaching. The virtual-gravitons drifts at a great velocity toward the source of flux which decreases the magnitude of . Further, the test particle is massive (another star or planet), and the momentum transferred by one virtual-graviton is negligible. Therefore, it requires a high graviton exchange rate to produce a measurable force in the test particle. In short, the gravity at the galactic scale is weak but long-ranged.
In contrast, the flux created by an observer at the micro-scale, say a sub-atomic particle consisting of a few hundred gravitons or less, is light and limited in range. The resulting drift velocity of virtual-gravitons toward the source is small, which gives a high value of . Further, the momentum transfer by one virtual-graviton to the test particle is also high as the test particle is lightweight (another sub-atomic particle). Therefore, gravity at the micro-scale might be a short-range but strong force. The strong interaction or the nuclear force might be the gravitational force at the quantum level, and the gluons are the gravitons. It is also in line with the assumption that gravitons are quanta of matter and gravitation, both.
2.3.3. Possibility of black holes
Referring to the Eq. (24), the force is directly proportional to . A significant number of system-gravitons are required to generate a massive gravitational force, which leads to a high graviton exchange rate and steeper vacuum energy gradient, therefore, a considerable . But a high graviton exchange rate and steeper vacuum energy gradient lower the value of . To offset the diminishing product of , a black hole needs a massive volume, so the product is high nevertheless. It suggests that a black hole cannot be incredibly dense [46].
2.4. Composite universal gravitational constant,
A constant is introduced in the force equations valid for a binary system. Suppose a new mass is introduced to this system such that . The force acting on is expressed in Eq, (28) where is the separation between .
The derivation assums that is accelerated under the influence of and is the epicenter for . Similarly, the flux is accelerating under the influence of with as the epicenter. The first term in Eq, (28) results from coupling with the unused flux of , as it appeared in Eq. (23). Since the force between is required, the first term in Eq, (28) is ignored.
Similarly, the force between and is recalculated in the backdrop of (supposedly) infinite entities, arranged in the decreasing order of . The constant G approaches a value denoted by such that
For any experimentation on Earth involving gravity, the value of has contributions from the entire observable universe. In short, “mass out there influences inertia here," - which is roughly Mach’s principle. Further, since the contribution is from entities that may be situated several lightyears away, the constant relative motion of Earth will lead to a varying value of [18,19,20,21]. This unique situation is reflected by the 1998 CODATA decision to increase the relative uncertainty from 0.013% to 0.15 % [22].
Further, researchers pointed out that measurements show that varies significantly with the orientation of the test masses relative to the system of fixed stars [23,24,25]. changes with the orientation by at least 0.054%, and as the precision of measurements increased, the disparity between the values increased [see references in [23]]. The same is reflected in Eq. (29) that includes the cross-sectional area of the test particle.
2.5. vs
presented in the matter-vacuum equilibrium hypothesis is a function of the energy of virtual-gravitons available for exchange. It is, in turn, a function of the square of the observer’s velocity in the local IFoR. introduced in relativity theory is a function of the square of the velocity of an observer. Essentially, both are a dimensionless function of the kinetic energy of the observer.
For the present hypothesis to be accurate, and must be identical. Let be defined in a similar manner to , then the following expression is obtained
The integrand in Eq. (30) gives unity when integrated from 0 to c. Therefore, the integrand can be the PDF of virtual-gravitons energy. The PDF is plotted in Figure 4 and drastically differs from the PDF assumed in Figure 1. Figure 4 shows an ever-increasing probability of finding a virtual-graviton with higher KE. It points out that there is an abundance of vacuum energy density consistent with predictions made by QFT. However, unlike GR, there is no issue with enormous vacuum energy density [47] as the energy itself is not a source of gravitation but a mediator.
3. Concluding remarks
The notion of quantum of matter has always existed, though under different names and definitions, and so has graviton exchange as a gravity mediator. Built on these ideas is the vacuum model as a continuous collection of virtual-gravitons exchanged between matter entities. The movement of virtual-gravitons is similar to electrons in a conductor where the drift velocity of the electrons is small, but the current flows at the speed of EM waves. The exchange of gravitons results in an equilibrium where matter continuously erodes in the vacuum while the vacuum condenses as matter. When the equilibrium rate is taken at a constant, it leads to the discussion time and time dilation.
The force resulting from the collision of drifting virtual-gravitons with a test particle leads to apparent effects such as length contraction and the concept of relativistic mass. When the expression of force is approximated for a star-planet system, it is revealed that the force does not decrease in a Keplerian fashion. Further, when the force is calculated in the presence of a supposedly infinite system of masses, the force constant tends to some quasi-constant value while also confirming Mach’s hypothesis.
Ultimately, an attempt is made to discover the kinetic energy distribution of virtual-gravitons in the vacuum - a cornerstone in the matter-vacuum equilibrium theory. It is realized that the derivative of the function of the relativity theory can be taken as the said PDF. It points to an enormous vacuum energy density, possibly resolving the cosmological constant problem as both QM and GR now advocates for a colossal .
The present theory rests on the existence of gravitons with non-trivial mass. It has been proposed that gluons and gravitons are the same entity, making the strong force a short-range form of gravity. The theory may be validated by estimation of per Eq. (29), which involves constants like the diffusivity constant of vacuum energy, and mass of graviton, among other things.
Finally, mechanical gravity theories like Le Sage’s theory and Fatio’s theory have existed since before the time of Newton. While these theories could arrive at an inverse square law and mass proportionality, they can never arrive at concepts like time dilation and quantum entanglement. However, mechanical theories of gravity are essential to understand the origin of and the working of the universe at a small scale, which got missed by Newton and Einstein. This article hopes to bridge this same disconnect between the universe’s working at the micro and the macro scale.
Appendix A. Structure of matter
Fatio [35] assumed matter is a cage of infinitely slender beams to ensure every part of the matter interacts with the vacuum super-fluid. Fatio’s idea of matter being highly porous isn’t far-fetched when viewed in the context of present knowledge of the structure of matter. However, Fatio’s structure of matter runs into the problem of infinity [35]. This section explores the structure of matter that ensures the porosity of matter without running into the infinity problem.
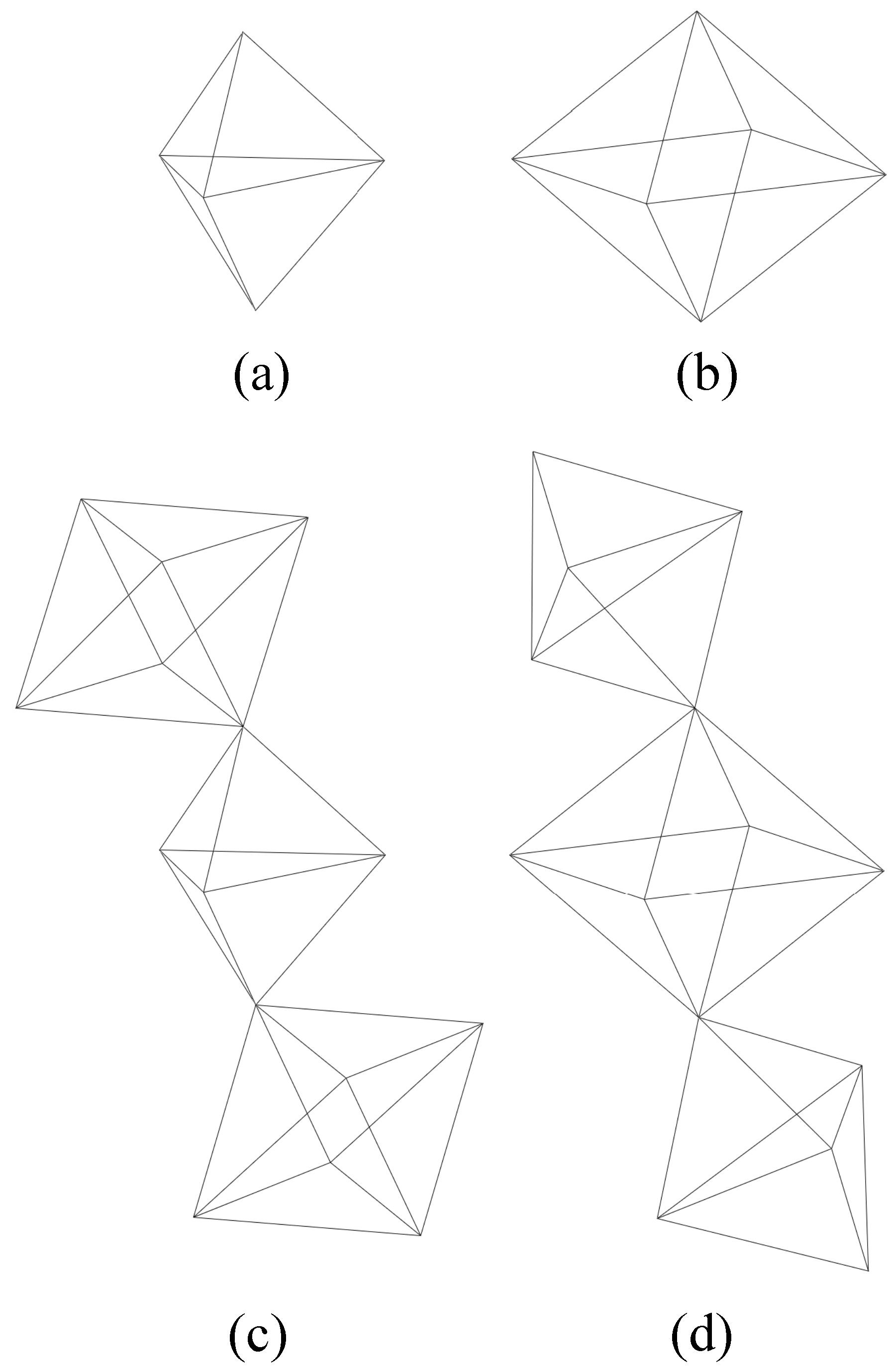
Since a graviton is also a quantum of matter, let the graviton represent the first generation of matter. The second generation of matter might be simple three-dimensional structures formed by graviton arrangements, as shown in Figure A1a,b. Each node in the figures represents a graviton that is held together by electrostatic attraction. A simple bipyramid and octahedral arrangement of the gravitons ensures that each graviton can interact with the surrounding. There can be several such arrangements. but only two are shown for representation. As shown in Figure A1c,d, several of the second-generation structures might share a common node to form the third generation. The interaction of several third-generation structures might similarly form higher generations.
In short, the matter is assumed to have an orderly structure, not just a pile of gravitons lumped together. An orderly arrangement of gravitons inside matter ensures that every graviton interacts with the vacuum super-fluid.
Figure A1.
Assumed structure and generation of matter that ensures interaction of every part of matter with vacuum.
Figure A1.
Assumed structure and generation of matter that ensures interaction of every part of matter with vacuum.
References
- Isham, C.J. Prima facie questions in quantum gravity. In Canonical gravity: From classical to quantum; Springer, 1994; pp. 1–21.
- Kiefer, C. Conceptual problems in quantum gravity and quantum cosmology. International Scholarly Research Notices 2013, 2013. [Google Scholar] [CrossRef]
- Rovelli, C. Notes for a brief history of quantum gravity. arXiv preprint gr-qc/0006061 2000. [Google Scholar]
- Carlip, S. Is quantum gravity necessary? Classical and Quantum Gravity 2008, 25, 154010. [Google Scholar] [CrossRef]
- Jefimenko, O.D. On the experimental proofs of relativistic length contraction and time dilation. Zeitschrift für Naturforschung A 1998, 53, 977–982. [Google Scholar] [CrossRef]
- Sastry, G. Is length contraction really paradoxical? American Journal of Physics 1987, 55, 943–946. [Google Scholar] [CrossRef]
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In Collected Papers; Springer, 1937; pp. 172–197.
- Hecht, E. Einstein never approved of relativistic mass. The Physics Teacher 2009, 47, 336–341. [Google Scholar] [CrossRef]
- Okun, L.B. The concept of mass. Physics today 1989, 42, 31–36. [Google Scholar] [CrossRef]
- Adler, C.G. Does mass really depend on velocity, dad? American Journal of Physics 1987, 55, 739–743. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford Jr, W.K.; Thonnard, N.; Burstein, D. Rotational properties of 23 SB galaxies. The Astrophysical Journal 1982, 261, 439–456. [Google Scholar] [CrossRef]
- Bosma, A. 21-cm line studies of spiral galaxies. II. The distribution and kinematics of neutral hydrogen in spiral galaxies of various morphological types. The Astronomical Journal 1981, 86, 1825–1846. [Google Scholar] [CrossRef]
- Morgan, E. Estimating the vacuum energy density–an overview of possible scenarios. Jozef Stefan Institute 2005. [Google Scholar]
- Moreva, E.; Brida, G.; Gramegna, M.; Giovannetti, V.; Maccone, L.; Genovese, M. Time from quantum entanglement: an experimental illustration. Physical Review A 2014, 89, 052122. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.C.; Lee, J. Gravity as a quantum entanglement force. Journal of the Korean Physical Society 2015, 66, 1025–1030. [Google Scholar] [CrossRef]
- Krisnanda, T.; Tham, G.Y.; Paternostro, M.; Paterek, T. Observable quantum entanglement due to gravity. npj Quantum Information 2020, 6, 1–6. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian dynamics as an alternative to dark matter. Annual Review of Astronomy and Astrophysics 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Barukčić, I. Newton’s gravitational constant big g is not a constant. Journal of Modern Physics 2016, 7, 510–522. [Google Scholar] [CrossRef]
- Rothleitner, C.; Schlamminger, S. Invited review article: Measurements of the Newtonian constant of gravitation, G. Review of Scientific Instruments 2017, 88, 111101. [Google Scholar] [CrossRef] [PubMed]
- Quinn, T.; Speake, C. The Newtonian constant of gravitation—a constant too difficult to measure? An introduction, 2014.
- Wu, J.; Li, Q.; Liu, J.; Xue, C.; Yang, S.; Shao, C.; Tu, L.; Hu, Z.; Luo, J. Progress in precise measurements of the gravitational constant. Annalen der Physik 2019, 531, 1900013. [Google Scholar] [CrossRef]
- Mohr, P.J.; Taylor, B.N.; Newell, D. The fundamental physical constants. Physics Today 2007, 60, 52–55. [Google Scholar] [CrossRef]
- Gershteyn, M.L.; Gershteyn, L.I.; Gershteyn, A.; Karagioz, O.V. Experimental evidence that the gravitational constant varies with orientation. arXiv preprint physics/0202058 2002. [Google Scholar]
- Will, C.M. Relativistic gravity in the solar system. II. Anisotropy in the Newtonian gravitational constant. The Astrophysical Journal 1971, 169, 141. [Google Scholar] [CrossRef]
- Iorio, L. Observational constraints on spatial anisotropy of G from orbital motions. Classical and Quantum Gravity 2011, 28, 225027. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Is there an Aether? Nature 1951, 168, 906–907. [Google Scholar] [CrossRef]
- Dirac, P. Is there an Æther? Nature 1952, 169, 702–702. [Google Scholar] [CrossRef]
- Sinha, K.; Sivaram, C.; Sudarshan, E. Aether as a superfluid state of particle-antiparticle pairs. Foundations of Physics 1976, 6, 65–70. [Google Scholar] [CrossRef]
- Sinha, K.; Sivaram, C.; Sudarshan, E. The superfluid vacuum state, time-varying cosmological constant, and nonsingular cosmological models. Foundations of Physics 1976, 6, 717–726. [Google Scholar] [CrossRef]
- Sinha, K.; Sudarshan, E. The superfluid as a source of all interactions. Foundations of Physics 1978, 8, 823–831. [Google Scholar] [CrossRef]
- Urban, M.; Couchot, F.; Sarazin, X.; Djannati-Atai, A. The quantum vacuum as the origin of the speed of light. The European Physical Journal D 2013, 67, 58. [Google Scholar] [CrossRef]
- Trippe, S. A simplified treatment of gravitational interaction on galactic scales. arXiv preprint arXiv:1211.4692 2012. [Google Scholar] [CrossRef]
- Platscher, M.; Smirnov, J.; Meyer, S.; Bartelmann, M. Long range effects in gravity theories with Vainshtein screening. Journal of Cosmology and Astroparticle Physics 2018, 2018, 009. [Google Scholar] [CrossRef]
- Ali, A.F.; Das, S. Cosmology from quantum potential. Physics letters B 2015, 741, 276–279. [Google Scholar]
- Pushing gravity : new perspectives on Le Sage’s theory of gravitation / edited by Matthew R. Edwards.; Apeiron: Montreal, 2002.
- Múnera, H.A. A Le Sagian atomic-type model for propagation and generation of gravity. In Should the Laws of Gravitation be Reconsidered?–The Scientific Legacy of Maurice Allais; 2011; pp. 385–422. [Google Scholar]
- Maxwell, J.C. Atom. Encyclopaedia Britannica 1875, 9, 46–47. [Google Scholar]
- Poincaré, H.; Maitland, F. Science and method; Courier Corporation, 2003.
- Zamyatnin, Y.S.; Konovalov, V.Y. Probability of nuclear fisson and effective fisson cross sections: Datasheet from Landolt-Börnstein - Group I Elementary Particles, Nuclei and Atoms · Volume 16A1: “Low Energy Neutrons and their Interaction with Nuclei and Matter. Part 1” in SpringerMaterials. 2000. [Google Scholar] [CrossRef]
- Anderson, E. Problem of time in quantum gravity. Annalen der Physik 2012, 524, 757–786. [Google Scholar] [CrossRef]
- Isham, C.J. Canonical quantum gravity and the problem of time. In Integrable systems, quantum groups, and quantum field theories; Springer, 1993; pp. 157–287.
- Anderson, E. Problem of time in quantum gravity. Annalen der Physik 2012, 524, 757–786. [Google Scholar] [CrossRef]
- Zeh, H.D.; Page, D.N. The physical basis of the direction of time, 1990.
- Lebowitz, J.L.; others. Boltzmann’s entropy and time’s arrow. Physics today 1993, 46, 32–32. [Google Scholar] [CrossRef]
- Gold, T. The arrow of time. American Journal of Physics 1962, 30, 403–410. [Google Scholar] [CrossRef]
- Celotti, A.; Miller, J.C.; Sciama, D.W. Astrophysical evidence for the existence of black holes. Classical and Quantum Gravity 1999, 16, A3. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Reviews of modern physics 1989, 61, 1. [Google Scholar] [CrossRef]
| 1 | If the assumption is wrong then this term represents a slow decaying, test particle independent force that needs further investigation. |
Figure 1.
Probability density function of kinetic energy of a graviton
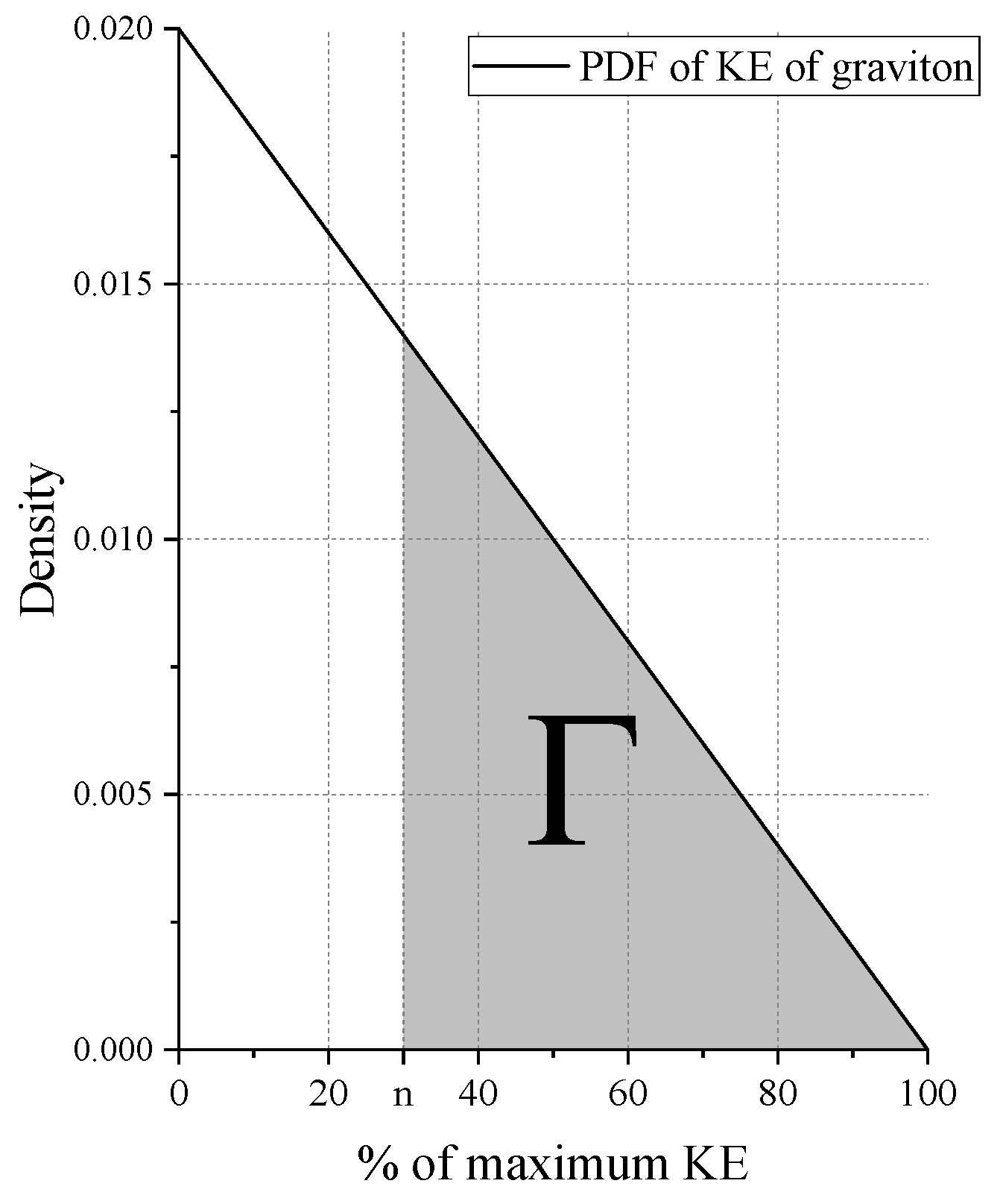
Figure 4.
Probability density function of the kinetic energy of virtual-gravitons based on .
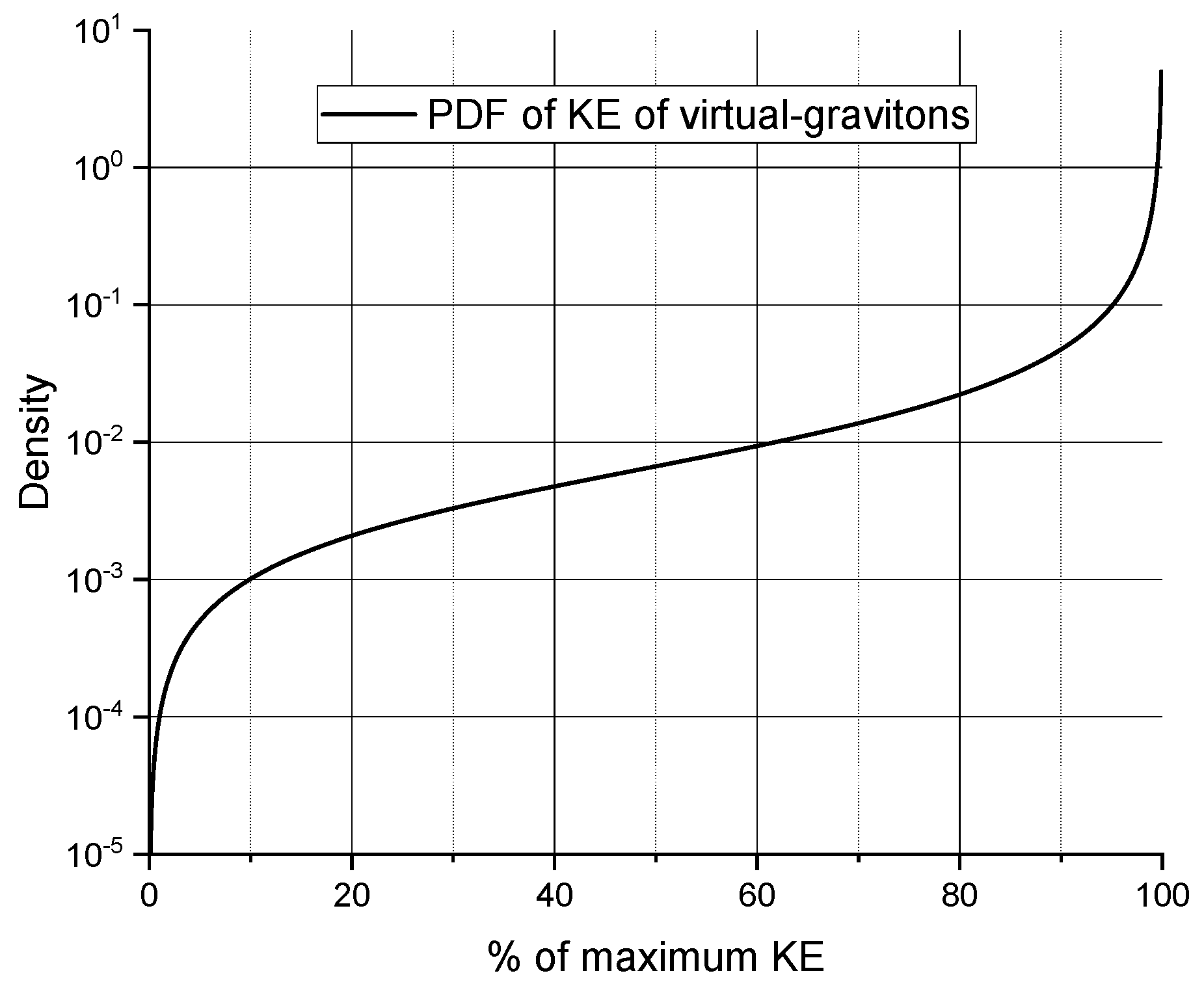
Table 1.
The primed variables are measured in the test particle frame or the moving frame, and
| Relation | Equilibrium | SR |
| Time | ||
| Length | ||
| Mass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






