Prerpints.org logo
Preprint
Article

Comparative Study of Different Ion-exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate

Altmetrics

Downloads

212

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 January 2023

Posted:

19 January 2023

You are already at the latest version

Alerts
Abstract
The application of diffusion dialysis using various types of ion-exchange membranes for the separation of sulfuric acid and nickel sulfate has been evaluated. The process of dialysis separation of a real waste solution from an electroplating facility containing 252.3 g/L of sulfuric acid, 20.9 g/L of nickel ions and small amounts of zinc, iron, copper ions, etc. has been studied. Heterogeneous cation-exchange membrane containing sulfo groups and heterogeneous anion-exchange membranes with different thicknesses (from 145 μm to 550 μm) and types of fixed groups (4 samples with quaternary amino groups and 1 sample with secondary and tertiary amino groups) are used. The diffusion fluxes of sulfuric acid, nickel sulfate, and the total and osmotic fluxes of the solvent are determined. The use of a cation-exchange membrane does not allow separation of the components, since the fluxes of both components are low and comparable in magnitude. The use of anion-exchange membranes makes it possible to efficiently separate sulfuric acid and nickel sulfate. At the same time, the thin dialysis membrane turns out to be the most effective, as well as the membranes with quaternary amino groups, and the membrane with secondary and tertiary amino groups proved to be the least effective.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

In general, dialysis is a membrane separation process of solution components in which transport is driven primarily by concentration differences [1]. If an ion-exchange membrane is used in the dialysis, such process is called diffusion dialysis (DD) [2]. DD is a perspective method used for separating organic and inorganic components [3], [4] extracting metal ions from mixtures [5]. For example, nickel recuperation in the process of lithium-ion accumulators recycling [6], nickel extraction from used catalyst [7], separation of nonferrous metals salts from acids [2], including separation during galvanic wastewaters processing [8], [9], [10], [11], [12], [13]. Using an anion-exchange membrane (AEM) for separating nickel sulfate and sulfuric acid allows to extract about 66-72% of sulfuric acid, depending on conditions of the dialysis procedure [2], [14].
DD eliminates the costs of migration ion transport, which leads to a considerable decrease in energy consumption, compared to electrodialysis (ED) [15]. A simple and unexpansive equipment is another advantage of DD over ED. Neither DC power supply nor polarizing electrodes, which are often made from expensive materials, such as platinized titanium, are required for DD. At the same time, galvanic plants wastewaters processing is relevant both in terms of decreasing environmental pollution and saving non-renewable resources by their extraction and return them to the production. However, there is a problem of achieving sufficient performance for industrial applications. In this regard, the study is aimed to evaluate the efficiency and practical applicability of DD for separating nickel sulfate and sulfuric acid using various types of ion-exchange membranes (IEMs). Only industrially produced IEMs were used for DD. At the same time, the efficiency of using both dialysis IEM and conventional electrodialysis IEMs in DD will be given. In addition, all experiments were performed on a real waste solution of an electroplating facility.

2. Materials and Methods

2.1. Ion-Exschange Membranes

In this work, heterogeneous AEMs made on the basis of strongly basic anion-exchange aminated polystyrene resins cross-linked with divinylbenzene (samples 1, 2, 5, Table 1) were used, as well as a heterogeneous cation-exchange membrane (CEM) based on sulfonated polystyrene cross-linked with divinylbenzene (sample No. 3). In addition, a weakly basic AEM (sample No. 4) and a thin dialysis membrane (sample No. 6) were studied.
The membranes had different thicknesses, reinforcing mesh, ionogenic group types and ion-exchange capacities (Table 1). Samples № 1-3 were provided by MEGA a. s. (Prague, Czech Republic), samples № 4, 5 by LLC Innovation Enterprise Shekinoazot (Tula, Russia), sample № 6 by Tianwei Membrane Corporation Ltd (Weifang High-tech Zone, Shandong, China). Samples 1-5 were conditioned according to a standard procedure, after which CEMs were converted to H+-form and AEMs were converted to OH--form. At this stage, IEM samples were separated to determine the exchange capacity. Sample 6, which was used for dialysis, had not been treated with alkaline solution and had remained in Cl--form after the conditioning. Next, the IEMs were converted into the form of sulfate anions as a result of 48 hours exposure to 1 M sulfuric acid solution and then were washed with deionized water. Ion-exchange capacity was measured by acid-base back titration. For this, sample 6 had been previously converted to OH--form. Moisture content and thickness in the Table 1 are given in the H+-form for CEMs and in the form of sulfate anions for AEMs.

2.2. Method of Dialisys

The study of DD separation process was carried out in a dual chamber flow dialyzer (Figure 1a). To ensure flowability, an inert polyethylene mesh-separator was arranged in each chamber. Circulation of the solution was ensured by a Heidolph Pumpdrive 510 peristaltic pump (Heidolph Instruments GmbH & Co, Schwabach, Germany). The feed tank contained the processed solution, as which a real waste solution of an electroplating facility, containing mostly sulfuric acid and nickel (Table 2) was used. Processed solution was pumped through the first chamber. The total volume of the processed solution was 0.5 L. Deionized water circulated through the second chamber. Since the driving force behind the dialysis process is the concentration gradient between solutions separated by an IEM, portions of deionized water were changed two times per day at the initial stage and once per day at the final stage to sustain it. The volume of each portion of deionized water was 5 L. At certain intervals during the experiment concentrations of sulfuric acid and nickel sulfate in the processed solution and dialysate were measured, as well as volume of the processed solution. Sulfuric acid concentration was measured by EasyPlus Automated Titrator (N.V. Mettler-Toledo S.A., Zaventem, Belgium), using acid-base potentiometric titration. Ni2+ ions concentration was measured using complexometric titration. The solutions’ densities during the dialysis were measured with an areometer.
Fluxes of nickel sulfate and sulfuric acid through the IEM were determined based on the experimental results according to the formula:
j i = Δ n i − n a l i Δ t ⋅ S ,
where i was sulfuric acid or nickel sulfate, Δni was the change in the amount of the i substance in the processed solution over a period of time Δt, n a l i was the amount of the i substance taken with a sample for solution analysis, S was the IEM area. Recovery of sulfuric acid and loss of nickel sulfate ( χ t i ) calculated according to the equation
χ t i = n 0 i − n t i − ∑ 0 t n a l i n 0 i − ∑ 0 t n a l i ⋅ 100 % ,
where t was the time by which the value χ t i was reached, n 0 i and n t i were the amount of the substance of the i-component in the processed solution at the initial time and at time t, respectively. Average flux of sulfuric acid and nickel sulfate ( j t i ¯ ) in time t were calculated by
j t i ¯ = n 0 i − n t i − ∑ 0 t n a l i t ⋅ S .
During the dialysis process, a diffusion flux of an electrolyte (jdif) which was directed to an area with a lower concentration occurs due to a chemical potential gradient (Figure 1b). The drag flux of water was transferred with the electrolyte (jh). So, (jh) has the same direction as a diffusion flux of an electrolyte. In addition, as two solutions with different concentrations were separated by an IEM, an osmotic water flux (jos), opposite to diffusion flux, occurs. Thus, the total volume water flux ( j H 2 O ) to the processed solution chamber was defined as the difference between the osmotic flux and the drag flux
j H 2 O = j o s   −   j h .
Thereby, a change of the processed solution volume was defined by a decrease through a diffusion flux of dissolved substance, which was connected to a transfer of water as a part of hydration shells (drag water flux), and an increase as a result of an osmotic water flux.
The osmotic water flux may be defined as
j o s = P H 2 O ⋅ π s o l − π H 2 O ,
where P H 2 O was the water permeability of the IEM, π s o l и π H 2 O were the osmotic pressures of the processed and dialysate solutions, respectively. The Van't Hoff equation or the equation (6) can be used to calculate the osmotic pressure
π = R T V ¯ H 2 O ⋅ ν m φ M H 2 O ,
where π was the osmotic pressure, R was universal gas constant, T was temperature, V ¯ H 2 O and M H 2 O were partial molar volume and molecular weight of the solvent, ν was the Van’t Hoff coefficient, m was molality of electrolyte (amount of a solute divided by the mass of the solvent), φ was molal osmotic coefficient [16].
However, the task of defining osmotic pressure values in concentrated solutions, in which properties deviate from ideal solutions greatly, was quite complex. It included the problem of determination of activity coefficients and osmotic coefficients of electrolytes. Thermodynamic properties of many electrolyte solutions were defined experimentally, but this data cannot be used for solutions containing more than one electrolyte. Furthermore, theoretical derivation was extremely difficult for all cases but solutions containing either one electrolyte or two binary electrolytes. Thus, work [17] was dedicated to model ion composition of sulfuric acid and defining osmotic coefficients of solutions with concentrations up to 6 mol/L. The authors used method based on modified Debye-Hückel theory, developed in a famous series of studies including applied to multicomponent systems [18], [19], [20], [21]. It was shown, that results obtained using this model agree well with the experimental data. Wherein, this model used a number of fitting parameters and virial coefficients representing forces of ion-ion interactions for a range of electrolytes. However, application of this method was not verified for a system considered in this study. In [22] osmotic pressures were defined according to the Van’t Hoff equation and model [17] for a solution containing copper and nickel sulfates given that their ratio was a constant value. It was shown that the experimental data of osmotic pressure values in these solutions agrees well with the results obtained using model [17] and did not agree with the results calculated according to the Van’t Hoff equation. The problem of defining osmotic coefficients and activity coefficients for individual electrolyte solutions, taking hydration and ion association into account, were solved in [23], [24]. In some studies, the authors disregarded the presence of the second component in the solution and considered the parameters for a solution with one solute [11].
In general, a precise calculation of all the ion forms in concentrated solutions containing several components was a quite difficult task requiring separate consideration. Thus, total concentrations of hydrogen ions, which present as a proton and in a hydro-sulfuric anion in solution, and nickel ions concentration were defined in this study. Thermodynamic properties of the system, such as osmotic pressure or degree of dissociation were not determined.
The estimation of the total water flux was calculated based on the following reasoning. The weight loss of the processed solution was equal to the sum of masses of water, sulfuric acid and nickel sulfate, which transferred to the dialysate. The total water flux was calculated using the formula
j H 2 O = Δ V ⋅ ρ s − m H 2 S O 4 − m N i S O 4 ρ H 2 O ⋅ S ⋅ Δ t ,
where ΔV was the change of processed solution volume during the time Δt, ρs was the processed solution density, ρ H 2 O was the water density (1000 kg/m3), m H 2 S O 4 and m N i S O 4 were the masses of sulfuric acid and nickel sulfate which transferred to the dialysate during the time Δt. The water drag flux was calculated using the formula
j h = j H 2 S O 4 ⋅ 2 h H + + h S O 4 2 − + j N i S O 4 ⋅ h N i 2 + + h S O 4 2 − ⋅ M H 2 O ρ H 2 O ,
where h H + , h S O 4 2 − и h N i 2 + were the solvation number of the H+, S O 4 2 − and Ni2+ ions. A similar approach was used to estimate the water drag flux carried in the hydration shell of ions was used in [11]. The adopted solvation numbers were 2 for H+, 5 for S O 4 2 − and 5 for Ni2+ [25], [26], [27], [28]. The osmotic flux was calculated as a difference between total water flux and drag water flux using the formula (4).
Formula (5) and Van’t Hoff equation could be used to estimate P H 2 O value
P H 2 O = j o s R ⋅ T ⋅ Δ C ,
where ΔC was the difference of ions concentration between the processed solution and dialysate, which was calculated using the sulfuric acid and nickel sulfate concentration and the Van’t Hoff coefficients. According to [29] the P H 2 O was determined by formula
P H 2 O = D H 2 O ⋅ C H 2 O ,   1 m ⋅ V ¯ H 2 O R ⋅ T ⋅ l ,
where D H 2 O was the water diffusion coefficient in the membrane, C H 2 O ,   1 m was the water concentration inside membrane at the feed interface. Formula (8) showed that the water permeability included membrane thickness. It allowed to compare the membrane water permeability for the reverse osmosis membranes, ultra- and nanofiltration membranes, which had a similar thickness [29]. However, in presented study IEMs had different thicknesses. It was well known, that the diffusion flux might be determined using formula
j i = P i ⋅ Δ C l ,
where Pi was the coefficient of membrane diffusion permeability [29]. Then the water permeability coefficient P H 2 O * was proposed to compare the properties of membranes with different thicknesses. P H 2 O * could be calculated by the formula
P H 2 O * = j o s ⋅ l R ⋅ T ⋅ Δ C

3. Results

3.1. Sulfuric Acid and Nickel Sulfate Transfer through Membranes

The sulfuric acid and nickel sulfate fluxes defined in the process of DD for IEMs of different types are shown in Figure 2. Analysis of obtained results shows that an essential difference occurs in the of the values of fluxes passing through AEMs and CEM. Thus, sulfuric acid practically is not transferred through the CEM in the presence of comparable nickel sulfate flux (Figure 2, grey squares). The results obtained agree well with the results of studying heterogeneous CEMs diffusion permeability showing that, with the same concentrations, sulfuric acid flux is lower than sodium chloride flux [30]. During dialysis, a decrease in the flux of nickel sulfate through the CEM from 0.04 to 0.02 mol/(m2 h) is observed, while its concentration in the processed solution decreases by 4 times, to 0.07 mol/L. The flux of sulfuric acid also decreases from 0.09 to 0.01 mol/(m2·h), which is accompanied by a decrease in the concentration of sulfuric acid in the processed solution to 0.9 mol/L. So, these components cannot be separated, which makes it impractical to use a CEM for this process.
The highest values of the flux and transfer rate of sulfuric acid are naturally observed for the thinnest dialysis TWDDA3 membrane (Figure 2a). As the membrane thickness increases, the H2SO4 transfer rate decreases. Ralex AMHPES, Ralex AMHPP and MA-41 membranes, which differ only in the material of the reinforcing mesh and the degree of grinding of the ion-exchange resin, have very similar characteristics of the DD process. An interesting fact is that the rate of transfer of sulfuric acid through the MA-40 membrane was the lowest compared to all other AEMs. Perhaps this is due to the fact that the value of the ion exchange capacity of this membrane is higher than that of all other studied samples of AEMs. Moreover, in acidic solutions, all ionogenic groups of the MA-40 membrane will be in the protonated state, in contrast to solutions with a neutral or alkaline environment. This might lead to a significant difficulty in the transport of co-ions through the membrane compared to membranes with a lower exchange capacity, which explains the low diffusion transfer rates.
The nickel sulfate flux through the AEMs does not exceed 0.025 mol/m2 h for all samples, except for the dialysis TWDDA3 membrane (Figure 2c). For this membrane, an almost linear increase with time in the flux of nickel sulfate is observed value of 0.08 mol/m2·h (Figure 2c), which is significantly higher compared to all other samples. The dependences of the nickel sulfate flux on time for almost all membranes have an increasing character. This is due to a decrease in the concentration of sulfuric acid in the processed solution as a result of its transfer through the membrane, resulting in an increase in the flux of nickel sulfate. This effect is especially pronounced for the TWDDA3 membrane. The concentration of sulfuric acid in the processed solution decreases very quickly (Figure 3, curve 3), and if at the beginning of the experiment it is significantly, 6-9 times higher than the concentration of nickel sulfate, then after 27 hours the ratio becomes almost the same and further in solution, the concentration of nickel sulfate begins to exceed the concentration of sulfuric acid, as a result of which the transfer of nickel sulfate increases. In this case, the concentration of nickel sulfate changes little during the experiment (Figure 3, curves 2, 4).
The concentration ratios for all the studied membranes change in a similar way, only the rate of decrease in the concentration of sulfuric acid differs (Table 3). Thus, the time to reach the same ratio of the concentrations of sulfuric acid and nickel sulfate in the processed solution for the MA-41 membrane is about 150 h, and for the TWDDA3 membrane, about 27 h (Figure 3). At the same time, for all AEMs, the flux of nickel sulfate remains significantly lower than the flux of sulfuric acid (Figure 2, Table 3).
Based on the experimental data obtained, the time of reaching 80, 85, 90 and 95% recovery of sulfuric acid, the loss of nickel sulfate by this time, and the average fluxes of sulfuric acid and nickel sulfate were calculated (Table 3, Figure 4). The time of achieving the desired levels of sulfuric acid recovery is comparable for both Ralex membranes and the MA-41 membrane and is 100-170 hours. The longest recovery is achieved on the MA-40 membranes (from 180 to 300 hours) and the dialysis TWDDA3 membrane is the most effective. The time of reaching 95% sulfuric acid recovery is 30 hours.
For all membranes, except for Ralex AMHPES, nickel sulfate losses increase insignificantly with an increase in the degree of sulfuric acid recovery from 80 to 95% (Figure 4b). At the same time, the highest losses of nickel sulfate are observed for membranes MA-40 (up to 16%) and MA-41 (11-15%), the lowest – for the TWDDA3 sample (does not exceed 1 %) (Figure 4b, Table 3). However, for the Ralex AMHPES membrane, a sharp increase in the loss of nickel sulfate by almost 3 times (from 3 to 9%) is observed with an increase in the degree of sulfuric acid recovery from 80 to 95%.
The values of the average fluxes of sulfuric acid naturally decrease with increasing dialysis time due to a decrease in the concentration gradient between the chambers, while the change in the values of the average fluxes of nickel sulfate from time for different membranes does not have a general pattern (Table 3). With the increase in dialysis time, the flux of nickel sulfate is expected to increase due to a decrease in the flux of sulfuric acid and an increase in the concentration of nickel sulfate in the processed solution. Indeed, for TWDDA3 and Ralex AMHPES membranes, an increase in the average flux of nickel sulfate by 10 and 7 times is observed with an increase in the degree of sulfuric acid recovery from 80 to 95%. In this case, some, not proportional to the change in flux, increase in the concentration of nickel sulfate in solution is observed. However, for the remaining three membranes, there is a tendency towards a decrease in the average flux, which is most pronounced for the Ralex AMHPP and MA-41 membranes. At the same time, the concentration of nickel sulfate, as in the case of TWDDA3 and Ralex AMHPES membranes, increases with the increase in time of the dialysis process. Separately, it should be noted that in the case of the MA-41 membrane, the concentration of nickel sulfate in the processed solution increases very slightly. So, if for the rest of the membranes there is an increase in concentration from the initial value of 0.30 M to 0.37–0.40 M, for the MA-41 membrane, the concentration of nickel sulfate does not exceed 0.31 M. Such features of the change in the value of the average flux of nickel sulfate and the change in the content of nickel sulfate connected with water transport in the DD process, which will be discussed below. Thus, the task of separating sulfuric acid and nickel sulfate is achieved using all AEMs, but the most effective is the thin dialysis TWDDA3 membrane.

3.2. Water Transport during Diffusion Dialysis

The phenomenon of “positive” and “negative” osmosis is described in [31]. It consists in an abnormally high transfer of the solvent or in a transfer of a solvent from a more concentrated solution to a more diluted one through an IEM during dialysis. The reason for this phenomenon is that in the process of dialysis, due to the difference in the mobilities of the counter- and co-ions at the outer boundaries of the membrane / electrolyte solution, an electric potential difference is formed, leading to the flow of the solution inside the membrane. This flow will be directed towards the concentrated solution in the case of a more mobile counter-ion (“positive osmosis”). Conversely, in the case of a more mobile co-ion, the direction of the solution flow inside the membrane will be towards the diluted solution (“negative osmosis”).
Figure 5 shows the total water flux during dialysis for the studied membranes. Negative flux values indicate that the osmotic flux exceeds the drag water flux and the amount of solvent in the processed solution increases. It is observed in the case of a CEM (Figure 5b).
It is shown that during the entire process of dialysis, osmosis exceeds the reverse drag water flux. The value of the osmotic flux decreases by 3 times, which is associated with a decrease in the concentration gradient between the processed solution and the diluted one. At the same time, the observed result does not contradict the concept of “positive and negative osmosis”. In the case of a CEM, the co-ion is less mobile and thus the direction of the flow of the solution inside the membrane is directed towards a more concentrated solution. Thus, the observed decrease in the concentration of sulfuric acid in the processed solution is the result of not only its diffusion transfer through the membrane, but also dilution due to the osmotic transfer of water from a diluted to a concentrated electrolyte solution.
In the case of AEMs, the dependences have a different shape. For the dialysis TWDDA3 membrane, there is a decrease in the total water flux by more than 21 times up to negative values. Negative values are reached after 40 hours of the DD, which corresponds to 97% removal of sulfuric acid from the processed solution and a residual concentration of 0.22 mol/L sulfuric acid and 0.39 mol/L nickel sulfate. At the same time, the dependence of the nickel sulfate concentration on the dialysis time has an extremum, and the time of reaching the maximum concentration of nickel sulfate in the processed solution (about 25 hours) apparently corresponds to the moment when the osmotic flux begins to increase and dominate over the drag water flux and “negative osmosis” due to the higher mobility of H+ co-ions compared to sulfate anions. In general, during dialysis, there is a slight increase in the concentration of nickel sulfate, associated with a decrease in the amount of solvent in the processed solution.
For the MA-40 membrane, there is an increase in the amount of total water flux with the time of the process from negative values at the beginning of the experiment, when the osmotic transfer is higher than the transfer of water with solutes, to positive ones. Until the end of the experiment, the total water flux remains positive, which indicates the predominant contribution of “negative osmosis" and drag water flux. It leads to the transfer of the solvent from a more concentrated to a less concentrated solution against the osmotic flux. For other AEMs (Ralex AMHPES, Ralex AMHPP and MA-41 membranes), the dependence of the total water flux on the time of the dialysis process is extremal. At the same time, a significant difference in the values of the total water fluxes through AEMs with similar composition and structure (MA-41 membrane and both Ralex ones) is observed. Thus, in the case of the MA-41 membrane, the maximum value of the total water flux is 3.5·10-5 m3/(m2·h), while for Ralex AMHPES and Ralex AMHPP membranes it is 7.1·10-5 and 8.5·10-5 m3/(m2·h), respectively. It should also be noted that the final composition of the processed solution is approximately the same for all the studied membranes.
Perhaps, the kinetic factor is of great importance: due to the high rate of transfer of sulfuric acid through the thin dialysis TWDDA3 membrane, the counter osmotic flux of water is inhibited. Another extreme case is the Ralex CMHPES membrane, for which the total fluxes of sulfuric acid and nickel sulfate are very low and the osmotic flux leads to a significant increase in the amount of the solvent in the processed solution. The remaining membranes occupy an intermediate position and the amount of the total water flux correlates with the amount of sulfuric acid flux through them.
Estimation of the water permeability coefficient of the studied membranes shows that, as expected, the highest values are found for the CEM (Figure 6). In this case, the dependence of the water permeability coefficient on the concentration difference for the CEM is practically absent. So, the dependences for AEMs are increasing.
Comparison of the water permeability of AEMs shows that the dialysis TWDDA3 membrane and Ralex AMHPES membrane have a slightly higher permeability than others. However, the values of the water permeability of all AEMs are similar.

4. Conclusions

The DD of the real waste solution of an electroplating facility, containing mostly sulfuric acid and nickel sulfate using different ion-exchange membrane types is studied. The sulfuric acid and the nickel sulfate fluxes are similar for the cation-exchange membrane. Besides, the total water flux through the cation-exchange membrane directs opposite to the diffusion fluxes and the volume of the processed solution is increased by 3 times. Thus, the use of a cation-exchange membrane in the DD process does not allow the separation of sulfuric acid and nickel sulfate. However, using the anion-exchange membranes in the DD process provides the separation of sulfuric acid and nickel sulfate. As expected, the thinnest dialysis membrane is the most effective. The time of reaching 95% recovery of sulfuric acid is 30.5 h which is about 5 times less than for the next most efficient Ralex AMHPES membrane. The weakly basic anion-exchange membrane MA-40 is less effective than other anion-exchange membranes. The total water fluxes and diffusion fluxes through all the anion-exchange membranes are directed equally most of the DD time. The values of the water permeability coefficient of ion-exchange membranes are estimated. The highest values of the water permeability coefficient are observed for the cation-exchange membrane. The values of the water permeability coefficient of all anion-exchange membranes are similar.
In general, it is found that the use of all strongly basic anion-exchange membranes makes the separation of sulfuric acid and nickel sulfate by diffusion dialysis possible. Despite the longer time required to achieve a high degree of separation compared to using a dialysis membrane, the use of conventional electrodialysis membranes may be economically justified due to their lower cost.

Author Contributions

Conceptualization, S.L. and N.L.; methodology, S.L. and N.L.; formal analysis, S.L. and N.L.; investigation, N.K., N.R. and J.L; writing—original draft preparation, S.L., N.L. and J.L.; writing—review and editing, S.L. and N.L.; visualization, N.L.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, project number FZEN-2020-0022.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors are grateful to Dr. O.A. Demina and Dr. I.V. Falina for their help in discussing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Koros, W.J.; Ma, Y.H.; Shimidzu, T. Terminology for membranes and membrane processes (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 1479–1489. [Google Scholar] [CrossRef]
  2. Luo, J.; Wu, C.; Xu, T.; Wu, Y. Diffusion dialysis-concept, principle and applications. J. Memb. Sci. 2011, 366, 1–16. [Google Scholar] [CrossRef]
  3. Vasil’eva, V.I.; Vorob’Eva, E.A. Dynamics of the separation of amino acid and mineral salt in the stationary dialysis of solutions with an MK-40 profiled sulfo group cation exchange membrane. Russ. J. Phys. Chem. A 2012, 86, 1726–1731. [Google Scholar] [CrossRef]
  4. Vasil’eva, V.; Goleva, E.; Pismenskaya, N.; Kozmai, A.; Nikonenko, V. Effect of surface profiling of a cation-exchange membrane on the phenylalanine and NaCl separation performances in diffusion dialysis. Sep. Purif. Technol. 2019, 210, 48–59. [Google Scholar] [CrossRef]
  5. Zhang, C.; Zhang, W.; Wang, Y. Diffusion dialysis for acid recovery from acidic waste solutions: Anion exchange membranes and technology integration. Membranes (Basel). 2020, 10, 1–23. [Google Scholar] [CrossRef]
  6. Sonoc, A.C.; Jeswiet, J.; Murayama, N.; Shibata, J. A study of the application of Donnan dialysis to the recycling of lithium ion batteries. Hydrometallurgy 2018, 175, 133–143. [Google Scholar] [CrossRef]
  7. Bendova, H.; Weidlich, T. Application of diffusion dialysis in hydrometallurgical separation of nickel from spent Raney Ni catalyst. Sep. Sci. Technol. 2018, 53, 1218–1222. [Google Scholar] [CrossRef]
  8. Ng, P.K.; Snyder, D. Mass Transport Characterization of Donnan Dialysis: the Nickel Sulfate System. Proc. - Electrochem. Soc. 1981, 81–2, 71–87. [Google Scholar] [CrossRef]
  9. Yan, J.; Wang, H.; Fu, R.; Fu, R.; Li, R.; Chen, B.; Jiang, C.; Ge, L.; Liu, Z.; Wang, Y.; et al. Ion exchange membranes for acid recovery: Diffusion Dialysis (DD) or Selective Electrodialysis (SED)? Desalination 2022, 531. [Google Scholar] [CrossRef]
  10. Merkel, A.; Čopák, L.; Dvořák, L.; Golubenko, D.; Šeda, L. Recovery of spent sulphuric acid by diffusion dialysis using a spiral wound module. Int. J. Mol. Sci. 2021, 22. [Google Scholar] [CrossRef]
  11. Ruiz-Aguirre, A.; Lopez, J.; Gueccia, R.; Randazzo, S.; Cipollina, A.; Cortina, J.L.; Micale, G. Diffusion dialysis for the treatment of H2SO4-CuSO4 solutions from electroplating plants: Ions membrane transport characterization and modelling. Sep. Purif. Technol. 2021, 266, 118215. [Google Scholar] [CrossRef]
  12. Gueccia, R.; Randazzo, S.; Chillura Martino, D.; Cipollina, A.; Micale, G. Experimental investigation and modeling of diffusion dialysis for HCl recovery from waste pickling solution. J. Environ. Manage. 2019, 235, 202–212. [Google Scholar] [CrossRef] [PubMed]
  13. Gueccia, R.; Aguirre, A.R.; Randazzo, S.; Cipollina, A.; Micale, G. Diffusion dialysis for separation of hydrochloric acid, iron and zinc ions from highly concentrated pickling solutions. Membranes (Basel). 2020, 10, 1–17. [Google Scholar] [CrossRef]
  14. Xu, T.; Weihua, Y. Tuning the diffusion dialysis performance by surface cross-linking of PPO anion exchange membranes—simultaneous recovery of sulfuric acid and nickel from electrolysis spent liquor of relatively low acid concentration. J. Hazard. Mater. 2004, 109, 157–164. [Google Scholar] [CrossRef] [PubMed]
  15. Luo, J.; Wu, C.; Xu, T.; Wu, Y. Diffusion dialysis-concept, principle and applications. J. Memb. Sci. 2011, 366, 1–16. [Google Scholar] [CrossRef]
  16. Robinson, R.A.; Stokes, R.H. Electrolyte solutions. The Measurement and Interpretation of Conductance, Chemical Potential and Diffusion in Solutions of Simple Electrolytes.; Second edi.; Butterworths Scientific Publications: London, 1959. [CrossRef]
  17. Pitzer, K.S.; Roy, R.N.; Silvester, L.F. Thermodynamics of Electrolytes. 7. Sulfuric Acid. J. Am. Chem. Soc. 1977, 99, 4930–4936. [Google Scholar] [CrossRef]
  18. Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1972, 77, 268–277. [Google Scholar] [CrossRef]
  19. Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J. Phys. Chem. 1973, 77, 2300–2308. [Google Scholar] [CrossRef]
  20. Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. III. Activity and osmotic coefficients for 2-2 electrolytes. J. Solution Chem. 1974, 3, 539–546. [Google Scholar] [CrossRef]
  21. Pitzer, K.S.; Kim, J.J. Thermodynamics of Electrolytes. IV. Activity and Osmotic Coefficients for Mixed Electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef]
  22. Van Gauwbergen, D.; Baeyens, J.; Creemers, C. Modeling osmotic pressures for aqueous solutions for 2-1 and 2-2 electrolytes. Desalination 1997, 109, 57–65. [Google Scholar] [CrossRef]
  23. Sergievskii, V. V.; Rudakov, A.M. Dependence of the osmotic coefficients and average ionic activity coefficients on hydrophobic hydration in solutions. Russ. J. Phys. Chem. A 2016, 90, 1567–1573. [Google Scholar] [CrossRef]
  24. Rudakov, A.M.; Sergievskii, V. V.; Nagovitsyna, O.A. Dependences of the osmotic coefficients of aqueous calcium chloride solutions on concentration at different temperatures. Russ. J. Phys. Chem. A 2017, 91, 2361–2365. [Google Scholar] [CrossRef]
  25. Adapa, S.; Malani, A. Cation hydration by confined water and framework-atoms have crucial role on thermodynamics of clay swelling. Sci. Rep. 2022, 12, 1–19. [Google Scholar] [CrossRef] [PubMed]
  26. Kiriukhin, M.Y.; Collins, K.D. Dynamic hydration numbers for biologically important ions. 2002, 99, 155–168. [CrossRef]
  27. Ohtaki, H.; Radnai, T. Structure and Dynamics of Hydrated Ions. Chem. Rev. 1993, 93, 1157–1204. [Google Scholar] [CrossRef]
  28. Vchirawongkwin, V.; Rode, B.M.; Persson, I. Structure and dynamics of sulfate ion in aqueous solution-an ab initio QMCF MD simulation and large angle X-ray scattering study. J. Phys. Chem. B 2007, 111, 4150–4155. [Google Scholar] [CrossRef] [PubMed]
  29. Mulder, M. Basic Principles of Membrane Technology; 2nd ed.; Springer Dordrecht: Dordrecht, 1996; ISBN 978-0-7923-4248-9.
  30. Demina, O.A.; Kononenko, N.A.; Falina, I. V.; Demin, A. V. Theoretical estimation of differential coefficients of ion-exchange membrane diffusion permeability. Colloid J. 2017, 79, 317–327. [Google Scholar] [CrossRef]
  31. Schlögl, R. Elektrodiffusion in freier Lösung und geladenen Membranen. Zeitschrift fur Phys. Chemie 1889, 1, 305–339. [Google Scholar] [CrossRef]
Preprints 67579 g001
Figure 1. Scheme of DD set-up (a) and scheme of electrolyte and water fluxes in the process of DD (b).
Figure 1. Scheme of DD set-up (a) and scheme of electrolyte and water fluxes in the process of DD (b).
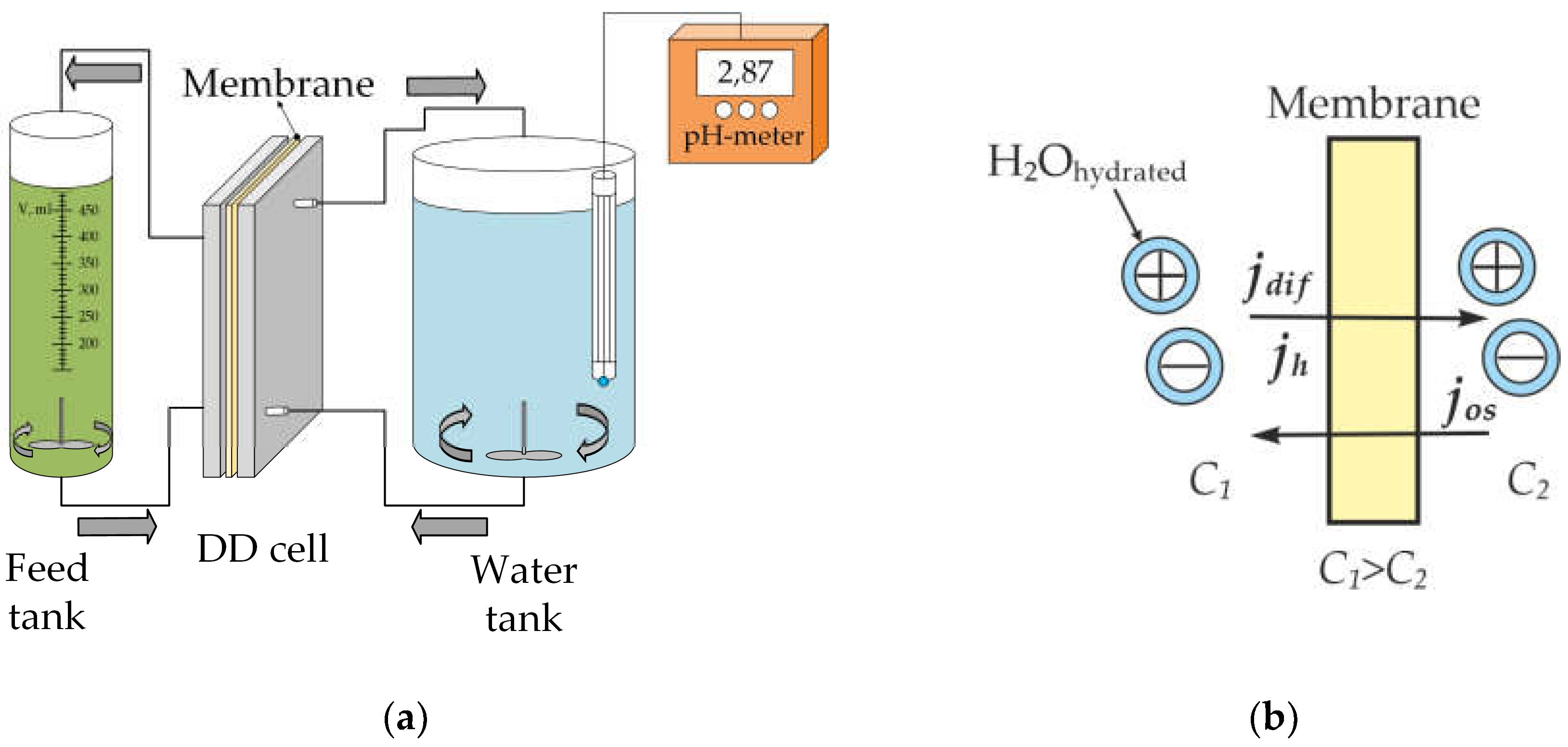
Preprints 67579 g001
Preprints 67579 g002
Figure 2. Kinetic dependence of the fluxes of sulfuric acid (a), the initial section of this dependence (b) and nickel sulfate (c) for membranes of various types during DD. The data caption on all figures corresponds to the caption given in (a).
Figure 2. Kinetic dependence of the fluxes of sulfuric acid (a), the initial section of this dependence (b) and nickel sulfate (c) for membranes of various types during DD. The data caption on all figures corresponds to the caption given in (a).
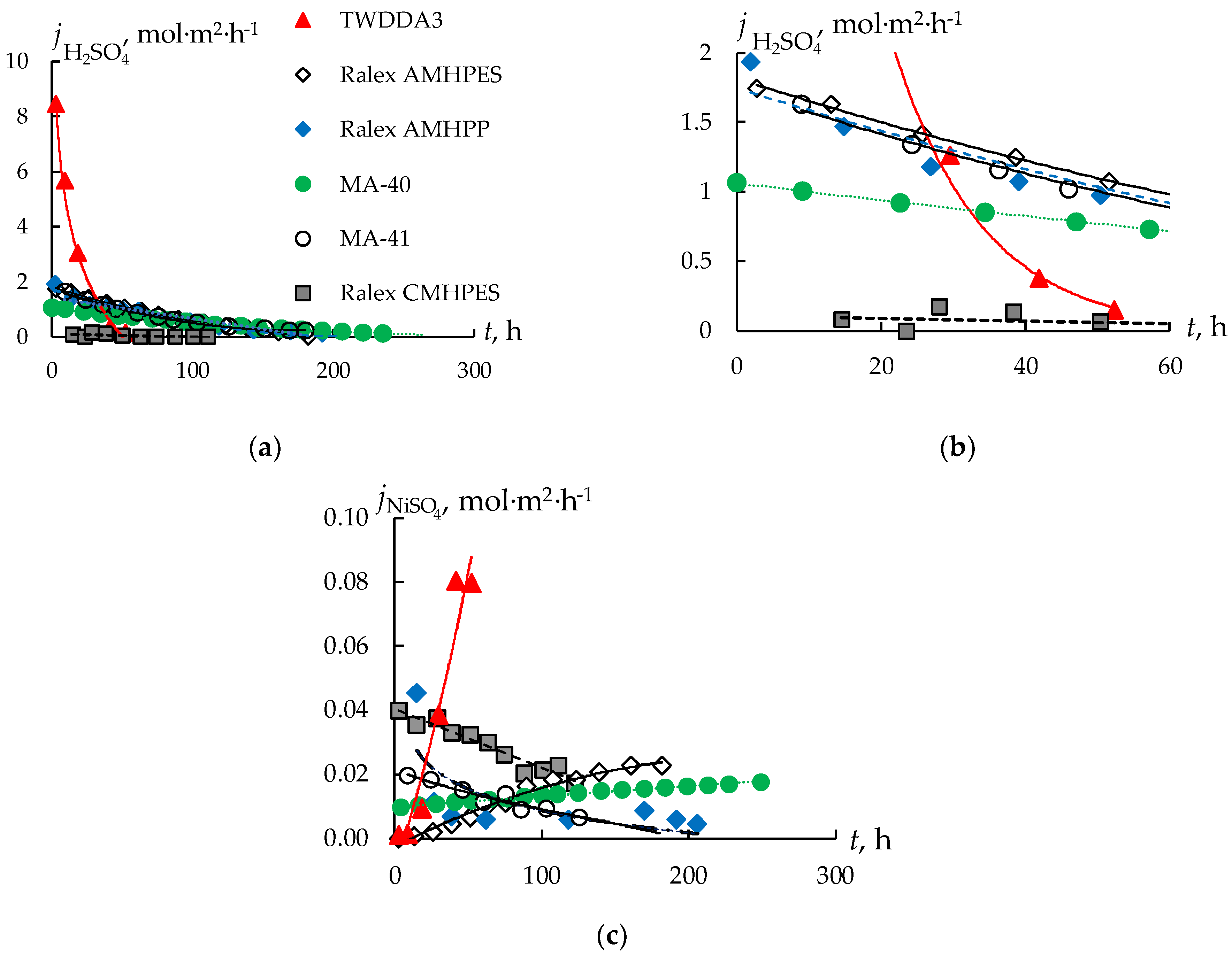
Preprints 67579 g002
Preprints 67579 g003
Figure 3. Kinetic dependences of the concentration of sulfuric acid (1, 3) and nickel sulfate (2, 4) in the processed solution during the DD process with the MA-41 membrane (1, 2) and TWDDA3 membrane (3, 4).
Figure 3. Kinetic dependences of the concentration of sulfuric acid (1, 3) and nickel sulfate (2, 4) in the processed solution during the DD process with the MA-41 membrane (1, 2) and TWDDA3 membrane (3, 4).
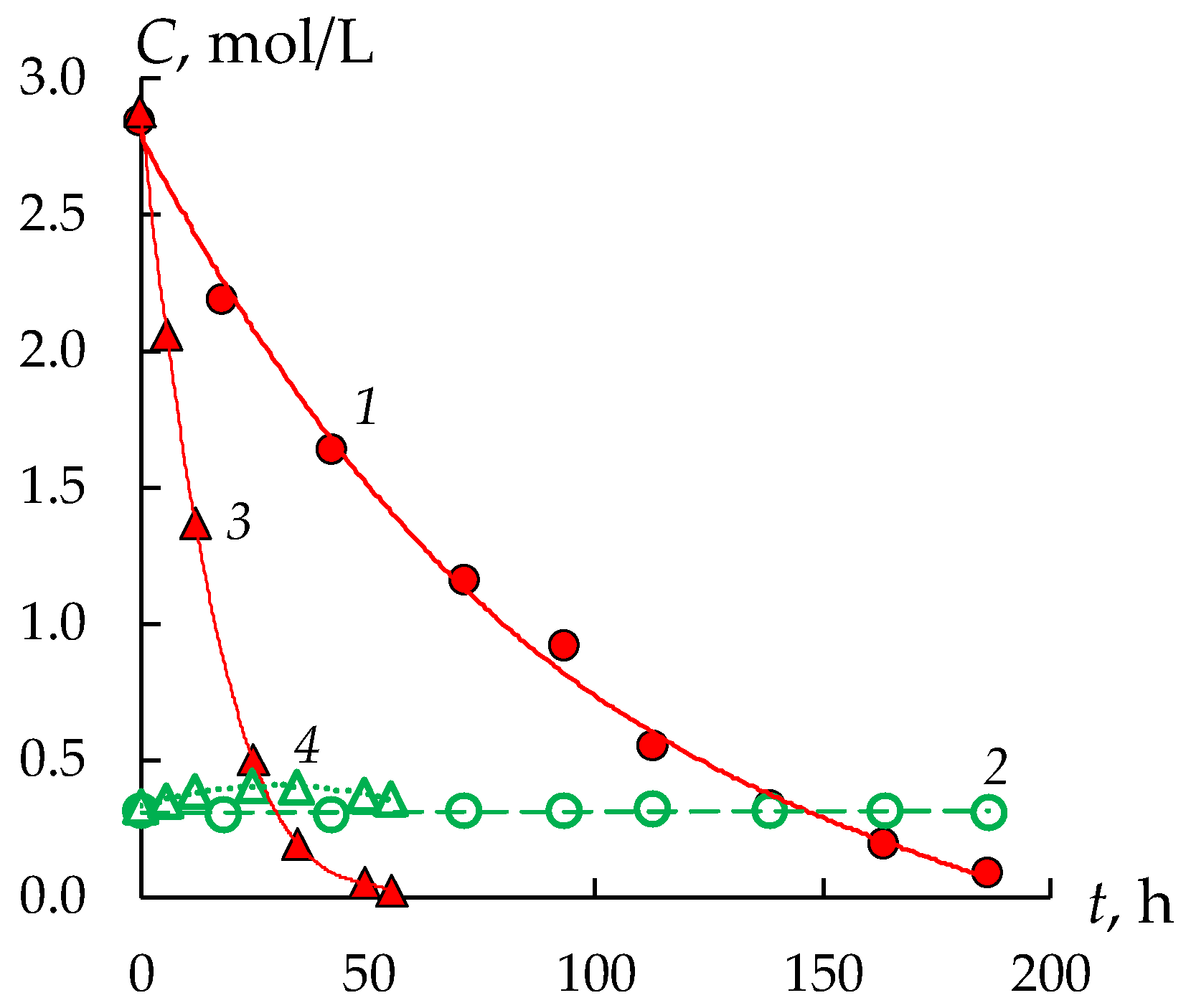
Preprints 67579 g003
Preprints 67579 g004
Figure 4. The time of reaching 80-95% recovery of sulfuric acid (a) and the loss of nickel sulfate (b) from the solution for the studied membranes. The signature of the data in the figures corresponds to the signature given in (a).
Figure 4. The time of reaching 80-95% recovery of sulfuric acid (a) and the loss of nickel sulfate (b) from the solution for the studied membranes. The signature of the data in the figures corresponds to the signature given in (a).
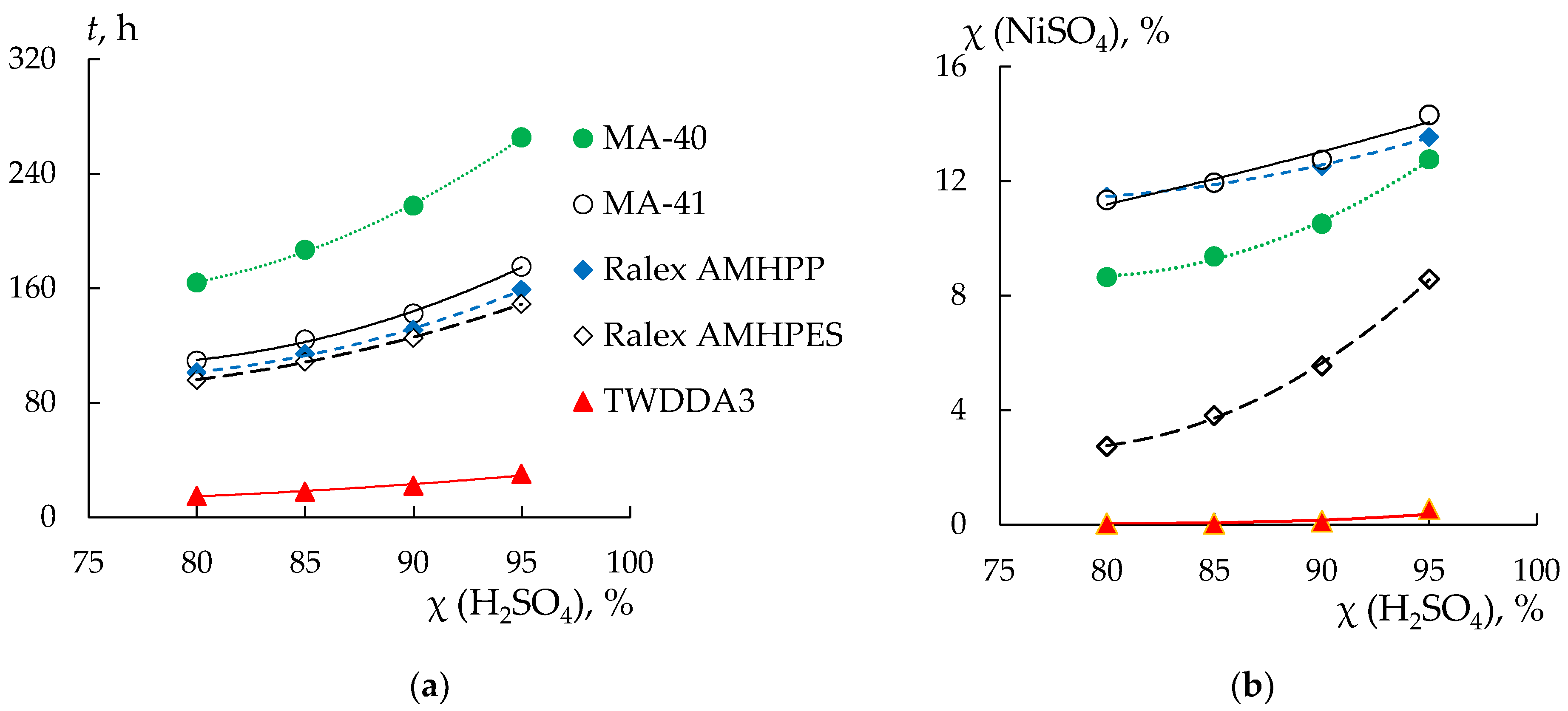
Preprints 67579 g004
Preprints 67579 g005
Figure 5. Total water flux through different types of AEMs (a) and CEM (b) during dialysis.
Figure 5. Total water flux through different types of AEMs (a) and CEM (b) during dialysis.
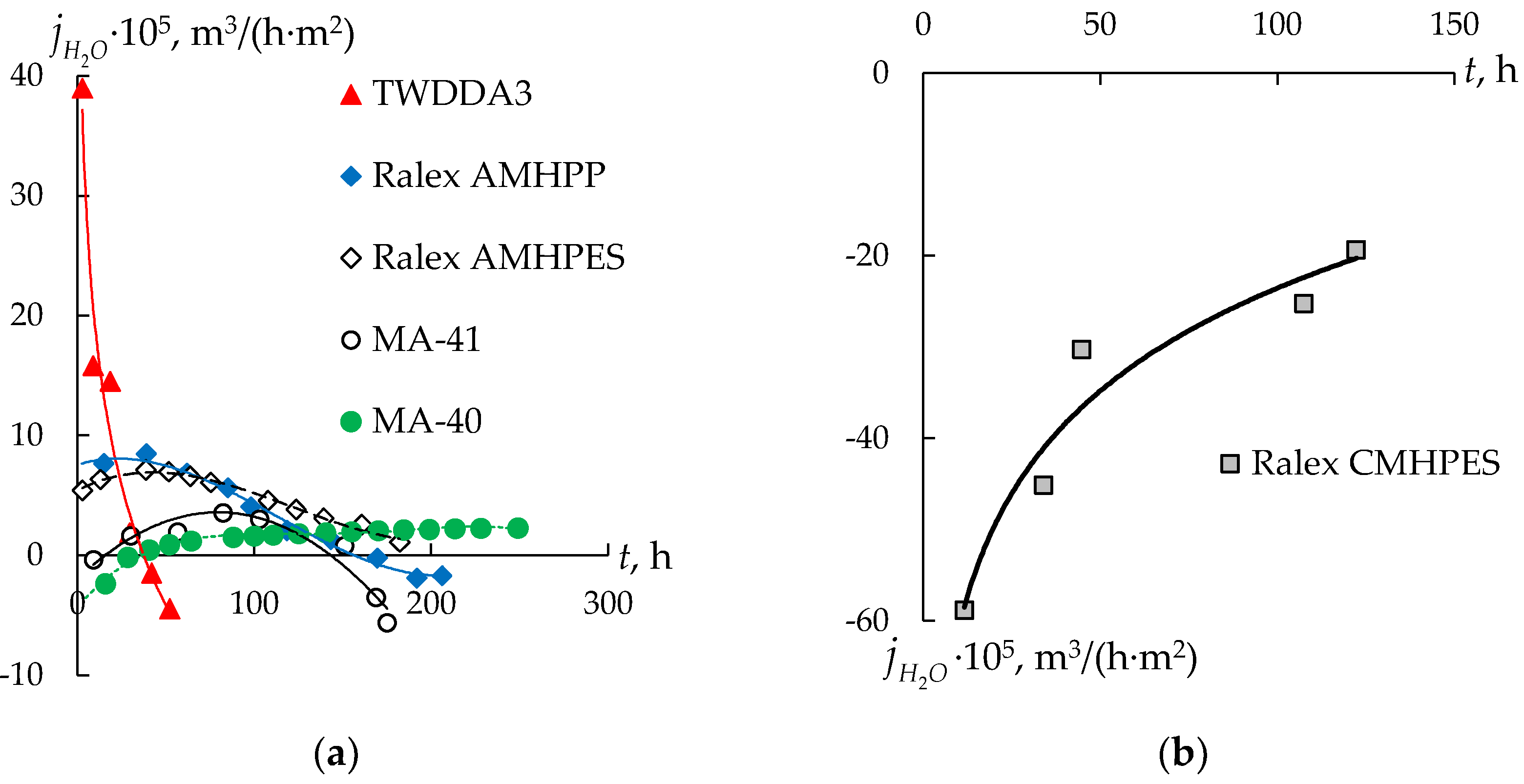
Preprints 67579 g005
Preprints 67579 g006
Figure 6. Water permeability coefficient of the membranes depending on the concentration difference (a) and values of the membranes water permeability coefficient at ΔС = 3.5 mol/L (b).
Figure 6. Water permeability coefficient of the membranes depending on the concentration difference (a) and values of the membranes water permeability coefficient at ΔС = 3.5 mol/L (b).
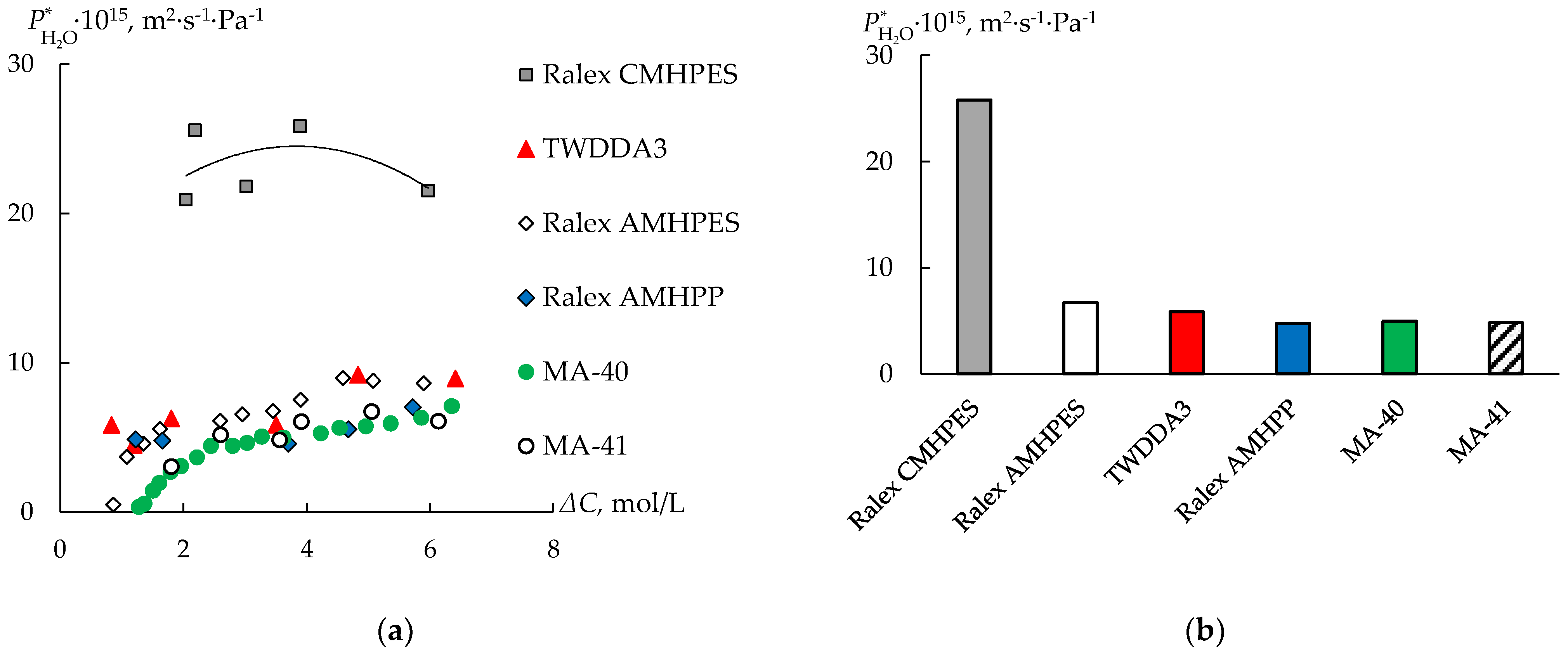
Preprints 67579 g006
Table 1. The physical-chemical properties of IEMs.
Table 1. The physical-chemical properties of IEMs.
Sample No. Membrane Ionogenic groups Reinforcing
mesh		 Q, mmol/g l, μm
1 Ralex AMHPES quaternary
amino groups		 polyester 1.05 550
2 Ralex AMHPP quaternary
amino groups		 polypropylene 0.97 550
3 Ralex CMHPES sulfo groups polyester 1.16 530
4 МА-40 secondary and
tertiary amino groups		 nylon 2.15 520
5 МА-41 quaternary
amino groups		 nylon 0.54 420
6 TWDDA3 quaternary
amino groups		 Polyphenylene
oxide		 0.49 145
Table 2. The composition of the waste solution*.
Table 2. The composition of the waste solution*.
Substance Concentration, g/L
Н2SO4 252.3
Ni 20.9
Zn 2.3
Fe 1.08
Cu 0.90
Sn 0.080
Sb 0.050
Cd 0.045
Pb 0.015
As 0.003
* Data provided by the plant. The content of metals takes into account all ionic forms in terms of a simple substance.
Table 3. Average fluxes of sulfuric acid (mol·m-2·s-1) and nickel sulfate through various AEMs upon reaching 80-95% recovery of sulfuric acid from solution.
Table 3. Average fluxes of sulfuric acid (mol·m-2·s-1) and nickel sulfate through various AEMs upon reaching 80-95% recovery of sulfuric acid from solution.
χ (H2SO4), % 80 85 90 95
TWDDA3
H2SO4 4.63 4.64 4.48 3.95
NiSO4 0.001 0.003 0.004 0.010
MA-41
H2SO4 1.02 0.96 0.88 0.77
NiSO4 0.016 0.016 0.015 0.010
MA-40
H2SO4 0.66 0.62 0.56 0.49
NiSO4 0.0003 0.001 0.002 0.003
Ralex AMHPES
H2SO4 1.12 1.06 0.98 0.87
NiSO4 0.001 0.003 0.004 0.007
Ralex AMHPP
H2SO4 1.08 1.03 0.94 0.82
NiSO4 0.012 0.011 0.010 0.010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated