Prerpints.org logo
Preprint
Article

Predicting Earthquake-Induced Landslides by Using a Stochastic Modelling Approach Which Combines Preparatory and Triggering Factors: A Case Study of the Coseismic Landslides Occurred on January and February 2001 in El Salvador, CA

Altmetrics

Downloads

177

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 January 2023

Posted:

19 January 2023

You are already at the latest version

Alerts
Abstract
In January and February 2001, El Salvador was hit by two strong earthquakes that triggered thousands of landslides, causing 1,259 fatalities and extensive damage. The analysis of aerial and SPOT-4 satellite images taken a few days after the events allowed us to map 6,491 coesismic landslides, which occurred in 14 study areas extending for about 400 km2. Four different Multivariate Adaptive Regression Splines (MARS) models were produced by using different covariate sets and landslide inventories, the latter containing the slope failures triggered by an extreme rainfall event of November 2009 and those induced by the earthquakes of 2001. Moreover, two validation scenarios were employed, including the 25% and 95% of the mapped landslides, respectively. The results of our experiment revealed that: (i) MARS algorithm provides reliable predictions of coesismic landslides; (ii) models calibrated with rainfall-induced landslides predict with acceptable accuracy landslides caused by deep earthquakes and distributed over vast areas; (iii) the best accuracy is achieved by models trained with both preparatory and trigger variables; (iv) a small portion of the landslides produced by an earthquake can be used to calibrate MARS predictive models that help to identify slopes where yet unreported landslides may have occurred.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

In El Salvador, CA, landslides are among the most destructive natural processes, which can cause mass fatalities and devastation in the built environment [1]. They may occur either due to heavy rains (rainfall-induced landslides) or as a secondary event of an earthquake (earthquake-induced landslides). The extreme rainfall events that frequently affect the Central American region are indeed responsible for activating gravitational phenomena consisting of shallow and fast-moving flow landslides that may cause severe economic damage and fatalities [2]. Additionally, seismic events can produce hundreds to thousands of gravitational phenomena, which may cause more damage and victims than the earthquake itself, a situation that occurs in the country, often affected by high-intensity phenomena. Indeed, among the various secondary effects of a seismic event (i.e., tsunamis, fires and liquefaction phenomena), 71.1% of deaths worldwide result from landslides [3]. Landslides usually occur during or shortly after a seismic event and have different spatial distributions according to slope gradient, lithology, earthquake magnitude and hypocentral and epicentral distances [4,5,6,7,8]. A number of studies observed a correlation between earthquake intensity and landslide occurrence [9,10]. Keefer identified a critical Richter Magnitude of 4.0 and observed that the area affected by gravitational phenomena grows progressively up to 500,000 km2 for an earthquake having a magnitude of 9.2 [9]. However, this correlation may present exceptions. A landslide indeed could be initiated even by a weak shaking if the failure of a slope is imminent before the seismic event or if the involved material includes weakly cemented and/or incoherent rocks. Volcanic rocks, widely distributed across the country, are among these lithologies, as they are usually characterized by higher mobility than non-volcanic rocks due to differences in material properties such as granularity, collapsibility and water content [11,12]. These geological conditions can significantly increase the frequency of gravitational phenomena triggered and the areas affected by landslides compared to areas that experienced comparable magnitudes [13,14].
Damage due to coseismic landslides is closely related to economic development and the ability to prevent and reduce disasters. Developed countries indeed have the economic and scientific resources to project and manage structures designed to contain blocks of rock and stop or divert both slow and rapid flows [15,16]. They may also activate direct or indirect protection and alarm systems to favor a prompt and rapid general evacuation. Projecting effective defensive engineering structures and alarm systems requires knowing where landslides are more likely to occur. This information, which is also fundamental for land use planning aimed at mitigating landslide risk, is provided by landslide susceptibility maps.
Landslide susceptibility reflects the probability of slope failure occurrence in a given area [17,18,19]. Mapping of landslide susceptibility can be achieved by using a variety of methods, among which the stochastic approach is the most popular choice [20,21,22,23,24]. This methodology is based upon the hypothesis that "the past is the key to the future" [25,26,27]. Therefore, future landslides are more likely to be triggered under the same environmental conditions that have produced past and present slope failures. The first step of landslide susceptibility modelling through a stochastic approach is selecting a mapping unit, which usually corresponds to square grid cells derived from Digital Elevation Models (DEM) or to slope units limited by streams and water divides. Then, a value of the dependent and independent variables is assigned to each mapping unit. The dependent variable is usually dichotomous (0: absence of landslide; 1: presence of landslide). The values of the selected independent variables (also known as covariates or predictors), which serve as proxies for the preparatory factors mainly controlling landslide occurrence in the study area, are usually derived from DEMs and from already available thematic maps, such as geological or land use maps. Finally, multivariate statistical techniques or machine learning algorithms are usually employed to model the relationships between landslide spatial distribution and the variability of the predictors, to calculate a probability value of landslide occurrence for each mapping unit. The most common statistical and machine learning methods employed for this aim are logistic regression [18,28,29,30,31], discriminant analysis [26,32,33], support vector machines [34,35] or random forests [36]. Comprehensive reviews of the most popular methods for landslide susceptibility zonation can be found in [26,37,38,39]. Landslide susceptibility zonation usually relies on independent variables that reflect only preparatory factors, assuming that the geographical distribution of the landslide inventories is not affected by the pattern of the trigger (either rainfall or earthquake), which is thus considered as spatially homogeneous. However, if a homogenous pattern of the trigger can be assumed for single and relatively small areas, this hypothesis does not apply when modelling large areas or multiple study areas that may experience different intensity of the trigger. In other words, when landslide susceptibility is assessed at regional scale or in different areas spread over a large territory, it is necessary to consider not only variables that express preparatory factors but also variables that represent the pattern and intensity of the trigger.
This paper focuses on predicting the landslides triggered by two earthquakes of magnitude 7.7 and 6.6, occurred in El Salvador in January and February 2001, respectively, which triggered thousands of slope failures and caused more than 1,150 fatalities. The main aim of this study was to evaluate the ability of rainfall- and earthquake induced landslide susceptibility models to predict the geographical distribution of the coseismic slope failures occurred in 2001 under two possible calibration and validation scenarios. One where most landslides are known (i.e., 75%), and the other where only a minor portion of the gravitational phenomena occurred are identified (i.e., 5%). A comparable and more than acceptable predictive ability of these scenarios might suggest that an inventory of slope failures built just after the triggering event, even if incomplete, may help to rapidly generate reliable landslide susceptibility maps.
The experiment was performed in fourteen sectors of El Salvador, accounting for a total extent of 397 km2. Eight sectors (92 km2) were strongly hit by the January earthquake whereas most of the landslides triggered by the February earthquake occurred in the other six sectors (305 km2). The modelling strategy was based on both rainfall- and earthquake-triggered landslide susceptibility models. The first model was calibrated by using an inventory of thousands of landslides triggered on November 7-8, 2009, by the combined action of Hurricane Ida and the low-pressure system 96E, in a sector extending 287 km2 along the slopes of the San Vicente Volcano, El Salvador [40]. The rainfall-triggered model, which was trained by using only eleven preparatory factors, used as independent variables, was applied to all fourteen study areas to verify its ability to predict the position of the coseismic landslides that occurred in January and February 2001. On the other hand, the earthquake-induced landslide predictive models were calibrated by using both preparatory and trigger variables, the latter reflecting the intensity of ground shaking.
The article is organized as follows. Section 2 describes the available data and the methods employed to map the coseismic landslides and to calibrate and validate the predictive models. Section 3 describes the inventory of the coseismic landslides and shows the results of models training and testing. The results are discussed in Section 4, which also reports the main conclusions of the study.

2. Materials and Methods

2.1. Study areas

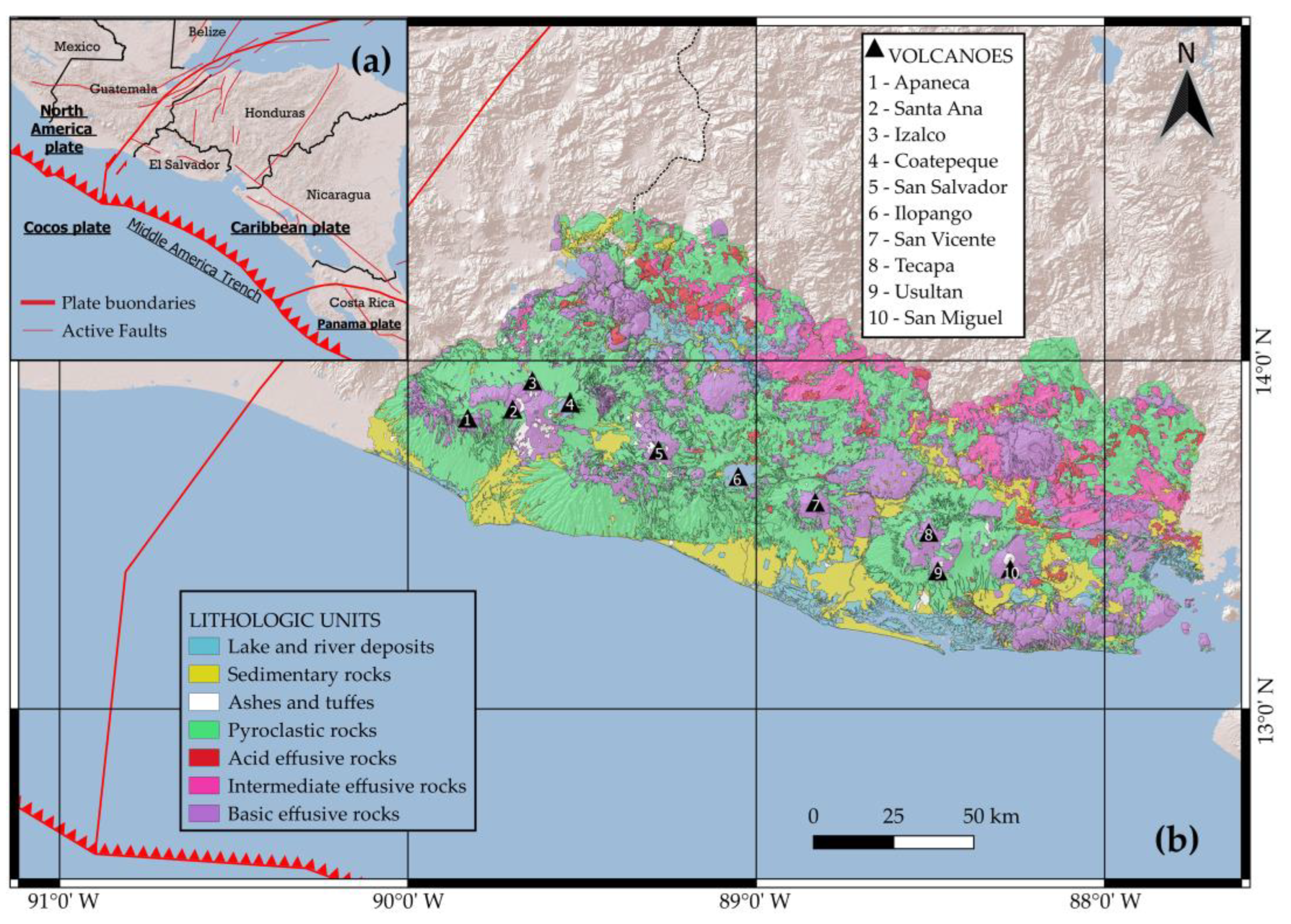
The intricate geodynamic context in which the small country of El Salvador is located is characterized by the convergence of the Cocos plate with the Caribbean plate, through the Middle America Trench, with a rate of about 7 cm/year [41]. This active tectonic environment is responsible for several active volcanoes in the country, aligned in the direction of WNW-ESE, which have frequently erupted and deposited widespread and poorly consolidated tephra in many parts of the country [13]. These lithologies, combined with acid pyroclastites and acid and basic effusive rocks, ensure that volcanic rocks represent 95% of the outcropping lithologies in the country (Figure 1).
The combination of the geodynamic context, responsible for medium and high earthquakes, steep slopes due to rugged volcanic ranges, incoherent rocks and a subtropical climate characterized by heavy storms, cause a high probability of earthquake- and rainfall-induced landslides occurrence in most of the country. The consequences of these gravitational phenomena are devastating for the country, which is the smallest country in Central America but the one with the highest population density (310 inhabitants/km2). Indeed, the fertility of the soils around the volcanoes, oriented WNW-ESE due to the tectonic assessment [42], has generated a situation in which a large part of the population lives in the areas of the country most susceptible to the gravitational phenomena. 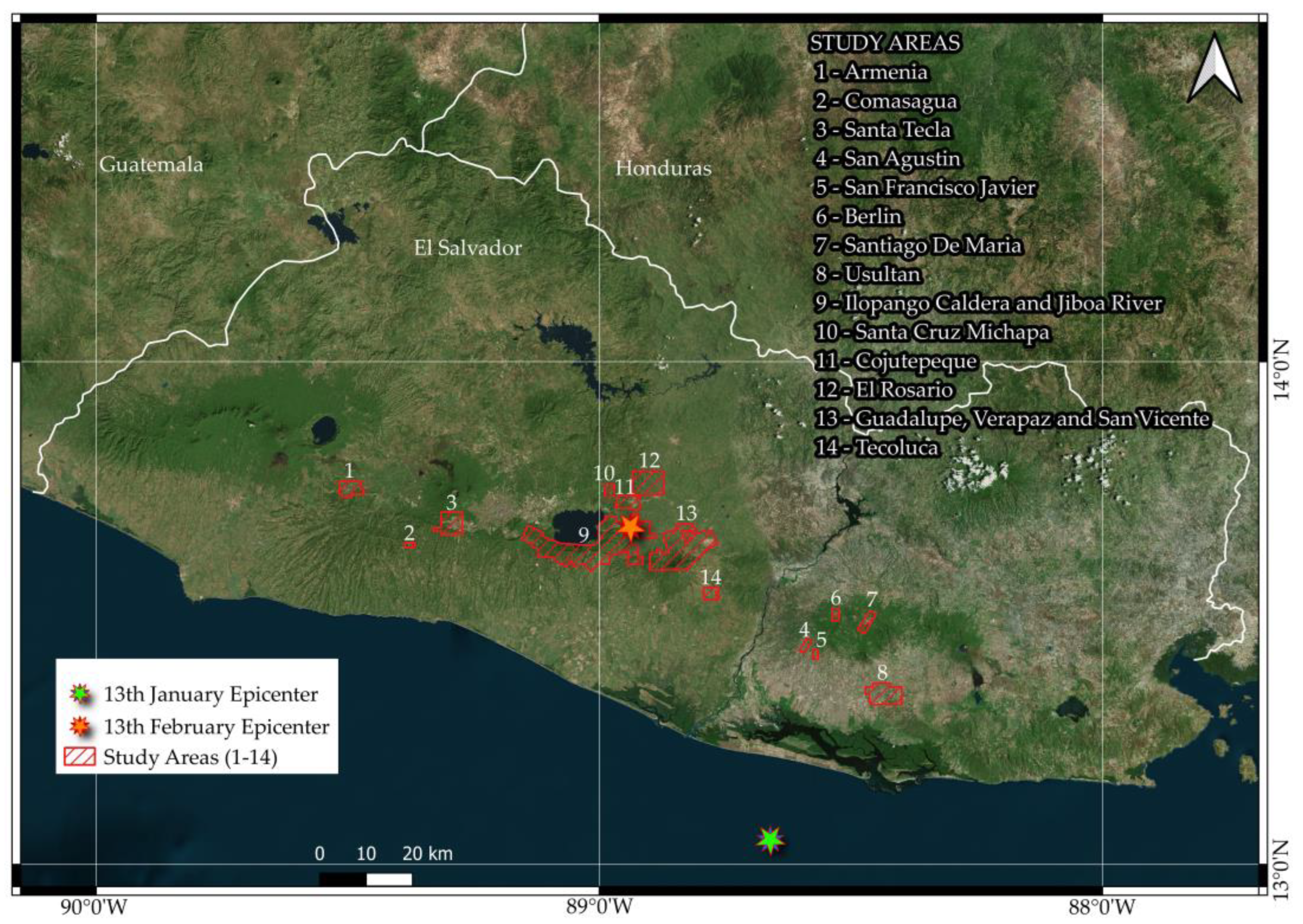As a confirmation of that, El Salvador has the highest ratio of destroyed houses to affected risks of Central America [43]. 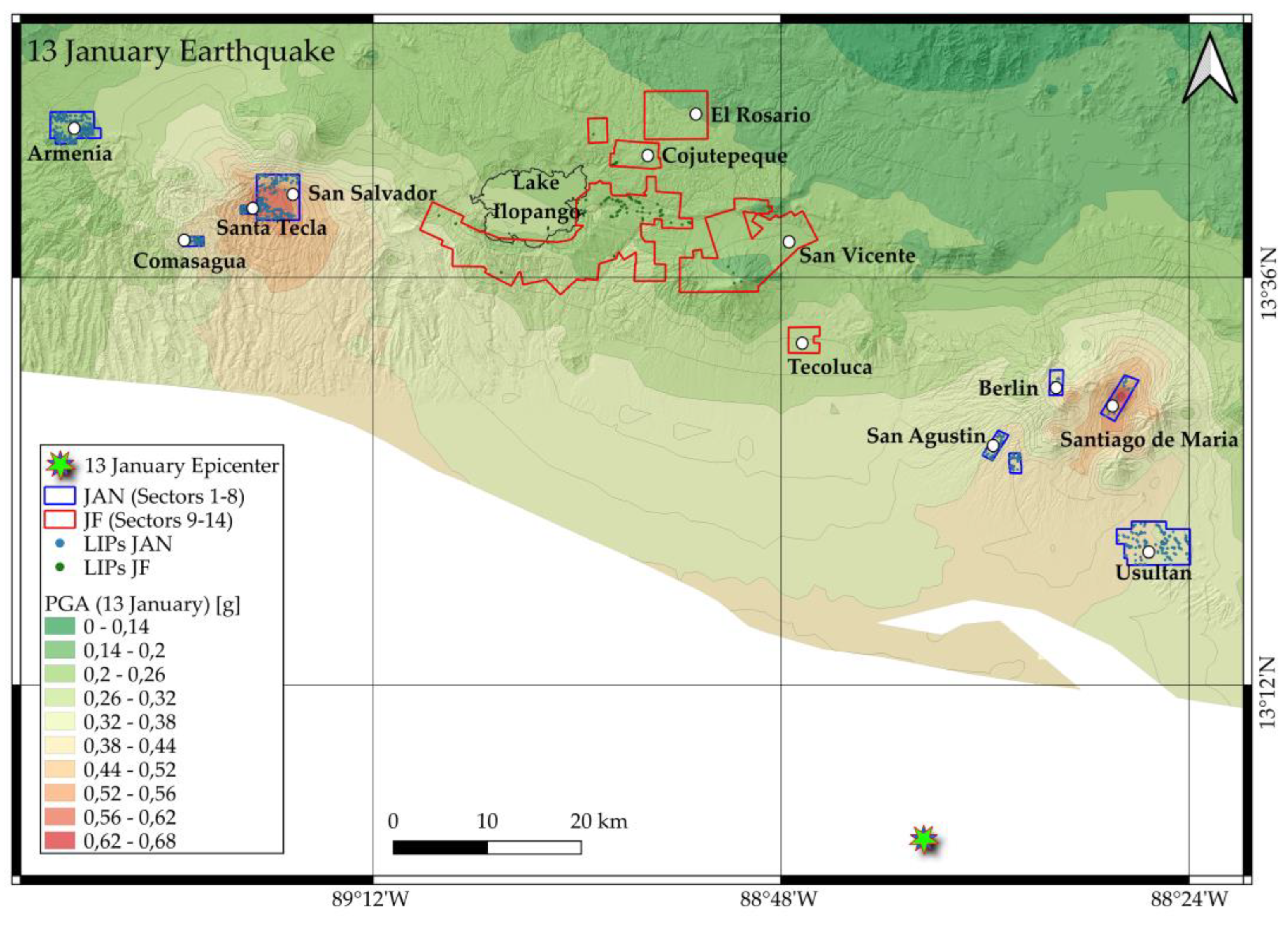This work was carried out in fourteen sectors along the volcanic chain (Figure 2), which were among the areas most affected by the two intense earthquakes occurred in the first two months of 2001.
The first eight study areas, numbered from 1 to 8, were selected because of the high number of landslides triggered by the January 2001 earthquake. Sectors 1 to 3 are in the south-western part of the country, close to the San Salvador volcano, whereas sectors 4 to 8 are located in the southern-eastern portion of El Salvador. Sectors from 9 to 14 are placed in the south-central part of the country and were selected because they were close to the February 2001 earthquake epicenter and strongly affected by coseismic landslides. Table 1 reports the extent, average and standard deviation of altitude and slope angle, and the main outcropping lithology of all the study areas.

2.2. The 2001 earthquakes

El Salvador has been severely affected by medium and high-intensity earthquakes that have triggered numerous gravitational phenomena capable of generating massive devastation of residential areas and many casualties. Bommer et al. [40] report that the country is experiencing earthquakes from two major seismic sources. The first source of seismicity originates deep earthquakes in the Benioff-Wadati zones of the subducted Cocos plate beneath the Caribbean plate, characterized by relatively high magnitude values (surface wave magnitude Ms and moment magnitude Mw often with values > 6.0), capable of involving large areas of El Salvador. Numerous seismic phenomena with this genesis were witnessed in the last century, many of them were particularly destructive and had dramatic impacts on the country. Among them, the September 1915 event, Ms 7.8, which caused destruction in the country's western area, and the earthquake of Ms 7.3 occurred in June 1982, which caused 49 victims and hundreds of earthquake-induced landslides. The second source of seismicity is a zone of upper-crustal earthquakes that coincides with the volcanoes array, orientated WNW-ESE [40]. These intraplaque earthquakes occur at relatively lower hypocentral depths. Since the main Salvadoran cities are located just along the volcanoes' alignment, it is not hard to figure out the catastrophic consequences of the seismic events that can occur, often with more significant damage than seismic phenomena with genesis in Benioff-Wadati zones. Among the most significant events in the last century with this genesis, there are the earthquake of 8 June 1917 (Ms 6.7), which caused 101 victims, the 20 December 1936 (Ms 6.1) event, which resulted in more than 200 victims and the 10 October 1986 event (Ms 7.5), which produced more than 1,500 fatalities.
On 13 January 2001, the country was hit by a violent earthquake, belonging to the first source of seismicity, at a depth of 60 km with a magnitude of 7.7 Mw (Figure 3). This event caused thousands of gravitational phenomena, causing 844 fatalities and 5,565 injured, with the destruction of over 100,000 buildings. The difference in terms of damage and fatalities between this event and the one of 1982, which had similar magnitude, are related to the increase of the elements at risk. A rapid expansion of the urban areas has indeed occurred during this time span, which continued to grow mainly towards the flanks of the volcanoes, as revealed by the difference between the topographical maps of the country dating back to the year 1981 and aerial photos of 2001.
Exactly one month later, on 13 February 2001, El Salvador experienced a further intense earthquake, which added more destruction to the country. This event, belonging to the second source of seismicity, was of Mw 6.6 with a hypocenter placed at 10 km depth, resulting in 315 fatalities and 3,399 injured caused by ground-shaking and landslides (Figure 3).
Nearly 45,000 homes were destroyed and 16,000 seriously damaged. This earthquake affected areas comparable to those affected by the 1936 event, with the same genesis. Once again, the increased risk factors have led to more damage and more victims.
Most of the landslides triggered by the 2001 earthquakes were shallow debris flows, but there were also numerous slides as well as debris and rock falls according to Cruden & Varnes's classification of landslides [44]. Moreover, both earthquakes triggered a few large and deep landslides that were highly damaging.
There are several doubts about whether these two earthquakes are related. However, some studies [42,45] reported that normal faulting subduction earthquakes in Central America tend to be followed by either large thrust events or shallow intraplate events within four years. This trend can also be observed in El Salvador, where earthquakes belonging to the second type of seismic genesis have occurred even after a month, as in the case of the earthquakes of 2001. To mention other examples of this trend, Bommer et al. [40] cite examples of 1915 subduction earthquakes, 1932 and 1982, followed by 1917, 1936 and 1986 intra-crustal earthquakes, respectively.
El Salvador is in a tropical-humid climate system, characterized by a dry season from November to April and a wet season from May to October, where about 75% of annual precipitation falls. The earthquakes of 2001 occurred in the first two months of the year, thus during the dry season, as confirmed by the precipitation data recorded close to the study areas. Furthermore, the cumulative precipitation in the 12 months preceding the earthquakes of 2001 was lower than the annual average recorded at the same gauge stations in the 29 years before the earthquakes (Table 2).
In addition, November 2000 was the last month that experienced rainfall, which was lower than the average, and the following months until the earthquakes of 2001, unlike the averages of previous years, were without rains. These data suggest that the water's content has not played a decisive role in the genesis of gravitational phenomena, a situation that could have increased the extension, the amount, and the damage caused by the landslides, due to a possible increase in volume weight and decrease in the cohesion of soils and outcropping rocks.

2.3. Mapping strategy

Landslide inventories are valuable tools for investigating landscape susceptibility to these phenomena. When investigating the slopes response to a specific triggering event, the archive must exclude the landslides occurred before and after that event. In stochastic and empirical assessment of landslide susceptibility, the presence or absence of a gravitational phenomenon within a selected mapping unit is employed as dependent variable. Thus, the accuracy and degree of completeness of the inventory largely affect the predictive performance of the models [46,47,48,49,50].
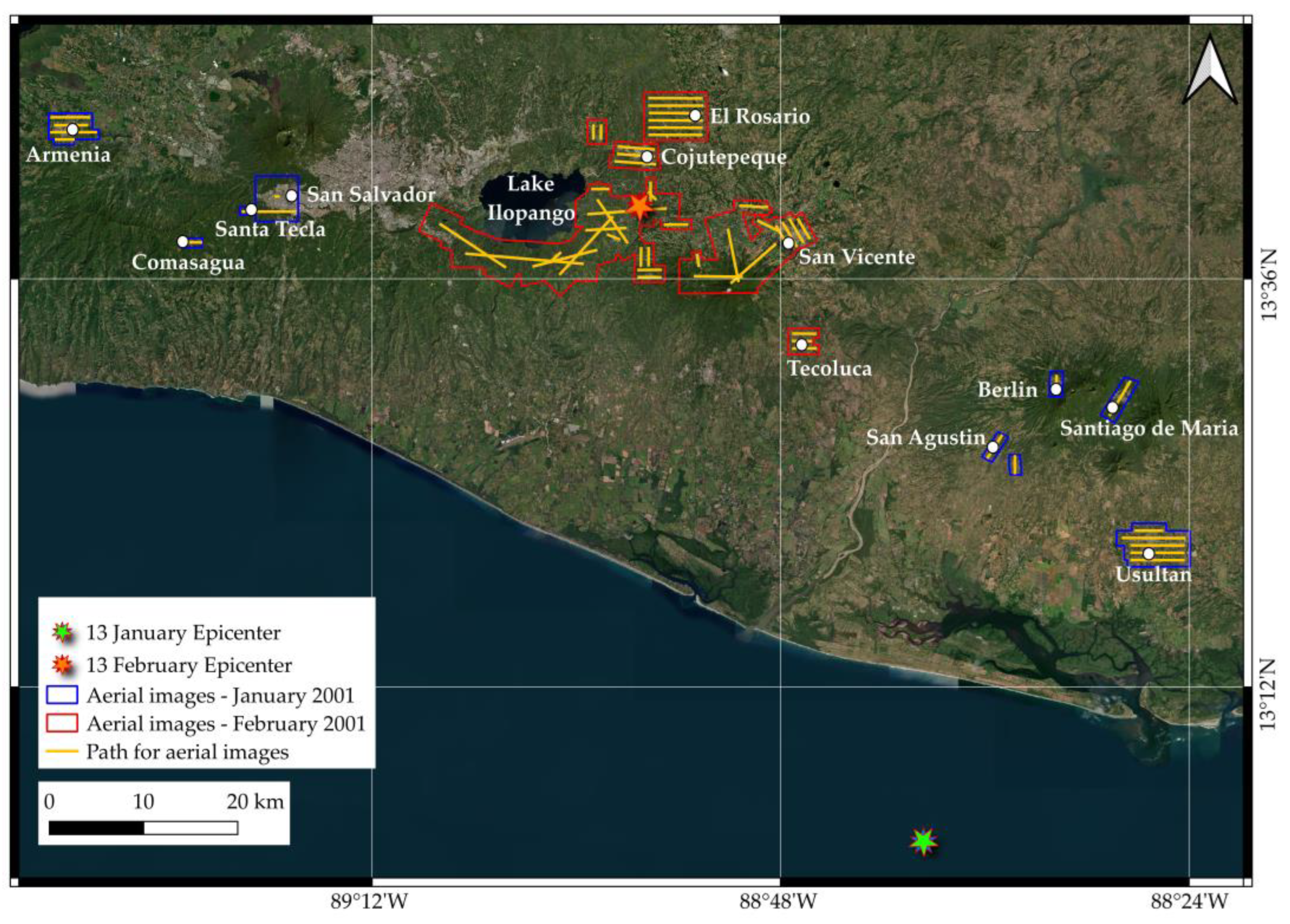
Since the 2001 landslide inventories available to date are incomplete, as they only include the main gravitational phenomena, the first step of this study was preparing a complete inventory of the slope failures triggered by the two earthquake events in the study areas. To this aim, aerial photos provided by the CNR (Centro Nacional de Registros de El Salvador - Instituto Geográfico y del Catastro Nacional) were employed. As regards the January earthquake, 136 aerial photos covering an area of 91.85 km2 were analyzed, while 313 aerial photos acquired over an area of 305.72 km2 were employed to identify the landslides triggered by the February earthquake (Figure 4).
Recognizing and mapping landslides in tropical areas, where vegetation recovers rapidly, requires aerial/satellite images taken not long after the event [38]. The employed aerial photos were taken in the days just after the earthquakes, when displaced materials had not yet been removed. The aerial images cover the areas of the country that were most heavily affected by the 2001 earthquakes. These correspond to sectors of the eastern and western parts of the country, in the case of the January earthquake, and to the central sector in the case of the February earthquake. In order to exclude from the analysis slope failures triggered by a previous seismic or rainy event, SPOT-4 satellite images with 10-m spatial resolution (European Space Agency), acquired before the 2001 events, were analyzed and the landslides already visible in these images were removed. In addition, in the areas covered by the February 2001 aerial photos, SPOT-4 satellite images of 21 January (Scene ID: 1 611-323 01-01-21 16:44 1 P) were also analyzed to identify those landslides triggered by the January earthquake.
In this study, the landslides were recognized, and their bodies were mapped as vector polygons. Then, the highest point of each landslide crown was identified, assuming that the environmental properties of these points, known as LIPs (Landslide Identification Points) [20,51,52,53], reflect the pre-failure conditions that favored the initiation of the landslides.

2.4. Dependent and independent variables

Landslide susceptibility assessment involves the division of the study area into mapping units, which usually correspond to grid cells or slope units [54,55,56]. As grid cell partition is largely and effectively employed in landslide susceptibility mapping [8,57,58], this strategy was employed in our experiment. The study areas were subdivided into 10-m pixels resulting from the resampling of a 5-m cell DEM of the European Space Agency (ESA). This cell size was selected aiming to find a compromise between spatial resolution and computation time needed to train and test the models [57], taking into account that a 10-m cell partition has been successfully employed in previous studies [29,59].
In this study, the dependent variable is dichotomous, taking the value of 1 when a pixel hosts one or more LIPs and the value of 0 when it does not intersect a LIP or a landslide body. As regards independent variables, they were selected according to data availability and their supposed direct or indirect relationships with the spatial distribution of the slope failures occurred in the study areas [60]. The following eleven predictors, which reflect preparatory factors, were selected: Aspect (ASP), Catchment Area (C_AR), Convergence Index (C_IND), Downslope Curvature (D_CUR), Elevation (ELE), Geology (GEO), Normalized Difference Vegetation Index (NDVI), Slope (SLO), Topographic Positioning Index (TPI), Topographic Wetness Index (TWI) and Upslope Curvature (U_CUR). Additionally, two trigger (i.e., depending on the earthquake characteristics) variables were also employed as covariates, namely: Peak Ground Accelerations (PGA) and distance from the hypocenter (DIST). The first was obtained by rasterizing the PGA values from both earthquakes from the USGS ShakeMap website [61], while the second by producing a distance raster from the epicenter coordinates known through the USGS website.
Table 3 summarizes the list of variables employed to model the landslide spatial distribution.

2.5. Modelling technique

The likelihood of landslide occurrence at each 10-m grid cell of the study area was calculated by using Multivariate Adaptive Regression Splines (MARS; [62]) as modelling technique. MARS is a non-parametric regression method, useful for handling complex data and able to model non-linear relationships between dependent and independent variables, splitting their range into an optimized number of linear branches. The extreme values of these intervals, called knots, allow an optimal linear function known as basis function (BF). The result will be a weighted sum of terms which include a basis function or the product of two or more of them. The MARS regression function is expressed as (1):
  y = f x = α + ∑ i = 1 N β i h i x
where y is the dependent variable predicted by the function f(x), α is the constant, each hi(x) is a BF and βi its coefficients, whereas N is the number of functions.
Calibration and validation of the MARS models were carried out by using the following packages of the R software: "raster" [63], "usdm" [64], "splitstackshape" [65], "pROC" [66], "ROCR" [67], "caret" [68] and "earth" [69].

2.6. Calibration and validation strategy

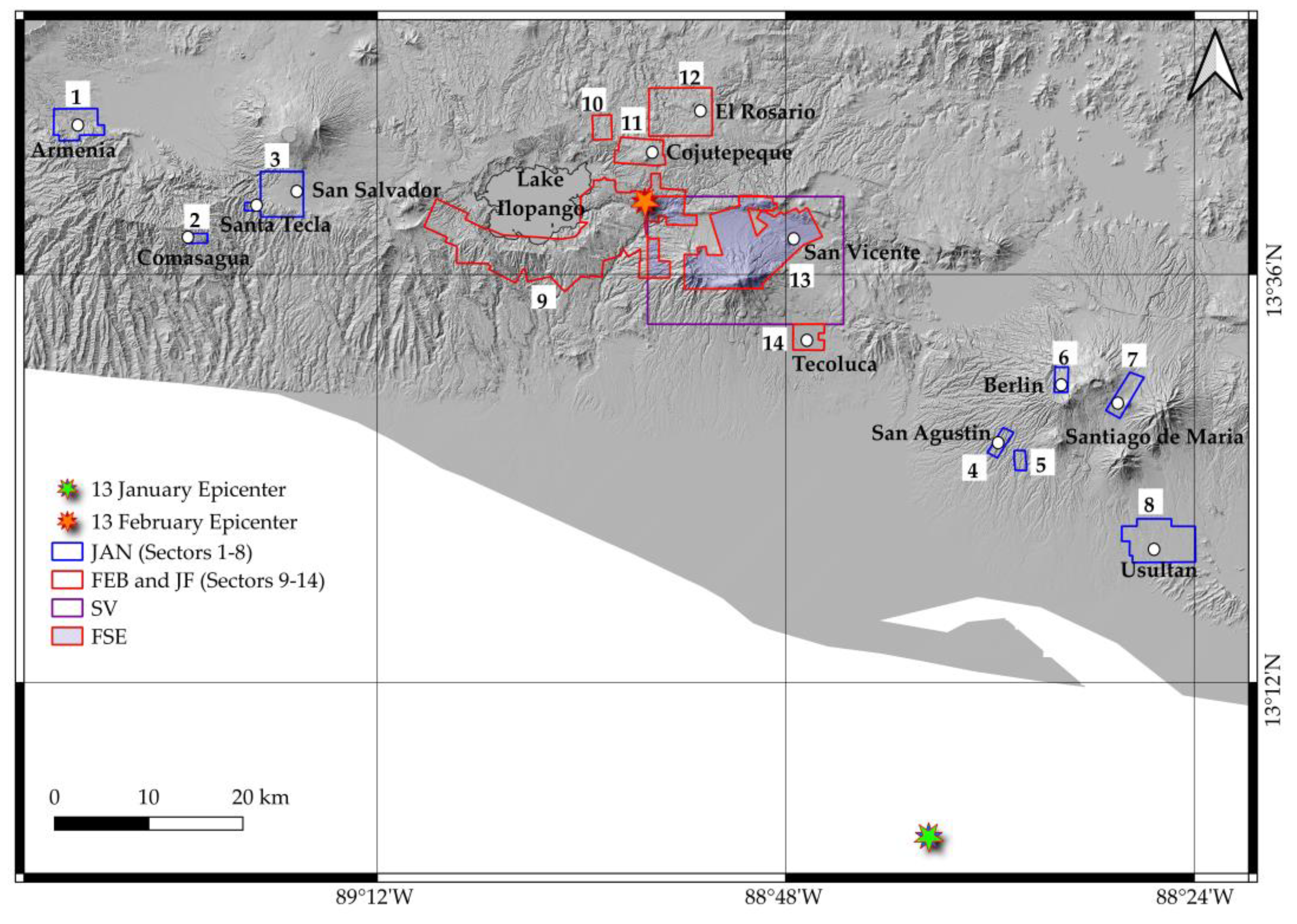
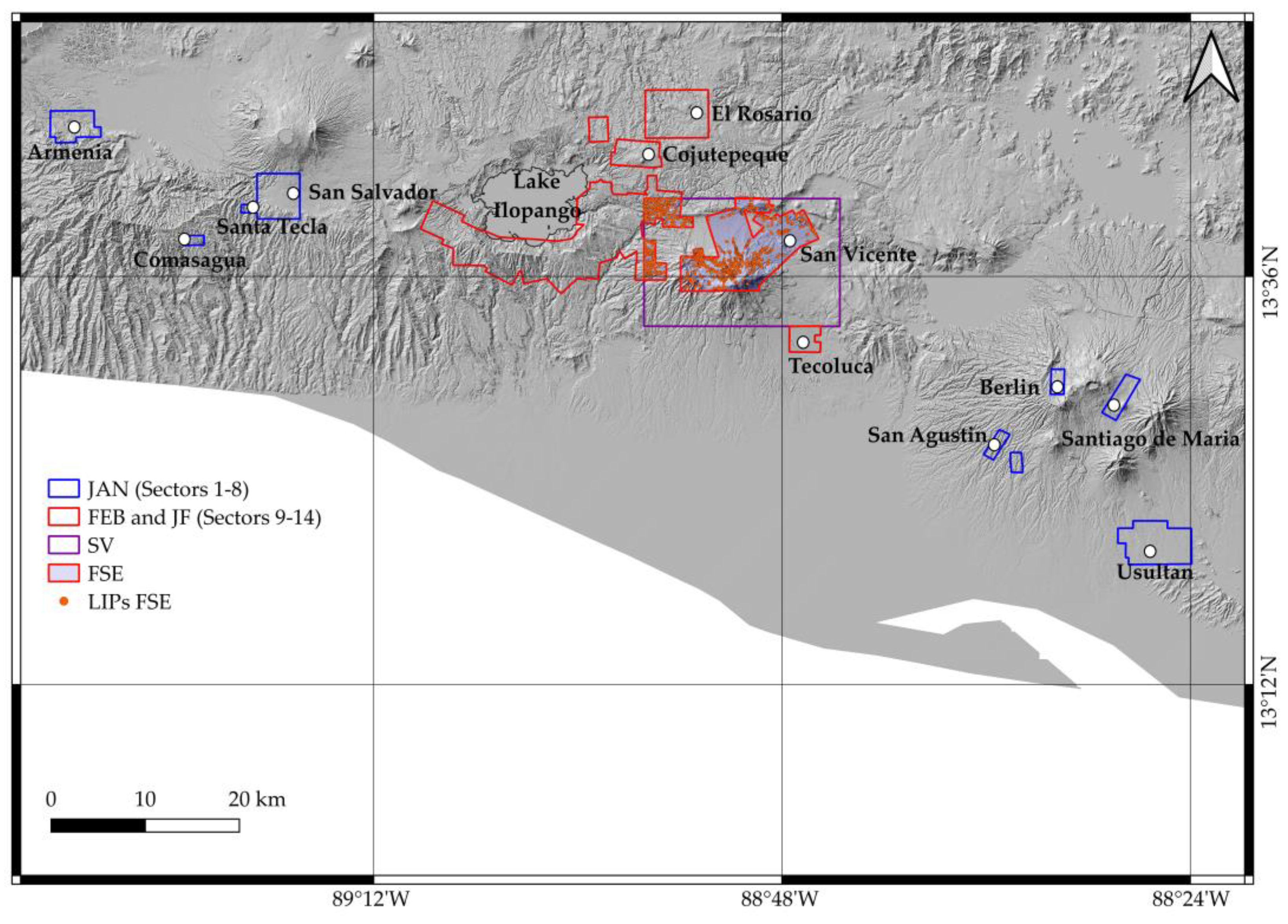
In this study, landslide predictive models were calibrated and validated using five datasets (Figure 5; Table 4), which correspond to the fourteen study sectors (JAN, FEB and JF), to the area of the San Vicente (SV) volcano landslide inventory prepared by Mercurio et al. [40] and to the intersection between the latter and sectors 9 and 13 (FSE).
These datasets are matrices where rows correspond to the pixels of a specific area, while columns report the values of the dependent and independent variables calculated for each pixel. The dataset of rainfall-triggered landslides (i.e., SV) includes only preparatory covariates, whereas those of the coseismic landslides (i.e., JAN, FEB, JF and FSE) report the values of both preparatory and trigger variables.
The MARS predictive models were prepared using different calibration datasets or sets of predictors (Table 5). The models named M1 were trained with the datasets SV, which include rainfall-induced landslides and eleven independent variables reflecting preparatory factors. The M1 model calibrated with the dataset SV was then transferred to all fourteen study sectors of El Salvador, calculating for each pixel of these areas a probability (PSV) of landslide occurrence. The values of PSV were then employed as a new predictor when training the M3 model. The M2, M3 and M4 models were calibrated with the earthquake-induced landslides of January and February 2001. The variables PGA and DIST were used in the M2 model as the only covariates, and in the M3 model in addition to PSV. The M4 model contains both preparatory and triggering independent variables.
The predictive ability of the M1 models was evaluated by comparing the PSV values and the presence or absence of coseismic landslides in the datasets JAN, FEB, JF and FSE.
Calibration and validation of the MARS models consisted of the following steps. First, we randomly selected ten subsets from each dataset, which include all the event cells and the same number of non-event cells. The subsets of cells extracted from the SV dataset were used to train ten M1 models. Second, we extracted two calibration samples from the ten subsets of all the datasets excluding SV, by randomly selecting the 75% and the 5% of the event cells, respectively. The remaining event cells (25% and 95%, respectively) were included in the validation samples. Both calibration and validation samples were completed by randomly picking the same number of non-event cells. Thus, this second step produced twenty calibration and twenty validation samples from the datasets JAN, FEB, JF and FSE. The two ratios of event/non-event cells were chosen in order to evaluate the predictive performance of the MARS models under two different scenarios: the first one, in which the position of a large part (i.e., 75%) of the earthquake-induced landslides is known; the second scenario simulates the situation just after the earthquake occurrence, when only a very small part (i.e., 5%) of the landslides have been identified.
The probability of landslide occurrence was calculated for each cell of the validation samples by averaging the score obtained from the ten MARS model runs (one for every calibration sample). This strategy was applied to increase the stability of the landslide predictions and mitigate the rare-events issue [18,28,70,71]. For all the validation samples, a receiver operating characteristics (ROC) curve [39,72,73,74] was prepared by using the average MARS score to predict the value of the dependent variable at each pixel (0: LIP absence; 1: LIP presence). The ROC curve plots sensitivity (true positive rate) against 1 – specificity (false positive rate). Then, the Area Under the ROC (AUC) curves were calculated, thus obtaining, for each of the models M1 to M4 and both the validation scenarios, ten AUC values for the prediction of the datasets JAN, FEB, JF and FSE. This procedure lead to a total of 320 AUC values. An AUC value close to 0.5 reveals a random prediction whereas a value of 1.0 reflects a perfect ability to discriminate between event and non-event pixels. AUC values larger than 0.7, 0.8 and 0.9 were considered as acceptable, excellent, and outstanding, respectively [75]. The Wilcoxon signed-rank test was employed to identify significant differences between the models' predictive skill performance, by setting the level of significance at 0.01.

3. Results

3.1. The 2001 earthquake-induced landslide inventories

The landslide inventory of the dataset JAN was obtained by analyzing eight sets of aerial photos taken a few days after the earthquake of 13 January 2001. These images cover eight inhabited sectors extending for 91.85 km2 (Figure 6), which have experienced the most significant damage due to the seismic shaking and the consequent landslides. These were mainly rotational slides, debris/earth flows and earth/rock falls.
The inventory consists of 997 LIPs, each hosted by a 10-m pixel. The percentage of event cells (i.e., cells hosting at least one LIP), compared to the total number of pixels (1,260,811) of the study area, is equal to 0.08%, while the cells intersecting the landslide polygons are 9,556, which correspond to the 0.76% of the total pixels. The JF inventory include the LIPs and landslides caused by the January earthquake in the areas covered by the aerial images taken after the February event (sectors 9 to 14, counted from West to East, are respectively: Ilopango south and Rio Jiboa, S. Cruz Michapa, Cojutepeque, El Rosario, San Vicente and Tecoluca; red polygons of Figure 6). These landslides were identified by analyzing images of the SPOT-4 satellite, dated 21 January 2001. In these sectors, with relatively low January PGA values, 123 LIPs were mapped, each placed in one 10-m cell and accounting for 0.002% of the total number of cells of the area under examination. When landslide bodies are considered, unstable pixels cover the 0.2% of the area.
When JAN and JF inventories are merged, the percentage of the LIPs and landslide pixels in relation to the total area (sectors 1 to 14) are significantly reduced (0.017 and 0.30, respectively), due to the low PGA values within sectors 9 to 14. However, the landslides triggered in these sectors, despite being about one tenth of the number of the JAN landslides, cover a significantly higher number of pixels (Table 6). This can be explained considering that the steepest slopes are characterized by thick deposits of poorly consolidated, late Pleistocene and Holocene Tierra Blanca rhyolitic tephras erupted from Ilopango caldera, an area particularly susceptible to the initiation of gravitational phenomena [49,53]. In fact, in that region, the January earthquake resulted in a low number of debris flows and rotational slides, which, however, have large extent. This is also demonstrated by the number of gravitational phenomena larger than 10,000 m2, which are respectively two and twenty-two in the JAN and the JF datasets. However, the two gravitational phenomena, both occurred in sector 3 (Las Colinas neighborhood of Santa Tecla, west of the capital San Salvador), caused the worst damage and the largest number of victims. One of these is a complex landslide (rotational slide + earth flows) covering an area of about 200,000 m3, where approximately 585 people lost their life. This landslide, sadly become famous for the devastation it has generated, was about 800 m long and 150 m wide, with a 50 m high escarpment activated on the north side of El Balsamo Ridge, which is composed by the andesitic cinders and some interbedded tephra of the El Balsamo Formation [40]. The second event, located at approximately 2.5 km from the first landslide, is a debris flow about 1,500 m long, which also starting from the north side of El Balsamo Ridge reached and destroyed a sector of the Carrera Panamericana, the most crucial road in the country, which connects the capital with the western part of El Salvador. The highway interruption has hindered the arrival of aid, creating enormous damage to the population. However, the absence of small landslides in sectors 9 to 14 compared to that of sectors 1 to 8 (41.42%) could be also related to the different resolution of the images used for mapping, as phenomena with an extension of less than 100 m2 are hardly detectable in a satellite analysis with a 10-m resolution.
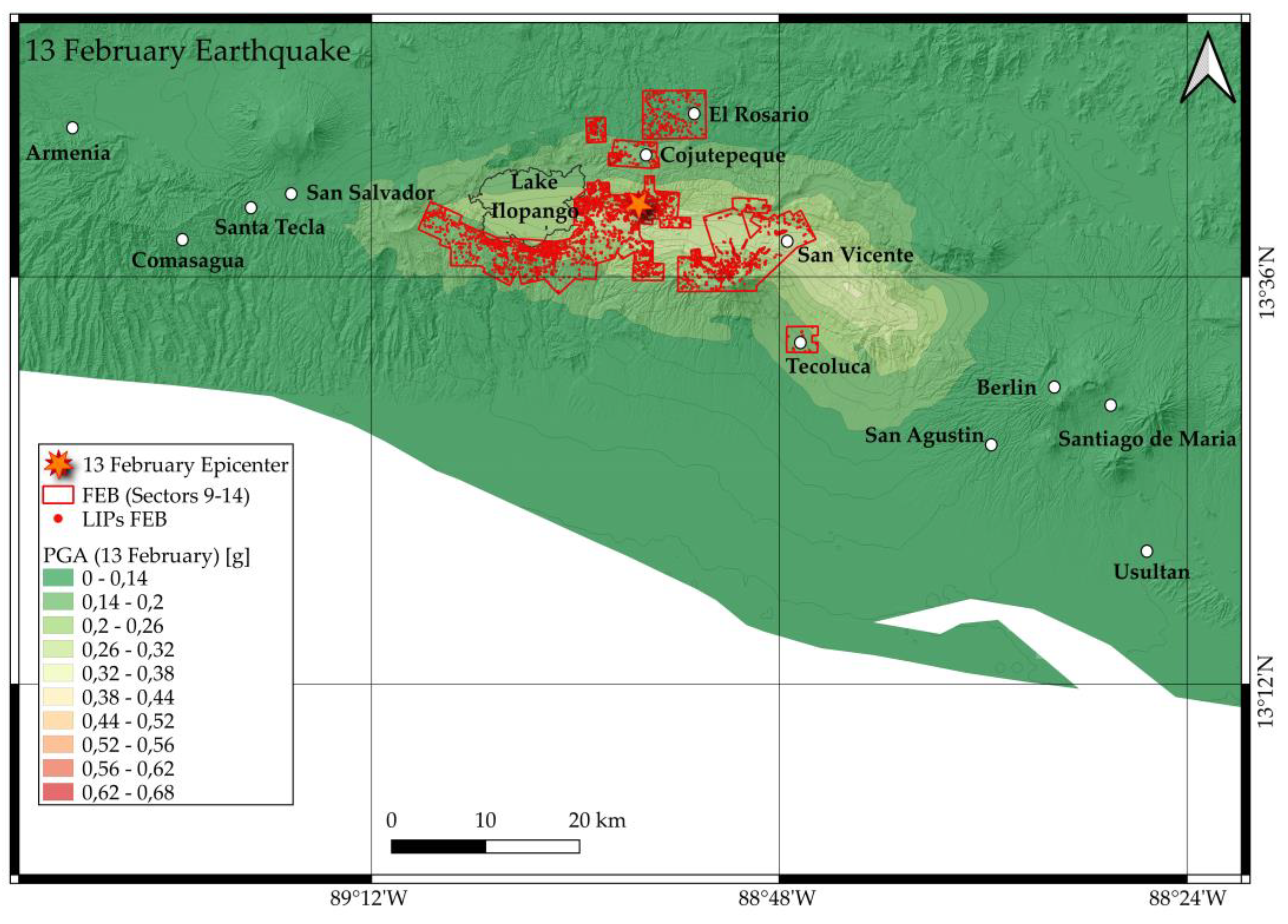
The seismic phenomenon of the 13 February triggered thousands of landslides in the country's central sector. Many landslides occurred where slopes are covered by thick and slightly consolidated deposits of rhyolitic tephras of the Tierra Blanca Formation originated by eruptions from the Ilopango Caldera.
Landslides mapping was carried out in aerial photos taken a few days after the event in areas that experienced very high PGA and suffered the most significant damage (sectors 9 to 14, Figure 7). The landslides also included in the JF inventory have been discarded, except for those that have been reactivated.
The FEB inventory include 5,371 LIPs intersecting 5,344 pixels. The percentage of event cells of the FEB dataset is 0.09%. The extent of the landslide bodies is 123,488 pixels, which account for 2.12% of the study area. This seismic event triggered landslides similar to those of the JAN dataset, but their frequency and size are higher (Table 7).
Among the many large-scale phenomena that have occurred, large rotational flows of debris have been mapped in the area close to the epicenter, corresponding to areas near the Jiboa River, fortunately with low population densities. As a matter of fact, thousands of gravitational phenomena have been detected in the Tierra Blanca Formation (GEO4), some of which have caused the damming of the river for hundreds of meters, causing the formation of an artificial lake that could have caused a high hydrogeological risk downstream.

3.2. The Ida/96E 2009 inventory

The SV inventory [40] covers an area of 287 km2 around the flanks of the San Vicente Volcano and includes the LIPs of 5,609 landslides triggered between 7 and 8 November 2009 [76] by an extreme rainfall event. That was caused by the combined action of the Hurricane Ida and the low-pressure system 96E, which produced 350 mm in 24 h, in an area of about 400 km2, located between Ilopango Lake and San Vicente Volcano (Figure 8).
The rainfall triggered numerous and large debris flows which caused fatalities and massive damage, with an estimated economic loss of approximately a quarter of a billion dollars [77]. The FSE inventory was generated by overlapping the areas of the datasets FEB and SV. The intersection extents for 107 km2 and includes the whole sector 13 and 12.5% of the sector 9 of the FEB study areas (Figure 9). The FSE dataset contains 1,587 LIPs pertaining to the landslides triggered by the February earthquake, which are mainly earth/debris flows.

3.3. Predictive performance of the MARS models

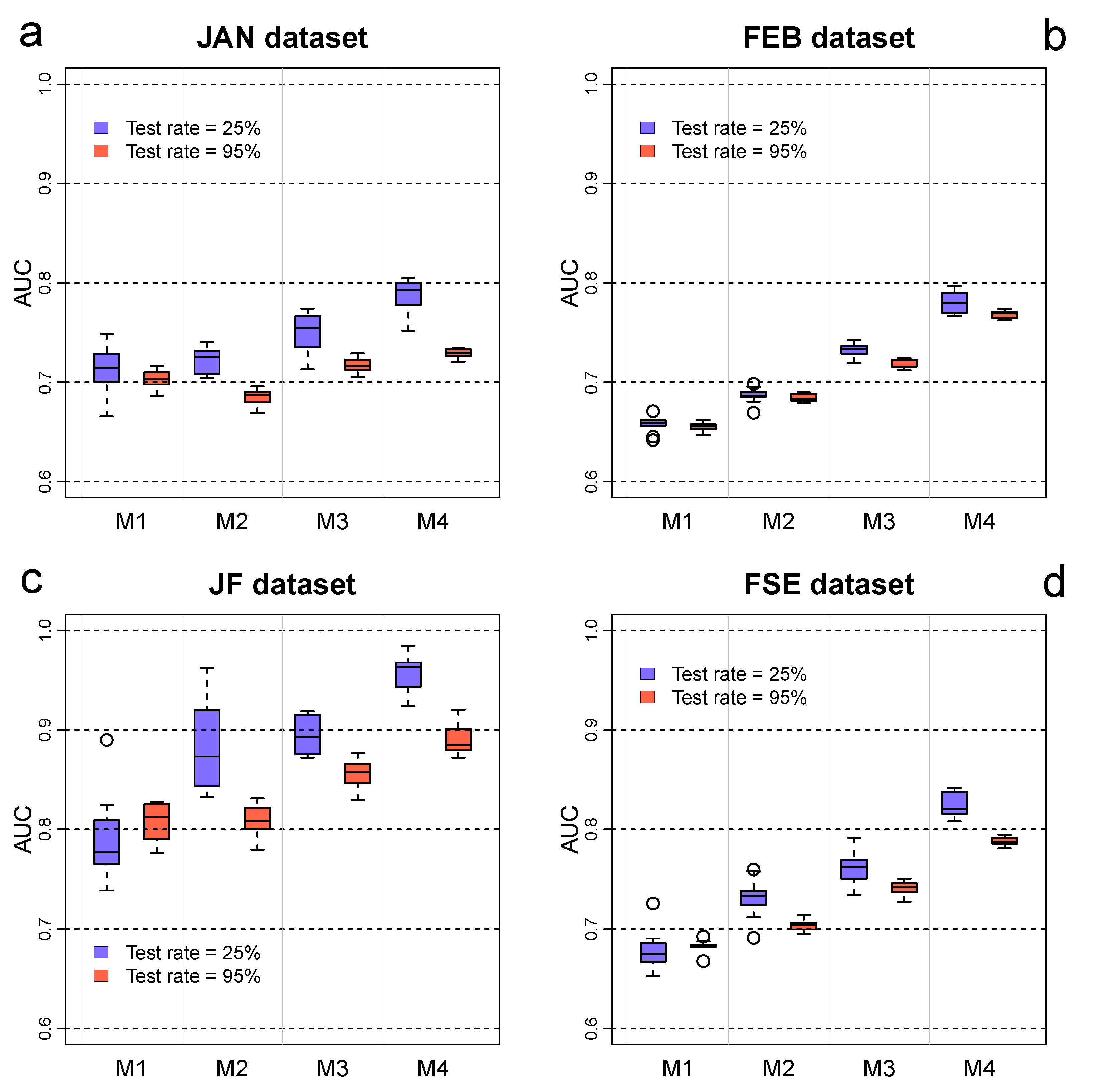
Inventories and variables used for calibrating and validating M1, M2, M3 and M4 models are shown on Table 5. The predictive skill of the models measured on the validation samples of the datasets JAN, FEB, JF and FSE for both scenarios are revealed by the boxplots of Figure 9. These reflect, for each model and dataset, the variability and skewness of the ten AUC values calculated by applying the calibration and validation strategy described in section 2.6. The skewness display, for each group of ten AUCs, their first quartile (Q1), median and third quartile (Q3), the minimum and maximum values within 1.5 times the interquartile range (IQR) above Q3 and below Q1 and eventually outliers outside 1.5 of IQR. Moreover, Table 8 shows the average and standard deviation values of the AUC groups.
The M1 models, which were calibrated with all the rainfall-induced landslides occurred near the San Vicente volcano and then transferred to the study areas, exhibit average AUC values ranging from 0.66 to 0.81. Overall, the accuracy of these models is poorer than that of the other models, except for what observed in the datasets JAN and JF, where M1 models perform similarly to M2 models or even better when validation is carried out with 95% of the landslides of the dataset JAN. In both validation scenarios, the performance of the M1 models is not acceptable for the datasets FEB and FSE whereas it is acceptable in the dataset JAN [75]. The M1 models show the best performance in the dataset JF, achieving a mean AUC of approximately 0.79 and 0.81 when the validation samples include the 25% and 95% of the landslides, respectively.
The M2 models, which include as predictors the variables PGA and DIST, achieved mean AUC values in the range of 0.68 – 0.88. Their performance is better than that exhibited by the M1 models, except for the dataset JAN when the calibration samples include only the 5% of the LIPs. In this case, as well as in both validation scenarios applied to the dataset FEB, the predictive skill of the M2 models is not acceptable. On the other hand, their ability to discriminate between stable and unstable cells of the datasets FSE and JF is acceptable and excellent, respectively.
The validation of the M3 models revealed mean AUC values in the range 0.72 – 0.90, significantly higher than those achieved by the M1 and M2 models in all the datasets. The predictive ability of the M3 models, which were fitted using the covariates PGA, DIST and PSV, is acceptable in the datasets JAN, FEB and FSE, and excellent in the datasets JF.
The M4 models were trained with all the independent variables available, excluding PSV. The validation results reveal a further improvement of the predictive ability of the M4 models compared to that exhibited by the other models. In both validation scenarios, the AUC average values, which are in the range 0.73 – 0.96, indeed exceed the acceptability threshold in the datasets JAN, FEB and FSE, whereas are excellent when applied to the JF datasets.
For both the validation scenarios, the best predictive ability of the four tested models is observed in the dataset JF (mean AUC: 0.81 – 0.96), which contain the landslides triggered in sectors 9 to 14 by the January earthquake. Conversely, the models exhibited some inaccuracy in discriminating between stable and unstable cells of the datasets JAN and FEB, showing mean AUC values in the ranges 0.69 – 0.79 and 0.66 – 0.77, respectively.
Overall, when learning samples include the 75% of the observed landslides, the models M2 to M4 exhibit a significantly better accuracy (mean AUC: 0.69 – 0.96) than that achieved when calibrated using only 5% of the landslides (mean AUC: 0.68 – 0.89). However, except for the dataset JF, differences in terms of mean AUC values are small and even not significant for the models M2 and M4 in the dataset FEB. Moreover, as regards M1 models, there is no significant difference of accuracy when validation is carried out with 25% and 95% of the landslides. On the other hand, validation samples containing the 95% of the landslides lead to more stable predictive skill (SD: 0.004 – 0.019) than that obtained when validating the models with the 25% of the event cells (SD: 0.007 – 0.043).

4. Discussion and Conclusions

In January and February of 2001, El Salvador was hit by two intense seismic phenomena of different nature, which produced thousands of gravitational phenomena. Both 2001 earthquakes triggered similar landslides, but their distribution varied because of different earthquake source parameters, such as magnitude, epicentral distance and hypocentral depth. Indeed, earthquakes with large hypocentral depths tend to produce a relatively low number of gravitational phenomena spread over large areas. In contrast, phenomena that occur at relatively low hypocentral depth usually produce a high number of landslides concentrated in areas close to the epicenter [9]. The seismic event of January, having a hypocentral depth of 60 km, triggered 1,200 gravitational phenomena across 398 km2; whereas 5,371 landslides, spread over 305 km2, were induced by the February event, which had a hypocentral depth of 10 km. The difference in hypocentral depth caused different spatial distributions of PGA and MMI (Modified Mercalli Intensity). In fact, their values decreased from the hypocenter to a greater distance in the January event compared to the February one. The slow decay of PGA values, which is observed for earthquakes with deep and offshore genesis, triggers gravitational phenomena over larger areas than earthquakes with most superficial genesis. Conversely, the latter are characterized by a higher concentration of slope failures around the hypocenter.
In this work, four different MARS models (M1 to M4) were produced by using different predictor sets and landslide inventories, the latter containing the slope failures triggered by the Ida/96E event of November 2009 (M1) and those induced by the earthquakes of January and February 2001 (M2 to M4). Moreover, two different calibration-validation scenarios were employed. In the first scenario, three quarters of the observed landslides were used for calibrating the models M2 to M4 whereas the remaining quarter was included in the validation samples. This scenario is frequently used to produce and validate landslide susceptibility models [40,58,70,78,79]. In the second scenario, the learning samples contain only 5% of the earthquake-induced landslides, using the remaining 95% of the LIPs for validation.
The AUC values calculated for each model, dataset, and validation scenario, which are summarized by Table 8 and boxplots of Figure 10, reveal that the MARS algorithm provides reliable predictions of the spatial distribution of earthquake-induced landslides. Indeed, 75% of the 320 values of AUC that were computed in this experiment exceed the threshold of acceptability (AUC > 0.7) and a quarter of them even reveals excellent predictive skill of the models (AUC > 0.8). A general growing trend of predictive skill from M1 to M4 can be observed, except in the datasets JAN and JF where predictive performance of M1 and M2 models is similar. Conversely, when landslides triggered by the February earthquake are considered (i.e., datasets FEB and FSE), M2 models’ predictive ability is clearly better than that achieved by the M1 models, which do not achieve acceptable accuracy. This could be explained by a weaker control of the earthquake variables (i.e., PGA and DIST) on the spatial distribution of the January landslides, due to higher hypocentral depth and largest distance between epicenter and observed slope failures with respect to February events. On the other hand, the higher accuracy of M3 models compared to M2 models, which is observed in all the four datasets, reveal that a rainfall-induced landslide susceptibility model, even if calibrated outside the validation area, can significantly improve the predictive ability of a model containing only trigger variables. However, the fact that the best accuracy is achieved by the M4 models, highlights the need to include preparatory variables measured in the same area where validation is performed.
Figure 10 and Table 8 clearly reveal that stable and unstable cells of the dataset JF are discriminated with better accuracy than that achieved in the other datasets. This is consistent with the larger size of the landslides induced by the January earthquake that were identified in the sectors 9 to 14. In fact, due to the coarser resolution of the SPOT-4 satellite images with respect to that of the aerial photos employed to map the slope failures of the other datasets, JF includes only landslides extending more than 100 m2. This could have led to a stronger link between controlling factors and triggered landslides. Furthermore, as this dataset only include large and evident landslides, it may have fewer mapping errors. On the other hand, the larger standard deviation of AUC values observed in the dataset JF can be explained by the smaller size of the calibration and validation samples, due to lower number of LIPs.
The AUC values also show that models’ predictive skill observed in the dataset FSE is better than that achieved in the dataset FEB. Based on these results, we could infer that rainfall-triggered landslide susceptibility models help more in predicting seismic-induced slope failures occurred if focusing in the same area where models were calibrated.
Comparing the performance of the models M2 to M4 achieved with the two different percentage of validation LIPs (i.e., 25 and 95%), it is worth noting that the gap of mean AUC is never greater than 0.07, being 0.03 on average. Moreover, the mean AUC values observed with the second validation scenario always exceed the threshold of acceptability except for the M2 model in the dataset JAN and in the dataset FEB, where also performance validated with the 25% of the LIPs is not acceptable. These results suggest that reliable predictive models of earthquake-triggered landslides can be obtained even when only a small portion of the slope failures have been identified. Therefore, in this situation which is typical of the first moments immediately after a triggering event, predictive models such as those used in this work can help to quickly identify slopes where unmapped mass movements may have occurred. Indeed, even after more than twenty years, only one fifth of the landslides identified in this work were already known. The latter were the main landslides that had hit the inhabited centers and that had been mapped immediately after the events to aid civil protection operations.
Based on the results of this experiment, the following main conclusions can be drawn for the areas of El Salvador (CA) that were most affected by the earthquakes of 2001.
  • Overall, the MARS algorithm provides reliable predictions of the spatial distribution of earthquake-induced landslides.
  • MARS models calibrated with rainfall-induced landslides (i.e., M1 models), even if exported from other areas, are able to predict with acceptable accuracy landslides distributed over vast areas, caused by deep earthquakes such as the one of January 2001.
  • When MARS models based only on seismic covariates (i.e., M2 models) include as predictor the probability of occurrence of rainfall-induced landslides (i.e., M3 models), even when transferred from other areas, a significant increase of accuracy can be observed.
  • The models containing both preparatory and trigger variables (i.e., M4 models) achieve the best accuracy in predicting the spatial distribution of earthquake-induced landslides.
  • Even when only a small part of the landslides produced by an earthquake is known, as usually occurs shortly after the event, it is possible to use them to calibrate models, such as those used in this work, that help to identify slopes where yet unreported landslides may have occurred.
The results of this experiment and the main conclusions listed above suggest that the approach presented in this work can be useful for predicting the distribution on the Salvadoran territory of landslides caused by earthquakes like those occurred in January and February of 2001. Seismic events with similar characteristics occur quite frequently in El Salvador due to the continuous subduction of the Cocos Plate beneath the Caribbean Plate, which generates severe offshore earthquakes resulting in intraplate phenomena in a relatively short time. Therefore, it is useful to provide the country with landslide susceptibility maps, calibrated also with slope failures induced by extreme rain events, which occur with greater frequency than earthquake-induced landslides. Indeed, as observed in our experiment, these maps can be used as a basis for identifying slopes where a future seismic event is most likely to cause landslides. On the other hand, in case a high magnitude earthquake occurs, and the position of some landslides caused by the same event is known, the models based on predisposing variables can be integrated with trigger variables such as PGA and distance from the epicenter, in order to obtain predictive maps that may help local civil protection to identify sites potentially affected by others and unknown earthquake-induced landslides.

Concluding remarks

Author Contributions

Conceptualization, Claudio Mercurio, Edoardo Rotigliano and Christian Conoscenti; methodology, Claudio Mercurio, Laura Paola Calderón-Cucunuba, Abel Alexei Argueta-Platero, Grazia Azzara, Chiara Cappadonia, Chiara Martinello, Edoardo Rotigliano and Christian Conoscenti; software, Claudio Mercurio, Laura Paola Calderón-Cucunuba, Abel Alexei Argueta-Platero, Chiara Martinello and Christian Conoscenti; validation; Claudio Mercurio, Chiara Cappadonia, Edoardo Rotigliano and Christian Conoscenti; formal analysis, Claudio Mercurio, Laura Paola Calderón-Cucunuba, Abel Alexei Argueta-Platero, Grazia Azzara, Chiara Martinello and Christian Conoscenti; investigation; Claudio Mercurio, Grazia Azzara, Chiara Martinello, Chiara Cappadonia and Christian Conoscenti; resources, Claudio Mercurio, Abel Alexei Argueta-Platero, Grazia Azzara, Chiara Martinello and Christian Conoscenti; data curation, Claudio Mercurio, Laura Paola Calderón-Cucunuba, Grazia Azzara, Chiara Martinello, Chiara Cappadonia, and Christian Conoscenti; writing—original draft preparation, Claudio Mercurio, Laura Paola Calderón-Cucunuba and Christian Conoscenti; writing—review & editing, Claudio Mercurio, Laura Paola Calderón-Cucunuba, Chiara Martinello and Christian Conoscenti; visualization, Claudio Mercurio, Abel Alexei Argueta-Platero, Grazia Azzara, Chiara Cappadonia and Christian Conoscenti; supervision, Chiara Cappadonia, Edoardo Rotigliano and Christian Conoscenti; project administration, Chiara Cappadonia, Edoardo Rotigliano and Christian Conoscenti; funding acquisition, Christian Conoscenti. All authors have read and agreed to the published version of the manuscript.

Funding

This research was developed in the framework of the CASTES project (AID 11726), funded by the Italian Agency for Development Cooperation (AICS) and coordinated by prof. Christian Conoscenti (https://castes.agronomia.ues.edu.sv).

Data Availability Statement

The landslide inventories, Digital Elevation Model and geologic layers adopted for this study can be acquired from any of the authors. The NDVI values obtained can be downloaded from the website MODIS Satellite from modis.gsfc.nasa.gov/data. Peak Ground Accelerations and Epicentral Distance values can be generated by rasterization of layers available from the USGS Shakemap website (earthquake.usgs.gov/data/shakemap).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rose, W.I.; Bommer, J.J.; López, D.L.; Carr, M.J.; Major, J.J. Natural Hazards in El Salvador; Geological Society of America, 2004. [Google Scholar] [CrossRef]
  2. Quesada-Román, A.; Campos-Durán, D. Natural Disaster Risk Inequalities in Central America. Pap. Appl. Geogr. 2022. [Google Scholar] [CrossRef]
  3. Marano, K.D.; Wald, D.J.; Allen, T.I. Global Earthquake Casualties Due to Secondary Effects: A Quantitative Analysis for Improving Rapid Loss Analyses. Nat. Hazards 2010, 52, 319–328. [Google Scholar] [CrossRef]
  4. Agnesi, V.; Carrara, A.; Macaluso, T.; Monteleone, S.; Pipitone, G.; Sorriso-Valvo, M. (Preliminary Observations of Slope Instability Phenomena Induced by the Earthquake of November 1980 on the Upper Valley of Sele River). Geol. Appl. e Idrogeol. 1982, 17, 79–93. [Google Scholar]
  5. Agnesi, V.; Carrara, A.; Macaluso, T.; Monteleone, S.; Pipitone, G.; Sorriso-Valvo, M. (Typological and Morphological Features of Slope Instability Phenomena Induced by the 1980 Earthquake, Upper Sele Valley, Southern Italy). Geol. Appl. Idrogeol. 1983, 18, 309–341. [Google Scholar]
  6. A. Carrara, V.A.T.M.S.M.G.P. Slope Movements Induced by the Southern Italy Earthquake of November 1980. IAEG 1986, 2, 237–250. [Google Scholar]
  7. Agnesi, V.; Camarda, M.; Conoscenti, C.; Di Maggio, C.; Serena Diliberto, I.; Madonia, P.; Rotigliano, E. A Multidisciplinary Approach to the Evaluation of the Mechanism That Triggered the Cerda Landslide (Sicily, Italy). Geomorphology 2005, 1–2, 101–116. [Google Scholar] [CrossRef]
  8. Rotigliano, E.; Cappadonia, C.; Conoscenti, C.; Costanzo, D.; Agnesi, V. Slope Units-Based Flow Susceptibility Model: Using Validation Tests to Select Controlling Factors. Nat. Hazards 2012, 61, 143–153. [Google Scholar] [CrossRef]
  9. Keefer, D.K. Landslides Caused by Earthquakes. Geol. Soc. Am. Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
  10. Martino, S.; Prestininzi, A.; Romeo, R.W. Earthquake-Induced Ground Failures in Italy from a Reviewed Database. Nat. Hazards Earth Syst. Sci. 2014, 14, 799–814. [Google Scholar] [CrossRef]
  11. Legros, F. The Mobility of Long-Runout Landslides. Eng. Geol. 2002, 63, 301–331. [Google Scholar] [CrossRef]
  12. Hayashi, J.N.; Self, S. A Comparison of Pyroclastic Flow and Debris Avalanche Mobility. J. Geophys. Res. Solid Earth 1992, 97, 9063–9071. [Google Scholar] [CrossRef]
  13. Bommer, J.; Benito, B.; Ciudad-Real, M.; Lemoine, A.; López-Menjívar, M.; Madariaga, R.; Mankelow, J.; Méndez de Hasbun, P.; Murphy, W.; Nieto-Lovo, M.; et al. The El Salvador Earthquakes of January and February 2001: Context, Characteristics and Implications for Seismic Risk. [CrossRef]
  14. Jibson, R.W.; Crone, A.J.; Harp, E.L.; Baum, R.L.; Major, J.J.; Pullinger, C.R.; Escobar, C.D.; Martínez, M.; Smith, M.E. Landslides Triggered by the 13 January and 13 February 2001 Earthquakes in El Salvador. Spec. Pap. Geol. Soc. Am. 2004. [Google Scholar] [CrossRef]
  15. Chen, H. Controlling Factors of Hazardous Debris Flow in Taiwan. Quat. Int. 2006, 147, 3–15. [Google Scholar] [CrossRef]
  16. Larsen, M.C.; Wieczorek, G.F. Geomorphic Effects of Large Debris Flows and Flash Floods, Northern Venezuela, 1999. Zeitschrift fur Geomorphol. Suppl. 2006. [Google Scholar]
  17. Brabb, E.E. Innovative Approaches to Landslide Hazard and Risk Mapping 1985, 1, 17–22.
  18. Vargas-Cuervo, G.; Rotigliano, E.; Conoscenti, C. Prediction of Debris-Avalanches and -Flows Triggered by a Tropical Storm by Using a Stochastic Approach: An Application to the Events Occurred in Mocoa (Colombia) on 1 April 2017. Geomorphology 2019, 339, 31–43. [Google Scholar] [CrossRef]
  19. Martinello, C.; Mercurio, C.; Argueta-Platero, A.A.; Cappadonia, C.; Rotigliano, E.; Conoscenti, C. Prediction of the spatial distribution of landslides generated from earthquakes by using an approach which combines a rainfall-induced inventory and static with seismic parameters. Submitted to MDPI Remote Sensing.
  20. Lombardo, L.; Cama, M.; Maerker, M.; Rotigliano, E. A Test of Transferability for Landslides Susceptibility Models under Extreme Climatic Events: Application to the Messina 2009 Disaster. Nat. Hazards 2014, 74, 1951–1989. [Google Scholar] [CrossRef]
  21. Khalaj, S.; BahooToroody, F.; Mahdi Abaei, M.; BahooToroody, A.; De Carlo, F.; Abbassi, R. A Methodology for Uncertainty Analysis of Landslides Triggered by an Earthquake. Comput. Geotech. 2020, 117, 1–13. [Google Scholar] [CrossRef]
  22. Bahootoroody, F.; Khalaj, S.; Leoni, L.; De Carlo, F.; Di Bona, G.; Forcina, A. Reliability Estimation of Reinforced Slopes to Prioritize Maintenance Actions. Int. J. Environ. Res. Public Health 2021, 18, 1–12. [Google Scholar] [CrossRef] [PubMed]
  23. Conoscenti, C.; Martinello, C.; Alfonso-Torreño, A.; Gómez-Gutiérrez, Á. Predicting Sediment Deposition Rate in Check-Dams Using Machine Learning Techniques and High-Resolution DEMs. Environ. Earth Sci. 2021. [Google Scholar] [CrossRef]
  24. Cappadonia, C.; Cafiso, F.; Ferraro, R.; Martinello, C.; Rotigliano, E. Rockfall Hazards of Mount Pellegrino Area (Sicily, Southern Italy). J. Maps 2021, 17, 29–39. [Google Scholar]
  25. Carrara, A.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Gis Technology in Mapping Landslide Hazard. In; Springer, Dordrecht, 1995; pp. 135–175. [CrossRef]
  26. Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic Landslide Hazard Assessment at the Basin Scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
  27. Furlani, S.; Ninfo, A. Is the Present the Key to the Future? Earth-Science Rev. 2015, 142, 38–46. [Google Scholar] [CrossRef]
  28. Heckmann, T.; Gegg, K.; Gegg, A.; Becht, M. Sample Size Matters: Investigating the Effect of Sample Size on a Logistic Regression Susceptibility Model for Debris Flows. Nat. Hazards Earth Syst. Sci. 2014, 14, 259–278. [Google Scholar] [CrossRef]
  29. Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of Susceptibility to Earth-Flow Landslide Using Logistic Regression and Multivariate Adaptive Regression Splines: A Case of the Belice River Basin (Western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
  30. Allison, P.D. Logistic Regression Using the SAS System: Theory and Application, SAS Institute Inc., Cary, NC Available online:. Available online: http://www.sciepub.com/reference/248083 (accessed on 26 November 2020).
  31. Nowicki Jessee, M.A.; Hamburger, M.W.; Allstadt, K.; Wald, D.J.; Robeson, S.M.; Tanyas, H.; Hearne, M.; Thompson, E.M. A Global Empirical Model for Near-Real-Time Assessment of Seismically Induced Landslides. J. Geophys. Res. Earth Surf. 2018, 123, 1835–1859. [Google Scholar] [CrossRef]
  32. Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the Quality of Landslide Susceptibility Models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
  33. Carrara, A.; Crosta, G.; Frattini, P. Comparing Models of Debris-Flow Susceptibility in the Alpine Environment. Geomorphology 2008. [Google Scholar] [CrossRef]
  34. Brenning, A. Spatial Prediction Models for Landslide Hazards: Review, Comparison and Evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
  35. Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial Prediction Models for Shallow Landslide Hazards: A Comparative Assessment of the Efficacy of Support Vector Machines, Artificial Neural Networks, Kernel Logistic Regression, and Logistic Model Tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
  36. Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How Can Statistical Models Help to Determine Driving Factors of Landslides? Ecol. Modell. 2012, 239, 27–39. [Google Scholar] [CrossRef]
  37. Yilmaz, I. Landslide Susceptibility Mapping Using Frequency Ratio, Logistic Regression, Artificial Neural Networks and Their Comparison: A Case Study from Kat Landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
  38. Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth-Science Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
  39. Frattini, P.; Crosta, G.; Carrara, A. Techniques for Evaluating the Performance of Landslide Susceptibility Models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
  40. Mercurio, C.; Martinello, C.; Rotigliano, E.; Argueta-Platero, A.A.; Reyes-Martínez, M.E.; Rivera-Ayala, J.Y.; Conoscenti, C. Mapping Susceptibility to Debris Flows Triggered by Tropical Storms: A Case Study of the San Vicente Volcano Area (El Salvador, CA). 2021. [Google Scholar] [CrossRef]
  41. Dewey, J.W.; Suárez, G. Seismotectonics of Middle America. Neotectonics North Am. 1991, 309–321. [Google Scholar] [CrossRef]
  42. Bommer, J.J.; Benito, M.B.; Ciudad-Real, M.; Lemoine, A.; López-Menjívar, M.A.; Madariaga, R.; Mankelow, J.; Méndez de Hasbun, P.; Murphy, W.; Nieto-Lovo, M.; et al. The El Salvador Earthquakes of January and February 2001: Context, Characteristics and Implications for Seismic Risk. Soil Dyn. Earthq. Eng. 2002. [Google Scholar] [CrossRef]
  43. Campos-Durán, D.; Quesada-Román, A. Intensive and Extensive Risk in Central America Between 1990 and 2015. Anuário do Inst. Geociências - UFRJ 2017, 40, 234–249. [Google Scholar] [CrossRef]
  44. Cruden, D.M.; and Varnes, D.J. (1996) Landslide Types and Processes. In Turner, A.K. and Shuster, R.L., Eds., Landslides Investigation and Mitigation, Transportation Research Board, Special Report No. 247, 36-75. - References - Scientific Research Publishing. Available online: https://www.scirp.org/(S(czeh2tfqyw2orz553k1w0r45))/reference/ReferencesPapers.aspx?ReferenceID=1855371 (accessed on 16 November 2020).
  45. Lomnitz, C.; Elizarrarás, S.R. El Salvador 2001: Earthquake Disaster and Disaster Preparedness in a Tropical Volcanic Environment. Seismol. Res. Lett. 2001, 72, 346–351. [Google Scholar] [CrossRef]
  46. Galli, M.; Ardizzone, F.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Comparing Landslide Inventory Maps. Geomorphology 2008, 94, 268–289. [Google Scholar] [CrossRef]
  47. Steger, S.; Brenning, A.; Bell, R.; Glade, T. The Propagation of Inventory-Based Positional Errors into Statistical Landslide Susceptibility Models. Nat. Hazards Earth Syst. Sci. 2016, 16, 2729–2745. [Google Scholar] [CrossRef]
  48. Steger, S.; Brenning, A.; Bell, R.; Glade, T. The Influence of Systematically Incomplete Shallow Landslide Inventories on Statistical Susceptibility Models and Suggestions for Improvements. Landslides 2017, 14, 1767–1781. [Google Scholar] [CrossRef]
  49. Rotigliano, E.; Martinello, C.; Agnesi, V.; Conoscenti, C. Evaluation of Debris Flow Susceptibility in El Salvador (CA): A Comparisobetween Multivariate Adaptive Regression Splines (MARS) and Binary Logistic Regression (BLR). Hungarian Geogr. Bull. 2018, 67, 361–373. [Google Scholar] [CrossRef]
  50. Martinello, C.; Mercurio, C.; Cappadonia, C.; Hernández Martínez, M.Á.; Reyes Martínez, M.E.; Rivera Ayala, J.Y.; Conoscenti, C.; Rotigliano, E. Investigating Limits in Exploiting Assembled Landslide Inventories for Calibrating Regional Susceptibility Models: A Test in Volcanic Areas of El Salvador. Appl. Sci. 2022, 12. [Google Scholar] [CrossRef]
  51. Rotigliano, E.; Agnesi, V.; Cappadonia, C.; Conoscenti, C. The Role of the Diagnostic Areas in the Assessment of Landslide Susceptibility Models: A Test in the Sicilian Chain. Nat. Hazards 2011, 58, 981–999. [Google Scholar] [CrossRef]
  52. Cama, M.; Lombardo, L.; Conoscenti, C.; Agnesi, V.; Rotigliano, E. Predicting Storm-Triggered Debris Flow Events: Application to the 2009 Ionian Peloritan Disaster (Sicily, Italy). Nat. Hazards Earth Syst. Sci. 2015, 15, 1785–1806. [Google Scholar] [CrossRef]
  53. Rotigliano, E.; Martinello, C.; Hernandéz, M.A.; Agnesi, V.; Conoscenti, C. Predicting the Landslides Triggered by the 2009 96E/Ida Tropical Storms in the Ilopango Caldera Area (El Salvador, CA): Optimizing MARS-Based Model Building and Validation Strategies. Environ. Earth Sci. 2019, 78. [Google Scholar] [CrossRef]
  54. Carrara, A.; Guzzetti, F. Geographical Information Systems in Assessing Natural Hazards. Nuevos Sist. Comun. e Inf. 1995, 2013–2015. [Google Scholar]
  55. Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide Hazard Evaluation: A Review of Current Techniques and Their Application in a Multi-Scale Study, Central Italy. In Proceedings of the Geomorphology; Elsevier, December 1 1999; Vol. 31; pp. 181–216. [Google Scholar] [CrossRef]
  56. Hansen, A. 1984. Landslide Hazard Analysis. In: Brunsden, D. & Prior, D.B. (Eds.), Slope Instability, John Wiley and Sons, New York, Pp. 523-602. Available online: http://www.sciepub.com/reference/209033 (accessed on 1 October 2022).
  57. Cama, M.; Lombardo, L.; Conoscenti, C.; Rotigliano, E. Improving Transferability Strategies for Debris Flow Susceptibility AssessmentApplication to the Saponara and Itala Catchments (Messina, Italy). Geomorphology 2017, 288, 52–65. [Google Scholar] [CrossRef]
  58. Martinello, C.; Cappadonia, C.; Conoscenti, C.; Agnesi, V.; Rotigliano, E. Optimal Slope Units Partitioning in Landslide Susceptibility Mapping. J. Maps 2020. [Google Scholar] [CrossRef]
  59. Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of Differences in Resolution and Sources of Controlling Factors for Gully Erosion Susceptibility Mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
  60. Shao, X.; Xu, C. Earthquake-Induced Landslides Susceptibility Assessment: A Review of the State-of-the-Art. Nat. Hazards Res. 2022. [Google Scholar] [CrossRef]
  61. Wald, D.J.; Worden, C.B.; Thompson, E.M.; Hearne, M. ShakeMap Operations, Policies, and Procedures. Earthq. Spectra 2022, 38, 756–777. [Google Scholar]
  62. Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
  63. Hijmans, R.J. Geographic Data Analysis and Modeling [R Package Raster Version 3.6-3]. 2022.
  64. Package “usdm” Type Package Title Uncertainty Analysis for Species Distribution Models. 2022.
  65. Mahto Ananda Package “splitstackshape” Type Package Title Stack and Reshape Datasets After Splitting Concatenated Values. 2018.
  66. Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.C.; Müller, M. PROC: An Open-Source Package for R and S+ to Analyze and Compare ROC Curves. BMC Bioinformatics 2011, 12, 1–8. [Google Scholar]
  67. Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing Classifier Performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef] [PubMed]
  68. Max Kuhn Contributions from Jed Wing, A.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B. ; Core Team, the R.; Benesty, M.; et al. Package “caret” Title Classification and Regression Training Description Misc Functions for Training and Plotting Classification and Regression Models. 2018, 2.
  69. Milborrow, S. Notes on the Earth Package. 2021.
  70. Van Den Eeckhaut, M.; Hervás, J.; Jaedicke, C.; Malet, J.P.; Montanarella, L.; Nadim, F. Statistical Modelling of Europe-Wide Landslide Susceptibility Using Limited Landslide Inventory Data. Landslides 2012, 9, 357–369. [Google Scholar]
  71. Svoray, T.; Michailov, E.; Cohen, A.; Rokah, L.; Sturm, A. Predicting Gully Initiation: Comparing Data Mining Techniques, Analytical Hierarchy Processes and the Topographic Threshold. Earth Surf. Process. Landforms 2012, 37, 607–619. [Google Scholar] [CrossRef]
  72. Javidan, N.; Kavian, A.; Pourghasemi, H.R.; Conoscenti, C.; Jafarian, Z.; Rodrigo-Comino, J. Evaluation of Multi-Hazard Map Produced Using MaxEnt Machine Learning Technique. Sci. Reports 2021 111 2021, 11, 1–20. [Google Scholar] [CrossRef]
  73. Conoscenti, C.; Agnesi, V.; Cama, M.; Caraballo-Arias, N.A.; Rotigliano, E. Assessment of Gully Erosion Susceptibility Using Multivariate Adaptive Regression Splines and Accounting for Terrain Connectivity. L. Degrad. Dev. 2018, 29, 724–736. [Google Scholar] [CrossRef]
  74. Conoscenti, C.; Rotigliano, E. Predicting Gully Occurrence at Watershed Scale: Comparing Topographic Indices and Multivariate Statistical Models. Geomorphology 2020, 359. [Google Scholar] [CrossRef]
  75. Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; ISBN 9780471722144. [Google Scholar]
  76. Avila, L.A.; Cangialosi, J. Tropical Cyclone Report.
  77. Avila, R. “Síntesis de Los Informes de Evaluación Técnica de Las Lluvias Del 7 y 8 de Noviembre 2009 En El Salvador: Análisis Del Impacto Físico Natural y Vulnerabilidad Socio Ambiental”.
  78. Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A GIS-Based Automated Procedure for Landslide Susceptibility Mapping by the Conditional Analysis Method: The Baganza Valley Case Study (Italian Northern Apennines). Environ. Geol. 2006, 50, 941–961. [Google Scholar] [CrossRef]
  79. Costanzo, D.; Chacón, J.; Conoscenti, C.; Irigaray, C.; Rotigliano, E. Forward Logistic Regression for Earth-Flow Landslide Susceptibility Assessment in the Platani River Basin (Southern Sicily, Italy). Landslides 2014, 11, 639–653. [Google Scholar] [CrossRef]
Preprints 67380 g001
Figure 1. Location and geological setting of the study area. El Salvador is located in Central America, where the Cocos Plate is subducted beneath the Caribbean Plate into the Middle American Trench (a); geological setting of El Salvador, mainly characterized by the volcanoes chain and by the large outcropping of volcanic rocks (b).
Figure 1. Location and geological setting of the study area. El Salvador is located in Central America, where the Cocos Plate is subducted beneath the Caribbean Plate into the Middle American Trench (a); geological setting of El Salvador, mainly characterized by the volcanoes chain and by the large outcropping of volcanic rocks (b).
Preprints 67380 g001
Preprints 67380 g002
Figure 2. Location of the fourteen study areas: sectors 1-3 and 4-8 were heavily affected by the earthquake of 13 January 2001; sectors 9-14 were severely affected by the earthquake of 13 February 2001.
Figure 2. Location of the fourteen study areas: sectors 1-3 and 4-8 were heavily affected by the earthquake of 13 January 2001; sectors 9-14 were severely affected by the earthquake of 13 February 2001.
Preprints 67380 g002
Preprints 67380 g003
Figure 3. Main earthquakes (Mw > 5.5) that affected El Salvador. The earthquakes that hit the country on 13 January and 13 February 2001 are highlighted.
Figure 3. Main earthquakes (Mw > 5.5) that affected El Salvador. The earthquakes that hit the country on 13 January and 13 February 2001 are highlighted.
Preprints 67380 g003
Preprints 67380 g004
Figure 4. Positions of the epicenters, paths and areas covered by the aerial images employed to map the landslides occurred in January and February 2001.
Figure 4. Positions of the epicenters, paths and areas covered by the aerial images employed to map the landslides occurred in January and February 2001.
Preprints 67380 g004
Preprints 67380 g005
Figure 5. Locations of the datasets used for the landslide susceptibility modelling.
Figure 5. Locations of the datasets used for the landslide susceptibility modelling.
Preprints 67380 g005
Preprints 67380 g006
Figure 6. PGA values and LIPs related to the seismic event of Mw 7.7 of 13 January 2001 in the fourteen study areas.
Figure 6. PGA values and LIPs related to the seismic event of Mw 7.7 of 13 January 2001 in the fourteen study areas.
Preprints 67380 g006
Preprints 67380 g007
Figure 7. PGA values of the seismic event of 13 February 2001 and LIPs of the landslides triggered in the FEB study areas.
Figure 7. PGA values of the seismic event of 13 February 2001 and LIPs of the landslides triggered in the FEB study areas.
Preprints 67380 g007
Preprints 67380 g008
Figure 8. LIPs of the landslides triggered by the seismic event 13 February 2001 in the intersection between FEB and SV study areas (FSE).
Figure 8. LIPs of the landslides triggered by the seismic event 13 February 2001 in the intersection between FEB and SV study areas (FSE).
Preprints 67380 g008
Preprints 67380 g009
Figure 9. Box plots of the AUC values achieved by the M1, M2, M3 and M4 models, measured on the validation samples of the datasets JAN, FEB, JF and FSE for both validation scenarios (Scenario 1: test rate 25%; Scenario 2: test rate: 95%).
Figure 9. Box plots of the AUC values achieved by the M1, M2, M3 and M4 models, measured on the validation samples of the datasets JAN, FEB, JF and FSE for both validation scenarios (Scenario 1: test rate 25%; Scenario 2: test rate: 95%).
Preprints 67380 g009
Table 1. Extent, average and standard deviation of altitude and slope angle, and the main outcropping lithology classes. GEO1: soft rocks (intermediate basic effusive rocks and subordinate pyroclastites); GEO2: hard rocks (intermediate basic effusive rocks); GEO3: medium rocks (acid effusive and acid intermediate rocks); GEO4: very soft soils (Tierra Blanca: acidic pyroclastites, subordinate volcanic epiclastites and acid effusive rocks); GEO5: soft soils (Quaternary sedimentary deposits); GEO6: hard soils (acid pyroclastic rocks, volcanic epiclastites); GEO7: medium soils (volcanic epiclastites and pyroclastites, locally effusive basic-intermediate rocks).
Table 1. Extent, average and standard deviation of altitude and slope angle, and the main outcropping lithology classes. GEO1: soft rocks (intermediate basic effusive rocks and subordinate pyroclastites); GEO2: hard rocks (intermediate basic effusive rocks); GEO3: medium rocks (acid effusive and acid intermediate rocks); GEO4: very soft soils (Tierra Blanca: acidic pyroclastites, subordinate volcanic epiclastites and acid effusive rocks); GEO5: soft soils (Quaternary sedimentary deposits); GEO6: hard soils (acid pyroclastic rocks, volcanic epiclastites); GEO7: medium soils (volcanic epiclastites and pyroclastites, locally effusive basic-intermediate rocks).
Sector Area [km2] Altitude [m a.s.l.] Slope angle [°] Two main lithology
classes
Mean Std.dev. Mean Std.dev.
1 15.41 577.73 64.19 15.10 11.22 GEO7 (83.92%) GEO2 (15.39%)
2 2.31 1039.00 50.69 25.17 10.02 GEO2
(84.42%)		 GEO7 (15.58%)
3 23.89 975.86 70.16 14.71 12.96 GEO7 (42.38%) GEO4 (26.70%)
4 3.98 286.16 41.14 20.51 10.71 GEO7 (100.00%) -
5 2.66 287.80 31.01 16.38 9.41 GEO7 (98.44%) GEO1 (1.56%)
6 3.89 1008.35 85.91 12.11 9.23 GEO1 (72.80%) GEO7 (27.20%)
7 8.29 862.50 70.54 11.05 8.79 GEO1 (50.97%) GEO7 (49.03%)
8 31.42 78.34 22.40 3.29 4.28 GEO7 (95.32%) GEO5
(1.81%)
9 155.32 618.41 122.58 24.23 12.43 GEO7 (30.17%) GEO6 (27.98%)
10 5.32 685.48 28.97 16.46 12.00 GEO6 (56.19%) GEO4 (41.14%)
11 13.79 781.87 74.31 16.09 10.14 GEO2 (51.69%) GEO6
(31.39%)
12 34.80 699.61 51.11 16.30 10.01 GEO2 (10.39%) GEO6
(73.24%)
13 87.65 833.88 365.10 17.93 13.55 GEO4 (36.26%) GEO1 (31.78%)
14 8.84 266.62 39.17 5.12 5.55 GEO6
(90.25%)		 GEO2 (8.57%)
Table 2. Precipitation in the 12 months preceding the seismic events of 2001 and the average annual precipitation in the period 1971-1999 in the fourteen areas under consideration.
Table 2. Precipitation in the 12 months preceding the seismic events of 2001 and the average annual precipitation in the period 1971-1999 in the fourteen areas under consideration.
Sector 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Rainfall [mm]
Mar 2000-Feb 2001 		1166 1614 1614 1571 1571 1571 1571 1571 1632 1632 1632 1632 1632 1632
Average rainfall [mm] 1971-1999 1657 1847 1847 1650 1650 1650 1650 1650 1836 1836 1836 1836 1836 1836
Table 3. Independent variables used to model rainfall- and earthquake-induced landslides.
Table 3. Independent variables used to model rainfall- and earthquake-induced landslides.
Independent variable Application for
rainfall-induction / earthquake-induction landslide susceptibility
(Y: yes, N: no)		 Type Reference
ASP Aspect Y/Y Preparatory Geospatial Data Abstraction Library QGis
C_AR Catchment Area Y/Y Preparatory SAGA GIS
C_IND Convergence Index Y/Y Preparatory SAGA GIS
D_CUR Downslope Curvature Y/Y Preparatory SAGA GIS
ELE Elevation Y/Y Preparatory 10-m DEM resampled from a 5-m DEM from ESA
DIST Epicentral Distance N/Y Trigger USGS website
GEO Geology Y/Y Preparatory Geological map from Schmidt-Thomé
(modified)
NDVI Normalized Difference Vegetation Index Y/Y Preparatory Terra/MODIS Satellite NASA
PGA Peak Ground Acceleration N/Y Trigger USGS Shakemap
SLO Slope Y/Y Preparatory Geospatial Data Abstraction Library QGis
TPI Topographic Positioning
Index		 Y/Y Preparatory Geospatial Data Abstraction Library QGis
TWI Topographic Wetness
Index		 Y/Y Preparatory SAGA GIS
U_CUR Upslope Curvature Y/Y Preparatory SAGA GIS
Table 4. Datasets used to calibrate and validate the landslide predictive models.
Table 4. Datasets used to calibrate and validate the landslide predictive models.
Dataset code Area Trigger Landslides date
SV San Vicente area (Mercurio et al., 2021) Rainfall Nov, 2009
JAN Sectors 1 to 8 Earthquake Jan, 2001
FEB Sectors 9 to 14 Earthquake Feb, 2001
JF Sectors 9 to 14 Earthquake Jan, 2001
FSE Intersections between FEB and SV areas Earthquake Feb, 2001
Table 5. Inventories and independent variables used in M1, M2, M3, M4 models.
Table 5. Inventories and independent variables used in M1, M2, M3, M4 models.
Inventory for Calibration Model
M1 M2 M3 M4
SV (rainfall-induction) X
JAN, JF, FEB, FSE (earthquake-induction) X X X
Independent variables
PSV X
Ten preparatory variables X X
Two trigger variables X X X
Area/Inventory for validation
JAN, JF, FEB, FSE (earthquake-induction) X X X X
Table 6. Amounts and characteristics of the landslides triggered by the January earthquake in sectors 1 to 14.
Table 6. Amounts and characteristics of the landslides triggered by the January earthquake in sectors 1 to 14.
Sector Area of the sector (km2) N° of LIPs %
of event cells
 N° of landslides extending < 100 m2; (%) N° of
landslides extending 100-1,000 m2; (%)		 N° of
landslides extending 1,000-1,0000 m2; (%)		 N° of landslides extending > 10,000 m2; (%) Landslides
average extent in m2 		% of landslide cells
1 15.41 245 0.10 84 (34.29) 143 (58.37) 18 (7.35) 0 (0) 297.69 1.24
2 2.31 128 0.52 67 (52.34) 57 (44.53) 4 (3.13) 0 (0) 190.91 3.16
3 23.89 296 0.10 107 (36.15) 159 (53.72) 28 (9.46) 2 (0.68) 870.79 1.45
4 3.98 67 0.07 38 (56.72) 29 (43.28) 0 (0) 0 (0) 145.82 0.39
5 2.66 43 0.15 27 (62.79) 14 (32.56) 2 (4.65) 0 (0) 151.94 0.74
6 3.89 8 0.02 1 (12.50) 6 (75.00) 1 (12.50) 0 (0) 328.59 0.19
7 8.29 17 0.01 1 (5.88) 16 (94.12) 0 (0) 0 (0) 267.09 0.06
8 31.42 193 0.05 88 (45.60) 103 (56.37) 2 (1.04) 0 (0) 116.19 0.31
JAN (1-8) 91.85 997 0.08 413 (41.42) 527 (52.86) 55 (5.52) 2 (0.20) 407.13 0.76
9 155.32 93 0.0025 0 (0) 19 (20.43) 55 (59.14) 19 (20.43) 8,744.50 0.27
10 5.32 1 0.0018 0 (0) 0 (0) 0 (0) 1 (100) 19,571.39 0.44
11 13.79 23 0.0136 0 (0) 8 (34.78) 15 (65.22) 0 (0) 2,079.28 0.35
12 34.80 0 0 0 (0) 0 (0) 0 (0) 0 (0) 0 0
13 87.65 6 0.004 0 (0) 1 (16.67) 3 (50.00) 2 (33.33) 10,263.87 0.05
14 8.84 0 0 0 (0) 0 (0) 0 (0) 0 (0) 0 0
JF (9-14) 305.72 123 0.002 0 (0) 28 (22.77) 73 (59.34) 22 (17.89) 7,660.25 0.20
JAN+JF (1-14) 397.57 1,120 0.017 413 (36.88) 555 (49.56) 128 (11.42) 24 (2.14) 3,585.67 0.30
Table 7. Amounts and characteristics of the gravitational phenomena of landslides belonging to sectors 9 to 14 related to the February earthquake.
Table 7. Amounts and characteristics of the gravitational phenomena of landslides belonging to sectors 9 to 14 related to the February earthquake.
Sector Area of the sector (km2) N° of LIPs %
of event cells		 N° of landslides extending < 100 m2; (%) N° of
landslides extending 100-1,000 m2; (%)		 N° of
landslides extending 1,000-1,0000 m2; (%)		 N° of landslides extending > 10,000 m2; (%) Landslides average extent in m2 % of landslide cells
9 155.32 3650 0.10 427 (11.70) 2,145 (58.77) 955 (26.16) 123 (3.37) 1,694.63 2.47
10 5.32 186 0.33 32 (17.20) 119 (63.98) 34 (18.28) 1 (0.54) 789.50 4.68
11 13.79 279 0.16 91 (32.62) 151 (54.12) 37 (13.26) 0 (0) 554.75 1.58
12 34.80 209 0.06 6 (2.87) 144 (68.90) 57 (27.27) 2 (0.96) 1,093.83 1.16
13 87.65 1029 0.07 172 (16.72) 563 (54.71) 267 (25.95) 27 (2.62) 1,500.60 1.56
14 8.84 18 0.02 8 (44.44) 10 (55.56) 0 (0) 0 (0) 126.75 0.08
FEB (9-14) 305.72 5,371 0.092 736 (13.70) 3,132 (58.31) 1,350 (25.13) 153 (2.85) 1,538.26 2.12
Table 8. AUC mean and standard deviation (SD) calculated for the four models and datasets, with the two validation scenarios (Scenario 1: test rate 25%; Scenario 2: test rate: 95%).
Table 8. AUC mean and standard deviation (SD) calculated for the four models and datasets, with the two validation scenarios (Scenario 1: test rate 25%; Scenario 2: test rate: 95%).
Scenario 1 AUC_JAN_mean AUC_JAN_SD AUC_FEB_mean AUC_FEB_SD AUC_JF_mean AUC_JF_SD AUC_FSE_mean AUC_FSE_SD
M1_25 0.711 0.027 0.658 0.008 0.789 0.043 0.679 0.020
M2_25 0.723 0.013 0.687 0.008 0.880 0.042 0.731 0.020
M3_25 0.749 0.020 0.732 0.007 0.895 0.019 0.763 0.017
M4_25 0.787 0.017 0.780 0.010 0.958 0.020 0.825 0.012
Scenario 2 AUC_JAN_mean AUC_JAN_SD AUC_FEB_mean AUC_FEB_SD AUC_JF_mean AUC_JF_SD AUC_FSE_mean AUC_FSE_SD
M1_95 0.703 0.009 0.655 0.004 0.808 0.019 0.683 0.006
M2_95 0.685 0.008 0.684 0.004 0.809 0.015 0.704 0.006
M3_95 0.717 0.007 0.720 0.005 0.855 0.015 0.742 0.007
M4_95 0.729 0.004 0.768 0.004 0.889 0.015 0.788 0.004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated