Prerpints.org logo
Preprint
Article

WEA: A Node Importance Algorithm in Weighted Networks

Altmetrics

Downloads

188

Views

32

Comments

0

Submitted:

13 January 2023

Posted:

23 January 2023

You are already at the latest version

Alerts
Abstract
The heterogeneous structure implies that a few nodes may be crucial in maintaining network structural and functional properties. Identifying these crucial nodes correctly and quickly is a primary issue as contemporarily may face the mushrooming of large-scale datasets. Besides, the ‘weight issue’ is always ignored in this field which edge weight may play a positive/negative role in contributing to the node importance in different weighted networks. This paper provides a novel algorithm, Weighted Expectation Algorithm (WEA), which aims to ensure accuracy and speed of computation by taking advantage of dynamic programming to better handle the task of large-scale networks. Additionally, the weight issue that edge weights may contribute differently is addressed by a simply quantitative definition. Two standard experiments show WEA can maintain the network structure in connectivity well (by the lowest average robustness 0.192) and identify the node importance better in the spreading function test of spreading dynamics (by the highest average Kendall’s tau-b 0.678). In addition, the time complexities of different algo-rithms are evaluated, and their time-consuming are tested, proving that WEA consumes a rela-tively short time.
Keywords: 
Subject: Computer Science and Mathematics  -   Geometry and Topology

1. Introduction

Network relationships exist in many complex systems, which involve all aspects of human social activities. For instance, power networks [1], social networks [2,3,4], and epidemic spread networks [5,6]. The notion of the network is widely used to depict the complex relationships between different entities [7], and the topology characteristics often play an essential role in network information mining. For a long time, researchers have focused on the research of unweighted networks, such as the node importance [7,8], the edge importance [9], and the link prediction based on it [10,11]. While, the issue of the node importance is essentially basic, and some algorithms to measure the importance of the nodes are proposed based on the network's primary topology feature. For instance, Degree Centrality is a classic, simple, and effective algorithm for unweighted networks, directly measuring the number of neighbors for each node to calculate its importance; The K-core Centrality (KC) [12] is proposed to suggest that a node’s topological location contributes more to its node importance than its first-order neighbor, and it often gets good performance in random network and scale-free network (but poor in small world network). Most of these first proposed ones are generally aimed at unweighted networks.
However, in reality, it is evident that a weighted network always carries more abundant information and is more capable of describing various complex systems [7,13]. For instance, in a traffic network, where edges represent roads and nodes represent intersections, the importance of nodes can be counted by analyzing the traffic flow as edge weight which can finally boost the traffic resource optimization [14]; On social networks, for example where weight represents the time of interactions between two nodes, adding the weighted information into account can better understand the networks’ topological functions and the evolution of a society [15,16]; Setting trade volume as weight in a large-scale economic network makes it possible to reveal the high economic potential nodes and helps the analysis of the stability and robustness of an economic system [17]; Also, the weight notion is essential in the study and application of the identification of the protein complex [18]. Many other weighted networks are being studied, like the PPI network [19], the power grid network [20,21], and the citation network [22,23]. It indicates that the direction of weighted node importance contemporarily is pretty basic.
Generally, from the perspective of complex network construction, existing methods can be classified into four categories: Neighborhood-based methods, Path-based methods, Location-based methods, and Iterative refinement-based methods, respectively. Of course, the combinatorial ones consist of two or several of these four, and those types always have high time complexity. Concisely, we primarily discuss the four basic ones. The representative earliest method based on neighborhood is Degree Centrality (DC) which performs well in studying network vulnerability on scale-free network and exponential network. However, being judged too simple since the original DC only uses a few topology information. Its weighted version then be widely used, the Node strength (Weighted Degree Centrality, WD), mainly stems from the conclusion that in the study of real networks, the degree is always correlated with Node strength [24]. Then, innumerable algorithms belonging to this category emerged, including the well-known H-index. However, H-index can hardly suit undirected weighted networks. In a recent study, Gao et al. improved H-Index and proposed another (HI) [25] that can apply to undirected networks. As for the Path-based methods, Betweenness Centrality (BT) [26] and Closeness Centrality (CL) [27] are the most classical ones, and they can well suit weighted networks. BT measures how much the shortest path goes through a node to show its hub function to control the information flow where the distribution has a power law. It performs well in scale-free networks. CL measures all the distance from the observed node to any other ones in the network to show an average propagation length of the information in the network. Still, owing to its feature, BT tends to miss the information of node importance that is not in the defined path, and some information in the defined path will be over-emphasized in computing. Location-based methods argue that the node located in the core will have much more spreading ability than the nodes in the periphery [7]. After the proposal of the unweighted K-core, many improved versions have emerged. An impressive one can be W-Core decomposition (WC) [28], which decomposes the calculation of node importance into two factors, degree strength and node strength, through a small number of adjustable parameters. Similar to WC, Marius Eidsaa et al. proposed S-Core decomposition (SC) [29], where the nearest integer to the node strength is recorded to be the importance score every time and then considered to be its core number. These two algorithms, based on KC, can well collect the edge weight contribution to the importance of its linked nodes. Nevertheless, whatever the KC, WC, or SC, they have two drawbacks: One is the careless classification mainly because usually, a considerable number of nodes belonging to the same core will be considered at the same importance score; Another, these three perform poorly in Barabasi Albert (BA) networks and tree-like networks, where the core values of all nodes are minimal and indistinguishable [7]. A very typical iterative refinement-based method is Eigenvector Centrality (EC) [30]. Algorithms in this class usually can fully consider the information of multi-order neighbors. While different from the previous ones, they reach a steady state after iterative computing and output the sorting results. Due to too much iteration, practically, it makes EC kindred algorithms inefficient.
Although many algorithms, including EC, WC, and SC, can be applied to unweighted and weighted networks, the parameters of these algorithms need to be manually assigned by pre-estimation. Furthermore, some could not reach accurate outcomes. HI aimed to solve that problem to gain better convergence and stronger robustness. Nonetheless, it becomes more time-consuming, even if it is more capable of accurately evaluating node importance. In some situations, some algorithms based on corresponding methods can ensure the sorting an excellent accuracy, such as HI, but inevitably make themselves more time-consuming.
To the best of our knowledge, until current days, few works have considered the negative weight contribution to the node importance, whereas widely exist in reality and need a framework to quantify the calculation.
Table 1. Different types of centrality Algorithms.
Table 1. Different types of centrality Algorithms.
Classification Representative Ones Advantages Disadvantages
Neighborhood-based methods Degree Centrality Easy to calculate Accounting less information
HI (improved H-Index) Excellent accuracy High time
complexity
Path-based methods Betweenness Centrality Accurate in in scale-free
networks		 Relatively high time
complexity,
Only focus on the path nodes
information
Closeness Centrality More information
to support accuracy		 Relatively high time
complexity
Location-based methods K-Core Some types of networks can be well evaluated Without weight information, poor
performance in BA
network and tree-like networks
W-Core Moderate accuracy Need parameters, poor
performance in BA
network and tree-like networks
S-Core Moderate accuracy Need parameters, poor
performance in BA
network and tree-like networks
Iterative refinement-based methods Eigenvector Centrality Fully consider multi-order neighbor information Need parameters, inefficient for
conducting
To sum up, the mentioned above have achieved some satisfactory outcomes in some aspects, but they also have inherent limitations [31,32]. On the one hand, almost all existing algorithms do not consider whether the weights are positive or negative for the connection strength of the nodes. That means there is an absence of a unified framework to define the positive/negative contribution from the weight to the node importance (the weight issue), which over simplified the network situation in the real world [7]. On the other hand, a dilemma is that accuracy and time complexity are incompatible for most node importance algorithms. The computational complexity makes applying these algorithms a daunting task, which leads to some tasks for large-scale networks not being conducted well [7].
An instance can well illustrate the ‘weight problem’: In the global Covid-19 transmission networks, nodes always represent cities or places. If the weight represents the number of airline seats between two cities, it implies the weight is positively related to the importance of the linked nodes. In comparison, if the weight represents the airline distance between two cities, the weight is negatively connected to the nodes. Until now, few works have considered the negative weight contribution to the node importance, whereas it widely exists in reality. Regarding the second issue, one method is Dynamic programming (DP), which can significantly reduce the time complexity of computations with specific characteristics (with its development in topology). Therefore, we may appropriately solve the second issue by appealing to a design that DP optimizes.
In response to the second issue, we need a brief description of Dynamic programming mechanism. DP is often used to solve optimization problems, such as the shortest path problem and the 0-1 knapsack problem. Moreover, NP-Hard problems are usually involved in 'optimal ' issues as they often have many possible solutions and are inclined to be addressed by DP. Generally, if DP can optimize an algorithm, it should possess two main features: The optimality of substructure and the repeatability of subproblems. The optimality of the substructure means the optimal solution to the original problem can be derived from the optimal solution to its subproblems. The repeatability of subproblems means that during the process of tackling subproblems, even though the decision sequences differ, they produce repetitive states when reaching the same stage. Similar to the divide-and-conquer method, an original problem is decomposed in DP, and the subproblems are firstly solved. Then the solution to the original problem is obtained from the solution to these subproblems. In other perspectives, DP is to save every step outcome of the subproblems in each iteration and then make better use of these outcomes for the coming computing for the original problem.
Inspired by the above mentions, this paper proposed a Weighted Expectation Algorithm (WEA), which well solved the ‘weight problem’. Meanwhile, it can guarantee an accurate calculation with a low time complexity for each node importance score of the network. Experiments on connectivity and the SIR propagation model show that WEA outperforms in accuracy, and the time-consuming testing shows it possesses a high efficiency. Since adopting the idea of Dynamic programming, the time complexity of WEA is O(dmaxEGN), where EG is the total edge numbers, N is the total node numbers and dmax is the maximum degree of the network nodes.

2. Methodology

To better measure the node importance of weighted networks, the influence from weights always needs to be considered based on topology structure and the value [33]. For instance, WC considers both the influence of weights and degrees. We refer to the notion of possible world semantics in the uncertainty graph domain, proposing a possibility importance score factor. The information carried by the weight and its contribution to the node importance is defined as the score of the node under different degree possibilities. A node final importance score is obtained by calculating the set of all the scores in different degree possibilities.
WEA is relatively simple and efficient, which can be divided into three steps: (1). According to the node connected to strength with the weights’ meaning, the weights are pre-processed specifically; (2). The node score Pr (be elaborated in the following) to its importance score factor is calculated through Dynamic programming under all of its degree possibilities; (3). Similar to expectation calculating, a cumulative calculation of Pr scores extract the node’s final importance score.

2.1. Preliminaries

Problem definition. Given a network H(V,E,W), typically a weighted one, where V is node set, E is edge set, and the element eij in E represents the edge between node i and node j. The weight value is Wij. W denotes the weight matrix where the minimum and maximum values are represented by wmin and wmax, respectively. The aim is to produce a set P ranked by the node importance scores, which contains all the nodes in the largest connected subgraph of H without any duplication.
Quantitative definition for the positive/negative weight. We set a ‘bridge’ (2.2 Equation (4)) for positive and negative contribution weight values. In absolute value, the increase in the positive contribution value to the node importance corresponds to the rise in the negative contribution value, but the sign of the contribution is the opposite.
Possible World Semantics. Possible World Semantics (Pr equation) is redefining the contribution of the weighted edges in calculating node importance. Possible World Semantics interprets probability data as a set of deterministic instances called possible worlds, each associated with the probability that can be observed in the real world. Therefore, an uncertain network with t edges can be considered a set of 2t possible deterministic networks.
Preprints 67363 g001
Figure 1. An example of possible world: A graph with 3 edges.
Figure 1. An example of possible world: A graph with 3 edges.
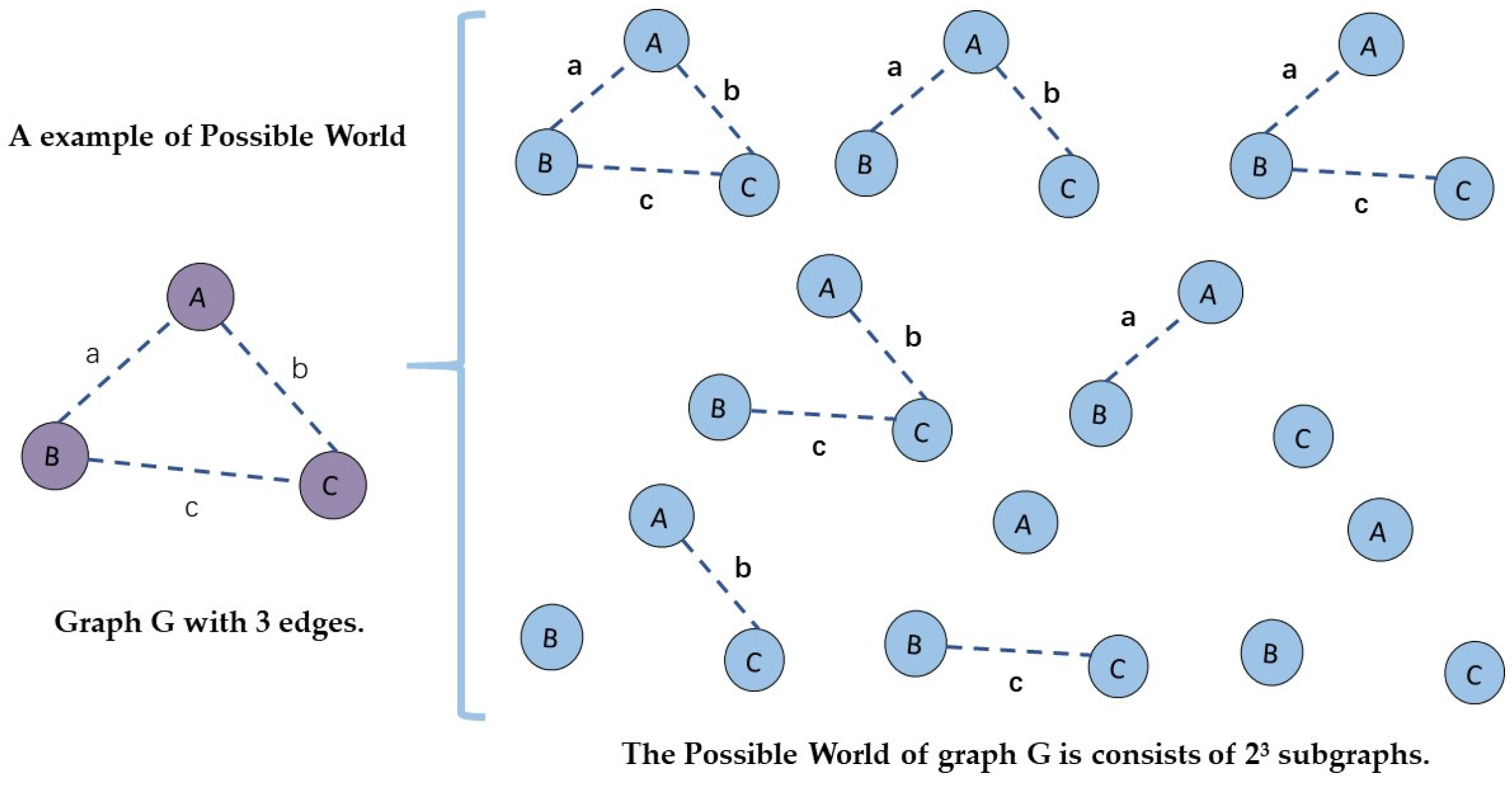
Preprints 67363 g001
Given a target graph G(V,E,W), its subgraph G′(V′,E′,W′) consists of node set V′, edge set E′ and weight set W′, where E ′ ⊆ E , V ′ ⊆ V and W ′ ⊆ W . Use Pr(G′) to denote the probabilities of graph G′(V′,E′,W′), the equation is [34,35,36]:
Pr G ′ = ∏ ϵ ∈ E ′ w i j ′ ∏ e ∈ E / E ′ 1 − w i j ′
The degree of node i in graph G′ be noted as deg(i, G′), abbreviated as deg(i), and c ∈ ( 1 , 2 , … , d e g ( i ) ) is a corresponding factor, called possible importance score in this paper. Thus, we got the following equation [34,35,36]:
Pr [ d e g ( i , G ″ ) ≥ c ] = ∑ G i ′ ∈ G i ″ ≥ c Pr ( G i ′ )
where Gi’ represents any one of the collection of all the possible subgraphs that belong to graph Gi″ (Where i has a degree no less than the inter c). In this paper, we defined any Gi″ could only be made up of one form in this two: First, only consists of node i; Second, consist of node i and some or all of its first-order neighbor nodes [9] and the normalized weight links that between them. The G i ″ ≥ c means { G i ′ ⊆ G i ″ | deg ( i , G ′ ) ≥ c } .
Dynamic programming (DP). DP is a method to solve certain types of sequential decision problems (if DP can solve). The original problem f0 is its aim and a sequence F with a finite number of elements, say F=(f1,f2,f3…), including all the subproblems that sever the original problem.

2.2. Pre-Processing of the Edge Weights

Below is a standard normalized W:
w i j ′ = w i j − w m i n w m a x − w m i n
Note that the value of w i j ′ falls in [0, 1] rather than (0, 1). To avoid the w i j ′ value sitting on the boundary (the value of 0 or 1 caused by w i j = w m i n or w i j = w m a x ), we modify Equation (3) by adding an adaptive parameter l to ensure that w i j ′ ∈ ( 0 , 1 ) . In addition, it is worth noticing that the edge weight could positively or negatively contribute to a node’s importance when given different networks. Therefore, we designed the following normalization equation:
w i j ′ = w i j − ( w min − l ) ( w max + l ) − ( w min − l ) = w i j − w min + l w max − w min + 2 l ,     w i j ∼ C i w i j ′ = w i j − ( w min − l ) ( w max + l ) − ( w min − l ) = 1 − w i j − w min + l w max − w min + 2 l ,     w i j ∼ 1 / C i
Where w i j ′ is the weight of the observed edge. w m a x and w m i n are the maximum and minimum values of edge weight in the weighted network H respectively; Set l as an adaptive constant which makes no influence on the result as it is a normalization tool, and for concision, we set it as the average value of edge weights l = ∑ l N G w E G , where EG is the total number of edges of the target network H. N G i is the number of the node i’s neighbors; Ci is the importance score of node i; The ~ represents a positive correlation.
Thus, after normalization is accomplished by Equation (4), the larger the weight is, the closer to 1 it is, and vice versa, but it will never touch the boundary.

2.3. Dynamic Programming for the Node Importance Calculation

Theoretically, the results of Equation (4) will be used in Equations (1) and (2) for calculating Pr [ d e g ( i , G ″ ) ≥ c ] . Accounting for this process is highly time-consuming, especially in large-scale network computing. It is now handled with the help of the DP by a combination process of Equations (5)–(8) [34,35]:
X ( p , q ) = w i j X ( p − 1 , q − 1 ) + ( 1 − w i j ) X ( p − 1 , q )
Let p and q be two integers, where p ∈ ( 0 , 1 , 2 , … , d e g ( i ) ) , q ∈ ( 0 , 1 , 2 , … , p ) , and p≥q; E(i)={e1,e2,e3,…,edeg(i)} is a set of consisting all the edges that connected to node i; notably, the operation between set A and set B: A\B represents taking complement of set B in set A. And let E’(i) be a subset of E(i), where E ′ ( i ) ⊆ E ( i ) ; deg(i|E’(i)) is the defined degree of node i in subset G’(V,E\(E(i)\E’(i))). Equation X(p,q)=Pr[deg(|{e1,e2,…,ep})=q] means, given the ordered edge set { e 1 , e 2 , … , e d e g ( i ) } , when node i’s degree equals q, the probability score of node i is Pr[deg(i)]=q. Under this definition, with integer q meets each q ∈ [ 0 , p ] , we can take p through each of the integer values in the natural number set [0,deg(i)], and, for any node i with a degree t in graph Gi′(has 2t subgraphs, recorded in set Gi′’), this can realize a traversal for all the scores of the subgraphs in the possible world Gi′’ by each inside traversal on all of its corresponding linked degrees for all of the linked degrees’ possibilities. This traversal process can be seen as the nested ‘for‘ loops in coding.
Function X is a definition for DP in case it meets the boundary conditions, which is also indispensable for the calculation [34,35]:
X ( 0 , 0 ) = 1 X ( p , − 1 ) = 0 ,   ∀ p ∈ [ 0 ,   d e g ( i ) ] ; X ( p , q ) = 0 ,   ∀ p ∈ [ 0 ,   d e g ( i ) ] ,   q ∈ [ p + 1 , c ] ;
Once let Pr ( d e g ( i ) = c ) = ∑ q = 0 deg ( i ) X ( d e g ( i ) , q ) we have[34,35]:
Pr ( d e g ( i ) ≥ c ) = ∑ m = c d e g ( i ) Pr [ d e g ( i ) = m ] = 1 − ∑ m = 0 c − 1 Pr ( d e g ( i ) = m )
Where the inter m is a degree flag that used during the traversal computing. And then we have [34,35]:
Pr [ d e g ( i ) ≥ m + 1 ] = Pr [ d e g ( i ) > m ] − Pr [ d e g ( i ) = m ]
As can be seen, the original problem f0 is to compute the Pr[deg(i,G’’≥c)], and the subproblems is to compute each G i ′ score in the set G i ″ . That means, started by the situation of c=0, every Pr[deg(i)≥c)] can be find through the Pr[deg(i)=c)] as the integer c increasing by 1 each time.
It can be inferred that the time complexity of the above DP is O(dmaxEG).

2.4. Rank Nodes According to Importance

After implementing the DP (described in 2.2), for any node i in G, we obtained the deg(i) probability distribution of the possible world scenarios ( c i ∈ { 1 , 2 , … , d e g ( i ) } ), which correspond to the deg(i) importance scores c. Notably, the final importance score corresponding to node i is defined as:
C i = ∑ c = 1 d e g ( i ) c Pr ( d e g ( i ) ≥ c )
Before the execution of WEA, P is set to be a backup subset to the node-set V. Set V is traversed when the above-described steps are performed, and all nodes in G are ordinally sorted in P according to the node scores granted by WEA. X is a structure to record nodes and their corresponding importance. The following is a pseudocode description of WEA:
Algorithm: Weighted Expectation Method (WEA)
  Input: A Weighted Network H(V,E,W)
  Output: Importance Ranking of All Vertices in Target G(V,E,W’)
  1: W ′ ← ∅ ;
  2: for each e ∈ E do:
  3:  calculate w i j by using formula (2);
  4:   W ← W ′ ∪ w i j ;
  5: end for
  6: P ← Initialize an empty Priority queue;
  7: for each i ∈ G ( V , E , W ′ ) do:
  8:  compute Pr ( deg ( i ) ≥ c ) by using formula (5)-(8);
  9:  compute C i by using formula (9);
  10:    X ← ∅ Initial an empty structure;
  11:    X.NodeImportance ← [ i , C i ] ;
  12:     P . push(X);
  13:    end for
  15: return P;
  End
Where [ i , C i ] can be seen as a Structure kindred thing in the C language, H is the original network, and G is the target graph extracted from H by taking four pre-operations: (1). Deleting the self-loop edges; (2). Taking the maximum connected subgraph; (3). Determine whether it is a directed network (if directed, combine the directed edges between the linked nodes as a whole and to be its new weight); (4). Normalizing the edge weights.
It can be seen that WEA is also suitable for computing tasks in unweighted networks.
Table 2. Time complexity comparison table for the node importance sorting algorithms in multiple weighted networks.
Table 2. Time complexity comparison table for the node importance sorting algorithms in multiple weighted networks.
BT EC CL WC SC HI WEA
O ( n 3 ) O ( n 3 ) O ( m a x ( e , n l o g n ) ) O ( n 3 ) O ( n 3 ) O ( n 3 ) O ( d max E G N )
It is cited why the network edge numbers and the max degree can be used to represent the time complexity is: There are two traversals in WEA, it needs to traverse each nodes of the dataset, and for each node, it needs to traverse each edge of it (if it has).

3. Experiments

Two typical tests, named by Connectivity and SIR propagation model, have been used to verify this proposed WEA.

3.1. Connectivity Test

The connectivity verification [36] is a classic way to verify accuracy for sorting algorithms in the field of node importance [7] (and edge importance [9]), which is mainly reflected by the size changing of the current largest connected subgraph during the deleting nodes (or edges) process. During this, if the drop rate of the site is fast, the graph structure collapses rapidly, proving that the more important nodes in the graph are removed. In other words, the algorithm performs efficiently in sorting important nodes. Precisely, the connectivity r always be depicted as [37,38]:
r = N v ′ N v
Where N v is the total node numbers contained in the largest connected component in the graph before the test is executed; N v ′ represents the current numbers of nodes contained in the maximum connectivity component during the removal of the nodes by corresponding sorted order.
The well-known robustness metrics always be used to assess the effect of removing the nodes on the connectivity [37,38]:
R = 1 N ′ ∑ n = 1 N ′ r n
Where r n refers to each time the current ratio r during this iteratively nodes deleting; 1/N’ can be seen as a normalization factor to ensure that graphs in different sizes can be compared equally. Besides, for better evaluation, f is set to represent the ratio of the deleted nodes numbers and those in the original largest connected component.

3.2. Dynamic Spreading Test (SIR Propagation Model)

Another classical test of the node importance is the susceptible-infected-recovered model (SIR), which regarded the node importance rank as the node spreading power sorting [39,40,41]. Its’ aim is to test the correlation between the tested algorithm and the SIR sorting. The higher the correlation with Sir ranking, the better the performance of the tested algorithm. The higher the correlation value is, the better the tested algorithm performs. During the SIR propagation, each node in the target graph G is taken in turns as the seed node for infection, and then observe the influence of the epidemic disease spreads out. 500 independent SIR propagation simulations are conducted for each node in this experiment. Then the average number of recovery nodes in the network for this 500 SIR propagation simulation’s end is recorded as the node importance score. Eventually, all the nodes in G are sorted according to their importance scores. The most usual correlation analysis is to find the value of Kendall’s tau-b between each tested algorithm and SIR sorting.
It is needed to introduce Kendall’s tau-b correlation coefficients [42,43]: The sets X ( x 1 , x 2 , x 3 , … , x N ) and Y ( y 1 , y 2 , y 3 , , … , y N ) are the sequence of the orderly sorting nodes that derived from the tested algorithm and the SIR propagation simulation, respectively. Then the corresponding x s and x t in sequence X along with y s and y t in sequence Y are taken arbitrarily to form two tuples, ( x s , y s ) and ( x t , y t ) respectively, where for integer variables s and t suit s ≠ t , s ≤ N , and t ≤ N . If x s < x t , y s < y t or x s > x t , y s > y t they are concordant; If x s < x t , y s > y t or x s > x t , y s < y t , they are discordant; Else they are neither concordant nor discordant. Thus, Kendall’s tau-b is defined as:
τ b ( X , Y ) = 2 ( n c − n d ) N ( N − 1 )
Where n c and n d are the number of concordant and discordant, respectively.
Notably, according to the heterogeneous mean-field theory, the epidemic threshold in unweighted SIR is approximate to:
β C ≈ < k a v g > < k a v g 2 > − < k a v g >
The < k a v g > and the < k a v g 2 > denote the mean degree and mean square of degree, respectively. The heterogeneous mean field theory ensures the expectations of each node infecting neighbor nodes are regular, considered as E x p ( i ) = ∑ K a v g p i N . p i is the probability of infection in the average case (broadly, p i is a constant in unweighted SIR). Considering WEA is suitable for weighted networks, and in order to make the experimental results more objective, we selected the weighted SIR (WSIR) type for verification, which takes advantage of the threshold that differs from the original one [44]:
β C ′ ≈ < k > l ( < k 2 > − < k > )
We take l as the average edge weight value in the graph G (where l is defined in 2.2).

3.3. Datasets

In need of verifying the accuracy of sorting between WEA and the compared algorithms, the selected nine publicly-available real networks for experiments: (1) Email_dnc (Directed) [45]: Email network in the 2016 Democratic National Committee email leak; (2) Inf_USAir97 [45]: An American Airlines network; (3) Eco_everglades [45]: A eco-system of Florida Everglades; (4) Rt_bahrain [45]: Twitter social network (Undirected); (5) Windsurfers [46]: Natural disaster network; (6) Lesmis (Les Misérables) [46]: Social network of characters from Victor Hugo’s book; (7) Blocks [45]: The symmetrical power of the network from Gordon Royle, from University of Western Australia; and (8) C. elegans neural network (Caenorhabditis elegans, the undirected available on the website Koneck) [46]: The neural network of Caenorhabditis elegans. (9).Tech_caida (Directed) [45]: The relationships network of caida.
Table 3 lists some rudimentary topology characteristics of the eight real networks. D is to show whether this network is directed or not. V is the number of nodes, E G is the number of edges, K a v g is the average degree, W a v g is the average weight of each network, W m a x is the average weight of each network, T is the average triangle numbers formed by edges. Cc is the global clustering coefficient, and φ is the assortativity coefficient.
Since one central point of this work is to study the problem of how the weight be used to represent the link strength between two nodes, we define the different direction edge weight values as the component of the link strength between two nodes. In practice, it needs to consider the situations. For instance, it is required to consider the offset of the values when addressing a directed economic network. While, in some other situations, the values in two directed edges between two nodes typically shall be added as a whole for the edge weight computation.
Operations (1)–(4) are conducted for the above datasets. Firstly, the self-loops are removed if they exist; Secondly, the maximum connected subgraph is taken for the next computing; Thirdly, if they are directed, such as Email_dnc, the edge weight values between two nodes are added as a whole as their new weight value; Lastly, the weights for computing are pre-normalized by formula (4) and those weight values are assigned to be the weights of G.
Note that the absence of the self-loops ensures a better comparison and unified computing. Plus, if two or more nodes from one algorithm score the same, they are considered to be ranked in a tie, and their order in the node importance ranking will be randomly arranged. And then, the directed edges should be dealt with (if the network has).

4. Results

Seven algorithms were selected for conducting the comparison with WEA on those attached datasets, including the classical weighted version of the BT [26], CL [27], EC [30], WC [28], SC [29], the improved algorithm (HI) [25] developed by Lue et al. and the WD [24]. To validate the experiment, we chose two mainstream tests to measure the node importance sorting: Connectivity test and SIR test. We adopt the operations described above for each dataset (say network H). Then obtain the target graph G, and all the algorithms are conducted on it.
During the tests, if two or more nodes calculated by this algorithm score the same, their rankings are considered tied.

4.1. Figures, Tables and Schemes

The figures of connectivity verification have been attached below.
Table 4. Robustness R values for each algorithm on different datasets, of which WEA are always bold by the best.
Table 4. Robustness R values for each algorithm on different datasets, of which WEA are always bold by the best.
Robustness BT EC CL WC SC HI WD WEA
Email_dnc 0.020 0.083 0.062 0.050 0.045 0.041 0.017 0.017
USAir97 0.140 0.143 0.417 0.158 0.141 0.293 0.129 0.128
Eco_everglades 0.507 0.500 0.506 0.501 0.500 0.488 0.500 0.440
Rt_bahrain 0.044 0.254 0.142 0.074 0.066 0.069 0.033 0.039
Windsurfers 0.476 0.479 0.493 0.444 0.435 0.468 0.432 0.426
Lesmis 0.164 0.177 0.232 0.269 0.173 0.152 0.157 0.151
Blocks 0.311 0.179 0.310 0.270 0.179 0.304 0.178 0.178
C.elegans_neural 0.341 0.450 0.421 0.403 0.416 0.394 0.375 0.340
Tech_caida 0.013 0.122 0.047 0.029 0.026 0.011 0.010 0.010
Average value 0.224 0.265 0.265 0.292 0.224 0.220 0.246 0.192
Table 5. Kendall’s tau-b correlation coefficients for each algorithm, the best-performed results are emphasized in bolds.
Table 5. Kendall’s tau-b correlation coefficients for each algorithm, the best-performed results are emphasized in bolds.
WSIR (tau-b) BT EC CL WC SC HI WD WEA
Email_dnc 0.372 0.657 0.531 0.536 0.628 0.715 0.519 0.557
USAir97 0.436 0.873 0.141 0.848 0.813 0.217 0.820 0.890
Eco_everglades 0.225 0.778 0.184 0.743 0.778 0.250 0.715 0.832
Rt_bahrain 0.131 0.423 0.523 0.511 0.685 0.580 0.573 0.588
Windsurfers 0.375 0.322 0.322 0.615 0.549 0.745 0.686 0.716
Lesmis 0.272 0.685 0.274 0.756 0.713 0.674 0.546 0.561
Blocks 0.071 0.944 0.055 0.647 0.668 0.113 0.843 0.920
C.elegans_neural 0.279 0.419 0.236 0.668 0.650 0.557 0.620 0.678
Tech_caida 0.161 0.238 0.263 0.310 0.415 0.306 0.259 0.357
Average value 0.258 0.593 0.281 0.626 0.655 0.462 0.620 0.678
To compare the time-consuming of the algorithms outputting the result, the running time of different algorithms is recorded in Table 6. All the algorithms are conducted on the dataset in a Desktop computer with detailed information: Intel(R) Core (TM) i5-10400 CPU @2.90 GHz, RAM 16.0 GB, 64-bit operation system. The maximum iterate by 30000 times is set to EG for each dataset to ensure an outcome. Besides, the pretreatment of dealing with edge weights of directed datasets is not counted in the running time.

5. Discussion

In Table 6, we compared the time complexity of WEA with that of other algorithms, and as can be seen, the performance of WEAs’ is pretty well.
The figure varied for each algorithm in each dataset and presented vivid outcomes. A steeper downward curve means that the network structure collapses faster. The value R is to engrave the overall trend better. A smaller R corresponds to an entire faster network collapsing and thus, indicates the nodes deleted by the corresponding algorithm in order of its priority possess high importance.
There is no difficulty in finding WEA line with minimal robustness in eight networks. The connectivity curve of WEA tends to decline rapidly (which makes the structure collapse rapidly) in the figure of each dataset. The algorithm’s overall robustness is judged by measuring the area among the connectivity curve, x-axis, and y-axis (recorded as the value R). For example, in Figure 2 (b), according to the connectivity curve drawn by WEA, the decline in the early stage is relatively fast, and in the later stage, it is relatively gentle (the inflection point is around 0.17 of the ordinate value) which means that when about the first 17% of nodes are deleted, the network structure almost collapsed, and the number of the crucial nodes functioning in maintaining the network connection drops sharply. Furthermore, in Figure 2(g), the curves of WEA and SC almost coincide, which may be caused by the small number of nodes in the data set. In Figure 2(d), being inferior to WD, the curve of WEA performs at the second because of some inherent properties of the Dataset: As seen in Table 3, the value of Cc is too small.
As shown in Table 4, as the best performance value is boldly marked, the robustness (R) of WEA on the eight datasets is the lowest among all the algorithms. Compare the average R of each data, WEA is the lowest, at 0.192, followed by that of SC and classic BT. The results indicate that WEA sorting can always make the robustness value the lowest in deleting the nodes. This means WEA is more suitable for keeping accuracy in finding important node tasks.
Weighted SIR test can well test the algorithms’ performance in Dynamic spreading, so as to show whether the node importance rank is sound. We adopt it under the most proper β c ′ to ensure the infected seed has an adequate spreading and performs well in each dataset.
Table 5 records each Kendall’s tau-b of these algorithms by its performance. As the best-performed results are emphasized in bold, Kendall’s tau-b of WEA in the WSIR test often gains the maximum values among most of the dataset, indicating that, in verifying the node importance, WEAs’ sorting is much closer to the results of the propagation simulation. Although, in the Rt_bahrain, SC obtains Kendall’s tau-b with 0.685 that higher than WEA and in the small datasets of Lesmis and Blocks, its value of WC and EG is higher than WEA’s (may be, under the SIR testing, WEA is not that superior at measuring the node spreading ability which possess the higher ratios of the node numbers to the edge numbers, calculated for 0.59 for Rt_bahrain, 0.30 for Lesmis, and 0.51 for Blocks respectively, which are dramatically high than other datasets). Nevertheless, WEA still wins those compared algorithms with the highest average Kendall’s tau-b. That is to say, the important nodes found by WEA possess a more substantial spreading capability, thereby indicating that WEA is more suitable for finding important nodes.
As seen in Table 6, each time, WEA has the second performance at the overall time-consuming of 160.67 Seconds, followed the WD with a total of 16.40 Seconds. The most time-consuming is BT at 6487.26 Seconds totally, and the second time-costing is CL which at the total of 3291.21 Seconds.
Even if the running time for WD is less than WEA, WEA can better ensure accuracy by a considerable time-consuming.

6. Conclusions and Outlooks

Aiming to address two issues: 1. The computing accuracy is always incompatible with low complexity. 2. Weight may contribute positively or negatively to the node’s importance, but there is an absence of a quantitative definition to deal with these two situations. This work proposes WEA, a new index for the node importance mining that considers the local topology information. Due to the design that takes advantage of Dynamic programming, WEA can significantly reduce time complexity but still guarantee high computing accuracy, which can well fit large-scale networks task. Meanwhile, by using a compact bridge (Equation (3)), WEA can make the types of negative/positive weight contribution networks be computed quantitatively and equally. Moreover, Equation (4) has portability that can be easily assembled with many other algorithms. Experimental verifications also showed WEA's high sorting accuracy and low time complexity. We mentioned in the dynamic spreading test that WEA is not that superior at measuring the node spreading function, maybe for the potential of the extremely high ratio (the node numbers to the edge numbers). Because WEA possesses the feature of flexible unlimited decimals, it ensures a precise importance score for each node. In general, as a new index, WEA is more precise and faster than the compared ones.
Based on this work, some further exploration can be done. Firstly, find some ultra-optimization ways to exert in large-scale network computing. Secondly, given the current hot trend of the relative node importance, it developed to be a challenging issue whether the statistical method can mine some invisible parts of the network from the topology information of the already known network parts since most networks possess prominent statistical characteristics, such as small world network.
Most algorithms choose the research object with conventional unweighted/weighted static networks. However, some networks in other forms are always ignored, such as dynamic networks [47,48] or spatiotemporal networks [49]. For example, an interesting issue can be how to quickly and accurately identify abnormal nodes in dynamic networks, criminal nodes in the blockchain, and social software, which will have great potential applications.
As for the current node importance research, there is a domain differentiation. Some algorithms may be more suitable for some specific fields or situations than others; in fact, the distinction between them is also for specific occasions. It is a good phenomenon because it is difficult to have an algorithm that can cover every different situation. However, the verification for these algorithms also has some domain differentiation. For example, BT performs poorly in SIR but very well in connectivity. Although this is the inevitable result of the algorithm’s applicability, this is a negative phenomenon. At present, many algorithms have been proposed, and some of them are rarely innovative. In the future, it is expected to summarize the application fields of existing algorithms and the testing methods [7,50].

Author Contributions

Conceptualization, L.J. Chen., MJ. and NZ.; methodology, LJ. Chen. and MJ.; software, LJ. Chen., ZL. and JL.; validation, ZL. and LJ. Chen.; formal analysis, LJ. Chen. and JL.; investigation, LJ. Chen.; resources, NZ.; data curation, JL. and MJ; writing—original draft preparation, NZ.; writing—review and editing, JW.; visualization, LJ. Chen. and ZL; supervision, NZ. and JW.; project administration, NZ.; funding acquisition, NZ. All authors have read and agreed to the published version of the manuscript. Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

This work has been supported by the National Natural Science Foundation of China and the China Postdoctoral Science Foundation Project under Grant Nos. 62066048 and 2020M673312. Data Driven Software Engineering innovation team of Yunnan province of China No. 2017HC012, State Key Laboratory of Computer Architecture No. CARCH201813.

Data Availability Statement

Data Availability Statements in section “MDPI Research Data Policies” at Network Data | Network Repository and Networks (konect.cc).

Conflicts of Interest

The authors declare no conflict of interests.

References

  1. Zhang, X.; Ma, C.; Timme, M. Vulnerability in dynamically driven oscillatory networks and power grids. Chaos 2020, 30. [Google Scholar]
  2. Li, A.-W.; Xiao, J.; Xu, X.-K. The Family of Assortativity Coefficients in Signed Social Networks. Ieee Transactions on Computational Social Systems 2020, 7, 1460–1468. [Google Scholar] [CrossRef]
  3. Fanjin, Z.; Jie, T.; Xueyi, L.; Zhenyu, H.; Yuxiao, D.; Jing, Z.; Xiao, L.; Ruobing, X.; Kai, Z.; Xu, Z.; et al. Understanding WeChat User Preferences and "Wow" Diffusion arXiv. arXiv 2021, 14, 14. [Google Scholar]
  4. Bian, R.; Koh, Y.S.; Dobbie, G.; Divoli, A.J.A.C.S. Identifying top-k nodes in social networks: a survey. 2019, 52, 1–33.
  5. Zhang, L.; Zhu, J.; Wang, X.; Yang, J.; Liu, X.F.; Xu, X.-K. Characterizing COVID-19 Transmission: Incubation Period, Reproduction Rate, and Multiple-Generation Spreading. Frontiers in Physics 2021, 8. [Google Scholar] [CrossRef]
  6. Brockmann, D.; Helbing, D. The Hidden Geometry of Complex, Network-Driven Contagion Phenomena. Science 2013, 342, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
  7. Lu, L.; Chen, D.; Ren, X.-L.; Zhang, Q.-M.; Zhang, Y.-C.; Zhou, T. Vital nodes identification in complex networks. Physics Reports-Review Section of Physics Letters 2016, 650, 1–63. [Google Scholar]
  8. Al-garadi, M.A.; Varathan, K.D.; Ravana, D. Identification of influential spreaders in online social networks using interaction weighted K-core decomposition method. Physica a-Statistical Mechanics and Its Applications 2017, 468, 278–288. [Google Scholar] [CrossRef]
  9. Zhao, N.; Li, J.; Wang, J.; Li, T.; Yu, Y.; Zhou, T. Identifying significant edges via neighborhood information. Physica a-Statistical Mechanics and Its Applications, 2020; 548. [Google Scholar]
  10. Li, J.; Peng, X.; Wang, J.; Zhao, N. A Method for Improving the Accuracy of Link Prediction Algorithms. Complexity 2021. [Google Scholar] [CrossRef]
  11. Ma, G.; Yan, H.; Qian, Y.; Wang, L.; Dang, C.; Zhao, Z. Path-based estimation for link prediction (Apr, 10.1007/s13042-021-01312-w, 2021). International Journal of Machine Learning and Cybernetics 2021, 12, 2459–2459. [Google Scholar] [CrossRef]
  12. Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nature Physics 2010, 6, 888–893. [Google Scholar] [CrossRef]
  13. Liu, X.; Tang, T.; Ding, N.J.E.I.J. Social network sentiment classification method combined Chinese text syntax with graph convolutional neural network. 2022, 23, 1–12.
  14. Zhang, G.; Jia, H.; Yang, L.; Li, Y.; Yang, J. Research on a Model of Node and Path Selection for Traffic Network Congestion Evacuation Based on Complex Network Theory. Ieee Access 2020, 8, 7506–7517. [Google Scholar] [CrossRef]
  15. Medo, M.; Mariani, M.S.; Lu, L. The fragility of opinion formation in a complex world. Communications Physics 2021, 4. [Google Scholar] [CrossRef]
  16. Liu, X.; Ding, N.; Liu, C.; Zhang, Y.; Tang, T.J.A.I. Novel social network community discovery method combined local distance with node rank optimization function. 2021, 51, 4788–4805.
  17. Garas, A.; Argyrakis, P.; Rozenblat, C.; Tomassini, M.; Havlin, S. Worldwide spreading of economic crisis. New Journal of Physics 2010, 12. [Google Scholar] [CrossRef]
  18. Wu, Z.; Liao, Q.; Liu, B.J.B.I.B. A comprehensive review and evaluation of computational methods for identifying protein complexes from protein–protein interaction networks. 2020, 21, 1531–1548.
  19. Zhou, J.; Xiong, W.; Wang, Y.; Guan, J. Protein Function Prediction Based on PPI Networks: Network Reconstruction vs Edge Enrichment. Frontiers in Genetics 2021, 12. [Google Scholar] [CrossRef] [PubMed]
  20. Panigrahi, P.; Maity, S. Structural vulnerability analysis in small-world power grid networks based on weighted topological model. International Transactions on Electrical Energy Systems 2020, 30. [Google Scholar] [CrossRef]
  21. Zou, Y.; Li, H.J.F.I.P. Study on Power Grid Partition and Attack Strategies Based on Complex Networks. 2022, 750.
  22. Butun, E.; Kaya, M. Predicting Citation Count of Scientists as a Link Prediction Problem. Ieee Transactions on Cybernetics 2020, 50, 4518–4529. [Google Scholar] [CrossRef]
  23. Kim, M.; Baek, I.; Song, M. Topic Diffusion Analysis of a Weighted Citation Network in Biomedical Literature. Journal of the Association for Information Science and Technology 2018, 69, 329–342. [Google Scholar] [CrossRef]
  24. Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. 2004, 101, 3747–3752.
  25. Gao, L.; Yu, S.; Li, M.; Shen, Z.; Gao, Z. Weighted h-index for Identifying Influential Spreaders. Symmetry 2019, 11. [Google Scholar] [CrossRef]
  26. Simard, F.; Magnien, C.; Latapy, M. Computing betweenness centrality in link streams. 2021.
  27. Rahim Taleqani, A.; Vogiatzis, C.; Hough, J. Maximum closeness centrality-clubs: a study of dock-less bike sharing. 2020, 2020.
  28. Garas, A.; Schweitzer, F.; Havlin, S. A k-shell decomposition method for weighted networks. New Journal of Physics 2012, 14. [Google Scholar] [CrossRef]
  29. Eidsaa, M.; Almaas, E. s-core network decomposition: A generalization of k-core analysis to weighted networks. Physical Review E 2013, 88. [Google Scholar] [CrossRef]
  30. Bengtsson, A.K.; Holfve Sabel, M.-A. Applications of eigenvector centrality to small social networks. 2016.
  31. Albert, R.; Barabasi, A.L. Statistical mechanics of complex networks. Reviews of Modern Physics 2002, 74, 47–97. [Google Scholar] [CrossRef]
  32. Mizruchi, R. Applied Network Analysis: A Methodological Introduction. Contemporary Sociology 1984, 13, 205. [Google Scholar] [CrossRef]
  33. Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proceedings of the National Academy of Sciences of the United States of America 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
  34. Bonchi, F.; Gullo, F.; Kaltenbrunner, A.; Volkovich, Y. In Core decomposition of uncertain graphs; ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 2014; 2014.
  35. Yang, B.; Wen, D.; Qin, L.; Zhang, Y.; Chang, L.; Li, R.-H. Ieee, Index-based Optimal Algorithm for Computing K-Cores in Large Uncertain Graphs. In 2019 Ieee 35th International Conference on Data Engineering, 2019; pp 64-75.
  36. Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–U122. [Google Scholar] [CrossRef]
  37. Schneider, C.M.; Moreira, A.A.; Andrade, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proceedings of the National Academy of Sciences of the United States of America 2011, 108, 3838–3841. [Google Scholar] [CrossRef]
  38. Ren, X.-L.; Gleinig, N.; Helbing, D.; Antulov-Fantulin, N.J.P. Generalized network dismantling. 2019, 116, 6554–6559.
  39. Kiss, I.Z.; Miller, J.C.; Simon, P.L. Mathematics of Epidemics on Networks Volume 46. Interdisciplinary Applied Mathematics, 2017. [Google Scholar] [CrossRef]
  40. Gubar, E.; Zhu, Q.; Taynitskiy, V. In Optimal control of multi-strain epidemic processes in complex networks, International Conference on Game Theory for Networks, 2017; Springer: 2017; pp 108–117.
  41. Li, R.; Wang, W.; Di, Z.J.P.A.S.M. Applications, i., Effects of human dynamics on epidemic spreading in Côte d’Ivoire. 2017, 467, 30–40.
  42. Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
  43. Quintero-Rincón, A.; Carenzo, C.; Ems, J.; Hirschson, L.; Muro, V.; D'Giano, C. Spike-and-wave epileptiform discharge pattern detection based on Kendall's Tau-b coefficient. 2019.
  44. Sun, Y.; Liu, C.; Zhang, C.-X.; Zhang, Z.-K. Epidemic spreading on weighted complex networks. Physics Letters A 2014, 378, 635–640. [Google Scholar] [CrossRef]
  45. Nesreen Ahmed, R.A.R. Rong Zhou Network Repository. Available online: https://networkrepository.com/networks.php (accessed on 9 August 2022).
  46. KUNEGIS, J. Konect. Available online: http://konect.cc/networks/ (accessed on 9 August 2022).
  47. Zambon, D.; Alippi, C.; Livi, L. Concept Drift and Anomaly Detection in Graph Streams. 2017, PP, 1-14.
  48. Bian, R.; Koh, Y.; Dobbie, G.; Divoli, A. In Network Embedding and Change Modeling in Dynamic Heterogeneous Networks, the 42nd International ACM SIGIR Conference, 2019; 2019.
  49. Wangli; Haosup; sup; Zhaoxiang; Recognition, Z.J.P. Wangli; Haosup; sup; Zhaoxiang; Recognition, Z.J.P. Spatiotemporal Distilled Dense-Connectivity Network for Video Action Recognition. 2019.
  50. Ferraz, D.; Rodrigues, F.A.; Yamir, M.J.P.R. Fundamentals of spreading processes in single and multilayer complex networks. 2018, S0370157318301492-.
Preprints 67363 g002
Figure 2. The changes in connectivity in nine real networks vary when nodes are removed. The horizontal coordinate denotes the node removal ratio f, and the vertical coordinate denotes the largest connectivity coefficient value r while removing nodes according to the tested algorithm sorting. Each sub-figure (a–h) of the figure demonstrates the performance of conducting the test in the publicly real network data. All of the sub-figures, showed that the R value in WEA line always plummeted fastest, and the line often fell dramatically into an approximate reaching bottom in r quickly.
Figure 2. The changes in connectivity in nine real networks vary when nodes are removed. The horizontal coordinate denotes the node removal ratio f, and the vertical coordinate denotes the largest connectivity coefficient value r while removing nodes according to the tested algorithm sorting. Each sub-figure (a–h) of the figure demonstrates the performance of conducting the test in the publicly real network data. All of the sub-figures, showed that the R value in WEA line always plummeted fastest, and the line often fell dramatically into an approximate reaching bottom in r quickly.
Preprints 67363 g002
Table 3. The basic topology characteristics of the eight real networks.
Table 3. The basic topology characteristics of the eight real networks.
Datasets D V EG Kavg Wavg Wmax T Cc φ
Email_dnc Y 1892 37400 40 27.14 10.00 13200 0.22 -0.15
USAir97 N 332 2126 12 0.07 0.53 36500 0.63 -0.21
Eco_everglades N 69 911 26 22.54 3132.5 211 0.58 -0.27
Rt_bahrain N 4676 7979 3 1347997193.06 1348062538.00 97 0.02 -0.22
Windsurfers N 43 336 16 3.59 47.00 1096 0.56 -0.26
Lesmis N 77 254 6 3.74 61.00 32 0.57 -0.17
Blocks N 300 584 3 27.14 100.00 3 0.66 -0.35
C.elegans_neural Y 279 4296 29 3.74 61.00 33 0.65 -0.16
Tech_caida Y 26475 106800 4 2.67 4.00 4 0.21 -0.20
Table 6. The time-consuming of running different algorithms.
Table 6. The time-consuming of running different algorithms.
Time (Seconds) BT EC CL WC SC HI WD WEA
Email_dnc 24.78 1.39 10.02 6.61 8.20 2.63 0.36 5.45
USAir97 0.89 0.08 0.64 0.31 1.43 0.68 0.14 1.70
Eco_everglades 0.13 5.15 0.06 0.03 0.07 0.87 0.03 0.53
Rt_bahrain 147.35 4.45 17.01 41.70 10.42 6.13 2.71 3.92
Windsurfers 0.18 0.04 0.02 0.02 0.03 0.49 0.02 0.16
Lesmis 0.21 0.09 0.04 0.03 0.12 0.15 0.07 0.06
Blocks 0.12 0.22 0.02 0.02 0.05 0.23 0.02 0.03
C.elegans_neural 1.57 0.25 0.64 0.25 0.33 0.06 0.08 1.09
Tech_caida 6312.03 843.78 3262.76 1011.53 1281.32 962.13 12.97 147.73
Total time 6487.26 885.45 3291.21 1060.50 1301.97 971.37 16.40 160.67
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated