Not Hydraulic but an Adsorption Water Transport occurs in the Xylem of Land Plants

1. Introduction

Hales [1] established the view of a pulled fluid movement in plants on the basis of experiments with plant cuttings.

The concept of water transport within vessels and tracheids - considered as tubes - of the xylem of intact plants was mainly developed by Boehm [2], Dixon and Joly [3] and Renner [4] on plant cuttings and samples.

The textbook opinion of plant moisture movement is based on an assumed, hydraulic volume flow in the xylem. It is supposed to take place in continuous: "... water threads hanging from the water evaporating leaf cells, ..” [2] (Translated from German). In order to ensure the cohesion of the fluid even under a presumed high tensile stress, e.g. at growth heights above 10 meters, the tensioned water threads must be in a metastable state, since under these conditions (superheated state) they should physically boil with bubble formation (“embolism”) already at ambient temperature and tearing off.

According to cohesion theory there should not form bubbles (“emboli”) filled with gas or water vapor, and should not be already contained in the xylem which would prevent the suspected hydrodynamic fluid flow. In fact, gases or water vapor bubbles are ubiquitously found in living plants [5,28].

The hydraulic of physics is part of fluid mechanics and the Hagen/Poiseuille law applies to hydraulic volume flow in ideal capillary pipes or tubes [6]. The vessels and tracheids of the xylem do not possess ideal properties of pipes or tubes (Compare section 2.2), as required by the hydraulic cohesion theory. Unlike ideal pipes, the walls of the vessels and tracheids interact with the transported water. The latter penetrates (imbibes) the dead cell walls and the cells can shrink and swell. Due to the interaction with water, the cells serve as source or sink for the transported fluid. Therefore, since the properties of natural xylem do not conform to the basic law of fluid flow, the continuity equation [7] (No reaction of the wall material with the moved fluid), is not satisfied by the cohesion theory [8].

The non-existence of ideal capillary pipes/tubes as hydraulic pathways of water, can be considered as an excluding criteria for long-distance fluid-flow transport in plants according to cohesion theory.

Many plant physiologists nevertheless consider the theory to be valid, but it does not go unchallenged. See for example: [9,10,11,12]. Textbook authors as [13,14,15] express doubts regarding the current doctrine of water transport in plants. [8] reject the cohesion theory and conclude: "... that the arguments of the proponents of the cohesion theory are completely misleading".

2. Controversies with the concept of long-distance water transport, the cohesion-tension theory

“The cohesion-tension theory has been a controversial subject for more than a century and continues to generate lively debate.” [16]. The theory tries to give an answer to the question, according to which principle the water transport in intact, living plants from the root to the leaf takes place. It is supposed to be a hydraulic suction driven flow in pipes, but this is not true.

2.1. In xylem there is no hydraulic suction driven flow

The transpiration of plant as well as many other diffusion processes, can be physically described by Fick's laws. Referring to the first law the authors [16] write: „This equation accounts only for movement in response to a concentration gradient, and not for movement in response to other forces (e.g., pressure, electric fields, and so on)”. So not in response to a pressure- driven volume flow as one suspects with the hydraulic cohesion theory. Later in their book, the authors contradict themselves on this point and incorrectly assume that in plant water transport a pressure-driven volume flow according to Poiseuille would result from a diffusion process, which is not true.

An attempt is made to construct such a process: “As water evaporates from the surface film that covers the cell walls of the mesophyll water withdraws farther into the interstices of the cell wall, and surface tension causes a negative pressure of the liquid phase.” [16].

This assumption of a withdrawal of the water away from its destination the atmosphere, is contradicted by several researchers. [17] contradicts this assumption: "... that even under extreme evaporation conditions no withdrawal could be expected”. [18] contradicts this as well: “The large tensions that potentially could be present in the cell wall generally do not occur in living cells since water is usually available and gets ‘pulled’ into the interstices, thus filling them.” [19] notes for the above described reversal of the transport direction of water (“ .. water withdraws ..”) from the atmosphere to the root, that such a reversal of movement is unlikely but could occur when the relative humidity of the surrounding atmosphere exceeds RH = 0,98. However, this does not describe moisture release (transpiration), but rather moisture uptake via the leaf.

2.2. The xylem is not composed of pipes/tubes

The proponents of cohesion theory mistakenly consider the vessels and tracheids of the xylem as tubes in which the Hagen/Poiseuille flow law is supposed to apply, which is not established. Plants are cut open from experimenters and plumbing suction or pressure is applied to the samples open on both sides [20,21]. Samples cut from plants are spun in centrifuges by Ziegler et al. [22] to impose a flow on the moisture present in the xylem. The aim is to obtain results with specimens identical to the behaviour of rooted, intact plants, but this is already prevented by the destructive experimental design.

Strasburger [23] devoted himself to answering the question: is a volume flow-wise movement according to Poiseuille possible? Consists the xylem of ideal tubes/capillaries, yes or no? He writes about his experiments on Aristolochia sipho and Vitis vinifera, among others: "Since capillarity has played and continues to play such an important role in explaining water ascension in plants, it is worthwhile to examine directly what the plant waterways are capable of achieving as capillaries. This is all the more worthwhile because the walls of these waterways are in an imbibed state, and this raises the question of whether this state does not influence their conductivity”. And concludes from this further: "For the tubular system of the plant, in which the water moves, the same laws must also apply as for other tubular systems, ...". As a result of his experiments on the "capillarity" of plant waterways, published with measured values (Figure 1), Strasburger [23] writes: " ... that the capillarity level for water in the vessels of plants is considerably lower than in glass capillaries ...", “ .. where the measured value ... was often half that calculated for glass capillaries." (The passages in quotation marks are translated from German).

From the finding in [23] that the vessels of the xylem do not behave like glass capillaries he concludes: "There remains almost only the assumption that an interaction between the imbibed wall and the content of the vessels influences the shape of the meniscus, flattens it and thus reduces its load-bearing capacity" (Translated from German). In other words, at least the investigated vessels of the xylem of Aristolochia sipho and of Vitis vinifera, do not correspond to the properties of impenetrable glass capillaries on which the equation of capillary fluid flow was empirically derived. See e.g. in [6].

Thus the need mentioned above: “.., the same laws must also apply as for other tubular systems, ..." does not fit the presumed “tubular system” of the plant. The results of the experiments speak against tubular systems assumed in plants and thus against the cohesion theory.

The elimination of a fluid mechanical water transport in plants in the sense of the cohesion theory - the non-existence of pipes/tubes [23] - is also described in [24]: ".. by the walls of the trachea which, as is well known, though very permeable to water, ..". Referring to doubts about the cohesion theory in [25]: "A more serious difficulty is the fact that wood does not contain ideal capillaries ... ", and Sitte et al. [26] point out: " ... so it is clear that the pathways do not correspond to ideal capillaries: ..” (Translated from German). Thus, the questioning of the cohesion theory is confirmed by several researchers. Therefore, the cohesion theory with its hydraulic view [5] cannot be accepted for water movement in living plants. How is water really moved?

3. The diffusive/adsorptive principle of water transport at the xylem/wood matrix

3.1. Physicochemical relationships between water and wood that are important for long-distance moisture transport

Since water is transported from the root to the leaf in the xylem (Figure 2 at b b) and there is a high affinity between water and xylem, some physicochemical relationships of wood that are important for understanding water transport are then discussed in more detail in 3.1. Moist wood can be considered as an anisotropic gel [27]. "In the case of wood, an analogy exists to an aqueous solution. The wood can be thought of as being partially dissolved in the sorbed water. As with a true solution this water is held at a vapor pressure p, lower than the saturated vapor pressure p₀ of pure water" [27]. Damp wood is in equilibrium at a defined water content, depending on the type of wood, with a certain relative humidity RH. The relative humidity RH of the air is defined as p/p₀ where p means the existing water vapor pressure is generally lower than the saturation water vapor pressure p₀

RH = p/p₀  (T, p = constant)

(1)

(RH multiplied by 100 is the percentage relative humidity).

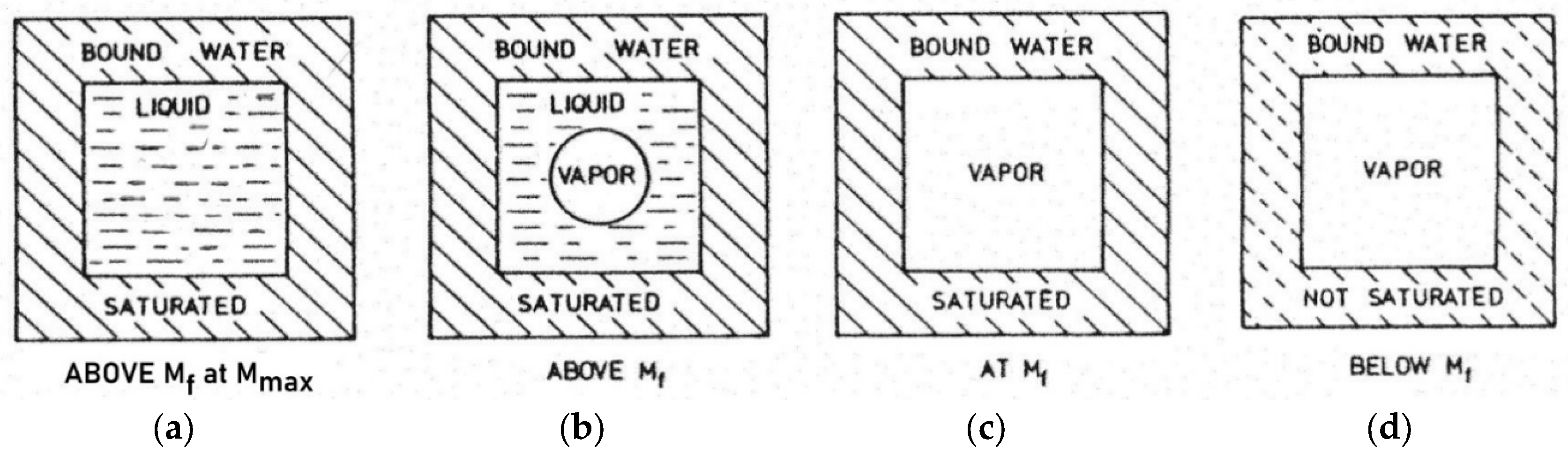
In the wood of living plants, water may be present in three main forms: 1) easily movable liquid water completely or partially filling the cell cavities in Figure 3 at a and b. 2) water vapor in the cell cavities at c and d and 3) bound water in the cell wall at a, b, c and d.

"The liquid water in the cell cavities is sometimes called ‘free’ water to distinguish it from the cell-wall water which may then be called ‘bound’ water. This is because it is attracted or bound to the wood with stronger forces than those which hold the so-called ‘free’ water.“ [27].

The terms "free" and “bound” are relative because the water is subjected to more or less large adsorptive van der Waals force fields depending on the water content in the cell cavities and is therefore not in the same thermodynamic state as ordinary liquid water in a large container.

The point of water content at which a given xylem cell has lost its cavity water or "free" water and contains only water vapor in the lumen, but the cell walls are still fully saturated, is called the fiber saturation point M_f (Figure 3 at c). Near the fiber saturation point (sometimes called the: fiber saturation range), several technical wood properties change in addition to physicochemical ones.

Legend: " a) The parenchyma covering the root tip. b b) The wood body composed of tracheids in tangential section. The tracheids ... ; their upper part is filled with air, the lower part with water. All conducting structures, which are in contact with the parenchyma of the root or the leaves, show a spiral pattern on the wall, so that the water can easily pass through the large thinned surfaces. ......, c) The leaf parenchyma, which gets the water from the spiral vessels and loses it by transpiration." (Translated from German).

Figure 2. Reduced tangential section of a coniferous plant in [28].

Figure 2. Reduced tangential section of a coniferous plant in [28].

The outward epidermis with cuticle and stomata in the leaf at c) and the cambium, cortex and bark of the woody body at b b), are not drawn in [28].

Cambium, cortex and bark form the almost hermetic closure of the xylem to the outside. In fact, according in [29], one of the foci of the water transport principle is based on the "hermetic closure" of its tracheal pathways to the outside.

Figure 3. Schematic, idealized representation of the moisture distribution in the cross-section of a wood cell: a above the fiber saturation point M_f at the maximum water content M_max, b above the fiber saturation point M_f, c at the fiber saturation point M_f and d below M_f. Based on [27].

Figure 3. Schematic, idealized representation of the moisture distribution in the cross-section of a wood cell: a above the fiber saturation point M_f at the maximum water content M_max, b above the fiber saturation point M_f, c at the fiber saturation point M_f and d below M_f. Based on [27].

For different species, the moisture content of fiber saturation point M_f is generally between 25% and 35%, based on dry wood. The maximum moisture content M_max in Figure 3 at a, can range from about 30% (Pock wood: 31%) to more than 230% (Balsa wood: 767%). The maximum moisture content is rarely reached in living wood. Even at maximum water content M_max moisture is retained almost without tension by the adsorption force fields of the wood at any growth height. Only when a drop of water is placed on the upper interface of a branch cut off at two points and held vertically with maximum water content in the woody part, does a drop escape at the bottom. At this high moisture value M_max it can additionally no longer be held by the adsorption force in the wood compared to the gravitational force and drips off.

To maintain the vital water transport in the apoplast from the root via the stem to the leaf, a continuous liquid film must be present in the xylem, the moisture content in the xylem must be greater than the fiber saturation M_f. Below this value, water transport is only possible in insufficient amount in vapor form. Trapped air can make the matrix more hydrophobic, its possible rehydration therefore more difficult. Among other things, it follows: "Already the conduction channels of the seedlings are filled with water and remain filled accordingly ..." [29] (Translated from German). A main task, that the pathways are not emptied too far in the course of transpiration but remain "filled accordingly", comes to the closing movements of the stomata and the almost hermetic closure of the conducting tissue to the outside. The nearly airtight closure of the wood could be measured by [30] using absolute pressure sensors in sapwood. While July/August in stem of Pedula pendula, the moisture/vapor pressure of the wood rarely dropped to 0.0043 MPa absolute pressure (corresponding to the boiling range of water at 30 °C). In contrast, the pressure more often rose to more than 0.8 MPa. The maintenance of these significant deviations from normal pressure indicate a high airtight closure of the stem.

3.2. Water transport is driven by transpiration, a diffusional process

Just before sunrise and adequate water supply, the plant should be almost completely hydrated. There is no net movement of moisture. From this state of equilibrium, the stomata open in the leaf after sunrise, and transpiration starts. During it, water evaporates from a thin film covering the walls of the leaf intercellular surface belonging to the apoplast. The phase transition from water film to vapor during evaporation, represents a diffusive process. The latter is part of transpiration. The reason for evaporation is the clear concentration gradient for water between the liquid phase of the intercellular walls with high water concentration and the water vapor phase of the outside air with low water concentration. The atmosphere is relatively dry and can: "... dehydrate the plant" [16]. Without any energy input of their own, rooted land plants exploit the external concentration gradient between moist soil and relatively dry atmosphere for water transport from root to stem to top. The diffusive evaporation of water during transpiration physically follows Fick's first law:

J = - D · A · Δc/Δx

(2)

In equation (2) J [mol/s] means the quantity of a substance diffused per unit time, D its diffusion coefficient [m²/s], A the crossed area [m²] and Δc/Δx the concentration gradient [mol/m³ · m] of the substance. The quantity of a substance diffused per unit time J [mol/s], is directly proportional to the size of the diffusion coefficient D [m²/s], der crossed area A [m²] and the driving concentration gradient Δc/Δx [mol/m³ · m]. The minus sign occurs because the direction of net diffusion is towards regions of lower concentration.

The movement of water vapor from respiratory cavities outward to the atmosphere within the transpiration process also occurs by diffusion. The moist intercellular area A of the respiratory cavities, adjacent to the outside air when the stomata are open, is huge. By additional action of wind, a large concentration gradient Δc/Δx of water vapor between leaf interior and atmosphere may be maintained at the leaf surface. Wind amplifies the quantity of total stomatal and cuticular transpiration.

The transpiration- or diffusion- rate E [mol/m² · s] of water between foliage and atmosphere measured in many studies reflects about 70-75% of the amount of water taken up by the root, moved and released to the atmosphere by transpiration (diffusion) [31]. For example, the transpiration- diffusion- rate of a Tradescantia zebrina plant [32] in still air E = 1.5 · 10^-3 [mol/ m² · s] and for strongly moving air almost three times the amount (= 4.4 · 10^-3 [mol/ m² · s]) was measured (Experimental conditions: 23°C ±2°C, relative humidity of ambient air RH = 0.65, stomata width = 15 µm).

Transpiration requires a high amount of energy, which can dehydrate the plant. The energy must be supplied by the environment of the plant. The molar heats of vaporization of water ΔH₀ at standard pressure and 30°C is: ΔH₀ = 43,7 kJ. For comparison: the enthalpy change by warming-up one mole of water ΔH_w from 30 °C to 31°C needs significantly less energy: ΔH_w = 0,075 kJ [43]. Transpiration involves a simultaneous transfer of energy and mass.

In the apoplast too, a concentration gradient Δc/Δx develops between the water-bearing root xylem which is higher in moisture to the water-releasing intercellular walls in the leaves which have lower moisture concentration but without phase change. Spontaneously, the water diffuses down the physiological concentration range from the root to the intercellular walls in the leaf. A purely diffusive water transport is superimposed on its path in the xylem by a desorption/adsorption process triggered by the partial dehydration of the plant via the effect of van der Waals forces in the apoplast (Compare section 3.4). The huge outer and inner surface A of root and leaf, as well as the huge inner apoplastic surface of root, stem and leaf, allow - in addition to the factors described above - a potentially high thermodynamic mass movement triggered by diffusive transpiration.

3.3. Support for the diffusive plant water transport in vascular bundle with heavy water HDO under non-invasive conditions

Heavy water HDO, diluted with normal water, has almost the same physiological properties as normal water and can be used in plants, for example, as a tracer for the movement of water. HDO can be quantitatively determined within rooted plants by mass spectroscopy. [33] discovered on young Vicia faba plants, which had been grown in nutrient solution and then adjusted in diluted heavy water HDO, that the tracer, only after about 25-30% of the total water of the plant had evaporated, could be detected in the transpiration water after about five to eight hours (Depending on the transpiration rate). During the transport process in the plant, there was a measurable exchange between vascular water and the cellular water of the surrounding parenchyma tissue. This shows that during its movement in the plant transversely to the shoot axis, the water shifts molecularly beyond the xylem conducting bundles by de- and re-wetting, so to speak "on a broad front", and does not flow in ideal capillaries according to Hagen/Poiseuille (Cohesion theory). Result: "The water in the vascular bundle of the plant is in diffusion equilibrium with the total water of the plant" [33] (Translated from German).

3.4. Inside xylem, a de- and an adsorptive water transport superimposes the diffusive moisture movement

In the hermetically sealed, porous system of the xylem, a diffusive movement of water in response to a concentration gradient (3.2) can be superimposed on additional physicochemical transport processes, such as desorption/dehydration (3.4.1) and subsequent adsorption/rehydration (3.4.2). These sorption processes between wood and water are based on physisorption. The holding and moving adsorption forces are relatively weak induced dipole and van der Waals forces respectively, acting from wood to water and from water to water. Physisorption is often characterized by the formation of multiple adsorption layers (“multilayers”) [12]. The moisture de- and adsorption overlap reversibly in the physiological moisture range of the xylem between M_f and M_max, where water transport takes place [34].

3.4.1. Desorption (Dehydration)

Based on the assumed moisture saturation of a land plant in the morning, after opening the stomata first the imbibed mesophyll cell walls lose water in vapor form to the atmosphere. Endergonically ("energy-consuming") this is controlled by the prevailing environmental conditions. The extent of desorption of the leaves discussed here can be quantified, for example, by measuring their temporally decreasing moisture content (Figure 4).

The investigation of the daily water content variation of the needles of Pinus ponderosa according to Figure 4, shows a maximum at a moisture content of about 155% in the night hours and a minimum of 125% in the afternoon, both related to dry weight. The daily water loss by desorption in this study is about 30%. From the measurements it is clear from this example that the water loss is not immediately compensated. The observed daily fluctuations occur. It is not until the following night at 24 o'clock that the approximate 155 % of the initial value is reached again after water adsorption from the root. As a result of the concept of local equilibrium [36] it can be concluded that the measured moisture content of the total needles corresponds approximately with the xylem moisture content which was not measured. This is because: "... most cells in a typical leaf are within 0.5 mm of a minor vein" [16]. After long lasting moisture loss of the leaves, the water loss continues also in the wood at the trunk down to the root: As daily maximum of the water content in the sapwood was measured in the outer 10 annual rings of the trunk of three different Picea abies trees in [37] with 4 samples each, on average = 175 % moisture content and as daily minimum also in the three spruces with the same sample size on average = 150% (Late summer 1967, moisture content measured at 1,3 m stem height, tree age approximately 75 years with a mean height of approximately 27 m, pure Norway spruce [Picea abies] forest near Munich/Germany). The daily water loss of the wood in this study [37] is 25%. For the fiber saturation point M_f of the sapwoods of Picea abies, a value of 35% is given in tables, and for its maximum moisture content M_max = 201% in [44]. Here between both values the moisture content of the wood remained under favourable growing conditions.

Using hydroponics [38] was able to measure the transpiration losses and water supply of trees simultaneously and separately. On a 3,12 m tall Canadian poplar (Populus x canadensis), it was shown that the tree began to take up water through the root only after reaching a saturation deficit after dehydration of the total plant of about 3 kg of water. The externally forced dehydration of plants described above changes not only the moisture content but also the energy ratio of the water to the wood. This is crucial for water transport in the xylem: dehydration leads to new endergonic ("energy-consuming") formation of free adsorption sites, or free interfaces for water [27]. They are energy-rich and form a thermodynamic energy store. Depending on the temporal adsorptive reoccupation with water (rehydration), the storage can be maintained for more or less time.

3.4.2. Adsorption (Rehydration)

With sufficient water supply from the root, the energy storage wood (formed after desorption of water) will exergonically ("energy-releasing") and spontaneously, adsorb water and move it almost without tension. For water involved in this physical reaction, the so-called free energy G is a measure of the driving force of the reaction.

The decrease in molar free energy ΔG_s of water, associated with the adsorption of liquid water by a hygroscopic material such as wood is given by the following equation

ΔG_s = - R · T · ln (RH)

(3)

where ΔG_s [J/mol] is the molar free energy of water, R [J/mol · K] is the gas constant, T [K] is temperature (in degrees Kelvin) and RH the relative humidity of the atmosphere surrounding the moist hygroscopic material.

Equation (3) is valid for reversible processes. Reversibility applies in the physiological, liquid water containing region above M_f for the de- and adsorption processes considered here, and thus for the region of water transport [34]. Equation (3) can therefore be applied in this moisture concentration range.In principle, a spontaneous change going toward equilibrium, such as the adsorption of water, can be used to do work, including water transport against gravity.

With the adsorption process there is - at constant temperature and pressure - a relationship between the maximum (non-expansion) work w_max,s and the change in free energy ΔG_s [39]:

w_max,s = ΔG_s (T, p = constant)

(4)

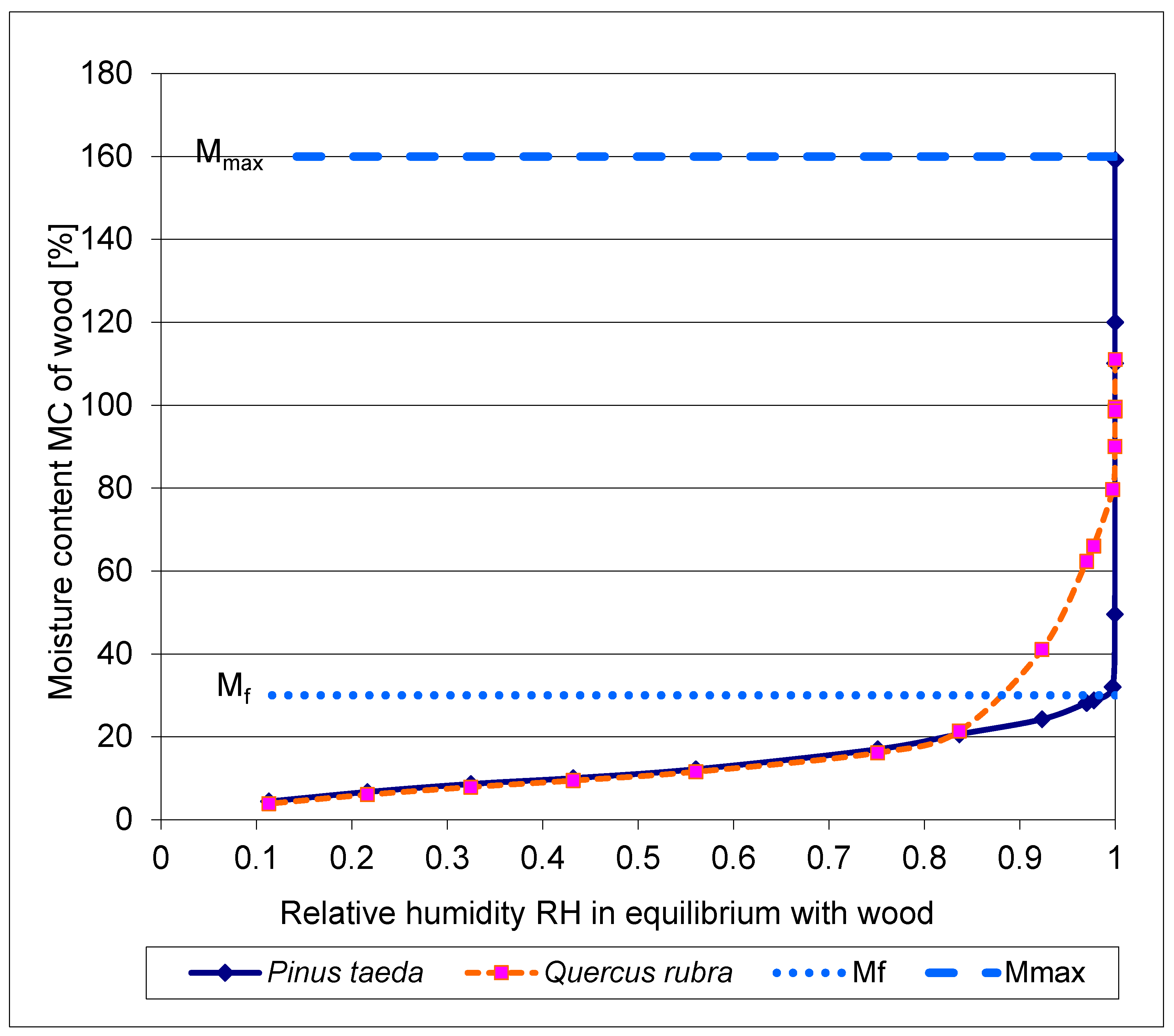
3.5. The desorption isotherms of moist wood of Pinus taeda and Quercus rubra

The desorption isotherm of water-saturated wood, respectively of a coniferous tree Pinus taeda and a deciduous tree Quercus rubra, is shown in Figure 5.

To the aim of their work the authors point out in [40]: "Specifically, it should provide insight into the fundamental driving force for the transport of water in wood ...". In [41] similar studies on Picea mariana are performed.

Using special relative humidity measurement methods beyond the isopiestic method above RH = 0.955, characteristic desorption curves are obtained over the entire range of moisture content. These are the tension plate, the pressure plate and the pressure membrane methods.

For undisturbed water transport in the xylem from root to apex, the continuous presence of liquid water, i.e. above the fiber saturation concentration M_f, is crucial. According to [40], "liquid" water is present in the physiological range of the wood of Pinus taeda and Quercus rubra above a relative humidity of about RH = 0.98 (Figure 5). This region is above a moisture content corresponding to the fiber saturation point M_f (Figure 3 in a and b).

For comparison with the leaf moisture conditions (at the inner side of the stomata), the relative humidity amounts to RH = 0.95 (25 °C) [42]. The authors in [16] mention: ” .. a value of nearly 1 ..." for the relative humidity inside a leaf.

During the desorption (dehydration) of the wood, starting from the maximum water content M_max (for Pinus taeda = 160%, for Quercus rubra = 120% in [40]), the range around M_f coincides with the loss of liquid water in the cell cavities of the xylem (Figure 3 at c). M_f is assumed to be = 30% for Pinus taeda and M_f = 25% for Quercus rubra.

The abrupt transition of water content at M_f from the so-called over-hygroscopic- (above M_f) to the hygroscopic- range (below M_f) in the coniferous wood of Pinus taeda appears remarkable.

In the hardwood of Quercus rubra, the decrease in concentration from the over-hygroscopic moisture range to the hygroscopic range is much less abrupt than in the softwood plant. This may be related to the fact that there is always more living parenchyma in hardwood than in softwood.

Figure 5. Comparison of the de-sorption isotherms of Pinus taeda and Quercus rubra, measured at 30 °C over the entire range [40]. For clarity, the range of fiber saturation point M_f (≈ 30%) and maximum water content M_max (≈160%), is plotted for Pinus taeda only.

Figure 5. Comparison of the de-sorption isotherms of Pinus taeda and Quercus rubra, measured at 30 °C over the entire range [40]. For clarity, the range of fiber saturation point M_f (≈ 30%) and maximum water content M_max (≈160%), is plotted for Pinus taeda only.

3.6. Energetic consideration of sorptive plant water transport on moist wood of Pinus taeda

Using the measuement results from [40] in column 1 (“Moisture content”) and 2 (“Relative humidity”) of Table 1, it is possible to calculate the decrease in molar free energy ΔG_s, according to (3), listed in column 3 (“Calculated”), made during spontaneous adsorptive rewetting of the wood from M_f to M_max. During the adsorption of one mole of water m_w (m_w = 0,018 kg) for example from M_f to M_max of the wood of Pinus taeda, ΔG_s = 7,1 [J/mol] free energy is released (Table 1). According to (4), this value corresponds to molar (lifting-) work w_max,s ≙ 7,1 [N · m/mol]. Without loss, one can adsorptively raise the mass m_w of one mole of water by the height h = w_max,s/(m_w · g) ≈ 40 m (with: g = 9,81 [m/s²] and: N = kg · m/s²). Using measurements of the desorption isotherm on Picea mariana in [41], similar calculations are made for Picea mariana in [12].

4. Conclusions

This paper presents a natural description of plant water transport. The hydraulic suction of water in plants, which is postulated in textbooks, is not found in nature. There are no ideal tubes in the xylem, which could be the basis for a hydraulic flow of water in plants. Land plants can be dehydrated (Desorption) during transpiration, caused by the relatively dry atmosphere. Related to the fixed xylem matrix, a water gradient between higher moisture concentration in the root and lower in the intercellular space of leaf is formed. The subsequent rehydration of the xylem (Adsorption) starts from the water-containing central cylinder of the root. Superimposed on the diffusive mass transport between high moisture concentrations in the root and lower in the leaf, is a dehydrating/rehydrating (Desorption/adsorption) moisture movement in the xylem. The latter is based on the high affinity between mobile water and fixed xylem respectively wood. During the day, with persistent transpiration, the plant's moisture stores are partially emptied. The result is van der Waals forces present and released during dehydration extend into the space and the energy stores in the xylem are formed. The adsorptive replenishment of the water/energy stores, simultaneously with the transport of water, is usually delayed. A tensioned spring can serve as mechanical comparison to the thermodynamic energy storage described. The value of the results presented above is in understanding the actual, thermodynamic (not-hydraulic) basis and model for long-distance water movement in rooted plants. The findings will be useful for future research.