Prerpints.org logo
Preprint
Article

Pulsed Thermography Dataset for Training Deep Learning Models

Altmetrics

Downloads

246

Views

231

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 January 2023

Posted:

26 January 2023

You are already at the latest version

Alerts
Abstract
Pulsed thermography is a vital technique in the nondestructive evaluation field. However, its data analysis can be complex and requires skilled experts. Advances in deep learning have yielded exceptional results, including image segmentation. Therefore, many efforts have been made to apply deep learning methods to data processing for nondestructive evaluation. Despite this, there is currently no public Pulsed thermographic dataset available for evaluating various spatial-temporal deep methods of segmenting pulsed thermographic data. This article aims to provide such a dataset and assess the performance of commonly used deep learning-based instance segmentation models on it. Additionally, the impact of the number of frames and data transformations on model performance is examined. The findings suggest that suitable preprocessing methods can effectively reduce the data size without compromising the deep models’ performance.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Pulsed thermography (PT) has been a popular non-destructive evaluation (NDE) method in recent decades due to its speed and high accuracy. It is particularly suitable for detecting near-surface defects in metal, carbon fiber reinforced polymers (CFRP), or polyvinyl chloride (PVC) materials. As a result, it has been used in many areas, such as the automotive and aerospace industries. In recent years, deep learning has seen significant advancements in various image processing tasks, such as image classification [1,2,3], object detection [4,5,6], image segmentation [7,8,9] and video understanding [10,11]. To evaluate the performance of these deep learning based algorithms, publicly available datasets, such as ImageNet [12], PASCAL [13], and COCO [14] for image classification; Cityscapes [15], and ADE20K [16] for image segmentation, are commonly used. These datasets play a crucial role in the development of algorithms. The availability of high-quality datasets in NDE field is also essential to provide benchmarks for different deep learning methods. However, collecting datasets in the NDE field poses several challenges:

1.1. imbalanced dataset

One of the challenges in using artificial intelligence (AI) in the NDE field is dealing with imbalanced datasets [17]. In NDE, the majority of components being tested are free of defects or damage, while only a small proportion of them are defective. If an AI model is trained on such data without proper preprocessing, it may tend to consistently predict that the components are sound. This can render the model ineffective.

1.2. limited data

PT data are more difficult to obtain than normal images. This is because PT experiments typically require the use of an expensive infrared camera with an additional heat source and must be performed by specialists in a dedicated laboratory. In addition, a computer-controlled trigger system is usually required. These factors make the PT data more challenging to collect and scarce.

1.3. Labeling challenge

The labeling challenge is multi-faceted. On the one hand, it requires skilled expertise to properly analyze PT data and accurately label it. The model aims to replicate this knowledge. On the other hand, the validation of the absence/presence of defects is usually challenging because, in the NDE field, most defects are hidden under the surface of the object. Accurate validation can often be performed using either destructive testing or CT scanning. The former method damages the object, and the latter is often costly.
In the field of NDE, although there are a number of methods for instance, segmentation in defect detection [18,19,20]. However, the datasets used for these methods are often not publicly available due to internal regulations. This paper aims to address this issue by providing a well-designed yet relatively simple dataset that can be used to support future research in evaluating AI algorithms. The dataset can be found at https://www.kaggle.com/datasets/ziangwei/irtpvc. Additionally, we have tested several popular instance segmentation methods with optimized hyperparameters. In summary, the contribution of this work is threefold: 1. a carefully designed publicly available PT dataset for PVC components containing defects of different sizes and depths. 2. Experiments with several popular encoder-decoder based defect segmentation models on this dataset. 3. Investigation of the efficiency improvement by using appropriate data transform methods and by using fewer frames as models’ input.

2. Related work

2.1. Pulsed thermography technology

Pulsed thermography is an active thermography technique in which a heat source is used to excite the object with a heat pulse. An infrared camera then records a video of the object to measure the cooling process on the surface of the object, which can be described, using a 1d formulation, by the following equation [21,22,23]:
y ( z , t ) = T 0 + Q e π t e x p ( − z 2 4 α t )
e = k ρ c p
Where α represents the thermal diffusivity of the sample. k is the sample’s thermal conductivity. c p is the heat capacity of the sample. e denotes the material’s thermal effusivity. It describes the materials’ capability of exchanging thermal energy with their surroundings. z is the depth. At the surface of the sample where z is zero, the equation can be simplified to:
y ( t ) = T 0 + Q e π t
Since the sound region has homogeneous materials, its thermal diffusivity and conductivity are similar. However, the material of the defective area has different parameters, resulting in a distinct thermal behavior. This difference forms the theoretical basis for PT as a method for non-destructive testing.
PT has been extensively applied to a variety of materials, such as CFRP [19] and glass fiber reinforced materials [24]. In [25], different active thermography methods, including pulsed thermography and lock-in thermography, are investigated for the inspection of spot welds. The study also evaluates different heating methods and data post-processing approaches to identify the optimal combination. Additionally, infrared thermography has been used in the protection of cultural heritage; in [26], the authors employ infrared thermography to inspect panel painting samples for incipient defects.

2.2. Deep learning-based methods used in thermography for NDE

The advancement of deep learning-based methods has led to improved results in data classification and segmentation for PT data. In [20], Mask-RCNN has been applied to the synthetic experimental pulsed thermographic dataset to detect abnormal regions. In [19], authors have employed an U-Net model to segment the defect regions on curved CFRP samples with a pulsed thermography technique. Faster-RCNN models with Inception V2 and Inception Resnet V2 architectures are trained to identify defects within composite materials using thermographic images in [27]. Average precision is used to assess the models’ performance. The results show that the model with Inception V2 outperforms the one with Inception Resnet V2. A hydrogen deep neural network that incorporates temporal and spatial information on the infrared data to detect the defects in composite and coating material is proposed in [28]. In [29], the authors use PT to detect the impact damage within the composite samples. They employ a support vector machine to classify the defective areas from the healthy area. They report the classification results ranging from 78.7 % to 93.5 %. In [30], recurrent neural networks and feed-forward neural networks are investigated to detect defects within some non-planar CFRP specimens. The results indicate that a long short-term memory neural network outperforms a feed-forward neural network when dealing with time-dependent information. A feed-forward neural network to classify the defects into different categories is proposed [31]. Two models are trained on raw data and Thermographic Signal Reconstruction (TSR) coefficients, respectively. The model using TSR coefficients outperforms the other one using the raw data.
As the use of generative adversarial networks (GANs) has become increasingly popular, they have also been applied to processing thermographic data. A GAN-based thermal image argumentation method is proposed to enhance the visibility of defects in CFRP components in [32]. In [33], the authors introduce IRT-GAN, which is trained on six thermographic data. These data are fully simulated for composite materials with different types. The model takes TSR coefficients as input and is able to produce segmented images.

2.3. Public available thermographic dataset

There are some publicly available infrared image or video datasets, such as PTB-TIR [34] for pedestrian tracking and LLVIP [35] for low-light vision. However, most of them are not for NDE tasks. In [36], the authors present a pulsed thermographic dataset. It contains two kinds of composite material samples: carbon and glass fiber-reinforced plastic. However, the dataset is not provided to the public and is not annotated for machine learning applications. Thermography databases from Laval University are demonstrated in [37]. The databases include infrared measurements for materials such as composite materials, plexiglass, steel, aluminum, etc. The focus of the study is on defect segmentation in single infrared images. It does not consider temporal information between thermal frames. To the best of our knowledge, a well-documented, publicly available PT dataset for defect segmentation that considers both spatial and temporal information is yet to be developed.

3. Data preparation and preliminaries

3.1. Specimens’ information and data acquisition

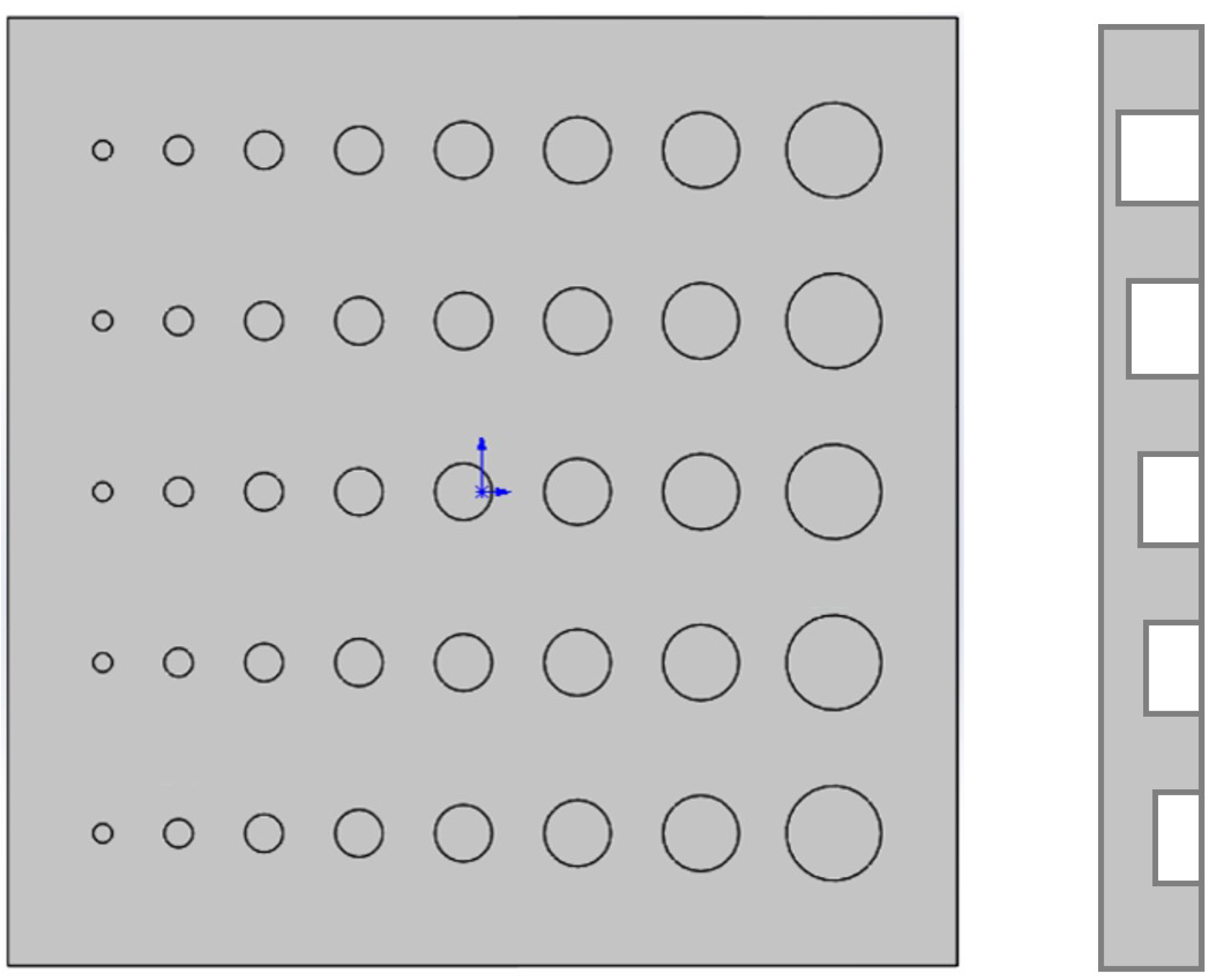
In this work, We present the PVC-Infrared dataset for deep learning, which is a PT dataset that consists of 19 PT measurements for 19 PVC specimens respectively. Each specimen has a dimension of 100 mm × 100 mm × 5 mm. On the bottom side of the specimens, cylindrical holes (without going through the specimen) of different sizes and depths were created to simulate subsurface defects, as shown in Figure 1. This figure illustrates all possible locations, sizes, and depths of the cylindrical holes that could exist. The diameter of the holes ranges from 2 mm to 10 mm, and the depth varies from 2.5 mm to 4.5 mm from the bottom side. Figure 2 shows CAD images of eight specimens from bottom view. Figure 3 presents a comparison of the visualization of a CAD image and an optical image of a specimen.
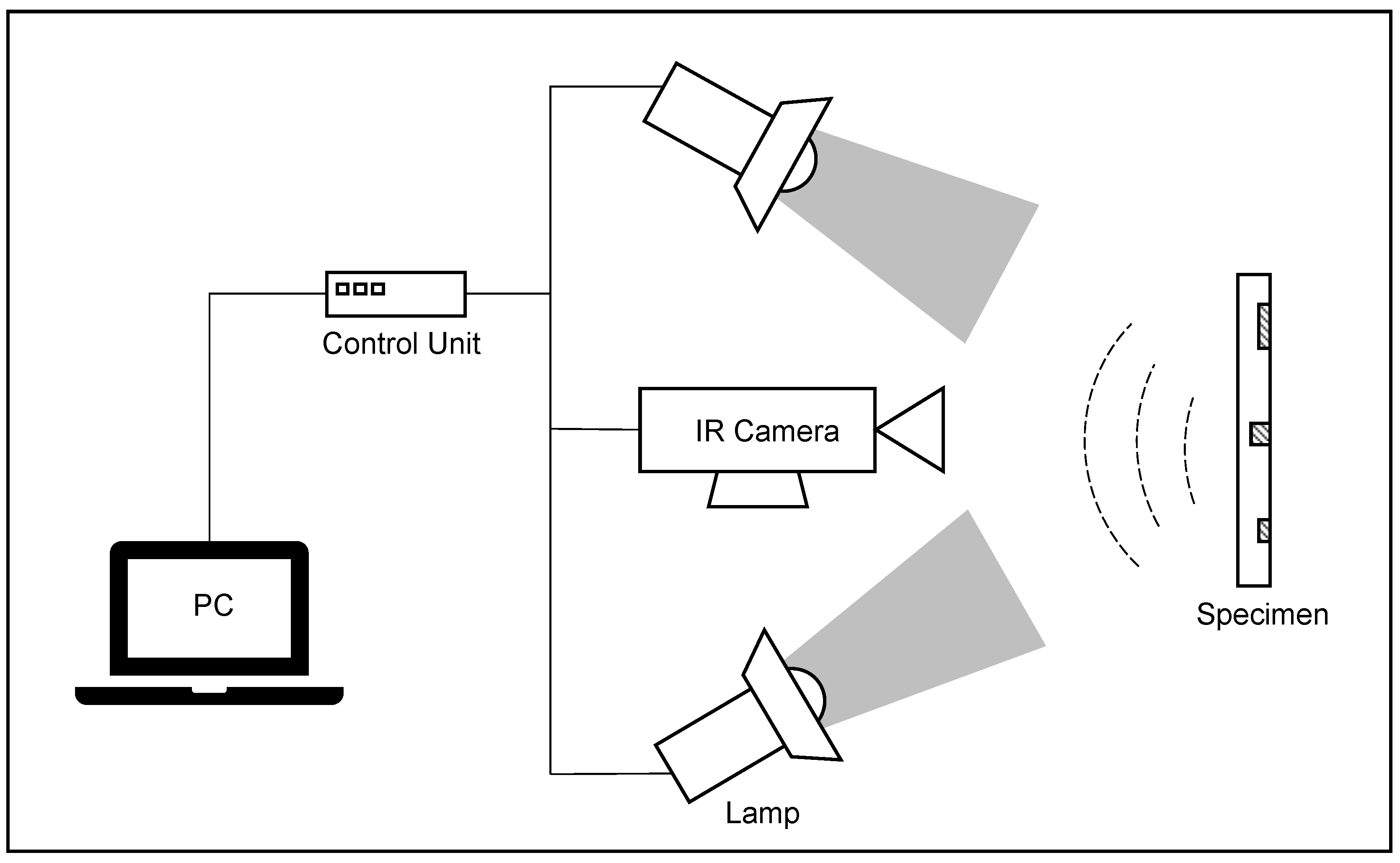
Figure 4 shows the experimental setup. The camera and lamps are controlled by a computer via a control unit for synchronization. A trigger signal is at first sent to the infrared camera to start recording. The overall recording time can be pre-defined. After a specific time interval, the lamps are triggered to flash. The infrared camera used in this experiment is FLIR SC5000. Two lamps from Broncolor, each with a power of 6.4 KJ, are used as heat sources to warm up the specimen. The camera records the infrared video with an image resolution of 320 × 256 for 181 seconds at a frequency of 10 Hz, resulting in a 320 × 256 × 1810 video per measurement.

3.2. Pulsed phase thermography

Pulsed phased thermography (PPT) is proposed in [38,39]. With this method, the phase of the thermal image sequence is calculated using a discrete Fourier transform (DFT). The formula for the transform is:
y k = 1 N ∑ n = 0 N − 1 x n e − i 2 π k n N = R e k + i I m k
Where x n is a pixel value at image frame n. R e k and I m k denote the real part and imaginary part of the Fourier transform. The phase Φ k and amplitude A k of DFT can be calculated with:
Φ k = a t a n ( I m k R e k )
A k = R e k 2 + I m k 2
We focused on the phase images of DFT results, as it shows better contrast of the abnormal regions. Often the first 5 to 10 phase images will provide adequate representations of the raw infrared data.

3.3. Principal component thermography

Principal component thermography (PCT) is introduced in [40]. Similar to PPT, here, Singular Value Decomposition (SVD) along the thermal image sequence is performed. Specifically, the 3D thermal video, which has the size of ( N , W , H ) is at first reshaped to ( N , W H ) with a raster-like operation. With the following formula, SVD can be performed:
X = U Γ V T
Where X represents the N × W H raw data matrix. U is a W H × N matrix. The matrix Γ has the size of N × N . The matrix V T is the transpose of an N × N matrix. When the matrix A is arranged so that its columns contain time variations and its rows contain spatial variations, the columns of the matrix U contain the Empirical Orthogonal Functions (EOFs). Typically, the first few EOFs contain the most relevant information of the original data and are used for further analysis.

3.4. Data labeling

The labeling of the data is done manually. At first, both PCT and PCT are applied to all the PT data. The transformed images are then visually inspected to identify the one with the best contrast of the defective regions. Manual labeling is then conducted by placing circles on the transformed images. The labels are reliable because all the defects are known and can be directly validated, as they are visible from the bottom side of the specimens.
Preprints 67863 g005
Figure 5. Pulsed phase thermography images for a specimen.
Figure 5. Pulsed phase thermography images for a specimen.
Preprints 67863 g005
Preprints 67863 g006
Figure 6. Principal component thermography images for a specimen.
Figure 6. Principal component thermography images for a specimen.
Preprints 67863 g006

4. Experiments with deep models for defect segmentation

4.1. U-net

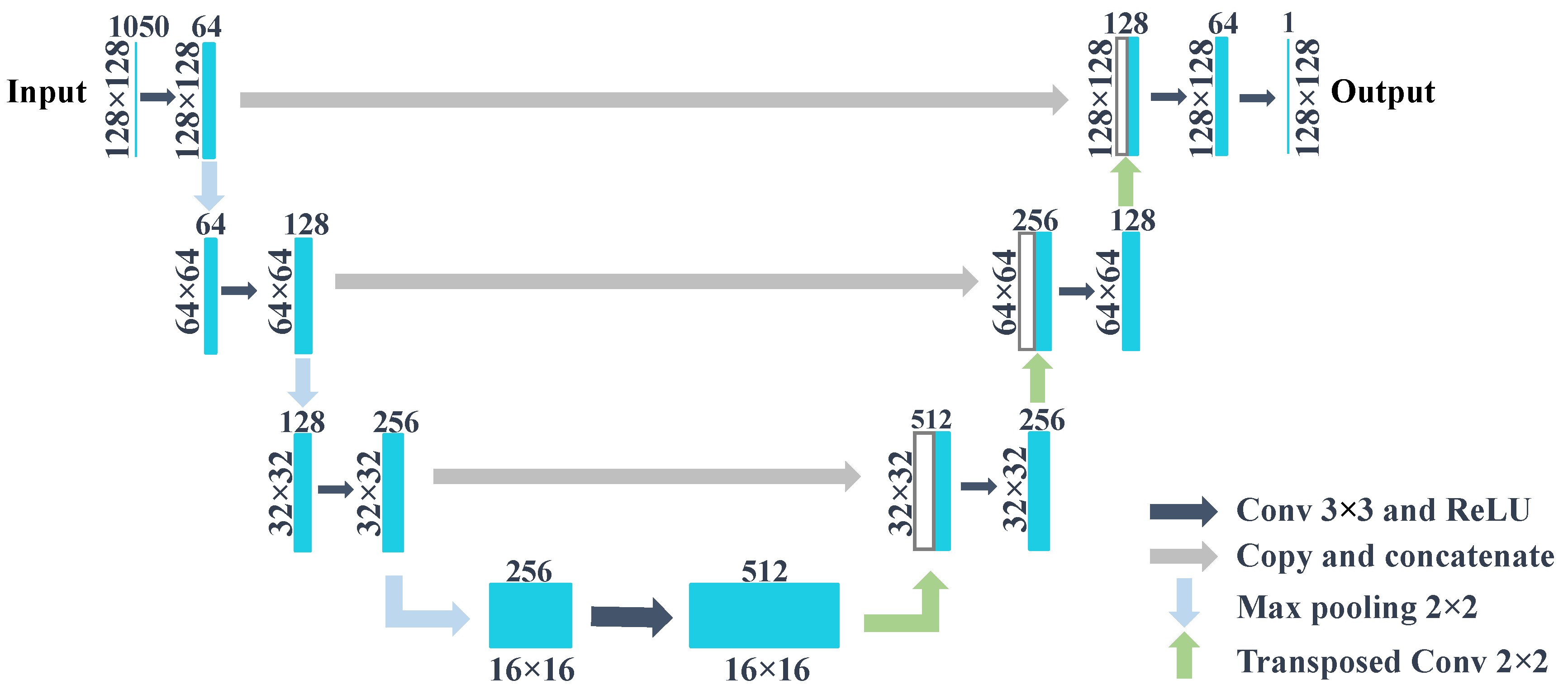
Introduced in [7], U-Net is a robust neural network architecture for biomedical image segmentation. It has two main components: the encoding stage and the decoding stage. The encoding stage is composed of several convolutional neural network blocks, each followed by a max pooling operation. The decoding part usually consists of the same number of transposed convolution blocks for upsampling. Thus the output will have the same dimension as the input data. Between the encoding stage and the decoding stage, there are also skip connections, which perform copy and concatenation of the feature maps and enable output images to have high resolution. In this work, we use a lightweight version of U-Net as shown in Figure 7, where we use only one convolutional layer instead of a double convolutional layer as an operation block.
Preprints 67863 g007
Figure 7. U-Net architecture presented in [19].
Figure 7. U-Net architecture presented in [19].
Preprints 67863 g007

4.2. SegNet

SegNet, proposed in [9], is similar to the U-Net architecture, which has encoding and decoding stages. The main difference is that, in SegNet, only the locations where max pooling is performed, which can also be referred to as pooling indices, are copied and used for upsampling to the decoding stage at the skip connection instead of copying the entire feature map from the encoding stage. Compared to the original SegNet, we have employed fewer steps both at the encoding and the decoding stages. The model architecture used is illustrated in Figure 8.
Preprints 67863 g008
Figure 8. SegNet architecture adapted from a figure in [9].
Figure 8. SegNet architecture adapted from a figure in [9].
Preprints 67863 g008

4.3. Model pre-training

Various models pre-trained on optical images such as VGG net [2] or ResNet [3] can be used as encoders to improve the performance of the encoder-decoder model due to their well-designed network architecture.
Additionally, these models are often pre-trained on large datasets of standard images, such as ImageNet dataset or COCO dataset. However, these pre-trained models cannot be directly used for our application, as the PT data we have contains many more image channels (each frame can be thought of as a channel in a 2.5D image) than the typical 3-channel RGB image. To address this, we modified the parameters in the first layer of the pre-trained models so that they can process the PT data by following this formula:
w j ′ = ∑ 1 C w i C ′
Where the w i denotes the neuron’s weights at the ith channel of the network’s first layer. C is the original channel number, which is 3 for the RGB channels. C ′ denotes the new channel number, which is 1000 in our case. w j ′ is the new weights. With this method, we are able to take advantage of the ImageNet pre-trained VGG11 models on the PT data.

4.4. Experiments on the original dataset

The data are split into three sections: training, validation, and testing. The training set includes 13 measurements, while both the validation and test sets consist of 3 measurements each. Various models are used in this study, including a modified version of U-Net and SegNet, as well as versions of U-Net and SegNet that used a VGG11 encoder backbone [41]. The latter two models were also trained with and without pre-trained parameters to evaluate the impact of model pre-training on performance.
For the training, stochastic gradient descent (SGD) is used as an optimizer, The models are trained for 3000 epochs. The loss function used here is binary cross entropy. The loss can be calculated with the following formula:
L = − 1 N ∑ i = 1 N y i · l o g ( p ( y i ) ) + ( 1 − y i ) · l o g ( 1 − p ( y i ) )
Where y i is the model’s prediction, it can be either 0 or 1 for binary classification. p ( y i ) is a model’s prediction of probability in [0, 1]. N represents the sample number.
The quantitative results on the test set of the original dataset are presented in the Table 1. We use Intersection over Union (IoU) on the test set for evaluation. To be specific, the average value of the IoUs (Average IoU) obtained on the three test samples is calculated. U-Net with VGG11 as encoder has reached the highest IoU over the other models with a model of 91.4MB. U-Net with pre-trained VGG11 as encoder has achieved comparable results, which suggests that the model pretraining did not contribute to the model’s performance. Figure 10 shows the visualization maps of results by U-Net and SegNet. They can both generate satisfactory segmentations for the defects. U-Net tends to classify more pixel to the foreground than SegNet. The models process measurements at 1-2 FPS on a machine equipped with two Intel Xeon E5-2630 v4 @ 2.20GHz CPUs, which is relatively slow, especially for industrial deployment.
Table 1. Results on test dataset of original data.
Table 1. Results on test dataset of original data.
Average IoU Model size
U-Net 0.683 18.4 MB
SegNet 0.668 17.2 MB
U-Net VGG11 0.722 91.4 MB
U-Net VGG11 pre-trained 0.712 91.4 MB
SegNet VGG11 0.588 95.3 MB
SegNet VGG11 pre-trained 0.599 95.3 MB

4.5. Efficient data segmentation methods

Deep models possess strong feature-extraction capabilities. As a result, it is logical to apply them directly to raw data. However, thermal videos tend to be large in size, which can consume a significant amount of computational resources. This can make it impractical for industrial deployment. In this section, we will investigate two approaches to reduce the size of PT data to mitigate this problem.

4.5.1. Experiment with transformed data

Manually inspecting a large number of frames per pulsed thermographic measurement can be time-consuming and tedious. To address this issue, Pulsed Phase Thermography (PPT) [38], Principal Component Thermography (PCT) [40], and Thermographic Signal Reconstruction (TSR) [42] are often applied to extract the most relevant information from the original PT data and create a more compact representation. This reduces the number of images that need to be inspected. This suggests that these methods can be seen as effective data preprocessing methods to reduce the size of training data for deep models. Smaller training data size also consumes notably less computational cost for training deep models. We select the first 10 images that are generated by PCT and PPT as training data. We have experimented with two models on the transformed data. Here we use Adam [43] as optimizer, the other hyperparameters are consistent with those in section 4.4 The performance of the models on the transformed data is shown in Table 2. In addition, the models process the transformed data approximately 3 × faster than the model for the original data.
Table 2. Results on validation dataset of transformed data.
Table 2. Results on validation dataset of transformed data.
Average IoU Model size
U-Net on original data 0.748 18.4 MB
SegNet on original data 0.729 17.2 MB
U-Net on PPT 0.732 14.5 MB
SegNet on PPT 0.717 13.3 MB
U-Net on PCT 0.638 14.5 MB
SegNet on PCT 0.625 13.3 MB

4.5.2. Experiment with fewer thermal frames

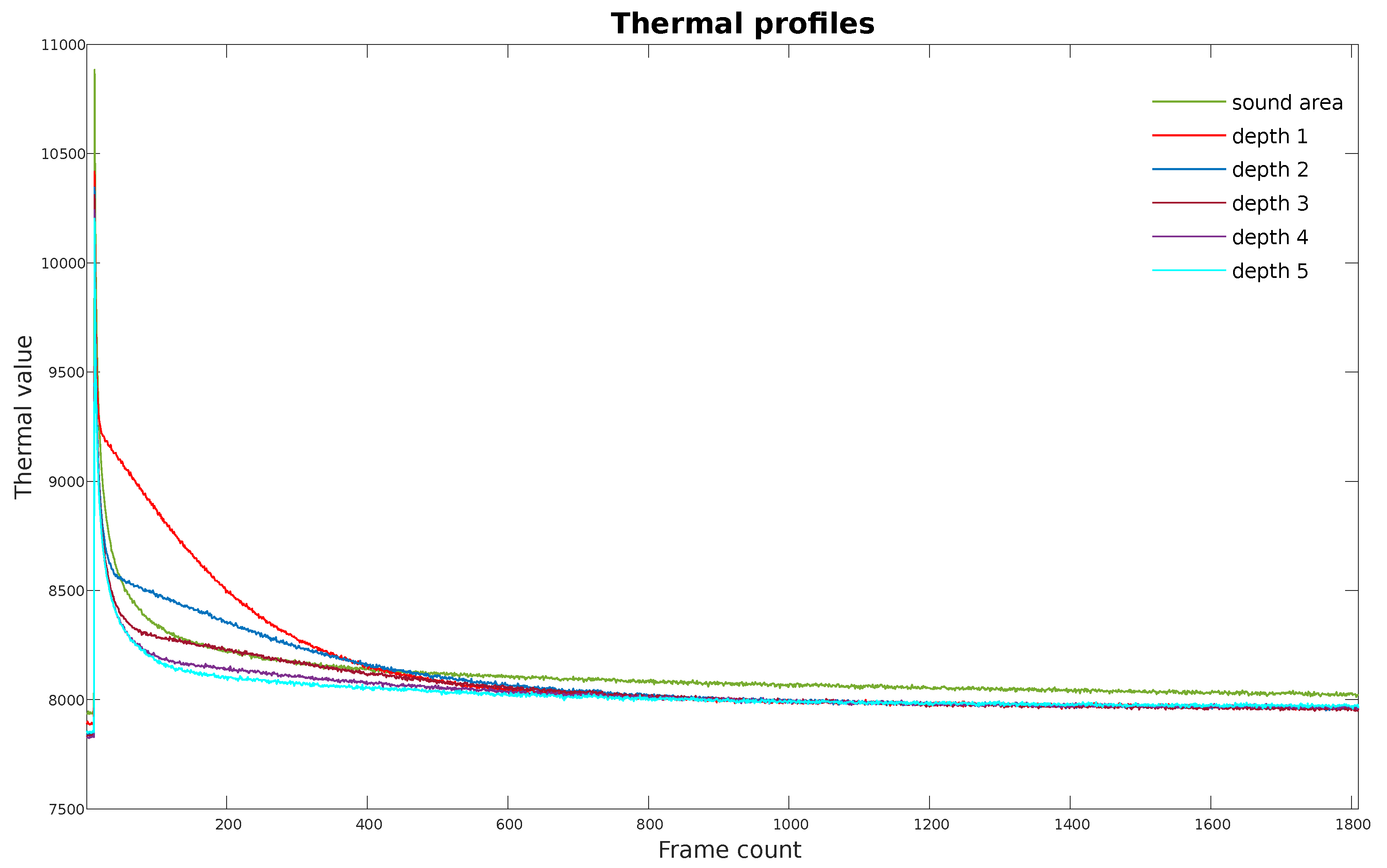
Figure 9 compares six thermal profiles from different areas (one from the sound area and five from different defective areas) of the thermographic measurement and shows that the main thermal value difference occurs in the early stage. The most relevant information might also lie within this region. Therefore, using only the initial part of the thermal sequence as input data may be beneficial for the deep models to focus. We use Average IoU on the validation dataset as a metric to assess the effect of frame number on the models’ performance. Table 3 shows the results of the experiment on the validation set. Interestingly, with the whole original measurement, the result is not the best. The best results were obtained with the initial 200 frames. This indicates that many of the trailing frames do not contribute to the defect evaluation and can be excluded. The training hyperparameters are consistent with those in Section 4.4. When processing the dataset with 140 or 200 frames, the models run 2 to 3 × faster than the models for the original dataset.
Preprints 67863 g009
Figure 9. Thermal profiles comparison from sound area and defective areas with different defect depths.
Figure 9. Thermal profiles comparison from sound area and defective areas with different defect depths.
Preprints 67863 g009
Table 3. Results (Average IoU) with only leading frames of thermal sequence on validation dataset. One original measurement contains 1810 frames.
Table 3. Results (Average IoU) with only leading frames of thermal sequence on validation dataset. One original measurement contains 1810 frames.
1810 200 140 100 50 25
U-Net 0.748 0.762 0.729 0.728 0.705 0.467
SegNet 0.729 0.769 0.730 0.727 0.723 0.478
Preprints 67863 g010
Figure 10. Visualization of segmentation results. The green mask represents the segmentations, and the yellow contour represents the ground truth area. The first row shows PCT images of the testing data. The second row shows the results obtained using SegNet, and the third row shows the results obtained using U-Net.
Figure 10. Visualization of segmentation results. The green mask represents the segmentations, and the yellow contour represents the ground truth area. The first row shows PCT images of the testing data. The second row shows the results obtained using SegNet, and the third row shows the results obtained using U-Net.
Preprints 67863 g010

5. Discussion

Datasets are crucial for the advancement of applied AI. However, publicly available PT datasets are scarce due to difficulties in data acquisition. We present a PT dataset for training deep learning models. It contains 19 measurements collected on 19 PVC specimens with planted defects. The dataset includes planted defects with known depth and size in specific locations. These defects are also visible from the bottom side of each specimen, allowing for easy and accurate labeling. This is in contrast to the completely hidden defects, which are more common in the NDE field.
Additionally, the dataset is larger than many NDE data for AI applications, such as the datasets used in [19] and [18], which typically have a smaller number of specimens (fewer than 10). A larger dataset can reduce the risk of the models’ overfitting.
We conducted experiments using several deep encoder-decoder models for defect segmentation on the original dataset. Among them, U-Net VGG11, without using the pre-trained parameters, achieves the best performance overall. The results also suggest that using a pre-trained model does not necessarily enhance the model’s performance, as observed for both U-Net and SegNet. Additionally, incorporating VGG11 as the encoder backbone of U-Net improves the model’s performance significantly, which is not the case for SegNet.
The results in Table 2 show that on the transformed datasets, the performance of the models can be similar to what they do on the original dataset. However, the transformed dataset is significantly smaller, and the training and inference time of the models can be reduced accordingly. This indicates that PCT and PPT are effective data transformation methods and can reduce the data size without losing relevant information.
Further than this, as we observed in the thermal profiles, the most evident difference in the thermal values between sound areas and defective areas occurs early on in the measurement. We have studied this issue by only using the leading frames as training data. As shown in Table 3, when the models use only the first 50, 100, 140, or 200 images, the performance of the models is barely decreased. However, these models can process data up to 3 × faster than the models processing the original data. Interestingly, with 200 frames, the models even reach better results than when the entire dataset is used. This suggests that a large portion of the raw thermal data contains redundant information that is not relevant for defect localization.
This work also has some limitations. One limitation is that the depth of defects is not taken into account. This is essential for applications where the defect’s depth is crucial. Another limitation is that the model is only tested on the defects in one shape. It would be valuable to evaluate the model’s ability to detect defects of various shapes. Additionally, exploring more methods for selecting frames during training could lead to further improvements in model efficiency.

6. Conclusions

In this work, we present PVC-Infrared dataset for deep learning, a dataset for defect detection using pulsed thermography as an NDE method. We hope that this dataset will be of benefit to further research work. Additionally, we experiment with various deep models, including U-Net, SegNet and variants of these models with VGG net as backbone, on both the original dataset and transformed datasets using PPT and PCT. Furthermore, we experiment with the models using only the leading thermal frames of the PT measurement, given the assumption that they should contain more relevant information than the other thermal frames. In both cases, the results can be comparable to the results on the original data. Using fewer frames, the deep model can even outperform the one using the whole dataset. These findings suggest that using the entire dataset is not necessary for a deep learning-based automated defect segmentation task. This highlights the potential for improving the efficiency of deep learning methods for PT data processing, particularly in industrial deployments. For future work, depth information of defects should also be taken into account. In addition, it would be meaningful to test the models on a PT dataset with defects in other shapes.

Author Contributions

Ziang Wei: methodology, data labeling, training the models and original drafting of the manuscript. Ahmad Osman: supervision, expertise in AI, manuscript review and editing. Bernd Valeske: supervision, funding acquisition, manuscript review and editing. Xavier Maldague: supervision, manuscript review and editing.

Funding

This research was supported by the European Regional Development Fund (ERDF).

Data Availability Statement

The PT dataset used in the paper can be accessed via the URL https://www.kaggle.com/datasets/ziangwei/irtpvc. The dataset is available for academic and research use only. Papers using this dataset are kindly requested to refer to this paper.

Acknowledgments

Support from Fraunhofer IZFP is gratefully acknowledged. David Müller is acknowledged for the design and preparation of the test specimen used in the paper within his research on the evaluation of deep learning approaches for quantitative defect testing and reconstruction with thermography. Udo Netzelmann is acknowledged for providing advice for the experimental setup.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AI Artificial Intelligence
PT Pulsed Thermography
PPT Pulsed Phase Thermography
PCT Principal component Thermography
TSR Thermographic Signal Reconstruction
NDE Nondestructive Evaluation
IoU Intersection over Union
CFRP Carbon Fiber Reinforced Polymers

References

  1. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Communications of the ACM 2017, 60, 84–90. [CrossRef]
  2. Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
  3. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
  4. Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, pp. 580–587.
  5. Girshick, R. Fast r-cnn. Proceedings of the IEEE international conference on computer vision, 2015, pp. 1440–1448.
  6. Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 779–788.
  7. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.
  8. Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 2881–2890.
  9. Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE transactions on pattern analysis and machine intelligence 2017, 39, 2481–2495. [CrossRef]
  10. Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, 2014, pp. 1725–1732.
  11. Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 7794–7803.
  12. Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255.
  13. Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. International journal of computer vision 2010, 88, 303–338. [CrossRef]
  14. Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. European conference on computer vision. Springer, 2014, pp. 740–755.
  15. Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 3213–3223.
  16. Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Scene parsing through ade20k dataset. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 633–641.
  17. Chakravarthy, A.D.; Bonthu, S.; Chen, Z.; Zhu, Q. Predictive models with resampling: A comparative study of machine learning algorithms and their performances on handling imbalanced datasets. 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA). IEEE, 2019, pp. 1492–1495.
  18. Wei, Z.; Osman, A.; Gross, D.; Netzelmann, U. Artificial intelligence for defect detection in infrared images of solid oxide fuel cells. Infrared Physics & Technology 2021, 119, 103815. [CrossRef]
  19. Wei, Z.; Fernandes, H.; Herrmann, H.G.; Tarpani, J.R.; Osman, A. A deep learning method for the impact damage segmentation of curve-shaped cfrp specimens inspected by infrared thermography. Sensors 2021, 21, 395. [CrossRef]
  20. Fang, Q.; Ibarra-Castanedo, C.; Maldague, X. Automatic defects segmentation and identification by deep learning algorithm with pulsed thermography: Synthetic and experimental data. Big Data and Cognitive Computing 2021, 5, 9. [CrossRef]
  21. Chung, Y.; Lee, S.; Kim, W. Latest advances in common signal processing of pulsed thermography for enhanced detectability: A review. Applied Sciences 2021, 11, 12168. [CrossRef]
  22. Fleuret, J.R.; Ebrahimi, S.; Ibarra-Castanedo, C.; Maldague, X.P. Independent component analysis applied on pulsed thermographic data for carbon fiber reinforced plastic inspection: a comparative study. Applied Sciences 2021, 11, 4377. [CrossRef]
  23. Ibarra-Castanedo, C.; Genest, M.; Servais, P.; Maldague, X.P.; Bendada, A. Qualitative and quantitative assessment of aerospace structures by pulsed thermography. Nondestructive Testing and Evaluation 2007, 22, 199–215. [CrossRef]
  24. Jensen, F.; Terlau, M.; Sorg, M.; Fischer, A. Active Thermography for the Detection of Sub-Surface Defects on a Curved and Coated GFRP-Structure. Applied Sciences 2021, 11, 9545. [CrossRef]
  25. Verspeek, S.; Ribbens, B.; Maldague, X.; Steenackers, G. Spot Weld Inspections Using Active Thermography. Applied Sciences 2022, 12, 5668. [CrossRef]
  26. Yao, Y.; Sfarra, S.; Lagüela, S.; Ibarra-Castanedo, C.; Wu, J.Y.; Maldague, X.P.; Ambrosini, D. Active thermography testing and data analysis for the state of conservation of panel paintings. International Journal of Thermal Sciences 2018, 126, 143–151. [CrossRef]
  27. Bang, H.T.; Park, S.; Jeon, H. Defect identification in composite materials via thermography and deep learning techniques. Composite Structures 2020, 246, 112405. [CrossRef]
  28. Luo, Q.; Gao, B.; Woo, W.L.; Yang, Y. Temporal and spatial deep learning network for infrared thermal defect detection. Ndt & E International 2019, 108, 102164. [CrossRef]
  29. Alhammad, M.; Avdelidis, N.; Ibarra-Castanedo, C.; Torbali, M.; Genest, M.; Zhang, H.; Zolotas, A.; Maldgue, X. Automated Impact Damage Detection Technique for Composites Based on Thermographic Image Processing and Machine Learning Classification. Sensors 2022, 22, 9031. [CrossRef]
  30. Tao, Y.; Hu, C.; Zhang, H.; Osman, A.; Ibarra-Castanedo, C.; Fang, Q.; Sfarra, S.; Dai, X.; Maldague, X.; Duan, Y. Automated Defect Detection in Non-planar Objects Using Deep Learning Algorithms. Journal of Nondestructive Evaluation 2022, 41, 1–11. [CrossRef]
  31. Duan, Y.; Liu, S.; Hu, C.; Hu, J.; Zhang, H.; Yan, Y.; Tao, N.; Zhang, C.; Maldague, X.; Fang, Q.; others. Automated defect classification in infrared thermography based on a neural network. NDT & E International 2019, 107, 102147. [CrossRef]
  32. Liu, K.; Li, Y.; Yang, J.; Liu, Y.; Yao, Y. Generative principal component thermography for enhanced defect detection and analysis. IEEE Transactions on Instrumentation and Measurement 2020, 69, 8261–8269. [CrossRef]
  33. Cheng, L.; Tong, Z.; Xie, S.; Kersemans, M. IRT-GAN: A generative adversarial network with a multi-headed fusion strategy for automated defect detection in composites using infrared thermography. Composite Structures 2022, 290, 115543. [CrossRef]
  34. Liu, Q.; He, Z.; Li, X.; Zheng, Y. PTB-TIR: A thermal infrared pedestrian tracking benchmark. IEEE Transactions on Multimedia 2019, 22, 666–675. [CrossRef]
  35. Jia, X.; Zhu, C.; Li, M.; Tang, W.; Zhou, W. LLVIP: A visible-infrared paired dataset for low-light vision. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 3496–3504.
  36. Erazo-Aux, J.; Loaiza-Correa, H.; Restrepo-Giron, A.D.; Ibarra-Castanedo, C.; Maldague, X. Thermal imaging dataset from composite material academic samples inspected by pulsed thermography. Data in brief 2020, 32, 106313. [CrossRef]
  37. Fang, Q.; Ibarra-Castanedo, C.; Maldgue, X. University Laval Infrared Thermography Databases for Deep Learning Multiple Types of Defect Detections Training. Engineering Proceedings 2021, 2, 8032. [CrossRef]
  38. Maldague, X.; Marinetti, S. Pulse phase infrared thermography. Journal of applied physics 1996, 79, 2694–2698. [CrossRef]
  39. Maldague, X.; Largouët, Y.; Couturier, J.P. A study of defect depth using neural networks in pulsed phase thermography: modelling, noise, experiments. Revue générale de thermique 1998, 37, 704–717. [CrossRef]
  40. Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Composite structures 2002, 58, 521–528. [CrossRef]
  41. Iglovikov, V.; Shvets, A. Ternausnet: U-net with vgg11 encoder pre-trained on imagenet for image segmentation. arXiv preprint arXiv:1801.05746.
  42. Shepard, S.M. Advances in pulsed thermography. Thermosense XXIII. SPIE, 2001, Vol. 4360, pp. 511–515. [CrossRef]
  43. Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. ICLR (Poster), 2015.
Preprints 67863 g001
Figure 1. An example of specimens with defects in all possible sizes in all possible locations. The right part of the image shows all the possible depths of the defects, ranging from 2.5 mm to 4.5 mm from the right surface (bottom).
Figure 1. An example of specimens with defects in all possible sizes in all possible locations. The right part of the image shows all the possible depths of the defects, ranging from 2.5 mm to 4.5 mm from the right surface (bottom).
Preprints 67863 g001
Preprints 67863 g002
Figure 2. Visualization of eight specimens from the bottom side.
Figure 2. Visualization of eight specimens from the bottom side.
Preprints 67863 g002
Preprints 67863 g003
Figure 3. Images for a specimen, left image is the CAD visualization, right image is an optical image for it.
Figure 3. Images for a specimen, left image is the CAD visualization, right image is an optical image for it.
Preprints 67863 g003
Preprints 67863 g004
Figure 4. Setup of the PT experiment.
Figure 4. Setup of the PT experiment.
Preprints 67863 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated