Improving Deep Echo State Network with Neuronal Similarity-based Iterative Pruning Merging Algorithm

Preprint

Article

Improving Deep Echo State Network with Neuronal Similarity-based Iterative Pruning Merging Algorithm

Altmetrics

Downloads

129

Views

Comments

A peer-reviewed article of this preprint also exists.

Qingyu Shen,Hanwen Zhang,

Yao Mao^*

Qingyu Shen,Hanwen Zhang,

Yao Mao^*

This version is not peer-reviewed

Submitted:

22 January 2023

Posted:

30 January 2023

You are already at the latest version

Alerts

Abstract

Recently, a layer-stacked ESN model named deep echo state Network (DeepESN) has been established. As an interactional model of recurrent neural network and deep neural network, investigations of DeepESN are of significant importance in both areas. Optimizing the structure of neural networks remains a common task in artificial neural networks, and the question of how many neurons should be used in each layer of DeepESN must be stressed. In this paper, our aim is to solve the problem of choosing the optimized size of DeepESN. Inspired by the sensitive iterative pruning algorithm, a neuronal similarity-based iterative pruning merging algorithm (NS-IPMA) is proposed to iteratively prune or merge the most similar neurons in DeepESN. Two chaotic time series prediction tasks are applied to demonstrate the effectiveness of NS-IPMA. The results show that the DeepESN pruned by NS-IPMA outperforms unpruned DeepESN with the same network size, and NS-IPMA is a feasible and superior approach to improving the generalization performance of DeepESN.

Keywords:

Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity

1. Introduction

Recurrent neural networks (RNNs) represent a consolidated computational abstraction for learning with variable length time series data [1]. As a simplified paradigm of RNN, the echo state network [2,3] (ESN) provides a prominent reduction in the computational cost compared to other paradigms of RNNs(e.g. ([4], LSTM), ([5], GRU)), for which the hidden layer of ESN is constructed by a randomly generated reservoir instead of independent neurons and the output weights of ESN are trained by a simple linear regression rather than backpropagation algorithm. Thus, ESN has a successful application in various time series prediction problems (e.g. [6,7,8,9]).

Deep neural networks [10] (DNNs) have the potential to learn data representations at various levels of abstraction and are being increasingly stressed in the machine learning community. Recently, a layer-stacked ESN model named deep echo state network (DeepESN) has been established and investigated, theoretically and experimentally, by Gallicchio, etc. The inherent characterization of the system dynamics developed at the different layers of DeepESN is experimentally analyzed in [11] and theoretically explained in[12]; A theoretical foundation for the study of DeepESN from a dynamical system point of view is introduced in [13]; Further details on the analysis and advancements of DeepESN could be found in [14]. As an interactional model of RNN and DNN, investigations of DeepESN are of significant importance in both areas. On the one hand, DeepESN expands our knowledge on how the information with memory attracted by RNN is extracted by hierarchical neural networks, on the other hand, DeepESN helps us better understand how the abstract intrinsic representations of time series extracted by DNN are recalled in reservoirs. Furthermore, DeepESN has richer nonlinear representation capacity and less computational complexity, and better predictive performance than single layer ESN [15].

Optimizing the structure of neural networks remains a common task in artificial neural networks, and the same question of how many neurons should be used in each layer must be stressed in all types of neutral network. If the neurons are too few, the architecture does not satisfy the error demand by learning from the data, whereas if the neurons are too many, learning leads to the well-known overfitting problem [16]. As far as we know, little research has been carried out on optimizing architecture of DeepESN. For research that has already been carried out on DeepESN, the same number is commonly assigned in each layer, which is acceptable but not optimal. In this paper, our aim is to solve the problem of choosing the optimized size of DeepESN, especially the number of neuron in different layers.

In 2014, a sensitive iterative pruning algorithm (SIPA) was proposed by Wang and Yan [17] to optimize the simple cycle reservoir network (SCRN), the algorithm was used to prune the least sensitive neurons one by one according to the sensitive analysis, the results showed that the SIPA method can optimize the structure and improve the generalization performance of the SCRN, meanwhile, pruning out redundant neurons could contribute to reducing the calculation and improving the computing efficiency of the network. Inspired by these advantages of SIPA, we wanted to apply a similar iterative pruning approach on DeepESN. However, SCRN is a kind of minimal-complexity ESN with simple cycle topology, the topology of DeepESN is much more complex than SCRN. Pruning a neuron in the network will raise perturbations on adjacent neurons, resulting in unstable network performance, in SIPA, the perturbations could be eliminated by adjusting the input weights into the perturbed neurons to minimum the distance of its input signal before and after pruning. Due to the hierarchical structure of reservoirs in DeepESN, perturbation raised by pruning a neuron in the lower layer will propagate into higher layers layer by layer, leading to greater instability of network performance and difficulty of perturbation elimination.

In order to overcome above difficulty, a new neuronal similarity-based iterative pruning merging algorithm (NS-IPMA) is proposed to iteratively prune out or merge the most similar neurons in DeepESN. In NS-IPMA, a pair of most similar twin neurons, which is regarded as redundant neurons in the network, are selected out iteratively, then, if they exist in different layers, the one in higher layer will be pruned out, if they are in a same resverior, they will be merged into one neuron, which works as the substitution of antecedent twin neurons. Quantive estimation of neuronal similarity plays an essential role in determining the redundant neurons which should be pruned out, Four neuronal similarity estimation criteria of NS-IPMA approach were attempted, including the inverse of Euclidean distance, Pearson’s correlation, Spearman’s correlation and Kendall’s correlation. Reducing the network size is a directly effective approach to improve generalization performance of neural network, because pruning out neurons will lead to reduction of network size, to verify the effectiveness of NS-IPMA method. The The DeepESNs pruned by the NS-IPMA method were compared with unpruned DeepESNs, whose number of neurons in each reservoir is the same. The pruned DeepESN and the unpruned DeepESN were compared with equal layer number advancements equal total neruon number.The results of the experiment on two chaotic time series prediction tasks showed that the NS-IPMA method has good network structure adaptability, and the DeepESNs pruned by NS-IPMA methed have better generalization performance and better robustness than the unpruned DeepESNs, indicating that the NS-IPMA methed is a feasible and superior approach to improving the generalization performance of DeepESN. NS-IPMA method provides a novel approach for choosing the appropriate network size of DeepESN, it also has application potential in other RNNs and DNNs.

This paper is organized as follows. DeepESN and entropy quantification of reservoir richness is detailly introduced in Section 2, SIPA and new proposed NS-IPMA are described in Section 3, experiments and results are presented and discussed in Section 4. Section 5 draws the conclusions.

2. Deep echo state network

2.1. Leakey integrator echo state network

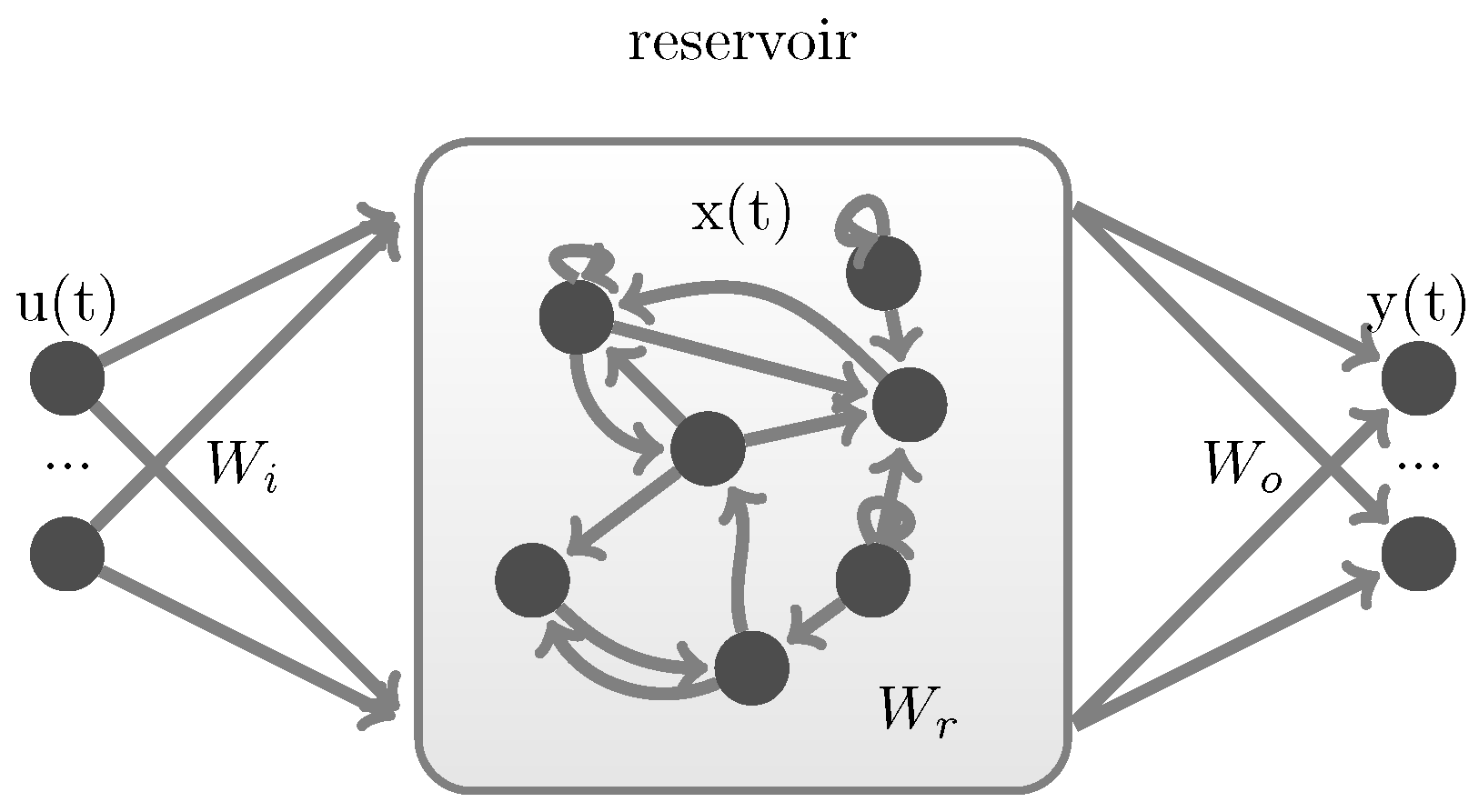
A leakey integrator echo state network [18],(LI-ESN), as shown in Figure 1, is a recurrent neural network with three layers: input layer

u (t) \in R^{N_{u} \times 1}

, hidden layer

x (t) \in R^{N_{x} \times 1}

, output layer

y (t) \in R^{N_{y} \times 1}

. t notes time sequence order. The hidden layer is regarded as a reservoir, which holds the memory of foregone information, and

x (t)

is refreshed by state transition function:

x (t) = α x (t - 1) + (1 - α) tanh (W_{i} u (t - 1) + W_{r} x (t - 1)),

(1)

where

W_{i} \in R^{N_{x} \times N_{u}}

is the input weight matrix randomly generated before training,

W_{r} \in R^{N_{x} \times N_{x}}

is the reservoir weight matrix previously given before training.

α \in [0, 1]

is the leaky parameter.

tanh (•)

is the activation function of the hidden layer. The reservoir weights in

W_{r}

must be initialized to satisfy the echo state property (ESP) [19,20], denoting by

ρ (•)

the spectral radius operator (

i . e .

the largest absolute eigenvalue of its matrix argument), the necessary condition for the ESP is expressed as follows:

ρ ((1 - α) I + α W_{r}) < 1 .

(2)

Accordingly,the values in matrix

W_{r}

are randomly selected from a uniform distribution(e.g.

U [- 1, 1]

), and then rescaled to satisfy above condition in equation 2.

The output

y (t)

can be calculated through a linear combination of reservoir states as follows:

y (t) = W_{o} x (t),

(3)

where

W_{o} \in R^{N_{y} \times N_{x}}

is the output weight matrix.

During training, the states of reservoir neurons are collected in a training state matrix

X_{t r a i n} = [x (1), x (2) \dots x (L_{t r a i n})]

, and an output target matrix

Y_{t r a i n} = [\hat{y} (1), \hat{y} (2) \dots \hat{y} (L_{t r a i n})]

is collected correspondingly, where

L_{t r a i n}

is the number of training samples.

The output weights in

W_{o}

can be calculated by ridge regression as follows:

W_{o} = {({(X_{t r a i n}^{T} X_{t r a i n} + λ I)}^{- 1} X_{t r a i n}^{T} Y_{t r a i n})}^{T},

(4)

where

{(•)}^{T}

represents matrix transpose,

{(•)}^{- 1}

represents matrix inversion,

λ I

is a regularization term ensuring

X_{t r a i n}^{T} X_{t r a i n}

is invertible.

2.2. Deep echo state network

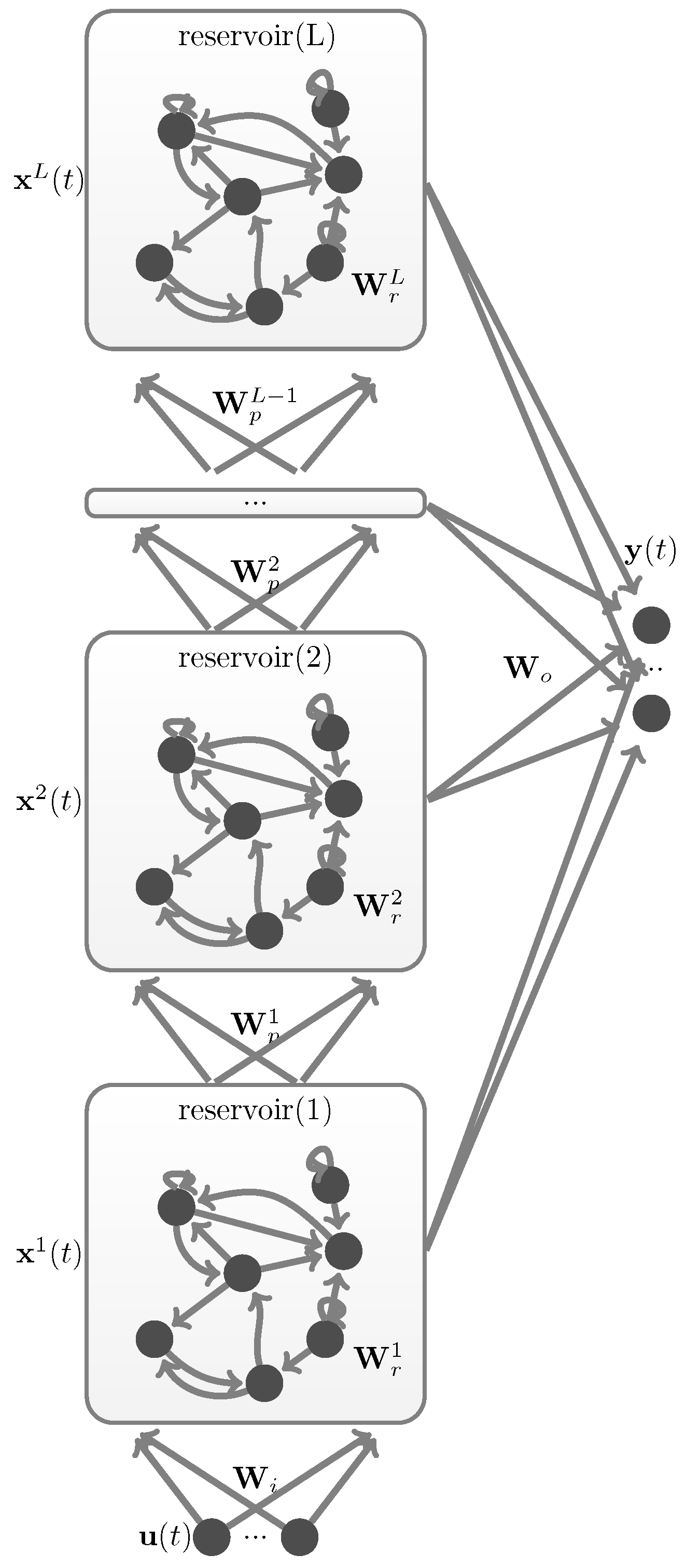
DeepESN was first introduced by Gallicchio [11,14], as a stacked reservoir computing (RC) architecture, multiple reservoir layers are stacked one on top of each other. The state transition functions of hidden layers in DeepESN are expressed as:

\{\begin{matrix} x^{1} (t) = α^{1} x^{1} (t) + (1 - α^{1}) tanh (W_{i} u (t - 1) + W_{r}^{1} x^{1} (t - 1)), & l = 1 \\ x^{l} (t) = α^{l} x^{l} (t) + (1 - α^{l}) tanh (W_{p}^{l - 1} x^{l - 1} (t - 1) + W_{r}^{l} x^{l} (t - 1)), & l \in [2, L] \end{matrix}

(5)

where the superscript(1 and l) is the layer notation,with totally L hidden layers in the network.

x^{l} (t) \in R^{N_{x}^{l} \times 1}

represents the l-th hidden layer (i.e. reservoir

(l)

) with

N_{x}^{l}

neurons inside,

W_{i} \in R^{N_{x}^{1} \times N_{u}}

is the input weight matrix of the first hidden layer,

W_{r}^{l} \in R^{N_{x}^{l} \times N_{x}^{l}}

is the reservoir weight matrix of the l-th hidden layer,

W_{p}^{l - 1} \in R^{N_{x}^{l - 1} \times N_{x}^{l}}

is the propagate weight matrix which connects reservoir

(l - 1)

to reservoir

(l)

Figure 2. Structure of DeepESN.

As in the standard LI-ESN approach, the reservoir weights of a DeepESN are initialized subject to similar stability constraints. In the case of DeepESN, such constraints are expressed by the necessary condition for the ESP of deep RC networks [13], described by the following equation:

max_{l \in [1, L]} ρ ((1 - α^{l}) I + α^{l} W_{r}) < 1,

(6)

a same leaky parameter (

α^{l} \equiv α

) in each layer is considered in this paper.

The values in each reservoir matrix

{W_{r}^{l} | l \in [1, L]}

are randomly initialized from a uniform distribution (e.g.

U [- 1, 1]

), after that, each

W_{r}^{l}

is spectral normalized by its spectral radius and rescaled by a same reservoir scaling paramerter

γ_{r}

to meet the demand of equation 6.

W_{r}^{l} \leftarrow \frac{γ_{r} W_{r}^{l}}{ρ (W_{r}^{l})}, l \in [1, L] .

(7)

The values in input weight matrix

W_{i}

are randomly selected from a uniform distribution

U [- γ_{i}, γ_{i}]

, where

γ_{i}

is the input scaling parameter. The values in each propagate weight matrix

{W_{p}^{l} | l \in [1, L - 1]}

are randomly selected from a uniform distribution

U [- γ_{p}, γ_{p}]

where

γ_{p}

is the propagate scaling parameter.

The output equation and the training equation of DeepESN are formed by concatenating all hidden neurons in each reservoirs together, denoting

\tilde{x} {(t)}^{T} = [x^{1} {(t)}^{T} x^{2} {(t)}^{T} \dots x^{L} {(t)}^{T}]

and substituting

\tilde{x} (t)

for

x (t)

in equation 3 and equation 4:

y (t) = W_{o} \tilde{x} (t),

(8)

W_{o} = {({({\tilde{X}}_{t r a i n}^{T} {\tilde{X}}_{t r a i n} + λ I)}^{- 1} {\tilde{X}}_{t r a i n}^{T} Y_{t r a i n})}^{T} .

(9)

2.3. Architechiecural richness of DeepESN

The components of the state should be as diverse as possible to provide a richer pool of dynamics from which the trainable part can appropriately combine. From an information-theoretic point of view, this form of richness could be measured by means of the entropy of instantaneous reservoir states [1]. Here an efficient estimator of Renyi’s quadratic entropy is introduced: suppose that we have N independent and identically distributed samples

{v_{1}, \dots, v_{N}}

for the continuous random variable

V

, An estimation of Renyi entropy directly from sampling data is defined as:

H_{2} (V) = - log (\frac{1}{N^{2}} \sum_{i = 1}^{N} \sum_{j = 1}^{N} G_{κ \sqrt{2}} (v_{j} - v_{i})),

(10)

where

G_{κ \sqrt{2}} (•)

is a Gauss kernel function with standard deviation

κ \sqrt{2}

κ

could be determined by Silverman’s rule:

κ = σ (V) {(4 N^{- 1} {(2 d + 1)}^{- 1})}^{\frac{1}{d + 4}},

(11)

where

σ (V)

is standard deviation and d is the data dimensionality.

Average state entropy (ASE) is obtained by time average of instantaneous Renyi’s quadratic estimation of reservoir neurons.

\begin{matrix} H (t) = H_{2} (\tilde{x} (t)), \end{matrix}

(12)

\begin{matrix} A S E = \frac{1}{S} \sum_{t = 1}^{S} H (t), \end{matrix}

(13)

where S is the sample number. ASE gives us a research perspective independent of learning aspect, higher ASE values are preferable and denote richer dynamics in reservoirs[1].

3. Pruning deep echo state network with neuronal similarity-based iterative pruning merging algorithm

3.1. Sensitive iterative pruning algorithm on simple cycle reservoir network

The simple cycle reservoir network(SCRN)is a kind of minimum complexity ESN, which has a cycle topology in the reservoir [21]. Every reservoir neuron is unidirectionally connected to its two adjacent neurons, A SIPA method is introduced to choose the right network size of SCRN through iteratively pruning out the least sensitive neurons [17].

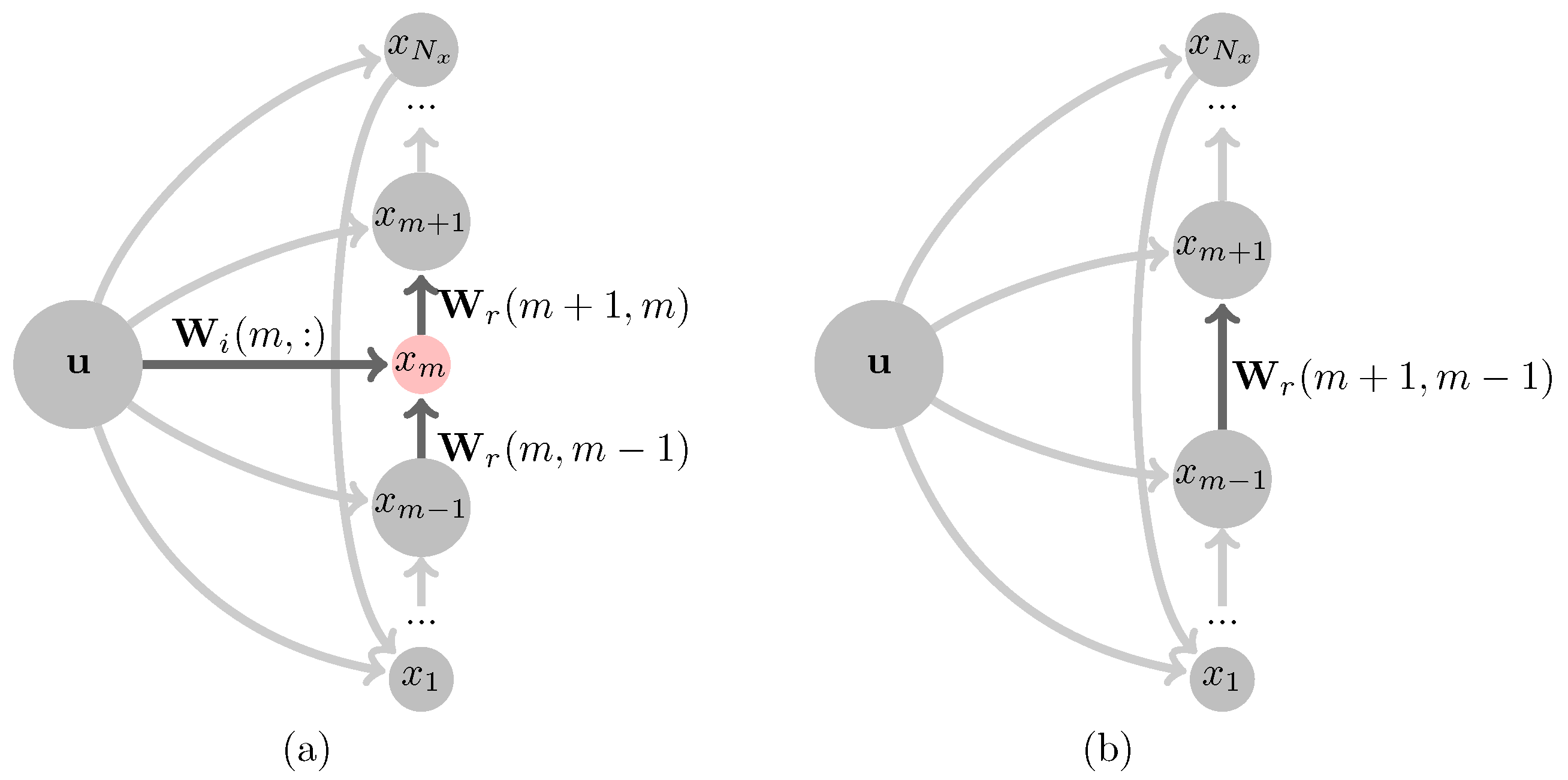
SIPA method is carried out in the following steps:

Step 1.: Establish an SCRN with a large enough reservoir and satisfactory performance.
Step 2.: Select a neuron to be pruned using the sensitive criterion [22] (assume $x_{m}$ is to be pruned), as diagramed in Figure 3, remove all weights connected to $x_{m}$ as follows:

$\{\begin{matrix} W_{i} (m, :) \leftarrow & 0 \\ W_{r} (m, m - 1) \leftarrow & 0 \\ W_{r} (m + 1, m) \leftarrow & 0 \end{matrix}$

(14)
Step 3.: Establish a new link between two neighbors of pruned neuron, the link weight is determined to eliminate the perturbation caused by pruning, denating the input to $x_{m + 1}$ before pruning $I_{o} = W_{i} (m + 1, :) u + W_{r} (m + 1, m) x_{m}$ , the input to $x_{m + 1}$ after pruning $I_{n} = W_{i} (m + 1, :) u + W_{r} (m + 1, m - 1) x_{m - 1}$ , the perturbation is eliminated and the original reservoir behavior is maintained as long as $I_{n}$ is set as close as possible to $I_{o}$ , by solving the following optimization problem:

$min_{W_{r} (m + 1, m - 1)} | | I_{o} - I_{n} {| |}_{2} .$

(15)
Step 4.: Adjust the output weights by retraining the network.Then calculate the training error.
Step 5.: Repeat steps 2-4 until the training error or the reservoir size reaches an acceptable range.

The key to a successful application of SIPA is Step 3. In Step 2, a reservoir perturbation is triggered by pruning, making the performance of the pruned network unpredictable. Thus, the essential task of Step 3 is to reduce the effects of perturbation so that the rest neurons remain unchanged and the network performance is approximately as good as before.

3.2. Neuronal similarity-based iterative pruning merging algorithm on deep echo state network

Due to the simple topology of SCRN, only one neuron (

x_{m + 1}

) receives input from the pruned neuron (

x_{m}

). The perturbation elimination in SCRN is easy to perform. However, the topology of DeepESN is much more complicated, more extensive perturbation will be raised by pruning one neuron in DeepESN because, in a highly coupled reservoir, perturbation at any neuron will be diffused to every neuron of same reservoir. In addition, in hierarchically stacked reservoirs, perturbation in lower layer will be transmitted to every higher layer above. It is very difficult to eliminate all of these perturbations.

The merging method is designed to solve this difficulty, this coincides with Islam’s idea [23], two neurons are merged by averaging their input weights. Consider the following ideal scenario: Merging two identical twin neurons in a same reservoir will derive a new neuron that is identical to anteceden two twins, this new burned neuron could act as eqivalent substitution for anteceden two twins. Conseqently, a neuron is pruned without leading any perturbation through superimposing the output weights of the merged twins as well. This ideal perturbation-free merging has the prerequisite that two identical neurons to be found in the same reservoir, the more similar the two merged neurons are, the weaker perturbation will be raised by merging. Neuronal similarity could be assessed by some quantitative relations of the collected training state matrix. Distance and correlation are commonly used to quantify similarity, four similarity estimation criteria are given in this paper including the inverse of Euclidean distance (

E D

), Pearson’s correlation coefficient (

P C

),Spearman’s correlation coefficient (

S C

) and Kendall’s correlation coefficient (

K C

) as follows:

Noting the total number of neurons in all reservoirs

M = \sum_{l = 0}^{L} N_{x}^{l}

, renote the train state matrix

{\tilde{X}}_{t r a i n} = {[\begin{matrix} x^{1} (1) & x^{1} (2) & \dots & x^{1} (L_{t r a i n}) \\ x^{2} (1) & x^{2} (2) & \dots & x^{1} (L_{t r a i n}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x^{L} (1) & x^{L} (2) & \dots & x^{L} (L_{t r a i n}) \end{matrix}]}_{(M \times L_{t r a i n})} = [\begin{matrix} n_{1} \\ n_{2} \\ ⋮ \\ n_{M} \end{matrix}],

(16)

where

L_{t r a i n}

is the number of training samples,

n_{i}

is the historical state of i-th neuron state during training. The similarity of

n_{i}

and

n_{j}

is derived by:

\begin{matrix} E D (i, j) & = \frac{1}{‖ n_{i} - n_{j} ‖_{2}}, \end{matrix}

(17)

\begin{matrix} P C (i, j) & = \frac{σ_{n_{i} n_{j}}}{\sqrt{σ_{n_{i} n_{i}} σ_{n_{j} n_{j}}}}, \end{matrix}

(18)

\begin{matrix} S C (i, j) & = 1 - \frac{6 \sum_{t = 1}^{L_{t r a i n}} d_{t}^{2}}{L_{t r a i n} ({L_{t r a i n}}^{2} - 1)}, \end{matrix}

(19)

\begin{matrix} K C (i, j) & = \frac{c - d}{\frac{1}{2} L_{t r a i n} (L_{t r a i n} - 1)}, \end{matrix}

(20)

where

σ_{n_{i} n_{j}}

represents cross-correlation of

n_{i}

and

n_{j}

σ_{n_{i} n_{i}}

and

σ_{n_{j} n_{j}}

represents autocorrelation of

n_{i}

and

n_{j}

d_{t}

is the rank difference of

n_{i} (t)

and

n_{j} (t)

, c is the number of concordant pairs and d is the number of discordant pairs in

n_{i}

and

n_{j}

. NS-IPMA based on different similarity estimation criteria are named correspondingly, for instance, ES-IPMA means NS-IPMA based on the inverse of Euclidean distance criterion, etc.

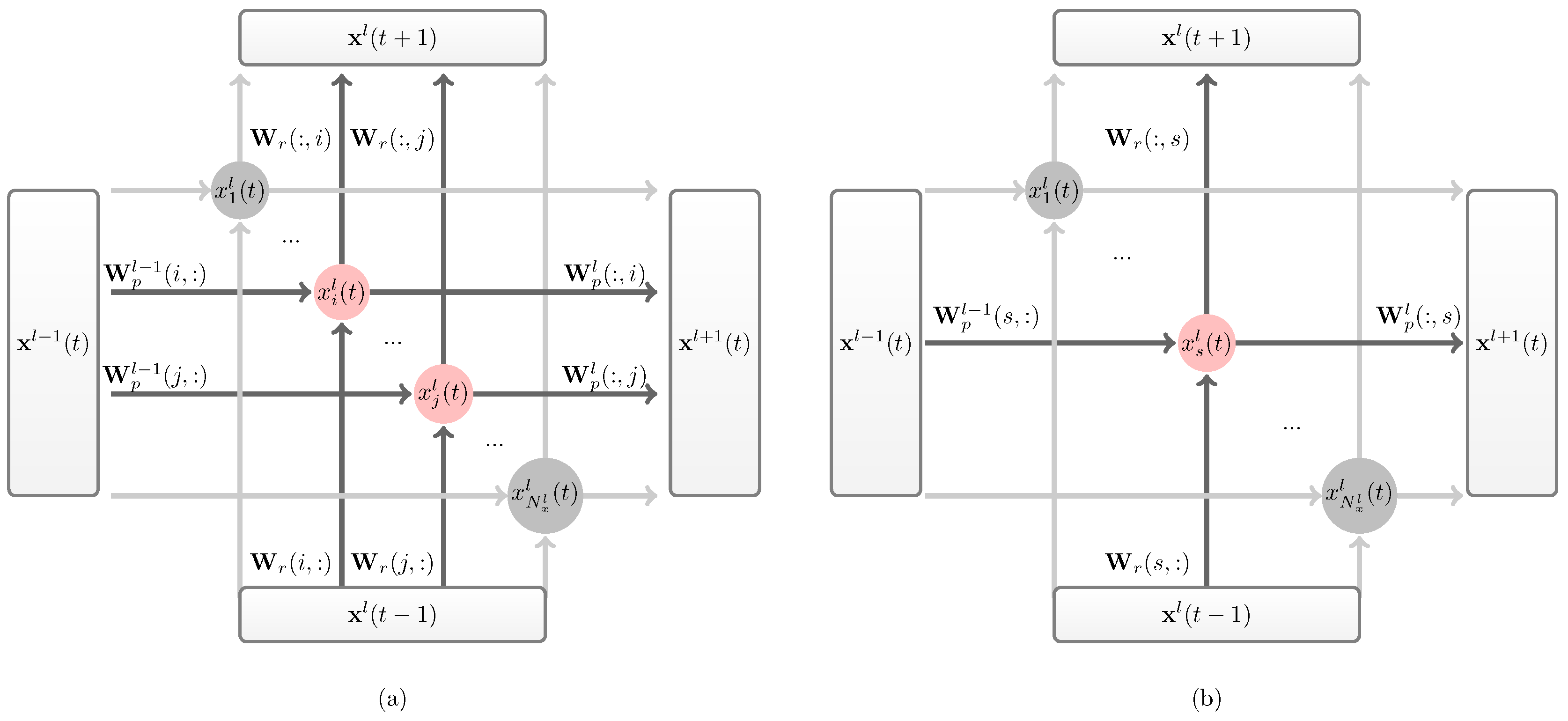
The NS-IPMA method is carried out in the following steps:

Step 1.

Initially generate a performable DeepESN with large enough reservoirs by tuning hyperparameters to minimize the average of training and validate error using Particle Swarm Optimization (PSO) algorithm, please refer to A for more detail on hyperparameter tuning. This DeepESN is a primitive network to implement.

Step 2.

Washout the reservoirs, activate the reservoirs using train samples to obtain the training state matrix.

Step 3.

Quantify the similarity of each two neurons (using one criterion of equation 17 - 20) and select a pair of the most similar neurons.

Step 4.

(1).: If selected neurons are in the same reservoir (note as $x_{i}^{l}$ and $x_{j}^{l}$ ), merge them. As diagramed in Figure 4, $x_{s}^{l}$ is the son neurons merged as the substitute of its parents $x_{i}^{l}$ and $x_{j}^{l}$ . l is the reservoir layer where $x_{i}^{l}$ and $x_{j}^{l}$ exists in. Related weight matrix $W_{p}^{l - 1}$ , $W_{p}^{l}$ and $W_{r}^{l}$ is refreshed as follows1:

$\{\begin{matrix} W_{p}^{l - 1} (s, :) \leftarrow \frac{W_{p}^{l - 1} (i, :) + W_{p}^{l - 1} (j, :)}{2} \\ W_{r}^{l} (s, :) \leftarrow \frac{W_{r}^{l} (i, :) + W_{r}^{l} (j, :)}{2} \\ W_{r}^{l} (:, s) \leftarrow W_{r}^{l} (:, i) + W_{r}^{l} (:, j) \\ W_{p}^{l} (:, s) \leftarrow W_{p}^{l} (:, i) + W_{p}^{l} (:, j) \end{matrix}$

(21)
(2).: If selected neurons are in different reservoirs(note as $x_{i}^{m}$ and $x_{j}^{l}$ ), prune one in high layer (assume $m < l$ ). Related weight matrix $W_{p}^{l - 1}$ , $W_{p}^{l}$ and $W_{r}^{l}$ is refreshed as follows1:

$\{\begin{matrix} W_{p}^{l - 1} (j, :) \leftarrow 0 \\ W_{r}^{l} (j, :) \leftarrow 0 \\ W_{r}^{l} (:, j) \leftarrow 0 \\ W_{p}^{l} (:, j) \leftarrow 0 \end{matrix}$

(22)

Step 5.

Adjust the output weights by retraining the network.Then estimate the performance of the current network.

Step 6.

Repeat steps 2-5 until the training error or the network size reaches an acceptable range.

4. Experiments and results

4.1. Datasets

4.1.1. Mackey-Glass chaotic time-seriers

Mackey-Glass time series [24] is a standard benchmark for chaotic time series forecast models where ESN has been successfully applied to demonstrate good performance. The 31 order Mackey-Glass time series is defined in the following differential equation:

\frac{d x}{d t} = 0.2 \frac{x_{31}}{1 + {x_{31}}^{11}} - 0.1 x, x_{31} = x (t - 31),

(23)

the Mackey Glass dataset (

M G

) is sampled with a sample frequency of 4Hz. A Python library[25] was used to generate this dataset.

4.1.2. Lorenz chaotic time series

The Lorenz time series prediction [26] is another benchmark problem for ESN. The Lorenz dynamic system is described by the following equations:

\{\begin{matrix} \frac{d x}{d t} & = - \frac{34}{3} (x - y); \\ \frac{d y}{d t} & = - \frac{298}{11} (x - y) + x z; \\ \frac{d z}{d t} & = - \frac{17}{7} z + x y \end{matrix}

(24)

The initial values are set as

[x (0), y (0), z (0)] = [0.5, 0, - 0.5]

,the Lorenz z axis dataset (LZ) is sampled with a sample frequency of

12.5

Hz.

Before the experiments, both datasets are shifted by its mean to remove the DC bias.

4.2. Experiments

4.2.1. Next spot prediction task

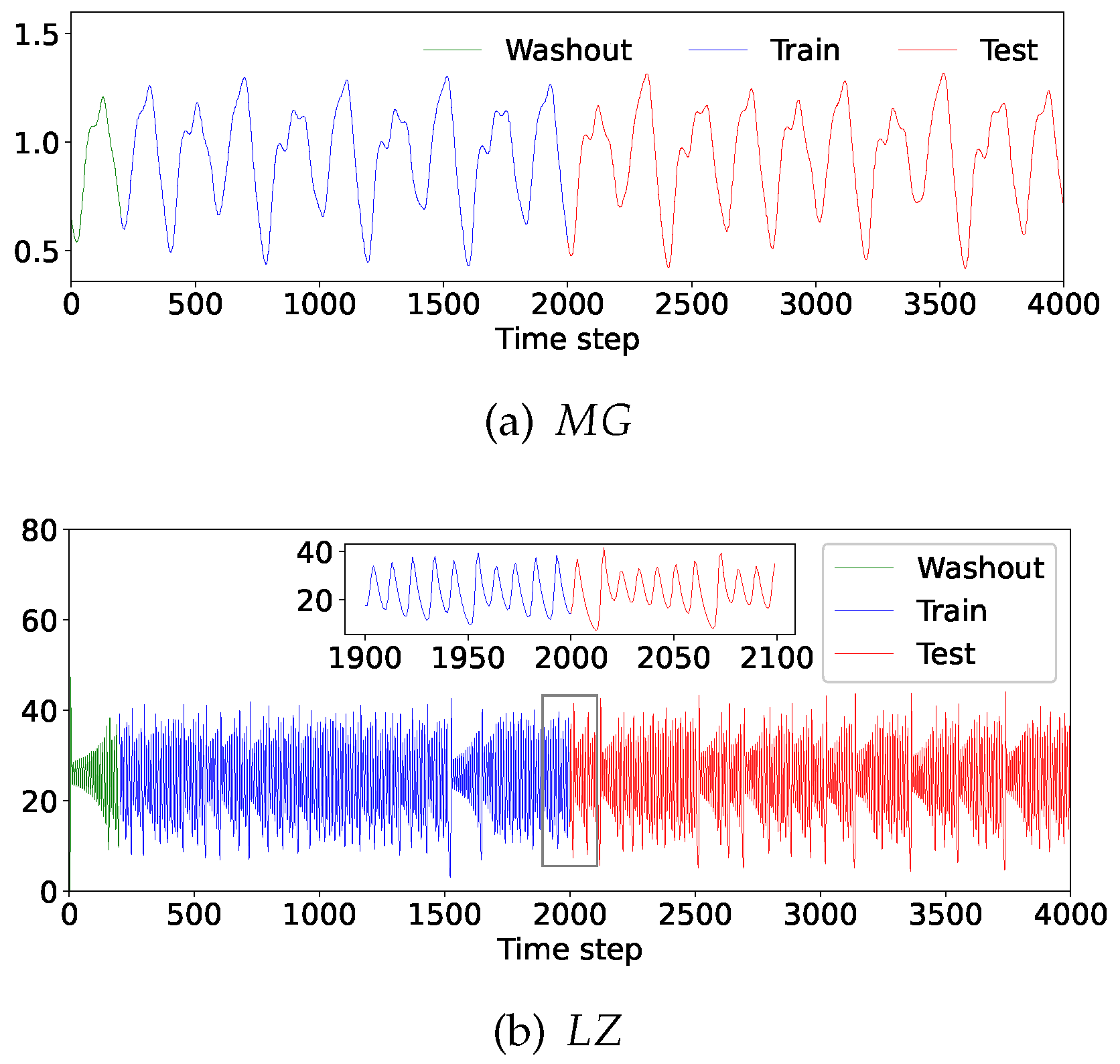
In the next spot prediction experiment, the last four continuous spots were considered the input and the next spot was considered the desired output, i.e.

{u (t - 3), u (t - 2), u (t - 1), u (t)}

was used to predict

u (t + 1)

. The number of the train samples and the test samples was 1800 and 2000, 200 samples before the first training sample were used to wash out the initial transient(see Figure 5). The reservoir diversity was quantized by the ASE(see: 2.3) of combined training and testing neuron states activated by training and testing samples. the predictive error performance was quantized by normalized root mean square error:

N R M S E = \sqrt{\sum_{t = 1}^{T} \frac{∣ y (t) - \hat{y} (t) ∣^{2}}{T ∣ y (t) - \bar{y} (t) ∣^{2}}},

(25)

where T is sample number,

\hat{y} (t)

is desired output,

y (t)

is the readout output and

\bar{y} (t)

is average of

y (t)

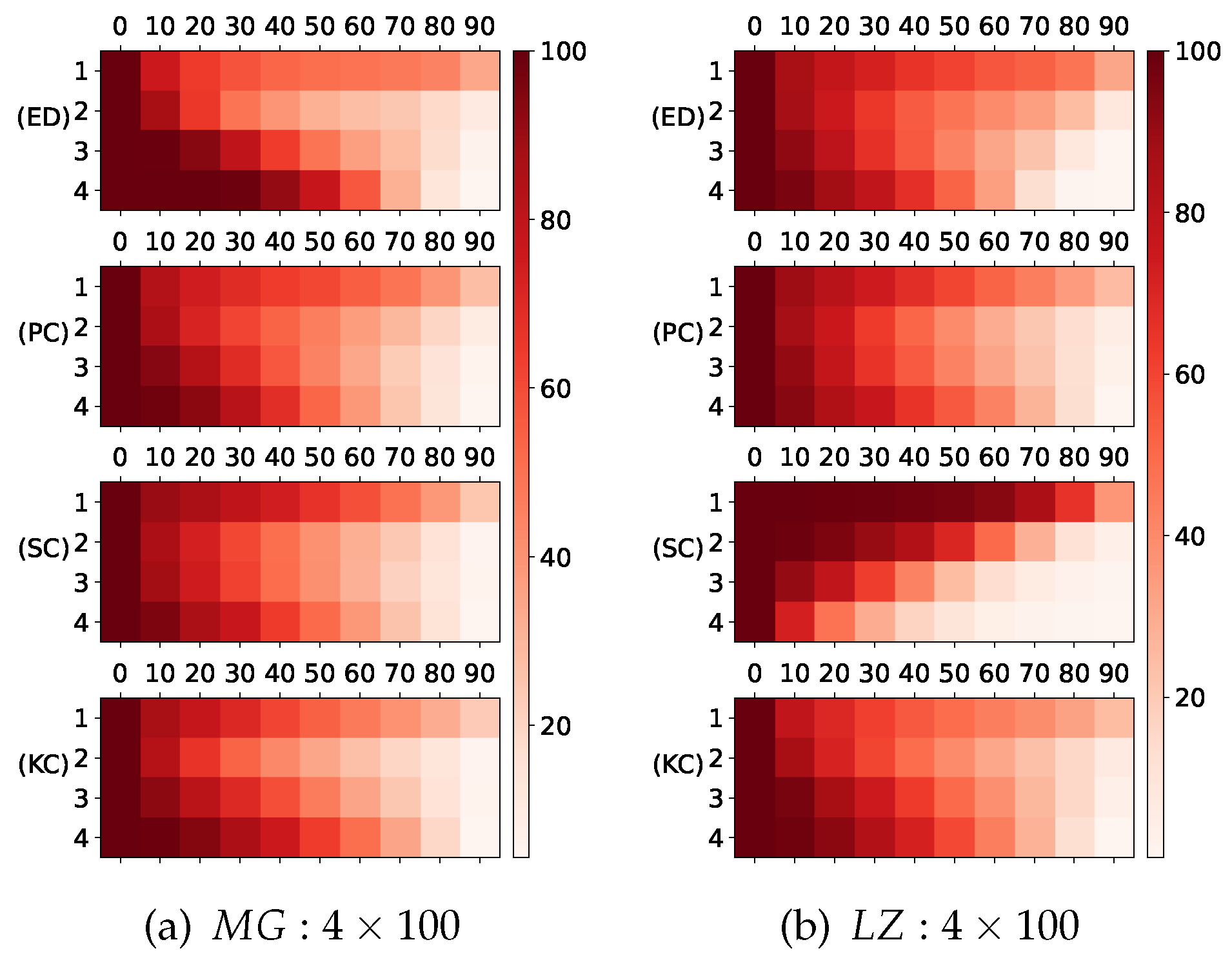
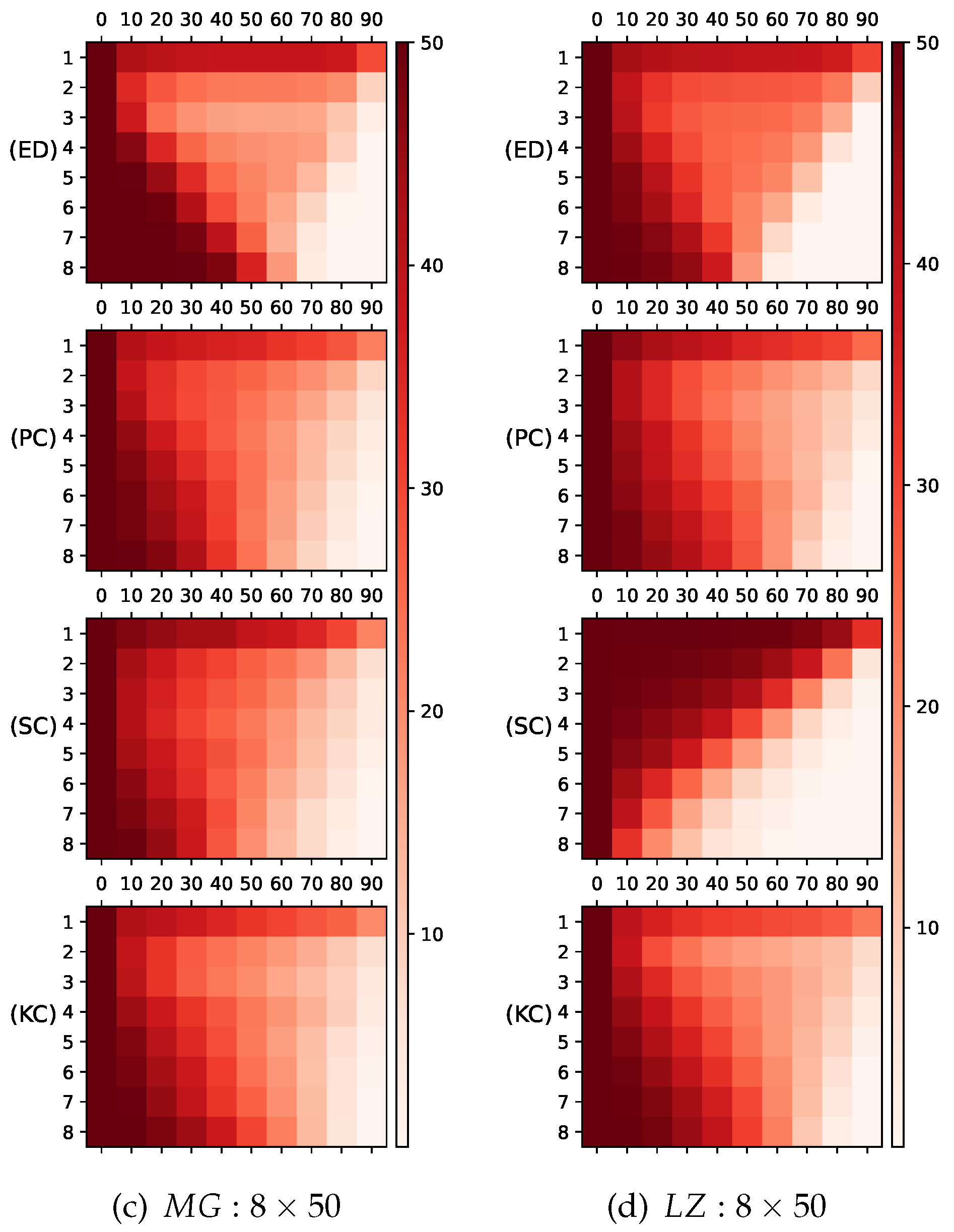
Two different initial reservoir size conditions of DeepESN were performed in both dataset, the first is 4 stacked reservoir with 100 neurons in each reservoir (Abbreviated to:

4 \times 100

) and the second is 8 stacked reservoir with 50 neurons in each reservoir (Abbreviated to:

8 \times 50

).All experiments were carried out under two different initial conditions on two datasets, model hyperparameters tuned by PSO were recorded in Table A1.

4.2.2. Ablation experiment and control experiment

In order to demonstrate the effectiveness of different similarity estimation criteria, the worst-case scenario of NS-IPMA, Neuron iterative pruning merging algorithm without similarity estimation (IPMA), was investigated as an ablation experiment. in IPMA, the similarity of each two neurons was assigned by random values. Thus, two random neurons would be recognized as the most similar neuron pairs and would be pruned (or merged).

To verify the effectiveness of NS-IPMA method. The pruned DeepESNs were compared with a control experiment, the unpruned DeepESN, whose number of neurons in each reservoir is the same, the pruned DeepESN and the unpruned DeepESN were compared with equal layer number, equal total neruon number and same hyperparameters. The unpruned DeepESN is a standard benchmark that indicates the evolutionary characteristic of network performance by reducing network size. 90 percentage of neurons of random initalized DeepESNs were continuous pruned by different criterion based NS-IPMA methods (ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA) and non-criterion based IPMA,during pruning, networks were silhouetted and the performance were evaluated once 10 percentage of neurons had been pruned, these pruned groups were compared with unpruned DeepESN. All experiments were repeated for 20 times and all results were averaged through 20 independent replications.

Figure 6. The number of remaining neurons in each layer of peuned DeepESN, which was processed by different similarity estimation criteria based NS-IPMA methods. The vertical axis indicates layer index, the horizontal axis indicates percentage of pruned neurons in the initial total number of neurons, the mesh color indicates the number of remained neurons, the darker color indicates more neurons are reamained. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

4.3. Results and disscusion

4.3.1. Hierarchical structure

During pruning, the number of remaining neurons in each reservoir of pruned DeepESN, which was processed by different similarity estimation criterion based NS-IPMA, are shown in Figure 5 As NS-IPMA goes on, we observed significantly reduction of the neuron number in high layers at a later stage, the reason was because the discard policy, of which when a redundant pair of most similar neuron in different reservoirs were found, the neuron in higher layers would be pruned out. Lower layer reservoirs are the foundation of higher layer reservoirs, too few neurons in lower layers brings risk of insufficient information presentation and extracion in higher layers. Thus, the NS-IPMA methods have good network structure adaptability.

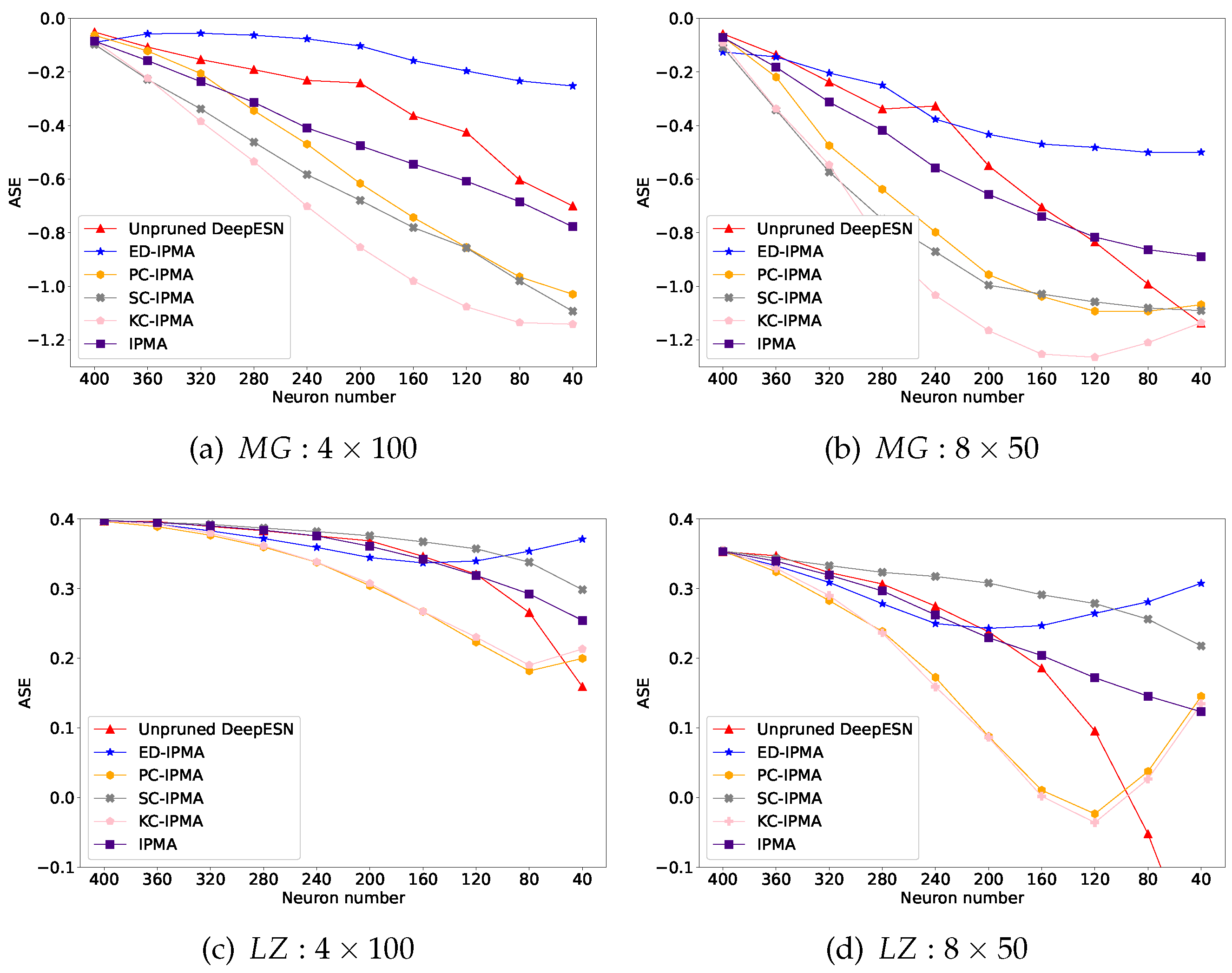
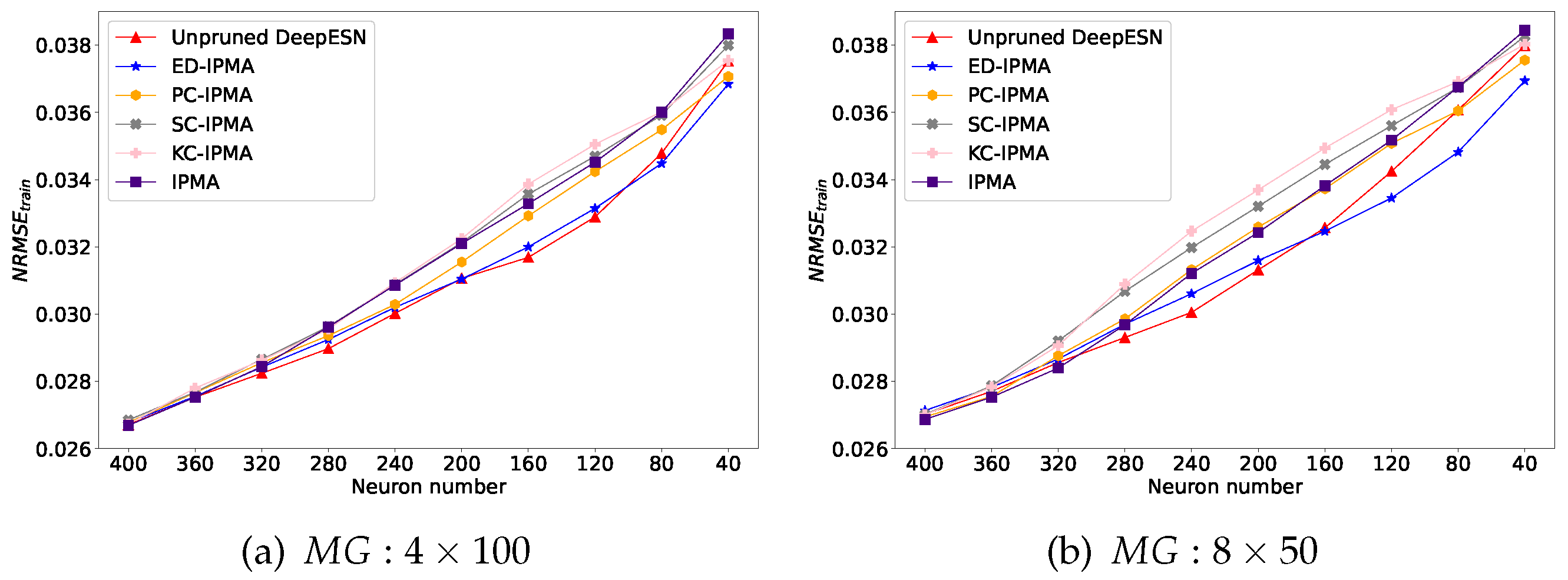
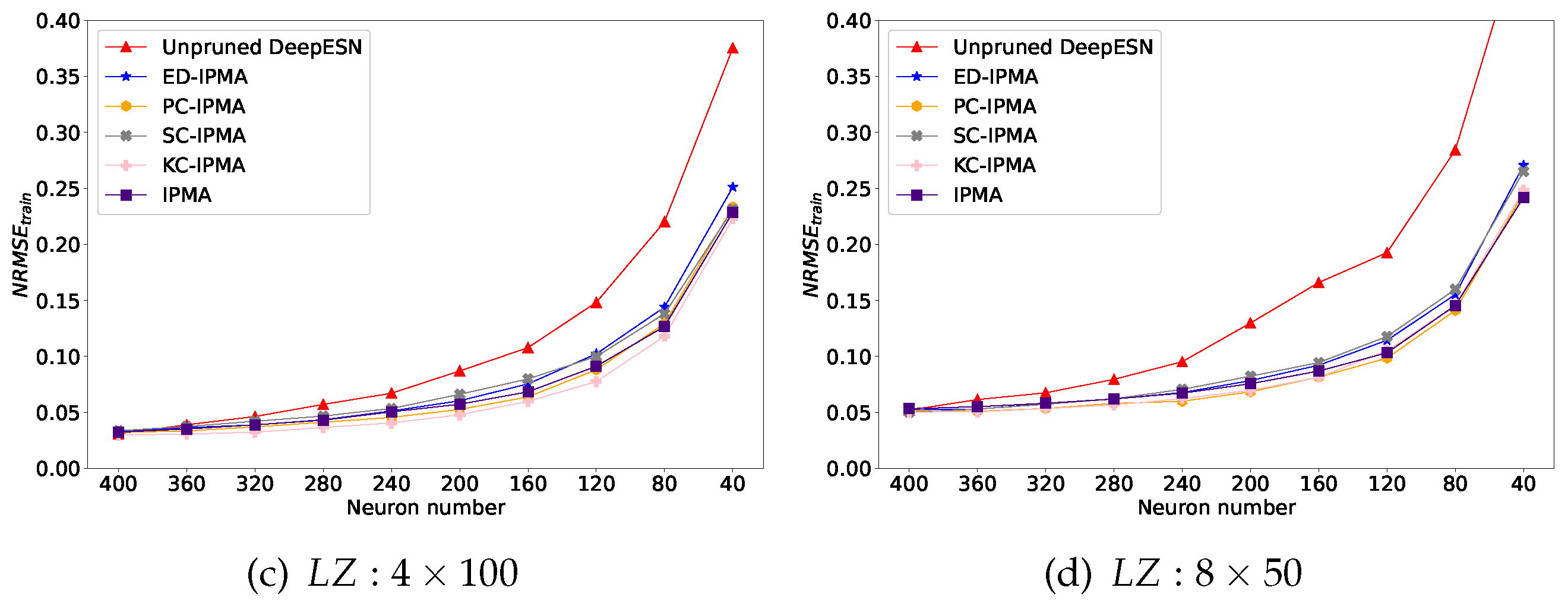
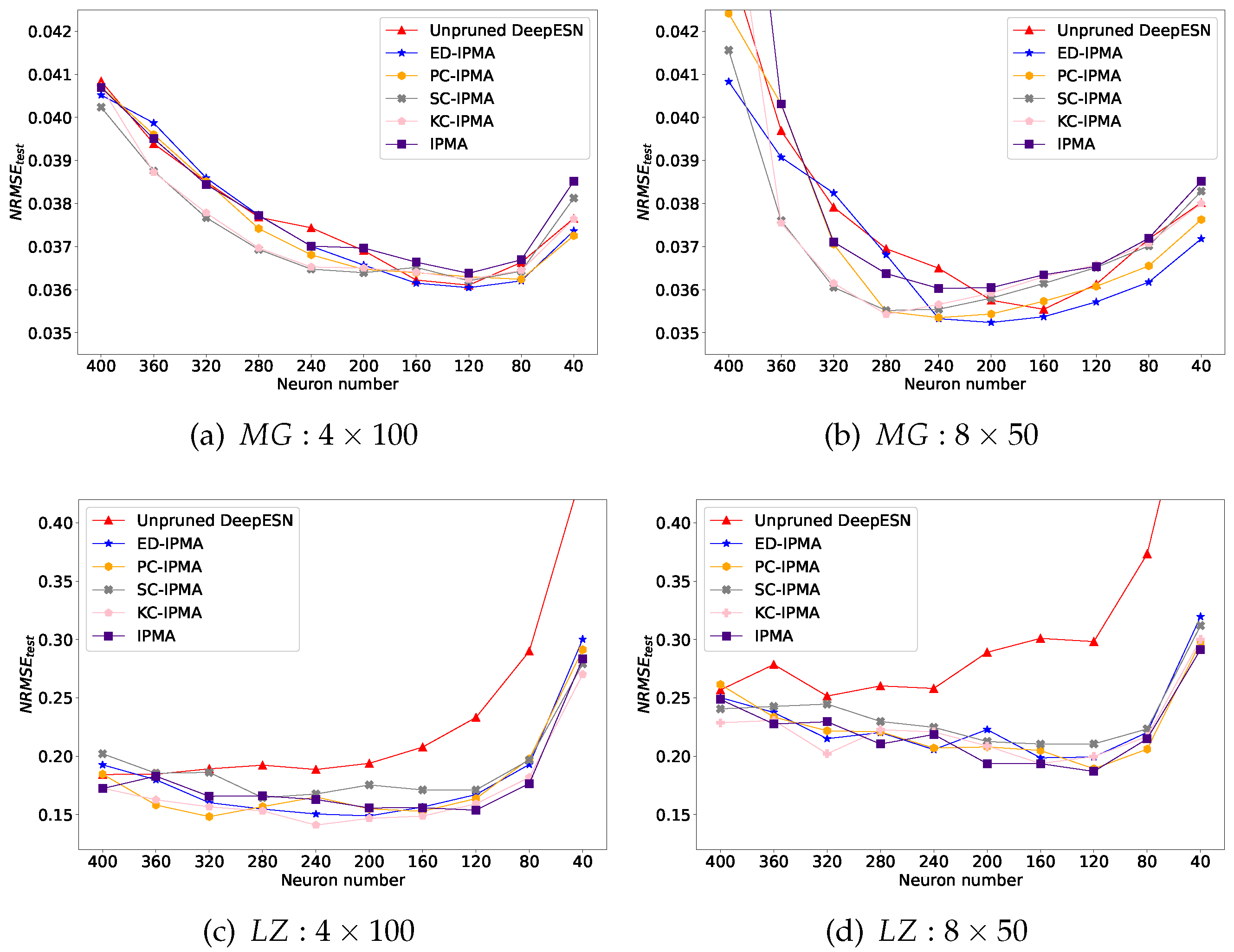
4.3.2. Reservoir diversity and error performance

The quantitative performance comparations (ASE, training NRMSE, and testing NRMSE) of unpruned DeepESN and DeepESN, which was pruned by IPMA and different similarity estimation criterion based NS-IPMA, are illustrated in Figure 7, Figure 8 and Figure 9 The results on the two datasets were similar but different. On the whole, as reservoir size reduces, ASE will decrease and training NRMSE will increase, confirming that the model with more neurons has better information representation ability and better training effect. Initially, testing NRMSE is greater than training NRMSE, this phenomenon is called overfitting. As the reservoir size reduces, The training error went down and the overfitting is improved. confirming that the reducing the network size is a directly effective approach to improve generalization performance of the network. There is no doubt that pruning neurons will lead to reduction of network size, that is the reason why the unpruned DeepESN is tested as a benchmark. A successful pruning algorithm should outperform this benchmark. Furthermore, the minimum testing NRMSE condition is choosen to compare the extreme generalization performance of each experiment group, which was recorded in Table 1.

Similarly, from Figure 7, the DeepESN pruned by ED-IPMA maintains a minimum ASE loss as the number of neurons decreases, we suspect that there are some hidden relationships between Euler distance and Renyi’s quadratic entropy; from Table 1, the pruned DeepESNs have a samller standard deviation of the minimum testing NRMSE compared to the unpruned DeepESN, indicating that NS-IPMA method has good robustness.

On MG dataset: from Figure 9a,b, In the early stage, the testing error of DeepESN pruned by SC-IPMA and KC-IPMA drops rapidly; later, DeepESN pruned by ED-IPNA and PC-IPMA out stand from crowd when the majority of neurons are pruned. From Table 1, although ED-IPMA achieved the best extreme generalization performance, the pruned DeepESNs have no obvious improvement on the mean value of minimum testing NRMSE compared to the unpruned DeepESN.

On LZ dataset: from Figure 8 c,d and Figure 9c,d, and Table 1, the taining error, testing error, and extreme generalization performance of pruned DeepESNs are all significantly improved compared with unpruned DeepESN, and the diversity of different similarity estimation criteria are not prominent, non-criterion based IPMA method perfomed as good as criterion based NS-IPMA methods.

In summary, all these experimental results showed that the NS-IPMA method is a successful approach to improving the generalization performance of DeepESN, which is specific in, under most circumstances of our designed experiments, the DeepESN pruned by NS-IPMA has better generalization performance than the standard unpruned DeepESN.

5. Conclusions

In our research, a new Iterative Pruning Merging algorithm was proposed to simplify the architecture of DeepESN. As to which neurons should be pruned out, four different similarity estimation criteria were attempted. The unpruned DeepESNs is a benchmark that indecates the evolutionary characteristic of network performance by reducing network size, the effectiveness of proposed methed was experimentally verified by comparing pruned DeepESNs with unpruned DeepESNs in the same network size. The results showed that these NS-IPMA methods have good network structure adaptability, and the DeepESNs pruned by NS-IPMA methed have better generalization performance and better robustness than unpruned DeepESNs, indicating that NS-IPMA methed is a feasible and superior approach to improving the generalization performance of DeepESN. The NS-IPMA method provides a novel approach for choosing the appropriate network size of DeepESN, one could start with a larger model than necessary reservoir size, then prune or merge some similar neurons to obtain a better DeepESN model, one could select a simple architecture with small computation requirements while keeping the testing error acceptable.

However, there are still some shortcomings in our work: First, the problem of how to choose the redundant neurons to be pruned out, or what the best neuronal similarity estimation criterion should be, remains unsolved. Second, only the hierarchical structure, the reservoir diversity, and the overall error performance are investigated, more evolutionary characteristics of different reservoirs, such as their spectral radius, resulting from the NS-IPMA method are not analyzed. Third, the effects of pruning and merging are not clearly distinguished. Further research on the NS-IPMA method is expected to be carried out.

Appendix A. Hyperparameter tuning

Table A1. Hyperparameters applied under different initial resverior size on different datasets.

Dataset	$M G$	$M G$	$L Z$	$L Z$
Initial size	$4 \times 100$	$8 \times 50$	$4 \times 100$	$8 \times 50$
$α$	0.92	0.92	0.92	0.92
$γ_{r}$	0.8	0.8	0.8	0.8
${γ_{i}}^{* 1}$	0.373 84	0.253 14	0.096 31	0.064 94
${γ_{p}}^{* 2}$	0.211 36	0.241 62	0.335 51	0.347 11
$λ$	$1 \times 10^{- 10}$	$1 \times 10^{- 10}$	$1 \times 10^{- 10}$	$1 \times 10^{- 10}$

*1 Tuned by PSO in the range of [1 × 10⁻⁵, 10]; *2 Tuned by PSO in the range of [0.1, 5].

As defined in Section 2.2, hyperparameters(

α

γ_{i}

γ_{r}

γ_{p}

and

λ

) play essential roles in the performance of DeepESN, so as in the successful application of NS-IPMA.

α

and

γ_{r}

affect stability of reservoirs,

α = 0.92

and

γ_{r} = 0.8

are set to satisfy equation 6;

λ

affects the generalization performance, a small regularization facter

λ = 1 \times 10^{- 10}

is chosen to make the output weights better fit the training samples.

γ_{i}

adjusts the strength of input signal into the first layer of DeepESN,

γ_{p}

adjusts the strength of input signal into higher layers of DeepESN, thus,

γ_{i}

is optimized on the LI-ESN which is the first layer of DeepESN, after that

γ_{p}

is optimized on the DeepESN after higher layers hierarchically stacked on original LI-ESN. The tuned results are recorded in Table A1.

References

Gallicchio, C.; Micheli, A. Architectural richness in deep reservoir computing. Neural Computing and Applications 2022. [Google Scholar] [CrossRef]
Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
Zhang, S.; He, K.; Cabrera, D.; Li, C.; Bai, Y.; Long, J. Transmission Condition Monitoring of 3D Printers Based on the Echo State Network. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
Che, Z.P.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Scientific Reports 2018, 8. [Google Scholar] [CrossRef] [PubMed]
Xu, X.; Ren, W. Prediction of Air Pollution Concentration Based on mRMR and Echo State Network. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
Zhang, M.; Wang, B.; Zhou, Y.; Sun, H. WOA-Based Echo State Network for Chaotic Time Series Prediction. Journal of the Korean Physical Society 2020, 76, 384–391. [Google Scholar] [CrossRef]
Zhang, M.; Wang, B.; Zhou, Y.; Gu, J.; Wu, Y. Prediction of Chaotic Time Series Based on SALR Model with Its Application on Heating Load Prediction. Arabian Journal for Science and Engineering 2021, 46, 8171–8187. [Google Scholar] [CrossRef]
Zhou, J.; Wang, H.; Xiao, F.; Yan, X.; Sun, L. Network traffic prediction method based on echo state network with adaptive reservoir. Software-Practice & Experience 2021, 51, 2238–2251. [Google Scholar] [CrossRef]
Baek, J.; Choi, Y. Deep Neural Network for Predicting Ore Production by Truck-Haulage Systems in Open-Pit Mines. Applied Sciences 2020, 10. [Google Scholar] [CrossRef]
Gallicchio, C.; Micheli, A.; Pedrelli, L. Deep reservoir computing: A critical experimental analysis. Neurocomputing 2017, 268, 87–99. [Google Scholar] [CrossRef]
Gallicchio, C.; Micheli, A.; Silvestri, L. Local Lyapunov exponents of deep echo state networks. Neurocomputing 2018, 298, 34–45. [Google Scholar] [CrossRef]
Gallicchio, C.; Micheli, A. Echo State Property of Deep Reservoir Computing Networks. Cognitive Computation 2017, 9, 337–350. [Google Scholar] [CrossRef]
Gallicchio, C.; Micheli, A. Deep Echo State Network (DeepESN): A Brief Survey. ArXiv 2017, abs/1712.04323. [CrossRef]
Gallicchio, C.; Micheli, A. Why Layering in Recurrent Neural Networks? A DeepESN Survey. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN); pp. 1–8. [CrossRef]
Thomas, P.; Suhner, M.C. A New Multilayer Perceptron Pruning Algorithm for Classification and Regression Applications. Neural Processing Letters 2015, 42, 437–458. [Google Scholar] [CrossRef]
Wang, H.; Yan, X. Improved simple deterministically constructed Cycle Reservoir Network with Sensitive Iterative Pruning Algorithm. Neurocomputing 2014, 145, 353–362. [Google Scholar] [CrossRef]
Jaeger, H.; Lukoševičius, M.; Popovici, D.; Siewert, U. Optimization and applications of echo state networks with leaky- integrator neurons. Neural networks: the official journal of the International Neural Network Society 2007, 20 3, 335–52. [Google Scholar] [CrossRef]
Yildiz, I.B.; Jaeger, H.; Kiebel, S.J. Re-visiting the echo state property. Neural Networks 2012, 35, 1–9. [Google Scholar] [CrossRef] [PubMed]
Gallicchio, C.; Micheli, A. Architectural and Markovian factors of echo state networks. Neural Networks 2011, 24, 440–456. [Google Scholar] [CrossRef]
Rodan, A.; Tino, P. Minimum complexity echo state network. newblock IEEE Transactions on Neural Networks 2011, 22, 131–144. [Google Scholar] [CrossRef]
Castellano, G.; Fanelli, A.; Pelillo, M. An iterative pruning algorithm for feedforward neural networks. IEEE Transactions on Neural Networks 1997, 8, 519–531. [Google Scholar] [CrossRef]
Islam, M.M.; Sattar, M.A.; Amin, M.F.; Yao, X.; Murase, K. A New Adaptive Merging and Growing Algorithm for Designing Artificial Neural Networks. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2009, 39, 705–722. [Google Scholar] [CrossRef] [PubMed]
Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197 4300, 287–9. [Google Scholar] [CrossRef]
Maat, J.R.; Malali, A.; Protopapas, P. TimeSynth: A Multipurpose Library for Synthetic Time Series in Python, 2017. https://github.com/TimeSynth/TimeSynthh.
Chao, K.H.; Chang, L.Y.; Xu, F.Q. Smart Fault-Tolerant Control System Based on Chaos Theory and Extension Theory for Locating Faults in a Three-Level T-Type Inverter. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]

Figure 1. Structure of LI-ESN.

Figure 3. Connection weight coefficients diagram of neurons in reservoir of SCRN before(a) and after(b) pruning a neuron by SIPA.

Figure 4. Connection weight coefficients diagram of neurons in reservoir(l) of DeepESN before(a) and after(b) merging a neuron by NS-IPMA.

Figure 5. (a)

M G

and (b)

L Z

datasets.

Figure 5. (a)

M G

and (b)

L Z

datasets.

Figure 7. ASE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Figure 7. ASE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Figure 8. Training NRMSE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Figure 8. Training NRMSE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Figure 9. Testing MRMSE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Figure 9. Testing MRMSE Comparation of unpruned DeepESN and DeepESN pruned by IPMA, ED-IPMA, PC-IPMA, SC-IPMA, KC-IPMA. (a):Initial 4 layer reservoirs with 100 neurons in each reservoir on

M G

dataset;(b):Initial 8 layer reservoirs with 50 neurons in each reservoir on

M G

dataset; (c):Initial 4 layer reservoirs with 100 neurons in each reservoir on

L Z

dataset;(d):Initial 8 layer reservoirs with 50 neurons in each reservoir on

L Z

dataset.

Table 1. Minimum testing NRMSE condition of each experiment group.

	Group	Unpruned DeepESN	Pruned DeepESN
	Method	-	ED-IPMA	PC-IPMA	SC-IPMA	KC-IPMA	IPMA
	$N R M S E_{t e s t}$ (Mean)	0.036 105	0.036 046	0.036 240	0.036 206	0.036 243	0.036 380
$M G : (4 \times 100)$	$N R M S E_{t e s t}$ (Std.)	0.000 483	0.000 388	0.000 221	0.000 281	0.000 144	0.000 291
	Neuron number	120	120	80	120	120	120
	$N R M S E_{t e s t}$ (Mean)	0.035 544	0.035 238	0.035 350	0.035 516	0.035 427	0.036 030
$M G : (8 \times 50)$	$N R M S E_{t e s t}$ (Std.)	0.000 699	0.000 346	0.000 516	0.000 533	0.000737	0.000 338
	Neuron number	160	200	240	280	280	240
	$N R M S E_{t e s t}$ (Mean)	0.184 285	0.148 812	0.152 775	0.164 455	0.140 930	0.155 667
$L Z : (4 \times 100)$	$N R M S E_{t e s t}$ (Std.)	0.043 201	0.026 072	0.024 417	0.022 953	0.031 862	0.027 816
	Neuron number	400	200	160	280	240	200
	$N R M S E_{t e s t}$ (Mean)	0.251 535	0.198 581	0.189 230	0.210 376	0.193 678	0.186 933
$L Z : (8 \times 50)$	$N R M S E_{t e s t}$ (Std.)	0.044 484	0.027 631	0.024 995	0.033 404	0.029 164	0.024 092
	Neuron number	320	160	120	160	160	120

Bold values indicate the best validation performance of all methods.

1	if $l = 1$ , $W_{i}$ perform as $W_{p}^{l - 1}$ ;if $l = L$ , $W_{p}^{l}$ does not exist.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Improving Deep Echo State Network with Neuronal Similarity-based Iterative Pruning Merging Algorithm

Abstract

1. Introduction

2. Deep echo state network

2.1. Leakey integrator echo state network

2.2. Deep echo state network

2.3. Architechiecural richness of DeepESN

3. Pruning deep echo state network with neuronal similarity-based iterative pruning merging algorithm

3.1. Sensitive iterative pruning algorithm on simple cycle reservoir network

3.2. Neuronal similarity-based iterative pruning merging algorithm on deep echo state network

4. Experiments and results

4.1. Datasets

4.1.1. Mackey-Glass chaotic time-seriers

4.1.2. Lorenz chaotic time series

4.2. Experiments

4.2.1. Next spot prediction task

4.2.2. Ablation experiment and control experiment

4.3. Results and disscusion

4.3.1. Hierarchical structure

4.3.2. Reservoir diversity and error performance

5. Conclusions

Appendix A. Hyperparameter tuning

References

MDPI Initiatives

Important Links

Subscribe