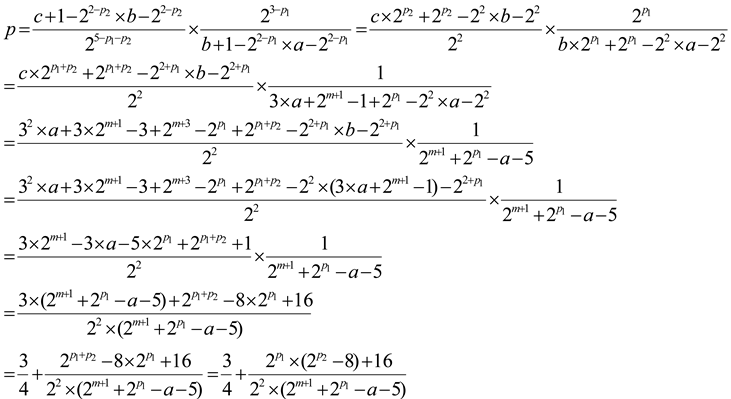The Collatz Conjecture is a famous math conjecture, named after mathematician Lothar Collatz, who introduced the idea in 1937. It is also known as the 3x + 1 conjecture, the Ulam conjecture etc. Many mathematicians have tried to prove it true or false and have expanded it to more digits scale. But until today, it has not yet been proved.

The Collatz Conjecture concerns sequences of positive integers in which each term is obtained from the previous one as follows: if the previous integer is even, the next integer is the previous integer divided by 2, till to odd. If the previous integer is odd, the next term is the previous integer multiply 3 and plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence.

Here is an example for a typical integer x = 27, takes up to 111 steps, increasing or decreasing step by step, climbing as high as 9232 before descending to 1.

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.

If the conjecture is false, there should exists some starting number which gives rise to a sequence that does not contain 1. Such a sequence would either enter a repeating cycle that excludes 1, or increase without bound. No such sequence has been found by human and computer after verified a lot of numbers can reach to 1. It is very difficult to prove these two cases exist or not.

This paper will try to prove the conjecture true from a special view. Because any even can become odd through $÷2^k$ operation, this paper will research only odd characters in the conjecture sequence. The equivalence conjecture become: with random starting odd x, do $(\times 3+1)÷2^k$ operation repeatedly, it always converges to 1. The above sequence can be written as following, in which numbers on arrows are k in $÷2^k$ in each step:

If odd x do n times $(\times 3+1)÷2^k$ calculation build odd y, we can get:

In which p₁…p_n is k in $÷2^k$ operation in each step.

For example: $(7\times 3+1)÷2=11$,$(11\times 3+1)÷2=17$, then $17=\frac{3^2\times 7+3+2}{2^2}$

Suppose odd x can converge to 1 through $(\times 3+1)÷2^k$ calculation, then y=1, get:

We know $(1\times 3+1)÷2^2=1$, and can do any times this kind of operation. That is to say, 1 do random n steps $(\times 3+1)÷2^2$ operation can converge to 1, have:

Below we use this model to prove and search for solution of Formula (1) for any odd x converging to 1.

First with odd x do reform:

$x=a_m\times 3^m+a_{m-1}\times 3^{m-1}+...+a_1\times 3+a_0$, a_m…a₀=0, 1 or 2. Then:

If a_m>1 or a_m=1 but

$(a_{m-1}\times 3^{n+m-1}+...+a_1\times 3^{n+1}+a_0\times 3^n)>(3^{n+m-1}+3^{n+m-2}\times 2^2...+3^n\times 2^{2(m-1)})$, make

$x=3^{m+1}-3^m+a_{m-1}\times 3^{m-1}+...+a_1\times 3+a_0$ or:

Build identical equation:

If x can converge to 1, Formula (1) and Formula (2) should be equivalence. Below we try to reform Formula (2) to form of Formula (1), if successful, it proves that equation for Formula (1) has solution.

First let:

$(3^{n+m-1}+3^{n+m-2}\times 2^2...+3^n\times 2^{2(m-1)})-(a_{m-1}\times 3^{n+m-1}+...+a_1\times 3^{n+1}+a_0\times 3^n)=t_n\times 3^n$, because x is odd, this is odd minus even, t_n should be odd.

Because the max value of x-3^m is $2\times 3^{m-1}+2\times 3^{m-2}+...+2\times 3+2$, min value is $-3^{m-1}+1$, then t_n has a range:

from $(3^{m-1}+3^{m-2}\times 2^2...+2^{2(m-1)})-(2\times 3^{m-1}+2\times 3^{m-2}+...+2\times 3+2)$ to $(3^{m-1}+3^{m-2}\times 2^2...+2^{2(m-1)})-(-3^{m-1}+1)$.

Change t_n to binary form and let:

$t_n\times (2+1)\times 3^{n-1}+3^{n-1}\times 2^{2m}-3^{n-1}=t_{n-1}\times 3^{n-1}$, this is just with 3ⁿ part multiply (2+1) become 3^n-1 part, and plus corresponding part in Formula (2), minus corresponding part in Formula (1). From now on, t_n-1 become even. Continue:

$t_{n-1}\times (2+1)\times 3^{n-2}+3^{n-2}\times 2^{2m+2}-3^{n-2}\times 2^{p_1}=t_{n-2}\times 3^{n-2}$, and let 2^p1 equal to max value of even part(or the lowest bit of odd part).

Watch Formula (1) and Formula (2), in general, if do not consider 2^p1+… part (because we consider 2^p1+… as max value of even part of t_i-2) in Formula (1), corresponding parts in Formula (2) are bigger than corresponding part in Formula (1). Hence after a few times of $t_{i-1}\times (2+1)$, value of t_i-2 is mainly determined by corresponding part in Formula (2). And, after $t_{i-1}\times (2+1)$, odd part should add 1 or 2 bits, if add 1 bit, $+2^{2m+2}$ should operate in MSB bit, if add 2 bits, $+2^{2m+2}$ should operate in MSB-1 bit. Both cases odd part add 2 bits after $+2^{2m+2}$ operation, if MSB bit of t_i-2 is 2^k, k should be odd.

For example:

Continue:

$t_{n-2}\times (2+1)\times 3^{n-3}+3^{n-3}\times 2^{2m+4}-3^{n-3}\times 2^{p_1+p_2}=t_{n-3}\times 3^{n-3}$, let 2^p1+p2 equal to max value of even part. Because LSB bit no. of odd part of t_i increases continuously, this can be finished easily.

Watch t_i(i<n and decreases step by step), during iteration, the count of succession 1 in the highest part should be unchanged or increased. Why? This is because of characters of odd multiply 3 and $+2^{2m}$ operation. If t_i-1 is with form 10…, obviously, count of succession 1 in highest part of t_i-2 is unchanged or increased. If t_i-1 is with form 111…, after do $\times (2+1)$, should become 101…, do $+2^{2m}$,become 111…, count of succession 1 in highest part is also unchanged or increased. Other cases can be proved easily. Some cases can increase, for example, if t_i-1 is with form 110110…, t_i-2 becomes 1110…

Do this iteration continuously, count of succession 1 in the highest part of odd part of t_i is unchanged or increased, LSB bit no. is also increased. Hence, finally, t_i can become form of 11…, just $2^k\times (2^j-1)$ form (k+j=odd). Stop here, do not do $\times (2+1)$ again, odd x already converge to 1. Do $-2^{2(n+m)}$ operation, it should operate in MSB+1 bit, because MSB bit no. of $+2^{2k}$ is forever equal to MSB+1 bit no. of the previous item. Hence minus result can be equal to $-2^{p_1+p_2+...+p_n}$, thus prove the Collatz Conjecture and get solution of Formula (1).

Below give a specific example, x=7.

We know, with 7 do $(\times 3+1)÷2^k$, have:

Suppose:

Build:

$*(2+1) \mathrm{and}+2^6: (2^5+2^3+2)\times (2+1)\times 3^{n-2}+2^6\times 3^{n-2}=(2^7+2^5+2^4+2^3+2^2+2)\times 3^{n-2}$,

Let p₁=1, and delete item 2:

Let p₁+p₂=2, and delete item 2²:

Let p₁+p₂+p₃=4, and delete item 2⁴:

Let p₁+p₂+p₃+p₄=7, and delete item 2⁷:

Now become 111…, the highest bit is 2¹³, iteration finished, steps n=5. And

This way, we get a solution for Formula (1), in which the value of n and p_i is exactly same with the result got from calculating directly.

If we calculate directly with odd through $(\times 3+1)÷2^k$ operation, the odd sequence built (called Sequence (1)) has no obvious convergence regularity, elements in the sequence vary sometimes big, sometimes small. But if we do operation as introduced in above section, convergence regularity of the odd sequence built (called Sequence (2)) is more obvious.

First, if add two corresponding elements in each step in these two odd sequences, should be exactly 2^k(k is different with different elements). Such as

$7+9=16,11+21=32,17+47=64$… in above example.

In general, first element in Sequence (2) is:

and first element in Sequence (1) is x:

$x=3^m+a_{m-1}\times 3^{m-1}+...+a_1\times 3+a_0$, then

$x+a=3^m+3^{m-1}+3^{m-2}\times 2^2...+2^{2(m-1)}=2^{2m}$, is just the same form with Formula (2), and 2m should be the MSB+1 bit no. of x or a(along with the increase of a in Sequence (2), 2m should be the MSB+1 bit no. of a, because each corresponding part in Formula (2) is bigger than which in Formula (1)).

Below prove next elements also satisfy above regularity.

Suppose a in Sequence (2) and x in in Sequence (1) satisfy above regularity, and:

$a=2^m+a_{m-1}\times 2^{m-1}+...+a_1\times 2+1$,

$x=2^{m+1}-a$, then

$3a+2^{m+1}-1=3\times 2^m+3\times a_{m-1}\times 2^{m-1}+...+3\times a_1\times 2+3+2^{m+1}-1$,

$3x+1=3\times 2^{m+1}-3\times 2^m-3\times a_{m-1}\times 2^{m-1}-...-3\times a_1\times 2-3+1$,

This states that the lowest bit of odd part of (3x+1) and (3a+2^m+1-1) is equal, and add these two odd parts should be 2ⁱ(i<k).

Above regularity states that the original odd sequence has no obvious regularity is because it is only the partial part, not the whole part.

Second, research into odd multiplying 3, any odd can be written in binary form 1…1, both the highest and lowest bit is 1, after $\times 3$, although total bit number increases, first substep is to shift bit 1 to the middle of the result, second substep may make carry to higher bit due to 1+1 in the middle of the result(1-bits in the middle of odd also satisfy this regularity). Both substeps are beneficial to our final goal, because we need many 1 bits in final result. $+2^{2k}$ operation ensure succession 1 bits in the highest part, -1 operation reduce count of isolated 1 bits in the lowest part. Hence 0-bits in the odd part in t_i should shift right or bit-count reduce in each step, and its weight in total t_i should reduce step by step till to 0, when the odd part converges to 1...1. Build a simple weight model:

Where 2^2k is the corresponding adding part in t_i in that step. Because obviously $2^{2k}<t_i$ in each step, simply we can use w_i represent the weight of value of all 0 bits in odd part in t_i. We can also think $2^{2k}$ as the sum of t_i and its corresponding part in original sequence, the conclusion we final got is same. Specially, with any odd a, which highest bit is 2^m, define w_i for this odd:

Although the denominator may be bigger than which in Definition (1), the regularity is same.

Note: if odd is with form 1...1, without 0 bits, try to find its corresponding original odd strictly using method introduced above, if not found, abandon it, if found, ignore some previous steps till w(i) or w_[a] is not equal to 0. Only weight function value of 11 is always equal to 0 till to convergence, it is not worth worrying about. These cases do not influence our research.

Observe w_i, it should reduce step by step, and model value can and must converge to 0, because there is no possibility to exist a convergence value, which its corresponding odd part in t_i is not 1...1, and its model value can remain unchanged in next steps through multiplying 3 operation and other two operations. Thus odd part must converge to 1...1, could not diverge or converge to other odds.

t_i sequence in above example is: 9,42,188,816,3456,14336

odd part sequence is: 9,21,47,51,27,7

w_i sequence is(according to Definition (1)):

(2+4)/4=1.5,(4+16)/16=1.25,64/64=1,(64+128)/256=0.75,512/1024=0.5,0/4096=0

Through above introduction we know, with odd we do $(\times 3+1)÷2^k$ operation in the Collatz Conjecture, on the contrast, with odd we do $(\times 3+2^m-1)÷2^k$ in above iteration method. We can easily prove that odd 1…10a(a is in binary base) is equivalent to odd 10a in second method, count of succession 1 bits in the head part only represent the iteration steps roughly.

In fact, only one case 0 bits in t_i do not shift right or bit-count reduce when t_i has not converged. This is:

101->1011.

This case w_i do not change, both are 1/4, according to Definition (2). But next step 1011->11, t_i converges, hence this case is not worth worrying about.

Below we prove it strictly.

Suppose with odd a do $(\times 3+1)÷2^k$ operation, and use x represent iteration steps. We can reform w_i as following(according to Definition (1)), the numerator part is exactly equal to 0 bits in t_i:

Obviously w(x) is continuous derivable when a in odd domain definition and x in positive integer domain definition, and is bounded(>=0).

Now we try to take the derivative of w(x).

Here the derivation definition of the numerator and denominator is: (y(x+1)-y(x))/(x+1-x).

Then the derivation of the numerator is:

The derivation of the denominator is: $2^{2k_x+2}-2^{2k_x}=3\times 2^{2k_x}$

Then

Where b is the odd after odd a doing x steps $(\times 3+1)÷2^k$ operation. that is:

Observe w^’(x), we know when b>3 w^’(x)<0, w(x) monotonically decreases. Only when b=1(this case $2^{p_{x+1}}$ should equal to 4), or when b=3, $2^{p_{x+1}}=2$, W^’(x)=0. Second case of b=3 is the except case introduced above, the corresponding odd part of t_i is with form ‘101’, is not worth worrying about. First case is convergence case.

Totally, this kind of iteration calculation has these cases after doing as following:

Case 1: odd tail part decreases one bit, head part does not increase one bit, this case tail part should insert one bit of 1 and with zero or more 0 changing to 1, totally 1 bits weight should increase in tail part.

Case 2: odd tail part decreases one bit, head part increases one bit, if corresponding odd in (× 3+1)÷2^k sequence change bigger, is just because tail part carry one bit of 1 to head part; if corresponding odd change smaller, is just we need.

Case 3: odd tail part decreases two bits, head part does not increase one bit, tail part 0 bits should shift right.

Case 4: odd tail part decreases two bits, head part increases one bit.

Case 5: odd tail part decreases three or more bits, head part increases zero or one bit.

All these cases, w(x) function are decreased step by step except some cases introduced above.

Does it exist some odds which its w_i tends to 0 but not equal to 0 forever? In fact, it exists some odds which 0-bits distribution are similar and w_i decreases if they exist in same sequence. Such as, 10001 and 110001(+2⁵) or 11000011(*4-1), 10001 and 1100001(insert 0). Because the $(\times 3+2^m-1)÷2^k$ operation limits the varying of the highest part of odd, these odds could not be possible to appear in the same sequence, also could not repeatedly appear.

For example:

10001->101001->1011101->11001011->11011->111, could not produce similar 0-bits distribution.

Below prove it from another view.

Suppose odd a is in $(\times 3+1)÷2^k$ operation sequence, its corresponding odd in $(\times 3+2^m-1)÷2^k$ operation sequence is b, which highest bit is 2^m, then according to Definition (2), $w_{[b]}=\frac{\mathrm{a}-1}{2^{\mathrm{m}+1}}$.

Next Step, b become odd c, then $w_{[c]}=\frac{3\mathrm{a}+{1-2}^{\mathrm{p}}}{2^{\mathrm{m}+1}\times 4}$, where 2^p is the lowest bit of odd part.

$\frac{w_{[c]}}{w_{[b]}}=\frac{3\mathrm{a}+{1-2}^{\mathrm{p}}}{4\times (a-1)}=\frac{3}{4}-\frac{2^p-4}{4\times (a-1)}<\frac{3}{4}+\frac{1}{2\times (a-1)}$,

When a is big enough, for example a>=2¹⁰+1, $\frac{w_{[c]}}{w_{[b]}}<0.751$.

This means when odd in $(\times 3+1)÷2^k$ operation sequence is big enough, next step, w_i is smaller than which multiply 0.751 in current step.

In above example, for first odd, $w_{[10001]}=\frac{7}{16}$, for other odds, $w_{[110001]}=\frac{7}{32}$, $w_{[11000011]}=\frac{15}{64}$, $w_{[1100001]}=\frac{15}{64}$, w_i for all other odds is equal to or bigger than w_i *0.5 for first odd.

Any odds have this same regularity. Because when the tail part of the odds remain unchanged or insert 0(any tail position), the numerator part is same or bigger than 2 times of original, and the denominator become same or 2 times of original, when the head part(successive 1 part) of the odds add one 1, the denominator become 2 times again, then the final value should be bigger than 0.5 times than original.

In above example, obviously, first odd could not become other odds in within 3 steps(case of huge odds is same). But 0.751*0.751*0.751=0.423564751<0.5, it is contradictious.

If steps increase, it is also not possible to become other odds, because if steps increase, count of 1 in head part should also increase, this consumes many steps, there are no enough steps left to finish the need deformation.

We know, normally if only think about varying of head part, it needs 2 or 3 steps periodly to finish adding one 1 to head part, if tail part carry one bit of 1 to head part, it minus 1 step. And tail part is not possible to carry 1 bit two times to head part when head part add two 1 successively, because each time head part add one 1 or tail part carry 1 bit to head part, highest part of tail part produces two more 0 bits, it could not produce carrying bit successively. This is to say, normally in long odd sequence, each time head part add one 1, it at least need about 2 more steps(we ignore odds needing only 1 step to add one 1 to head part in first step here, and we also ignore odds with form 10111(many many 1)..., because although this kind of odds need 2 steps to finish adding one 1 to head part successively during some steps, it decreases count of successive 1 in tail part after each step, this is not good for changing to similar 0-bits distribution).

We know loop odd sequence and divergence odd sequence both are long sequence which has much more than 4 elements(3 steps). Suppose any huge start odd a(its corresponding odd in $(\times 3+1)÷2^k$ sequence is bigger than 2¹⁰+1), a add x bits of 1 in head part and become huge odd b with similar 0-bits distribution of a, it at least need y steps to finish. Then w_[b] should be bigger than 0.5^x times of W_[a] from calculation directly, and should be smaller than 0.751^y times of W_[a] through iteration calculation character introduced in above. This is:

But, no matter whether the deformation is finished or not, only to finish adding enough bits of 1 to head part, it need at least more than 2x steps(about 2.5x steps), there is no enough steps to do tail deformation. So far, the needing steps from these two angles may be contradictious.

Hence it could not be possible to exist a sequence which exists a loop or w_i tends to 0 but not equal to 0 forever when all odds in the sequence are big enough. Once one corresponding odd in $(\times 3+1)÷2^k$ sequence become smaller than 2¹⁰+1, it become case of small odd, and all small odds can be proved to converge easily manually.

To avoid proving weight function W_[a] converging to 0(it is not easily to prove strictly the numerator part equal to 0 finally), we build its complement weight function. Build:

$w_{c[a]}=\frac{\mathrm{a}}{2^{\mathrm{m}+1}}$, the highest bit of a is 2^m

Through the proof and introduction above, we know W_c[a] monotonically increases except when corresponding odd b_i in $(\times 3+1)÷2^k$ sequence of a_i is 1 or 3, and these except cases are not worth worrying about. And we also know the convergence state of W_c[a] is $\frac{2^{\mathrm{k}}-1}{2^{\mathrm{k}}}$.

How much does W_c[a] increase in each step? Suppose odd a₀,a₁,a₂ are three elements in order in $(\times 3+2^m-1)÷2^k$ sequence, a₀ is equal to a, then

$w_{c[a_0]}=\frac{\mathrm{a}}{2^{\mathrm{m}+1}}$,$w_{c[a_1]}=\frac{3\mathrm{a}+2^{\mathrm{m}+1}-1}{2^{\mathrm{m}+3}}$,$w_{c[a_2]}=\frac{3^2\mathrm{a}+3\times 2^{\mathrm{m}+1}-3+2^{m+3}-2^p}{2^{\mathrm{m}+5}}$, where 2^p is 2^k in first step $(\times 3+2^m-1)÷2^k$ operation.

Observe this formula, when 2^p is equal to 2 or 4, $\frac{w_{c[a_2]}-w_{c[a_1]}}{w_{c[a_1]}-w_{c[a_0]}}$ is $\ge \frac{3}{4}$, suppose this ratio is $\frac{3}{4}$, then

When n->∞, $w_{c[a_n]}=\frac{\mathrm{a}}{2^{\mathrm{m}+1}}+\frac{2^{m+1}-a-1}{2^{m+3}}\times 4=\frac{2^{m+1}-1}{2^{\mathrm{m}+1}}$, this is a convergence state, and we know, in actual case, it needs a limit number n steps to reach to(or bigger than) $\frac{2^{m+1}-1}{2^{\mathrm{m}+1}}$, because the ratio is $\ge \frac{3}{4}$.

when 2^p is bigger than 4, $\frac{w_{c[a_2]}-w_{c[a_1]}}{w_{c[a_1]}-w_{c[a_0]}}$ is $<\frac{3}{4}$, but still $>\frac{1}{2}$, W_c[a] also increases, this time, there is not any other limit, it can increase till to its convergence state. And more importantly, when 2^p is bigger than 4, converging speed become more faster, because corresponding odd in $(\times 3+1)÷2^k$ sequence become smaller.

Of course, W_c[a] can converge in $\frac{2^{\mathrm{k}}-1}{2^{\mathrm{k}}}$(k is any positive integer), not only $\frac{2^{\mathrm{m}+1}-1}{2^{\mathrm{m}+1}}$. This increases the convergence chance of W_c[a].

Is it possible that W_c[a] increases continuously but never equal to $\frac{2^{\mathrm{k}}-1}{2^{\mathrm{k}}}$? For example, 87/128, 177/256, 357/512, 717/1024…(here does not consider ratio temporarily).

It is not possible. Observe the varying of fraction in lowest terms of W_c[a], the denominator part is equal, smaller, or 2 times of previous(because the numerator part at least can be divided by 2 in each step) in each step, when is equal, the numerator part should increase, it is possible to converge, when is 2 times of previous, the total value also increase, when is smaller, the total value should not only bigger than the value of front W_c[a] with same denominator part(if exist), but also bigger than all W_c[a] follow it. And in long sequence, usually appear the smaller case, it has many chances to appear $\frac{2^{\mathrm{k}}-1}{2^{\mathrm{k}}}$, especially when the front element is already close to its convergence state. For example, suppose 177/256 is in sequence, if some following element with same denominator part 256 appear after many steps, its value should be bigger than all the elements between 177/256 and itself, it is much possible to equal to 255/256.

Continuously observe W_c[a], even in the 2 times case, elements are closer to convergence state by themselves. Suppose the denominator part of fraction in lowest terms of $w_{c[a_1]}=\frac{3\mathrm{a}+2^{\mathrm{m}+1}-1}{2^{\mathrm{m}+3}}$ is 2^m+2,

We know 2^m<a<2^m+1-1, if a is not equal to 11…101, which is very close to its convergence state 11…1, the above formula is <0. Thus proved the above conclusion.

Below give an example of start number 27 in $(\times 3+1)÷2^k$ odd sequence to verify, some decimals are written in the form which is easily to be judged equal to, bigger or smaller than 0.75.

Odds in $(\times 3+2^m-1)÷2^k$ sequence are:

37,87,97,209,441,917,1887,1927,1957,3959,3993,8037,16151,16209,32505,65141,130479,130627,65369,130821,261767,261861,523863,523969,1048097,2096433,4193225,8386989,16774787,8387697,16775849,33552381,67105787,16776639,16776783,16776891,4194243,2097129,4194269,8388555,1048571,262143

W_c[a] sequence:

37/64,87/128,97/128,209/256,441/512,917/1024,1887/2048,1927/2048,1957/2048,3959/4096,3993/4096,8037/8192,16151/16384,16209/16384,32505/32768,65141/65536,130479/(65536*2),130627/(65536*2),65369/65536,130821/(65536*2),261767(65536*4),261861/(65536*4),523863/(65536*8),523969/(65536*8),1048097/(65536*16),2096433/(65536*32),4193225/(65536*64),8386989/(65536*128),16774787/(65536*256),8387697/(65536*128),16775849/(65536*256),33552381/(65536*512),67105787/(65536*1024),16776639/(65536*256),16776783/(65536*256),16776891/(65536*256),4194243/(65536*64),2097129/(65536*32),4194269/(65536*64),8388555/(65536*128),1048571/(65536*16),262143/262144

$w_{c[a_{i+1}]}-w_{c[a_i]}$ sequence:

13/128,10/128,15/256,23/512,35/1024,53/2048,40/2048,30/2048,45/4096,34/4096,51/8192,77/16384,58/16384,87/32768,131/65536,197/(65536*2),148/(65536*2),111/(65536*2),83/(65536*2),125/(65536*4),94/(65536*4),141/(65536*8),106/(65536*8),159/(65536*16),239/(65536*32),359/(65536*64),539/(65536*128),809/(65536*256),607/(65536*256),455/(65536*256),683/(65536*512),1025/(65536*1024),769/(65536*1024),144/(65536*256),108/(65536*256),81/(65536*256),15/(65536*64),11/(65536*64),17/(65536*128),13/(65536*128),1/(65536*16)

$\frac{w_{c[a_{i+2}]}-w_{c[a_{i+1}]}}{w_{c[a_{i+1}]}-w_{c[a_i]}}$ sequence:

10/13≈0.77,0.75,0.77,0.76,0.76,0.755,0.75,0.75,0.76,0.75,0.755,0.753,0.75,0.753,0.752,0.751,0.75,0.748,0.753,0.752,0.75,0.752,0.75,0.752,0.751,0.751,0.750,0.750,0.749,0.751,0.750,0.750,0.749,0.75,0.75,0.741,0.73,0.77,0.76,0.62

Through above we know $w_{c[a_1]}=\frac{3\mathrm{a}+2^{\mathrm{m}+1}-1}{2^{\mathrm{m}+3}}$, it can be written in following forms:

$w_{c[a_1]}=\frac{2\mathrm{a}+[\frac{b-1}{2}]}{2^{\mathrm{m}+2}}$ b-1<>0 mod 4, or

$w_{c[a_1]}=\frac{\mathrm{a}+[\frac{b-1}{4}]}{2^{\mathrm{m}+1}}$, b-1≡0 mod 4, in which b is the corresponding odd of a in $(\times 3+1)÷2^k$ sequence, b-1 reflects the 0-bits in the tail part of a.

Then Collatz Conjecture can be described as: With any odd a in range of 2^k to 2^k+1-1, set its initial goal set is 2^j+1-1(j<=k), its tail part is b, do operation: try to do (b-1) divided by 4, if can not, shift left one bit of a, plus the result of shifting right one bit of b(the 0-bits in the tail part of a), and add 2^k+2-1 to goals set of a, this operation makes the 0-bits in the tail part of a shift right or count reduce; if can, a plus the result of (b-1) divided by 4, this operation not only makes the 0-bits in the tail part of a shift right or count reduce, but also reduces the odds count about 1/4 to its goal 2^k+1-1, furthermore, if the last result is even, it can reduce a fraction of using 2^k+1 as denominator, this makes it can reach its previous goal 2^j+1-1(j<k) possibly. Do these operations repeatedly, it have unlimited chances to reach one of its goal set.

Through above we know, if $(\times 3+1)÷2^k$ sequence have only /2 and(or) /4 cases, the sequence can never converge, /2 case makes goal of a in $(\times 3+2^m-1)÷2^k$ sequence larger, /4 case needs ∞ steps. But it is not possible in long sequence, this is determined by the regularity of tail binary bits of odd doing $(\times 3+1)÷2^k$ operation. Odds of form with *10…01(many 0), both its initial value and result can do (-1)/4, Odds of form with *11…11(many 1), both its initial value and result can do (-1)/2, these two cases can become other forms after several steps, and once become other forms, it needs many steps to become back to many 1 or 0 forms(if become back to form with similar distribution, 0 or 1 count should reduce). Odds with other forms, themselves and their following steps can appear alternately /2, /4, /2^k cases.

6. (*3+2. ^m-1)/2^k Tree And Its Regularity

Characters of 2^k are very regular, if we set odds of $(\times 3+1)÷2^k$ between 4^p+4^p-1+…+1 and 4^p+1+4^p+…+1 as one layer, call 2^k are the properties of these odds after doing $(\times 3+1)÷2^k$ operation, we can find each layer count of 2^2p+1, 2^2p,…2², 2 are 1, 1 2 4, 1 2 4 8 16…, their positions have equal interval space, 2^2p+1 is in the middle between 4^p and 4^p+1, 2^2p is in the middle of left part…, first position and step length of odds of different 2^k property are different afer doing $(\times 3+1)÷2^k$ operation in different layers. In brief, characters of 2^k are very regular, we do not introduce in detail. Here we still put focus on $(\times 3+2^m-1)÷2^k$ odds. See following tree:

…

L6: 129(321.1) 131(81.3) 133(327.1) 135(165.2) 137(333.1) 139(21.5) 141(339.1) 143(171.2) 145(345.1) 147(87.3) 149(351.1) 151(177.2) 153(357.1) 155(45.4) 157(363.1) 159(183.2) 161(369.1) 163(93.3) 165(375.1) 167(189.2) 169(381.1) 171(3.8) 173(387.1) 175(195.2) 177(393.1) 179(99.3) 181(399.1) 183(201.2) 185(405.1) 187(51.4) 189(411.1) 191(207.2) 193(417.1) 195(105.3) 197(423.1) 199(213.2) 201(429.1) 203(27.5) 205(435.1) 207(219.2) 209(441.1) 211(111.3) 213(447.1) 215(225.2) 217(453.1) 219(57.4) 221(459.1) 223(231.2) 225(465.1) 227(117.3) 229(471.1) 231(237.2) 233(477.1) 235(15.6) 237(483.1) 239(243.2) 241(489.1) 243(123.3) 245(495.1) 247(249.2) 249(501.1) 251(63.4) 253(507.1) 255

L5: 65(161.1) 67(41.3) 69(167.1) 71(85.2) 73(173.1) 75(11.5) 77(179.1) 79(91.2) 81(185.1) 83(47.3) 85(191.1) 87(97.2) 89(197.1) 91(25.4) 93(203.1) 95(103.2) 97(209.1) 99(53.3) 101(215.1) 103(109.2) 105(221.1) 107(7.6) 109(227.1) 111(115.2) 113(233.1) 115(59.3) 117(239.1) 119(121.2) 121(245.1) 123(31.4) 125(251.1) 127

L4: 33(81.1) 35(21.3) 37(87.1) 39(45.2) 41(93.1) 43(3.6) 45(99.1) 47(51.2) 49(105.1) 51(27.3) 53(111.1) 55(57.2) 57(117.1) 59(15.4) 61(123.1) 63

L3: 17(41.1) 19(11.3) 21(47.1) 23(25.2) 25(53.1) 27(7.4) 29(59.1) 31

L2: 9(21.1) 11(3.4) 13(27.1) 15

L1: 5(11.1) 7

L0: 3

In above tree, a.b in () means result is a*2^b after front odd doing $(\times 3+2^m-1)÷2^k$ operation. m_th layer has 2^m elements, the last element is the convergence state. Characters of 2^k are also very regular, for example, upward from a specific layer, positions of 2 are 1+2i(i>=0), upward from another specific layer, positions of 2² are 4+4i, positions of 2³ are 2+8i, positions of 2⁴ are 14+16i…, this can be easily proved strictly. For example, odds of position 2+8i in m layer are 2^m+1-1+(2+8i)*2,(0=<i<=[(2^m-1-1)/4])

Can be divided by 2³, result is odd if m+1>3. And because the highest bit of the result odd is 2^m, it must be in m-1 layer, downward one layer from m layer.

Through above, we can easily prove that if the property of an odd is 2¹, it moves upward one layer, if the property of an odd is 2², it moves forward in the same layer, if the property of an odd is 2^k(k>2), it moves downward k-2 layers.

In this tree, because element count of each layer is 2 times of which of the downward layer, we can transform all positions to one specific layer. M-1 layer transform to m layer do *2, m+1 layer transform to m layer do /2, etc. Then all transformed positions can not exceed 2^m!

Below we try to prove odds in any layer can converge. Normally, we suppose the research sequence is long huge(odds in $(\times 3+1)÷2^k$ sequence are huge) sequence.

Suppose a is an odd in m-1 layer, its highest bit is 2^m.

Pos of a in m-1 layer is: $\frac{a-2^m+1}{2}$,

$3\times a+2^{m+1}-1=b\times 2^{p_1}$, b is in layer m-p₁+1

Pos of b in m-p₁+1 layer is: $\frac{b-2^{m-p_1+2}+1}{2}$,

Pos of b in m-1 layer is: $\frac{b-2^{m-p_1+2}+1}{2^{3-p_1}}$

$3^2\times a+3\times 2^{m+1}-3+2^{m+3}-2^{p_1}=c\times 2^{p_1+p_2}$, is in layer m+3-p₁-p₂

Pos of c in m+3-p₁-p₂ layer is: $\frac{c-2^{m+4-p_1-p_2}+1}{2}$

Pos of c in m-1 layer is: $\frac{c-2^{m+4-p_1-p_2}+1}{2^{5-p_1-p_2}}$

$\frac{c-2^{m+4-p_1-p_2}+1}{2^{5-p_1-p_2}}-\frac{b-2^{m-p_1+2}+1}{2^{3-p_1}}=\frac{c+1-2^{2-p_2}\times b-2^{2-p_2}}{2^{5-p_1-p_2}}$, ratio p is:

Next try to prove the average value of ratio p is >=3/4 in long valid sequence.

Only these cases ratio p<3/4: p₂=1, p₁>=2; p₂=2, p₁>=3. When 2^m+1-a>>$2^{p_1}-5$ (corresponding odd in $(\times 3+1)÷2^k$ sequence is very big), $2^{p_1}-5$ can be ignored, $2^{m+1}+2^{p_1}-a-5\approx 2^{m+1}-a$. Then:

If p_k appear 2,1,2,1,2,1,2,1..., p_(2,1)+ p_(1,2)≈3/2, average p≈3/4.

If p_k appear 2,1,1,2,1,1,2..., p_(2,1)+ p_(1,1) + p_(1,2)>9/4, average p>3/4.

If p_k appear 3,1,3,1,3,1,3,1..., p_(3,1)+ p_(1,3)<3/2, average p<3/4(>1/2). but this sequence means: first downward one layer, then upward one layer, then downward one layer…, all movements are in the two layers, it must overstep the boundary of the tree(sequence is invalid) or converge.

If p_k appear 2,1,3,1,2,1,3,1…, p_(2,1)+ p_(1,3)+p_(3,1) +p_(1,2)<12/4, average p<3/4, this serial number could be possible to appear frequently, because the property of the front and back number of 2 are same, and 3 also. In most instances, front and back property are different. Front and back property are same for two numbers frequently are less cases.

If p_k appear 2,1,3,2,1,3,2…, average p<3/4, but this sequence means: first forward in one layer, upward one layer, and downward one layer, and forward in that layer…, all movements are in the two layers, it must overstep the boundary of the tree or converge.

If p_k appear 2,1,3,1,3,2,1,3,1,3,2..., average p<3/4, but all movements are in the two layers, it must overstep the boundary of the tree or converge.

If p_k appear 2,1,3,1,3,2,2,1,3,1,3,2..., average p<3/4, but all movements are in the two layers, it must overstep the boundary of the tree or converge.

Summary, all <3/4 cases in above are invalid or can converge possibly. And we know, Normally (3,1),(4,1),(5,1)…,(3,2),(4,2),(5,2)…appear less times in long sequence, because they are beneficial to convergence. The ratio of them is <3/4 is usually just because the ratio is >3/4 in front of them. In fact, (1,1), (1,2), (2,1), (2,2) appear frequently in long sequence. This case, average ratio p>=3/4.

Above calculation is roughly, mainly because a in above formula changes each time, but the final conclusion is correct. We can also prove it from another view. From ratio formula we know, cases of (forward,upward), (downward,upward), (downward,forward) ratio<3/4; cases of (upward,upward), (downward,downward), (upward,downward), (upward,forward) ratio>3/4; case of (forward,forward) ratio =3/4. cases of >3/4 is more than cases of <3/4. And most importantly, in long huge sequence, the general trend of the sequence is upward in the tree(general forward and downward trend increase the convergence speed), cases of (upward,upward), (upward,forward), (forward,forward) should appear frequently, (upward,upward) should appear most times. Because one step can only upward one layer, and one step can downward one more layers, we can think successive upward steps as one step to achieve reciprocity operation, then the accumulation ratio is big, this guarantee the average ratio is >=3/4.

For example, if appear (4,1) or (4,2), normally it should upward 2 or more layers before to guarantee general upward trend. If front sequence is (1,1,4), then ratio sequence is about:

If think front upward steps as one step, then front ratio is about: ratio sequence of (4,1) is about: back ratio is about:

If 2^m+1-a is very big(huge sequence), ${(\frac{3}{4})}^2+\frac{31}{2^2\times (2^{m+1}-a)}$>>$\frac{80}{2^2\times (2^{m+1}-a)}$, p_f-(3/4)>>|p_b-(3/4)|, the average ratio is >3/4.

Other cases are similar, then average ratio is >=3/4.

Even in extreme case (upward,forward,upward), the ratio is about 3/4, and this case is not possible to appear frequently in long sequence.

This way, proved the above conclusion. In fact the average ratio is >3/4(we expand the range just for convenient explanation), so we can use proportional sequence of ratio 3/4 to estimate.

After a do n times $(\times 3+2^m-1)÷2^k$ operation, pos in m-1 layer is:

When n->∞,

When first number property $2^{p_1}$>4(this is very easy to achieve in long sequence), and when n->∞, the final position is >2^m-1, is contradictory. This means, the sequence should become small sequence(once one element become a small odd in our range, the sequence becomes), or converge before a limit steps, or overstep the boundary of the tree(it is not possible in real world).

Still has one puzzle, the transformed positions of equivalence elements(add binary 1s in head) of elements in left half part in m-1 layer are all in right half part in m-1 layer, it is as if exist many loops. It is of course not correct, this is because, although they are equivalence, their functions are different. Other odds can change to them, and they can also converge. Through proof in previous section, odd a can not make a loop in long huge sequence because adding x bits of binary 1 in head, needs about 2.5x steps, and W_[a] transformation needs less than 2.4207x steps(this regularity can also be found in above tree). And, if some long sequence exist loops, the transformation position(to m-1 layer) can never reach to or bigger than 2^m-1, it is also contradictory.

Maybe it is possible to use proportional sequence of ratio 3/4 to estimate the convergence steps for some long huge sequence(guarantee the average ratio is >3/4). For some odds in m-1 layer, if start odd can reach to or bigger than 2^m-1 in limit steps n using ratio 3/4, indicates that the convergence step count should <=n; if can not reach to forever, indicates should use average ratio>3/4, but we don't know the suitable value of ratio, we can do $(\times 3+2^m-1)÷2^k$ operation several steps until found a suitable odd as start odd and do estimation again.

T_i has many other characters, for example, its odd part should be with form 3*y after first step, this can be easily proved:

With odd x, first operation is: 3x+2^2k-1, 2^2k-1 can be divided by 3 exactly, then total value is with form 3y.

Continue to watch t_i, from this step, within each few steps, odd part should be back to form 3*y(suppose it has not yet converged before this step), this is because each next step has 2^2k-2^p1+…pi part, when p_1+…p_i is even, total value is with form 3*y. This also limits the varying range of the odd part.

And after a few steps, y should be with binary form 101...1, since this time, if step count is big enough, with each some steps, the head part of y increase a 01 pair. In fact, if odd part of t_i is written in 3y,3y+1,3y+2 form, the head part of the binary form of y increases 01 pair continuously. From the example of starting odd x=27, this regularity can be obviously observed, here do not list the result. This indicates again that this kind of iteration calculation has determined direction, and gradually regularly converges.

This way, we have proved that the Collatz Conjecture is true.