Preprint
Article
Simulated Local EPR Correlation: CHSH = 3
Altmetrics
Downloads
723
Views
401
Comments
5
A peer-reviewed article of this preprint also exists.
supplementary.zip (677.75KB )
This version is not peer-reviewed
Quantum Information and Quantum Computing
Submitted:
03 February 2023
Posted:
06 February 2023
Read the latest preprint version here
Alerts
Abstract
A statistical simulation is presented which reproduces the correlation obtained from EPR coincidence experiments without non-local connectivity. Defining spin under the quaternion group reveals hyper-helicity, a hitherto missed attribute of spin. Including this in the treatment, reveals two complementary properties: spin polarization and spin coherence. The former has a CHSH value of 2, and spin coherence has a CHSH = 1 giving CHSH = 3 for an EPR pair. The simulation here gives 2.995. We suggest that Nature has CHSH=3 being considerable more than predicted from quantum mechanics of $2\sqrt{2}$. There are no Local Hidden Variables. We suggest that quaternion spin is more fundamental than Dirac spin. A computer program which performs the simulation without non-local connectivity is described.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
Introduction
We consider the correlation obtained from coincidence EPR experiments [1,2,3]. An EPR pair, [4], is defined as two particles that were originally in a singlet state and separated, [5]. In that process, we assume no non-local entanglement persists so the pair forms a product state.
This paper is the third of three in which quaternion spin is presented. In the first paper, [6], the Dirac equation is modified by changing the symmetry of a spin from SU(2) to the quaternion group. This introduces a bivector, which is the origin of helicity. The second paper [7] shows that the correlation from helicity accounts for the anti-symmetric part of spin, not present in Dirac spin, [8], giving the missing correlation in EPR experiments.
We repeat that helicity is not the usual particle-physics definition, [9].
In this paper a computer simulation generates the correlation from both polarization and coherence and combines these, see Eq.(1) to give an apparent violation of Bell’s inequalities (BI), [10].
Analysis of the simulation leads us to predict that Nature has a CHSH value of 3 rather than the CHSH = value from quantum theory. We suggest that this is convincing evidence that quaternion spin replace Dirac spin in some applications. The simulation code in both FORTRAN and C are found at the end, giving respectively CHSH values of 2.995 and 3.045. We use the value of 2.995.
First, quaternion spin is described after which the statistical simulation is presented. The results agree with the experimental data and are discussed. The derivation of the superposition principle, Eq.(1), for this system is given in Appendix 1 and computer program links in Appendix 2.
Quaternion Spin
Since EPR pairs have no connectivity between them, only one spin is treated. A Dirac spin is represented by two states, where is the axis of quantization in the Lab Fixed Frame (LFF) . Quaternion spin, [6], has in addition, helicity giving spin four states, . The operator associated with polarized states is the Pauli spin vector whereas that associated with the helicity states is the bivector ,7], in terms of the Levi-Civita tensor.
As a spin approaches a polarizing filter in direction , these properties are contracted giving measured values of and . This causes the helicity to cease as the polarization is formed in response to the field.
In appendix 1, the expectation values are found for the two distinct processes, giving and for Alice’s spin. When these are combined, , the result is a superposition of two phases, one for the (3) spin axis and the other for the orthogonal (1) spin axis, see Figure 1,
The vector coupoing of the two mirror states, [6], shown in Figure 1. presess oppositely, producing a purely coherent spin state of magnitude one. This equation generates all the simulated correlation in this paper.
The angle defines the filter orientation. The angle is the Local Variable (LV) that orients the two-dimensional spin in 3D space and deserves its own section. .
The Local Variable
Consider Figure 2 which depicts the separation process. First note Alice is in a RH frame and Bob is in a LH frame. Conservation of angular momentum requires that must be (in practice we use ). As they separate, the EPR pair must precess in the same direction to maintain conservation of angular momentum. The two states, however, have opposite helicities when Bob’s frame is changed to a RH frame.
Multiple repeats of EPR experiments from a random source mean that varies between 0 and but must be the same for both Alice and Bob. The value of is solely responsible for the correlation. Observed coincidence events deterministically depend upon the relationship between and .
The state operator here describes one particle rather than a statistical operator over an ensemble. The state of a single particle, , is, by definition, pure [11]. A product state is between two pure states, and therefore, describe two particles,
Alice and Bob are correlated by their common axis because in their entangled state, before separation, they shared the same coordinate frame. Use this to calculate the correlation from a product state, [7]
In the usual treatment, the spin is in the LFF with the vector , giving the cosine angle in Eq.(3).
Quaternion spin has structure so a Body frame is needed, BFF, and this is expressed by where now is different for every spin in general and is related to the LFF by
as is the field vector. We assume that the LFF axes (Z,X) and the BFF axes are coplanar, thereby requiring . Therefore, in the LFF, see Eq.(3), is modified with each spin orientation, and is given by
Likewise, Bob has . Now the product state in Eq.(3) has a common history from its entangled state via . As they separate, is the same for the two. A structured particle can do that, whereas a point particle cannot. Our main assumption is that an EPR pair separates with a handshake which fixes a common variable between them through and which they carry with them. Without this assumption, the correlation can only be classical.
The variable is local but not hidden. Presented here is a theory with no Local Hidden variables, LHV. BI are only used as a quantitative measure of correlation in the CHSH form, [1]. With no LHV, Bell’s theorem is inapplicable and should be always satisfied.
Click Events
Without providing details, the treatment shows that when the spins are in polarized states, only one of the two phases remain in Eq.(1), and either one will do. In contrast, coherences have both phases present. We assume that upon filtering, only one of the two spin axes aligns, and the other randomizes. This process is usually called wave function “collapse” into the observed value. Here the state is found deterministically by the dependence of the relative magnitudes of the two phases (the real parts). Once known, a spin up or down is determined from the sign of the coherence terms (the imaginary part). Take Eq.(1) and write it as
For polarization we use either axis, but for coherences the axis that aligns with the filter is the larger of the two
For both polarization and coherence, a left spinning axis gives a +1 click and a right spinning axis gives a -1 click (or vice versa),
Choosing the axis most aligned overlooks the mechanism. However when a particle with two axes approaches a field, a calculation similar to that of Scully et al [12] determines the outcome. The process here is not only local, but also deterministic.
The computer simulation programs these by the integer function, “Click” see Appendix 2. We distinguish polarizations from coherence by introducing parameters k and kp. For polarizations, k = kp and for coherences, k = - kp. The programs therefore chooses either a polarized state or a coherent state as produced at the source. Alice and Bob states only differ by their common variable changing to . The FORTRAN code that determines clicks from polarized states is given by
Phase = cos(thArad )*(cos(thRad)-sin(thRad))
if (Phase.GT.0.) then
click = +1
elseif (Phase.LE.0.) then
click = -1
endif
Here thArad = and thRad = . Figure 3 shows the simulated correlation from one axis, gives polarization as a triangle. In this figure the quantum mechanical EPR correlation of is decomposed into two parts: the triangle, and the difference between the minus cosine and the triangle which we call the French Mustache. It is the Mustache that raises the quantum CHSH value to 2.828.
The code for determining the clicks from coherent states is given by ( Eq.(1))
PhaseCC = cos(2*thArad )*(cos(thRad)-sin(thRad))
PhaseSS = sin(2*thArad )*(sin(thRad)+cos(thRad))
PhaseM = max(PhaseCC,PhaseSS)
if (phaseM.EQ.PhaseCC) then
Phase = sin(thArad)*(cos(thRad)-sin(thRad))
elseif (phaseM.EQ.PhaseSS) then
Phase =cos(thArad)*(sin(thRad)+cos(thRad))
endif
if (Phase.GT.0.) then
click = +1
elseif (Phase.LT.0.) then
click = -1 endif
This is plotted in Figure 4 with CHSH = 0.968 showing that quaternion spin gives more correlation than from quantum theory, CHSH = 0.828
Figure 5 is the full simulated plot which is the sum of the simulated polarization Figure 3, and the simulated coherence, Figure 4. These give a CHSH value of 2.995. Note that this CHSH value is a sum of polarization, 2.027 and coherence Figure 4, 0.968, consistent with Eq.(1).
The theoretical CHSH value for polarizations is 2, whereas in Figure 3 it is 2.027. There is residual quaternion correlation that remains as shown in Figure 6. A small mismatch and a cross over occur close to the horizontal axis. We call this residual quaternion correlation. It is hardly discernible. Considering it might be an artifact, various tests did not remove it. The calculation was done at higher resolutions with no change. This, along with its similar symmetry to the other coherence supports this to be a real feature.
From the inset in Figure 6, there are two discontinuities at and . Removing these features by moving the middle triangle down gives an inverted triangle, but also gives a CHSH value of zero. The discontinuities, therefore, are necessary for the residue to be physical. We assert this residual contribution to coherence is due to correlation in the polarization states. If confirmed, the polarization exceeds BI, ([10]), by a small amount and violates his theorem ([13].
Discussion of the Simulation
The Factor 2 in Coherence
Changing the functions to test other “guesses” or varying the parameters gave no improvement over the use of Eqs.(6) and (7). There is little, if any, flexibility. Changes mostly leads to a complete collapse of the correlation.
In order to get the two periods in the Mustache function, Figure 4, it was necessary to change thARad to 2*thARad for the two coherentcaxes. Only the value 2 works, with 1.9 and 2.1 giving nonsense. This only applies to the magnitude of the coherence and not (in fact is wrong) for the polarizations. The origin is the Clebsch-Gordan coupling of the two spins 1/2 from the and axes to give the resonant spin a value of 1. This doubles the magnetic moment and the Larmor frequency too. Note, however, to maintain the two components in Figure 1 as mirror images, only the components can form. Equation (1) is derived for the two axes in a field, and does not treat the the spin 1 resonance spin.
The CHSH value of 2.995 is larger than the expected from quantum theory . In the discussion we argue the 2.995 value is physically reasonable and gives support for quaternion spin over Dirac spin.
Determining the Correlation
Any two incompatible physical attributes, say position and momentum, require two different experiments, and the results of each are collected separately. It appears that EPR pairs create this complementary distinction without our experimental intervention. At the source a pair separates into a coherent (two axes) state of zero angular momentum. In free flight, the axis of linear momentum is spun by the hyper-helicity and it is this action that randomizes the polarization to zero. In free flight we find that spin displays no polarization. Only helicity is present apart from whatever property the spinning Y axis generates.
When the particle encounters an anisotropic field, one of the two spins is pulled and this stops the axis from spinning. At the point of measurement, the geometric arrangement of the polarizing field relative to the spin orientation leads to a competition as to which of the two magnetic axes will align. Some orientations leave little choice since one axis is closer, but in other orientations it is a toss-up. This is the origin of spin coherence which gives an apparent violation of BI.
In the simulation, we separate one axis events (polarization) from two axes events (coherence) and collect the events in different bins. Correlation in EPR coincidence experiments is measured by counting the clicks and organizing them as,
Here for simplicity, we write the even coincidences as and the odd as . The correlations from polarization and coherence are defined,
The superscripts p and c enforce distinction between polarized and coherent clicks. There are 4 states, 2 polarized and 2 coherent.
From Eqs.(8) and (9) notice that the value of the correlations should not depend upon now many coincidences are produced as long as they are statistical. More coincidences improve the accuracy but do not change the values. However, the number of clicks is finite and those obtained from experiment in Eq.(8) must be distributed between those of Eq.(9). We address this in the next section while here we calculate the correlations from both polarization and coherence by assuming for convenience the same number of clicks for each,
Coincidence experiments presently cannot distinguish if the clicks arise from polarized pairs or coherent pairs. If we allow that distinction, then we can express the total number of clicks in Eq.(8) as,
The equal and non-equal coincidences in Eq.(8) obey,
Note, however, this decomposition into p and c clicks does not change the total number of clicks produced. Rather it supposes there are two types of measurement outcomes. Hence the total number of particles remains constant and the experimental correlation is divided between the two contribution as discussed in the next section.
Quantum Coherence
The total number of coincidences realized in an experiment must be distributed between the polarization and coherence, Eq.(9). How this occurs gives insight into the nature of quantum coherence.
As noted, Eq.(11) does not conserve clicks between the LHS and the RHS. The number of coincidences collected in Eq.(8) is different from the number used in Eq.(9). We now address that point.
Consider first Figure 7. This shows the two axes of Alice’s spin oriented in the (1,1) quadrant of the BFF. Bob, far away, shares the same BBF and his is oriented oppositely in the (-1,-1) quadrant [14]. The two axes of each spin couple to produce a resonance fringe, [15] seen from the vector addition of the two axes for each spin, Figure 1. We now call this quaternion spin. Reversing the signs of the components along the axis is another orientation which also produces quaternion spin in the odd quadrants shown by the dotted lines. These four vectors that represent coherence between the two spin axes giving a resultant resonance spin of magnitude one, as shown in the bottom part of the figure. From this we can rationalize the correlation observed in coincidence experiments.
In the Figure 7 no field vectors, for Alice on her side and for Bob on his side, are shown but we consider different scenarios that occur in coincidence experiments at setting that have different values of .
If or along the axis, then the two spins are aligned parallel and anti-parallel. This causes rapid precession about thereby averaging the components along , This is Dirac’s spin, up or dn. There is only polarization present. Any coherence is average out as is evident from the correlation in Figure 5 at settings of zero and . Likewise if the filters are set to or , they lie along and there is neither polarization nor coherence.
Equation (1) shows the superposition depicted in Figure 1 which creates a coherent spin state of magnitude one, see also bottom frame of Figure 7. In free flight, this resonance-produced quaternion spin is the only manifestation possible. From the theory [6], this resonance occurs only in isotropy whence the two axes of a spin are indistinguishable. Applying a field destroys the indistinguishably, and thereby the resonance cannot form. One of the two axes is pulled to the field direction and the other randomizes. Note that the sense of two spinning axes of quaternion spin is opposite, so depending on which axis aligns, the spin is measured to be either up or dn, or more precisely spinning left or right.
When the filters are arranged such that one axis is clearly closer to the field, when is less than about 22.5 degrees or greater than 67.5 in the (1,1) quadrant, then their is little choice and one axis is favoured to align. These produce the polarized states of Figure 5. They are depicted as the single vector images on the LHS and RHS of the quaternion spin in Figure 7. The axes not shown are still present, but are averaged by its spinning partner.
As increases towards , the situation changes and a choice must be made between the two axes. The maximum correlation results when various coherent axes interfere. When equals the field axes coincide with the spins. The vector strongly interacts at and . Indeed the vector sum of these two is parallel to giving strong correlation. Likewise the axis is parallel to .
To express actual experiments, set the filter angles, , to a specific value and place it on Figure 7. Then as the fixed value of is rotated about the figure, it comes into and out of phase with the polarization and coherence. If four experiments are performed such that is rotated around Figure 7, then at every value of both filter angles simultaneously encounter points of high angular momentum. The angles with the greatest correlation is shown on the RHS of Figure 7, and gives a sum of correlation give by,
thereby revealing the origin of the CHSH form of BI.
The RHS figure can be flipped about the line , axis to treat the mirror state. The results are identical.
Using these notions show that polarization and coherence are credibly produced in varying amounts with and the number of coincidences is divided between polarization and coherence. Present coincidence experiments are unable to distinguish these, each simply recording a click. The only data are the numbers in Eq.(8). Suppose, however, that an experimental method was developed to distinguish between polarized and coherent states. This required using the LV to build a filter based upon exploiting the difference between that LV and the filter angle, . Using this filter allows distinction betwen polarized and coherent states similar to a Stern-Gerlach filter that separates polarized states. This filter, however, is designed to divert the polarizaed states and coherent states into different bins as expressed in Eq.(9). To determine how these might be distributed, Eq.(11) is re-written but now requiring that the total number of particles is conserved,
to give,
With the data from Eq.(8), we only need the correct polarized data from Eq.(12) if this equation is to be satisfied.
We simulated experiments with 2 million events. The large number was needed for accuracy. The values of both and were varied, the former in steps of clicks with the latter varying in steps of 1 click. We chose quantum correlation as an example, at different angles. These are tabulated in Table (8).
The first two entries are found by inspection. The first with physically gives only polarization. Likewise the case displays neither polarization nor coherence since neither can form.
The last two entries were calculated as described, and the values shown were found by requiring the experimental and calculated correlation to lie with a tolerance: . By varying the tolerance, one distribution was found for each as shown in the table. Typical tolerance was .
For the entries show that polarization dominates coherence, consistent with one axis being pulled. This suggests that polarizations predominantly lie on either side of the axis. In contrast, for degrees the situation is reversed with coherence dominating. This shows that coherence lies predominantly between degrees to .
We suggest that these numbers illustrate expected results from coincidence experiments that involve two complementary physical attributes rather than one. Note that the Pol. and Coh. entries in the Table can be interchanged with no effect. The Table, however, verifies that clicks can be conserved, such that the experimental data are distributed between the two elements carried by a spin.
Click Analysis
The simulated data allows us to distinguish between polarized and coherent events. Figure 9 gives the raw click data from the 4 types using the notation,
The raw click-counts are normalized to the total number of clicks per event, . From inspection of Figure 9, the two polarized triangles subtract , to give the observed polarization correlation, and add to zero.
The origin of the EPR correlation is visible in Figure 10. Plotted there are the sums and differences of mixing polarization with coherence, and . Both of these give a cosine-like function when subtracted, and are the origin of the quaternion correlation. Therefore, Nature fundamentally treats correlation as the difference between the number of different events: here polarization minus coherence. In contrast, sums of mixed polarizations and coherences give nothing useful and are, like the others when added, of no physical interest.
The quaternion coherence, , has more correlation but a similar structure to the quantum correlation. From the raw data, Figure 9, the quaternion correlation , resembles two opposing sine waves and the following gives a good fit,
Discussion
Figure 5 and Figure 11 shows the quaternion spin carries more correlation than quantum theory predicts. From Figure 4 the difference between the quaternion and quantum correlation is CHSH = 0.968 - 0.828 = 0.141. In addition, a residue of 0.027 correlation remained in the polarization, although it is extracted in Figure 6. The dominating contribution to coherence is Eq.(17), suggesting that two opposing sine functions describe the coherence correlations between Alice with Bob.
Note that the residual quaternion correlation, Figure 6 has a similar symmetry to Figure 11 and both are reflected at .
Table (1) lists four values of the CHSH inequalities. The value of 2 quantifies the Invisible Boundary [16], between polarization and coherence. Quantum theory gives the value of which is less than that from the theory here of 2.995. We suggest Nature has a value of 3 for the following reasons.
Quantum theory entangles states and treats spin as polarized up and dn only. Dirac spin has no structure whereas quaternion spin does, giving more degrees of freedom and more correlation. The usual entangled quantum calculation gives correlation of and the follows from the cosine of angle at . Entanglement is partly responsible for reducing the observed correlation from 3. In contrast, the simulated correlation treats the process without entanglement.
The question then concerns the value of 2.995. First, looking at the simulated coherence, Eq.(17), the prefactor is 1/4. The CHSH values leading to 2.995 are and . This suggests a convergence to which leads to a CHSH value of 3. For an EPR pair that means that two thirds of the correlation is polarization and one third is quantum coherence.
Spin
In this treatment, non-local entanglement is replaced by helicity. The Dirac spin is replaced with quaternion spin. Both these features come from changing the symmetry from SU(2) to .
The origin of spin is the Dirac equation, found by applying conservation of energy and mass when linearizing the Klein-Gordon equation into the four dimensional Dirac field, [17]. His gamma matrices are the vectors. Spin, however, is measured to have only two states, , not four. On the other hand, Dirac’s equation reveals two spins, of which each is opposite in every way, like mirror images, see Figure 7, bottom image, center which satisfies just that. This is also evident from the reflection of the data points about in Figure 9. Dirac concluded that his theory describes a particle and its antimatter twin, leading to hole theory and the sea of electron concept. Quaternion spin puts this in doubt. If the structure of quaternion spin is accepted, then the matter-antimatter pair Dirac proposed is replaced by a single spin with two spinning axes shown in Figure 7 and Figure 1. Dirac’s vision of a matter-antimatter pair may well occur at high energies where quaternion spin is formed and decays. Normal temperatures are much lower where quaternion spin is stable.
The orientation of the 2D plane is perpendicular to the direction of linear momentum. This leads to a visualization which is geometrically identical to that of a photon, see Figure 13, and the two spin axes form their own “World Sheet”, [18].
When the Dirac equation is changed to reflect quaternion spin, indeed two mirror states result [6], see Figure 7 again, which are, perhaps, the most fundamental particles in Nature. They have no parity, only reflection, but combine into states of even parity, polarization, and odd parity, coherence.
Recall that in free flight, the plane formed from the two axes is spun by the quaternion so that they display no net polarization. Likewise, when encountering a measurement probe, the magnetic moments on the axes are pulled and one axis lines up. The helicity stops. This is a view of complementarity, with only one element of reality being evident at any instant, although they both simultaneously exist on the same particle.
Considering that Nature has CHSH = 3, quaternion spin misses only CHSH = 0.005 of the correlation which is smaller than the residual correlation 0f 0.027 found in the polarization states. This alone is strong evidence for quaternion spin over Dirac spin.
By using quantum theory and local entanglement in normal situation, we are missing about five percent of the correlation available.
Spin carries helicity as an element of reality, and quaternions exist in the hypersphere of four dimensions. Spin extends to this space which is beyond our visualization, but nonetheless it remains an element of reality beyond our dimension. The only part of a quaternion that is visible to us is the stereographic projection from onto our Minkowski spacetime.
Bell
The CHSH form of Bell’s inequalities provides a valuable quantitative measure of correlation. This enables us to separate classical (polarization) from quantum (helicity). Bell’s theorem is distinct from his inequalities and asserts in Bell’s words [13],
If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local.
In this work, there are no hidden variables and therefore Bell’s theorem does not apply.
The evidence supporting this type of non-locality, however, is solely from coincidence experiments. EPR pairs have been studied extensively as shown in the works of [1,2,3]. There are many spin-offs such as quantum teleportation [19] and others, like delayed choice, [20], and the study of GHZ states, [5], There is no other evidence for non-locality and persistent entanglement over spacetime. All these experiments are stated as violating BI which then from Bell’s theorem are designated as unequivocal proof that Nature is fundamentally non-local. Quaternion spin gives an alternate explanation.
Using the mechanism described in the Section on Quantum coherence, a filter can be build that exploits the difference . In principle we can separate polarization from coherence and then do an experiment on each. Polarization then gives CHSH=2 and coherence gives CHSH=1. This agrees with the simulated value of CHSH=2.995. The sum of the two give the observed value which appears to violate BI, but, as we have emphasized, there are no hidden variables and no non-locality required. This is the stark opposite conclusion that universally states the violation is evidence for non-local connectivity. The treatment here is local.
Some critics might suggest that the treatment here is actually a LHV model, and then invoke Bell’s theorem to reject such a model can violated BI. They argue that any violation must be due to loopholes. There are no loopholes in the treatment here, and no conspiracies because the LV, , is fully characterized and can be manipulated by a filter. This is consistent with the analysis of Lewis ([21]) who stated:
“But if the mechanism can be uncovered, then we can take it into account in our dealings with measuring devices, and the threat of skepticism (due to conspiracies) recedes.”
If quaternion spin is accepted, then quantum information technologies must learn how to filter and manipulate thereby giving them access to 30 percent of the correlation that qubits miss.
When a violation of BI is observed, it should be viewed as evidence that there is some other process taking place. This leads to new experiments to resolve and characterize the cause of that violation. In the past Bell’s theorem has been, however, misleading, with enormous effort expended over the last 50 years to exploit persistent entanglement by using non-locality as a property of Nature.
We do not criticize local entanglement and only assert that non-local entanglement is untenable. We view local entanglement as an essential property of quantum theory. Indeed we concur with Schrödinger who famously stated, [22], that entanglement was not “a” but “the” difference from classical. Entanglement is a fundamental property of quantum theory but not of Nature. It simplifies calculations, but the price is missing correlation and structure.
Note however that the simulated CHSH = 2.027 for polarization shows that a local realistic theory can violate BI. It is of interest to pursue this further.
Conclusions
We find the two complementary properties exist simultaneously. This supports Einstein in the famous Einstein-Bohr debates, [23]. However, only one property can be realized at any instant, thereby supporting Bohr’s notion of complementarity. Coherence and polarization do not commute and are incompatible elements of reality. They influence each other. The spinor spins the polarization; the indistinguishably of the two polarization axes creates the parity for the helicity to know which way to spin.
According to the treatment here, however, EPR are validated in asserting that quantum theory is incomplete. Quantum mechanics is a theory of measurement but not of Nature.
The existence of quaternion spin requires accepting that Nature has reality beyond our spacetime; that there is information lost; [24], and there are properties in Nature we cannot observe. Some limitations of quantum mechanics can be addressed by replacing Dirac spin with quaternion spin, and entanglement with helicity.
The violation of Bell’s inequalities is not evidence for non-locality, a difficult concept to grasp, but rather evidence for the existence of hyper-helicity and other hidden variables that are responsible for local realism.
Acknowledgments
The author is grateful to Pierre Leroy, (programmer) and Chantal Roth, PhD (programmer) for their help and patience with simulation methods. I thank Pierre who converted the FORTRAN Program to C. The author also gratefully acknowledges Richard Gill, mathematician, Leiden University, who tenaciously played the role of Devil’s Advocate which helped clarify some aspects of Bell’s theory.
Appendix 1. Superposed quaternion spin
Define the lab and body frames by the unit vectors,
Require to be coplanar with and related by the LV ,
Define the polarizing filter in the XZ plane,
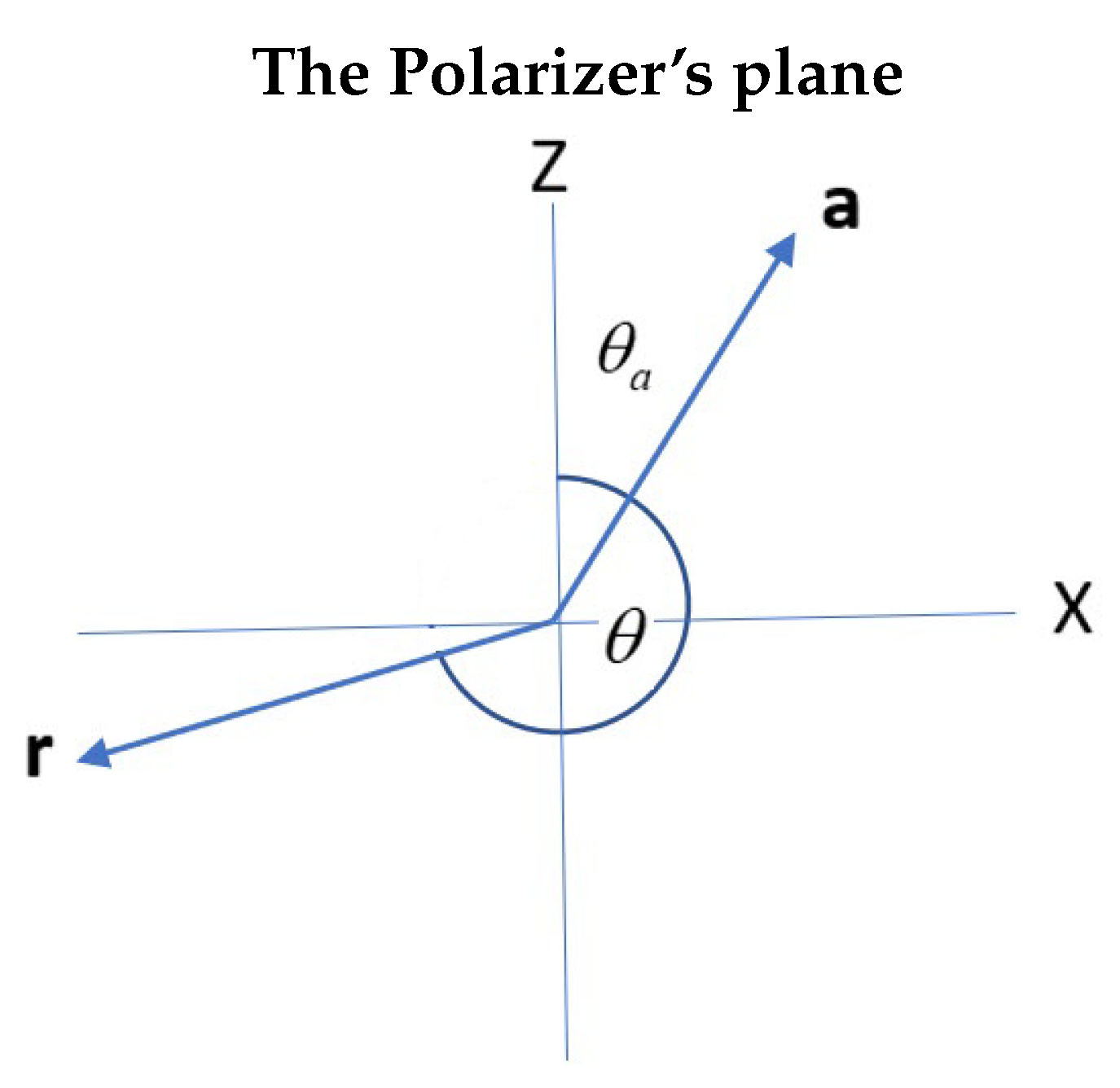
Figure 14 shows these components.
Figure 14.
Depiction of the LFF with the filter angle and the LHV .
Define the sum of the two attributes: polarization and coherence and we seek the expectation values from each,
These involve the quantum trace over the state,
which depends upon the state operator for a single spin in a pure state .
Quaternion rotation
From reference [6], the quaternion spins in the hyper-space and the states are unit quaternions,
Here is the precession frequency of the helicity. Applying this quaternion to a Pauli vector shows the bivector, causes precession around the axis,
Projecting this equation shows the spin components in the BFF are rotated in the polarization plane, , as expected,
The quaternion state only spins the axis of linear momentum L or R. Equation((31) is not the usual expectation value used in polarization space. Being in the hyper-space, the helicity is not observable. Only the effect on the two polarizations spinning is seen. This is consistent with the usual particle physics definition of helicity.
This calculation shows quaternion spin is extrinsic and not hidden like the intrinsic angular momentum of Dirac spin,
Polarization
Since quaternion spin has two spin axes, we define the state operator in the BFF by
where . Calculate the trace in the BFF
Here the second rank Cartesian identity is
In our case the contravariant and covariant vectors are equal and the following properties are needed [25],
Finally substitute the BFF vectors with the LFF vectors from Eqs.(26) and (27) to give
so the dot and cross products are
Giving the result as a superposition of two frequencies
The exponentials are unit quaternions.
The simulation shows that the coherent states require that must be doubled to to agree with experiment, see the section “Discussion of the simulation” for a possible suggestion. The theory as it now stands does not predict this feature whereas a more detailed calculation should reveal the actual mechanism by which the resonance spin is decomposed into two spins of 1/2 in an anisotropic environment.
Appendix 2. The FORTRAN code
The program is written in FORTRAN. From the following link the program is available along with some useful files to plot the figures.
- Resources including the data in .txt files; and Excel program; Gnu plotting; and FORTRAN code with instructions
- FORTRAN Code by Bryan Sanctuary
- Converted to C by Pierre Leroy.
- Some of the unpublished papers are available from my blog Bryan’s Blog.
References
- Clauser, J. F. , Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880.
- Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 1: 14 (8), 15 October 1944.
- Weihs, G. , Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
- Einstein, Albert, Boris Podolsky, and Nathan Rosen. “Can quantum-mechanical description of physical reality be considered complete?.” Physical review 47.10 (1935): 777.
- Greenberger, D. M. , Horne, M. A., Shimony, A., & Zeilinger, A. (1990). Bell’s theorem without inequalities. American Journal of Physics, 58(12), 1131-1143.
- Sanctuary, B. Extrinsic Quaternion Spin. Preprints 2023, 2023020055. [Google Scholar] [CrossRef]
- Sanctuary, B. Spin with Hyper-helicity. . Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
- Schwartz, M. D. (2014). Quantum field theory and the standard model. Cambridge University Press.
- Bell, John S. “On the Einstein Podolsky Rosen paradox.” Physics Physique Fizika 1.3 (1964): 195.
- Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624.
- Fano, Ugo. “Description of states in quantum mechanics by density matrix and operator techniques.” Reviews of modern physics 29.1 (1957): 74.
- Scully, Marlan O., Willis E. Lamb Jr, and Asim Barut. “Theory of the Stern-Gerlach apparatus.” Found. Phys.;(United States) 17.6 (1987).
- Bell, J. S. “Speakable and Unspeakable in Quantum Mechanics” (Cambridge University Press, 1987), 2004. See “Locality in quantum mechanics: reply to critics. Epistemological Letters”, Nov. 1975, pp 2–6.
- Sanctuary, B. C. “The two dimensional spin and its resonance fringe. arXiv:0707.1763 (2007).
- Sanctuary, B. C. “Structure of a spin 1/2. arXiv:0908.3219 (2009).
- Wick, David. “The Infamous Boundary: Seven decades of heresy in quantum physics.” Springer Science and Business Media, 2012.
- Peskin, M. E. , Schroeder, D. V. ( Boulder, CO.
- Maldacena, J. , Susskind, L. ( 61(9), 781–811.
- Bennett, C. H. , Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1995). “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels.” Physical review letters, 70(13), 1895.
- Lewis, Peter J. "Conspiracy theories of quantum mechanics." The British journal for the philosophy of science (2006).
- Kim, Y. H. , Yu, R., Kulik, S. P., Shih, Y., & Scully, M. O. (2000). Delayed “choice” quantum eraser. Physical Review Letters, 84(1), 1.
- Schrödinger, E. , “Discussion of probability relations between separated systems”. Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563 (1935).
- Jammer, M. (1974). Philosophy of Quantum Mechanics. the interpretations of quantum mechanics in historical perspective.
- Braunstein, Samuel L., and Arun K. Pati. “Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox.” Physical review letters 98.8 (2007): 080502.
- Snider, Robert F., “Irreducible Cartesian Tensors”, Vol.43, De Gruyter Studies in Mathematical Physics, de Gruyter, Berlin, 2018.
Figure 1.
The two polarization axes, each spins of 1/2, form quaternion spin of even parity and spin of 1 from the coupling of two mirror states.
Figure 1.
The two polarization axes, each spins of 1/2, form quaternion spin of even parity and spin of 1 from the coupling of two mirror states.
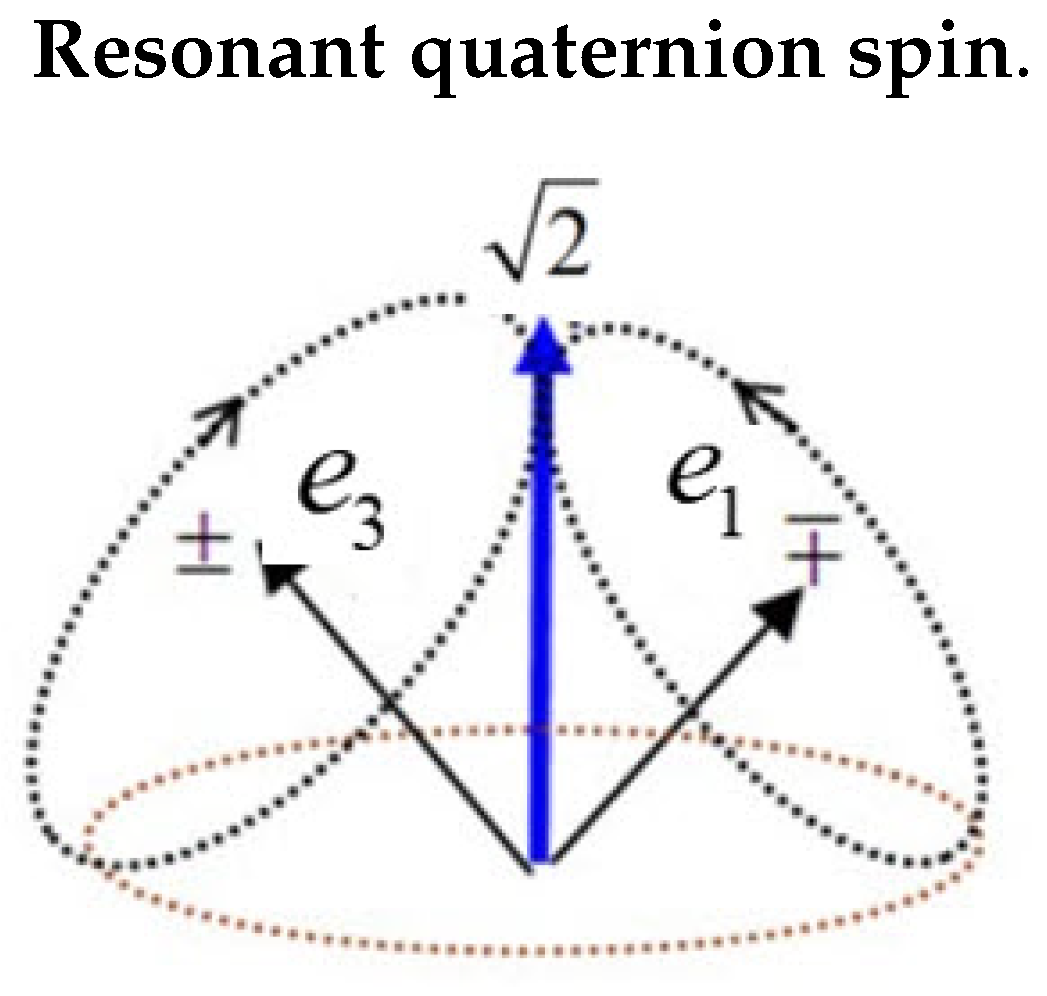
Figure 2.
Alice goes right in a RH coordinate frame and Bob goes left in a LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. Note in the center figure that Alice and Bob start off with the same but opposite orientation in the BFF indicated by .
Figure 2.
Alice goes right in a RH coordinate frame and Bob goes left in a LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. Note in the center figure that Alice and Bob start off with the same but opposite orientation in the BFF indicated by .
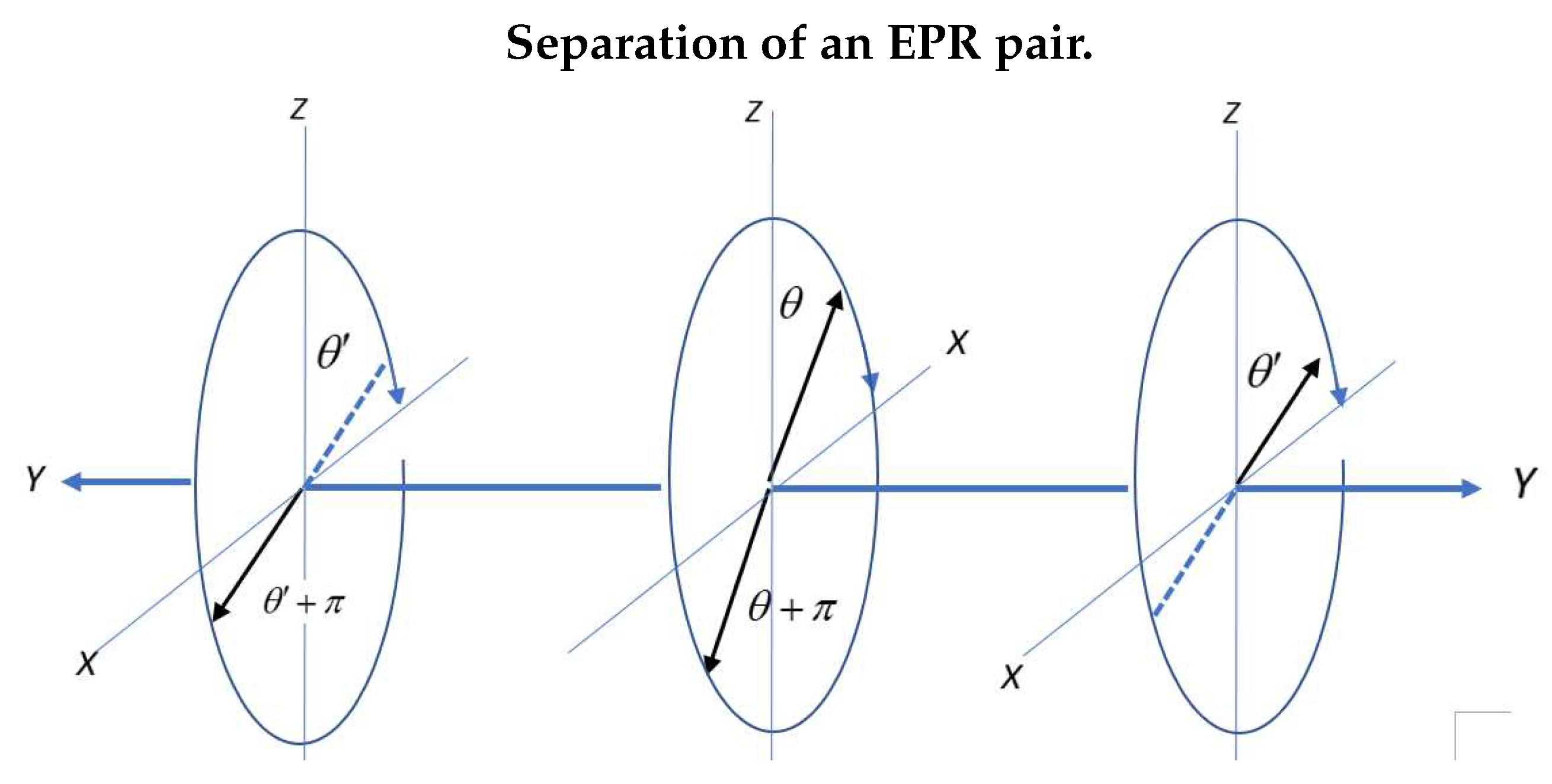
Figure 3.
Plotting intensity versus the angle difference . The full quantum correlation is given by . This is separated into a triangle, giving the polarizations, and the coherences, giving the French Mustache. The results of the simulation are given by the blue points. The CHSH values are listed.
Figure 3.
Plotting intensity versus the angle difference . The full quantum correlation is given by . This is separated into a triangle, giving the polarizations, and the coherences, giving the French Mustache. The results of the simulation are given by the blue points. The CHSH values are listed.
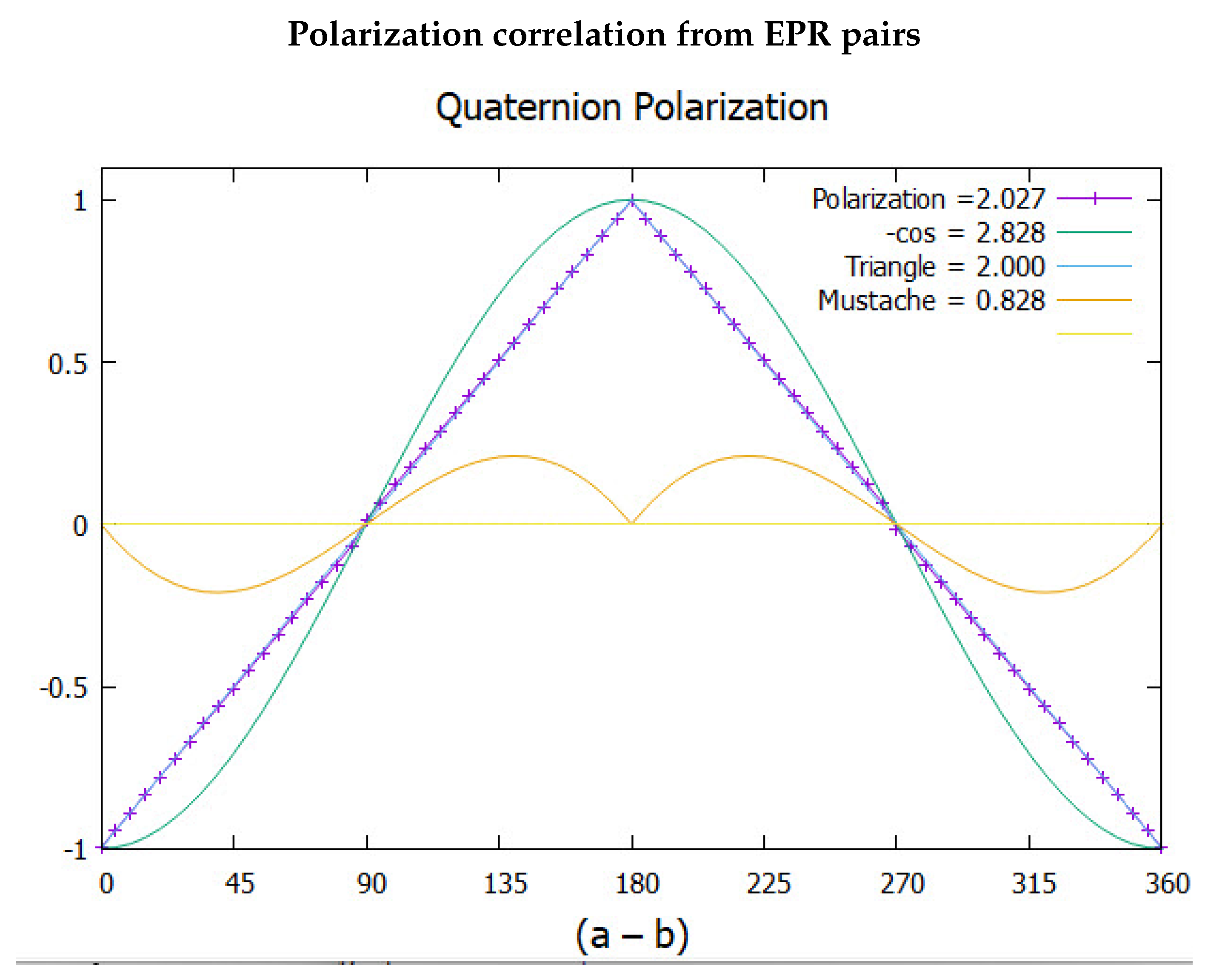
Figure 4.
Same as Figure 3, but plotting the simulated coherence.
Figure 4.
Same as Figure 3, but plotting the simulated coherence.
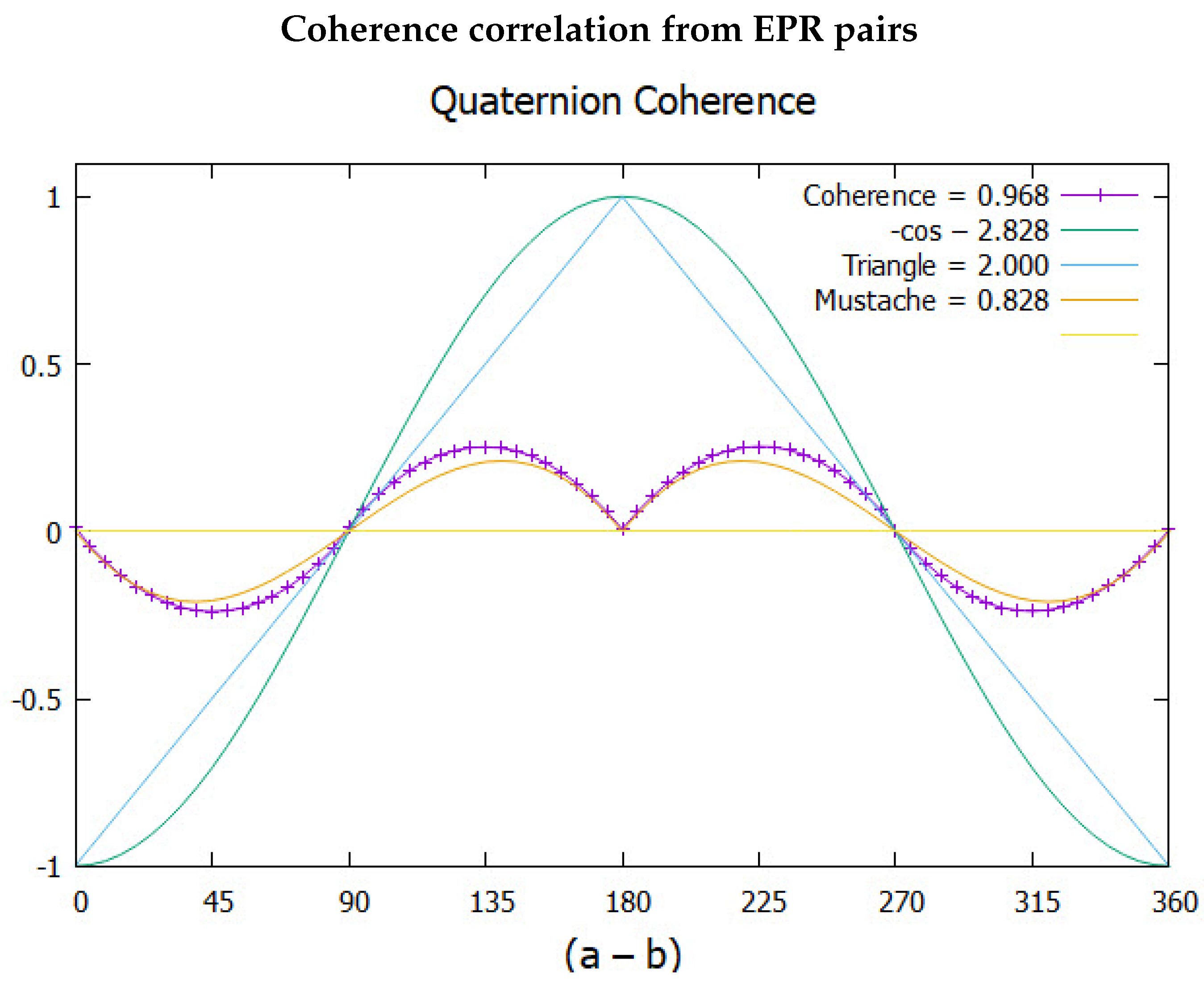
Figure 5.
Same as Figure 3, but plotting the full correlation as the sum of that from polarization and coherence. The simulated plot is decomposed into contributions from polarization and two coherent modes, respectively the French Mustache and a, hardly discernible, residual quaternion correlation.
Figure 5.
Same as Figure 3, but plotting the full correlation as the sum of that from polarization and coherence. The simulated plot is decomposed into contributions from polarization and two coherent modes, respectively the French Mustache and a, hardly discernible, residual quaternion correlation.
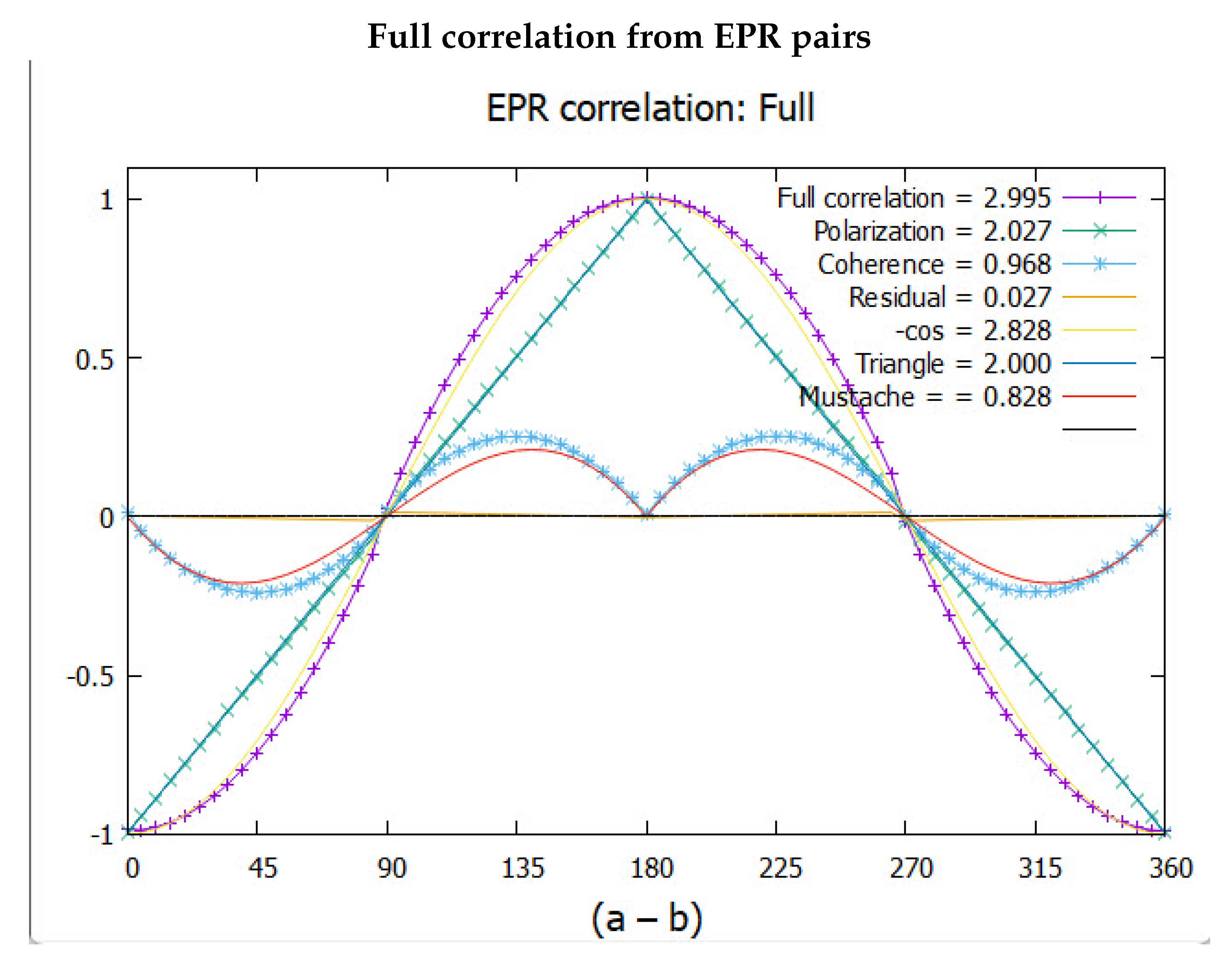
Figure 6.
A blow up of the simulated polarization compared to an exact triangle. The insert shows it over 2.
Figure 6.
A blow up of the simulated polarization compared to an exact triangle. The insert shows it over 2.
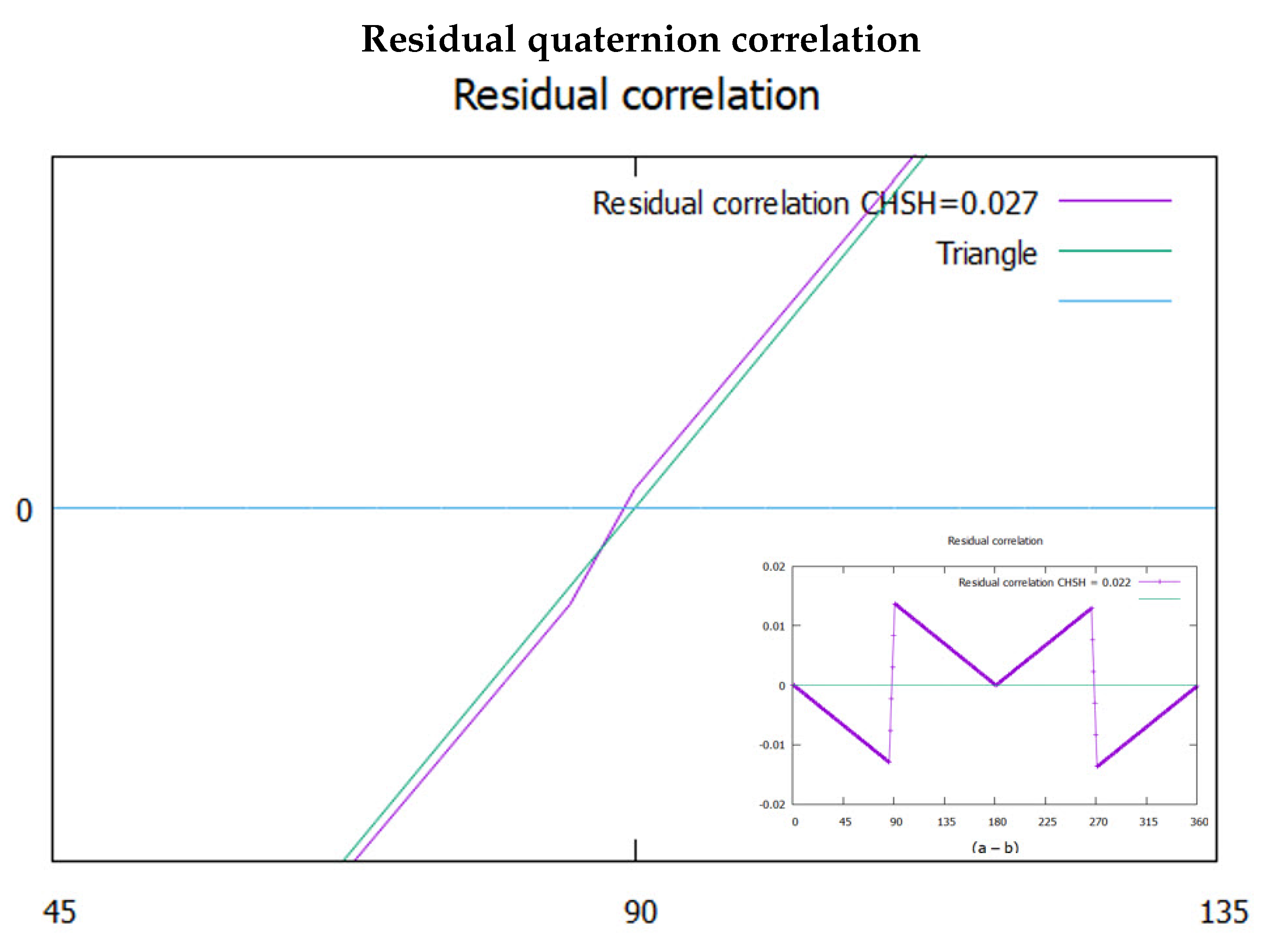
Figure 7.
Alice’s spin (red lines in the (1,1) quadrant) and Bob’s spin (blue lines in the (-1,-1) quadrant) are oriented antiparallel in the BFF. All vectors are unit. The addition of the two axes of a spin results creates the quaternion spin depicted of magnitude one. the settings that give the maximum violation of the CHSH inequality. Bottom:. Two axes interfering to produce the coherent resonance spin. This is coherence, and how quaternion spin seems to appear. Depicted on the LHS and RHS are the two possible polarized states. The missing axes ( on the left and on the right) are still there, but are averaged, leaving only the polarized state.
Figure 7.
Alice’s spin (red lines in the (1,1) quadrant) and Bob’s spin (blue lines in the (-1,-1) quadrant) are oriented antiparallel in the BFF. All vectors are unit. The addition of the two axes of a spin results creates the quaternion spin depicted of magnitude one. the settings that give the maximum violation of the CHSH inequality. Bottom:. Two axes interfering to produce the coherent resonance spin. This is coherence, and how quaternion spin seems to appear. Depicted on the LHS and RHS are the two possible polarized states. The missing axes ( on the left and on the right) are still there, but are averaged, leaving only the polarized state.
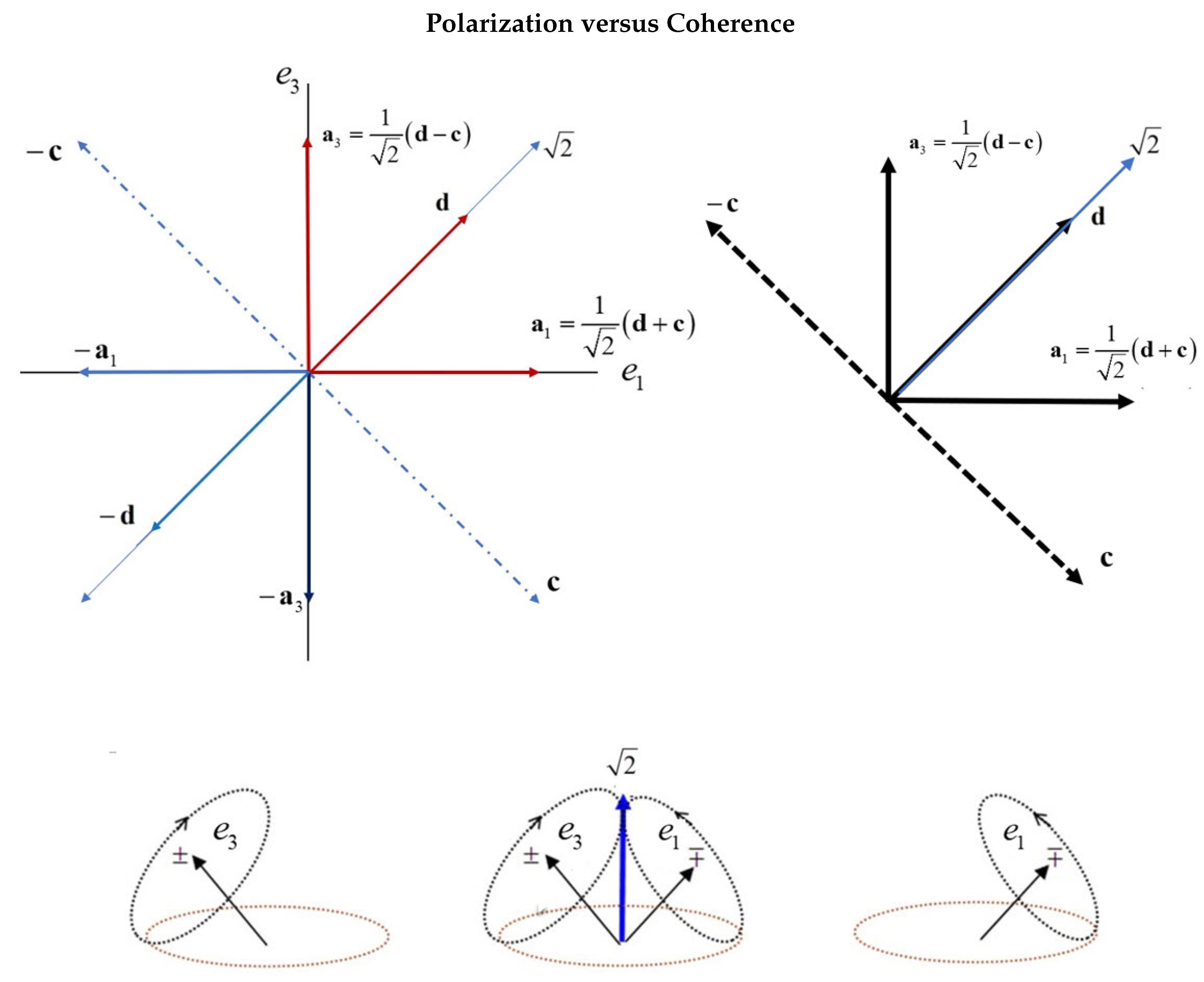
Figure 8.
Some ways the experimental clicks can be distributed between polarization and coherence.

Figure 9.
The normalized raw clicks, Eq.(10).
Figure 9.
The normalized raw clicks, Eq.(10).
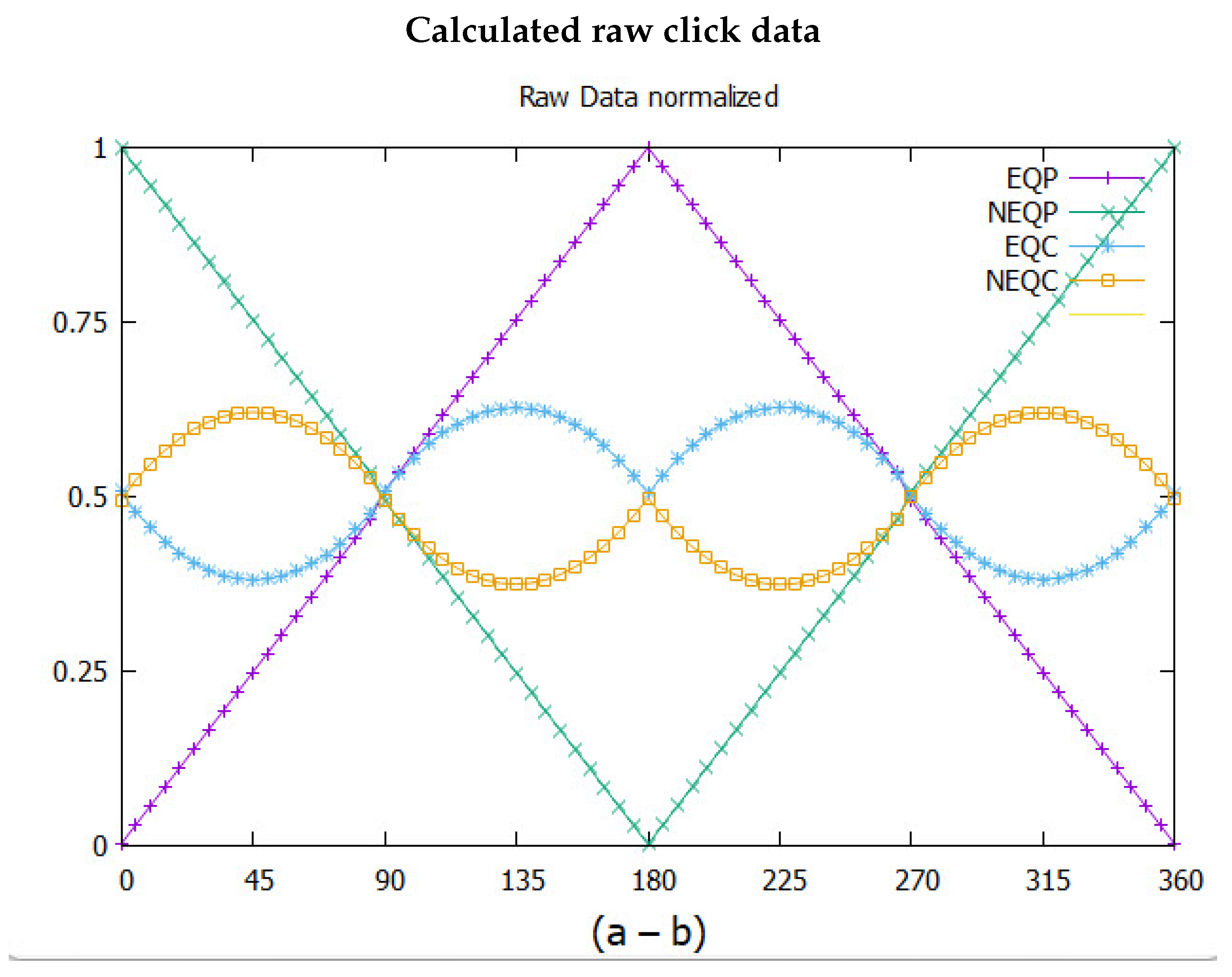
Figure 10.
Adding coherence and polarization clicks gives the upper two nonphysical curves. Subtraction gives two cosines-like curves of magnitude one which are superposed on the lower curve and form the EPR correlation.
Figure 10.
Adding coherence and polarization clicks gives the upper two nonphysical curves. Subtraction gives two cosines-like curves of magnitude one which are superposed on the lower curve and form the EPR correlation.
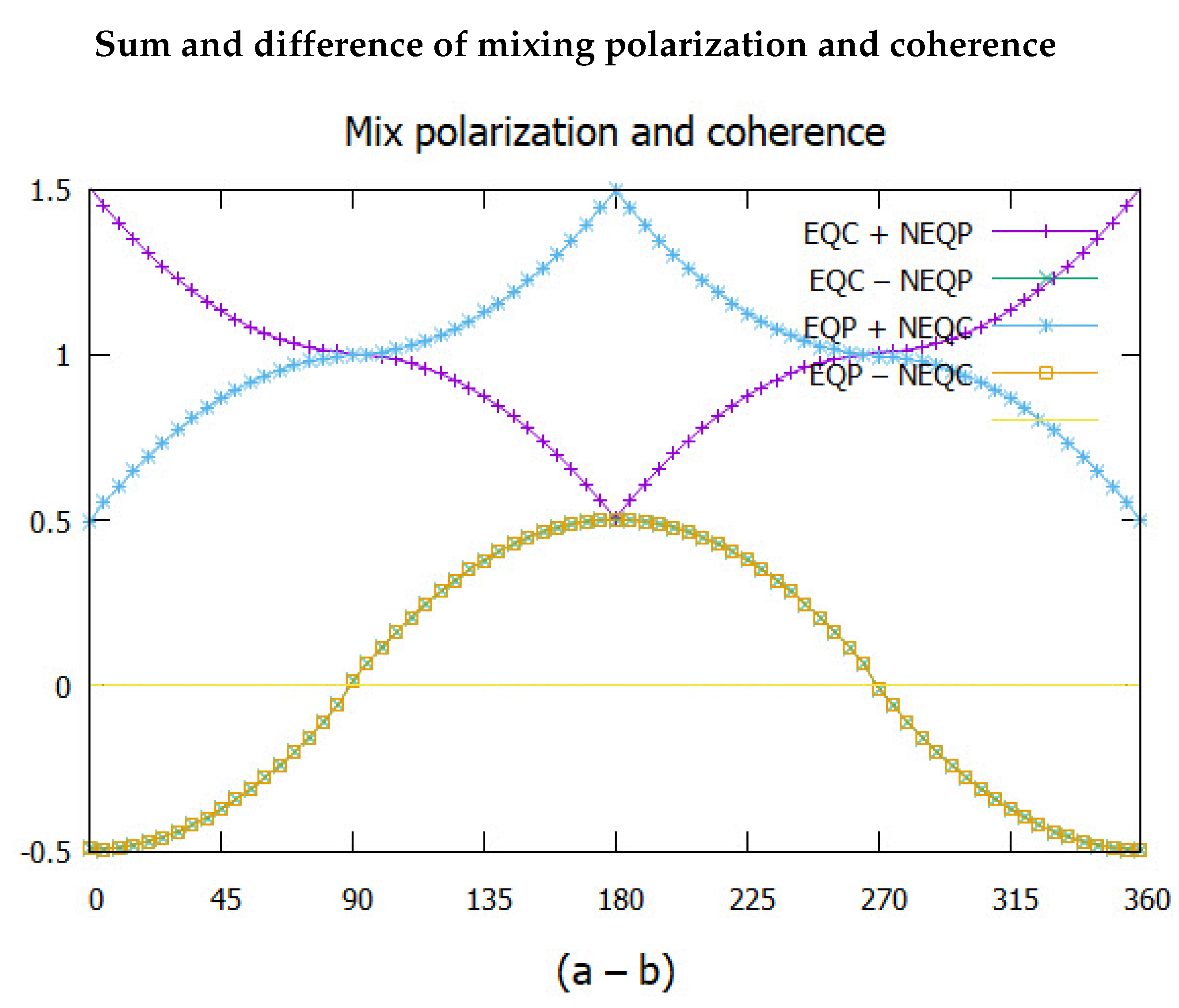
Figure 11.
The function given in Eq.(17) compared to the simulation. Also shown is the correlation from quantum theory.
Figure 11.
The function given in Eq.(17) compared to the simulation. Also shown is the correlation from quantum theory.
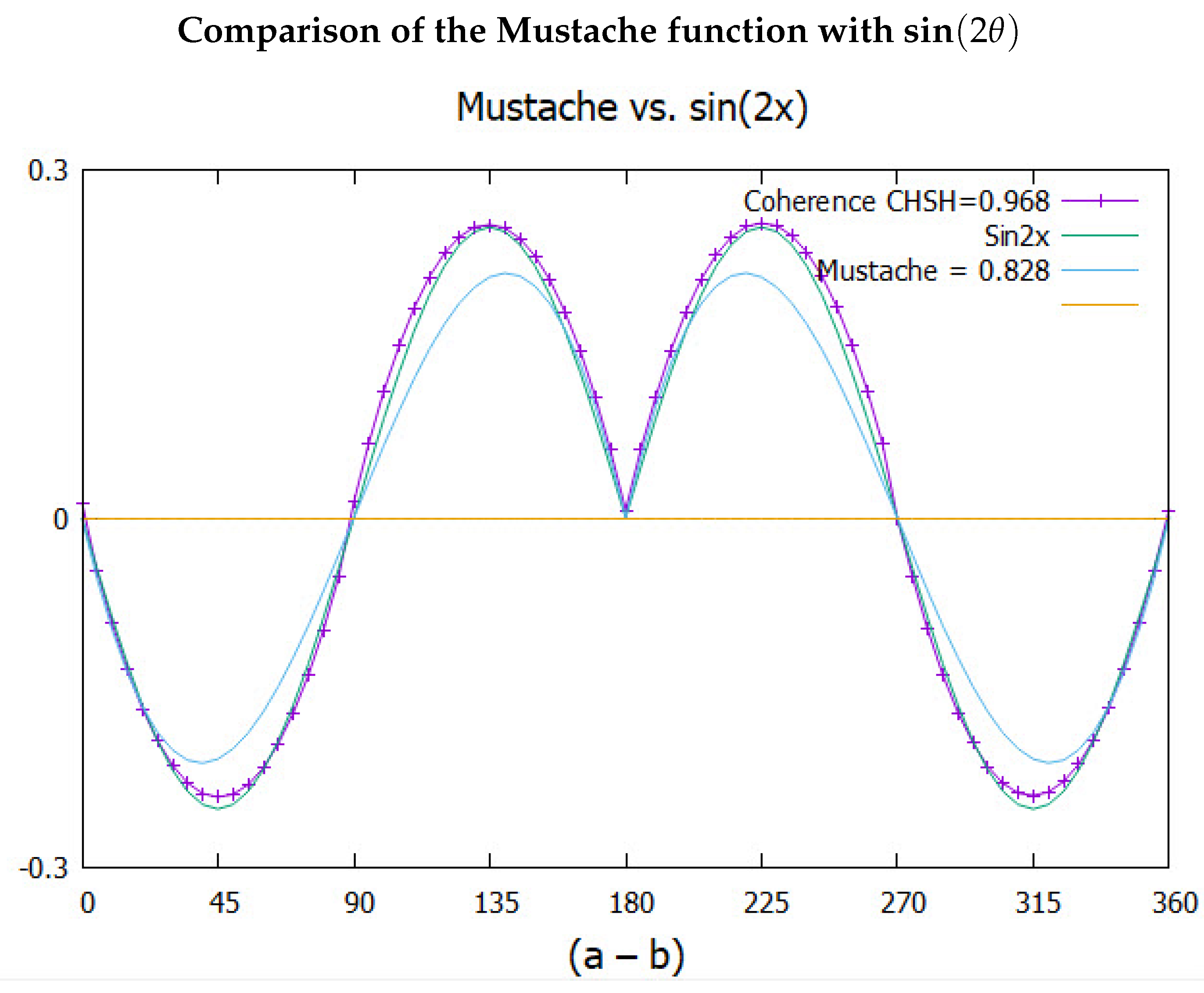
Figure 12.
Values of the CHSH inequalities from classical to Nature.

Figure 13.
Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
Figure 13.
Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





