Preprint
Article
EPR Correlations Using Quaternion Spin
Altmetrics
Downloads
723
Views
401
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (1.33MB )
This version is not peer-reviewed
Quantum Information and Quantum Computing
Submitted:
12 July 2024
Posted:
17 July 2024
You are already at the latest version
Alerts
Abstract
{We present a statistical simulation replicating the correlation observed in EPR coincidence experiments without needing non-local connectivity. We define spin coherence as a spin attribute that complements polarization by being anti-symmetric and generating helicity. Point particle spin becomes structured with two orthogonal magnetic moments, each with a spin of $\frac{1}{2}$—these moments couple in free flight to create a spin-1 boson. Depending on its orientation in the field, when it encounters a filter, it either decouples into two independent fermion spins of $\frac{1}{2}$, or it remains a boson and precesses without decoupling. The only variable in this study is the angle that orients a spin on the Bloch sphere, first identified in the 1920s. There are no hidden variables. The new features introduced in this work result from changing the spin symmetry from SU(2) to the quaternion group, $Q_8$, which complexifies the Dirac field. The transition from a free-flight boson to a measured fermion is the reason for the observed violation of Bell's Inequalities and resolves the EPR paradox.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
We consider the correlation obtained from coincidence EPR experiments, [1,2,3]. Here, we define an EPR pair, [4], as two particles initially in a singlet state and then separate, [5]. In that process, we assume no non-local entanglement persists, so the pair forms a product state.
We have develop a spin theory, [6], which includes a Pauli bivector, , [7]. From this change, spin becomes structured and geometrically equivalent to a photon, Figure 1, [6]. It has two orthogonal spins axes, and , which are reflections of each other, and in free-flight, these couple to give a composite boson spin of magnitude 1, . We show that the observed violation of Bell’s Inequalities, (BI) [8], results from the decoupling of this boson spin-1 in a polarizing field, giving the usual fermion spin-. The process epitomizes and formalizes the wave-particle duality for spin.
We refer to the two-state point particle spin- as a measured electron, , a fermion, which is the solution to the Dirac equation, [9]. It has two states of up and down, where is a vector on the Bloch sphere. The complementary property to the measured spin polarization is the helicity [7]. The boson electron, , exists only in free flight (isotropy) and displays helicity, which spins the axis of linear momentum either L or R. As a boson electron encounters a polarizing field, it transitions to the fermion electron. These are consequences of complexifying the Dirac equation, [6].
After discussing the origin of EPR correlation, we review quaternion, or Q-spin [6], without details. We then use Q-spin to simulate the EPR correlation, which reproduces the violation of BI without non-locality. The computer simulation generates the correlation from polarization and coherence, giving CHSH correlation, [1], of respectively 2 and 1 for a total of 3. QM uses a singlet state to give CHSH = . The simulation treats all EPR pairs, with no missing coincidences, and they are statistically independent
This paper is the third of four in which quaternion spin, or Q-spin, is presented. In the first paper, [6], the Dirac equation is modified to include a bivector, which is the origin of the complementary property to spin polarization, the helicity. The second paper, [7], shows correlation between an EPR pair is conserved after separation. The fourth, [10], summarizes some consequences of using Q-spin, which replaces Dirac’s two-point particles, the matter-antimatter pair, with one structured particle. Q-spin is one particle with four states, whereas Dirac’s equation gives two particles with two states each.
2. EPR Correlation
The correlation arising from an EPR pair is plotted in Figure 2 versus where the angles are the filter settings at Alice and Bob. The coincidence data gives a cosine similarity, which violates BI. In contrast, a product state does not violate BI with a CHSH = 2. This is displayed in the figure as a triangle. Subtracting the two separates the part responsible for the BI violation, with CHSH = 0.828. We call this the mustache function, and Bell’s theorem, [11], asserts this can only arise from non-locality. In contrast, here, we attribute the missing correlation to quantum coherence which, until this work, has not been formulated. This is easily seen by taking the usual singlet state,
and the outer product of Eq.(1), gives a matrix and defines the pure state operator, ,
The off-diagonal components, are responsible for the mustache function.
Using Eq.(2), we obtain the EPR correlation from an entangled state as shown in [6], . Dropping the two off-diagonal terms gives a product state, . The unit vectors, and denote the filter vectors.
In EPR coincidence experiments, the observed correlation is inconsistent with the product state but gives the full correlation. One of the many statements of the EPR paradox [12] is the conclusion that entanglement must be maintained over spacetime. Bell’s Theorem justifies this, [11], but how such non-local connectivity is maintained is not understood and defies rational explanation, [13,14,15]. These difficulties can be overcome by introducing the bivector, which Geometric Algebra justifies, [16].
The geometric product is the sum of the symmetric scalar product and the anti-symmetric wedge product. This leads to the well-known relationship between the spin components of
The bivector, , plays no role in determining the observed spin polarization because it traces out. Define the helicity, [7], as the complementary attribute to the polarization,
Using this anti-symmetric, anti-Hermitian second rank tensor operator in the same calculation as given above for a product state gives the missing correlation, [7],
Adding this to the product of cosines recovers the full correlation, , suggesting the observed violation of BI is a result of helicity. This is an example of the Conservation of Geometric Correlation, [7]. Non-locality plays no role here.
2.1. Quaternion Spin
The details of this section are found in [6].
Spin is obtained from the Dirac equation, a four-dimensional real field represented by the four anti-commuting gamma matrices, . Dirac found two spins of , each with two states and mirror images of each other. He interpreted the two as a matter-antimatter pair despite the negative energy issues, [17].
However, there is no bivector in the Dirac equation, [18], and introducing one is our departure from the usual development. Multiplying one gamma matrix by the imaginary number, chosen to be , is the only fundamental change introduced in this work. Dirac’s gamma field is then replaced by . The subscript s denotes spin spacetime, [6], which differs from Minkowski space where Dirac’s spin is defined. There are two solutions to the complexified Dirac equation: reflective or mirror states. They have no parity. Dirac interpreted the two mirror image states as a matter-antimatter pair.
Introducing a bivector changes the Clifford algebra from that of Minkowski space, to for spin spacetime. Dirac’s two spins have SU(2) symmetry. Introducing a bivector changes the symmetry to the quaternion group, .
The bivector complexifies the Dirac field, which is the primary motivation behind Twistor theory, [19,20]. The Dirac equation becomes non-Hermitian, [6], so spin spacetime is complex, giving helicity states as complex conjugates. The ± in the gamma matrices above is due to complexification.
As shown elsewhere, [6], the non-Hermitian Dirac equation further separates into distinct spaces under parity symmetry. One space is of even parity and describes a 2D disc obeying . The second space is the hypersphere, generating a unit quaternion that spins the axis of linear momentum, Figure 1. In free flight, a spin is a spinning disc of angular momentum. Despite the coupling of the two fermionic axes to give a composite boson, the helicity causes the polarization to average out. In free flight, an electron is a boson of odd parity, , with only helicity states of L or R, Figure 1.
The upper central frame of Figure 3 shows a free-flight boson formed from coupling the mirror states of the two fermionic axes (3,1). When encountering a field, illustrated by the longer arrow, the indistinguishably is broken and, depending on its orientation relative to the boson spin, either the boson precesses uncoupled, lower middle panel, or if the field is closer to one of the two fermionic axes, the boson decouples into a fermion as shown in the left and right panels. This recovers Dirac spin, which obeys Dirac’s equation, and is the spin- that we measure.
How the resonant spin decouples depends upon the filter strength and its orientation relative to the resonant spin. This is discussed in the following section.
2.2. Q-spin in a Polarizing Field
The complementary attributes of spin, polarization, and coherence, simultaneously exist. We express Q-spin, , possessing both properties,
There are two components, one for each axis, , , [6]. Contracting this complex spin with a field vector gives a unit quaternion, .
We combine these two axes which constructively interfere to produce a purely resonance spin being a boson of spin-1,
The expectation values are obtained for a single Q-spin in a vector field being the product of three quaternions (see [6] Eq.(43)),
The first quaternion is a phase (see Eq.(30) of [6]); the second is a geometric factor that orients the spin disc in the Body Fixed Frame, BFF; and the last is a field quaternion that sets the field position in the Laboratory Fixed Frame, LFF. Since Q-spin has structure, the body and lab frames are needed.
There are several practical ways of expressing Eq.(8), [6], and these lead to two mechanisms for the transition from a free-flight boson to a measured fermion, depicted in Figure 3.
The Least Action Principle is used that states the axis that aligns is the closest to the polarizing field vector. Note that the two axes have opposite magnetic moments; hence, the field orientation determines whether the plus or minus state is observed.
2.3. Separating an EPR Pair
Initially, in a singlet state at the source, an EPR pair separates, and the two independent particles move towards their respective filters. In the process, they conserve linear momentum, angular momentum, and helicity, see Figure 4. The discs depict a separation process, with the middle disc showing Alice and Bob’s anti-parallel boson spins. Alice’s spin moves right, and Bob’s moves left. Alice’s initial orientation at the source is set by the angle . The axis of linear momentum, Y, spins with helicity being either left or right. Bob’s orientation is to conserve angular momentum. Both spin around the Y axis in the same direction, maintaining them as anti-parallel in free flight.
Note that Alice and Bob are in opposite frames. Alice is in a right-handed frame by the right-hand rule, and Bob is in a left. The two frames are related by complex conjugation, so whereas they both have the same sense of precession, their helicities are opposite when Bob is viewed from a RH frame.
In the following, we obtain the correlation from coincidence experiments in different cases.
2.4. Correlation from an EPR Pair
In the absence of the filters and , the correlation is given by the product of Q-spins for Alice and Bob,
The spins are anti-correlated at separation, which requires to differ between Alice and Bob by , see Figure 4. Also, the helicities of Alice and Bob’s spins are opposite, expressed by the complex conjugation. The second term reverses the helicity of both, so the correlation is real. This is similar to forming polarized light with photons. As expected, after leaving a common source in free-flight before encountering filters, the correlation between Alice and Bob is -1, consistent with the two spins remaining anti-parallel and anti-correlated from the source up to the filter.
2.5. Approaching a Filter
As the spins of Alice and Bob approach their randomly set filters, the correlation between the two resonance states is
This is identical to the correlation from a singlet state that maintains entanglement, , but Eq.(10) is a product state with no entanglement. Using Q-spin, the correlation is maintained by the common angle without any non-local connectivity between Alice and Bob.
However, to get this result, both the spins of Alice and Bob must be complex. If one spin is polarized, there is no helicity, and only the scalar part of the quaternion is present,
We separated the phase needed for anti-correlation. Only the product state survives even if one spin is coherent,
To get the full correlation, Eq.(10), Alice and Bob’s particles must be boson spins. If one or the other has decoupled into a fermion, only a product state is possible. That means the correlation from coherence can only be measured when the spins of both Alice and Bob are oriented within the same 45o wedge as seen in Figure 5. The boson axis, labeled with 1’s, represents Alice and Bob’s anti-parallel bosons as they approach their (space-like separated) fields. When they do respond to their fields, the anti-parallel bosons reorient, being pulled to the nearest field axis where they precess. The processes at Alice and Bob are completely independent, and therefore local.
2.6. Interpretation of the CHSH Inequality
Coupling of angular momentum is common in all spectroscopes [21], including transport properties of gases, [22,23]. In our case, the resonance spin is stable in free-flight but will eventually decouple as it approaches a polarizing field. At a given distance, the decoupling depends upon the orientation of a spin relative to the filter and its strength relative to the spin-spin coupling within Q-spin.
Consider now that the filter settings for both Alice and Bob are shown in Figure 5. Bob’s is one of and , and Alice’s settings is one of either or , with and . There are four experiments expressed in the CHSH inequality, whence Alice and Bob have correlations of , , , and . The LFF is fixed by the filter settings, and Q-spins impinge on the filters at random angles of from a random source. The figure shows two orientations each labeled by a "1", and which bisect two of the filter cones. We chose these settings because Alice and Bob’s bosons are then close to their filter, only 22.5o away, and remain bosons as they align with their filter and precess about it. Therefore, their contribution to the correlation is from coherence, coh. If, in contrast, an experiment is, say, , then Alice is still only from , but now Bob is 112.5o from his. Whereas Alice remains a boson, Bob’s boson must decouple when encountering his filter at . Using this experiment, the contribution to the correlation is from polarization, pol, Eq.(12).
When considering the possible outcomes for coincidences, there are four types: pol:pol, pol:coh, coh:pol, coh:coh, and only the coh:coh coincidences contribute to the correlation from coherence.
The maximum correlation for the S=CHSH inequality for the four experiments is determined by the filter setting as shown in Figure 5, giving,
Consider the correlation from one experiment, shown in Figure 5. If Alice and Bob’s spins reorient as bosons, their precessions will look like shown in Figure 6. Spin makes an angle of with a field direction. That is for spin-1 bosons as shown in Figure 6. A spin has thereby supporting the assertion that the bosons remain intact within the cone.
3. Simulation Model
In contrast to a structureless point particle, Q-spin displays four internal motions with four axes. First the axis of linear momentum is spun by a quaternion. The two fermion axes can precess about their axes which maintain mirror symmetry, and couple to give the fourth axis the boson.
In [6], Q-spin in a polarizing field, Eq.(8), is expressed in different ways which show the projections of Alice and Bob’s spins onto the boson axis, , and the decoupled axes, and . From these expressions in the LFF, the correlation between Alice and Bob is due to a competition between axes using the Least Action Principle. Consider Eq.(14) of [6] given by,
To know which axis aligns, note the two terms are projections of the two BFF spin axes along the field axis,
3.1. Quaternion Algorithm
Consider a boson in a polarizing field, (upper middle panel of Figure 3) showing the two coupled axes giving the boson. We can deterministically know which axis will align when it decouples. Before decoupling, we must double the angle to account for the double Larmor frequency and write the two coupled boson axes as,
The larger axis will become polarized, and its sign gives a + or − click. Without doubling the angle, , the simulation fails. The doubling gives the mustache function in Figure 7 and a CHSH correlation of 1.
Of course, the same is done for Bob, and the coincidences from both Alice and Bob combine their clicks into equal coincidences or unequal coincidences, .
If Alice and Bob’s spins are outside the 45o wedge, the boson spin is assumed to have decoupled into a fermion. Then only one axis remains, Figure 3, and we choose either. The usual Larmor frequency for a fermion is proportional to and does not double the angle. Then, we determine if that axis is positive or negative, indicating a plus or minus click. Using a single axis gives the triangle, Figure 7, and a CHSH value 2.
To summarize, coherence depends upon two axes. First, determine the larger axis,
and then use the sign of that axis to determine the click values. Since varies from 0 to , the magnitudes and signs of the projected axes vary.
For polarization, use only one axis, and we chose .
The sign also deterministically evaluates spin up or down.
The simulation determines the correlation between classical axes. It is not a quantum simulation; instead, it is a model that the treatment here suggests. It is known that classical simulations can account for the correlation without non-locality, [24,25], see also [26]. We note the total correlation from polarization and coherence gives a total of CHSH=3, in contrast to that from an entangled state of .
3.2. Simulation Results
The FORTRAN and C code, available with this paper, determines clicks from polarized states and coherent events using the above algorithms. Additionally we provide several text files which are outputs from the simulation, along with the plotting code for Gnuplot.
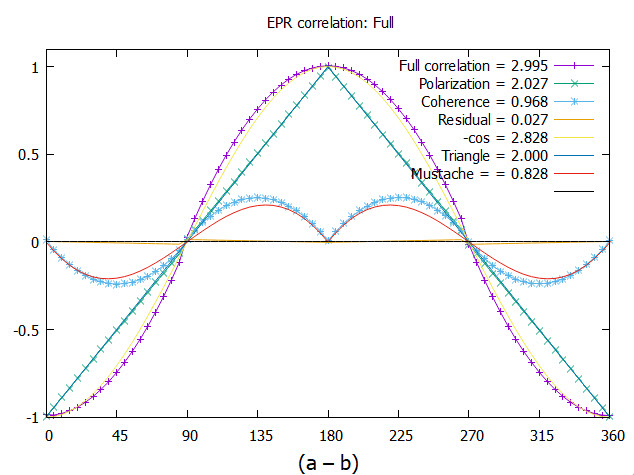
The results are given in Figure (Figure 7. The simulated correlation from either polarization axis gives the polarization as the triangle, with a CHSH = 2.027. The mustache coherence, which depends on the coupling of the two axes into one axis, is shown in the same figure and gives a CHSH = 0.968. The simulation gives a total CHSH value of 2.995, or almost 3. The simulation gives more correlation than from a singlet state, CHSH = 2.828.
The theoretical CHSH value for polarizations is 2, whereas in Figure 7, it is 2.027. The residual correlation remains as shown in Figure 8. A cross-over occurs close to the horizontal axis. It is hardly discernible. Considering it might be an artifact, various tests did not remove it. This has symmetry similar to the mustache coherence and supports this as a natural feature in the model. We expected the cross-over in Figure 8 to be at zero and have not determined why it is shifted. The two discontinuities at and are necessary for the residue to be physical (without them, there is no correlation of 0.027). We assert that this residual contribution to coherence is due to correlation in the polarization states. If confirmed, the polarization exceeds BI, [8], by a small amount and violates his theorem [11].
3.3. Determining the Correlation
Polarization and coherence are complementary properties, meaning they are not manifest simultaneously [27,28]. Pauli stated [29], “Intuitively, observables are complementary if the experimental arrangements allowing their unambiguous definitions are mutually exclusive." In out case, the angle, , is taken as random, but can be in the control of the experimenter and can be used, in principle, to distinguish polarization from coherence. In this sense, Pauli’s statement is consistent here.
The correlation between equal coincidence events (), , and unequal events(), is given by
which gives the minus cosine similarity in EPR coincidence experiments.
Using Q-spin, the coincidence events are complementary. Sometimes, an event gives a boson correlation, and other times, it gives a polarization correlation. However, complementary properties do not exist in the same space. Polarization belongs to a convex set, a disc with . Quaternion space, the hypersphere, is also convex. Since we treat a single EPR pair, both polarization and coherent states are pure. The two complementary attributes of spin are extreme points on their distinct convex spaces.
With no mixed states, we must only distinguish between polarized (pol) and coherent (coh) states. Introduce Boolean operators that ensure complementarity,
where or , with the sum of the contributions being the total number of events, .
Suppose that it is possible to filter the system such that the experiments can distinguish between the two, then we can write the total correlation as collecting the different events in different bins,
The correlation from each is evaluated to obtain the complete correlation as shown in Figure 7 being the sum of the two contributions. Note that the value of a correlation is independent of the total number of clicks, so for the calculation, we did the following: first in Eq.(20), assume and and the polarization algorithm was used to give the triangle in Figure 7. Then we set and and calculated the mustache curve using the coherence algorithm.
We find that the correlation at the source from an entangled singlet is divided between correlation from polarization and coherence. This is consistent with the Conservation of Geometric Correlation, [7], which states that the total correlation at the source is conserved between particles upon separation.
A filter, as mentioned, might be constructed by polarizing the beam at the source for Alice and Bob, adjust to be the same for all EPR pairs, and then arrange the filters at the desired angle relative to the polarized source. Additionally, a filter might vary the strengths of the applied field to inhibit or promote decoupling.
3.4. The Mustache Function
The correlation between bosons is responsible for the mustache function. Q-spin coherent correlation resembles two opposing sine waves reflected at . The following gives a good fit,
This is plotted in Figure 9 along with the simulated data points which match Eq.(21). Also plotted for comparison is the correlation from quantum theory. The simulation gives more correlation, CHSH = 1, than obtained from the singlet state and QM, CHSH = 0.828. We propose, [10], the difference is due to the singlet state being an approximation.
The doubling of the filter angles, is due to the boson magnetic moment of which gives two periods over . The first period starts off at where Alice and Bob’s spins are anti-correlated. As moves to , the anti-correlation means that the magnetic quantum numbers, m, must be opposite between Alice and Bob. This makes the mustache negative up to . At that point, the two bosons become correlated, with equal magnetic quantum numbers, rendering the boson correlation positive.
The second period starts at , but the bosons remain correlated up to , after which they are again anti-correlated. Therefore, the boson correlation in the second period starts off positive. The sign of the boson correlation is in tandem with the sign of the correlation from polarization.
We view the correlations from polarization (pol) and coherences (coh) as distinct. By dropping the coherent terms, only fermion electrons remain and the correlation is the triangle in Figure 7. Putting back the boson spins bisect the BFF quadrants. However, recall that to give correlation from coherence, both Alice and Bob must be bosons, coh-coh. There are four types of coincidences between them: pol-pol, pol-coh, coh-pol, and coh-coh. Therefore, only of the coincidences lead to coherence, which is the origin of that factor in Eq.(21)
4. Discussion
We find that the two complementary properties exist simultaneously. This supports Einstein in the famous Einstein-Bohr debates, [12]. However, only one property can be realized at the same instance, supporting Bohr’s notion of complementarity, [30]. Coherence and polarization are incompatible elements of reality. They influence each other. The spinor spins the polarization; the indistinguishability of the two polarization axes creates the mirror states for the helicity to know which way to spin.
Figure 10 lists four values of the CHSH inequalities. The value of 2 quantifies the Infamous Boundary [31], between polarization and coherence. Quantum theory gives the value of , which is less than that from the simulation of 2.995, which is close to 3. The value three results from modeling the three axes of Q-spin: the two polarized and one coherent, suggesting a CHSH = 1 for each axis.
The CHSH values leading to 2.995 from the simulation are and . This suggests a convergence to , which is correlation per axis. This leads to a CHSH value of 3, which supports equal contributions from each axis.
4.1. Spin
In this treatment, non-local entanglement is replaced by helicity. The Dirac spin is replaced with Q-spin. Both these features come from changing the symmetry from SU(2) to . The visualization of Q-spin, which is geometrically identical to a photon in free flight, see Fig (Figure 1), carries a 2D spin plane that forms its own “World Sheet”, [32]. The 2D structure of Q-spin admits anyons [33], consistent with a boson and a fermion on one particle. This is not possible in 3D or for a point particle.
When the Dirac equation is changed to include Q-spin, the two resulting mirror states have no parity, only reflection, but they combine into states of even parity polarization and odd parity coherence. The mirror states that Dirac interpreted as a matter-antimatter pair represent, for Q-spin, two magnetic axes on one particle. The two reflective axes are orthogonal, in phase, and precess oppositely with equal energy from the upper middle panel in Figure 3. Q-spin resolves Dirac’s negative energy issue.
If Q-spin was formed at the Big Bang, producing no anti-matter, then the baryon asymmetry problem, [34], is solved.
Spin carries helicity as an element of reality, and quaternions exist in the hypersphere of four spatial dimensions. Spin extends to these spaces beyond our visualization but remains an element of reality beyond our dimension. The only part of a quaternion visible to us is the stereographic projection from onto our Minkowski space. From that, we observe a spinning axis.
According to the treatment here, however, EPR is validated in asserting that quantum theory is incomplete. Quantum mechanics is a theory of measurement but not of Nature. It does not include those higher dimensions of the hypersphere needed for the coherence; it does not include anti-Hermitian operators as elements of reality, nor the complexity of spin spacetime. Despite being contrary to accepted philosophy, the treatment here gives an alternate, deterministic, and locally realistic description of the microscopic.
In calculating expectation values, the state operator is given in reference [7], which includes only the polarization axes and not the bivector for helicity. This is justified because a bivector is not physically observable in our spacetime.
In the BFF, Q-spin is expressed by Eq.(6.14) with two axes, and projected along the field direction. The magnitude of those projections determines which axis is favored to align, whereas if both axes are more or less equally projected, being in a wedge, then the resonance spin of magnitude 1 is favored.
To repeat, in free flight, Q-spin acts like a boson with odd parity, and in a perturbing field, it acts like a fermion with even parity.
4.2. Bell
Bell’s theorem states that no local theory can exceed his inequality and asserts in his own words [11],
If [a hidden-variable theory] is local, it will not agree with quantum mechanics; if it agrees with quantum mechanics, it will not be local.
Since we have shown that coherence accounts for the violation of BI, thereby obviating non-locality, this statement by Bell cannot be supported. Bell’s Inequalities are classical and quantitatively express correlations between real variables in our 3D space. His classical theorem proves that a classical system cannot violate his upper bound. In contrast, Q-spin is quantum, with two complementary attributes in different convex spaces. It carries helicity, or coherence, in addition to polarization, and the variables are complex. Bell’s theorem does not apply to quantum systems, and no conclusions concerning non-locality and quantum theory can be drawn from any of his works, [11]. The only value of BI is that they quantitatively define the “Infamous boundary", [31], between the classical and quantum worlds via a CHSH value of two.
In this work, there are no Hidden Variables. The only variable is local, , relating spin and Minkowski spaces. Non-locality cannot be concluded when BI is violated, [35]. Instead, the opposite follows, as shown here: the violation is evidence of local realism.
4.3. Conclusions
The existence of Q-spin requires accepting that Nature has reality beyond our spacetime, that there is information lost; [36], and that there are properties in Nature we cannot observe. Some limitations of quantum mechanics can be addressed by replacing Dirac spin with Q-spin and entanglement with helicity.
However, we can show that an entangled singlet state is an approximation [10]. For this reason, the quantum correlation of is less than the simulated value of CHSH=3. This violates Tsirel’son’s bound, [37]. Entanglement is a fundamental property of quantum theory but not of Nature. It simplifies calculations by dropping coherent terms, but the price is lost correlation and structure.
Q-spin, if accepted, changes our fundamental view of Nature and requires a re-examination of areas of quantum theory that have hitherto relied on Bell’s Theorem to justify non-local connectivity, [1,2,3,38,39,40,41,42,42].
The violation of Bell’s inequalities is not evidence for non-locality, an impossible concept to grasp, but rather evidence for the existence of helicity and other properties of Nature that constitute local realism.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org. It contains the simulation programs is C and FORTRAN. Additionally, Gnuplot code is given along with the .text files that give most of the figures in this paper.
Funding
This research received no external funding.
Acknowledgments
The author is grateful to Pierre Leroy (programmer) and Chantal Roth (programmer), for their help and patience with simulation methods. I thank Pierre, who converted the FORTRAN Program to C.
Conflicts of Interest
The authors declare no conflicts of interest in writing the manuscript; or in the decision to publish the results.
References
- Clauser, J. F., Horne, M. A., Shimony, A., Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880.
- Aspect, Alain, Jean Dalibard, and Gérard Roger. "Experimental test of Bell’s inequalities using time-varying analyzers." Physical review letters 49.25 (1982): 1804.Aspect, Alain (October 15 1976). "Proposed experiment to test the non separability of quantum mechanics". Physical Review D. 14 (8): 1944–1951.
- Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
- Einstein, Albert, Boris Podolsky, and Nathan Rosen. "Can quantum-mechanical description of physical reality be considered complete?." Physical Review 47.10 (1935): 777.
- Greenberger, D. M., Horne, M. A., Shimony, A., & Zeilinger, A. (1990). Bell’s theorem without inequalities. American Journal of Physics, 58(12), 1131-1143.
- Sanctuary, B. Quaternion Spin.Mathematics 2024, 12(13), 1962; [CrossRef]
- Sanctuary, B. Spin helicity. Preprints 2023, 2023010571. [CrossRef]
- Bell, John S. "On the Einstein Podolsky Rosen paradox." Physics Physique Fizika 1.3 (1964): 195.
- Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624.
- Sanctuary, B. Quaternion-Spin and Some Consequences. Preprints 2023, 2023121277. [CrossRef]
- Bell, J. S. "Speakable and Unspeakable in Quantum Mechanics" (Cambridge et al., 1987), 2004. See "Locality in quantum mechanics: reply to critics. Epistemological Letters", Nov. 1975, pp 2–6.".
- Jammer, M. (1974). Philosophy of Quantum Mechanics. The interpretations of quantum mechanics from a historical perspective.
- Newton to Bentley, February 25 1692/3, The Correspondence of Isaac Newton, ed. H. W. Turnbull (Cambridge: Cambridge University Press, 1961),.
- Einstein, Albert. Born-Einstein Letters 1916-1955: Friendship, Politics, and Physics in Uncertain Times. Palgrave Macmillan, 2014.
- Mullin, W. J. (2017). Quantum weirdness. Oxford University Press.
- Doran, C., Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
- Dirac, P. A. M. (1930). "A Theory of Electrons and Protons". Proc. R. Soc. Lond. A. 126 (801): 360–365.
- Peskin, M. E., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
- Penrose, Roger. "Twistor algebra." Journal of Mathematical Physics 8.2 (1967): 345-366.
- Penrose, Roger. "Solutions of the Zero-Rest-Mass Equations." Journal of Mathematical Physics 10.1 (1969): 38-39.
- Herzberg, Gerhard. Molecular Spectra and molecular structure-Vol I. Vol. 1. Read Books Ltd, 2013.
- Turfa, A. F., Connor, J. N. L., Thijsse, B. J., & Beenakker, J. J. M. (1985). A classical dynamics study of Senftleben-Beenakker effects in nitrogen gas. Physica A: Statistical Mechanics and its Applications, 129(3), 439-454.
- Sanctuary, B. C., J. J. M. Beenakker, and J. A. R. Coope. "Influence of nuclear spin couplings on the thermomagnetic torque in HD." The Journal of Chemical Physics 60.8 (1974): 3352-3353.
- Annila, A. (2021). Quantum Entanglement: Bell’s Inequality Trivially Violated Also Classically. Available at SSRN 4388586.
- Arto Annila, Marten Wikstrom, 2021, viXra:2112.0118 Quantum Entanglement: Bell’s Inequality Trivially Violated Also Classically. Category: Quantum Physics.
- Geurdes, H. (2023) Bell’s Theorem and Einstein’s Worry about Quantum Mechanics. Journal of Quantum Information Science, 13, 131-137. [CrossRef]
- Kiukas, J., Lahti, P., Pellonpää, JP. et al. Complementary Observables in Quantum Mechanics. Found Phys 49, 506–531 (2019). [CrossRef]
- Busch, P., Grabowski, M., Lahti, P.: Operational Quantum Physics, LNP 31. Springer, New York, 1994, 2nd Corrected Printing (1997).
- Dirac, Paul Adrien Maurice. The principles of quantum mechanics. No. 27. Oxford University Press, 1981.
- Bohr, Niels. "Can quantum-mechanical description of physical reality be considered complete?." Physical Review 48.8 (1935): 696.
- Wick, David. "The Infamous Boundary: Seven decades of heresy in quantum physics." Springer Science and Business Media, 2012.
- Maldacena, J., Susskind, L. (2013). Cool horizons for entangled black holes. Fortschritte der Physik, 61(9), 781-811.
- Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Physical review letters, 49(14), 957.
- Baryon asymmetry. (2024, April 6). In Wikipedia. https://en.wikipedia.org/wiki/Baryon asymmetry.
- Abellán, Carlos, et al. "Challenging local realism with human choices." arXiv preprint arXiv:1805.04431 (2018).
- Braunstein, Samuel L., and Arun K. Pati. "Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox." Physical review letters 98.8 (2007): 080502.).
- Tsirel’son, B. S. (1987). Quantum analogs of the Bell inequalities. The case of two spatially separated domains. Journal of Soviet Mathematics, 36, 557-570.
- Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical review letters, 70(13), 1895.
- Kim, Y. H., Yu, R., Kulik, S. P., Shih, Y., & Scully, M. O. (2000). Delayed "choice" quantum eraser. Physical Review Letters, 84(1), 1.
- Van Raamsdonk, M. (2010). Building up spacetime with quantum entanglement. General Relativity and Gravitation, 42(10), 2323-2329.
- Bashar, M. A., Chowdhury, M. A., Islam, R., Rahman, M. S., and Das, S. K., "A Review and Prospects of Quantum Teleportation," 2009 International Conference on Computer and Automation Engineering, 2009, pp. 213-217. [CrossRef]
- Gisin, N., Ribordy, G., Tittel, W., Zbinden, H., Quantum cryptography. Reviews of modern physics, 74(1), 145, 2002.
Figure 1.
Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
Figure 1.
Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
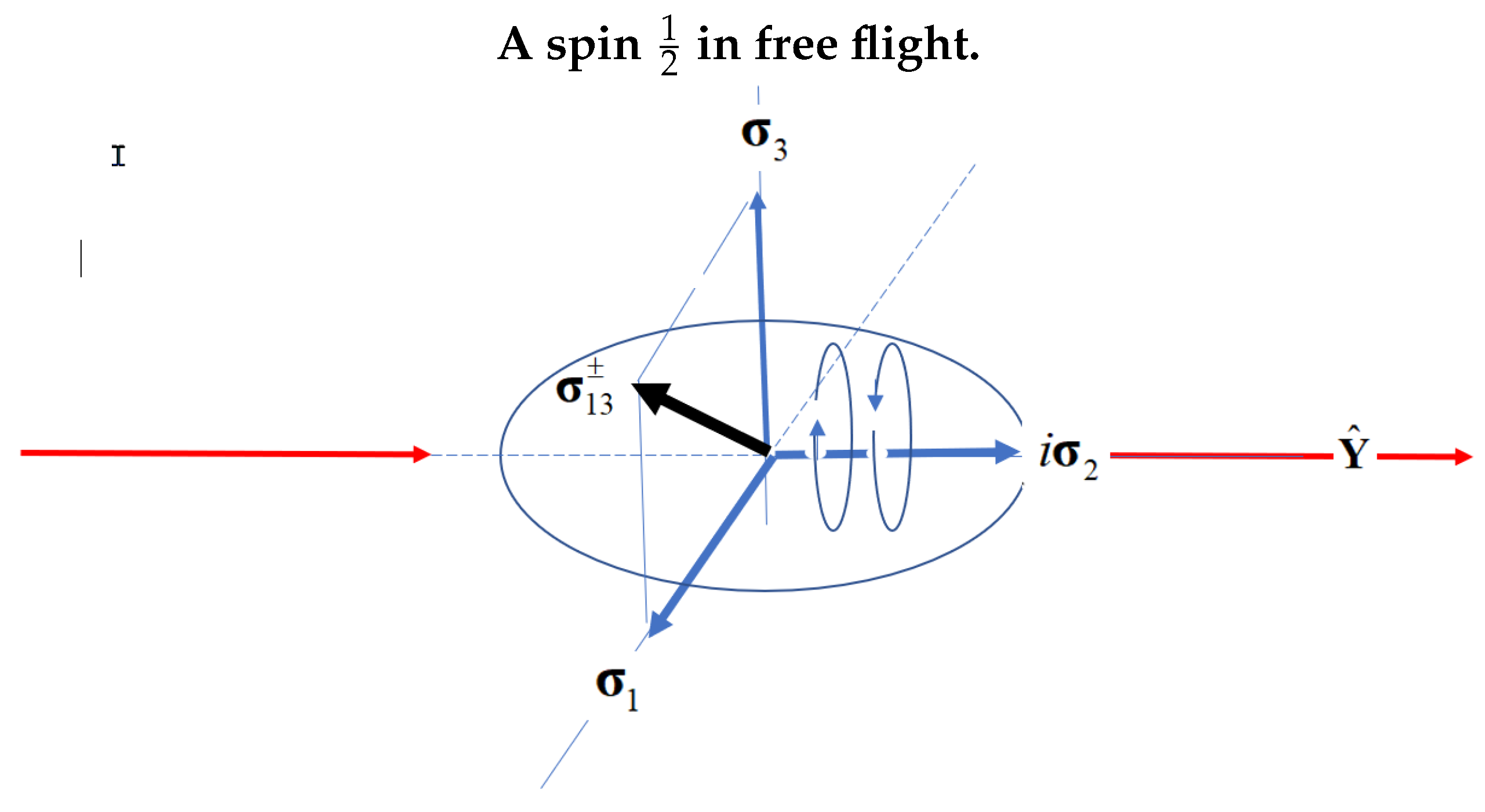
Figure 2.
The full correlation from quantum mechanics with CHSH = is decomposed into product states with CHSH = 2, and the difference between the two which gives the mustache function with CHSH = 0.828.
Figure 2.
The full correlation from quantum mechanics with CHSH = is decomposed into product states with CHSH = 2, and the difference between the two which gives the mustache function with CHSH = 0.828.
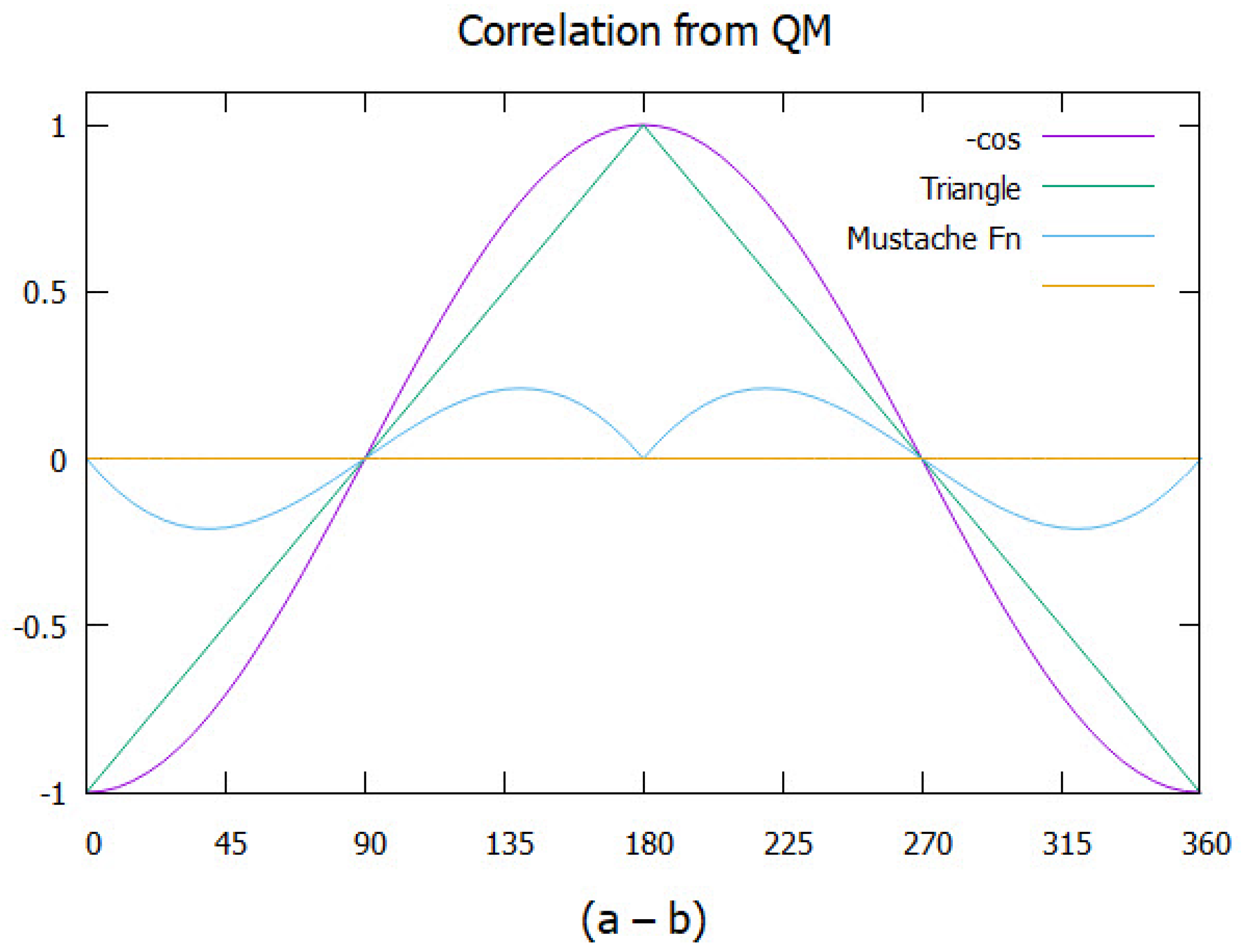
Figure 3.
The longer arrow denotes the direction of the polarizing field.
Middle top: The two mirror states in free flight, and , couple to give a boson spin-1.
Left and right: The fermionic axis closer to the field axis aligns, and the boson decouples. These two panels do not indicate two particles but one Q-spin depicted with one or the other axis aligned with the field.
Middle bottom: When the boson spin is close to the field, it initially precesses as a spin one without decoupling.
Figure 3.
The longer arrow denotes the direction of the polarizing field.
Middle top: The two mirror states in free flight, and , couple to give a boson spin-1.
Left and right: The fermionic axis closer to the field axis aligns, and the boson decouples. These two panels do not indicate two particles but one Q-spin depicted with one or the other axis aligned with the field.
Middle bottom: When the boson spin is close to the field, it initially precesses as a spin one without decoupling.
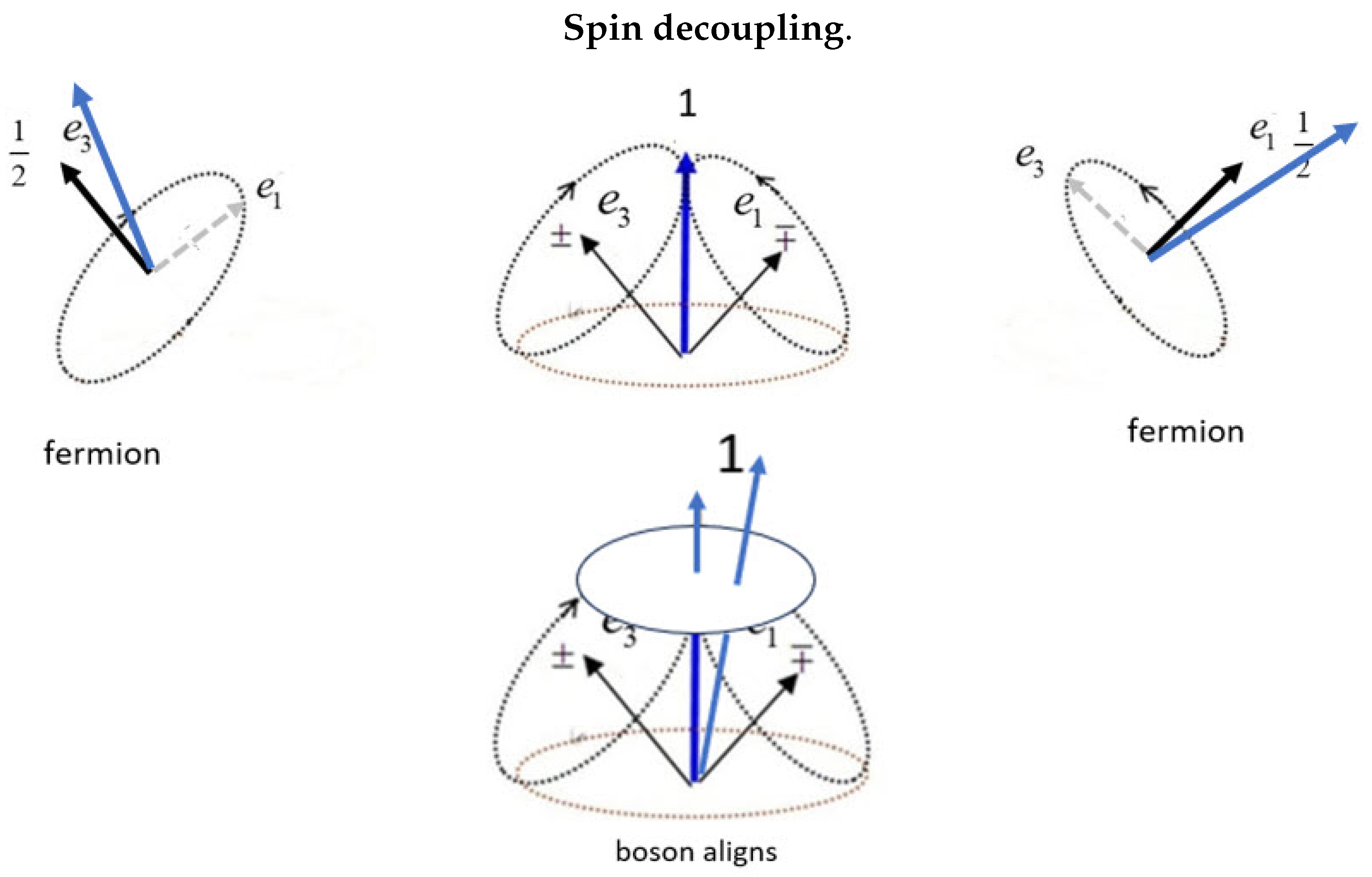
Figure 4.
Alice goes right in an RH coordinate frame, and Bob goes left in an LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. In the center figure, Alice and Bob start with the same but opposite orientation in the BFF indicated by .
Figure 4.
Alice goes right in an RH coordinate frame, and Bob goes left in an LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. In the center figure, Alice and Bob start with the same but opposite orientation in the BFF indicated by .
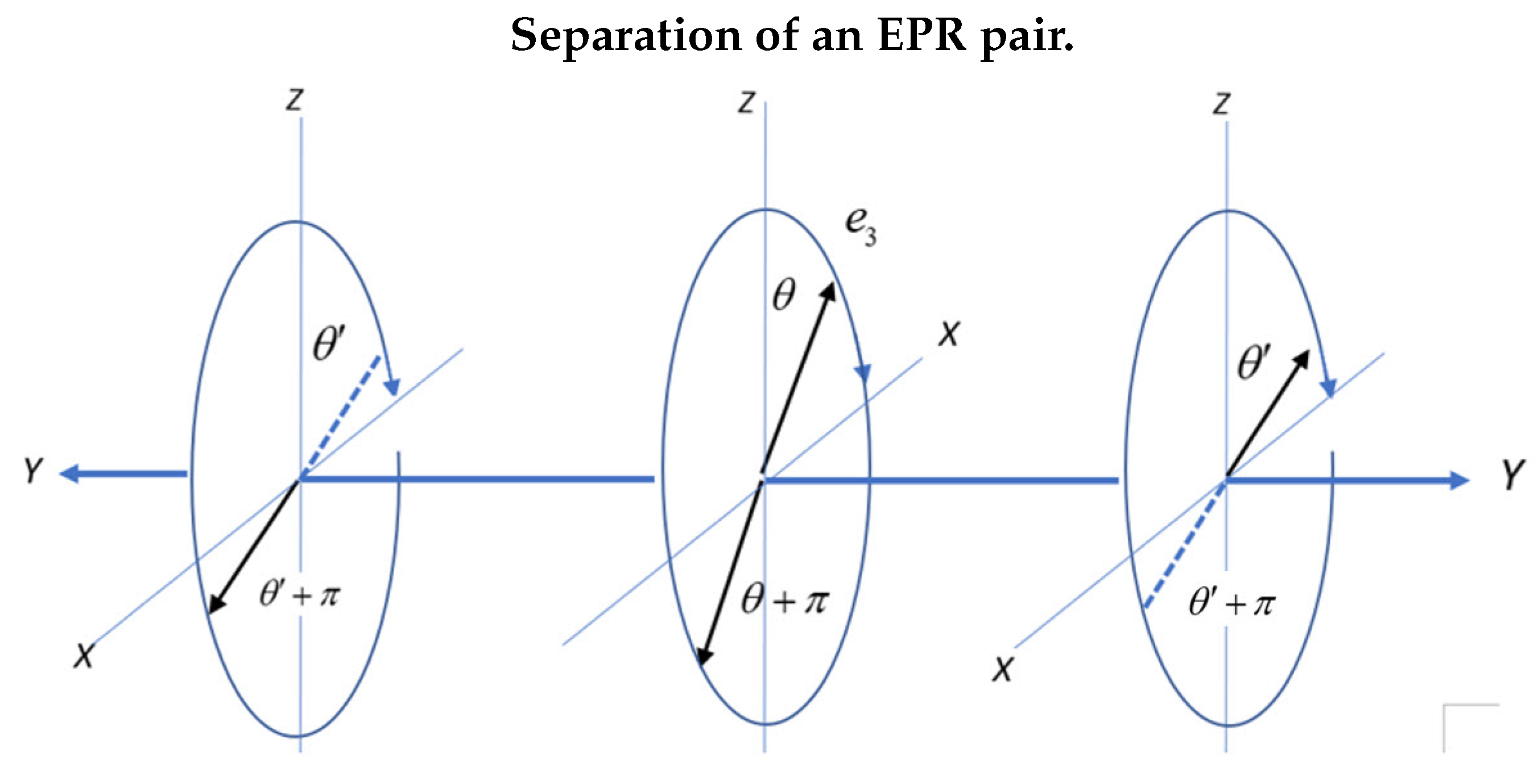
Figure 5.
Showing Alice and Bob’s spins by looking along their common axis of linear momentum, orthogonal to the screen. The heavy lines are possible filter settings in the LFF, XZ plane. Bob’s settings are or . Alice’s has settings of either , or . Also shown, bisecting two of the four 45o cones, are arrows labeled “1". These are the two antiparallel boson spins of Alice and Bob impinging on their filters. Within the two 45o wedges, Alice and Bob’s spins are bosons.
Figure 5.
Showing Alice and Bob’s spins by looking along their common axis of linear momentum, orthogonal to the screen. The heavy lines are possible filter settings in the LFF, XZ plane. Bob’s settings are or . Alice’s has settings of either , or . Also shown, bisecting two of the four 45o cones, are arrows labeled “1". These are the two antiparallel boson spins of Alice and Bob impinging on their filters. Within the two 45o wedges, Alice and Bob’s spins are bosons.
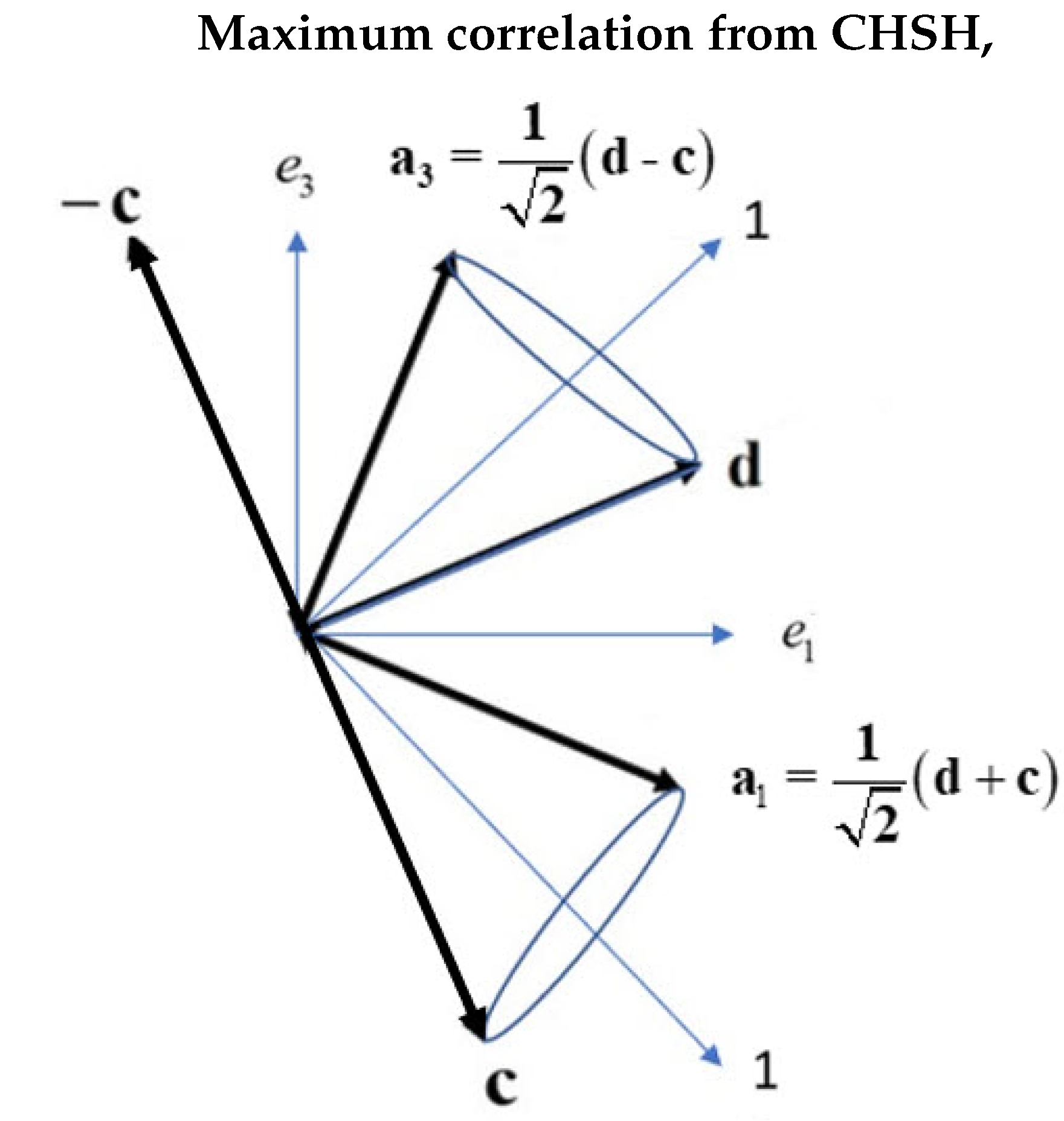
Figure 6.
Displaying the maximum correlation from coherence. Alice sets her filter to , and her boson spin of 1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at 45o from . Alternately, Alice can set her filter angle to , and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin of magnitude 1 precesses about its axis with an angle of 45o.
Figure 6.
Displaying the maximum correlation from coherence. Alice sets her filter to , and her boson spin of 1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at 45o from . Alternately, Alice can set her filter angle to , and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin of magnitude 1 precesses about its axis with an angle of 45o.
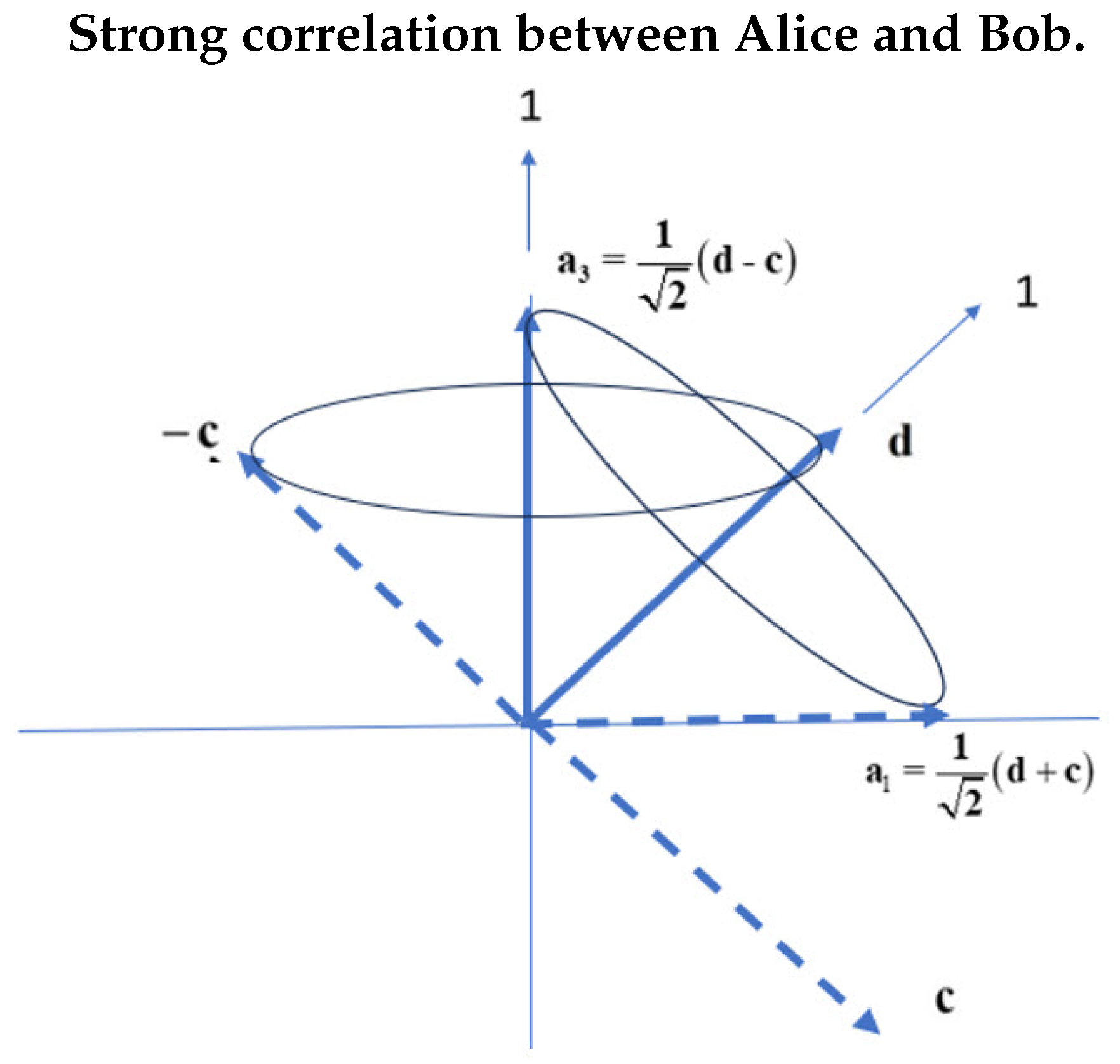
Figure 7.
Plotting EPR correlation versus the angle difference . The blue points give the results of the simulation. The CHSH values are listed and the full correlation is the sum of polarization, the triangle, and coherence, the mustache. Note the, hardly discernible, residual quaternion correlation along the horizontal axis.
Figure 7.
Plotting EPR correlation versus the angle difference . The blue points give the results of the simulation. The CHSH values are listed and the full correlation is the sum of polarization, the triangle, and coherence, the mustache. Note the, hardly discernible, residual quaternion correlation along the horizontal axis.
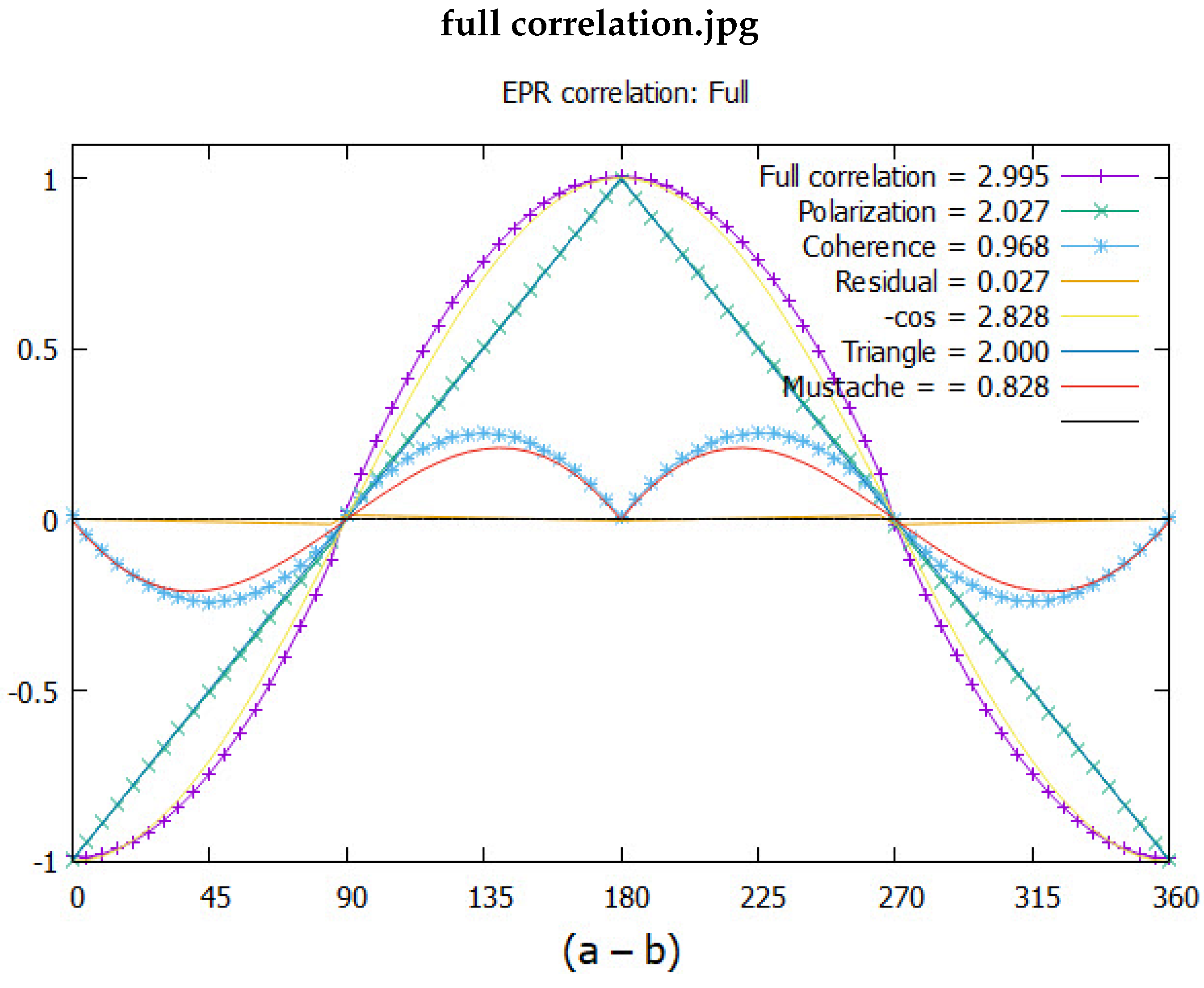
Figure 8.
A blow-up of the simulated polarization compared to an exact triangle. The insert shows it over 2.
Figure 8.
A blow-up of the simulated polarization compared to an exact triangle. The insert shows it over 2.
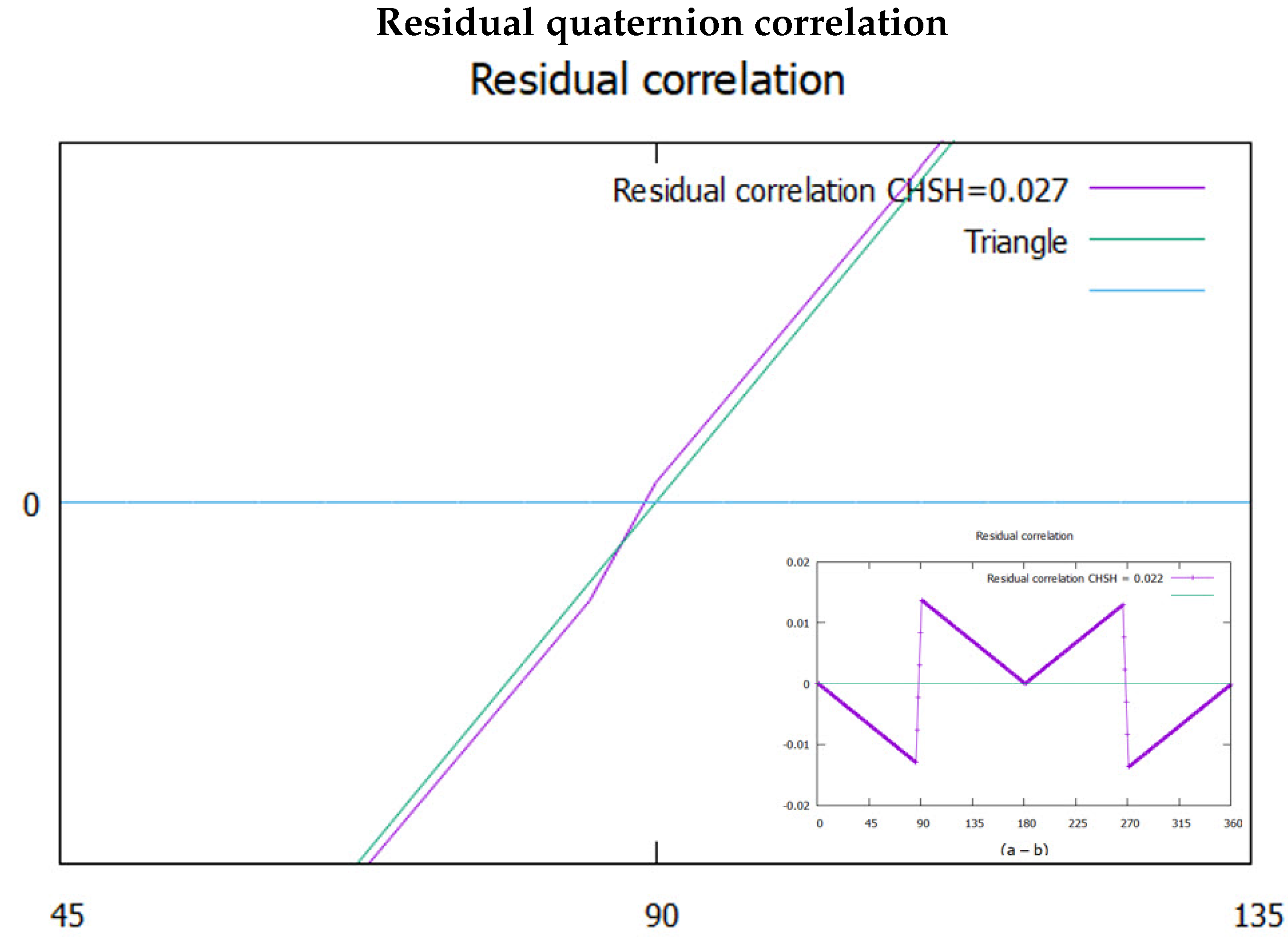
Figure 9.
The function given in Eq.(21) compared to the simulation. Also shown is the smaller correlation from quantum theory.
Figure 9.
The function given in Eq.(21) compared to the simulation. Also shown is the smaller correlation from quantum theory.
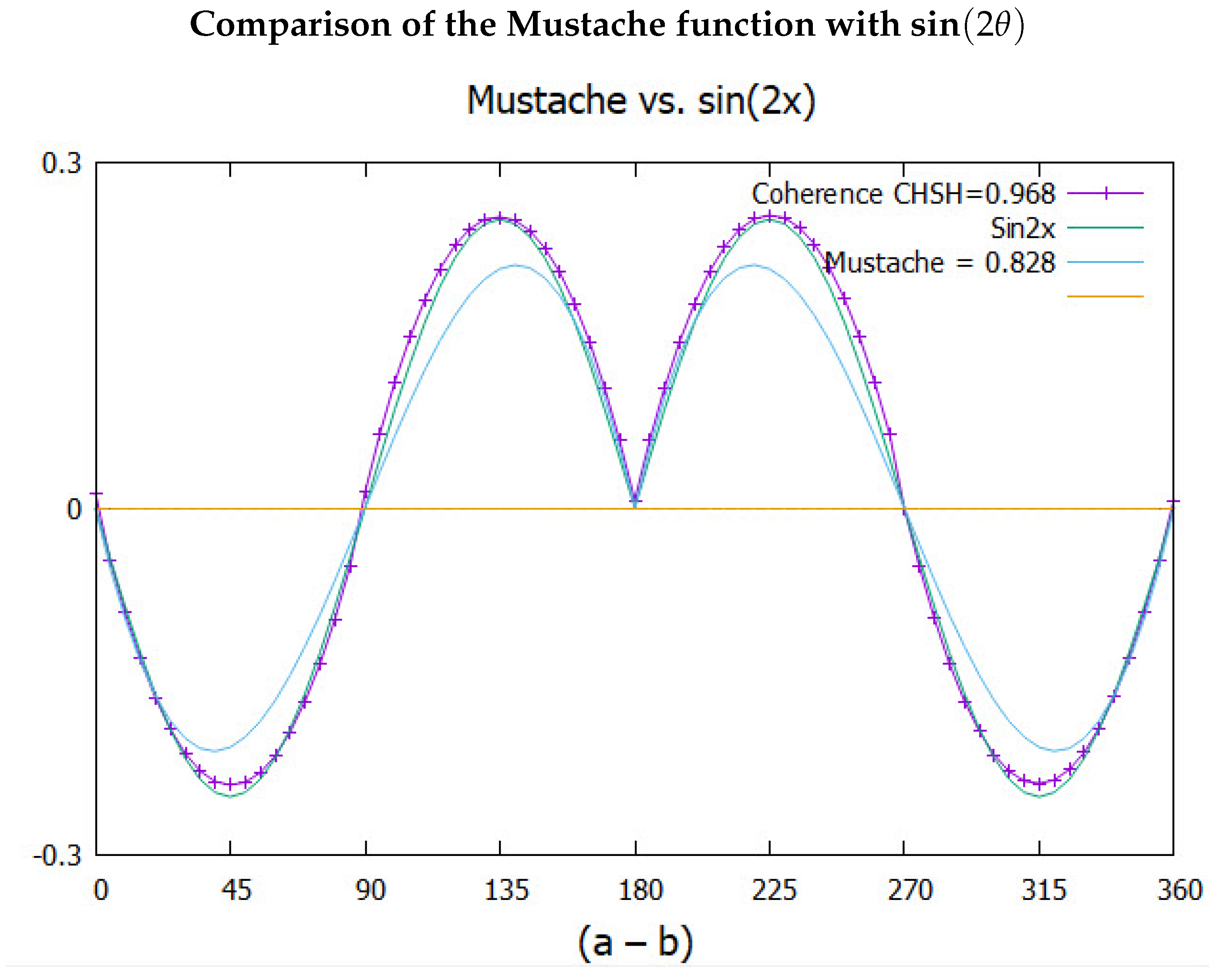
Figure 10.
Values of the CHSH inequalities from classical to Nature.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





