Prerpints.org logo
Preprint
Article

Spin Helicity

Altmetrics

Downloads

242

Views

164

Comments

0

This version is not peer-reviewed

Quantum Information and Quantum Computing

Submitted:

14 June 2024

Posted:

17 June 2024

You are already at the latest version

Alerts
Abstract
Under the quaternion group, $Q_8$, spin helicity emerges as an element of reality, and complementary to spin polarization. Here we show that the correlation in EPR coincidence experiments is conserved upon separation from a singlet, being divided between polarization and coherence. Including helicity accounts for the violation of Bell's Inequalities without non-locality.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

Introduction

Spin helicity, as defined in particle physics, [1], is the projection of spin along the axis of linear momentum, p · σ . If the helicity is positive, spin is in the state, + , n ^ , and if it is negative, the state is − , n ^ . Here n ^ in a unit vector on the Bloch sphere. We abandon this definition of helicity in this paper.
A significant difference between quantum and classical systems is that the former have complementary properties, like position and momentum, p , r − = − i ℏ where p = − i ℏ d d r whereas classical systems all commute. The complementary properties of spin polarization has not been formulated, see, however, [2], and here we find it to be the spin helicity.
By complementary, we mean that, in addition to not commuting, there exist distinct inverse or complementary spaces for the two properties. Position-momentum are represented in inverse Fourier spaces. That spin components do not commute, σ i , σ j − = 2 ε i j k i σ k , does not make σ i and σ j complementary because they belong to the same vector space. These two components are incompatible, not complementary.
The purpose of this paper is to define helicity as the coherent and complementary property to spin polarization. That is, helicity is an element of reality, [3]. We show that the correlation between two spins, initially in a singlet state, is divided between the polarization and coherence once they separate. The contribution from both violates Bell’s Inequalities (BI), [4,5] .
Upon separation we assume entanglement is lost under the assumption of locality. Nonetheless, the contribution to the correlation from helicity makes up for the loss due to dropping the entanglement.

The Singlet State and Separation

Our view of a singlet state is based upon the cancellation of polarization. Looking at the usual definition of the singlet, we express two generic states each for Alice and Bob, | ± 〉 i , by the up/down polarized states, and so the singlet state is constructed in the usual way
| Ψ 12 〉 = 1 2 | + 〉 1 | − 〉 2 − | − 〉 1 | + 〉 2
These states for each spin display orthogonalities: 〈 m | n 〉 = δ m n . By generic we mean that n ^ is not specified and any direction may emerge as long as it is the same for both Alice and Bob.
State vectors, like Eq.(1), do not display coherence, so taking its outer product of gives a 4 × 4 matrix which is the state operator, [6],
ρ 12 = Ψ 12 Ψ 12 = 1 4 I 1 I 2 − σ 1 · σ 2 = 1 2 0 0 0 0 0 1 − 1 0 0 − 1 1 0 0 0 0 0
The polarized states are diagonal, ± ± , and the coherent states are off-diagonal, ± ∓ , in the representation of Eq.(1). The resulting matrix is the entangled state, ρ 12 , and can be represented as the tensor product between the two identity matrices, I i and the scalar product between the two Pauli spin vectors. The off-diagonal coherent terms are responsible for the entanglement and preclude the product state. If those two coherent states are dropped, then the singlet state becomes a product state,
ρ ψ 12 − → off - diagonal drop ρ product 12 = ρ 1 + ρ 1 − + ρ 1 − ρ 2 + = 1 2 I 1 + σ Z 1 1 2 I 2 − σ Z 2 + 1 2 I 1 − σ Z 1 1 2 I 2 + σ Z 2 = 1 4 I 1 I 2 − σ Z 1 σ Z 2
According to Bell’s Theorem, [7], product states cannot account for the violation of BI. However, rather than assert this means that the violation is due to non-locality, here we find it is due to the dropped coherent terms (the two off-diagonal terms in Eq.(2)). The violation of BI is due entirely to the presence of correlation due to coherence, thereby obviating non-locality.
We define an EPR pair as the two particles that separate from a singlet state, and one moves to Alice and the other to Bob. We assume there is no entanglement between the two particles after separation.
To reflect the experimental configuration where the two filters are co-planar, we set ϕ a b = 0 , E a , b = − cos θ a b → ϕ a b = 0 − cos θ a − θ b , where E ( a , b ) represents the quantum correlation between EPR pairs.

The Local Singlet

The expectation value for the correlation is defined by the quantum trace over the operators, [8].
A B = Tr A † B ρ
where † is the operator adjoint. The correlation due to polarization of the spins between different filter settings is given by
E a , b = Tr 1 , 2 σ a 1 σ b 2 ρ 12 = a · σ 1 σ 2 · b
Remove the filter components a and b to focus on the expectation value only
σ 1 σ 2 = − 1 2 Tr 1 σ 1 σ 1 · 1 2 Tr 2 σ 2 σ 2 = − U ̲ ̲ · U ̲ ̲ = − U ̲ ̲
using,
1 2 Tr σ σ = 1 2 Tr σ X σ X X X + σ Y σ Y Y Y + σ Z σ Z Z Z = 1 2 Tr I X X + Y Y + Z Z = X X + Y Y + Z Z ≡ U ̲ ̲
Here U ̲ ̲ is the totally symmetric second rank tensor being the identity in 3D Cartesian space. Notice the antisymmetric contributions in the product, σ i σ j , i ≠ j , trace to zero, and are omitted.
We then find the usual result for the spin correlation from quantum mechanics,
E a , b = − a · U ̲ ̲ · b = − a · b = − cos θ a − θ b
which gives the maximum correlation from the singlet state. This calculation is done before the singlet separates into an EPR pair. The EPR paradox states that coincidence experiments, [5,9,10], show that the entangled state appears to remain intact over spacetime after separation. Bell’s Theorem concludes, [7], only non-local connectivity between Alice and Bob can explain the violation of BI. Here we show it is due to correlation between Alice and Bob’s helicities.
From Eq.(6), note the contraction between Alice and Bob. The only source of correlation between EPR pairs in this treatment is through this contraction. The two U ̲ ̲ ’s must share the same coordinate frame in order to be fully correlated. This frame is determined as the EPR pair separates, [11].

The Product State

Using Eq.(3) gives the correlation from the product states, (pol),
E pol a , b = a · Tr 1 , 2 σ 1 σ 2 ρ product 12 · b = − a · 1 2 Tr 1 σ 1 σ Z 1 1 2 Tr 2 σ 2 σ Z 2 · b = − a · Z Z · b = − cos θ a cos θ b
and this result can only satisfy, and not violate, BI.

The Source

As the particles leave the source, the filters and their settings, a and b , are far away and we do not need the quantum trace,
σ 1 σ 2 → remove trace σ 1 σ 1 · σ 2 σ 2
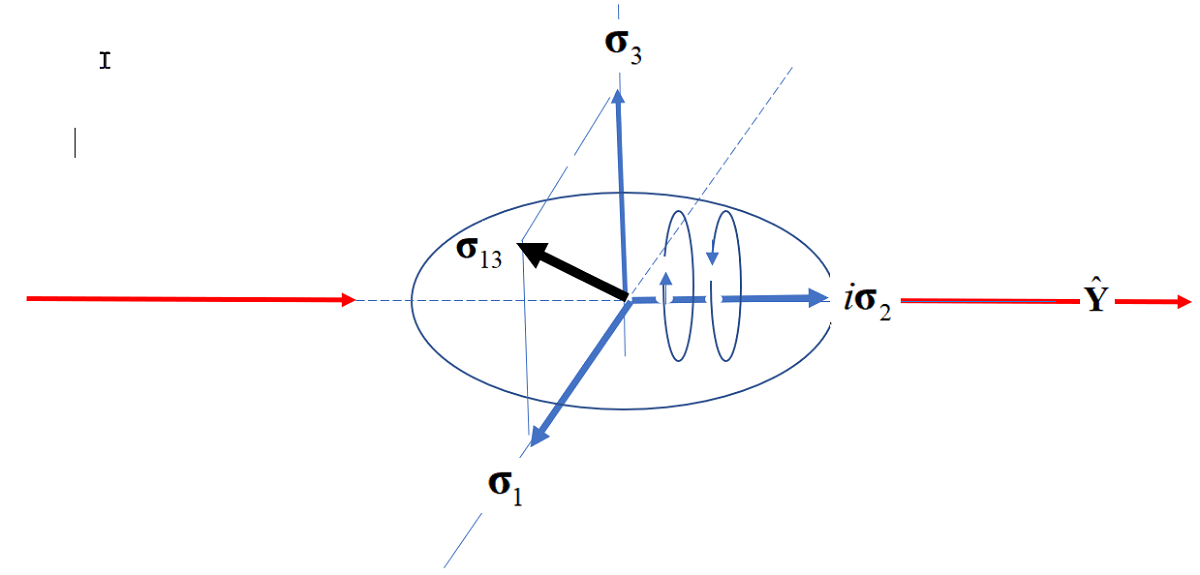
and the operator describing a spin in free flight is the dyadic, σ σ , see e , g . Eq.(6). This can be expressed using Geometric Algebra, [12] which for three-dimensional real space is
σ i σ j = δ i j + ε i j k i σ k
giving a bivector, and the three components of the Levi-Civita tensor, ε ̲ ̲ ̲ . The antisymmetric parts make no contribution to the spin polarization because they trace out, see, e.g. Eq.(7). To obtain those lost terms, we must find the correlation from the second term in Eq.(11), which is a bivector, i σ , and renders spin complex, [13,14].

The Helicity

We define the geometric helicity as a second rank operator by
h ̲ ̲ g ≡ ε ̲ ̲ ̲ · i σ
which is anti-Hermitian and rotates the plane perpendicular to the bivector, i σ . The helicity, h ̲ ̲ g , is antisymmetric, odd to parity, indicating helicity spins left or right. The correlation due to coherence (coh), in coincidence polarizing experiments is defined and given by
E a , b coh = a · h ̲ ̲ g 1 · h ̲ ̲ g 2 · b = − sin θ a sin θ b
That is,
E a , b coh = a · Tr 12 h ̲ ̲ g 1 † · h ̲ ̲ g 2 ρ product 12 · b = − a · ε ̲ ̲ ̲ · 1 2 Tr 1 σ 1 σ Z · b · ε ̲ ̲ ̲ · 1 2 Tr 2 σ 2 σ Z = − a · ε ̲ ̲ ̲ · 1 2 Tr 1 σ 1 σ 1 · Z · b · ε ̲ ̲ ̲ · 1 2 Tr 2 σ 2 σ 2 · Z = − a · ε ̲ ̲ ̲ · Z · b · ε ̲ ̲ ̲ · Z = − a × Z · b × Z = − sin θ a Y · Y sin θ b = − sin θ a sin θ b
where the three vectors, a , b , Z , are coplanar for ϕ a b = 0 . Assuming a and b lie in the Z X plane, then Y is the axis of linear momentum which is the same for both Alice and Bob.

The Conservation of Geometric Correlation

The correlation between two spins in a local singlet is:
E a , b = − a · U ̲ ̲ · b = − cos θ a − θ b
The correlation from a separated EPR pair arises from both the polarization of the spins and their coherent helicity,
E a , b = − a · Z Z · b − a × Z · b × Z = − cos θ a cos θ b − sin θ a sin θ b = − cos θ a − θ b
Correlation is preserved between the entangled local singlet and the product state of a separated EPR pair which can be expressed as being divided between the polarization and the coherence,
E a , b ︷ local = E a , b pol + E a , b coh ︷ separated
This articulates the Conservation of Geometric Correlation between an isotropic singlet and its EPR pair. There are several equivalent ways to express this, but its fundamental origin is the geometric product, Eq.(11). This result can also be generalized to n-tuples, [15] and correlation is always conserved.

Conclusions

Spin helicity is an anti-symmetric and anti-Hermitian bivector, Eq.(12), which is an element of reality of spin under quaternion symmetry, [2]. We suggest that spin is more fully defined by, σ → Σ which includes both the Pauli vector and bivector, and defines Q-spin,
Σ ≡ σ + h ̲ ̲ g
Contracting with a unit vector gives a unit quaternion, a · Σ . Spin processes become a product of quaternions and hence a rotation.
There is no bivector in the Dirac equation, however, it is shown elsewhere, [2], that one is easily introduced. The main requirement for the Dirac field is the gamma matrices must anticommute. Both ( γ 0 , γ 1 , γ 2 , γ 3 ) and ( γ s 0 , γ s 1 , i γ s 2 , γ s 3 ) satisfy this (the subscript “s" denotes spin spacetime). The Clifford algebra changes from the usual spacetime, C ℓ 1 , 3 , to C ℓ 2 , 2 , [2]. The latter algebra is isomorphic to quaternion algebra leading to the group, Q 8 . Dirac chose the former Clifford algebra, and here we have examined the latter, [2]. Following this, parity arguments lead to further separation of the C ℓ 2 , 2 into two complementary spaces: a 2D polarization spacetime, C ℓ 1 , 2 and the space of quaternions, H.
In free flight only helicity is manifest, [2], but when encountering a probe field, the helicity ceases and the usual polarized Dirac spin with two states emerges. Helicity, h ̲ ̲ g , and angular momentum, σ , are incompatible elements of reality. They epitomize the wave-particle duality of quantum theory.
Formulating spin this way, Eq.(12), makes spin complex, [13,14], and gives it the structure of a spinning disc of polarization. It has four states: the usual two states of up and down when measured; and two helicity states of L and R in free-flight. In contrast, the usual definition of helicity (as the projection of the spin vector onto the axis of linear momentum) is interpreted as giving the spin state of up and down. That is, helicity in particle physics is not independent of spin, whereas here the helicity and spin polarization are distinct.
It is our view that the only physically reasonable definition of entanglement restricts it to local situations. Stretching out entangled “EPR" channels, [16], to “connect" to a distant partner to account for correlation, rather than two partners knowing their right from left, is something Occam would have no difficulty with.
If one wishes to accept that spin always carries values of either ± 1 2 , as is assumed in the definition of qubits, and reject helicity, then non-locality appears to be the only alternative, [7].
However, the treatment here shows the violation of BI is not evidence for non-locality [17], but rather for local realism. Bell’s Theorem states that no classical system of real variables forming a single convex set, can exceed his inequalities, but his theorem is not applicable to complex complementary quantum variables with two convex sets.
These ideas are supported by a computer simulation, [11], which brings out additional features and properties of quaternion spin.

References

  1. Griffiths, David (2009). Introduction to Elementary Particles. pp. 59–60. ISBN 978-3-527-40601-2.
  2. Sanctuary,B.QuaternionSpin.Preprints2024,2023020055. [CrossRef]
  3. Einstein, Albert, Boris Podolsky, and Nathan Rosen. “Can quantum-mechanical description of physical reality be considered complete?.” Physical review 47.10 (1935): 777.
  4. Bell, John S. “On the Einstein Podolsky Rosen paradox." Physics Physique Fizika 1.3 (1964): 195.
  5. Clauser, J. F., Horne, M. A., Shimony, A., Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880.
  6. Fano, Ugo. “Description of states in quantum mechanics by density matrix and operator techniques." Reviews of modern physics 29.1 (1957): 74.
  7. Bell, J. S. (2004). p. 139 or 147, Speakable and unspeakable in quantum mechanics: Collected papers on quantum philosophy. Cambridge university press.
  8. Von Neumann, John. Mathematical foundations of quantum mechanics. Princeton university press, 1955.
  9. Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951.
  10. Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
  11. Sanctuary,B.C.,Non-localEPRCorrelationsusingQuaternionSpin.Preprints2023,2023010570. [CrossRef]
  12. Doran, C., Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
  13. Penrose, Roger. “Twistor algebra." Journal of Mathematical physics 8.2 (1967): 345-366.
  14. Penrose, Roger. “Solutions of the Zero-Rest-Mass Equations." Journal of mathematical Physics 10.1 (1969): 38-39.
  15. Sanctuary,B.C.(1976).Multipole operators for anarbitrary number of spins. The Journal of Chemical Physics, 64(11),4352-4361.
  16. Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical review letters, 70(13), 1895.
  17. Big Bell Test Collaboration. “Challenging local realism with human choices." Nature 557.7704 (2018): 212-216.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated