Duality Principles and Numerical Procedures for a Large Class of Non-convex Models in the Calculus of Variations

Preprint

Article

Duality Principles and Numerical Procedures for a Large Class of Non-convex Models in the Calculus of Variations

Altmetrics

Downloads

4092

Views

3880

Comments

Fabio Botelho^*

This version is not peer-reviewed

Submitted:

19 June 2023

Posted:

19 June 2023

Read the latest preprint version here

Alerts

Abstract

This article develops duality principles and numerical results for a large class of non-convex variational models. The main results are based on fundamental tools of convex analysis, duality theory and calculus of variations. More specifically the approach is established for a class of non-convex functionals similar as those found in some models in phase transition. Finally, in the last section we present a concerning numerical example and the respective software.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 49N15

1. Introduction

In this section we establish a dual formulation for a large class of models in non-convex optimization.

The main duality principle is applied to double well models similar as those found in the phase transition theory.

Such results are based on the works of J.J. Telega and W.R. Bielski [2,3,15,16] and on a D.C. optimization approach developed in Toland [17].

About the other references, details on the Sobolev spaces involved are found in [1]. Related results on convex analysis and duality theory are addressed in [5,7,8,10,14].

Finally, in this text we adopt the standard Einstein convention of summing up repeated indices, unless otherwise indicated.

In order to clarify the notation, here we introduce the definition of topological dual space.

Definition 1.1

(Topological dual spaces). Let U be a Banach space. We shall define its dual topological space, as the set of all linear continuous functionals defined on U. We suppose such a dual space of U, may be represented by another Banach space

U^{*}

, through a bilinear form

{〈 \cdot, \cdot 〉}_{U} : U \times U^{*} \to R

(here we are referring to standard representations of dual spaces of Sobolev and Lebesgue spaces). Thus, given

f : U \to R

linear and continuous, we assume the existence of a unique

u^{*} \in U^{*}

such that

\begin{matrix} f (u) = {〈 u, u^{*} 〉}_{U}, \forall u \in U . \end{matrix}

(1)

The norm of f , denoted by

{∥ f ∥}_{U^{*}}

, is defined as

\begin{matrix} {∥ f ∥}_{U^{*}} = sup_{u \in U} {| {〈 u, u^{*} 〉}_{U} {| : ∥ u ∥}_{U} \leq 1} \equiv ∥ u^{*} ∥_{U^{*}} . \end{matrix}

(2)

At this point we start to describe the primal and dual variational formulations.

2. A general duality principle non-convex optimization

In this section we present a duality principle applicable to a model in phase transition.

This case corresponds to the vectorial one in the calculus of variations.

Let

Ω \subset R^{n}

be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω .

Consider a functional

J : V \to R

where

J (u) = F (\nabla u_{1}, \dots, \nabla u_{N}) + G (u_{1}, \dots, u_{N}) - {〈 u_{i}, f_{i} 〉}_{L^{2}},

and where

V = {u = (u_{1}, \dots, u_{N}) \in W^{1, p} (Ω; R^{N}) : u = u_{0} on \partial Ω},

f \in L^{2} (Ω; R^{N}),

and

1 < p < + \infty .

We assume there exists

α \in R

such that

α = inf_{u \in V} J (u) .

Moreover, suppose F and G are Fréchet differentiable but not necessarily convex. A global optimum point may not be attained for J so that the problem of finding a global minimum for J may not be a solution.

Anyway, one question remains, how the minimizing sequences behave close the infimum of J.

We intend to use duality theory to approximately solve such a global optimization problem.

Denoting

V_{0} = W_{0}^{1, p} (Ω; R^{N})

Y_{1} = Y_{1}^{*} = L^{2} (Ω; R^{N \times n})

Y_{2} = Y_{2}^{*} = L^{2} (Ω; R^{N \times n})

Y_{3} = Y_{3}^{*} = L^{2} (Ω; R^{N}),

at this point we define,

F_{1} : V \times V_{0} \to R

G_{1} : V \to R

G_{2} : V \to R

G_{3} : V_{0} \to R

and

G_{4} : V \to R,

\begin{matrix} F_{1} (\nabla u, \nabla ϕ) & = & F (\nabla u_{1} + \nabla ϕ_{1}, \dots, \nabla u_{N} + \nabla ϕ_{N}) + \frac{K}{2} \int_{Ω} \nabla u_{j} \cdot \nabla u_{j} d x \\ + \frac{K_{2}}{2} \int_{Ω} \nabla ϕ_{j} \cdot \nabla ϕ_{j} d x \end{matrix}

(3)

and

G_{1} (u_{1}, \dots, u_{n}) = G (u_{1}, \dots, u_{N}) + \frac{K_{1}}{2} \int_{Ω} u_{j} u_{j} d x - {〈 u_{i}, f_{i} 〉}_{L^{2}},

G_{2} (\nabla u_{1}, \dots, \nabla u_{N}) = \frac{K_{1}}{2} \int_{Ω} \nabla u_{j} \cdot \nabla u_{j} d x,

G_{3} (\nabla ϕ_{1}, \dots, \nabla ϕ_{N}) = \frac{K_{2}}{2} \int_{Ω} \nabla ϕ_{j} \cdot \nabla ϕ_{j} d x,

and

G_{4} (u_{1}, \dots, u_{N}) = \frac{K_{1}}{2} \int_{Ω} u_{j} u_{j} d x .

Define now

J_{1} : V \times V_{0} \to R

J_{1} (u, ϕ) = F (\nabla u + \nabla ϕ) + G (u) - {〈 u_{i}, f_{i} 〉}_{L^{2}} .

Observe that

\begin{matrix} J_{1} (u, ϕ) & = & F_{1} (\nabla u, \nabla ϕ) + G_{1} (u) - G_{2} (\nabla u) - G_{3} (\nabla ϕ) - G_{4} (u) \\ \leq & F_{1} (\nabla u, \nabla ϕ) + G_{1} (u) - {〈 \nabla u, z_{1}^{*} 〉}_{L^{2}} - {〈 \nabla ϕ, z_{2}^{*} 〉}_{L^{2}} - {〈 u, z_{3}^{*} 〉}_{L^{2}} \\ + sup_{v_{1} \in Y_{1}} {{〈 v_{1}, z_{1}^{*} 〉}_{L^{2}} - G_{2} (v_{1})} \\ + sup_{v_{2} \in Y_{2}} {{〈 v_{2}, z_{2}^{*} 〉}_{L^{2}} - G_{3} (v_{2})} \\ + sup_{u \in V} {{〈 u, z_{3}^{*} 〉}_{L^{2}} - G_{4} (u)} \\ = & F_{1} (\nabla u, \nabla ϕ) + G_{1} (u) - {〈 \nabla u, z_{1}^{*} 〉}_{L^{2}} - {〈 \nabla ϕ, z_{2}^{*} 〉}_{L^{2}} - {〈 u, z_{3}^{*} 〉}_{L^{2}} \\ + G_{2}^{*} (z_{1}^{*}) + G_{3}^{*} (z_{2}^{*}) + G_{4}^{*} (z_{3}^{*}) \\ = & J_{1}^{*} (u, ϕ, z^{*}), \end{matrix}

(4)

\forall u \in V, ϕ \in V_{0}, z^{*} = (z_{1}^{*}, z_{2}^{*}, z_{3}^{*}) \in Y^{*} = Y_{1}^{*} \times Y_{2}^{*} \times Y_{3}^{*}

Here we assume

K, K_{1}, K_{2}

are large enough so that

F_{1}

and

G_{1}

are convex.

Hence, from the general results in [17], we may infer that

\begin{matrix} inf_{(u, ϕ) \in V \times V_{0}} J (u, ϕ) & = & inf_{(u, ϕ, z^{*}) \in V \times V_{0} \times Y^{*}} J_{1}^{*} (u, ϕ, z^{*}) . \end{matrix}

(5)

On the other hand

inf_{u \in V} J (u) \geq inf_{(u, ϕ) \in V \times V_{0}} J_{1} (u, ϕ) \geq inf_{u \in V} Q_{J} (u) = inf_{u \in V} J (u),

where

Q_{J} (u)

refers to a standard quasi-convex regularization of J.

From these last two results we may obtain

inf_{u \in V} J (u) = inf_{(u, ϕ, z^{*}) \in V \times V_{0} \times Y^{*}} J_{1}^{*} (u, ϕ, z^{*}) .

Moreover, from standards results on convex analysis, we may have

\begin{matrix} inf_{u \in V} J_{1}^{*} (u, ϕ, z^{*}) & = & inf_{u \in V} {F_{1} (\nabla u, \nabla ϕ) + G_{1} (u) \\ - {〈 \nabla u, z_{1}^{*} 〉}_{L^{2}} - {〈 \nabla ϕ, z_{2}^{*} 〉}_{L^{2}} - {〈 u, z_{3}^{*} 〉}_{L^{2}} \\ + G_{2}^{*} (z_{1}^{*}) + G_{3}^{*} (z_{2}^{*}) + G_{4}^{*} (z_{3}^{*})} \\ = & sup_{(v_{1}^{*}, v_{2}^{*}) \in C^{*}} {- F_{1}^{*} (v_{1}^{*} + z_{1}^{*}, \nabla ϕ) - G_{1}^{*} (v_{2}^{*} + z_{3}^{*}) - {〈 \nabla ϕ, z_{2}^{*} 〉}_{L^{2}} \\ + G_{2}^{*} (z_{1}^{*}) + G_{3}^{*} (z_{2}^{*}) + G_{4}^{*} (z_{3}^{*})}, \end{matrix}

(6)

where

C^{*} = {v^{*} = (v_{1}^{*}, v_{2}^{*}) \in Y_{1}^{*} \times Y_{3}^{*} : - div {(v_{1}^{*})}_{i} + {(v_{2}^{*})}_{i} = 0, \forall i \in {1, \dots, N}},

F_{1}^{*} (v_{1}^{*} + z_{1}^{*}, \nabla ϕ) = sup_{v_{1} \in Y_{1}} {{〈 v_{1}, z_{1}^{*} + v_{1}^{*} 〉}_{L^{2}} - F_{1} (v_{1}, \nabla ϕ)},

and

G_{1}^{*} (v_{2}^{*} + z_{2}^{*}) = sup_{u \in V} {{〈 u, v_{2}^{*} + z_{2}^{*} 〉}_{L^{2}} - G_{1} (u)} .

Thus, defining

J_{2}^{*} (ϕ, z^{*}, v^{*}) = F_{1}^{*} (v_{1}^{*} + z_{1}^{*}, \nabla ϕ) - G_{1}^{*} (v_{2}^{*} + z_{3}^{*}) - {〈 \nabla ϕ, z_{2}^{*} 〉}_{L^{2}} + G_{2}^{*} (z_{1}^{*}) + G_{3}^{*} (z_{2}^{*}) + G_{4}^{*} (z_{3}^{*}),

we have got

\begin{matrix} inf_{u \in V} J (u) & = & inf_{(u, ϕ) \in V \times V_{0}} J_{1} (u, ϕ) \\ = & inf_{(u, ϕ, z^{*}) \in V \times V_{0} \times Y^{*}} J_{1}^{*} (u, ϕ, z^{*}) \\ = & inf_{z^{*} \in Y^{*}} \{inf_{ϕ \in V_{0}} \{sup_{v^{*} \in C^{*}} J_{2}^{*} (ϕ, z^{*}, v^{*})\}\} . \end{matrix}

(7)

Finally, observe that

\begin{matrix} inf_{u \in V} J (u) \\ = & inf_{z^{*} \in Y^{*}} \{inf_{ϕ \in V_{0}} \{sup_{v^{*} \in C^{*}} J_{2}^{*} (ϕ, z^{*}, v^{*})\}\} \\ \geq & sup_{v^{*} \in C^{*}} \{inf_{(z^{*}, ϕ) \in Y^{*} \times V_{0}} J_{2}^{*} (ϕ, z^{*}, v^{*})\} . \end{matrix}

(8)

This last variational formulation corresponds to a concave relaxed formulation in

v^{*}

concerning the original primal formulation.

3. Another duality principle for a simpler related model in phase transition with a respective numerical example

In this section we present another duality principle for a related model in phase transition.

Let

Ω = [0, 1] \subset R

and consider a functional

J : V \to R

where

J (u) = \frac{1}{2} \int_{Ω} {({(u^{'})}^{2} - 1)}^{2} d x + \frac{1}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}},

and where

V = {u \in W^{1, 4} (Ω) : u (0) = 0 and u (1) = 1 / 2}

and

f \in L^{2} (Ω) .

A global optimum point is not attained for J so that the problem of finding a global minimum for J has no solution.

Anyway, one question remains, how the minimizing sequences behave close the infimum of J.

We intend to use duality theory to approximately solve such a global optimization problem.

Denoting

V_{0} = W_{0}^{1, 4} (Ω)

, at this point we define,

F : V \to R

and

F_{1} : V \times V_{0} \to R

F (u) = \frac{1}{2} \int_{Ω} {({(u^{'})}^{2} - 1)}^{2} d x,

and

F_{1} (u, ϕ) = \frac{1}{2} \int_{Ω} {({(u^{'} + ϕ^{'})}^{2} - 1)}^{2} d x .

Observe

F (u) \geq inf_{ϕ \in V_{0}} F_{1} (u, ϕ) \geq Q_{F} (u), \forall u \in V,

where

Q_{F} (u)

refers to a quasi-convex regularization of

F .

We define also

F_{2} : V \times V_{0} \to R,

F_{3} : V \times V_{0} \to R

and

G : V \times V_{0} \to R

F_{2} (u, ϕ) = \frac{1}{2} \int_{Ω} {({(u^{'} + ϕ^{'})}^{2} - 1)}^{2} d x + \frac{1}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}},

\begin{matrix} F_{3} (u, ϕ) & = & F_{2} (u, ϕ) + \frac{K}{2} \int_{Ω} {(u^{'})}^{2} d x \\ + \frac{K_{1}}{2} \int_{Ω} {(ϕ^{'})}^{2} d x \end{matrix}

(9)

and

\begin{matrix} G (u, ϕ) & = & \frac{K}{2} \int_{Ω} {(u^{'})}^{2} d x \\ + \frac{K_{1}}{2} \int_{Ω} {(ϕ^{'})}^{2} d x \end{matrix}

(10)

Observe that if

K > 0, K_{1} > 0

is large enough, both

F_{3}

and G are convex.

Denoting

Y = Y^{*} = L^{2} (Ω)

we also define the polar functional

G^{*} : Y^{*} \times Y^{*} \to R

G^{*} (v^{*}, v_{0}^{*}) = sup_{(u, ϕ) \in V \times V_{0}} {{〈 u, v^{*} 〉}_{L^{2}} + {〈 ϕ, v_{0}^{*} 〉}_{L^{2}} - G (u, ϕ)} .

Observe that

inf_{u \in U} J (u) \geq inf_{((u, ϕ), (v^{*}, v_{0}^{*})) \in V \times V_{0} \times {[Y^{*}]}^{2}} {G^{*} (v^{*}, v_{0}^{*}) - {〈 u, v^{*} 〉}_{L^{2}} - {〈 ϕ, v_{0}^{*} 〉}_{L^{2}} + F_{3} (u, ϕ)} .

With such results in mind, we define a relaxed primal dual variational formulation for the primal problem, represented by

J_{1}^{*} : V \times V_{0} \times {[Y^{*}]}^{2} \to R

, where

J_{1}^{*} (u, ϕ, v^{*}, v_{0}^{*}) = G^{*} (v^{*}, v_{0}^{*}) - {〈 u, v^{*} 〉}_{L^{2}} - {〈 ϕ, v_{0}^{*} 〉}_{L^{2}} + F_{3} (u, ϕ) .

Having defined such a functional, we may obtain numerical results by solving a sequence of convex auxiliary sub-problems, through the following algorithm.

1.: Set $K \approx 150$ and $K_{1} = K / 20$ and $0 < ε ≪ 1 .$
2.: Choose $(u_{1}, ϕ_{1}) \in V \times V_{0},$ such that $∥ u_{1} ∥_{1, \infty} ≪ K / 4$ and $∥ ϕ_{1} ∥_{1, \infty} ≪ K / 4 .$
3.: Set $n = 1 .$
4.: Calculate $(v_{n}^{*}, {(v_{0}^{*})}_{n})$ solution of the system of equations:

$\frac{\partial J_{1}^{*} (u_{n}, ϕ_{n}, v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial v^{*}} = 0$

and

$\frac{\partial J_{1}^{*} (u_{n}, ϕ_{n}, v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial v_{0}^{*}} = 0,$

that is

$\frac{\partial G^{*} (v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial v^{*}} - u_{n} = 0$

and

$\frac{\partial G^{*} (v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial v_{0}^{*}} - ϕ_{n} = 0$

so that

$v_{n}^{*} = \frac{\partial G (u_{n}, ϕ_{n})}{\partial u}$

and

${(v_{0}^{*})}_{n}^{*} = \frac{\partial G (u_{n}, ϕ_{n})}{\partial ϕ}$
5.: Calculate $(u_{n + 1}, ϕ_{n + 1})$ by solving the system of equations:

$\frac{\partial J_{1}^{*} (u_{n + 1}, ϕ_{n + 1}, v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial u} = 0$

and

$\frac{\partial J_{1}^{*} (u_{n + 1}, ϕ_{n + 1}, v_{n}^{*}, {(v_{0}^{*})}_{n})}{\partial ϕ} = 0$

that is

$- v_{n}^{*} + \frac{\partial F_{3} (u_{n + 1}, ϕ_{n + 1})}{\partial u} = 0$

and

$- {(v_{0}^{*})}_{n} + \frac{\partial F_{3} (u_{n + 1}, ϕ_{n + 1})}{\partial ϕ} = 0$
6.: If $max {∥ u_{n} - u_{n + 1} ∥_{\infty}, ∥ ϕ_{n + 1} - ϕ_{n} ∥_{\infty}} \leq ε$ , then stop, else set $n : = n + 1$ and go to item 4.

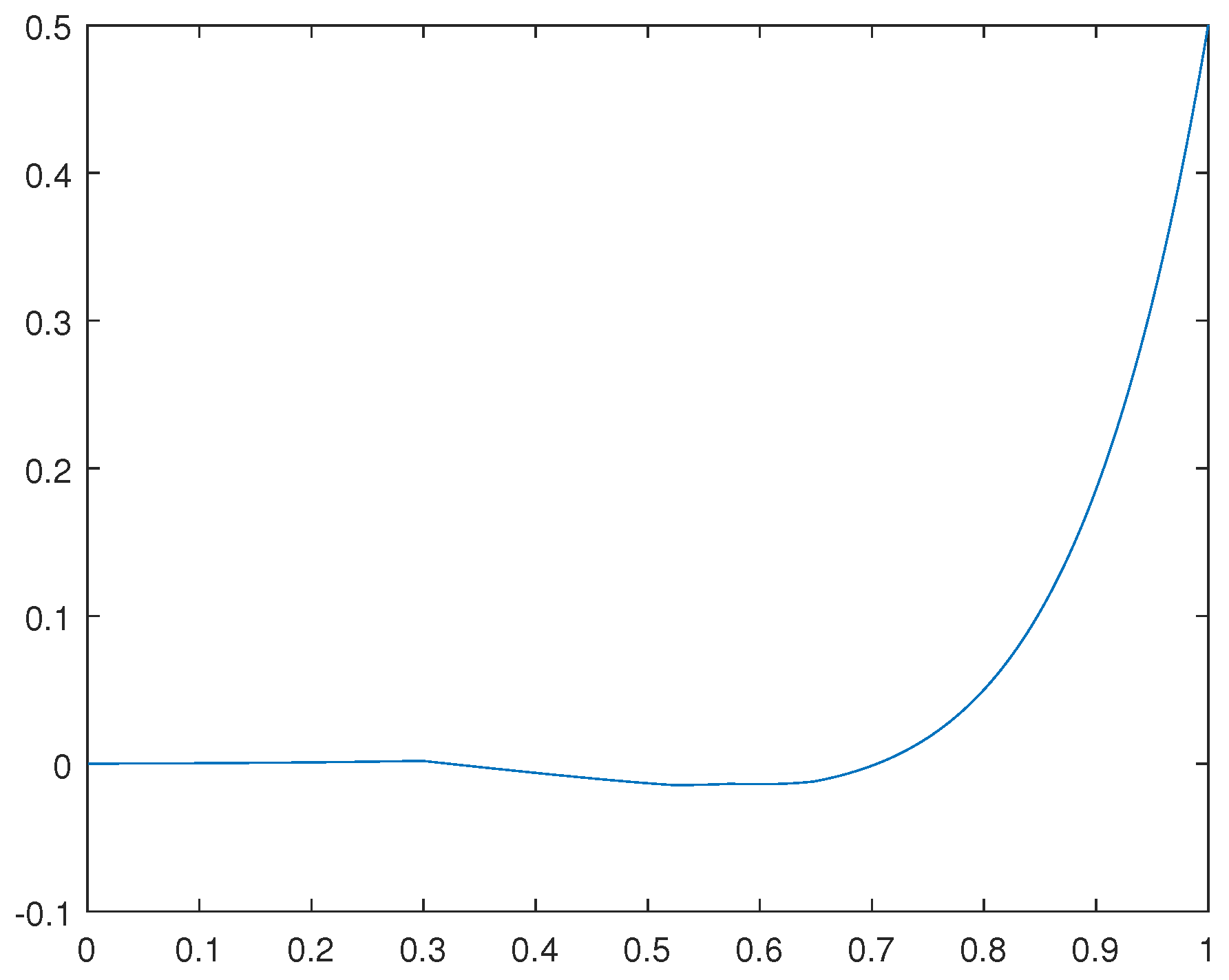
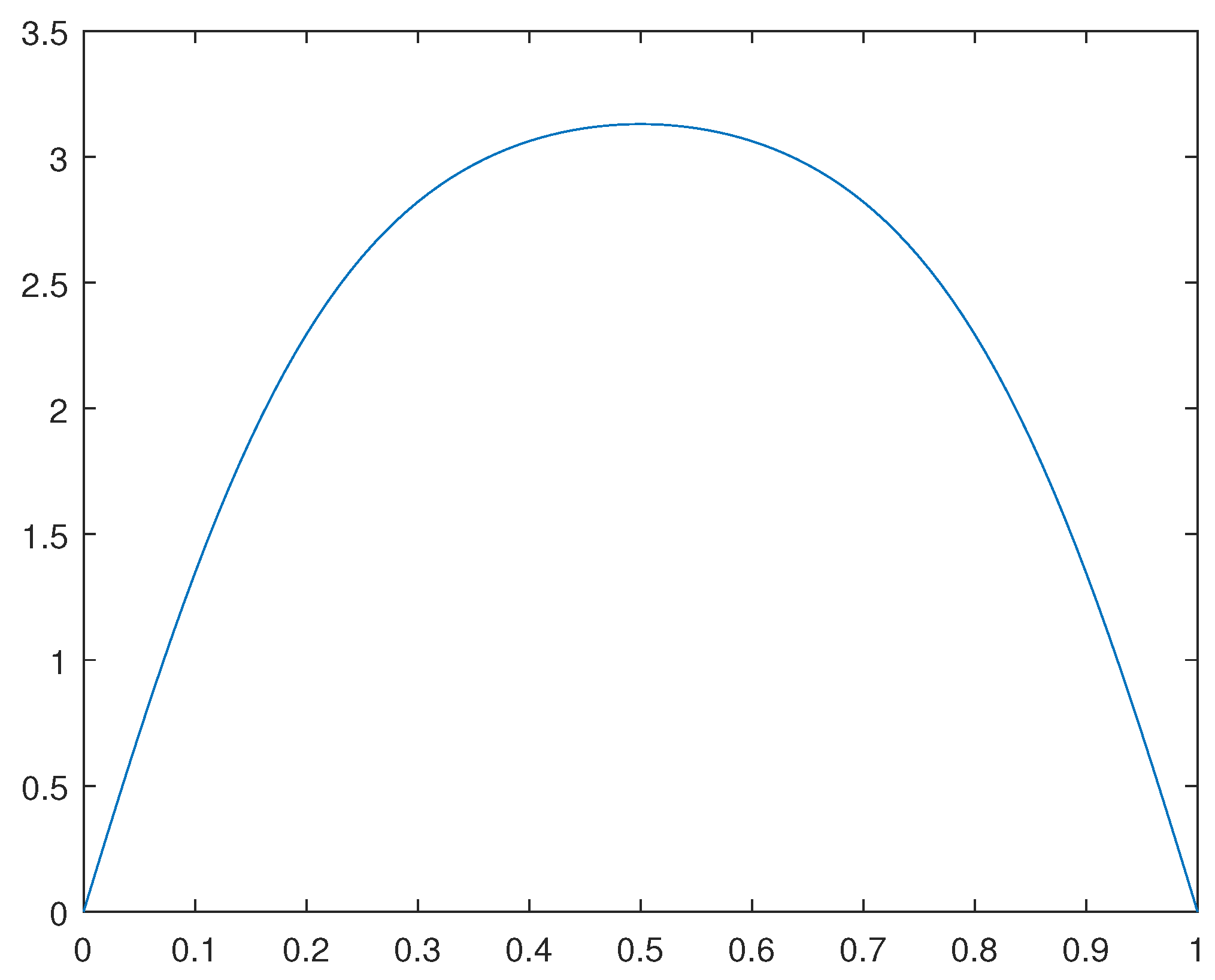
For the case in which

f (x) = 0

, we have obtained numerical results for

K = 1500

and

K_{1} = K / 20

. For such a concerning solution

u_{0}

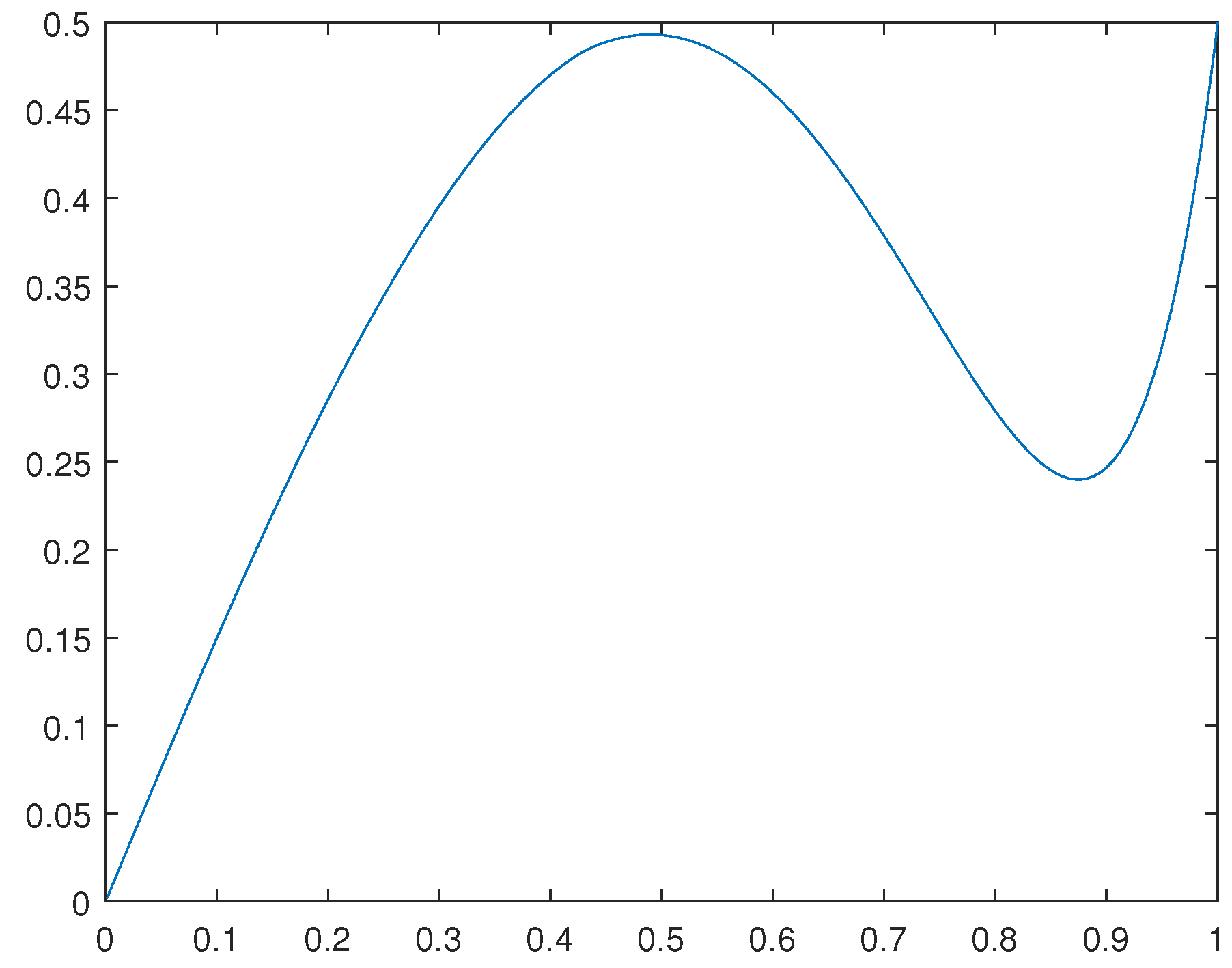
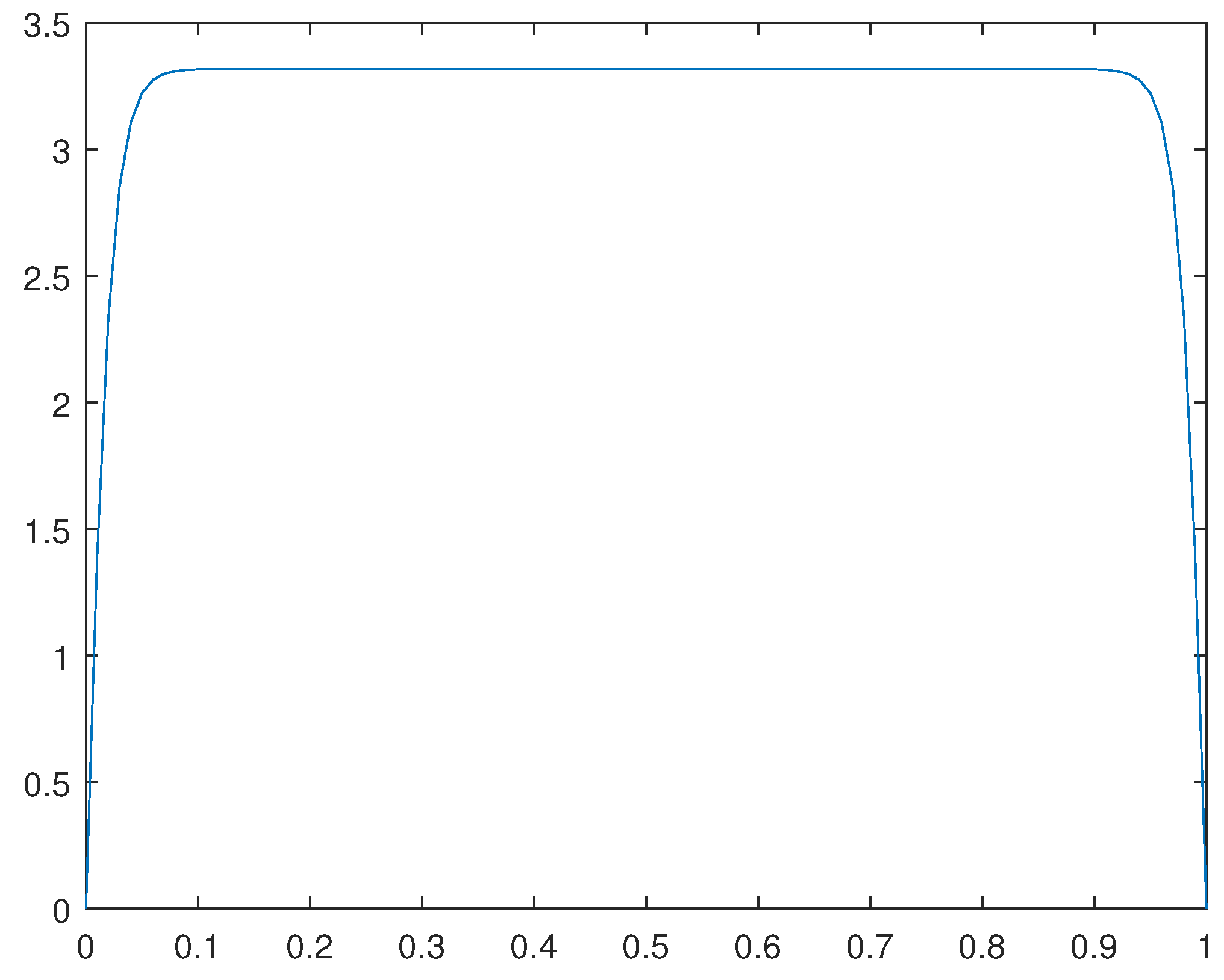
obtained, please see Figure 1. For the case in which

f (x) = sin (π x) / 2

, we have obtained numerical results for

K = 100

and

K_{1} = K / 20

. For such a concerning solution

u_{0}

obtained, please see Figure 2.

Remark 3.1.

Observe that the solutions obtained are approximate critical points. They are not, in a classical sense, the global solutions for the related optimization problems. Indeed, such solutions reflect the average behavior of weak cluster points for concerning minimizing sequences.

4. A convex dual variational formulation for a third similar model

In this section we present another duality principle for a third related model in phase transition.

Let

Ω = [0, 1] \subset R

and consider a functional

J : V \to R

where

J (u) = \frac{1}{2} \int_{Ω} min {{(u^{'} - 1)}^{2}, {(u^{'} + 1)}^{2}} d x + \frac{1}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}},

and where

V = {u \in W^{1, 2} (Ω) : u (0) = 0 and u (1) = 1 / 2}

and

f \in L^{2} (Ω) .

A global optimum point is not attained for J so that the problem of finding a global minimum for J has no solution.

Anyway, one question remains, how the minimizing sequences behave close to the infimum of J.

We intend to use the duality theory to solve such a global optimization problem in an appropriate sense to be specified.

At this point we define,

F : V \to R

and

G : V \to R

\begin{matrix} F (u) & = & \frac{1}{2} \int_{Ω} min {{(u^{'} - 1)}^{2}, {(u^{'} + 1)}^{2}} d x \\ = & \frac{1}{2} \int_{Ω} {(u^{'})}^{2} d x - \int_{Ω} | u^{'} | d x + 1 / 2 \\ \equiv & F_{1} (u^{'}), \end{matrix}

(11)

and

G (u) = \frac{1}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}} .

Denoting

Y = Y^{*} = L^{2} (Ω)

we also define the polar functional

F_{1}^{*} : Y^{*} \to R

and

G^{*} : Y^{*} \to R

\begin{matrix} F_{1}^{*} (v^{*}) & = & sup_{v \in Y} {{〈 v, v^{*} 〉}_{L^{2}} - F_{1} (v)} \\ = & \frac{1}{2} \int_{Ω} {(v^{*})}^{2} d x + \int_{Ω} | v^{*} | d x, \end{matrix}

(12)

and

\begin{matrix} G^{*} ({(v^{*})}^{'}) & = & sup_{u \in V} {- {〈 u^{'}, v^{*} 〉}_{L^{2}} - G (u)} \\ = & \frac{1}{2} \int_{Ω} {({(v^{*})}^{'} + f)}^{2} d x - \frac{1}{2} v^{*} (1) . \end{matrix}

(13)

Observe this is the scalar case of the calculus of variations, so that from the standard results on convex analysis, we have

inf_{u \in V} J (u) = max_{v^{*} \in Y^{*}} {- F_{1}^{*} (v^{*}) - G^{*} (- {(v^{*})}^{'})} .

Indeed, from the direct method of the calculus of variations, the maximum for the dual formulation is attained at some

{\hat{v}}^{*} \in Y^{*}

Moreover, the corresponding solution

u_{0} \in V

is obtained from the equation

u_{0} = \frac{\partial G ({({\hat{v}}^{*})}^{'})}{\partial {(v^{*})}^{'}} = {({\hat{v}}^{*})}^{'} + f .

Finally, the Euler-Lagrange equations for the dual problem stands for

\{\begin{matrix} {(v^{*})}^{''} + f^{'} - v^{*} - sign (v^{*}) = 0, & in Ω, \\ {(v^{*})}^{'} (0) = 0, {(v^{*})}^{'} (1) = 1 / 2, \end{matrix}

(14)

where

sign (v^{*} (x)) = 1

v^{*} (x) > 0,

sign (v^{*} (x)) = - 1,

v^{*} (x) < 0

and

- 1 \leq sign (v^{*} (x)) \leq 1,

v^{*} (x) = 0 .

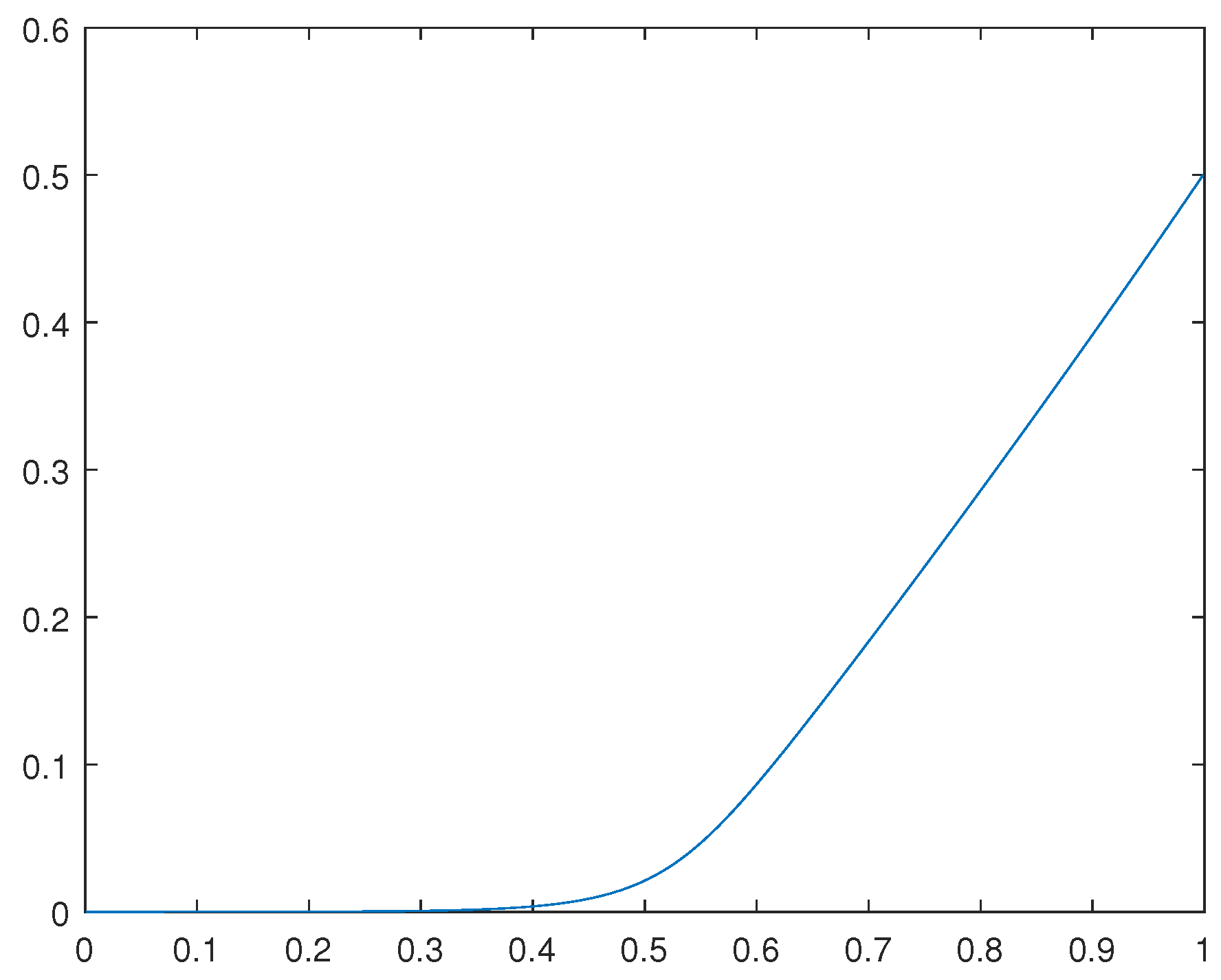
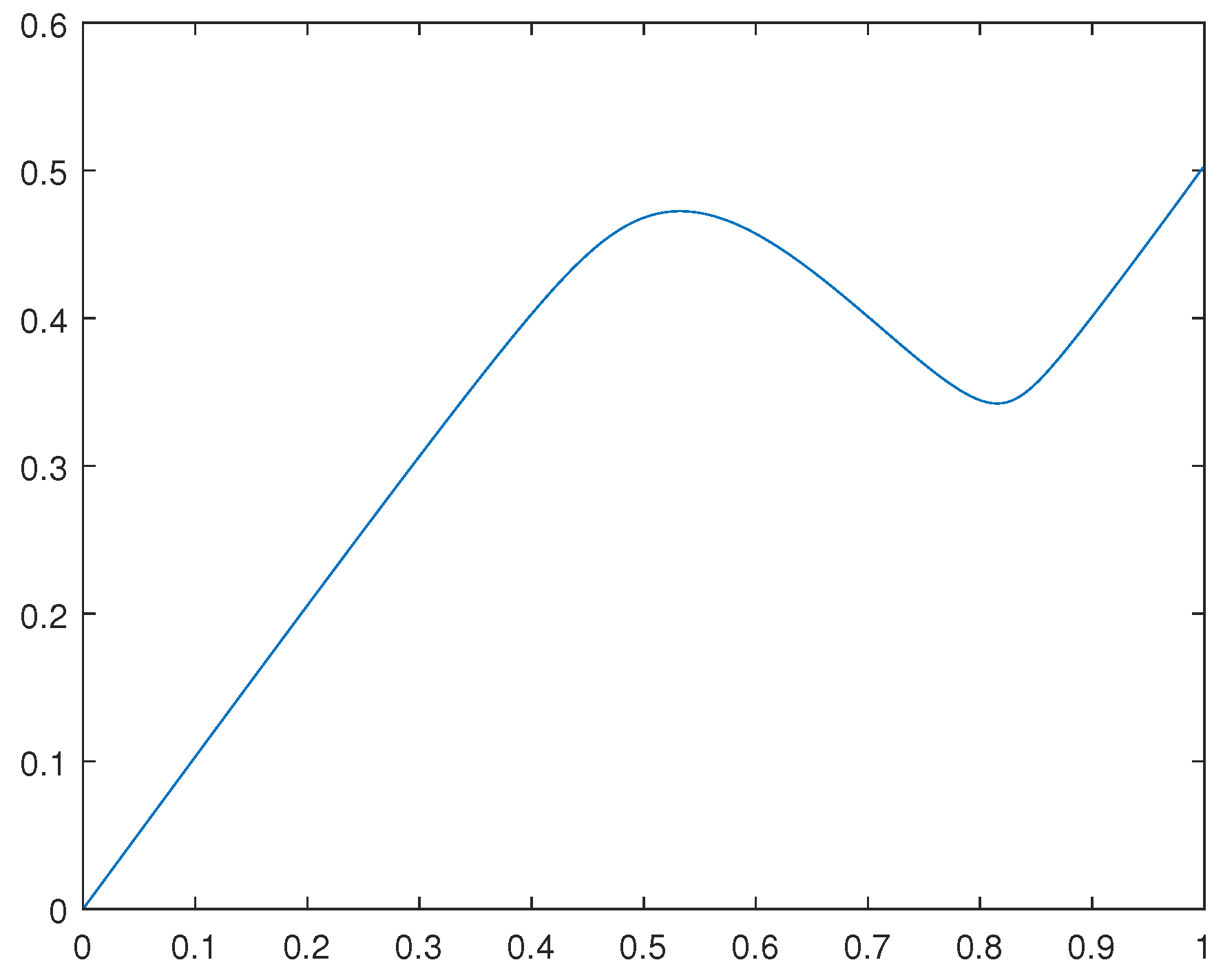
We have computed the solutions

v^{*}

and corresponding solutions

u_{0} \in V

for the cases in which

f (x) = 0

and

f (x) = sin (π x) / 2 .

For the solution

u_{0} (x)

for the case in which

f (x) = 0

, please see Figure 3.

For the solution

u_{0} (x)

for the case in which

f (x) = sin (π x) / 2

, please see Figure 4.

Remark 4.1.

Observe that such solutions

u_{0}

obtained are not the global solutions for the related primal optimization problems. Indeed, such solutions reflect the average behavior of weak cluster points for concerning minimizing sequences.

4.1. The algorithm through which we have obtained the numerical results

In this subsection we present the software in MATLAB through which we have obtained the last numerical results.

This algorithm is for solving the concerning Euler-Lagrange equations for the dual problem, that is, for solving the equation

\{\begin{matrix} {(v^{*})}^{''} + f^{'} - v^{*} - sign (v^{*}) = 0, & in Ω, \\ {(v^{*})}^{'} (0) = 0, {(v^{*})}^{'} (1) = 1 / 2 . \end{matrix}

(15)

Here the concerning software in MATLAB. We emphasize to have used the smooth approximation

| v^{*} | \approx \sqrt{{(v^{*})}^{2} + e_{1}},

where a small value for

e_{1}

is specified in the next lines.

*************************************

1.: clear all
2.: $m_{8} = 800;$ (number of nodes)
3.: $d = 1 / m_{8};$
4.: $e_{1} = 0.00001;$
5.: $f o r i = 1 : m_{8}$

$y o (i, 1) = 0.01;$

$y_{1} (i, 1) = sin (π * i / m_{8}) / 2;$

$e n d;$
6.: $f o r i = 1 : m_{8} - 1$

$d y_{1} (i, 1) = (y_{1} (i + 1, 1) - y_{1} (i, 1)) / d;$

$e n d;$
7.: $f o r k = 1 : 3000$ (we have fixed the number of iterations)

$i = 1;$

$h_{3} = 1 / \sqrt{v o {(i, 1)}^{2} + e_{1}};$

$m_{12} = 1 + d^{2} * h_{3} + d^{2};$

$m_{50} (i) = 1 / m_{12};$

$z (i) = m_{50} (i) * (d y_{1} (i, 1) * d^{2});$
8.: $f o r i = 2 : m_{8} - 1$

$h_{3} = 1 / \sqrt{v o {(i, 1)}^{2} + e_{1}};$

$m_{12} = 2 + h_{3} * d^{2} + d^{2} - m 50 (i - 1);$

$m 50 (i) = 1 / m_{12};$

$z (i) = m_{50} (i) * (z (i - 1) + d y_{1} (i, 1) * d^{2});$

$e n d;$
9.: $v (m_{8}, 1) = (d / 2 + z (m_{8} - 1)) / (1 - m_{50} (m_{8} - 1));$
10.: $f o r i = 1 : m_{8} - 1$

$v (m_{8} - i, 1) = m_{50} (m_{8} - i) * v (m_{8} - i + 1) + z (m_{8} - i);$

$e n d;$
11.: $v (m_{8} / 2, 1)$
12.: $v o = v;$

$e n d;$
13.: $f o r i = 1 : m_{8} - 1$

$u (i, 1) = (v (i + 1, 1) - v (i, 1)) / d + y_{1} (i, 1);$

$e n d;$
14.: $f o r i = 1 : m_{8} - 1$

$x (i) = i * d;$

$e n d;$

$p l o t (x, u (:, 1))$

********************************

5. An improvement of the convexity conditions for a non-convex related model through an approximate primal formulation

In this section we develop an approximate primal dual formulation suitable for a large class of variational models.

Here, the applications are for the Kirchhoff-Love plate model, which may be found in Ciarlet, [11].

At this point we start to describe the primal variational formulation.

Let

Ω \subset R^{2}

be an open, bounded, connected set which represents the middle surface of a plate of thickness h. The boundary of

Ω

, which is assumed to be regular (Lipschitzian), is denoted by

\partial Ω

. The vectorial basis related to the cartesian system

{x_{1}, x_{2}, x_{3}}

is denoted by

(a_{α}, a_{3})

, where

α = 1, 2

(in general Greek indices stand for 1 or 2), and where

a_{3}

is the vector normal to

Ω

, whereas

a_{1}

and

a_{2}

are orthogonal vectors parallel to

Ω .

Also,

n

is the outward normal to the plate surface.

The displacements will be denoted by

\hat{u} = {{\hat{u}}_{α}, {\hat{u}}_{3}} = {\hat{u}}_{α} a_{α} + {\hat{u}}_{3} a_{3} .

The Kirchhoff-Love relations are

\begin{matrix} {\hat{u}}_{α} (x_{1}, x_{2}, x_{3}) = u_{α} (x_{1}, x_{2}) - x_{3} w {(x_{1}, x_{2})}_{, α} \\ and {\hat{u}}_{3} (x_{1}, x_{2}, x_{3}) = w (x_{1}, x_{2}) . \end{matrix}

(16)

Here

- h / 2 \leq x_{3} \leq h / 2

so that we have

u = (u_{α}, w) \in U

where

\begin{matrix} U & = & \{u = (u_{α}, w) \in W^{1, 2} (Ω; R^{2}) \times W^{2, 2} (Ω), \\ u_{α} = w = \frac{\partial w}{\partial n} = 0 on \partial Ω\} \\ = & W_{0}^{1, 2} (Ω; R^{2}) \times W_{0}^{2, 2} (Ω) . \end{matrix}

It is worth emphasizing that the boundary conditions here specified refer to a clamped plate.

We also define the operator

Λ : U \to Y \times Y

, where

Y = Y^{*} = L^{2} (Ω; R^{2 \times 2})

, by

Λ (u) = {γ (u), κ (u)},

γ_{α β} (u) = \frac{u_{α, β} + u_{β, α}}{2} + \frac{w_{, α} w_{, β}}{2},

κ_{α β} (u) = - w_{, α β} .

The constitutive relations are given by

N_{α β} (u) = H_{α β λ μ} γ_{λ μ} (u),

(17)

M_{α β} (u) = h_{α β λ μ} κ_{λ μ} (u),

(18)

where:

{H_{α β λ μ}}

and

\{h_{α β λ μ} = \frac{h^{2}}{12} H_{α β λ μ}\}

, are symmetric positive definite fourth order tensors. From now on, we denote

{{\bar{H}}_{α β λ μ}} = {H_{α β λ μ}}^{- 1}

and

{{\bar{h}}_{α β λ μ}} = {h_{α β λ μ}}^{- 1}

Furthermore

{N_{α β}}

denote the membrane force tensor and

{M_{α β}}

the moment one. The plate stored energy, represented by

(G \circ Λ) : U \to R

is expressed by

(G \circ Λ) (u) = \frac{1}{2} \int_{Ω} N_{α β} (u) γ_{α β} (u) d x + \frac{1}{2} \int_{Ω} M_{α β} (u) κ_{α β} (u) d x

(19)

and the external work, represented by

F : U \to R

, is given by

F (u) = {〈 w, P 〉}_{L^{2}} + {〈 u_{α}, P_{α} 〉}_{L^{2}},

(20)

where

P, P_{1}, P_{2} \in L^{2} (Ω)

are external loads in the directions

a_{3}

a_{1}

and

a_{2}

respectively. The potential energy, denoted by

J : U \to R

is expressed by:

J (u) = (G \circ Λ) (u) - F (u)

Define now

J_{3} : \tilde{U} \to R

J_{3} (u) = J (u) + J_{5} (w) .

where

J_{5} (w) = 10 \int_{Ω} \frac{a^{K b w}}{ln (a) K^{3 / 2}} d x + 10 \int_{Ω} \frac{a^{- K (b w - 1 / 100)}}{ln (a) K^{3 / 2}} d x .

In such a case for

a = 2.71

K = 185

b = P / | P |

Ω

and

\tilde{U} = {{u \in U : ∥ w ∥}_{\infty} \leq 0.01 and P w \geq 0 a . e . in Ω},

we get

\begin{matrix} \frac{\partial J_{3} (u)}{\partial w} & = & \frac{\partial J (u)}{\partial w} + \frac{\partial J_{5} (u)}{\partial w} \\ \approx & \frac{\partial J (u)}{\partial w} + O (\pm 3.0), \end{matrix}

(21)

and

\begin{matrix} \frac{\partial^{2} J_{3} (u)}{\partial w^{2}} & = & \frac{\partial^{2} J (u)}{\partial w^{2}} + \frac{\partial^{2} J_{5} (u)}{\partial w^{2}} \\ \approx & \frac{\partial^{2} J (u)}{\partial w^{2}} + O (850) . \end{matrix}

(22)

This new functional

J_{3}

has a relevant improvement in the convexity conditions concerning the previous functional J.

Indeed, we have obtained a gain in positiveness for the second variation

\frac{\partial^{2} J (u)}{\partial w^{2}},

which has increased of order

O (700 - 1000) .

Moreover the difference between the approximate and exact equation

\frac{\partial J (u)}{\partial w} = 0

is of order

O (\pm 3.0)

which corresponds to a small perturbation in the original equation for a load of

P = 1500 N / m^{2},

for example. Summarizing, the exact equation may be approximately solved in an appropriate sense.

6. An exact convex dual variational formulation for a non-convex primal one

In this section we develop a convex dual variational formulation suitable to compute a critical point for the corresponding primal one.

Let

Ω \subset R^{2}

be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω .

Consider a functional

J : V \to R

where

J (u) = F (u_{x}, u_{y}) - {〈 u, f 〉}_{L^{2}},

V = W_{0}^{1, 2} (Ω)

and

f \in L^{2} (Ω) .

Here we denote

Y = Y^{*} = L^{2} (Ω)

and

Y_{1} = Y_{1}^{*} = L^{2} (Ω) \times L^{2} (Ω) .

Defining

V_{1} = {{u \in V : ∥ u ∥}_{1, \infty} \leq K_{1}}

for some appropriate

K_{1} > 0

, suppose also F is twice Fréchet differentiable and

det \{\frac{\partial^{2} F (u_{x}, u_{y})}{\partial v_{1} \partial v_{2}}\} \neq 0,

\forall u \in V_{1} .

Define now

F_{1} : V \to R

and

F_{2} : V \to R

F_{1} (u_{x}, u_{y}) = F (u_{x}, u_{y}) + \frac{ε}{2} \int_{Ω} u_{x}^{2} d x + \frac{ε}{2} \int_{Ω} u_{y}^{2} d x,

and

F_{2} (u_{x}, u_{y}) = \frac{ε}{2} \int_{Ω} u_{x}^{2} d x + \frac{ε}{2} \int_{Ω} u_{y}^{2} d x,

where here we denote

d x = d x_{1} d x_{2} .

Moreover, we define the respective Legendre transform functionals

F_{1}^{*}

and

F_{2}^{*}

F_{1}^{*} (v^{*}) = {〈 v_{1}, v_{1}^{*} 〉}_{L^{2}} + {〈 v_{2}, v_{2}^{*} 〉}_{L^{2}} - F_{1} (v_{1}, v_{2}),

where

v_{1}, v_{2} \in Y

are such that

v_{1}^{*} = \frac{\partial F_{1} (v_{1}, v_{2})}{\partial v_{1}},

v_{2}^{*} = \frac{\partial F_{1} (v_{1}, v_{2})}{\partial v_{2}},

and

F_{2}^{*} (v^{*}) = {〈 v_{1}, v_{1}^{*} + f_{1} 〉}_{L^{2}} + {〈 v_{2}, v_{2}^{*} 〉}_{L^{2}} - F_{2} (v_{1}, v_{2}),

where

v_{1}, v_{2} \in Y

are such that

v_{1}^{*} + f_{1} = \frac{\partial F_{2} (v_{1}, v_{2})}{\partial v_{1}},

v_{2}^{*} = \frac{\partial F_{2} (v_{1}, v_{2})}{\partial v_{2}} .

Here

f_{1}

is any function such that

{(f_{1})}_{x} = f, in Ω .

Furthermore, we define

\begin{matrix} J^{*} (v^{*}) & = & - F_{1}^{*} (v^{*}) + F_{2}^{*} (v^{*}) \\ = & - F_{1}^{*} (v^{*}) + \frac{1}{2 ε} \int_{Ω} {(v_{1}^{*} + f_{1})}^{2} d x + \frac{1}{2 ε} \int_{Ω} {(v_{2}^{*})}^{2} d x . \end{matrix}

(23)

Observe that through the target conditions

v_{1}^{*} + f_{1} = ε u_{x},

v_{2}^{*} = ε u_{y},

we may obtain the compatibility condition

{(v_{1}^{*} + f_{1})}_{y} - {(v_{2}^{*})}_{x} = 0 .

Define now

A^{*} = {v^{*} = (v_{1}^{*}, v_{2}^{*}) \in B_{r} (0, 0) \subset Y_{1}^{*} : {(v_{1}^{*} + f_{1})}_{y} - {(v_{2}^{*})}_{x} = 0, in Ω},

for some appropriate

r > 0

such that

J^{*}

is convex in

B_{r} (0, 0) .

Consider the problem of minimizing

J^{*}

subject to

v^{*} \in A^{*} .

Assuming

r > 0

is large enough so that the restriction in r is not active, at this point we define the associated Lagrangian

J_{1}^{*} (v^{*}, φ) = J^{*} (v^{*}) + {〈 φ, {(v_{1}^{*} + f)}_{y} - {(v_{2}^{*})}_{x} 〉}_{L^{2}},

where

φ

is an appropriate Lagrange multiplier.

Therefore

\begin{matrix} J_{1}^{*} (v^{*}) & = & - F_{1}^{*} (v^{*}) + \frac{1}{2 ε} \int_{Ω} {(v_{1}^{*} + f_{1})}^{2} d x + \frac{1}{2 ε} \int_{Ω} {(v_{2}^{*})}^{2} d x \\ + {〈 φ, {(v_{1}^{*} + f)}_{y} - {(v_{2}^{*})}_{x} 〉}_{L^{2}} . \end{matrix}

(24)

The optimal point in question will be a solution of the corresponding Euler-Lagrange equations for

J_{1}^{*} .

From the variation of

J_{1}^{*}

v_{1}^{*}

we obtain

- \frac{\partial F_{1}^{*} (v^{*})}{\partial v_{1}^{*}} + \frac{v_{1}^{*} + f}{ε} - \frac{\partial φ}{\partial y} = 0 .

(25)

From the variation of

J_{1}^{*}

v_{2}^{*}

we obtain

- \frac{\partial F_{1}^{*} (v^{*})}{\partial v_{2}^{*}} + \frac{v_{2}^{*}}{ε} + \frac{\partial φ}{\partial x} = 0 .

(26)

From the variation of

J_{1}^{*}

φ

we have

{(v_{1}^{*} + f)}_{y} - {(v_{2}^{*})}_{x} = 0 .

From this last equation, we may obtain

u \in V

such that

v_{1}^{*} + f = ε u_{x},

and

v_{2}^{*} = ε u_{y} .

From this and the previous extremal equations indicated we have

- \frac{\partial F_{1}^{*} (v^{*})}{\partial v_{1}^{*}} + u_{x} - \frac{\partial φ}{\partial y} = 0,

and

- \frac{\partial F_{1}^{*} (v^{*})}{\partial v_{2}^{*}} + u_{y} + \frac{\partial φ}{\partial x} = 0 .

so that

v_{1}^{*} + f = \frac{\partial F_{1} (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{1}},

and

v_{2}^{*} = \frac{\partial F_{1} (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{2}} .

From this and Equations (25) and (26) we have

\begin{matrix} - ε {(\frac{\partial F_{1}^{*} (v^{*})}{\partial v_{1}^{*}})}_{x} - ε {(\frac{\partial F_{1}^{*} (v^{*})}{\partial v_{2}^{*}})}_{y} \\ + {(v_{1}^{*} + f_{1})}_{x} + {(v_{2}^{*})}_{y} \\ = & - ε u_{x x} - ε u_{y y} + {(v_{1}^{*})}_{x} + {(v_{2}^{*})}_{y} + f = 0 . \end{matrix}

(27)

Replacing the expressions of

v_{1}^{*}

and

v_{2}^{*}

into this last equation, we have

- ε u_{x x} - ε u_{y y} + {(\frac{\partial F_{1} (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{1}})}_{x} + {(\frac{\partial F_{1} (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{2}})}_{y} + f = 0,

so that

{(\frac{\partial F (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{1}})}_{x} + {(\frac{\partial F (u_{x} - φ_{y}, u_{y} + φ_{x})}{\partial v_{2}})}_{y} + f = 0, in Ω .

(28)

Observe that if

\nabla^{2} φ = 0

then there exists

\hat{u}

such that u and

φ

are also such that

u_{x} - φ_{y} = {\hat{u}}_{x}

and

u_{y} + φ_{x} = {\hat{u}}_{y} .

The boundary conditions for

φ

must be such that

\hat{u} \in W_{0}^{1, 2} .

From this and Equation (28) we obtain

δ J (\hat{u}) = 0 .

Summarizing, we may obtain a solution

\hat{u} \in W_{0}^{1, 2}

of equation

δ J (\hat{u}) = 0

by minimizing

J^{*}

A^{*}

Finally, observe that clearly

J^{*}

is convex in an appropriate large ball

B_{r} (0, 0)

for some appropriate

r > 0

7. Another primal dual formulation for a related model

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular boundary denoted by

\partial Ω .

Consider the functional

J : V \to R

where

\begin{matrix} J (u) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{2} \int_{Ω} {(u^{2} - β)}^{2} d x \\ - {〈 u, f 〉}_{L^{2}}, \end{matrix}

(29)

α > 0, β > 0, γ > 0

V = W_{0}^{1, 2} (Ω)

and

f \in L^{2} (Ω) .

Denoting

Y = Y^{*} = L^{2} (Ω)

, define now

J_{1}^{*} : V \times Y^{*} \to R

\begin{matrix} J_{1}^{*} (u, v_{0}^{*}) & = & - \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x - {〈 u^{2}, v_{0}^{*} 〉}_{L^{2}} \\ + \frac{K_{1}}{2} \int_{Ω} {(- γ \nabla^{2} u + 2 v_{0}^{*} u - f)}^{2} d x + {〈 u, f 〉}_{L^{2}} \\ + \frac{1}{2 α} \int_{Ω} {(v_{0}^{*})}^{2} d x + β \int_{Ω} v_{0}^{*} d x, \end{matrix}

(30)

Define also

A^{+} = {u \in V : u f \geq 0, a . e . in Ω},

V_{2} = {{u \in V : ∥ u ∥}_{\infty} \leq K_{3}},

and

V_{1} = V_{2} \cap A^{+}

for some appropriate

K_{3} > 0

to be specified.

Moreover define

B^{*} = {v_{0}^{*} \in Y^{*} : ∥ v_{0}^{*} ∥_{\infty} \leq K}

for some appropriate

K > 0

to be specified.

Observe that, denoting

φ = - γ \nabla^{2} u + 2 v_{0}^{*} u - f

we have

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial {(v_{0}^{*})}^{2}} = \frac{1}{α} + 4 K_{1} u^{2}

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial u^{2}} = γ \nabla^{2} - 2 v_{0}^{*} + K_{1} {(- γ \nabla^{2} + 2 v_{0}^{*})}^{2}

and

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial u \partial v_{0}^{*}} = K_{1} (2 φ + 2 (- γ \nabla^{2} u + 2 v_{0}^{*} u)) - 2 u

so that

\begin{matrix} det {δ^{2} J_{1}^{*} (u, v_{0}^{*})} \\ = & \frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial {(v_{0}^{*})}^{2}} \frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial u^{2}} - {(\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*})}{\partial u \partial v_{0}^{*}})}^{2} \\ = & \frac{K_{1} {(- γ \nabla^{2} + 2 v_{0}^{*})}^{2}}{α} - \frac{γ \nabla^{2} + 2 v_{0}^{*} + 4 α u^{2}}{α} \\ - 4 K_{1}^{2} φ^{2} - 8 K_{1} φ (- γ \nabla^{2} + 2 v_{0}^{*}) u + 8 K_{1} φ u \\ + 4 K_{1} (- γ \nabla^{2} u + 2 v_{0}^{*} u) u . \end{matrix}

(31)

Observe now that a critical point

φ = 0

and

(- γ \nabla^{2} u + 2 v_{0}^{*} u) u = f u \geq 0

Ω

Therefore, for an appropriate large

K_{1} > 0

, also at a critical point, we have

\begin{matrix} det {δ^{2} J_{1}^{*} (u, v_{0}^{*})} \\ = & 4 K_{1} f u - \frac{δ^{2} J (u)}{α} + K_{1} \frac{{(- γ \nabla^{2} + 2 v_{0}^{*})}^{2}}{α} > 0 . \end{matrix}

(32)

Remark 7.1.

From this last equation we may observe that

J_{1}^{*}

has a large region of convexity about any critical point

(u_{0}, {\hat{v}}_{0}^{*})

, that is, there exists a large

r > 0

such that

J_{1}^{*}

is convex on

B_{r} (u_{0}, {\hat{v}}_{0}^{*}) .

With such results in mind, we may easily prove the following theorem.

Theorem 7.2.

Assume

K_{1} ≫ max {1, K, K_{3}}

and suppose

(u_{0}, {\hat{v}}_{0}^{*}) \in V_{1} \times B^{*}

is such that

δ J_{1}^{*} (u_{0}, {\hat{v}}_{0}^{*}) = 0 .

Under such hypotheses, there exists

r > 0

such that

J_{1}^{*}

is convex in

E^{*} = B_{r} (u_{0}, {\hat{v}}_{0}^{*}) \cap (V_{1} \times B^{*})

δ J (u_{0}) = 0,

and

- J (u_{0}) = J_{1} (u_{0}, {\hat{v}}_{0}^{*}) = inf_{(u, v_{0}^{*}) \in E^{*}} J_{1}^{*} (u, v_{0}^{*}) .

8. A third primal dual formulation for a related model

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular boundary denoted by

\partial Ω .

Consider the functional

J : V \to R

where

\begin{matrix} J (u) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{2} \int_{Ω} {(u^{2} - β)}^{2} d x \\ - {〈 u, f 〉}_{L^{2}}, \end{matrix}

(33)

α > 0, β > 0, γ > 0

V = W_{0}^{1, 2} (Ω)

and

f \in L^{2} (Ω) .

Denoting

Y = Y^{*} = L^{2} (Ω)

, define now

J_{1}^{*} : V \times Y^{*} \times Y^{*} \to R

\begin{matrix} J_{1}^{*} (u, v_{0}^{*}, v_{1}^{*}) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{1}{2} \int_{Ω} K u^{2} d x \\ - {〈 u, v_{1}^{*} 〉}_{L^{2}} + \frac{1}{2} \int_{Ω} \frac{{(v_{1}^{*})}^{2}}{(- 2 v_{0}^{*} + K)} d x \\ + \frac{1}{2 (α + ε)} \int_{Ω} {(v_{0}^{*} - α (u^{2} - β))}^{2} d x + {〈 u, f 〉}_{L^{2}} \\ - \frac{1}{2 α} \int_{Ω} {(v_{0}^{*})}^{2} d x - β \int_{Ω} v_{0}^{*} d x, \end{matrix}

(34)

where

ε > 0

is a small real constant.

Define also

A^{+} = {u \in V : u f \geq 0, a . e . in Ω},

V_{2} = {{u \in V : ∥ u ∥}_{\infty} \leq K_{3}},

and

V_{1} = V_{2} \cap A^{+}

for some appropriate

K_{3} > 0

to be specified.

Moreover define

B^{*} = {v_{0}^{*} \in Y^{*} : ∥ v_{0}^{*} ∥_{\infty} \leq K_{4}}

and

D^{*} = {v_{1}^{*} \in Y^{*} : ∥ v_{1}^{*} ∥ \leq K_{5}},

for some appropriate real constants

K_{4}, K_{5} > 0

to be specified.

Remark 8.1.

Define now

H_{1} (u, v_{0}^{*}) = - γ \nabla^{2} + 2 v_{0}^{*} + 4 α u^{2}

For an appropriate function (or, in a more general fashion, an appropriate bounded operator)

M_{1}

define

E^{*} = {(u, v_{0}^{*}) \in V_{1} \times B^{*} : \sqrt{4 α} | u | \geq \sqrt{| M_{1} + γ \nabla^{2} |} and 2 v_{0}^{*} + M_{1} \geq ε_{1}} .

Since for

(u, v_{0}^{*}) \in V_{1} \times B^{*}

we have

u f \geq 0, in Ω

, so that for

u_{1}, u_{2} \in V_{1}

we have

sign (u_{1}) = sign (u_{2}) in Ω,

we may infer that

E^{*}

is a convex set.

Moreover if

(u, v_{0}^{*}) \in E^{*}

, then

\sqrt{4 α} | u | \geq \sqrt{| M_{1} + γ \nabla^{2} |}

so that

4 α u^{2} \geq M_{1} + γ \nabla^{2}

and

2 v_{0}^{*} + M_{1} \geq ε_{1}

so that

H_{1} (u, v_{0}^{*}) = - γ \nabla^{2} + 2 v_{0}^{*} + 4 α u^{2} \geq ε_{1} .

Such a result we will be used many times in the next sections.

Observe that, defining

φ = v_{0}^{*} - α (u^{2} - β)

we may obtain

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*}, v_{1}^{*})}{\partial u^{2}} = - γ \nabla^{2} + K + \frac{α}{α + ε} 4 u^{2} - 2 φ \frac{α}{α + ε}

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*}, v_{1}^{*})}{\partial {(v_{1}^{*})}^{2}} = \frac{1}{- 2 v_{0}^{*} + K}

and

\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*}, v_{1}^{*})}{\partial u \partial v_{1}^{*}} = - 1

so that

\begin{matrix} det \{\frac{\partial^{2} J_{1}^{*} (u, v_{0}^{*}, v_{1}^{*})}{\partial u \partial v_{1}^{*}}\} \\ = & \frac{\partial^{2} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})}{\partial {(v_{1}^{*})}^{2}} \frac{\partial^{2} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})}{\partial u^{2}} - {(\frac{\partial^{2} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})}{\partial u \partial v_{1}^{*}})}^{2} \\ = & \frac{- γ \nabla^{2} + 2 v_{0}^{*} + 4 \frac{α^{2}}{α + ε} u^{2} - 2 \frac{α}{α + ε} φ}{- 2 v_{0}^{*} + K} \\ \equiv & H (u, v_{0}^{*}) . \end{matrix}

(35)

However, at a critical point, we have

φ = 0

so that, we define the non-active but convex restriction

C^{*} = {(u, v_{0}^{*}) \in V_{1} \times B : {(φ)}^{2} \leq ε},

for a small parameter

ε > 0 .

From such results, assuming

K ≫ max {K_{3}, K_{4}, K_{5}},

and

0 < ε ≪ ε_{1} ≪ 1

, we have that

H (u, v_{0}^{*}) > 0, in C^{*} \cap E^{*} .

With such results in mind, we may easily prove the following theorem.

Theorem 8.2.

Suppose

(u_{0}, {\hat{v}}_{0}^{*}, {\hat{v}}_{1}^{*}) \in E_{1}^{*} = (E^{*} \cap C^{*}) \times D^{*} \times B^{*}

is such that

δ J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) = 0 .

Under such hypotheses, defining

C_{{\hat{v}}_{0}^{*}} = {u \in V_{1} : (u, {\hat{v}}_{0}^{*}) \in E_{1}^{*}},

we have that

δ J (u_{0}) = 0

and

\begin{matrix} J (u_{0}) & = & inf_{u \in V_{1} \cap C_{{\hat{v}}_{0}^{*}}} J (u) \\ = & J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) \\ = & inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} \{sup_{v_{0}^{*} \in B^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} \\ = & sup_{v_{0}^{*} \in B^{*}} \{inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} . \end{matrix}

(36)

Proof.

The proof that

δ J (u_{0}) = 0

and

J (u_{0}) = J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*})

may be easily made similarly as in the previous sections.

Moreover, from the hypotheses, we have

J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) = inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} J_{1}^{*} (u, v_{1}^{*}, {\hat{v}}_{0}^{*})

and

J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) = sup_{v_{0}^{*} \in B^{*}} J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, v_{0}^{*}) .

From this, from a standard saddle point theorem and the remaining hypotheses, we may infer that

\begin{matrix} J (u_{0}) & = & J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) \\ = & inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} \{sup_{v_{0}^{*} \in B^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} \\ = & sup_{v_{0}^{*} \in B^{*}} \{inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} . \end{matrix}

(37)

Moreover, observe that

\begin{matrix} J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) & = & inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} J_{1}^{*} (u, v_{1}^{*}, {\hat{v}}_{0}^{*}) \\ \leq & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{K}{2} \int_{Ω} u^{2} d x \\ + {〈 u^{2}, {\hat{v}}_{0}^{*} 〉}_{L^{2}} - \frac{K}{2} \int_{Ω} u^{2} d x \\ - \frac{1}{2 α} \int_{Ω} {({\hat{v}}_{0}^{*})}^{2} d x - β \int_{Ω} {\hat{v}}_{0}^{*} d x \\ + \frac{1}{2 (α + ε)} \int_{Ω} {({\hat{v}}_{0}^{*} - α (u^{2} - β))}^{2} d x - {〈 u, f 〉}_{L^{2}} \\ \leq & sup_{v_{0}^{*} \in Y^{*}} \{\frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + 〈 u^{2}, v_{0}^{*} 〉 \\ - \frac{1}{2 α} \int_{Ω} {(v_{0}^{*})}^{2} d x - β \int_{Ω} v_{0}^{*} d x \\ + \frac{1}{2 (α + ε)} \int_{Ω} {(v_{0}^{*} - α (u^{2} - β))}^{2} d x - {〈 u, f 〉}_{L^{2}}\} \\ = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{2} \int_{Ω} {(u^{2} - β)}^{2} d x \\ - {〈 u, f 〉}_{L^{2}}, \forall u \in V_{1} \cap C_{{\hat{v}}_{0}^{*}} . \end{matrix}

(38)

Summarizing, we have got

J (u_{0}) = J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) \leq inf_{u \in V_{1} \cap C_{{\hat{v}}_{0}^{*}}} J (u) .

From such results, we may infer that

\begin{matrix} J (u_{0}) & = & inf_{u \in V_{1} \cap C_{{\hat{v}}_{0}^{*}}} J (u) \\ = & J_{1}^{*} (u_{0}, {\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}) \\ = & inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} \{sup_{v_{0}^{*} \in B^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} \\ = & sup_{v_{0}^{*} \in B^{*}} \{inf_{(u, v_{1}^{*}) \in (V_{1} \cap C_{{\hat{v}}_{0}^{*}}) \times D^{*}} J_{1}^{*} (u, v_{1}^{*}, v_{0}^{*})\} . \end{matrix}

(39)

The proof is complete. □

9. An algorithm for a related model in shape optimization

The next two subsections have been previously published by Fabio Silva Botelho and Alexandre Molter in [5], Chapter 21.

9.1. Introduction

Consider an elastic solid which the volume corresponds to an open, bounded, connected set, denoted by

Ω \subset R^{3}

with a regular (Lipschitzian) boundary denoted by

\partial Ω = Γ_{0} \cup Γ_{t}

where

Γ_{0} \cap Γ_{t} = \emptyset .

Consider also the problem of minimizing the functional

\hat{J} : U \times B \to R

where

\hat{J} (u, t) = \frac{1}{2} {〈 u_{i}, f_{i} 〉}_{L^{2} (Ω)} + \frac{1}{2} {〈 u_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})},

subject to

\{\begin{matrix} {(H_{i j k l} (t) e_{k l} (u))}_{, j} + f_{i} = 0 in Ω, \\ H_{i j k l} (t) e_{k l} (u) n_{j} - {\hat{f}}_{i} = 0, on Γ_{t}, \forall i \in {1, 2, 3} . \end{matrix}

(40)

Here

n = (n_{1}, n_{2}, n_{3})

denotes the outward normal to

\partial Ω

and

U = {u = (u_{1}, u_{2}, u_{3}) \in W^{1, 2} (Ω; R^{3}) : u = (0, 0, 0) = 0 on Γ_{0}},

B = \{t : Ω \to [0, 1] measurable : \int_{Ω} t (x) d x = t_{1} | Ω |\},

where

0 < t_{1} < 1

and

| Ω |

denotes the Lebesgue measure of

Ω .

Moreover

u = (u_{1}, u_{2}, u_{3}) \in W^{1, 2} (Ω; R^{3})

is the field of displacements relating the cartesian system

(0, x_{1}, x_{2}, x_{3})

, resulting from the action of the external loads

f \in L^{2} (Ω; R^{3})

and

\hat{f} \in L^{2} (Γ_{t}; R^{3}) .

We also define the stress tensor

{σ_{i j}} \in Y^{*} = Y = L^{2} (Ω; R^{3 \times 3}),

σ_{i j} (u) = H_{i j k l} (t) e_{k l} (u),

and the strain tensor

e : U \to L^{2} (Ω; R^{3 \times 3})

e_{i j} (u) = \frac{1}{2} (u_{i, j} + u_{j, i}), \forall i, j \in {1, 2, 3} .

Finally,

{H_{i j k l} (t)} = {t H_{i j k l}^{0} + (1 - t) H_{i j k l}^{1}},

where

H^{0}

corresponds to a strong material and

H^{1}

to a very soft material, intending to simulate voids along the solid structure.

The variable t is the design one, which the optimal distribution values along the structure are intended to minimize its inner work with a volume restriction indicated through the set B.

The duality principle obtained is developed inspired by the works in [2,3]. Similar theoretical results have been developed in [10], however we believe the proof here presented, which is based on the min-max theorem is easier to follow (indeed we thank an anonymous referee for his suggestion about applying the min-max theorem to complete the proof). We highlight throughout this text we have used the standard Einstein sum convention of repeated indices.

Moreover, details on the Sobolev spaces addressed may be found in [1]. In addition, the primal variational development of the topology optimization problem has been described in [10].

The main contributions of this work are to present the detailed development, through duality theory, for such a kind of optimization problems. We emphasize that to avoid the check-board standard and obtain appropriate robust optimized structures without the use of filters, it is necessary to discretize more in the load direction, in which the displacements are much larger.

9.2. Mathematical formulation of the topology optimization problem

Our mathematical topology optimization problem is summarized by the following theorem.

Theorem 9.1.

Consider the statements and assumptions indicated in the last section, in particular those refereing to Ω and the functional

\hat{J} : U \times B \to R .

Define

J_{1} : U \times B \to R

J_{1} (u, t) = - G (e (u), t) + {〈 u_{i}, f_{i} 〉}_{L^{2} (Ω)} + {〈 u_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})},

where

G (e (u), t) = \frac{1}{2} \int_{Ω} H_{i j k l} (t) e_{i j} (u) e_{k l} (u) d x,

and where

d x = d x_{1} d x_{2} d x_{3} .

Define also

J^{*} : U \to R

\begin{matrix} J^{*} (u) & = & inf_{t \in B} {J_{1} (u, t)} \\ = & inf_{t \in B} {- G (e (u), t) + {〈 u_{i}, f_{i} 〉}_{L^{2} (Ω)} + {〈 u_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})}} . \end{matrix}

(41)

Assume there exists

c_{0}, c_{1} > 0

such that

H_{i j k l}^{0} z_{i j} z_{k l} > c_{0} z_{i j} z_{i j}

and

H_{i j k l}^{1} z_{i j} z_{k l} > c_{1} z_{i j} z_{i j}, \forall z = {z_{i j}} \in R^{3 \times 3}, such that z \neq 0 .

Finally, define

J : U \times B \to R \cup {+ \infty}

J (u, t) = \hat{J} (u, t) + I n d (u, t),

where

I n d (u, t) = \{\begin{matrix} 0, & if (u, t) \in A^{*}, \\ + \infty, & otherwise, \end{matrix}

(42)

where

A^{*} = A_{1} \cap A_{2},

A_{1} = {(u, t) \in U \times B : {(σ_{i j} (u))}_{, j} + f_{i} = 0, in Ω, \forall i \in {1, 2, 3}}

and

A_{2} = {(u, t) \in U \times B : σ_{i j} (u) n_{j} - {\hat{f}}_{i} = 0, on Γ_{t}, \forall i \in {1, 2, 3}} .

Under such hypotheses, there exists

(u_{0}, t_{0}) \in U \times B

such that

\begin{matrix} J (u_{0}, t_{0}) & = & inf_{(u, t) \in U \times B} J (u, t) \\ = & sup_{\hat{u} \in U} J^{*} (\hat{u}) \\ = & J^{*} (u_{0}) \\ = & \hat{J} (u_{0}, t_{0}) \\ = & inf_{(t, σ) \in B \times C^{*}} G^{*} (σ, t) \\ = & G^{*} (σ (u_{0}), t_{0}), \end{matrix}

(43)

where

\begin{matrix} G^{*} (σ, t) & = & sup_{v \in Y} {{〈 v_{i j}, σ_{i j} 〉}_{L^{2} (Ω)} - G (v, t)} \\ = & \frac{1}{2} \int_{Ω} {\bar{H}}_{i j k l} (t) σ_{i j} σ_{k l} d x, \end{matrix}

(44)

{{\bar{H}}_{i j k l} (t)} = {H_{i j k l} (t)}^{- 1}

and

C^{*} = C_{1} \cap C_{2},

where

C_{1} = {σ \in Y^{*} : σ_{i j, j} + f_{i} = 0, in Ω, \forall i \in {1, 2, 3}}

and

C_{2} = {σ \in Y^{*} : σ_{i j} n_{j} - {\hat{f}}_{i} = 0, on Γ_{t}, \forall i \in {1, 2, 3}} .

Proof.

Observe that

\begin{matrix} inf_{(u, t) \in U \times B} J (u, t) & = & inf_{t \in B} \{inf_{u \in U} J (u, t)\} \\ = & inf_{t \in B} \{sup_{\hat{u} \in U} \{inf_{u \in U} \{\frac{1}{2} \int_{Ω} H_{i j k l} (t) e_{i j} (u) e_{k l} (u) d x \\ + {〈 {\hat{u}}_{i}, {(H_{i j k l} (t) e_{k l} (u))}_{, j} + f_{i} 〉}_{L^{2} (Ω)} \\ - {〈 {\hat{u}}_{i}, H_{i j k l} (t) e_{k l} (u) n_{j} - {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})}\}\}\} \\ = & inf_{t \in B} \{sup_{\hat{u} \in U} \{inf_{u \in U} \{\frac{1}{2} \int_{Ω} H_{i j k l} (t) e_{i j} (u) e_{k l} (u) d x \\ - \int_{Ω} H_{i j k l} (t) e_{i j} (\hat{u}) e_{k l} (u) d x \\ + {〈 {\hat{u}}_{i}, f_{i} 〉}_{L^{2} (Ω)} + {〈 {\hat{u}}_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})}\}\}\} \\ = & inf_{t \in B} \{sup_{\hat{u} \in U} \{- \int_{Ω} H_{i j k l} (t) e_{i j} (\hat{u}) e_{k l} (\hat{u}) d x \\ {〈 {\hat{u}}_{i}, f_{i} 〉}_{L^{2} (Ω)} + {〈 {\hat{u}}_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})}\}\} \\ = & inf_{t \in B} \{inf_{σ \in C^{*}} G^{*} (σ, t)\} . \end{matrix}

(45)

Also, from this and the min-max theorem, there exist

(u_{0}, t_{0}) \in U \times B

such that

\begin{matrix} inf_{(u, t) \in U \times B} J (u, t) & = & inf_{t \in B} \{sup_{\hat{u} \in U} J_{1} (u, t)\} \\ = & sup_{u \in U} \{inf_{t \in B} J_{1} (u, t)\} \\ = & J_{1} (u_{0}, t_{0}) \\ = & inf_{t \in B} J_{1} (u_{0}, t) \\ = & J^{*} (u_{0}) . \end{matrix}

(46)

Finally, from the extremal necessary condition

\frac{\partial J_{1} (u_{0}, t_{0})}{\partial u} = 0

we obtain

{(H_{i j k l} (t_{0}) e_{k l} (u_{0}))}_{, j} + f_{i} = 0 in Ω,

and

H_{i j k l} (t_{0}) e_{k l} (u_{0}) n_{j} - {\hat{f}}_{i} = 0 on Γ_{t}, \forall i \in {1, 2, 3},

so that

G (e (u_{0})) = \frac{1}{2} {〈 {(u_{0})}_{i}, f_{i} 〉}_{L^{2} (Ω)} + \frac{1}{2} {〈 {(u_{0})}_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})} .

Hence

(u_{0}, t_{0}) \in A^{*}

so that

I n d (u_{0}, t_{0}) = 0

and

σ (u_{0}) \in C^{*} .

Moreover

\begin{matrix} J^{*} (u_{0}) & = & - G (e (u_{0})) + {〈 {(u_{0})}_{i}, f_{i} 〉}_{L^{2} (Ω)} + {〈 {(u_{0})}_{i}, {\hat{f}}_{i} 〉}_{L^{2} (Γ_{t})} \\ = & G (e (u_{0})) \\ = & G (e (u_{0})) + I n d (u_{0}, t_{0}) \\ = & J (u_{0}, t_{0}) \\ = & G^{*} (σ (u_{0}), t_{0}) . \end{matrix}

(47)

This completes the proof. □

9.3. About a concerning algorithm and related numerical method

For numerically solve this optimization problem in question, we present the following algorithm

1.: Set $t_{1} = 0.5 in Ω$ and $n = 1$ .
2.: Calculate $u_{n} \in U$ such that

$J_{1} (u_{n}, t_{n}) = sup_{u \in U} J_{1} (u, t_{n}) .$
3.: Calculate $t_{n + 1} \in B$ such that

$J_{1} (u_{n}, t_{n + 1}) = inf_{t \in B} J_{1} (u_{n}, t) .$
4.: If $∥ t_{n + 1} - t_{n} ∥_{\infty} < 10^{- 4}$ or $n > 100$ then stop, else set $n : = n + 1$ and go to item 2.

We have developed a software in finite differences for solving such a problem.

Here the software.

**************************************

1.: clear all

global P m8 d w u v Ea Eb Lo d1 z1 m9 du1 du2 dv1 dv2 c3

m8=27;

m9=24;

c3=0.95;

d=1.0/m8;

d1=0.5/m9;

Ea= $210 * 10^{5}$ ; (stronger material)

Eb=1000; (softer material simulating voids)

w=0.30;

P=-42000000;

z1=(m8-1)*(m9-1);

A3=zeros(z1,z1);

for i=1:z1

A3(1,i)=1.0;

end;

b=zeros(z1,1);

uo=0.000001*ones(z1,1);

u1=ones(z1,1);

b(1,1)=c3*z1;

for i=1:m9-1

for j=1:m8-1

Lo(i,j)=c3;

end; end;

for i=1:z1

x1(i)=c3*z1;

end;

for i=1:2*m8*m9

xo(i)=0.000;

end;

xw=xo;

xv=Lo;

for k2=1:24

c3=0.98*c3;

b(1,1)=c3*z1;

k2

b14=1.0;

k3=0;

while $(b 14 > 10^{- 3.5})$ and $(k 3 < 5)$

k3=k3+1;

b12=1.0;

k=0;

while $(b 12 > 10^{- 4.0})$ and $(k < 120)$

k=k+1;

k2

k3

k

X=fminunc(’funbeam’,xo);

xo=X;

b12=max(abs(xw-xo));

xw=X;

end;

for i=1:m9-1

for j=1:m8-1

$E 1 = L o {(i, j)}^{2} * (E a - E b);$

ex=du1(i,j);

ey=dv2(i,j);

exy=1/2*(dv1(i,j)+du2(i,j));

$S x = E 1 * (e x + w * e y) / (1 - w^{2});$

$S y = E 1 * (w * e x + e y) / (1 - w^{2});$

Sxy=E1/(2*(1+w))*exy;

dc3(i,j)=-(Sx*ex+Sy*ey+2*Sxy*exy);

end;

end;

for i=1:m9-1

for j=1:m8-1

f(j+(i-1)*(m8-1))=dc3(i,j);

end;

end;

for k1=1:1

k1

X1=linprog(f, $[]$ , $[]$ ,A3,b,uo,u1,x1);

x1=X1;

end;

for i=1:m9-1

for j=1:m8-1

Lo(i,j)=X1(j+(m8-1)*(i-1));

end;

end;

b14=max(max(abs(Lo-xv)))

xv=Lo;

colormap(gray); imagesc(-Lo); axis equal; axis tight; axis off;pause(1e-6)

end;

end;

****************************************************

Here the auxiliary Function ’funbeam’

function S=funbeam(x)

global P m8 d w u v Ea Eb Lo d1 m9 du1 du2 dv1 dv2

for i=1:m9

for j=1:m8

u(i,j)=x(j+(m8)*(i-1));

v(i,j)=x(m8*m9+(i-1)*m8+j);

end;

for i=1:m9

end;

u(m9-1,1)=0;

v(m9-1,1)=0;

u(m9-1,m8-1)=0;

v(m9-1,m8-1)=0;

for i=1:m9-1

for j=1:m8-1

du1(i,j)=(u(i,j+1)-u(i,j))/d;

du2(i,j)=(u(i+1,j)-u(i,j))/d1;

dv1(i,j)=(v(i,j+1)-v(i,j))/d;

dv2(i,j)=(v(i+1,j)-v(i,j))/d1;

end;

S=0;

for i=1:m9-1

for j=1:m8-1

E 1 = L o {(i, j)}^{3} * E a + (1 - L o {(i, j)}^{3}) * E b;

ex=du1(i,j);

ey=dv2(i,j);

exy=1/2*(dv1(i,j)+du2(i,j));

S x = E 1 * (e x + w * e y) / (1 - w^{2});

S y = E 1 * (w * e x + e y) / (1 - w^{2});

Sxy=E1/(2*(1+w))*exy;

S=S+1/2*(Sx*ex+Sy*ey+2*Sxy*exy);

end;

S=S*d*d1-P*v(2,(m8)/3)*d*d1;

***********************************************

For a two dimensional beam of dimensions

1 m \times 0.5 m

and

t_{1} = 0.63

we have obtained the following results:

1.: Case A: For the optimal shape for a clamped beam at left (cantilever) and load $P = - 4 10^{6} N j$ at $(x, y) = (1, 0.25)$ , please Figure 5.
2.: Case B :For the optimal shape for a simply supported beam at $(0, 0)$ and $(1, 0)$ and load $P = - 4 10^{6} N j$ at $(x, y) = (1 / 3, 0.5)$ , please Figure 6.

In the first case the mesh was $28 \times 24$ . In the second one the mesh was $27 \times 24$

10. A duality principle for a general vectorial case in the calculus of variations

In this section we develop a duality principle for a general vectorial case in variational optimization.

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω

. Let

J : V \to R

be a functional where

J (u) = G (\nabla u_{1}, \dots, \nabla u_{N}) - {〈 u, f 〉}_{L^{2}},

where

V = W_{0}^{1, 2} (Ω; R^{N})

and

f = (f_{1}, \dots, f_{N}) \in L^{2} (Ω; R^{N}) .

Here we have denoted

u = (u_{1}, \dots, u_{N}) \in V

and

{〈 u, f 〉}_{L^{2}} = {〈 u_{i}, f_{i} 〉}_{L^{2}},

so that we may also denote

J (u) = G (\nabla u) - {〈 u, f 〉}_{L^{2}} .

Assume

G (\nabla u) = \int_{Ω} g (\nabla u) d x

where

g : R^{3 N} \to R

is a differentiable function such that

g (y) \to + \infty

| y | \to \infty

. Moreover, suppose there exists

α \in R

such that

α = inf_{u \in V} J (u) .

It is well known that

\begin{matrix} α & = & inf_{u \in V} J (u) \\ = & inf_{u \in V} J^{* *} (u) \\ = & inf_{u \in V} {{(G \circ \nabla)}^{* *} (u) - {〈 u, f 〉}_{L^{2}}} . \end{matrix}

(48)

Under some mild hypotheses, from convexity, we have that

\begin{matrix} inf_{u \in V} {{(G \circ \nabla)}^{* *} (u) - {〈 u, f 〉}_{L^{2}}} \\ = & sup_{v^{*} \in A^{*}} {- {(G \circ \nabla)}^{*} (- d i v v^{*})} = - {(G \circ \nabla)}^{*} (f), \end{matrix}

(49)

where

A^{*} = {v^{*} \in Y = Y^{*} = L^{2} (Ω; R^{3 N}) : d i v v^{*} + f = 0} .

Now observe that the restriction

v = \nabla u

for some

u \in V

is equivalent to the restriction

curl v_{i} = 0, in Ω

where

v = {v_{i}} = {v_{i j}}_{j = 1}^{3}

\forall i \in {1, \dots, N},

with appropriate boundary conditions, so that with an appropriate Lagrange multiplier

ϕ = {ϕ_{i}}

, we obtain

\begin{matrix} {(G \circ \nabla)}^{*} (- d i v v^{*}) & = & sup_{u \in V} {{〈 u, - d i v v^{*} 〉}_{L^{2}} - G (\nabla u)} \\ = & sup_{u \in V} {{〈 \nabla u, v^{*} 〉}_{L^{2}} - G (\nabla u)} \\ \leq & inf_{ϕ \in Y^{*}} \{sup_{v \in Y} {{〈 v, v^{*} 〉}_{L^{2}} - G (v) + {〈 ϕ, curl v 〉}_{L^{2}}\} \\ = & inf_{ϕ \in Y^{*}} G^{*} (v^{*} + curl ϕ) . \end{matrix}

(50)

where we have denoted

curl v = {curl v_{i}}

and

curl ϕ = {curl ϕ_{i}} .

Joining the pieces, we have got

\begin{matrix} inf_{u \in V} J (u) & = & inf_{u \in V} {G (\nabla u) - {〈 u, f 〉}_{L^{2}}} \\ \geq & sup_{(v^{*}, ϕ) \in A^{*} \times Y^{*}} {- G^{*} (v^{*} + curl ϕ)}, \end{matrix}

(51)

where we recall that

Y = Y^{*} = L^{2} (Ω; R^{3 N}) .

We emphasize such a dual formulation in

(v^{*}, ϕ)

is convex (in fact concave).

11. A note on the Galerkin Functional

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω

Consider the functional

J : V \to R

where

\begin{matrix} J (u) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{4} \int_{Ω} u^{4} d x \\ - \frac{β}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}} \end{matrix}

(52)

Here

V = W_{0}^{1, 2} (Ω)

γ > 0, α > 0, β > 0 .

We denote also

Y = Y^{*} = L^{2} (Ω) .

At this point we define

A^{+} = {u \in V : u f \geq 0, in Ω},

V_{2} = {{u \in V : ∥ u ∥}_{\infty} \leq K_{3}},

for some appropriate real constant

K_{3} > 0

and

V_{1} = A^{+} \cap V_{2} .

Observe that

J^{'} (u) = - γ \nabla^{2} u + α u^{3} - β - f,

so that we define the Galerkin functional

J_{1} : V \to R

J_{1} (u) = \frac{1}{2} {∥ J^{'} (u) ∥}_{2}^{2} = \frac{1}{2} \int_{Ω} {(- γ \nabla^{2} u + α u^{3} - β u - f)}^{2} d x .

From this, we get

\begin{matrix} \frac{\partial^{2} J_{1} (u)}{\partial u^{2}} & = & (- γ \nabla u + α u^{3} - β u - f) 6 α u \\ + {(- γ \nabla^{2} + 3 α u^{2} - β)}^{2} . \end{matrix}

(53)

Define now

φ_{2} = (- γ \nabla^{2} u + α u^{3} - β u - f) 6 α u .

At this point, for an appropriate small real constant

ε_{1} > 0

and bounded constant operator

M_{1} > ε_{1}

, we set the intended non-active restriction

\sqrt{3 α} | u | \geq \sqrt{| M_{1} + γ \nabla^{2} + β |},

and define

B_{1} = {u \in V_{1} : \sqrt{3 α} | u | \geq \sqrt{| M_{1} + γ \nabla^{2} + β |}} .

Observe that since for

u \in V_{1}

we have

u f \geq 0

Ω

so that if

u_{1}, u_{2} \in V_{1}

then

sign (u_{1}) = sign (u_{2}), in Ω,

we may infer that

B_{1}

is a convex set.

Furthermore, if

u \in B_{1}

, then

\sqrt{3 α} | u | \geq \sqrt{| M_{1} + γ \nabla^{2} + β |},

so that

3 α u^{2} \geq M_{1} + γ \nabla^{2} + β,

and hence

δ^{2} J (u) = - γ \nabla^{2} + 3 α u^{2} - β \geq M_{1} > ε_{1} > 0 .

For a small parameter

ε > 0

we define the intended non-active restriction

φ_{2} \geq - ε u^{2}, in Ω,

and define

B_{2} = {u \in V_{1} : φ_{2} \geq - ε u^{2}, in Ω .

Observe that

φ_{2} \geq - ε u^{2},

is equivalent to

K_{7} u^{2} \geq - φ_{2} - ε u^{2} + K_{7} u^{2},

which is equivalent to

K_{7} u^{2} \geq max {0, - φ_{2}} - ε u^{2} + K_{7} u^{2}, in Ω .

This last inequality is equivalent to

\sqrt{K_{7}} | u | \geq \sqrt{max {0, - φ_{2}} - ε u^{2} + K_{7} u^{2}},

that is,

\sqrt{max {0, - φ_{2}} - ε u^{2} + K_{7} u^{2}} - \sqrt{K_{7}} | u | \leq 0, in Ω .

Observe now that for

K_{7} > 0

sufficiently large, we have that the function

\sqrt{max {0, - φ_{2}} - ε u^{2} + K_{7} u^{2}}

is convex on

V_{1}

Moreover, if

u \in V_{1}

, we have

u f \geq 0, in Ω,

so that similarly as above indicated, we may infer that

- \sqrt{K_{7}} | u |

is a convex function on

V_{1} .

Summarizing

\sqrt{max {0, - φ_{2}} - ε u^{2} + K_{7} u^{2}} - \sqrt{K_{7}} | u |

is a convex function on

V_{1}

so that

B_{2}

is a convex set.

Assuming

0 < ε ≪ ε_{1} ≪ 1

, define

B_{3} = B_{1} \cap B_{2}

, which is a convex set.

Summarizing, if

u \in B_{3}

, then

δ^{2} J_{1} (u) \geq 0 .

With such results in mind, we define the following convex optimization problem for finding a critical point of J.

Minimize

J_{1} (u) = \frac{1}{2} {∥ J^{'} (u) ∥}_{2}^{2} = \frac{1}{2} \int_{Ω} {(- γ \nabla^{2} u + α u^{3} - β u - f)}^{2} d x,

subject to

u \in B_{3} .

Observe that a critical point

u_{0} \in B_{3}

J_{1}

, from such a concerning convexity of

J_{1}

on the convex set

B_{1}

, is also such that

J (u_{0}) = min_{u \in B_{3}} J_{1} (u) .

Finally, we may also define the convex optimization problem of minimizing

\begin{matrix} J_{3} (u) & = & K_{1} J_{1} (u) + J (u) \\ = & \frac{K_{1}}{2} \int_{Ω} {(- γ \nabla^{2} u + α u^{3} - β u - f)}^{2} d x \\ + \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{4} \int_{Ω} u^{4} d x \\ - \frac{β}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}}, \end{matrix}

(54)

subject to

u \in B_{3} .

Here

K_{1} > 0

is a large real constant.

Such a functional

J_{3}

is also convex on

B_{3}

so that a critical point

u_{0} \in B_{3}

of J is also a critical point of

J_{3}

, and thus

J_{3} (u_{0}) = min_{u \in B_{3}} J_{3} (u) .

12. A note on the Legendre-Galerkin functional

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω

Consider the functional

J : V \to R

where

\begin{matrix} J (u) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{α}{4} \int_{Ω} u^{4} d x \\ - \frac{β}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}} \end{matrix}

(55)

Here

V = W_{0}^{1, 2} (Ω)

γ > 0, α > 0, β > 0 .

We denote also

Y = Y^{*} = L^{2} (Ω)

and

F_{1} : V \to R

F_{2} : V \to R

and

F_{3} : V \to R

F_{1} (u) = \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x,

F_{2} (u) = \frac{α}{4} \int_{Ω} u^{4} d x,

F_{3} (u) = \frac{β}{2} \int_{Ω} u^{2} d x .

Moreover, we define

F_{1}^{*}, F_{2}^{*}, F_{3}^{*} : Y^{*} \to R

\begin{matrix} F_{1}^{*} (v_{1}^{*}) & = & sup_{u \in V} {{〈 u, v_{1}^{*} 〉}_{L^{2}} - F_{1} (u)} \\ = & \frac{1}{2} \int_{Ω} \frac{{(v_{1}^{*})}^{2}}{- γ \nabla^{2}} d x, \end{matrix}

(56)

\begin{matrix} F_{2}^{*} (v_{2}^{*}) & = & sup_{u \in V} {{〈 u, v_{2}^{*} 〉}_{L^{2}} - F_{2} (u)} \\ = & \frac{3}{4} \int_{Ω} \frac{{(v_{2}^{*})}^{4 / 3}}{α^{1 / 3}} d x, \end{matrix}

(57)

\begin{matrix} F_{3}^{*} (v_{3}^{*}) & = & sup_{u \in V} {{〈 u, v_{3}^{*} 〉}_{L^{2}} - F_{3} (u)} \\ = & \frac{1}{2 β} \int_{Ω} {(v_{3}^{*})}^{2} d x . \end{matrix}

(58)

Observe now that these three last suprema are attained through the equations,

v_{1}^{*} = \frac{\partial F_{1} (u)}{\partial u} = - γ \nabla^{2} u,

v_{2}^{*} = \frac{\partial F_{2} (u)}{\partial u} = α u^{3}

v_{3}^{*} = \frac{\partial F_{3} (u)}{\partial u} = β u .

From such results, at a critical point, we obtain the following compatibility conditions

u = \frac{v_{1}^{*}}{- γ \nabla^{2}} = {(\frac{v_{2}^{*}}{β})}^{1 / 3} = \frac{v_{3}^{*}}{β} .

From such relations we have

\frac{v_{1}^{*}}{- γ \nabla^{2}} = \frac{v_{3}^{*}}{β},

and

v_{2}^{*} = α {(\frac{v_{3}^{*}}{β})}^{3},

so that

v_{1}^{*} = - γ \nabla^{2} (\frac{v_{3}^{*}}{β}),

and

v_{2}^{*} = α {(\frac{v_{3}^{*}}{β})}^{3} .

Moreover, we define the functional

F_{4}^{*} : Y^{*} \to R,

F_{4}^{*} (v^{*}) = sup_{u \in V} {{〈 u, v_{1}^{*} + v_{2}^{*} - v_{3}^{*} 〉}_{L^{2}} - {〈 u, f 〉}_{L^{2}}} .

Therefore

F_{4}^{*} (v^{*}) = \{\begin{matrix} 0, & if v_{1}^{*} + v_{2}^{*} - v_{3}^{*} - f = 0, in Ω, \\ + \infty, & otherwise . \end{matrix}

(59)

Hence, a critical point of J corresponds to the solution of the following system of equations

v_{1}^{*} = - γ \nabla^{2} (\frac{v_{3}^{*}}{β}),

v_{2}^{*} = α {(\frac{v_{3}^{*}}{β})}^{3},

and

v_{1}^{*} + v_{2}^{*} - v_{3}^{*} - f = 0, in Ω .

From this last equation we may obtain

v_{1}^{*} = - v_{2}^{*} + v_{3}^{*} + f,

so that the final equations to be solved are

- v_{2}^{*} + v_{3}^{*} + f + γ \nabla^{2} (\frac{v_{3}^{*}}{β}) = 0

and

v_{2}^{*} - α {(\frac{v_{3}^{*}}{β})}^{3} = 0, in Ω,

with the boundary conditions

u = \frac{v_{3}^{*}}{β} = 0, on \partial Ω .

With such results in mind, we define the Legendre-Galerkin functional

J^{*} : {[Y^{*}]}^{2} \to R

, where

\begin{matrix} J^{*} (v^{*}) & = & \frac{1}{2} \int_{Ω} {(- v_{2}^{*} + v_{3}^{*} + f + \frac{γ \nabla^{2} v_{3}^{*}}{β})}^{2} d x \\ + \frac{1}{2} \int_{Ω} {(v_{2}^{*} - α {(\frac{v_{3}^{*}}{β})}^{3})}^{2} d x . \end{matrix}

(60)

At this point, defining

φ = v_{2}^{*} - α {(\frac{v_{3}^{*}}{β})}^{3},

we obtain

\frac{\partial^{2} J^{*} (v^{*})}{\partial {(v_{2}^{*})}^{2}} = 2;

\frac{\partial^{2} J^{*} (v^{*})}{\partial {(v_{3}^{*})}^{2}} = {(- 1 - \frac{γ \nabla^{2}}{β})}^{2} + \frac{9 α^{2} {(v_{3}^{*})}^{4}}{β^{6}} + O (φ),

\frac{\partial^{2} J^{*} (v^{*})}{\partial v_{2}^{*} \partial v_{3}^{*}} = \frac{- 3 α {(v_{3}^{*})}^{2}}{β^{3}} + (- 1 - \frac{γ \nabla^{2}}{β}) .

From such results we may infer that

\begin{matrix} det (\frac{\partial^{2} J^{*} (v^{*})}{\partial v_{2}^{*} \partial v_{3}^{*}}) & = & \frac{\partial^{2} J^{*} (v^{*})}{\partial {(v_{2}^{*})}^{2}} \frac{\partial^{2} J^{*} (v^{*})}{\partial {(v_{3}^{*})}^{2}} - {(\frac{\partial^{2} J^{*} (v^{*})}{\partial v_{2}^{*} \partial v_{3}^{*}})}^{2} \\ = & {(- 1 - \frac{γ \nabla^{2}}{β} + 3 α \frac{{(v_{3}^{*})}^{2}}{β^{3}})}^{2} + O (φ) \end{matrix}

(61)

Observe that a critical point

φ = 0

so that

δ^{2} J^{*} (v^{*}) > 0

at a neighborhood of any critical point.

At this point we define

A^{+} = \{v^{*} = (v_{2}^{*}, v_{3}^{*}) \in {[Y^{*}]}^{2} : \frac{v_{3}^{*}}{β} f \geq 0, in Ω\},

D^{*} = {v^{*} = (v_{2}^{*}, v_{3}^{*}) \in {[Y^{*}]}^{2} : ∥ v^{*} ∥_{\infty} \leq K},

for an appropriate real constant

K > 0

Finally, for an appropriate finite dimensional model version, in a finite differences or finite elements context, we assume

- γ \nabla^{2} - β < 0,

and define

E^{*} = A^{+} \cap D^{*}

We also define

C_{1}^{*} = {v^{*} = (v_{2}^{*}, v_{3}^{*}) \in E^{*} : φ^{2} \leq ε, in Ω},

for a small real constant

ε > 0,

C_{2}^{*} = \{v^{*} = (v_{2}^{*}, v_{3}^{*}) \in E^{*} : (- 1 - \frac{γ \nabla^{2}}{β} + 3 α \frac{{(v_{3}^{*})}^{2}}{β^{3}}) \geq ε_{1}\},

and

C^{*} = C_{1}^{*} \cap C_{2}^{*} .

Similarly as in the in the book [6], in Chapter 8, at section 8.7, in the proof of Theorem 8.7.1 at pages 299, 300 and 301, we may prove that

C^{*}

is a convex set.

Furthermore, for

0 < ε ≪ ε_{1} ≪ 1,

we have that

J^{*}

is convex on

C^{*}

Summarizing, we may define the following convex optimization problem to obtain a critical point of the primal functional J,

Minimize J^{*} (v_{2}^{*}, v_{3}^{*}) subject to v^{*} = (v_{2}^{*}, v_{3}^{*}) \in C^{*} .

We call

J^{*}

the Legendre-Galerkin functional associated to J.

12.1. Numerical examples

We have obtained numerical solutions for two one-dimensional examples.

1.: For $γ = 1.0,$ $α = 3.0,$ $β = 30.0,$ $f \equiv 10, in Ω = [0, 1] .$

For the respective solution please see Figure 7.
2.: For $γ = 0.01,$ $α = 3.0,$ $β = 30.0,$ $f \equiv 10, in Ω = [0, 1] .$

For the respective solution please see Figure 8.

References

R.A. Adams and J.F. Fournier. Sobolev Spaces, 2nd ed.; Elsevier: New York, NY, USA, 2003. [Google Scholar]
W.R. Bielski, A. W.R. Bielski, A. Galka, J.J. Telega, The Complementary Energy Principle and Duality for Geometrically Nonlinear Elastic Shells. I. Simple case of moderate rotations around a tangent to the middle surface. Bulletin of the Polish Academy of Sciences, Technical Sciences, Vol. 38, No. 7-9, 1988.
W.R. Bielski and J.J. Telega, A Contribution to Contact Problems for a Class of Solids and Structures, Arch. Mech., 37, 4-5, pp. 303-320, Warszawa 1985.
J.F. Annet, Superconductivity, Superfluids and Condensates, 2nd edn. (Oxford Master Series in Condensed Matter Physics, Oxford University Press, Reprint). 2010.
F.S. Botelho, Functional Analysis, Calculus of Variations and Numerical Methods in Physics and Engineering, CRC Taylor and Francis, Florida, 2020.
F.S. Botelho, Advanced Calculus and its Applications in Variational Quantum Mechanics and Relativity Theory, CRC Taylor and Francis, Florida, 2021.
F.S. Botelho, Variational Convex Analysis, Ph.D. thesis, Virginia Tech, Blacksburg, VA -USA, (2009).
F. Botelho, Topics on Functional Analysis, Calculus of Variations and Duality, Academic Publications, Sofia, (2011).
F. Botelho, Existence of solution for the Ginzburg-Landau system, a related optimal control problem and its computation by the generalized method of lines, Applied Mathematics and Computation, 218, 11976-11989, (2012). [CrossRef]
F. Botelho, Functional Analysis and Applied Optimization in Banach Spaces, Springer Switzerland, 2014.
P.Ciarlet, Mathematical Elasticity, Vol. II – Theory of Plates, North Holland Elsevier (1997).
J.C. Strikwerda, Finite Difference Schemes and Partial Differential Equations, SIAM, second edition (Philadelphia, 2004).
L.D. Landau and E.M. Lifschits, Course of Theoretical Physics, Vol. 5- Statistical Physics, part 1. (Butterworth-Heinemann, Elsevier, reprint 2008).
R.T. Rockafellar, Convex Analysis, Princeton Univ. Press, (1970).
J.J. Telega, On the complementary energy principle in non-linear elasticity. Part I: Von Karman plates and three dimensional solids, C.R. Acad. Sci. Paris, Serie II, 308, 1193-1198; Part II: Linear elastic solid and non-convex boundary condition. Minimax approach, ibid, pp. 1313.
A.Galka and J.J.Telega Duality and the complementary energy principle for a class of geometrically non-linear structures. Part I. Five parameter shell model; Part II. Anomalous dual variational priciples for compressed elastic beams. Arch. Mech. 1995, 677-698, 699–724.
J.F. Toland, A duality principle for non-convex optimisation and the calculus of variations, Arch. Rat. Mech. Anal., 71, No. 1 (1979), 41-61. [CrossRef]

Figure 1. Solution

u_{0} (x)

for the case

f (x) = 0

Figure 1. Solution

u_{0} (x)

for the case

f (x) = 0

Figure 2. Solution

u_{0} (x)

for the case

f (x) = sin (π x) / 2

Figure 2. Solution

u_{0} (x)

for the case

f (x) = sin (π x) / 2

Figure 3. Solution

u_{0} (x)

for the case

f (x) = 0

Figure 3. Solution

u_{0} (x)

for the case

f (x) = 0

Figure 4. Solution

u_{0} (x)

for the case

f (x) = sin (π x) / 2

Figure 4. Solution

u_{0} (x)

for the case

f (x) = sin (π x) / 2

Figure 5. Density

t (x, y)

for the Case A.

Figure 5. Density

t (x, y)

for the Case A.

Figure 6. Density

t (x, y)

for the Case B.

Figure 6. Density

t (x, y)

for the Case B.

Figure 7. Solution

u (x) = v_{3} (x) / β

for the example 1.

Figure 7. Solution

u (x) = v_{3} (x) / β

for the example 1.

Figure 8. Solution

u (x) = v_{3} (x) / β

for the example 2.

Figure 8. Solution

u (x) = v_{3} (x) / β

for the example 2.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Duality Principles and Numerical Procedures for a Large Class of Non-convex Models in the Calculus of Variations

Abstract

1. Introduction

2. A general duality principle non-convex optimization

3. Another duality principle for a simpler related model in phase transition with a respective numerical example

4. A convex dual variational formulation for a third similar model

4.1. The algorithm through which we have obtained the numerical results

5. An improvement of the convexity conditions for a non-convex related model through an approximate primal formulation

6. An exact convex dual variational formulation for a non-convex primal one

7. Another primal dual formulation for a related model

8. A third primal dual formulation for a related model

9. An algorithm for a related model in shape optimization

9.1. Introduction

9.2. Mathematical formulation of the topology optimization problem

9.3. About a concerning algorithm and related numerical method

10. A duality principle for a general vectorial case in the calculus of variations

11. A note on the Galerkin Functional

12. A note on the Legendre-Galerkin functional

12.1. Numerical examples

References

MDPI Initiatives

Important Links

Subscribe