Preprint
Article
Duality Principles and Numerical Procedures for a Large Class of Non-convex Models in the Calculus of Variations
Altmetrics
Downloads
4092
Views
3880
Comments
1
This version is not peer-reviewed
Submitted:
11 September 2023
Posted:
12 September 2023
Read the latest preprint version here
Alerts
Abstract
This article develops duality principles and numerical results for a large class of non-convex variational models. The main results are based on fundamental tools of convex analysis, duality theory and calculus of variations. More specifically the approach is established for a class of non-convex functionals similar as those found in some models in phase transition. Finally, in some sections we present concerning numerical examples and the respective softwares.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
MSC: 49N15
1. Introduction
In this section we establish a dual formulation for a large class of models in non-convex optimization.
The main duality principle is applied to double well models similar as those found in the phase transition theory.
Such results are based on the works of J.J. Telega and W.R. Bielski [2,3,15,16] and on a D.C. optimization approach developed in Toland [17].
About the other references, details on the Sobolev spaces involved are found in [1]. Related results on convex analysis and duality theory are addressed in [5,7,8,10,14].
Finally, in this text we adopt the standard Einstein convention of summing up repeated indices, unless otherwise indicated.
In order to clarify the notation, here we introduce the definition of topological dual space.
Definition 1.1
(Topological dual spaces). Let U be a Banach space. We shall define its dual topological space, as the set of all linear continuous functionals defined on U. We suppose such a dual space of U, may be represented by another Banach space , through a bilinear form (here we are referring to standard representations of dual spaces of Sobolev and Lebesgue spaces). Thus, given linear and continuous, we assume the existence of a unique such that
The norm of f , denoted by , is defined as
At this point we start to describe the primal and dual variational formulations.
2. A general duality principle non-convex optimization
In this section we present a duality principle applicable to a model in phase transition.
This case corresponds to the vectorial one in the calculus of variations.
Let be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by
Consider a functional where
and where
and
We assume there exists such that
Moreover, suppose F and G are Fréchet differentiable but not necessarily convex. A global optimum point may not be attained for J so that the problem of finding a global minimum for J may not be a solution.
Anyway, one question remains, how the minimizing sequences behave close the infimum of J.
We intend to use duality theory to approximately solve such a global optimization problem.
Denoting , , , at this point we define, , , , and by
and
and
Define now ,
Observe that
.
From the general results in [17], we may infer that
On the other hand
From these last two results we may obtain
Moreover, from standards results on convex analysis, we may have
where
and
Thus, defining
we have got
Finally, observe that
This last variational formulation corresponds to a concave relaxed formulation in concerning the original primal formulation.
3. Another duality principle for a simpler related model in phase transition with a respective numerical example
In this section we present another duality principle for a related model in phase transition.
Let and consider a functional where
and where
and
A global optimum point is not attained for J so that the problem of finding a global minimum for J has no solution.
Anyway, one question remains, how the minimizing sequences behave close the infimum of J.
We intend to use duality theory to approximately solve such a global optimization problem.
Denoting , at this point we define, and by
and
Observe that
In order to restrict the action of on the region where the primal functional is non-convex, we redefine a not relabeled
and define also
and
by
and
Denoting we also define the polar functional by
Observe that
With such results in mind, we define a relaxed primal dual variational formulation for the primal problem, represented by , where
Having defined such a functional, we may obtain numerical results by solving a sequence of convex auxiliary sub-problems, through the following algorithm (in order to obtain the concerning critical points, at first we have neglected the constraint ).
- 1.
- Set and and
- 2.
- Choose such that and
- 3.
- Set
- 4.
- Calculate solution of the system of equations:andthat isandso thatand
- 5.
- Calculate by solving the system of equations:andthat isand
- 6.
- If , then stop, else set and go to item 4.
At this point, we present the corresponding software in MAT-LAB, in finite differences and based on the one-dimensional version of the generalized method of lines.
Here the software.
***********************
- 1.
-
clear allm8=300;d=1/m8;K=0.1;K1=120;for i=1:m8vo(i,1)=i*d/10;yo(i,1)=sin(i*d*pi)/2;end;k=1;b12=1.0;while andk=k+1;for i=1:m8-1duo(i,1)=(uo(i+1,1)-uo(i,1))/d;dvo(i,1)=(vo(i+1,1)-vo(i,1))/d;end;m9=zeros(2,2);m9(1,1)=1;i=1;m80(1,1,i)=-f1-K;m80(1,2,i)=-f1;m80(2,1,i)=-f1;m80(2,2,i)=-f1-K1;m50(:,:,i)=m80(:,:,i)*inv(m12);z(:,i)=inv(m12)*y11(:,i)*;for i=2:m8-1;m80(1,1,i)=-f1-K;m80(1,2,i)=-f1;m80(2,1,i)=-f1;m80(2,2,i)=-f1-K1;m50(:,:,i)=inv(m12)*m80(:,:,i);end;U(1,m8)=1/2;U(2,m8)=0.0;for i=1:m8-1U(:,m8-i)=m50(:,:,m8-i)*U(:,m8-i+1)+z(:,m8-i);end;for i=1:m8u(i,1)=U(1,i);v(i,1)=U(2,i);end;b12=max(abs(u-uo))uo=u;vo=v;u(m8/2,1)end;for i=1:m8y(i)=i*d;end;plot(y,uo)**************************************
For the case in which , we have obtained numerical results for and . For such a concerning solution obtained, please see Figure 1. For the case in which , we have obtained numerical results also for and . For such a concerning solution obtained, please see Figure 2.
Remark 3.1.
Observe that the solutions obtained are approximate critical points. They are not, in a classical sense, the global solutions for the related optimization problems. Indeed, such solutions reflect the average behavior of weak cluster points for concerning minimizing sequences.
3.1. A general proposal for relaxation
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
Consider a functional where
where
, is convex and Fréchet differentiable, and
where is also Fréchet differentiable.
Assume there exists such that
where for each is an open connected set such that is regular. We also suppose
Define
and define also
At this point we define
and
where
Moreover, we propose the relaxed functional
Observe that clearly
4. A convex dual variational formulation for a third similar model
In this section we present another duality principle for a third related model in phase transition.
Let and consider a functional where
and where
and
A global optimum point is not attained for J so that the problem of finding a global minimum for J has no solution.
Anyway, one question remains, how the minimizing sequences behave close to the infimum of J.
We intend to use the duality theory to solve such a global optimization problem in an appropriate sense to be specified.
At this point we define, and by
and
Denoting we also define the polar functional and by
and
Observe this is the scalar case of the calculus of variations, so that from the standard results on convex analysis, we have
Indeed, from the direct method of the calculus of variations, the maximum for the dual formulation is attained at some .
Moreover, the corresponding solution is obtained from the equation
Finally, the Euler-Lagrange equations for the dual problem stands for
where if if and
if
We have computed the solutions and corresponding solutions for the cases in which and
For the solution for the case in which , please see Figure 3.
For the solution for the case in which , please see Figure 4.
Remark 4.1.
Observe that such solutions obtained are not the global solutions for the related primal optimization problems. Indeed, such solutions reflect the average behavior of weak cluster points for concerning minimizing sequences.
4.1. The algorithm through which we have obtained the numerical results
In this subsection we present the software in MATLAB through which we have obtained the last numerical results.
This algorithm is for solving the concerning Euler-Lagrange equations for the dual problem, that is, for solving the equation
Here the concerning software in MATLAB. We emphasize to have used the smooth approximation
where a small value for is specified in the next lines.
*************************************
- 1.
- clear all
- 2.
- (number of nodes)
- 3.
- 4.
- 5.
- 6.
- 7.
-
(we have fixed the number of iterations)
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
********************************
5. An improvement of the convexity conditions for a non-convex related model through an approximate primal formulation
In this section we develop an approximate primal dual formulation suitable for a large class of variational models.
Here, the applications are for the Kirchhoff-Love plate model, which may be found in Ciarlet, [11].
At this point we start to describe the primal variational formulation.
Let be an open, bounded, connected set which represents the middle surface of a plate of thickness h. The boundary of , which is assumed to be regular (Lipschitzian), is denoted by . The vectorial basis related to the cartesian system is denoted by , where (in general Greek indices stand for 1 or 2), and where is the vector normal to , whereas and are orthogonal vectors parallel to Also, is the outward normal to the plate surface.
The displacements will be denoted by
The Kirchhoff-Love relations are
Here so that we have where
It is worth emphasizing that the boundary conditions here specified refer to a clamped plate.
We also define the operator , where , by
The constitutive relations are given by
where: and , are symmetric positive definite fourth order tensors. From now on, we denote and .
Furthermore denote the membrane force tensor and the moment one. The plate stored energy, represented by is expressed by
and the external work, represented by , is given by
where are external loads in the directions , and respectively. The potential energy, denoted by is expressed by:
Define now by
where
In such a case for , , in and
we get
and
This new functional has a relevant improvement in the convexity conditions concerning the previous functional J.
Indeed, we have obtained a gain in positiveness for the second variation which has increased of order
Moreover the difference between the approximate and exact equation
is of order which corresponds to a small perturbation in the original equation for a load of for example. Summarizing, the exact equation may be approximately solved in an appropriate sense.
5.1. A duality principle for the concerning quasi-convex envelope
In this section, denoting
we define the functional , where
where
and,
We define also
and
It is a well known result from the modern Calculus of Variations theory that
At this point we denote
and
Observe that
, where
and
Also
and
in an appropriate tensor sense.
Here it is worth highlighting we have denoted,
where we recall that
in an appropriate tensorial sense.
Summarizing, defining by
we have got
Remark 5.1.
This last dual functional is concave and such a concerning inequality corresponds a duality principle for the relaxed primal formulation.
We emphasize such results are extensions and in some sense complement the original duality principles in the works of Telega and Bielski, [2,3,15].
Moreover, if is such that
it is a well known result from the Legendre transform proprieties that the corresponding such that
and
is also such that
and
From this and
we obtain
Also, from the modern calculus of variations theory, there exists a sequence such that
and
From this and the Ekeland variational principle, there exists such that
and
so that
and
Assume now we are dealing with a finite dimensional version of such a model, in a finite elements of finite differences context, for example.
In such a case we have
for an appropriate
From continuity we obtain
Summarizing, we have got
Here we highlight such last results are valid just for this finite-dimensional model version.
6. An exact convex dual variational formulation for a non-convex primal one
In this section we develop a convex dual variational formulation suitable to compute a critical point for the corresponding primal one.
Let be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by
Consider a functional where
and
Here we denote and
Defining
for some appropriate , suppose also F is twice Fréchet differentiable and
Define now and by
and
where here we denote
Moreover, we define the respective Legendre transform functionals and as
where are such that
and
where are such that
Here is any function such that
Furthermore, we define
Observe that through the target conditions
we may obtain the compatibility condition
Define now
for some appropriate such that is convex in
Consider the problem of minimizing subject to
Assuming is large enough so that the restriction in r is not active, at this point we define the associated Lagrangian
where is an appropriate Lagrange multiplier.
Therefore
The optimal point in question will be a solution of the corresponding Euler-Lagrange equations for
From the variation of in we obtain
From the variation of in we obtain
From the variation of in we have
From this last equation, we may obtain such that
and
From this and the previous extremal equations indicated we have
and
so that
and
Replacing the expressions of and into this last equation, we have
so that
Observe that if
then there exists such that u and are also such that
and
The boundary conditions for must be such that
From this and equation (34) we obtain
Summarizing, we may obtain a solution of equation by minimizing on .
Finally, observe that clearly is convex in an appropriate large ball for some appropriate
7. Another primal dual formulation for a related model
Let be an open, bounded and connected set with a regular boundary denoted by
Consider the functional where
, and
Denoting , define now by
Define also
and
for some appropriate to be specified.
Moreover define
for some appropriate to be specified.
Observe that, denoting
we have
and
so that
Observe now that a critical point and in .
Therefore, for an appropriate large , also at a critical point, we have
Remark 7.1.
From this last equation we may observe that has a large region of convexity about any critical point , that is, there exists a large such that is convex on
With such results in mind, we may easily prove the following theorem.
Theorem 7.2.
Assume and suppose is such that
Under such hypotheses, there exists such that is convex in ,
and
8. A third primal dual formulation for a related model
Let be an open, bounded and connected set with a regular boundary denoted by
Consider the functional where
, and
Denoting , define now by
where is a small real constant.
Define also
and
for some appropriate to be specified.
Moreover define
and
for some appropriate real constants to be specified.
Remark 8.1.
Define now
For an appropriate function (or, in a more general fashion, an appropriate bounded operator) define
for some small parameter
Moreover, define
Since for we have , so that for we have
we may infer that is a convex set.
Moreover if , then
so that
and
so that
Such a result we will be used many times in the next sections.
Observe that, defining
we may obtain
and
so that
However, at a critical point, we have so that, for a fixed we define the non-active but convex restriction
for a small parameter
From such results, assuming and , we have that
for and
With such results in mind, we may easily prove the following theorem.
Theorem 8.2.
Suppose is such that
Under such hypotheses, we have that
and
Proof.
The proof that
and
may be easily made similarly as in the previous sections.
Moreover, observe that for sufficiently large, we have
so that this and the other hypotheses, we have also
and
From this, from a standard saddle point theorem and the remaining hypotheses, we may infer that
Moreover, observe that
Summarizing, we have got
From such results, we may infer that
The proof is complete. □
9. An algorithm for a related model in shape optimization
The next two subsections have been previously published by Fabio Silva Botelho and Alexandre Molter in [5], Chapter 21.
9.1. Introduction
Consider an elastic solid which the volume corresponds to an open, bounded, connected set, denoted by with a regular (Lipschitzian) boundary denoted by where Consider also the problem of minimizing the functional where
subject to
Here denotes the outward normal to and
where
and denotes the Lebesgue measure of
Moreover is the field of displacements relating the cartesian system , resulting from the action of the external loads and
We also define the stress tensor by
and the strain tensor by
Finally,
where corresponds to a strong material and to a very soft material, intending to simulate voids along the solid structure.
The variable t is the design one, which the optimal distribution values along the structure are intended to minimize its inner work with a volume restriction indicated through the set B.
The duality principle obtained is developed inspired by the works in [2,3]. Similar theoretical results have been developed in [10], however we believe the proof here presented, which is based on the min-max theorem is easier to follow (indeed we thank an anonymous referee for his suggestion about applying the min-max theorem to complete the proof). We highlight throughout this text we have used the standard Einstein sum convention of repeated indices.
Moreover, details on the Sobolev spaces addressed may be found in [1]. In addition, the primal variational development of the topology optimization problem has been described in [10].
The main contributions of this work are to present the detailed development, through duality theory, for such a kind of optimization problems. We emphasize that to avoid the check-board standard and obtain appropriate robust optimized structures without the use of filters, it is necessary to discretize more in the load direction, in which the displacements are much larger.
9.2. Mathematical formulation of the topology optimization problem
Our mathematical topology optimization problem is summarized by the following theorem.
Theorem 9.1.
Consider the statements and assumptions indicated in the last section, in particular those refereing to Ω and the functional
Define by
where
and where
Define also by
Assume there exists such that
and
Finally, define by
where
where
and
Under such hypotheses, there exists such that
where
and where
and
Proof.
Observe that
Also, from this and the min-max theorem, there exist such that
Finally, from the extremal necessary condition
we obtain
and
so that
Hence so that and
Moreover
This completes the proof. □
9.3. About a concerning algorithm and related numerical method
For numerically solve this optimization problem in question, we present the following algorithm
- 1.
- Set and .
- 2.
- Calculate such that
- 3.
- Calculate such that
- 4.
- If or then stop, else set and go to item 2.
We have developed a software in finite differences for solving such a problem.
Here the software.
**************************************
- 1
-
clear allglobal P m8 d w u v Ea Eb Lo d1 z1 m9 du1 du2 dv1 dv2 c3m8=27;m9=24;c3=0.95;d=1.0/m8;d1=0.5/m9;Ea=; (stronger material)Eb=1000; (softer material simulating voids)w=0.30;P=-42000000;z1=(m8-1)*(m9-1);A3=zeros(z1,z1);for i=1:z1A3(1,i)=1.0;end;b=zeros(z1,1);uo=0.000001*ones(z1,1);u1=ones(z1,1);b(1,1)=c3*z1;for i=1:m9-1for j=1:m8-1Lo(i,j)=c3;end; end;for i=1:z1x1(i)=c3*z1;end;for i=1:2*m8*m9xo(i)=0.000;end;xw=xo;xv=Lo;for k2=1:24c3=0.98*c3;b(1,1)=c3*z1;k2b14=1.0;k3=0;while andk3=k3+1;b12=1.0;k=0;while andk=k+1;k2k3kX=fminunc(’funbeam’,xo);xo=X;b12=max(abs(xw-xo));xw=X;end;for i=1:m9-1for j=1:m8-1ex=du1(i,j);ey=dv2(i,j);exy=1/2*(dv1(i,j)+du2(i,j));Sxy=E1/(2*(1+w))*exy;dc3(i,j)=-(Sx*ex+Sy*ey+2*Sxy*exy);end;end;for i=1:m9-1for j=1:m8-1f(j+(i-1)*(m8-1))=dc3(i,j);end;end;for k1=1:1k1X1=linprog(f,,,A3,b,uo,u1,x1);x1=X1;end;for i=1:m9-1for j=1:m8-1Lo(i,j)=X1(j+(m8-1)*(i-1));end;end;b14=max(max(abs(Lo-xv)))xv=Lo;colormap(gray); imagesc(-Lo); axis equal; axis tight; axis off;pause(1e-6)end;end;
****************************************************
Here the auxiliary Function ’funbeam’
function S=funbeam(x)
global P m8 d w u v Ea Eb Lo d1 m9 du1 du2 dv1 dv2
for i=1:m9
for j=1:m8
u(i,j)=x(j+(m8)*(i-1));
v(i,j)=x(m8*m9+(i-1)*m8+j);
end;
end;
for i=1:m9
end;
u(m9-1,1)=0;
v(m9-1,1)=0;
u(m9-1,m8-1)=0;
v(m9-1,m8-1)=0;
for i=1:m9-1
for j=1:m8-1
du1(i,j)=(u(i,j+1)-u(i,j))/d;
du2(i,j)=(u(i+1,j)-u(i,j))/d1;
dv1(i,j)=(v(i,j+1)-v(i,j))/d;
dv2(i,j)=(v(i+1,j)-v(i,j))/d1;
end;
end;
S=0;
for i=1:m9-1
for j=1:m8-1
ex=du1(i,j);
ey=dv2(i,j);
exy=1/2*(dv1(i,j)+du2(i,j));
Sxy=E1/(2*(1+w))*exy;
S=S+1/2*(Sx*ex+Sy*ey+2*Sxy*exy);
end;
end;
S=S*d*d1-P*v(2,(m8)/3)*d*d1;
***********************************************
For a two dimensional beam of dimensions and we have obtained the following results:
10. A duality principle for a general vectorial case in the calculus of variations
In this section we develop a duality principle for a general vectorial case in variational optimization.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by . Let be a functional where
where
and
Here we have denoted and
so that we may also denote
Assume
where is a differentiable function such that
as . Moreover, suppose there exists such that
It is well known that
Under some mild hypotheses, from convexity, we have that
where
Now observe that the restriction for some is equivalent to the restriction
where , with appropriate boundary conditions, so that with an appropriate Lagrange multiplier , we obtain
where we have denoted
and
Joining the pieces, we have got
where we recall that
We emphasize such a dual formulation in is convex (in fact concave).
11. A note on the Galerkin Functional
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by .
Consider the functional where
Here ,
We denote also
At this point we define
for some appropriate real constant and
Observe that
so that we define the Galerkin functional by
From this, we get
Define now
At this point, for an appropriate small real constant and bounded constant operator , we set the intended non-active restriction
and define
Observe that since for we have in so that if then
we may infer that is a convex set.
Furthermore, if , then
so that
and hence
For a small parameter we define the intended non-active restriction
and define
Observe that for and sufficiently large is convex in (positive definite Hessian) so that is a convex set. Assuming , define , which is a convex set.
Summarizing, if , then
With such results in mind, we define the following convex optimization problem for finding a critical point of J.
Minimize
subject to
Observe that a critical point of , from such a concerning convexity of on the convex set , is also such that
Finally, we may also define the convex optimization problem of minimizing
subject to
Here is a large real constant.
Such a functional is also convex on so that a critical point of J is also a critical point of , and thus
12. A note on the Legendre-Galerkin functional
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by .
Consider the functional where
Here ,
We denote also
and , and by
Moreover, we define by
Observe now that these three last suprema are attained through the equations,
From such results, at a critical point, we obtain the following compatibility conditions
From such relations we have
and
so that
and
Moreover, we define the functional by
Therefore
Hence, a critical point of J corresponds to the solution of the following system of equations
and
From this last equation we may obtain
so that the final equations to be solved are
and
with the boundary conditions
With such results in mind, we define the Legendre-Galerkin functional , where
At this point, defining
we obtain
From such results we may infer that
Observe that a critical point so that at a neighborhood of any critical point.
At this point we define
for an appropriate real constant .
Define now ,
for a small real constant
and
Similarly as done in the previous section, we may prove that is a convex set.
Furthermore, for we have that is convex on .
Summarizing, we may define the following convex optimization problem to obtain a critical point of the primal functional J,
We call the Legendre-Galerkin functional associated to J.
12.1. Numerical examples
We have obtained numerical solutions for two one-dimensional examples.
13. A general concave dual variational formulation for global optimization
Let be an open, bounded and connected set a regular (Lipschitzian) boundary denoted by
Consider a functional where
Here , and we also denote
Assume there exists such that
Furthermore, suppose G is three times Fréchet differentiable and there exists such that
Define now where,
where
and
Moreover, we define the polar functionals and , where
and
At this point we define the functional by
With such results in mind we define
and
for appropriated real constants and
Moreover, we define also the penalized functional where
Finally, we remark that for sufficiently small and sufficiently large, is concave in around a concerning critical point. We recall that a critical point
14. A related restricted problem in phase transition
In this section we develop a convex (in fact concave) dual variational for a model similar to those found in phase transition problems.
Let Consider the functional where
Here
We also denote and
Furthermore, we define the functionals G and by
and
Moreover we define by
and consider the problem of minimizing on the set
Already including the Lagrange multiplier concerning such restrictions, we define
Observe now that
where
Also,
where
From this we may infer that for some
Summarizing, denoting , and
we have got
We have developed numerical results by maximizing the dual functional for two examples, namely.
15. One more dual variational formulation
In this section we develop one more dual variational formulation for a related model.
Let and consider the functional defined by
where
We define also the relaxed functional , already including a concerning restriction and corresponding non-negative Lagrange multiplier , where
where
Observe that
Here, we highlight , for some real constant c.
Hence, denoting
and
we have obtained
Finally, for
we emphasize is concave on .
Here is a small regularizing real constant.
Remark 15.1.
The constraint is included to restrict the action of v on the region where the primal functional is non-convex, through an appropriate constant
16. A duality principle for a related relaxed formulation concerning the vectorial approach in the calculus of variations
In this section we develop a duality principle for a related vectorial model in the calculus of variations.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
For , consider a functional where
where
and
We assume and are Fréchet differentiable and F is also convex.
Also
where it is supposed to be Fréchet differentiable. Here we have denoted .
We define also by
where
and
Moreover, we define the relaxed functional by
where
Now observe that
, where
Here we have denoted
where and where
Furthermore, for , we have
Therefore, denoting by
we have got
Finally, we highlight such a dual functional is convex (in fact concave).
16.1. An example in finite elasticity
In this section we develop an application of results obtained in the last section to a model in non-linear elasticity.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
Concerning a standard model in non-linear elasticity, consider a functional where
where and
Here is a fourth-order and positive definite symmetric tensor (in an appropriate standard sense). Moreover, is a field of displacements resulting from the f load field action on the volume comprised by .
At this point, we define the functional , where
where
We define also the quasi-convex envelop of J, denoted by , as
It is a well known result from the modern calculus of variations theory that
Observe now that, denoting , and
we have that
, where ,
Hence, denoting
we have obtained
Remark 16.1.
This last dual functional is concave and such a concerning inequality corresponds a duality principle for the relaxed primal formulation.
We emphasize again such results are also extensions and in some sense complement the original duality principles in the works of Telega and Bielski, [2,3,15].
We emphasize such results are extensions and in some sense complement the original duality principles in the works of Telega and Bielski, [2,3,15].
Moreover, if is such that
it is a well known result from the Legendre transform proprieties that the corresponding such that
and
is also such that
and
From this and
we obtain
Also, from the modern calculus of variations theory, there exists a sequence such that
and
From this and the Ekeland variational principle, there exists such that
and
so that
and
Assume now we are dealing with a finite dimensional version of such a model, in a finite elements of finite differences context, for example.
In such a case we have
for an appropriate
From continuity we obtain
Summarizing, we have got
Here we highlight such last results are valid just for this finite-dimensional model version.
17. A model in superconductivity through an eigenvalue approach
In this section we intend to model superconductivity through a two phase eigenvalue approach.
Let be a straight wire corresponding to a one-dimensional super-conducting sample.
Consider the functional where
Here, in atomic units, is the total electronic charge, and we set corresponding to higher self-interacting energy which is related to a normal phase. We also set corresponding to a lower self-interacting energy which is related to a super-conducting phase and respective super-currents.
Moreover, we set and initially which is gradually decreased to .
Furthermore, we define
and
where corresponds to a normal phase and to a super-conducting one.
At this point we observe that the temperature is proportional the frequency of vibration for the normal phase.
We start the process with which in atomic units corresponds to a higher temperature and gradually decreases it to the value
Between and the system changes from an almost total normal phase to an almost total super-conducting phase, as expected.
We highlight that the temperature is proportional to the vibrational kinetics energy
so that for
and for a suitable vectorial function , we have
so that we may model the decreasing of temperature T through the decreasing of .
For , for the corresponding normal phase and super-conducting phase , please se Figure 11 and Figure 12, respectively.
For , for the corresponding normal phase and super-conducting phase , please se Figure 13 and Figure 14, respectively.
Finally, we have set which for large corresponds to the super-currents.
18. A simplified qualitative many body model for the hydrogen nuclear fusion
In this section we develop a qualitative simple model for the hydrogen nuclear fusion.
Let be a box in which is confined a gas comprised by an amount of ionized deuterium and tritium isotopes of hydrogen.
Though a suitable increasing in temperature, we intend to develop the following nuclear reaction
We recall that the ionized Deuterium atom comprises a proton and a neutron and the ionized Tritium atom comprises a proton and two neutrons.
Under certain conditions and at a suitable high temperature the ionized Deuterium and Tritium atoms react chemically resulting in an ionized Helium atom, comprised by two protons and two neutrons and resulting also in one more single energetic neutron. We emphasize the higher kinetics neutron energy level has many potential practical applications, including its conversion in electric energy.
At this point we denote by the masses of the ionized Deuterium, Tritium and Helium atoms, and the single neutron, respectively.
Therefore, we have the following mass relation
To simplify our analysis, in such a chemical reaction, denoting the total masses of ionized Deuterium, Tritium, Helium and single Neutrons by and we assume there is a real constant such that
With such statements and definitions in mind, we define the following functional J, where
where, in a simplified many body context,
Here refers to the particle densities.
Furthermore, we assume and , so that
and,
and the kinetics energy is expressed by
where we also assume
so that considering such a vibrational motion, the temperature T is proportional to , that is
Therefore, an increasing in T corresponds to a proportional increasing in
Summarizing, we have supposed
so that we represent the increasing in T through an increasing in
Moreover, we denote by the mass of a single neutron and by the mass of a single proton.
Thus, denoting also by the proportion of non-reacted and reacted masses respectively, we have the following constraints.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
Similar constraints are valid corresponding to the charge of a single proton.
We have also the following complementing constraints,
- 1.
- 2.
- 3.
- 4.
- 5.
With such results and statements in mind and simplifying the interacting terms, we re-define the functional J now denoting it by , here already including the Lagrange multipliers concerning the constraints, where
where the functional stands for
Remark 18.1.
In order to obtain consistent results it is necessary to set
In such a case, a higher temperature corresponding to a large , though such a nuclear reaction, will result in a small and a higher kinetics energy for the neutron field, corresponding to a large and closer to 1.
19. A more detailed mathematical description of the hydrogen nuclear fusion
In this section we develop in more details another model for the hydrogen nuclear fusion.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
Here such a set stands for a control volume in which an ionized gas (plasma) flows. Such a gas comprises ionized Deuterium and Tritium atoms intended, through a suitable higher temperature, to chemically react resulting in atoms of Hellion and a field of single energetic Neutrons.
Symbolically such a reaction stands for
We recall that the ionized Deuterium atom is comprised by a proton and a neutron and the ionized Tritium atom is comprised by a proton and two neutrons.
Moreover, the ionized Helium atom is comprised by two protons and two neutrons.
As previously mentioned, resulting from such a chemical reaction up surges also an energetic neutron which the higher kinetics energy has a great variety of applications, including its conversion in electric energy.
We highlight the model here presented includes electric and magnetic fields and the corresponding potential ones.
Denoting by t the time on the interval at this point we define the following density functions:
- 1.
- For the Deuterium field
- 2.
- For the Tritium field
- 3.
- For the Helium field
- 4.
- For the Neutron field
- 5.
- For the electronic field resulting from the ionization
Furthermore, we define also the related densities
- 1.
- 2.
For the chemical reaction in question we consider that one unit of mass of fractional proportion of ionized Deuterium and of ionized Tritium results in one unit of mass of fractional proportion of ionized Helium and of neutrons.
Symbolic, this stands for
Concerning the control volume in question and related surface control we assume such a volume has an initial (fot ) amount of ionized Deuterium of and an initial amount of ionized Tritium of The initial amount of ionized Helium and single neutrons are supposed to be zero.
On the other hand, about the surface control , we assume there is a part for which is allowed the entrance and exit of Deuterium and Tritium ionized atoms.
We assume also there is another part such that for which is allowed only the exit of ionized Helium atoms and neutrons, but not their entrance.
In is allowed the exit only (not the entrance) of ionized Deuterium and Tritium atoms.
Indeed, we assume the following relations for the masses:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- so that
- 8.
- 9.
- 10.
- 11.
- 12.
Here denotes the outward normal vectorial fields to the concerning surfaces.
Having clarified such masses relations, we define the functional
where
and where we assume and , so that
and
and the internal kinetics energy is expressed by
Here it is worth highlighting we have approximated the initially discrete set of indices s of particles as a continuous positive real variable s.
Moreover,
where and are appropriate real constants related to the respective charges.
Here is the fluid velocity field and
are fields of displacements for the corresponding atom fields.
Also denotes the magnetic potential, an external magnetic field and is the total magnetic field.
Moreover, is an induced electric field.
Finally,
for appropriate real positive constants
Such a functional J is subject to the following constraints:
- 1.
-
The momentum conservation equation for the fluid motionHere is the total density and P is the fluid pressure field.Furthermore,and
- (2)
- Mass conservation equation:
- (3)
-
Energy equationwhere we assume the Fourier lawwhere is the scalar field of temperature.Also,and
- (4)
- for an appropriate scalar function .
- (5)
- Mass relations
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- so that
where,
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (6)
-
Other mass constraints
- (a)
- (b)
- (c)
- (d)
- (e)
- 7.
- For the induced electric field, we must havewhere and are appropriate real constants related to the respective charges.
- 8.
- A Maxwell equation:where
- 9.
- Another Maxwell equation:where the total electric field stands forand where generically denotingwe have also
At this point we generically denote
Thus, already including the Lagrange multipliers concerning the restrictions indicated, the extended functional stands for
where,
Here we recall the following definitions and relations:
- 1.
- For the Deuterium field
- 2.
- For the Tritium field
- 3.
- For the Helium field
- 4.
- For the Neutron field
- 5.
- For the electronic field resulting from the ionization
- 1.
- 2.
Also,
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- so that
- 10.
- 11.
- 12.
Finally,
and where generically denoting
we have also
and,
20. A final mathematical description of the hydrogen nuclear fusion
In this section we develop in even more details another model for the hydrogen nuclear fusion.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
Here such a set stands for a control volume in which an ionized gas (plasma) flows. Such a gas comprises ionized Deuterium and Tritium atoms intended, through a suitable higher temperature, to chemically react resulting in atoms of Helium and a field of single energetic Neutrons.
Symbolically such a reaction stands for
We recall that the ionized Deuterium atom is comprised by a proton and a neutron and the ionized Tritium atom is comprised by a proton and two neutrons.
Moreover, the ionized Helium atom is comprised by two protons and two neutrons.
As previously mentioned, resulting from such a chemical reaction up surges also an energetic neutron which the higher kinetics energy has a great variety of applications, including its conversion in electric energy.
We highlight the model here presented includes electric and magnetic fields and the corresponding potential ones.
Denoting by t the time on the interval at this point we define the following density functions:
- 1.
- For a single Deuterium atom indexed by s:
- 2.
- For a single Tritium atom indexed by s:
- 3.
- For a single Helium atom indexed by s:
- 4.
- For the Neutron field:
- 5.
- For the electronic field resulting from the ionization
Furthermore, we define also the related densities
- 1.
- 2.
For the chemical reaction in question we consider that one unit of mass of fractional proportion of ionized Deuterium and of ionized Tritium results in one unit of mass of fractional proportion of ionized Helium and of neutrons.
Symbolically, this stands for
Concerning the control volume in question and related surface control we assume such a volume has an initial (fot ) amount of ionized Deuterium of and an initial amount of ionized Tritium of The initial amount of ionized Helium and single neutrons are supposed to be zero.
On the other hand, about the surface control , we assume there is a part for which is allowed the entrance and exit of Deuterium and Tritium ionized atoms.
We assume also there is another part such that for which is allowed only the exit of ionized Helium atoms and neutrons, but not their entrance.
In is allowed the exit only (not the entrance) of ionized Deuterium and Tritium atoms.
Indeed, we assume the following relations for the masses:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
-
so that
- 10.
- 11.
- 12.
Here denotes the outward normal vectorial fields to the concerning surfaces.
Having clarified such masses relations, denoting by the respective indexed number of particles at time t, we define the functional
where
and where we assume and , so that
and
and the internal kinetics energy is expressed by
Moreover,
where and are appropriate real constants related to the respective charges.
Here is the fluid velocity field and
are fields of displacements for the corresponding particle fields.
Also denotes the magnetic potential, an external magnetic field and is the total magnetic field.
Moreover, is an induced electric field.
Also,
for appropriate real positive constants
Finally,
where are small real positive constants.
Such a functional J is subject to the following constraints:
- 1.
-
The momentum conservation equation for the fluid motionHere is the total density and P is the fluid pressure field.Furthermore,and
- 2.
- Mass conservation equation:
- 3.
-
Energy equationwhere we assume the Fourier lawwhere is the scalar field of temperature.Also,and
- 4.
- for an appropriate scalar function .
- 5.
- Mass relations
- (a)
- (b)
- (c)
- (d)
- (e)
where,
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
-
so that
- (h)
- (i)
- 6.
-
Other mass constraints
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- 7.
- 8.
- For the induced electric field, we must havewhere and are appropriate real constants related to the respective charges.
- 9.
- A Maxwell equation:where
- 10.
- Another Maxwell equation:where the total electric field stands forand where generically denotingwe have also
At this point we generically denote
Thus, already including the Lagrange multipliers concerning the restrictions indicated, the extended functional stands for
where,
Here we recall the following definitions and relations:
- 1.
- For the Deuterium field
- 2.
- For the Tritium field
- 3.
- For the Helium field
- 4.
- For the Neutron field
- 5.
- For the electronic field resulting from the ionization
- 1.
- 2.
Also,
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
-
so that
- 10.
- 11.
- 12.
Finally,
and where generically denoting
we have also
and,
21. A qualitative modeling for a general phase transition process
In this section we develop a general qualitative modeling for a phase transition process.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
Such a set is supposed to a be a fixed volume in which an amount of mass of a substance A with a density function u will develop phase a transition for another phase with corresponding density function The total mass is suppose to be kept constant throughout such a process.
We model such transition in phase through a functional where
Here and
The phases corresponding to u and v are connected through a Lagrange multiplier E, which represents the chemical potential of the chemical process in question.
We assume the temperature is directly proportional to the internal kinetics energy where
For a internal vibrational motion, we assume approximately
for an appropriate frequency and vectorial function
Thus, the temperature is indeed proportional to , that is, symbolically, we may write
Therefore, we start with the system with a phase corresponding to and at . Gradually increasing the temperature to a corresponding , we obtain a transition to a phase corresponding to and .
At this point, we also define the index normalized corresponding densities
and
Finally, we have obtained some numerical results for the following parameters:
, ,
- 1.
-
We start with corresponding to and in .
- 2.
-
We end the process with corresponding to and in .
22. A mathematical description of a hydrogen molecule in a quantum mechanics context
In this section we develop a mathematical description for a hydrogen molecule.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by .
Observe that a single hydrogen molecule comprises two hydrogen atoms physically linked through their electrons.
We recall that each hydrogen atom comprises one proton, one neutron and one electron.
Since the electric charge interaction effects are much higher than those related to the respective masses, in a first analysis we neglect the single neutron densities.
Denoting and time , generically, for a particle at the atom in the molecule , we define the following general density:
Here we have the particle density in the atom with density , at the molecule with a global density .
Here we have also denoted, the particle mass, the mass of atom and the mass of molecule , so that we set the following constraints:
- 1.
- 2.
- 3.
At this point we denote for the atoms e of a hydrogen molecule:
- 1.
- : mass of electron in the atom , where
- 2.
- : mass of proton in the atom , where
Therefore, considering the respective indexed densities for the particles in question, we define the total hydrogen molecule density, denoted by as
Such system is subject to the following constraints:
- 1.
- From the proton in the atom :
- 2.
- For the proton in the atom :
- 3.
- For the atom :
- 4.
- For the atom :
- 5.
- For the electrons and , concerning the physical electronic link between the atoms:
- 6.
- For the total molecular density:
Therefore, already including the Lagrange multipliers, the corresponding variational formulation for such a system stands for , where
Here we denote
we assume
and
Finally,
Remark 22.1.
We highlight the two electrons which link the atoms are at same level of energy . Morever, each atom has its energy level and the molecule as a whole has also its energy level
23. A mathematical model for the water hydrolysis
In this section we develop a modeling for a chemical reaction known as the water hydrolysis.
Let be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by
In such a volume containing a total mass of water initially at the temperature 25 C with pressure 1 atm, we intend to model the following reaction
which as previously mentioned is the well known water hydrolysis.
We highlight stand for a water molecule which subject to an appropriate electric potential is decomposed into a ionized molecule and ionized atom.
It is also well known that the water symbol corresponds to a molecule with two hydrogen (H) atoms and one oxygen (O) atom.
Moreover, the oxygen atom O has 8 protons, 8 neutrons and 8 electrons whereas the hydrogen atom H has one proton, one neutron and one electron.
Remark 23.1.
Here we have assumed that a unit mass of reacts into a fractional mass of and a fractional mass of
Symbolically, we have:
To clarify the notation we set the conventions:
- 1.
- molecule generically corresponds to wave function .
- 2.
- molecule corresponds to wave function
- 3.
- hydrogen atom corresponds to wave function
At this point we define the following densities:
- 1.
- For the water density (for charges), denoted by , we havewhere is the mass of a single water molecule and generically refers to the hydrogen proton at the hydrogen atom concerning the molecular density and so on.
- 2.
- For the density, denoted by , we havewhere is the mass of a single molecule of .
- 3.
- For the ionized hydrogen atom have
where we have denoted is the mass of a single atom of .
Here and are appropriate real constants concerning a proton and an electron charge, respectively.
The system is subject to the following constraints:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
Already including the Lagrange multipliers for the constraints, the variational formulation for such system. denoted by the functional stands for
where
Here , , , , ,
Moreover,
where , , and
Furthermore,
where is an electric potential originated from an external electric field applied on
Finally,
24. A mathematical model for the Austenite and Martensite phase transition
In this section we consider a phase transition of a solid solution of () and carbon with a proportion of carbon, known as austenite, initially at a temperature above and close to and rapidly cooled to a temperature of about , developing a phase transition which generates a solid solution of () and carbon known as martensite.
Let be an open, bounded and connected set with a regular boundary denoted by which contains an amount of austenite at and which is rapidly cooled to a temperature on a time interval resulting a phase known as martensite.
We recall the of austenite phase presents a multi-faced cubic crystalline structure in a micro-structure with carbon atoms.
On the other hand, structure of the martensite phase has a cubic centralized crystalline structure in a micro-structure with carbon atoms.
At this point, we also recall that the (iron) atom has 26 protons, 26 electrons and 30 neutrons.
On the other hand a atom has 6 protons and this same number of electrons and neutrons.
Here we define the density function , representing the Austenite phase, where:
Similarly, we define the density function for the Martensite phase, which is denoted by , where:
For the corresponding to the Austenite phase, such density functions are subject to the following constraints:
Defining
and
we must have
where is a small real parameter related to crystalline structure dimensions.
We must have also,
and,
For the corresponding to the Austenite phase, such density functions are subject to the following constraints:
Defining
we must have
where is a small real parameter related to crystalline structure dimensions.
We must have also,
The other constraints for the densities are given by:
- 1.
- For the Austenite phase:
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- 2.
-
For the Martensite phase:
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- 3.
- For the total (iron) mass,
- 4.
- For the total Carbon mass
At this point we define the functional J which models such a pahse transition in question, where
where
Also,
Finally, , where
and,
Finally, for a field of displacements resulting from the action of a external load field and temperature variations, we define
where
and
Remark 24.1.
The system temperature is suppose to be directly proportional to , which is in this model is a known function obtained experimentally. Finally, the strain tensors and refer to austenite and martensite phases, respectively. Such tensors also depend on the temperature and must be also obtained experimentally.
References
- R.A. Adams and J.F. Fournier, Sobolev Spaces, 2nd edn. (Elsevier, New York, 2003).
- W.R. Bielski, A. W.R. Bielski, A. Galka, J.J. Telega, The Complementary Energy Principle and Duality for Geometrically Nonlinear Elastic Shells. I. Simple case of moderate rotations around a tangent to the middle surface. Bulletin of the Polish Academy of Sciences, Technical Sciences, Vol. 38, No. 7-9, 1988.
- W.R. Bielski and J.J. Telega, A Contribution to Contact Problems for a Class of Solids and Structures, Arch. Mech., 37, 4-5, pp. 303-320, Warszawa 1985.
- J.F. Annet, Superconductivity, Superfluids and Condensates, 2nd edn. (Oxford Master Series in Condensed Matter Physics, Oxford University Press, Reprint, 2010). 2010.
- F.S. Botelho, Functional Analysis, Calculus of Variations and Numerical Methods in Physics and Engineering, CRC Taylor and Francis, Florida, 2020.
- F.S. Botelho, Advanced Calculus and its Applications in Variational Quantum Mechanics and Relativity Theory, CRC Taylor and Francis, Florida, 2021.
- F.S. Botelho, Variational Convex Analysis, Ph.D. thesis, Virginia Tech, Blacksburg, VA -USA, (2009).
- F. Botelho, Topics on Functional Analysis, Calculus of Variations and Duality, Academic Publications, Sofia, (2011).
- F. Botelho, Existence of solution for the Ginzburg-Landau system, a related optimal control problem and its computation by the generalized method of lines, Applied Mathematics and Computation, 218, 11976-11989, (2012). [CrossRef]
- F. Botelho, Functional Analysis and Applied Optimization in Banach Spaces, Springer Switzerland, 2014.
- P.Ciarlet, Mathematical Elasticity, Vol. II – Theory of Plates, North Holland Elsevier (1997).
- J.C. Strikwerda, Finite Difference Schemes and Partial Differential Equations, SIAM, second edition (Philadelphia, 2004).
- L.D. Landau and E.M. Lifschits, Course of Theoretical Physics, Vol. 5- Statistical Physics, part 1. (Butterworth-Heinemann, Elsevier, reprint 2008).
- R.T. Rockafellar, Convex Analysis, Princeton Univ. Press, (1970).
- J.J. Telega, On the complementary energy principle in non-linear elasticity. Part I: Von Karman plates and three dimensional solids, C.R. Acad. Sci. Paris, Serie II, 308, 1193-1198; Part II: Linear elastic solid and non-convex boundary condition. Minimax approach, ibid, pp. 1313-1317 (1989).
- A.Galka and J.J.Telega Duality and the complementary energy principle for a class of geometrically non-linear structures. Part I. Five parameter shell model; Part II. Anomalous dual variational priciples for compressed elastic beams, Arch. Mech. 47 (1995) 677-698, 699-724.
- J.F. Toland, A duality principle for non-convex optimisation and the calculus of variations, Arch. Rat. Mech. Anal., 71, No. 1 (1979), 41-61. [CrossRef]
Figure 1.
solution for the case .
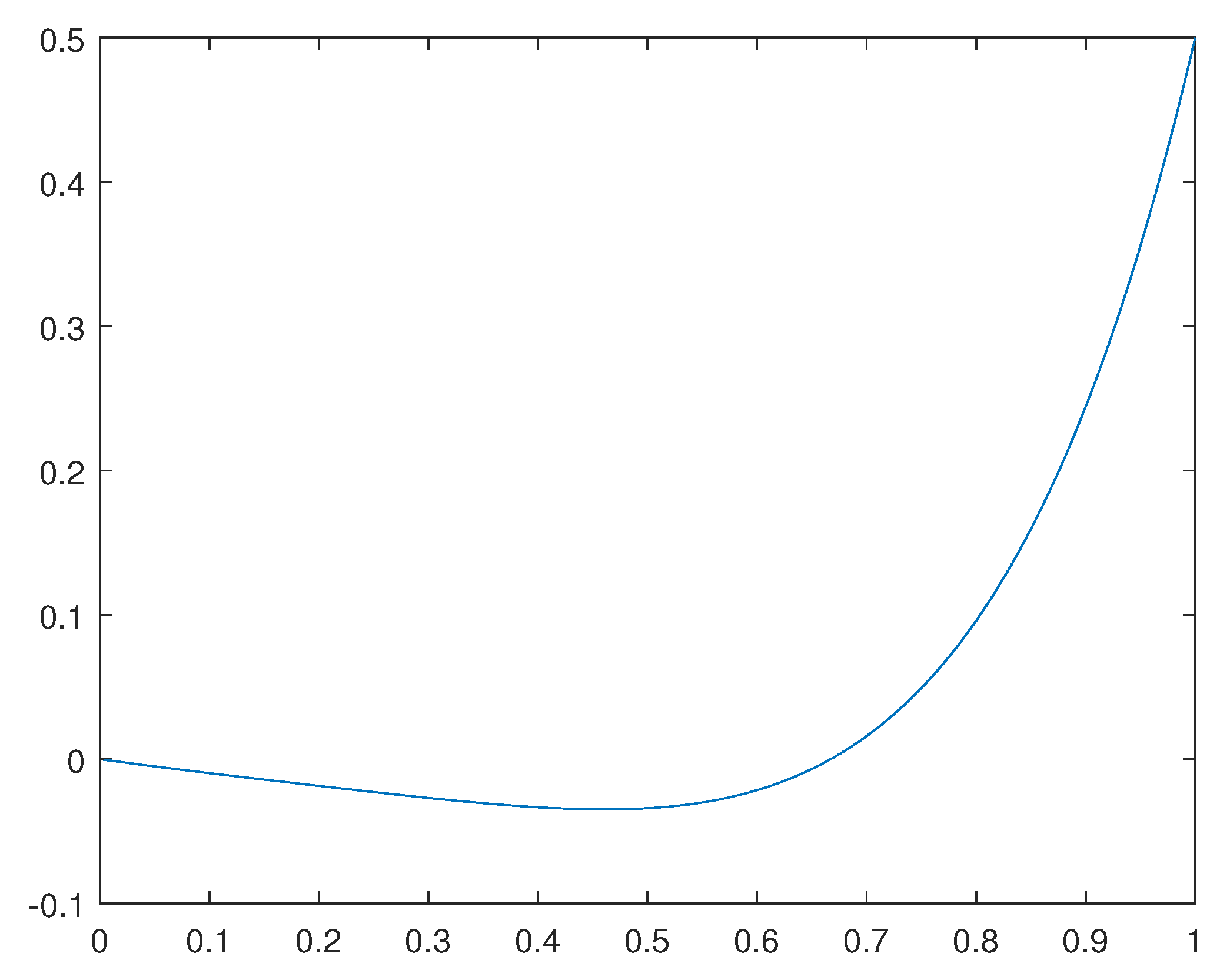
Figure 2.
solution for the case .
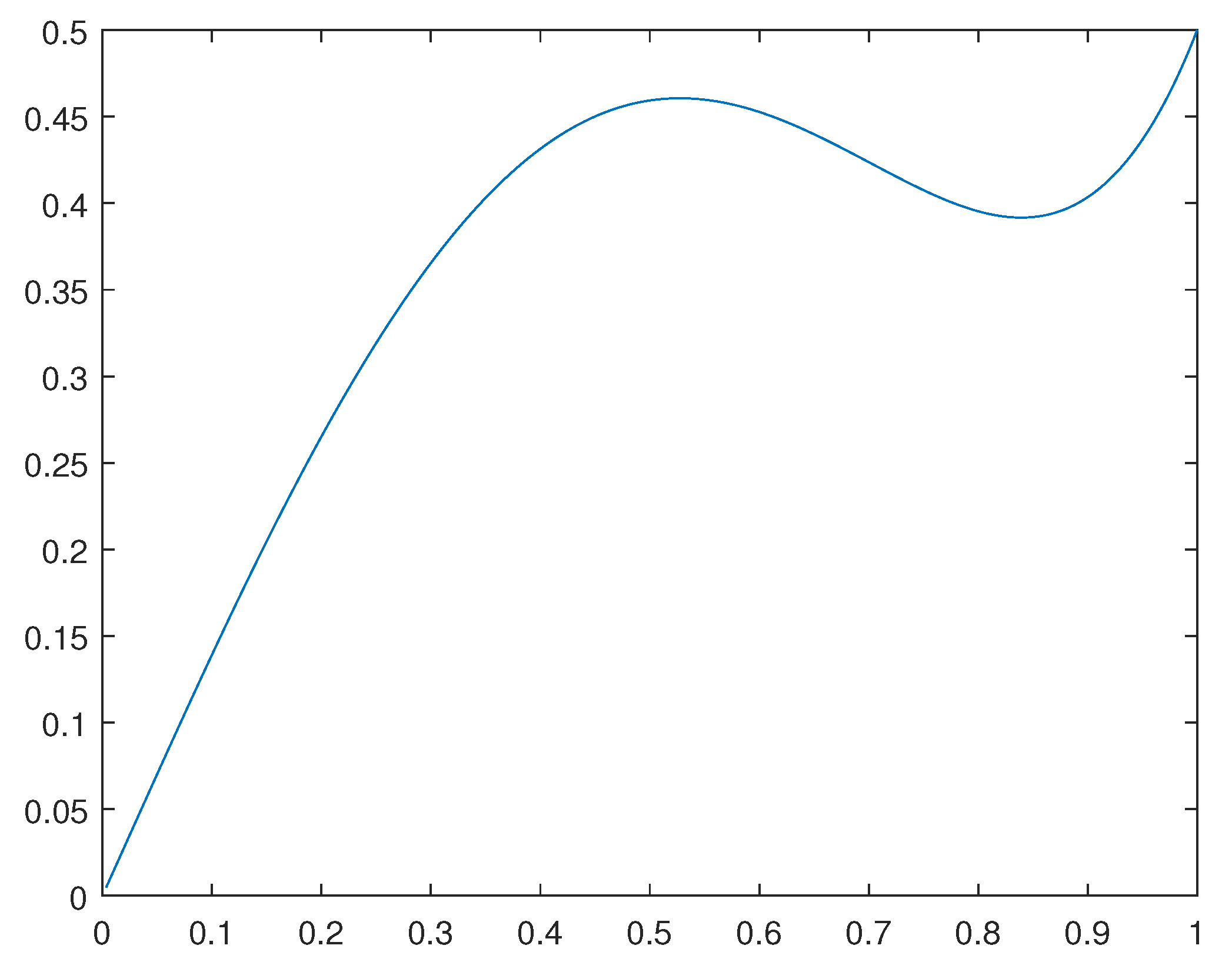
Figure 3.
solution for the case .
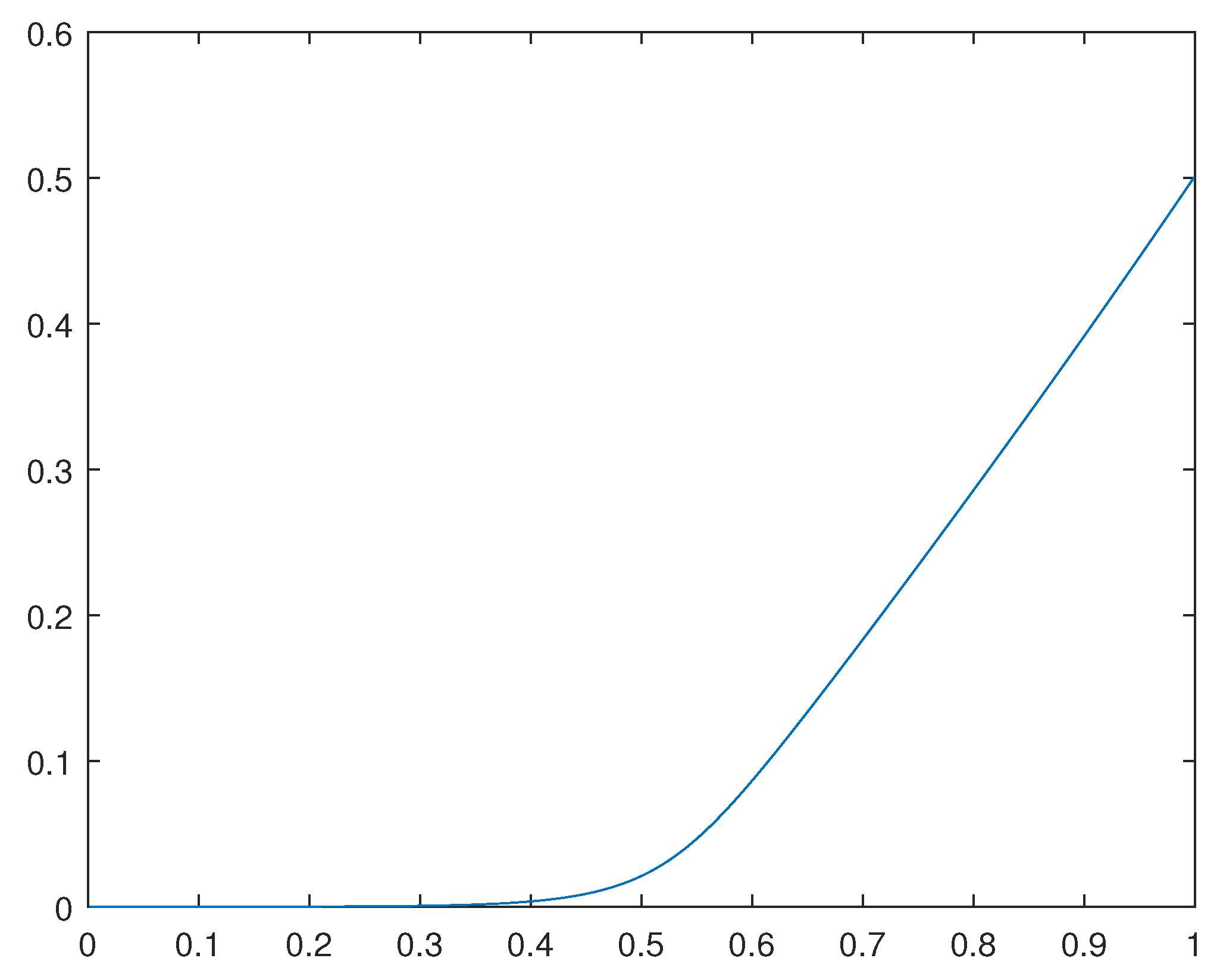
Figure 4.
solution for the case .
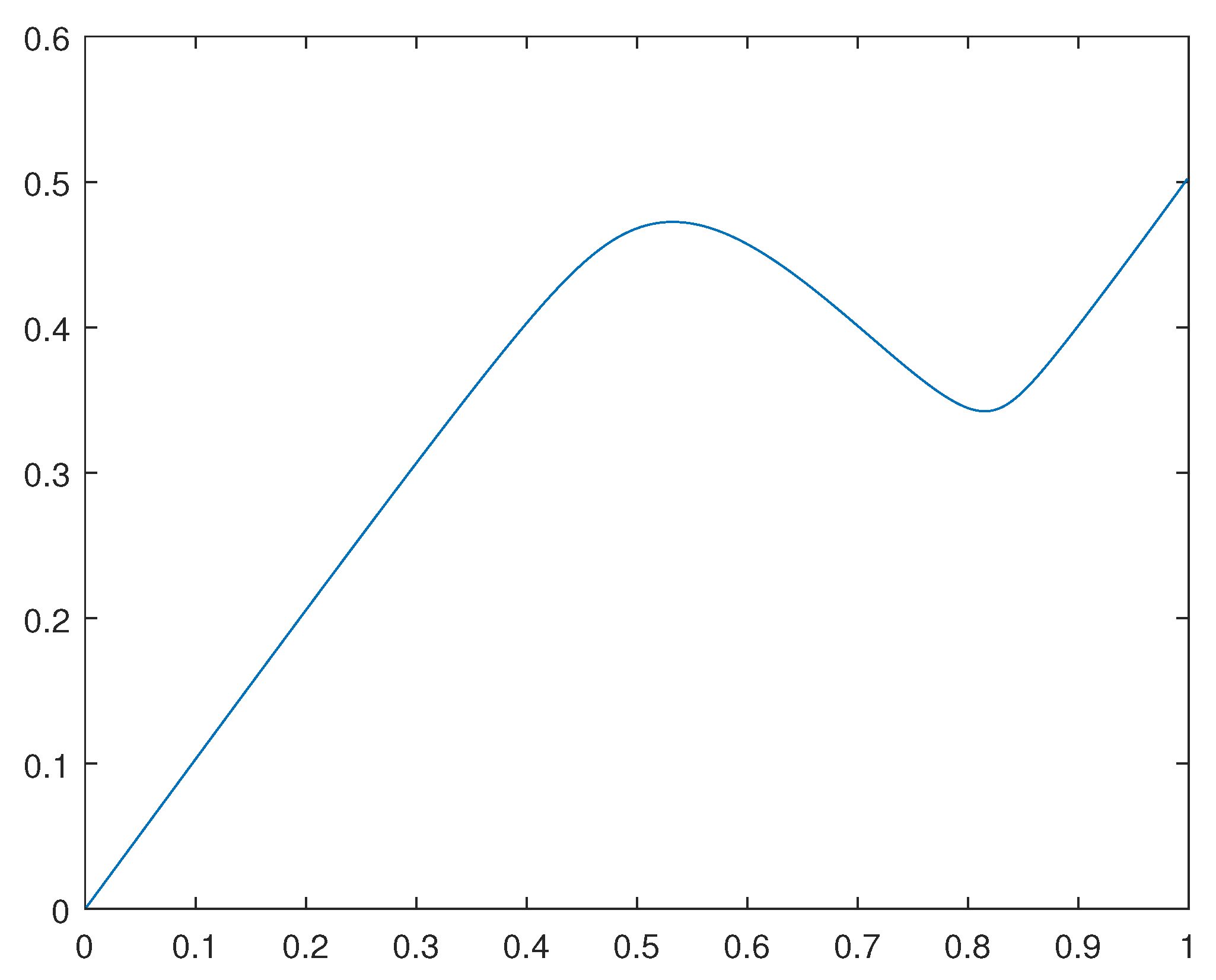
Figure 5.
Density for the Case A.

Figure 6.
Density for the Case B.

Figure 7.
Solution for the example 1.
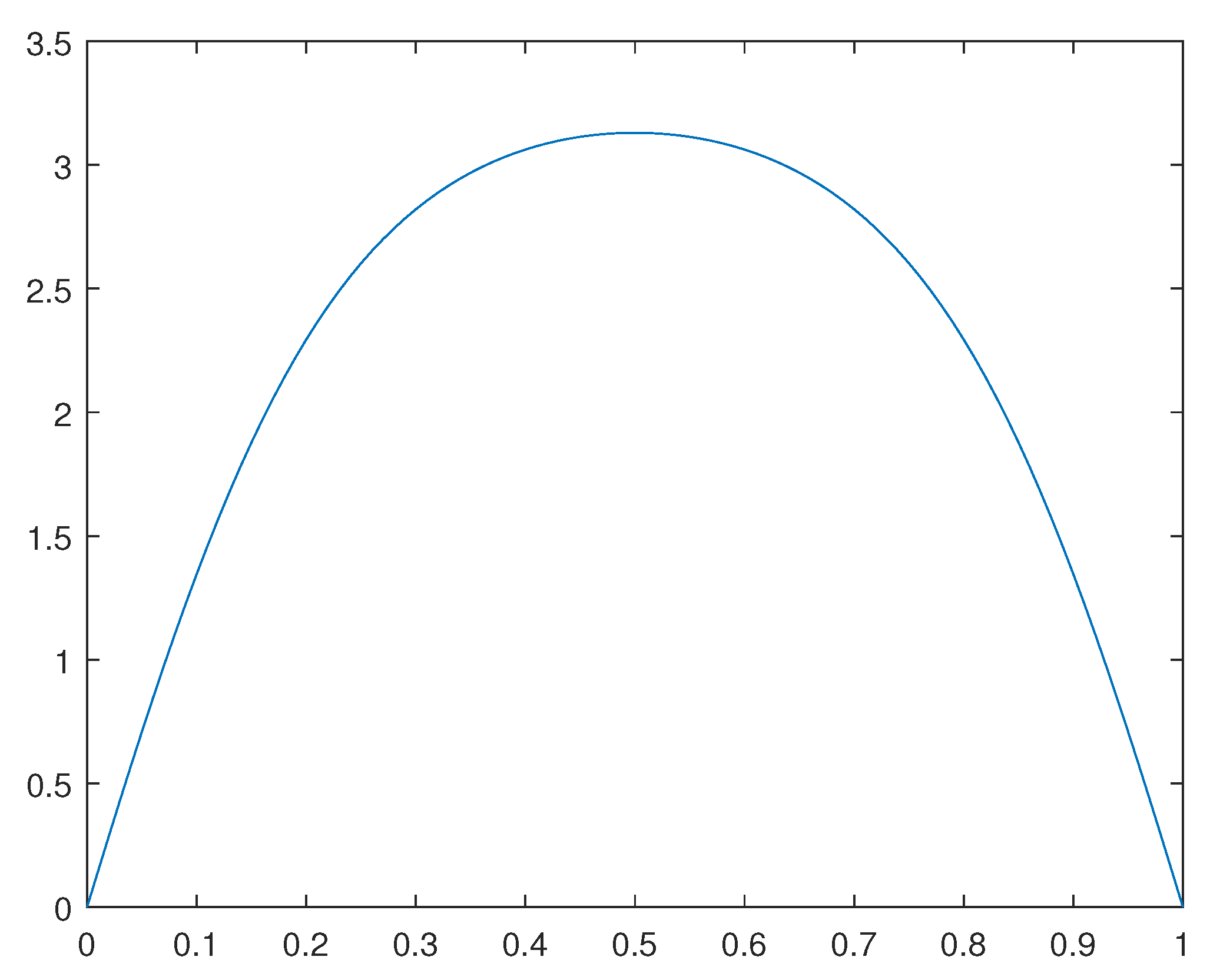
Figure 8.
Solution for the example 2.
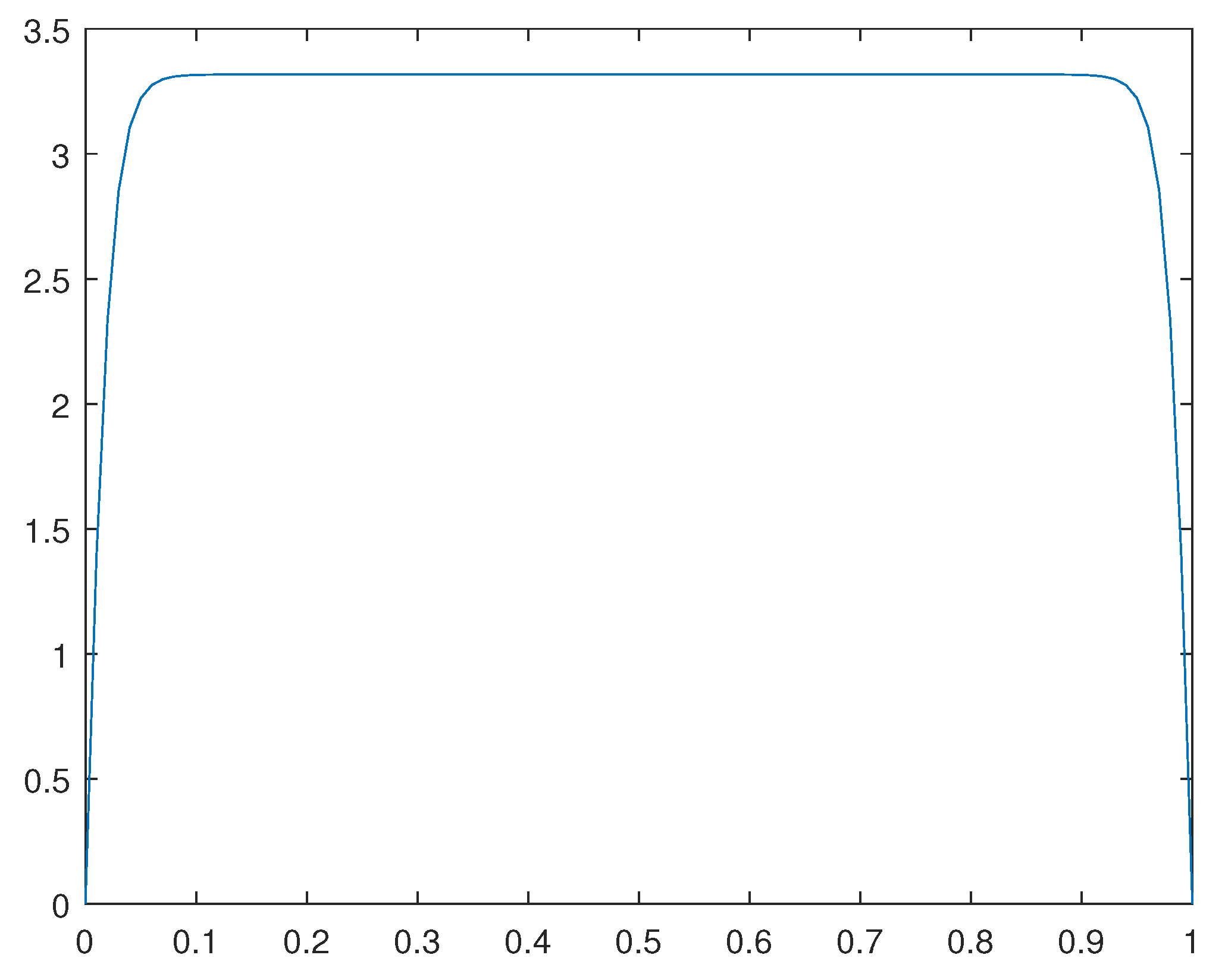
Figure 9.
Solution for the example A.
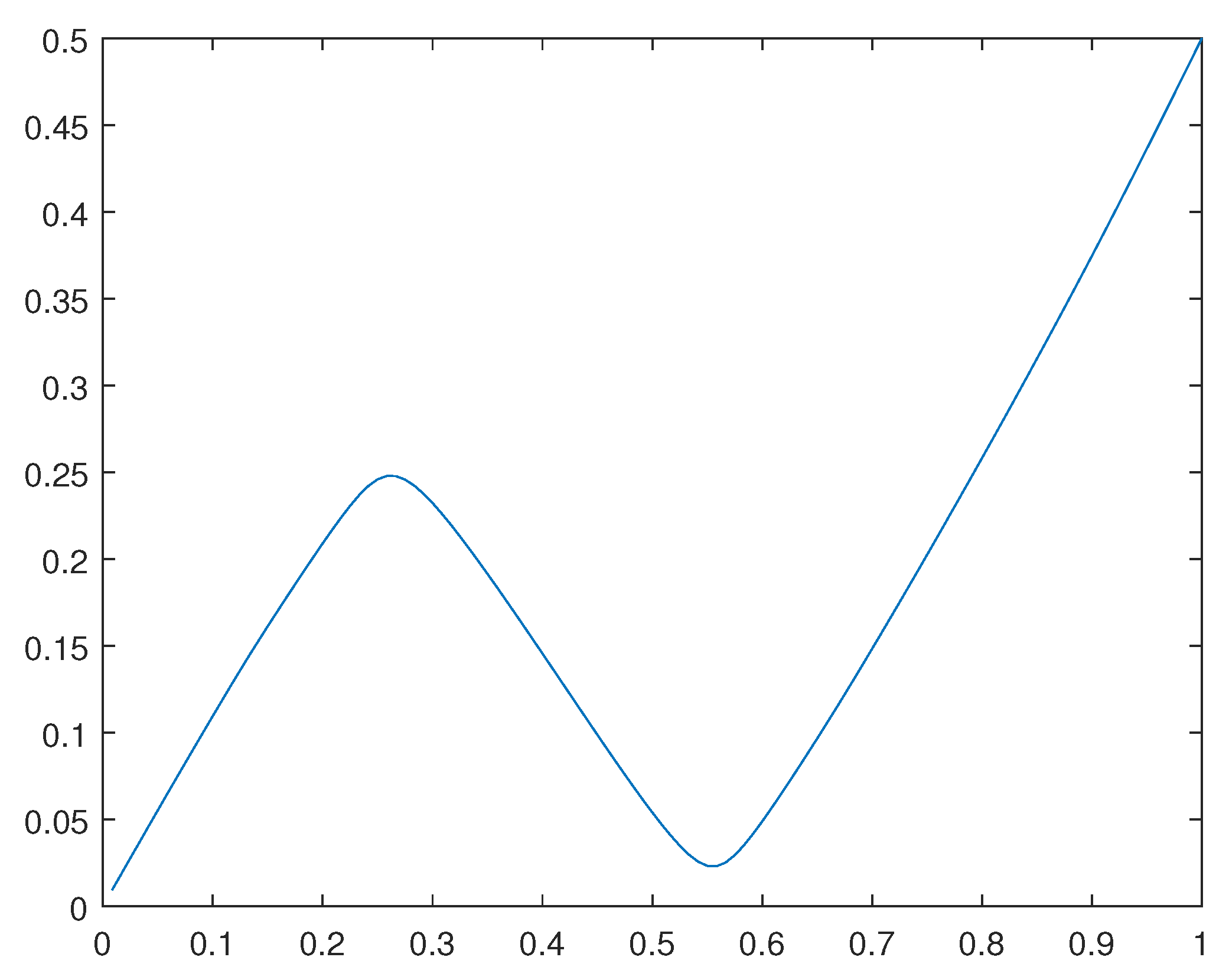
Figure 10.
Solution for the example B.
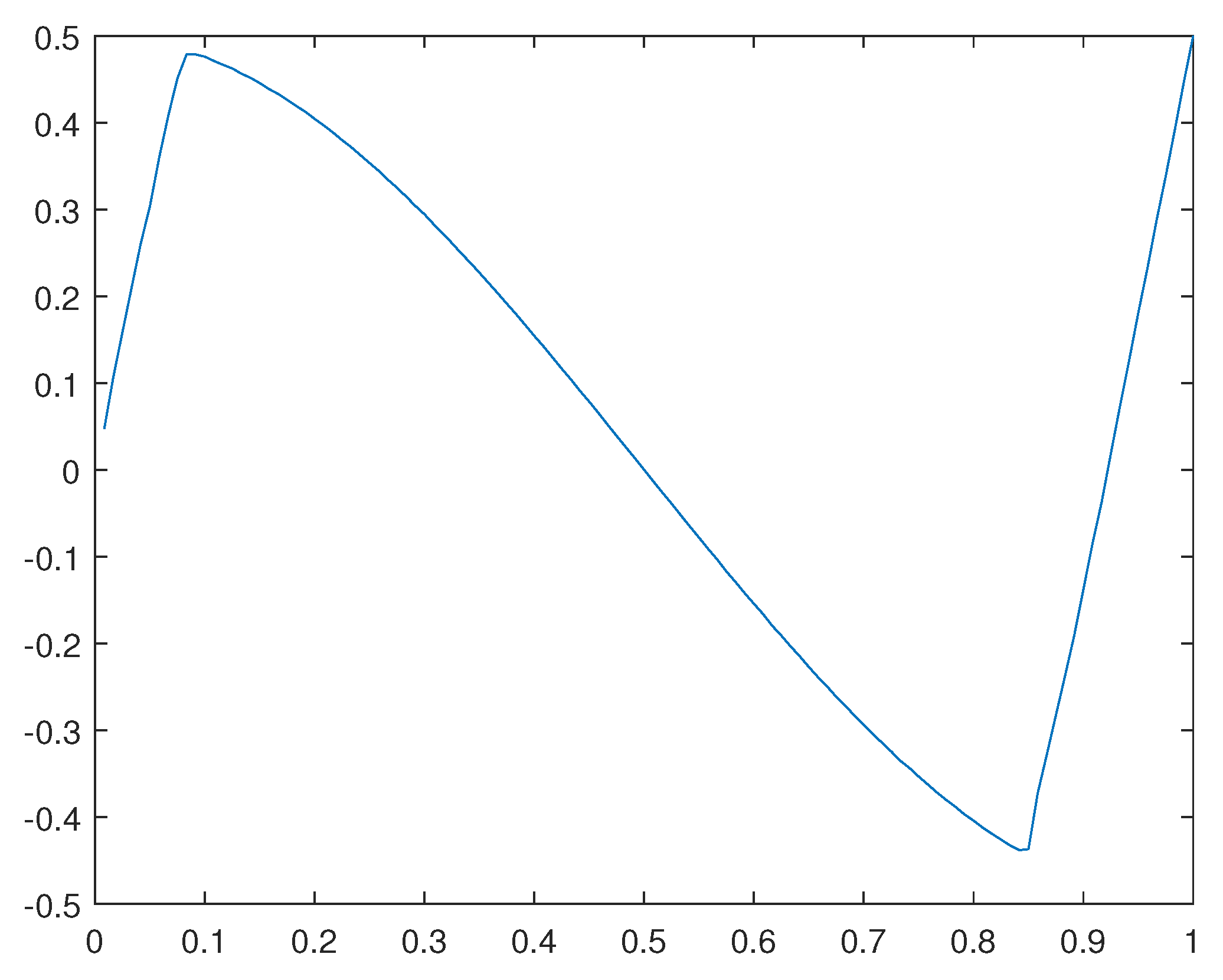
Figure 11.
Solution for the .
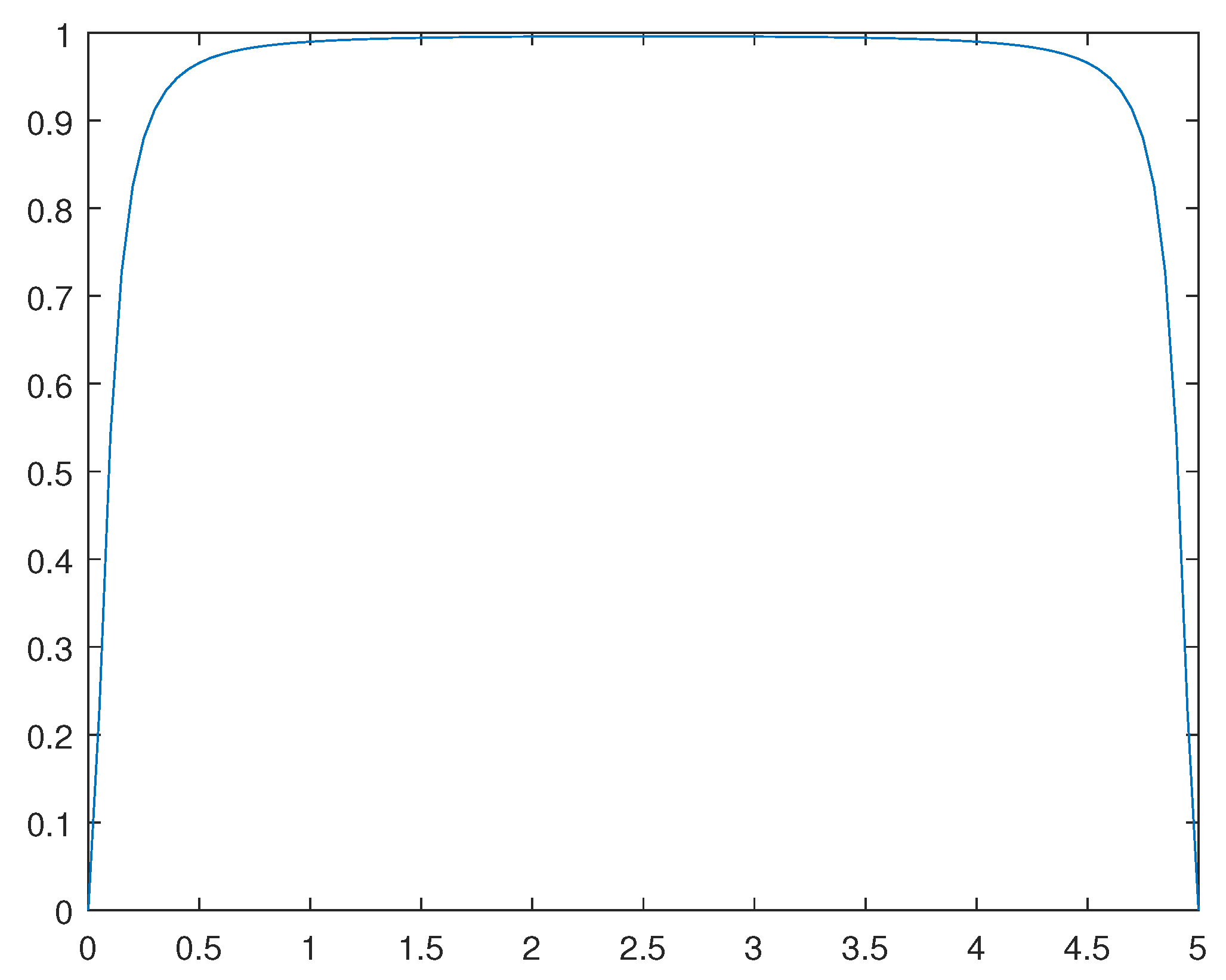
Figure 12.
Solution for the .
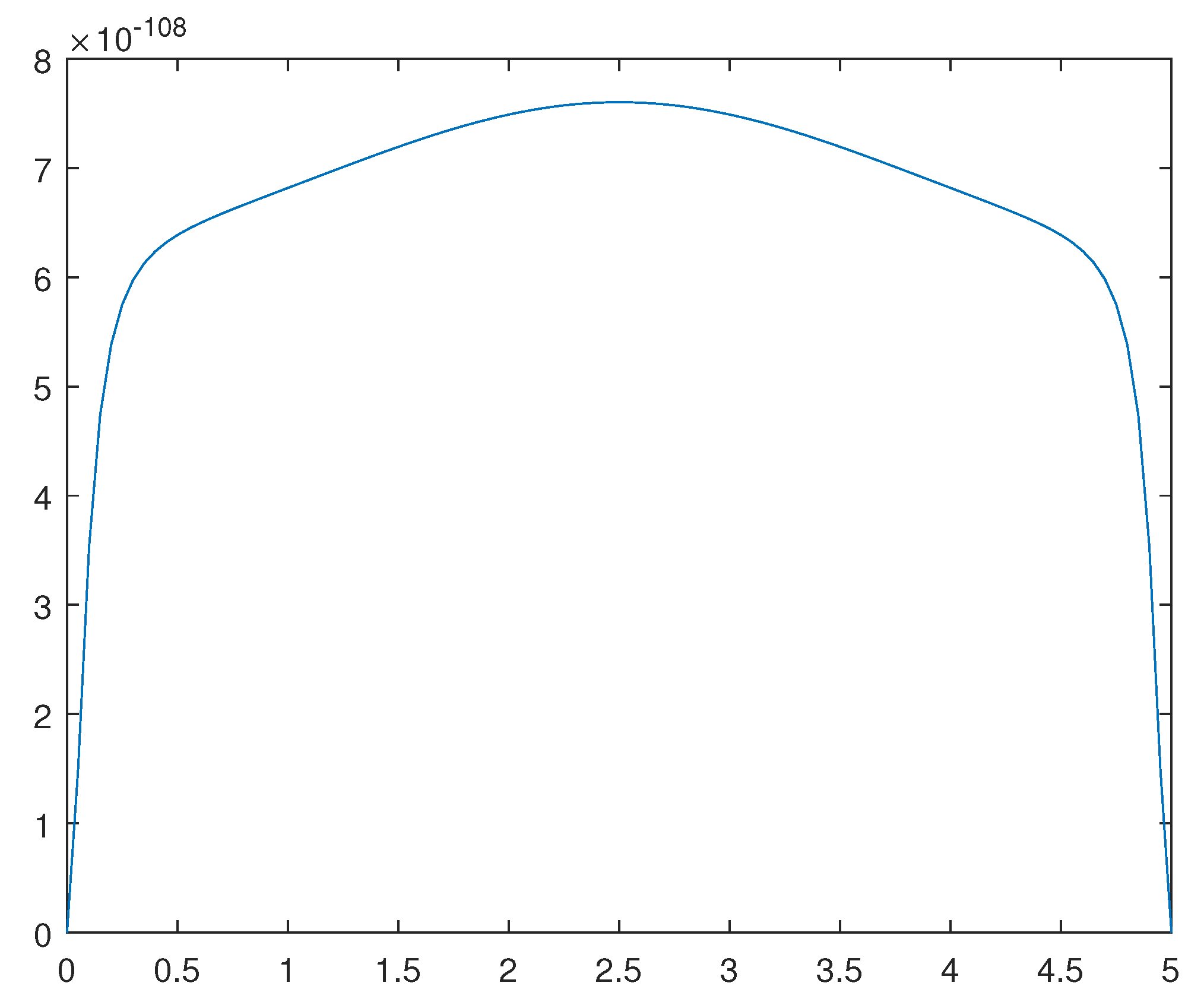
Figure 13.
Solution for the .
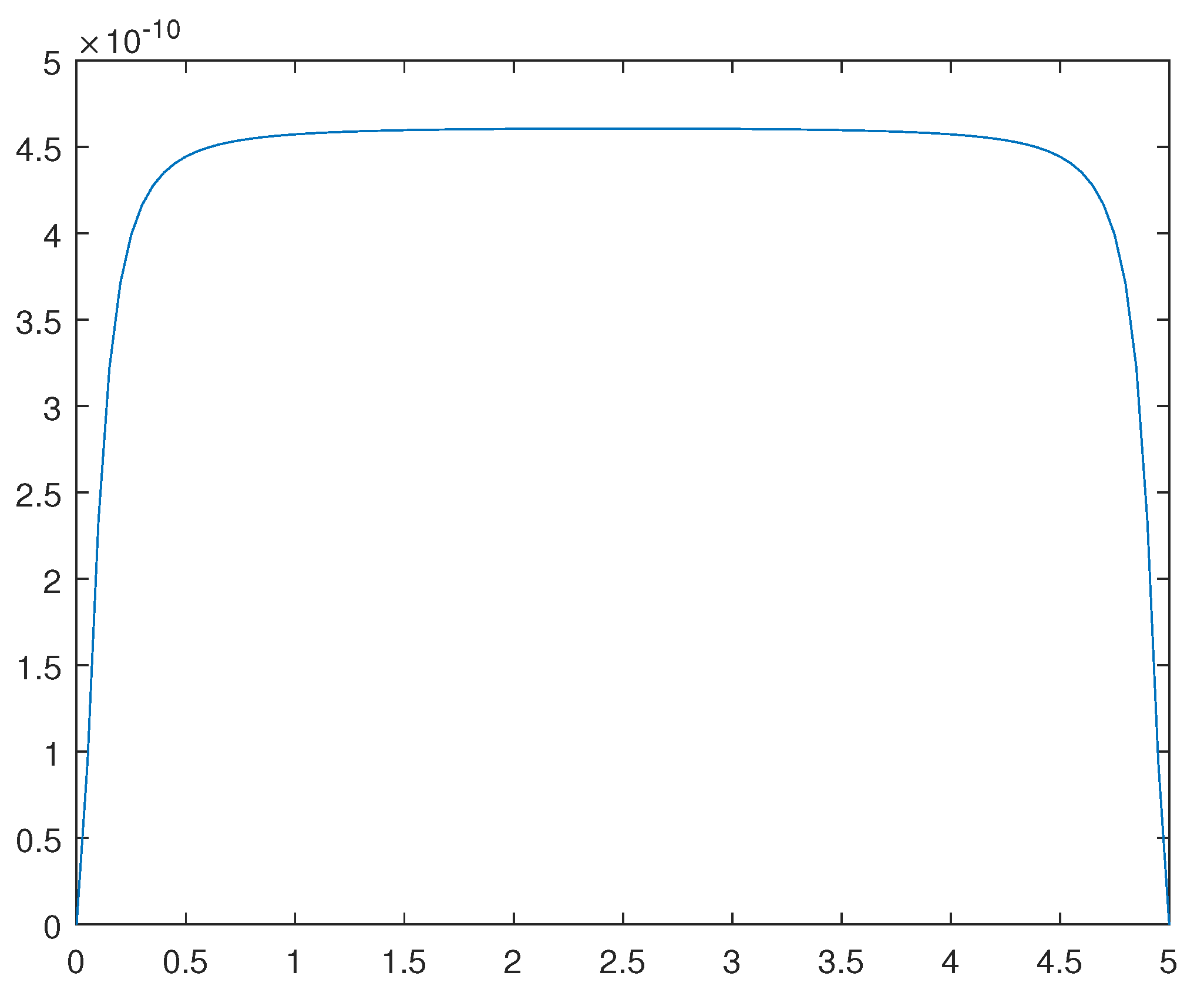
Figure 14.
Solution for the .
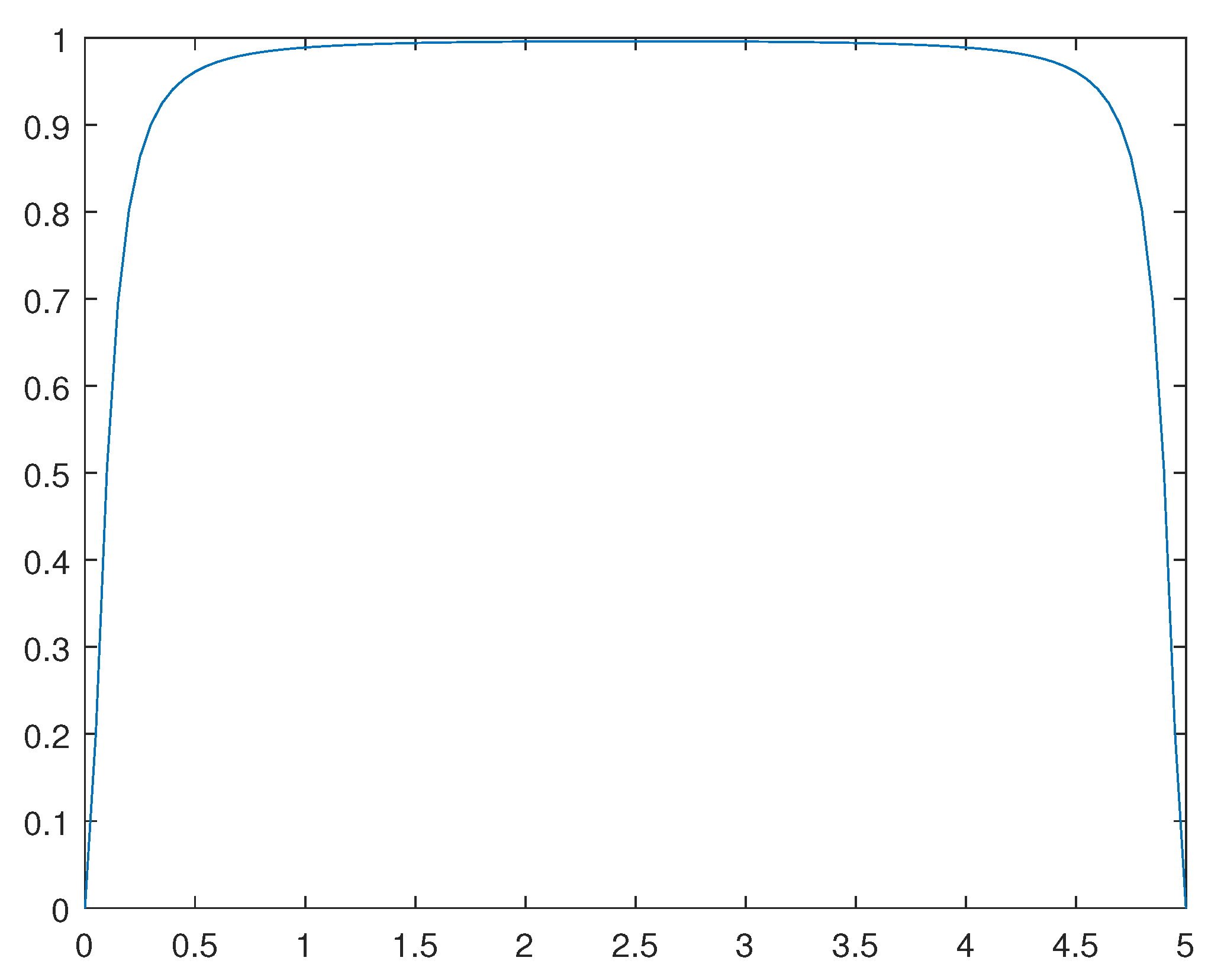
Figure 15.
Solution for .
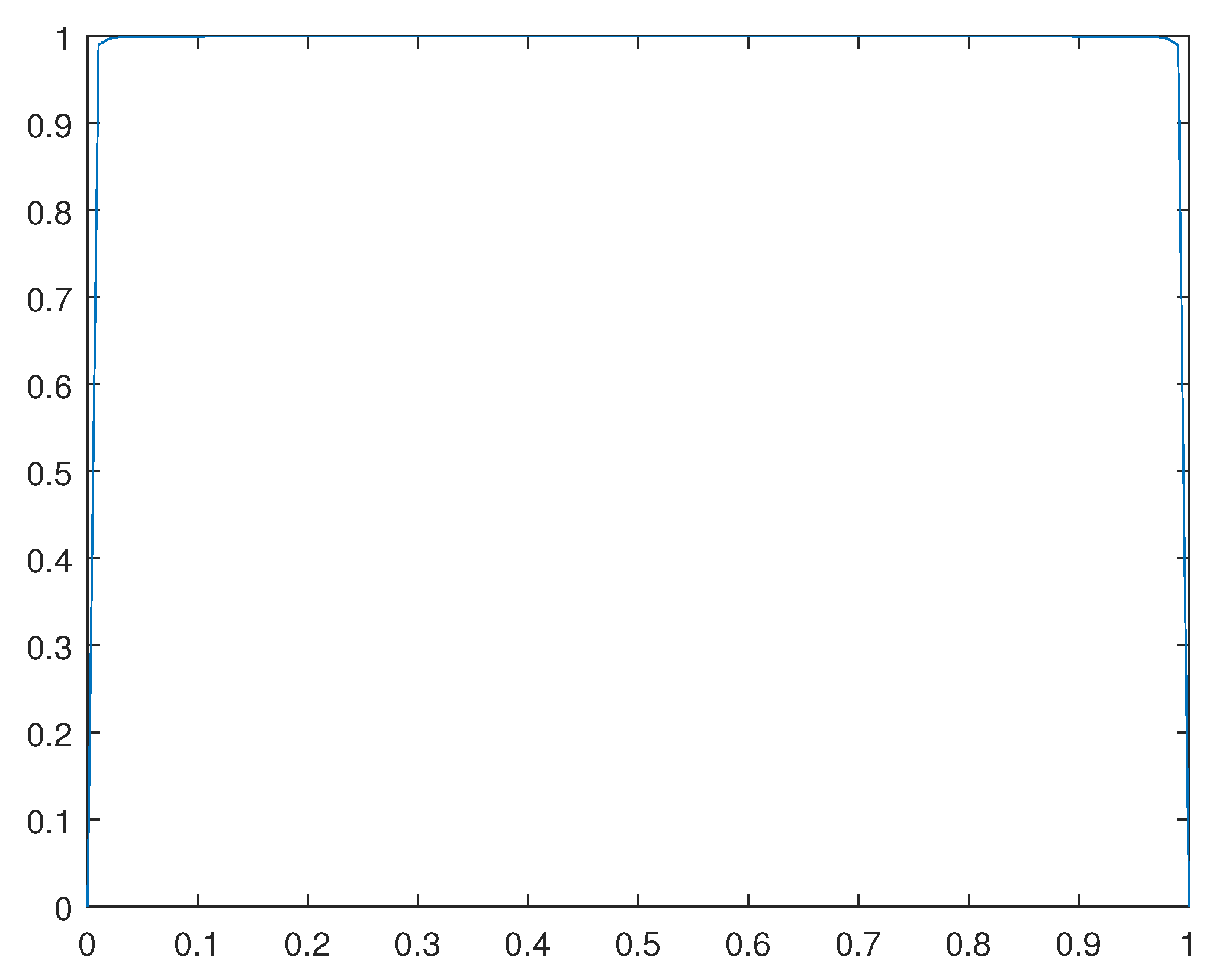
Figure 16.
Solution for .
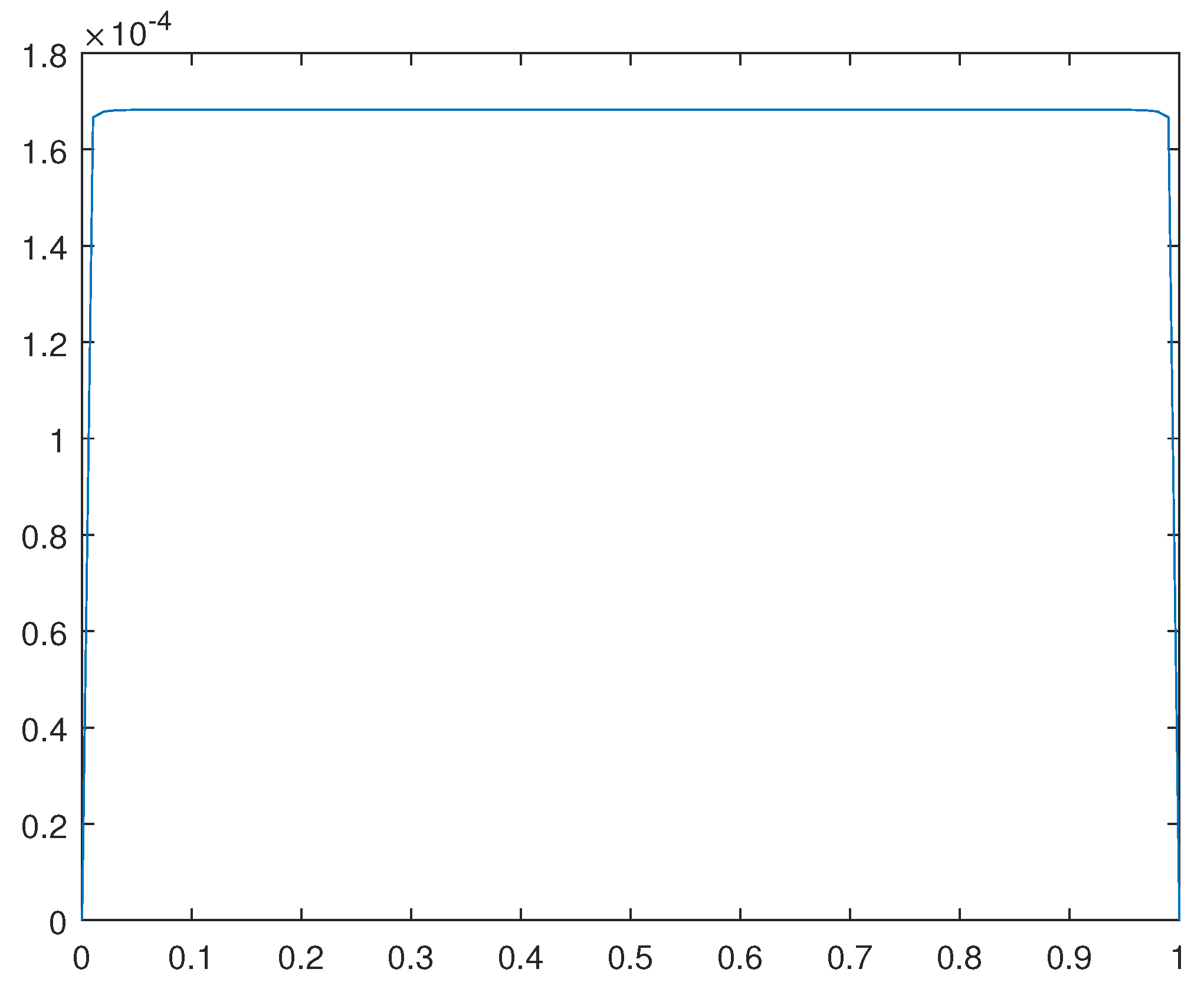
Figure 17.
Solution for .
Figure 18.
Solution for .
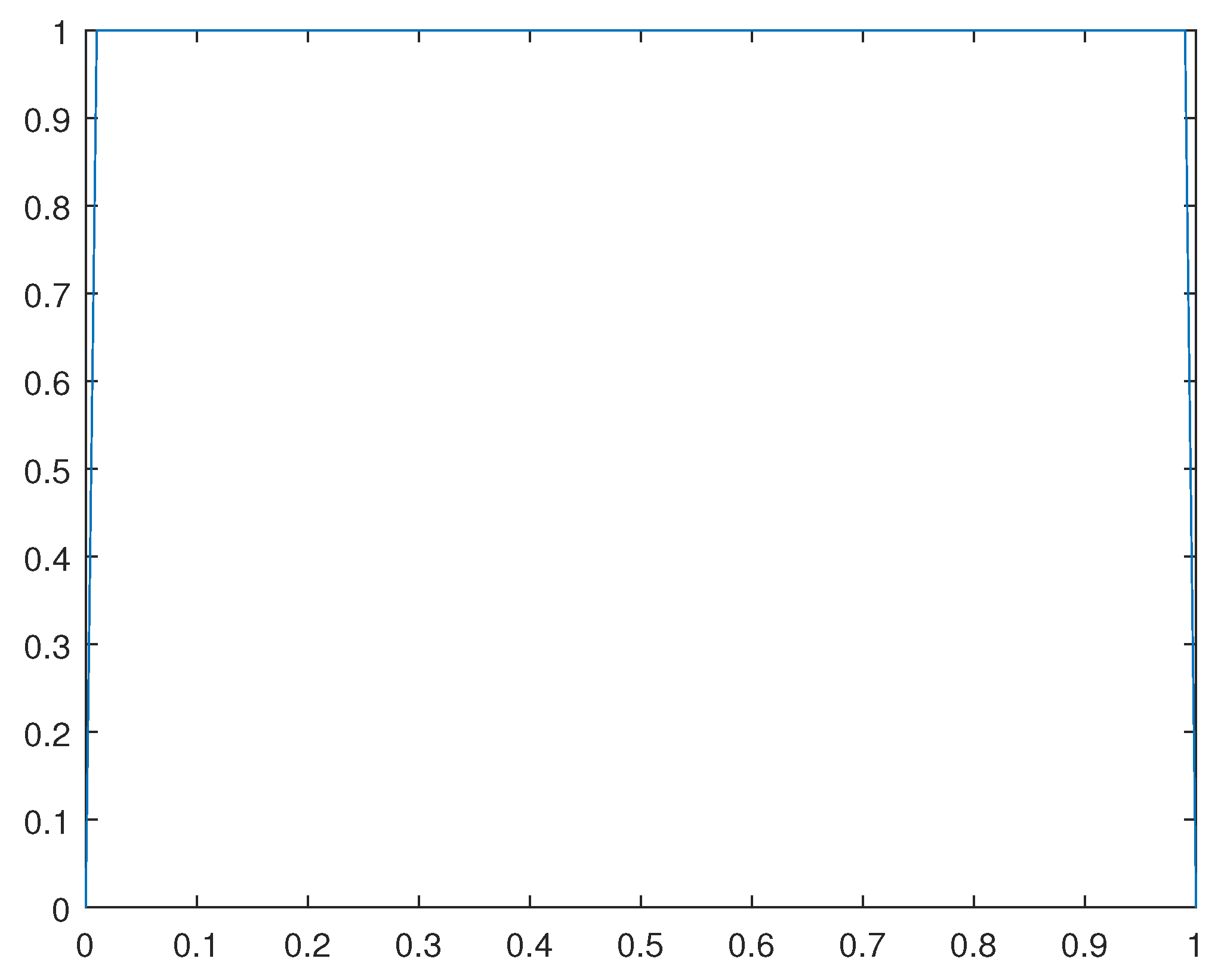
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





