Submitted:
02 February 2023
Posted:
03 February 2023
You are already at the latest version
Abstract
Keywords:
Introduction
Methods and Materials
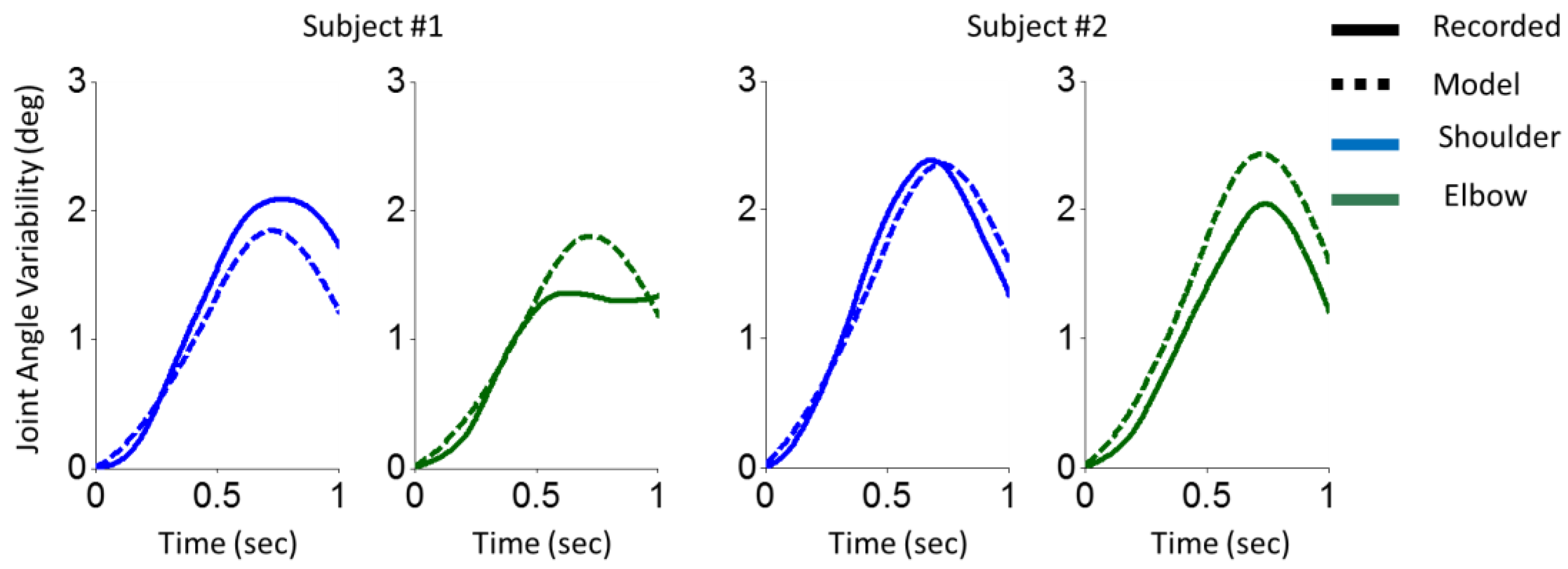
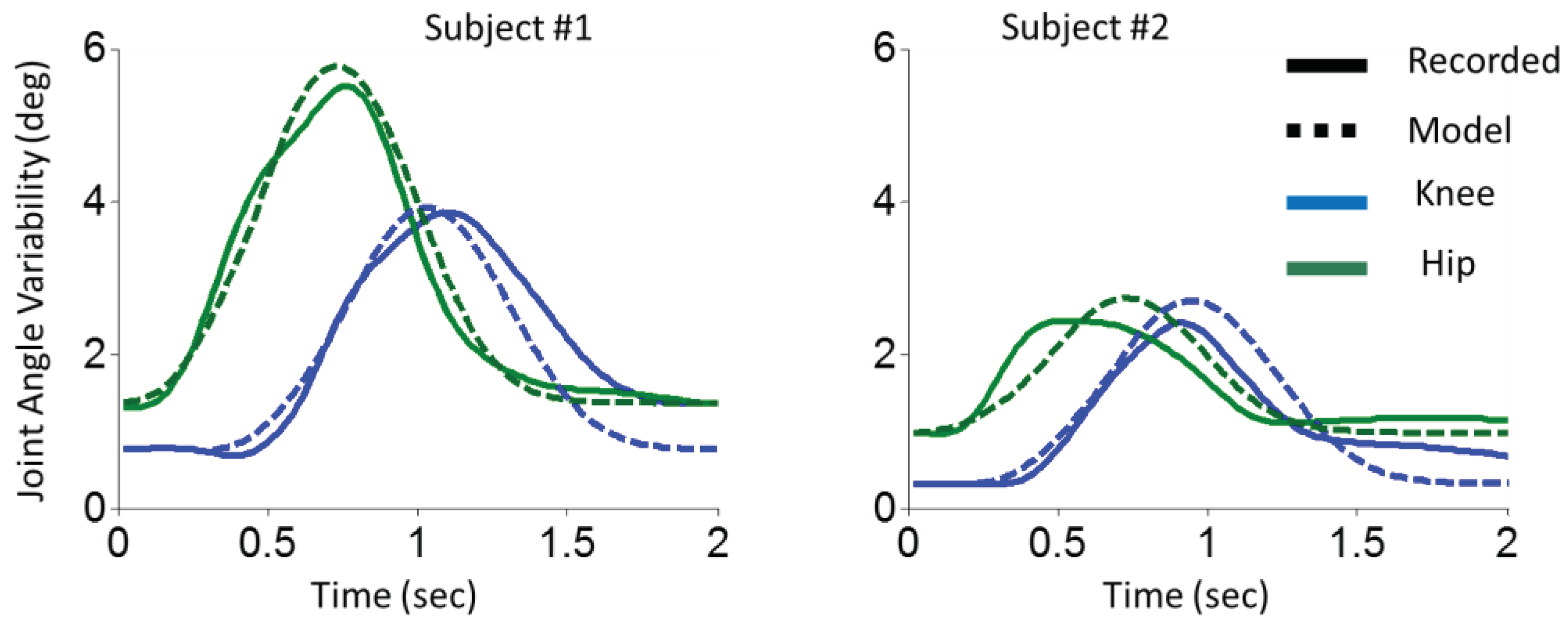
Results
Discussion and conclusion
Acknowledgments
Appendix A
Appendix B
Appendix C
References
- Bahrami, F., Riener, R., Jabedar-Maralani, P., & Schmidt, G. (2000). Biomechanical analysis of sit-to-stand transfer in healthy and paraplegic subjects. Clinical Biomechanics 15: 123–133. [CrossRef]
- Bhushan, N., & Shadmehr, R. (1999). Computational nature of human adaptive control during learning of reaching movements in force fields. Biological Cybernetics 81: 39–60. [CrossRef]
- Craig, J. J. (2005). Introduction to Robotics: Mechanics and Control. Pearson Education International, Third Edition.
- Darainy, M., Malfait, N., Gribble, P. L., Towhidkhah, F., & Ostry, D. J. (2004). Learning to Control Arm Stiffness Under Static Conditions. Journal of Neurophysiology 92: 3344–3350. [CrossRef]
- Emadi Andani, M., & Bahrami, F. (2012). COMAP: A new computational interpretation of human movement planning level based on coordinated minimum angle jerk policies and six universal movement elements. Human Movement Science 31: 1037–1055. [CrossRef]
- Emadi Andani, M., Bahrami, F., & Maralani, P. J. (2007). A Biologically Inspired Modular Structure to Control the Sit-to-Stand Transfer of a Biped Robot. 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. [CrossRef]
- Emadi Andani, M., Bahrami, F., & Jabehdar Maralani, P. (2009). AMA-MOSAICI: An automatic module assigning hierarchical structure to control human motion based on movement decomposition. Neurocomputing 72: 2310–2318. [CrossRef]
- Flanagan, J. R., & Wing, A. M. (1997). The Role of Internal Models in Motion Planning and Control: Evidence from Grip Force Adjustments during Movements of Hand-Held Loads. The Journal of Neuroscience 17: 1519–1528. [CrossRef]
- Flash, T., & Hogan, N. (1985). The coordination of arm movements: an experimentally confirmed mathematical model. The Journal of Neuroscience 5: 1688–1703. [CrossRef]
- Friedman, J., & Flash, T. (2009). Trajectory of the index finger during grasping. Experimental Brain Research 196: 497–509. [CrossRef]
- Haruno, M., Wolpert, D. M., & Kawato, M. (2003). Hierarchical MOSAIC for movement generation. International Congress Series 1250: 575–590. [CrossRef]
- Haruno, M., Wolpert, D. M., & Kawato, M. (2001). MOSAIC Model for Sensorimotor Learning and Control. Neural Computation 13: 2201–2220. [CrossRef]
- Janssen, W. G., Bussmann, H. B., & Stam, H. J. (2002). Determinants of the Sit-to-Stand Movement: A Review. Physical Therapy 82: 866–879. [CrossRef]
- Szendro, P., Vincze, G., & Szasz, A. (2001). Pink-noise behaviour of biosystems. European Biophysics Journal 30: 227–231. [CrossRef]
- Vaziri, S. (2006). Why Does the Brain Predict Sensory Consequences of Oculomotor Commands? Optimal Integration of the Predicted and the Actual Sensory Feedback. Journal of Neuroscience 26: 4188–4197. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




