Prerpints.org logo
Preprint
Article

A Generalized Series Expansion of the Arctangent Function Based on the Enhanced Midpoint Integration

Altmetrics

Downloads

197

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 February 2023

Posted:

06 February 2023

You are already at the latest version

Alerts
Abstract
In this work we derive a generalized series expansion of the acrtangent function by using the enhanced midpoint integration (EMI). Algorithmic implementation of the generalized series expansion utilizes a simple two-step iteration. This approach significantly improves the convergence and requires no surd numbers in computation of the arctangent function.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

In 2010, Adegoke and Layeni published an interesting relation for derivatives of the arctangent function [1]
d n d x n arctan ( x ) = ( − 1 ) n − 1 ( n − 1 ) ! ( 1 + x 2 ) n / 2 sin n arcsin 1 1 + x 2 , n ∈ N + .
Using this relation, they discovered a series expansion
arctan ( x ) = ∑ n = 1 ∞ 1 n x 2 1 + x 2 n / 2 sin n arcsin 1 1 + x 2 .
Equations (1) and (2) have some restrictions. Specifically, when n is even, equation (1) remains valid only at x ∈ [ 0 , ∞ ) , while equation (2) is valid only at x ∈ [ 0 , ∞ ) for ∀ n .
To resolve this problem, Lampret applied the signum function
sgn ( x ) = − 1 , x < 0 , 1 , x ≥ 0 ,
and proved that for complete coverage x ∈ ( − ∞ , ∞ ) , the equations (1) and (2) can be modified as [2]
d n d x n arctan ( x ) = sgn ( − x ) n − 1 ( n − 1 ) ! ( 1 + x 2 ) n / 2 sin n arcsin 1 1 + x 2
and
arctan ( x ) = sgn ( x ) ∑ n = 1 ∞ 1 n x 2 1 + x 2 n / 2 sin n arcsin 1 1 + x 2 ,
respectively.
Equations (3) and (4) represent a theoretical interest. In particular, Lampret noticed that from equation (3) it follows that [2]
sgn ( 0 ) n − 1 · ( n − 1 ) ! · sin n π 2 = ( − 1 ) ( n − 1 ) / 2 ( n − 1 ) ! , n odd , 0 , n even .
Comparing the following relation (see [3] for detailed derivation procedure by induction)
d n d x n arctan ( x ) = ( − 1 ) n ( n − 1 ) ! 2 i 1 ( x + i ) n − 1 ( x − i ) n
with equation (3), we can find the following identity
sgn ( − x ) n − 1 ( n − 1 ) ! ( 1 + x 2 ) n / 2 sin n arcsin 1 1 + x 2 = ( − 1 ) n ( n − 1 ) ! 2 i 1 ( x + i ) n − 1 ( x − i ) n .
It is not difficult to see that the relation (5) immediately follows from the identity (7). Therefore, relation (5) is just a specific case of the identity (7) occurring at x = 0 .
Identity (7) can be rewritten in form
sin n arcsin 1 1 + x 2 = − sgn ( x ) n − 1 ( 1 + x 2 ) n / 2 2 i 1 ( x + i ) n − 1 ( x − i ) n .
Therefore, from equation (4) it follows that
arctan ( x ) = sgn ( x ) ∑ n = 1 ∞ 1 n x 2 1 + x 2 n / 2 − sgn ( x ) n − 1 ( 1 + x 2 ) n / 2 2 i 1 ( x + i ) n − 1 ( x − i ) n
or
arctan ( x ) = i 2 ∑ n = 1 ∞ x n n 1 ( x + i ) n − 1 ( x − i ) n .
As we can see, this series expansion of the arctangent function is just a reformulation of equation (4) that follows due to identity (6).
In our previous publication [3], using the identity (6), we have derived the following series expansion of the arctangent function
arctan ( x ) = − 2 ∑ m = 1 ∞ ∑ n = 1 2 m − 1 ( − 1 ) n ( 2 m − 1 ) ( 1 + x 2 / 4 ) 2 m − 1 x 2 2 ( 2 m − n ) − 1 2 m − 1 2 n − 1 ,
from which at x = 1 we get a formula for π expressed in terms of the binomial coefficients
π 4 = − 2 ∑ m = 1 ∞ ∑ n = 1 2 m − 1 ( − 1 ) n ( 2 m − 1 ) ( 1 + 1 / 4 ) 2 m − 1 2 2 ( 2 m − n ) − 1 2 m − 1 2 n − 1
or
π 16 = ∑ m = 1 ∞ ∑ n = 1 2 m − 1 ( − 4 ) n − 1 ( 2 m − 1 ) 5 2 m − 1 2 m − 1 2 n − 1 .
Later, using again the same identity (6), we have also derived the following series expansion (see [4] and literature therein)
arctan ( x ) = 2 ∑ n = 1 ∞ 1 2 n − 1 g n ( x ) g n 2 ( x ) + h n 2 ( x ) ,
where the expansion coefficients are computed by two-step iteration
g n ( x ) = g n − 1 ( x ) ( 1 − 4 / x 2 ) + 4 h n − 1 ( x ) / x , h n ( x ) = h n − 1 ( x ) ( 1 − 4 / x 2 ) − 4 g n − 1 ( x ) / x ,
such that
g 1 ( x ) = 2 / x , h 1 ( x ) = 1 .
The series expansion (8) requires no surd numbers in computation and it is rapid in convergence.
As further development, in this work we derive a generalized series expansion of the arctangent function. Such an approach may be used to improve further convergence in computation of the arctangent function.

2. Derivation

Change of the variable x → x t in the equation (6) results in
∂ n ∂ t n arctan ( x t ) = ( − 1 ) n ( n − 1 ) ! x n 2 i 1 ( x t + i ) n − 1 ( x t − i ) n
or
∂ n ∂ t n x 1 + x 2 t 2 = ( − 1 ) n + 1 n ! x n + 1 2 i 1 ( x t + i ) n + 1 − 1 ( x t − i ) n + 1
since
∂ n ∂ t n arctan ( x t ) = ∂ n − 1 ∂ t n − 1 x 1 + x 2 t 2 .
There is an enhanced midpoint integration (EMI) formula (see [5] and literature therein for detailed derivation procedure)
∫ 0 1 f ( t ) d t = ∑ m = 1 M ∑ n = 0 ∞ ( − 1 ) n + 1 ( 2 M ) n + 1 ( n + 1 ) ! d n d t n f ( t ) t = m − 1 / 2 M .
It is interesting to note that if the upper summation bound associated with variable n is an integer N ≥ 1 , then we can also use
∫ 0 1 f ( t ) d t = lim M → ∞ ∑ m = 1 M ∑ n = 0 N ( − 1 ) n + 1 ( 2 M ) n + 1 ( n + 1 ) ! d n d t n f ( t ) t = m − 1 / 2 M .
It is easy to show that, excluding all zero terms occurring at odd values of the variable n, equation (10) can be rewritten in a more convenient form
∫ 0 1 f ( t ) d t = 2 ∑ m = 1 M ∑ n = 0 ∞ 1 ( 2 M ) 2 n + 1 ( 2 n + 1 ) ! d 2 n d t 2 n f ( t ) t = m − 1 / 2 M .
Although equation (11) requires even derivatives of the integrand at the points t = ( m − 1 / 2 ) / M , where m = 1 , 2 , 3 , … M , its application with help of the Computer Algebra System (CAS) may be very efficient in numerical integration. Specifically, such an approach may be especially useful for numerical integration for the highly oscillating functions. The interested readers can download the MATLAB code based on the integration formula (11) on the MATLAB Central website [6] (file ID #: 71037).
If an integrand represents a function of two variables f x , t , then the integration formula (11) reads as
∫ 0 1 f ( x , t ) d t = 2 ∑ m = 1 M ∑ n = 0 ∞ 1 ( 2 M ) 2 n + 1 ( 2 n + 1 ) ! ∂ 2 n ∂ t 2 n f ( x , t ) t = m − 1 / 2 M .
The arctangent function can be given as an integral
arctan ( x ) = ∫ 0 1 x 1 + x 2 t 2 d t .
Consequently, substituting the integrand from equation (13)
x 1 + x 2 t 2 = x 2 1 1 + i x t + 1 1 − i x t
into equation (12) and using equation (9) for differentiation, we can find that
arctan ( x ) = i ∑ m = 1 M ∑ n = 0 ∞ x 2 n + 1 ( 2 M ) 2 n + 1 ( 2 n + 1 ) 1 ( x m − 1 / 2 M + i ) 2 n + 1 − 1 ( x m − 1 / 2 M − i ) 2 n + 1 .
Series expansion (14) is rapid in convergence. However, it requires algebraic manipulations with complex numbers. Therefore, it is very desirable to exclude them. This can be achieved by induction based on two-step iteration
α n ( x , t ) = α n − 1 ( x , t ) ( 1 − 1 / ( x t ) 2 ) + 2 β n − 1 ( x , t ) / ( x t ) , β n x , t = β n − 1 x , t 1 − 1 / x t 2 − 2 α n − 1 x , t / x t ,
and
α 1 ( x , t ) = 1 / ( x t ) , β 1 ( x , t ) = 1 ,
that transforms equation (14) into the following series expansion
arctan ( x ) = 2 ∑ m = 1 M ∑ n = 1 ∞ 1 ( 2 n − 1 ) ( 2 m − 1 ) 2 n − 1 α n ( x , γ m , M ) α n 2 ( x , γ m , M ) + β n 2 ( x , γ m , M ) ,
where the argument is
γ m , M = m − 1 / 2 M .
Equation (15) is a generalization of the equation (8). Consistency between these two equations can be observed by taking M = 1 . In particular, substitution M = 1 into series expansion (15) of the arctangent function implies that t = γ 1 , 1 = 1 / 2 . Consequently, from equation (15) we get equation (8), where the expansion coefficients are
g 1 ( x ) = α 1 ( x , γ 1 , 1 ) , h 1 ( x ) = β 1 ( x , γ 1 , 1 ) , g n ( x ) = α n ( x , γ 1 , 1 ) , h n ( x ) = β n ( x , γ 1 , 1 ) .
The following is a Mathematica code that generates graphs shown in Figure 1 (this code can be copy-pasted directly to the Mathematica notebook): Preprints 68265 i001
Graphs in Figure 1 are generated by using series expansion (15) truncated at n max = 10 . Blue, red and green curves correspond to integer M taken to be 1, 2 and 3, respectively.

3. Convergence

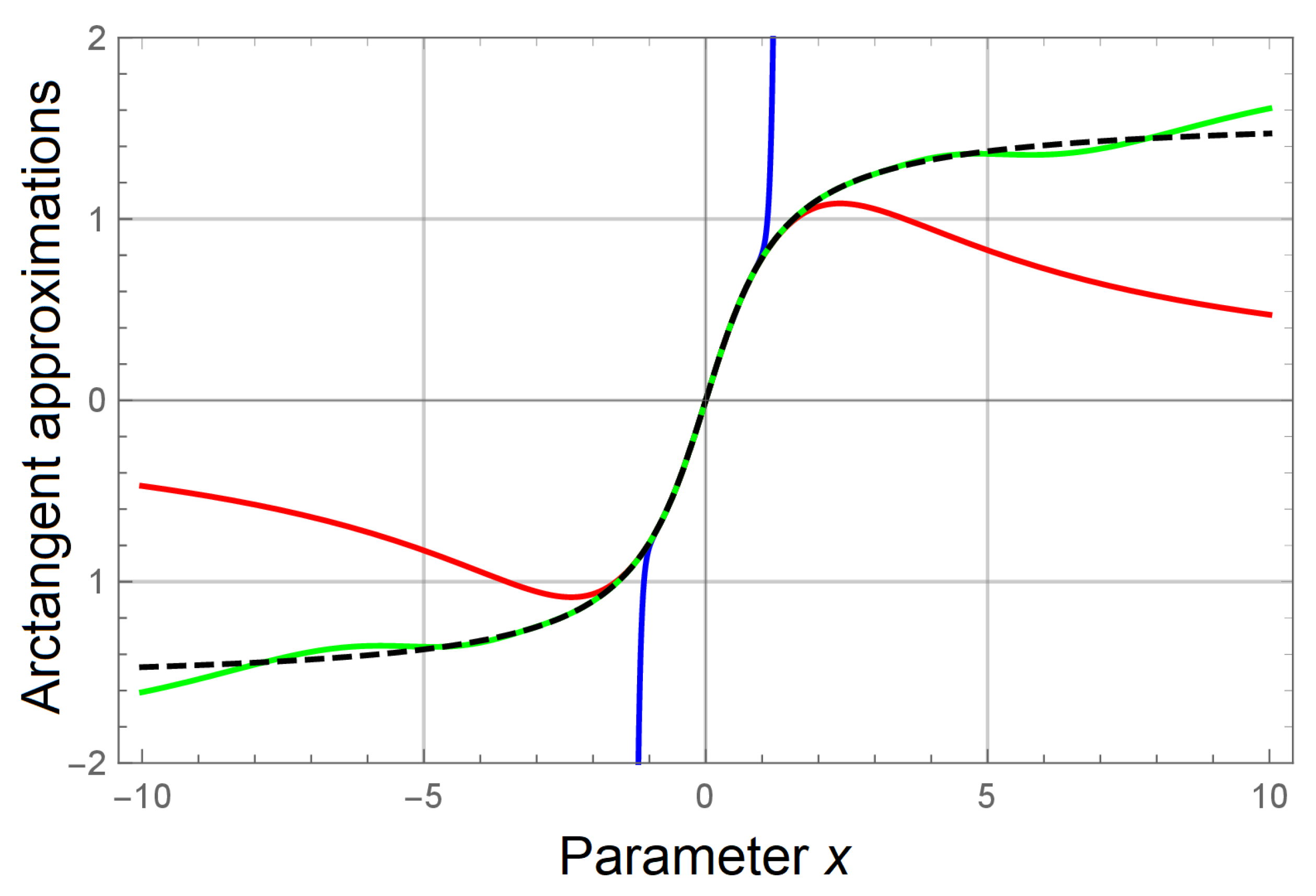
Consider Figure 2 showing approximation curves of the arctangent function arctan ( x ) by using equations (15), (16) and (17) truncated at n max = 10 . The blue curve corresponding to the Maclaurin expansion series
arctan ( x ) = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 , | x | ≤ 1 ,
diverges beyond − 1 and 1 due to finite radius of convergence. Although one can resolve this issue by using an elementary relation
arctan x = π 2 − arctan 1 x , x > 0 , 0 , x = 0 , − π 2 − arctan 1 x , x < 0 ,
our objective is just to visualize the convergence. The red curve shows the Euler series expansion [7,8]
arctan x = ∑ n = 0 ∞ 2 2 n n ! 2 2 n + 1 ! x 2 n + 1 1 + x 2 n + 1 .
The green curve illustrates the series expansion (15) at M = 1 . The black dashed curve depicts the original arctangent function for comparison. As we can see from Figure 2, even at smallest M the series expansion (15) provides more rapid convergence as compared to the Euler series expansion (17).
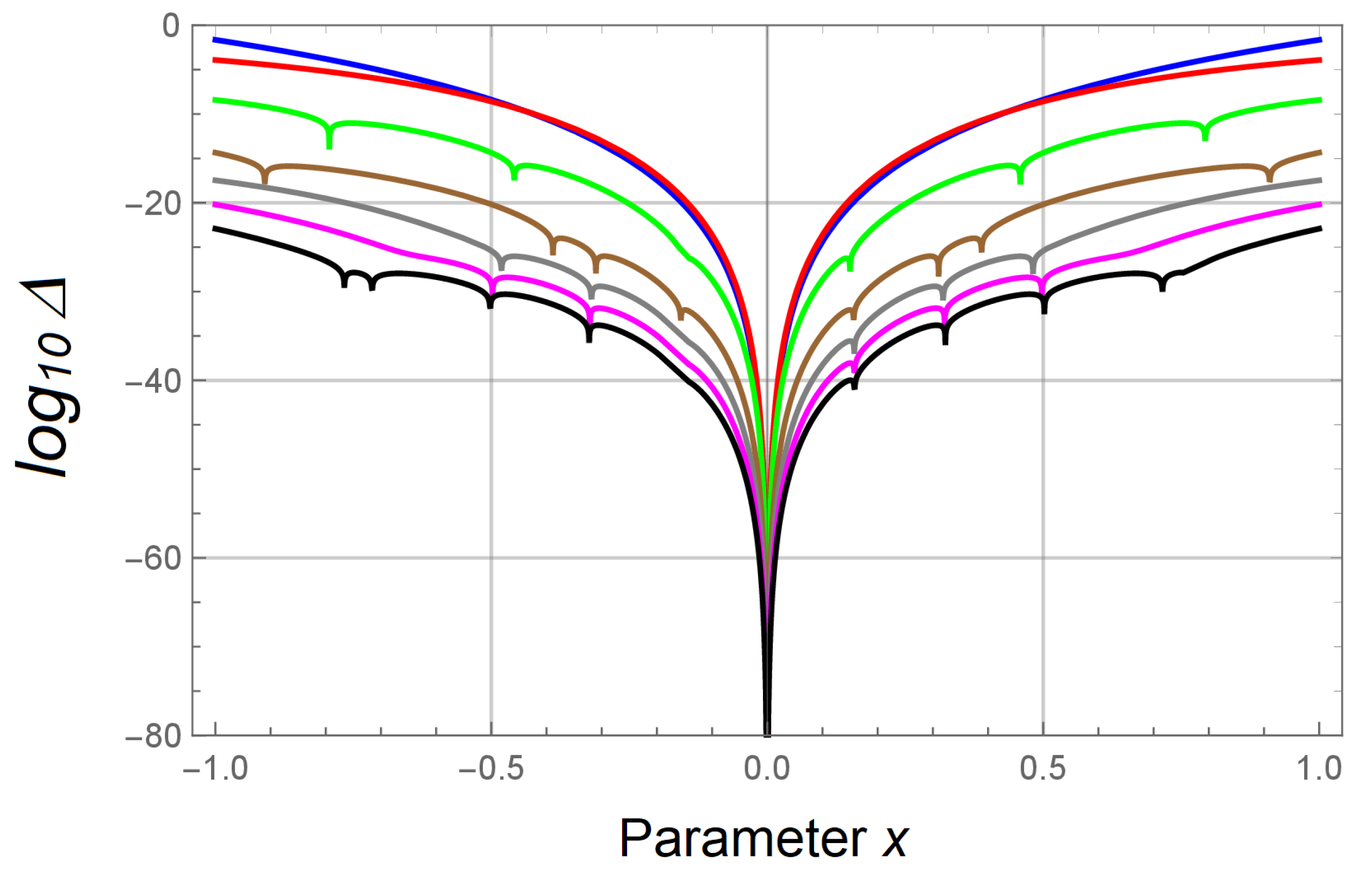
Figure 3 shows the logarithms of absolute difference log 10 Δ between the arctangent function and its approximations provided by equations (15), (16) and (17). All curves are also computed with truncating integer n max = 10 in all these equations. The blue and red curves correspond to equations (16) and (17) while the green, brown, gray, magenta and black curves correspond to equation (15) when M is equal to 1, 2, 3, 4 and 5, respectively. As we can see from this figure, increase of the integer M leads to a rapid decrease of the absolute difference Δ by many orders of the magnitude. These results indicate that the series expansion (15) provides increasing convergence with increasing M. Consequently, the series expansion (15) may be promising for efficient computation digits of π in the Machin-like formulas [4,9,10,11,12,13,14,15] without undesirable surd numbers since computation of any irrational numbers is itself a big challenge.
Our empirical results show that even using already known Machin-like formulas with sufficiently large integers in actangent arguments, the expansion series (15) at any M ≥ 1 can provide more than 17 digits of π at each increment by 1 of the variable n. It is interesting to note that this convergence rate is faster than that of provided by Chudnovsky formula generating 14 to 16 digits of π per increment [9,12]. Nowadays, Chudnovsky formula remains most efficient for computing digits of π due to its rapid convergence and other advantages in algorithmic implementation. Historically, however, there were several records that appeared due to application of the Machin-like formulas in computing π and, in 2002, an algorithm, developed by Kanada on the basis of self-checking pair of the Machin-like formulas, beat the record providing more than a trillion digits of π for the first time [10,12]. Therefore, discovery of new Machin-like formulas and rapidly convergent series expansions of the arctangent function may be promising for computing digits of the constant π .

4. Conclusions

We derived a generalized series expansion (15) of the arctangent function by using the EMI formula (12). Computational test we performed reveals that such a generalization significantly improves convergence in computation of the arctangent function.

Author Contributions

S.M.A. developed the methodology, wrote the codes and prepared a draft version of the manuscript. R.S., R.K.J and B.M.Q. verified, reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This work is supported by National Research Council Canada, Thoth Technology Inc., York University and Epic College of Technology.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
EMI Enhanced midpoint integration
CAS Computer algebra system

References

  1. Adegoke, K.; Layeni, O. The higher derivatives of the inverse tangent function and rapidly convergent BBP-type formulas for pi. Appl. Math. E-Notes 2010, 10, 70–75. [Google Scholar] [CrossRef]
  2. Lampret, V. The higher derivatives of the inverse tangent function revisited. Appl. Math. E-Notes 2011, 11, 224–23. [Google Scholar]
  3. Abrarov, S.M.; Quine, B.M. A simple identity for derivatives of the arctangent function. Available online: https://doi.org/10.48550/arXiv.1605.02843 (accessed on 1 February 2023).
  4. Abrarov, S.M.; Siddiqui, R.; Jagpal, R.K.; Quine, B.M. A new form of the Machin-like formula for π by iteration with increasing integers. J. Integer Seq. 2022, 25((4)), 22.4.5. [Google Scholar] [CrossRef]
  5. Abrarov, S.M.; Quine, B.M. A formula for pi involving nested radicals. Ramanujan J. 2018, 46, 657–665. [Google Scholar] [CrossRef]
  6. Abrarov, S.M. Array numerical integration by enhanced midpoint rule (file ID: 71037). Available online: https://tinyurl.com/bdf8pt2m (accessed on 1 February 2023).
  7. Castellanos, D. The ubiquitous π. Math. Mag. 1988, 61(2), 67–98. [Google Scholar] [CrossRef]
  8. Chien-Lih, H. An elementary derivation of Euler’s series for the arctangent function. Math. Gaz. 2005, 89, 469–470. [Google Scholar] [CrossRef]
  9. Berggren, J.L.; Borwein, J.M.; Borwein, J. Pi: a source book, 3rd ed.; Springer: New York, USA, 2004. [Google Scholar]
  10. Calcut, J.S. Gaussian integers and arctangent identities for π. Amer. Math. Monthly 2009, 116(6), 515–530. [Google Scholar] [CrossRef]
  11. Nimbran, A.S. On the derivation of Machin-like arctangent identities for computing pi (π). Math. Student 2010, 79((1-4)), 171–186. [Google Scholar]
  12. Agarwal, R.P.; Agarwal, H.; Sen, K.S. Birth, growth and computation of pi to ten trillion digits. Adv. Differ. Equ. 2013, 100. [Google Scholar] [CrossRef]
  13. Wetherfield, M.R.; Chien-Lih, H. Computing pi: lists of Machin-type (inverse cotangent) identities for pi/4. Available online: http://www.machination.eclipse.co.uk (accessed on 1 February 2023).
  14. A Wolfram notebook playing with Machin-like formulas. Available online: https://www.wolframcloud.com/obj/exploration/MachinLike.nb (accessed on 1 February 2023).
  15. Gasull, A.; Luca, F.; Varona, J.L. Three essays on Machin’s type formulas. Available online: https://doi.org/10.48550/arXiv.2302.00154 (accessed on 2 February 2023).
Preprints 68265 g001
Figure 1. Arctangent approximations computed by using series expansion (15) truncated at n max = 10 . Blue, red and green curves correspond to M taken to be 1, 2 and 3, respectively.
Figure 1. Arctangent approximations computed by using series expansion (15) truncated at n max = 10 . Blue, red and green curves correspond to M taken to be 1, 2 and 3, respectively.
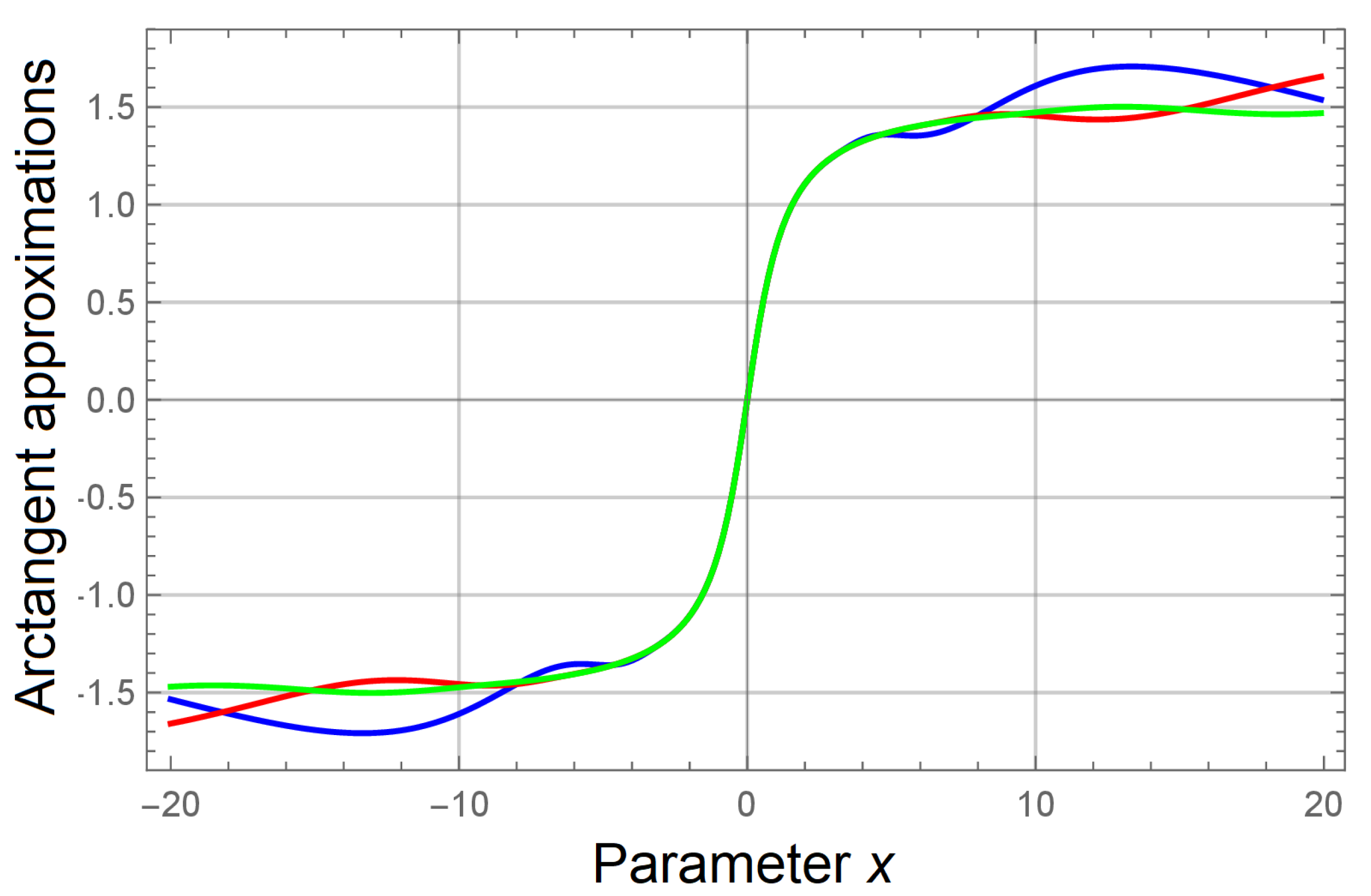
Preprints 68265 g001
Preprints 68265 g002
Figure 2. Arctangent approximations computed by series expansions (16) (blue), (17) (red) and (15) (green) truncated at n max = 10 . Integer M in equation (15) is taken to be equal to 1. The dashed black curve shows the original artangent function.
Figure 2. Arctangent approximations computed by series expansions (16) (blue), (17) (red) and (15) (green) truncated at n max = 10 . Integer M in equation (15) is taken to be equal to 1. The dashed black curve shows the original artangent function.
Preprints 68265 g002
Preprints 68265 g003
Figure 3. Logarithms of absolute difference l o g 10 Δ between original arctangent function and series expansions (16) (blue), (17) (red) and (15) (green-to-black) truncated at n max = 10 . Integer M in the series expansion (15) is taken to be 1 (green), 2 (brown), 3 (gray), 4 (magenta) and 5 (black).
Figure 3. Logarithms of absolute difference l o g 10 Δ between original arctangent function and series expansions (16) (blue), (17) (red) and (15) (green-to-black) truncated at n max = 10 . Integer M in the series expansion (15) is taken to be 1 (green), 2 (brown), 3 (gray), 4 (magenta) and 5 (black).
Preprints 68265 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated