A Relational Semantics for Ockham’s Modalities

Preprint

Article

A Relational Semantics for Ockham’s Modalities

Altmetrics

Downloads

159

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 February 2023

Posted:

06 February 2023

You are already at the latest version

Alerts

Abstract

This article aimed at providing some extension of the modal square of opposition in the 1 light of Ockham’s account of the modal operators. Moreover, we shall set forth some significant 2 remarks on the de re-de dicto distinction and on the modal operator of contingency by means of a 3 Boolean algebra called Bitstring Semantics. This generalisation starting from Ockham’s account of 4 modalities will allow us to take into consideration whether Ockham’s thought on this matter holds 5 water or not, and in which case it should be changed in order to make it coherent.

Keywords:

Subject: Arts and Humanities - Philosophy

0. Introduction

The article is structured as follows.1

A first, more historical part will be entirely dedicated to the set-up of Ockham’s account of modal propositions and their possible readings. It will be considered the de re-de dicto distinction in Ockham’s thought first of all, providing some informal rules regarding this distinction deduced from Ockham’s account (Section 1).

Then, Ockham’s account of contingency and its application to the modal squares provided in Ockham’s commentary on Aristotle’s De Interpretatione. This brings to two modal hexagons that will be drawn as generalisations of the modal square, by means of the application of contingency, as Ockham defines it, within those modal squares provided in the above-mentioned commentary (Section 2).

Finally, a formal section will be devoted to a formal semantics of Ockham’s modal statements. More especially, it will consist in a set of two kinds of logical forms, whether de re and de dicto, and a corresponding second-order logic where modalities are viewed as a dyadic predicate including properties and worlds. After devising a Boolean semantics, according to which the meaning of formulas corresponds to their model sets or ordered truth-conditions, Ockham’s statements of (non-)contingency will then be redefined by means of an external use of negation, and our algebraic translation of logical relations will result in a final structure including sixteen modal statements into a hexadecagon of modal statements (Section 3).

1. Ockham’s Account

In medieval logic, there are two possible readings of a modal proposition. A modal proposition can be read either in sensu compositionis (compound sense) or in sensu divisionis (divided sense)2. Ockham3 defines the compound sense as follows:

In the sense of composition it is always asserted that such a mode is truly predicated of the proposition corresponding to the dictum in question. For example, by means of "That every man is an animal is necessary" it is asserted that the mode "necessary" is truly predicated of the proposition "Every man is an animal", the dictum of which is "That every man is an animal".4

Therefore, in the compound sense what is taken under consideration is the proposition, or better the dictum, namely the categorical proposition to which the modal operator is linked. The proposition is then true if the dictum satisfies the requirements of the modal operator attached to it. For example, assume that there is a proposition de necessario, i.e., a proposition having necessity as a modal operator, and it is taken in the compound sense, then that proposition is true iff the categorical proposition or dictum is a necessary proposition, such as in case of “every man is an animal”. Hence it is called “compound sense” because the dictum is taken as a composite, as a unitary entity that can be necessary, possible, etc.

Regarding the divided sense, Ockham states:

However, the sense of division of such a proposition is always equipollent to a proposition taken with a mode and without such a dictum. For example, "That every man is an animal is necessary"; in the sense of division is equipollent to "Every man is of necessity (or necessarily) an animal".”5

The divided sense does not have a dictum but the modal operator “divides” the subject from the predicate by introducing a changing of the copula. Ockham clearly says a proposition in divided sense is true or false according to the references of the terms involved in the proposition. In order to evaluate if the proposition is true, it is required to go through the individuals that are denoted by the subject and to rewrite the proposition at stake in the correspondent singular propositions:

“It is necessary that every man is white” is true in the divided sense

iff

“This man (hoc) is white” and “That man is white”, etc., are all true and necessary.6

If it is the case that every singular term, i.e. “this man”, “that man”, stand for “man” so that all the singular propositions are true and necessary, the proposition taken in the divided sense is true and necessary as well.

Ockham also states that the compound sense requires that the proposition is taken materially (materialiter) while the latter is taken significatively (significative) in the divided sense. Regarding the former, the term “materially” can be better understood looking at the well-known medieval supposition theory. A term has a material supposition (suppositio materialis) when terms stand for themselves, e.g. “dog has three letters”. Hence, in case of the compound sense, the modal proposition stands for itself, or better for its dictum. Indeed, a proposition taken in the compound sense is true or false according to its dictum. In the opposite side, a proposition in the divided sense is taken significatively (significative).7 This means that the truth-value of a modal proposition taken in divided sense is based on the meanings of the terms involved in that proposition. By the means of the singular propositions, it can be verified whether the relation between the subject and the predicate is that one that is required by the modal operator inside the modal proposition.

Another way to understand the distinction can be the following: the divided sense is extensional, because it is based on the references of the terms involved in the singular proposition, while the compound sense is intensional, for it is based on the analysis of the proposition apart from the reference of the terms involved. Finally, it can be said that the compound/divided sense distinction is based on the fact that the truth-value of a proposition changes if we consider either the subject in its relation with the predicate or the proposition as a whole. In other words, the distinction is based on a mereological distinction: what applies to the proposition as a whole does not apply to the subject as a part of the whole and vice versa.

It is quite important to distinguish between these two senses for the same modal proposition can have different truth-values according to these different readings. For example, this proposition “it is necessary that every truth is true” is true in the compound sense, but false in the divided sense. Indeed, not every singular proposition of that proposition is necessary. There are some truths that become “stale”, as Hegel would say, and are not necessary, at least in the sense of being always true. It is also possible that a modal proposition is false in the compound sense, but true in the divided sense. Ockham gives this example:

An example: “both parts of a contradiction can be true” is false in the sense of composition and true in the sense of division, since each singular is true.8

Furthermore, the truth-conditions of a proposition taken in divided sense are actually based on the truth-conditions of the compound sense, for when it is required to establish whether a proposition is true in the divided sense, it is also required to reduce that proposition to its singular propositions. Nevertheless, all the singular proposition can be only taken in compound sense: indeed, note that each singular is taken always in a compound sense because it is impossible to divide it further. For in a singular proposition there is nothing else that can be “divide”, that is it is not possible to go further in the analysis of the reference, but the singular proposition is that makes the reference of a term clear. In other words, a singular proposition can be taken only in a compound sense for it is basically an atomic proposition.

Put it succinctly, it is necessary to distinguish those different readings. There is a also a syntactic distinction that requires some attention and especially in its relation with these two possible readings, so with the semantic level.

Let us take one modal operator, such as possibility. This is a cum dicto form:

⋄(S is P)

In this form, the modal operator is attached to the dictum. The modal operator is always external and it is always a noun in the form “it is possible that”. The dictum has this form: S is in the accusative case and P is a verb in an infinitive verb.

There is also a sine dicto form:

S is ⋄ P

In this case the modal operator is either a verb (S can be P) or an adverb (S is possibly P). In this form, there is not any dictum at all but the modal operator is internal.

Now, a proposition sine dicto is always taken in the divided sense for an internal modal operator “divides” always the subject from the predicate so that the relationship between them must be always verified by looking at the singular propositions. A proposition cum dicto can be either in divided or compound sense. So, in case of a cum dicto form it is required to clarify which reading of the modal proposition is considered. As a result of that, a cum dicto proposition that is taken in the divided sense is equivalent to the same proposition sine dicto.9

All in all, when there is a cum dicto form, there is an ambiguity between divided and compound sense. Hence, in order to avoid any ambiguity, it is possible to unify the semantical level (compound and divided sense) and the syntactical level (cum dicto-sine dicto) as follows:

\underset{\underset{de dicto}{︸}}{C o m p o u n d s e n s e - cum dicto} \underset{\underset{de re}{︸}}{D i v i d e d s e n s e - sine dicto}

Therefore, hereafter we shall refer just to the modern distinction de dicto/de re to denote both the semantical aspect and the syntactical aspect included in Ockham’s account.

Before considering the modal squares and their extensions, it is required to set up some rules aimed at describing in which case there is a proposition that is either de re or de dicto. These rules could be called “a posteriori rules” because they are deduced from Ockham’s account.10 We shall take only the case of necessity and possibility11 into account. Indeed, Ockham’s squares that will be considered here involved just necessity and possibility.

The set-up of this rules is based on the truth-values of the dictum:

(a): A dictum is true and cannot be false: ( $D^{⊤}$ ), e.g. “every man is an animal”.
(b): A dictum is false and cannot be true: ( $D^{⊥}$ ), e.g. “every white thing is a black thing”.
(c): A dictum can be either true or false: ( $D^{⊤ / ⊥}$ ), e.g. “every man is white”.

Given that, it can be said that:

□ / ⋄ \forall / \exists (D^{⊤}) is always de dicto

In Ockham’s account, propositions such as “it is necessary/possible that every/some man is an animal” are always a de dicto, even if it can be also true de re. Indeed, a proposition de dicto is necessary/possible iff the dictum is necessary/possible. So, if the dictum is true and cannot be false it can be said to be necessary, so possible (ab necesse ad posse). As a result of that, when there are dicta such as “Socrates is Socrates” or “Socrates is a man”, there will always be a proposition de dicto.

By contrast when a dictum is false and cannot be true, we have that:

□ / ⋄ \forall / \exists (D^{⊥}) is always de re

A proposition like “every living being is a corpse” is true de re both in case of possibility and necessity but it is not true de dicto. It is false that “it is necessary/possible that every living being is a corpse”, for it is false that “it is necessary/possible that every living being is not a living being”. However, it is true that “every living being can be a corpse”. It is also true that “every living being is necessarily a corpse” in the sense that “every living being must sooner or later die”. So, every “opposition” such as “every white thing is black” is always de re.

Finally, if the dictum is true but can be false and vice versa, we have:

□ / ⋄ \forall / \exists (D^{⊤ / ⊥}) is always de dicto or de re

For example, “every animal is a man” is false but can be true both de dicto and de re: “it is possible that every animal is a man” and “every animal can be a man”.

2. Extension of Ockham’s Modal Squares

Whereas the standard version of the modal square involves all the four alethic modal operators at the same time, though it included neither universals nor particulars, the modal logic of 14th century tried to include quantified propositions within the modal square. The necessity to introduce quantified propositions and to involve all the alethic modalities produce a splitting of the standard modal square in different squares having for example just two modal operators in the top and bottom sides, as universals and particulars.

From his side, Ockham provides three squares in his commentary on De Interpretatione. We shall focus on two of them involving necessity and possibility.

In the first squares, necessity in the up side (universals), possibility in the bottom side (particulars). Assuming that M means “being a man”, W means “being white”, whereas A stands for the affirmative universal, E for the negative universal, I for the affirmative particular and O for the negative particular, this results in the square

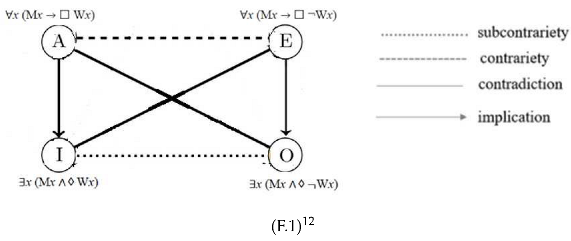
They are all de re, but Ockham clearly says that this square can be also re-write with all the propositions in a de dicto form13. Indeed, as we have said, the dictum “every/some man is white” can be both true and false (

D^{⊤ / ⊥}

The same holds for the second square in which the same dictum is involved (e.g. “every/some man is white”). However, this square has possibility in the top side (universals) and necessity in the bottom side (particulars):

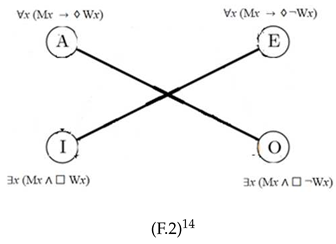
This square is incomplete because the universals (“every man can be white” – “every man can not be white”) are not contrary for they can be both true the same time. In the same way, the two particulars (“some man is necessarily white” – “some man is necessarily not white”) are not subcontraries for they can be both false at the same time.15

These two squares can be extended by introducing the modal operator of contingency. The first of it is required to briefly define what is contingent as a modal operator according to Ockham.16

Given that ∇ means “it is contingent that” and that

Δ

means “it is not contingent that” or “it is determinate that”, Ockham defines propositions de contingenti, so having contingency as modal operator, as follows17:

Universal de contingenti:

\nabla \forall x (S x \to P x) = ⋄ \forall x (S x \to P x) \land ⋄ \forall x (S x \to \neg P x) / \forall x (S x \to ⋄ P x) \land \forall x (S x \to ⋄ \neg P x)

Particular de contingenti:

\nabla \exists x (S x \land P x) = ⋄ \exists x (S x \land P x) \land ⋄ \exists x (S x \land \neg P x) / \exists x (S x \land ⋄ P x) \land \exists x (S x \land ⋄ \neg P x)

These definitions are based on one side of De Morgan’s rules that Ockham knows and clearly defines in [13]:19

\neg (A \land B) \leftrightarrow (\neg A) \lor (\neg B)

So, these are the negation of the propositions de contingenti:

Δ \forall x (S x \to P x) = □ \exists x (S x \land P x) \lor □ \exists x (S x \land \neg P x) = \exists x (S x \land □ P x) \lor \exists x (S x \land □ \neg P x

)

Δ \exists x (S x \land P x) = □ \forall x (S x \to P x) \lor □ \forall x (S x \to \neg P x) = \forall x (S x \to □ P x) \lor \forall x (S x \to □ \neg P x

Note that Ockham clearly points out that contingency and non-contingency are negation-symmetric ([19]: 118). There are no differences between “It is contingent that S is P” and “It is contingent that S is not P”.20

Ockham gives these examples:21

It is contingent that every man is an animal = every man can be an animal and every man can not be an animal
It is not contingent that every man is an animal = it is necessary that some man is an animal or it is necessary that some man is not an animal22
It is contingent that some man is white = some man can be white and some man can not be white
It is not contingent that some man is white = every man is necessarily white or every man is necessarily not white

Contingency is the conjunction of opposite simultaneous possibilities. Which kind of opposition is at stake here? That one between the propositions de possibili “some man can be white” and “some man can not be white”. That is to say subcontrariety. Note indeed that two subcontraries can be conjunct for they can be both true at the same: when it is possible to conjunct two subcontraries de possibili, there is a proposition de contingenti, “it is contingent that some man is white”.

Similarly, the negation of a proposition such as “it is contingent that some man is white” is equivalent to the disjunction of the negations of “some man can be white” and “some man can not be white”. Therefore, we have: “every man is necessarily white” or “every man is necessarily not white”. These propositions are contraries, so either one or the other can be true. This is a disjunction.

In addition, Ockham states that a proposition de contingenti implies not only one proposition de possibili, but two propositions, the subcontraries de possibili,23 just like a logical conjunction implies both the conjuncts:

De dicto

$\nabla \forall x (S x \to P x) \to ⋄ \forall x (S x \to P x)$
$\nabla \forall x (S x \to P x) \to ⋄ \forall x (S x \to \neg P x)$
$\nabla \exists x (S x \land P x) \to ⋄ \exists x (S x \land P x)$
$\nabla \exists x (S x \land P x) \to ⋄ \exists x (S x \land \neg P x)$

De re

$\nabla \forall x (S x \to P x) \to \forall x (S x \to ⋄ P x)$
$\nabla \forall x (S x \to P x) \to \forall x (S x \to ⋄ \neg P x)$
$\nabla \exists x (S x \land P x) \to \exists x (S x \land ⋄ P x)$
$\nabla \exists x (S x \land P x) \to \exists x (S x \land ⋄ \neg P x)$

By constrast, a proposition de necessario implies the negation of the proposition de contingenti,24 just like a disjunction implies the logical disjunction:

De dicto

$□ \forall x (S x \to P x) \to Δ \forall x (S x \to P x)$
$□ \forall x (S x \to \neg P x) \to Δ \forall x (S x \to P x)$
$□ \exists x (S x \land P x) \to Δ \exists x (S x \land P x)$
$□ \exists x (S x \land \neg P x) \to Δ \exists x (S x \land P x)$

De re

$\exists x (S x \land □ P x) \to Δ \forall x (S x \to P x)$
$\exists x (S x \land □ \neg P x) \to Δ \forall x (S x \to P x)$
$\forall x (S x \to □ P x) \to Δ \exists x (S x \land P x)$
$\forall x (S x \to □ \neg P x) \to Δ \exists x (S x \land P x)$

Finally, what is contingent is said to be incompatible to (repugnans) both necessary and impossible. Therefore, contingent is what is usually called “two-sided possibility”: a proposition de contingenti such as “it is contingent that some man is white” is incompatible with both “every man is necessarily white” and “every man is necessarily not white”.25

To sum up, by introducing contingency to the squares above-presented, these two new figures can be drawn:

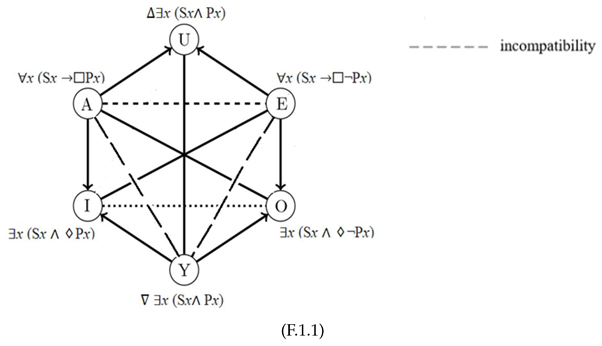
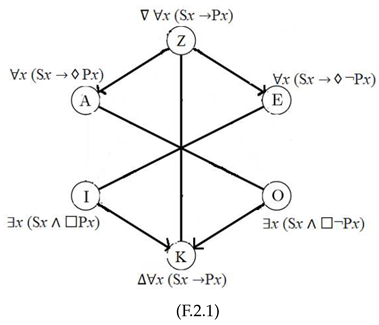
These are the extensions of Ockham’s modal squares following Ockham’s claims about contingency. (F.1.1) is the standard modal hexagon, that one provided by [1]. However, Ockham’s modal hexagon (F.1.1) does not have a relation of subcontrariety between U, I and O that should be present in the standard modal hexagon. So, Ockham’s modal hexagon is partially incomplete.

(F.2.1) is also an incomplete version of the standard modal hexagon for (F.2) is an incomplete version of the square of opposition. However, this latter figure shows that the modal hexagon in quantified modal logic is split in two different version, (F.1.1) and (F.2.1). In other words, the standard modal hexagon must be redefined in order to account for all the propositions de contingenti in quantified modal logic so that we cannot admit only one version of it, but two different versions, i.e. F.1.1 and F.2.1.

A final remark concerning Ockham’s application of the negation within the modal propositions that are conjoined in a proposition de contingenti. Regarding negation, there are two possible applications:

internal: e.g., “every S is possibly not P”.
external: e.g., “not every S is possibly P” = “some S is possibly not P”.

Ockham takes only internal negation into account, without considering the external one. This is what makes possible our application of those propositions de contingenti within the modal squares. Indeed, let us consider the case in which “it is contingent that every S is P” would be equivalent to “it is possible that every S is P and it is possible that some S is not P”, so having an external negation as a second conjunct. Starting from that, the proposition “it is not contingent that every S is P” is equivalent to “it is necessary that some S is not P or it is necessary that every S is P”. As a result, contingency will not be related to all the four angles of the square (A,E,O,I) but just to A and O de possibili and de necessario. Therefore, external negation seems to make impossible to drawn a standard modal hexagon in quantified modal logic, whereas internal negation helps to construct a regular hexagon of quantified modal logic. In the next sections we shall see how, starting from Ockham’s account and external negation, this would lead to an even more complicated resulting structure.

3. Logical Analysis

The point in the following is to set forth a systematic theory of modal statements, both by streamlining them into a basic logical form and then devising a corresponding formal semantics where modalities are turned into relations standing between propositions and possible worlds.

3.1. Syntax

Let us attempt to streamline Ockham’s logical theory of quantified modal statements into the language of first-order logic, in order to obtain a comprehensive formalisation of it. For this purpose, these statements include two kinds of quantifiers (universal and existential) and four modal operators (necessity, possibility, non-contingency or determinacy, and contingency) that can be switched to each other and result in either de dicto or de re formulas.

A first way to account for these modal statements is ordinary language. Let

Q

= {A,E,I,O} a set of 4 quantifying expressions (“Every is (not) ...”, “Some is (not) ...”), and let

M = {□, ⋄, Δ, \nabla}

a set of 4 modal operators (necessity, possibility, non-contingency or determinacy, and contingency). It results in a cardinal set of

4 \times 4 \times 2 = 32

modal statements; in the first group (i)–(xvi) of statements, the quantifying expressions occur de dicto (with a broad scope), whereas they occur de re (with a narrow scope) in the second group (xvii)–(xxxii).

De dicto statements

M Q : “ It is \dots that \dots S is \dots P ”

$□ Q$ :

“It is necessary that ... S is ... P”

(i): □A: “It is necessary that every S is P”
(ii): □E: “It is necessary that every S is not P”
(iii): □I: “It is necessary that some S is P”
(iv): □O: “It is necessary that some S is not P”

$⋄ Q$ :

“It is possible that ... S is ... P”

(v): ⋄A: “It is possible that every S is P”
(vi): ⋄E: “It is possible that every S is not P”
(vii): ⋄I: “It is possible that some S is P”
(viii): ⋄O: “It is possible that some S is not P”

$Δ Q$ :

“It is determinate that ... S is ... P”

(ix): $Δ$ A: “It is determinate that every S is P”
(x): $Δ$ E: “It is determinate that every S is not P”
(xi): $Δ$ I: “It is determinate that some S is P”
(xii): $Δ$ O: “It is determinate that some S is not P”

$\nabla Q$ :

“It is contingent that ... S is ... P”

(xiii): ∇A: “It is contingent that every S is P”
(xiv): ∇E: “It is contingent that every S is not P”
(xv): ∇I: “It is contingent that some S is P”
(xvi): ∇O: “It is contingent that some S is not P”

De re statements

Q M : “ \dots S is \dots \dots P ”

A $M$ :

“... S is ... ... P”

(xvii): A□: “Every S is necessarily P”
(xviii): A⋄: “Every S is possibly P”
(xix): A $Δ$ : “Every S is determinately P”
(xx): A∇: “Every S is contingently P”

E $M$ :

“... S is ... not P”

(xxi): E□: “Every S is necessarily not P”
(xxii): E⋄: “Every S is possibly not P”
(xxiii): E $Δ$ : “Every S is determinately not P”
(xxiv): (xxiv) E∇: “Every S is contingently not P”

I $M$ :

“Some S is ... P”

(xxv): I□: “Some S is necessarily P”
(xxvi): I⋄: “Some S is possibly P”
(xxvii): I $Δ$ : “Some S is determinately P”
(xxviii): I∇: “Some S is contingently P”

O $M$ :

“Some S is ... not P”

(xxix): O□: “Some S is necessarily not P”
(xxx): O⋄: “Some S is possibly not P”
(xxxi): O $Δ$ : “Some S is determinately not P”
(xxxii): O∇: “Some S is contingently not P”

A second way to account for the meaning of modal statements is by means of first-order logic, in order to show subsequently which are logically equivalent. Formal logic renders the previous informal statements (i)–(xxxii) in terms of quantified expressions and their affirmed and negated components. The basic logical form of modal statements relies upon 3 main components, that is: one modal operator, one quantifier, and one predicative expression. Given that these components may be either affirmed or denied, let ± a general operator symbolizing either the affirmation or negation of components. Assuming the validity of the following classical equivalences:

A \to B = \neg (A \land B) \neg \neg A = A \forall x A x = \neg \exists x \neg A x

the 32 modal statements may be rephrased as follows according to the two kinds of scope between quantifiers and modalities:

De dicto modal statements:

\pm ⋄ \pm \exists x (S x \land \pm P x)

(i) □A:

\neg ⋄ \exists x (S x \land \neg P x) = □ \forall x (S x \to P x)

(ii) □E:

\neg ⋄ \exists x (S x \land P x) = □ \forall x (S x \to \neg P x)

(iii) □I:

\neg ⋄ \neg \exists x (S x \land P x) = □ \exists x (S x \land P x)

(iv) □O:

\neg ⋄ \neg \exists x (S x \land \neg P x) = □ \exists x (S x \land \neg P x)

(v) ⋄A:

⋄ \neg \exists x (S x \land \neg P x) = ⋄ \forall x (S x \to P x)

(vi) ⋄E:

⋄ \neg \exists x (S x \land P x) = ⋄ \forall x (S x \to \neg P x)

(vii) ⋄I:

⋄ \exists x (S x \land P x)

(viii) ⋄O:

⋄ \exists x (S x \land \neg P x)

(ix)

Δ

□ \forall x (S x \to P x) \lor □ \exists x (S x \land \neg P x)

(x)

Δ

□ \forall x (S x \to \neg P x) \lor □ \exists x (S x \land P x)

(xi)

Δ

□ \exists x (S x \land P x) \lor □ \forall x (S x \to \neg P x)

(xii)

Δ

□ \exists x (S x \land \neg P x) \lor □ \forall x (S x \to P x)

(xiii) ∇A:

⋄ \forall x (S x \to P x) \land ⋄ \exists x (S x \land \neg P x)

(xiv) ∇E:

⋄ \forall x (S x \to \neg P x) \land ⋄ \exists x (S x \land P x)

(xv) ∇I:

⋄ \exists x (S x \land P x) \land ⋄ \forall x (S x \to \neg P x)

(xvi) ∇O:

⋄ \exists x (S x \land \neg P x) \land ⋄ \forall x (S x \to P x)

De re modal statements:

\pm \exists x (S x \land \pm ⋄ \pm P x)

(xvii) A□:

\forall x (S x \to □ P x)

(xviii) E□:

\forall x (S x \to □ \neg P x)

(xix) I□:

(\exists x) (S x \land □ P x)

(xx) O□:

(\exists x) (S x \land □ \neg P x)

(xxi) A⋄:

\forall x (S x \to ⋄ P x)

(xxii) E⋄:

\forall x (S x \to ⋄ \neg P x)

(xxiii) I⋄:

\exists x (S x \land ⋄ P x)

(xxiv) O⋄:

\exists x (S x \land ⋄ \neg P x)

(xxv) A

Δ

\forall x (S x \to □ P x) \lor (x) (S x \to □ \neg P x)

(xxvi) E

Δ

\forall x (S x \to □ \neg P x) \lor \forall x (S x \to □ P x)

(xxvii) I

Δ

\exists x (S x \land □ P x) \lor \exists x (S x \land □ \neg P x)

(xxviii) O

Δ

\forall x (S x \to □ \neg P x) \lor \forall x (S x \to □ P x)

(xxix) A∇:

\forall x (S x \to ⋄ P x) \land \forall x (S x \to ⋄ \neg P x)

(xxx) E∇:

\forall x (S x \to ⋄ \neg P x) \land \forall x (S x \to ⋄ P x)

(xxxi) I∇:

\exists x (S x \land ⋄ P x) \land \exists x (S x \land ⋄ \neg P x)

(xxxii) O∇:

\exists x (S x \land ⋄ \neg P x) \land \exists x (S x \land ⋄ P x)

Note that the above renderings of contingency and determinacy differ from Ockham’s versions, as we already said in the end of Section 2. The difference lies in the occurrence of negation: contingency means that it is possible for a given statement and its negation to be true. Now consider the statement ∇A: “It is contingent that every man is an animal”, where contingency applies to the universal affirmative A. We already saw that, according to Ockham, the latter means that it is possible that every man is an animal and it is possible that no man is an animal. Now such an interpretation makes an internal use of negation in its second conjunct, “No man is an animal" (i.e. “Every man is not an animal”), whereas our previous definition of contingency means that, according to ∇A, it is possible that every man is an animal and it is possible that not every man is an animal, i.e. it is possible that some man is not an animal. In other words, our suggestion definition of contingency makes an external use of negation in its second conjunct. Due to this discrepancy with Ockham, the following proposes a systematic way to account for the modal statements (i)–(xxxii) and their mutual logical relations.

3.2. Semantics

Possible world semantics (or relational semantics) is the standard way to afford the truth-conditions of modal statements, all the more that Kripke’s models helps to catch the plural meaning of necessity and possibility in modal frames and their various accessibility relations between worlds. Instead of following that path, however, the next sections intend to catch Ockham’s view of modalities by means of a special relational semantics: Bitstring Semantics, in which the meaning of a statements relies upon a partition of logical space. We assume in the following that necessity is treated as a S5 modality, and the point is to determine all logical interrelations between any modal statements. It results in an updated theory of opposition for (i)–(xxxii), with the help of a Boolean algebra to redefine the variety of logical relations between arbitrary formulas.

3.2.1. Relational Statements

First of all, let us rephrase the logical form of modal statements in order to make sense of the modal operators. Following the modern view of necessity as truth in all possible worlds, another way to say that is by claiming that, for example, every S is necessarily P if, and only if, S is P at every given world. Let P be a dyadic relation between an individual and a world, such that

P a w

reads “(the individual) a is P at w”. Then the de dicto and de re modal statements can be rephrased into these new logical forms of second-order logic, by quantifying over possible worlds:

De dicto modal statements:

\pm \exists x \pm \exists w \pm P x w

De re modal statements:

\pm \exists w \pm \exists x \pm P x w

The above reformulation of modal statements clearly shows that de re modal statements merely switch the ordering of quantifiers as they occur in their de dicto counterparts, recalling that modality is viewed now as a second kind of quantifier ranging over worlds. Apart from ontological scruples regarding what entities may occur in a world, a purely logical approach to the matter enables to think of a relational statement like “a is P at w” (about being at) as a relational expression that is on a par with “a loves b” (about loving). Thus “being at” and “loving” are two equally dyadic predicates.

3.2.2. Relational Semantics

Once that analogy is admitted, we can construct a model for modal statements in which a world includes three kinds of entities: properties, individuals, and worlds. This means that a world may include another world as an element. Besides that, a minimal number of two individual values

a, b

is required in order to make a difference between worlds at which everyone is P and someone (but not everyone) is P. Given that the modal statements (i)–(xxxii) let the predicate expression

S x

unchanged, models needn’t include a second property S and may include only P to make sense of these modal statements.26

Thus, let

w_{i}^{*}

be a minimal set for modal statements, including two individuals

a, b

and (at least), one property P, and two possible worlds

w_{1}, w_{2}

. The truth-value of a modal statement consists in knowing which individuals satisfy the property P in which possible world, accordingly.

w_{1}^{*} = {P a w_{1}, P a w_{2}, P b w_{1}, P b w_{2}}

w_{2}^{*} = {P a w_{1}, P a w_{2}, P b w_{1}, \neg P b w_{2}}

w_{3}^{*} = {P a w_{1}, P a w_{2}, \neg P b w_{1}, P b w_{2}}

w_{4}^{*} = {P a w_{1}, \neg P a w_{2}, P b w_{1}, P b w_{2}}

w_{5}^{*} = {\neg P a w_{1}, P a w_{2}, P b w_{1}, P b w_{2}}

w_{6}^{*} = {P a w_{1}, P a w_{2}, \neg P b w_{1}, \neg P b w_{2}}

w_{7}^{*} = {P a w_{1}, \neg P a w_{2}, P b w_{1}, \neg P b w_{2}}

w_{8}^{*} = {\neg P a w_{1}, P a w_{2}, P b w_{1}, \neg P b w_{2}}

w_{9}^{*} = {P a w_{1}, \neg P a w_{2}, \neg P b w_{1}, P b w_{2}}

w_{10}^{*} = {\neg P a w_{1}, P a w_{2}, \neg P b w_{1}, P b w_{2}}

w_{11}^{*} = {\neg P a w_{1}, \neg P a w_{2}, P b w_{1}, P b w_{2}}

w_{12}^{*} = {P a w_{1}, \neg P a w_{2}, \neg P b w_{1}, \neg P b w_{2}}

w_{13}^{*} = {\neg P a w_{1}, P a w_{2}, \neg P b w_{1}, \neg P b w_{2}}

w_{14}^{*} = {\neg P a w_{1}, \neg P a w_{2}, P b w_{1}, \neg P b w_{2}}

w_{15}^{*} = {\neg P a w_{1}, \neg P a w_{2}, \neg P b w_{1}, P b w_{2}}

w_{16}^{*} = {\neg P a w_{1}, \neg P a w_{2}, \neg P b w_{1}, \neg P b w_{2}}

It can be shown that each of the above 16 possible worlds satisfies or doesn’t satisfy 1 among 6 kinds of truth-condition

W_{i} (X)

(where

X \in

(i)–(xxxii)), which are model sets (i.e. sets of sets of elements) for the modal statements27

W_{1} (X) = \forall x \forall w P x w

W_{2} (X) = \exists x \forall w P x w \land \exists x \exists w P x w \land \exists x \exists w \neg P x w

W_{3} (X) = \forall x \exists w P x w \land \forall x \exists w \neg P x w

W_{4} (X) = \exists x \forall w P x w \land \exists x \forall w \neg P x w

W_{5} (X) = \exists x \exists w P x w \land \exists x \exists w \neg P x w \land \exists x \forall P \neg P x w

W_{6} (X) = \forall x \forall w \neg P x w

3.2.3. Bitstring Semantics

Now the truth-value of any modal statement X can be codified in terms of a bitstring, i.e. an ordered set of Boolean bits 1 (or 0) meaning that X satisfies (or does not satisfy) the corresponding model set. The modal statements (i)–(xxxii) can be explained by means of

n = 6

models sets, accordingly:

W (X) = 〈 W_{1} (X), . . ., W_{6} (X) 〉

The set-theoretical import of that semantics entails that conjunction and disjunction of statements are rendered as the intersection and union of their corresponding bits, accordingly. Thus, for any matching formulas

X, Y

W_{i} (X_{1}) \cap W_{i} (X_{2}) = m i n (W_{i} (X_{1}), W_{i} (X_{2})) W_{i} (X_{1}) \cup W_{i} (X_{2}) = m a x (W_{i} (X_{1}), W_{i} (X_{2}))

Given that modal statements have been understood as mixed quantified statements, no wonder if a number of them are equivalent with each other, i.e. have the same characteristic bitstring. Indeed: any statement including two quantifiers of the same sort (universal, or particular) is equivalent with its switched counterpart, so that; e.g. the de dicto statement (i), “It is necessary that every S is P” means the same as its de re counterpart (xvii), “Every S is necessarily P”. This appears in the following list of the characteristic bitstrings for modal statements X, including only 16 ordered values for a total of 32 formulas:

(1)

W (□

A) =

W

(A□) = 100000

(2)

W (□

E) =

W

(E□) = 000001

(3)

W (□

I) = 110110

(4)

W (□

O) = 010111

(5)

W (⋄

A) = 101000

(6)

W (⋄

E) = 001001

(7)

W (⋄

I) =

W

(I⋄) = 111110

(8)

W (⋄

O) =

W

(O⋄) = 011111

(9)

W (Δ

A) =

W (Δ

E) =

W (Δ

I) =

W (Δ

O) =

W

(I∇) =

W

(O∇) = 110111

(10)

W (\nabla

A) =

W (\nabla

E) =

W (\nabla

I) =

W (\nabla

O) =

W

(A∇) =

W

(E∇) = 001000

(11)

W

(I□) = 110100

(12)

W

(O□) = 000111

(13)

W

(A⋄) = 111000

(14)

W

(E⋄) = 001011

(15)

W

Δ

) =

W

Δ

) = 100001

(16)

W

(I∇) =

W

(O∇) = 011110

It is worthwhile to note three things in the above bitstrings. First, all these include Ockham’s four contingent and determinate statements: U = (15), Y = (16), K = (9), and Z = (10). Second, there are some equivalences between the de dicto and de re versions of contingency and determinacy, so that our formalisation altered Ockham’s interpretations without going beyond the four statements

U, Y, K, Z

. And third, the above equivalences match with the famous Barcan Formulas by accepting the following equivalences:

\forall x □ F x \leftrightarrow □ \forall x F x \exists x ⋄ F x \leftrightarrow ⋄ \exists x F x

An expected objection to the above equivalences is that an individual may exist in a possible world without existing in the actual world, thus invalidating the entailment relation from

⋄ \exists x F x

\exists x ⋄ F x

. Although the main reason of this equivalence in our semantics is that no clear-cut distinction is made between possible worlds and the actual world, a theoretical reason may be advanced to defend it as well (see [6]): if there a world at which an object, say a, is F, so a may be F is the actual world without being so after all. Our model set assumes a set of constant individuals, such that whatever exists in a world also exists in all the other ones. But even in the contrary case, it seems that the Barcan Formulas would still hold because a given property F may be satisfied by one individual whichever: if there is a world at which something is F, so something is F in the actual world without requiring that it is one and the same individual in both cases. For how to individuate an object without specifying its properties? This philosophical issue is left open in the present paper, and our point is just to claim that the above logical equivalences cannot be taken to be counterintuitive without some special philosophical assumptions.

3.2.4. Logical Relations

Finally, the characteristic bitstring of modal statements can be used to identify the logical relations between any pair of them. These relations deal with models that any two formulas can share or not. For any two formulas

X, Y

, that they are compatible means that they can share the same model; if, on the contrary, they are incompatible, this means that they cannot share any model or, in other words, that any model of the first formula X (symbol:

W^{+} (X) = W_{i} (X) = 1

) is a counter-model of the second formula Y (symbol:

W^{-} (Y) = W_{i} (Y) = 0

). This results in the well-known set of the four Aristotelian relations of opposition, including two cases of compatibility and one pattern of the entailment relation (viz. subalternation). Thus, for any models

W^{+}

and counter-models

W^{-}

of related statements

X, Y

X and Y are contraries (symbol:

c t

) only if every model of X is a counter-model of Y:

W^{+} (X) \subseteq W^{-} (Y)

W^{+} (Y) \subseteq W^{-} (X)

X and Y are contradictories (symbol:

c d

) if, and only if, every model of X is a counter-model of Y:

W^{+} (X) = W^{-} (Y)

X and Y are subcontraries (symbol:

s c t

) only if every counter-model of X is a model of Y:

W^{-} (X) \subseteq W^{+} (Y)

W^{-} (X) \subseteq W^{+} (Y)

Y is subaltern to X (symbol:

s b

) only if every model of X is a model of Y and every counter-model of Y is a counter-model of X

W^{+} (X) \subseteq W^{+} (Y)

W^{-} (Y) \subseteq W^{-} (X)

And finally, X and Y are independent from each other (symbols: ind) whenever they don’t satisfy any of the above conditions –they can be either true or false together, in other words.

The set of 16 modal statements leads to a set of 16(16 – 1)/2 = 120 logical interrelations, as depicted in the following table where the ordering of related formulas only matters with subalternation28:

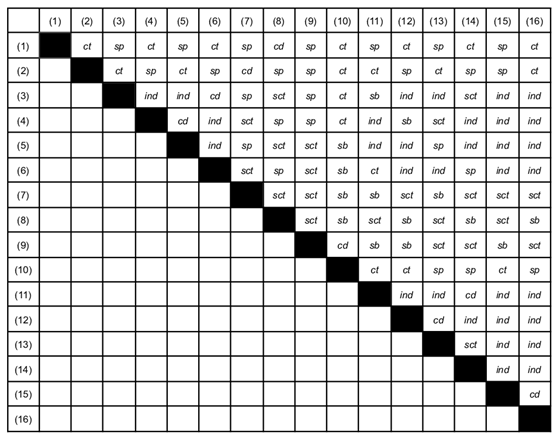
3.2.5. Increasing Diagrams

Another way to depict these logical relations is by means of a diagram. It has already been recalled in a previous section that the “Aristotelian square" included a modal version of categorical propositions, and the extension of necessity and possibility to contingency naturally led to Blanché’s hexagon. In addition, two other diagrammatic versions of modal logic were implemented under the impetus of works around other logicians: on the one hand, [2] noticed that the history of logic contained a logical octagon of quantified modal logic behind the work of Buridan and [5] provided a formal semantics for it; on the other hand, [3] devised a further dodecagon in showing that Avicenna, proposed a set of logical relations between 12 statements. In light of the preceding, one can surmise a closure of this increasing extension from the square onward: there cannot be more than 16 modal statements in their de re-de dicto versions. The corresponding diagram extends the previous figures into a logical hexadecagon, accordingly:

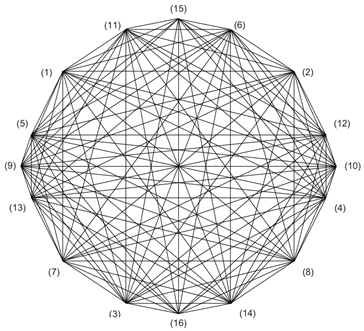
and our semantics helps to show that each of these formulas codified by 6 ordered bits forms an exhaustive number of

2^{6} = 64

distinct statements (from antilogies:

000000 = ⊥

, to tautologies:

111111 = ⊤

Note finally that each of the implication relations between both de dicto and de re modal statements (see Section 2) is established in a Boolean way: each antecedent is a superaltern of its consequent, so that, e.g., the first implication

\nabla \forall x (S x \to P x) \to ⋄ \forall x (S x \to P x)

is a more customary way to claim that (10) entails (5) because the latter is subaltern to the former. (See the above exhaustive table of logical relations between (1)-(16)).

Conclusion

We gave a survey of Ockham’s theory of modal statements, based on a de re-de dicto distinction in the use of modalities and its extension to the cases of contingency and determinacy (or non-contingency). Then we proposed a reformulation of modal statements in a systematic way, by means of both a second-order translation and a corresponding relational semantics where statements are codified by bitstrings. Finally, we showed that Ockham’s modal statements reduce to an exhaustive set of sixteen formulas, thereby leading to a comprehensive hexadecagon that encompasses the previous extensions from the Aristotelian square to Ockham’s hexagon and Buridan’s octagon of logical relations between these modal statements.

Let us recall that such a semantics relies on a special interpretation of necessity as truth in all possible worlds, i.e. models where the accessibility relation is an equivalent relation in terms of Kripke semantics. We favoured an alternative, Boolean semantics of ordered model sets, however, in order to construct an algebraic theory of logical relations between matching formulas (i.e. sharing the same logical form; see [20]). An interesting development of the proposed Bitstring Semantics would consist in constructing model sets for non-equivalent accessibility relations, thus applying to temporal, epistemic or deontic interpretations of the modal operators. But this project goes beyond our present purpose to make sense of Ockham’s proper theory of modalities with modern formal tools. At any rate, such a special Boolean semantics has already been developed in other separate works (see e.g. [4,18]) and could turn out to be a nice trade-off between Kripke semantics and the prior algebraic tradition of modal logic.

Another prospect is to extend the logical form of Ockham’s modal statements, by also negating the subject term S of the categorical statements A,E,I,O. Such an extension was devised by previous logicians (see especially [9]) and this amounts to proposing a modal version of Keynesian categorical propositions (wherein S is always negated), whereas Ockham sticked to a modal version of Aristotelian categorical propositions (wherein S is always affirmed).29

Acknowledgments

In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.” Authors must identify and declare any personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results”.

References

Blanché, R.; Davy, G. Structures intellectuelles. Les Études Philosophiques 21, 541–542.
Campos-Benítez, J. M. The medieval octagon of opposition for sentences with quantified predicates. History and Philosophy of Logic 2014, 35, 354–368. [Google Scholar] [CrossRef]
Chatti, S. (2015). “Les carrés d’Avicenne”. In Ben Aziza, H & Chatti, S (eds.): Le carré et ses extensions: Approches théoriques, pratiques et historiques, publications de la Faculté des Sciences Humaines et Sociales de Tunis.
Demey, L. Boolean considerations on John Buridan’s octagons of opposition. History and Philosophy of Logic 2019, 40, 116–134. [Google Scholar] [CrossRef]
Demey, L.; Steinkrüger, P. The logical geometry of John Buridan’s modal octagon. Tijdschrift voor Filosofie 2017, 79, 217–223. [Google Scholar]
Hayaki, R. Contingent Objects and the Barcan Formula. Erkenntnis 2006, 64, 87–95. [Google Scholar] [CrossRef]
Hintikka, J. (1973). Time and Necessity: Studies in Aristotle’s Theory of Modality. Oxford: Oxford University Press.
Karger, Elizabeth (1976). A Study of William of Ockham’s Modal Logic. Ph.D. dissertation, University of California.
Keynes, J. N. 1884. Studies and Exercises in Formal Logic, 1st ed., London: Macmillan.
Knuuttila, S. (1993). Modalities in Medieval Philosophy. London, New York: Routledge; second edition, 2020.
Moktefi, A.; Schang, F. Another Side of Categorical Propositions: The Keynes–Johnson Octagon of Oppositions. History and Philosophy of Logic 2023, 43, 309–326. [Google Scholar] [CrossRef]
Normore, Calvin G. (1975). The Logic of Time and Modality in the Later Middle Ages: The Contribution of William of Ockham. Ph.D. dissertation, University of Toronto.
Ockham, William of. (1974). Summa Logicae (Opera Philosophica et Theologica), Vol. I, ed. P. Boehner, G. Gal & S. Brown, St Bonaventure Institute, New York.30.
Ockham, William of. (1978). Expositio in librum Perihermeneias (Opera Philosophica), Vol. II, ed. A. Gambatese & S. Brown, St Bonaventure Institute, New York.
Ockham, William of. (1980). Quodlibeta septem (Opera Philosophica et Theologica), Vol. IX, ed. J.C. Wey, St Bonaventure Institute, New York.31.
Pizzi Claudio E., A. Possibility and Dyadic Contingency. Journal of Logic, Language and Information 2022, 31, 451–463. [Google Scholar] [CrossRef]
Read, S. (2021). “Modality in Medieval Philosophy”. In O. Bueno and S. Shalkowski (eds.): The Routledge Handbook of Modality, New York and London, Routledge, 344–354.
Schang, F. End of the Square? South American Journal of Logic 2018, 4, 485–505. [Google Scholar]
Simons, P. Approaching the Alethic Modal Hexagon of Opposition. Logical Universalis 2012, 6, 109–118. [Google Scholar] [CrossRef]
Yi, B. Categorical Propositions and Existential Import: A Post-modern Perspective. History and Philosophy of Logic 2021, 42, 307–373. [Google Scholar] [CrossRef]

1	These two historical sections (Section 1, pp. 1-4, and Section 2, pp. 4-9) are written by D. Falessi; while Section 3, pp. 9-16, dedicated to a logical reformulation of modal statements starting from Ockham’s account, are by F. Schang. Needless to say, the conclusion and all the sections are the result of a common work of discussion and sharing opinions and ideas.
2	See also [10,17] for the medieval theories of modal logic.
3	For a fully-fledged explanation of Ockham’s account of modalities, see [8,12]. We shall consider here just the de re and de dicto readings, the status of contingency as a modal operator, and the modal squares.
4	[13] II, 9, 13-17, transl. p. 109.
5	[13] II, 9, 19-23, transl. p. 109.
6	[13] II, 10, 11-24.
7	See [13] III-1, 20, 30-38.
8	[15], II, q. 5, 131 67-69, transl. p. 112.
9	[13] II, 10, 2-4.
10	It is required to justify those rules from a formal point of view. This will be done in section 3.2.3.
11	Note that, hereby, “possibility” is taken in its one-sided reading, i.e. possibility that is opposite to impossibility but subaltern to necessity. See also [7].
12	[14], II, c. 7, §9, 489, 133-134.
13	“It must be known that this square is valid either if all the propositions involved are taken in a compound sense or something equivalent to a compound sense or in a divided sense or something equivalent to a divided sense.” [[14], II, c. 7, §9, 489, 135-137].
14	[14], II, c. 7, §9, 489, 133-134.
15	See [14], II, c. 7, §9, 491, 172-177.
16	For a more abstract approach to the concepts of contingency and non-contingency, see e.g.[16].
17	[13], III-3, 15, 647, 17; [14], II, c. 7, §9, 491, 178 – 492,196.
18	Ockham seems to consider that, for example, the universal de contingenti de dicto is equivalent to both $⋄ \forall x (S x \to P x) \land ⋄ \forall x (S x \to \neg P x)$ and $\forall x (S x \to ⋄ P x) \land \forall x (S x \to ⋄ \neg P x)$ . This is not valid, as we shall see in section 3.2.3. By contrast, $□ \exists x (S x \land P x) \lor □ \exists x (S x \land \neg P x) = \exists x (S x \land □ P x) \lor \exists x (S x \land □ \neg P x)$ and $□ \forall x (S x \to P x) \lor □ \forall x (S x \to \neg P x) = \forall x (S x \to □ P x) \lor \forall x (S x \to □ \neg P x)$ , in the cases $Δ \forall x (S x \to P x)$ and $Δ \exists x (S x \land P x)$ , are valid (see again section 3.2.3). Ockham provides little information of propositions de contingent de re, and we shall not consider it in this paper.
19	“It should also be noted that the contradictory opposite of a conjunctive proposition is a disjunctive proposition composed of the contradictories of the parts of the conjunctive (opposita contradictorie copulativae est una disiunctiva composita ex contradictoriis partium copulativae).” [13], II, 32, 348, 22-23, transl. p. 187.
20	[13], III-3, §15, 647, 12-15.
21	[13] III-3, 15, 647, 24-33; [14], II, c. 7, §9, 491, 184 – 492,196.
22	Note that the dicta “every man is an animal” and “some man is an animal” are of the form ( $D^{⊤}$ ) and hence they are de dicto.
23	[13], III-3, 12, 640, 38-44.
24	[13], III-3, 12, 639, 15-18.
25	[13], III-3, 13, 643, 25-28.
26	Or course, one can conceive a situation in which something is not S; but this requires another, more complex logical form of modal statements in which the subject term S can be either affirmed or negated. See the Conclusion about this prospect.
27	These models sets are such that, in order of appearance: $W_{1} (X)$ : Every x is P at any w; $W_{2} (X)$ : Some x is P at every w, and Some x is P at some (but not every) w; $W_{3} (X)$ : Every x is P at some (but not every) w; $W_{4} (X)$ : Some x is P at every w and Some x is not P at every w; $W_{5} (X)$ : Some x is P at some (but not every) w, and Some x is not P at every w; $W_{6} (X)$ : Every x is not P at every w.
28	Note that the boxes to the left of the black boxes are left empty because they are trivially the same kind of relation as the ones depicted to the right of the black boxes: for any paired formulas X,Y standing into a given relation R, R(X,Y) = R(Y,X); except for subalternation, R = $s b$ , however: the converse relation of subalternation is superalternation, so that $s b (X, Y$ ) iff $s p (Y, X$ ).
29	A Bitstring Semantics for both Aristotelian and Keynesian categorical propositions has been recently set forth (see [11]). Its modal de re and de dicto version remain to be made by now, by applying modal operators into logical forms like $\pm ⋄ \pm \exists x (\pm S x \land \pm P x), or \pm \exists x \pm ⋄ (\pm S x \land \pm P x) .$
30	The translation of Part II of the Summa logicae is provided by: A.J. Freddoso & H. Schuurman (1980), Ockham’s Theory of Propositions. Part II of the Summa Logicae, St. Augustine’s Press, South Bend.
31	The translation of Quodlibeta septem is provided by: A.J. Freddoso & F. E. Kelley (1998), Quodlibetal Questions: Quolibets 1-7, v. I-II, Yale University Press, Yale.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Relational Semantics for Ockham’s Modalities

Abstract

0. Introduction

1. Ockham’s Account

2. Extension of Ockham’s Modal Squares

3. Logical Analysis

3.1. Syntax

3.2. Semantics

3.2.1. Relational Statements

3.2.2. Relational Semantics

3.2.3. Bitstring Semantics

3.2.4. Logical Relations

3.2.5. Increasing Diagrams

Conclusion

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe