Submitted:
03 February 2023
Posted:
06 February 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Inverse Finite Element Method review
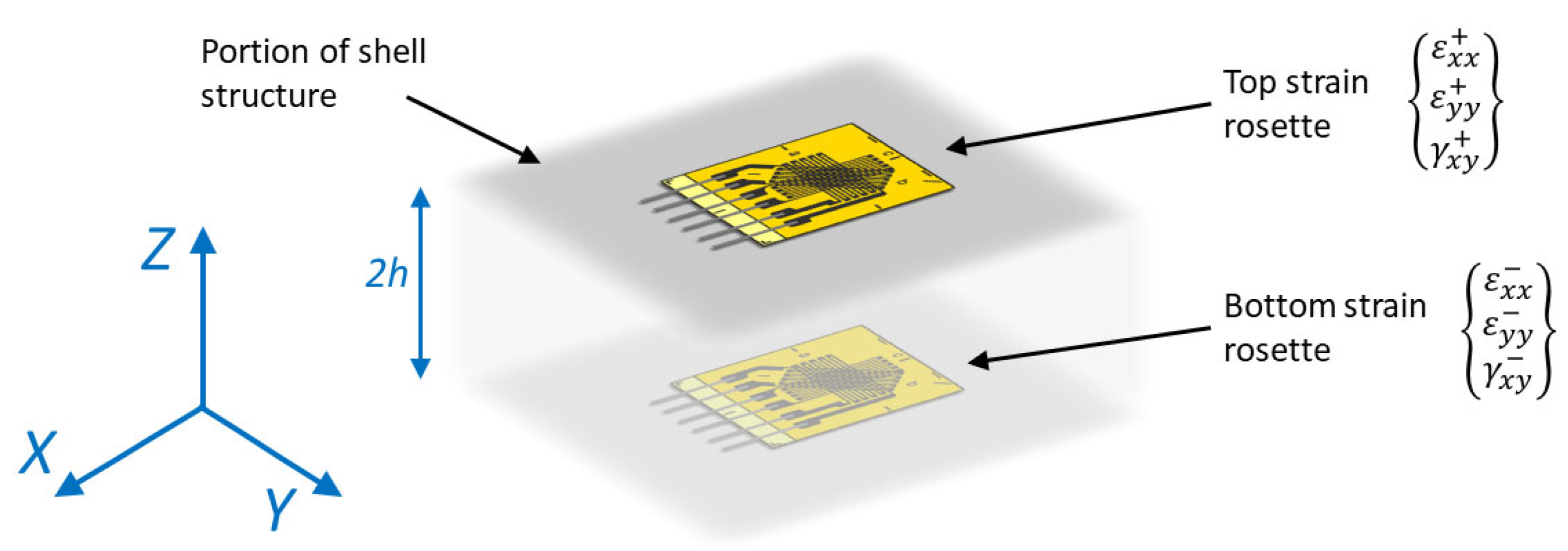
2.1. Input strain formulation
2.2. Numerical strain formulation
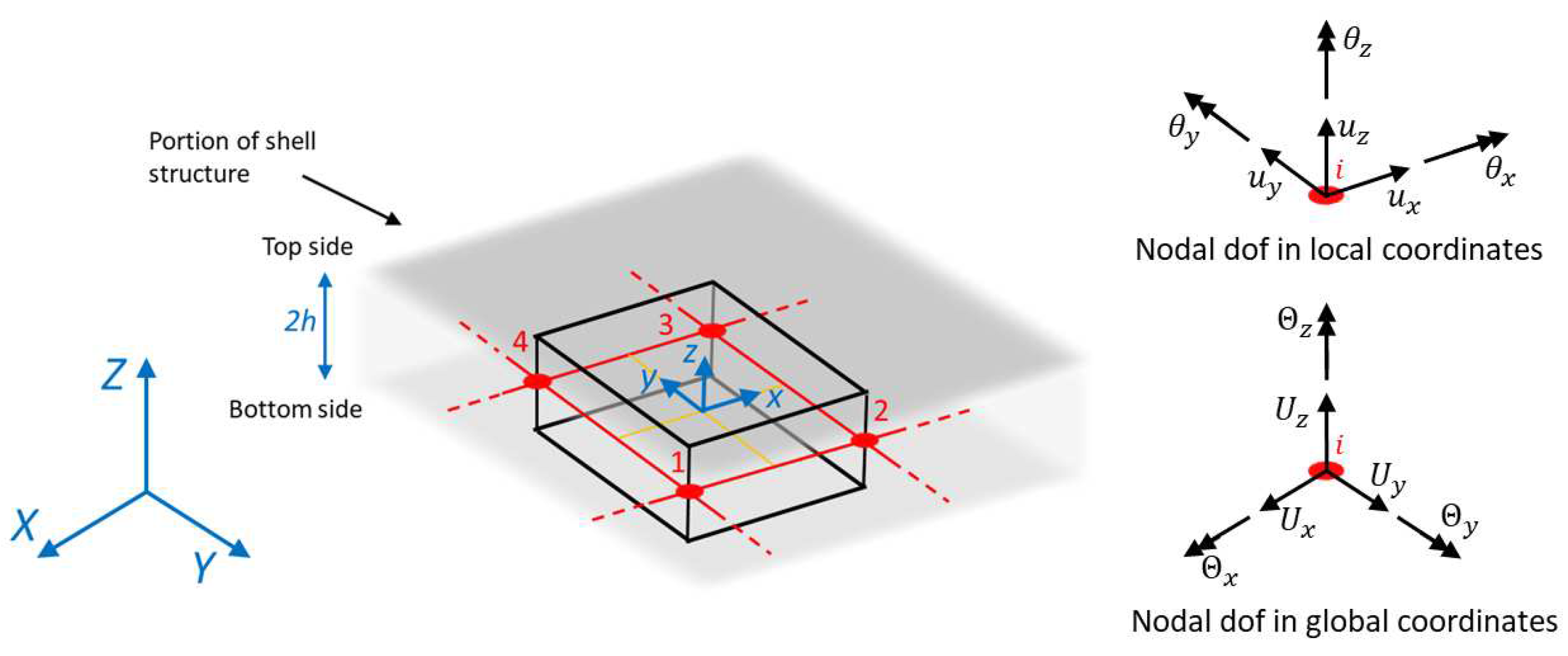
2.3. Matrix formulation
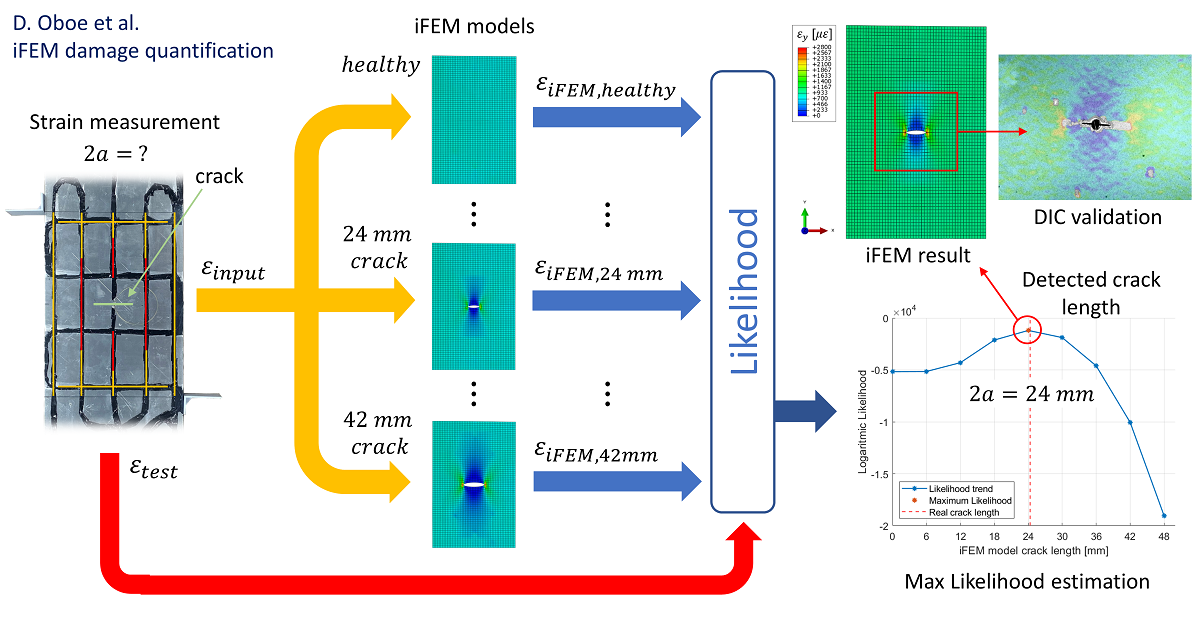
3. Crack size estimation technique
3.1. Crack size estimation overview
3.2. Crack propagation routine
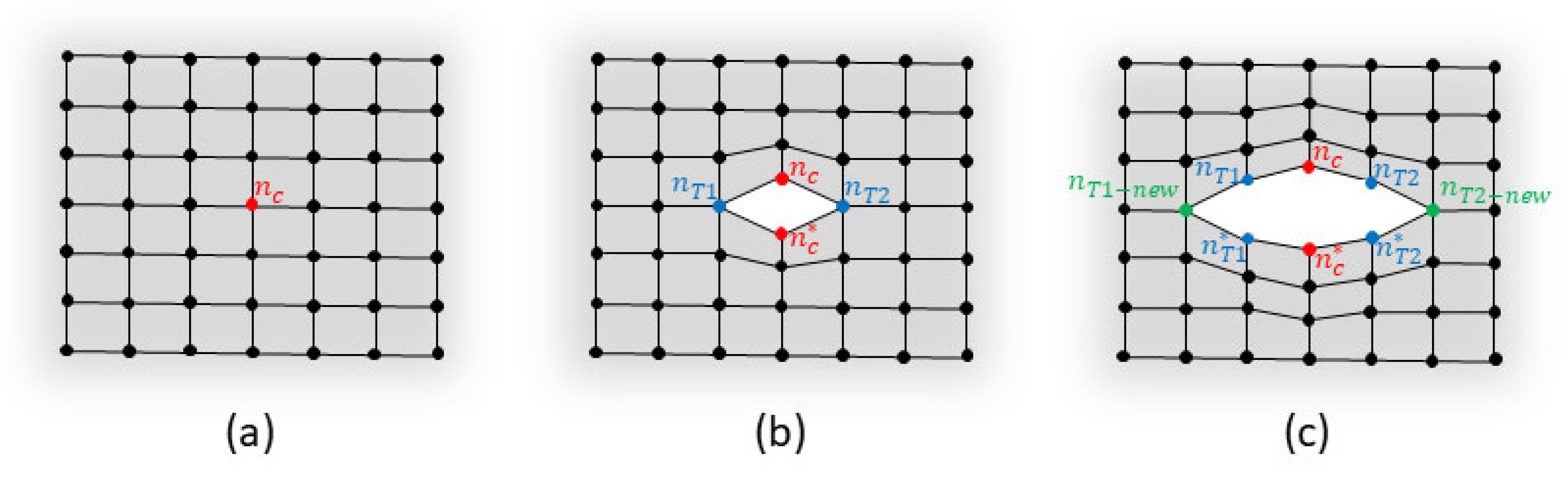
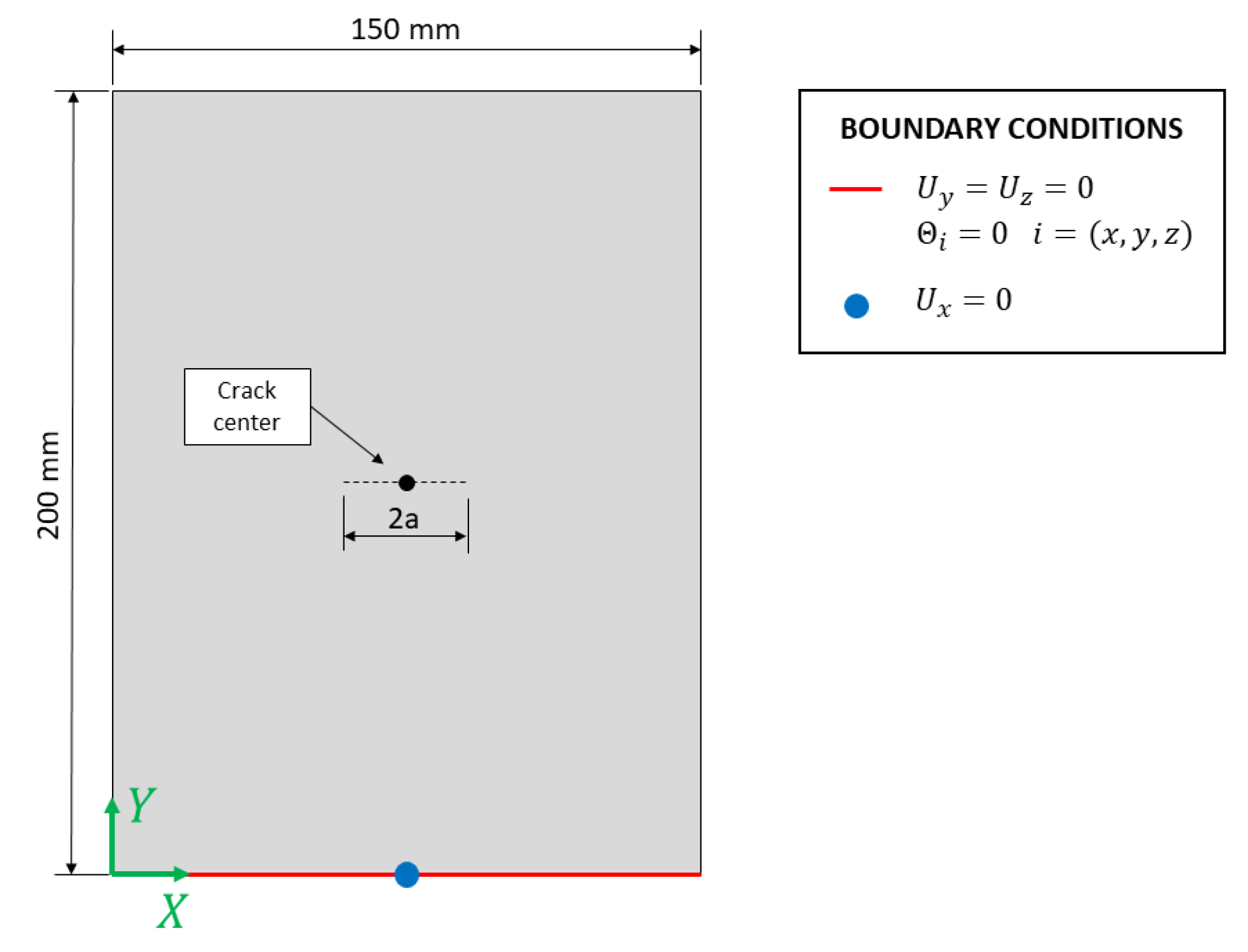
- The central position of the crack is identified as one node of the undamaged iFEM mesh, as highlighted by the red node in Figure 3a. This localization can be based on several approaches, such as visual inspection of the structure or automatic localization with a specific algorithm. The present research will not investigate any particular localization technique and the crack center is supposed to be known from any visual or automatic inspection, however, the approach described remains valid for any general localization method.
- The crack is introduced in the mesh by doubling the node corresponding to the crack center and modifying the connectivity matrix to unlink the elements (Figure 3b). The crack is supposed to propagate under a pure Mode I loading, thus its orientation is perpendicular to the first principal stress. Finally, the two nodes identifying the crack tips are highlighted in blue in Figure 3b. This procedure, together with the crack center identification, is detailed in Algorithm 1.
- The crack is further propagated perpendicularly to the first principal stress. The two nodes on the crack tip’s locations are doubled and the connectivity matrix is further modified to unlink the elements, as shown in Figure 3c and detailed in Algorithm 2.
- Repeat step 3 several times, opening one node per time, until the most likely crack length is reached according to the procedure detailed in Section 3.3.
| Algorithm 1: Crack center identification and introduction on an undamaged structure. | |
| 1: | Identify the position () of the crack center |
| 2: | Find the maximum principal stress direction from the sensor’s measurements |
| 3: | Find the nearest node of the mesh to the crack center → Center node |
| 4: | Identify the two crack tip nodes and as the nearest nodes to the crack center and perpendicular to the maximum principal stress direction |
| 5: | Double the Center node → update the node matrix |
| 6: | Update the connectivity matrix to unlink the elements in correspondence of |
| 7: | Compute the crack length: norm() |
| 8: | Compute and invert the iFEM matrix |
| Algorithm 2: Crack propagation from an existing damage condition. | |
| 1: | Identify the two nodes and as the nearest nodes to the crack tip and perpendicular to the maximum principal stress direction |
| 2: | Identify the new crack tip 1 between and as the farthest node from → |
| 3: | Identify the two nodes and as the nearest nodes to the crack tip and perpendicular to the maximum principal stress direction |
| 4: | Identify the new crack tip 2 between and as the farthest node from → |
| 5: | Double the crack tip nodes: and → update the node matrix |
| 6: | Update the connectivity matrix to unlink the elements in correspondence of and |
| 7: | Update the crack tip location: and |
| 8: | Compute the crack length: norm() |
| 9: | Compute and invert the iFEM matrix |
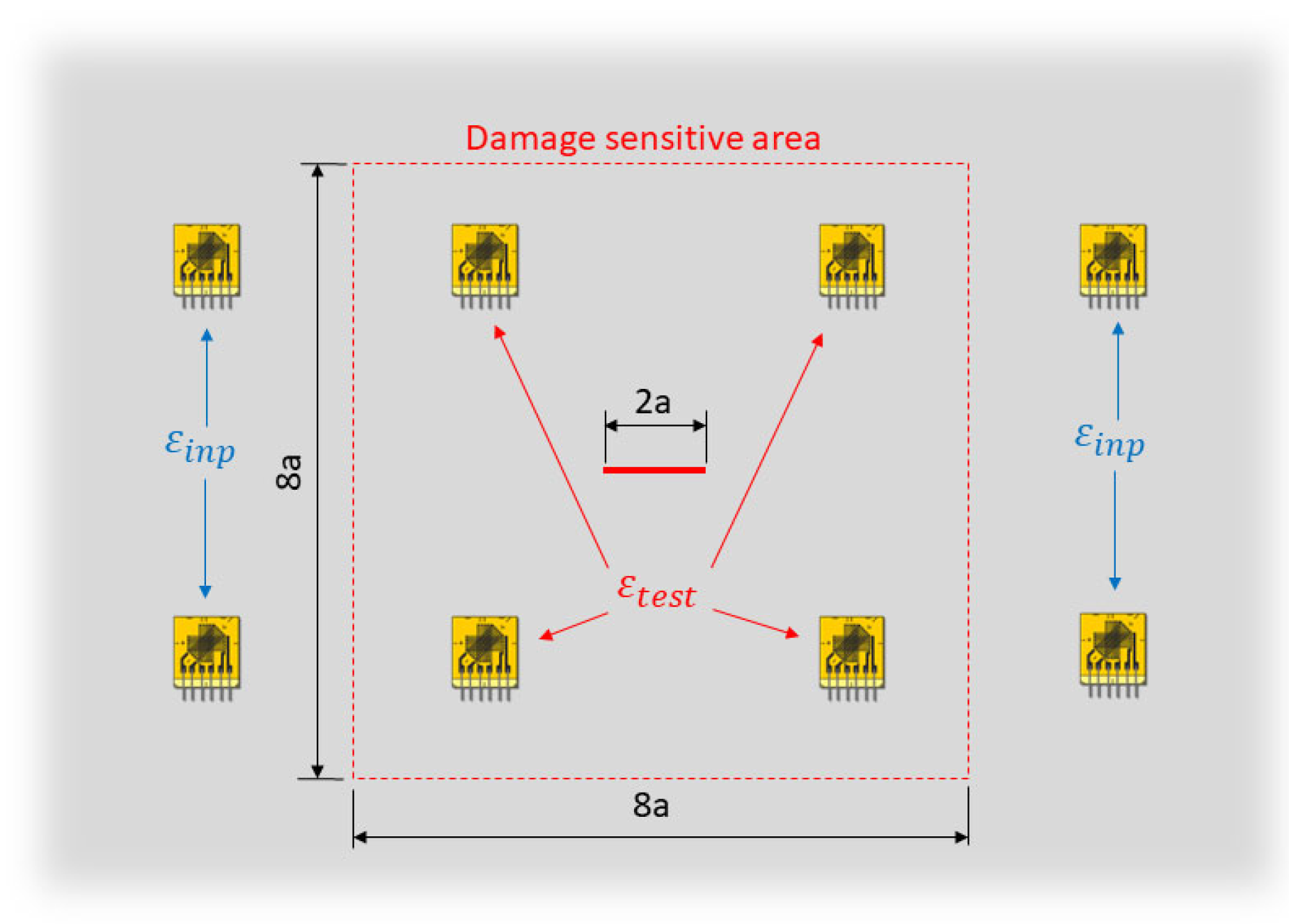
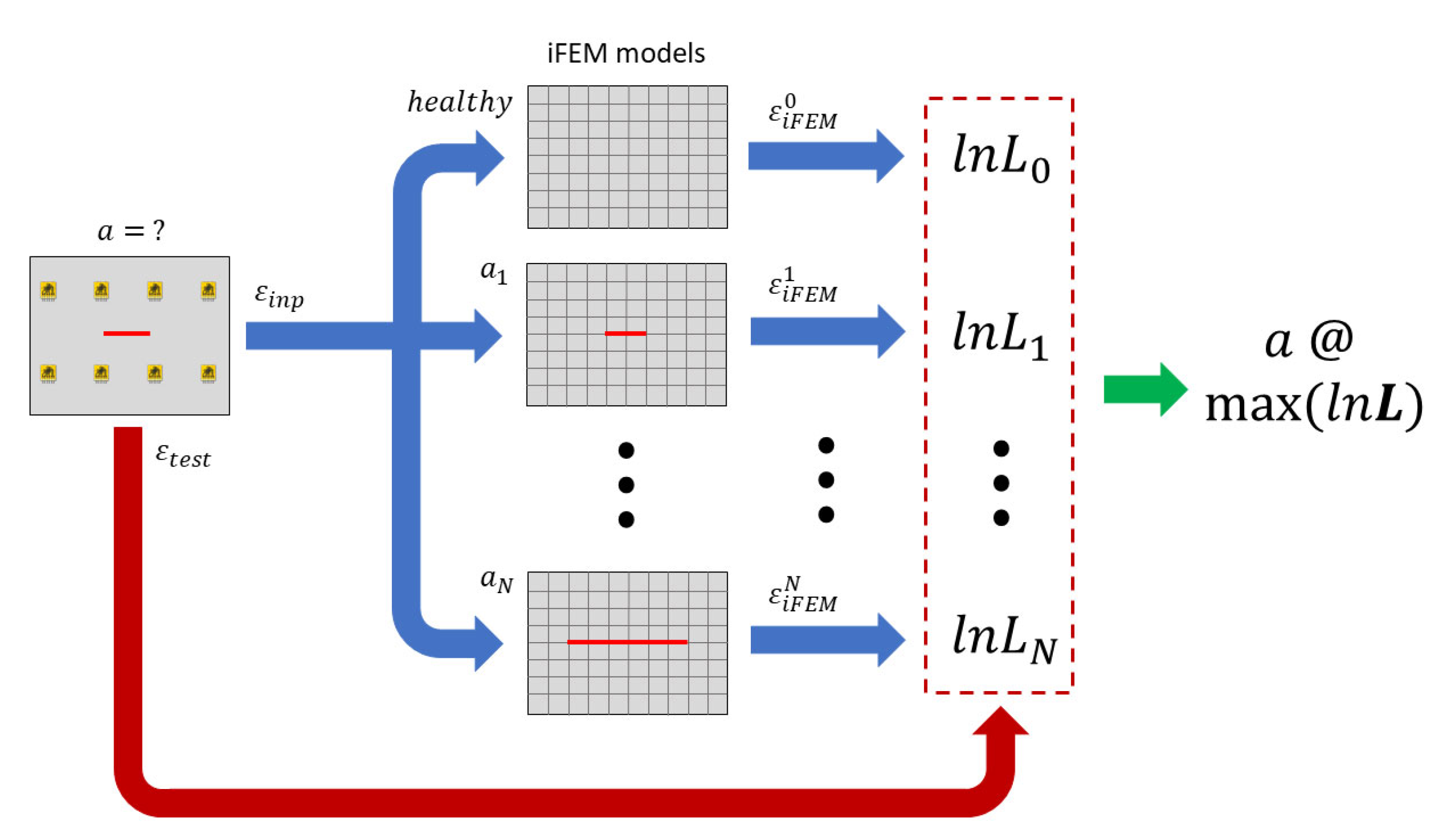
3.3. Damage state diagnosis
- An input sensor network () to feed the iFEM algorithm and compute the displacement and the strain field on the whole structure
- A test sensor network () to compare the strain field computed by the iFEM () with the experimental measurements acquired on the structure.
- The input sensor network is composed only of sensors sufficiently far from the damaged area to acquire the far-field strain. Thus, these strain measurements will not be affected by the presence of the damage, whatever is the actual damage condition considered.
- The test sensor network is composed of sensors located in the area of influence of the damage, where the observations can be correlated to the actual damage state.
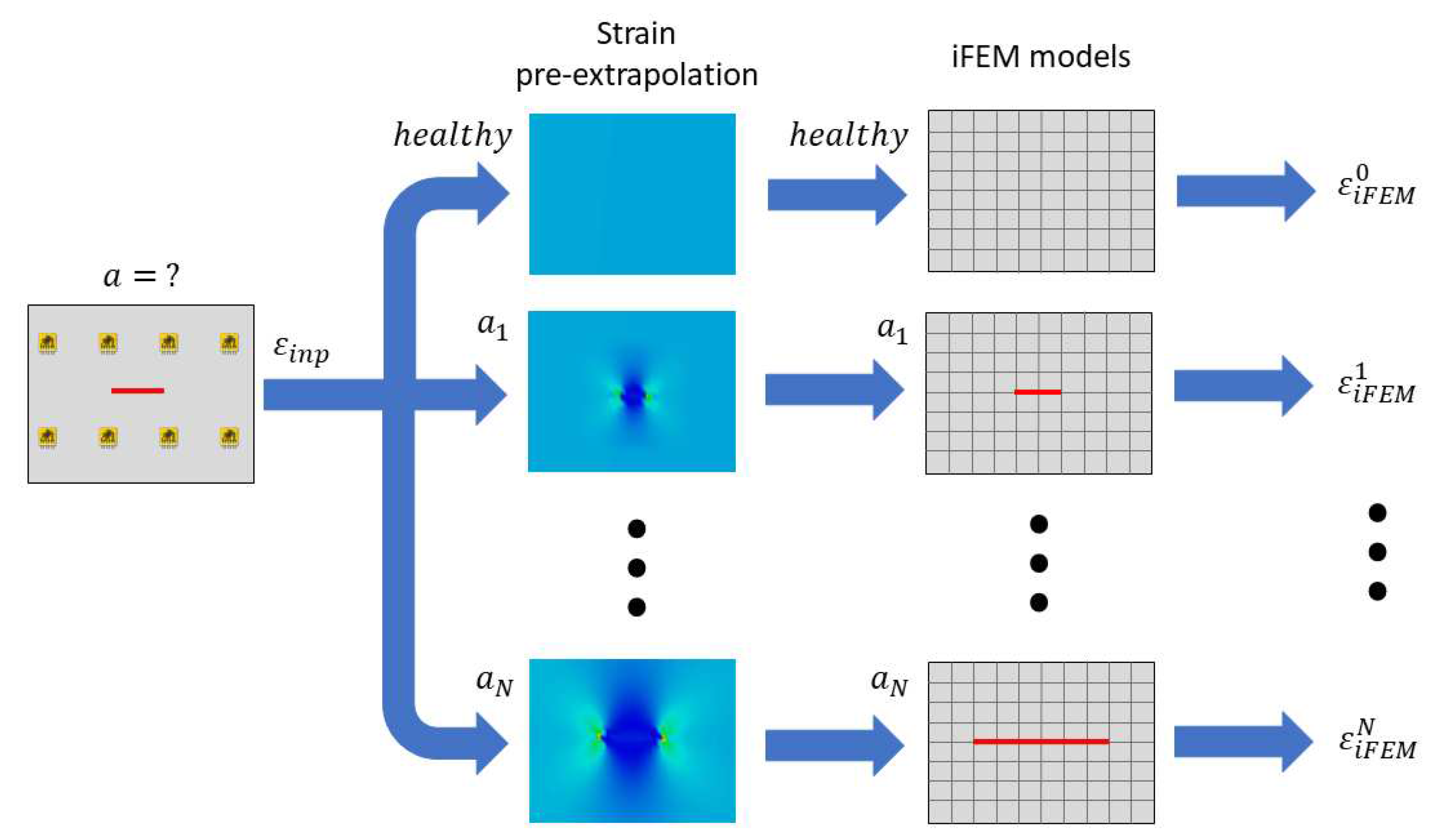
3.4. Crack strain field pre-extrapolation
3.4.1. Pre-extrapolation framework overview
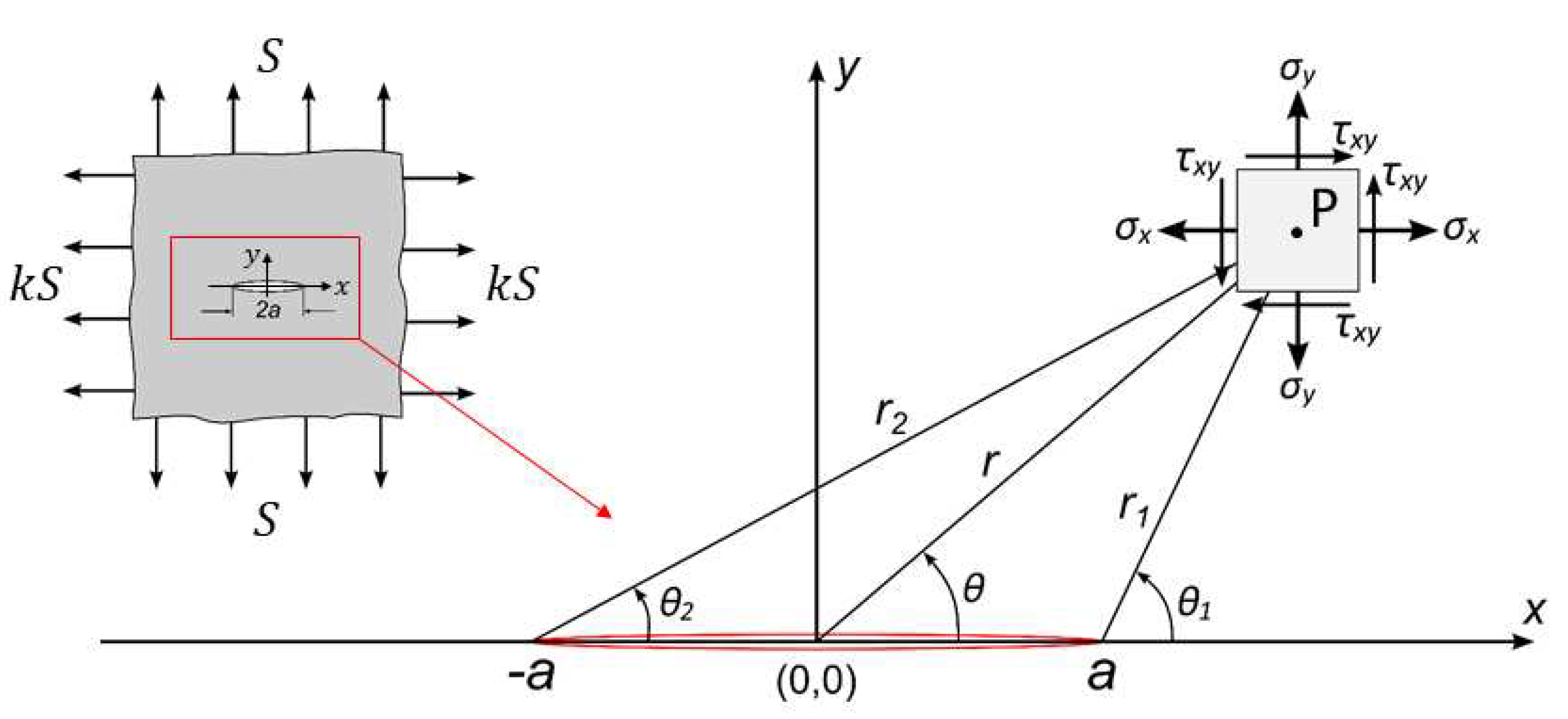
3.4.2. Physics-based strain pre-extrapolation for a crack in an infinite plate
- A global pre-extrapolation, based on a data-driven approach, is computed on the whole structure to obtain the far-field strain value. In the present analysis, a bi-linear polynomial fitting is adopted, however, other techniques (for example the SEA) can be selected according to the specific case study. Notice that, each strain component (, , ) is independently pre-extrapolated on each side of the structure.
- A local pre-extrapolation better predicts the strain field in the damage-sensitive area with a physics-based approach. This takes as input the far-field strain computed by the data-driven pre-extrapolation to compute the specific strain field induced by the crack.
4. Case study
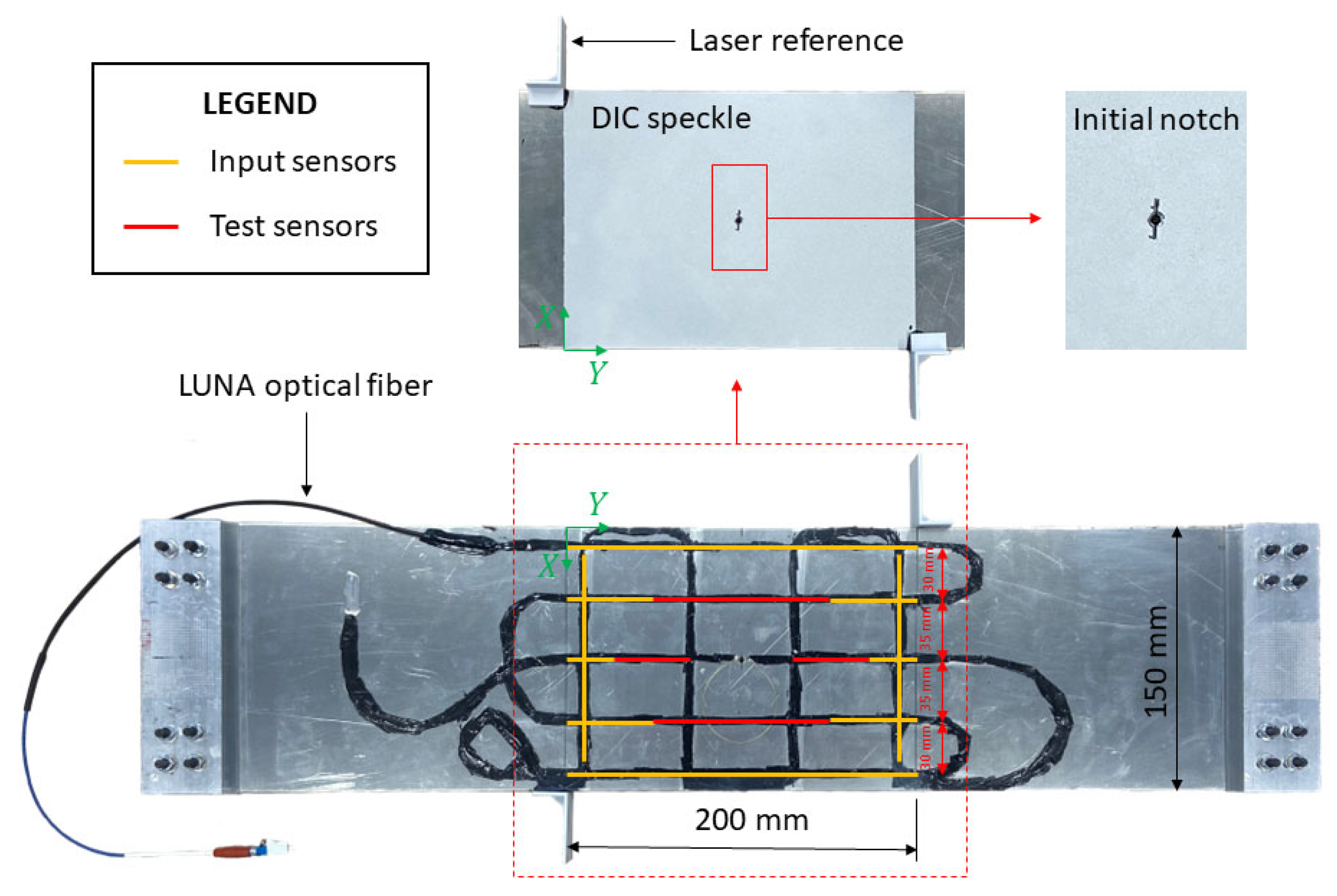
4.1. Specimen and sensor network
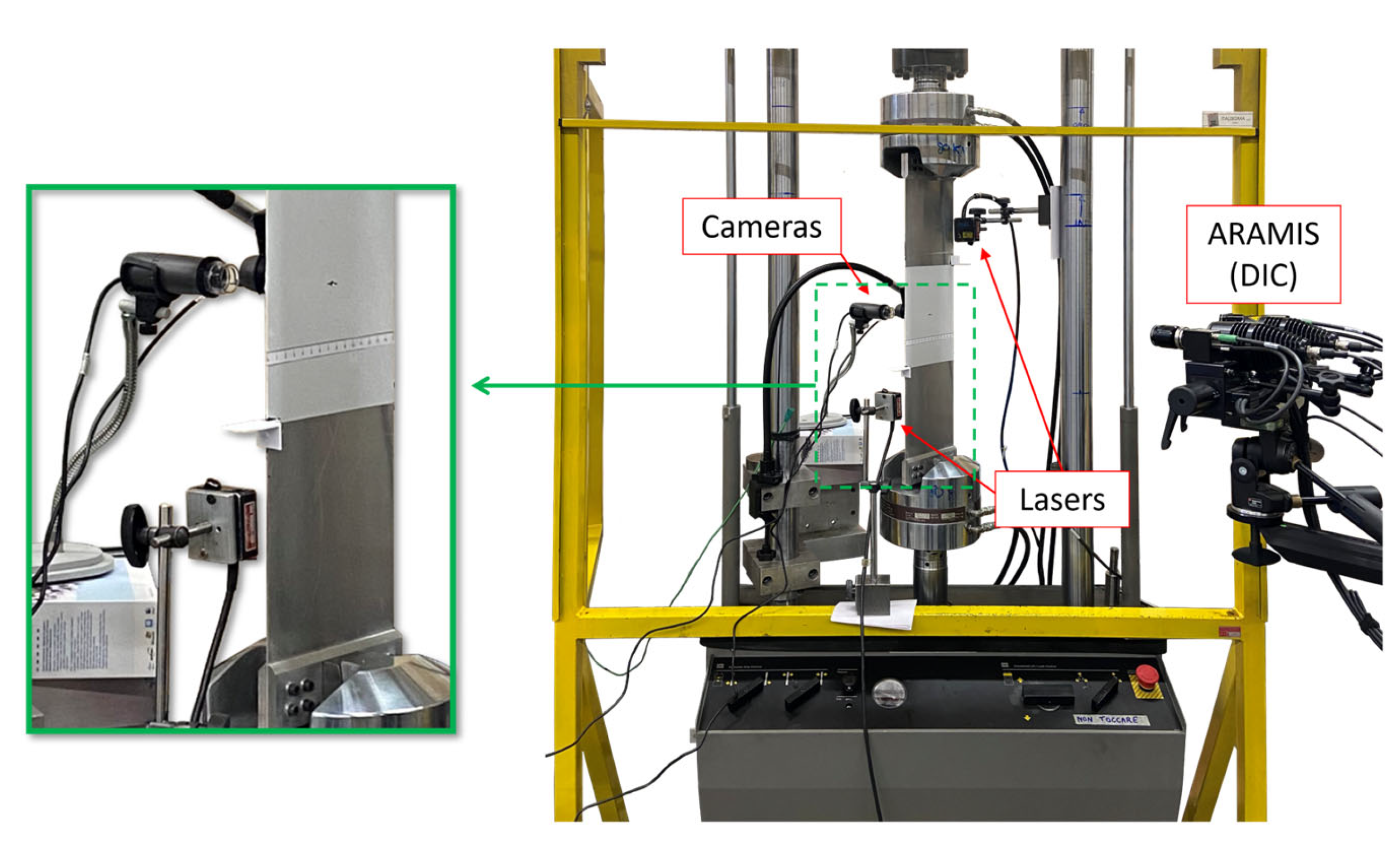
4.2. Test rig
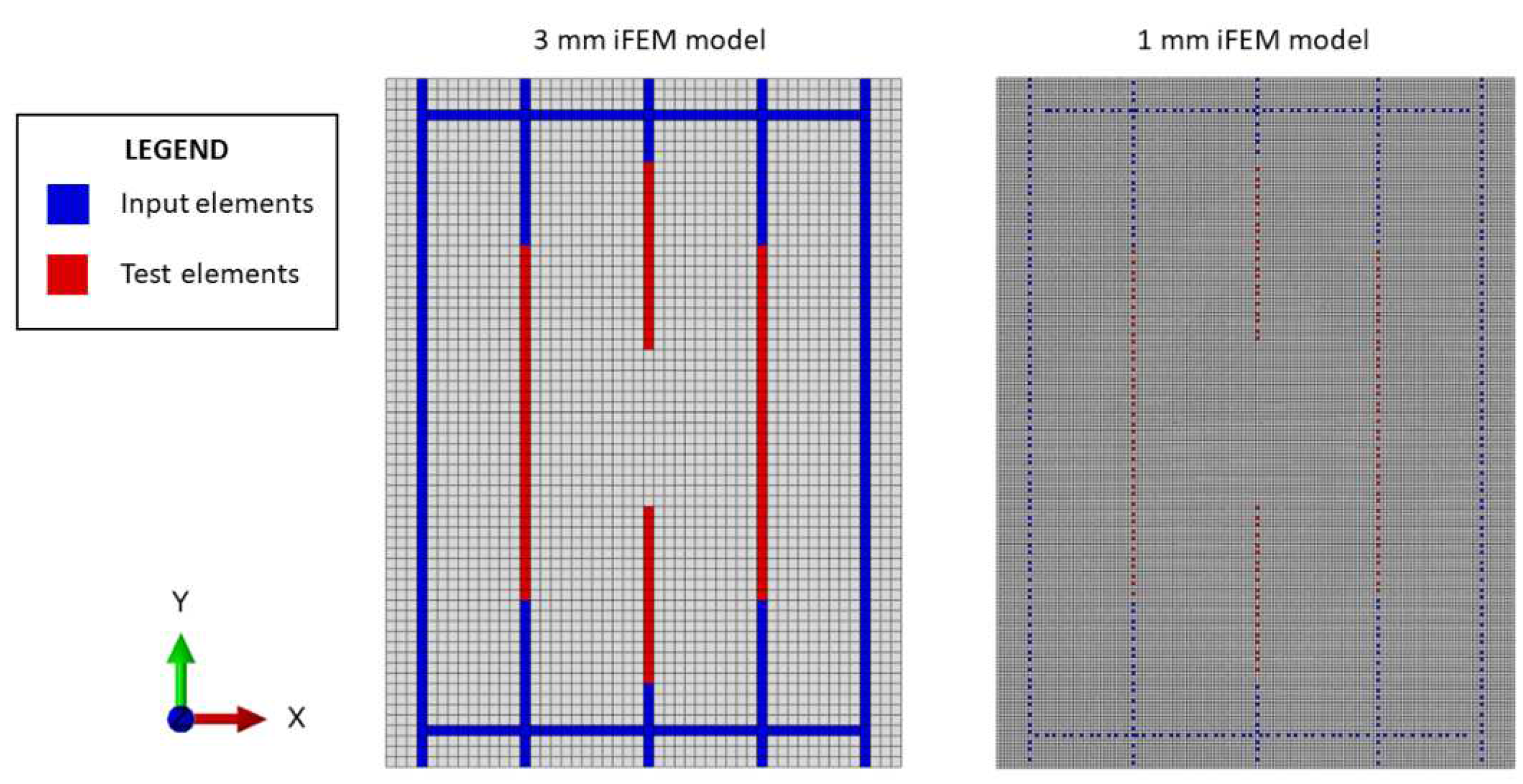
4.3. iFEM models
- a mesh with element’s size (namely model), thus the structure is discretized by a total number of 3,300 inverse elements
- a mesh with element’s size (namely model), thus the structure is discretized by a total number of 30,000 inverse elements
5. Results and Discussion
5.1. Fatigue propagation experimental results
5.2. iFEM results with the 3 mm model
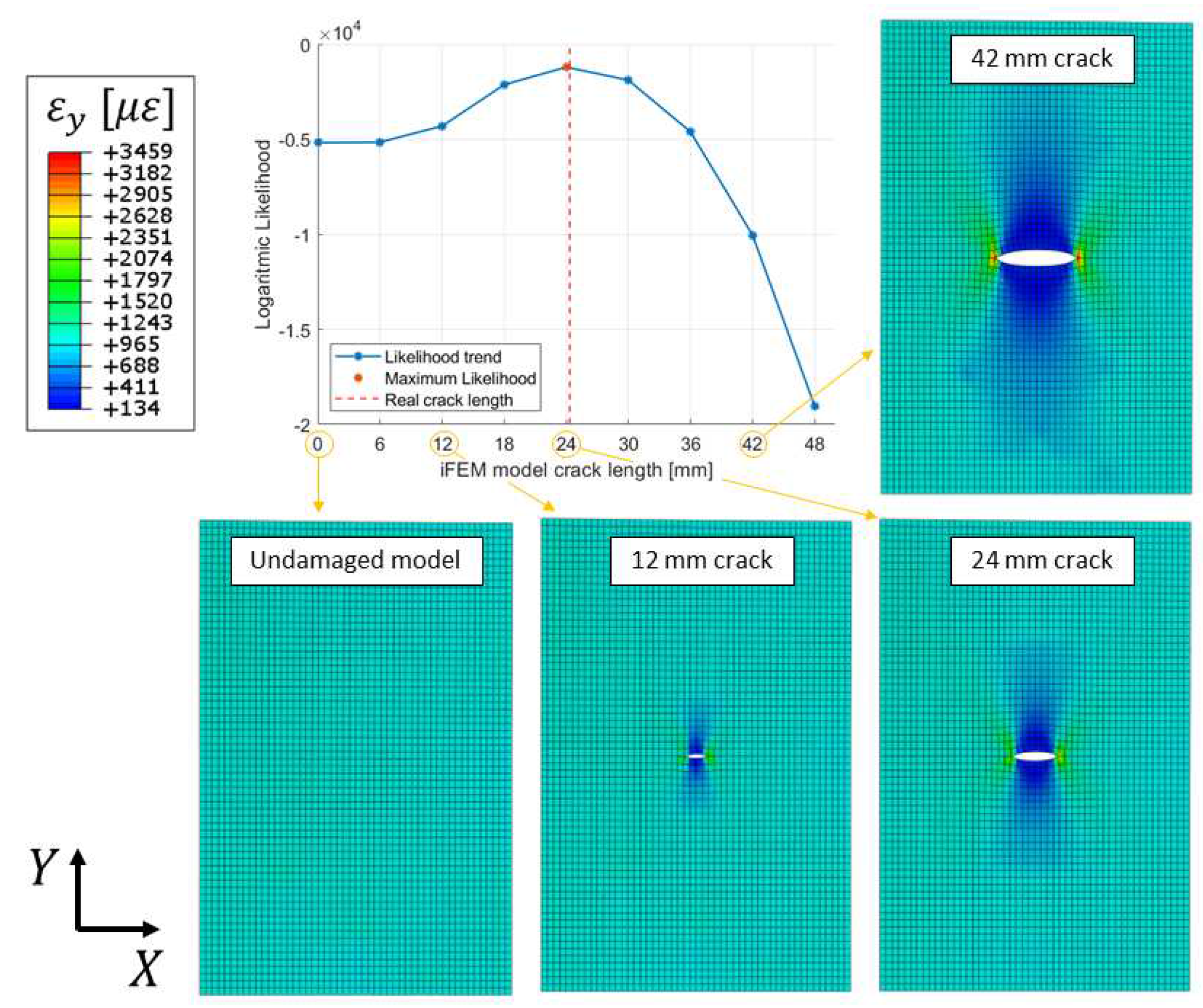
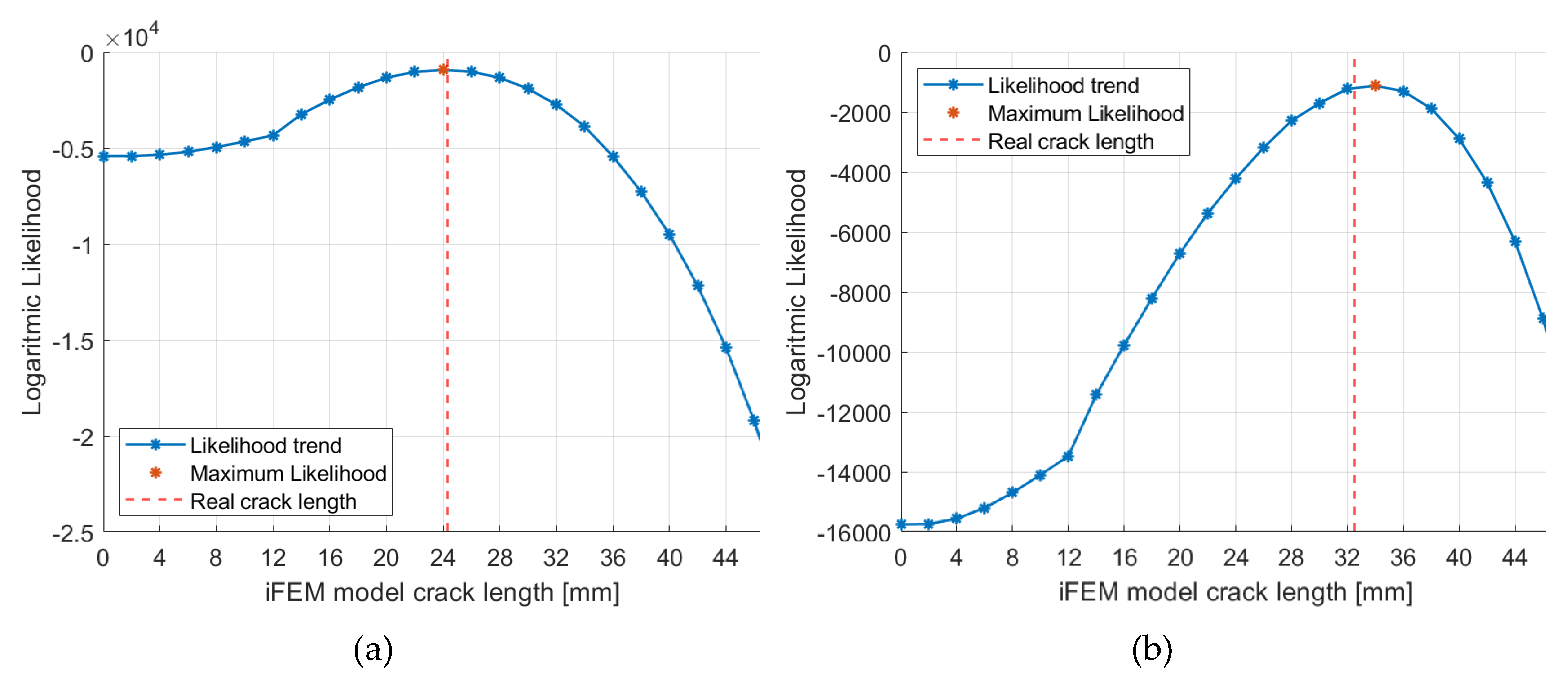
5.2.1. Likelihood trends
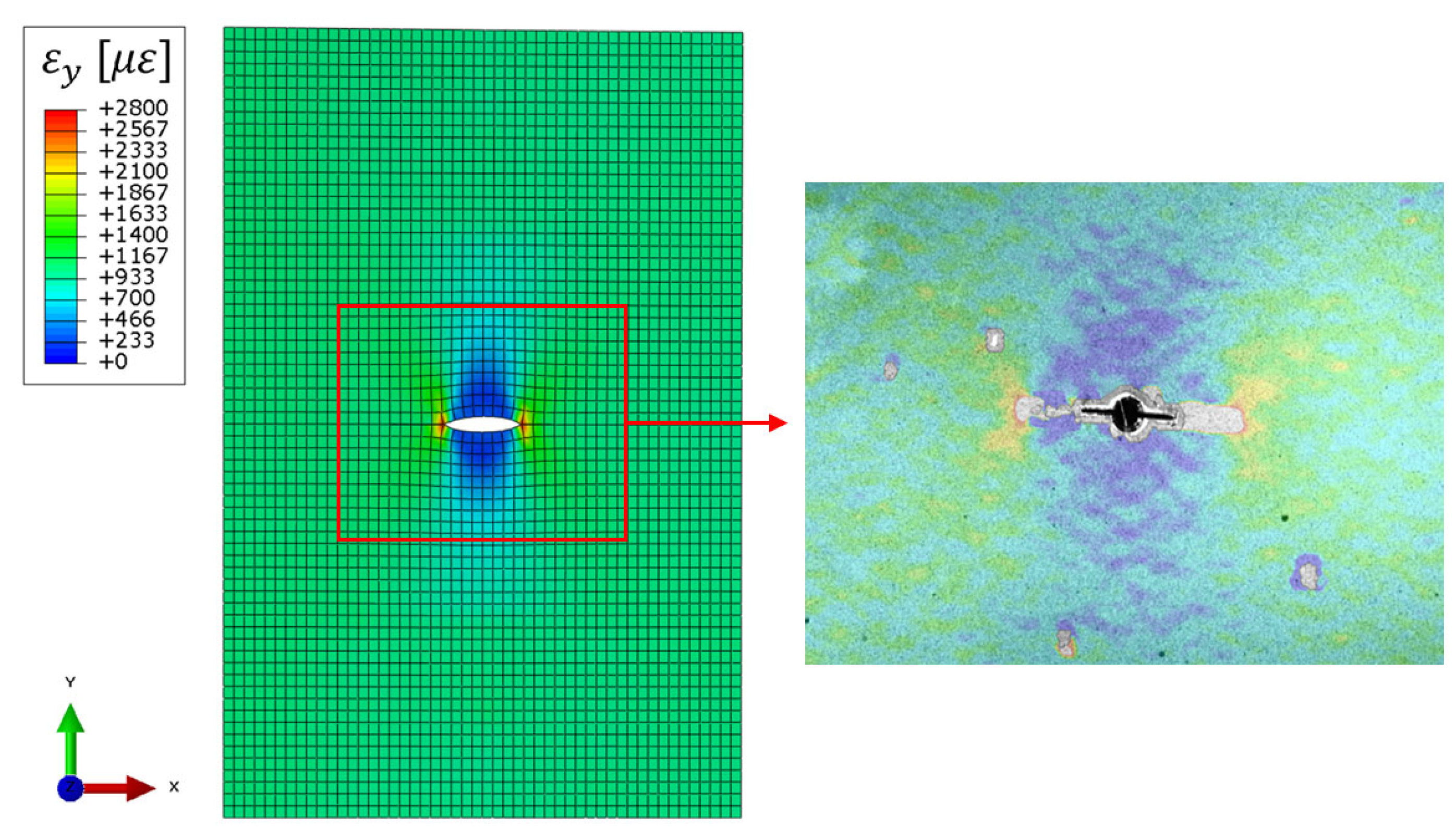
5.2.2. iFEM strain and displacement fields evaluation
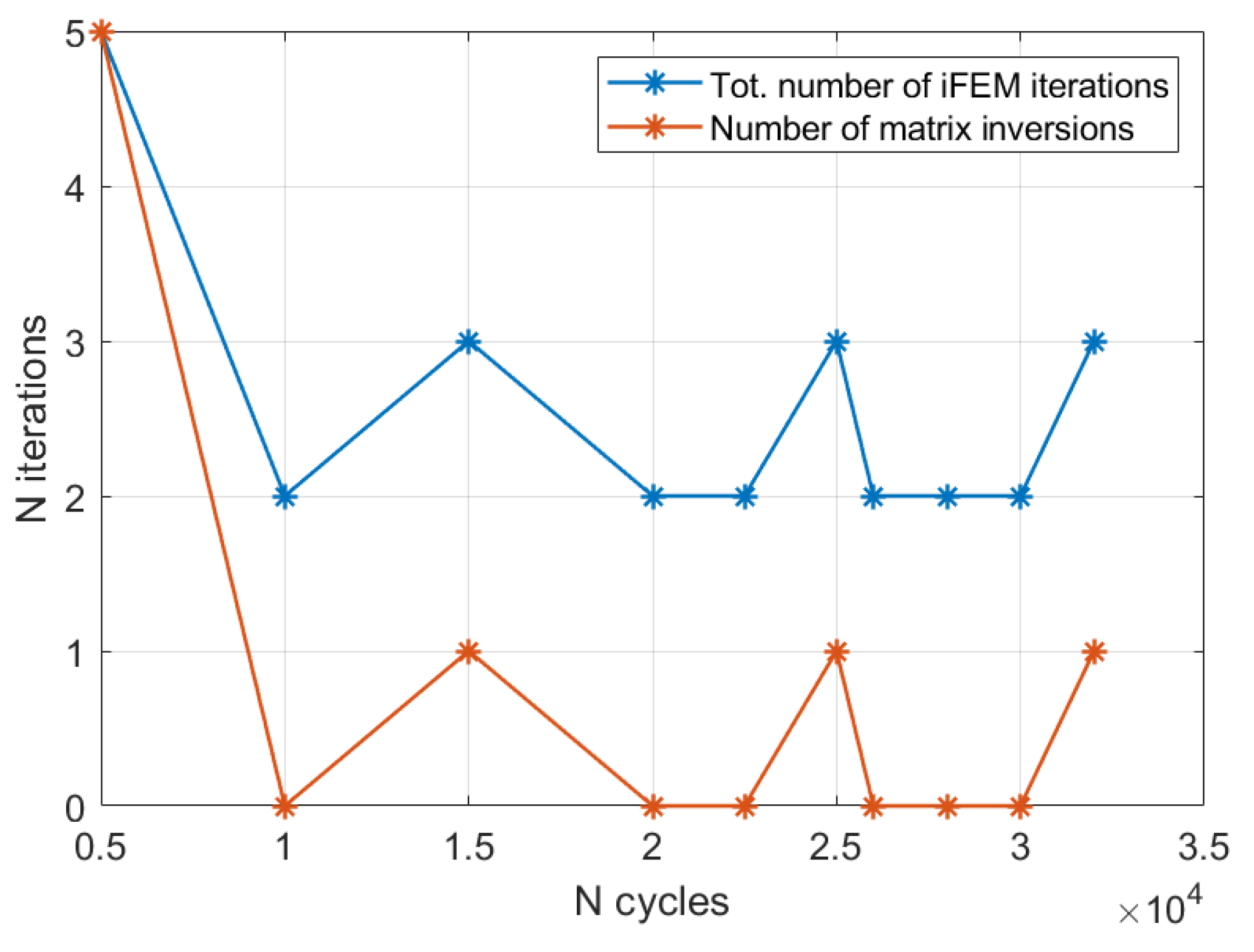
5.2.3. Automatic crack size estimation framework
- The model update and the damage diagnosis are carried out online, where the needed models are generated on-demand, although this may require a significant computation burden
- A database of damage scenarios can be generated offline considering the most relevant damage mechanisms of the structure (e.g. the crack’s nucleation from rivet holes). Then, the real-time algorithm will just load the required models, in which the matrix has been already inverted, and perform an efficient damage diagnosis.
- The damage diagnosis procedure is carried out offline at specified intervals, in parallel with respect to the structure’s operation. With this approach, the a priori definition of the damage scenarios and the database creation is not necessary since the computation does not have strict requirements in terms of computational time. The offline procedure computes the new damage condition of the structure, which can be uploaded on the real-time Digital-Twin and used until the next model’s update. The offline damage diagnosis and model update can be carried out on-demand, for example, based on some real-time damage indices, or at specified intervals according to the expected damage growth rate.
- A combination of the approaches described can be adopted according to the specific case. For example, an initial database can be created, and then, once the damage location is identified, additional models are generated on-demand.
| Algorithm 3: Real-time crack size estimation procedure without a priori creation of a database of damage scenarios. | |
| 1: | Define the undamaged iFEM model (mesh, connectivity, BC, etc.) |
| 2: | Set the initial state variables: = undamaged iFEM model (mesh, connectivity, BC, etc.) (zero initial crack length) (time instant counter) (zero initial detected crack length) |
| 3: | Identify the crack center |
| 4: | Define the input () and the test () sensor networks |
| 5: | while experimental data acquisition ON do |
| 6: | |
| 7: | Acquire the new experimental measurements and |
| 8: | find ( (index of the previous iteration iFEM model) |
| 9: | (iteration counter) |
| 10: | (, ) = Compute the iFEM results ((, , ) (Algorithm 4) |
| 11: | |
| 12: | while do |
| 13: | |
| 14: | |
| 15: | if does not exist do |
| 16: | if do |
| 17: | = crack introduction from (Algorithm 1) |
| 18: | else |
| 19: | = crack propagation from (Algorithm 2) |
| 20: | end |
| 21: | Get the new from |
| 22: | end |
| 23: | (, ) = Compute the iFEM results ((, , ) (Algorithm 4) |
| 24: | if do |
| 25: | (store the detected crack length) |
| 26: | |
| 27: | |
| 28: | (exit from the while loop) |
| 29: | end |
| 30: | end |
| 31: | end |
| Algorithm 4: iFEM computation subroutine with physics-based strain pre-extrapolation. | |
| 1: | Pre-extrapolate the strain field with the physics-based approach considering the crack length |
| 2: | Define the iFEM input vector |
| 3: | Compute the iFEM displacement field using Equation (10) |
| 4: | Compute the iFEM strain field using Equation (5) |
| 5: | Compute the Logarithmic Likelihood () between and using Equation (12). |
5.3. iFEM results with the 1 mm model
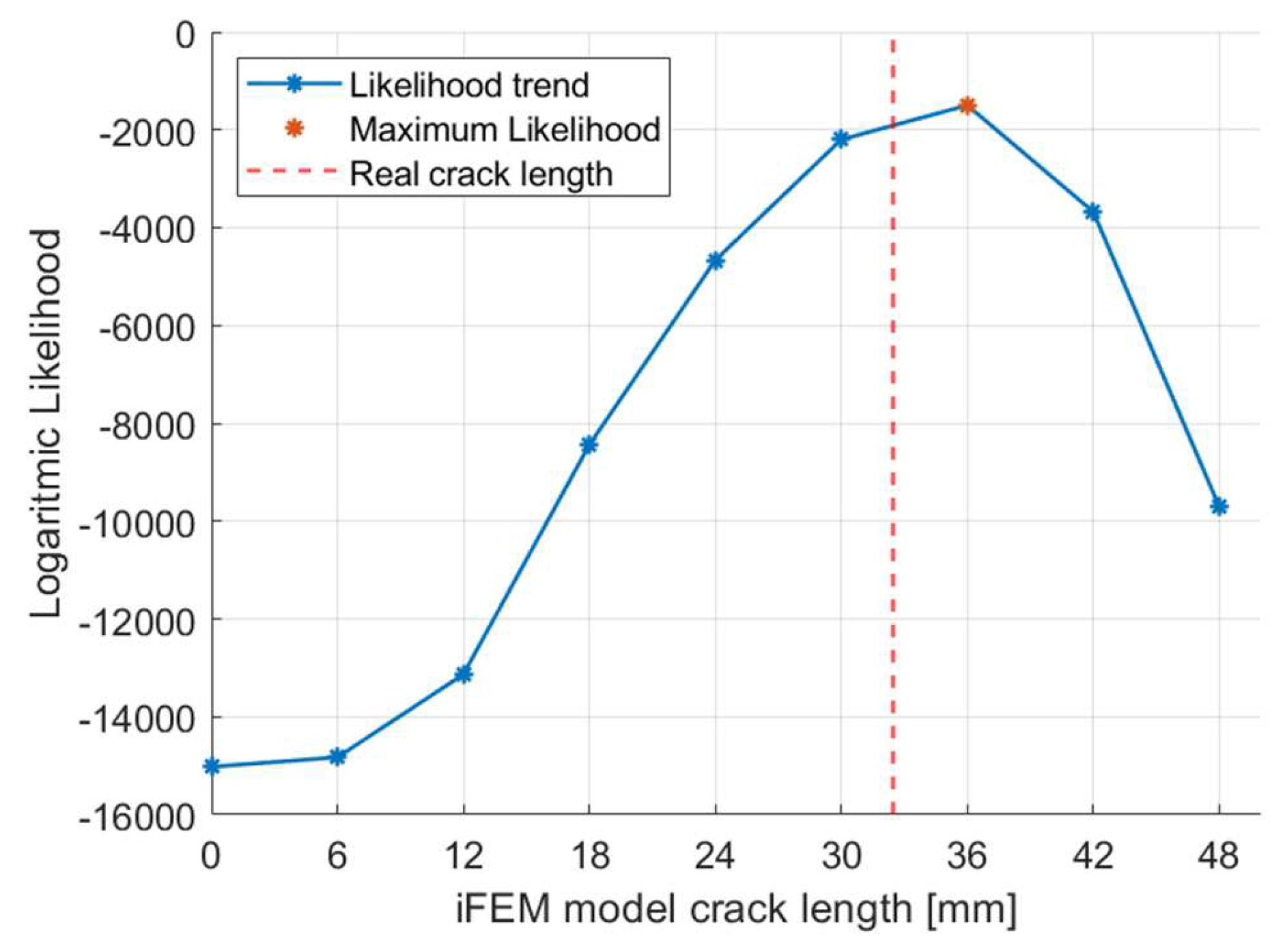
5.3.1. Likelihood trends
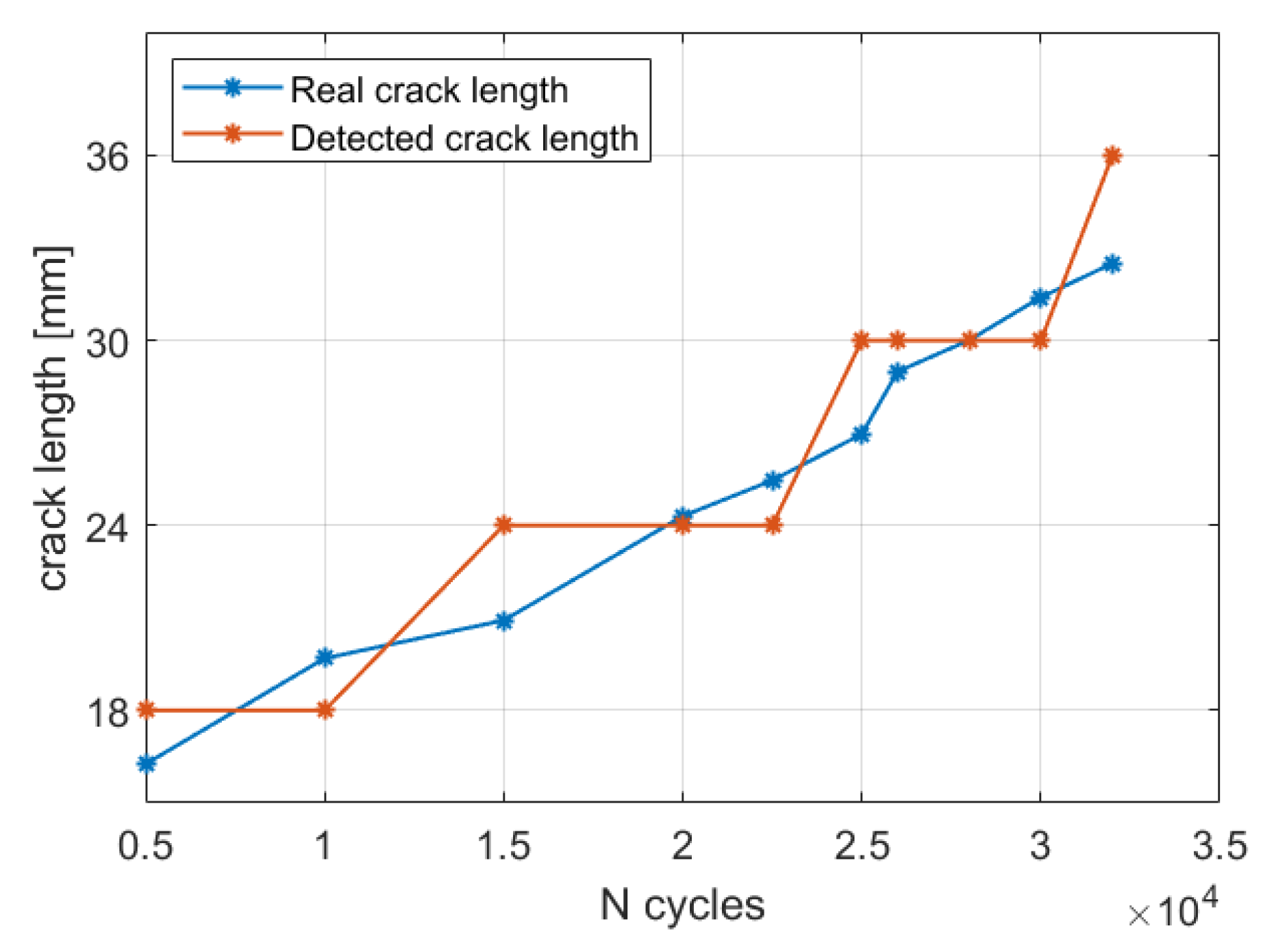
5.3.2. Crack size estimation results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The authors naively considered likelihood function as proportional to damage probability density function in presence of a non‐informative prior knowledge on damage extent. |
References
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-Based Structural Health Monitoring Using Output-Only Measurements under Changing Environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley and Sons, 2012; ISBN 9781119994336. [Google Scholar]
- Lambinet, F.; Sharif Khodaei, Z. Measurement Platform for Structural Health Monitoring Application of Large Scale Structures. Meas. J. Int. Meas. Confed. 2022, 190. [Google Scholar] [CrossRef]
- Alavi, A.H.; Hasni, H.; Jiao, P.; Borchani, W.; Lajnef, N. Fatigue Cracking Detection in Steel Bridge Girders through a Self-Powered Sensing Concept. J. Constr. Steel Res. 2017, 128, 19–38. [Google Scholar] [CrossRef]
- Warner, J.; Bomarito, G.; Hochhalter, J.; Leser, W.; Leser, P.; Newman, J. A Computationally-Efficient Probabilistic Approach to Model-Based Damage Diagnosis. Int. J. Progn. Heal. Manag. 2017, 8. [Google Scholar] [CrossRef]
- Sbarufatti, C. Optimization of an Artificial Neural Network for Fatigue Damage Identification Using Analysis of Variance. Struct. Control Heal. Monit. 2017, 24, 1–17. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Manes, A.; Giglio, M. Performance Optimization of a Diagnostic System Based upon a Simulated Strain Field for Fatigue Damage Characterization. Mech. Syst. Signal Process. 2013, 40, 667–690. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the Digital Twin: A Systematic Literature Review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Informatics 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Wagg, D.J.; Worden, K.; Barthorpe, R.J.; Gardner, P. Digital Twins: State-of-The-Art and Future Directions for Modeling and Simulation in Engineering Dynamics Applications. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2020, 6. [Google Scholar] [CrossRef]
- Peng, F.; Zheng, L.; Peng, Y.; Fang, C.; Meng, X. Digital Twin for Rolling Bearings: A Review of Current Simulation and PHM Techniques. Meas. J. Int. Meas. Confed. 2022, 201, 111728. [Google Scholar] [CrossRef]
- Glaessgen, E.H.; Stargel, D.S. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. Collect. Tech. Pap. - AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf. 2012, 1–14. [Google Scholar] [CrossRef]
- Seshadri, B.R.; Krishnamurthy, T. Structural Health Management of Damaged Aircraft Structures Using the Digital Twin Concept. 25th AIAA/AHS Adapt. Struct. Conf. 2017, 1–13. [CrossRef]
- Gockel, B.T.; Tudor, A.W.; Brandyberry, M.D.; Penmetsa, R.C.; Tuegel, E.J. Challenges with Structural Life Forecasting Using Realistic Mission Profiles. Collect. Tech. Pap. - AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf. 2012, 1–11. [Google Scholar] [CrossRef]
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering Aircraft Structural Life Prediction Using a Digital Twin. Int. J. Aerosp. Eng. 2011, 2011. [Google Scholar] [CrossRef]
- Tuegel, E.J. The Airframe Digital Twin: Some Challenges to Realization. Collect. Tech. Pap. - AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf. 2012, 1–8. [Google Scholar] [CrossRef]
- Johansen, S.S.; Nejad, A.R. On Digital Twin Condition Monitoring Approach for Drivetrains in Marine Applications. Proc. Int. Conf. Offshore Mech. Arct. Eng. - OMAE 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Ritto, T.G.; Rochinha, F.A. Digital Twin, Physics-Based Model, and Machine Learning Applied to Damage Detection in Structures. Mech. Syst. Signal Process. 2021, 155, 107614. [Google Scholar] [CrossRef]
- Moghadam, F.K.; Nejad, A.R. Online Condition Monitoring of Floating Wind Turbines Drivetrain by Means of Digital Twin. Mech. Syst. Signal Process. 2022, 162, 108087. [Google Scholar] [CrossRef]
- Tao, F.; Cheng, J.; Qi, Q.; Zhang, M.; Zhang, H.; Sui, F. Digital Twin-Driven Product Design, Manufacturing and Service with Big Data. Int. J. Adv. Manuf. Technol. 2018, 94, 3563–3576. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in Manufacturing: A Categorical Literature Review and Classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Fedorko, G.; Molnár, V.; Vasiľ, M.; Salai, R. Proposal of Digital Twin for Testing and Measuring of Transport Belts for Pipe Conveyors within the Concept Industry 4.0. Meas. J. Int. Meas. Confed. 2021, 174. [Google Scholar] [CrossRef]
- Wang, M.; Feng, S.; Incecik, A.; Królczyk, G.; Li, Z. Structural Fatigue Life Prediction Considering Model Uncertainties through a Novel Digital Twin-Driven Approach. Comput. Methods Appl. Mech. Eng. 2022, 391, 114512. [Google Scholar] [CrossRef]
- Kefal, A.; Emami, I.; Yildiz, M.; Tessler, A. A Smoothed IFEM Approach for Efficient Shape-Sensing Applications : Numerical and Experimental Validation on Composite Structures. Mech. Syst. Signal Process. 2021, 152, 107486. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells. NASA/TM-2003-212445, 2003. [Google Scholar]
- Tessler, A.; Spangler, J. Inverse FEM for Full-Field Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells. Proc. 2nd Eur. Work. Struct. Heal. Monit. Munich, Ger. 2004. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape Sensing of 3D Frame Structures Using an Inverse Finite Element Method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Bao, H.; Xu, Q. Optimal Sensor Placement Based on Eigenvalues Analysis for Sensing Deformation of Wing Frame Using IFEM. Sensors (Switzerland) 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. An Inverse Finite Element Method for Beam Shape Sensing: Theoretical Framework and Experimental Validation. Smart Mater. Struct. 2014, 23. [Google Scholar] [CrossRef]
- Chen, K.; Cao, K.; Gao, G.; Bao, H. Shape Sensing of Timoshenko Beam Subjected to Complex Multi-Node Loads Using Isogeometric Analysis. Meas. J. Int. Meas. Confed. 2021, 184, 109958. [Google Scholar] [CrossRef]
- Wang, J.; Ren, L.; You, R.; Jiang, T.; Jia, Z.; Wang, G. xin Experimental Study of Pipeline Deformation Monitoring Using the Inverse Finite Element Method Based on the IBeam3 Element. Meas. J. Int. Meas. Confed. 2021, 184, 109881. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, L.; Bao, H.; Du, J. Shape Sensing of Variable Cross-Section Beam Using the Inverse Finite Element Method and Isogeometric Analysis. Meas. J. Int. Meas. Confed. 2020, 158, 107656. [Google Scholar] [CrossRef]
- You, R.; Ren, L. An Enhanced Inverse Beam Element for Shape Estimation of Beam-like Structures. Meas. J. Int. Meas. Confed. 2021, 181, 109575. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and Stress Monitoring of a Chemical Tanker Based on Inverse Finite Element Method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and Stress Monitoring of a Panamax Containership Using Inverse Finite Element Method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Li, M.; Kefal, A.; Cerik, B.C.; Oterkus, E. Dent Damage Identification in Stiffened Cylindrical Structures Using Inverse Finite Element Method. Ocean Eng. 2020, 198. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A Quadrilateral Inverse-Shell Element with Drilling Degrees of Freedom for Shape Sensing and Structural Health Monitoring. Eng. Sci. Technol. an Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Least-Squares Variational Method for Full-Field Reconstruction of Elastic Deformations in Shear-Deformable Plates and Shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Shape Sensing of a Complex Aeronautical Structure with Inverse Finite Element Method. Sensors 2021, 21, 342–351. [Google Scholar] [CrossRef]
- Niu, S.; Zhao, Y.; Bao, H. Shape Sensing of Plate Structures through Coupling Inverse Finite Element Method and Scaled Boundary Element Analysis. Meas. J. Int. Meas. Confed. 2022, 190, 110676. [Google Scholar] [CrossRef]
- Zhao, F.; Bao, H. An Improved Inverse Finite Element Method for Shape Sensing Using Isogeometric Analysis. Meas. J. Int. Meas. Confed. 2021, 167, 108282. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Tessler, A. Real-Time Displacement Monitoring of a Composite Stiffened Panel Subjected to Mechanical and Thermal Loads. Meccanica 2015, 50, 2487–2496. [Google Scholar] [CrossRef]
- Papa, U.; Russo, S.; Lamboglia, A.; Del Core, G.; Iannuzzo, G. Health Structure Monitoring for the Design of an Innovative UAS Fixed Wing through Inverse Finite Element Method (IFEM). Aerosp. Sci. Technol. 2017, 69, 439–448. [Google Scholar] [CrossRef]
- Colombo, L.; Sbarufatti, C.; Giglio, M. Definition of a Load Adaptive Baseline by Inverse Finite Element Method for Structural Damage Identification. Mech. Syst. Signal Process. 2019, 120, 584–607. [Google Scholar] [CrossRef]
- Li, M.; Kefal, A.; Oterkus, E.; Oterkus, S. Structural Health Monitoring of an Offshore Wind Turbine Tower Using IFEM Methodology. Ocean Eng. 2020, 204, 107291. [Google Scholar] [CrossRef]
- Kefal, A. An Efficient Curved Inverse-Shell Element for Shape Sensing and Structural Health Monitoring of Cylindrical Marine Structures. Ocean Eng. 2019, 188. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Kefal, A.; Yildiz, M. A Comparative and Review Study on Shape and Stress Sensing of Flat/Curved Shell Geometries Using C0-Continuous Family of IFEM Elements. Sensors (Switzerland) 2020, 20, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Kefal, A.; Yildiz, M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors (Switzerland) 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Abdollahzadeh, M.A.; Tabrizi, I.E.; Kefal, A.; Yildiz, M. A Combined Experimental/Numerical Study on Deformation Sensing of Sandwich Structures through Inverse Analysis of Pre-Extrapolated Strain Measurements. Meas. J. Int. Meas. Confed. 2021, 185, 110031. [Google Scholar] [CrossRef]
- Kefal, A.; Tabrizi, I.E.; Tansan, M.; Kisa, E.; Yildiz, M. An Experimental Implementation of Inverse Finite Element Method for Real-Time Shape and Strain Sensing of Composite and Sandwich Structures. Compos. Struct. 2021, 258, 113431. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. A Novel Approach for Displacement and Stress Monitoring of Sandwich Structures Based on the Inverse Finite Element Method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Kefal, A.; Tessler, A.; Oterkus, E. An Enhanced Inverse Finite Element Method for Displacement and Stress Monitoring of Multilayered Composite and Sandwich Structures. Compos. Struct. 2017, 179, 514–540. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Isogeometric IFEM Analysis of Thin Shell Structures. Sensors (Switzerland) 2020, 20, 2685. [Google Scholar] [CrossRef]
- Colombo, L.; Oboe, D.; Sbarufatti, C.; Cadini, F.; Russo, S.; Giglio, M. Shape Sensing and Damage Identification with IFEM on a Composite Structure Subjected to Impact Damage and Non-Trivial Boundary Conditions. Mech. Syst. Signal Process. 2021, 148, 107163. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Comparison of Strain Pre-Extrapolation Techniques for Shape and Strain Sensing by IFEM of a Composite Plate Subjected to Compression Buckling. Compos. Struct. 2021, 262, 113587. [Google Scholar] [CrossRef]
- Tessler, A.; Riggs, H.R.; Macy, S.C. A Variational Method for Finite Element Stress Recovery and Error Estimation. Comput. Methods Appl. Mech. Eng. 1994, 111, 369–382. [Google Scholar] [CrossRef]
- Tessler, A.; Hughes, T.J.R. A Three-Node Mindlin Plate Element with Improved Transverse Shear. Comput. Methods Appl. Mech. Eng. 1985, 50, 71–101. [Google Scholar] [CrossRef]
- Tessler, A.; Riggs, H.R.; Freese, C.E.; Cook, G.M. An Improved Variational Method for Finite Element Stress Recovery and a Posteriori Error Estimation. Comput. Methods Appl. Mech. Eng. 1998, 155, 15–30. [Google Scholar] [CrossRef]
- Riggs, H.R.; Tessler, A.; Chu, H. C1-Continuous Stress Recovery in Finite Element Analysis. Comput. Methods Appl. Mech. Eng. 1997, 143, 299–316. [Google Scholar] [CrossRef]
- Oboe, D.; Sbarufatti, C.; Giglio, M. Physics-Based Strain Pre-Extrapolation Technique for Inverse Finite Element Method. Mech. Syst. Signal Process. 2022, 177, 109167. [Google Scholar] [CrossRef]
- Poloni, D.; Oboe, D.; Sbarufatti, C.; Giglio, M. Towards a Stochastic Inverse Finite Element Method : A Gaussian Process Strain Extrapolation. Mech. Syst. Signal Process. 2023, 189. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Yang, H.; Huang, H. Direct Damage Index Based on Inverse Finite Element Method for Structural Damage Identification. Ocean Eng. 2021, 221, 108545. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Jia, D.; Qiu, S.; He, W. Structural Damage Identification Using Strain Mode Differences by the IFEM Based on the Convolutional Neural Network (CNN). Mech. Syst. Signal Process. 2022, 165, 108289. [Google Scholar] [CrossRef]
- Kefal, A.; Diyaroglu, C.; Yildiz, M.; Oterkus, E. Coupling of Peridynamics and Inverse Finite Element Method for Shape Sensing and Crack Propagation Monitoring of Plate Structures. Comput. Methods Appl. Mech. Eng. 2022, 391, 114520. [Google Scholar] [CrossRef]
- Westergaard, H.M. Bearing Pressures and Cracks. J. Appl. Mech. 1939, 6, A49–A53. [Google Scholar] [CrossRef]
- Eftis, J.; Liebowitz, H. On the Modified Westergaard Equations for Certain Plane Crag Problems. Int. J. Fract. Mech. 1972, 8, 383–392. [Google Scholar] [CrossRef]
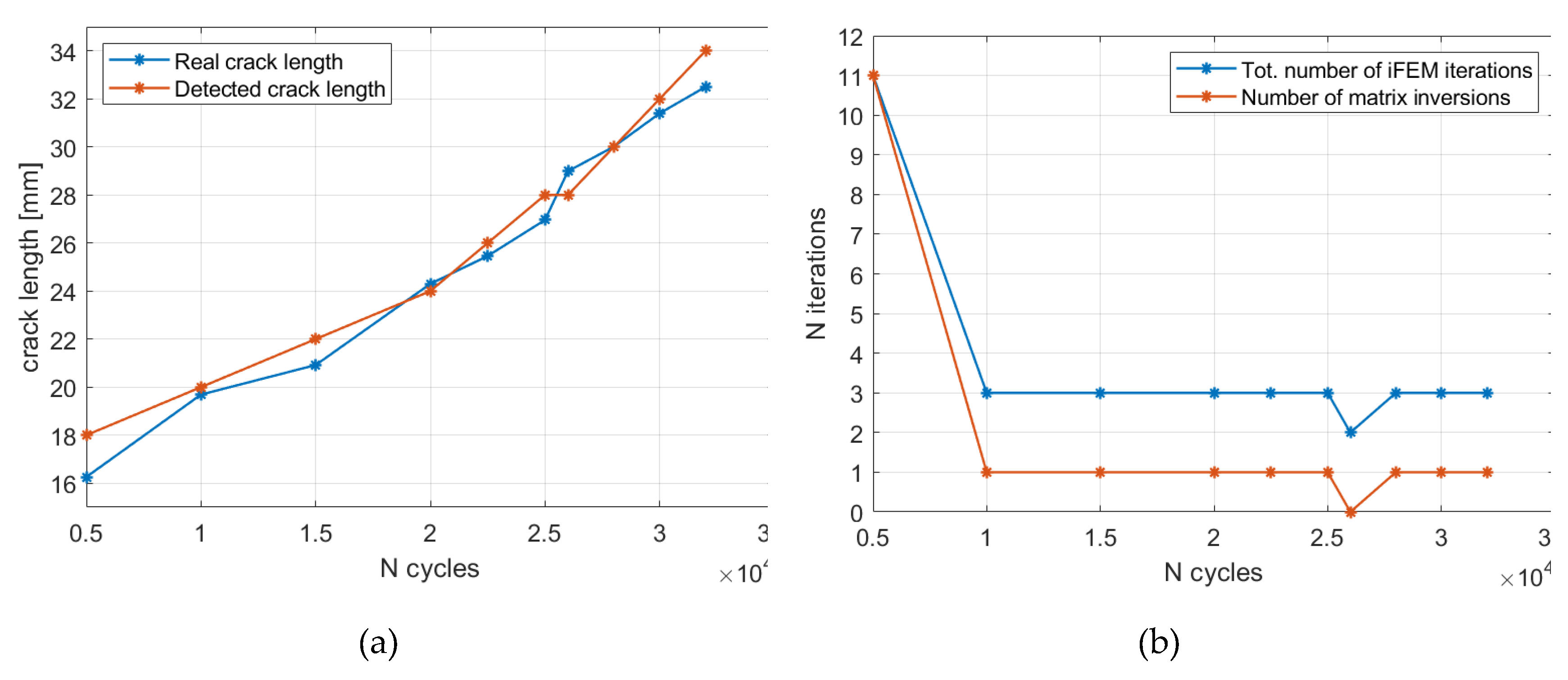
| N cycles | ] |
|---|---|
| 5,000 | 16.26 |
| 10,000 | 19.69 |
| 15,000 | 20.92 |
| 20,000 | 24.30 |
| 22,500 | 25.46 |
| 25,000 | 26.96 |
| 26,000 | 28.99 |
| 28,000 | 30.01 |
| 30,000 | 31.40 |
| 32,000 | 32.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





