Preprint
Article
Modeling of Soil Water Erosion in Tunisia Using Geospatial Data and Integrated Approach of RUSLE and GIS
Altmetrics
Downloads
322
Views
129
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 February 2023
Posted:
06 February 2023
You are already at the latest version
Alerts
Abstract
Soil erosion is one of the most important environmental problems which can have various negative consequences, such as land degradation affecting the sustainable development and the agricultural production, especially for developing countries like Tunisia. Moreover, soil erosion is a major problem around the world because of its effects on soil fertility by nutriment loss and siltation in water bodies. Apart from this, soil erosion by water is the most serious type of land loss in several regions both locally and globally. This study evaluated regional soil erosion risk through the derivation of appropriate factors, using the Revised Universal Soil Loss Equation (RUSLE), which was applied to establish a soil erosion risk map of the whole Tunisian territory and to identify the vulnerable areas of the country. RUSLE model take into account all the factors playing a major role in erosion processes, namely the erodibility of soils, topography, land use, rainfall erosivity and anti-erosion farming practices. The equation is thus implemented under Geographic Information System (GIS) “Arc GIS Desktop”. The results indicated that Tunisia has a serious risk of soil water erosion, showing that 6.43% of the total area of the country is affected by a very high soil loss rate estimated at more than 30 t/ha/year and 4.20% are affected by high mean annual soil loss ranging from 20 to 30 t/ha/year. The most eroded areas were identified in west southern, central and western parts of the country. The spatial erosion map can be used as a decision support document to guide decision-makers towards better land management and provide the opportunity to develop management strategies for soil erosion prevention and control in the global scale of Tunisia.
Keywords:
Subject: Environmental and Earth Sciences - Soil Science
1. Introduction
Large-scale soil erosion was known to be one of the most severe problems that can lead to environmental damage [1,2] and consequences affecting the political, social and economic aspects of countries [3], particularly the developing countries. The most dominant agent of the soil erosion is the water [4], removing the soil surface materials and including detachment, transportation and deposition of the particles by rainfall and runoff. Soil erosion caused by water is defined as the breakdown of soil structure and detachment of soil particles due to falling raindrops and water flow exceeding a critical threshold [5]. The raindrops, with which soil particles (sediments) are detached, hit the topsoil of ground surface by splash during rainfall. The detached sediments can be transported to rills. The rills were gradually joined together to form large channels leading to gully erosion. The natural process of the removal of soil particles by water runoff and their redistribution downslope represents one of the main types of soil degradation [6]. It can cause negative consequences on soil productivity, human health and the earth’s environment, as well as on habitat which can have gradual degradation [7,8]. Many researchers have focused their studies on soil erosion by water to assess soil erosion losses in different regions of the world using remote sensing and GIS technology [5,9,10,11,12,13]. The Land Use and Land Cover (LULC) can influence the soil erosion process in a positive or negative way [14]. Human activities can accelerate the process of erosion, transport, and sedimentation such as urbanization, mining and construction of roads, highways and dams [8].
More than 80 soil erosion models [15,16,17,18,19,20,21,22,23], with varying degrees of complexity, have been developed to evaluate potential soil loss for different spatial and temporal scales [24,25], such as the Universal Soil Loss Equation (USLE), which was developed by Wischmeier and Smith in 1965 from measurements on elementary experimental plots respecting exact dimensions [26]. However, this model had certain limitations since it only took into account sheet erosion processes at the scale of the plot [27,28,29]. To remove these limitations, the model has been improved, modified and revised in several versions by integrating runoff factors to adapt it to the scale of a rainfall event [30]. Indeed, the USLE model has moved to MUSLE model "Modified Universal Soil Loss Equation", taking into account the topographic complexity through the use of the Digital Elevation Model (DEM) and anti-erosive practices. Finally, the RUSLE “Revised Universal Soil Loss Equation” improves the determination of the different factors of soil water erosion [31]. This new Revised USLE equation maintains the basic structure of USLE but uses new algorithms to calculate and estimate the individual factors. RUSLE model takes the form of a mathematical equation that uses erosion factors as inputs to estimate the mean annual soil losses resulting from sheet and rill erosion [32]. It is an empirical model that brings together the factors affecting the rate of water erosion, namely the kinetic energy of intense rainfall, soil properties, terrain characteristics, soil protection by vegetation cover and anthropogenic practices. This model does not consider erosion processes such as detachment, transport and deposition to estimate soil loss. The revised Wischmeier equation is combined with GIS techniques to assess soil loss rate and its spatial distribution across different land covers, taking into account the advantages offered by GIS and geospatial data [33,34,35] that can lead to more efficient, more precise and less time-consuming results [36], thus helping to guide decision-making. RUSLE model is not used to estimate the amount of sediment migrating from a specific watershed, but the amount of soil lost from any area [37]. For this, the model retains the same form as the equation used in the USLE model.
The RUSLE model involves the spatial combination of the different factors contributing to soil erosion. It was used to calculate soil losses (A) which is a multiplicative function taking into account the erosivity and the aggressiveness of rainfall and runoff (R factor) [megajoules millimeter hour−1 hectare−1 year−1], the soil erodibility (K factor) [ton hour megajoules− 1 millimeter− 1] and the resistance of the environment (C, P and LS factors) [dimensionless]. LS in RUSLE equation is generally the combination of L and S, representing the effect of the topography on erosion rates [38]. The RUSLE model has been used worldwide and adapted according to the climatic, topographic and soil context [9,10,39,40]. It is still used widely to estimate soil erosion all over the world [41] and can be used to estimate soil erosion for large areas, up to country level [42].
Therefore, modeling of soil water erosion in Tunisia using geospatial data and integrated approach of RUSLE and GIS aimed to estimate the spatial distribution of soil erosion of the overall study area, which can be useful to contribute to a better understanding of the soil degradation of large-scale areas. The spatial soil erosion map produced, can serve as a useful input for deriving land planning and management strategies and provide an opportunity to develop a decision plan for soil erosion prevention for better control and protection of both natural and man-made resources available in Tunisia.
2. Materials and Methods
2.1. Description of the study area
The republic of Tunisia, located in the North of African continent, is situated between 30°13’ and 37°20’ north latitude and 7°32’ and 11°36’ east longitude (Figure 1). It is located also in the south part of the Mediterranean Sea and bordered by Lybia at the South-East and by Algeria at the West. The study area covers 155084 km2, including the two main islands (Jerba and Kerkennah) but without the other small islands, such as Kneiss, Zembra, Kuriat, Galite and Chikly. Tunisia is the smallest country in North Africa, with a coastline on the North and East having around 1,300 km.
Tunisia has different types of landscapes, with mountainous areas in the North-West (Figure 2), upper and lower Steppe areas in the center and wide plains in the East. The depressions of the great Chotts mark the beginning of the Sahara in the South, with the mountains of Dhahar and the plains of Jeffara. The lowest altitude is 27 m below sea level, relating to the chott areas, and the highest is 1549 m above sea level, in Jbel el Chaambi, with an average elevation of 256 m for the whole study area.
Tunisia has ten different bioclimatic zones (Figure 3), characterized by three factors: the mean annual precipitation which decreases from North to South, the highest mean temperature of the hottest month (August) and the mean lowest temperature of the coldest month (January) [43]. The winter in Tunisia is soft and humid with temperatures between 8°C and 15°C and the summer is hot and dry with temperatures between 22°C and 35°C which can even exceed 40°C in August. Its northern part has a humid higher, humid lower and sub-humid bioclimate with an average annual rainfall, for the previous 31 years (from 1990 to 2020), of 650-736 mm. The central regions have a semi-arid higher, semi-arid middle, semi-arid lower and arid-higher bioclimate with 250-650 mm annual rainfall. The southern part has an arid lower, Saharan higher and Saharan lower bioclimate with 37-250 mm annual rainfall.
2.2. Methodology and data source processing
The cartographic documents are generally produced at local scales. However, these data are often without recent updating, incomplete and sometimes non-existent, such as geographical reference data on topography, precipitation, land cover, etc... Similarly, georeferenced digital data on a small scale are mostly scarce or obsolete. On the other hand, the use of online databases on a global scale has become available these last years. Furthermore, the spatial analysis and modeling are facilitated mainly because of the existence of satellite data which has become very easy to have continuously. Indeed, the raster mode with a simple data structure and a regular shape of the grid is very convenient to keep geometric properties common to all layers of information, thus facilitating the combination of different layers, since all numeric values are dependent on the same base unit, the pixel.
In addition, these data need to be tested in several case studies on a global scale. That is why, one of the objectives of this study is to assess the potential of existing digital data for spatialized modeling in a GIS of soil water erosion in the current Tunisian context. It can be in some cases considered as an alternative to overcome the problem of lack of data.
The choice of RUSLE model (Equation 1) in this study was motivated by the fact that this model does not differ conceptually from the original soil loss equation (USLE) of Wischmeier and Smith [26]. On the contrary, it improves the quality of the environmental parameters which define the role of each factor. Also, the input data for this model is easier to access compared to other more recent models, which require more sophisticated data.
The RUSLE is written as: A=R*K*LS*C*P
Where:
A is the soil loss per unit area, expressed in the units of K and the period selected for R;
R is the rainfall and runoff erosivity factor;
K is the soil erodibility factor;
LS is the slope length and slope steepness factor;
C is the crop management factor;
P is the support practice factor.
RUSLE model was used to estimate the yearly average of soil loss due to water erosion, by taking into account the five factors indicated in equation (1). The latter has been applied using GIS and geospatial data composed of: (1) Climatic data including a 31-year average annual precipitation downloaded from the NASA-POWER meteorological parameters, taken from NASA's MERRA-2 assimilation model and necessary for computing the rainfall and Runoff Erosivity factor (R). (2) Soil map of Tunisia extracted from FAO Digital Soil Map of the Word (DSMW), essential for calculating the soil erodibility factor (K). (3) Global Digital Elevation Model (ASTER GDEM), which is used to calculate the topographic factor (LS). (4) LULC map of Tunisia extracted from ESRI 2020 Global Land Cover and used to calculate and map the vegetative cover factor (C) as well as the support and management practice factor (P).
Each of the factors was derived separately in raster format based on rainfall pattern, soil type, topography and LULC data in the context of soil water erosion modeling, in order to generate global scale maps. However, the current study, that deal with the estimation of soil erosion by water, did not consider development stage of the crops. Furthermore, the season variability effects were not taken into account.
The geospatial data with different types and origins are listed in Table 1. Figure 4 shows the flowchart of the method used for the estimation of each factor and for the analysis of soil loss based on the RUSLE model and GIS technique.
The following parts of this article make a brief description of the various factors showed in equation (1) and present the results obtained after modeling and analysis of geospatial data.
2.2.1. Rainfall and runoff erosivity factor (R-factor)
The estimation of the R factor requires knowledge of the kinetic energies and the average intensity over 30 min of the raindrops that fall each time, over a long period of up to 30 years [44]. But this direct method requires precipitation records at high resolutions to calculate R-factor. Other authors have developed alternative formulas when these data are not available. The equations most used to calculate the R factor using only annual precipitation are those of Renard and Freimund [45] (Equations 2 and 3), whose expressions are:
Where: R is the measure of rainfall erosivity and Pi is the average annual precipitation (mm).
R = 0.0483. Pi1.61 if 𝑃𝑖 < 850 𝑚𝑚
R = 587,8 -1,219 Pi +0,004105. Pi 2 if 𝑃𝑖 > 850 𝑚𝑚
The estimation of rainfall and runoff erosivity using rainfall data with long-time intervals has been conducted by many authors for different regions of the world [36,46]. To calculate the average annual R-factor values in this study, a 31-year average annual data has been used and an interpolation of this data was applied to have a representative rainfall distribution map which is used as input for calculation of R-factor, knowing that the rainfall data available for the study area is not homogenous. This parameter, expressed in (MJ.mm.ha−1. h−1.year−1), takes into consideration the influence of climatic aggressiveness on soil loss [47].
To generate the R-factor for the whole Tunisia, a 31-year average annual precipitation from 1990 to 2020 required for this study, was downloaded freely, as a Comma-Separated Values (CSV) file, from the National Aeronautics and Space Administration (NASA) Prediction of Worldwide Energy Resources known as POWER project which was initiated in 2003. It provides access to solar and meteorological data sets for the entire globe and particularly over regions where surface measurements are sparse or nonexistent. The meteorological parameters are based upon the MERRA-2 assimilation model. The monthly and annual precipitation data are derived from NASA's Global Precipitation Measurement (GPM). and an interpolation of this data was applied to have a representative rainfall distribution map which was used as input for calculation of R-factor. Since the mean annual precipitation in Tunisia does not exceed 850 mm, equation 3 was used to calculate the rainfall-runoff erosivity factor, taking into account the bioclimatic map of Tunisia which has been developed for climatically homogeneous areas. The Inverse Distance Interpolation (IDW) method was used to minimize the calculation error and above all to optimize the processing time on the ArcGIS software. It is a method that consists in creating, from the aggregated points and the corresponding information, a value grid with a certain continuity.
2.2.2. Soil erodibility (K-factor)
The soil erodibility K, expressed in [t. h. MJ−1.mm−1], determines the resistance of different types of soil to erosion, knowing that soils are more or less sensitive to water erosion. This K factor is determined according to the characteristics of the soil: infiltration capacity, retention texture and susceptibility to particle removal. The infiltration and the high cohesion of the materials increase the soil resistance to removal and gullying of particles. The high rate of sand stabilizes the structure of the soil and makes it less sensitive to climatic aggression. Similarly, the organic matter improves the physical and chemical properties (cohesion, structural stability, porosity) of the soil, increasing the ability to retain water, and strengthens resistance to erosion [48]. Thus, the higher the percentage of sand, the more the soil is permeable, which implies a low value of the K-factor and vice versa. Bolline and Rousseau (1978) [49] established the classification, in Table 2 interpreting the soil susceptibility index.
Table 1.
Description of the data sources.
| Erodibility (K) | Type of soil |
|---|---|
| K < 0.10 | Soil highly resistant to erosion |
| 0.10 à 0.25 | Soil fairly resistant to erosion |
| 0.25 à 0.35 | Soil moderately resistant to erosion |
| 0.35 à 0.45 | Soil with low erosion resistance |
| >0.45 | Soil with very low resistance to erosion |
However, soil erodibility is not constant, as it varies not only with soil type, but also with seasons and cultivation techniques. The soil map of Tunisia was prepared using FAO Digital Soil Map of the Word Shapefile (DSMW), where the soil data layer has been clipped, according to the country boundaries relative to the study area, in the ArcGIS Desktop environment. K-factor was calculated using Williams (1995) [50] formula (Equations 4) and FAO Digital Soil Map.
The raster dataset of the FAO/UNESCO Digital Soil Map of the World (DSMW) has a spatial resolution of 5 * 5 arc minutes and is in geographic projection.
Where:
is a factor that gives low soil erodibility factor for soils with high coarse-sand content and high value for soil with little sand.
is a factor that gives low soil erodibility factor for soils with high clay to silt ratios.
is a factor that reduces soil erodibility for soils with extremely high sand content.
is a factor that reduces soil erodibility factor with high coarse-sand contents and high value for soil with little sand.
The factors are calculated using these equations (Equations 5, 6, 7 and 8)
Where, ms is the percent sand content (0.05-2.0) mm diameter particles,
msilt is the percent silt content (< 0.002) mm diameter particles,
mc is the percent clay content (0.05-2.0) mm diameter particles,
orgC is the percent organic carbon of the layer (%).
2.2.3. Topographic factor (LS-factor)
The two parameters that constitute the topographic factor are slope gradient and slope length factor were estimated, here in this study, through an ASTER Global Digital Elevation Model (ASTER GDEM) with a 30 m resolution downloaded freely from (https://search.earthdata.nasa.gov/downloads/) [73]. The DEM of Tunisia’s territory is ranged from -27 m to 1549 m (Figure 2). The latter was incorporated into GIS to determine accurately the slope gradient (S) and slope length (L), taking into account that the effect of slope length and degree of slope interaction should always be considered together [51]. So, to create the slope length and steepness (LS-factor), equivalent to topographic factor and relief factor, respectively, flow direction and flow accumulation maps were created after the filling process of DEM data by the use of the GIS extension Arc Hydro Tools. The flow accumulation was determined for each cell by the flow that flows through that cell. The greater the flow accumulation value, the easier the area will form runoff and vice versa. The slope map in degree, required to estimate the LS factor, shows that most of the slope of Tunisia is ranged from 0 to 10° which represent about 95,54 % from total area (Figure 9).
In 1985, Moore and Burch [52] developed the equation below (Equation 9) to compute the length-slope factor:
The equation (9) has been applied by many researchers [51,53,54]. The exponent value m can be taken equal to 0.4 while the value of n can be taken equal to 1.3 [53,54,55].
Where:
𝐿𝑆: is slope steepness–length factor.
𝐴𝑠: is the flow accumulation (in meters).
𝜃: is the slope angle (in radians).
𝑚 = 0.4 – 0.6 and n = 1.2 – 1.3.
In general, as the length of the slope increases, the total soil erosion and the soil erosion per unit area increase due to the gradual accumulation of runoff water in the downhill direction of the slope. As the steepness of the slope increases, the velocity and erosivity of the runoff increase.
2.2.4. Vegetative cover factor (C-factor)
It is a dimensionless factor presenting the effectiveness of the vegetation cover in relation to the susceptibility of the soil to erosion [56]. Vegetation cover and its spatial distribution play an important role in reducing the effects of runoff by amortizing the impact of rainwater on an area [15].
According to several studies, this RUSLE factor that can range from zero for water and a very well protected soil with very strong cover effects, to 1 for a surface that produces a lot of runoffs (bare soil) and leaves the soil very susceptible to water erosion [57]. Several authors consider that C-factor is around 0.01 (1/100) under dense forest, 0.05 (5/100) under grasslands and 0.24 (24/100) under crops (Table 3). Other researchers have adopted the calculation of C-factor by new simplified approaches: use of remote sensing techniques such as the classification of satellite images [58,59] and vegetation indices [60] or use of the Land Use/Land Cover (LULC) map and class assignment for each entity [61]. In fact, C-factor reflect the effect of LULC, cropping and management practices on the rate of soil erosion [62,63,64,65].
C-factor was determined, in this study based on the literature, by assigning a value for each type of LULC extracted from ESRI 2020 Global map of LULC, derived from ESA Sentinel-2 imagery at 10 m resolution and downloaded freely from https://livingatlas.arcgis.com/landcover/ for all land masses on the planet. Two Individual GeoTIFF scenes (32S_20200101-20210101 and 32R_20200101-20210101) covering the Tunisian territory, have been downloaded from Esri 2020 Land Cover Downloader application. These scenes were joined to form a mosaic image and the values of the C-factor (Table 3) for 7-class LULC types covering the study area were used in the data analysis to build the C-factor map for the year 2020 at 10 m resolution, performing the analysis in ArcGIS and then converted to a grid with 30 x 30 m spatial resolution.
2.2.5. Support and management practice factor (P-factor)
This factor, which is dimensionless, represents soil protection based on anti-erosion cultivation techniques that reduce runoff speed and thus reduce the risk of water erosion. It varies according to the landscaping carried out, namely cultivation on a level curve, in alternating strips or on terraces, reforestation in benches, ridging and ridging [15].
The P-factor is between 0 and 1, in which the value 0 represents a very good environment of resistance to erosion and the value 1 shows an absence of anti-erosion practice [72]. Wischmeier and Smith (1978) [15] established the classification according to the slope in percent (Table 4), showing that this factor can be distributed according to two zones: the cultivated zones and the other zones.
3. Results and discussion
In this part, the results of the processing as well as the calculations of each factor made for the spatialization of the soil loss rates in the study area will be presented in more details. After applying the RUSLE model, an assessment of the impacts of erosion at the regional scale of Tunisia will also be detailed in this section.
3.1. Spatial distributions of RUSLE factors
3.1.1. R-factor
The rainfall erosivity factor quantifies the effects of rainfall aggressiveness and therefore reflects the amount and rate of runoff associated with a rainfall event. It was calculated from annual average precipitation data recorded over a time interval of 31 years (from 1990 to 2020).
After calculation, the values of the R factor in Tunisia range from 24.29 to 1859.84 MJ.mm.h-1. ha-1. year-1. However, the average value in the entire country is 473.73 MJ.mm.h-1. ha-1. year-1. The maximum value is observed in the North-West part of Tunisia and the minimum value is observed in the South.
The maps in Figure 5 and Figure 6 show that precipitation and erosivity factor (R-factor) decrease gradually from the South towards the extreme North-West part of Tunisia. In addition, it is important to note that rainfall and runoff erosivity factor is a crucial factor in assessing soil erosion for future LULC and climate change.
3.1.2. K-factor
The physic-chemical properties of soils, such as organic matter, fine sand, clay and silt contents were obtained from the FAO-UNESCO Soil Map of the World. The percentage of organic matter (OM) depends on the presence and nature of the vegetation on the ground as well as on the use of the latter.
Determination of the K factor was performed using equations 4, 5, 6, 7 and 8 from Williams (1995) [50] and the soil map of Tunisia (Figure 7), extracted from the FAO-UNESCO Digital Soil Map of the Word (DSMW) shapefile [74]. The soil erodibility spatial distribution map (Figure 8) shows that the values of K-factor range from 0.10 to 0.19 t. h. MJ-1.mm-1. According to the classification of Bolline and Rosseau (1978) [49], the soils in Tunisia are therefore all classified as soil fairly resistant to erosion.
3.1.3. LS-factor
The slope map (Figure 9) is obtained by the Slope tool in Spatial analyst which was then used to calculate the steepness of the slopes. The mean value of the slope throughout the country is 2.24° with a standard deviation of 3.50° and values above 10° especially in the South-East, Center and North-West of the country.
Knowing that the LS factor is the derivative product of equation (9) of Moore and Burch (1985) [52], the equation of this product is formulated on Map Algebra's Raster Calculator following the syntax:
LS = Power ("Flow Accumulation" * Cell size / 22.13,0.4) * Power (Sin ("Slope in degree" * 0.0174533) / 0.0896,1.3)
Such that “Slope in degree” represents the slope map as represented by Figure 9 and the cell size represents the spatial resolution of the ASTER GDEM equal to 30 m. To convert the slope to radians, it was multiplied by 0.0174533, since 1 degree = 0.0174533 radians.
Thus, the following LS topographic factor map was obtained (Figure 10), showing that the value range of the LS factor is between 0 and 12.41. However, the average value in the whole country is 1.09.
3.1.4. C-factor
The vegetation cover factor map shows that the values vary from 0 to 1 over the whole country. The minimum values are found in the northern part of the country, where according to the LULC map (Figure 11), there are mainly dense forests and cultivated areas corresponding to well protected soil with very strong cover effects. On the other hand, the value of C-factor (Figure 12) is close to 1 going south, especially on bare soil that produces a lot of runoffs and leaves the soil very susceptible to water erosion.
3.1.5. P-factor
The support and management practice factor explains the effects of agricultural practices that can minimize the impact of rainwater and reduce the rate of runoff, and thus logically reduce soil loss (Wischmeier and Smith, 1978) [15].
The determination of the P-factor required the establishment of the map of agricultural and non-agricultural land (Figure 13) from the LULC map of Tunisia extracted from ESRI 2020 Global map, derived from ESA Sentinel-2 as well as the slope map in percent.
The values of the P-factor in agricultural areas decrease as the slope decreases and vice versa on steep terrain. These values vary from 0.1 on low slope land to 0.33 on very steep land. The other non-agricultural areas are all classified as areas without erosion control practices, which are assigned the value P = 1 (Figure 14).
The results of the calculations on each factor can be summarized as follows:
- The values of the erosivity factor of the rains vary from 24.29 to 1859.84 MJ.mm.h-1. ha-1. year-1 with an average of 473.73 MJ.mm.h-1. ha-1. year-1 over the whole country.
- The soil erodibility K-factor is classified as fairly resistant to erosion, with values varying from 0.10 to 0.19 t. h. MJ-1.mm-1.
- The value range of the topographic factor LS is between 0 and 12.41, with an average value of 1.09 over the whole country.
- The values of the vegetative cover C-factor vary from 0 to 1.
- The values of the support and management practice factor vary from 0.1 to 0.33 for agricultural land and are equal to 1 for non-agricultural land.
3.2. Calculation of soil loss rate and quantification of erosion
The modeling of the factors involved in water erosion of soils has enabled the quantification and spatialization of this phenomenon.
The RUSLE model gives an approximation of the average value of soil loss, expressed in tons per hectare per year, on a given scale of study. This approximation is based on the joint product of the five factors described above. In this study, the modeling is essentially carried out on ArcGIS. To estimate and map the spatial distribution of soil losses for the entire Tunisian territory, the maps of the five factors, seen in the previous sections, were projected according to the same coordinate system "Universal Transverse Mercator (UTM) zone 32 N using the Datum: WGS 1984" with a spatial resolution of 30 m x 30 m for each. We then proceeded to the calculation pixel by pixel by the RUSLE equation (1) with the "Raster calculator" tool and the "Map Algebra" function in ArcMap.
The application of this model allowed the establishment of the map of Figure 15, displaying the average values and the distribution of soil loss rates for the whole country.
By carrying out the calculation according to the empirical and spatialized model RUSLE on ArcGIS, the average value range of soil losses in Tunisia was obtained, varying from 0 to a maximum value of 619.44 t/ha/year. These results have been subdivided into 5 classes, according to Kefi et al. (2012) [9], represented in Table 5.
Despite a large domination of very low soil erosion by water, representing 56.34 % of the total area of Tunisian territory, 10.64 % of the total area are severely exposed to water erosion of the soil (High and very high soil erosion).
4. Conclusions
This study was the first to provide complete and detailed water soil erosion map for Tunisia at a country scale. The RUSLE model, an empirical model to assess soil losses per year, has been conducted to evaluate soil losses in Tunisia which were mapped at a 30 m cell size. The usage of the RUSLE equation is significantly facilitated by its deployment in Geographic Information Systems (GIS) and the use of geospatial data, provided over vast regions, such as the global territory of Tunisia. So, the use of this approach contributed to regional soil erosion risk assessment through the rapid derivation of appropriate indices.
Therefore, this study has found an adequate method that integrates geospatial data and GIS with the RUSLE model to estimate the spatial distribution of soil water erosion in whole Tunisia and provide spatial erosion map. The quantification of water soil erosion losses is an essential approach to spatialize the zones most sensitive to water erosion. Consequently, this approach can give, in practice, relevant results for the potential evaluation of soil losses at the regional scale and make an important contribution to regional soil erosion risk assessment through the derivation of appropriate factors, despite the few studies that have been carried out for the modeling of soil erosion at the scale of countries around the world.
Soil erosion by water is a natural phenomenon that may or may not be accelerated by various agents. The impact of soil erosion depends on several parameters. In this study, the rates of soil loss by water erosion were listed according to five different classes, including: very low, low, moderate, high and very high.
There is normally a tolerable amount of soil loss in the natural cycle of the earth's elements, so that soils can maintain their long-term productivity. Tolerable soil loss is the maximum annual amount of soil that can be removed without affecting the long-term natural productivity of soil covering the slope of an area. The limit value is set in this study at 10 t/ha/year.
The results indicated that 6.43% of the Tunisia’s surface, corresponding to 9989.66 km2, was affected by a very high soil loss rates (>30 t ha−1 y−1). 4.20% of the total area of the country, corresponding to 6535.02 km2, was affected by a high soil loss rates ranging from 20 to 30 (t ha−1 y−1). These results can be useful to identify the vulnerable areas of the country and to develop a less time-consuming decision plan more efficient for soil erosion prevention and control. This integrated approach, based on GIS and erosion model, can be useful to contribute to a better understanding of the soil degradation of large-scale areas in Tunisia, for better preserving and protecting both natural and man-made resources available in the country.
References
- Wang, B.; Zheng, F.; Römkens, M.J.M.; Darboux, F. Soil erodibility for water erosion: A perspective and Chinese experiences. Geomorphology 2013, 187, 1–10. [Google Scholar] [CrossRef]
- Keesstra, D.S.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- Hessel, R.; Wyseure, G.; Panagea, I.S.; Alaoui, A.; Reed, M.S.; van Delden, H.; Muro, M.; Mills, J.; Oenema, O.; Areal, F.; van den Elsen, E.; Verzandvoort, S.; Assinck, F.; Elsen, A.; Lipiec, J.; Koutroulis, A.; O’Sullivan, L.; Bolinder, M.A.; Fleskens, L.; Kandeler, E.; Montanarella, L.; Heinen, M.; Toth, Z.; Hallama, M.; Cuevas, J.; Baartman, J.E.M.; Piccoli, I.; Dalgaard, T.; Stolte, J.; Black, J.E.; Chivers, C.A. Soil-Improving Cropping Systems for Sustainable and Profitable Farming in Europe. Land 2022, 11, 780. [Google Scholar] [CrossRef]
- Gao, J. and Wang, H. Temporal analysis on quantitative attribution of karst soil erosion: a case study of a peak-cluster depression basin in Southwest China. Catena 2018, (172): 369–377.
- Karydas, C. G.; Panagos, P. Modelling monthly soil losses and sediment yields in Cyprus, International Journal of Digital Earth 2016, Vol. 9, No. 8, 766–787.
- Buryak, Z.A.; Narozhnyaya, A.G.; Gusarov, A.V.; Beylich, A.A. Solutions for the Spatial Organization of Cropland with Increased Erosion Risk at the Regional Level: A Case Study of Belgorod Oblast, European Russia. Land 2022, 11, 1492. [Google Scholar] [CrossRef]
- Sun, L.; Wan, S.; Luo, W. Biochars Prepared from Anaerobic Digestion Residue, Palm Bark, and Eucalyptus for Adsorption of Cationic Methylene Blue Dye: Characterization, Equilibrium, and Kinetic Studies. Bioresour. Technol. 2013, 140, 406–413. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Wetland and Its Degradation in the Yellow River Source Zone. In Landscape and Ecosystem Diversity, Dynamics and Management in the Yellow River Source Zone; Springer: Berlin, Germany, 2016; pp. 209–232. [Google Scholar]
- Kefi, M. ; Yoshino, K; Setiawan, Y. Assessment and mapping of soil erosion risk by water in Tunisia using time series MODIS data. Paddy Water Environ 2012, 10:59–73.
- Sidi Almouctar, M.A.; Wu, Y.; Zhao, F.; Dossou, J.F. Soil Erosion Assessment Using the RUSLE Model and Geospatial Techniques (Remote Sensing and GIS) in South-Central Niger (Maradi Region). Water 2021, 13, 3511. [Google Scholar] [CrossRef]
- Ganasri, B.P.; Ramesh, H. Assessment of Soil Erosion by RUSLE Model Using Remote Sensing and GIS - A Case Study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- El Jazouli, A.; Barakat, A.; Khellouk, R.; Rais, J.; El Baghdadi, M. Remote Sensing and GIS Techniques for Prediction of Land Use Land Cover Change Effects on Soil Erosion in the High Basin of the Oum Er Rbia River (Morocco). Remote. Sens. Appl. Soc. Environ. 2019, 13, 361–374. [Google Scholar] [CrossRef]
- Spalevic, V.; Barovi´c, G.; Vujaˇci´c, D.; Curovi´c, M.; Behzadfar, M.; Djurovi´c, N.; Dudi´c, B.; Billi, P. The Impact of Land Use Changes on Soil Erosion in the River Basin of Miocki Potok, Montenegro. Water 2020, 12, 2973. [Google Scholar] [CrossRef]
- Kastridis, A.; Kamperidou, V. Influence of Land Use Changes on Alleviation of Volvi Lake Wetland (North Greece). Soil Water Res. 2016, 10, 121–129. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall-Erosion Losses—A Guide to Conservation Planning. Agriculture Handbook No. 537; U.S. Department of Agriculture: Washington, DC, USA, 1978; p. 58. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). Agricultural handbook No. 703; U.S. Department of Agriculture: Washington, DC, USA, 1997; p. 407. [Google Scholar]
- Kirkby, M.J.; Irvine, B.J.; Jones, R.J.A.; Govers, G.; Boer, M.; Cerdan, O.; Daroussin, J.; Gobin, A.; Grimm, M.; Le Bissonnais, Y.; et al. The PESERA coarse scale erosion model for Europe. I.Model rationale and implementation. Eur. J. Soil Sci. 2008, 59, 1293–1306. [Google Scholar] [CrossRef]
- Karydas, C.G.; Panagos, P. The G2 erosion model: An algorithm for month-time step assessments. Environ Res. 2018, 161:256-267.
- Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European Soil Ersoion Model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Processes Landf. 1998, 23, 527–544. [Google Scholar] [CrossRef]
- Gavrilovic, Z.; Stefanovic, M.; Milovanovic, I.; Cotric, J.; Milojevic, M. Torrent classification-Base of rational management of erosive regions. IOP Conf. Ser. Earth Environ. Sci. 2008, 4, 012039. [Google Scholar] [CrossRef]
- Dragiˇcevi´c, N.; Karleuša, B.; Ožani´c, N. A. Review of the Gavrilovi´c method (erosion potential method) application. Gradevinar. 2016, 68, 715–725. [Google Scholar]
- Batista, P.V.G.; Davies, J.; Silva, M.L.N.; Quinton, J.N. On the evaluation of soil erosion models: Are we doing enough? Earth-Sci. Rev. 2019, 197, 102898. [Google Scholar] [CrossRef]
- Igwe, P.U.; Onuigbo, A.A.; Chinedu, O.C.; Ezeaku, I.I.; Muoneke, M.M. Soil Erosion: A Review of Models and Applications. Int. J. Adv. Eng. Res. Sci. 2017, 4, 237341. [Google Scholar]
- Karydas, C. G.; Panagos, P.; Gitas, I. Z. A Classification of Water Erosion Models According to Their Geospatial Characteristics. International Journal of Digital Earth 2014, Vol. 7, No. 3, 229–250. [Google Scholar] [CrossRef]
- Kefi, M.; Yoshino, K.; City, T. Evaluation of the Economic Effects of Soil Erosion Risk on Agricultural Productivity Using Remote Sensing: Case of Watershed in Tunisia. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2010, 38, 930. [Google Scholar]
- Wischmeier, W.H. , Smith D.D. Predicting Rainfall-Erosion Losses from Cropland East of the Rocky Mountains: Guide for Selection of Practices for Soil and Water Conservation. Washington, D.C., USDA, Agricultural Research Service. 1965.
- Bera, A. Assessment of soil loss by universal soil loss equation (USLE) model using GIS techniques: a case study of Gumti River Basin, Tripura, India. Model Earth Syst Environ. 2017, 3:29.
- Elaloui, A.; Marrakchi, C.; Fekri, A. et al. USLE-based assessment of soil erosion by water in the watershed upstream Tessaoute (Central High Atlas, Morocco). Model Earth Syst Environ. 2017, 3:873–885.
- Pham, T.G.; Degener, J.; Kappas, M. Integrated universal soil loss equation (USLE) and geographical information system (GIS) for soil erosion estimation in A Sap basin: Central Vietnam. Int Soil Water Conserv Res. 2018, 6:99–110.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K. Predicting soil erosion by water. A guide to conservation planning with the revised universal soil loss equation (RUSLE). Agric. Handbook 703. US Govt Print Office, Washington, DC. 1993.
- Maqsoom, A.; Aslam, B.; Hassan, U.; Kazmi, Z.A.; Sodangi, M.; Tufail, R.F.; Farooq, D. Geospatial Assessment of Soil Erosion Intensity and Sediment Yield Using the Revised Universal Soil Loss Equation (RUSLE) Model. ISPRS Int. J. Geo-Inf. 2020, 9, 356. [Google Scholar] [CrossRef]
- Xue, J.; Lyu, D.; Wang, D.; Wang, Y.; Yin, D.; Zhao, Z.; Mu, Z. Assessment of Soil Erosion Dynamics Using the GIS-Based RUSLE Model: A Case Study of Wangjiagou Watershed from the Three Gorges Reservoir Region, Southwestern China. Water 2018, 10, 1817. [Google Scholar] [CrossRef]
- Tang, Q. , Xu, Y., Bennett, S.J., Li, Y. Assessment of soil erosion using RUSLE and GIS: a case study of the Yangou watershed in the Loess Plateau, China. Environmen. Earth Sci. 2015, 73 (4), 1715–1724.
- Ganasri, B.P.; Ramesh, H. Assessment of soil erosion by RUSLE model using remote sensing and GIS-A case study of Nethravathi Basin. Geosci. Front 2016, 7(6), 953–961. [Google Scholar] [CrossRef]
- Ghosal, K.; Bhattacharya, S.D. A review of RUSLE Model. J. Indian Soc. Remote Sens. 2020. 1–19.
- Tzioutzios, C.; Kastridis, A. Multi-Criteria Evaluation (MCE) Method for the Management of Woodland Plantations in Floodplain Areas. Int. J. Geo-Inf. 2020, 9, 725. [Google Scholar] [CrossRef]
- Rawat, K.S.; Mishra, A.K.; Bhattacharyya, R. Soil Erosion Risk Assessment and Spatial Mapping Using LANDSAT-7 ETM+, RUSLE, and GIS—A Case Study. Arab. J. Geosci. 2016, 9, 288. [Google Scholar] [CrossRef]
- Van Remortel, R.D.; Maichle, R.W.; Hickey, R.J. Computing the LS factor for the Revised Universal Soil Loss Equation through array-based slope processing of digital elevation data using a C++ executable. Computers & Geosciences 2004, 30: 1043–1053.
- Efthimiou, N.; Lykoudi, E.; Psomiadis, E. Inherent Relationship of the USLE, RUSLE Topographic Factor Algorithms and Its Impact on Soil Erosion Modelling. Hydrol. Sci. J. 2020, 65, 1879–1893. [Google Scholar] [CrossRef]
- Biswas, S.S.; Pani, P. Estimation of Soil Erosion Using RUSLE and GIS Techniques: A Case Study of Barakar River Basin, Jharkhand, India. Modeling Earth Syst. Environ. 2015, 4, 42. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K. A new European slope length and steepness factor (LS-factor) for modeling soil erosion by water. Geosciences 2015, 5 (2), pp. 117-126.
- Yang, Q.; Guo, M.; Li, Z.; Wang, C. Extraction and analysis of China soil erosion topographic factor Soil Water Convers. China 2013, pp. 17-21.
- National Institute of Meteorology. Climatological Report for summer 2021 in Tunisia: Hottest summer on record since 1950. Climate Product Department-Deputy Direction of Climatology 2021, pp. 1-16. Available online: https://www.meteo.tn/ (accessed on 18 September 2022).
- Sadiki, A.; Bouhlassa, S.; Auajjar, J.; Faleh, A.; Macaire, J.J. Utilisation d’un SIG pour l’évaluation et la cartographie des risques d’érosion par l’Equation universelle des pertes en sol dans le Rif oriental (Maroc): cas du bassin versant de l’oued Boussouab. Bull l’Inst Sci Rabat Sect Sci Terre 2004, 26:69–79.
- Renard, K.G.; Freimund, J.R. Using Monthly Precipitation Data to Estimate the R Factor in the Revised USLE. Journal of Hydrology 1994, 157, 287–306. [Google Scholar] [CrossRef]
- Pangali Sharma, T.P.; Zhang, J.; Khanal, N.R.; Prodhan, F.A.; Nanzad, L.; Zhang, D.; Nepal, P. A Geomorphic Approach for Identifying Flash Flood Potential Areas in the East Rapti River Basin of Nepal. Int. J. Geo-Inf. 2021, 10, 247. [Google Scholar] [CrossRef]
- Thapa, P. Spatial Estimation of Soil Erosion Using RUSLE Modeling: A Case Study of Dolakha District, Nepal. Env. Syst. Res. 2020, 9, 15. [Google Scholar] [CrossRef]
- El Hage Hassan, H. Les apports d'un SIG dans la connaissance des évolutions de l'occupation du sol et de la limitation du risque érosif dans la plaine de la Bekaa (Liban): exemple d'un secteur du Bekaa el Gharbi. 2011. Doctoral thesis. Orleans.
- Bolline, A.; Rousseau, P. Erodibilité des sols de moyenne en haute Belgique. Utilisation d’une méthode de calcul du facteur K de l’équation universelle de perte en terre. Bull. Soc. Géogr. de Liège 1978, 14, 4. pp. 127–140. [Google Scholar]
- Williams, J.R. Chapter 25: The EPIC model. In V.P. Singh (ed.) Computer models of watershed hydrology. Water Resources Publications 1995, p. 909-1000.
- Moore, I.D.; Wilson, J.P. Length-slope factors for the Revised Universal Soil Loss Equation: Simplified method of estimation. Journal of soil and water conservation 1992, Sep 1;47(5):423-428.
- Moore, I.D.; Burch, G. J. Physical Basis of the Length Slope Factor in the Universal Soil Loss Equation. Soil Science Society America Journal 1986, 50: 1294–1298.
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil attribute prediction using terrain analysis. Soil science society of america journal 1993, Mar;57(2):443-52.
- Jain, M.K.; Kothyari, U.C. Estimation of soil erosion and sediment yield using GIS. Hydrological Sciences Journal. 2000, Oct 1;45(5):771-86.
- Van der Knijff, J. M.; Jones, R.J.A.; Montanarella, L. Soil erosion risk: assessment in Europe. 2000.
- Garouani, A.; Chen, H.; Lewis, L.; Triback, A.; Abahrour, M. Cartographie de l'utilisation du sol et de l'érosion à partir d'images satellitaires et du SIG IDRISI au Nord Est du Maroc, Télédétection 2008, vol 8, n°3, p 193-201.
- Negese, A.; Fekadu, E.; Getnet, H. Potential Soil Loss Estimation and Erosion-Prone Area Prioritization Using RUSLE, GIS, and Remote Sensing in Chereti Watershed, Northeastern Ethiopia. Air, Soil and Water Research 2021,14.
- Karydas, C.G.; Sekuloska, T.; Silleos, G.N. Quantification and site-specification of the support practice factor when mapping soil erosion risk associated with olive plantations in the Mediterranean island of Crete. Environmental Monitoring and Assessment 2009, Feb;149:19-28.
- Lazzari, M.; Gioia, D.; Piccarreta, M.; Danese, M.; Lanorte, A. Sediment yield and erosion rate estimation in the mountain catchments of the Camastra artificial reservoir (Southern Italy): a comparison between different empirical methods. Catena 2015, p323–339. [Google Scholar] [CrossRef]
- Vatandaşlar, C.; Yavuz, M. Modeling cover management factor of RUSLE using very high-resolution satellite imagery in a semiarid watershed. Environmental Earth Sciences 2017, Jan;76:1-21.
- Borrelli, P.; Marker, M.; Panagos, P.; Schutt, B. Modeling Soil Erosion and River Sediment Yield for an Intermountain Drainage Basin of the Central Apennines, Italy. Catena 2014, 114: 45–58.
- Sekiyama, A.; Mihara, M. Determining C factor of universal soil loss equation (USLE) based on remote sensing. International Journal of Environmental and Rural Development. 2016, p72. [Google Scholar]
- Shawul, A.A.; Chakma, S. Spatiotemporal detection of land use/land cover change in the large basin using integrated approaches of remote sensing and GIS in the Upper Awash basin, Ethiopia. Environmental Earth Sciences 2019, vol. 78, no. 5.
- Sewnet, A. Land use/cover change at Infraz watershed by using GIS and remote sensing techniques, northwestern Ethiopia. International Journal of River Basin Management 2015, vol. 14, no. 2, pp. 133–142.
- Chakilu, G.G.; Moges, M.A. Assessing the land use/cover dynamics and its impact on the low flow of Gumara watershed, upper Blue Nile basin, Ethiopia. Hydrology: Current Research 2017, vol. 8, no. 1.
- Guo, Q.K.; Liu, B.Y.; Yun, X.I.E.; Liu, Y.N.; Yin, S.Q. Estimation of USLE crop and management factor values for crop rotation systems in China. Journal of Integrative Agriculture 2015, 14(9), 1877–1888. [Google Scholar] [CrossRef]
- Hurni, H. Erosion-productivity-conservation systems in Ethiopia.1985, 654-674.
- Tiruneh, G.; Ayalew, M. Soil loss estimation using geographic information system in enfraz watershed for soil conservation planning in highlands of Ethiopia. International Journal of Agricultural Research, Innovation and Technology (IJARIT). 2015, 5(2355-2020-1587):21-30.
- Ewunetu, A.; Simane, B.; Teferi, E.; Zaitchik, B.F. Land cover change in the blue nile river headwaters: farmers’ perceptions, pressures, and satellite-based mapping. Land 2021, 10(1), 68. [Google Scholar] [CrossRef]
- Erdogan, H.E.; Erpul, G.; Bayramin, I. Use of USLE/GIS methodology for predicting soil loss in a semiarid agricultural watershed. Turkey: Department of Soil Science, University of Ankara 2006.
- Swarnkar, S.; Malini, A.; Tripathi, S.; Sinha, R. Assessment of uncertainties in soil erosion and sediment yield estimates at ungauged basins: an application to the Garra River basin, India. Hydrology and Earth System Sciences 2018, Apr 24;22(4):2471-85.
- Lufafa, A.; Tenywa, M.M.; Isabirye, M.; Majaliwa, M.J.G.; Woomer, P.L. Prediction of soil erosion in a Lake Victoria basin catchment using a GIS-based Universal Soil Loss model. Agricultural systems 2003, 76(3), 883–894. [Google Scholar] [CrossRef]
- The ASTER Global Digital Elevation Model V003. Available online: https://search.earthdata.nasa.gov/downloads (accessed on 12 February 2022).
- FAO. Digital Soil Map of the World (DSMW)|Land & Water|Food and Agriculture Organization of the United Nations Land & Water|Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/land-water/land/landgovernance/land-resources-planning-toolbox/category/details/en/c/1026564/ (accessed on 2 April 2022).
Figure 1.
Location map of the study area.
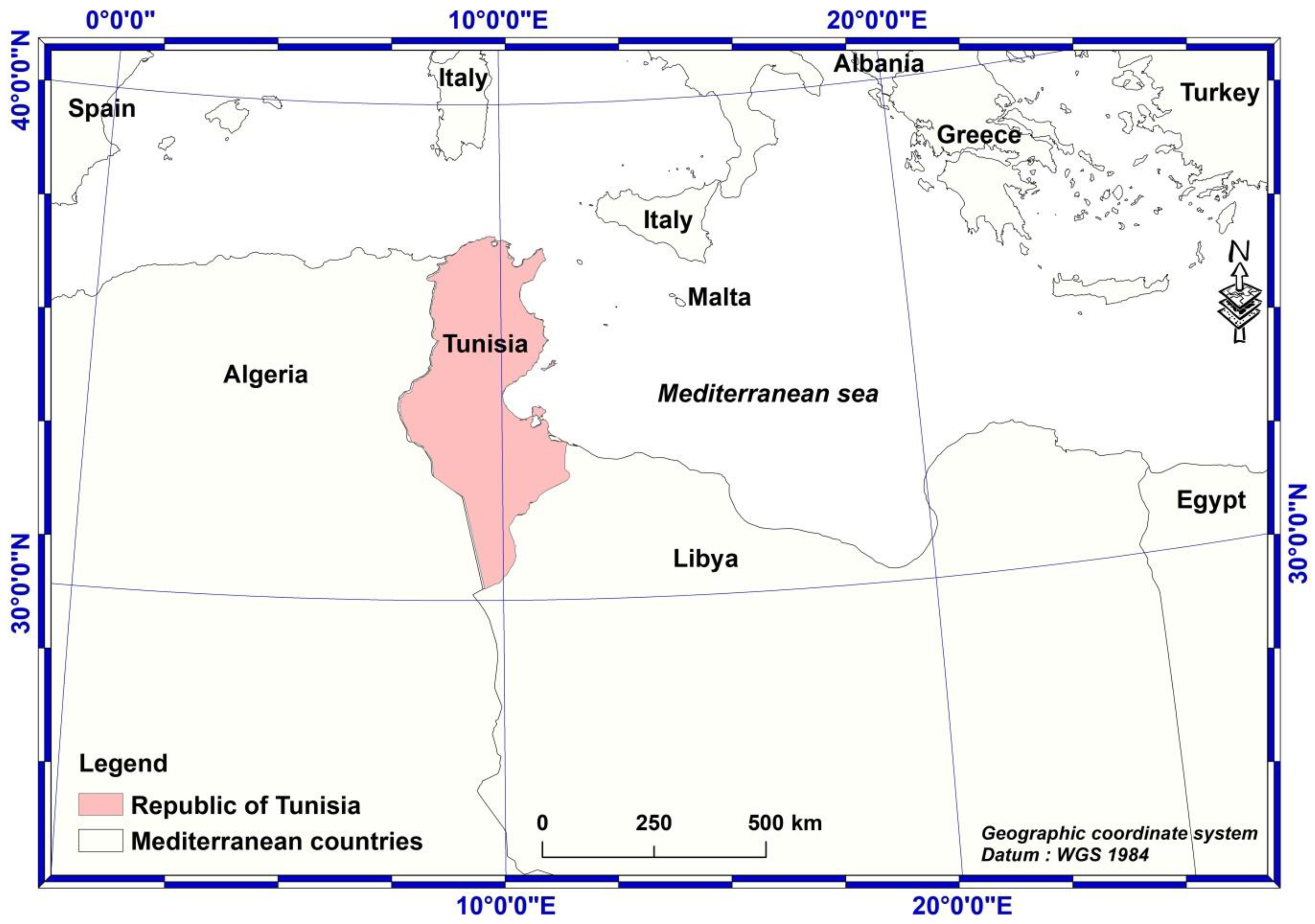
Figure 2.
Distribution of altitudes in Tunisia generated from ASTER DEM data.
Figure 3.
Bioclimatic map of Tunisia.
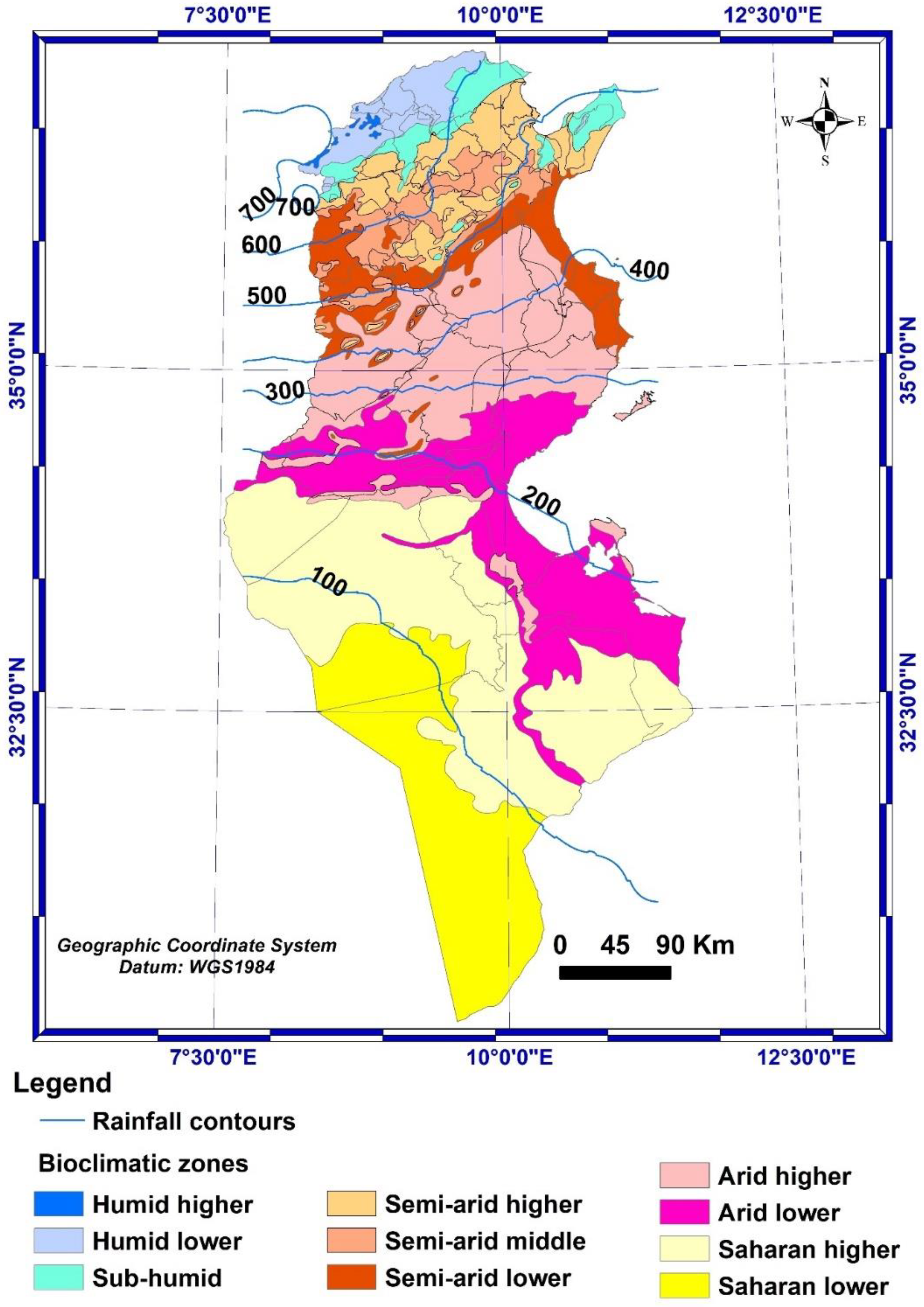
Figure 4.
Flow chart for the analysis of soil loss based on the RUSLE model and GIS technique.
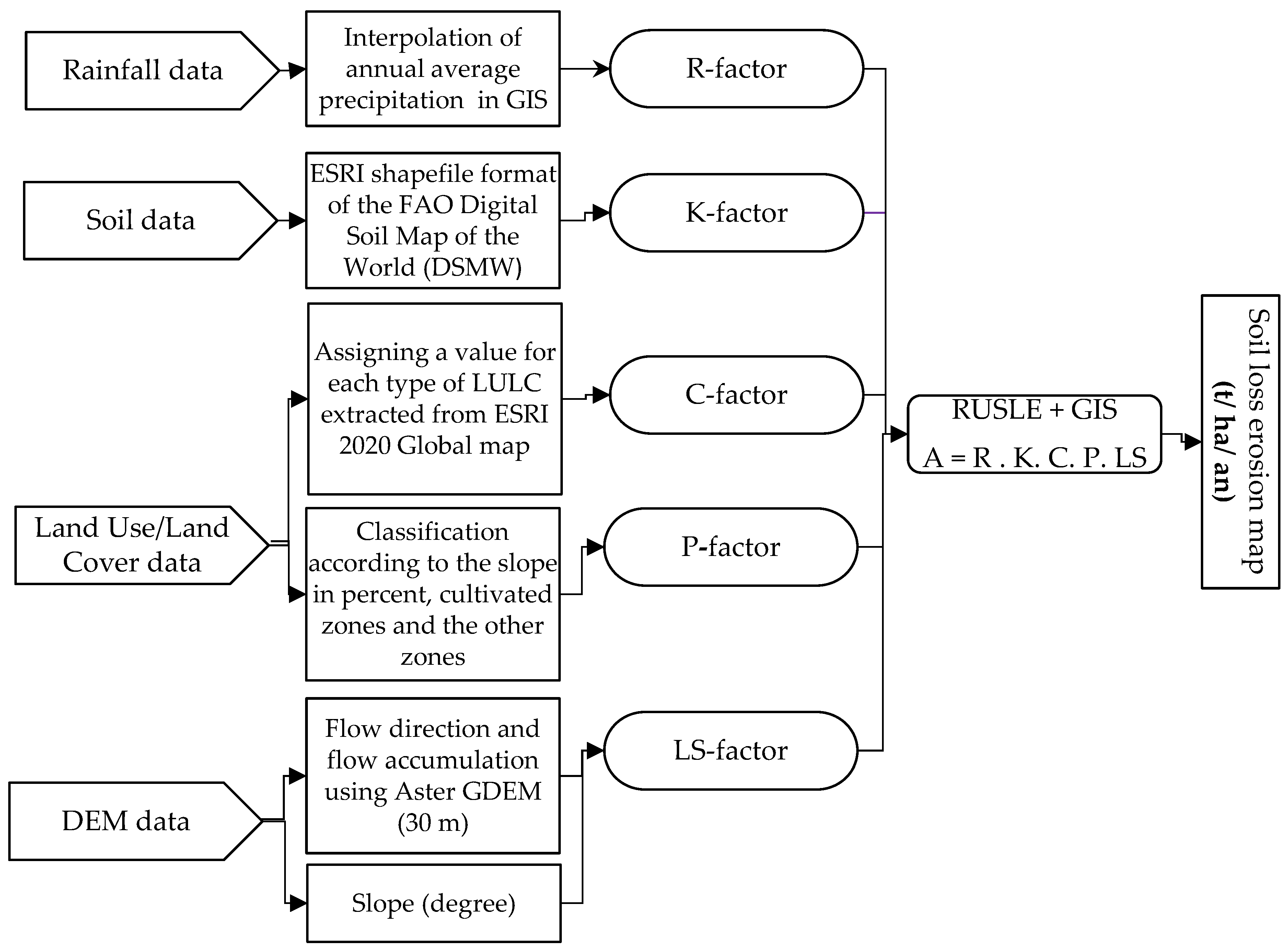
Figure 5.
Map of mean annual rainfall of Tunisia.
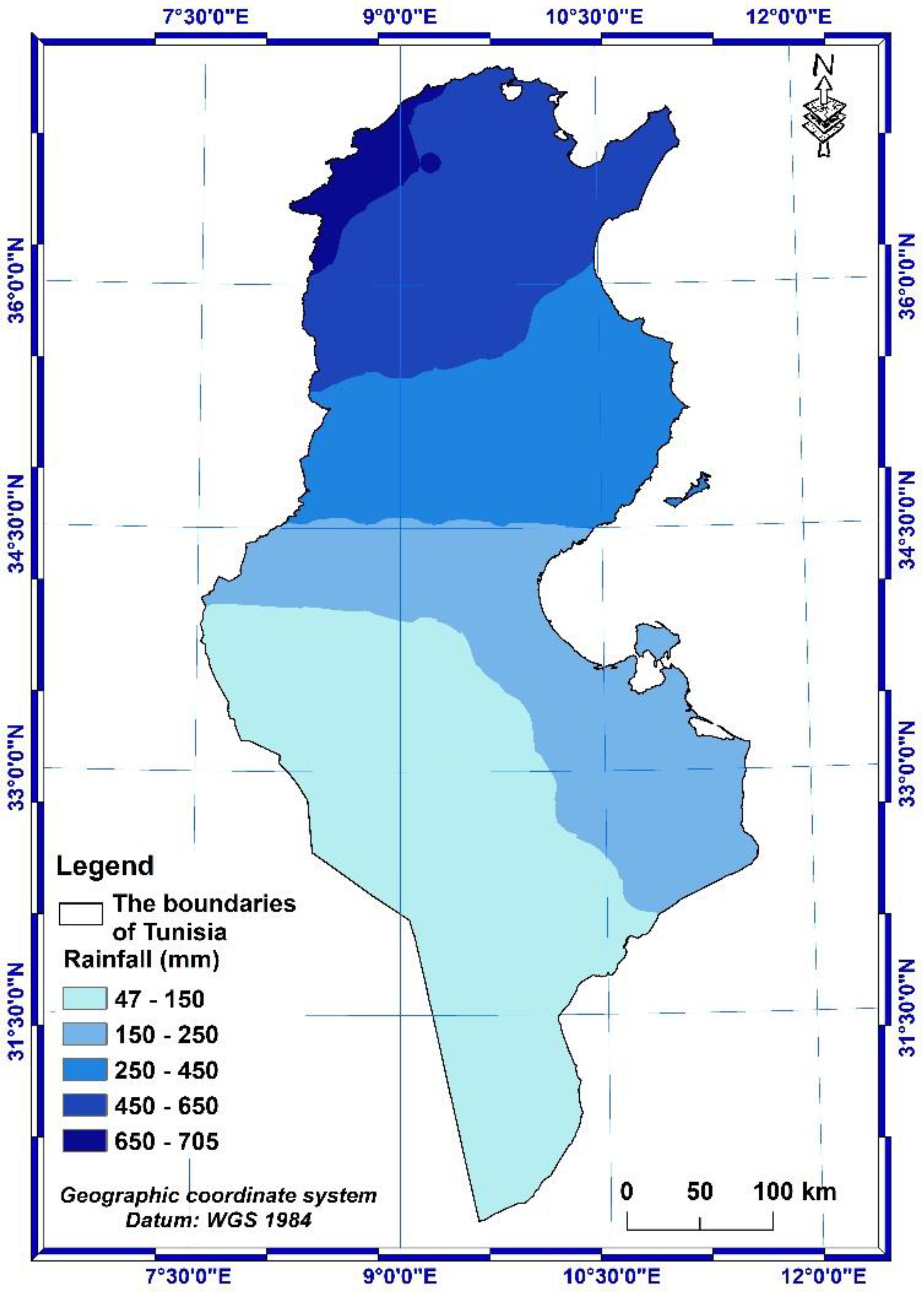
Figure 6.
R-factor spatial distribution of Tunisia.
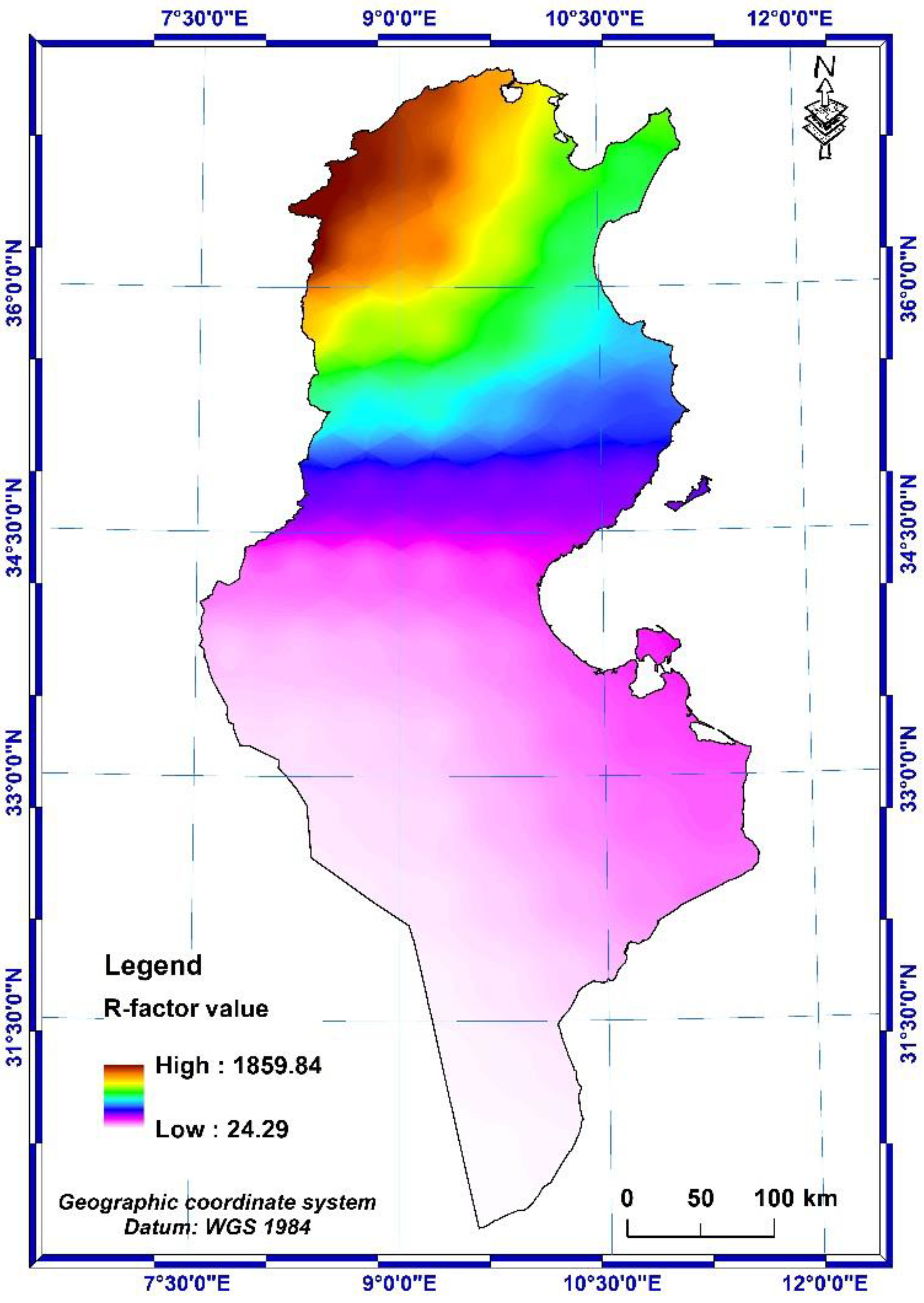
Figure 7.
Soil map of Tunisia.
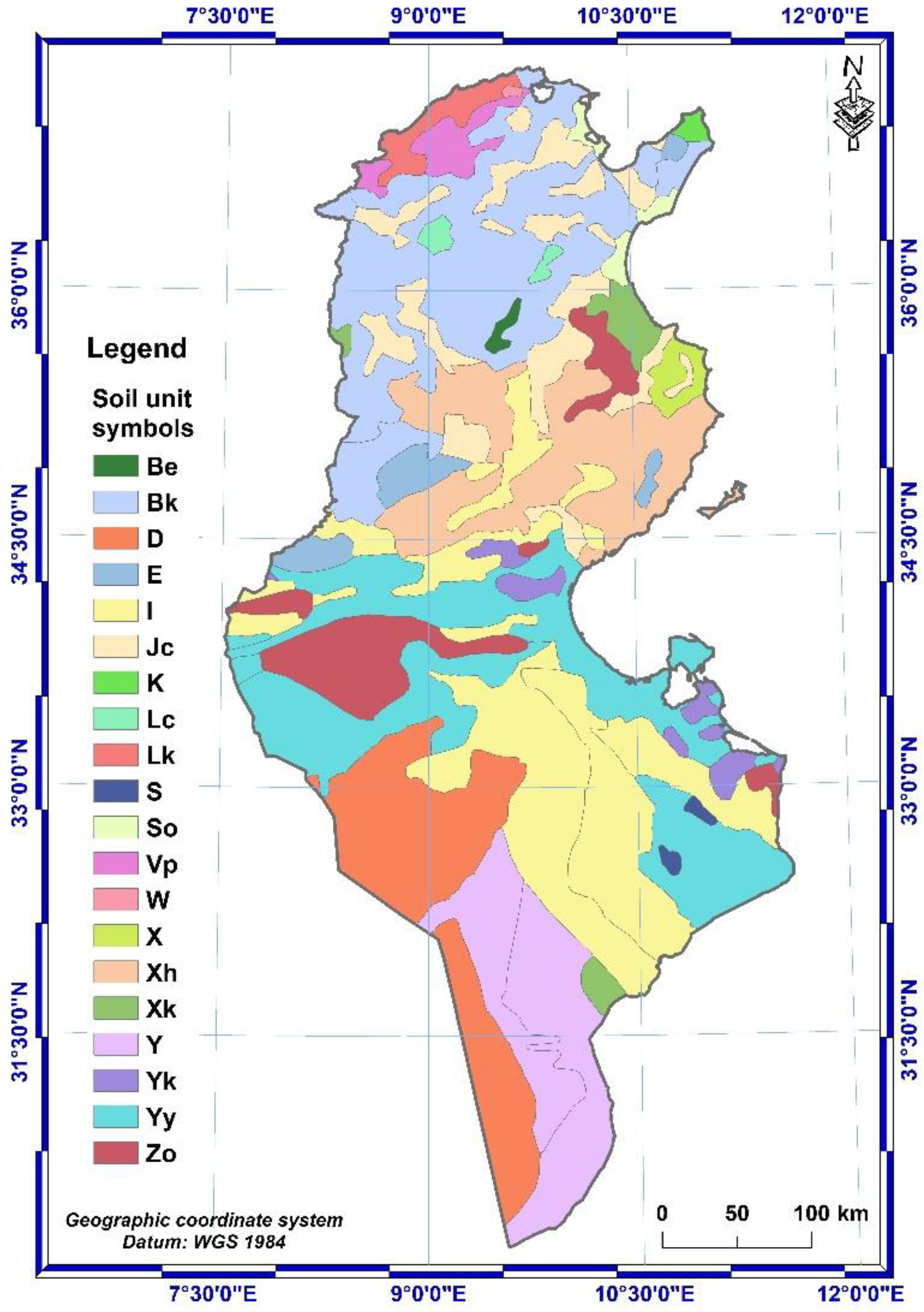
Figure 8.
K-factor spatial distribution. (Extracted from the FAO-UNESCO Soil Map of the World).
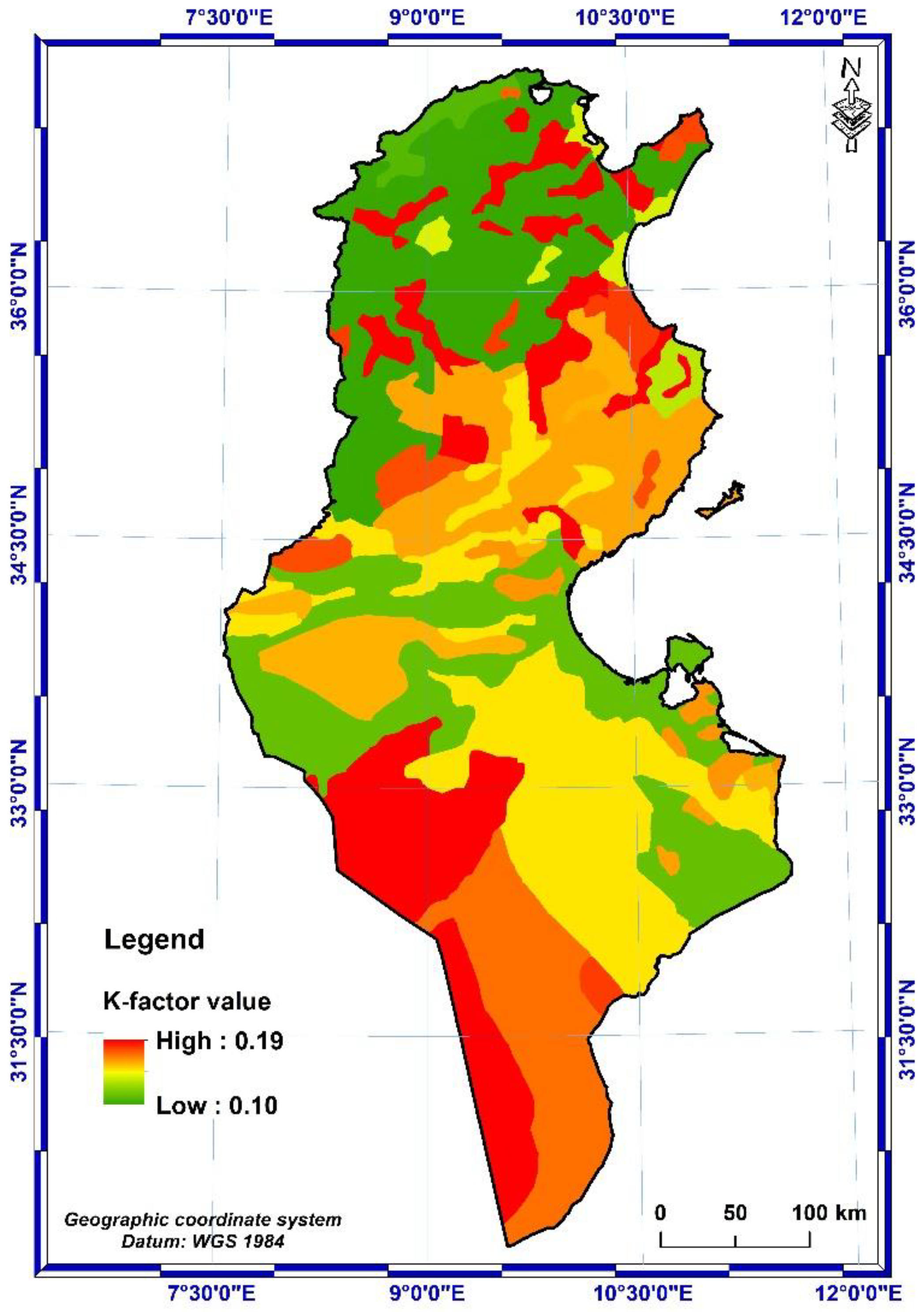
Figure 9.
Slope map of Tunisia.
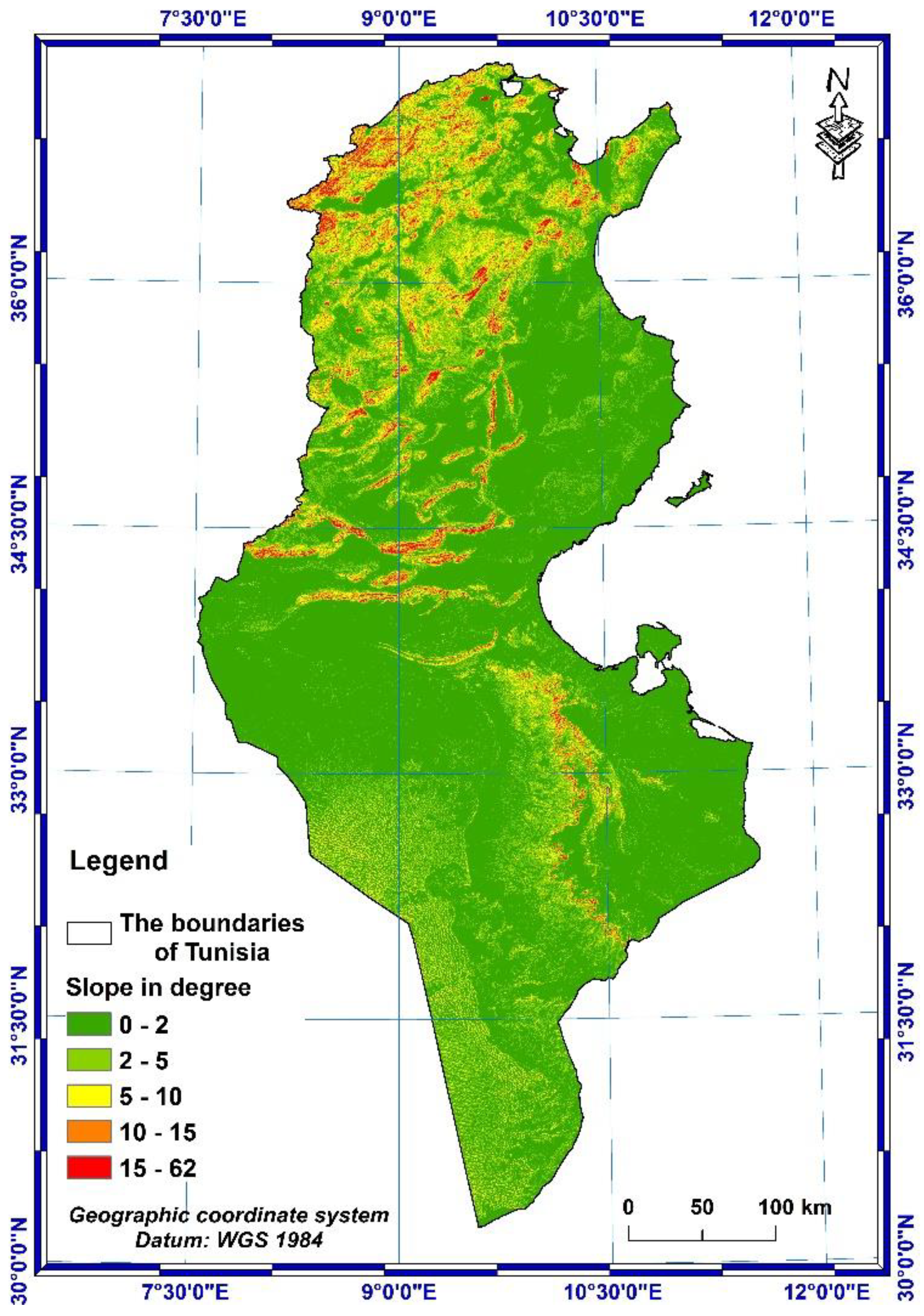
Figure 10.
LS-factor spatial distribution.
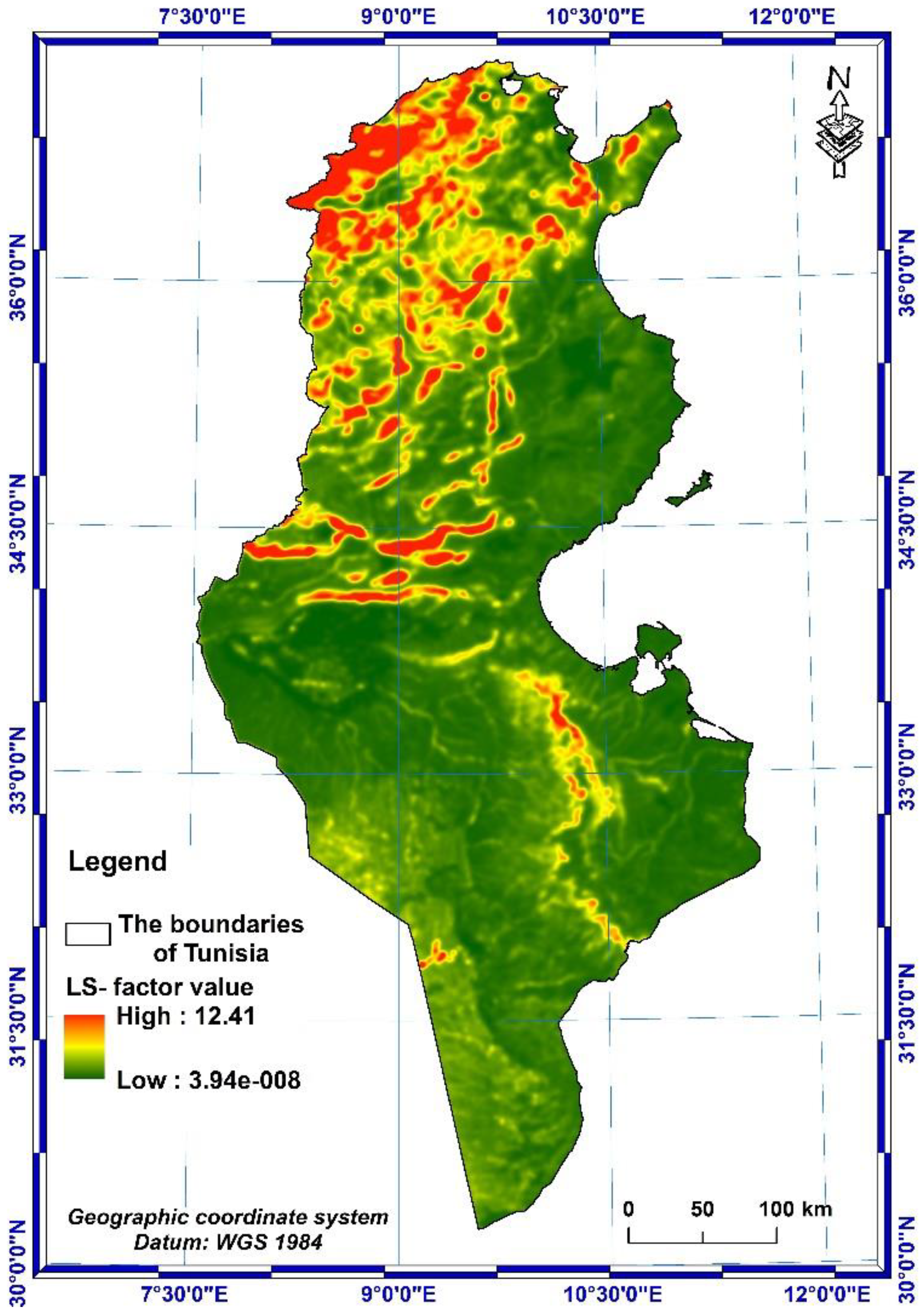
Figure 11.
Land Use-Land Cover map of Tunisia.
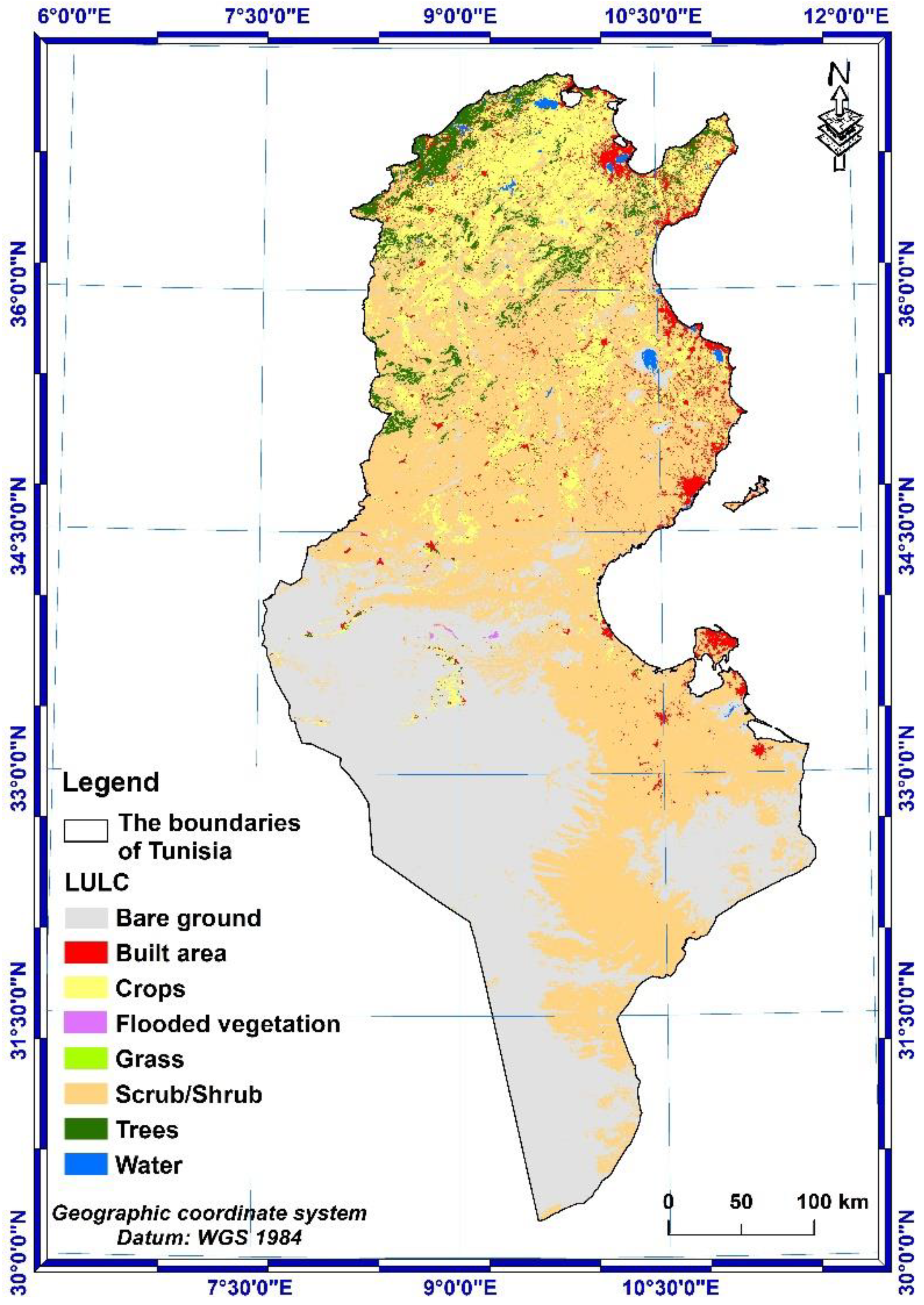
Figure 12.
C-factor spatial distribution.
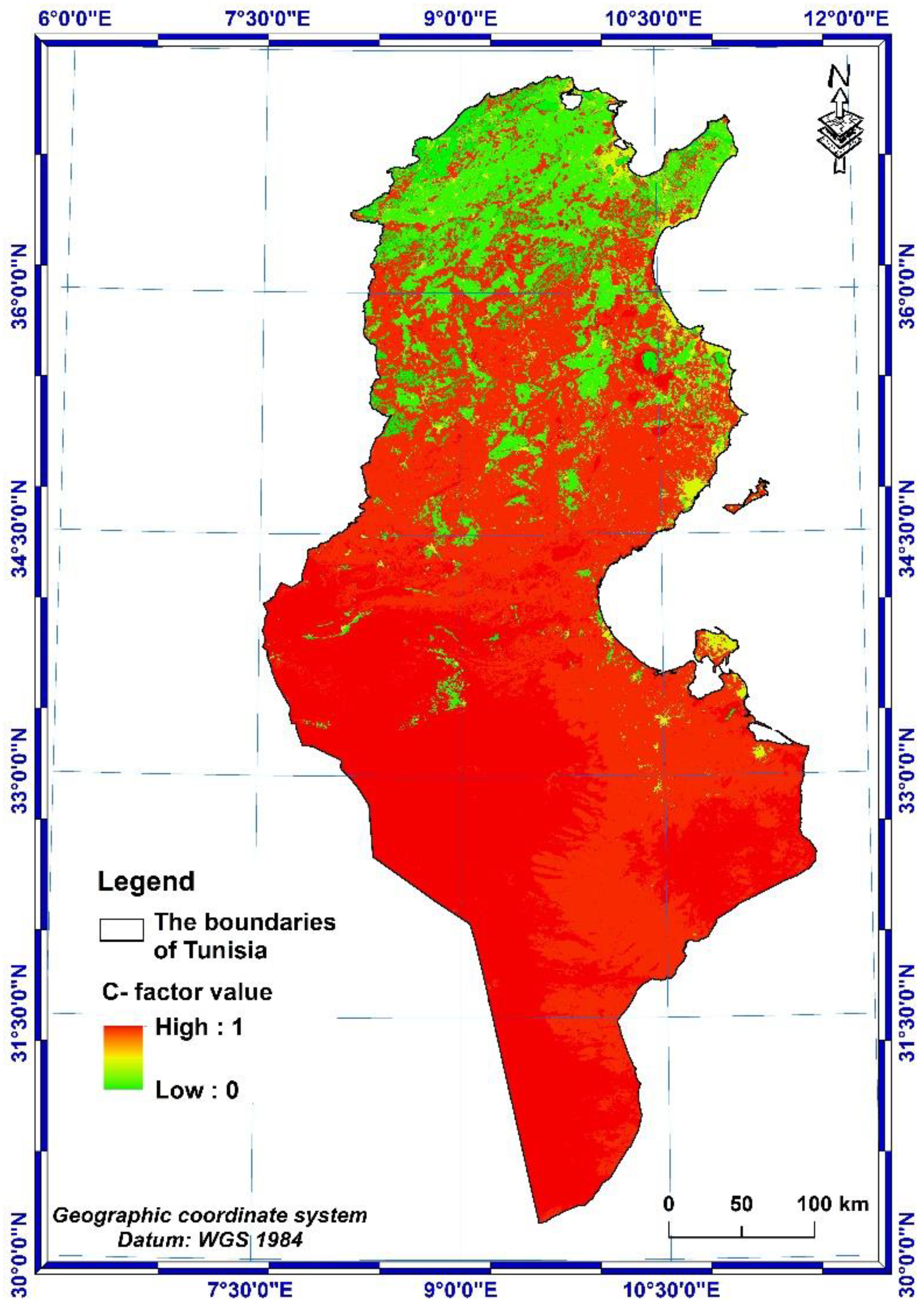
Figure 13.
Agricultural and non-agricultural lands of Tunisia.
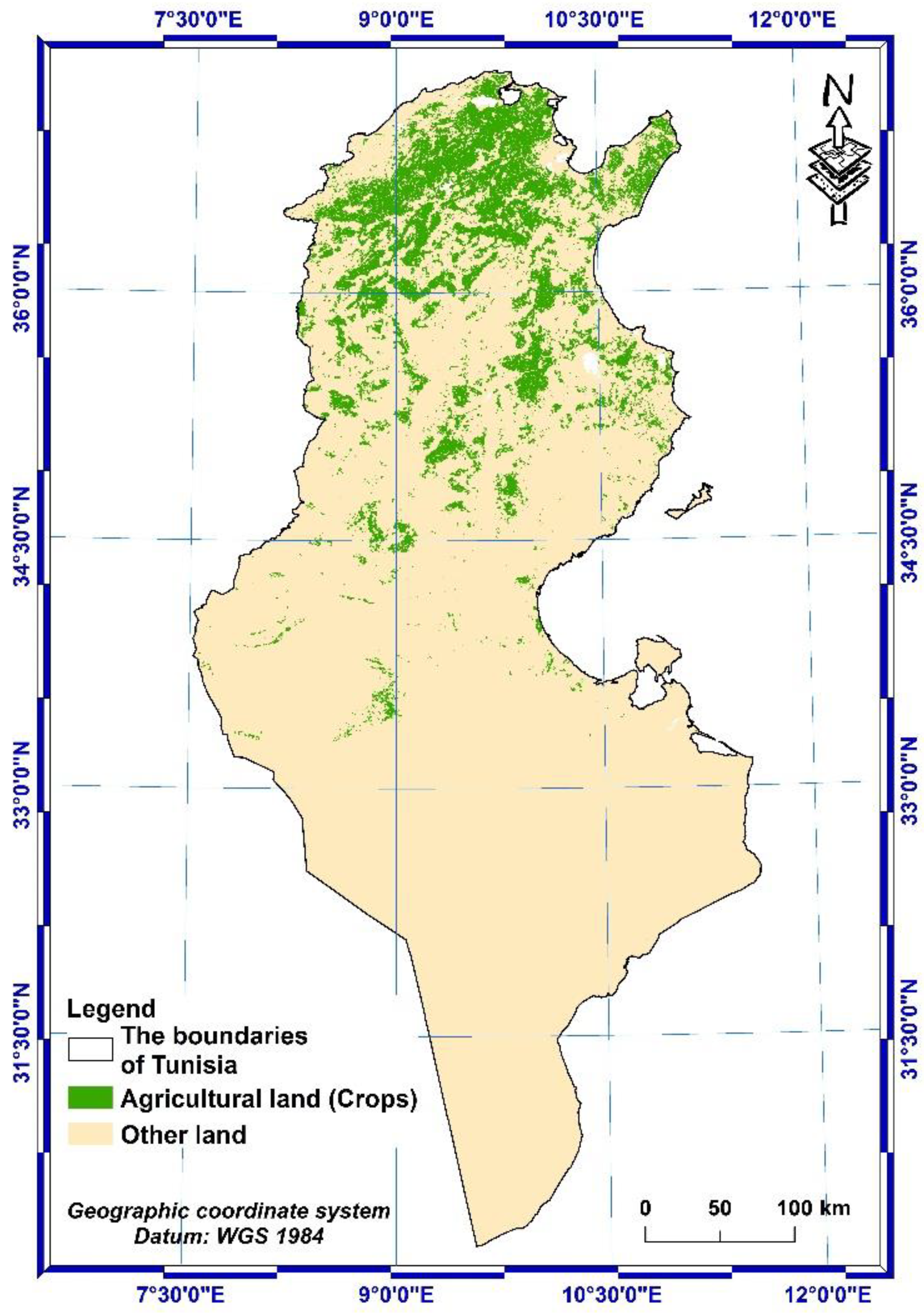
Figure 14.
P-factor spatial distribution.
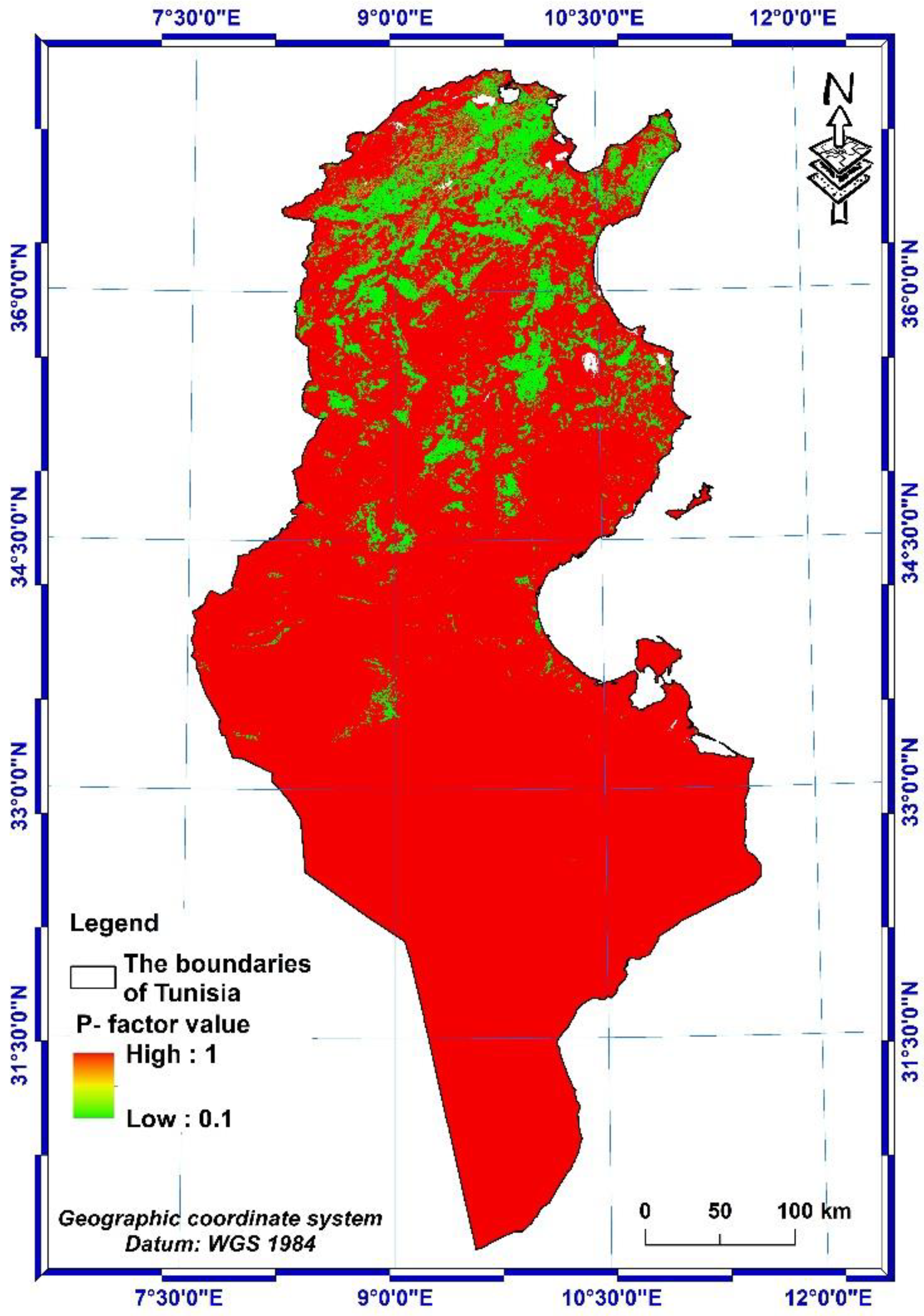
Figure 15.
Soil loss map of Tunisia.
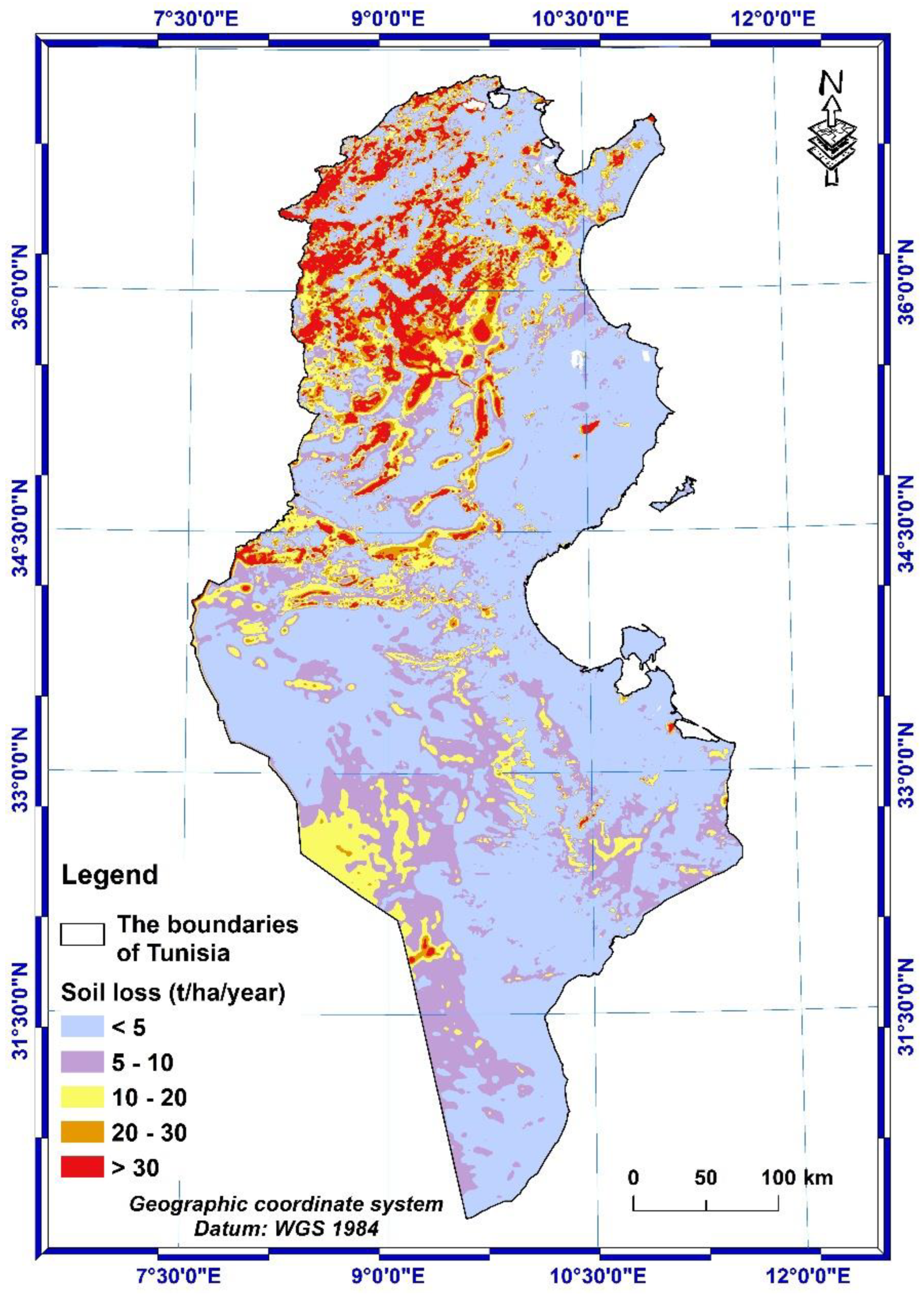
Table 1.
Description of the data sources.
| N° | Type of Data | Data description | Name of the service that provide the data | Link |
|---|---|---|---|---|
| 1 | Rainfall data | Monthly and annual precipitation data derived from NASA's Global Precipitation Measurement (GPM)-CSV file format | National Aeronautics and Space Administration (NASA) Prediction of Worldwide Energy Resources (POWER project) | https://power.larc.nasa.gov/data-access-viewer/ |
| 2 | Soil data | FAO Digital Soil Map of the World (DSMW)-ESRI shapefile format | Food and Agriculture Organization of the United Nations | https://data.apps.fao.org/map/catalog/srv/eng/catalog.search#/home |
| 3 | DEM data | Terra Advanced Spaceborne Thermal Emission and Reflection Radiometer-Global Digital Elevation Model (ASTER-GDEM)-Version 3-Grid format at 30m resolution | NASA’s Earth Observing System Data and Information System (EOSDIS) | https://search.earthdata.nasa.gov/download/ |
| 4 | LULC data | ESRI 2020 Global Land Use Land Cover from Sentinel-2 (TIF file format) | The map is derived from ESA Sentinel-2 imagery at 10 m resolution. | https://livingatlas.arcgis.com/landcover/ |
Table 3.
C-factor value of different soil types.
| LULC type | C-factor | Source |
|---|---|---|
| Cropland | 0.24 | Guo et al., 2015 [66] |
| Forest (Dense) | 0.01 | Hurni, 1985 [67] |
| Grassland | 0.05 | Tiruneh and Ayalew, 2015 [68] |
| Shrubland | 0.2 | Tiruneh and Ayalew, 2015 [68] |
| Bare land | 0.6 | Ewunetu et al., 2021 [69] |
| Waterbody | 0 | Erdogan et al., 2006 [70]; Swarnkar el al., 2018 [71] |
| Settlement | 0.15 | Hurni, 1985 [67] |
Table 4.
P-factor reference values adopted from Wischmeier and Smith (1978) [15].
Table 4.
P-factor reference values adopted from Wischmeier and Smith (1978) [15].
| Slope (%) | P- Factor | |
|---|---|---|
| Agricultural land | 0 – 5 | 0.1 |
| 5 – 10 | 0.12 | |
| 10 – 20 | 0.14 | |
| 20 – 30 | 0.19 | |
| 30 – 50 | 0.25 | |
| 50 – 100 | 0.33 | |
| Other land | All | 1 |
Table 5.
Soil loss distribution.
| Score scale | Soil loss class (t/ha/year) | Area (km2) | Area percentage (%) | Indicator |
|---|---|---|---|---|
| 1 | < 5 | 87559,33 | 56,34 | Very low |
| 2 | 5 - 10 | 32854,00 | 21,14 | Low |
| 3 | 10 - 20 | 18471,60 | 11,89 | Moderate |
| 4 | 20 - 30 | 6535,03 | 4,21 | High |
| 5 | > 30 | 9989,66 | 6,43 | Very high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







