Stark Broadening of Al IV Spectral Lines

Preprint

Article

Stark Broadening of Al IV Spectral Lines

Altmetrics

Downloads

148

Views

Comments

A peer-reviewed article of this preprint also exists.

Milan S. Dimitrijević^*,

Magdalena D. Christova

Milan S. Dimitrijević^*,

Magdalena D. Christova

This version is not peer-reviewed

Submitted:

04 February 2023

Posted:

07 February 2023

You are already at the latest version

Alerts

Abstract

Stark widths for 23 transitions in Al IV have been calculated employing modified semiempirical method. The results are obtained for an electron density of 10^17 cm−3 and temperatures from 10,000 K up to 160,000 K. The results obtained in this investigation are used for the examination of the influence of Stark broadening in Al IV stellar spectra, as well as to check Stark width regular behavior and similarites within Al IV spectrum.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

Data on spectral line profiles, broadened by interactions with surrounding charged particles (Stark broadening) are of interest in many research fields as astrophysics (e.g. [1]), laboratory plasma ([2,3,4,5]) inertial fusion experiments ([6,7]), laser design and development ([8]), laser produced plasma research ([9,10,11]) and plasmas in technology ([12,13]). Particular interest for such data exists in astrophysics,where they are needed e.g. for stellar abundances investigations, stellar atmospheres modelling, spectral lines analysis and synthesis, radiative transfer etc.

The most interesting celestial objects for Stark brodening data applications are white dwarfs, where this is the principal presure broadening mechanism. The importance of Stark broadening has been investigated recently in DO, DB (see e.g., [14]), DA dwarfs (see e.g., [15]) and also in B subdwarfs (see e.g., [16]) and A and late B type stars (see e.g., [15]).

Astrophysical significance of aluminium is due to its high cosmic abundance, since it is the twelfth most common element in the Universe, and its spectral lines are commonly present in stellar spectra. For example, Smiljanic et al. [17] investigated aluminium abundances in giants and dwarfs and their implications on stellar and galactic chemical evolution using two samples: i) more than 600 dwarfs of the solar neighborhood and of open clusters and ii) low- and intermediate-mass clump giants in six open clusters. Carretta et al. [18] determined aluminium abundances for 90 red giant branch (RGB) stars in NGC 2808, and Smith [19] derrived atmospheric abundance of aluminium for a sample of forty normal, superficially normal, and HgMn type main-sequence late-B stars

Recently, Elabidi [21] used quantum mechanical theory [22,23] to calculate 20 Al IV lines belonging to 2p⁶–3s, 3s–3p and 3p–3d transitions. All these lines are in UV but in astronomy are particularly convenient spectral lines in the visible. In the case of Al IV such lines are from 4s–4p and 4p–4d transitions which are in Jℓ coupling. Here we calculated, using the modified semiempirical method [20], Stark widths for 23 lines and multiplets which are all in the visible part of the spectrum, so very convenient for astronomical observations and plasma diagnostics. The obtained results enable also to examine the influence of Stark broadening on Al IV spectral lines in DB and DO white dwarfs and A type stars. Moreover, the similarities of Stark widths within multiplets and supermultiplets may be checked for the cas of Jℓ coupling.

2. Theory

The modified semiempirical method (MSE) has been developed for the theoretical determination of line widths and shifts of isolated spectral lines which are emitted or absorbed by non-hydrogenic ions perturbed by their interaction with surrounding electrons. It may be particularly useful if we have not enough atomic data for the adequate application of a more precise theoretical method. In this formalism, the full width at half intensity maximum (FHWM) is given as [20]:

W_{M S E} = N \frac{8 π}{3} \frac{ℏ^{2}}{m^{2}} {(\frac{2 m}{π k T})}^{1 / 2} \frac{π}{\sqrt{3}} \frac{λ^{2}}{2 π c} \times

\times {\sum_{ℓ_{i} \pm 1} \sum_{L_{i^{'}} J_{i^{'}}} {\vec{R}}^{2} [n_{i} ℓ_{i} L_{i} J_{i}, n_{i} (ℓ_{i} \pm 1) L_{i^{'}} J_{i^{'}}] \tilde{g} (x_{ℓ_{i}, ℓ_{i} \pm 1}) +

+ \sum_{ℓ_{f} \pm 1} \sum_{L_{f^{'}} J_{f^{'}}} {\vec{R}}^{2} [n_{f} ℓ_{f} L_{f} J_{f}, n_{f} (ℓ_{f} \pm 1) L_{f^{'}} J_{f^{'}}] \tilde{g} (x_{ℓ_{f}, ℓ_{f} \pm 1}) +

+ (\sum_{i^{'}} {\vec{R}}_{i i^{'}}^{2})_{Δ n \neq 0} g (x_{n_{i}, n_{i} + 1}) + (\sum_{f^{'}} {\vec{R}}_{f f^{'}}^{2})_{Δ n \neq 0} g (x_{n_{f}, n_{f} + 1})} .

(1)

Here, the index i is for the initial and index f for the final atomic energy level. The square of the matrix element

{{\vec{R}}^{2} [n_{k} ℓ_{k} L_{k} J_{k}, (ℓ_{k} \pm 1) L_{k^{'}} J_{k^{'}}], k = i, f}

may be expressed in the following maner:

{\vec{R}}^{2} [n_{k} ℓ_{k} L_{k} J_{k}, n_{k} (ℓ_{k} \pm 1) L_{k}^{'} J_{k}^{'}] =

\frac{ℓ_{>}}{2 J_{k} + 1} Q [ℓ_{k} L_{k}, (ℓ_{k} \pm 1) L_{k}^{'}] Q (J_{k}, J_{k}^{'}) {[R_{n_{k}^{*} ℓ_{k}}^{n_{k}^{*} (ℓ_{k} \pm 1)}]}^{2} .

(2)

Here,

ℓ_{>} = \max (ℓ_{k}, ℓ_{k} \pm 1)

and

{(\sum_{k^{'}} {\vec{R}}_{k k^{'}}^{2})}_{Δ n \neq 0} = {(\frac{3 n_{k}^{*}}{2 Z})}^{2} \frac{1}{9} ({n_{k}^{*}}^{2} + 3 ℓ_{k}^{2} + 3 ℓ_{k} + 11) .

(3)

In Equation (1)

x_{ℓ_{k}, ℓ_{k^{'}}} = \frac{E}{Δ E_{ℓ_{k}, ℓ_{k^{'}}}}, k = i, f

E = \frac{3}{2} k T

is the electron kinetic energy and

Δ E_{ℓ_{k}, ℓ_{k^{'}}} = | E_{ℓ_{k}} - E_{ℓ_{k^{'}}} |

is the energy difference between levels

ℓ_{k}

and

ℓ_{k} \pm

1 (

k = i, f

x_{n_{k}, n_{k} + 1} \approx \frac{E}{Δ E_{n_{k}, n_{k} + 1}},

where for

Δ n \neq 0

, the energy difference between energy levels with

n_{k}

and

n_{k}

+1,

Δ E_{n_{k}, n_{k} + 1}

is represented by the following equation:

Δ E_{n_{k}, n_{k} + 1} = 2 Z^{2} E_{H} / n_{k}^{* 3},

(4)

where

n_{k}^{*} = {[E_{H} Z^{2} / (E_{i o n} - E_{k})]}^{1 / 2}

is the effective principal quantum number, N electron density, T temperature, Z the residual ionic charge (e.g. Z=4 for Al IV),

E_{i o n}

the appropriate spectral series limit,

Q (ℓ L, ℓ^{'} L^{'})

, multiplet factor and

Q (J, J^{'})

line factor [24]. Gaunt factors which are needed for calculation are denoted as

g (x)

[25,26] and

\tilde{g} (x)

[20]. Radial integrals

[R_{n_{k}^{*} ℓ_{k}}^{n_{k}^{*} ℓ_{k} \pm 1}]

are calculated by using the Coulomb approximation [27] with the help of tables in [28].

In some cases, these tables are not applicable, because the values are out of them, in particular for higher principal quantum numbers, in such a case one can use the procedure described in Ref. [29].

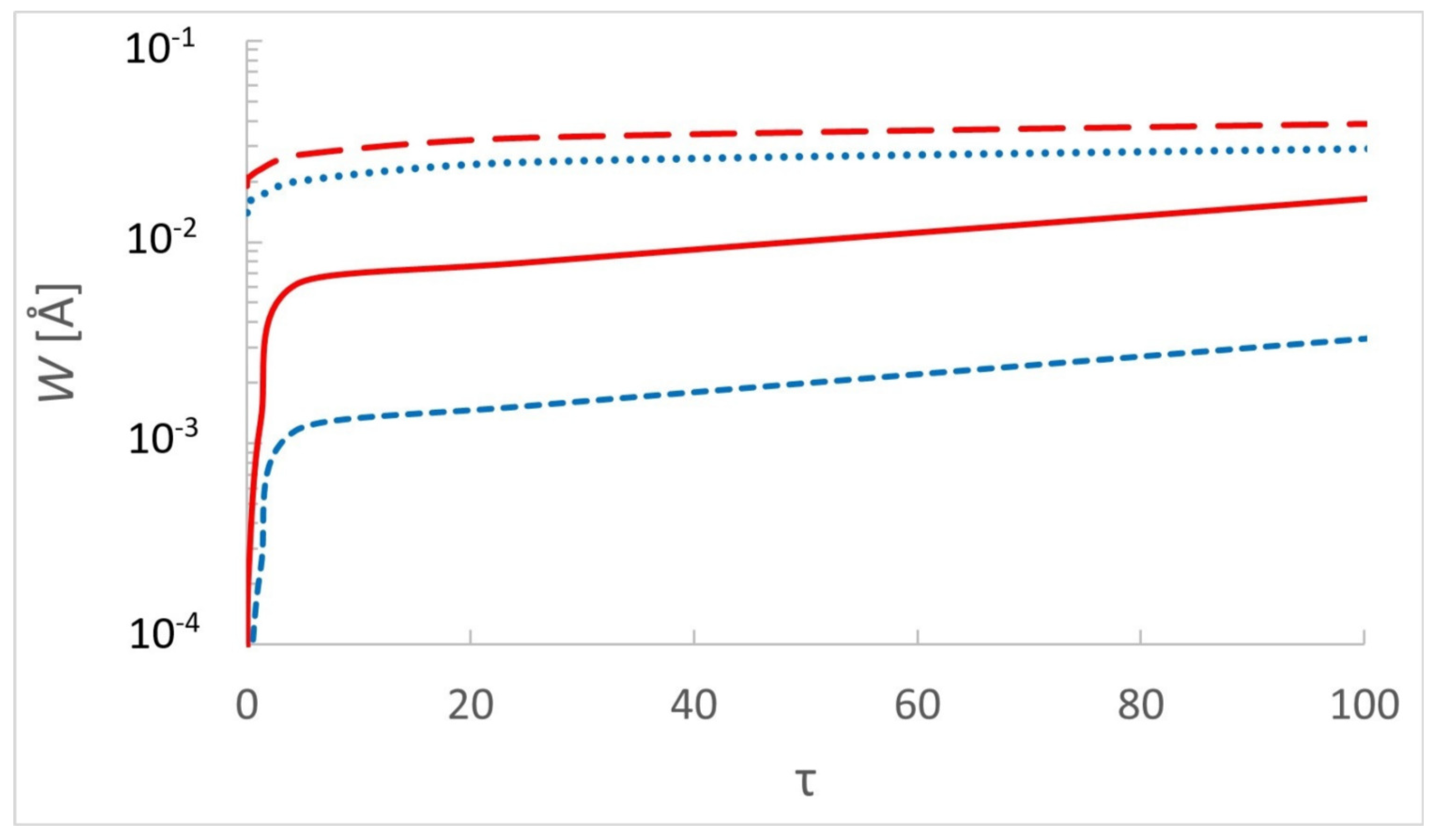
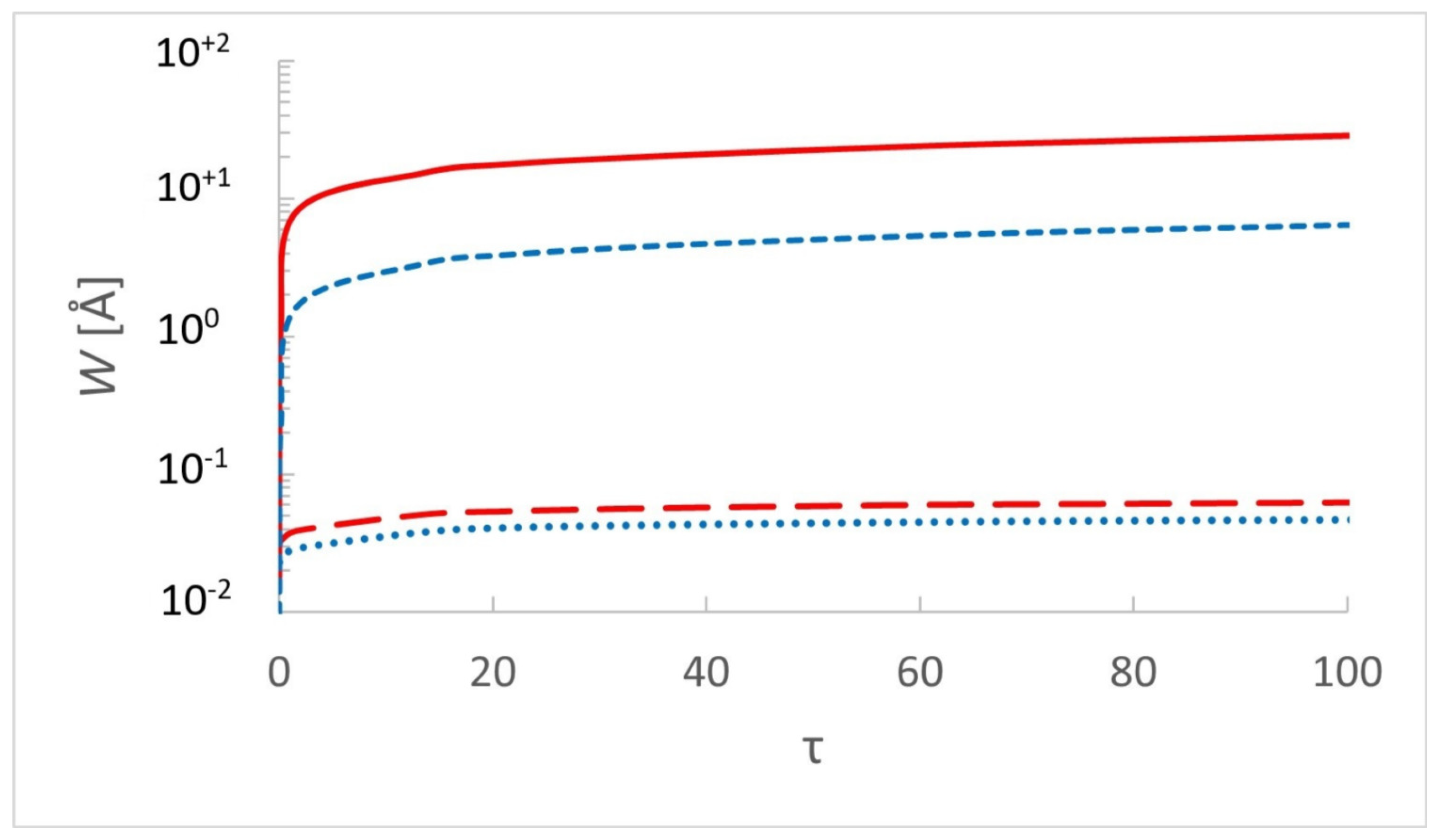
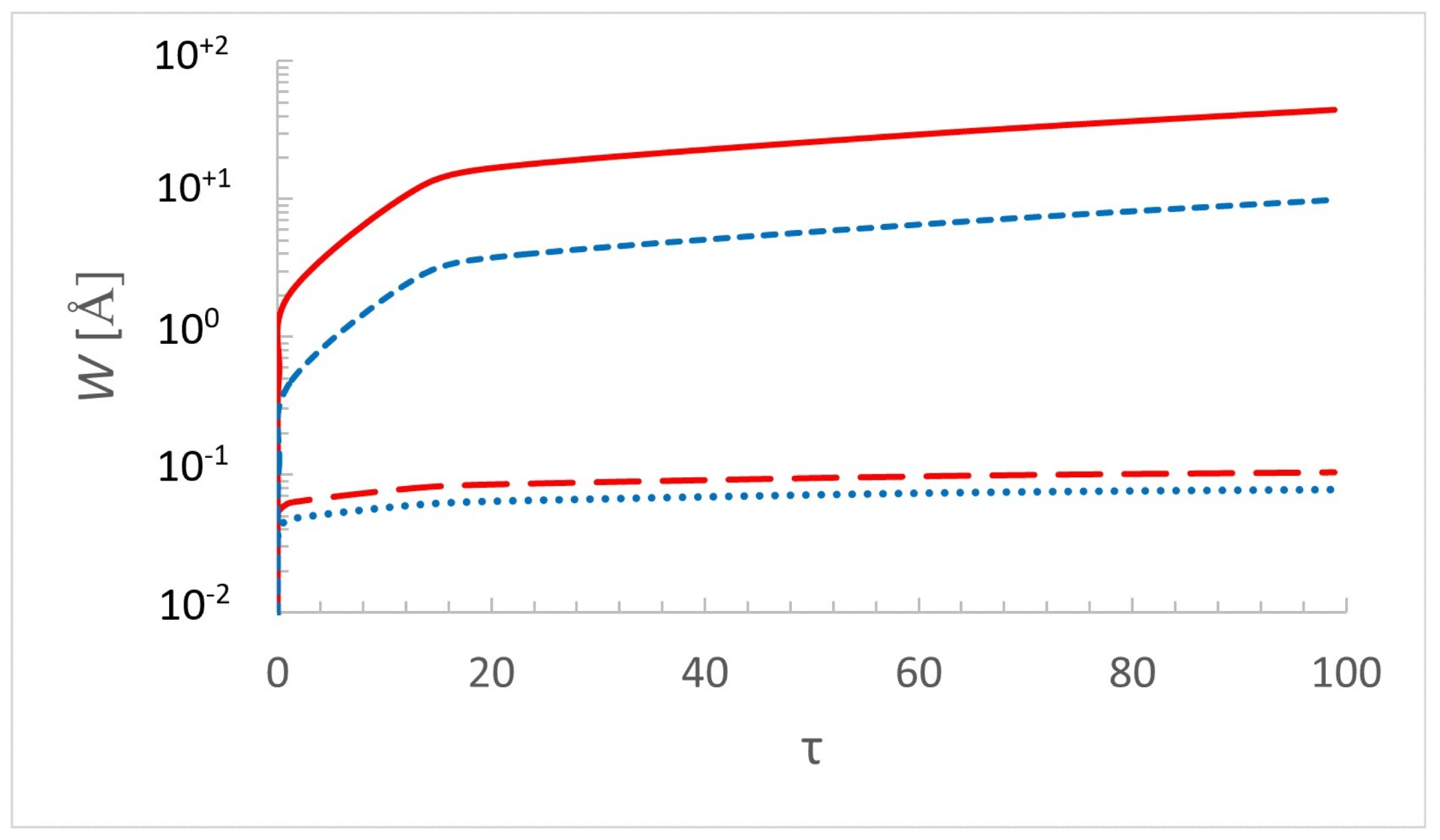
3. Results

We calculated Stark Full widths at half intensity maximum (FWHM), by employing the modified semiempirical method [20]. The set of atomic energy levels, which need to be included as input data have been taken from [30,31]. In Table 1 are given the obtained results for electron-impact (Stark) FWHM for 23 Al IV transitions, calculated for an electron density of 10¹⁷ cm⁻³ and electron temperatures of 10,000, 20,000, 40,000, 80,000 and 160,000 K. Theoretical errors of our calculations are within the limit of 40 per cent. Concerning the dependence of results on electron density, it is linear if the influence of Debye screening is negligible. This influence should be checked only for high densities. We draw attention as well that the wavelengths given in Table 1 are not observed ones but they are calculated using atomic energy levels, so that they are not identical with observed ones. In Table 1 is also provided the value of

3 k T / 2 Δ E

. This is the ratio of mean energy of free electrons and the energy difference between closest perturbing level and the closer of initial and final levels (

Δ E

), and it shows which type of collisions contribute to the line width. For values which are lower than one, dominate the elastic collisions. Namely in such a case the energy of colliding electrons is below the threshold for excitation of atomic energy levels. When it increases above this value, the contribution of inelastic collisions increases.

There is no experimental or other theoretical data for Stark broadening of Al IV transitions investigated here.

The presented here results for Al IV Stark wdths are from six multiplet, three belonging to the spectral series with parent term ²

P_{1 / 2}^{o}

: 4s ²[1/2]^o–4p ²[1/2], 4s ²[1/2]^o–4p ²[3/2] and 4p ²[1/2]–4d ²[3/2]^o, and three belonging to the spectral series with parent term ²

P_{3 / 2}^{o}

: 4s ²[3/2]^o–4p ²[1/2], 4p ²[1/2]–4d ²[1/2]^o, and 4p ²[1/2]–4d ²[3/2]^o. We have also four supermultiplets: 4s ²[K]^o–4p ²[K’] and 4p ²[K]–4d ²[K’]^o, in spectral series with parent terms ²

P_{1 / 2}^{o}

and ²

P_{3 / 2}^{o}

This gives us opportunity to check similarities of Stark widths within the present Al IV multiplets and supermultiplets.Namely, when such similarities are present, this may be used for example to check are the existing experimental or theoretical values consistent, and also to use existing data to estimate needed line widths which are unknown.

Wiese and Konjević [32] found, analysing experimental data from literature, that if we express Stark widths in angular frequency units, differences within the same multiplet should usually not exceede several per cent and about 30 per cent in the case of a supermultiplet. It is interesting to check this for Al IV transitions presnted here, which are in Jℓ coupling scheme. In oder to do this, we present in Table 2 Stark widths expressed in Ångströms and angular frequency units for T=80,000 K.

For the transformation of Stark widths between Å and angular frequency units one can use the following relation:

W (\overset{˚}{A}) = \frac{λ^{2}}{2 π c} W (s^{- 1}),

(5)

where c is the speed of light.

If we analyse data in Table 2 we can see that in the spectral series with parent term ²

P_{1 / 2}^{o}

, in the case of multiplet 4s ²[1/2]^o–4p ²[1/2], the greatest width is 64% larger from the smallest one if expressed in Ångströms and 17% if the widths are in angular frequency units. For 4s ²[1/2]^o–4p ²[3/2] multiplet these values are 94% and 12%, and for 4p ²[1/2]–4d ²[3/2]^o 1.7% and 11%, respectively. For the spectral series with parent term ²

P_{3 / 2}^{o}

, these values are 62.5% and 9.5% in the case of 4s ²[3/2]^o–4p ²[1/2] multiplet, 65% and 0.4% for 4p ²[1/2]–4d ²[1/2]^o multiplet, and 60.5% and 0.5% for 4p ²[1/2]–4d ²[3/2]^o multiplet.

We can see that for considered Al IV transition in Jℓ coupling, these differences may be of the order of 10-20 per cent if expressed in angular frequency units which enables a rough check of consistency of existing experimental and theoretical data or an approximate check during experiment or calculation.

In the case of supermultiplet 4s ²[K]^o–4p ²[K’], belonging to the spectral series with parent term ²

P_{1 / 2}^{o}

, the maximal difference when line width is expressed in Ångströms is 210% and 89% if the widths are in angular frequency units. For the 4p ²[K]–4d ²[K’]^o supermultiplet, which belongs to the same spectral series, these values are 166% and 61%. The similar situation is and for supermultiplets in spectral series with the parent term ²

P_{3 / 2}^{o}

. For supermultiplet 4s ²[K]^o–4p ²[K’] these values are 124% and 85% respectively, while for 4p ²[K]–4d ²[K’]^o they are169% and 93%. We can see that the prediction [32] that the differences of Stark widths in angular frequency units, within the same supermultiplet usually not exceede about 30 per cent, in the case of Al IV transition in Jℓ coupling, considered here, is not satisfied.

4. On the Stark Broadening in Stellar Atmospheres

The obtained results are used here to show the influence of electron impacts on Al IV lines (Stark broadening) in stellar spectra. In order to demonstrate this influence we compared Stark and Doppler widths for different Rosseland optical depths, taking into account the transition with the largest (2s²2p⁵(²

P_{1 / 2}^{o}

)4s ²[1/2]^o–2s²2p⁵(²

P_{1 / 2}^{o}

)4p ²[3/2],

λ

= 4250.2 Å) and the smallest (2s²2p⁵(²

P_{3 / 2}^{o}

)4p ²[5/2]–2s²2p⁵(²

P_{3 / 2}^{o}

)4d ²[3/2]^o,

λ

= 3411.8 Å) Stark width values from Table 1. In Figure 1 are presented ratios of Stark and Doppler widths for an A type star atmospheric model with effective temperature

T_{e f f}

= 8500 K and logarithm of surface gravity log g = 4.5 [34]. Recently, we performed a similar investigation for Zn III specrral lines in UV part of the spectrum [33].

As a difference, Al IV spectral lines considered here are all in the visible part of the spectrum. For UV Zn III lines we found that Doppler width is dominant for all considered Rosseland optical depths and that the Stark broadening could be neglected. In the case of Al IV lines in the visible, for higher values of Rosseland opacity or deeper atmospheric layers, Stark broadening may be a correction which increases the accuracy. In Figure 2 , such analysis is performed for a model of DB white dwarf atmosphere with

T_{e f f}

= 25,000 K and log g = 4.5 [35].

One can see that for such atmospheric model Stark width is dominant for both transitions and for all investigated Rosseland optical depths, even more than in the case of previously investigated Zn III UV multiplets. For DO white dwarf atmosphere model with

T_{e f f}

= 60,000 K and log g = 4.5 [35] (see Figure 3), we can see the difference in the influence of Stark broadening on UV and optical spectral lines. Namely, in the case of Al IV Stark broadening dominates for both transitions and for all Rosseland optical depths of interest, while for Zn III UV lines, Stark broadening is dominant for higher values of Rosseland optical depth, while for lower ones Doppler broadening is higher, but in most cases comparable to the Stark.

This is a demonstration of the influence of wavelength values. Namely in Stark broadening theories the wavelength enters as a square and the expression for Doppler width is linear with wavelength. So, with the increase of wavelength, Stark widths increase faster than Doppler ones. So, in visible part of the spectrum the influence of Stark broadening will be higher in comparison with Doppler broadening, than in UV part.

5. Conclusions

We calculated Stark widths for 23 Al IV transitions in Jℓ coupling, with the help of the modified semiempirical method [20]. For the considered transitions, which are all in the visible part of the spectrum, there are no other experimental or theoretical data. With the help of the obtained data we investigated the influence of Stark broadening on Al IV spectral lines in the visible part of the spectrum, in atmospheres of A-type stars and DB and DO white dwarfs. In comparison with lines in UV, the influence of Stark broadening in the visible part of the spectrum is higher due to the influence of higher wavelengths. We also used the obtained results to check regularities and similarities among Al IV Stark widths within multiplets and supermultiplets and found that in the case of Jℓ coupling (investigated here), differences of Stark widths within multiplets of Al IV transitions considered here are 10-20 per cent, while within investigated supermultiplets there is no similarities which would be useful for the check of consistency of experimental or theoretical results.

The Al IV Stark widths presented in this article will also enter in STARK-B database (http://stark-b.obspm.fr/ (accessed on 27 January 2023), [36,37], which enters in Virtual Atomic and Molecular Data Center VAMDC (http://www.vamdc.org/ (accessed on 27 January 2023), [38,39]).

The presented spectral line widths of Al IV, broadened by collisions with surrouning electrons (Stark broadening) may be used for many topics in astrophysics like for modelling of stellar atmospheres, abundance determination of zinc, analysis and synthesis of Al IV lines in stellar spectra, opacity calculations, investigation, modelling and diagnostics of laboratory plasmas as well as for various technological applications in particular for optimisation of cutting, welding, melting and piercing of aluminium by lasers. They also may be used for the diagnostic and modelling of an electrodynamic macro-particle accelerator arc plasma created by the evaporation of an Al-foil [40,41] and for diagnostics of plasmas generated during incipient laser ablation of aluminum in air [42].

Author Contributions

Both authors were involved in the preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

All obtained data are in the paper.

Acknowledgments

This work has been supported with a STSM visit grant E-COST-GRANT-CA17126-0085105c for M.S.D. within the framework of COST Action CA 17126 “Towards Understanding and Modelling Intense Electronic Excitation, TUMIEE”. Thanks also to Technical University of Sofia for the provided help.

Conflicts of Interest

The authors declare no conflict of interest

References

Beauchamp, A.; Wesemael, F.; Bergeron, P. Spectroscopic Studies of DB White Dwarfs: Improved Stark Profiles for Optical Transitions of Neutral Helium. Astrophys. J. Suppl. Ser. 1997, 108, 559–573. [Google Scholar] [CrossRef]
Konjević, N. Plasma broadening and shifting of non-hydrogenic spectral lines: Present status and applications. Phys. Rep. 1999, 316, 339–401. [Google Scholar] [CrossRef]
Torres, J.; van de Sande, M.J.; van der Mullen, J.J.A.M.; Gamero, A.; Sola, A. Stark broadening for simultaneous diagnostics of the electron density and temperature in atmospheric microwave discharges. Spectrochim. Acta B 2006, 61, 58–68. [Google Scholar] [CrossRef]
Belostotskiy, S.G.; Ouk, T.; Donnelly, V.M.; Economou, D.J.; Sadeghi, N.J. Gas temperature and electron density profiles in an argon dc microdischarge measured by optical emission spectroscopy. Appl. Phys. 2010, 107, 053305. [Google Scholar] [CrossRef]
Zhou, Y.; Li, H.; Jung, J.-E.J.; Ki, N.S.; Donnelly, V.M. Effects of N₂ and O₂ plasma treatments of quartz surfaces exposed to H₂ plasmas. J. Vac. Sci. Technol. A 2022, 40, 053002. [Google Scholar] [CrossRef]
Griem, H.R. Plasma spectroscopy in inertial confinement fusion and soft X-ray laser research. Phys. Fluids 1992, 4, 2346–2361. [Google Scholar] [CrossRef]
Iglesias, E.; Griem, H.R.; Welch, B.; Weaver, J. UV Line Profiles of B V from a 10-Ps KrF-Laser-Produced Plasma. Astrophys. Space Sci. 1997, 256, 327–331. [Google Scholar] [CrossRef]
Wang, J.S.; Griem, H.R.; Huang, Y.W.; Böttcher, F. Measurements of line broadening of B V Hα and Lδ in a laser-produced plasma. Phys. Rev. A 1992, 45, 4010–4014. [Google Scholar] [CrossRef]
Gornushkin, I.B.; King, L.A.; Smith, B.W.; Omenetto, N.; Winefordner, J.D. Line broadening mechanisms in the low pressure laser-induced plasma. Spectrochim. Acta 1999, 54, 1207–1217. [Google Scholar] [CrossRef]
Nicolosi, P.; Garifo, L.; Jannitti, E.; Malvezzi, A.M.; Tondello, G. Broadening and self-absorption of the resonance lines of H-like light ions in laser-produced plasmas. Nuovo Cimento B 1978, 48, 133–151. [Google Scholar] [CrossRef]
Sorge, S.; Wierling, A.; Röpke, G.; Theobald, W.; Suerbrey, R.; Wilhein, T. Diagnostics of a laser-induced dense plasma by hydrogen-like carbon spectra. J. Phys. B 2000, 33, 2983–3000. [Google Scholar] [CrossRef]
Yilbas, B.S.; Patel, F.; Karatas, C. Laser controlled melting of H12 hot-work tool steel with B₄C particles at the surface. Opt. Laser Technol. 2015, 74, 36–42. [Google Scholar] [CrossRef]
Hoffman, J.; Szymański, Z.; Azharonok, V. Laser controlled melting of H12 hot-work tool steel with B4C particles at the surface. AIP Conf. Proc. 2006, 812, 469–472. [Google Scholar] [CrossRef]
Dimitrijević, M.S.; Christova, M.D. Stark widths of Lu II spectral lines. Eur. Phys. J. D 2021, 75, 172. [Google Scholar] [CrossRef]
Majlinger, Z.; Dimitrijević, M.S.; Srećković, V. Stark broadening of Zr IV spectral lines in the atmospheres of chemically peculiar stars. Mon. Not. R. Astron. Soc. 2020, 470, 1911–1918. [Google Scholar] [CrossRef]
Hamdi, R.; Ben Nessib, N.; Milovanović, N.; Popović, L.Č.; Dimitrijević, M.S.; Sahal-Bréchot, S. Stark Widths of Ar II Spectral Lines in the Atmospheres of Subdwarf B Stars. Atoms 2017, 5, 26. [Google Scholar] [CrossRef]
Smiljanic, R.; Romano, D.; Bragaglia, A.; Donati, P.; Magrini, L.; et al. The Gaia -ESO Survey: Sodium and aluminium abundances in giants and dwarfs. Implications for stellar and Galactic chemical evolution. A&A 2016, 589, A115. [Google Scholar]
Carretta, E.; Bragaglia, A.; Lucatello, S.; Gratton, R.G.; D’Orazi, V.; Sollima, A. Aluminium abundances in five discrete stellar populations of the globular cluster NGC 2808. A&A 2018, 615, A17. [Google Scholar] [CrossRef]
Smith, K.C. Elemental abundances in normal late-B and HgMn stars from co-added IUE spectra II. Magnesium, aluminium and silicon. A&A 1993, 276, 393–408. [Google Scholar]
Dimitrijević, M.S.; Konjević, N. Stark widths of doubly- and triply-ionized atom lines. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 451–459. [Google Scholar] [CrossRef]
Elabidi, H. Systematic trends of Stark broadening parameters with spectroscopic charge Z within the neon isoelectronic sequence from Mg III to Br XXVI. JQSRT 2021, 259, 107407. [Google Scholar] [CrossRef]
Elabidi, H.; Ben Nessib, N.; Sahal-Bréchot, S. Quantum mechanical calculations of the electron-impact broadening of spectral lines for intermediate coupling. J. Phys. B 2004, 37, 63–71. [Google Scholar] [CrossRef]
Elabidi, H.; Ben Nessib, N.; Cornille, M.; Dubau, J.; Sahal-Bréechot, S. Electron impact broadening of spectral lines in Be-like ions: quantum calculations. J. Phys. B 2008, 41, 025702. [Google Scholar] [CrossRef]
Shore, B.W.; Menzel, D. Generalized Tables for the Calculation of Dipole Transition Probabilities. Astrophys. J. Suppl. Ser. 1965, 12, 187–214. [Google Scholar] [CrossRef]
Griem, H.R. Semiempirical Formulas for the Electron-Impact Widths and Shifts of Isolated Ion Lines in Plasmas. Phys. Rev. 1968, 165, 258–266. [Google Scholar] [CrossRef]
Griem, H.R. Spectral line Broadening by Plasmas; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
Bates, D.R.; Damgaard, A. The Calculation of the Absolute Strengths of Spectral Lines. Philos. Trans. R. Soc. Lond. Ser. A 1949, 242, 101–122. [Google Scholar] [CrossRef]
Oertel, G.K.; Shomo, L.P. Tables for the Calculation of Radial Multipole Matrix Elements by the Coulomb Approximation. Astrophys. J. Suppl. Ser. 1968, 16, 175–218. [Google Scholar] [CrossRef]
Van Regemorter, H.; Dy Hoang, B.; Prud’homme, M. Radial transition integrals involving low or high effective quantum numbers in the Coulomb approximation. J. Phys. B 1979, 12, 1053–1061. [Google Scholar] [CrossRef]
Martin, W.C.; Zalubas, R. Energy Levels of Aluminium, Al I through Al XIII. J. Phys. Chem. Ref. Data 1979, 8, 817–864. [Google Scholar] [CrossRef]
Kramida, A.; Ralchenko, Y.; Reader, J. NIST ASD Team. NIST Atomic Spectra Database (ver. 5.10); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021; Available online: https://physics.nist.gov/asd (accessed on 20 January 2023).
Wiese, W.L.; Konjević, N. Regularities and similarities in plasma broadened spectral line widths (Stark widths). J. Quant. Spectrosc. Radiat. Transf. 1982, 28, 185–198. [Google Scholar] [CrossRef]
Dimitrijević, M.S.; Christova, M.D. Stark Broadening of Zn III Spectral Lines. Universe 2022, 8, 430. [Google Scholar] [CrossRef]
Kurucz, R.L. Model atmospheres for G, F, A, B, and O stars. Astrophys. J. Suppl. Ser. 1979, 40, 1–340. [Google Scholar] [CrossRef]
Wesemael, F. Atmospheres for hot, high-gravity stars. II. Pure helium models. Astrophys. J. Suppl. Ser. 1981, 45, 177–257. [Google Scholar] [CrossRef]
Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N.; Ben Nessib, N. The STARK-B database VAMDC node: A repository for spectral line broadening and shifts due to collisions with charged particles. Phys. Scr. 2015, 90, 054008. [Google Scholar] [CrossRef]
Sahal- Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database. Available online: http://stark-B.obspm.fr (accessed on 27 January 2023).
Dubernet, M.L.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bartschat, K.; Boudon, V.; Braams, B.J.; Chung, H.K.; Daniel, F.; Delahaye, F.; et al. The virtual atomic and molecular data centre (VAMDC) consortium. J. Phys. B 2016, 49, 074003. [Google Scholar] [CrossRef]
Albert, D.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bollard, P.; Boudon, V.; Delahaye, F.; Del Zanna, G.; Dimitrijević, M.S.; Drouin, B.J.; et al. A Decade with VAMDC: Results and Ambitions. Atoms 2020, 8, 76. [Google Scholar] [CrossRef]
Rolader, G.E.; Batteh, J.H. Thermodynamic and electrical properties of railgun plasma armatures. IEEE Transactions on Plasma Sci. 1989, 17, 439–445. [Google Scholar] [CrossRef]
Dimitrijević, M.S.; Djurić, Z.; Mihajlov, A.A. Stark broadening of Al III and Cu IV lines for diagnostic of the rail gun arc plasma. J. Phys. D 1994, 27, 247–252. [Google Scholar] [CrossRef]
Pakhal, H. R.; Lucht, R. P.; Laurendeau, N. M. Spectral measurements of incipient plasma temperature and electron number density during laser ablation of aluminum in air. Appl. Phys. B 2008, 90, 15–27. [Google Scholar] [CrossRef]

Figure 1. Dependence of Stark and Doppler full widths at half intensity maximum of Al IV 2

s^{2}

p^{5}

(^{2}

P_{1 / 2}^{o}

)4s

^{2}

[1/2]^o–2

s^{2}

p^{5}

(^{2}

P_{1 / 2}^{o}

)4p

^{2}

[3/2] ,

λ

= 4520.2 Å (red, Stark—solid line, Doppler—long dashes) and 2

s^{2}

p^{5}

(^{2}

P_{3 / 2}^{o}

)4p

^{2}

[5/2]–2

s^{2}

p^{5}

(^{2}

P_{3 / 2}^{o}

)4d

^{2}

[3/2]^o,

λ

= 3411.8 Å(blue, Stark—dashes, Doppler—dots) spectral lines, on the Rosseland optical depth in the atmosphere of an A type star. Model of stellar atmosphere [34] is with parameters

T_{e f f}

= 8500 K and log g = 4.5.

Figure 1. Dependence of Stark and Doppler full widths at half intensity maximum of Al IV 2

s^{2}

p^{5}

(^{2}

P_{1 / 2}^{o}

)4s

^{2}

[1/2]^o–2

s^{2}

p^{5}

(^{2}

P_{1 / 2}^{o}

)4p

^{2}

[3/2] ,

λ

= 4520.2 Å (red, Stark—solid line, Doppler—long dashes) and 2

s^{2}

p^{5}

(^{2}

P_{3 / 2}^{o}

)4p

^{2}

[5/2]–2

s^{2}

p^{5}

(^{2}

P_{3 / 2}^{o}

)4d

^{2}

[3/2]^o,

λ

= 3411.8 Å(blue, Stark—dashes, Doppler—dots) spectral lines, on the Rosseland optical depth in the atmosphere of an A type star. Model of stellar atmosphere [34] is with parameters

T_{e f f}

= 8500 K and log g = 4.5.

Figure 2. Same as in Figure 2 but for the atmosphere of a DB white dwarf. The atmosphere model from [35] with parameters

T_{e f f}

= 25,000 K and log g = 8.

Figure 2. Same as in Figure 2 but for the atmosphere of a DB white dwarf. The atmosphere model from [35] with parameters

T_{e f f}

= 25,000 K and log g = 8.

Figure 3. Same as in Figure 2 but for the atmosphere of a DO white dwarf. The atmosphere model from [35] with parameters

T_{e f f}

= 60,000 K and log g = 8.

Figure 3. Same as in Figure 2 but for the atmosphere of a DO white dwarf. The atmosphere model from [35] with parameters

T_{e f f}

= 60,000 K and log g = 8.

Table 1. In this table are presented FWHM - Full Widths at Half Intensity Maximum (W) for Al IV spectral lines broadened by impacts with surrounding electrons, for an electron density of

10^{17}

{cm}^{- 3}

and temperatures from 10,000 K to 160,000 K. In last column the quantity

3 k T / 2 Δ E

is given, where

Δ E

is the energy difference type of collisions contributing to line broadening. When it is lower than one, collisions are elastic. Starting with the value of one, with its increase increases the influence of inelastic collisions.

Table 1. In this table are presented FWHM - Full Widths at Half Intensity Maximum (W) for Al IV spectral lines broadened by impacts with surrounding electrons, for an electron density of

10^{17}

{cm}^{- 3}

and temperatures from 10,000 K to 160,000 K. In last column the quantity

3 k T / 2 Δ E

is given, where

Δ E

Transition	T [K]	W [Å]	3kT/2 $Δ$ E
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$	10000.	1.07	0.471
	20000.	0.754	0.942
$λ$ = 4515.6 Å	40000.	0.533	1.88
	80000.	0.410	3.77
	160000.	0.352	7.53
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$	10000.	0.643	0.471
	20000.	0.455	0.942
$λ$ = 3261.3 Å	40000.	0.322	1.88
	80000.	0.250	3.77
	160000.	0.215	7.53
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2]	10000.	2.00	0.471
	20000.	1.42	0.943
$λ$ = 4520.2 Å	40000.	1.00	1.89
	80000.	0.776	3.77
	160000.	0.671	7.54
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{2}^{o}$	10000.	0.747	2.36
	20000.	0.554	4.73
$λ$ = 3485.1 Å	40000.	0.429	9.45
	80000.	0.345	18.9
	160000.	0.296	37.8
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	10000.	0.710	3.99
	20000.	0.543	7.98
$λ$ = 3279.5 Å	40000.	0.422	16.0
	80000.	0.340	31.9
	160000.	0.294	63.8
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	10000.	1.38	3.99
	20000.	1.05	7.98
$λ$ = 4550.5 Å	40000.	0.817	16.0
	80000.	0.659	31.9
	160000.	0.571	63.8
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [5/2]^o	10000.	0.506	2.32
	20000.	0.381	4.64
$λ$ = 3492.1 Å	40000.	0.303	9.28
	80000.	0.248	18.6
	160000.	0.213	37.1
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{2}^{o}$	10000.	0.780	2.36
	20000.	0.578	4.73
$λ$ = 3482.3 Å	40000.	0.446	9.45
	80000.	0.358	18.9
	160000.	0.307	37.8
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	10000.	0.741	3.99
	20000.	0.565	7.98
$λ$ = 3277.0 Å	40000.	0.437	16.0
	80000.	0.352	31.9
	160000.	0.305	63.8
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$	10000.	1.33	0.545
	20000.	0.940	1.09
$λ$ = 5224.1 Å	40000.	0.668	2.18
	80000.	0.520	4.36
	160000.	0.448	8.72
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$	10000.	0.830	0.545
	20000.	0.587	1.09
$λ$ = 3916.5 Å	40000.	0.415	2.18
	80000.	0.320	4.36
	160000.	0.276	8.72
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]	10000.	0.684	0.545
	20000.	0.484	1.09
$λ$ = 4291.9 Å	40000.	0.342	2.18
	80000.	0.263	4.36
	160000.	0.225	8.72
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]	10000.	0.606	0.545
	20000.	0.429	1.09
$λ$ = 4544.1 Å	40000.	0.303	2.18
	80000.	0.232	4.36
	160000.	0.198	8.72
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	10000.	0.589	1.89
	20000.	0.441	3.77
$λ$ = 3279.6 Å	40000.	0.348	7.55
	80000.	0.287	15.1
	160000.	0.249	30.2
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	10000.	0.387	2.71
	20000.	0.294	5.43
$λ$ = 3108.0 Å	40000.	0.236	10.9
	80000.	0.195	21.7
	160000.	0.166	43.4
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	10000.	0.977	1.89
	20000.	0.731	3.77
$λ$ = 4210.3 Å	40000.	0.575	7.55
	80000.	0.474	15.1
	160000.	0.412	30.2
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	10000.	0.624	2.71
	20000.	0.473	5.43
$λ$ = 3931.7 Å	40000.	0.381	10.9
	80000.	0.313	21.7
	160000.	0.267	43.4
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	10000.	0.829	1.89
	20000.	0.619	3.77
$λ$ = 3797.4 Å	40000.	0.485	7.55
	80000.	0.399	15.1
	160000.	0.347	30.2
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	10000.	0.546	2.71
	20000.	0.412	5.43
$λ$ = 3569.2 Å	40000.	0.329	10.9
	80000.	0.270	21.7
	160000.	0.231	43.4
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [5/2]^o	10000.	0.704	2.94
	20000.	0.540	5.88
$λ$ = 3532.0 Å	40000.	0.437	11.8
	80000.	0.363	23.5
	160000.	0.310	47.0
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	10000.	0.372	2.71
	20000.	0.278	5.43
$λ$ = 3411.8 Å	40000.	0.217	10.9
	80000.	0.176	21.7
	160000.	0.149	43.4
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [5/2]^o	10000.	0.458	2.94
	20000.	0.347	5.88
$λ$ = 3377.7 Å	40000.	0.276	11.8
	80000.	0.226	23.5
	160000.	0.192	47.0
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [7/2]^o	10000.	0.511	2.10
	20000.	0.381	4.20
$λ$ = 3499.1 Å	40000.	0.295	8.39
	80000.	0.238	16.8
	160000.	0.204	33.6

Table 2. In the table are presented electron-impact broadening (Stark broadening) Full Widths at Half Intensity Maximum (W) in [Å] and in [

10^{12}

s^{- 1}

] units for Al IV spectral lines, for an electron density of

10^{17}

{cm}^{- 3}

and T = 80,000 K.

Table 2. In the table are presented electron-impact broadening (Stark broadening) Full Widths at Half Intensity Maximum (W) in [Å] and in [

10^{12}

s^{- 1}

] units for Al IV spectral lines, for an electron density of

10^{17}

{cm}^{- 3}

and T = 80,000 K.

Transition	$λ$ [Å]	W [Å]	W [ $10^{12}$ $s^{- 1}$ ]
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$	4516.	0.410	0.379
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$	3261.	0.250	0.442
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4s $^{2}$ [1/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2]	4520.	0.776	0.715
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{2}^{o}$	3485.	0.345	0.535
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	3279.	0.340	0.596
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	4551.	0.659	0.599
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [5/2]^o	3492.	0.248	0.383
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{2}^{o}$	3482.	0.358	0.556
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4p $^{2}$ [3/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{1 / 2}^{o}$ )4d $^{2}$ [3/2 $]_{1}^{o}$	3277.	0.352	0.618
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$	5224.	0.520	0.359
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$	3917.	0.320	0.393
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]	4292.	0.263	0.269
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4s $^{2}$ [3/2]^o–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]	4544.	0.232	0.212
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	3280.	0.287	0.502
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{1}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	3108.	0.195	0.380
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	4210.	0.474	0.504
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [1/2 $]_{0}$ –2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	3932.	0.313	0.382
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [1/2]^o	3797.	0.399	0.521
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	3569.	0.270	0.400
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [3/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [5/2]^o	3532.	0.363	0.548
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [3/2]^o	3412.	0.176	0.284
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [5/2]^o	3378.	0.226	0.373
Al IV 2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4p $^{2}$ [5/2]–2 $s^{2}$ 2 $p^{5}$ $(^{2}$ $P_{3 / 2}^{o}$ )4d $^{2}$ [7/2]^o	3499.	0.238	0.366

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Stark Broadening of Al IV Spectral Lines

Abstract

1. Introduction

2. Theory

3. Results

4. On the Stark Broadening in Stellar Atmospheres

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe