1. Introduction
Every meteorologist including the author from very beginning of her/his career learned that the Earth gravity on a point-mass in atmosphere (
mA) at location
rA consists of Earth gravitation and centrifugal force with the Earth center (
O) as the origin of the position vector
rA (
Figure 1).
The solid Earth “shrinks” into a point-mass located at the Earth center with the entire Earth mass to get the Earth gravitation. With such a treatment, the Earth gravitation on
mA, given by
F(
rA), is between the Earth point-mass
MO (at point
O) and atmospheric point-mass
mA,
where
G = 6.67408×10
-11Nm
2kg
-2, is the Newtonian gravitational constant; and
M = 5.98×10
24 kg is the mass of the Earth. Since
F(
rA) in Eq.(1) is calculated through shrinking the solid Earth into a point-mass
MO. It is not true and therefore should be called the untrue Earth gravitation.
Let
Ω be the Earth’s angular velocity with |
Ω| = 2π/(86164 s). Combining the untrue gravitation (
F with the centrifugal force (
FC) on the point-mass
mA
leads to the effective gravity (
geff, sometimes called normal gravity, or apparent gravity) [
1] (pp 12-14)
The effective gravity
geff is non-radial (not in the direction of
rA) but changes little with latitude or height. The rotation causes equatorial bulge and polar flattening, i.e., uniform ellipsoidal Earth. Let
k be the unit vector perpendicular to the ellipsoidal Earth surface. The effective gravity
geff at the Earth surface is given by (
https://glossary.ametsoc.org/wiki/Gravity)
where
φ is the latitude.
To solve the non-radial nature of
geff, orthogonal curvilinear coordinate systems, i.e., the geopotential coordinates (more accurately called the effective geopotential coordinates) have been used. Among them, the oblate spheroid coordinate system (
λ,
φ,
z) with (
i,
j,
k) the corresponding unit vectors is optimal since it describes the ellipsoidal shape more accurately. However, the error is less than 0.17% between polar spherical coordinate and oblate spherical coordinate systems [
2] (P.92). The geophysically realistic, ellipsoidal, analytically tractable (GREAT) coordinates was presented [
3] to make that the horizontal coordinate surfaces coincide with the effective geopotential (Φ
eff) surfaces and to ensure that there is no component of effective gravity (
geff) in any direction tangential to coordinate surfaces (i.e., no horizontal compoenent in
geff),
where the direction of
k is defined as the vertical in meteorology. The effective geopotential Φ
eff is given by [
2] (P.46, Equation 3.5.2) [
5,
6]
where
z is the height of the point mass in atmosphere with z = 0 at the Earth ellipsoidal surface. Vertical integration of (5b) from
z = 0 to the height of the point mass in atmosphere (
z) leads to
where
Z is the effective geopotential height of the point mass. The two heights (
z and
Z) are numerically interchangeable for most meteorological purpose (see website:
https://glossary.ametsoc.org/wiki/Geopotential_height). The effective gravity
geff with no horizontal component has been used in atmospheric dynamics and modeling as if it were the true gravity.
A question arises:
Is it reasonable to shrink the solid Earth into a point-mass with the entir Earth mass (M) concentrated at the Earth center (O) in calculating the Earth gravitation? The answer is
NO because the solid Earth contains infinite number of point-masses. The Newton’s law of universal gravitation in today’s language states that every point-mass attracts every other point mass by a force acting along the line intersecting the two points. The force is proportional to the product of the two point-masses, and inversely proportional to the square of the distance between them (see website
https://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation.)
Let r be the position vector of a point inside the solid Earth, σ(r) be the mass density, and dΠ be the infinitesimally small volume (around r). The point-mass at r is represented by
The Newton’s gravitation of point-mass
dm(
r) on a point mass
mA at location
rA in atmosphere is given by
The gravitation of the whole Earth on the point-mass
mA is the volume integration (
Figure 2) [
4] (P.72, Equation 6.4),
where Π is the Earth volume. Let
σ0 be the averaged mass density of the solid Earth. Then Eq.(7b) becomes
Combine the true gravitational force (
FN) and the centrifugal force (
FC) on the point mass
A in atmosphere
Correspondingly the true Earth gravity on the point mass
mA in atmosphere [using Eqs.(2) and (9)] is given by
Here, g is the true gravity; δg, with evident horizontal components, is the true gravitational acceleration minus untrue gravitational acceleration, and called the gravity disturbance vector. δg is a major variable and quantified by gravity field models along with observations in geodesy and solid Earth dynamics, however, it is totally neglected in atmospheric dynamics and modeling.
The gravity disturbance vector δ
g was recently found important in ocean dynamics especially in Ekman transport [
7]. However, importance of δ
g in large-scale atmospheric dynamics has not been recognized. The objective of this study is to show the importance of δ
g in atmospheric dynamics.
4. Discussion
The effective gravity geff used in large-scale atmospheric dynamics and modeling is untrue since it is obtained from shrinking the Earth into a point-mass with entire mass concentrated at the Earth center. The true gravity g minus the effective gravity geff is the gravity disturbance vector δg (δg = g – geff). The effect of δg in atmospheric dynamics is studied through replacing geff by g. Seven non-dimensional numbers (A, B, C, D, E1, E2, E3) are defined to identify importance of horizontal component of δg versus the horizontal temperature gradient (A number), the pressure gradient force (B number), the Coriolis force (C number), the traditional geostrophic vorticity (D number), the components of traditional Q vector (E1, E2 numbers), and the components of traditional Omega equation (E3 number).
Two reputable, independent, and openly available datasets (a) ICGEM EIGEN-6C4 and (b) NCEP/NCAR Reanalysis long term mean data are used to compute the seven numbers.
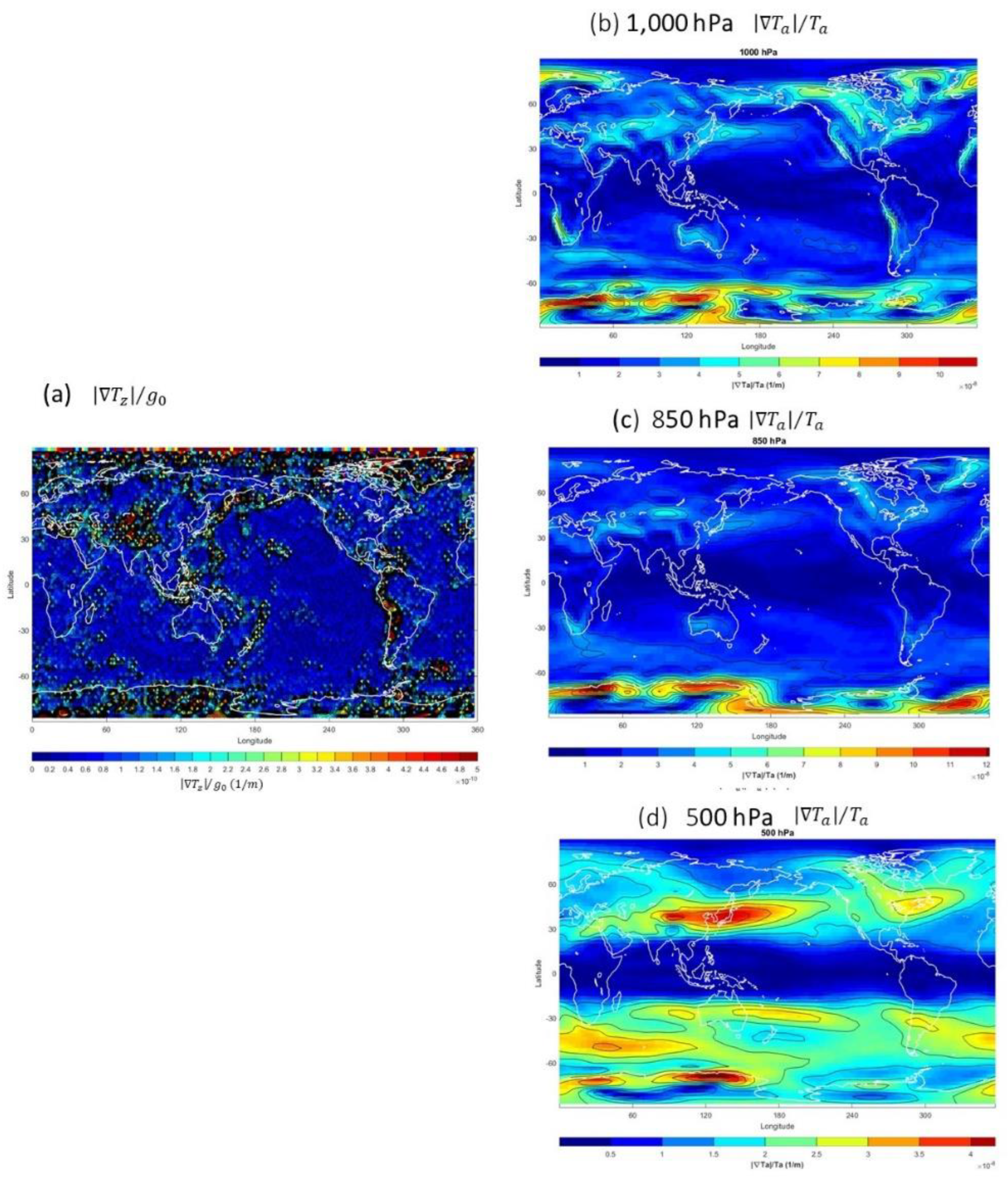
Table 8 presents these numbers at 12 pressure levels in troposphere (1,000 – 100 hPa). Among them, only the
A number is smaller than 0.0198×10
-2 in the whole troposphere, which means that the effect of δ
g on the thermal wind relation is negligible. The
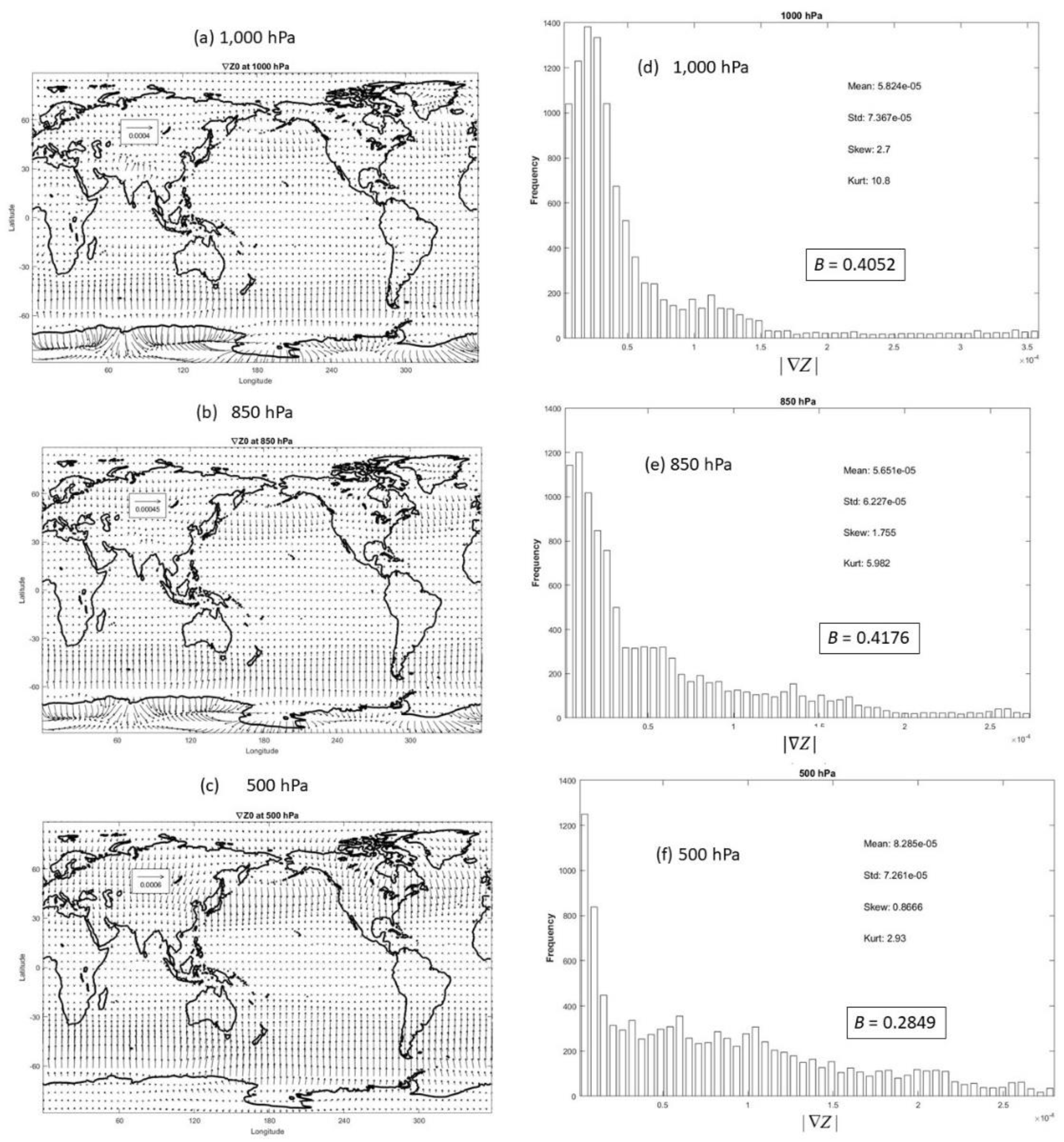
B number varies from 0.4176 (max) at 850 hPa to 0.1630 (min) at 200 hPa with a mean of 0.2792 and the
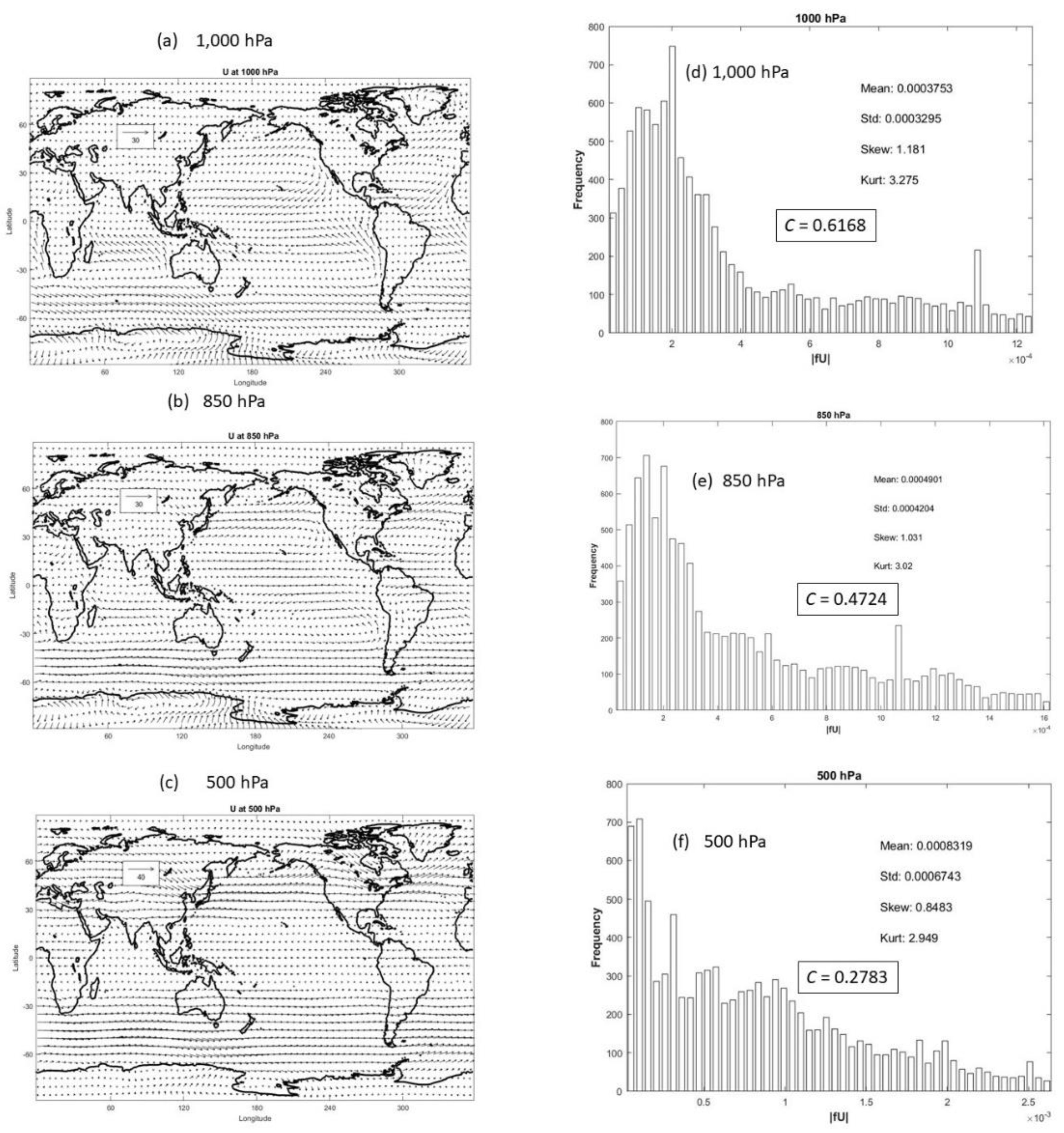
C number changes from 0.6168 (max) at 1,000 hPa to 0.1573 (min) at 200 hPa with a mean of 0.3052 in the troposphere. Both
B and
C numbers are greater than 0.27 for 1,000-500 hPa, and show that δ
g is non-negligible in comparison to
geff in the geostrophic wind especially in lower troposphere (1,000-500 hPa). The
D number varies from 1.3381 (max) at 500 hPa to 0.6712 (min) at 1,000 hPa with a mean of 1.0718, and shows that δ
g is comparable to
geff in the geostrophic vorticity. The
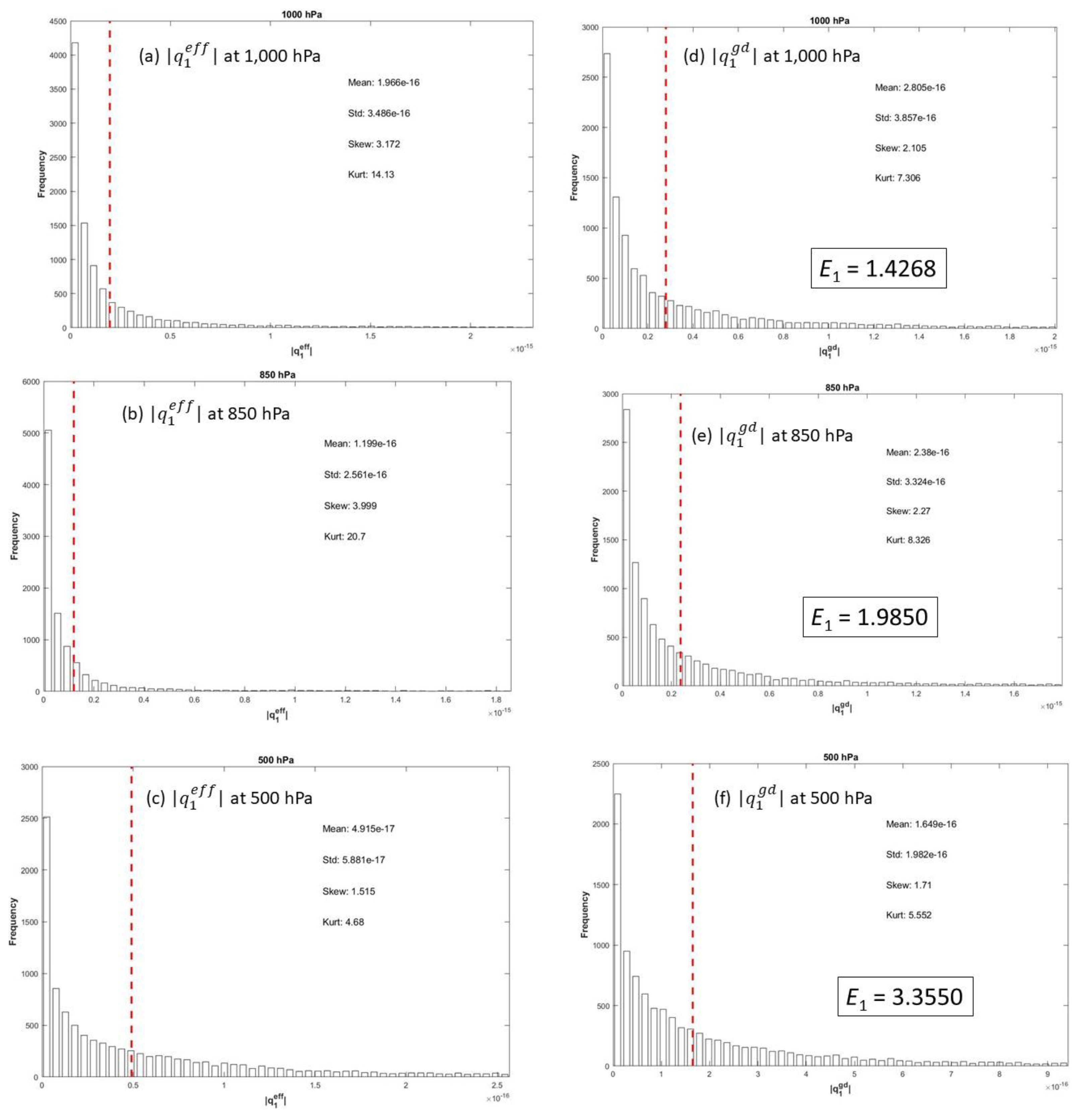
E1 number varies from 4.3834 (max) at 100 hPa to 1.4268 (min) at 1,000 hPa with a mean of 2.9313 and the
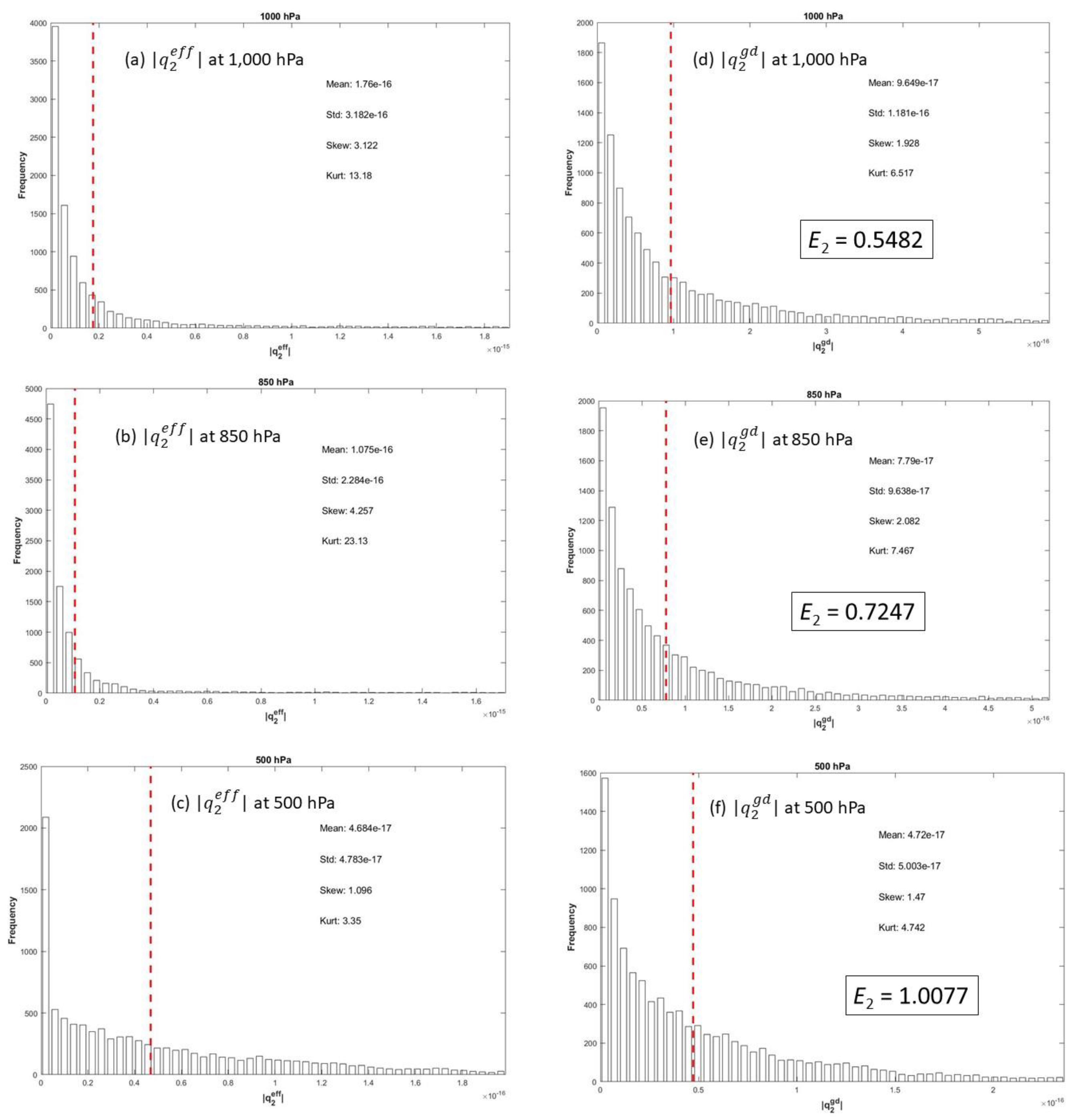
E2 number changes from 1.0570 (max) at 600 hPa to 0.5482 (min) at 1,000 hPa with a mean of 0.8211. Both
E1 and
E2 numbers show that δ
g is comparable to
geff in in the Q vector. The
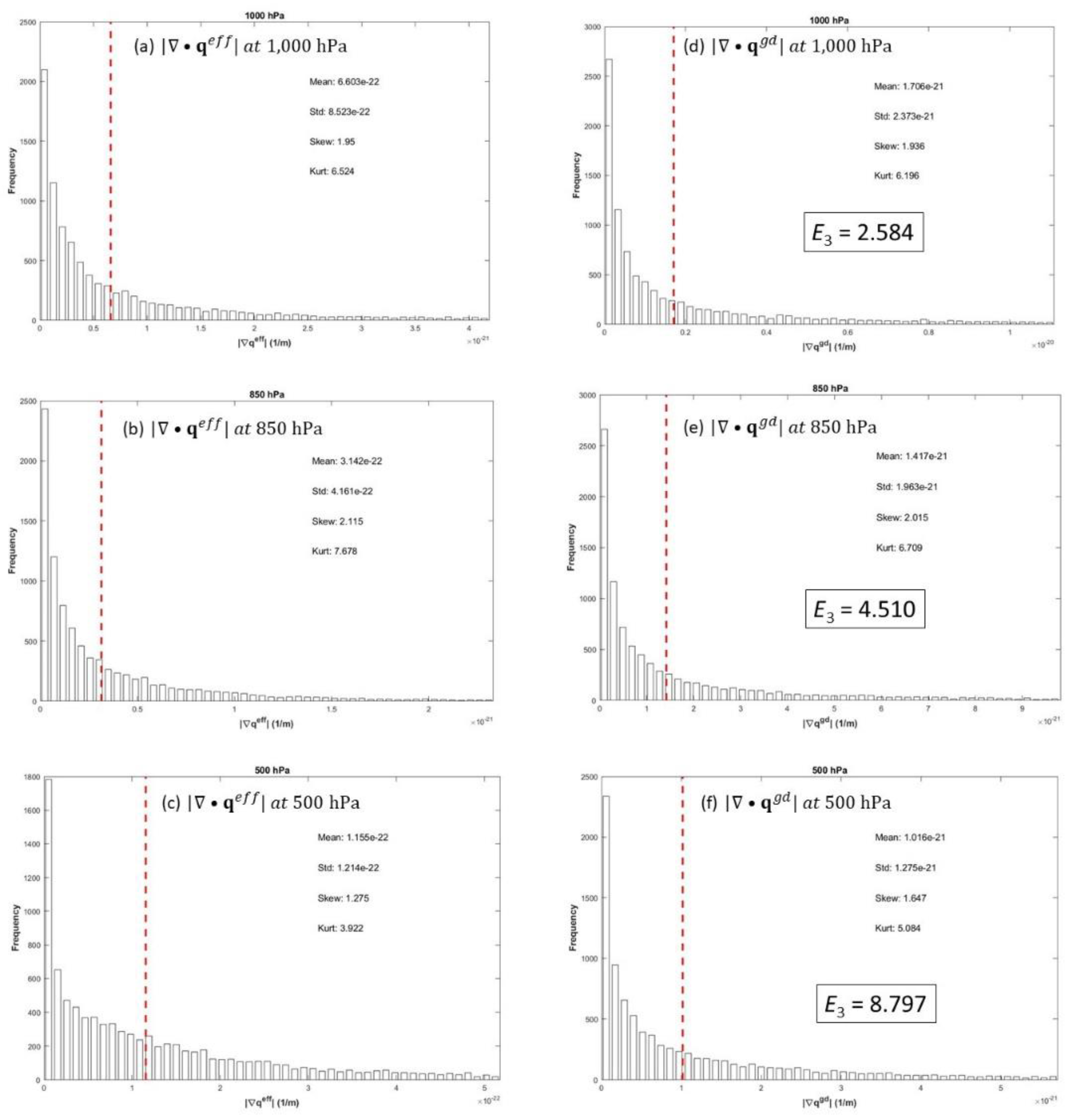
E3 number varies from 11.713 (max) at 100 hPa to 2.584 (min) at 1,000 hPa with a mean of 7.271, and shows that δ
g is extremely important in comparison to
geff in the Omega equation. In summary, the true gravity g should replace the effective gravity
geff, or the true geopotential (Φ = Φ
eff -
T) should replace the effective geopotential (Φ
eff) in large-scale atmospheric dynamics and modeling.
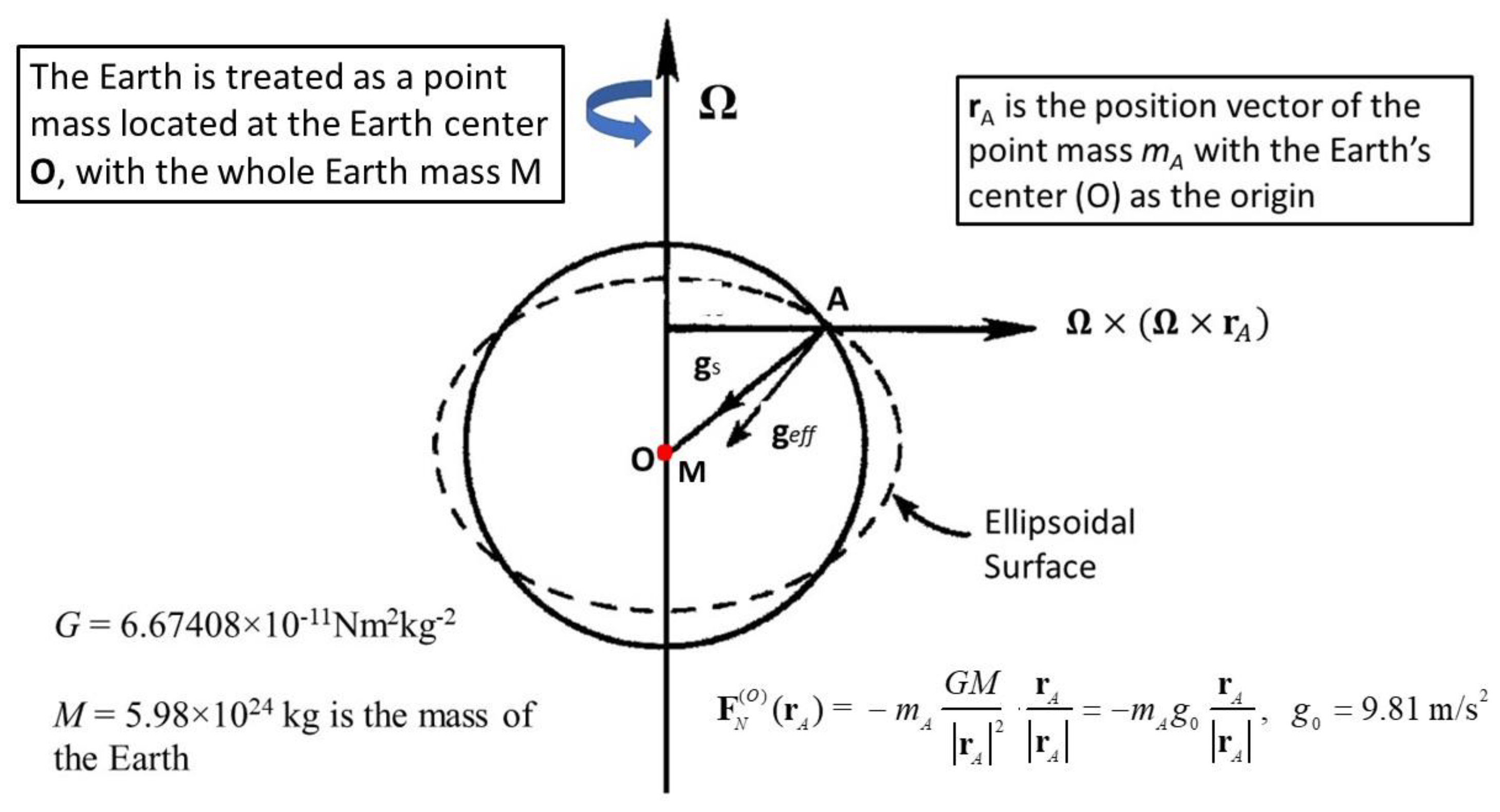
Figure 1.
In dynamic meteorology, the solid Earth shrinks into a point-mass (shown as the red dot) located at the Earth center (O) with the entire Earth mass. The Earth gravitation (untrue) on the point-mass mA in the atmosphere is between the point-mass MO and point-mass mA, and represented by F. Combination of the untrue Earth gravitational and centrifugal accelerations leads to the effective gravity geff, which is used in atmospheric modeling ever since.
Figure 1.
In dynamic meteorology, the solid Earth shrinks into a point-mass (shown as the red dot) located at the Earth center (O) with the entire Earth mass. The Earth gravitation (untrue) on the point-mass mA in the atmosphere is between the point-mass MO and point-mass mA, and represented by F. Combination of the untrue Earth gravitational and centrifugal accelerations leads to the effective gravity geff, which is used in atmospheric modeling ever since.
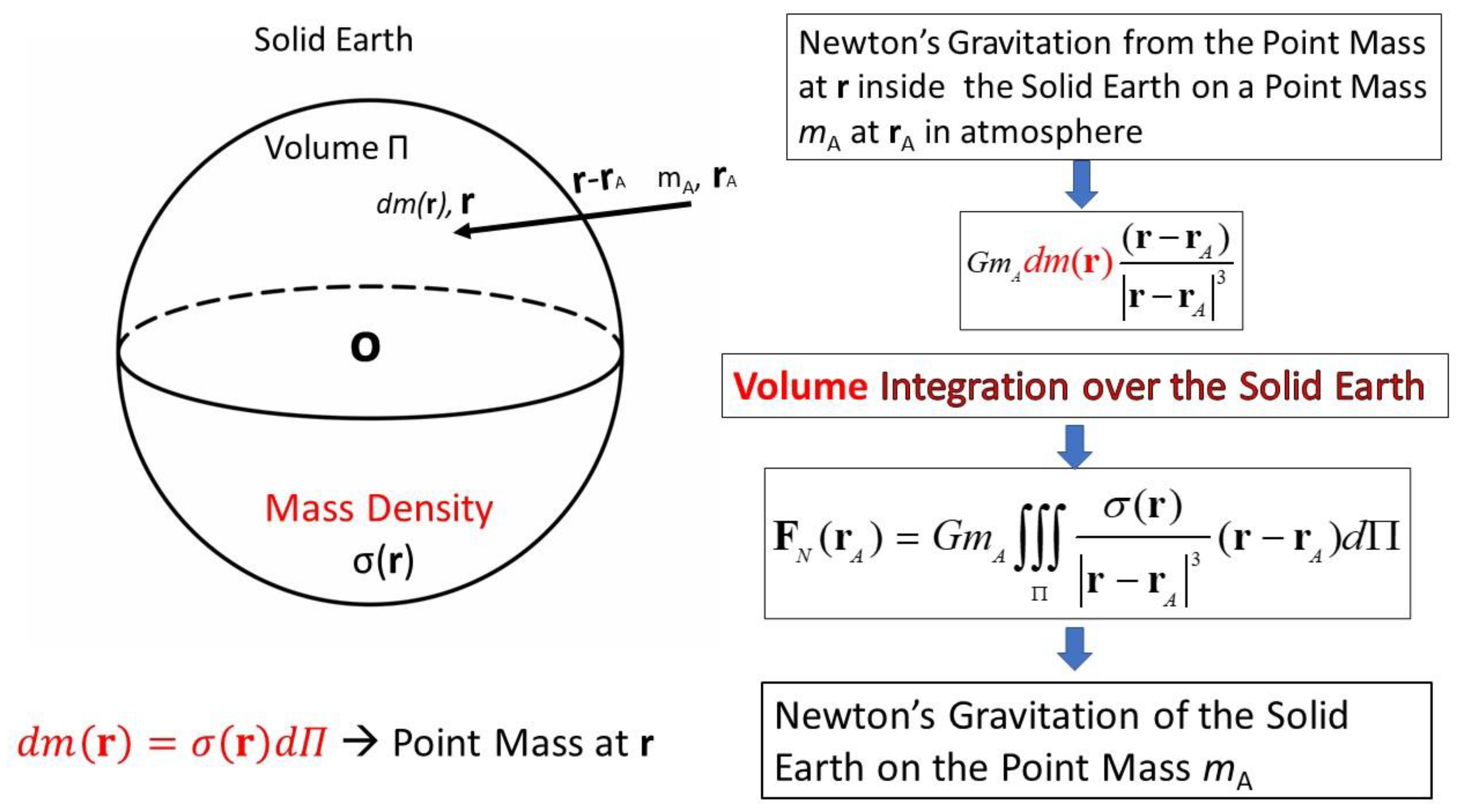
Figure 2.
Figure 2. The true Earth gravitation on a point mass mA at rA [i.e., FN(rA)] is the volume integration of Newton’s universal gravitation over all point-masses inside the Earth
Figure 2.
Figure 2. The true Earth gravitation on a point mass mA at rA [i.e., FN(rA)] is the volume integration of Newton’s universal gravitation over all point-masses inside the Earth
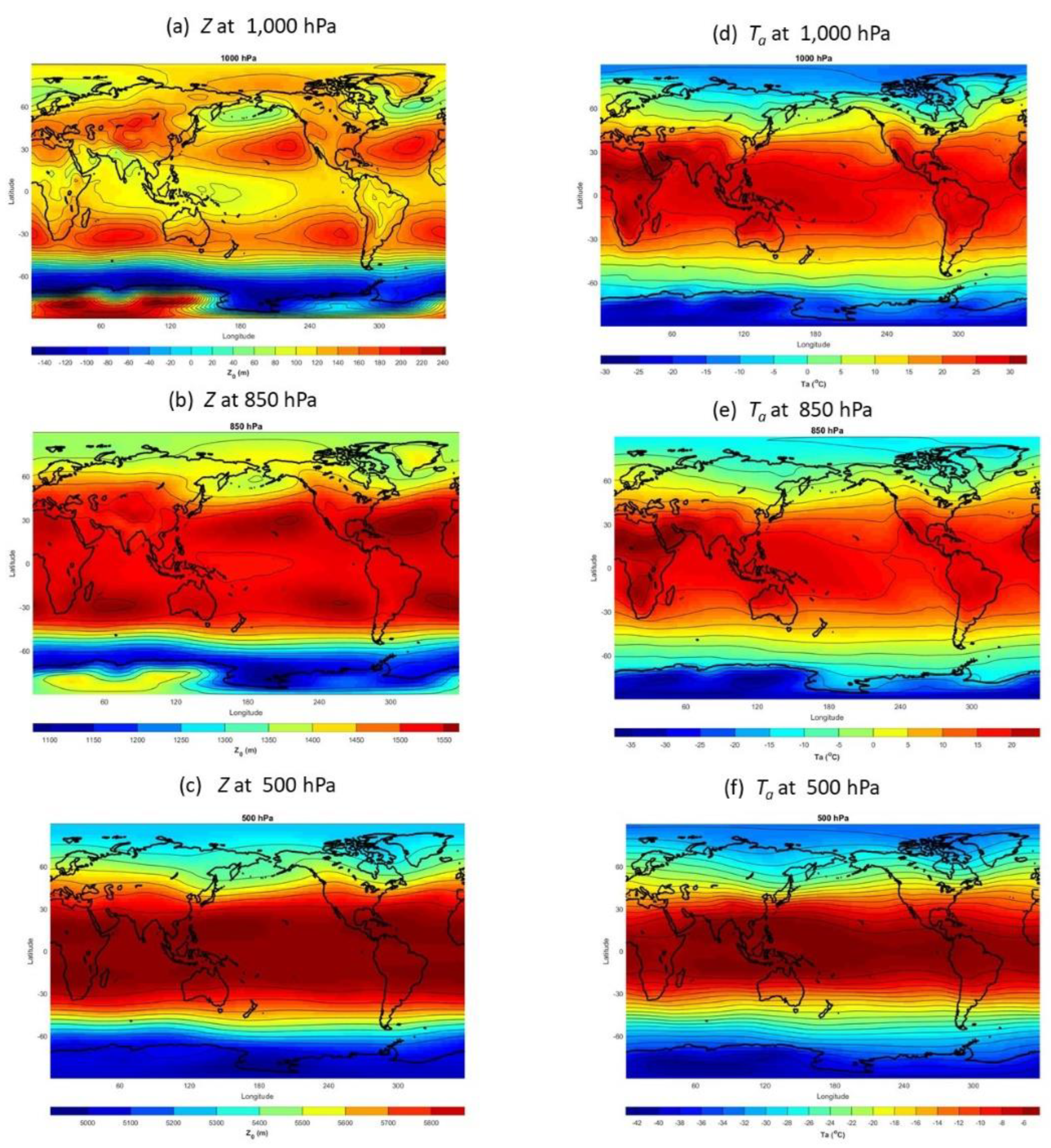
Figure 4.
Long-term annual mean data with 2.5
o×2.5
o resolution on the three pressure levels: geopotential height (
Z) at (a) 1,000 hPa, (b) 500 hPa, and (c) 100 hPa, and temperature (
Ta) at (d) 1,000 hPa, (e) 500 hPa, and (f) 100 hPa. The data were calculated from the long-term monthly mean
Z and
Ta obtained online at the website:
https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.derived.html.
Figure 4.
Long-term annual mean data with 2.5
o×2.5
o resolution on the three pressure levels: geopotential height (
Z) at (a) 1,000 hPa, (b) 500 hPa, and (c) 100 hPa, and temperature (
Ta) at (d) 1,000 hPa, (e) 500 hPa, and (f) 100 hPa. The data were calculated from the long-term monthly mean
Z and
Ta obtained online at the website:
https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.derived.html.
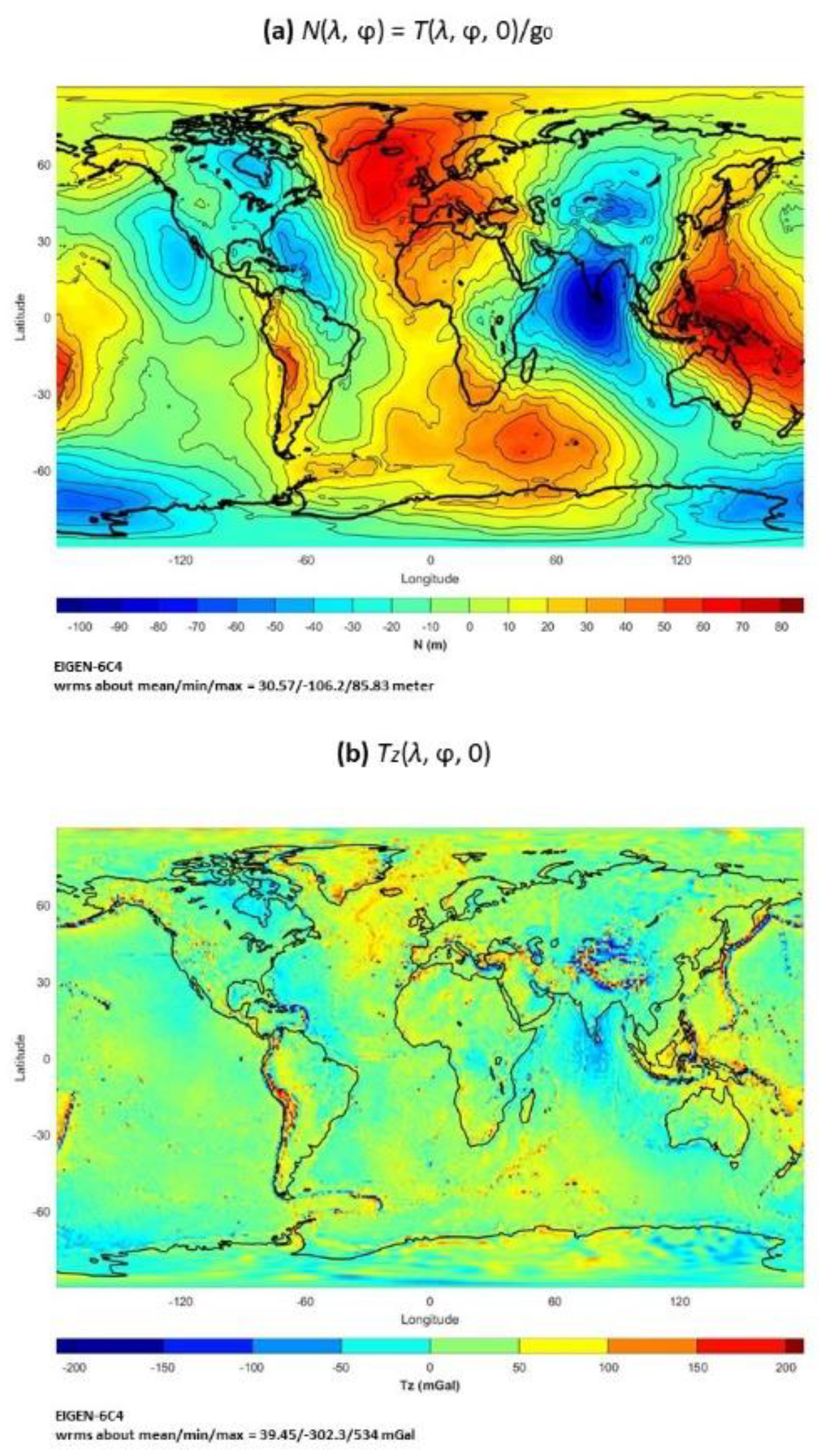
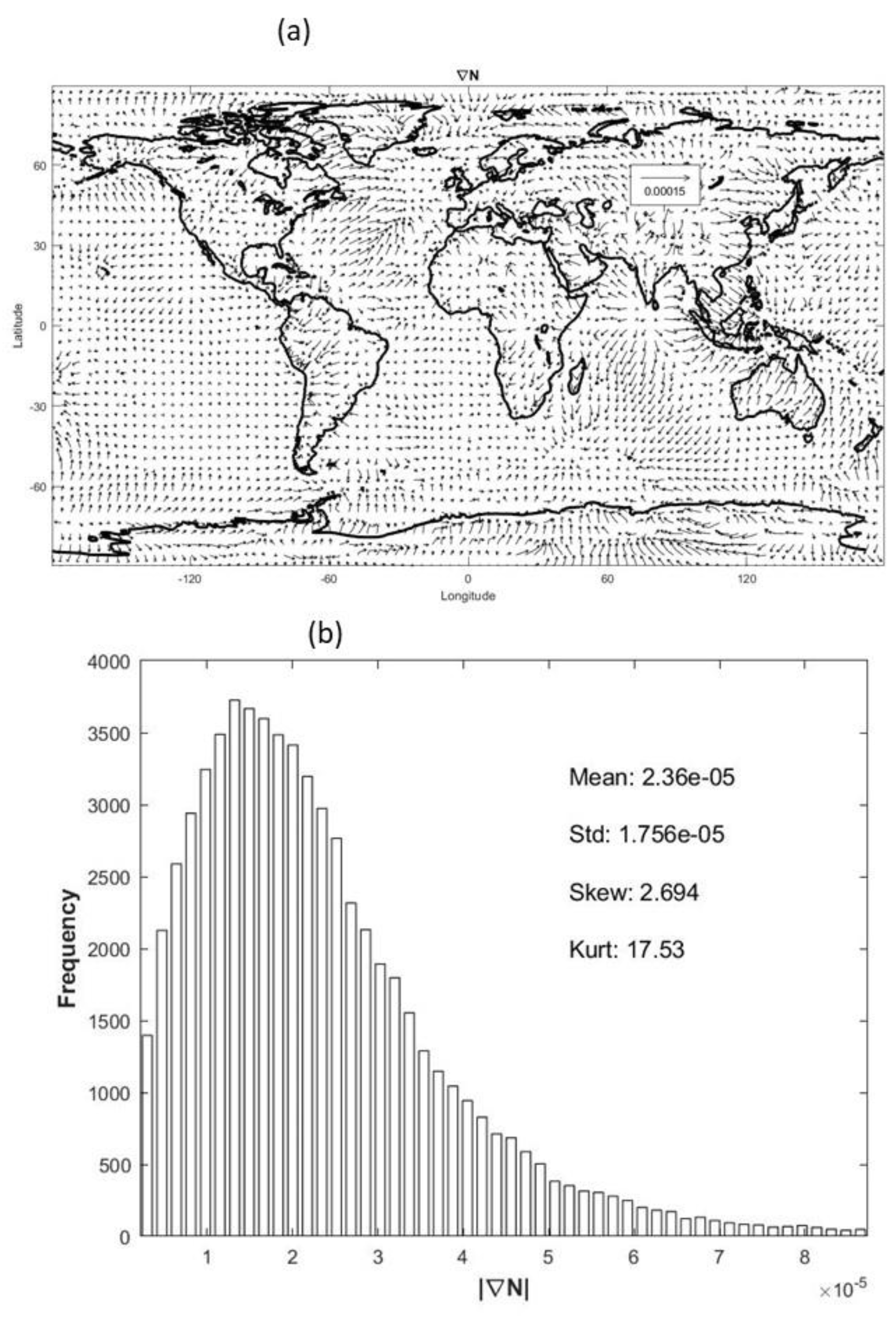
Figure 5.
(a) Vector plot of zN and (b) histogram of |zN |with four statistical parameters (mean, standard deviation, skewness, kurtosis).
Figure 5.
(a) Vector plot of zN and (b) histogram of |zN |with four statistical parameters (mean, standard deviation, skewness, kurtosis).
Figure 6.
Vector plot of on (a) 1,000 hPa, (b) 850 hPa, and (c) 500 hPa, and histograms of || with four statistical parameters (mean, standard deviation, skewness, kurtosis) and B number on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 6.
Vector plot of on (a) 1,000 hPa, (b) 850 hPa, and (c) 500 hPa, and histograms of || with four statistical parameters (mean, standard deviation, skewness, kurtosis) and B number on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 7.
Vector plots of long-term annual mean wind vectors (U) on (a) 1,000 hPa, (b) 850 hPa, and (c) 500 hPa, and histograms of |U| with four statistical parameters (mean, standard deviation, skewness, kurtosis) and
C number on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa. The long-term annual mean wind vector U were calculated from the long-term monthly mean wind vector U obtained online at the website:
https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.derived.html.
Figure 7.
Vector plots of long-term annual mean wind vectors (U) on (a) 1,000 hPa, (b) 850 hPa, and (c) 500 hPa, and histograms of |U| with four statistical parameters (mean, standard deviation, skewness, kurtosis) and
C number on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa. The long-term annual mean wind vector U were calculated from the long-term monthly mean wind vector U obtained online at the website:
https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.derived.html.
Figure 8.
Horizontal distributions of (a) zTz|/g0 , and Ta|/Ta on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa.
Figure 8.
Horizontal distributions of (a) zTz|/g0 , and Ta|/Ta on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa.
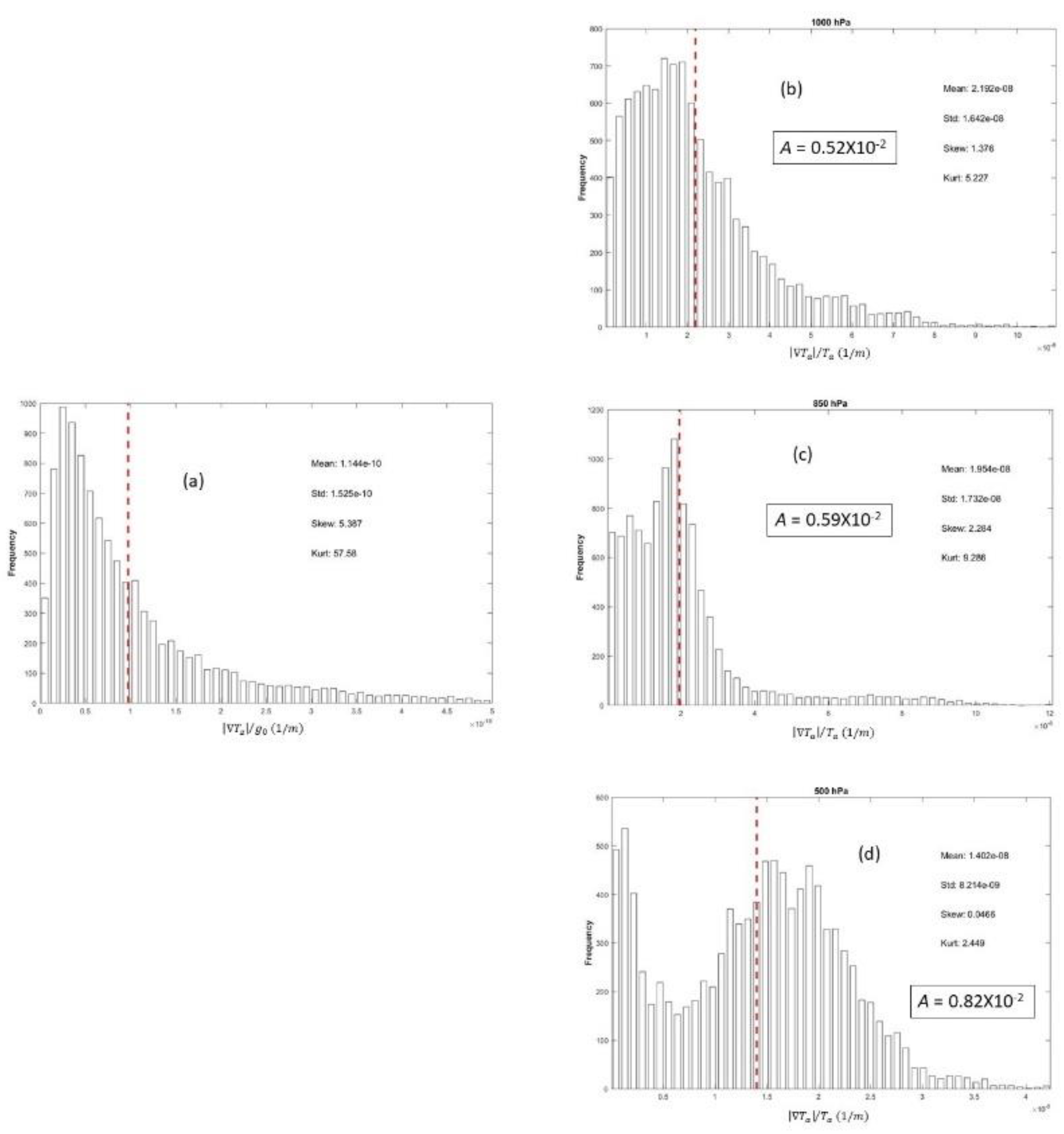
Figure 9.
Histograms of (a) zTz|/g0 , andTa|/Ta with four statistical parameters (mean, standard deviation, skewness, kurtosis) and A number on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa. The red dashed lines show the mean values from the corresponding histograms.
Figure 9.
Histograms of (a) zTz|/g0 , andTa|/Ta with four statistical parameters (mean, standard deviation, skewness, kurtosis) and A number on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa. The red dashed lines show the mean values from the corresponding histograms.
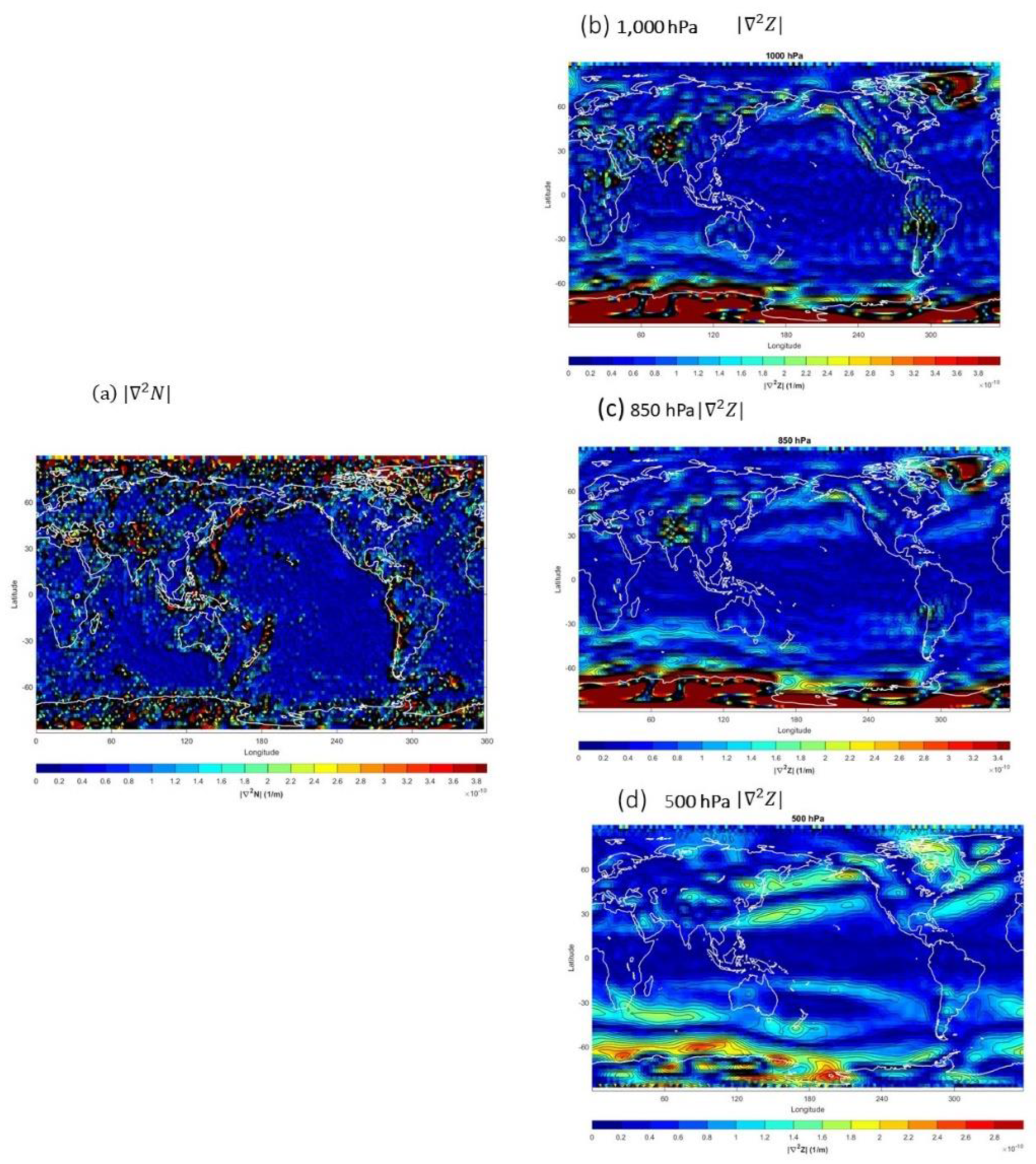
Figure 10.
Horizontal distributions of (a) N| and 2Z| on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa.
Figure 10.
Horizontal distributions of (a) N| and 2Z| on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa.
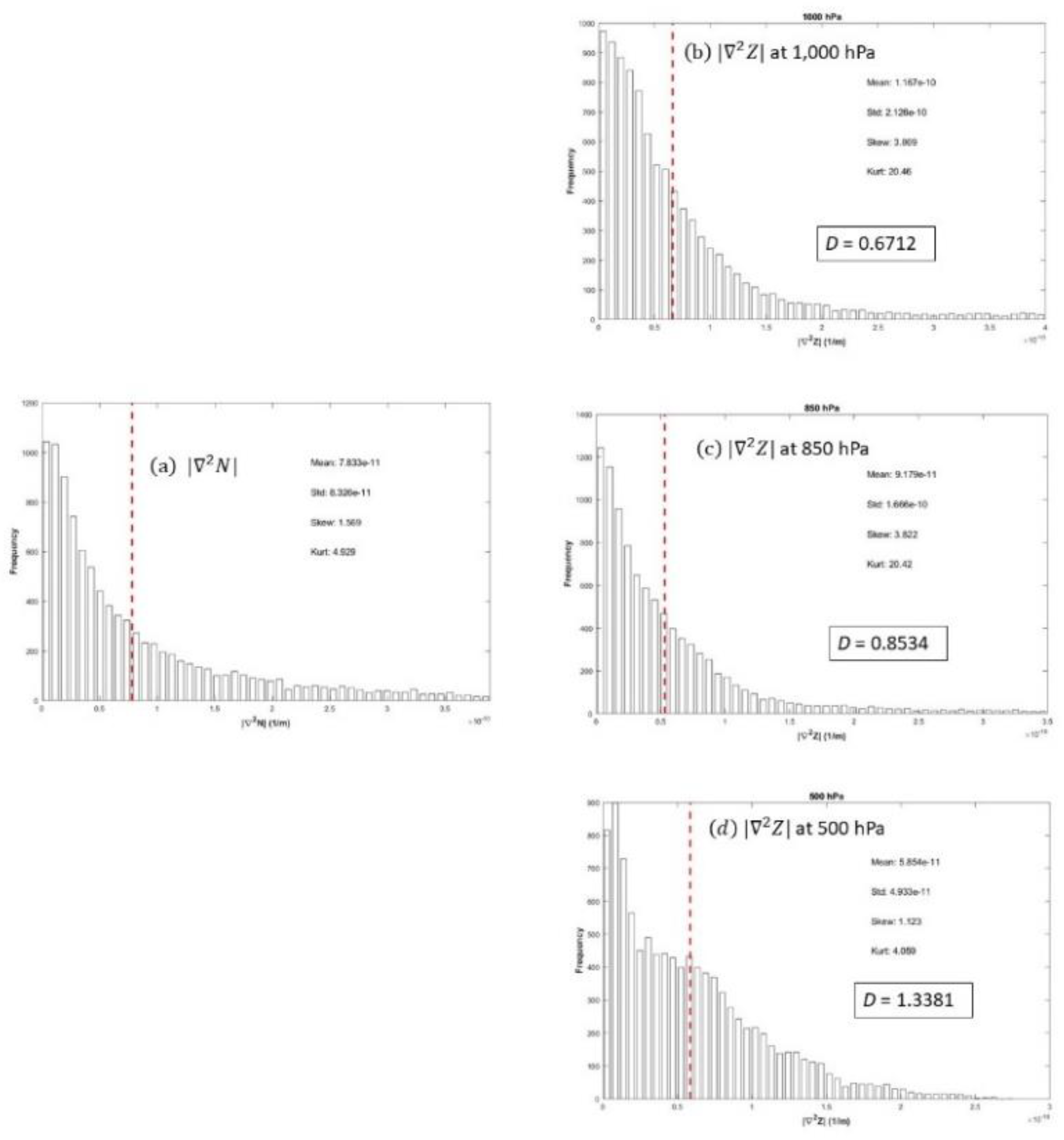
Figure 11.
Histograms of (a) N|, and 2Z| with four statistical parameters (mean, standard deviation, skewness, kurtosis) and D number on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa. The red dashed lines show the mean values from the corresponding histograms.
Figure 11.
Histograms of (a) N|, and 2Z| with four statistical parameters (mean, standard deviation, skewness, kurtosis) and D number on (b) 1,000 hPa, (c) 850 hPa, and (d) 500 hPa. The red dashed lines show the mean values from the corresponding histograms.
Figure 12.
Horizontal distributions of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 12.
Horizontal distributions of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
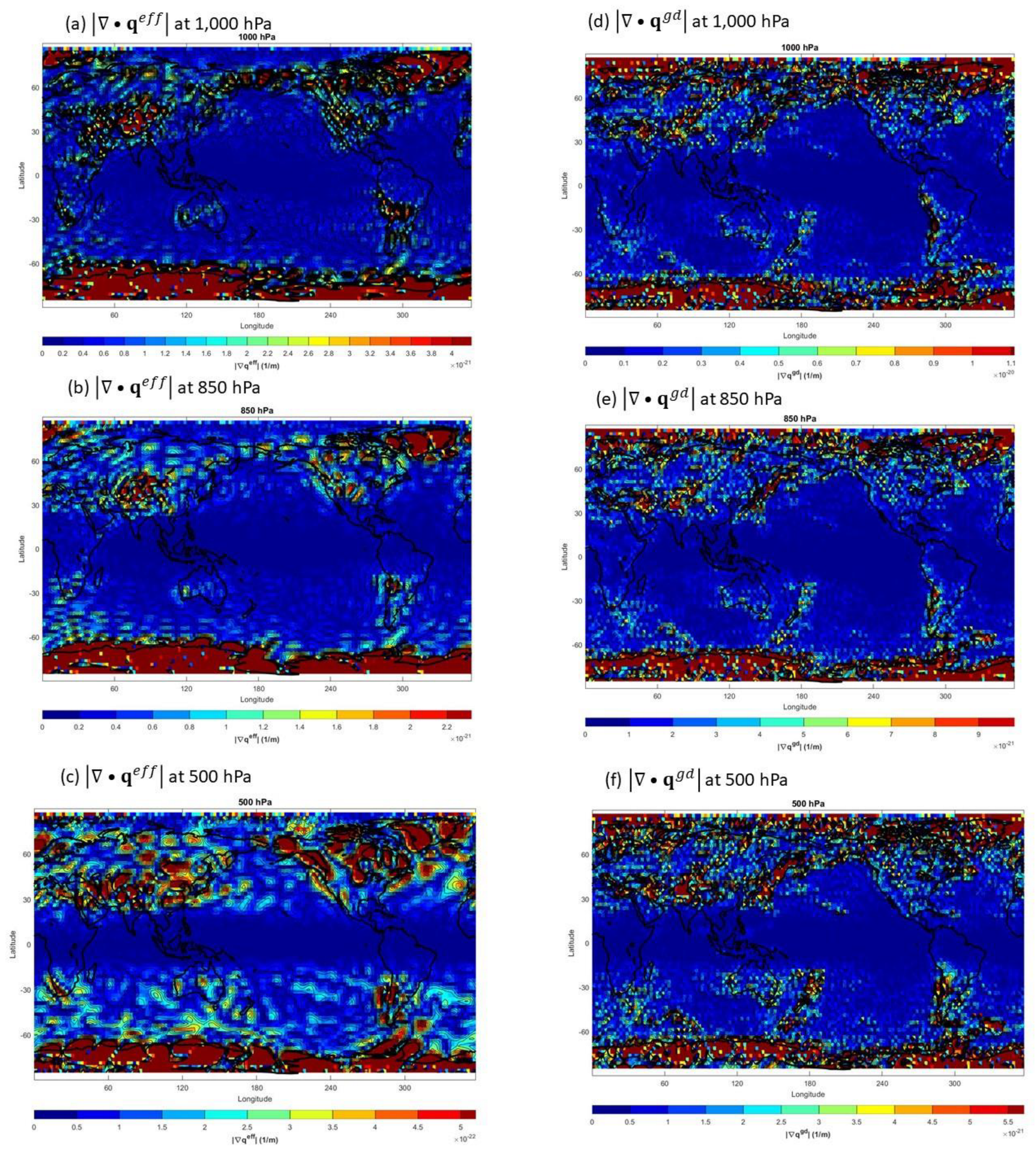
Figure 13.
Horizontal distributions of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 13.
Horizontal distributions of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 14.
Histograms of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E1 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
Figure 14.
Histograms of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E1 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
Figure 15.
Histograms of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E2 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
Figure 15.
Histograms of on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E2 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
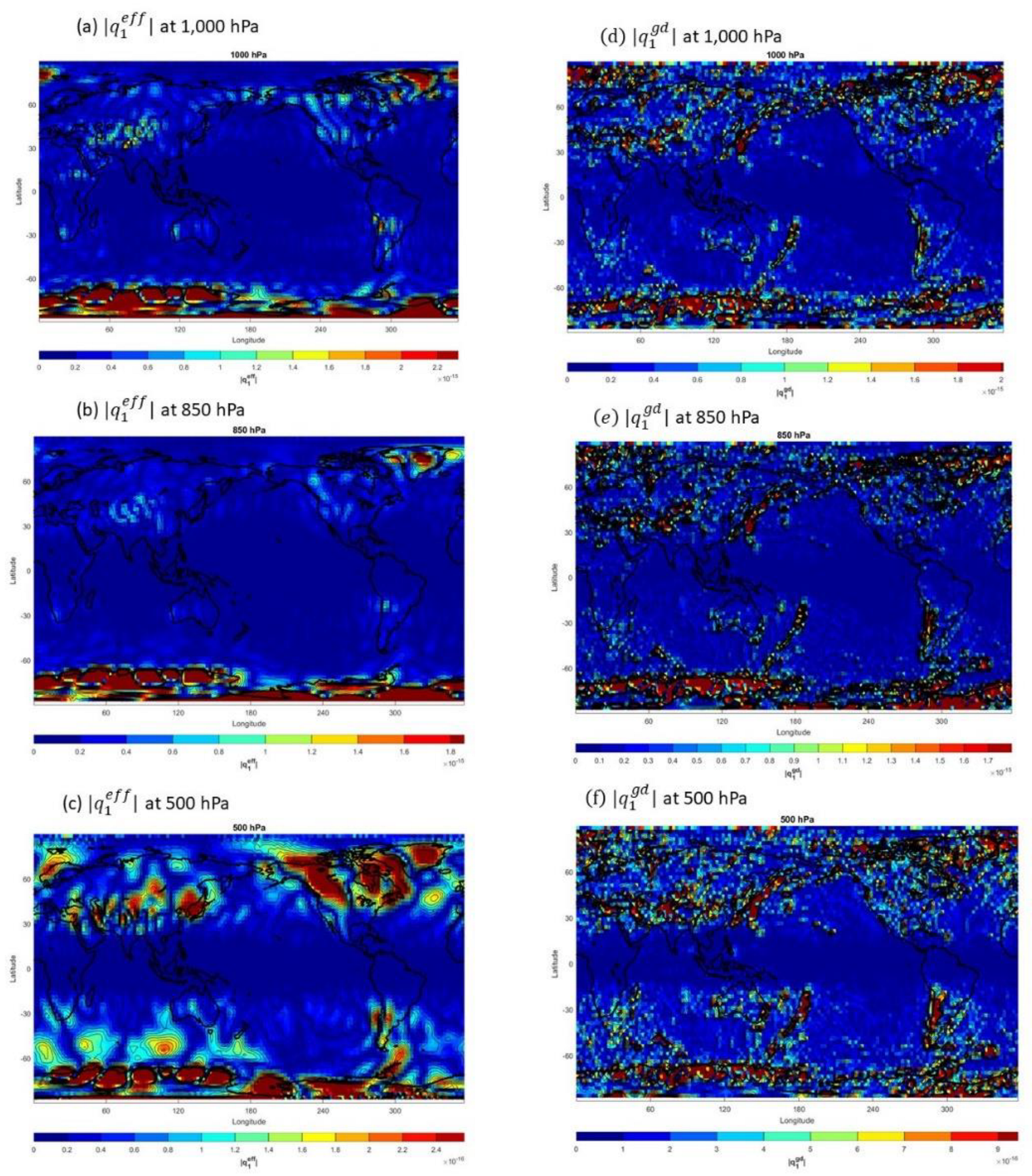
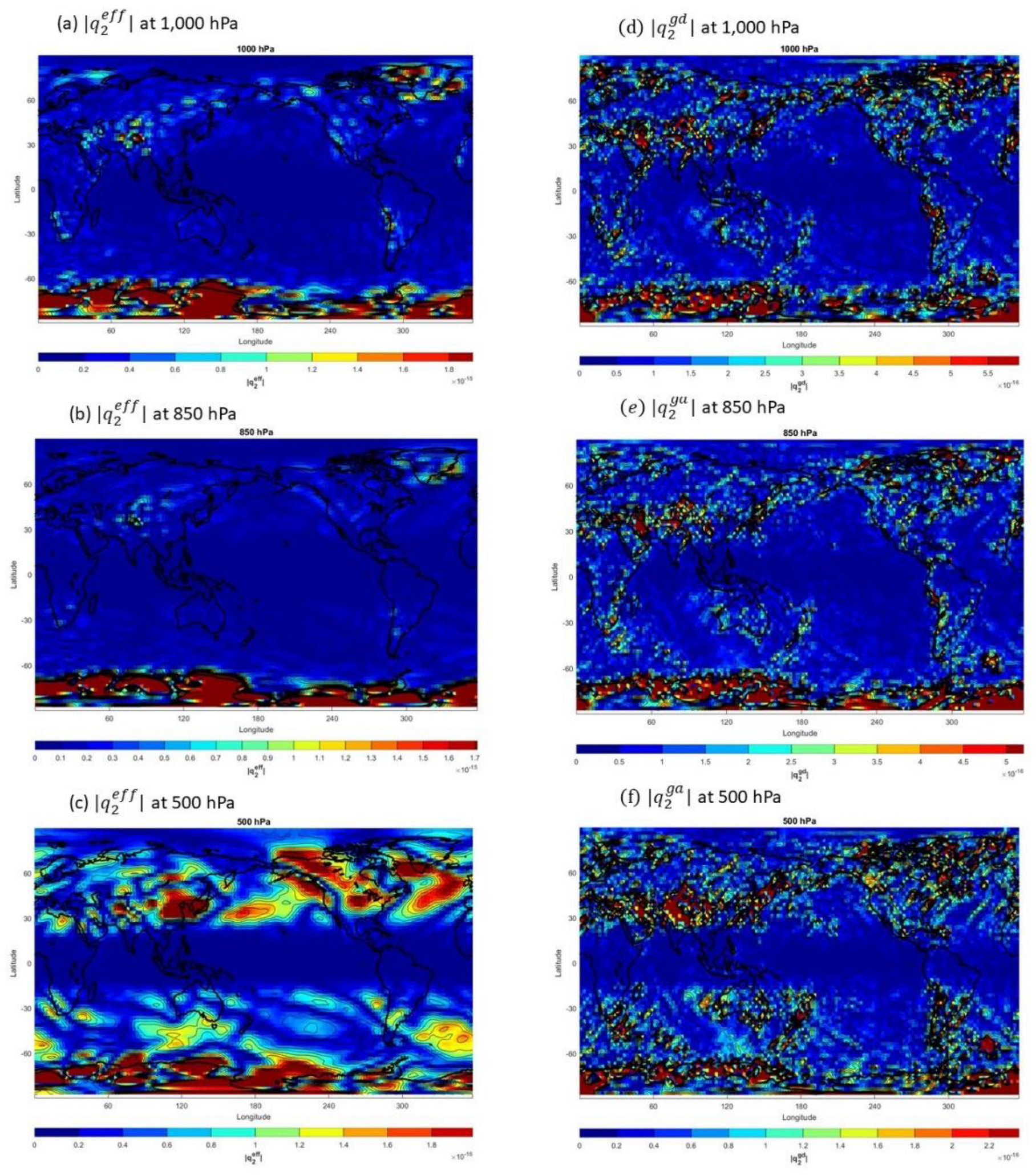
Figure 16.
Horizontal distributions of eff| on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of gd| on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 16.
Horizontal distributions of eff| on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of gd| on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa.
Figure 17.
Histograms of eff| on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of gd| on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E3 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
Figure 17.
Histograms of eff| on (a) 1,000 hPa, (b) 850 hPa, (c) 500 hPa, and of gd| on (d) 1,000 hPa, (e) 850 hPa, and (f) 500 hPa with four statistical parameters (mean, standard deviation, skewness, kurtosis) and E3 number on (d), (e), and (f). The red dashed lines show the mean values from the corresponding histograms.
Table 1.
Global means of zN |and annual at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional B-number.
Table 1.
Global means of zN |and annual at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional B-number.
| Pressure Level (hPa) |
) (10-5) |
zN | ) (10-5) |
B-number |
| |
|
2.360 |
|
| 1,000 |
5.824 |
|
0.4052 |
| 925 |
5.686 |
|
0.4151 |
| 850 |
5.651 |
|
0.4176 |
| 700 |
6.153 |
|
0.3836 |
| 600 |
6.870 |
|
0.3435 |
| 500 |
8.285 |
|
0.2849 |
| 400 |
10.27 |
|
0.2298 |
| 300 |
12.68 |
|
0.1861 |
| 250 |
13.78 |
|
0.1713 |
| 200 |
14.48 |
|
0.1630 |
| 150 |
14.40 |
|
0.1639 |
| 100 |
12.63 |
|
0.1869 |
Table 2.
Global means of (g0) and annual |fU| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional C-number.
Table 2.
Global means of (g0) and annual |fU| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional C-number.
| Pressure Level (hPa) |
Mean (|fU|) (mGal) |
Mean (g0) (mGal) |
C-number |
| |
|
23.15 |
|
| 1,000 |
37.53 |
|
0.6168 |
| 925 |
45.52 |
|
0.5086 |
| 850 |
49.01 |
|
0.4724 |
| 700 |
60.46 |
|
0.3829 |
| 600 |
69.59 |
|
0.3327 |
| 500 |
83.19 |
|
0.2783 |
| 400 |
103.3 |
|
0.2241 |
| 300 |
128.8 |
|
0.1797 |
| 250 |
140.7 |
|
0.1645 |
| 200 |
147.2 |
|
0.1573 |
| 150 |
143.7 |
|
0.1611 |
| 100 |
126.0 |
|
0.1837 |
Table 3.
Global means of zTz|/g0 and annual Ta|/Ta at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional A-number.
Table 3.
Global means of zTz|/g0 and annual Ta|/Ta at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional A-number.
| Pressure Level (hPa) |
Ta|/Ta )
(10-8 m-1) |
zTz|/g0)
(10-8 m-1) |
A-number |
| |
|
1.144×10-2
|
|
| 1,000 |
2.192 |
|
0.5219×10-2
|
| 925 |
2.025 |
|
0.5649×10-2
|
| 850 |
1.954 |
|
0.5855×10-2
|
| 700 |
1.885 |
|
0.6069×10-2
|
| 600 |
1.561 |
|
0.7329×10-2
|
| 500 |
1.402 |
|
0.8160×10-2
|
| 400 |
1.382 |
|
0.8278×10-2
|
| 300 |
1.168 |
|
0.9795×10-2
|
| 250 |
0.8997 |
|
1.2715×10-2
|
| 200 |
0.5773 |
|
1.9816×10-2
|
| 150 |
0.9135 |
|
1.2523×10-2
|
| 100 |
1.5140 |
|
0.7556×10-2
|
Table 4.
Global means of N| and annual 2Z| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional D-number.
Table 4.
Global means of N| and annual 2Z| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional D-number.
| Pressure Level (hPa) |
2Z|)
(10-10 m-1) |
N|)
(10-10 m-1) |
D-number |
| |
|
0.7833 |
|
| 1,000 |
1.167 |
|
0.6712 |
| 925 |
1.039 |
|
0.7539 |
| 850 |
0.9179 |
|
0.8534 |
| 700 |
0.7071 |
|
1.1078 |
| 600 |
0.5870 |
|
1.3344 |
| 500 |
0.5854 |
|
1.3381 |
| 400 |
0.6252 |
|
1.2529 |
| 300 |
0.7013 |
|
1.1169 |
| 250 |
0.7320 |
|
1.0701 |
| 200 |
0.7415 |
|
1.0564 |
| 150 |
0.7150 |
|
1.0955 |
| 100 |
0.6469 |
|
1.2109 |
Table 7.
Global means of gd| and annual eff| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional E3-number.
Table 7.
Global means of gd| and annual eff| at 12 pressure levels in the troposphere (treated as the order of magnitude) as well as the non-dimensional E3-number.
| Pressure Level (hPa) |
eff|)
(10-22 m-1) |
gd|)
(10-22 m-1) |
E3-number |
| 1,000 |
6.603 |
17.06 |
2.584 |
| 925 |
4.486 |
15.10 |
3.366 |
| 850 |
3.142 |
14.17 |
4.510 |
| 700 |
1.787 |
12.35 |
6.911 |
| 600 |
1.270 |
10.95 |
8.622 |
| 500 |
1.155 |
10.16 |
8.797 |
| 400 |
1.054 |
9.311 |
8.834 |
| 300 |
0.9258 |
6.939 |
7.495 |
| 250 |
0.7629 |
5.813 |
7.620 |
| 200 |
0.5760 |
4.416 |
7.667 |
| 150 |
0.6631 |
6.077 |
9.165 |
| 100 |
0.8011 |
9.383 |
11.713 |
Table 8.
Non-dimensional
A,
B,
C,
D,
E1,
E2,
E3 numbers at 12 pressure levels in the troposphere (obtained from the 4
th column of
Table 1,
Table 2,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7) to represent the importance of gravity disturbance vector δ
g in large-scale atmospheric dynamics and modeling.
Table 8.
Non-dimensional
A,
B,
C,
D,
E1,
E2,
E3 numbers at 12 pressure levels in the troposphere (obtained from the 4
th column of
Table 1,
Table 2,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7) to represent the importance of gravity disturbance vector δ
g in large-scale atmospheric dynamics and modeling.
| Pressure Level (hPa) |
A
ThermalWind |
B C
Geostrophic Wind |
D
GeostrophicVorticity/Ekman Pumping |
E1
Q1
|
E2
Q2
|
E3
Omega Equation |
| 1,000 |
0.0052 |
0.4052 |
0.6168 |
0.6712 |
1.4268 |
0.5482 |
2.584 |
| 925 |
0.0056 |
0.4151 |
0.5086 |
0.7539 |
1.6708 |
0.6205 |
3.366 |
| 850 |
0.0059 |
0.4176 |
0.4724 |
0.8534 |
1.9850 |
0.7247 |
4.510 |
| 700 |
0.0061 |
0.3836 |
0.3829 |
1.1078 |
2.8620 |
0.9097 |
6.911 |
| 600 |
0.0073 |
0.3435 |
0.3327 |
1.3344 |
3.3175 |
1.0570 |
8.622 |
| 500 |
0.0082 |
0.2849 |
0.2783 |
1.3381 |
3.3550 |
1.0077 |
8.797 |
| 400 |
0.0083 |
0.2298 |
0.2241 |
1.2529 |
3.3121 |
0.9395 |
8.834 |
| 300 |
0.0098 |
0.1861 |
0.1797 |
1.1169 |
3.0013 |
0.8091 |
7.495 |
| 250 |
0.0127 |
0.1713 |
0.1645 |
1.0701 |
3.2204 |
0.7786 |
7.590 |
| 200 |
0.0198 |
0.1630 |
0.1573 |
1.0564 |
3.1943 |
0.6829 |
7.667 |
| 150 |
0.0125 |
0.1639 |
0.1611 |
1.0955 |
3.4567 |
0.7789 |
9.165 |
| 100 |
0.0076 |
0.1869 |
0.1837 |
1.2109 |
4.3834 |
0.9965 |
11.713 |
| Mean |
0.0091 |
0.2792 |
0.3052 |
1.0718 |
2.9313 |
0.8211 |
7.271 |