Preprint
Article
Harnessing the Power of Online Inter-Class Tournaments to Imitate, Recombine, and Craft Innovative STEM Teaching Strategies
Altmetrics
Downloads
183
Views
79
Comments
0
This version is not peer-reviewed
Submitted:
08 February 2023
Posted:
10 February 2023
You are already at the latest version
Alerts
Abstract
There are increasing calls in education for deeper integration of disciplines and better preparation for the personal and job challenges of a fast-changing and smarter society. Thus, we need to search for new effective didactic strategies. However, current classrooms are isolated. They practically never connect. This hinders the exchange of ideas. It inhibits imitation and recombination, the basic blocks of cultural evolution and innovation. In this paper, we analyze online inter-class tournaments. These are lessons where entire elementary or middle school classes interconnect synchronously and play an educational game. These are new types of academic activities, and only possible thanks to digital communication technology. In this paper, we examine four online tournaments, we analyze how feasible it is to carry them out and the benefits they bring. One tournament is for teaching machine learning and statistics. The second one teaches the conservation of momentum in physics and an engineering optimization challenge. The third tournament is for learning to solve word problems. The fourth one is for teaching natural and sexual selection along with developing statistical and population thinking. We found that these inter-class tournaments are feasible to implement in schools and that they are a promising mechanism to facilitate imitation, recombination, and innovation of teaching strategies.

Keywords:
Subject: Social Sciences - Education
1. Introduction
There is an increasing demand in more integration across disciplines in K12 education [1] and better preparation for the personal and job challenges of a fast-changing and smarter society [2,3]. This is because, on the one hand, teaching in a more connected way, and more related to real-life problems, can make education more relevant, more meaningful, increase motivation to learn and improve student achievement [4,5]. On the other hand, students need a deeper understanding of core ideas of each discipline, and integration across disciplines helps to achieve a deeper understanding of each discipline. Thus, the call is to link concepts and skills learned from two or more disciplines in order to gain a deeper knowledge and understanding.
Therefore, teachers need to learn to teach connecting STEM disciplines. They should help students learn core STEM concepts and develop STEM skills such as rigorous argumentation, problem solving and modeling abilities [6]. They should help students understand core science concept [7] such as patterns, information, conservation laws, data and modeling, particulate nature of nature, energy and metabolism, and natural and sexual selection. Moreover, integration also means that STEM teachers should help students deal with key current national and global challenges: climate change, social inequalities, emotion and cognition, pandemics, impersonal trust [3,5]. They should also help students develop oral and written communication and argumentation, values and beliefs, attitudes, responsible citizenship, cooperation and teamwork. In addition, teachers should make students´ learning more meaningful and improve their preparation for the personal and job challenges of a fast changing and smarter society. They should do all that without hindering their teaching of each discipline.
One integration strategy is teaching real world applications. According to Grossmann ([8], pp. 146) “Interdisciplinarity has gained the most ground in applied fields, where the assumptions and common methods of different fields can be brought to bear on the same substantive questions and outcomes”. In the case of mathematics, an example is statistics. All disciplines are generating more and more data and at an increasing speed. This translates into an increased use of statistics in a growing number of disciplines [9]. Another example is mathematical modeling [4,10,11] and computational modeling [12,13,14,15]. There are also contents and practices in computational thinking that are gaining increasing importance in industry and consumer-oriented applications. Nevertheless, they do not yet have a place in the K12 curriculum. For example, agent-based modeling [13], machine learning [5], or natural language and image processing do not yet appear in the national curricula. These recent computational developments directly connect mathematics and computation with the social sciences, psychology, biology, and language. Here there is a huge potential for across discipline integration.
However, integration has several barriers. First, a significant proportion of students have poor understanding of the core ideas in the individual disciplines. Thus, for them, connecting ideas across disciplines is not straightforward at all [1,16]. This means that teachers are primarily concerned with teaching the core concepts of their discipline, and do not have time to spend exploring ways to integrate with other disciplines.
Second, the amount of knowledge of each discipline is increasing rapidly. It is a true explosion of ideas, methods and results. Thus, there are strong pressures on the curriculum to introduce new content in each discipline. These contents are also new for teachers. For example, we have now proposals of new curricula with concepts of computational thinking and the introduction of machine learning concepts in statistics [2,17].
Third, the new concepts of each discipline are not always intuitive. Sometimes they seem to contradict our intuitions or our previous knowledge. Teachers then have to invest time planning on how to teach these new ideas. For example, in Bayesian reasoning, use of adequate representations is critical for true understanding [18,19].
Fourth, there is a clear division of labor at schools. Teachers teach their discipline, in which they have been educated. Even in traditionally closely related disciplines, such as mathematics and physics, teachers teach only one discipline. The only exception is in the first levels of elementary education. However, even there, the teacher does not make an integration across disciplines. Teachers teach each discipline as a world apart from the others. Teachers teach the two critical disciplines, language and mathematics, as if they had nothing in common. Today, with the development of computer science in the area of natural language processing, both disciplines are increasingly closer. For example, in Large Language Models (LLM) such as ChatGPT [20], which is having a great impact on society, and in particular in research and education. However, mathematics and language remain completely separate in the curricula and at schools.
Fifth, we need to learn how to teach disciplines with a much deeper integration between them. This is something new for most teachers. They were not educated in the teaching of several different disciplines; let alone how to integrate them. There are still very few instances of teacher education in integrating disciplines [21].
Sixth, teaching is a very conservative profession, “pedagogical change offers the teacher little apparent benefit and a great apparent risk” ([22] pp. 55). In addition, integration poses a high risk. Activities that integrate disciplines could be very motivational, but can hinders high-quality instruction that help understand the practices and principles of each discipline [23].
Seventh, there is a lack of textbooks and materials with integrated disciplines. For example, there are no math-biology o math-social sciences school textbooks. Moreover, in each discipline its textbooks don´t have much integration with other disciplines. Therefore, this lack of materials requires teachers to invest a great deal of time and energy in studying other disciplines, meeting and exchanging ideas with other teachers, and beginning to try out new classroom alternatives.
Eight, it is still not completely clear how mathematics taught according to the curriculum helps to gain a better understanding of the other disciplines; nor do we understand other disciplines help students in learning math [16].
Ninth, there is a “structural isolation” in the teaching profession. Teachers teach behind closed doors ([24], pp. 51-52). This structural isolation between teachers and the impenetrable walls between classrooms makes it very difficult to compare, imitate, and exchange educational strategies.
Finally, teachers do not receive feedback about across-discipline integration from monitoring or evaluation systems. For example, class observation protocols and teacher evaluation reports don´t include information about integration. Additionally, national or state students´ tests don´t include knowledge that measure integration across disciplines.
Thus, across discipline integration has several formidable barriers to overcome. It is a completely new challenge. In addition, we need to learn to implement it in large scale.
2. Literature Review
2.1. Cultural Evolution: Imitation, Recombination, Innovation
Review of classroom practices show that almost no change has taken place over the last century [25,26]. Teachers mainly teach teacher-centered strategies. Some teachers are very effective when using such strategies. For example, on the Programme for International Student Assessment (PISA), the top-performing Organization for Economic Co-operation and Development (OECD) countries use more teacher-centered teaching practices in mathematics than other countries [27].
To best improve teaching that integrates disciplines, we need to research and understand how to design and manage communities of teachers that work together. These communities should focus on devising classroom practices that promote interdisciplinary learning. This type of research is new to the field of education and should be given more emphasis by educational researchers. The results of this research will be crucial to the success of classroom practices that promote integration across disciplines, and strategies that integrate educational research with classroom practice [28].
To do this, one of the main difficulties is that current classrooms are isolated. [22] compares a school to a nuclear power station. Since each component of a nuclear facility is causally interrelated with the others, it is much easier to trace the chain of events and thus pinpoint the source of any deficiency and correct it. Schools, on the other hand, have completely independent units (classrooms). What happens in one unit does not affect the others. They practically never connect or exchange information. There are very few opportunities for interaction with other classrooms. This situation hinders sharing ideas and strategists, copying and recombining them.
One tends to think that the problem is how to implement strategies carefully designed by authorities and experts. However, cultural evolution processes, needs the active participation of a large community. Moreover, innovations and change emerge from thousands of people attempting and interchanging ideas [29]. No one is really in charge. For example, in the history of the critical cultural evolutions of humankind, such as the jump from tribal to bigger societies, they did it without anyone having a global understanding of how it all fit together ([30], pp. 102). It is an incremental, bottom-up, rather random process. It occurs as a direct result of exchange, imitation and recombination, and not as an orderly top-down process developed according to a plan.
Additionally, the collective brain perspective suggests an optimal amount of interconnectivity. Too much interconnectivity is not always better. The diffusion of complex behavior requires a mechanism that goes beyond simple interconnection. Complex behavior follow a different adoption mechanism that the one required for simple ones. Two key components are reiteration and homophily. This means that individuals require repeated interactions, and that those interactions be with multiple peers, similar to them [31,32].
In summary, we need to facilitate and speed up mechanisms for developing new teaching practices that include across disciple integration. This is a deep cultural evolution process. It requires to device powerful mechanisms of inter-group connection, with the appropriate diffusion mechanisms. They should foster innovation and dissemination of new strategies. We have to device appropriate network topologies, closer to a fishing net than a fireworks display [33], that connects teachers and their classroom with other similar teachers and their classrooms. The process should consider reiteration and homophily. This means high frequency of interactions between teachers and between classrooms. Homophily means that the interactions should be with similar teachers and similar classrooms. We need to design collective learning strategies that promote social comparison, such as intergroup competition and intra group collaboration [34].
We must understand the mechanics of knowledge creation and mobilization. We should design ways to accelerate how teachers and schools identify problems and develop interventions and strategies [28,35]. We finally depend on the fact that we are smart because we have culture, not the other way around [36].
2.2. Lesson Study and Open Lessons
Teachers need well tested strategies. This means, teaching strategies developed in the classroom, and tested with students with similar grade levels, demographic and socio economic profiles. This is not a top-down process. Bottoms-up processes could be very effective, more sustainable and better to scale.
A popular bottoms-up practice is Lesson Study. It is a teacher professional development strategy, created in Japan in 1880. It is now increasingly widespread in Asia and the rest of the world [37]. It is a collaborative teaching improvement process. Its goal is to build strong and productive communities of teachers who share and learn from each other. According to ([25], pp. 181), when teachers work together, they build pedagogical capital. This is a scarce resource because isolation is endemic in schools. On the contrary, lesson study is teamwork. Several teachers work together designing, testing and improving a lesson. This process accelerates the production of effective lessons and lessons that aim to develop higher-order thinking skills [38]. It is a collective intelligence strategy to develop better lessons. They also help innovation in order to introduce new lessons adapted for new challenges. For example, lessons with integration across disciplines and that are also cross-border, integrating classes from different countries in a lesson [39,40,41].
After the team of teachers develop and test their lesson, a teacher performs it in public. In a school theater or gym, tens or hundreds of teachers actively observe this open or public class. Then, in the same place, the teachers analyze it. It is a large community of teachers observing and analyzing together a class on a key topic they have to teach and with students similar to theirs. It is a true collective brain in action.
Lesson Study and Open Lessons are powerful strategies that promotes collaborative work among teachers, who imitate and then improve strategies. However, they have some constraints [42]. They require a lot of time from teachers. They have to coordinate, find a common spot of time to meet and observe a classroom, visit other schools and review together recorded lessons. Another constraint is the lack of a constant comparison between classes since there is no competition between classes. Inter group competition is a core mechanism of cultural evolution [30]. “It pushes against the within-group forces of cultural evolution, which often favor self-interest, zero-sum thinking, collusion, and nepotism” ([30], pp. 360).
Contrary to other human endeavors, the lack of competition in education is due in part to a no pro-competitive culture. This is very curious, because there is competition in some popular school events. For example, in athletic Olympiads, and Math and Science Olympiads. There is also competition in team sports, and in musical contests. They are very popular in schools [43]. Moreover, inter-group competition increases intra-group cooperation [44]. Nevertheless, in schools there are practically no competition or tournaments between entire classes on academic subjects. On the contrary, in all schools there is a much stronger competition but of different nature. It is a competition between students in the same class. It is the competition generated by the usual students´ assessments. This intra-class competition inhibits collaboration.
3. Theoretical Framework
3.1. Inter-Group Play
Play is a natural educational strategy. Mammals and even birds play to learn [45]. For this reason, play to learn has great potential for teaching and learning [46,47]. That explains the interest in educational math games [48]. Play is the natural pedagogy. Thus, the proposed theoretical framework in this paper is play. However, a uniquely human type of play is competition play between groups. It is coalitional play fighting between two or more groups. Inter-group play is very popular, and are the basis of team sports. Ethnographic evidence with hunter-gatherers, until recently around, suggests that inter-group games are universal and they have been a basic learning strategy in the evolution of human culture. Dyadic play fighting occurs in many species, but only humans engage in coalitional play fighting [49].
Additionally, the massiveness and popularity of some team sports and the size of the entertainment industry based on team sports indicate that we have psychological components that make them attractive and engaging to all of us. “Participation in team sports such as ice hockey and soccer provides many children and adolescents with their first experience of intergroup competition, which may have lasting psychological effects” ([30], pp. 350). Moreover, “This shared experience seemed to create a collective sense of meaning and greater solidarity among the student body” ([30], pp. 351). According to Henrich [30] team sports and sports leagues “placed nonviolent intergroup competition at the center of people’s leisure time, where it often became part of their personal identity. Participation in team sports became central to raising children (well, at least boys)” ([30], pp. 360).
There is a long history of using team-games-tournaments (TGT) in classrooms for academic subjects [50,51]. For example, [52] proposes TGT, in which each week students from one class compete against members of other teams from the same class. In one of the earliest TGT in mathematics, [51] measured the effect of a non-computer based math game played within the classroom by teams. During the game, students received immediate feedback while each individual's score was public. Low ability students obtained a significant improvement.
However, at school the natural team is the class. Being in the same classroom for months and years creates a powerful sense of belonging and identity. Nevertheless, despite these facts, schools and teachers don´t use inter-class games for teaching.
In tournaments, we can differentiate several types. There are the tournaments in which a selected member of the class participates. This is what happens in the typical math Olympics. They are excellent events for finding and training talented students. Another type is team tournaments. Here each class selects teams, which represent the class. This option recruits more students than the previous one, but sometimes it could create conflicts inside the class. For example, conflicts about how many teams, who makes up those teams, and who is left out. The third option is when everyone in the classroom actively participate together in one team. If this type of tournament is frequent, week after week, then there is a greater chance of learning for all the students of the class.
A free benefit that automatically provides inter-class tournaments is a social dissemination mechanism. The frequent reiterated interactions between different schools enhance the diffusion of strategies. Moreover, the tournament designers can include a fishing net network topology between schools that facilitates interaction between similar schools, and therefore facilitates imitation. This mechanism of social interaction can be more efficient than other community learning strategies. It can also accelerate improvement and innovation. Inter-class tournaments simultaneously put a larger number of classes to work on a common activity. That is, a large number of students, teachers, and coordinators connect with each other. They then imitate more successful ideas and strategies. This is a great learning opportunity since population size correlates positively with the number and complexity of innovations [29,53]. These tournaments also manage to coordinate various groups that modify the activities. They test variants and adaptations of activities in order to improve the teaching of core concepts and crosscutting concepts. Thus, inter-class tournaments could also facilitate cultural evolution mechanisms for the innovation of new didactic activities that improve interdisciplinary integration. Moreover, inter-class tournaments where all students participate creates an environment that forces students of differing abilities to interact.
3.2. Research Questions
ICT makes it possible to implement online inter-class synchronous tournaments where students participate without leaving their schools. Teacher also interconnect frequently with other teachers through internet. These are experiences of frequent interconnection through the Internet between teachers. They facilitate the evolution of teaching strategies. For example, during the COVID-19 pandemic, in an internet-interconnected community of teachers, we found evidence of imitation and improvement of didactic strategies [54]. This leads to conjecture that in inter-class tournaments there may be a similar process between teachers. In this paper, we consider two research questions.
Research question 1: To what extent is it feasible to hold inter-class tournaments with topics from various disciplines where all students learn central ideas of each discipline and crosscutting concepts?
Research question 2: To what extent do inter-class tournaments help to innovate educational strategies?
In the next section, we review our experience of inter-class games and tournaments for teaching integrated STEM.
4. Research Findings
We analyze four inter-class tournament activities for elementary and middle school students. One is for teaching machine learning and statistical modeling. A second activity is to teach the conservation of momentum in physics and its practical application in an engineering optimization challenge. The third is for teaching word problems integrated with financial literacy. The fourth one is for teaching natural selection and sexual selection in evolutionary biology along with developing statistical and population thinking. In all these online inter-class tournaments, there is some degree of integration between science and mathematics curriculum. They additionally integrate meaningful engineering and technology challenges. We reviewed all four tournaments, looking for information on how teachers were imitating and recombining strategies, and how with teacher feedback the nature of tournament play evolved. Online interclass tournaments are a new type of academic activity unprecedented before the ICT age.
4.1. Machine Learning Inter-Class Tournament
This is a synchronous inter-class tournament [55,56]. Players have to detect patterns. For each round, the platform shows a box of certain size and color. The box is closed but it contains inside 12 cells (Figure 1). The box displayed on each round is the same for all classes. However, for each cell, the platform assigns a color black or white using hidden rules. For example, if the height of the box is larger than 6 centimeters and its color is yellow, then cell number 5 is white, otherwise is black.
After watching the new box and studying patterns between boxes and cells in previous rounds, each player must bet on the color, white or black, of his corresponding cell. After 2 minutes, time is over, and the box opens to display its contents. If the student´s prediction succeeds, he gets 2 points, if he does not, then he lose a point. Alternatively, each player can bet “gray”, meaning “I do not know,” and earn one point. Another option is betting by writing a model. This is a classification rule, typical of machine learning. If the rule predicts the right color for his cell, then the player earns 4 points. If the rule predicts the wrong color for the slot, then he loses 4 points. Thus, betting by writing a rule is appealing but also more risky because the loss is higher.
The platform displays the team's accumulated points and the national ranking. Students of the team have a different pattern detection problem than the rest of their team. However, all teams have the same set of pattern detection problems. This serves as individualized accountability for each student. Since time is short, the probability of having a team member solving the problem instead of the assigned student is very low.
Based on the grade level of the classes and the learning objectives of the math curriculum, the tournament coordinator selects the hidden rules. These rules define the complexity of the patterns. For example, on fourth grade the coordinator can use simple fractions for the hidden rules. For seventh grade, he can use linear inequalities for the hidden rules.
This game achieves a degree of integration between numbers, statistics, probability and supervised machine learning concepts. Additionally, in the preparation sessions before the actual tournaments, the teacher explains some applications. A typical one is diagnostic. The teacher suggests that students can think the box represents a car motor. That the characteristics of the box - length, width, height and color – represents characteristics or symptoms of the engine, such as hours of use, viscosity, temperature at which it boils, and color of the oil. The fact of opening the box corresponds to opening the motor, and the white or black color of the cell corresponds to whether or not the motor is faulty. There are several other diagnostic examples.
In [56] we found an idea diffusion process within the teams. They learn from other students different modeling strategies, at least in the case of simple patterns. The statistical analysis suggests that during the preparation for the tournament, some teams learned how to detect patterns, how to express them with rules (models), and then internally diffused those strategies. In the limited time of the study, students were successful in sharing only the simplest types of hidden input–output patterns. With more time, we could probably have detected the dissemination of modeling of more complex patterns.
In the process of implementation, throughout the years the tournament has been changing. Based on students' and teachers´ feedback, we have adjusted the learning objectives according to the grade level. Due to the inter-classroom competition, teachers were very interested in how other teachers were training their students. Which graphical representations were better to reach a deeper comprehension, and allowed faster and more accurate solutions? From the feedback of the teachers, we have incorporated pedagogical instructions to encourage students to keep the information, to use different representations, and to do and keep updating throughout the rounds several 2D scatter graphs. These suggestions have pushed several redesigns of the user interface of the game.
Additionally, from the interactions with teachers, the idea of including models emerged. Teachers suggested the didactic strategy that the models were autonomous bots, and students have to design efficient bots. The task of the students changed to design bots. It took the form of selecting variables and adjusting rules. We did several cycles of improvements, based on the ideas that teachers copied from each other, adjusted to their classes, recombined, and suggested to us.
We found that there is a great learning opportunity in the idea that students bet by writing rules. The rules use several learning objectives of the curriculum, such as a mix of categorical and numerical attributes, inequalities, scatter graphs, and linear and nonlinear equations and inequations. These changes are signs of a process of cultural evolution that was emerging in the community.
We observed a diffusion process throughout classrooms in the tournament. We found that students learned from each other different modelling strategies for simple patterns. Through the feedback from teachers, we incorporated pedagogical instructions and adjusted the user interface of the game to promote learning. Additionally, we introduced the idea of autonomous bots and students had to design efficient bots. Through cycles of improvement, we observed a process of cultural evolution emerging in the community, with students using categorical and numerical attributes, inequalities, scatter graphs, and linear and nonlinear equations and inequations.
4.2. The Conservation of Momentum Inter-Class Tournament
This is an inter-class tournament on predictions and explanations related to conservation of momentum [57]. It consists of a first session in which students answer a pretest on basic knowledge of the physics of movement. Students then participate in a 90 minutes session with four experiments. Later, in a third session, students participate in a synchronous tournament.
The experiments are the following (Figure 2). The first experiment is about predictions when jumping off a skateboard in various conditions, and then verifying by jumping in those same conditions. For example, the students have to predict whether the skateboard moves and to where, if the student jumps forward from the skateboard. In addition, the students have to predict what happens to the skateboard if the student jumps harder forward. Moreover, students have to predict what happens to the skateboard if the student jumps carrying a heavy backpack.
The second experiment is with a golf ball mounted in a toy truck and released by a slip. Again, students have to predict, and then verify their predictions. For example, the students have to predict what happens to the toy truck when the ball slides and falls to the ground. They also have to predict what happens to the toy truck if the angle of the slip is greater and the ball falls faster.
The third experiment is with a golf ball mounted in a toy truck that has a plastic tube mounted with an internal spring. When the spring is released, it launches golf ball. As before, the students have to predict, and then verify their predictions. For example, the students have to predict the motion of the toy truck for different retractions of the spring.
The fourth experiment is with rockets made from disposable plastic bottles. Students fill a fraction of the bottle with water and then they pump air up to a specified pressure using a bicycle cylinder. They have to first predict and then measure the optimal fraction of water for the rocket to rise the highest. To carry out the measurements, they must make several launches with different proportions of water and ensuring that the pressure is always the same. An interesting problem is to devise some way to measure height or reach. Here they can use knowledge of geometry. The students tabulate the data on paper or in a spreadsheet. In this way, the students can compare their measurements and find out how to synthesize the information using averages. Besides, the core science concepts, the activity promotes several math concepts that students must use. Among the main ones are fractions, measurement, statistics and geometry.
In ([57] Araya et al, 2017) we found that students who participated in the tournament learned significantly more than the rest. Students with weak academic performance who participated in the tournament improved the most, reducing the gap with the academically stronger students.
The inter-class tournament ends in a synchronized online activity. It is an online synchronous tests that contains questions that asks for a deeper understanding of the experiments. For example, it asks to explain how the rocket rises, what is the optimal fraction of water, and to explain their predictions with analogous reasoning using the skateboard and the toy trucks with slips and springs throwing golf balls. An interesting challenge is to explain why the optimal fraction of water is close to a third, and not the extremes.
As we implemented these activities, the teachers gave suggestions to make them closer to the curriculum, to make them more attractive to students, and to facilitate their implementation in the classroom. The teachers were interested in knowing how other classrooms implemented the activities. How much those students were learning? How did those students do on the post-test? What were the differences with their students? Why the differences occurred? Teachers copied the most successful teaching strategies and recombined them. Thus, the experimental activity underwent several changes. Among the important adjustments was incorporating launching the rocket at a certain angle (45 degrees, for example) and not straight up. This makes measurement easier. Another idea that emerged was to improve safety with skateboards. Initially, it was easy for some students to slip, which can lead to accidents. Another interesting addition was the spring release mechanism. The idea is to use a string that holds the contracted spring and sets it on fire with a match. The fire moves slowly and burns the string until it cuts it. This causes the spring to loosen. The phenomenon generates great expectations. This causes great excitement in the students, as it resembles a bomb fuse. Over time, various didactic strategies emerged to maintain a certain level of order in the class and achieve the participation of all in the experiments.
Thus, teachers made various adjustments to the experimental activity to make them more engaging, closer to the curriculum, and safer. This led to the implementation of ideas such as launching the rocket at a certain angle, improving skateboard safety, and incorporating a spring release mechanism. These adjustments created great expectations in the students and improved the maintenance of order in the classroom. The teachers also discussed how other classrooms implemented the activity, the learning outcomes, and the differences between their students. This allowed them to copy and recombine the most successful teaching strategies.
4.3. Word Problem Inter-Class Tournament
In this tournament, students play a computer-based board game [58]. Each player plays against a student from other school in a sequence of alternating rounds. The score of each student adds to the score of her class. The student has three beads to run through a spiral path of cells (Figure 3). The path ends at the center of the board, where the goal is located. On each turn, the student moves a lever that activates a raffle, from which a word problem randomly emerges. The solution of the word problem is the number of positions that the player has to move one of her three beads. The player chooses the most convenient bead. If she moves an incorrect number of positions, she loses points. If, after moving the bead, it ends up in a cell containing coins, then she wins the corresponding amount of points. If her bead arrives at a position with springboard with a number, then she has to move the bead forwards or backwards the corresponding number of positions. If the bead ends up in a position with a trap then her bead goes to the start cell. If her bead ends up in position containing one of their rival’s beads, then that rival’s bead goes back to the start cell. Therefore, the player has to select which bead to move in order to maximize her gain. The player that reaches the goal cell first obtains extra points and the play is over.
All players play synchronously. The tournament coordinator announces every 5 minutes the school ranking. He send in real time this information by videostreaming. Each class projects the videostreaming announcements in front of the classroom and using loudspeakers with a high volume level to create a tournament atmosphere.
During the game, the student has to solve several word games selected according to the learning objectives of the curriculum. On each round, the student also have to make strategic decisions to maximize her gain and minimize her opponent gains. The platform keeps the number of times the student solved correctly the word problems. It also knows the decisions the student used to maximize her gain.
We found an important social facilitation effect: a significant improvement on the performance of male students weak on math, and therefore a reduction on the performance gap between mathematically weak and strong male students. Female students weak on math also had a significant gain, but lower than the one obtained by weak male students.
These tournaments incorporate a new element, radically different from the previous ones. Each player does not respond or advance independently of the others, as it is in a race, a pattern bet, or a knowledge test. Now the student must make decisions taking into account what her opponent can do. Now, there is a phenomenon of mind reading. Each student has to guess what her opponent will do. In the language of game theory, it is a true game. On the one hand, the word problem comes out randomly, but according to the learning objectives of the curriculum selected by the tournament coordinator. A solution is always a number between 1 and 20. These are the number of positions that the player can advance. However, next comes the risk factor. The student has to choose which bead to move. In certain positions, the opponent can more easily attack him, and there are others where he can attack his opponent more successfully. On the other hand, there are movements that have a greater benefit than others do. There are more coins to collect. This combination of chance, deterministic problems, mind reading, risk, and reward establishes a connection with the world of financial decisions.
Over the years, this tournament has undergone several great changes. In the beginning, there were no word problems. Originally, teachers used the game for students to practice basic math concepts. For example, counting and arithmetic operations. However, some teachers suggested looking at how to include other learning objectives in the curriculum. One of the most demanded was the resolution of word problems. Given the attractiveness of the game and the students´ weaknesses in solving word problems [59], we worked with some teachers on different strategies to include them. We tested on several classrooms. We developed this further by incorporating an increasing number of learning objectives of the curriculum and adjusting it to the strands and grade levels. At the suggestion of teachers, we also included elements of a financial nature that support new learning objectives in the curriculum.
The synchronized inter-classroom competitions not only attracted the students, but also the teachers. The tournaments encouraged the search for strategies to teach how to solve efficiently word problems and strategies for moving beads on the board. There was a process of comparison and imitation among teachers. Then each teacher adapted the didactic strategies to the reality and level of her course.
This process of imitation, recombination, and diffusion of didactic strategies has allowed us to improve the tournaments. It has also led to an increase in the number of students who are attracted to solve word problems, and do it with greater accuracy and speed.
4.4. Natural and Sexual Selection Inter-Class Tournament
This is a synchronous inter-class tournament [60]. It involves organisms belonging to three species, each of a different color. The specie of red color feeds on the green specie, which in turn feeds on the blue specie, and the blue specie feeds on the red specie (Figure 4). Thus, the three species configure a not transitive cycle. At the beginning of the game, the platform assigns randomly a species to each team. It also assigns to each student of the team a herd of four organisms belonging to the team´s specie. Different teams can have organisms of the same species, but the game assigns organisms so that initially all species have approximately equal number of organisms. The game has several rounds. Each round corresponds to one generation. During the tournament students play six rounds, which take a total time of 60 to 90 minutes.
In each generation, the organisms live a maximum of 20 virtual days. They autonomously move chasing prey and avoiding predators. They do it according to their six innate traits, inherited from their parents, and to the instructions given to the whole herd by the student that owns it. On the on hand, each student, just before starting a round, specifies four parameters for her herd. For that, she uses four continuous sliders. The parameters are aggressiveness, exploratory attitude, punishment of uncooperative behavior, and imitation of the more energetic organism of the same species. On the other hand, all the innate traits of the organisms are binary: vision (short, long), velocity (slow, fast), ability to feel fear if close to predator (on, off), ability to feel hunger (on, off), ability to detect the remaining energy of preys (on, off), cooperativeness (on, off). The platform displays graphically all of these traits. Players can detect them by visual inspection. Furthermore, there are filters or digital inks with which the player can stain the organisms, and thus she can easily count traits in the populations.
At the beginning of each round, players must make two predictions about the distribution of two features in two species. The platform randomly assigns to each student the traits and species to track for the entire game. They are different from the assigned to other team members. Both traits predictions are about the proportion of the trait on the assigned species at the end of the generation. In addition, each player must make a binary prediction on the growth (increase, decrease) of the size of the population in each species. These predictions are a critical part of the educational aim of the game.
At the end of each round, each player has to select a sexual partner for each one of her female organism that survived the round. For each female organism, the platform displays a list with the 5 nearest male organisms. Once the student selects a male, the platform create an even number of offspring: half goes to the owner of the female organism and the other half goes to the owner of the male organism. The number of offspring is proportional to the energy accumulated by the female at the end of the 20 virtual days. The offspring inherit the traits from their parents according to a matrix unknown to the players.
The score of the team is the average of the score of its members. The score of a player is a mix between the agreements of the predictions and the size of the player herd. Every five minutes, the tournament coordinator announces the class ranking in order to create an exciting tournament atmosphere.
One objective of the game is to promote population thinking [61]. This is a particular and powerful way of thinking in evolutionary biology. This means that the student have to learn to rapidly inspect swarms of organisms, observe their traits, do data analysis and build models [62], detect patterns and tendencies, estimate cost and benefits of the traits, use those estimates to make predictions, and then contrast those predictions with what really happened in order to improve for the next round. We analyzed the performance of 181 students from 7 classrooms, where students took a pre and a post test on natural and sexual selection. The results provided preliminary evidence of learning of key components on natural selection.
This inter-class tournament brings several additional components. It is a game in which all the players are in the same space. Therefore, the interaction and complexity is much greater. It requires a mind reading of many more players. In addition, the player has two different types of controls: those that directly control the organisms’ features and those where the manipulation is through sexual selection.
In the first years, the tournament started as a game between teams within classes. It was not computer-based but used only concrete material. In the first two versions, students played a natural selection of physical traits game. The first version was about the natural selection of color. The second version was about the natural selection of beak size. After these successful experiences and the feedback received from several teachers and their classes, we developed a natural selection game of a non-physical trait. It was about the natural selection of cooperation. Students used hooks, some one-sided and others two-sided, with hooks at both ends. The hooks represent birds. Hooks hunt fishes represented by Christmas baubles. One-sided hooks fish alone, whereas two-sided hooks can hook onto each other in order to reach the baubles that were deeper down.
The teachers were giving various feedback to the game development team. The easiest game was the ones with physical traits. Introducing behavioral traits generated a fertile discussion among teachers. In the teachers' training and in the years that they taught biology, they did very little evolution, and if they included it, it was only of physical traits such as height or hair color. Therefore, the introduction of behavioral traits generated confusion among the professors. However, after successive cycles of trial and error, the conversation turned to how to teach the evolution of behavioral traits. Some teachers suggested starting by illustrating common behaviors close to students´ daily life. That included the domestication of dogs and horses. Professional breeders artificially selected them. In other words, the behavioral trait was aggressiveness. Another great challenge was the introduction of sexual selection. It is difficult content, and most teachers do not teach it. With the interclass competition, teachers got interested in knowing how teachers from other sections or schools introduced these ideas. They also wanted to know the response and learning of the corresponding students. There was a copy of concrete materials, stories, and teaching strategies. Natural selection is one of the central themes of biology. It is a great challenge to develop and learn effective teaching strategies that manage to dismantle deep-rooted misconceptions. Then we developed an online version with many more features, both physical and behavioral. The feedback of teachers and students were guiding the inclusion of game features. This is an example of a cultural evolution process of multiple micro adjustments and innovations throughout years of interactions.
In summary, teachers gave various feedback to the game development team on introducing behavioral traits, such as aggressiveness and cooperation, into the game. Their experience with evolution was limited to physical traits. Sexual selection was a not taught. Through trial and error, they discussed strategies to illustrate common behavioral traits in domesticated animals. We used the feedback of teachers and students to guide the development of an online version of the game with these more challenging and deep concepts. Teachers learn from each other what was working better. This is an example of a cultural evolution process, guided by multiple micro adjustments and innovations over time.
5. Discussion
In cooperative learning the most important element is positive interdependence: students should believe that they sink or swim together [63]. With the synchronous online inter-class tournaments, there is a common goal. All students share this common target. The platforms explicitly highlights this key element posting class rankings as students compete against other classes. The platform permanently publishes the class score reminding students of the shared target. Another key element is individual and group responsibility [63]. In these four type of tournaments, the platforms track the performance of each student. The games also includes instant feedback and metacognition. For example, in training sessions the teacher can freeze the game, as in basketball, and can pose open-ended questions that promote a deeper reflection. The teacher thus becomes a coach, constantly providing cognitive and emotional support to the class. Teachers also discuss their strategies with tournament organizers, as well as with other teachers of the tournament community.
Additionally, the coordinator of the tournament also has a fundamental role in promoting metacognition. This role is particularly intense in training sessions. She comments on the strategies developed by students from different classes, encourages comparison of strategies, and encourages them to reflect on mathematical concepts and methodologies. Finally, after several years of implementation, the community of teachers has been generating ideas that allow improvements on the games for next year's tournaments.
Another important characteristic on inter-class tournaments is synchrony. Students play inter-class tournaments at the same time and with announcements from the organizers that highlight synchrony. Interpersonal synchronization is important for many cooperative tasks. [64] has found that synchrony has significant positive social influences, such as a greater sense of similarity and affiliation. An example of the social impact of synchrony is in the evolution of language. Originally, it comes from grooming between peers. Next, it started collective laughter that synchronizes small groups. In a third stage, it started collective singing and dancing. This enhance synchronization to a higher level. This new stage increases social cohesion and collaboration [65]. In addition, with the effervescence triggered by synchronization, we are more willing to change our behavior. This is a great booster to integrate and feel part of a community, accept feedback and transform our practices.
We have analyzed our experience in more than a decade with four different types of inter-class tournaments. They connect mathematics and computational thinking topics with other STEM disciplines. We found that inter-class games are feasible to implement in schools. These are tournaments between classes from different schools with topics from various disciplines. In each case, the whole classes participated in teams or as a whole, and students learned central themes of each discipline. They also used and practiced some crosscutting concepts, such as data and patterns, and crosscutting skills, such as argumentation, cooperation, and teamwork. Moreover, we found that the tournaments generated great student motivation and that students not only enjoyed them but learned some basic citizens values and attitudes, such as fair competition with anonymous others and unknown teams.
To what extent do inter-class tournaments help develop educational activities that integrate various disciplines? The integration of different disciplines is a great challenge. However, inter-class tournaments offer a platform to help spread activities across disciplines. The innovative environment and effervescent atmosphere created facilitates trial and error. It helps teachers open their class to introduce core concepts from other disciplines. In the four types of tournaments shown in this work, there are some integration components. These successful experiences show us that this mechanism can be a strategy that helps overcome the barriers to integration. There are 10 difficult barriers to face, described at the beginning, but inter-class tournaments seem to be a way that makes it easier to lift those barriers.
To what extent do inter-class tournaments help to innovate educational strategies? The four examples of online inter-class tournaments presented in this paper, show evidence that there was a slow but constant process of cultural learning and innovation. Throughout the years, the nature of the games experienced some changes. Most of the feedback came from trial and error with different features, the reactions and performance of the students, and suggestions from teachers.
Until now, the scaling of educational strategies is a major challenge and one that remains pending. In recent decades, progress in mechanisms for educational scaling has been very limited. Although the technological development of the internet and social networks has allowed a much greater dissemination of information, this has not translated into changes in teaching practices. ICT has an enormous potential to address the challenges of large-scale Teacher Professional Development [66]. Both the coverage and speed of propagation of educational information, new curricula, seminars, webinars, educational websites, etc. have skyrocketed. However, this diffusion does not translate into a change in educational behaviors or educational beliefs [25].
These inter-class tournaments encourage a large community of classes, with their teachers and all their students, to interact under four conditions. First, the interaction is synchronous. This means an atmosphere of much more engagement, motivation, effervescence and cooperation. Second, this environment makes it easier for the organizer to disseminate messages, strategies and concepts. This synchronous interaction also makes it easy to receive feedback from teachers and students. Third, homophily. That is, students and teachers of the same grade level interact. They are students with similar interests and learning goals. Their teachers have to focus on teaching the same topics, and doing it in practically the same weeks. Fourth, reiteration. Many times in preparatory events as well as in the tournament, students and teachers from different schools are interacting. These repeated exchanges facilitate the creation of friendships and closed and permanent social networks [32,33].
The combination of these conditions facilitate the spread of ideas, innovation and change of strategies. It is a mechanism of cultural evolution different from that of standard teacher professional development and lesson study. In our experience, inter-class tournaments, are an alternative worth exploring and further developing. They are an alternative mechanism to enhance and accelerate the cultural evolution didactic strategies.
Online inter-class tournaments provide social interaction and learning opportunities between different schools. Teachers and coordinators can imitate more successful ideas and strategies. Helps teachers to modify activities and test variants for improved teaching of core concepts. They are a new type of academic activity unprecedented before the digital age. They connect entire K12 classrooms through digital communication, allowing for the exchange of ideas and strategies for the deeper integration of core math and science concepts, crosscutting skills, and meaningful learning. These tournaments promote imitation and recombination of didactic strategies. They are feasible to implement in schools and have the potential to greatly improve student preparation for the challenges of a fast-changing and smarter society. Furthermore, in inter-class tournaments all students participate. This characteristic creates an environment to foster interaction between students of different abilities, accelerating students´ learning.
Funding
This work was supported by the Chilean National Agency for Research and Development (ANID).
Acknowledgments
Support from ANID/ PIA/ Basal Funds for Centers of Excellence FB0003 is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Honey, M., Pearson, G., & Schweingruber, H. (eds.): STEM Integration in K-12 Education: Status, Prospects, and An Agenda for Research. National Academies Press, Washington, D.C. (2014).
- Isoda, M.; Araya, R.; Inprasitha, M. (2021) Developing Computational Thinking on AI and Big Data Era for Digital Society - Recommendations from APEC InMside I Project https://www.apec.org/Publications/2021/03/Developing-Computational-Thinking-on-AI-and-Big-Data-Era.
- Araya, R. (2021) What Mathematical Thinking Skills will our Citizens Need in 20 More Years to Function Effectively in a Super Smart Society? Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (Vol.1) Khon Kaen, Thailand.
- Maass, K., Geiger, V., Romero Ariza, M., & Goos, M. (2019). The role of mathematics in interdisciplinary STEM education. ZDM Mathematics Education, 51(6), 869-884. [CrossRef]
- Araya, R.; Isoda, M,; van der Mollen Moris, J. (2021) Developing Computational Thinking Teaching Strategies to Model Pandemics and Containment Measures. International Journal of Environmental Research and Public Health. 18(23), 12520. [CrossRef]
- Common Core State Standards (2011) http://www.corestandards.org/the-standards/mathematics.
- Krajcik, J., & Merritt, J., (2012) Engaging Students in Scientific Practices: What does constructing and revising models look like in the science classroom? Science Scope 35 (7) 6-8.
- Grossmann, M. (2021). How Social Science Got Better. Oxford University Press.
- Gibson, E. W. (2019) Leadership in Statistics: Increasing Our Value and Visibility, The American Statistician, 73(2), 109-116. [CrossRef]
- Carreira, S., & Blum, W. (2021) Mathematical modelling in the teaching and learning of mathematics: Part 2. Quadrante: Revista de Investigação em Educação Matemática.
- Borromeo-Ferri, R., Mena-Lorca, J., & Mena-Lorca, A. (2021). Fomento de la Educación - STEM y la Modelización Matemática para profesores. Kassel University Press.
- Tedre, M. & Denning, P. (2016). “The Long Quest for Computational Thinking.” Retrieved from http://denninginstitute.com/pjd/PUBS/long-quest-ct.pdf.
- Araya, R. (2022) Is it feasible to teach agent-based computational modeling to elementary and middle school students? Proceedings of the Singapore National Academy of Science.
- Araya, R. (2021) Enriching Elementary School Mathematical Learning with the Steepest Descent Algorithm. Mathematics. 9 (1197). [CrossRef]
- Araya R. (2021) Gamification Strategies to Teach Algorithmic Thinking to First Graders. In: Nazir S., Ahram T.Z., Karwowski W. (eds) Advances in Human Factors in Training, Education, and Learning Sciences. AHFE 2021. Lecture Notes in Networks and Systems, vol 269. Springer, Cham.
- English, L. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3(3). [CrossRef]
- Tedre, M., Toivonen, T., Kahila, J., Vartiainen, H., Valtonen, T., Jormanainen, I., & Pear, A. (2016) Teaching Machine Learning in K–12 Computing Education: Potential and Pitfalls. IEEE Access, 4. [CrossRef]
- Zhu, L., & Gigerenzer, G. (2006) Children can solve Bayesian problems: the role of representation in mental computation. Cognition, 98, (3), 287-308. [CrossRef]
- Bond, M. (2009) Decision-making: Risk school. Nature 461, 1189–1192. [CrossRef]
- van Dis, E; Bollen, J.; Zuidema, W.; van Rooij, R.; Bockting, C. (2023) ChatGPT: five priorities for Research. Nature 614, 224-226.
- Borromeo-Ferri, R. (2019). Teacher Education and Teacher Development. In Doig, B., Williams, J., Swanson, D., Borromeo Ferri, R., & Drake, P. (Eds.). Interdisciplinary mathematics education: The state of the art and beyond. Springer.
- Labaree, D. (2010). Someone Has to Fail. Harvard University Press.
- National Academies of Sciences, Engineering, and Medicine. (2021). Call to Action for Science Education: Building Opportunity for the Future. The National Academies Press. [CrossRef]
- Labaree, D. (2004). The Trouble with Ed Schools. Yale University Press.
- Cuban, L. (2013). Inside the Black Box of Classroom Practice Change Without Reform in American Education. Harvard Education Press.
- Vincent-Lancrin, S., et al.(2019) Measuring Innovation in Education 2019: What Has Changed in the Classroom? Educational Research and Innovation, OECD Publishing).
- OECD. (2016). Ten Questions for Mathematics Teachers…and How PISA Can Help Answer Them. OECD Publishing. [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. (2022). The Future of Education Research at IES: Advancing an Equity-Oriented Science. The National Academies Press. [CrossRef]
- Muthukrishna M, & Henrich J. (2016). Innovation in the collective brain. Phil. Trans. R. Soc. B 371 (20150192). [CrossRef]
- Henrich, J. (2020). The Weirdest People in the World, Farrat, Straus & Giroux.
- Guilbeault, D., & Centola, D. (2021). Topological measures for identifying and predicting the spread of complex contagions. Nat Commun 12 (4430). [CrossRef]
- Centola, D. (2018). How Behavior Spreads: The Science of Complex Contagions. Princeton University Press.
- Centola, D. (2021). Change. How to Make Big Things Happen. Little Brown Spark.
- Hulten, B., & DeVries, D. (1976). Team competition and group practice: Effects on student achievement and attitudes (Technical report 212). Baltimore: Johns Hopkins University Center for Social Organization of Schools.
- Farley-Ripple, E., May, H., Karpyn, A., Tilley, K., & McDonough, K. (2018). Rethinking connections between research and practice in education: A conceptual framework. Educational Researcher, 47(4), 235–245. [CrossRef]
- Henrich, J. (2022) Selective cultural processes generate adaptive heuristics. Less intuitive, hard-to-learn cognitive heuristics can thrive. Science, 376 (6588). [CrossRef]
- Isoda, M. (2015) The science of lesson study in the problem solving approach. In Inprasitha, M., Isoda, M., Wang-Iverson, P., & Yeap, B. Lesson Study Challenges in Mathematics Education. World Scientific.
- Inprasitha, M. (2015) Transforming education through lesson study: Thaliland´s decade-long journey. In Inprasitha, M., Isoda, M., Wang-Iverson, P., & Yeap, B. Lesson Study Challenges in Mathematics Education. World Scientific.
- Araya, R., & Collanqui, (2021) P. Are Cross-Border Classes Feasible for Students to Collaborate in the Analysis of Energy Efficiency Strategies for Socioeconomic Development While Keeping CO2 Concentration Controlled? Sustainability, 13 (1584). [CrossRef]
- Isoda, M.; Araya, R.; Eddy, C.; Matney, G.; Williams, J.; Calfucura, P.; Aguirre, C.; Becerra, P.; Gormaz, R.; Soto-Andrade, J.; Noine, T.; Mena-Lorca, A.; Olfos, R.; Baldin, Y.; Malaspina, U. (2018) Teaching Energy Efficiency: A Cross-Border Public Class and Lesson Study in STEM. Interaction Design and Architecture(s) Journal (IxD&A) N. 35, 2017, pp. 7 – 31.
- Wiemkem, R, Padmi, R., & Matney, G. (2021) Global Connections through Mathematical Problem Solving. Mathematics Teacher. Learning and Teaching PK-12. 114 (3) 219–226. [CrossRef]
- Yeap, B., Foo, P., & Soh, P. (2015). Enhancing Mathematics Teachers´ Professional Development through Lesson Study – A Case in Singapore. In Inprasitha, M, Isoda, M., Wang-Iverson, P., & Yeap, B. Lesson Study Challenges in Mathematics Education. 153-168. World Scientific. [CrossRef]
- Coleman, J. S., Hoffer, T., & Kilgore, S. (1982). High school achievement: Public, Catholic, and private schools compared. Basic Books.
- Majolo, B.., & Maréchal, L. (2017) Between-group competition elicits within-group cooperation in children. Scientific Reports 7(1). [CrossRef]
- Burghardt, G. (2005). The Genesis of Animal Play. MIT Press.
- Vygotsky, L. (1978) Mind in Society. The development of Higher Psychological Processes. Harvard University Press.
- Pellegrini, A. (2009). The Role of Play in Human Development. Oxford University Press.
- Devlin, K. (2011). Mathematics Education for a New Era: Video Games as a Medium for Learning. Peters/CRC Press.
- Sugiyama, M. S., Mendoza M., White F., & Sugiyama L. (2018) Coalitional Play Fighting and the Evolution of Coalitional Intergroup Aggression. Hum Nat. (3), 219-244. [CrossRef]
- Mevarech, Z., & Kramarski, B. (2014). Critical Maths for Innovative Societies. OECD Publications.
- Edwards, K., De Vries, D., & Snyder, J. (1972). Games and teams: a winning combination. Report 135. Center for Social Organization of Schools. Johns Hopkins University.
- Slavin, R. (2010). Co-operative learning: what makes groupwork work? In: Dumont, H., Istance,D., Benavides, F. (eds.) The Nature of Learning: Using Research to Inspire Practice. Educational Research and Innovation. OECD Publishing.
- Henrich, J.: (2016). The Secret of Our Success. Princeton University Press, Princeton (2016).
- Araya, R. (2021c) A collective brain to adapt teaching to quarantined first and second graders. IxD&A, 47, (21), 7 – 26.
- Araya R. (2007) What is inside this box: look at these other opened boxes for clues. Fifth Conference of the European Society for Research in Mathematics Education. Group 1: The role of Metaphors.
- Araya, R., Jiménez, A., Bahamondez, M., Dartnell, P., Soto-Andrade, J.,& Calfucura, P. (2014). Teaching Modeling Skills Using a Massively Multiplayer On Line Mathematics Game. World Wide Web Journal. 17 (2), 213-227. [CrossRef]
- Araya, R., Aguirre, C., Calfucura, P., & Jaure, P. (2017) Using Online Synchronous Interschool Tournaments to Boost Student Engagement and Learning in Hands-On Physics Lessons. Advances in Intelligent Systems and Computing, 84-94. [CrossRef]
- Araya, R., Aguirre, C., Bahamondez, M., Calfucura, P., & Jaure, P. (2016) Social Facilitation due to online inter-classrooms Tournaments. Lecture Notes in Computer Science. 9891. [CrossRef]
- U.S. Department of Education. Foundations for Success. (2008). Report of the National Mathematics Advisory Panel.
- Araya, R., Bahamondez, M., Contador, G., Dartnell, P. & Aylwin, M. (2013) Enseñanza de la Selección Natural con Juego Masivo por Internet. Congreso de Pedagogía, La Habana, Cuba.
- Mayr, R. (1982). The growth of biological thought: Diversity, evolution and inheritance. Harvard University Press.
- Holmes, N.G., Wieman, C., & Bonn, D.A. (2015) Teaching critical thinking. Proc Natl Acad Sci U S A. 112(36):11199-204. [CrossRef]
- Johnson, D., Johnson, R., & Johnson, E. (1984). Circles of Learning. Cooperation in the Classroom. Interaction Book Company.
- Rabinowitch T.C, & Knafo-Noam A (2015) Synchronous Rhythmic Interaction Enhances Children’s Perceived Similarity and Closeness towards Each Other. PLoS ONE 10(4): e0120878. [CrossRef]
- Gamble O., Gowlett, J., & Dunbar, R. (2014). Thinking Big. How the Evolution of Social Life Shaped the Human Mind. Thames & Hudson.
- Lim C., Tinio, V., Smith, M., Zou, E., & Modesto III, J. (2020) Teacher Professional Development at Scale in the Global South. In Panth, B., McLean, R. Anticipating and Preparing for Emerging Skills and Jobs. Springer. [CrossRef]
Figure 1.
Closed box, open box with booklet inside, and booklet with 12 cells
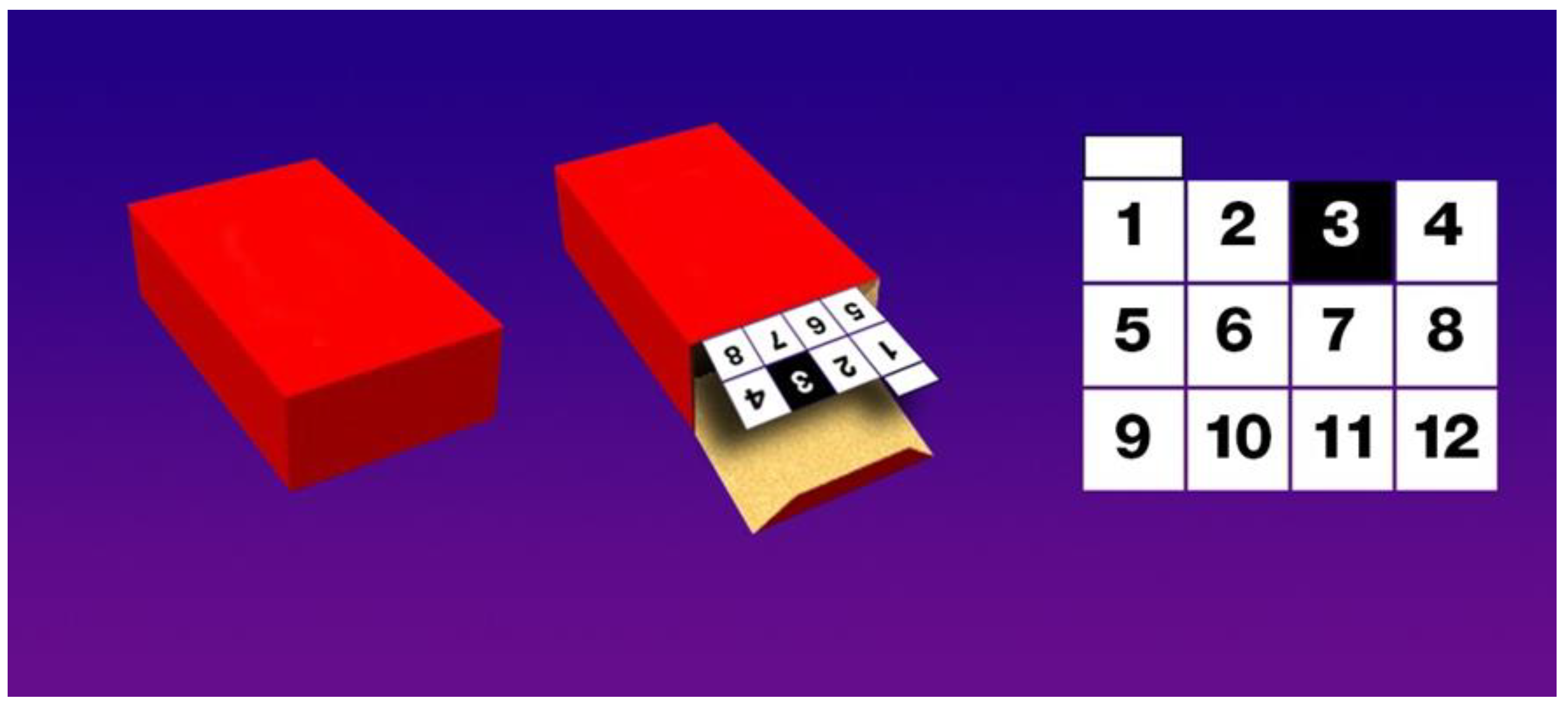
Figure 2.
Experiments 1, 2, 3 and 4.

Figure 3.
Experiments 1, 2, 3 and 4.
Figure 4.
Part of the screen with the organisms of the 3 species. The ones with white border are organisms that belong to the player. Those with a continuous border are male and the others are female.
Figure 4.
Part of the screen with the organisms of the 3 species. The ones with white border are organisms that belong to the player. Those with a continuous border are male and the others are female.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





