Prerpints.org logo
Preprint
Article

SFRRG: A Graph Neural Network Recommendation Model based on Feature and Structure Information

Altmetrics

Downloads

209

Views

58

Comments

0

Submitted:

10 February 2023

Posted:

13 February 2023

You are already at the latest version

Alerts
Abstract
With the rapid development of the Internet industry, the problem of information overload has arisen due to the abundance of information available online. Recommendation algorithms, as the core of recommendation systems, have been attracting much attention and are a hot topic of research for many experts and scholars. The classical recommendation algorithms are mainly divided into three major categories: collaborative filtering recommendation algorithms, content-based recommendation algorithms, and hybrid-based recommendation algorithms. Although these algorithms are widely used in various fields, with the proliferation of information, these traditional recommendation algorithms are no longer able to meet the needs of the times. To address this issue, recommendation systems have been developed to provide users with personalized and relevant information or products. Despite the wide use of recommendation algorithms, such as collaborative filtering, content-based filtering, and hybrid approaches, traditional recommendation algorithms have limitations and are no longer suitable for meeting the demands of the times. This paper proposes a new recommendation algorithm, SFRRG, that fuses structure and feature information in graph neural networks to improve the performance of the recommendation system in rating prediction. The effectiveness of the proposed algorithm is demonstrated through experiments on various data sets and compared with existing recommendation algorithms.
Keywords: 
Subject: Computer Science and Mathematics  -   Information Systems

1. Introduction

In recent years, with the development of science and the progress of society, the Internet industry has developed at a high speed. Although the proliferation of information has opened up people’s horizons and improved their standard of living, it has also caused the problem of information overload. Faced with such a huge amount of information, it is difficult for people to find the part they want quickly and accurately [1]. Therefore, the development of the Internet is like a double-edged sword, which not only brings people opportunities but also makes them face great challenges [2]. In order to solve the above problems, recommendation systems are created. A recommendation system is to provide the target users with products or information that they may be interested in. A recommendation system, also known as a recommender system, is a subclass of information filtering systems that seeks to predict the "rating" or "preference" a user would give to an item. Recommendation systems are utilized in a variety of areas and are most commonly recognized as playlist generators for video and music services, product recommenders for online stores, or content recommenders for social media platforms. There are several algorithms used for building recommender systems, including content-based filtering, collaborative filtering, and hybrid approaches. The goal of recommendation systems is to provide personalized and relevant suggestions to users, increasing their satisfaction and engagement with the product or service.
Recommendation algorithms, as the core of recommendation systems, have been attracting much attention and are a hot topic of research for many experts and scholars. The classical recommendation algorithms are mainly divided into three major categories: collaborative filtering recommendation algorithms, content-based recommendation algorithms, and hybrid-based recommendation algorithms [3]. Although these algorithms are widely used in various fields, with the proliferation of information, these traditional recommendation algorithms are no longer able to meet the needs of the times. For example, collaborative filtering recommendation algorithms not only suffer from the problem of data sparsity, but the most successful matrix decomposition algorithm of collaborative filtering recommendation algorithms, the learned embedding is inherently transductive. This means that potential feature embeddings learned for a user or item cannot be generalized to new users or new items. When a new user or a new item enters the system or a new rating is performed, it usually needs to be retrained [4]. This feature makes the matrix decomposition algorithm not suitable for certain application scenarios that require timely recommendations, such as news recommendations. Although content-based recommendation algorithms can alleviate this problem by using the content features of users or items [5], this capability is not always present and sometimes the content features of users or items may be difficult to extract. These problems are the reasons for poor recommendation results.
Deep learning has achieved remarkable results in the image and text domains, but it is still in its infancy in the graph data domain. In 2017, Kipf et al. [6] first migrated deep learning to the graph domain with powerful characterization capabilities, breaking the bottleneck of many graph computation tasks, and also laying the corresponding theoretical foundation for the subsequent field of graph deep learning. After that, the research on graph convolutional neural networks has been flourishing, and a large number of scholars have improved and optimized the original first-generation graph convolutional neural networks from different perspectives. However, the existing research on graph neural networks mainly focuses on the redefinition of the convolutional aggregation layer and the optimization of the network structure, and few models integrate the learning ability of a single classifier to improve the generalization ability of the final model from the perspective of integration. Graph neural networks complement the topological relationships between nodes and enrich the representational capabilities of the model, achieving remarkable results in various tasks. Its essence can be seen as an aggregation process of neighboring nodes, relying on the prior assumption that neighboring nodes on the graph usually have the same label, and it is difficult for graph neural networks to effectively characterize and predict isolated nodes or groups of nodes when presented with their states on the graph [7,8,9]. In such scenarios, which have little structural information, weakening the structural information and enhancing the node feature information can better improve the overall effectiveness of the model [10,11].
In this paper, we conduct an in-depth study on the above problems for the task of rating prediction in recommender systems. The purpose of this paper is to explore the performance of improving the existing model for node classification on graphs and to combine the characteristics of graph data structure to supplement the topological structure information among nodes based on the model prediction. In addition, the structure and feature information of nodes are unified and fused. The graph neural network model with fused structure and feature information is proposed termed SFRRG. The relationship between feature-similar nodes is captured by feature similarity calculation and feature graph reconstruction, which in turn enhances feature and structure information in the integration strategy. The model is used to learn its deep-level features from the rating matrix and to accomplish the rating prediction task of the recommendation system. Finally, experiments are conducted on data sets and compared with several existing recommendation algorithms to demonstrate the effectiveness and feasibility of the proposed algorithm in this paper.
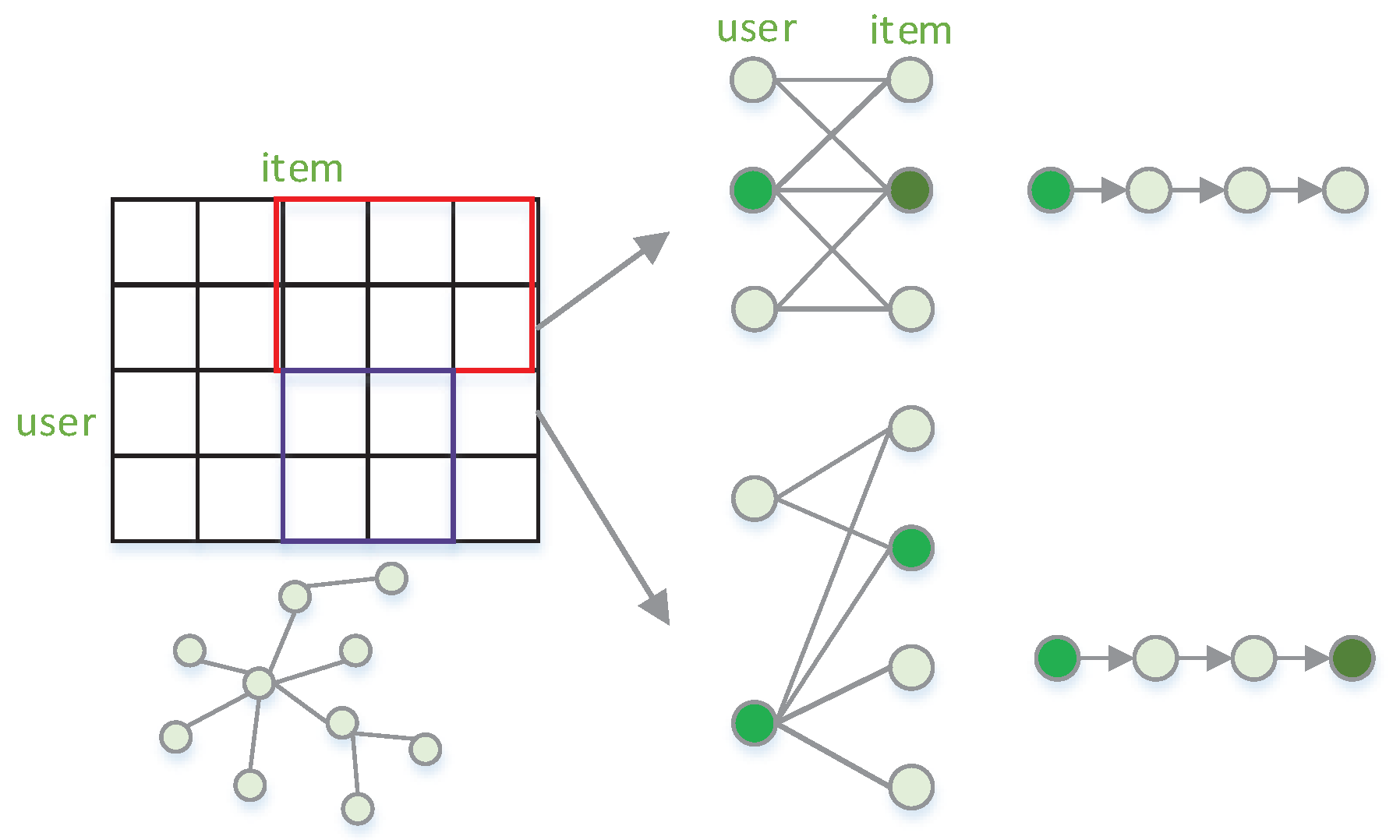
Preprints 68508 g001
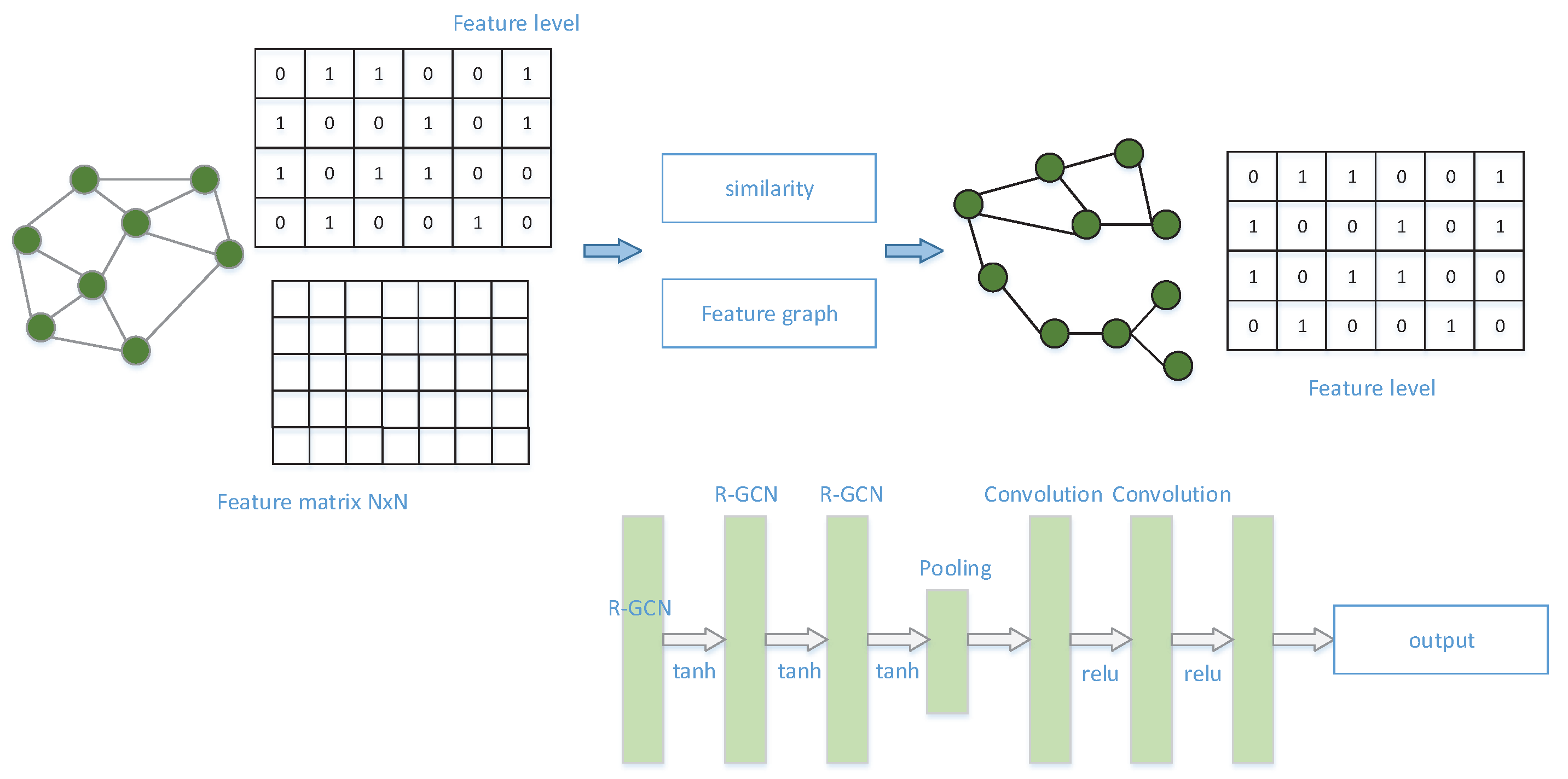
Figure 1. Recommender Systems Based on a Graph Neural Network.
Figure 1. Recommender Systems Based on a Graph Neural Network.
Preprints 68508 g001

2. Related Work

2.1. Recommender System

The recommendation algorithm of collaborative filtering has been widely followed and is one of the most popular recommendation algorithms today. This algorithm essentially collects groups of users with similar interest preferences as the target user and recommends items of interest to that group to the target user. In short, it is a predictive recommendation by collecting the history of user groups, connecting users and items, and mining the similarity in potential characteristics between users or items. Collaborative filtering recommendation algorithms can be subdivided into user-based collaborative filtering recommendation algorithms, project-based collaborative filtering recommendation algorithms, and model-based collaborative filtering recommendation algorithms. The earliest collaborative filtering recommendation algorithm is the user-based collaborative filtering recommendation algorithm. This algorithm was first used in email filtering systems and showed good performance at that time. However, the requirements of this type of algorithm are more demanding, and the user group with similar interests and preferences as the target user must be known in advance. In this way, the whole system needs to know the interest preferences of all users before it can make the next recommendation. Therefore, this type of algorithm can only be applied to small groups and is obviously inappropriate in the face of today’s Internet with a large user base. To address this shortcoming, automated recommendation systems have emerged [12]. This system uses the ratings collected from all users of the item to determine the user’s liking level. By calculating the similarity between users, a group of users with similar preferences to the target user is found, and the ratings of this group are used as a basis to make recommendations to the target user. The automated recommendation system has high performance, and it does not require the target user to specify users with similar preferences in advance, nor does it require users to know each other well, nor does it require knowledge of the content of all items in the whole system, so that it can spontaneously find user groups with similar preferences to the target user and thus discover the potential interest preferences of the target user. The emergence of automated recommendation systems has made collaborative filtering recommendation algorithms a hot topic at that time and widely followed [13].
Content-based recommendation algorithms do not require data from users other than the target user, and can accurately capture the user’s interest preferences, and the recommendation effect is relatively accurate. With the continuous development of science and technology, information retrieval technology and text processing technology are becoming more and more mature, and content-based recommendation algorithms have certain advantages in the recommendation of text-based content, but there are certain limitations in their application [14,15].
Along with the development of various recommendation algorithms, many hybrid-based recommendation algorithms emerged later. The hybrid-based recommendation algorithms combine the advantages of various algorithms to avoid the disadvantages and complement the strengths [16]. Specifically, they can be divided into two types according to the point in time when they are mixed in each hybrid recommendation algorithm. Pre-mix, and post-mix, which is a direct mix of several recommendation algorithms, is a mix at the method level. The hybrid strategies can be broadly classified into three types: hierarchical hybrid, inclusive hybrid, and complementary hybrid. Hierarchical blending is to use the results of one recommendation algorithm as the input of the next recommendation algorithm to obtain more accurate recommendation results by following the order of the processing flow. An inclusion hybrid is to integrate one recommendation algorithm into the framework of another recommendation algorithm. For example, in order to solve the sparsity problem of collaborative filtering recommendation algorithms, feature extraction is performed by content-based recommendation algorithms, which in turn enrich the preference model of users, as a way to calculate the similarity between users [17]. The last complementary mixture is obtained by selecting one recommendation algorithm to obtain the initial points or parameters, etc., necessary for another recommendation algorithm, such as the parameters of a Bayesian mixed-effects regression model through a Markov chain Monte Carlo approach [18]. This type of approach is to mix the recommendation results generated by different recommendation algorithms in different ways to provide comprehensive recommendation results to the target user. This hybrid approach improves the performance of the recommender system and satisfies the user’s needs.

2.2. Graph Neural Networks

A graph neural network (GNN) is a type of neural network for non-Euclidean data. The difference between a graph neural network and a traditional neural network is that a graph neural network targets non-Euclidean data, while a traditional neural network targets Euclidean data. Euclidean data, while traditional neural networks target Euclidean data, and graph neural networks can represent information of arbitrary depth from its neighborhood.
Spectral convolutional neural networks mainly rely on spectral graph theory [19,20,21] to act the convolutional kernel directly on the input signal in the spectral space. For example, Bruna et al. [22] made a breakthrough from the spectral space by spectrally decomposing the Laplacian matrix of the graph and using the obtained eigenvalues and eigenvectors to define convolutional operations in the spectral space. Kipf et al. [6] established a graph convolutional neural network (GCN) with the help of a first-order Chebyshev polynomial expansion. The spectral method will involve the calculation of eigenvalues and eigenvectors of the Laplacian matrix, and the eigendecomposition will greatly enhance the complexity of the model. On the basis of GCN, Wu et al. [23] proposed the SGC model, which removes the nonlinear transformation in the network layer. Klicpera et al [24] proposed the PPNP model by fusing the personalized PageRank algorithm and graph neural network, which decouples the feature transformation and feature propagation.PPNP and SGC, although starting from first-order graph convolutional neural networks, can be seen as a way to analyze the propagation of node features by aggregating functions to analyze the propagation of node features, which can be seen as a bridge between spectral and spatial methods [25]. Spatial convolutional neural networks discard the spectral decomposition operation of Laplacian matrices and define convolutional operations directly on the graph, i.e., for spatially similar neighborhoods, which greatly reduces the computational complexity of the model. Velic kovic et al. [26] proposed graph attention networks (GAT) to define graph convolution using the attention mechanism; the literature [27] extended graph neural networks from direct push learning to inductive learning; Xu et al. [28] proposed JKNet, which stitches together k convolutional layer outputs to alleviate the over smoothing phenomenon and increase the depth of graph neural network models. Existing studies have improved and optimized the aggregation strategy and network level from different perspectives [29], for example, GCN and GAT focus on structure-level neighbor aggregation, PPNP focuses on the transformation of features, and JKNet focuses on aggregation among distant nodes. The expressiveness of a single model is limited by its network layer design, and different models have natural preferences and focus [30,31,32]. It is difficult for a single model to consider all factors comprehensively, so this paper proposes to explore fusion integration learning to improve the expressiveness of existing models and eliminate the errors brought by such natural preferences to improve performance.

3. Methodology

 
Preprints 68508 g002
Figure 2. Schematic diagram of our model.
Figure 2. Schematic diagram of our model.
Preprints 68508 g002

3.1. Structure Information

A graph convolutional network can be viewed as a process of message passing. Message passing is a paradigm for aggregating information from neighboring nodes to update information from the central node, and this process can be expressed as follows:
x i k = γ k ( x i k − 1 , ϕ k ( x i k − 1 , x j k − 1 , e j , i ) ) ,
where x i k − 1 denotes the node features of node i in the k-1 layer; e j , i denotes the edge features from node j to node i, and γ and ϕ denote differentiable functions. The graph convolution operation then simulates the information transfer between adjacent nodes, which can capture the relationship between interconnected nodes. This process relies on the prior assumption1 that closely connected nodes on a graph usually have the same label.
a s s u m p t i o n 1 : i f x i l i n k t o x j l a b l e ( i ) = l a b l e ( j ) ,
Therefore, the first-order neighbor R s ( v i ) = { v k | ( v i , v k ∈ E s ) } of the fused node in the original graph structure G ( V , E S ) is used as its structural information in the process of model operations. Their first-order neighbors are considered here because graph neural networks play a major role in the aggregation process in first-order neighborhoods.

3.2. Feature Information

Based on this prior information of Assumption 1, the feature aggregation process of neighboring nodes of a graph convolutional neural network supplements the topological structure information between nodes and improves the accuracy of each graph task. However, in real business scenarios, some nodes have no neighbors or few neighbors, and using graph convolutional networks for these isolated nodes will produce a local over-smoothing phenomenon, which leads to degradation of node classification performance, so the graph structure of these isolated nodes is not much valuable.
Assuming that nodes x i and x j belong to different classes on the original graph structure graph, the final representations of nodes i and j can be expressed as follows under the action of a two-layer graph convolutional neural network layer.
H ( x i ) 2 = A g g 2 ( H ( x i ) 1 , H ( x j ) 1 ) ,
H ( x j ) 2 = A g g 2 ( H ( x j ) 1 , H ( x i ) 1 ) ,
From the above two formulations, it can be seen that the features of the nodes converge after the graph convolution transformation of these two nodes, producing a local over-smoothing phenomenon and thus failing to distinguish their true labels. Intuitively, in this scenario, weakening the structural information and enhancing the node feature information can better improve the overall effect of the model. Therefore, for such isolated nodes with little effective structural information, this paper relies on another prior assumption2 that nodes with high feature similarity usually have the same labels.
a s s u m p t i o n 2 : i f s i m ( x i , x j ) > t h r e s h o l d a b l e ( i ) = l a b l e ( j ) ,
Using the features of the nodes, a feature graph was reconstructed, and in the reconstructed graph structure, the local structure of nodes i and j were changed and the labels of their neighboring nodes mostly belonged to the same class. Under the prior assumption2, the confidence that nodes i and j are correctly classified becomes larger, thus improving the performance of the model.
s i m ( x i , x j ) = | x i ∩ x j | | x i ∪ x j | x i , x j ∈ { 0 , 1 } ( ∑ | x i − x j | p ) p − 1 o t h e r s
After calculating the similarity between nodes, a threshold d is set, and all nodes on the graph are traversed, and for each node, those node pairs with node similarity greater than the threshold are selected for edge concatenation operation, which completes the reconstruction of the feature graph.
A f ( i , j ) = 0 s i m ( x i , x j ) > d 1 o t h e r s
where A f denotes the adjacency matrix of the reconstructed feature graph G f ( V , E f ) . Based on the above definition, the neighbors R f ( v i ) = { v k | ( v i , v k ∈ E f ) } of node v i in the feature graph G f ( V , E f ) are fused as the feature information of the node.

3.3. Graph Neural Networks

3.3.1. Message Passing Layer

In order to handle different edge types, the relational graph convolution operator R-GCN is used here as the message-passing layer of GNN. message passing layer. The R-GCN layer has the following form.
x i ′ = W 0 x i + ∑ r ∈ R ∑ j ∈ N r ( i ) 1 | N r ( i ) | W r x j ,
The formula x i denotes the input feature vector of node i, x i ′ denotes the output feature vector of node i, R denotes the set of all possible ratings, and N r ( i ) denotes the set of neighbors of edge type r connected to node i. W0 and W r are learnable parameter matrices. Where W r is the parameter matrix used to handle different edge types, so the model is able to learn a large amount of information within the edge types, such as the average rating received by the target item, the path through which the two target nodes are connected, and other information. On further analysis, the W 0 x i part refers to the feature vector of the target node in the current layer, while the remaining part learns the feature vector of the nodes adjacent to the target node in the current layer. The inductive-based graph neural network model applies multiple R-GCN layers with tanh activation between the layers. The node feature vectors from all layers are connected and the obtained results are fed to the pooling layer, which transforms them into a graphical representation. The reason for applying R-GCN as the messaging layer of GNN is that R-GCN is not only suitable for application in entity classification problems and link prediction problems, but it takes into account the differences in the types of edges. Specifically, R-GCN will have different treatments for the layers at different locations. For the first layer, R-GCN will select the corresponding weights by the different types of edges and vertex labels and output them. For the middle and last layers, R-GCN multiplies the weights of the edges with the output of the previous layer and outputs them.

3.3.2. Pooling Layer

The feature descriptors are sorted uniformly, where each feature descriptor represents each vertex. Before these vertices are placed into a traditional 1D convolutional or dense layer, they are sorted in a uniform order. Specifically, in the sorting pool, each node representation is sorted according to the successive Weifeiler-Lehman colors of its previous layer feature representation. Then, standard one-dimensional convolutional layers are applied to these sorted representations, and finally the final graphical representation is learned by learning the global topology contained from the individual nodes as well as from the node sort. In short, the pooling layer is used to aggregate node features for the graphical representation. The specific formula is as follows.
g = c o n c a t ( h u , h v ) ,
where h u is the node representation of the target user, h v is the node representation of the target item, and g is the final graphical representation. The predicted ratings are output using the great likelihood algorithm. The specific formula is as follows.
r = w T θ ( W g ) ,

4. EXPERIMENTS

4.1. Datasets

In order to assess the efficacy of our approach, a series of in-depth experiments were performed on three actual datasets. The statistical characteristics of these datasets are outlined in Table 1.
Movielens is a well-known benchmark dataset commonly utilized in recommendation problems [33]. In our experiments, we employed two different versions of the dataset one with 100K interactions and the other with 1M interactions. The movie categories were included as item attribute information.
Yelp, a business recommendation dataset, was also used in our experiments. This dataset records customer ratings for various local businesses, and we added the category of each business as item attribute data to enhance the user-item interaction graph.
Table 1. Statistical information of datasets.
Table 1. Statistical information of datasets.
dataset users items categories interactions
Yelp 10002 10373 58 10
Movielens 1M 6040 3260 18 165.3
Movielens 100k 943 1152 19 103.9

4.2. Metrics

This experiment is an exploratory study for the task of rating prediction in a recommender system. One of the criteria to measure the goodness of a recommendation system is prediction accuracy. The two most commonly used metrics for prediction accuracy for scoring prediction tasks are the root mean square error (RMSE) and the mean absolute error (MAE). The mean absolute error is simple to calculate and is therefore widely used in the field of recommender systems, but it also has certain drawbacks. Because it is often the low-scoring items that are not easily predicted that have a greater impact and contribution to the MAE. Therefore, the performance of recommendation algorithms with small MAE values is not necessarily good, probably because they can better distinguish between items that users generally dislike and items that they extremely dislike, which is obviously not very meaningful. RMSE, on the other hand, divides the sum of the squares of the differences between users’ actual and predicted ratings of items by the number of all ratings available in the test set, and finally treats them with a root sign. The penalty for inaccurate predictions is increased, making the use of RMSE for recommendation system evaluation more stringent than the use of mean absolute error.
R M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 ,

4.3. Baselines

We compare our model with some relevant or current state-of-the-art methods.
  • GC-MC [34]. GC-MC is a seminal study in the area of graph neural networks for recommendation algorithms. It accomplishes a node embedding representation on the graph by utilizing a graph self-encoder on the user-item bipartite graph.
  • NGCF [35]. A collaborative filtering model that leverages the higher-order connections in user-goods interaction graphs to effectively integrate collaborative signals into the representation learning process in a clear and direct manner.
  • F-EAE [36]. They used deep learning to model interactions across two or more sets of objects. This model can be queried about new objects that were not available at training time, but for which interactions have since been observed.

4.4. Result Analysis

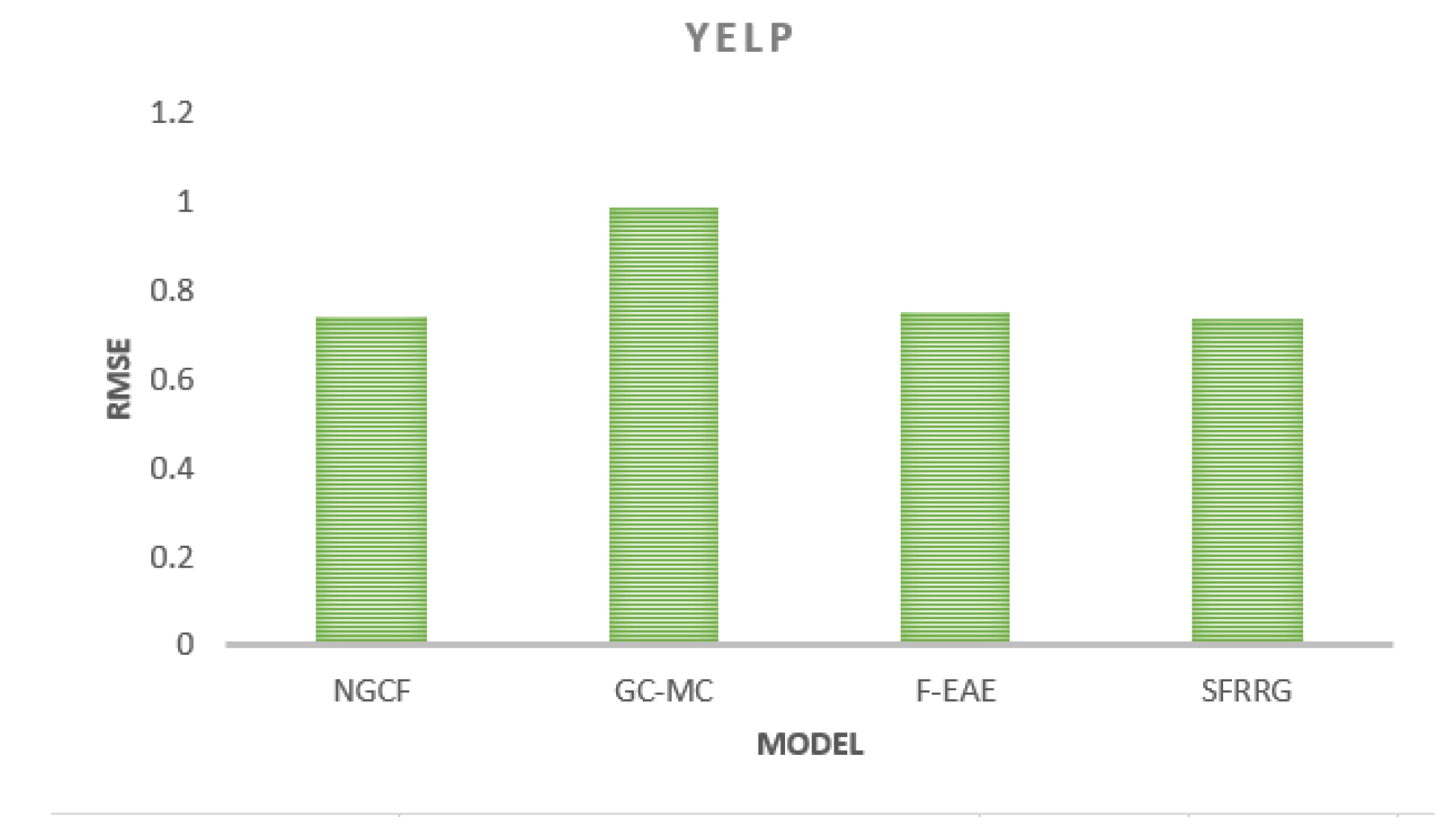
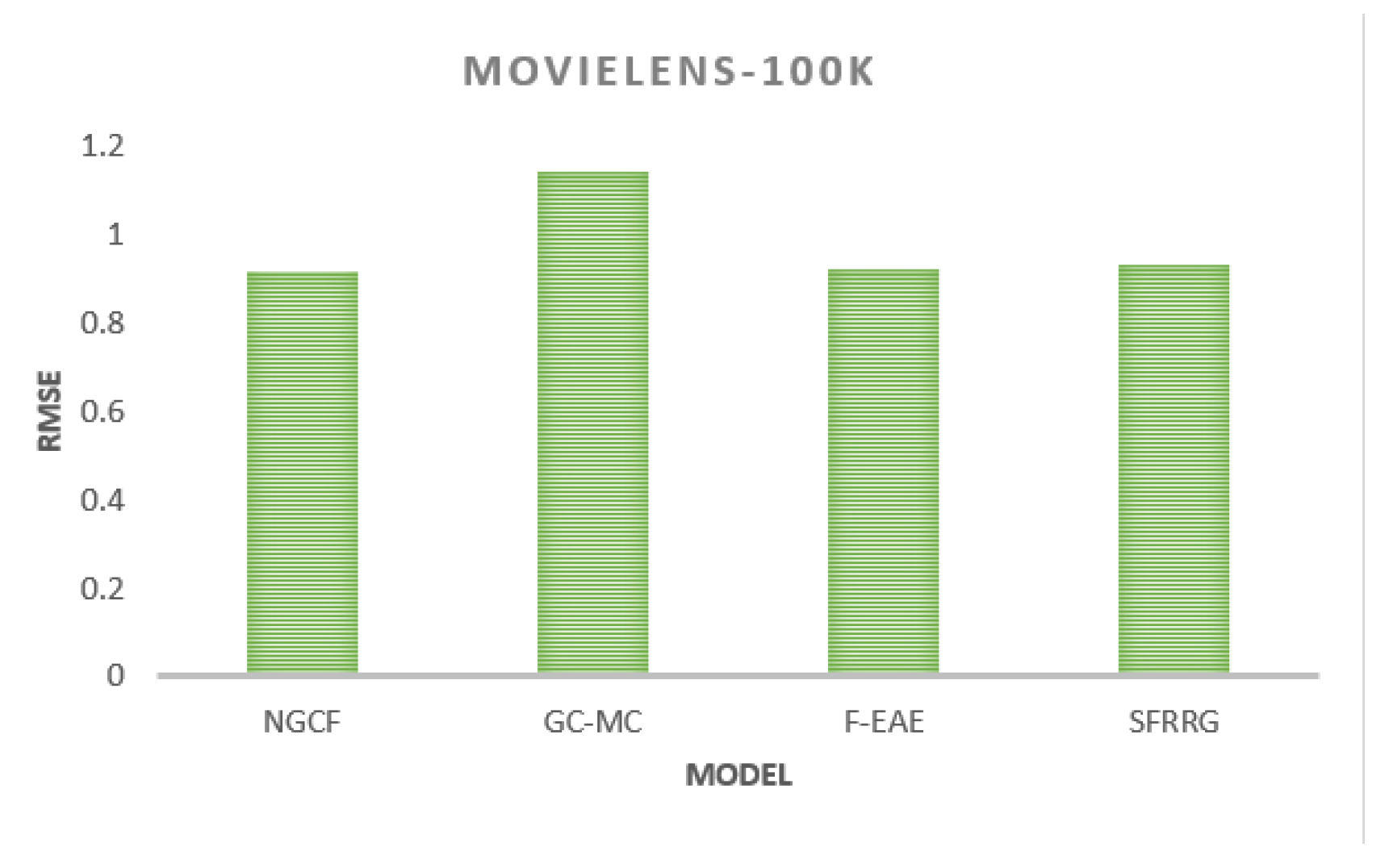
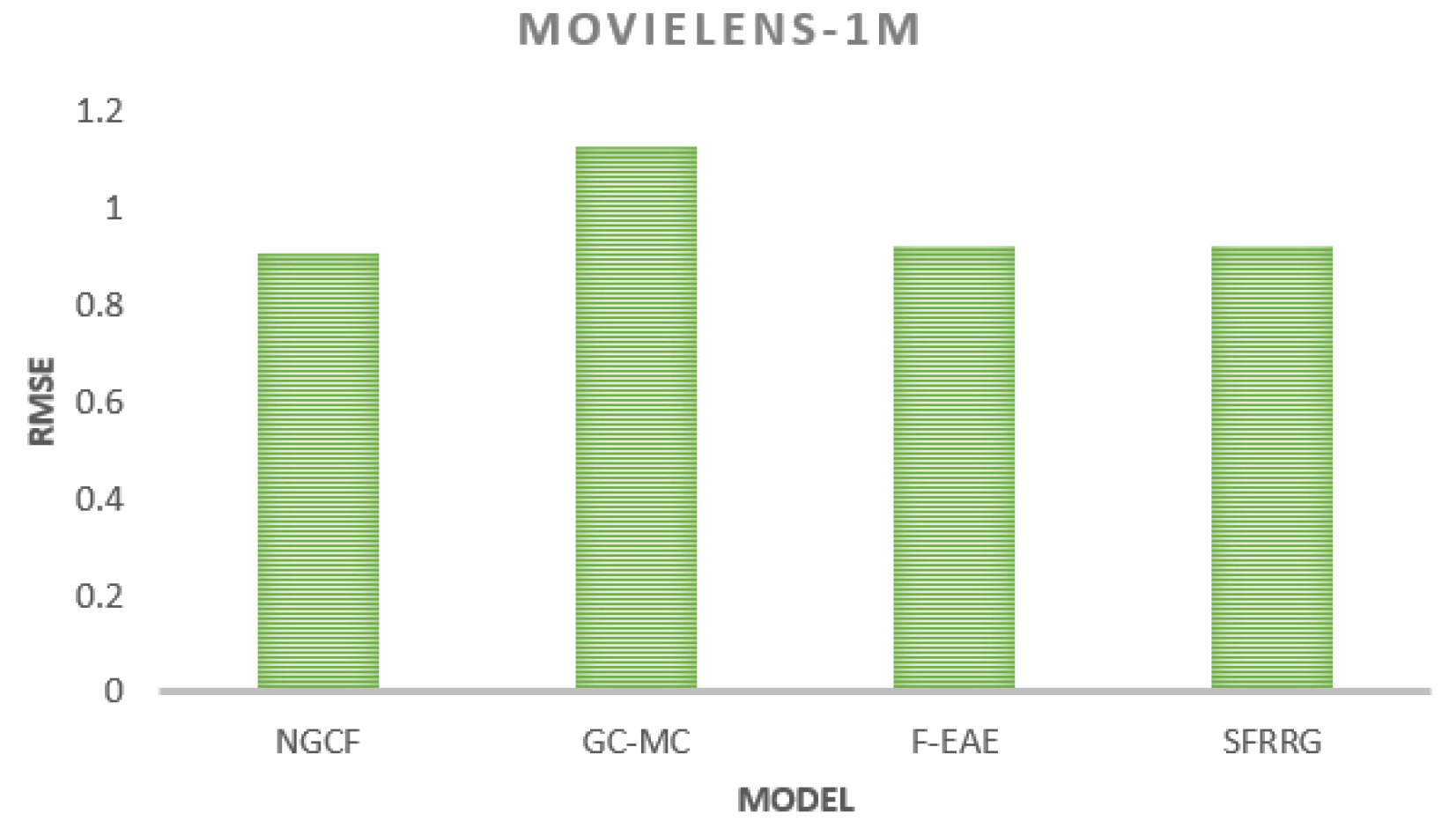
From the above two figures, the RMSE of SFRRG on the yelp rating dataset is 0.733, which is about 0.8% lower than that of NGCF, 24% lower than that of GC-MC, and 1.1% lower than that of F-EAE, and the recommendation accuracy is higher than that of other comparative algorithms. The RMSE of this algorithm is 0.916 on the MovieLens-100K dataset, which is about 1.3% lower than the NGCF algorithm and about 18.9% lower than the GC-MC algorithm. The RMSE of this paper’s algorithm SFRRG on the MovieLens-1M dataset is 0.904, which is about 1.8% lower than the NGCF algorithm, about 18.7% lower than the GC-MC algorithm, about 0.66% lower than the F-EAE algorithm, and about 1.5% lower than the SFRRG algorithm. 1.3% compared to the SFRRG algorithm. In summary, it shows the effectiveness of the data processing by this algorithm to improve the recommendation effect.
Preprints 68508 g003
Figure 3. Comparison of RMSE of each algorithm on Yelp dataset.
Figure 3. Comparison of RMSE of each algorithm on Yelp dataset.
Preprints 68508 g003
Preprints 68508 g004
Figure 4. Comparison of RMSE of each algorithm on MovieLens-l00K dataset.
Figure 4. Comparison of RMSE of each algorithm on MovieLens-l00K dataset.
Preprints 68508 g004
Preprints 68508 g005
Figure 5. Comparison of RMSE of each algorithm on MovieLens-lM dataset.
Figure 5. Comparison of RMSE of each algorithm on MovieLens-lM dataset.
Preprints 68508 g005

5. Conclusion and Future Work

Recommendation algorithms, as the core of recommendation systems, have been attracting much attention and are a hot topic of research for many experts and scholars. The classical recommendation algorithms are mainly divided into three major categories: collaborative filtering recommendation algorithms, content-based recommendation algorithms, and hybrid-based recommendation algorithms. Although these algorithms are widely used in various fields, with the proliferation of information, these traditional recommendation algorithms are no longer able to meet the needs of the times. Deep learning has achieved remarkable results in the image and text domains, but it is still in its infancy in the graph data domain. Graph neural networks complement the topological relationships between nodes and enrich the representational capabilities of the model, achieving remarkable results in various tasks. Its essence can be seen as an aggregation process of neighboring nodes, relying on the prior assumption that neighboring nodes on the graph usually have the same label, and it is difficult for graph neural networks to effectively characterize and predict isolated nodes or groups of nodes when presented with their states on the graph. In this paper, we conduct an in-depth study on the above problems for the task of rating prediction in recommender systems. The purpose of this paper is to explore the performance of improving the existing model for node classification on graphs and to combine the characteristics of graph data structure to supplement the topological structure information among nodes based on the model prediction. In addition, the structure and feature information of nodes are unified and fused. The graph neural network model with fused structure and feature information is proposed termed SFRRG. The relationship between feature-similar nodes is captured by feature similarity calculation and feature graph reconstruction, which in turn enhances feature and structure information in the integration strategy. The model is used to learn its deep-level features from the rating matrix and to accomplish the rating prediction task of the recommendation system. Finally, experiments are conducted on data sets and compared with several existing recommendation algorithms to demonstrate the effectiveness and feasibility of the proposed algorithm in this paper.

Conflicts of Interest

All authors have no conflict and declare that: (i) no support, financial or otherwise, has been received from any organization that may have an interest in the submitted work; and (ii) there are no other relationships or activities that could appear to have influenced the submitted work.

References

  1. C. Anderson, The long tail: Why the future of business is selling less of more. Hachette UK, 2006.
  2. G. Linden, B. Smith, and J. York, “Amazon. com recommendations: Item-to-item collaborative filtering,” IEEE Internet computing, vol. 7, no. 1, pp. 76–80, 2003. [CrossRef]
  3. Sarwar, G. Karypis, J. Konstan, and J. Riedl, “Item-based collaborative filtering recommendation algorithms,” in Proceedings of the 10th international conference on World Wide Web, 2001, pp. 285–295. [CrossRef]
  4. Y. Hu, Y. Koren, and C. Volinsky, “Collaborative filtering for implicit feedback datasets,” in 2008 Eighth IEEE international conference on data mining. Ieee, 2008, pp. 263–272. [CrossRef]
  5. S. Salmi, S. Mérelle, R. Gilissen, and W.-P. Brinkman, “Content-based recommender support system for counselors in a suicide prevention chat helpline: Design and evaluation study,” Journal of medical internet research, vol. 23, no. 1, p. e21690, 2021. [CrossRef]
  6. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” arXiv preprint arXiv:1609.02907, 2016. [CrossRef]
  7. X. He, L. Liao, H. Zhang, L. Nie, X. Hu, and T.-S. Chua, “Neural collaborative filtering,” in Proceedings of the 26th international conference on world wide web, 2017, pp. 173–182. [CrossRef]
  8. X. Wang, X. He, Y. Cao, M. Liu, and T.-S. Chua, “Kgat: Knowledge graph attention network for recommendation,” in Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 950–958. [CrossRef]
  9. Y. Wei, X. Wang, L. Nie, X. He, and T.-S. Chua, “Graph-refined convolutional network for multimedia recommendation with implicit feedback,” in Proceedings of the 28th ACM International Conference on Multimedia, 2020, pp. 3541–3549. [CrossRef]
  10. F. Ricci, L. Rokach, and B. Shapira, “Introduction to recommender systems handbook,” in Recommender systems handbook. Springer, 2010, pp. 1–35. [CrossRef]
  11. Y. Deldjoo, M. Schedl, B. Hidasi, Y. Wei, and X. He, “Multimedia recommender systems: Algorithms and challenges,” in Recommender systems handbook. Springer, 2022, pp. 973–1014. [CrossRef]
  12. B. Walek and V. Fojtik, “A hybrid recommender system for recommending relevant movies using an expert system,” Expert Systems with Applications, vol. 158, p. 113452, 2020. [CrossRef]
  13. S. Rui-min, Y. Fan, H. Peng, and X. Bo, “Pipecf: a dht-based collaborative filtering recommendation system,” Journal of Zhejiang University-SCIENCE A, vol. 6, pp. 118–125, 2005. [CrossRef]
  14. X. Yang, J. Guan, L. Ding, Z. You, V. C. Lee, M. R. M. Hasan, and X. Cheng, “Research and applications of artificial neural network in pavement engineering: a state-of-the-art review,” Journal of Traffic and Transportation Engineering (English Edition), vol. 8, no. 6, pp. 1000–1021, 2021. [CrossRef]
  15. D. Billsus and M. J. Pazzani, “User modeling for adaptive news access,” User modeling and user-adapted interaction, vol. 10, pp. 147–180, 2000. [CrossRef]
  16. Y. Wei, X. Wang, Q. Li, L. Nie, Y. Li, X. Li, and T.-S. Chua, “Contrastive learning for cold-start recommendation,” in Proceedings of the 29th ACM International Conference on Multimedia, 2021, pp. 5382–5390. [CrossRef]
  17. R. I. Kesuma and A. Iqbal, “Recommendation system for wedding service organizer using content-boosted collaborative filtering methods,” in IOP Conference Series: Earth and Environmental Science, vol. 537, no. 1. IOP Publishing, 2020, p. 012024.
  18. A. Mellit and S. Kalogirou, “Artificial intelligence and internet of things to improve efficacy of diagnosis and remote sensing of solar photovoltaic systems: Challenges, recommendations and future directions,” Renewable and Sustainable Energy Reviews, vol. 143, p. 110889, 2021. [CrossRef]
  19. A. Ng, M. Jordan, and Y. Weiss, “On spectral clustering: Analysis and an algorithm,” Advances in neural information processing systems, vol. 14, 2001.
  20. P. Mercado, F. Tudisco, and M. Hein, “Spectral clustering of signed graphs via matrix power means,” in International Conference on Machine Learning. PMLR, 2019, pp. 4526–4536.
  21. S. Habashi, N. M. Ghanem, and M. A. Ismail, “Enhanced community detection in social networks using active spectral clustering,” in Proceedings of the 31st Annual ACM Symposium on Applied Computing, 2016, pp. 1178–1181. [CrossRef]
  22. J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun, “Spectral networks and locally connected networks on graphs,” arXiv preprint arXiv:1312.6203, 2013.
  23. F. Wu, A. Souza, T. Zhang, C. Fifty, T. Yu, and K. Weinberger, “Simplifying graph convolutional networks,” in International conference on machine learning. PMLR, 2019, pp. 6861–6871.
  24. J. Gasteiger, A. Bojchevski, and S. Günnemann, “Predict then propagate: Graph neural networks meet personalized pagerank,” arXiv preprint arXiv:1810.05997, 2018.
  25. Q. Wang, Y. Wei, J. Yin, J. Wu, X. Song, and L. Nie, “Dualgnn: Dual graph neural network for multimedia recommendation,” IEEE Transactions on Multimedia, 2021. [CrossRef]
  26. P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Lio, and Y. Bengio, “Graph attention networks,” arXiv preprint arXiv:1710.10903, 2017.
  27. W. Hamilton, Z. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” Advances in neural information processing systems, vol. 30, 2017.
  28. K. Xu, C. Li, Y. Tian, T. Sonobe, K.-i. Kawarabayashi, and S. Jegelka, “Representation learning on graphs with jumping knowledge networks,” in International conference on machine learning. PMLR, 2018, pp. 5453–5462.
  29. Y. Wei, X. Wang, L. Nie, X. He, R. Hong, and T.-S. Chua, “Mmgcn: Multi-modal graph convolution network for personalized recommendation of micro-video,” in Proceedings of the 27th ACM International Conference on Multimedia, 2019, pp. 1437–1445. [CrossRef]
  30. J. Lee, I. Lee, and J. Kang, “Self-attention graph pooling,” in International conference on machine learning. PMLR, 2019, pp. 3734–3743.
  31. S. Yun, M. Jeong, R. Kim, J. Kang, and H. J. Kim, “Graph transformer networks,” Advances in neural information processing systems, vol. 32, 2019.
  32. Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon, “Dynamic graph cnn for learning on point clouds,” Acm Transactions On Graphics (tog), vol. 38, no. 5, pp. 1–12, 2019. [CrossRef]
  33. B. N. Miller, I. Albert, S. K. Lam, J. A. Konstan, and J. Riedl, “Movielens unplugged: experiences with an occasionally connected recommender system,” in Proceedings of the 8th international conference on Intelligent user interfaces, 2003, pp. 263–266. [CrossRef]
  34. R. v. d. Berg, T. N. Kipf, and M. Welling, “Graph convolutional matrix completion,” arXiv preprint arXiv:1706.02263, 2017.
  35. X. Wang, X. He, M. Wang, F. Feng, and T.-S. Chua, “Neural graph collaborative filtering,” in Proceedings of the 42nd international ACM SIGIR conference on Research and development in Information Retrieval, 2019, pp. 165–174. [CrossRef]
  36. J. Hartford, D. Graham, K. Leyton-Brown, and S. Ravanbakhsh, “Deep models of interactions across sets,” in International Conference on Machine Learning. PMLR, 2018, pp. 1909–1918.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated