Prerpints.org logo
Preprint
Article

Deep Learning for On-board Processing of Imaging Spectroscopy: A Survey

Altmetrics

Downloads

289

Views

132

Comments

0

Submitted:

09 February 2023

Posted:

13 February 2023

You are already at the latest version

Alerts
Abstract
Modern hyperspectral imaging technologies generate enormous datasets that could potentially transmit a wealth of information, but such a resource presents numerous difficulties for data analysis and interpretation. Deep learning techniques undoubtedly provide a wide range of potential for solving both traditional imaging tasks and exciting new problems in the spatial-spectral domain. This is true in the primary application area of remote sensing, where hyperspectral technology originated and has made the majority of its progress, but it may be even more true in the vast array of now existing and developing application areas that make use of these imaging technologies. The current review advances on two fronts: on the one hand, it is directed at domain experts who desire an updated overview of how deep learning architectures might work in conjunction with hyperspectral acquisition techniques to address specific tasks in various application sectors. On the other hand, by providing them with a picture of how deep learning technologies are applied to hyperspectral data from (near)real-time perspective. The contributions of this review include the existence of these two points of view and the inclusion of opportunities and important problems associated with the development of future CHIME mission to be launched by European Space Agency (ESA).
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Imaging spectroscopy in the visible to short-wave infrared (VSWIR) portion of the electromagnetic spectrum is a powerful Earth observation tool that evolved tremendously in the last 40 years (for a review see Rast and Painter [1]). A broad range of research fields and operational applications benefit from the unique capability of imaging spectroscopy sensors to accurately measure the spectral signature of Earth surface from remote sensing platforms, such as but not limited to monitoring of industrial activities, agriculture, ocean colour, as well as pre- and post-monitoring of natural hazards. Nowadays, several hyperspectral sensors are producing an almost continuous stream of data from airborne and spaceborne platforms i.e., AVIRIS-NG [2], EnMAP [3], PRISMA [4], EMITS [5] and future to-be-launched CHIME [6] and SBG [7]. Nearly all hyperspectral spaceborne sensors capture data with a bandwidth of ≈ 10 nm and a spatial resolution of ≈ 30 m. When combined with a relatively large swath (30km–150km), and repeated acquisition schemes, the produced data will need huge storage and computational power to be processed. Because of this and the increasing demand for rapid information and insights from Earth observation sensors, there is an urgent need for near real-time information extraction which is hardware friendly and can be embedded into airborne andor space-borne sensors. While multi-spectral sensors capture information in few spectral bands, HS sensors are capable of recording hundreds of spectral bands for each pixel. Therefore, an HS image can be considered as a multi-dimensional data cube which d(dimension)>150. Hence, the spectral signature [8], or fingerprint, of each pixel can be obtained. This signature can be used to extract information on the underlying surface and its properties in a quantitative way (e.g. quantitative retrieval of geop-physical properties) or for image classification (Figure 1).
For many applications i.e., Security, natural hazards, chemical leak detection, etc., is necessary to do the pixel-wise classification of Imaging spectroscopy. Pixel-wised classification is also known as image segmentation or semantic segmentation [10]. Hereafter throughout the document image segmentation and classification have been used interchangeably. It has been a recent trend to develop algorithms that can process data (near) real-time, and extract required information to prevent huge down-linking of data and further storage/processing costs [11]. For this goal, traditional machine learning techniques that require manual feature extraction are not a suitable candidate thus deep learning has found its place within the hyperspectral community [12,13]. Moreover, deep learning techniques can design features that are rarely possible by humans analyses [14]. Deep learning algorithms for on-board processing of HS data can be focused on data volume reduction [15,16], feature extraction [17], and target detection from raw data [18].
One should consider the limited memory and power supply on board as well as the quality of acquired data from the satellite to successfully deploy deep learning algorithms. The segmentation algorithms for HS imagery are often referred as supervised segmentation and using mainly spectral information that results in super-pixels [19] or homogeneous regions. In contrary, in computer vision and image processing community refer to both supervised and unsupervised methods and image classification normally is referred to assigning a label to every pixel in the whole imagery [18].
In early studies, Imaging spectroscopy segmentation was performed using a K-nearest neighbor classifier [20], support vector machines (SVMs) [21] and Gaussian un-mixing models [22]. Moreover, sparse signal representation methods have been used to classify noisy data with help of a learned dictionary [15]. These methods were extensively used before the emergence of deep learning techniques.
The objective of this paper is to evaluate various deep learning techniques in terms of network architecture, reliability, and the ability to handle noisy data. These factors play a crucial role in the implementation of deep learning for on-board applications. Additionally, the study will assess the capability of networks to be trained with limited training samples. The outcome of this analysis will inform the decision on which network architecture and configurations are optimal for onboard Imaging Spectroscopy segmentation.

2. Deep Learning for Imaging Spectroscopy Segmentation/Classification

We start with Convolutional Neural Networks (CNN) in different approaches (spectral, spatial, spectral–spatial). Other significant architectures we consider are Autoencoders, Deep Belief Networks, Generative Adversarial Networks, and Recurrent Neural networks. These architectures are flexible and adaptable to onboard Imaging spectroscopy processing as well. Discussion about challenges and new trends to handle them will be followed later in this section.

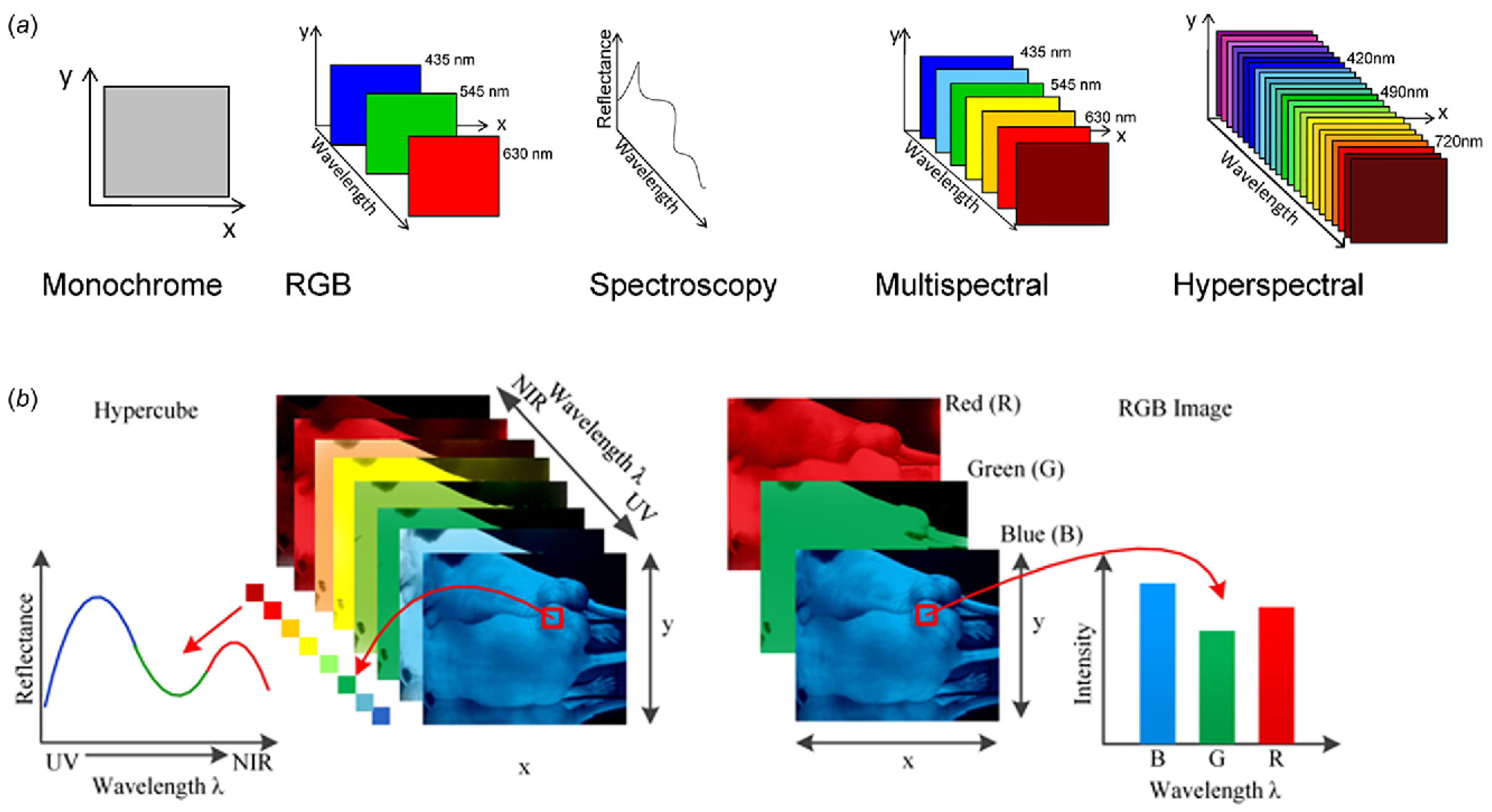
2.1. Spectral and Spatial Dimensions in Imaging Spectroscopy Processing

Hyperspectral data can be processed using different viewpoints. In early studies, pixel-wise processing was preferred using deep learning methods. This is done by extracting the spectral signature from each pixel and then comparing it to a known object’s spectral signature. We require some prior knowledge about the desired target in this approach. an example of such a study can be found in [23]. To reduce correlated information in spectral signature and remove redundant data, we can perform dimensionality reduction methods i.e.PCA [24], ICA [25], and autoencoders[26].
Dimensionality reduction is usually applied in addition to extracting features from the whole spectral span or on defined 2-dimensional patches (both spectral and spatial dimension dimensions). Extracting features in spectral-spatial dimensions requires extracting information from raw hyperspectral data cubes without applying prior knowledge and/or dimension reduction. This is heavy in computation thus there is a preference to work on sub-volumes instead of the whole data cube.

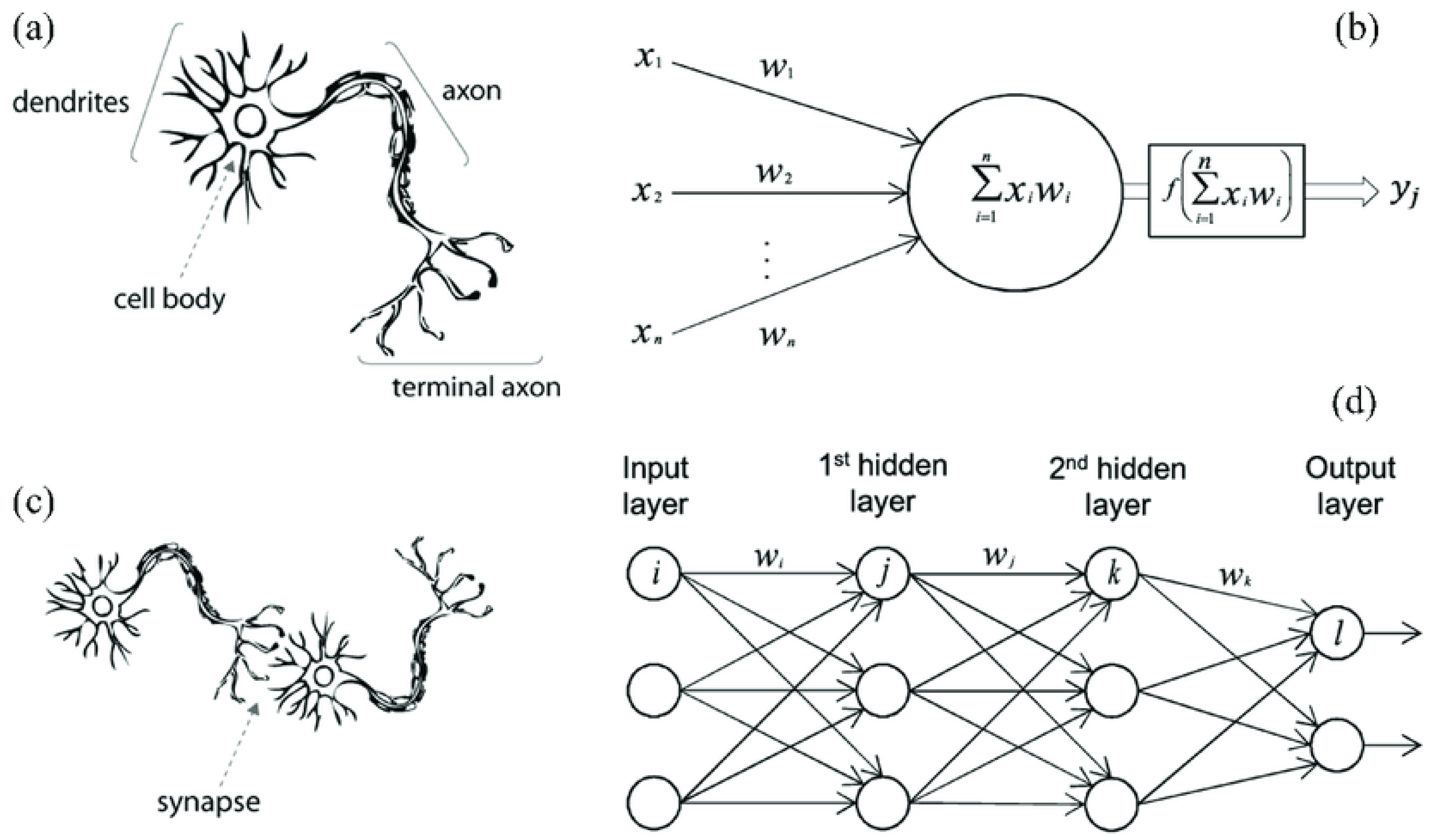
2.2. Convolutional Neural Networks

Artificial Neural Networks (ANNs) stemmed from biological neural systems. They contain an input layer, one or more hidden layer(s) and an output layer [27]. Historically, the development of neural networks has been based on the mathematical modeling of neurons in biological systems. Neurons are defined as the basic computational units in brains. Input is given to the neuron from the dendrite, the output is sent out via axon and the transmission is done through the synapse. A comparison of a biological neuron and the mathematical model in the neural network is provided in Figure 2.
A network with multiple hidden layers is called a deep neural network [29]. A simple drawing of a deep neural network is pictured in Figure 3.
For extracting information from images, Convolution Neural Networks (CNNs) have been introduced [31]. This type of network has been extensively used so far for different imagery analyses [32]. In CNN, the input image is constrained by its architecture. Normally, the neurons are arranged in three dimensions width ( w ) , height ( h ) , and depth ( d ) . Depth is the input depth, in the case of hyperspectral imagery, depth is the number of bands. By proceeding deeper into the network, it refers to the number of features of the input layer. In each layer, the neurons are connected to a selected number of neurons from the previous layer. This is to decrease the number of weights that needs to be defined [32].
CNN’s have also been combined with machine learning methods i.e.SVM to extract features and increase robustness toward over-fitting [33]. In this study, a target pixel and the spectral information of its neighbors are organized into a spectral–spatial multi-feature cube without extra modification of the CNN to classify land cover. Another example in [34] is a 2-channel deep CNN that has been used to do land cover classification combining spectral-spatial features. A hierarchical framework has been used for this purpose in [35]. Similarly, in [36] a method is proposed in which spatial and spectral features are extracted through CNNs from Imaging spectroscopy and Lidar. A pixel-wise classification using a 2-channel CNN and multi-source feature extraction was done in [37]. In [38] a framework for Imaging spectroscopy classification has been proposed that uses a fully-convolutional network to predict spatial features starting from multiscale local information and to fuse them with spectral features through a weighted method. This approach later performs classification using SVM.

2.2.1. Spectral Dimensional CNN

one-dimensional CNN (1D-CNN) is used to perform pixel-wise classification for Imaging spectroscopy processing. These networks apply to the spectral or spatial dimension. These networks are affected by noise easily thus making it challenging to use them for remote sensing, in general [39]. One solution is to use averaged spectrum from a group of neighboring pixels. This method best suits small-scale analyses such as crop segmentation [40]. Another solution is to perform PCA analyses before running CNN however, in the case of near real-time image processing, there is no room for heavy pre-processing tasks such as PCA. A different solution described in [41] uses a multi-scale CNN that applies to a pyramid of data that contains spatial features in multiple-scale. For small training samples, a band selection before CNN analysis has been proposed [42].

2.2.2. Spectral-Spatial Dimensions CNN

Working with both spectral and spatial features generally leads to better results in Imaging spectroscopy processing. In [43] a dual-stream channel CNN has been used that gets spectral features from the approach of [39], spatial features using the approach of [44] and a softmax regression classifier to combine those features. In [45] a combination of L2 norm and sparse constraint have been used with a similar combination of spectral-spatial features. In other studies, AlexNet [46] have been employed to do spatial-spectral analyses i.e. Densenet and architecrures like VGG-16 [38,47]. In [48] few-shot learning approach [49] has been used to learn a metric space that causes the samples of the same class to be close to each other to deal with the problem of a few training samples. Another way to improve accuracy while having a shortage of training information has been proposed in [50]. In this approach, the redundant information in the hidden layer is explored to find connections and improve the training process. Other examples of using spatial-spectral features together and improving the learning process can be found in [51,52,53]. They have used a variety of methods based on the super-pixel reconstruction of different features to improve the accuracy of segmentation and classification. The sensor-based feature learning is another method proposed by [54] in which five layers of spectral-spatial features were reconstructed according to sensor specifications. Another improvement to sensor-based training was explained in [55] which uses a novel architecture that actively processes input features into meaningful response maps for classification. All of the mentioned studies have used complex multi-step procedures that make them not suitable for (near)real-time processing of Imaging spectroscopy, however, the better performance of using multi-scale and multi-feature approaches has been proved according to mentioned studies in this section.

2.3. Auto-Encoders

To deal with the issue of limited training samples when processing Imaging spectroscopy, auto-encoders in different variations have been tested. For the first time in [56] PCA in spectral dimension was combined with auto-encoder in the other two dimensions to improve feature extraction for classification. In [57] and [58] stacked auto-encoders were employed in combination with PCA to flatten spectral dimension and followed by SVM and multi-layer perceptron (MLP) to perform classification. In [59] stacked auto-encoder was optimized for anomaly detection in Imaging spectroscopy. A combination of auto-encoders and CNN have been also tested in multi-scale approaches to extract features [60]. Another important point of using a stacked auto-encoder is the capability of handling noisy input. An example described in [61] used a stacked auto-encoder to generate feature maps from noisy input and then used super-pixel segmentation and majority voting. Another study used a pre-trained network by stacked encoders combined with logistic regression on noisy input to do supervised classification [62]. A framework based on stacked auto-encoders has been proposed to perform unsupervised classification on noisy input [63], this later was improved to an end-to-end classification pipeline for Imaging spectroscopys [64].

2.4. Deep Belief Networks, Generative Adversarial Networks, Recurrent Neural Networks

Deep belief networks (DBNs) have the capability of dimension reduction which makes them a good candidate to extract features. In [65] a DBN was combined with logistic regression to perform feature extraction. A combination of one- and two-layer DBN was combined with PCA. To perform (near)real-time anomaly detection DBN has been tested that also delivered promising results in extracting local objects [66]. A combination of DBN and wavelet transform has been also proposed by [67]. In [68,69] unsupervised classification was performed using DBNs and in the later study, an end-to-end classification framework based on DBNs and spectral angle distance metric were proposed. In Generative Adversarial Networks (GANs) two competing neural networks are used as generator and discriminator [70]. These networks have been used to perform classification when dealing with small training samples [71]. In similar cases, GANs have been employed to perform the final phase of Imaging spectroscopy classification using the discriminator agent [72,73,74]. Recurrent Neural Networks (RNNs) are mainly used to process time series. In the case of this, they are considered as sequences of a video series (each spectral band as a sequence), and RNNs are used to find similarities between time frames [75,76]. A combination of RNN to explore the spectral domain and LSTM(Long Short Term Memory) for exploring spatial features was proposed in [77]. RNNs have also been used to process mixed pixels in spectral dimension affected by noise [78].

2.5. Unsupervised and Semi-Supervised Approaches

Based on the fact that usually we face the problem of having limited training samples at hand semi-supervised and unsupervised approaches are getting more popular in the domain of Imaging spectroscopys. Examples can be found in [79,80] that use semi-supervised and layer-wise classification to process large-scale Imaging spectroscopys. Another example of performing pixel-wise classification can be found in [81] using an unsupervised method with CNN. First, inaccurate training samples were used and the classification was improved with a small set of accurately labeled training samples. In [82] to handle the limited training sample problem, a convolution-deconvolution network was used for unsupervised spectral-spatial feature learning. The convolution network was used to reduce dimensionality and deconvolution was used to reconstruct input data respectively. Another possibility that has been explored to deal with a few training samples is improving the training procedure as explained in [83] where unlabeled data is used in combination with a few labeled samples and RNN to classify Imaging spectroscopys. Another approach that was tested is using ResNet to learn spectral-spatial features from unlabeled data which also showed promising results [84].

2.6. Challenges in Imaging Spectroscopy Processing and New Trends for Handling Them

2.6.1. Limited Training Sets

The issue of having limited training samples remains a constant problem so far in the world of Imaging spectroscopy processing. New approaches have been explored in the direction of using semi-supervised techniques [85], self-supervising approaches [86] and domain adoption [87] which explores the discriminative input information to feed the neural network. Another approach is active transfer learning which used the most discriminative features from unlabeled input training samples [88].

2.6.2. Handling Noisy Data

To reconstruct high-quality input data for classification, some approaches are getting noticed. One study has explored super-resolutions in combination with transfer learning to reduce noise and improve the quality of the input training samples [89]. Other studies have used CNN with sparse signal reconstruction [90] and Laplacian pyramid network (LPN) [91] for enhancing input data. Another method explored presented in [92] uses structure tensors with a deep convolutional neural network to improve the quality and reduce noise.

2.7. Increase Speed and Accuracy

A new trend in the field of computer vision is using CapsuleNets (CapsNet) [93] which uses a set of nested neural layers. These networks increase the scalability of the model while increasing the speed of computation. Examples can be found in [94,95,96]. It was shown that by using spectral-spatial Capsnet the model converged quickly while avoiding over-fitting [97].

2.8. Hardware Accelerators

To increase the performance of HS data processing different hardware has been tested, such as computing clusters [98], GPUs and FPGAs (Field Programmable Gate Arrays) [99]. Recent advances in FPGAs have made them a suitable candidate to perform on-board image processing in both airborne and spaceborne platforms [100].
FPGA is a hardware unit consisting of an array of logic blocks, RAMs, hardcopy IPs, I/O pads, routing channels, etc [101]. It can be customized to perform different functions to be performed at different times and levels. A previous generation of similar technology was called ASICs [102]. FPGAs are more flexible and easier to program. It has shown lower power consumption and improved performance compared to on-board processing of hyperspectral imagery [103]. A few studies recently have performed different functions related to onboard HIS processing including data compression and image segmentation [104].
Older versions were using FPGAs for end-member extractions [103], another one used Xilinx Virtex-5 FPGA for automatic target detection [105] and Xilinx FPGA was used to perform end-member extraction for multiple targets [106]. Spectral signature un-mixing has been also tested on FPGA and graphical processing units (GPUs). Results have been competitive in terms of accuracy.
One study has used FPGA to demonstrate onboard processing capability to detect chemical plumes [107]. This study has been a pilot phase for developing an AI unit for the upcoming hyperspectral satellite to be launched by NASA JPL. A main drawback of using FPGA is the difficulty of its configuration and programming. For solving this OpenCL package from Intel and VITIS library (previously VHDL) from Xilinx have been developed [108]. Therefore, there have been limited studies on implementing deep learning for FPGA. Thus, our future step is going to be implementing deep learning on FPGA on the proposed hardware architecture for future CHIME missions [109].

3. Summary and Discussion

We explored the most recent trends in using deep learning for hyperspectral imagery. Almost all of the reviewed studies referred to limited training samples as a main limiting factor to employing deep learning widely in the HS image processing field. Another mentioned limiting factor is the lack of computation infrastructure and hardware in remote sensing-related studies. According to the review, there are many studies on using deep learning for land cover classification however there is still a gap in the studies on target and anomaly detection as well as data fusion and spectral unmixing. Segmentation of Imaging spectroscopy using deep learning is still a path less walked. Network architectures such as UNet, ResNet, and VNet are proven to be good choices to start with, although the application-based scenarios still need more work to be defined. Regarding the classification of Imaging spectroscopys, deep learning has shown to be effective, however since a lot of computational resources are required to perform deep learning and satisfactory results can be obtained from traditional classification approaches i.e.SVM, there is still reluctance in many users to employ deep learning. To handle the problem of limited training sets and noisy input data using GANs can be a good option to produce an augmented dataset and reduce noise in training samples. reinforcement learning can also be a good candidate that is worth further exploration. Since there is a trend to process Imaging spectroscopy onboard (using hardware accelerators) for both remote sensing and non-remote sensing applications, a summary of the most common methods according to their suitability for on-board implementation is provided in Table 1.
According to Table 1, conventional methods are easy to implement but need many training samples and traditional processing and updating procedures. Therefore, using CNN-based methods has found its place within the hyperspectral users’ community. Several versions of neural networks have been tested and in total deep CNN and 3D-kernel-CNN networks have shown very good results. Since we are focusing on optimizing network structure for onboard processing, GhostNets might be a good option as well. However, the accuracy might not be optimal. Other challenges when aiming for on-board processing of Imaging spectroscopy are noisy data and no atmospheric correction available at level zero data as a well limited training set. Therefore, we should focus on testing different network structures on simulated and real data similar to the upcoming CHIME mission shortly [114]. Overall, on-board processing of HS imagery is the new area of study that will open many new possibilities in the remote sensing domain.

4. Conclusion

Particularly in industries that profit from the computer-assisted interpretation of both visible and unseen (to the human sight) occurrences, the depth of information present in Imaging spectroscopy data is unquestionably attractive. However, cost-benefit analyses of industrial and professional Imaging spectroscopy technologies make it necessary for enabling elements to be present to activate their deployment potential. Machine learning technologies are expanding quickly in scope these days, and with the introduction of Deep Learning, they are changing the field of digital data analysis. By using a multidisciplinary approach and making our work accessible to practitioners, machine learning scientists, and domain experts, we attempted to examine what is currently occurring with the convergence of Imaging spectroscopy and deep learning technologies in this study. One of the key problems that developed as a barrier to high-quality scientific production is the publicly available datasets, even though pixel- and spectral-based analysis jobs may count on an order of thousands of training samples for Imaging spectroscopy volume. More generally, the quantity and caliber of data collected across the spectrum of disciplines continue to be a major obstacle to the creation of solid, efficient, and comprehensive Imaging spectroscopy-DL solutions. The provision of high-quality Imaging spectroscopy datasets can instead be encouraged by the investigation of various DL techniques for the RS field. Additionally, the ability to approach difficult visual tasks via DL solutions can be beneficial for other application domains where the penetration of Imaging spectroscopy technology is still far behind.

Author Contributions

Author Contributions: Nafiseh Ghasemi, as the research fellow with the Earth Observation Project Group CHIME, served as the main author of the article and was responsible for conducting the research and writing the manuscript. Jens Nieke, as the project manager of CHIME group, provided support for the research project and contributed to the overall direction of the study. Marco Celesti, as the CHIME mission scientist, supported the activities and fact-checked the information presented in the article. Gianluigi Di Cosimo, as the spacecraft manager, was responsible for checking the technical and system designs described in the article. All authors reviewed and approved the final manuscript.

Acknowledgments

The authors would like to thank European Space Agency (ESA) for providing support for doing the research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rast, M.; Painter, T.H. Earth Observation Imaging Spectroscopy for Terrestrial Systems: An Overview of Its History, Techniques, and Applications of Its Missions. Surveys in Geophysics 2019, 40, 303–331. [Google Scholar] [CrossRef]
  2. Vane, G.; Green, R.O.; Chrien, T.G.; Enmark, H.T.; Hansen, E.G.; Porter, W.M. The airborne visible/infrared imaging spectrometer (AVIRIS). Remote sensing of environment 1993, 44, 127–143. [Google Scholar] [CrossRef]
  3. Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sensing 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
  4. Pignatti, S.; Palombo, A.; Pascucci, S.; Romano, F.; Santini, F.; Simoniello, T.; Umberto, A.; Vincenzo, C.; Acito, N.; Diani, M.; et al. The PRISMA hyperspectral mission: Science activities and opportunities for agriculture and land monitoring. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS. IEEE; 2013; pp. 4558–4561. [Google Scholar]
  5. Green, R.O. The NASA Earth Venture Instrument, Earth Surface Mineral Dust Source Investigation (EMIT). In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2022; pp. 5004–5006. [Google Scholar]
  6. Nieke, J.; Rast, M. Towards the copernicus hyperspectral imaging mission for the environment (CHIME). IEEE, 2018, pp. 157–159.
  7. Miraglio, T.; Adeline, K.; Huesca, M.; Ustin, S.; Briottet, X. Assessing vegetation traits estimates accuracies from the future SBG and biodiversity hyperspectral missions over two Mediterranean Forests. International Journal of Remote Sensing 2022, 43, 3537–3562. [Google Scholar] [CrossRef]
  8. Shippert, P. Introduction to hyperspectral image analysis. Online Journal of Space Communication 2003, 2, 8. [Google Scholar]
  9. Mehta, N.; Shaik, S.; Devireddy, R.; Gartia, M.R. Single-cell analysis using hyperspectral imaging modalities. Journal of biomechanical engineering 2018, 140. [Google Scholar] [CrossRef]
  10. Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognition 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
  11. Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern trends in hyperspectral image analysis: A review. Ieee Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
  12. Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geoscience and Remote Sensing Magazine 2016, 4, 22–40. [Google Scholar] [CrossRef]
  13. Gao, F.; Wang, Q.; Dong, J.; Xu, Q. Spectral and spatial classification of hyperspectral images based on random multi-graphs. Remote Sensing 2018, 10. [Google Scholar] [CrossRef]
  14. He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature extraction with multiscale covariance maps for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 755–769. [Google Scholar] [CrossRef]
  15. Sun, W.; Zhang, L.; Zhang, L.; Lai, Y.M. A dissimilarity-weighted sparse self-representation method for band selection in hyperspectral imagery classification. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016, 9, 4374–4388. [Google Scholar] [CrossRef]
  16. Lorenzo, P.R.; Tulczyjew, L.; Marcinkiewicz, M.; Nalepa, J. Hyperspectral band selection using attention-based convolutional neural networks. IEEE Access 2020, 8, 42384–42403. [Google Scholar] [CrossRef]
  17. Wang, D.; Du, B.; Zhang, L.; Xu, Y. Adaptive spectral–spatial multiscale contextual feature extraction for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2020, 59, 2461–2477. [Google Scholar] [CrossRef]
  18. Nalepa, J.; Antoniak, M.; Myller, M.; Lorenzo, P.R.; Marcinkiewicz, M. Towards resource-frugal deep convolutional neural networks for hyperspectral image segmentation. Microprocessors and Microsystems 2020, 73, 102994. [Google Scholar] [CrossRef]
  19. Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–spatial classification of hyperspectral images with a superpixel-based discriminative sparse model. IEEE Transactions on Geoscience and Remote Sensing 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
  20. Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
  21. Van der Linden, S.; Janz, A.; Waske, B.; Eiden, M.; Hostert, P. Classifying segmented hyperspectral data from a heterogeneous urban environment using support vector machines. Journal of Applied Remote Sensing 2007, 1, 013543. [Google Scholar] [CrossRef]
  22. Altmann, Y.; Dobigeon, N.; McLaughlin, S.; Tourneret, J.Y. Nonlinear spectral unmixing of hyperspectral images using Gaussian processes. IEEE Transactions on Signal Processing 2013, 61, 2442–2453. [Google Scholar] [CrossRef]
  23. Yang, J.M.; Yu, P.T.; Kuo, B.C. A nonparametric feature extraction and its application to nearest neighbor classification for hyperspectral image data. IEEE Transactions on Geoscience and Remote Sensing 2009, 48, 1279–1293. [Google Scholar] [CrossRef]
  24. Fernandez, D.; Gonzalez, C.; Mozos, D.; Lopez, S. FPGA implementation of the principal component analysis algorithm for dimensionality reduction of hyperspectral images. Journal of Real-Time Image Processing 2019, 16, 1395–1406. [Google Scholar] [CrossRef]
  25. Fong, M. Dimension reduction on hyperspectral images. Univ. California, Los Angeles, CA, 2007. [Google Scholar]
  26. Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Du, P.; Marshall, S. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef]
  27. Cybenko, G. Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems 1989, 2, 303–314. [Google Scholar] [CrossRef]
  28. Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
  29. Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digital signal processing 2018, 73, 1–15. [Google Scholar] [CrossRef]
  30. Larochelle, H.; Bengio, Y.; Louradour, J.; Lamblin, P. Exploring strategies for training deep neural networks. Journal of machine learning research 2009, 10. [Google Scholar]
  31. Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. Ieee, 2017, pp. 1–6.
  32. Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional neural networks for medical image analysis: Full training or fine tuning? IEEE transactions on medical imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef]
  33. Leng, J.; Li, T.; Bai, G.; Dong, Q.; Dong, H. Cube-CNN-SVM: a novel hyperspectral image classification method. In Proceedings of the 2016 IEEE 28th International Conference on Tools with Artificial Intelligence (ICTAI). IEEE; 2016; pp. 1027–1034. [Google Scholar]
  34. Yang, J.; Zhao, Y.; Chan, J.C.W.; Yi, C. Hyperspectral image classification using two-channel deep convolutional neural network. In Proceedings of the 2016 IEEE international geoscience and remote sensing symposium (IGARSS). IEEE; 2016; pp. 5079–5082. [Google Scholar]
  35. Wei, Y.; Zhou, Y.; Li, H. Spectral-spatial response for hyperspectral image classification. Remote Sensing 2017, 9, 203. [Google Scholar] [CrossRef]
  36. Chen, Y.; Li, C.; Ghamisi, P.; Jia, X.; Gu, Y. Deep fusion of remote sensing data for accurate classification. IEEE Geoscience and Remote Sensing Letters 2017, 14, 1253–1257. [Google Scholar] [CrossRef]
  37. Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Transactions on Geoscience and Remote Sensing 2017, 56, 937–949. [Google Scholar] [CrossRef]
  38. Jiao, L.; Liang, M.; Chen, H.; Yang, S.; Liu, H.; Cao, X. Deep fully convolutional network-based spatial distribution prediction for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2017, 55, 5585–5599. [Google Scholar] [CrossRef]
  39. Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. Journal of Sensors 2015, 2015. [Google Scholar] [CrossRef]
  40. Sun, H.; Zheng, X.; Lu, X. A supervised segmentation network for hyperspectral image classification. IEEE Transactions on Image Processing 2021, 30, 2810–2825. [Google Scholar] [CrossRef] [PubMed]
  41. He, M.; Li, B.; Chen, H. Multi-scale 3D deep convolutional neural network for hyperspectral image classification. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP). IEEE; 2017; pp. 3904–3908. [Google Scholar]
  42. Li, Y.; Xie, W.; Li, H. Hyperspectral image reconstruction by deep convolutional neural network for classification. Pattern Recognition 2017, 63, 371–383. [Google Scholar] [CrossRef]
  43. Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote sensing letters 2017, 8, 438–447. [Google Scholar] [CrossRef]
  44. Slavkovikj, V.; Verstockt, S.; De Neve, W.; Van Hoecke, S.; Van de Walle, R. Hyperspectral image classification with convolutional neural networks. In Proceedings of the Proceedings of the 23rd ACM international conference on Multimedia, 2015, pp.; pp. 1159–1162.
  45. Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Transactions on Geoscience and Remote Sensing 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
  46. Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv preprint arXiv:1602.07360 arXiv:1602.07360 2016.
  47. Zhi, L.; Yu, X.; Liu, B.; Wei, X. A dense convolutional neural network for hyperspectral image classification. Remote Sensing Letters 2019, 10, 59–66. [Google Scholar] [CrossRef]
  48. Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep few-shot learning for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 2290–2304. [Google Scholar] [CrossRef]
  49. Li, F.F.; Fergus, R.; Perona, P. One-shot learning of object categories. IEEE transactions on pattern analysis and machine intelligence 2006, 28, 594–611. [Google Scholar]
  50. Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep&dense convolutional neural network for hyperspectral image classification. Remote Sensing 2018, 10, 1454. [Google Scholar]
  51. Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). IEEE; 2015; pp. 4959–4962. [Google Scholar]
  52. Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sensing Letters 2015, 6, 468–477. [Google Scholar] [CrossRef]
  53. Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE transactions on pattern analysis and machine intelligence 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
  54. Mei, S.; Ji, J.; Hou, J.; Li, X.; Du, Q. Learning sensor-specific spatial-spectral features of hyperspectral images via convolutional neural networks. IEEE Transactions on Geoscience and Remote Sensing 2017, 55, 4520–4533. [Google Scholar] [CrossRef]
  55. Fang, L.; Liu, G.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Hyperspectral image classification with squeeze multibias network. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 1291–1301. [Google Scholar] [CrossRef]
  56. Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 2013 9th international conference on information, Communications & Signal Processing. IEEE; 2013; pp. 1–5. [Google Scholar]
  57. Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE Journal of Selected topics in applied earth observations and remote sensing 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
  58. Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised spectral–spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geoscience and remote sensing letters 2015, 12, 2438–2442. [Google Scholar]
  59. Zhang, L.; Cheng, B. A stacked autoencoders-based adaptive subspace model for hyperspectral anomaly detection. Infrared Physics & Technology 2019, 96, 52–60. [Google Scholar]
  60. Yue, J.; Mao, S.; Li, M. A deep learning framework for hyperspectral image classification using spatial pyramid pooling. Remote Sensing Letters 2016, 7, 875–884. [Google Scholar] [CrossRef]
  61. Liu, Y.; Cao, G.; Sun, Q.; Siegel, M. Hyperspectral classification via deep networks and superpixel segmentation. International Journal of Remote Sensing 2015, 36, 3459–3482. [Google Scholar] [CrossRef]
  62. Xing, C.; Ma, L.; Yang, X. Stacked denoise autoencoder based feature extraction and classification for hyperspectral images. Journal of Sensors 2016, 2016. [Google Scholar] [CrossRef]
  63. Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J. A physics-based deep learning approach to shadow invariant representations of hyperspectral images. IEEE Transactions on Image Processing 2017, 27, 665–677. [Google Scholar] [CrossRef]
  64. Ball, J.E.; Wei, P. Deep Learning Hyperspectral Image Classification using Multiple Class-Based Denoising Autoencoders, Mixed Pixel Training Augmentation, and Morphological Operations. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2018; pp. 6903–6906. [Google Scholar]
  65. Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
  66. Ma, N.; Peng, Y.; Wang, S.; Leong, P.H. An unsupervised deep hyperspectral anomaly detector. Sensors 2018, 18, 693. [Google Scholar] [CrossRef]
  67. Huang, F.; Yu, Y.; Feng, T. Hyperspectral remote sensing image change detection based on tensor and deep learning. Journal of Visual Communication and Image Representation 2019, 58, 233–244. [Google Scholar] [CrossRef]
  68. Wang, M.; Zhao, M.; Chen, J.; Rahardja, S. Nonlinear unmixing of hyperspectral data via deep autoencoder networks. IEEE Geoscience and Remote Sensing Letters 2019, 16, 1467–1471. [Google Scholar] [CrossRef]
  69. Ozkan, S.; Kaya, B.; Akar, G.B. Endnet: Sparse autoencoder network for endmember extraction and hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 482–496. [Google Scholar] [CrossRef]
  70. Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE signal processing magazine 2018, 35, 53–65. [Google Scholar] [CrossRef]
  71. He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative adversarial networks-based semi-supervised learning for hyperspectral image classification. Remote Sensing 2017, 9, 1042. [Google Scholar] [CrossRef]
  72. Zhang, M.; Gong, M.; Mao, Y.; Li, J.; Wu, Y. Unsupervised feature extraction in hyperspectral images based on wasserstein generative adversarial network. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 2669–2688. [Google Scholar] [CrossRef]
  73. Zhan, Y.; Wu, K.; Liu, W.; Qin, J.; Yang, Z.; Medjadba, Y.; Wang, G.; Yu, X. Semi-supervised classification of hyperspectral data based on generative adversarial networks and neighborhood majority voting. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2018; pp. 5756–5759. [Google Scholar]
  74. Bashmal, L.; Bazi, Y.; AlHichri, H.; AlRahhal, M.M.; Ammour, N.; Alajlan, N. Siamese-GAN: Learning invariant representations for aerial vehicle image categorization. Remote Sensing 2018, 10, 351. [Google Scholar] [CrossRef]
  75. Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sensing 2017, 9, 298. [Google Scholar] [CrossRef]
  76. Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
  77. Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-convolutional LSTM based spectral-spatial feature learning for hyperspectral image classification. Remote Sensing 2017, 9, 1330. [Google Scholar] [CrossRef]
  78. Shi, C.; Pun, C.M. Superpixel-based 3D deep neural networks for hyperspectral image classification. Pattern Recognition 2018, 74, 600–616. [Google Scholar] [CrossRef]
  79. Ratle, F.; Camps-Valls, G.; Weston, J. Semisupervised neural networks for efficient hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2010, 48, 2271–2282. [Google Scholar] [CrossRef]
  80. Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Transactions on Geoscience and Remote Sensing 2015, 54, 1349–1362. [Google Scholar] [CrossRef]
  81. Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Transactions on geoscience and remote sensing 2016, 55, 645–657. [Google Scholar] [CrossRef]
  82. Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised spectral–spatial feature learning via deep residual Conv–Deconv network for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2017, 56, 391–406. [Google Scholar] [CrossRef]
  83. Wu, H.; Prasad, S. Semi-supervised deep learning using pseudo labels for hyperspectral image classification. IEEE Transactions on Image Processing 2017, 27, 1259–1270. [Google Scholar] [CrossRef]
  84. Feng, Q.; Zhu, D.; Yang, J.; Li, B. Multisource hyperspectral and LiDAR data fusion for urban land-use mapping based on a modified two-branch convolutional neural network. ISPRS International Journal of Geo-Information 2019, 8, 28. [Google Scholar] [CrossRef]
  85. Pan, B.; Shi, Z.; Xu, X. MugNet: Deep learning for hyperspectral image classification using limited samples. ISPRS Journal of Photogrammetry and Remote Sensing 2018, 145, 108–119. [Google Scholar] [CrossRef]
  86. Ghamisi, P.; Chen, Y.; Zhu, X.X. A self-improving convolution neural network for the classification of hyperspectral data. IEEE Geoscience and Remote Sensing Letters 2016, 13, 1537–1541. [Google Scholar] [CrossRef]
  87. Wang, Z.; Du, B.; Shi, Q.; Tu, W. Domain adaptation with discriminative distribution and manifold embedding for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters 2019, 16, 1155–1159. [Google Scholar] [CrossRef]
  88. Liu, P.; Zhang, H.; Eom, K.B. Active deep learning for classification of hyperspectral images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016, 10, 712–724. [Google Scholar] [CrossRef]
  89. Yuan, Y.; Zheng, X.; Lu, X. Hyperspectral image superresolution by transfer learning. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2017, 10, 1963–1974. [Google Scholar] [CrossRef]
  90. Lin, J.; Clancy, N.T.; Qi, J.; Hu, Y.; Tatla, T.; Stoyanov, D.; Maier-Hein, L.; Elson, D.S. Dual-modality endoscopic probe for tissue surface shape reconstruction and hyperspectral imaging enabled by deep neural networks. Medical image analysis 2018, 48, 162–176. [Google Scholar] [CrossRef]
  91. He, Z.; Liu, L. Hyperspectral image super-resolution inspired by deep Laplacian pyramid network. Remote Sensing 2018, 10, 1939. [Google Scholar] [CrossRef]
  92. Xie, W.; Shi, Y.; Li, Y.; Jia, X.; Lei, J. High-quality spectral-spatial reconstruction using saliency detection and deep feature enhancement. Pattern Recognition 2019, 88, 139–152. [Google Scholar] [CrossRef]
  93. Roy, P.; Ghosh, S.; Bhattacharya, S.; Pal, U. Effects of degradations on deep neural network architectures. arXiv preprint arXiv:1807.10108, arXiv:1807.10108 2018.
  94. Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J.; Pla, F. Capsule networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 2145–2160. [Google Scholar] [CrossRef]
  95. Wang, W.Y.; Li, H.C.; Pan, L.; Yang, G.; Du, Q. Hyperspectral image classification based on capsule network. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2018; pp. 3571–3574. [Google Scholar]
  96. Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep convolutional capsule network for hyperspectral image spectral and spectral-spatial classification. Remote Sensing 2019, 11, 223. [Google Scholar] [CrossRef]
  97. Yin, J.; Li, S.; Zhu, H.; Luo, X. Hyperspectral image classification using CapsNet with well-initialized shallow layers. IEEE Geoscience and Remote Sensing Letters 2019, 16, 1095–1099. [Google Scholar] [CrossRef]
  98. Wu, Z.; Li, Y.; Plaza, A.; Li, J.; Xiao, F.; Wei, Z. Parallel and distributed dimensionality reduction of hyperspectral data on cloud computing architectures. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016, 9, 2270–2278. [Google Scholar] [CrossRef]
  99. Gonzalez, C.; Sánchez, S.; Paz, A.; Resano, J.; Mozos, D.; Plaza, A. Use of FPGA or GPU-based architectures for remotely sensed hyperspectral image processing. Integration 2013, 46, 89–103. [Google Scholar] [CrossRef]
  100. Plaza, A.; Plaza, J.; Paz, A.; Sanchez, S. Parallel hyperspectral image and signal processing [applications corner]. IEEE Signal Processing Magazine 2011, 28, 119–126. [Google Scholar] [CrossRef]
  101. Kuon, I.; Tessier, R.; Rose, J. FPGA architecture: Survey and challenges. Foundations and Trends® in Electronic Design Automation 2008, 2, 135–253. [Google Scholar] [CrossRef]
  102. Mittal, S.; Gupta, S.; Dasgupta, S. FPGA: An efficient and promising platform for real-time image processing applications. 2008.
  103. González, C.; Mozos, D.; Resano, J.; Plaza, A. FPGA implementation of the N-FINDR algorithm for remotely sensed hyperspectral image analysis. IEEE transactions on geoscience and remote sensing 2011, 50, 374–388. [Google Scholar] [CrossRef]
  104. Lopez, S.; Vladimirova, T.; Gonzalez, C.; Resano, J.; Mozos, D.; Plaza, A. The promise of reconfigurable computing for hyperspectral imaging onboard systems: A review and trends. Proceedings of the IEEE 2013, 101, 698–722. [Google Scholar] [CrossRef]
  105. Bernabé, S.; Plaza, A.; Sarmiento, R.; Rodriguez, P.G.; et al. FPGA design of an automatic target generation process for hyperspectral image analysis. In Proceedings of the 2011 IEEE 17th International Conference on Parallel and Distributed Systems. IEEE; 2011; pp. 1010–1015. [Google Scholar]
  106. Lei, J.; Wu, L.; Li, Y.; Xie, W.; Chang, C.I.; Zhang, J.; Huang, B. A novel FPGA-based architecture for fast automatic target detection in hyperspectral images. Remote Sensing 2019, 11. [Google Scholar] [CrossRef]
  107. Theiler, J.; Foy, B.R.; Safi, C.; Love, S.P. Onboard CubeSat data processing for hyperspectral detection of chemical plumes. SPIE, 2018, Vol. 10644, pp. 31–42.
  108. Wang, Z.; Li, H.; Yue, X.; Meng, L. Briefly Analysis about CNN Accelerator based on FPGA. Procedia Computer Science 2022, 202, 277–282. [Google Scholar] [CrossRef]
  109. Omar, A.A.; Farag, M.M.; Alhamad, R.A. Artifical Intelligence: New Paradigm in Deep Space Exploration. IEEE, 2021, pp. 438–442.
  110. Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE transactions on geoscience and remote sensing 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
  111. Zheng, Z.; Zhong, Y.; Ma, A.; Zhang, L. FPGA: Fast patch-free global learning framework for fully end-to-end hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 5612–5626. [Google Scholar] [CrossRef]
  112. Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sensing 2017, 9, 67. [Google Scholar] [CrossRef]
  113. Paoletti, M.E.; Haut, J.M.; Pereira, N.S.; Plaza, J.; Plaza, A. Ghostnet for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 10378–10393. [Google Scholar] [CrossRef]
  114. Grøtte, M.E.; Birkeland, R.; Honoré-Livermore, E.; Bakken, S.; Garrett, J.L.; Prentice, E.F.; Sigernes, F.; Orlandić, M.; Gravdahl, J.T.; Johansen, T.A. Ocean Color Hyperspectral Remote Sensing With High Resolution and Low Latency—The HYPSO-1 CubeSat Mission. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–19. [Google Scholar] [CrossRef]
Preprints 68483 g001
Figure 1. Comparison between different visible-spectrum recording sensors, (a)in pixels, (b)wavelength representation. Image courtesy of Mehta et al.2018 [9].
Figure 1. Comparison between different visible-spectrum recording sensors, (a)in pixels, (b)wavelength representation. Image courtesy of Mehta et al.2018 [9].
Preprints 68483 g001
Preprints 68483 g002
Figure 2. Comparison between biological neuron in the brain and artificial neural networks (a)a single neuron in brain (b) A single neuron network (c)Synapse connection between neurons (d)multi-layer network with multiple neurons. Image courtesy of Jain et al.1996 [28].
Figure 2. Comparison between biological neuron in the brain and artificial neural networks (a)a single neuron in brain (b) A single neuron network (c)Synapse connection between neurons (d)multi-layer network with multiple neurons. Image courtesy of Jain et al.1996 [28].
Preprints 68483 g002
Preprints 68483 g003
Figure 3. Simple representation of deep neural network. Image courtesy of Larochelle et al.2009 [30].
Figure 3. Simple representation of deep neural network. Image courtesy of Larochelle et al.2009 [30].
Preprints 68483 g003
Table 1. A summary of the most commonly used image segmentation of hyperspectral imagery according to the most important features for onboard implementation.
Table 1. A summary of the most commonly used image segmentation of hyperspectral imagery according to the most important features for onboard implementation.
pixel-wise segmentation noise-robustness lightweight* easy implementation on board training-samples required
K-nearest neighbours No No Yes Yes high
SVM Yes No Yes Yes high
Spectral un-mixing Yes No Yes Yes high
Sparse signal representation [110] Yes No No No low
RNN Yes No No No high
CNN Yes No No Yes high
FCN [111] No Yes No Yes high
3D-kernel CNN [112] No Yes No No low
SVM-CNN No Yes No No high
multi-branch CNN No Yes No No low
deep CNN Yes Yes Yes Yes high
GhostNet [113] Yes Yes Yes No low
* low power and low latency
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated