Prerpints.org logo
Preprint
Article

The Design of Piecewise Integrated Composite Bumper Beam With Machine Learning Algorithm

Altmetrics

Downloads

206

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Advanced Carbon Fiber Reinforced Composite Materials

Submitted:

09 February 2023

Posted:

15 February 2023

You are already at the latest version

Alerts
Abstract
In the present study, piecewise integrated composite (PIC) bumper beam for passenger cars was proposed and design optimisation process for composite bumper beam against IIHS test was carried out with the help of machine learning. Several elements in IIHS bumper FE model have been assigned to be references, in order to collect training data which, allow the machine learning model to study the method of predicting loading types of each finite element. 2-D and 3-D implementations were provided by machine learning models, which determined stacking sequences of each finite element in PIC bumper beam. It was found that the PIC bumper beam, which was designed by machine learning model has direct impact on reducing the possibility of failure as well as increasing bending strength effectively than conventional composite bumper beam. Moreover, 3-D implementation produced better results compared with 2-D implementation since it was preferable to choose loading type information which was achieved from surroundings when the target elements were located either at corner or junction of planes instead of using information came from the same plane of target.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

Environmental issues have recently accelerated legislative actions worldwide targeting automotive industries and continuous demanding rigorous improvement for fuel efficiency, electric motor driving power system and structural compactness/lightness. Specifically, structural lightness is unceasingly required regardless of electric power system or capacity of auto-body, therefore, numerous works have been found so far. These works include topology optimisation, novel design methodologies and applying lightweight materials, such as non-ferrous light metals, thermoplastics, and fibre reinforced composites [1,2,3,4]. In particular, fibre reinforced composites have excellent specific strength, stiffness, and damping characteristics without sacrificing weight saving effect. Due to these beneficial properties, they have been used for structural materials of aircraft and space vehicles. As low-cost manufacturing technologies and mass production methods for composite structures have been established, the application of composite materials to leisure sport goods and auto-bodies are being increased nowadays [5,6,7,8,9].
Bumper beam is one of key parts in the vehicle to alleviate crash damages both for structure and passengers. Recent bumper beams are frequently made of composites in order to improve crashworthiness and structural lightness simultaneously. So far, entire region of composite bumper beams has been made based on conventional uni-style stacking sequences without changing sequences of composite plies or fibre orientations [10,11,12,13]. Jeong et al. [14] proposed a novel concept of PIC (Piecewise Integrated Composite), in which the loading type of bumper beam was analyzed and dissimilar stacking sequences, i.e., tension dominant, compression dominant and shear dominant, were assigned into five equally divided sub-regions of the composite bumper beam. However, intentionally divided sub-regions did not sufficiently reflect element-based dominant external loading types therefore, it is necessary to automatically assign dissimilar stacking sequences into each element to improve structural characteristics because each local part of the bumper beam is experiencing different types of loading during crash. Moreover, the best way to assign dissimilar stacking sequences into all elements is using machine learning technique. Accordingly, the PIC bumper beam design method with employing machine learning models was proposed in order to improve bending strength and structural lightweight effect of the product in the present study. Meanwhile, training data, which allow the machine learning model to study the method of predicting loading types of each finite element, were obtained from preliminary IIHS bumper beam FE analysis. Also, training data in the current study should contain information about stress triaxiality along with location in the form of coordinate values. Five different types of algorithms, which underlie on the machine learning model, were applied to guarantee the highest performance in view of improving bending strength and structural lightweight effect of the product [15,16,17]. Results of highest performance predicted loading type of each finite elements and robust stacking sequences against loading type were mapped into the entire region of bumper beam finite elements. Finally, the designed PIC bumper beam was verified in view of the strength improvement and structural weight saving effect by the IIHS bumper beam analysis.

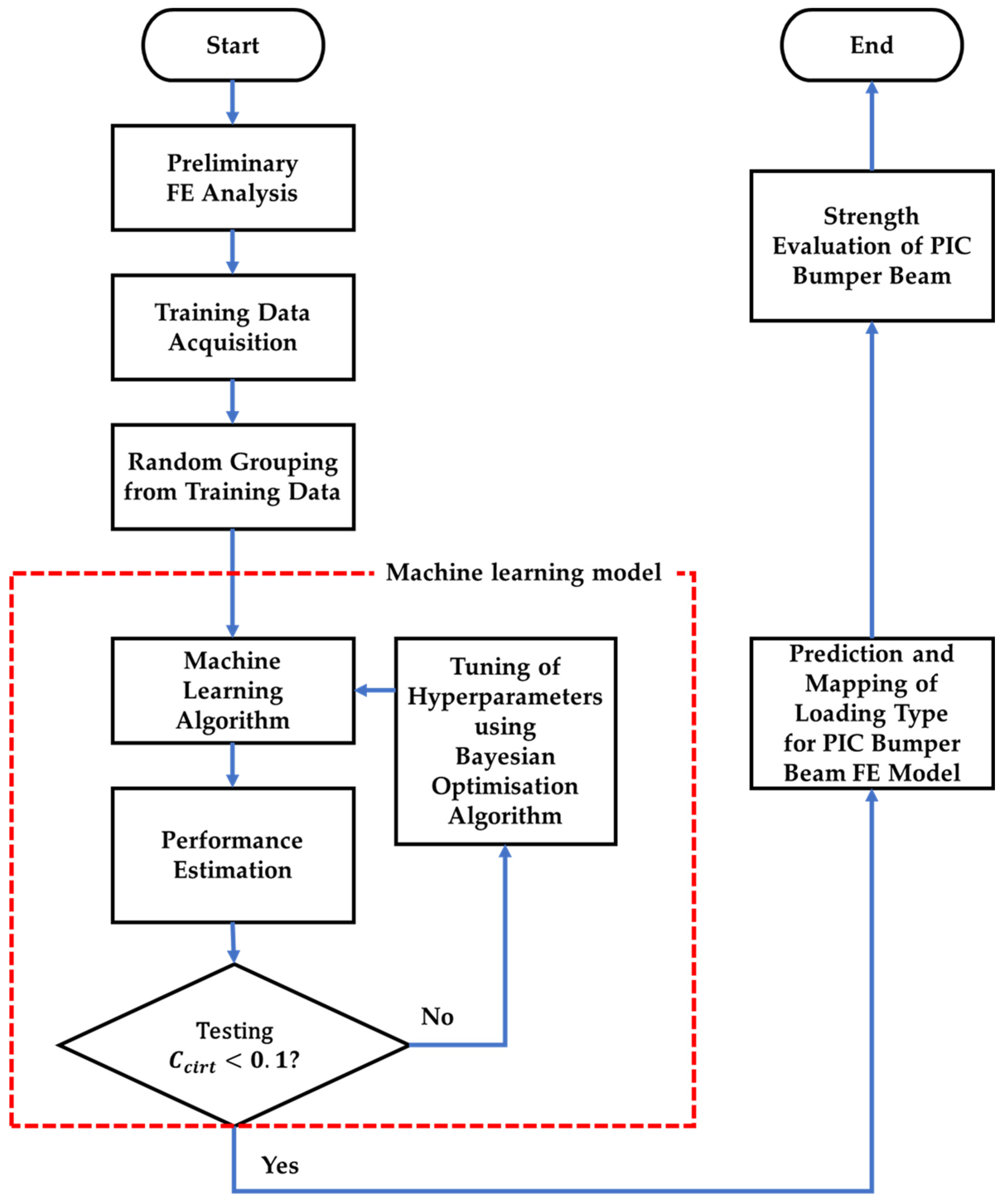
2. Outline of the PIC Bumper Beam Design Process

The PIC is assigning different stacking sequences for each shell element with a size of 4mm × 4mm as a similar form of mosaic and elements are assumed to have been perfectly bonded each other in order to increase robustness toward various external loading types. Firstly, a preliminary IIHS bumper FE analysis using aluminium bumper beam was carried out to achieve data, which are the input to machine learning model. For the material of the bumper beam during the preliminary FE analysis, aluminium alloy 7021 [18] was used since stress distribution within the beam is identical regardless of the material of the beam. Several elements among finite elements were chosen to be reference elements in order to collect stress triaxiality for judging the state of loading type, i.e., tension, compression, or shear with proper location. These data, resulted from reference elements, i.e., loading type and location were defined as training data, which are the input to machine learning model as explained previously.
Acquired training data are randomly assigned to five groups, i.e., each group contains 20% of training data for generalization’s sake [19]. One of groups is arbitrarily chosen for testing, the others for training which are put into machine learning algorithms, therefore, five times of trials are to be carried out per one iteration, which are known to be k-fold cross validation [20]. In the meantime, machine learning algorithms produce different performances according to their hyperparameter values. Mean value of accuracy and ROC (receiver operating characteristic)-AUC (area under the curve) are resulted from performance testing of machine learning algorithms. On condition that the results are not satisfactory, hyperparameters are tuned through the Bayesian optimisation algorithm and iterations are conducted until the lowest error or the highest performance is obtained. The iterative process, i.e., training group, machine learning algorithms, performance testing and hyperparameter tuning are known as machine learning model. When the results are acceptable, then loading types of unreferenced elements are able to be assigned and mapped into finite elements of the PIC bumper beam. Figure 1 shows the flowchart of PIC bumper beam design process.

3. Preliminary IIHS Bumper FE Analysis

The FE analysis was conducted with ANSYS LS-DYNA (ANSYS, Inc.), one of representative explicit finite element programs. The Belytschko-Lin-Tsay shell formulation is known to be suitable for expressing nonlinear anisotropic behavior of thin shell structure including complex load and large deformation with saving computation time [21]. Also, it was possible to track the through the thickness directional stresses at the top, mid and bottom surfaces of each element when the number of integration points was set to be three. For that reason, Belytschko-Lin-Tsay four node shell element with three integration points through the thickness direction were selected in order to model the thin-walled structures of bumper beam. Material model, which is able to be used for an elasto-plastic characteristics with an arbitrary stress as a function of strain curve and arbitrary strain rate dependency, was selected [22].
As previously noted, aluminium alloy 7021 was used for the material of the bumper beam during the preliminary FE analysis. Mechanical properties of aluminium alloy 7021 were summarised in Error! Reference source not found..
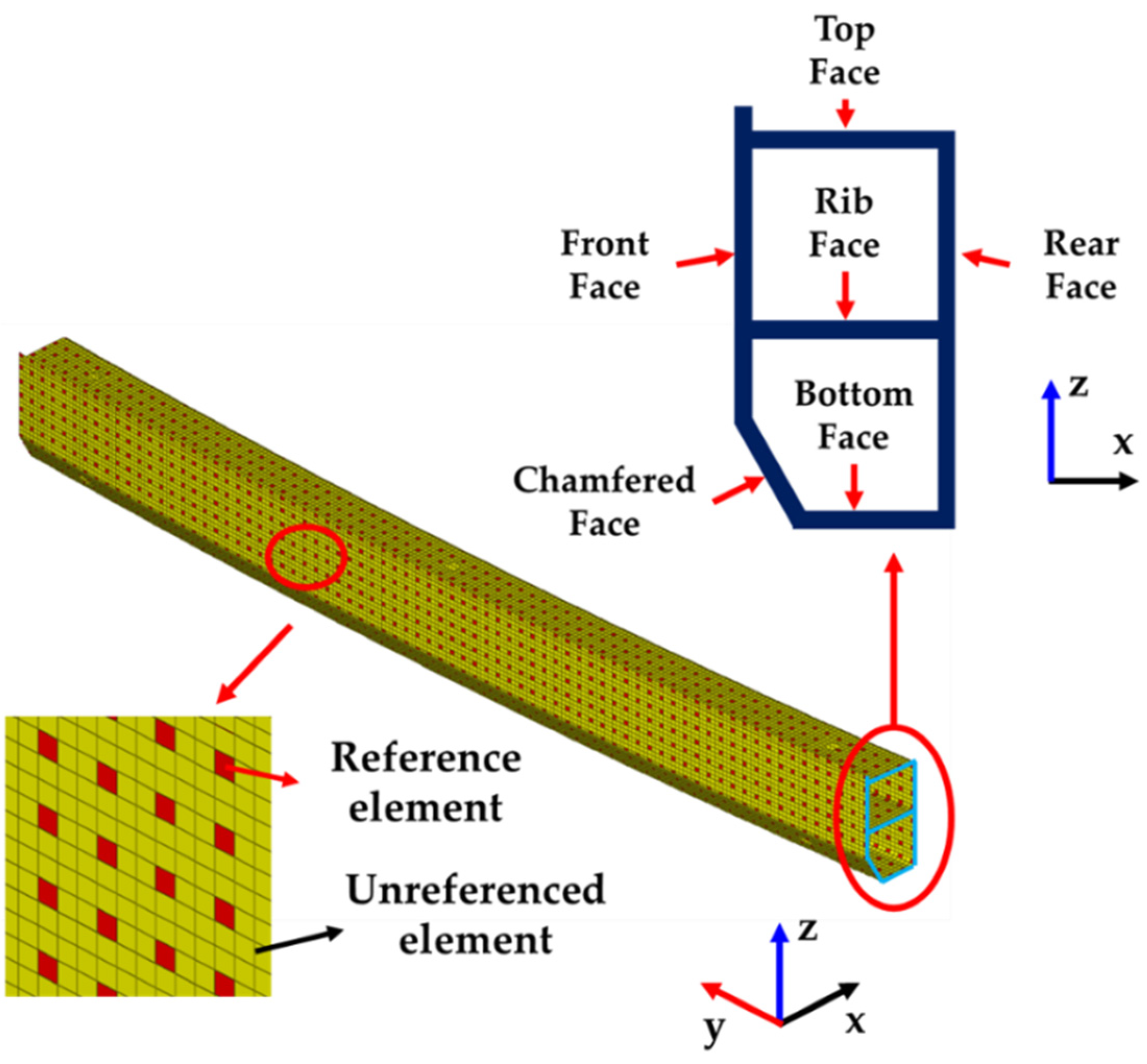
About 13% of total finite element were assigned to be references, in order to collect stress triaxiality for judging the state of loading type with proper location during IIHS bumper simulation. Stress triaxiality and coordinate location values for each reference element was included in training data. Total number of elements in bumper beam is about 9,500 and the reference element ratio is 12.8%, which is 1,210. 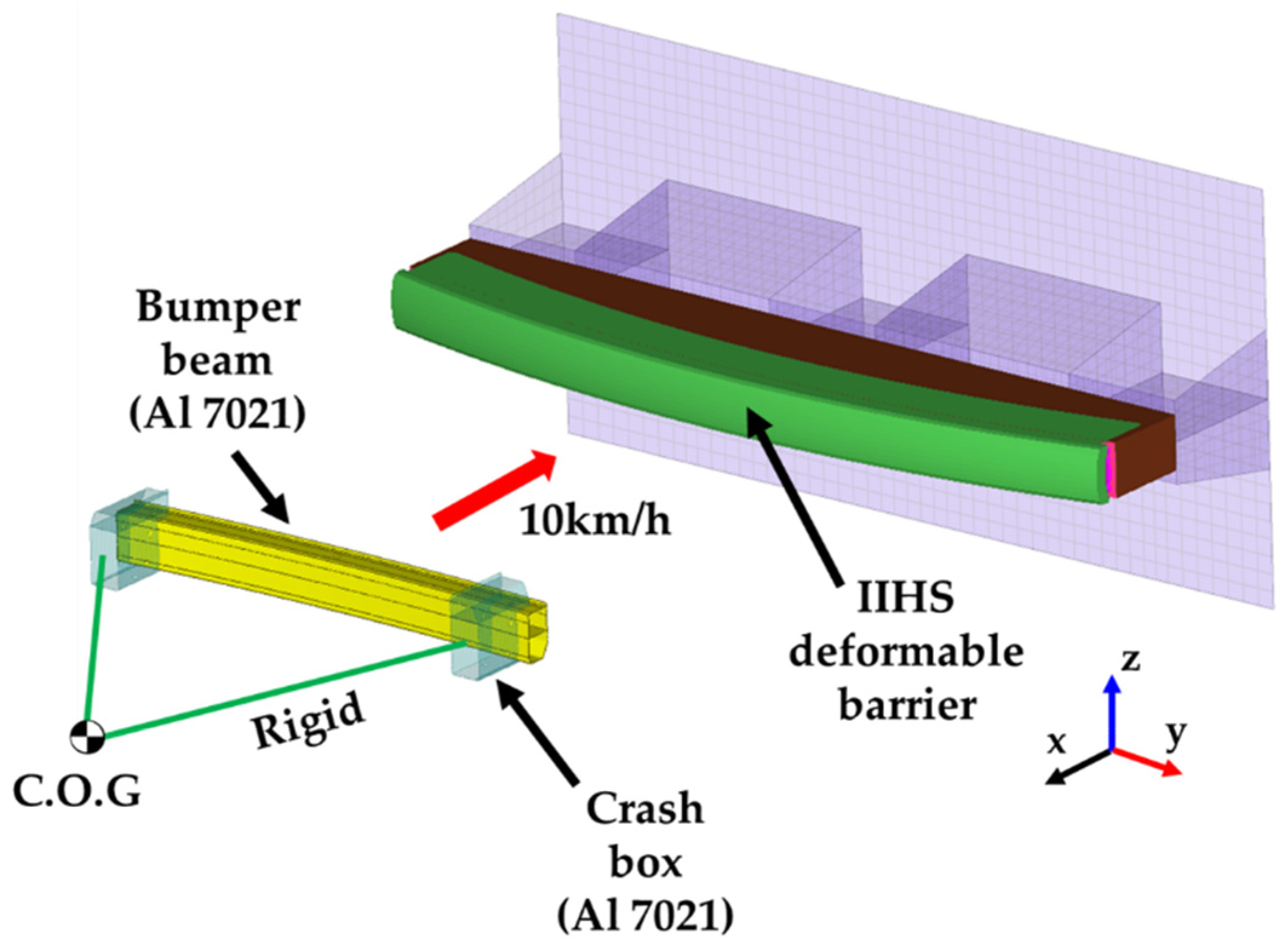Figure 2 shows the finite element bumper beam model with indicating reference elements and the cross-section of the bumper beam. Cross-sectional shape, total length, and radius of curvature for the bumper beam were designed with regard to the current product which was installed in a passenger car of “A” company. 2,200kg of the vehicle weight was considered as a form of concentrated mass element in the IIHS bumper crash analysis [14]. The IIHS bumper test is representatively used to measure the damage regions during the low-speed crash. In the meantime, the deformable barrier was modelled with 39,800 number of elements, based on the IIHS bumper test protocol [23]. The FE model for an automotive bumper beam and an IIHS standard deformable barrier including bumper crash boxes was illustrated in Figure 3. Aluminium alloy 7021 was used for the material of the bumper crash box which was firmly connected to rectangular cross-sectional to both ends of the bumper beam. As indicated in Figure 3, the initial speed was 10 km/h, and the vehicle mass of 2,200 kg was given to the point, in which the real centre of gravity of a passenger car was located. Consequently, it was found that 505 number of reference elements in tension, 593 in compression, and 112 in shear among 1,210 reference elements.

4. Training Data Acquisition and Random Grouping

As previously mentioned, the training data, which consist of stress triaxialities and coordinate location values, were obtained from preliminary IIHS bumper beam FE analysis.
There are two different implementations methods for random grouping, i.e., 2-dimentional(2-D) implementation and 3-dimensional(3-D) implementation. When the 2-D implementation is used, the training data is obtained from each face of bumper, i.e., the training data for top, front, chamfered, bottom, rear, and rib faces, respectively. Each training data regulates its own face, i.e., training data, which is obtained from top face is used only for predicting loading type of reference elements located in top face, etc. Meanwhile, training data in any faces are able to be used for any faces, on 3-D implementation.
Loading type of reference elements is determined through the stress triaxiality of each element. The definition of the stress triaxiality, is shown in Eq. (1).
η = σ m σ ¯
where σ m and σ ¯ are the mean principal stress and the von Mises stress, respectively [24].
Eqns. (2) and (3) show the definitions of mean principal stress and von Mises stress.
σ m = σ x + σ y + σ z   3
σ ¯ = 1 2 σ x − σ y 2 + σ y − σ z 2 + σ z − σ x 2 + 3 σ x y 2 + σ y z 2 + σ z x 2
When η is bigger than 0.1, loading type is considered to be tension dominant. Compression dominant loading type is believed if η is smaller than -0.1. In case η is bigger than -0.1 and smaller than 0.1, that element is subject to shear dominant loading [25].
Acquired training data are randomly divided into five groups, i.e., each group contains 20% of training data for the sake of generalization. As previously noticed, one of groups is arbitrarily chosen for testing, the others for training which are put into machine learning algorithms, therefore, five times of trials are to be carried out per one iteration, which are known to be k-fold cross validation.

5. Machine Learning Models

As previously mentioned in Ch.2, machine learning model consists of machine learning algorithms, performance estimation/testing and hyperparameter tuning.

5.1. Machine Learning Algorithms

Machine learning algorithms are able to characterise data for the sake of classification, regression, clustering, and outlier detection. In the present study, classification related machine learning algorithms were considered since it is indispensable to classify unknown data with decent prediction. Decision tree, ensemble decision tree (boosted and bagged), SVM (Support vector machine), and k-NN (k nearest neighbors) classification were chosen among classification algorithms according to their ability of classifying imbalanced data [26]. Each algorithm has several different parameters, i.e., hyperparameters, which are to be iteratively tuned based according to the Bayesian algorithm in order to optimise the results [27]. A detailed description of the classification used can be found as follows:

5.1.1. Decision Tree

Decision tree is normally used to compare unknown data to tree structure, which consists of root, branches and leaves. During the root process, unknown data are input to the decision tree algorithm and the output of the root process is transferred to various branches. Intermediate results for determining loading types of unknown data are generated based on the characteristics of training groups, which survive from criteria during the branch process. Final loading types of unknown data are unveiled in the leaf process. Decision tree has two hyperparameters, i.e., maximum number of splits and criteria, which was summarised in Table 2 [28].

5.1.2. Ensemble Method

There is a high possibility that the overfitting, which is indicating that predicted results of loading types are sufficiently good for training group, however, poor prediction is generated for unreferenced elements, happens when it involves too much branch processes. To reduce the effect of overfitting, it is recommended to apply the ensemble method, which merges outcomes from several branches into one value. In the present study, boosted decision tree and bagged decision tree are considered since they are considered to be representative machine learning algorithms with ensemble method. The boosted decision tree is applying the same algorithm model, which is previously used for the decision tree, iteratively and sequentially. Iterations are conducted with updated weighting factor, until the results fulfil the criterion. It requires maximum number of splits, number of learners, and learning rate as its hyperparameters. Bagged decision tree needs to apply several decision trees, which are generated by bootstrapping variations of the same decision tree algorithm model, parallelly at the same time. The best result is selected among aggregated ones based on a majority vote. The bagged decision tree needs two hyperparameters, i.e., maximum number of splits and number of learners. Table 3 shows the hyperparameters for the ensemble method [29].

5.1.3. SVM

SVM aims at forming the finest suitable decision limit or boundary, known as hyperplane, which separates n-dimensional space into loading types, making it easy to place a different point in the appropriate area. In SVM algorithm, extreme vector points called support vectors are chosen which help in creating a proper hyperplane. Hyperplane of SVM is defined as the best possible decision boundary out of various possible decision boundaries that accurately classifies the classes in n-dimensional space. Features of the training group determine the dimensions of the hyperplane. A hyperplane​ having maximum margins, which means the distance between two data points is maximum, is preferred. Kernel function, kernel scale, box constraint level, and multiclass method are hyperparameters, which are listed in Table 4 [30].
5.1.4. k-NN Classification
The k-NN classification is instance-based learning method used to classify objects based on their closest training group in the feature space. An object is classified by a majority vote of its neighbors, i.e., the object is assigned to the class that is most common amongst its k-nearest neighbors, where k is a positive integer. In the k-NN classification, the classification of a new test feature vector is determined by the classes of its k-nearest neighbors. Here, the k-NN classification was implemented using various distance metrics to locate the nearest neighbor. Number of neighbors, distance metric, and distance weight are its hyperparameters as shown in Table 5 [31].

5.2. Performance Testing

There are four types of cross validations, i.e., k-fold, holdout, leave-p-out and leave-one-out in order to estimate the performance of the machine learning algorithms [32]. In the present study, k-fold cross validation was selected among them since it is known to have an ability to reduce biases and classify loading types with low capacity of training data [33]. As mentioned in Ch. 2, acquired training data were randomly divided into five groups, i.e., each group contains 20% of training data for the sake of generalization. One of groups was arbitrarily chosen for testing, the others for training which were put into machine learning algorithms, therefore, five times of trials were carried out per one iteration.
The performance of the machine learning algorithms was estimated using the accuracy and the ROC-AUC value [34]. Accuracy is the proportion of correct predictions made by the model out of the total number of predictions as shown in Eqn. (4) [35].
A c c u r a c y   ( % ) = N u m b e r   o f   c o r r e c t   p r e d i c t i o n s T o t a l   n u m b e r   o f   p r e d i c t i o n s × 100
Accuracy is a widely used metric because of its simplicity and effectiveness, however, it contains the mixed information of tension, compression, and shear loading types. According to the possibility of imbalanced training data, which were produced from preliminary FE analysis, ROC-AUC might alleviate the misleading results by the imbalanced data [36]. ROC-AUC is suitable for estimating imbalanced loading type data, since they can separately show individual values for each loading type among training group. The ROC curve comes from ratios based on correctly predicted data and incorrectly predicted data, and the AUC means the area under the ROC curve. Generally, AUC takes values from 0 to 1, where a value of 0 indicates a perfectly inaccurate estimation, and a value of 1 reflects a perfectly accurate estimation. Less than 0.5 of AUC value suggests no discrimination, 0.7 to 0.8 is considered acceptable, 0.8 to 0.9 is considered excellent, and more than 0.9 is considered outstanding [37,38]. The convergence criterion ( C c r i t ) is defined as the change in accuracy as shown in Eqn. (5) [39].
C c r i t = A n − A n − 1 A n
where A n implies the accuracy value at the n- iteration. In order to meet the highest performance, the value for the convergence criterion was set to be 0.1. When the results were not satisfactory, hyperparameters were tuned based on Bayesian optimisation algorithm and iterative performance estimation and testing were conducted, which was detailed in the next chapter.

5.3. Hyperparameter Tuning with Bayesian Optimisation Algorithm

As previously mentioned, hyperparameters are tuned through the Bayesian optimisation algorithm, which is famous for more effective compared to the grid search or random search, and iterations are conducted until the lowest error or the highest performance is obtained on condition that the results are not satisfactory [40,41]. The main feature of optimising technique is to maximise the objective function, which is denoted by f along with hyperparameters as its independent variables. The output of the objective function is the performance of machine learning algorithms. Each iteration needs updating or tuning the hyperparameters within their own domain, which is represented by X . Accordingly, the Bayesian optimisation algorithm can be explained as Eqn. (6):
x * = arg ⁡ max x ∈ X ⁡ f x
where x denotes a set of hyperparameter values in the domain X , and x * is the set of hyperparameters that maximises the performance, i.e., the output of the objective function f [42]. Hyperparameters were tuned by the Expected-Improvement-Per-Second Plus, which provided fastest speed of the convergence criterion as well as prevented overexploiting possible ranges of hyperparameter domains from being illuded by the local maximum [43]. When the value of the convergence criterion became lower than 0.001, hyperparameter tuning was completed. Table 6 indicates the completely tuned hyperparameter values, which maximised the performance of each algorithm. Learning rate in the Boosted decision trees, Kernel scale and box constraint level of SVM were displayed by four decimal point.
Table 7 and Table 8 show the highest performances, i.e., accuracy and ROC-AUC value of 2-D and 3-D implementations. All values in the Table 7 are the average of values of top, front, chamfered, bottom, rear, and rib faces both for the accuracy and the ROC-AUC. The accuracy from the 3-dimensional implementation was higher than that of the 2-dimensional implementation. The k-NN classification showed the highest accuracy both for 2-dimensional and 3-dimensional implementations. As shown in Table 7 and Table 8, predicted ROC-AUC values for shear dominant loading type were smallest compared with either tensile or compressive ones, since the portion of shear dominant reference elements was lowest.

6. Prediction and Mapping of Loading Type of Unreferenced Elements

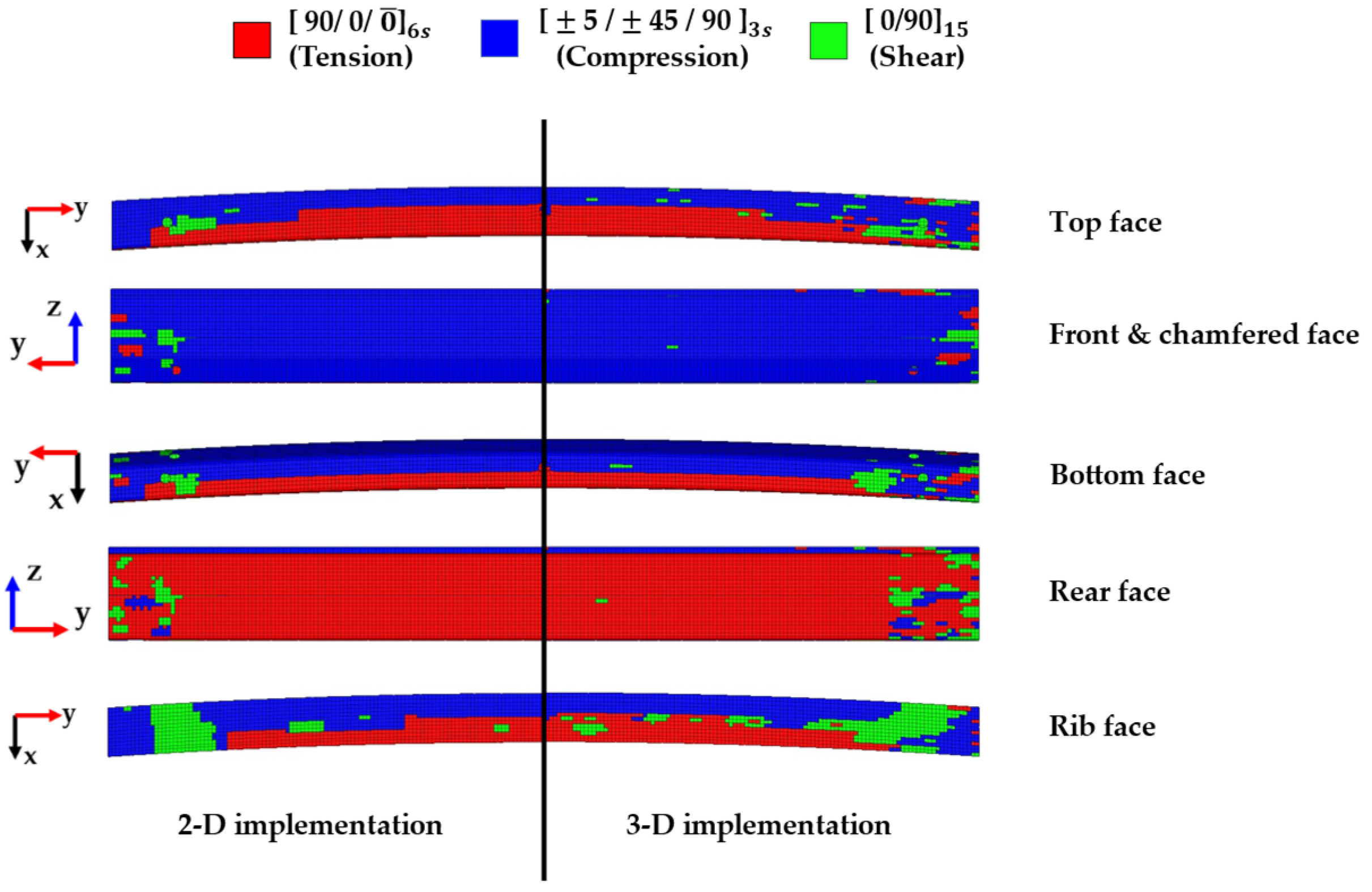
k-NN was applied to predict loading types of unreferenced finite elements in the PIC bumper beam with the input of coordinate location values of target locations since it was revealed to be the most excellent classification both for 2-D and 3-D implementations from the comparison of resultant performance of machine learning algorithms without further predictions using other machine learning algorithms. In the meantime, there are no previous results of loading types for unreferenced elements, i.e., no solutions are existing, it was unnecessary to calculate either accuracy or ROC-AUC values. Predicted results involved loading types and their locations, for unreferenced elements, therefore, they were mapped into the PIC bumper FE model. In the meantime, robust stacking sequences against each loading type were listed in Table 9 [44]. Also, these stacking sequences were mapped into the FE model as shown in Figure 4.
While machine learning algorithms were predicting dominant loading type at a certain face, only training data obtained from reference elements which were located at the same face during 2-D implementation. On the other hand, training data from reference elements, which were located at various faces depending on the metric values, were used for dominant loading type prediction in 3-D implementation as previously mentioned. From the Figure 4, it was observed that three different loading types were mixed together at both ends which were firmly connected to rectangular cross-sectional bumper crash boxes. 42.3%, 53.2%, and 4.5% of tension, compression, and shear dominant loading types were predicted for the entire PIC bumper beam FE model from 2-D implementation, whilst 42.1%, 50.4%, and 7.5% of tension, compression, and shear dominant loading types from 3-D implementation for the same bumper beam FE model. Also, each loading type areal difference was conspicuous in the rib face, i.e., tension dominant area from 3-D was 6.5% larger than that from 2-D, compression dominant area from 3-D was 12.5% smaller than that from 2-D, and shear dominant area from 3-D was 5.9% larger than that from 2-D, as observed from Figure 4. Meanwhile, loading type areas were the most similar from 2-D and 3-D on the front face. These results were summarised in Table 10.

7. Bending Strength Evaluation of PIC Bumper Beam

IIHS bumper analyses were performed using ANSYS LS-DYNA (ANSYS, inc.) in order to evaluate the bending strength of the PIC bumper beam based on the 2-D and 3-D implementations with employing machine learning model as well as a composite bumper beam with a conventional stacking sequence of [ 0 / ± 45 ] 5 S for comparison’s sake. Fully integrated shell formulation was selected to express nonlinear anisotropic behaviour with warpage under the function of improved transverse shear treatment for composite beam FE model [45]. Enhanced composite damage type material model, which are frequently used for describing material anisotropy with the help of the laminated shell theory, was selected for the whole composite part [22]. 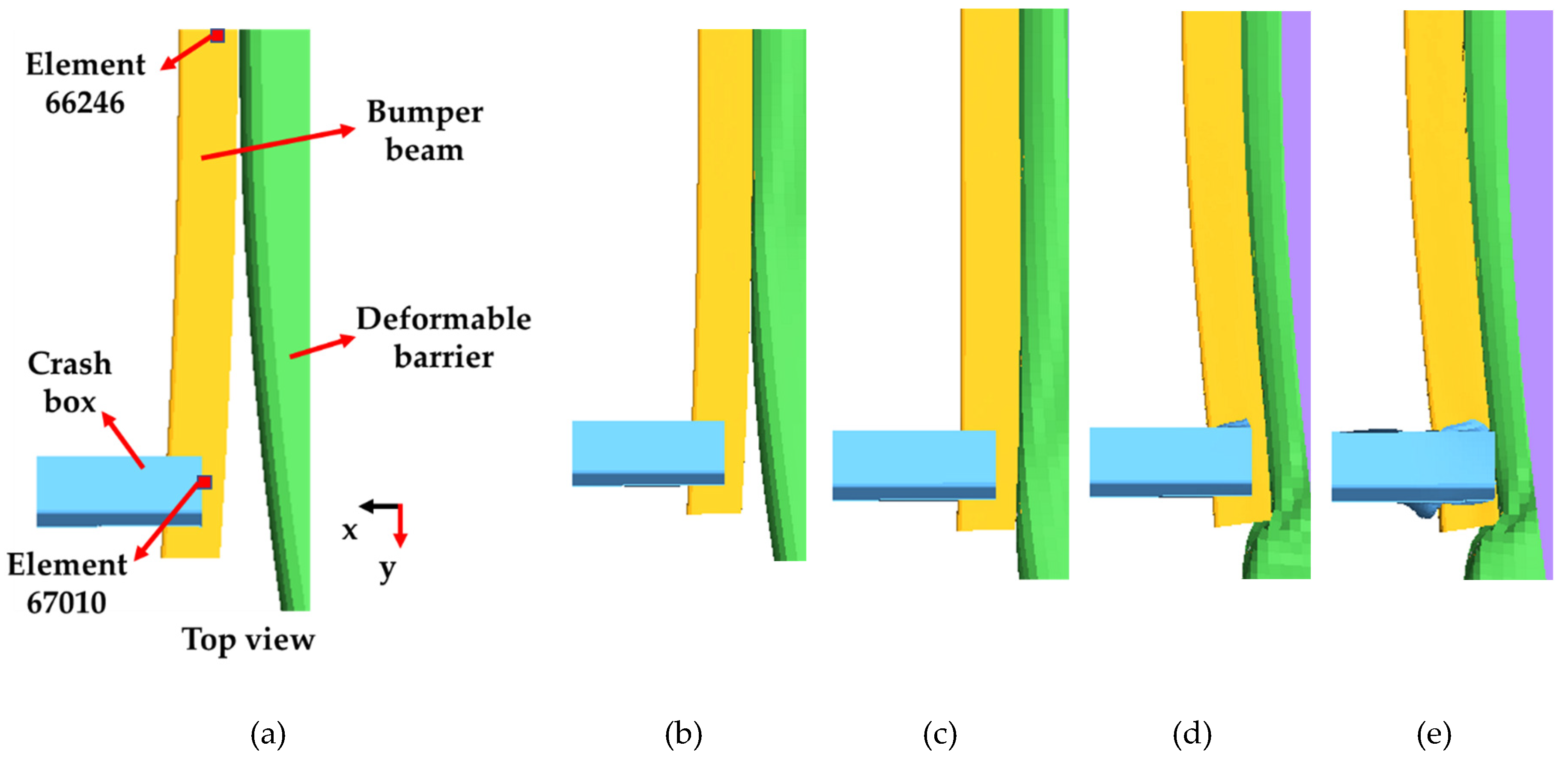Table 11 shows the mechanical properties of T700/2510 carbon fibre epoxy composite which were considered for the composite bumper beam [46]. Initial velocity, vehicle weight and miscellaneous details were the same as those used in preliminary IIHS bumper beam FE analysis. Deformation of PIC bumper beam and crash box was illustrated in Figure 5.
Beam was undergoing two types of deformation, i.e., bending type at centre part and buckling type along with cross-sectional direction at both ends which were connected to crash box. From Figure 5b, pure bending deformation of bumper beam was observed until 0.009 sec (C.O.G displacement: 24 mm), while buckling type crash box deformation started at 0.02 sec (C.O.G displacement: 54 mm) as shown in Figure 5c. Deformation of crash box initiated from the inner part and propagated to outer part owing to convex shape of the IIHS barrier. Bumper beam deformed to become a straight shape with respect to longitudinal direction and main deformation belonged to crash box at 0.035 sec (C.O.G displacement: 80 mm) as depicted in Figure 5d. In Figure 5e, maximum deformation of the bumper beam and crash box occurred at 0.045 sec (C.O.G displacement: 107 mm), elastic spring back started from this point.
Tsai-Wu indexes were investigated for specific elements, which were exposed to comparatively higher loading. The 66246th element and the 67010th element were chosen from the centre part and the RH end part of the composite bumper beam as visible in Figure 5a since these parts underwent severer deformation during FE analyses.
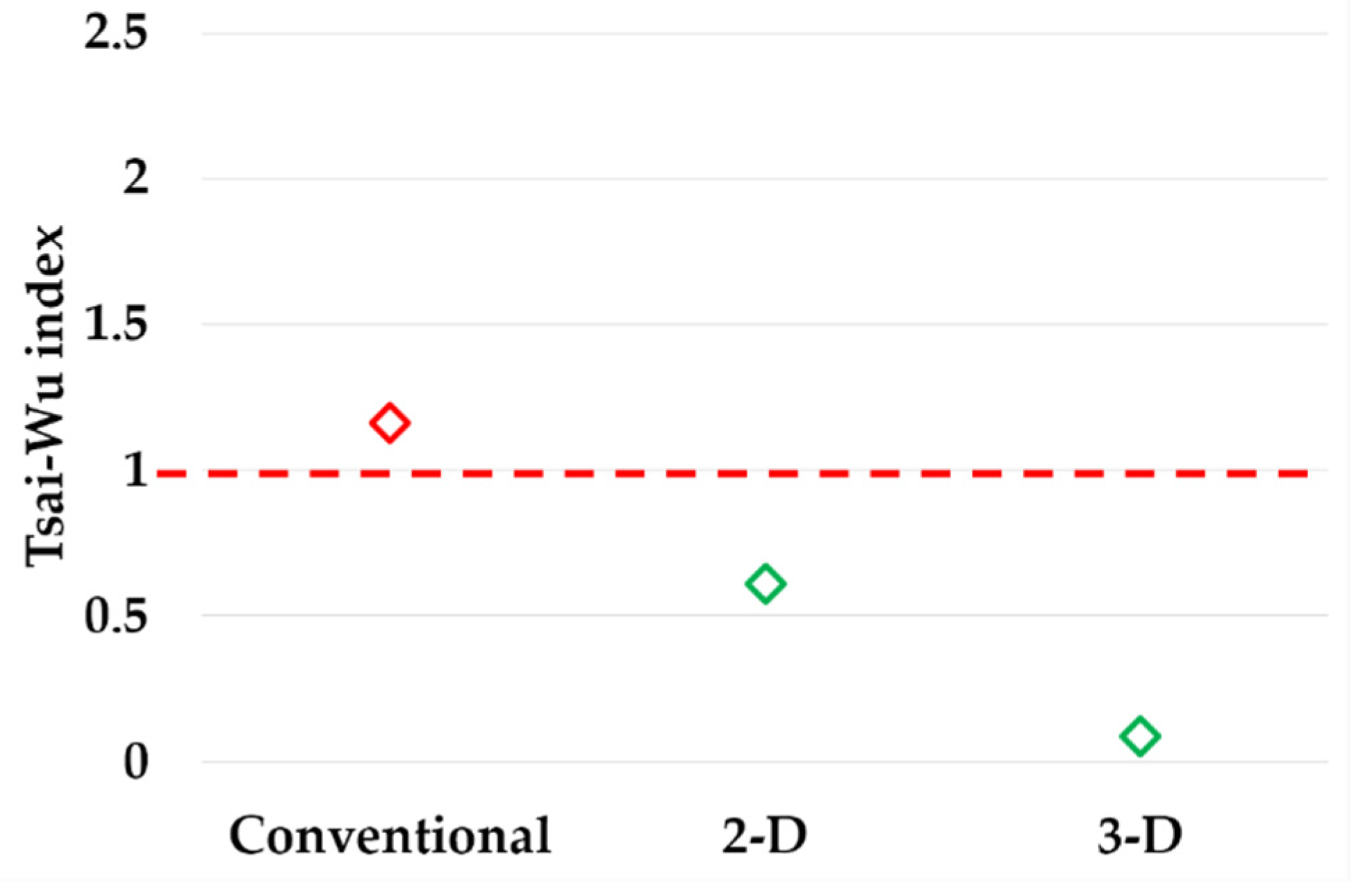
Dominant loading type for the 66246th element and the 67010th element were found to be shear, and decent loading type was predicted by the 3-D implementation, but the 2-D implementation predicted compression for the elements. As a result, the Tsai-Wu indexes for the 66246th element and the 67010th element were shown in Figure 6.
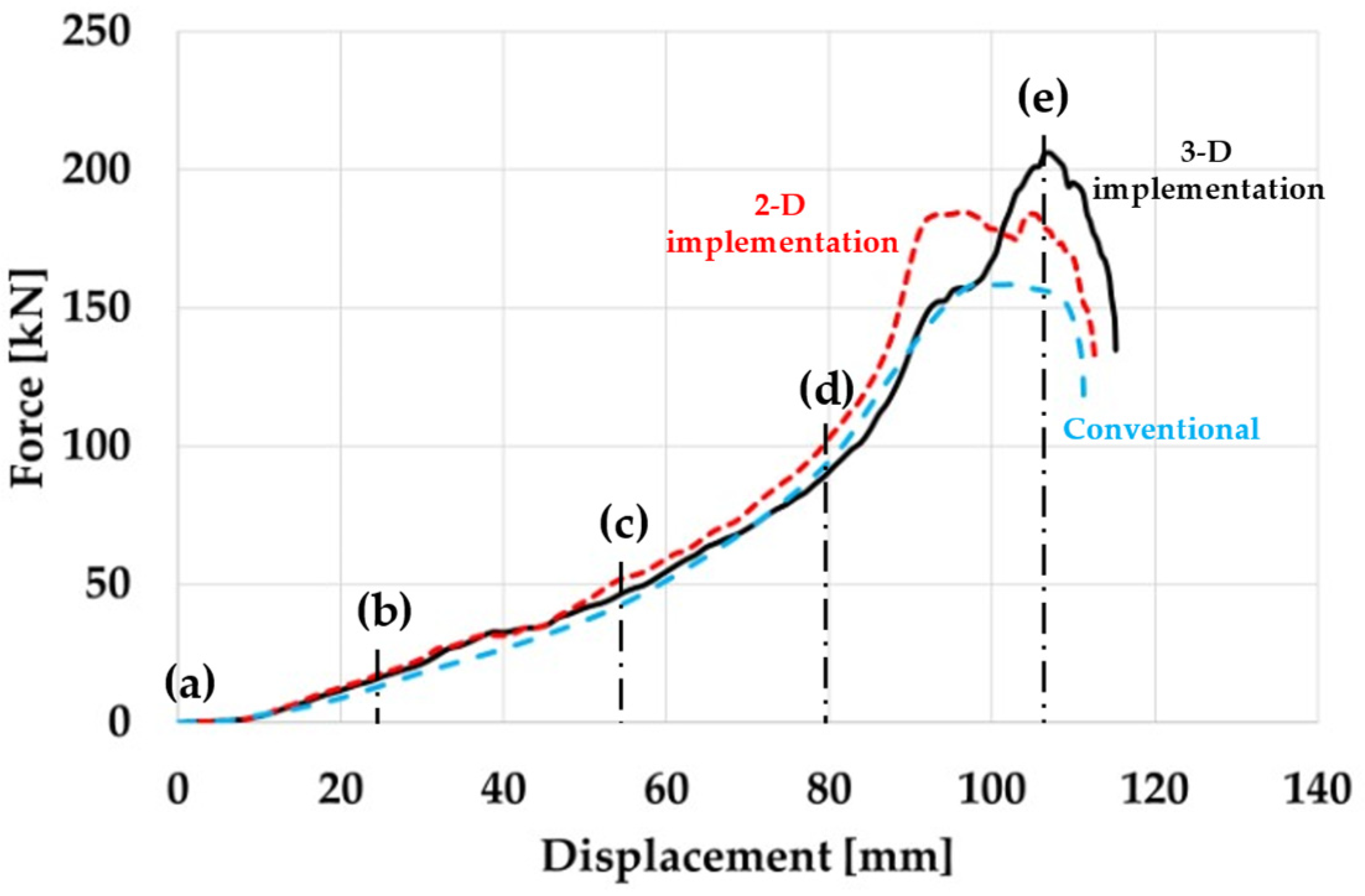
In Figure 6, the index, calculated based on the conventional composite beam, was found to be exceeding 1. The index for 2-D was close to 1, but the index for 3-D was the lowest, i.e., conventional composite beam was experiencing fracture, while PIC bumper beams were safe under the same level of external loading. It was found that the conventional stacking sequence did not sufficiently respond to external loading, and the PIC bumper beams were safe and effective. In the meantime, the Tsai-Wu indexes revealed that the PIC beam of 3-D implementation was safer compared with that of 2-D implementation. The force-displacement curve results of conventional composite bumper beam and PIC bumper beams were plotted in Figure 7. Each deformation of stage (a), (b), (c), (d), and (e) in Figure 5 were synchronised to points from (a) to (e) in Figure 7.
Force slope increased at point (d) because crash boxes and both end parts of composite bumper beam started to deform. Higher external load resisting ability of a composite bumper beam was dependent on the proper stacking sequences of both end parts.
The maximum bending strength of the conventional composite bumper beam was 158 kN, while that of the PIC bumper beam based on 2-D implementation was 184 kN, and 3-D implementation, 206 kN, i.e., the bending strength of PIC bumper beam of 3-D implementation was about 10.4% and 23.0% higher than that of 2-D implementation and that of conventional stacking sequence, respectively. The PIC bumper beams with machine learning model showed superior bending strength to conventional composite bumper. As previously observed, PIC bumper beam of 3-D implementation showed higher external load resisting ability compared to that of 2-D implementation. Therefore, it was found that the 3-D implementation was more effective to assign proper stacking sequences into exact places of composite bumper beam. If PIC bumper beams were designed targeting the same bending strength level of conventional composite bumper beam, 8% and 12% of weight saving effects could be achieved as summarised in Table 12.
From crashworthiness point of view, conventional composite bumper beam absorbed 6980 J during IIHS bumper crash analysis. Meanwhile, 2-D implemented, and 3-D implemented PIC bumper beams absorbed 8230 J and 8260 J, respectively. PIC bumper beam of 3-D implementation also showed slightly higher energy absorption characteristics than either conventional or 2-D implemented composite bumper beam. Therefore, PIC bumper beam design with machine learning has direct impact on reducing the possibility of failure as well as increasing bending strength effectively. Moreover, 3-D implementation produced better results compared with 2-D implementation since it was preferable to choose loading type information which was achieved from surroundings when the target elements were located either at corner or junction of planes instead of using information came from the same plane of target.

8. Conclusions

The PIC bumper beam with employing machine learning models was proposed in order to improve bending strength and structural lightweight effect, which were proved by IIHS bumper FE simulations. During simulation, composite bumper beam was undergoing two major types of deformation, i.e., bending type at centre part and buckling type along with cross-sectional direction at both ends which were connected to crash box. 2-D and 3-D implementations were provided by machine learning models, which determined stacking sequences of each finite element in PIC bumper beam. It was found that PIC bumper beams were safe and effective, however, the conventional composite bumper beam did not sufficiently withstand external loading. In the meantime, the Tsai-Wu indexes revealed that the PIC beam of 3-D implementation was safer compared with that of 2-D implementation. Also, dominant loading type for centre part and both end parts were found to be shear, and correct loading type was predicted by 3-D implementation, but the 2-D implementation predicted compression for parts.
Bending strength of 3-D implementation was about 10.4% and 23.0% higher than that of 2-D implementation and that of conventional stacking sequence. PIC bumper beam of 3-D implementation showed higher external load resisting ability compared to that of 2-D implementation. Therefore, it was found that the 3-D implementation was more effective to assign proper stacking sequences into exact places of composite bumper beam. If PIC bumper beams were designed targeting the same bending strength level of conventional composite bumper beam, 8% and 12% of weight saving effects could be achieved. Therefore, PIC bumper beam design with machine learning has direct impact on reducing the possibility of failure as well as increasing bending strength effectively.
From crashworthiness point of view, conventional composite bumper beam absorbed 6980 J during IIHS bumper crash analysis. Meanwhile, 2-D implemented, and 3-D implemented PIC bumper beams absorbed 8230 J and 8260 J, respectively. PIC bumper beam of 3-D implementation also showed slightly higher energy absorption characteristics than either conventional or 2-D implemented composite bumper beam. Moreover, 3-D implementation produced better results compared with 2-D implementation since it was preferrable to choose loading type information which was achieved from surroundings when the target elements were located either at conner or junction of planes instead of using information came from the same plane of target.

Author Contributions

Conceptualization, S.W.H and S.S.C.; methodology, S.W.H and S.S.C.; software, S.W.H and S.S.C.; validation, S.W.H and S.S.C.; formal analysis, S.W.H and S.S.C.; data curation, S.W.H.; writing—original draft preparation, S.W.H and S.S.C.; writing—review and editing, S.W.H and S.S.C.; visualization, S.W.H and S.S.C.; investigation, S.W.H and S.S.C.; resources, S.W.H and S.S.C.; project administration, S.S.C.; funding acquisition, S.S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2018R1D1A1B07051169). Also, this work was supported by the research grant of the Kongju National University in 2020.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bruggia, M.; Milanib, G. Optimal FRP reinforcement of masonry walls out-of-plane loaded: A combined homogenization–topology optimization approach complying with masonry strength domain. Comput Struct 2015, 153, 49–74. [Google Scholar] [CrossRef]
  2. Mirzendehdel, A.M.; Suresh, K. , Support structure constrained topology optimization for additive manufacturing. Comput Aided Des 2016, 81, 1–13. [Google Scholar] [CrossRef]
  3. Gholizadeh, S.; Ebadijalal, M. Performance based discrete topology optimization of steel braced frames by a new metaheuristic. Adv Eng Softw 2018, 123, 77–92. [Google Scholar] [CrossRef]
  4. Eckrich, M.; Arrabiyeh, PA; Dlugaj, AM; May, D. Structural topology optimization and path planning for composites manufactured by fiber placement technologies. Comput Struct 2022, 289, 115488. [CrossRef]
  5. Slater, C.; Otto, SR; Strangwood, M. The quasi-static and dynamic testing of damping in golf clubs shafts fabricated from carbon fibre composites. Procedia Eng 2010, 2, 3361–3366. [CrossRef]
  6. Kong, CD.; Lee, HS; Park, HB. Design and manufacturing of automobile hood using natural composite structure. Compos B Eng 2016, 91, 91,18–26. [CrossRef]
  7. Colonna, M.; Bon, FD.; Tarterini, F.; Moncalero, M.; Totaro, G.; Gioia, C.; Fabbri, P. Ski Boot Soles Based on a Glass Fiber/Rubber Composite with Improved Grip on Icy Surfaces. Procedia Eng 2016, 147, 372–377. [Google Scholar] [CrossRef]
  8. Muflikhun, MA.; Yokozeki, T. Experimental and numerical analysis of CFRP-SPCC hybrid laminates for automotive and structural applications with cost analysis assessment. Compos Struct 2021, 263, 113707. [Google Scholar] [CrossRef]
  9. Kulhan, T.; Kamboj, A.; Gupta, N.K.; Somani, N. Fabrication methods of glass fibre composites-a review. Funct. Compos. Struct 2022, 4, 022001. [Google Scholar] [CrossRef]
  10. Cheon, S.S.; Choi, J.H.; Lee, D.G. ; Development of the Composite Bumper Beam for Passenger Cars. Compos Struct 1995, 32, 491–499. [Google Scholar] [CrossRef]
  11. Hosseinzadeh, R.; Shokrieh, M.M.; Lessard, L.B. Parametric Study of Automotive Composite Bumper Beams Subjected to Low-velocity Impacts. Compos Struct 2005, 68, 419–427. [Google Scholar] [CrossRef]
  12. Belingardi, G.; Beyene, A.T.; Koricho, E.G. Geometrical Optimization of Bumper Beam Profile Made of Pultruded Composite by Numerical Simulation. Compos Struct 2013, 102, 217–225. [Google Scholar] [CrossRef]
  13. Kim, D.H.; Kim, H.G.; Kim, H.S. Design Optimization and Manufacture of Hybrid Glass/carbon Fiber Reinforced Composite Bumper Beam for Automobile Vehicle. Compos Struct 2015, 131, 742–752. [Google Scholar] [CrossRef]
  14. Jeong, C.H.; Oh, H.S.; Ham, S.W.; Kim, G.S.; Son, S.N.; Cho, Y.S.; Cheon, S.S. Crash simulation of a piecewisely-integrated composite bumper beams. Int. j. mech. prod. eng. 2018, 6, 37–40. [Google Scholar]
  15. Liang, L.; Sun, B. A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis. Bioengineering (Basel) 2019, 6, 104. [Google Scholar] [CrossRef] [PubMed]
  16. Zhenchao, Q.; Nanxi, Z.; Yong, L.; Wenliang, C. Prediction of mechanical properties of carbon fiber based on cross-scale FEM and machine learning. Compos Struct 2019, 212, 199–206. [Google Scholar] [CrossRef]
  17. Hürkamp, A.; Gellrich, S.; Ossowski, T.; Beuscher, J.; Thiede, S.; Herrmann, C.; Dröder, K. Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites. J. Manuf. Mater. Process. 2020, 4, 92. [Google Scholar] [CrossRef]
  18. Tisza, M. ; Czinege, I, Comparative study of the application of steels and aluminium in lightweight production of automotive part. Int. j. lightweight mater. manuf. 2018, 1, 229–238. [Google Scholar] [CrossRef]
  19. Arbameri, A.; Blaschke, T.; Chowdhuri, I.; Saha, A.; Chakrabortty, R.; Lee, S; Band, S. S, Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility. Remote Sens. 2020, 12, 3675. [CrossRef]
  20. Saha, A.; Pal, S.C.; Chowdhuri, I.; Islam, A.R.M.T.; Roy, P. ; Chakrabortty, R, Land degradation risk dynamics assessment in red and lateritic zones of eastern plateau, India: A combine approach of K-fold CV, data mining and field validation. Ecol. Inform. 2022, 69, 101653. [Google Scholar] [CrossRef]
  21. Key, S.W.; Hoff, C.C. , An improved constant membrane and bending stress shell element for explicit transient dynamics, Comput. Methods. Appl. Mech. Eng. 1995, 124, 33–47. [Google Scholar] [CrossRef]
  22. LS-DYNA manual R13.0 Vol II. Available online: https://www.dynasupport.com/manuals/ls-dyna-manuals/ls-dyna_manual_volume_ii_r13.pdf (accessed on 9 January 2023).
  23. Bumper test and rating protocol (Version VIII). Insurance institute for highway safety: https://www.iihs.org/media/07bf4085-8c25-4972-aa56-c06ff19dae05/L5AzKw/Ratings/Protocols/archive/test_protocol_bumper_vVIII_0910.pdf (28. Nov. 2022).
  24. Bai, Y.; Wierzbicki, T. , Application of extended Mohr-Coulomb criterion to ductile fracture. Int. j. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
  25. Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. j. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
  26. Bansal, M.; Goyal, A. ; Choudhary, A, A comparative analysis of K-Nearest Neighbor, Genetic, Support Vector Machine, Decision Tree, and Long Short Term Memory algorithms in machine learning. Decis. Anal. 2022, 3, 100071. [Google Scholar] [CrossRef]
  27. Fakhrmoosavi, F.; Kamjoo, E.; Kavianipour, M.; Zockaie, A.; Talebpour, A.; Mittal, A. , A Stochastic Framework Using Bayesian Optimization Algorithm to Assess the Network-level Societal Impacts of Connected and Autonomous Vehicles. Transp. Res. Part C Emerg. Technol. 2022, 136, 103663. [Google Scholar] [CrossRef]
  28. Roy, S.; Mondal, S.; Ekbal, A.; Desarkar, M.S. Dispersion Ratio based Decision Tree Model for Classification. Expert Syst. Appl. 2019, 116, 1–9. [Google Scholar] [CrossRef]
  29. Petković, M.; Ceci, M.; Pio,G.; Škrlj, B; Kersting, K.; Džeroski, S., Relational tree ensembles and feature rankings. Knowl. Based Syst. 2022, 5, 109254. [CrossRef]
  30. Richhariya, B.; Tanveer, M. EEG signal classification using universum support vector machine. Expert Syst. Appl. 2018, 106, 169–182. [Google Scholar] [CrossRef]
  31. Xiao, J. SVM and KNN ensemble learning for traffic incident detection. Physica A 2019, 517, 29–35. [Google Scholar] [CrossRef]
  32. Valente, G.; Castellanos, A.L.; Hausfeld, L.; Martino, F.; Formisano, E. , Cross-validation and permutations in MVPA: Validity of permutation strategies and power of cross-validation schemes. Neuroimage 2021, 238, 118145. [Google Scholar] [CrossRef]
  33. Anandan, B.; Manikandan, M. , Machine learning approach with various regression models for predicting the ultimate tensile strength of the friction stir welded AA 2050-T8 joints by the K-Fold cross-validation method. Mater. Today Commun. 2023, 34, 105286. [Google Scholar] [CrossRef]
  34. Raschka, S.; Mirjalili, V. Python Machine Learning, 2nd ed.; Packt Publishing: Birmingham, UK, 2019; pp. 230–240. [Google Scholar]
  35. Papalampidou, A.; Papoutsi, E.; Katsaounou, P.A. , Pulmonary nodule malignancy probability: a diagnostic accuracy meta-analysis of the Mayo model. Clin. Radiol. 2022, 77, 443–450. [Google Scholar] [CrossRef]
  36. Gajowniczek, K.; Ząbkowski, T. ImbTreeAUC: An R package for building classification trees using the area under the ROC curve (AUC) on imbalanced datasets. SoftwareX 2021, 15, 100755. [Google Scholar] [CrossRef]
  37. Mandrekar, J.N. , Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef]
  38. Hosmer, DW.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley and Sons: New York, USA, 2000; pp. 160–164. [Google Scholar]
  39. Querin, O. ; Victoria, M; Alonso, C.; Loyola, R.; Montrull, P. Topology Design Methods for Structural Optimization, 1st ed.; Academic Press: Massachusetts, USA, 2017; pp. 27–46. [Google Scholar]
  40. Alam, MS.; Sultana, N.; Hossain, SMZ., Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members. Appl. Soft Comput. 2021, 105, 107281. [CrossRef]
  41. Yang, L.; Shami, A. , On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
  42. Su, Z.; Wang, Y.; Tan, B.; Cheng, Q.; Duan, X.; Xu, D.; Tian, L.; Qi, T. , Performance prediction of disc and doughnut extraction columns using bayes optimization algorithm-based machine learning models. Chem. Eng. Process. 2023, 183, 109248. [Google Scholar] [CrossRef]
  43. Snoek, J.; Larochelle, H. ; Adams, RP, Practical Bayesian Optimization of Machine Learning Algorithms. arXiv 2012. [Google Scholar] [CrossRef]
  44. Denk, L.; Hatta, H.; Misawa, A.; Somiya, S. Shear fracture of C/C composites with variable stacking sequence. Carbon 2001, 39, 1505–1513. [Google Scholar] [CrossRef]
  45. LS-DYNA manual R13.0 Vol I. Available online: https://www.dynasupport.com/manuals/ls-dyna-manuals/ls-dyna_manual_volume_i_r13.pdf (accessed on 9th Jan. 2023).
  46. Tsai, S.W.; Melo, J.D.D. , A unit circle failure criterion for carbon fiber reinforced polymer composites. Compos. Sci. Technol. 2016, 123, 71–78. [Google Scholar] [CrossRef]
Preprints 68479 g001
Figure 1. Flowchart of PIC with machine learning model.
Figure 1. Flowchart of PIC with machine learning model.
Preprints 68479 g001
Preprints 68479 g002
Figure 2. FE bumper beam model.
Figure 2. FE bumper beam model.
Preprints 68479 g002
Preprints 68479 g003
Figure 3. Preliminary IIHS bumper analysis boundary conditions.
Figure 3. Preliminary IIHS bumper analysis boundary conditions.
Preprints 68479 g003
Preprints 68479 g004
Figure 4. Mapping results - 2-D implementation vs 3-D implementation.
Figure 4. Mapping results - 2-D implementation vs 3-D implementation.
Preprints 68479 g004
Preprints 68479 g005
Figure 5. Deformation of PIC bumper beam (3-D implementation): (a) Time: 0 s, COG displacement: 0 mm, (b) time: 0.009 s, COG displacement: 24 mm, (c) time: 0.02 s, COG displacement: 54mm (d): time: 0.035 s COG displacement: 80 mm, (e) time: 0.045 s, COG displacement: 107 mm.
Figure 5. Deformation of PIC bumper beam (3-D implementation): (a) Time: 0 s, COG displacement: 0 mm, (b) time: 0.009 s, COG displacement: 24 mm, (c) time: 0.02 s, COG displacement: 54mm (d): time: 0.035 s COG displacement: 80 mm, (e) time: 0.045 s, COG displacement: 107 mm.
Preprints 68479 g005
Preprints 68479 g006
Figure 6. Tsai-Wu index: (a) Centre part (element 66246), (b) end part (element 67010).
Figure 6. Tsai-Wu index: (a) Centre part (element 66246), (b) end part (element 67010).
Preprints 68479 g006
Preprints 68479 g007
Figure 7. Force-displacement curve of composite bumper beams.
Figure 7. Force-displacement curve of composite bumper beams.
Preprints 68479 g007
Table 1. Aluminium alloy 7021 mechanical properties.
Table 1. Aluminium alloy 7021 mechanical properties.
Mechanical properties Value
Density ρ 2,700 k g / m 3
Young’s modulus 70 GPa
Poisson’s ratio ν 0.3
Yield stress σ y 360 MPa
Table 2. Decision tree hyperparameters.
Table 2. Decision tree hyperparameters.
Machine learning
model		 Hyperparameter Variable
Decision tree Max. number of splits 1~1209
Split criterion Gini’s diversity index
Towing rule
Maximum deviance reduction
Table 3. Ensemble methods hyperparameters.
Table 3. Ensemble methods hyperparameters.
Machine learning
model		 Hyperparameter Variable
Boosted decision trees Max. number of splits 1 ~ 1209
Number of learners 10~500
Learning rate 0.001~1
Bagged decision trees Max. number of splits 1 ~ 1209
Number of learners 10 ~ 500
Table 4. SVM hyperparameters.
Table 4. SVM hyperparameters.
Machine learning
model		 Hyperparameter Variable
SVM Kernel function Gaussian
Linear
Quadratic
Cubic
Kernel scale 0.001~1000
Box constraint level 0.001~1000
Multiclass method One-vs-One
One-vs-All
Table 5. k-NN classification hyperparameters.
Table 5. k-NN classification hyperparameters.
Machine learning
model		 Hyperparameter Variable
k-NN classification Number of neighbors 1 ~ 605
Distance metric City block
Chebyshev
Correlation
Cosine
Euclidean
Hamming
Distance weight Equal
Inverse
Squared inverse
Table 6. Optimised hyperparameter using Bayesian algorithms.
Table 6. Optimised hyperparameter using Bayesian algorithms.
Machine learning
model		 Hyperparameter Values
Decision tree Max. number of splits 17
Split criterion Gini’s diversity index
Boosted decision trees Max. number of splits 1149
Number of learners 50
Learning rate 0.8987
Bagged decision trees Max. number of splits 694
Number of learners 214
SVM Kernel function Gaussian
Kernel scale 30.2498
Box constraint level 3.8962
Multiclass method One-vs-One
k-NN classification Number of neighbors 4
Distance metric City block
Distance weight Squared inverse
Table 7. Performances of 2-dimensional implementation.
Table 7. Performances of 2-dimensional implementation.
Machine learning
model		 Accuracy (%) ROC-AUC
Tension Compression Shear
Tree 84.2 0.85 0.88 0.73
Boosted decision trees 85.1 0.89 0.92 0.75
Bagged decision trees 81.1 0.90 0.91 0.75
SVM 85.9 0.89 0.90 0.62
k-NN classification 86.0 0.90 0.92 0.75
Table 8. Performances of 3-dimensional implementation.
Table 8. Performances of 3-dimensional implementation.
Machine learning
model		 Accuracy (%) ROC-AUC
Tension Compression Shear
Tree 85.4 0.95 0.94 0.80
Boosted decision trees 85.1 0.98 0.97 0.87
Bagged decision trees 85.3 0.98 0.97 0.87
SVM 86.2 0.96 0.94 0.62
k-NN classification 86.3 0.98 0.97 0.87
Table 9. Robust stacking sequences against each loading type.
Table 9. Robust stacking sequences against each loading type.
Dominant loading Stacking sequence
Tension [ 90 / 0 /   0 ¯ ] 6 s
Compression [ ± 5   / ± 45   /   90   ] 3 s
Shear [ 0 / 90 ] 15
Table 10. Predicted dominant loading type – 2-D implementation vs 3-D implementation.
Table 10. Predicted dominant loading type – 2-D implementation vs 3-D implementation.
Face 2-D implementation 3-D implementation
Tension Comp. Shear Tension Comp. Shear
Top 43.5% 53.3% 3.2% 41.2% 50.2% 8.6%
Front & chamfered 0.8% 97.5% 1.8% 2.1% 95.9% 2.0%
Bottom 20.7% 30.4% 2.1% 15.8% 29.5% 7.9%
Rear 95.5% 2.0% 2.5% 92.0% 2.8% 5.2%
Rib 30.0% 54.4% 15.6% 36.6% 41.9% 21.5%
Total 42.3% 53.2% 4.5% 42.1% 50.4% 7.5%
Table 11. Mechanical properties of T700/2510 carbon epoxy composite [46].
Table 11. Mechanical properties of T700/2510 carbon epoxy composite [46].
Properties Values
Density ,   [ ρ ] 1520   k g / m 3
Longitudinal   modulus ,   [ E 1 ] 126 GPa
Transverse   Modulus ,   [ E 2 ] 8.4 GPa
Shear   modulus ,   [ G 12 ] 4.23 GPa
Shear   modulus ,   [ G 23 ] 4.23 GPa
Poisson ’ s   ratio ,   [ v 12 ] 0.024
Axial   tensile   strength ,   [ X t ] 2172 MPa
Axial   compressive   strength ,   [ X c ] 1450 MPa
Transverse   tensile   strength ,   [ Y t ] 49 MPa
Transverse   compressive   strength ,   [ Y c ] 199 MPa
In - plane   shear   strength ,   S 155 MPa
Table 12. Mass of same bending strength level composite bumper beam.
Table 12. Mass of same bending strength level composite bumper beam.
Design method Bumper beam mass(kg) (%)
Conventional 1.31 -
2-D implementation 1.20 8%↓
3-D implementation 1.15 12%↓
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated