Prerpints.org logo
Preprint
Article

The Significance of Calibration to the Quantum-Mechanical De-Scription of Physical Reality

Altmetrics

Downloads

141

Views

26

Comments

0

This version is not peer-reviewed

Submitted:

09 February 2023

Posted:

16 February 2023

You are already at the latest version

Alerts
Abstract
This paper is a response to the EPR paper titled: "Can quantum-mechanical description of physical reality be considered complete?", published in Physical Review in 1935. A quantum-mechanical (QM) measurement function describes a distribution of local results, while each empirical measurement process produces one result as exact as allowed by a measuring instrument calibrated to a non-local unit standard. Repeating these empirical measurements produces a Gaussian distribution of measurement results. The QM and empirical measurement result distributions can be compared. To precisely compare a QM measurement function describing a distribution of eigenvectors to a distribution of repetitive empirical measurement results, it is necessary to determine, by calibration, the precision of the eigenvectors to the same standard as the empirical results, because each eigenvector evidences uncertainty relative to a standard. When the calibration process is recognized as formal as well as empirical, QM measurement function results and metrology measurement process results are unified.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

0. INTRODUCTION

Calibration is considered to be an adjustment of a measuring instrument to compensate for noise, distortion, and errors. This paper presents the concept that calibration also defines a minimum quantized unit. A minimum quantized unit changes the precision (in metrology practice) and determines the uncertainty (in quantum theory) of measurement results. Currently it is assumed that two metrology measurement results (e.g., x & p) will commute (i.e., xp = px). It is also recognized that two quantum measurement results generally do not commute (i.e., xp ≠ px). This paper develops how, when the minimum quantized unit is treated, all (metrology and quantum) measurement results do not generally commute at the minimum quantized unit. In response to the EPR paper [1] titled: "Can quantum-mechanical description of physical reality be considered complete?", published in the journal Physical Review in 1935, this paper presents how all measurement results are completed by including the precision determined by calibration to a non-local unit standard in both QM measurement functions and metrology measurement processes.

1. A MEASUREMENT RESULT QUANTITY

In a Euclidian space, the International Vocabulary of Metrology (VIM) [2] represents a measurement result as a quantity (lower case), the product of a numerical value (n) and a unit (u), with a ± population dispersion, equivalent to instrument calibration which establishes a mean u with a ± precision. In a normed vector space, a QM measurement function describes each measurement result as an eigenvalue of unity eigenvectors. A QM measurement function does not compare with a mean u because each eigenvector (uncalibrated) and mean u (empirically calibrated) are not correlated to each other. This discrepancy can be resolved by determining the precision of each eigenvector to a mean u and also to a standard. To accomplish this, the quantity calculus [3] function in (1) is proposed:
measure   result   Q u a n t i t y   Q = ∑ n = 0 n u n
When a quantity (i.e., a product) assumes all u are equal, then calibration (which equalizes the un to a standard) appears to be empirical. In Equation (1) each un is the smallest interval of an additive measure scale without any un calibration, including during the design or construction of empirical measuring instruments. Therefore, the property, relative size and precision of each un is only comparable locally (i.e., each un is calibrated to a local reference scale), or is comparable non-locally when each un is calibrated to U, a non-local standard Unit.
A quantity is expedient for experimental measurements. A Quantity, Equation (1), is a proper superset of a quantity. This paper proposes Equation (1) to represent the mathematical descriptions (functions) and empirical measurements (processes) that describe or produce all measurement results.

2. MODEL OF A RELATIVE MEASUREMENT SYSTEM

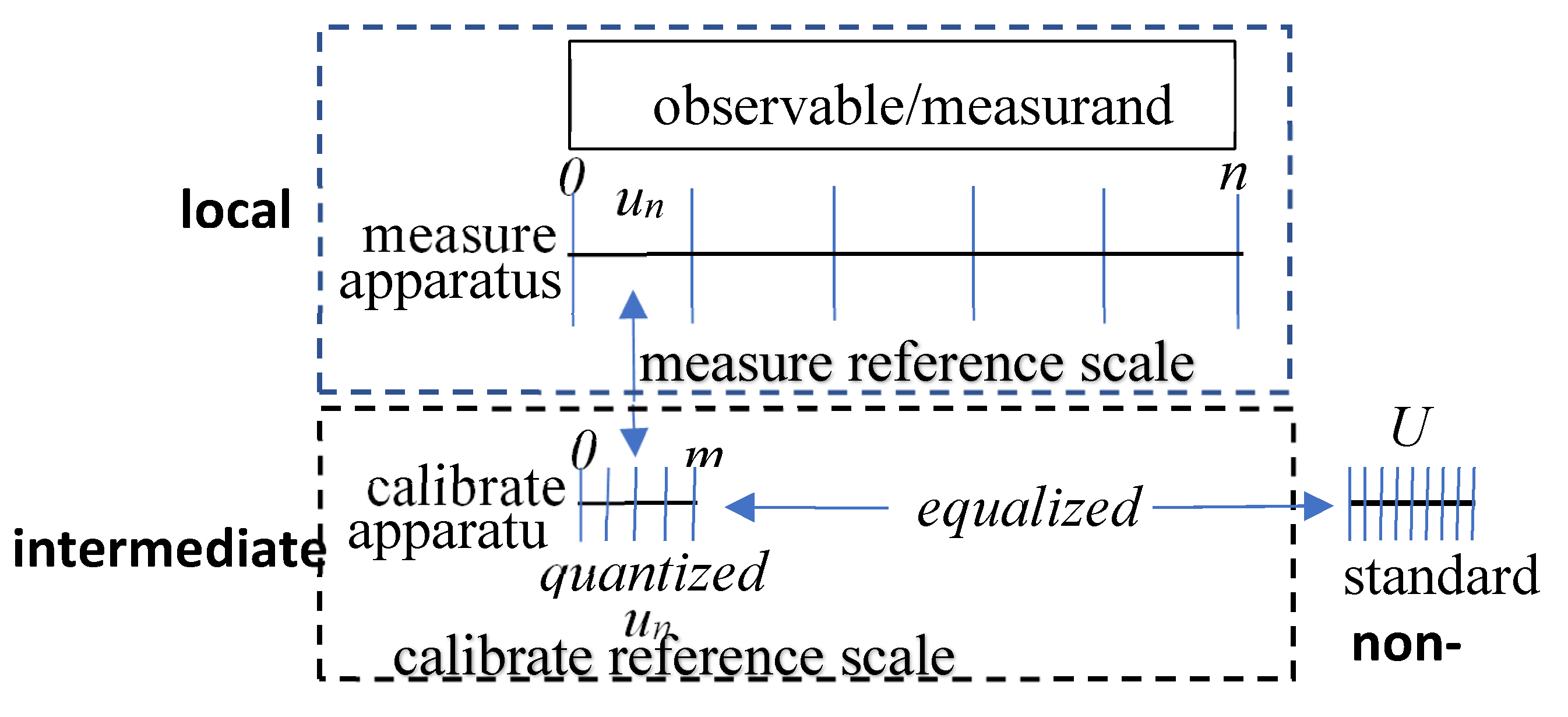
The local system includes the observable (quantum mechanics) or measurand (metrology) and the measure apparatus which provides an additive measure reference scale. The intermediate system (between the local and the non-local system) includes the calibrate apparatus which provides an equal interval calibrate reference scale. Each apparatus is without any noise or distortion, and represents a description (additive scale), function (equation) or process (empirical instrument). Figure 1 applies Equation (1) to establish a measurement result of an observable/measurand with a fixed numerical value ( n ⋅ m of 1/m states). Figure 1 brings together a representational measurement [4] (local) with the intermediate and non-local portions of a relative measurement system.
In Figure 1, the un intervals, where the mean interval is 1/n, quantify the measure reference scale; the m equal states, each defined to be 1/m, quantify the calibrate reference scale. Notice that the use of the measure and calibrate reference scales increases a continuous distribution's entropy by log n and log m respectively [5]. The calibrate reference scale quantizes and equalizes each un which determines the precision of each un to U. Quantizing and equalizing each un to U is termed un calibration. Then:
calibrated u n = u n ± 1 / m = u n m
On the measure reference scale, both n and un may vary due to noise (from outside the measurement system), distortion (from inside the measurement system), or quantization. In this paper a measure is correlated to a reference scale without un calibration, a measurement is with un calibration, and unm includes only quantization, not noise, distortion or errors. When a measure apparatus with the mean un = 1/n is applied repetitively to an n ⋅ m  numerical value observable, Equation (3) produces a distribution:
measurement   result   Quantities = ∑ n = 0 n u n ± 1 / m
Notice that by changing a quantity (product) to a Quantity (summation) it is clear that the un, each of which vary statistically plus or minus, are summed. In statistically rare cases the population dispersion created by each ±1/m is large (see 5.A, 5.B and 5.C below). The ±1/m · unm precision is determined by the calibrate reference scale and applies in all measurement functions/processes. When calibration is treated as only empirical, this effect is not treated and measurement discrepancies emerge.
Quantization (i.e., 1/m) also causes n uncertainty. W. Heisenberg formally presented quantum uncertainty in QM [6]. Relative Measurement Theory (RMT) [7] proved that the quantization of n at Planck scales causes Heisenberg's quantum uncertainty.
Only process measurement result Quantity population dispersion is caused by distortion and noise. Both function and process Quantity population dispersion is caused by the quantization of the calibrate reference scale.
A measurement function/process describes successive granularity. The measure reference scale has a mean unit = 1/n. Then 1/n > 1/m and 1/m = the quantization of the calibrate reference scale. Then 1/m ≥ the physical resolution of an instrument's transducer which converts the property of an observable's Quantity to a property of a reference scale.
As example, an analog voltmeter has a transducer which converts voltage (a property) into the position (another property) of a needle on a reference scale with an identified n uncertainty and unm precision of ±1/m. If the resolution of the transducer is a Planck (the most precise resolution possible), then the absolute value of the n uncertainty or unm precision is ≥ a Planck.
It is commonly assumed in QM measure functions that each eigenvector relates to a reference measurement standard, U in metrology. When the unm precision to U approaches the size of a measurement result Quantity only unm is valid to apply in a reference scale, because such unm precision produces an identifiable change to such a measurement result Quantity.

3. UNITS HAVE MULTIPLE DEFINITIONS

In a normed vector space an eigenvector equals a unity property (e.g., one unit length). In metrology, u represents a standard or a factor of a standard. In this paper, un represents an uncalibrated interval (which has a local property, undetermined relative size and undetermined precision) and unm represents a unit calibrated to U. Each unm has a non-local property, relative size and relative precision. The defined equal 1/m states may be treated as QM unity eigenvectors.
U standard, U (capitalized), is a non-local standard with a defined property and a defined numerical value. U represents one of the seven different BIPM base units (properties) or one of their derivations [8]. U may be without ± precision (i.e., exact). This paper recognizes that a non-local U defines the relative precision of unm, makes possible comparable measurement results, and U's numerical value is arbitrary only in the first usage.
un identifies each of the smallest intervals of a measure reference scale before any calibration.
unm is the calibrated numerical value of each un expressed in 1/m. The 1/m intervals are the smallest states of the calibrate reference scale. n and m may be represented as integers (counts) when 1/n and 1/m represent the smallest intervals or states of their respective reference scales.

4. ADDITIONAL DEFINITIONS

The International Vocabulary of Metrology (VIM) provides definitions of current metrology terminology. The following additional definitions, which do not include any noise or distortion, are related, where possible, to VIM definitions.
Quantity may be a product (q) or a sum (Q) as shown in Equation (1). In VIM a quantity is a product, because instrument calibration is assumed to establish sufficient unm precision when 1/m is not close in size to a measurement result Quantity.
Reference scale is the scale of a measure or calibrate reference apparatus local to an observable (i.e., the properties are locally comparable) and non-local to a U standard. A reference scale has equal (i.e., additive) uncalibrated intervals, where both the size relative to U and the precision of the intervals are not determined. A reference scale has a reference or zero point. VIM applies the term reference measurement standard for both concepts, similar to Maxwell's usage.
A measure apparatus has a reference scale and may have a transducer which converts an observable's property to a property of this reference scale. A measure apparatus determines the n of an observable.
A calibrate apparatus has a reference scale which is calibrated to a U whose property is consistent with this reference scale. The calibrate apparatus determines unm precision, ±1/m. The calibration of un does not average the unm precision.
Calibration or instrument calibration, is defined in VIM and generates a mean un. Calibration averages unm and commonly includes an adjustment of the n of a quantity as adjusting un in an empirical instrument is usually not practical.

5. EMPIRICAL EXAMPLES

A. Physical metre stick

A physical metre stick is 100 centimetres, or 100 un. Then n (e.g., 50) is a numerical value of un (a centimetre) and each un is calibrated to unm. When calibrated to U (a standard metre) u n m = U / 100 ± 1/m precision and n uncertainty = n ± 1/m, where each 1/m is one millimetre. The largest portion of the n · m population dispersion is determined by un calibration. 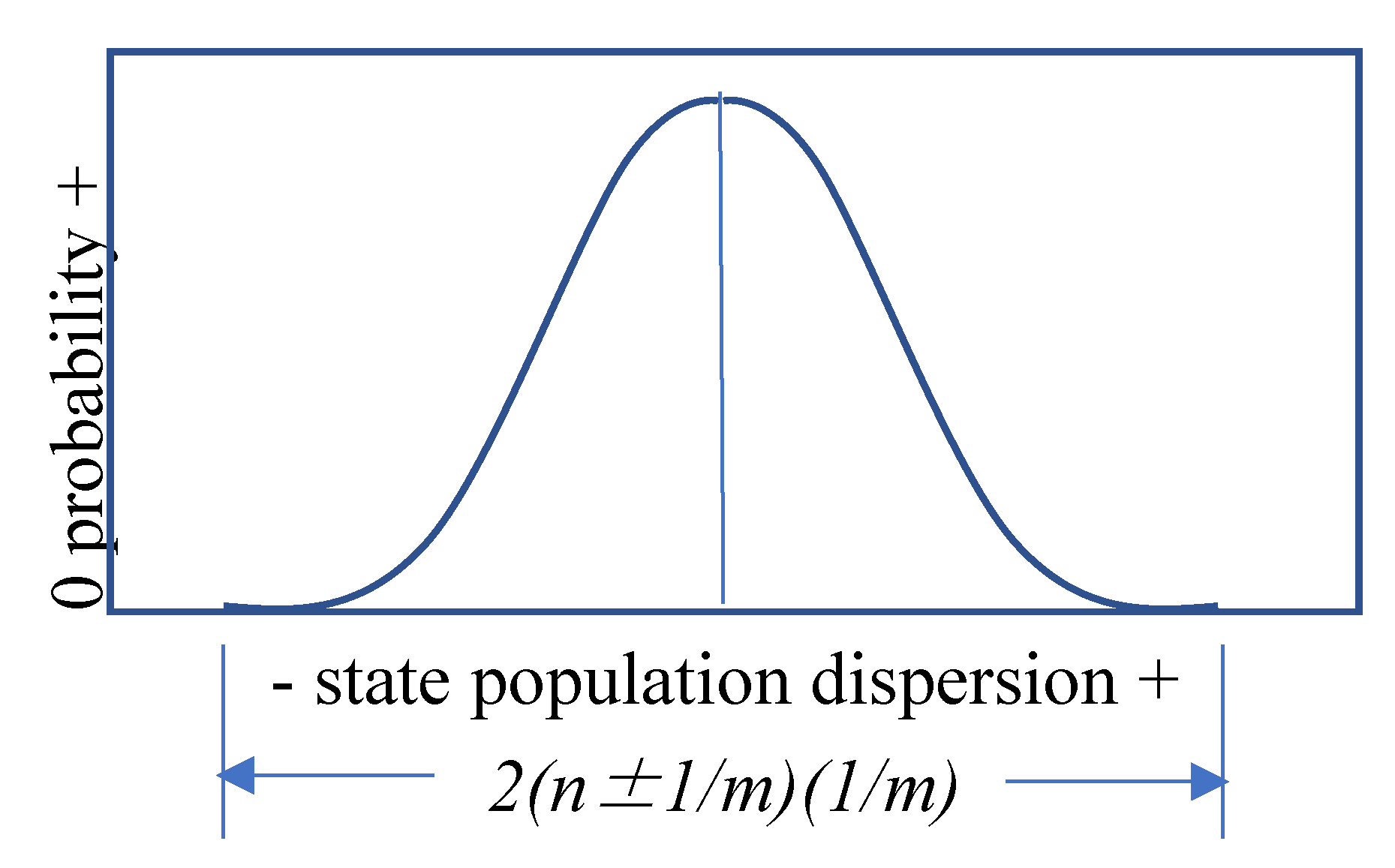In the rarest two cases, when n of the unm, all with a precision of +1/m, are summed and in another measurement of n of the unm, all with a precision of -1/m, are summed, the greatest population dispersion ( 2 n ± 1 / m 1 / m ) occurs, as shown in Figure 2 below.

B. Bell shaped normal measurement distributions

Figure 2 presents the characteristic bell shape (Gaussian) of a large distribution of repetitive experimental measurement results. This shape has been verified in many different forms of measurement results where noise and distortion have been minimized [9]. The bell shape (widening) unm precision population dispersion of a normal distribution in Figure 2 is further demonstrated in 5.C below.

C. Additive reference scale

An example of an additive reference scale is a thermometer which measures the property of thermodynamic temperature. Rather than marking the freezing and boiling points of water (points on a reference scale) and dividing the distance between them into equal units, this example demonstrates how additive intervals statistically increase population dispersion, producing a bell shaped measurement result distribution.
An instrument, consisting of a hollow glass tube with a reservoir filled with mercury at one end, fits inside another hollow glass tube that slides over the first. The two glass tubes are held together and placed in an adjustable temperature oven which has a resolution of 0.10 (degree). Then the outside glass tube is marked at the level of mercury which appears for the zero degree state and each 1.00 un above the zero mark. n + 1 marks (e.g., n = 100 in the Celsius system) or 101 marks are made to quantize the outside glass tube. Each of the 100 un is correlated by the oven to 1/0.1 =10 = unm 0.10 precision.
After 101 marks are made, the instrument is removed from the oven and an ice water bath is applied to the tube with mercury. The outside glass tube is now slid over the inside glass tube until the top of the inside mercury column lines up with the first mark on the outside glass tube. Now one mark on the outside glass tube is referenced to the temperature of ice water (00C) which is one reference point for thermodynamic temperature.
Consider the temperature of a glass of water in contact with the reservoir of the referenced measuring instrument. If the temperature of the water is 700, the 71st mark on the outside glass tube represents 700 ± 0.10 nominal precision or 70 worst case population dispersion. The ±0.10 nominal precision occurs when the ±0.10 unm precision of all 70 un is uniformly distributed.
The ±70 population dispersion occurs (very, very rarely) when each of the 70 un has the same +0.10 or -0.10 state precision which then sums. This statistical effect is ignored when defined equal units are applied (e.g., in an eigenvector representation of a measurement result). Notice there is also a 700 ± 0.10 numerical value of n uncertainty in this case.

D. Comparison of two measuring instrument results

The comparison of two measurement results (qa and qb) from two measuring instruments (a and b) is a ratio of their numerical values (na and nb) and the numerical values of their un (i.e., ua and ub), shown as: na · ua / nb · ub. The calibration of qa and qb to U refines ua into uam and ub into ubm. Then uam and ubm cancel because they are equalized by calibration. This allows accurate na/nb comparisons. Without the equalization of ua and ub by calibration the comparison of na/nb (a measurement) will change. This change is currently not understood and has been termed super-luminal transfer (ref). It is the unidentified (in theory) calibration of both ua and ub to U that creates what appears to be a super-luminal transfer. Such calibration is necessary to equalize the numerical values of uam and ubm, then a factor change in the numerical value of either uam and ubm need not impact the ratio na/nb. In this manner a numerical value of centimetres (e.g., 1/100 factor of a metre) is compared with a numerical value of a metre in 5.A, above. Calibration must occur in measurement theory as well as in experiments to allow accurate numerical value comparisons [10].
J. S. Bell, in his seminal paper [11]: "...there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote." Bell's mechanism is termed remote entanglement in this paper, to differentiate it from the well understood entanglement of two particles in close proximity. This appearance of remote entanglement is experimental evidence of calibration.
In the above example, the a and b measuring instruments are independent but the measurement results qa and qb, whose units (uam and ubm) are equalized by calibration, appear to "influence the reading of another instrument" (i.e., they are remotely entangled) across any distance. This Quantity based explanation of the comparison of two measuring instrument results, which identifies that calibration causes the mechanism Bell describes, is evidence of the significance of calibration to the quantum mechanical description of physical reality.

6. THE EFFECT OF U ON PRECISION AND POPULATION DISPERSION

Reviewing Equation (2), (above and reproduced here) the numerical value of the observable in Figure 1 is n · m of 1/m states. Each un is quantized and equalized to U by the calibrate reference scale, becoming unm:
calibrated u n = u n ± 1 / m = u n m
A common local property and common local un between measurement functions or processes are provided by a common reference scale. Then the non-local precision of un is determined by calibration to U. Notice that the n of U does not appear in Equation (2), but is required to determine unm. The n of U is arbitrary in the first usage, but required to determine measurement result precision. Equation (3) is modified to include the n uncertainty, producing:
measurement   result   Quantities = ∑ n = 0 n ± 1 / m u n ± 1 / m
Equation (4) identifies how different numerical values of Quantities will occur when the 1/m state is near a Planck size. Equation (4) is a measurement function that applies to measurement processes as well. From Equation (2):
u nm   precision = ± 1 / m
Assuming the un in Equation (4) are fixed then:
worst   case   sum   of   the   u nm   precision = ± n ± 1 / m 1 / m
population   dispersion   of   n = 2 n ± 1 / m 1 / m
Equation (7) identifies that the lowest probability measurement results have a population dispersion ~2n times 1/m. Equation (7) also explains how the Gaussian shape of a normal distribution in Figure 2 occurs.
Equation (7) identifies that every calibrated measurement result Quantity has a population dispersion which is understood when both the n and u of a Quantity are treated. In Equation (4) when n is large, the sum of each 1/m cancels, or close to cancels, very often (see 5.C) due to the central limit theorem's effect on a normal (i.e., symmetric) distribution of measurement results.
Conversely, when n is small (neutron spin measurements n = 2)[12], the sum of each ±1/m does not generally cancel. Thus two repetitive measurement result Quantities of the same observable when 1/m is near a Planck size, will likely be different. This appears in QM as repetitive measurement results that do not commute.

7. QUANTITY CALCULUS EXPLAINS PERPLEXING EXPERIMENTS

A. Heisenberg’s quantum uncertainty

In Heisenberg's quantum uncertainty analysis [13], Heisenberg identifies two properties, p = MV = momentum and x = position, each with a precision (i.e., un precision) of p1 and x1 that exhibit this uncertainty relationship: p1x1 h(h = a Planck). That is, when p1 increases, x1 decreases and h is the lower limit of the uncertainty. In his example p1 and x1 must be determined by comparing p and x at least two different times. Each comparison of p1 and x1 is a local comparison.
The time difference between two repetitive position measurements is: tn  = t n ′ − t n ″ . Converting Heisenberg's precision notation [below in brackets] into this paper's notation:
The position's qn precision = q 1 = x n ′ − x n ″ at . tn' - tn''
The velocity (V)'s vn precision = x n ′ − x n ″ t n ′ − t n ″ .
The momentum's pn precision = p 1 = M x n ′ − x n ″ t n ′ − t n ″ where M = mass (assumed constant).
This quantity calculus identifies that tn inversely changes x and p. This relationship applies to all such measure comparisons in theory and experiment. Heisenberg recognizes this inverse precision relationship: "Thus, the more the precisely [certainty] the position is determined, the less precisely [uncertainty] the momentum is known, and conversely."
However, QM does not currently identify that, the wavelength of light which is used to observe the x positions ("when the photon is scattered by the electron"), is also a measure reference scale interval of time. That is, a calibration process would define the wavelength of light applied, which determines the uncertainty. There is no error in Heisenberg's analysis here, only the lack of recognition of the calibration process.
This lack of recognition of the calibration process does lead to an error in understanding the Compton effect, where "the electron undergoes a discontinuous change in momentum". Relative measurement theory identified that this discontinuous change is due to calibration, not an interaction between the observable and the measuring instrument, as Heisenberg indicates (such interactions are empirical, not theoretical). C. Shannon [14] showed that a change in entropy (a discontinuity) always occurs when a continuous distribution is linearly transformed, in this case by the calibration of each measure reference scale interval, into a discrete distribution.

B. Double slit experiments

In the double slit experiments [15], two properties of each particle are measured. One measurement result quantity represents a frequency property, the other measurement result quantity represents an energy property. The slits provide the reference scale, while the sensing plate is both the frequency and energy transducer. An operator's selection of a pattern on the sensing plate determines which property is measured. Most particles have multiple properties, i.e., time, mass, energy, etc. In non-local measurements the selection of a property occurs by calibration of the measuring apparatus to a U. When calibration is assumed to be solely empirical, this property selection function of calibration is not recognized.

8. RELATING THIS PAPER TO OTHER MEASUREMENT THEORIES

In 1822, L. Euler identified that all measurement results are mutual relations [16]. In 1891, J. C. Maxwell [17] proposed that a measurement result is:
measurement   result   quantity   q = n ⋅ u
In Equation (8), n is a numerical value, and u is a unit ("taken as a standard of reference" [18]), which together form a mutual relation. Equation (8) is the basis of quantity calculus. From Maxwell's usage and quote, u is a mean that is equal (without ± precision) to a fixed standard unit. Equation (8) assumes that perfect precision is possible, well before Heisenberg's uncertainty identified such precision as impossible. This current paper has presented how Heisenberg's quantum uncertainty, or quantization, requires a precision function in Equation (8).
In the 20th century, QM offered a new measurement function, von Neumann's Process 1 which includes a statistical eigenvector operator [19]. Both von Neumann's Process 1 and Dirac's bra-ket notation treat a quantity as an inner product of eigenvalues and eigenvectors. The comparison of Equation (4) to Process 1 is straight forward when the equal 1/m states are treated as eigenvectors.
A Planck represents a very, very small quantization limit and the ~2n effect of quantization on population dispersion [see Equation (6)] is not usually recognized. Then, Maxwell's assumption that the mean un = U appears to have been acceptable [20]. This masks the quantized and statistical nature U exhibits at all scales. Currently QM also incorrectly assumes that the precision of repetitive measurement results can in theory be within a Planck of each other [21]. As presented in this paper, these assumptions break down when the unm precision is close in size to a measurement result Quantity.
In representational measurement theory [22], a measure and measurement are not differentiated. This theory does not recognize a quantity mutual relation; assumes measure result comparisons can occur without a reference scale or standard; treats a unit as arbitrary [23], which requires any calibration to be empirical [24]; and indicates that all measure result population dispersion is due to noise, distortion and errors in the measurement system [25].
All measurement results are uncertain. The statement in the EPR paper ("predict with certainty") that experimental measurement results (physical reality) can in theory be certain, is not rigorous. Experimental measurement results can only be as precise as a calibration process defines. This lack of certainty appears in metrology as ± precision. Precision, as used in this paper (without noise or distortion), is not empirical but a theoretical parameter of a measurement result.
Since a Quantity consisting of a numerical value and a calibrated un has not been applied in QM for almost 90 years, many perplexing effects have been noted. Measurement Unification, 2021 [26] explains how in the Stern-Gerlach experiments that J. S. Bell considered, the calibration of each instrument to the other is not recognized. Other explanations are given of quantum teleportation experiments, Mach-Zehnder interferometer experiments, Mermin's device (also based upon the Stern-Gerlach experiments), and the Schrödinger's Cat thought experiment. The explanations in Measurement Unification identify how un calibration unifies metrology processes and QM measurement functions.

9. CONCLUSION

Perhaps Maxwell's quantity, which assumed that the mean un = U, misled measurement theorists to treat calibration as an empirical process. QM evolved away from Maxwell's single dimension quantity with n and u towards a richer coordinate system with a magnitude and defined eigenvectors in multiple dimensions. However, the precise relationship of u and eigenvectors, determined by calibration, was not included in QM measurement functions. And when calibration is not part of a QM measurement function, the entropy change caused by calibration is not understood. The incompleteness identified in the EPR paper is resolved by including the precision determined by calibration to a non-local unit standard in both QM mathematical functions and metrology measurement processes.

Acknowledgments

The author acknowledges Luca Mari, Chris Field, Elaine Baskin, Richard Cember and the Entropy reviewers for their assistance.

References

  1. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete?, Physical Review, Vol 47, May 15, 1935. This paper is often referred to as the EPR paper.
  2. International Vocabulary of Metrology (VIM), third ed., BIPM JCGM 200:2012, quantity 1.1. 03 December 2022.
  3. J. de Boer, On the History of Quantity Calculus and the International System, Metrologia, Vol 31, page 405, 1995.
  4. D. H. Krantz, R. D. Luce, P. Suppes, A. Tversky, Foundations of Measurement, Academic Press, New York, 1971, Vol. 1, page 3, 1.1.2, Counting of Units. This three volume work is the foundational text on representational measure.
  5. Shannon, The Mathematical Theory of Communications, University of Illinois Press, Urbana, IL, 1963, page 91, para. 9. Shannon describes the entropy change due to a linear transformation of coordinates.
  6. W. Heisenberg, The physical content of quantum kinematics and mechanics, J.A. Wheeler, W.H. Zurek (Eds.), Quantum Theory and Measurement, Princeton University Press, Princeton, NJ (1983).
  7. K. Krechmer, Relative measurement theory (RMT), Measurement, 116 (2018), pp. 77-82.
  8. BIPM, the intergovernmental organization through which governments act together on matters related to measurement science and measurement standards, SI base units, https://www.bipm.org/en/measurement-units/si-base-units, 03 December 2022.
  9. Lyon, Why are Normal Distributions Normal? British Journal of the Philosophy of Science, 65 (2014), 621–649.
  10. E. Buckingham, On the physically similar systems: illustrations of the use of dimensional equations, Physical Review, Vol IV, No. 4, pages 345-376, 1914.
  11. J. S. Bell, The Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, Cambridge England, 1987, page 20, On the EPR paradox.
  12. G. Sulyok, S. G. Sulyok, S. Sponar, J. Erhart, G. Badurek, M. Ozawa and Y. Hasegawa, Violation of Heisenberg's error disturbance uncertainty relation in neutron-spin measurements, Physical Review A, 88, 022110 (2013).
  13. W. Heisenberg, p. 64. W. Heisenberg, p. 64. “Let q1 be the precision with which the value of q is known (q1 is, say, the mean error of q), therefore here the wavelength of light.
  14. Shannon, The Mathematical Theory of Communication.
  15. R. Feynman, The Feymann Lectures on Physics, Addison-Wesley Publishing Co., Reading, MA, 1966, page 1.1–1.8.
  16. L. Euler, Elements of Algebra, Chapter I, Article I, #3. Third ed., Longman, Hurst, Rees, Orme and Co., London England, 1822. “Now, we cannot measure or determine any quantity, except by considering some other quantity of the same kind as known, and pointing out their mutual relation.
  17. J. C. Maxwell, A Treatise on Electricity and Magnetism, 3rd Ed. (1891), Dover Publications, New York, 1954, p. 1.
  18. Ibid., The quote is Maxwell's.
  19. J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton University Press, Princeton NJ, USA, 1955, page 351, Process 1.
  20. Campbell, N. , Foundations of Science, Dover Publication, New York, NY, (1957), page 454.
  21. J. von Neumann, Mathematical Foundations, page 221.
  22. H. Krantz, Foundations of Measurement.
  23. Ibid., page 3.
  24. Ibid., page 32. “The construction and calibration of measuring devices is a major activity, but it lies rather far from the sorts of qualitative theories we examine here”.
  25. Ibid., Section 1.5.1.
  26. K. Krechmer, Measurement Unification, Measurement, Vol. 182, 21. 20 September.
Preprints 68449 g001
Figure 1. Relative measurement system.
Figure 1. Relative measurement system.
Preprints 68449 g001
Preprints 68449 g002
Figure 2. Normal distribution.
Figure 2. Normal distribution.
Preprints 68449 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated