Traceable Spectral Radiation Model of Radiation Thermometry

Preprint

Article

Traceable Spectral Radiation Model of Radiation Thermometry

Altmetrics

Downloads

153

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 February 2023

Posted:

16 February 2023

You are already at the latest version

Alerts

Abstract

Despite great technical capabilities, the theory of non-contact temperature measurement is usually not fully applicable to the use of measuring instruments in practice. While black body calibrations are in practice well established and easy to accomplish, this calibration protocol is never fully applicable to measurements of real objects under real conditions. Currently, the best approximation to real world radiation thermometry is grey body radiation thermometry, which is supported by most measuring instruments to date. Nevertheless, the metrological requirements necessitate traceability, therefore real body radiation thermometry is required for temperature measurements of real bodies. This article documents the current state of temperature calculation algorithms for radiation-thermometers and the creation of a traceable model for radiation thermometry of real bodies that uses a digital twin model of the system of measurement to compensate for the loss of data, caused by spectral integration, which occurs when thermal radiation is absorbed on the active surface of the sensor. To solve this problem, a hybrid model with variable scalar inputs is proposed, in which the scalar input parameters are calculated to correspond to the system of measurement. The method for calculating the effective parameters is proposed and verified with the theoretical model of non-contact thermometry. The sum of effective instrumental parameters is presented for different temperatures to show that the rule of radiation thermometry of grey bodies, according to which the sum of instrumental emissivity and instrumental reflectivity equals to 1, does not hold in radiation thermometry for real bodies. Using the derived models of radiation thermometry, the uncertainty of radiation thermometry due to the uncertainty of spectral emissivity is analysed by simulated measurements along the temperature ranges of various radiation thermometers, enabling traceable non-contact temperature measurements with known measurement uncertainty under any known conditions.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

Since the 2002 SARS outbreak in China, when non-contact thermometry was recognized as a practically convenient method for temperature measurement, radiation thermometry has continuously expanded to new industries and applications, including the consumer market. Thanks to the progress in the production of thermal radiation sensors in recent decades, the instrumentation in the field of radiation thermometry is now technologically advanced.

Despite practical advances, the theory of radiation thermometry with spectral-band sensors has not advanced in recent years. While non-contact temperature measurements are often made on grey bodies in practice, no methodology has yet been developed for measuring temperature of real bodies. The authors of this article strive to introduce traceability into the practice of radiation thermometry of real bodies. To achieve traceable measurements under real conditions, mathematical model of measurement must be derived and measurement uncertainty evaluated.

1.1. Radiation thermometry of black bodies

A black body is an ideal radiation source that has a maximum (or ideal, perfect) emissivity (of one) at all wavelengths (

ε (λ) = 1

) and does not reflect incident radiation. Therefore, the result of a non-contact temperature measurement on a black body always corresponds only to the temperature of the object and is independent of other environmental influences (neglecting the influence of the atmosphere).

While traceability is easily obtained by such measurements, the black body radiation thermometry method is only applicable to measurements on black bodies, which is an idealization of the method and only suitable (with negligible effects) when laboratory black bodies are used. In practice, laboratory black bodies are the best approximation of the black body with the highest achievable emissivity, which ideally approaches the emissivity of the black body (

ε (λ) \approx 1

). Despite the ease of measurement, black bodies are difficult to achieve in practice and are usually not feasible.

Established protocols for calibration of non-contact temperature measuring instruments, and consequently also most scientific publications in this field, mostly refer to calibrations of radiation thermometers which measure temperature of the black body. Such a calibration protocol is described by Murthy, Tsai and Saunders [1], König et al.[2], Donlon et al. [3], Boles [4], Kim et al.,[5] and Miklavec et al.[6].

Black body radiation thermometry is considered traceable and is therefore used by calibration laboratories to transfer radiation references. This means that black body calibrations are used to transfer reference measurements from the highest levels of traceability to lower levels.

The black body thermometry model is used by the simplest measurement instruments that operate with a fixed instrumental emissivity of 1 (e.g. transfer reference thermometers and many industrial sensors), and is also available in majority of radiation thermometers, which have adjustable setting of the instrumental emissivity that is set to 1.

1.2. Radiation thermometry of grey bodies

Grey body radiation thermometry is a simplification used for measuring grey bodies. It assumes that all influential quantities in the system of measurement are spectrally homogeneous and therefore independent of the observed wavelength. Based on this simplification the spectral behaviour could be summarized with scalar values.

While this simplification is theoretically close to the black body radiation thermometry, it extends the application of radiation thermometry to idealized real bodies, called grey bodies, which have spectrally uniform influence parameters (e.g. the emissivity and reflectivity of the object). These parameters, generally referred to as instrumental parameters, correspond to the entire system of measurement, which consists of the measured object (and its temperature), the environmental radiation and the measuring instrument. If the measuring instrument is calibrated and the instrumental parameters are correctly determined, only the temperature of actual grey bodies can be unambiguously measured.

This model and its variations are currently used by most radiation thermometers on the market with an adjustable emissivity parameter. This approach has been documented in numerous non-scientific sources (e.g. Fluke 4181 calibrator manual [7]) and thoroughly by Saunders [8], who modelled the response of a fixed instrumental emissivity radiation thermometer in calibration with a black body calibrator. Although the article focuses on calibration, the mathematical model is also applicable to measurements. The grey body model by Saunders utilized radiances (total radiant powers throughout spectrum, denoted

M

), obtained by the Sakuma–Hattori approximation of Planck’s law. Spectral interactions are not considered later in this model.

1.3. Radiation thermometry of real bodies

Currently the best practice in radiation thermometry of real bodies is to adjust the instrumental parameters depending on the temperature of the measured object.

This is often necessary even in radiation thermometry of grey bodies because of the thermal dependence of spectral influence parameters. While thermal dependence of influence parameters is expected and often documented for many materials, spectral interactions between the spectral distributions of spectral parameters and spectral radiances (spectrally defined radiant power, denoted with

M (λ)

) within the system of measurement are neglected in radiation thermometry of grey bodies, therefore the grey body radiation thermometry is not suitable for radiation thermometry of real bodies (with non-homogeneous distributions of spectral parameters).

In order to correctly perform radiation thermometry of real bodies, the instrumental parameters must take into account the current state of system of measurement, in particular the spectral radiances emitted and absorbed at each stage of the physical process of emission, propagation and absorption of thermal radiation within the active part of the sensor.

The objective of this study is to define a mathematical model for the process of non-contact temperature measurement and to define inverse models that serve to compensate for the inevitable influences within the physical model, such as reflection and atmospheric transmission.

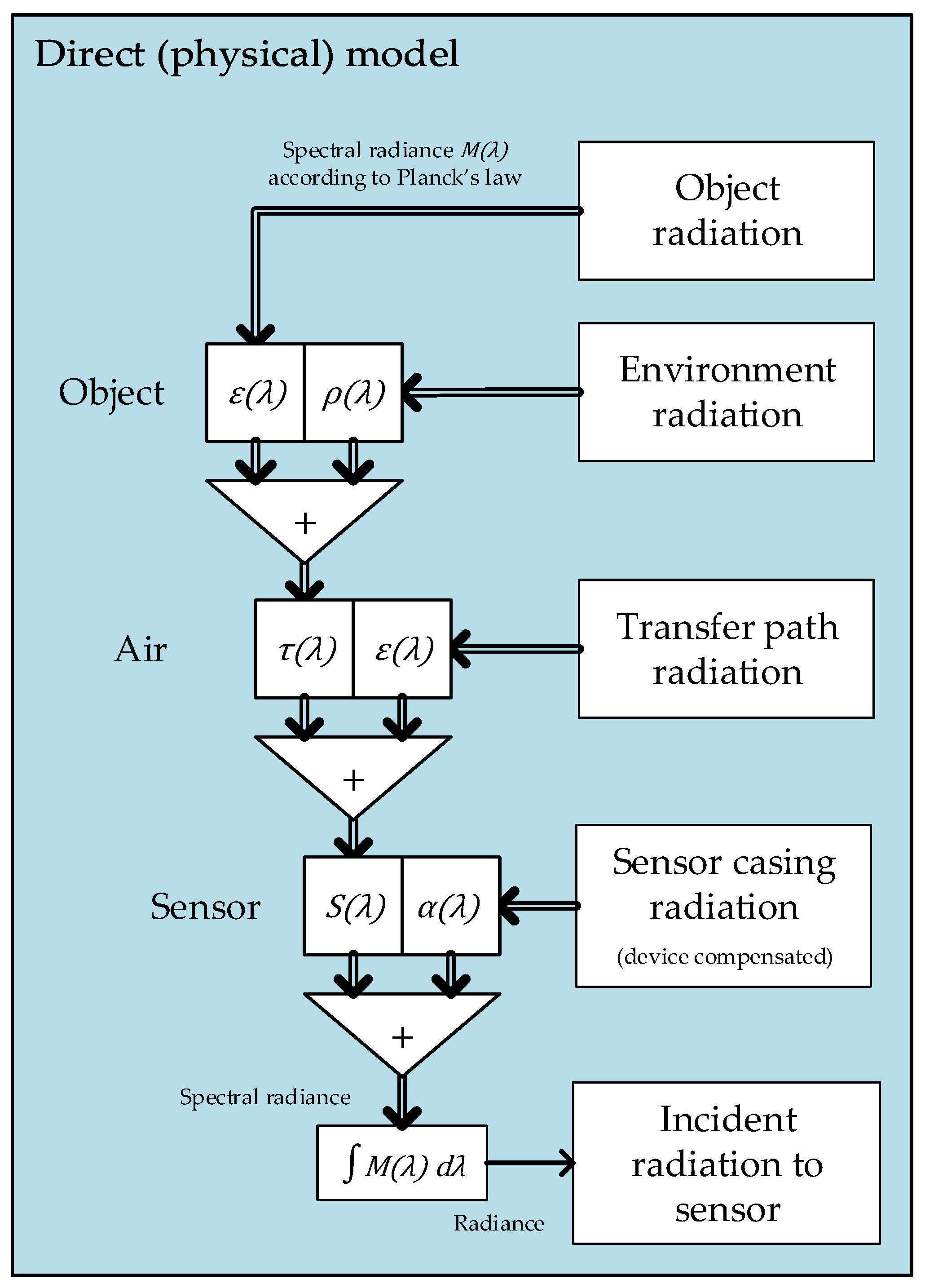
2. Defining the direct (physical) model

2.1. The process of radiation thermometry and the full system of measurement

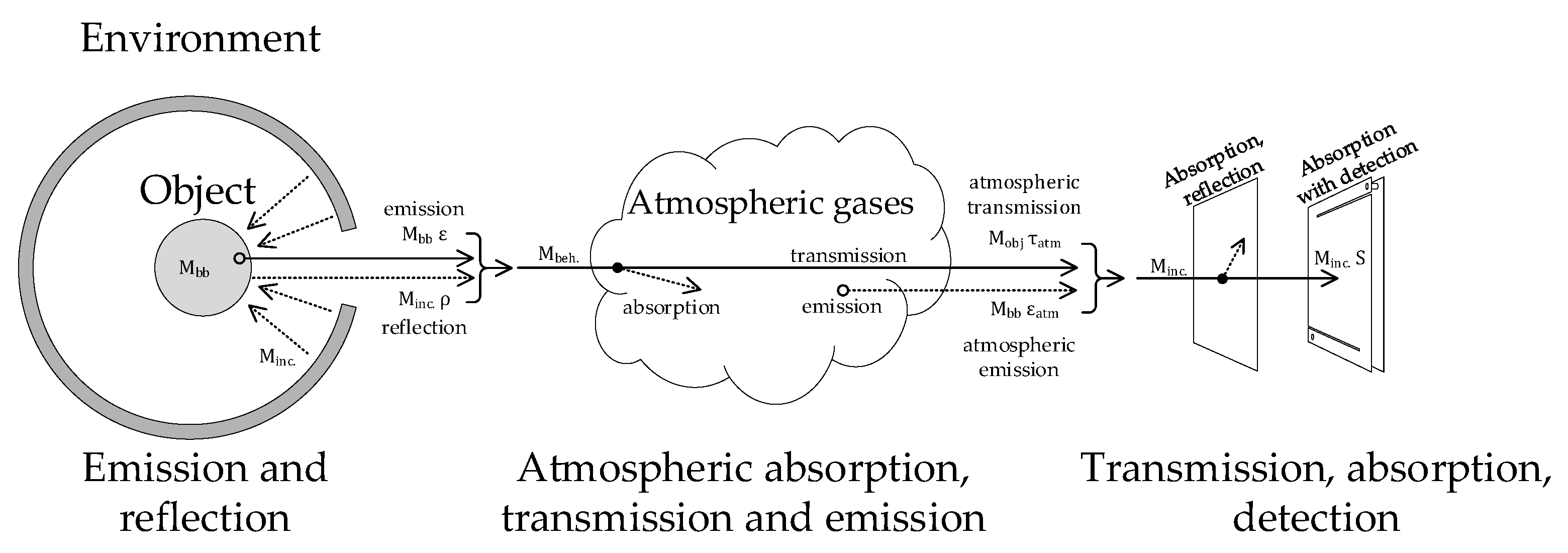
In radiation thermometry, the thermal radiation from objects is transferred to the radiation thermometer according to the physical laws of radiation. In measurement systems, influences of the environment are usually inevitable, therefore these influences are taken into account and compensated for in the measuring instrument. These influences include reflection, transmission through the air (and possibly optics and filter) and absorption to the sensor surface.

Radiation thermometer sensors measure the object’s radiant heat flux to its surface. Conventional thermometers use thermal sensors that absorb radiation on an exposed, absorbing surface, and convert it to the thermal radiation. This is the case with the most commonly used types of thermopile, MEMS and pyroelectric sensors.

Temperature difference between the exposed and the unexposed side of the absorbing surface is measured and calculated to the incident heat flux, using characteristic functions of the sensor that are beyond the scope of this research and are considered to be properly calibrated and traceable. The self-emission of the sensor is considered mathematically correctly compensated within the scope of this research, as it is purely dependent on the temperature of the sensor.

Output data of the sensor and the complementary input-output characteristic of the sensor is the incident radiance, which is assumed as compensated for natural heat dissipation, both through the case and through the optics. These influences are considered as mathematically easy to compensate and are beyond the scope of this research.

The incident radiance data of the sensor is later converted by another mathematical model (within the instrument) into the temperature of the radiation source, taking into account the inevitable influences of the environment and reflective properties of the object.

The operation and behaviour of the latter model, which is the inverse of the physical model, is the subject of this article. It represents the opposite of the physical model of radiation transfer, described in Figure 1.

2.2. Thermal radiation emission, transfer and absorption

Every black body with thermodynamic temperature above 0 K emits thermal radiation in the form of spectral radiance

M_{b b} (λ, T)

in accordance with Planck’s law (1),

M_{b b} (λ, T) = \frac{2 h c^{2}}{λ^{5}} {[e^{\frac{hc}{λ k_{B} T}} - 1]}^{- 1}

(1)

where

h

is the Planck constant,

k_{B}

is the Boltzmann constant,

c

is the speed of light in the medium,

λ

is the wavelength of emitted spectral radiance and

T

is the temperature of the black body.

The actual emission of real surfaces is the emission of the black body, spectrally weighted by the spectral emissivity of the surface.

A general form of interaction of radiation with the medium is described by Equation (2), where

M_{bb} (λ, T)

represents object’s blackbody emission,

M_{inc .} (λ)

represents incident radiation, which is reflected from the surface of a medium,

M_{beh .} (λ, T)

represents spectral radiance behind the object in the case of transmission through a translucent material and

M_{r e a l} (λ, T)

represents the radiation from the object after interaction, also called object radiation, consisting of all three radiant contributions,

M_{r e a l} (λ, T) = \underset{e m i s s i o n}{\underset{⏟}{M_{bb} (λ, T) \cdot ε (λ)}} + \underset{t r a n s m i s s i o n}{\underset{⏟}{M_{beh .} (λ, T) \cdot τ (λ)}} + \underset{r e f l e c t i o n}{\underset{⏟}{M_{inc .} (λ) \cdot ρ (λ)}}

(2)

where

τ (λ)

represents spectral transmissivity,

ε (λ)

spectral emissivity and

ρ (λ)

spectral reflectivity. Each of these spectral influence parameters is always bounded between 0 and 1.

Interaction of incident radiation with a medium at any wavelength is described by the equilibrium Equation (3).

ε (λ) + τ (λ) + ρ (λ) = 1

(3)

According to Kirchhoff’s law, emissivity

ε (λ)

is equal to absorptivity

α (λ)

at every wavelength (4).

ε (λ) = α (λ)

(4)

A scalar simplification of the general form of the object radiation (2) can be constructed (5),

M_{r e a l} (T) = M_{bb} (T) \cdot ε^{*} + M_{beh .} \cdot τ^{*} + M_{inc .} \cdot ρ^{*}

(5)

where the spectral radiance

M (λ)

is replaced by the radiance (total radiant power

M

over the whole spectrum) and the influence parameters are converted to scalar parameters accordingly, to preserve the original radiant power in the result.

2.3. Mathematical definition of the direct model

In radiation thermometry, numerous parameters interfere with the signal of interest, namely the radiation, emitted by the surface of the measured object.

2.3.1. Object’s emission and environmental radiation reflection

Figure 1 reveals the process flow of the direct model. First, the emission of the surface is calculated as the emission of the black body, reduced by the spectral emissivity factor.

According to Equation (3), the only complementary process of emission for real opaque surfaces is reflection. The reflection of the environmental radiation is reduced by the spectral reflectivity factor. The directional dependence is omitted from this (simplified) model. However, this does not affect the performance of the model, as long as the environmental radiation data are obtained in agreement with the directional reflectivity characteristic of the surface.

2.3.2. Atmospheric transmission and self-emission

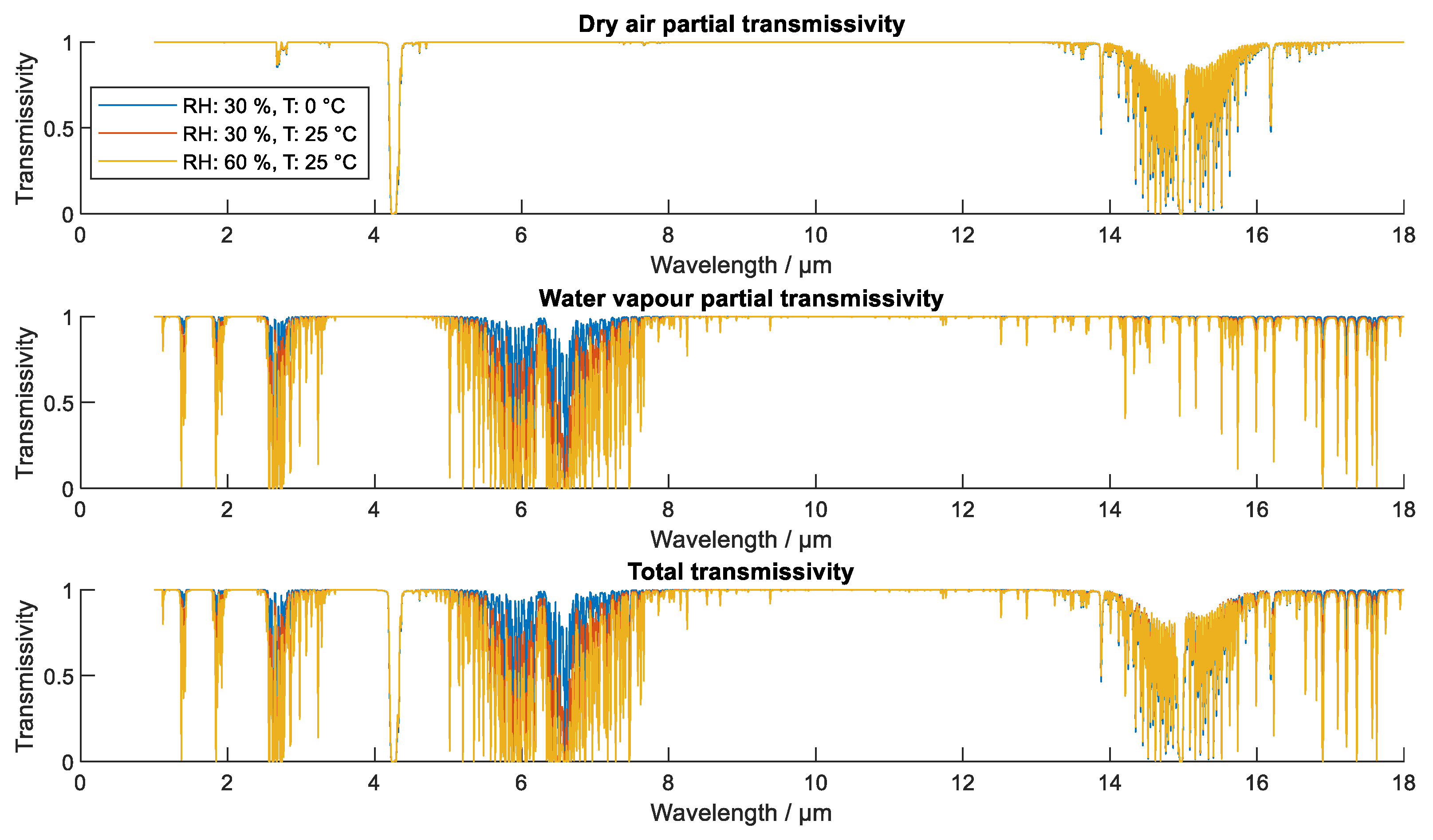
The combined emitted and reflected radiation travels through the atmosphere toward the radiation thermometer. During travel, the radiation is partially absorbed according to the spectral absorptivity of the air, while most of the radiation is transmitted according to the spectral transmissivity of the air. Due to Kirchhoff’s law (4), the spectral absorptivity is equal to the spectral emissivity, therefore the absorbed radiation is replaced by the proportional part of the atmospheric self-emission. The spectral transmissivity of the atmosphere is relatively high under the usual indoor conditions, as already determined by the authors for the purpose of this study [9]. The spectral transmissivity of the air is shown in Figure 2.

2.3.3. Transmission through the optical system of the measuring instrument

The transmission path may also include possible transparent windows and the optical system of the thermometer. However, publicly available spectral data for the optics of pyrometers and thermal imagers are limited, and the properties of the optics are usually measured and included in the spectral sensitivity characteristic of the measuring instrument, which is also the case for this model.

2.3.4. Sensor absorption and black body calibration

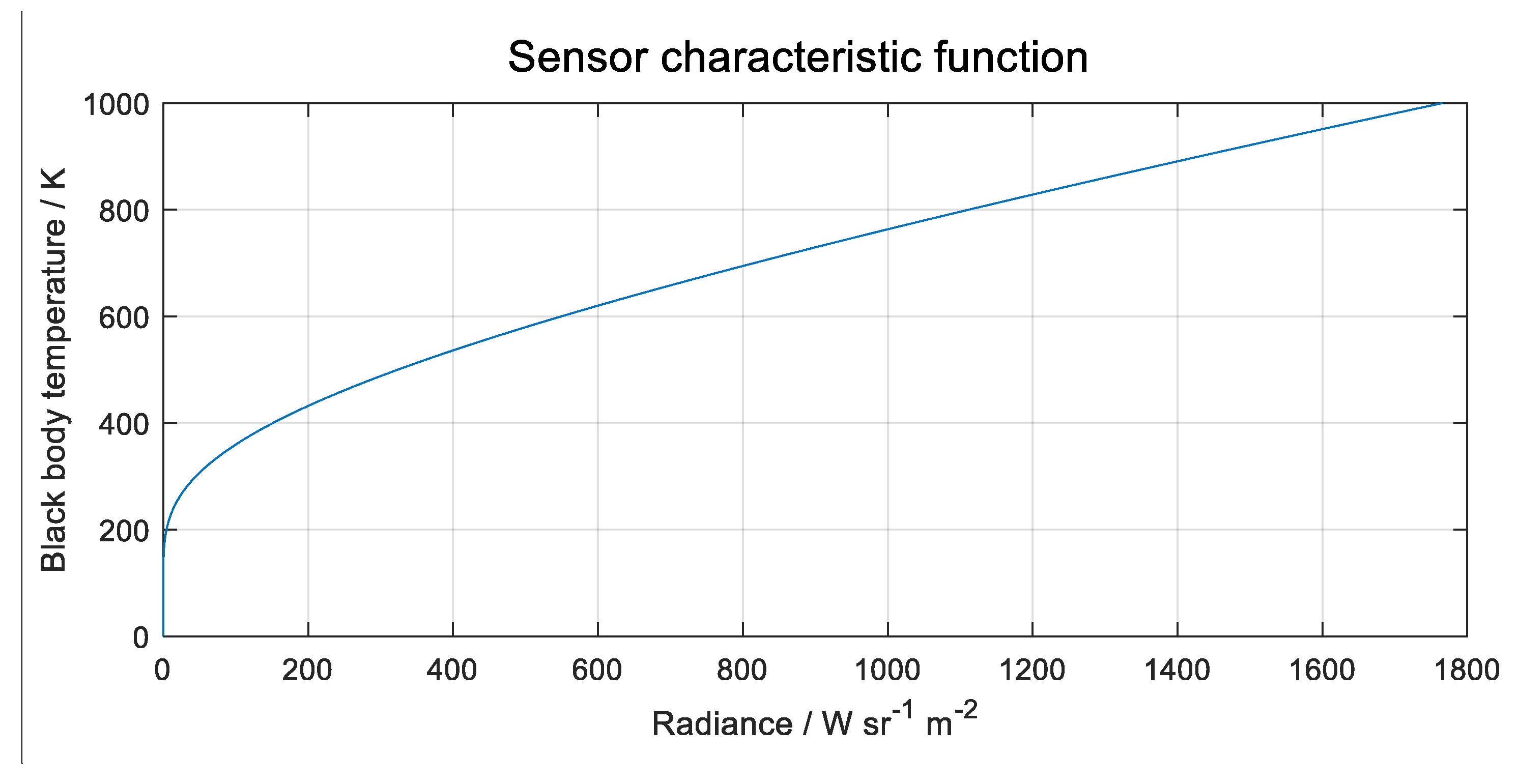
The combined thermal radiation is absorbed at the sensor. The sensor characteristic function is a conversion between the input quantity and the output quantity of a sensor. The input quantity of sensors for spectral-band radiation thermometry is the total absorbed radiant power over the sensitive spectrum. The effective measured radiant power is determined by the measured spectral radiance, the spectral sensitivity of the sensor and its geometry.

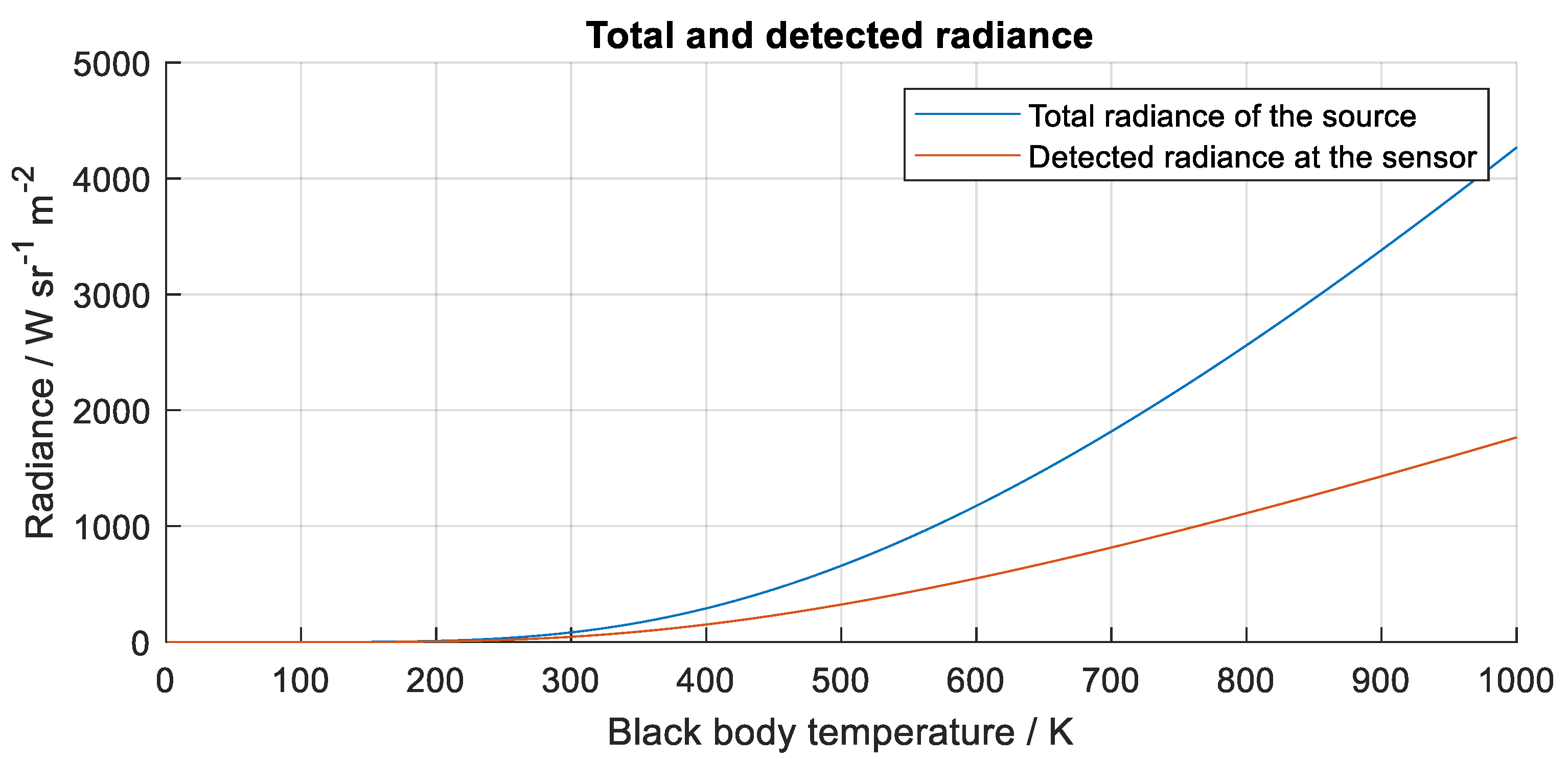
In radiation thermometry, the input quantity of a sensor is usually extended from radiant power to black body temperature for practical reasons. The sensor characteristic therefore converts the temperature of the black body (object temperature in Kelvin) into an output quantity, which in practice is the sensor value, but for the purpose of this research the sensor reading is simplified as the detected radiance and expressed directly in W sr^-1 m^-2.

Figure 3. The total radiance of the black body source at different temperatures and the detected fraction, forming the traceable characteristic response function of the sensor. VOx sensor characteristic from Figure 4 was used to generate this plot.

In practice, the characteristic of each sensor should be traceably determined by calibration on a black body radiator. For the purpose of this research, theoretical black body calibration is used because the emission is determined by Planck’s law and the spectral sensitivity of the sensor is known.

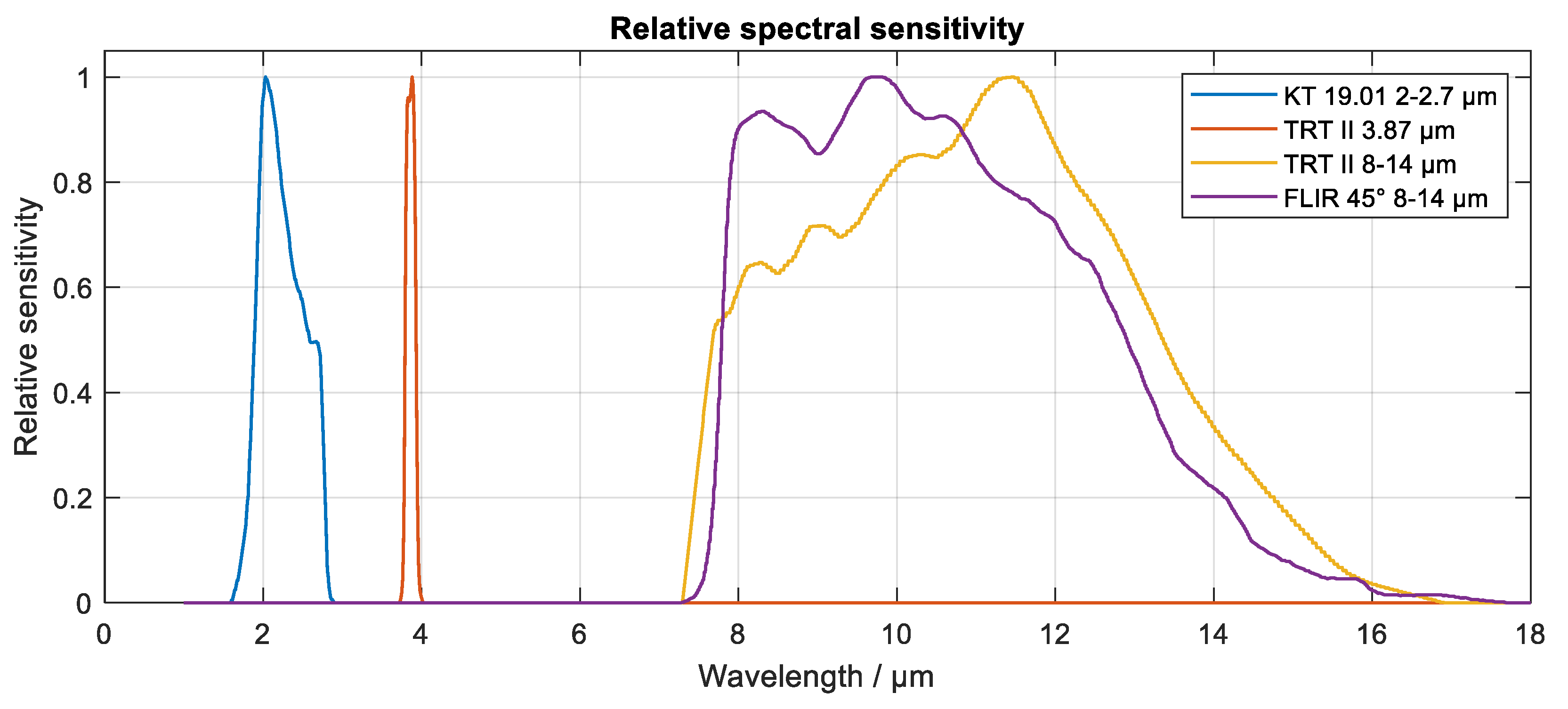
Figure 4. Spectral sensitivity of Heitronics KT19.01 radiation thermometer, spectral sensitivity of the high and the low temperature range of Heitronics Transfer Radiation Thermometer II (TRT II), digitized from Heitronics pyrometer documentation [10], and generic spectral sensitivity of vanadium oxide (VOx) based microbolometer detectors of FLIR thermal imagers [11] with 45° field of view optics.

The spectral sensitivity of the sensor describes the effective sensitivity of the sensor as a function of wavelength of the thermal signal. In the physical model of radiation thermometry, the spectral sensitivity can substitute the spectral absorptivity (6), as the actual parameter, relevant to response of a measuring instrument.

S (λ) = α (λ)

(6)

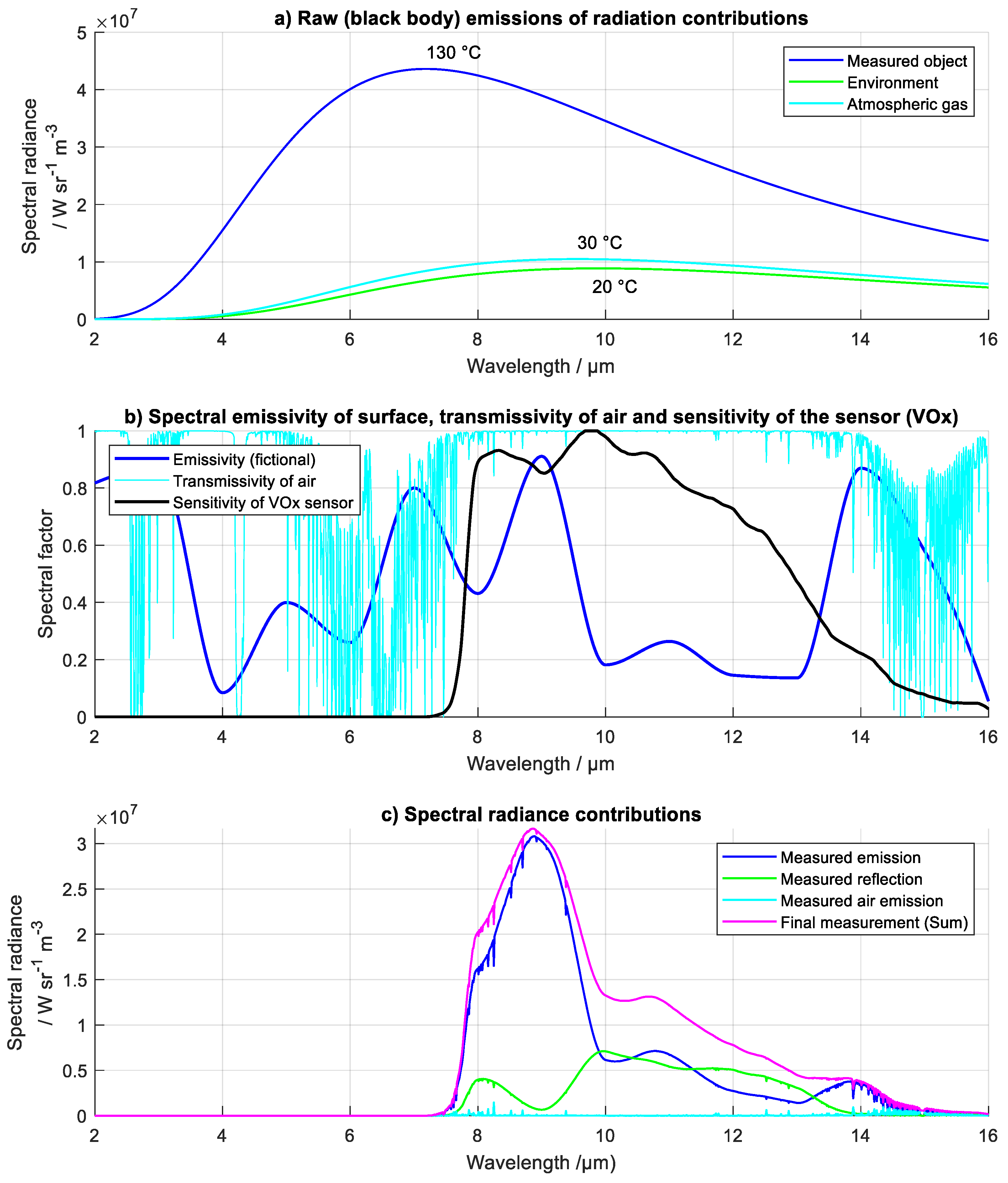
To obtain the sensor characteristic theoretically, the total incident power on the sensor is calculated by integrating the product of the pure blackbody emission, defined by Planck’s law, and the sensor sensitivity over all wavelengths. This product is described by Equation (7) and visible in Figure 6c, as the area under the graph of the sum of all contributing spectral radiances (displayed in magenta).

P = \int_{λ_{1}}^{λ_{2}} M_{b b} (λ, T) \cdot S (λ) d λ

(7)

Analytical solutions for the integration of Planck’s law are complex, impractical, and moreover infeasible when the discretely measured spectral sensitivity of the sensor and other influence parameters are taken into account. For this reason, we have opted for a fully numerical calculation of the sensor properties.

2.4. Final spectral interaction of the physical model

Considering the described properties of the physical laws, a direct model is generated in Figure 5. The rectangles represent the black body emissions, while the square and triangular operators represent the scaling and summation for the (spectral) radiance. The arrows with the double lines represent the spectral radiance, while the single line represents the radiance (the total radiant power without spectral information). The spectral information is lost during the spectral integration during absorption on the active surface of the sensor.

Figure 5. The direct (physical) model of radiation thermometry, describing the physical process of thermal emission, propagation, absorption and measurement of object (spectral) radiance.

A theoretical example of spectral behaviour within the direct model is shown in Figure 6. In this example, a random emissivity was generated that is intentionally non-homogeneous across the entire sensitivity spectrum of the sensor to emphasize the effect of a non-homogeneous spectral emissivity, as can occur with real objects.

Figure 6. Shown is the spectrally simulated behaviour of the direct model with a) the simulated spectral radiance of black body emissions, b) the spectral emissivity of surface, the spectral transmissivity of the air, and the spectral sensitivity of the sensor, and c) the partial and total spectral radiance, as absorbed in the sensor. The area under the sum of all contributions represents the signal output from the sensor.

3. Defining the inverse of the physical model

3.1. Inverse model of measurement

The direct model is based on a real physical model of conversion of object temperature to radiant power as a sensor value. The inverse model, i.e. the inverse of the physical model, is used for calculation from radiant power of a sensor to temperature of the object.

In all inverse models, inevitable influences of the measured object, environment and air, must be calculated and compensated for from the measured radiance. After compensation of these influences, only black body radiation of the measured object should be present in the resulting signal. This pure blackbody emission can be converted to the object temperature using a characteristic function, which is theoretically the inverse of Planck’s law.

3.1.1. Theoretically ideal spectral inverse of the direct model

Since the physical model is a spectral model, the inversion of this model results in a spectral inverse model. Spectral radiance cannot be retrieved from the sensor therefore, ideal traceable measurements should be made in spectral radiance, not total radiance. The ideal inverse model should therefore omit spectral integration. The correct combination of direct and inverse model is shown in Figure 7. However, spectral integration was omitted from the direct model to retain traceability, therefore this model is not practically feasible.

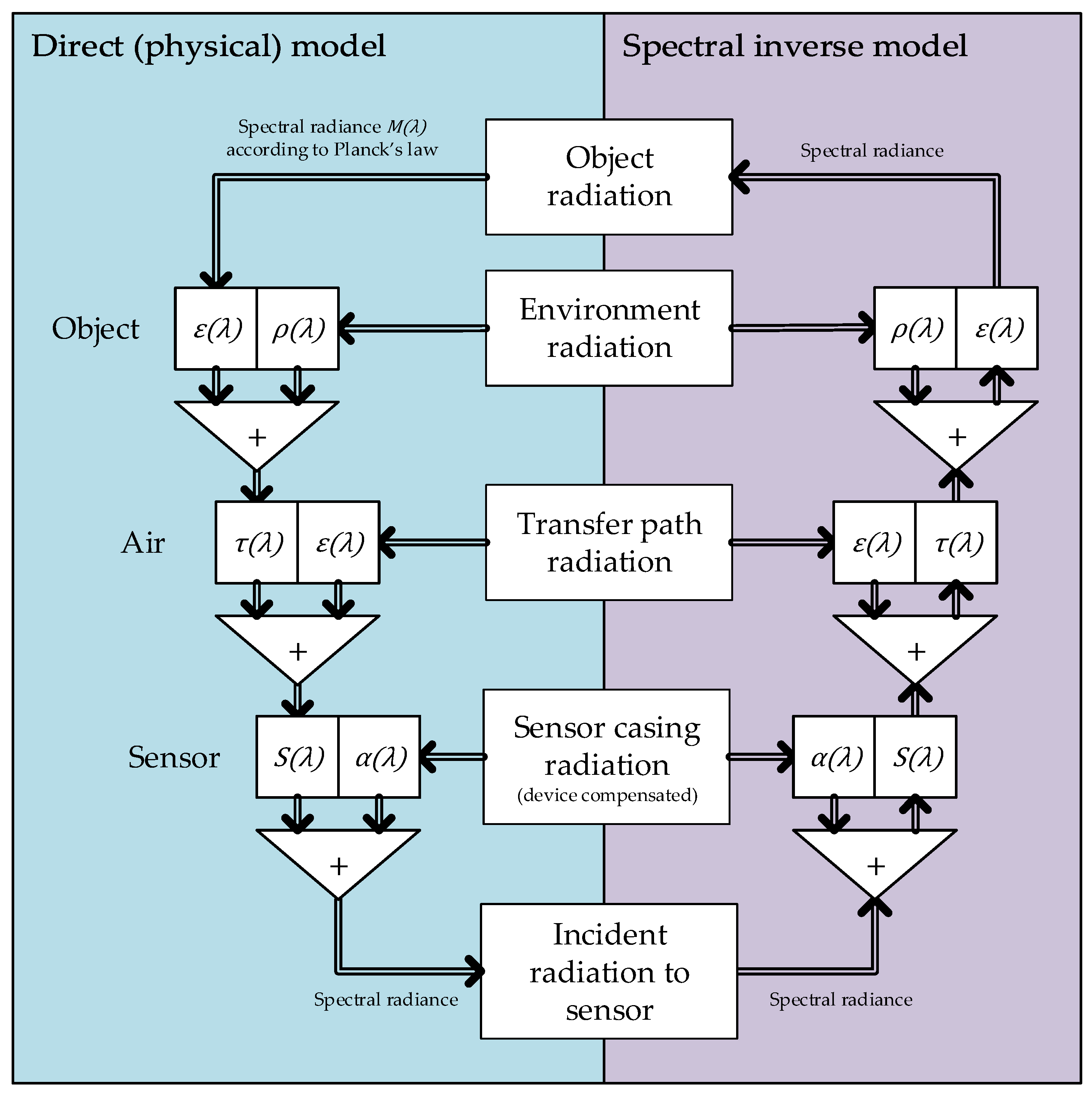
3.1.2. Scalar inverse model

Most existing radiation thermometers and thermal imagers currently use simplified scalar inverse model (Figure 8) and its derivatives. The scalar model is a generalization, used because the sensor reading is obtained as radiance (radiant power), which is a scalar number, rather than spectral radiance, which is defined as a spectrally distributed radiant power.

Parameters marked with prefix i are instrumental parameters. These are input parameters, defined as instrumental emissivity, instrumental reflectivity or instrumental transmissivity, that represent the scalar settings of an instrument’s mathematical model.

Ideal input parameters should correctly correspond to the system of measurement in under the given conditions. However, these parameter values are usually not known.

As a scalar simplification, this model is appropriate for grey body radiation thermometry, where spectral interactions are disregarded and neglected. The vast majority of instruments in the field of radiation thermometry currently operate according to this model, as can be seen from the scalar input values.

Since the settings of the measuring instruments are often unknown, these input parameters are usually estimated, taken from literature or determined experimentally usually without following the rules of traceability for the particular system of measurement. It is also common procedure to use constant instrumental parameters for all measurements of a given surface, regardless of the temperatures and spectral interactions involved.

Due to omission of processing of the spectral information of the signal, this model and method are considered inaccurate. An improved version of this model is needed to take full advantage of the available accuracy and traceability of radiation thermometry. To do this, the spectral interactions must be accounted for in the inverse model.

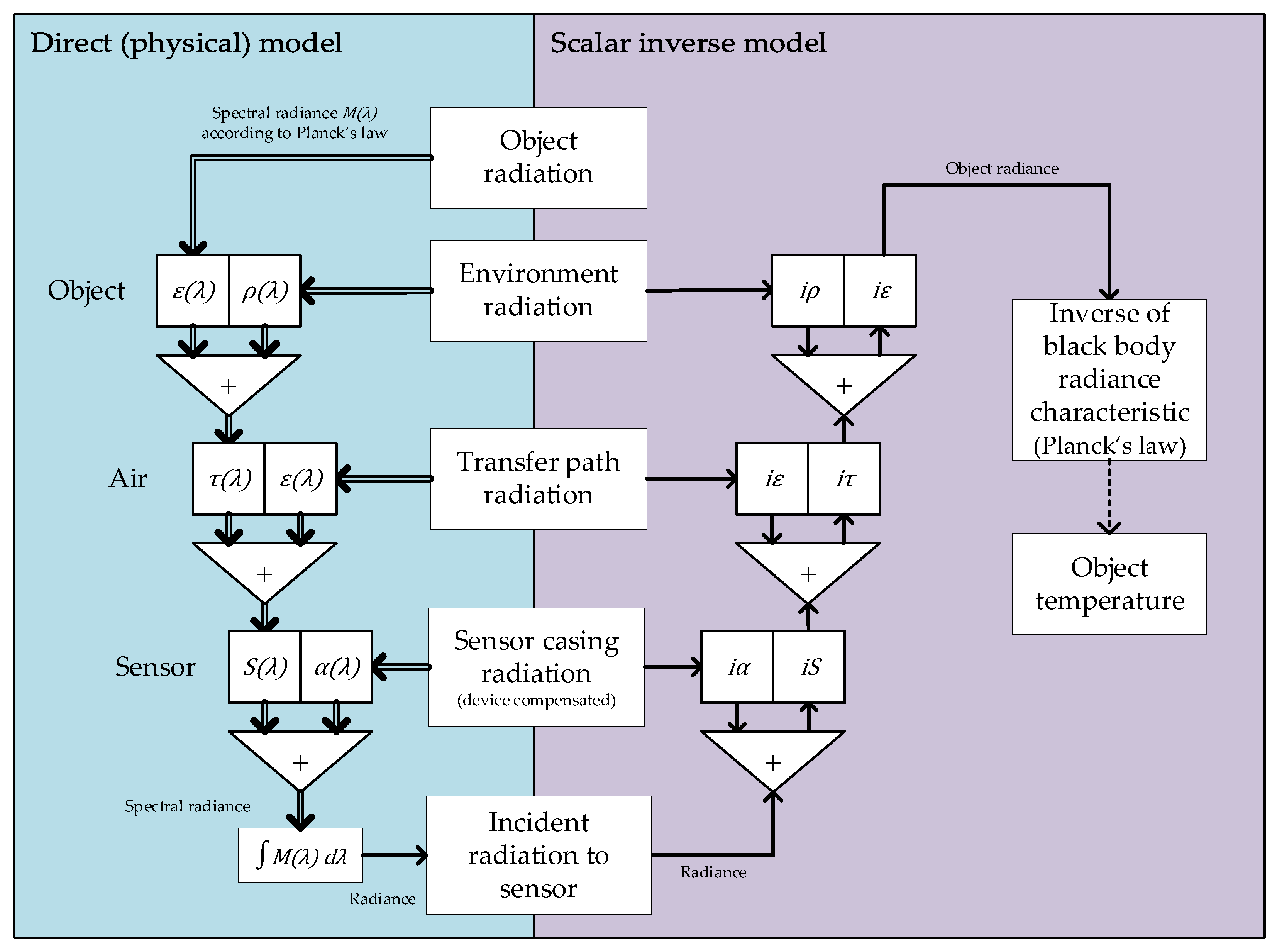
3.1.3. Hybrid model

In the scalar inverse model spectral effects are neglected, leading to a loss of traceability in non-contact temperature measurements of a real object. While an ideal inverse is not possible due to sensor limitations, resulting in a loss of spectral data, a workaround can be achieved by accurate measurement of influence parameters in the measurement process and calculation of the effective values of scalar parameters at different temperatures. 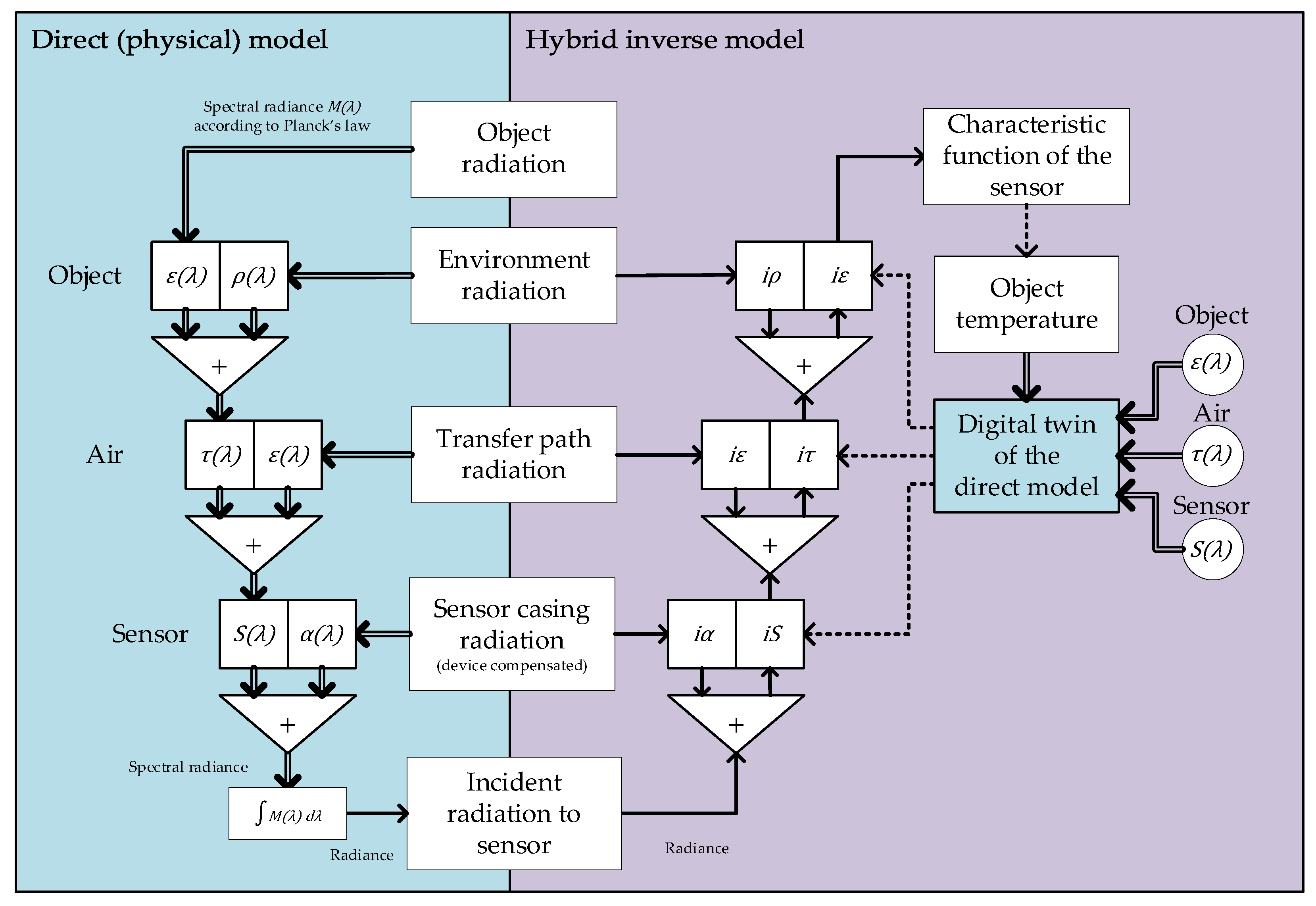A hybrid inverse model using this concept is proposed in Figure 9. The model operates as a scalar model, but the scalar parameters are continuously adjusted to account for spectral interactions.

For this purpose, the hybrid model uses a digital twin of the direct model, i.e. the digital simulation of the real process runs in parallel. To achieve this, the quantities of the direct model must be known. The spectral parameters are used to generate scalar parameters that are used by the scalar inverse model. Since the spectral distribution data of the signal is lost in the direct model, the full spectral operation of the direct model is simulated in the digital twin and used to compensate for the discrepancy between the scalar and the spectral inverse model. Since the effective emissivity depends on the spectral radiance and thus on the temperature of the object, a recursive relationship is established between the spectral representation of the object’s emission and its temperature. The calculated object temperature can thus be improved iteratively. It is important to note that optimization is only required to better define the spectral distribution of the signal. Therefore, small deviations and fast regression of the optimal results from the model are expected, but at least 2 iterations are required to correctly use the object temperature in an effective parameter simulation.

The hybrid model is a theoretical model. In practice, coefficients can also be determined experimentally, but a correct methodology is beyond the scope of this research.

3.1.4. Characteristic function of the sensor

This research is limited to incident radiance (radiant power), while actual sensors convert the output into an electrical signal which corresponds to the radiance. To calculate the temperature of the object, the input-output characteristic function of the sensor is used (Figure 10).

3.2. Optimized hybrid model

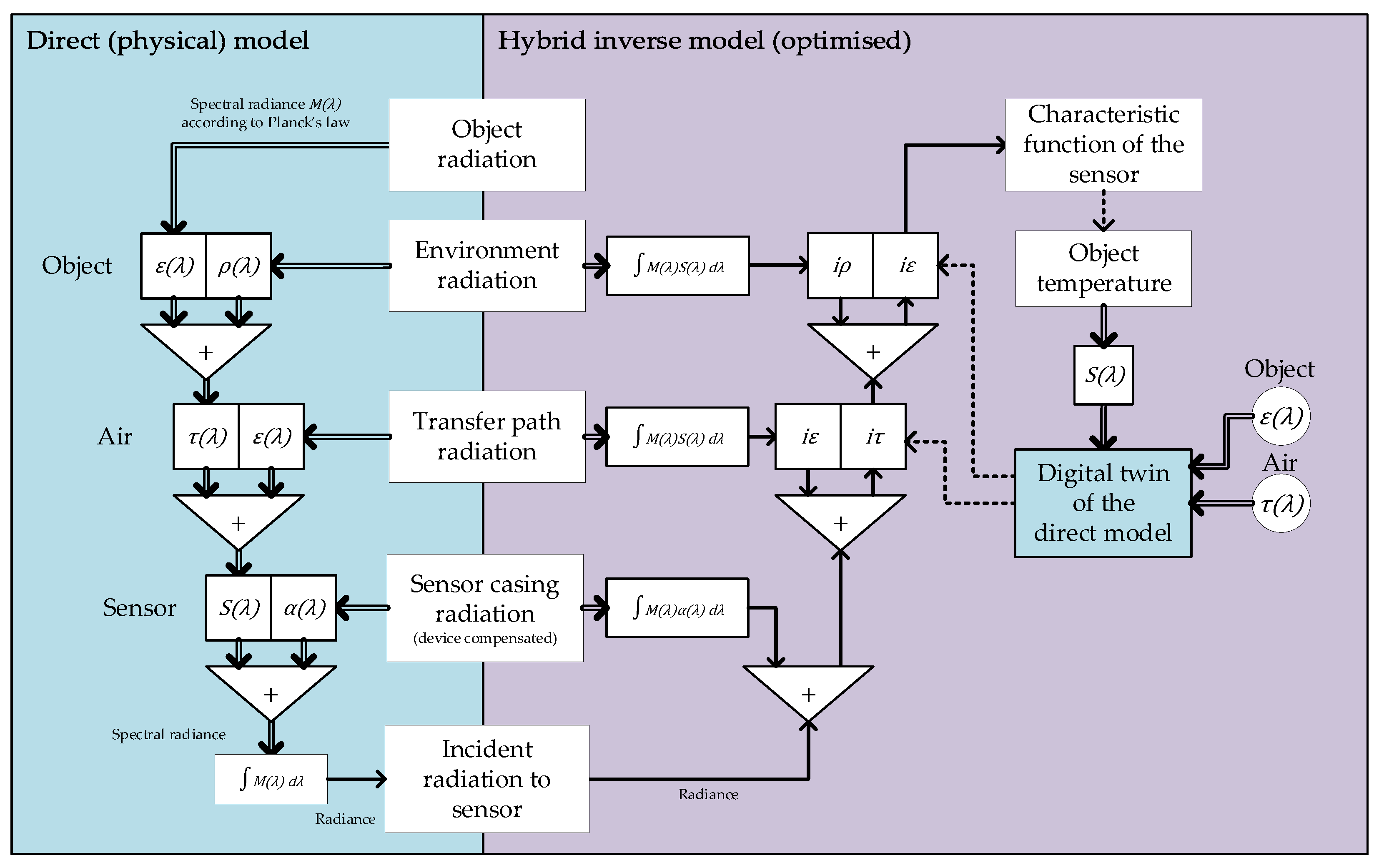
The spectral sensitivity of the sensor determines the characteristic transform between the temperature of the black body source and the measured incident radiant power at the sensor. In the direct model of radiation thermometry, the spectral sensitivity of the instrument is applied at the final stage of the measurement process, after emission and propagation to the measurement instrument. The spectral sensitivity the sensor is therefore applied proportionally to all radiations (and emissions) contributing to the signal and therefore has distributive properties in the model of radiation thermometry.

Due to distributive nature of spectral sensitivity in the direct model of radiation thermometry, sensitivity can also be applied to raw black body thermal emissions (of object, environment and air) prior to introduction of influence parameters. This can be utilized in the inverse model, to simplify and omit conversion of spectral sensitivity to instrumental sensitivity (effective scalar factor).

To optimize the hybrid inverse for easier calculation (Figure 11), the spectral sensitivity characteristic is therefore accounted for in the black body characteristic of the sensor for each of the radiant contributions, instead of being applied to the entire signal of the sensor at the beginning of the inverse model.

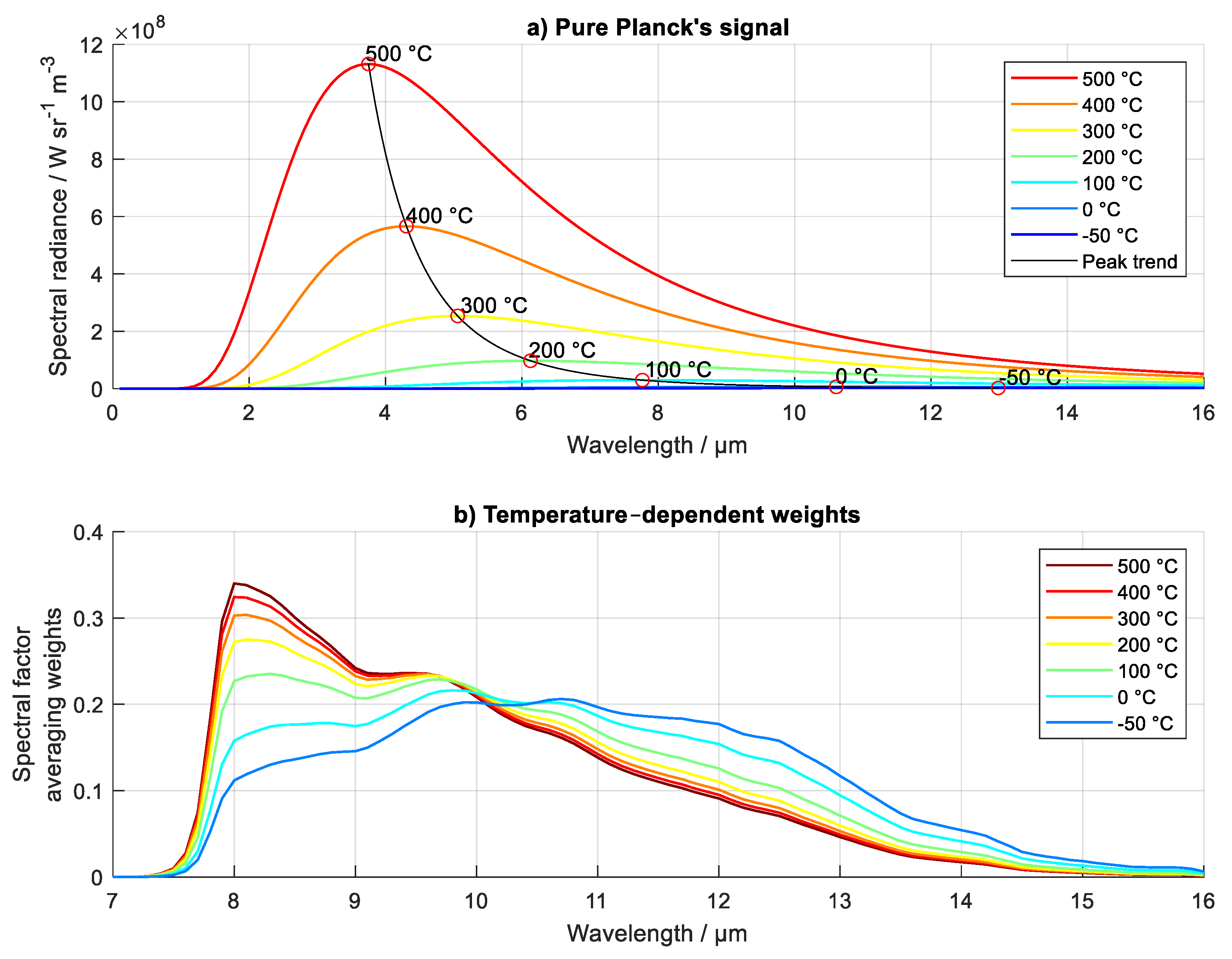
Based on the initial evaluation of the object temperature, the spectral radiance and consequently the spectral weights can be derived for averaging when conducting radiation thermometry of real bodies. Since the spectral representation varies less with increasing temperature, the errors in the initial object temperature variable, used to calculate spectral distribution of object emission, are attenuated at higher temperatures (above 600 K, where the peak trend of Planck’s law is steep). The error in the spectral distribution can be quickly reduced by iterating the process of calculating the emitted spectral radiance, and the apparent object temperature.

3.3. Conversion of spectral emissivity to an effective scalar value

Radiation thermometers usually allow scalar adjustment of emissivity. Regardless of the temperature of the measured object, the estimated or determined constant value is usually set by operators. However, this value does not correspond to the changing spectral representation of the measured signal, which leads to an error in the representation in the mathematical model.

3.3.1. Averaging in the spectral range of the measuring instrument

In the case of unknown spectral sensitivity of the sensor, uniformly weighted averaging in the spectral interval of the measuring instrument is usually used in practice (8).

ε^{*} = \frac{\int_{λ_{m i n}}^{λ_{m a x}} ε (λ) d λ}{λ_{m a x} - λ_{m i n}}

(8)

This is the simplest, but least accurate implementation of the spectral influence parameter in the inverse model of radiation thermometry, however it is fully metrologically compliant under the grey body assumption.

3.3.2. Experimentally obtained signal- and sensitivity-weighted mean

An experimental approach would require experimental calibration of the instrument emissivity setting under the reference conditions.

Values, obtained by adjusting emissivity setting of the instrument to match the measured and the reference temperature of a surface represent the empirically determined effective emissivity and correspond to the signal and sensitivity-weighted mean (Figure 12). However, this method is accurate only as long as the spectral representation of the signal does not change between calibration and measurement

Since the temperature dependence of the spectral radiance is not taken into account in a single measurement, calibration has to be performed over the entire temperature range.

This approach seems to be experimentally feasible, therefore methods of experimental evaluation of instrumental parameters for the given measuring instrument and sample combination will be addressed in detail in an article based on the ongoing research.

3.3.3. Calculated signal-weighted mean

In ideal case, spectral influence parameter could be spectrally compensated by the measuring instrument, however that would require knowledge of spectral radiance, which cannot be measured with conventional sensors.

A theoretically accurate implementation of spectral influence parameters in the scalar inverse model can be achieved by expressing with scalar factor the overall effect of the spectral influence parameter on the measurement, as detected by the sensor. For this, the direct model of radiation thermometry from chapter 2.4 can be utilized. By taking into account Planck’s law of black body emission, spectral influence parameters and possibly other spectral radiances in the system of measurement (e.g. environmental emission), spectral radiance contributions can be expressed for any stage of the direct (physical) model.

By definition, spectral influence parameters are defined as ratio between real and hypothetically ideal radiant response at specific wavelength. A scalar influence parameter corresponds to the ratio of the actual and theoretically ideal radiance throughout the measurement spectrum. In terms of radiation thermometry, these radiant contributions correspond to measured (spectral) radiance, as detected by the sensor.

The spectral emissivity can be converted into an effective scalar emissivity utilizing the expression for the measured spectral radiance of the emission

M_{e m i s s i o n}

in equation (9),

M_{e m i s s i o n} = \int^{​} M_{b b, o b j} (λ, T) ε (λ) τ_{a t m} (λ) S (λ) d λ = = ε^{*} \int^{​} M_{b, o b j} (λ, T) τ_{a t m} (λ) S (λ) d λ

(9)

where

M_{b b, o b j} (λ, T)

is the black body emission of the object at a given temperature,

ε (λ)

is the spectral emissivity of the object,

τ_{a t m} (λ)

is the spectral transmissivity of the atmosphere and

S (λ)

is the spectral sensitivity of the sensor.

The resulting formula for the effective emissivity scalar

ε^{*}

(10) corresponds to the definition of the emissivity in the given system of measurement, which describes the overall downscaling of the total radiance over the entire measurement spectrum:

ε^{*} = \frac{\int^{​} M_{b b, obj} (λ, T) ε (λ) τ_{a t m} (λ) S (λ) d λ}{\int^{​} M_{b b, obj} (λ, T) τ_{a t m} (λ) S (λ) d λ}

(10)

A rule can be derived for converting any spectral influence parameter to effective scalar value

f (λ) \to f^{*}

(11), which allows the conversion of any factor — emissivity, transmissivity or sensor absorptivity - under any conditions and in any phase of the inverse model. The scalar value is therefore equal to the ratio between the actual measured radiance contribution to the measured radiance and the ideal contribution, as it would be measured if the influence parameter was 1. Radiant contribution is considered as the (spectral) radiance of only the particular fraction of the measured radiance, which originates from a given source.

f^{*} (T) = \frac{M_{m e a s u r e d w i t h f (λ)} (T)}{M_{m e a s u r e d w i t h o u t f (λ)} (T)} = \frac{M_{r e a l} (T)}{M_{i d e a l} (T)}

(11)

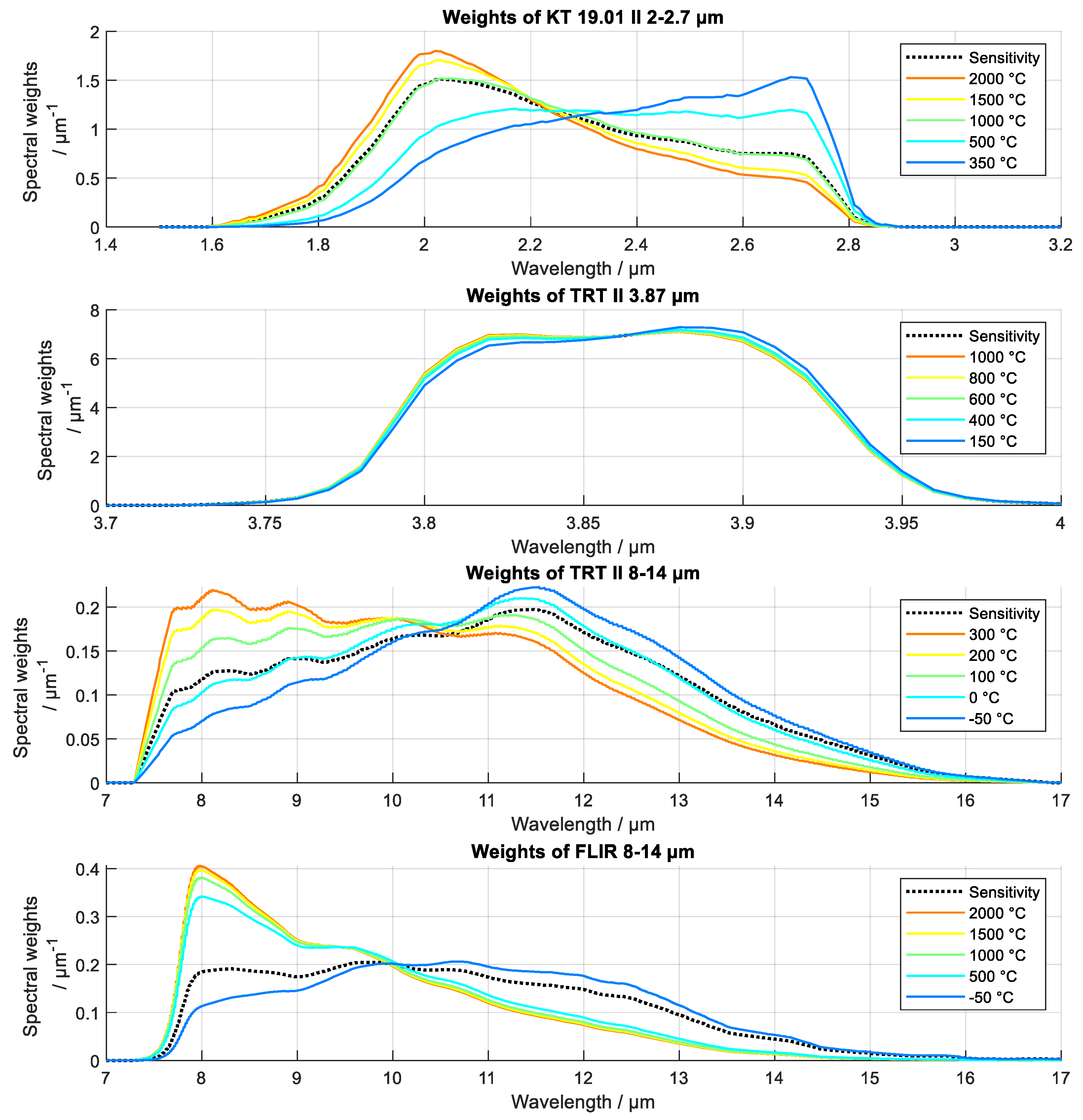
Spectral weights for averaging of the spectral emissivity, generated for different detectors, are shown in Figure 13. Detectors with different spectral sensitivities have different susceptibilities to anomalies in spectral emissivity due to temperature-induced shifts in the spectral representation of the measured radiance.

4. Results

4.1. Validation of the model of radiation thermometry with hybrid inverse

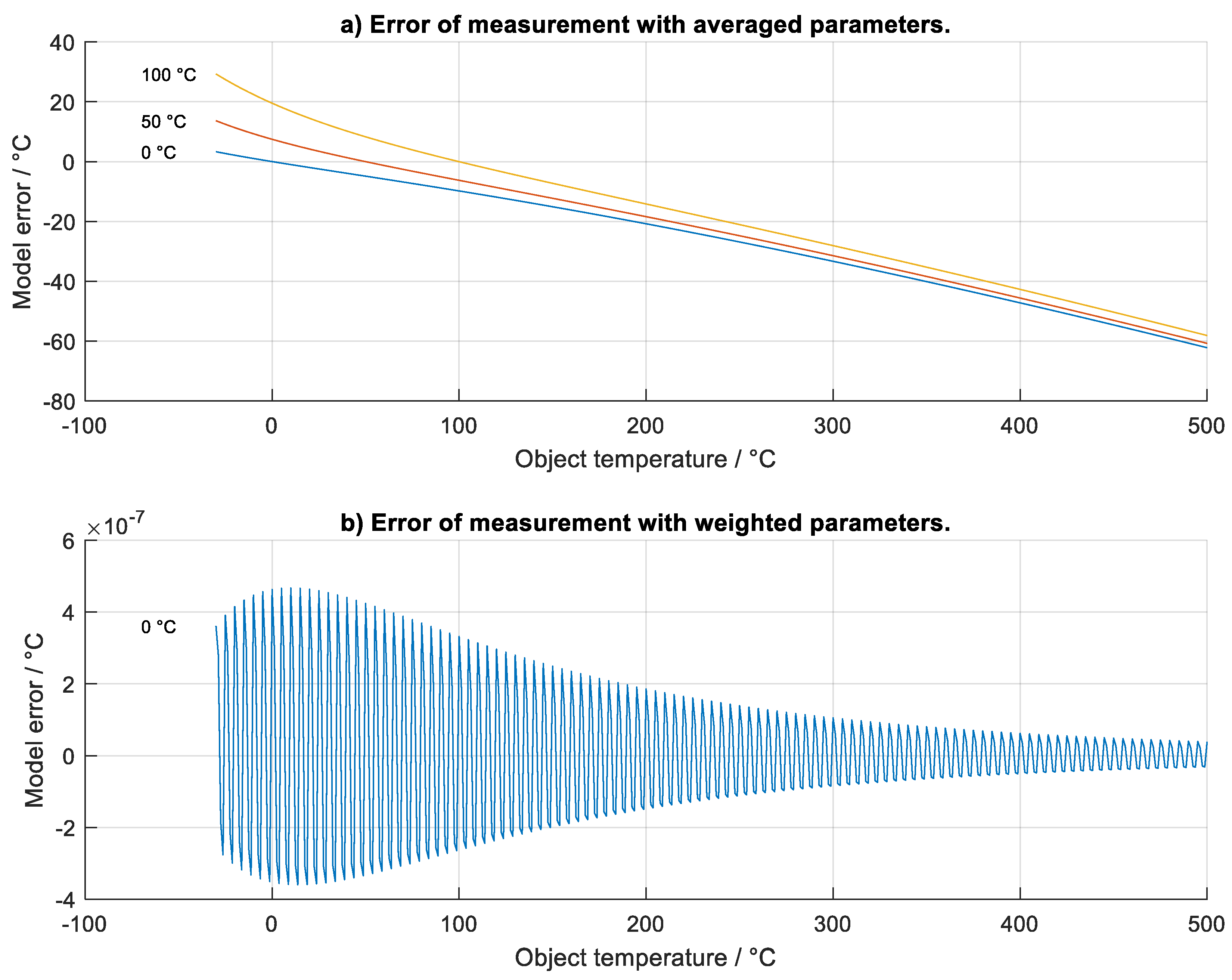
A measurement by radiation thermometry was simulated with a scalar and hybrid inverse model. The model errors, defined as the discrepancy between the theoretical output and the input of the model, are shown in Figure 14. The model with constant scalar values, obtained by averaging the spectral parameters, had large model errors. The model with effective scalar values weighted to the signal and the instrument had negligible error.

4.2. Effective scalarized parameters as instrumental settings

The equilibrium equation (

α (λ) + τ (λ) + ρ (λ) = 1

) is usually extended in practice to scalar operators (

i α + i τ + i ρ = 1

). This simplification is correct only if the measured surface is an ideal (spectrally homogenous) grey body or if the spectral distributions of the signals involved are equal, i.e. if there is radiative equilibrium.

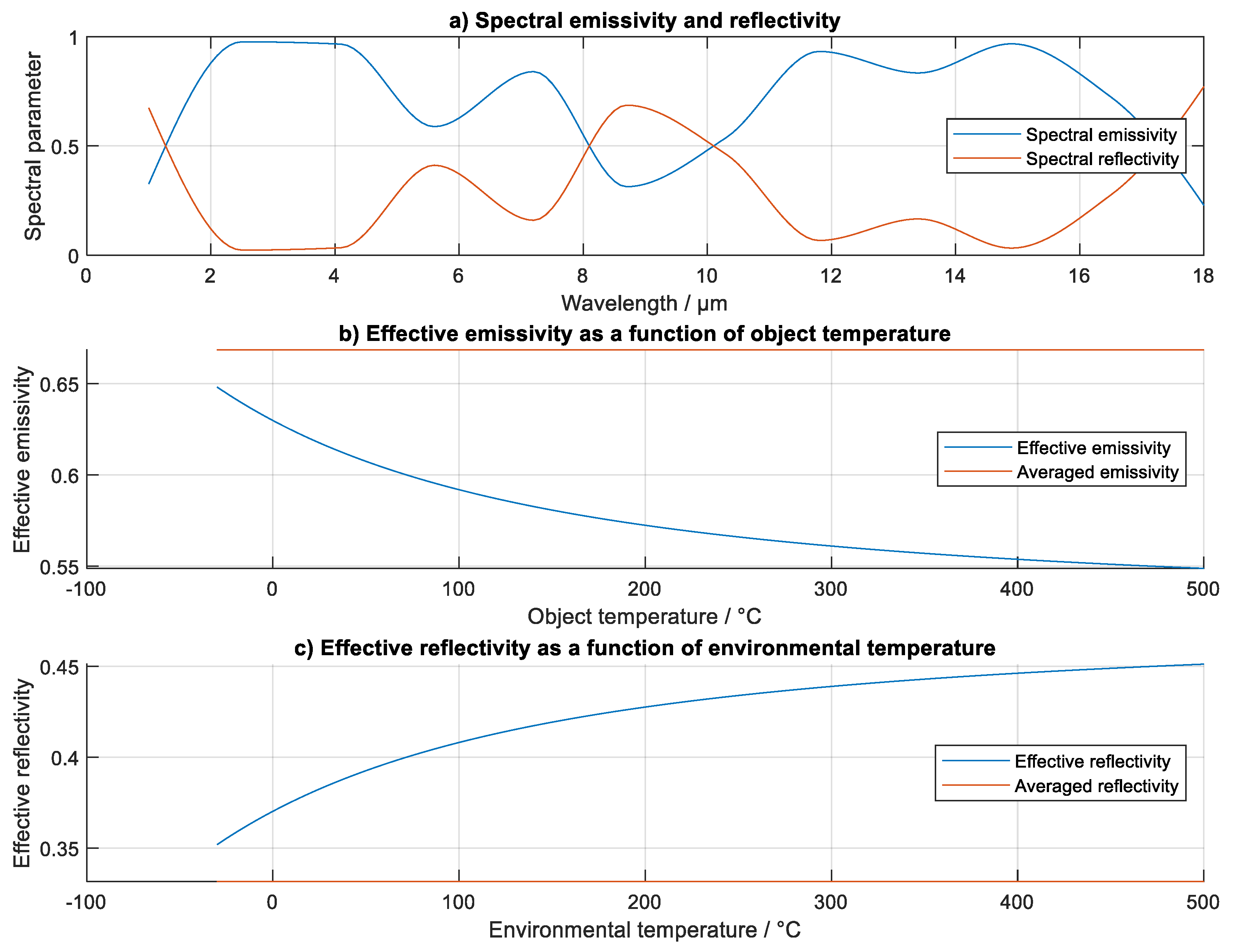
Under real conditions, the effective scalar equivalent value of a spectral parameter is determined by the spectral distribution of the spectral parameters, the signal, and the spectral sensitivity of the instrument. Since the spectral parameters are represented according to the signals involved, the effective scalar parameters are independent and therefore the sum of the three instrumental parameters is not necessarily equal to 1 when measured under real conditions. The effective and mean scalars of the emissivity and reflectivity of the object are shown in Figure 15, where each of the parameters is expressed as a function of the influenced value, in this case the temperature of the emitting object and the temperature of the environment, assuming thermal equilibrium of the environment, which is necessary to satisfy the assumption that the radiance is distributed according to Planck’s law.

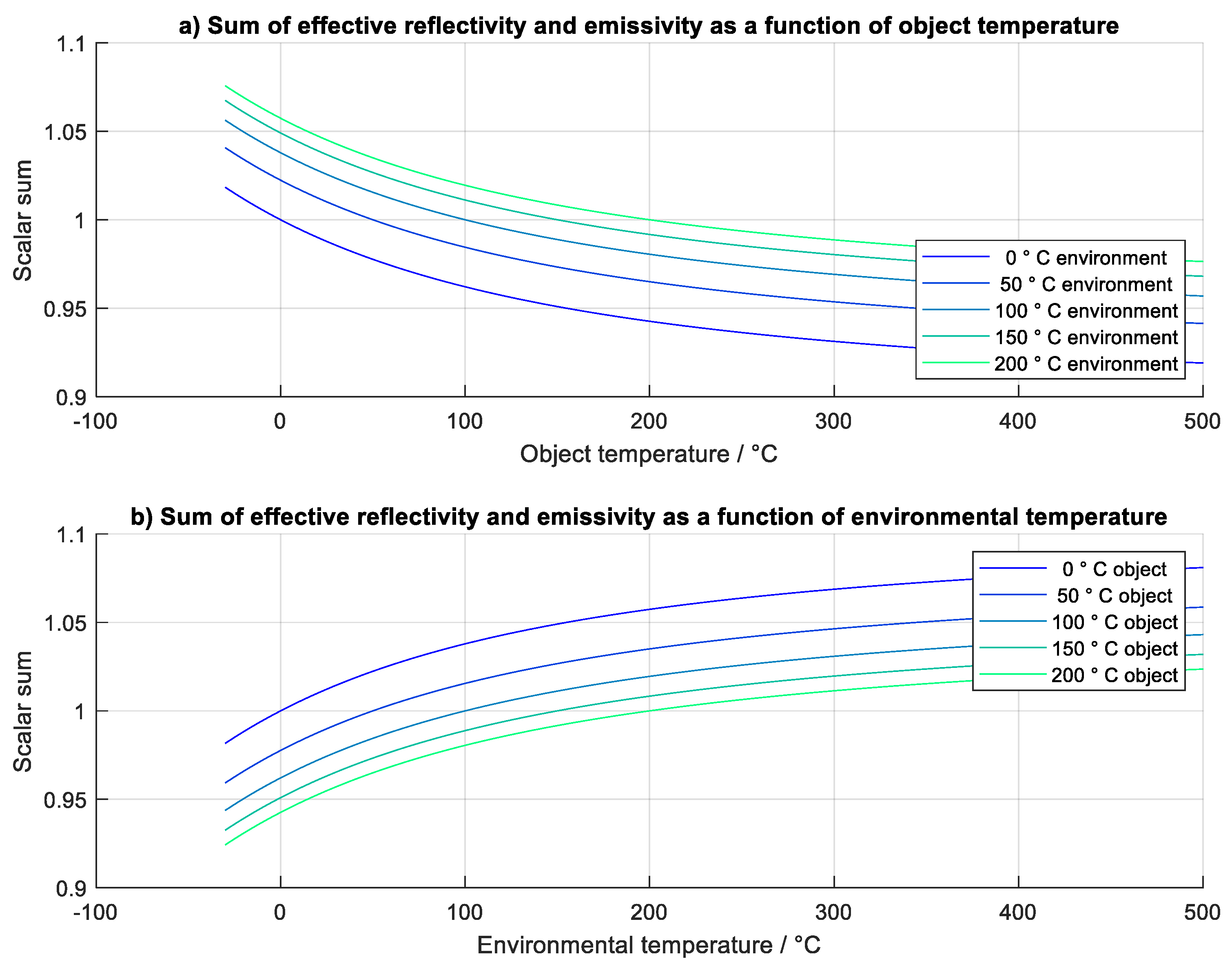
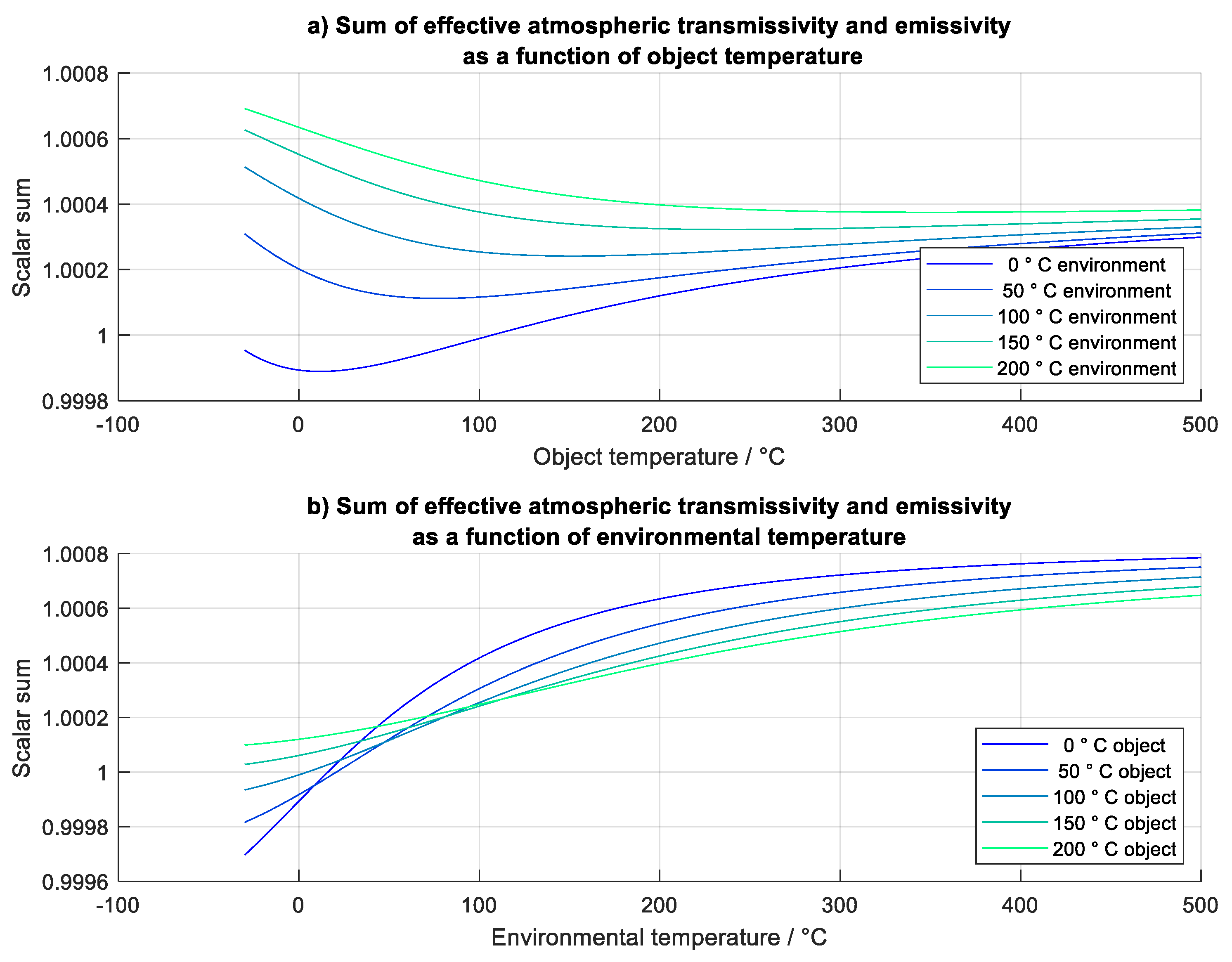
Unlike in the theory of radiation thermometry for grey bodies, the sum of effective parameters in radiation thermometry of real objects is not necessarily equal to 1. This is evident in Figure 16, where the sum of the two effective parameters is plotted as a function of the object and environmental temperature.

Transmissivity is set to 0 and omitted for opaque bodies. Considering that the model error, obtained from the plotted effective parameters in Figure 14 b was negligible, the effective parameters are considered valid.

The sum of the effective atmospheric emissivity and the transmissivity at fixed atmospheric temperature (Figure 17) also deviates from 1, but the effect is less pronounced.

4.3. Measurement uncertainty due to uncertainty of emissivity

The use of grey body measurement principles under real conditions is currently the standard practice in the field of radiation thermometry. Since the grey body simplification of spectral homogeneity never applies under real conditions, the uncertainty of spectral emissivity must be accounted for in the uncertainty of non-contact temperature measurement.

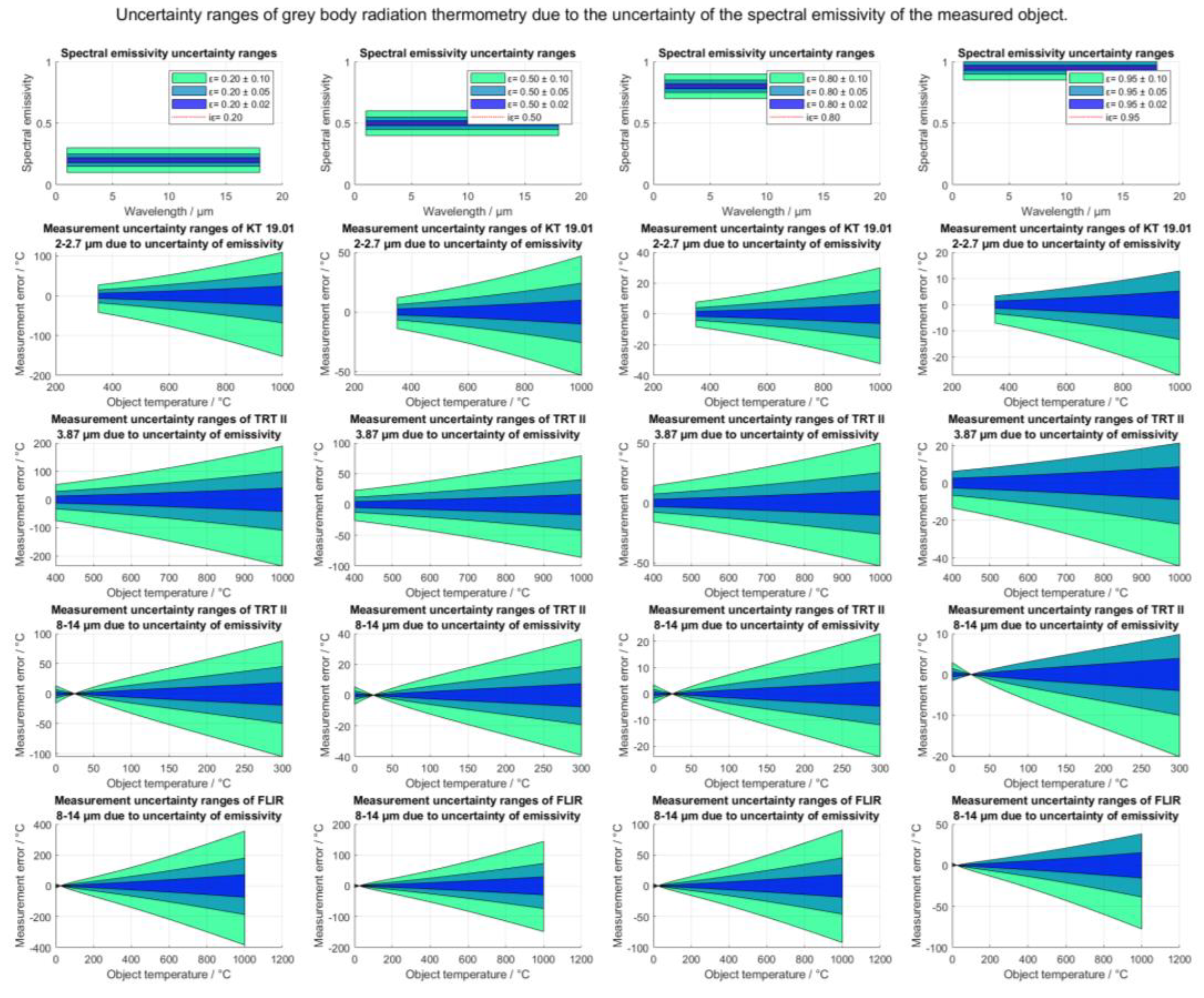
The highest measurement deviations are expected when spectral parameter (emissivity) is at its highest deviation along the full (measurement) spectrum. Deviations of spectral emissivity in narrow spectral bands always produce less or equal effect then deviations along the full spectrum (of measurement). Therefore, spectrally-local uncertainties of the spectral emissivity are considered to be included in the uncertainty budget of the uncertainty interval of the total spectrum. Therefore, the calculation of the measurement uncertainty interval is performed as the worst-case study, where the highest and the lowest expected deviation of the spectral emissivity (over the whole spectrum) define the uncertainty interval at the output of the measurement process. Note that the spectral emissivity is always bounded by 0 and 1, which causes the uncertainty of the emissivity to decrease near these limits.

Figure 18 shows the uncertainty intervals of grey body radiation thermometry due to uncertainty of emissivity. Although a (spectrally homogeneous) grey body was used in this figure, any case-specific (spectral) emissivity and the corresponding (spectral) uncertainty can be used for the uncertainty calculation. In such case, highest possible uncertainty should be used.

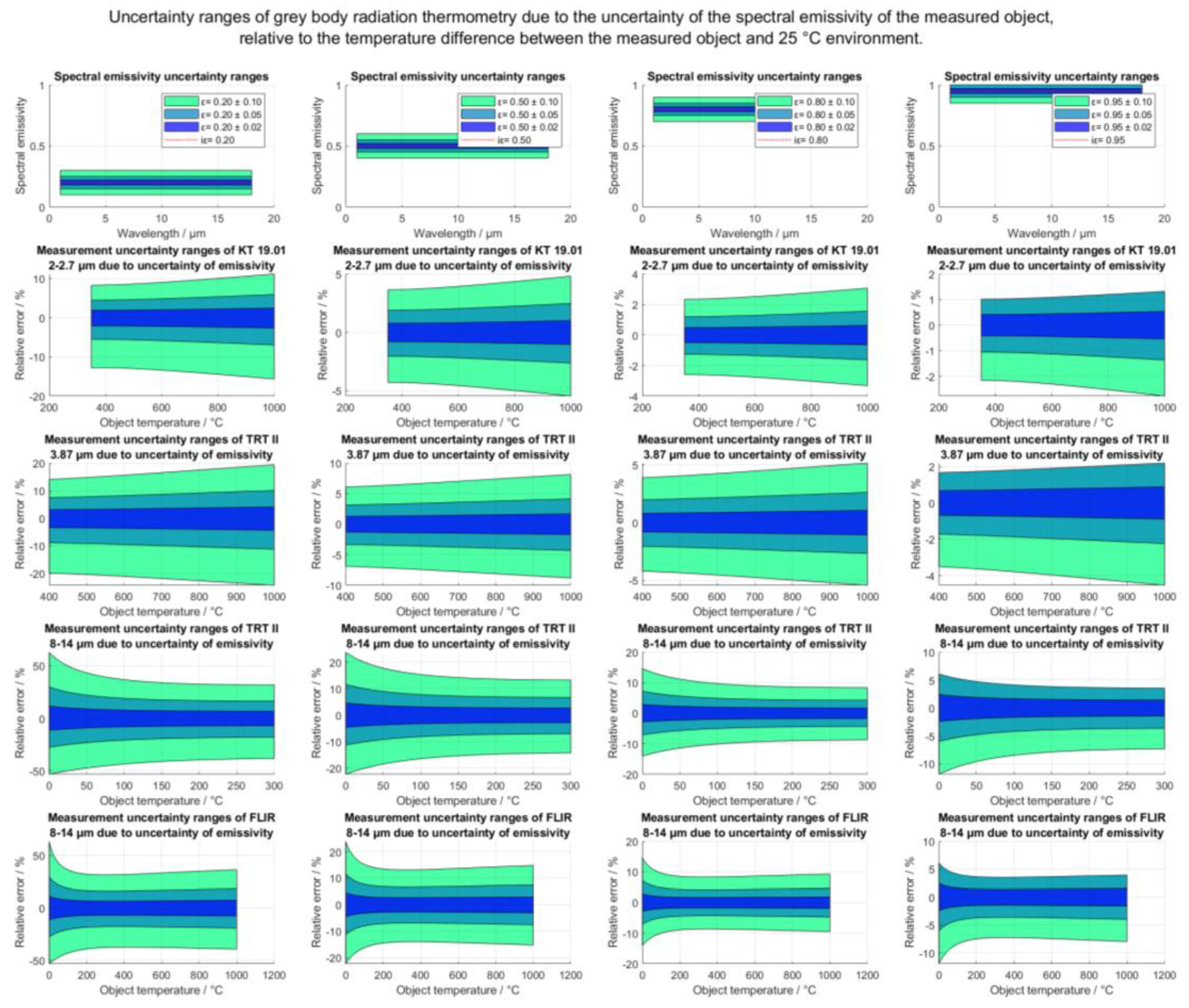
Similarly, the ranges of relative uncertainty are shown in Figure 19. The relative uncertainty is expressed as the ratio between the total measurement uncertainty and the temperature difference between the object and the reflected environment.

5. Discussion

5.1. State of the art in the field of radiation thermometry

Currently the field of radiation thermometry appears to be technologically well supported. Radiation thermometers with state of the art measuring capabilities are available for scientific, professional and consumer use.

Metrological conformity is in practice established for radiation thermometry of black bodies. Calibrations, conducted on black body sources are well established and documented in the literature, often also accredited and traceable to national or international standards.

Through theory and scalar inverse models, the use of radiation thermometers can be extended to grey bodies while retaining traceability, however this is generally not applicable to real conditions.

The literature search for radiation thermometry protocols for real bodies did not yield any existing results.

5.2. Theoretically derived mathematical model and hybrid inverse, validated by simulation

Based on the results of literature review, a physical model of radiation thermometry was defined and scalar and hybrid inverse models were derived. Considering the results of the model error simulation in Figure 14, the hybrid inverse model, where the instrumental parameters are set to the effective values, was validated as a correct approach for radiation thermometry of real objects, resulting in negligible conversion error. This approach requires an individual calculation of the effective scalar equivalent for each spectral parameter and an iterative calculation of the object temperature.

5.3. The use of the equilibrium equation for instrumental settings in radiation thermometry under real conditions is theoretically incorrect

As demonstrated by the simulation in Figure 14, the effective scalar equivalents of the spectral parameters do not necessarily sum to 1 (Figure 16) under real conditions. Therefore, the usual simplification of the equilibrium equation of the scalar inverse model (

i α + i τ + i ρ = 1

) is not valid under real conditions, when only a slight spectral non-homogeneity of the spectral factors exists.

The use of this equation under real conditions inevitably results in errors since the data of the spectral distribution of the signals are not taken into account, as shown in Figure 14.

To correctly account for the interactions between the spectral distributions of the influence parameters and the involved signals, the hybrid inverse model should be used, where the scalar influence parameters are determined as effective scalar parameters, corresponding to the signal-sensitivity-weighted mean of the spectral parameters from chapter 3.4.3.

5.4. Uncertainty of radiation thermometry due to uncertainty of spectral emissivity

Each surface can be classified as an idealized grey body with corresponding spectral homogeneity uncertainty. To assure traceability of measurements, input uncertainties must be evaluated and included in the total measurement uncertainty. A demonstration of the evaluation of uncertainty due to spectral emissivity is shown in Figure 18.

In general, the measurement uncertainty of any radiation thermometer is lowest near the apparent temperature of reflection and increases approximately linearly with the difference from the environment temperature. The Linearity was explored in Figure 19, where the measurement uncertainty is expressed in relation to the temperature difference between the measured object and the 25 °C environment.

The results in Figure 18 indicate that different sensors with different spectral sensitivities respond differently to measurement uncertainty, presumably due to different emission/reflection ratios in different spectral sensitivity ranges and at different object temperatures.

As can be seen from the simulation results, the measurement uncertainty increases with decreasing emissivity of the surface (at constant input uncertainty of the emissivity).

The spectral emissivity is always bounded by 0 and 1, which causes the uncertainty of the emissivity to decrease near these limits, directly decreasing input uncertainty of the process. As the emissivity uncertainty interval approaches emissivity 0, the total measurement uncertainty will seemingly increase to infinity. This is also logical, since non-emissive surfaces cannot be measured due to the lack of emission.

Another error was found to occur frequently when the compensation algorithms overestimate the influence of influence parameters. In this case, the compensated signal may be calculated to a negative incident radiance of the environment. Overcompensation is very problematic when low temperatures (below 0 °C) are measured at higher environmental temperatures, where emitted radiance is weak and easily exceeded by the environmental reflection compensation mechanism.

Author Contributions

Conceptualization, V.M. and I.P.; methodology, V.M. and I.P.; software, V.M.; validation, V.M.; formal analysis, V.M. and I.P.; investigation, V.M.; resources, V.M. and I.P.; data curation, V.M.; writing—original draft preparation, V.M.; writing—review and editing, I.P.; visualization, V.M.; supervision, I.P.; project administration, I.P.; funding acquisition, I.P. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge the financial support from the Slovenian Research Agency (research core funding No. P2-0225). The research was also supported partially by the Ministry of Economic Development and Technology, Metrology Institute of the Republic of Slovenia, in scope of contract 6401-18/2008/70 for the national standard laboratory for the field of thermodynamic temperature and humidity.

Data Availability Statement

All data, presented in this study, are publicly available from cited sources. Plot scripts in MATLAB environment are available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Murthy, B. Tsai and R. Saunders, “Radiative Calibration of Heat-Flux Sensors at NIST: Facilities and Techniques,” J Res Natl Inst Stand Technol., vol. 2, pp. 293-305, 1 Apr 2000. [CrossRef]
S. König, B. Gutschwager, R. D. Taubert and J. Hollandt, “Metrological characterization and calibration of thermographic cameras for quantitative temperature measurement,” J. Sens. Sens. Syst., vol. 9, pp. 425-442, 18 December 2020. [CrossRef]
J. Donlon and e. al., “A Second-Generation Blackbody System for the Calibration and Verification of Seagoing Infrared Radiometers,” Journal of atmospheric and oceanic technology, vol. 31, pp. 1104-1127, 2014. [CrossRef]
S. Boles, I. Pušnik, D. Mac Lochlainn, D. Fleming, I. Naydenova and S. Martin, “Development and characterisation of a bath-based vertical blackbody cavity calibration source for the range −30 °C to 150 °C,” Measurement : journal of the International Measurement Confederation [Print ed.], pp. 121-127, Aug. 2017. [CrossRef]
H.-I. Kim, B.-G. Chae, P.-G. Choi, M.-S. Jo, K.-M. Lee and H.-U. Oh, “Thermal Design of Blackbody for On-Board Calibration of Spaceborne Infrared Imaging Sensor,” Aerospace, vol. 5, p. 268, 16 May 2022. [CrossRef]
A. Miklavec, I. Pušnik, V. Batagelj and J. Drnovšek, “A large aperture blackbody bath for calibration of thermal imagers,” Measurement Science and Technology, pp. 1-8, 2013. [CrossRef]
Fluke Calibration, “Emissivity Compensation for Fluke Calibration 4180 Series Precision Infrared Calibrators,” Fluke calibration, Everett, WA U.S.A., 2012.
P. Saunders, “Calibration and use of low-temperature direct-reading radiation thermometers,” Measurement Science and Technology, vol. 2, 17 December 2008. [CrossRef]
V. Mlačnik and I. Pušnik, “Influence of Atmosphere on Calibration of Radiation Thermometers,” Sensors, vol. 21, no. 16, 2021. [CrossRef]
Heitronics Infrarot Messtechnik GmbH, Infrared radiation pyrometer KT19 II Operation instructions.
Teledyne FLIR LLC, “What is the typical spectral response for certain camera/lens combination?,” [Online]. Available: https://www.flir.com/support-center/Instruments/what-is-the-typical-spectral-response-for-certain-cameralens-combination/. [Accessed 26 March 2021].

Figure 1. Physical system of measurement in radiation thermometry with key influence parameters. Physical quantities and their notation correspond to Equation (2).

Figure 2. Spectral transmissivity of dry air, water vapour, and combination of both [9].

Figure 7. Theoretically ideal inverse of the direct model. Note that spectral integration is irreversible upon measurement. Therefore, measurement of spectral radiance is required for the ideal inverse model. Spectral integration was omitted from the direct model.

Figure 8. Model of radiation thermometry with the scalar inverse model. Parameters, beginning with i correspond to scalar instrumental parameters. Dotted lines represent transfer of non-radiation scalar data, such as temperature or calculated scalar equivalent of an influence parameter. The inverse black body radiance characteristic is a characteristic transformation between emitted radiance and temperature of a black body, which can be derived from Planck’s law.

Figure 9. Hybrid model of scalar and spectral quantities.

Figure 10. The characteristic function of the sensor with specific spectral sensitivity. The characteristic is obtained by inverting the simulation results of the direct characteristic in Figure 3.

Figure 11. Optimized hybrid inverse model utilizes distributive property of the model for spectral sensitivity.

Figure 12. (a) Spectral radiance, emitted by the black body, according to Planck's law. (b) Temperature–dependent weights for spectral factor averaging. VOx sensor sensitivity and black body spectral radiance have been used in this calculation. Note that with the spectral shift of the peak of the spectral radiance to the wavelengths outside the sensitivity range of the sensor (in this example at temperatures above 400 K), the instrumental emissivity is less sensitive to thermal changes.

Figure 13. Spectral weights for averaging of the spectral emissivity for different sensors. Spectral weights were calculated according to Equation (11) from spectral sensitivities from Figure 4.

Figure 14. Theoretical error of radiation thermometry, using scalar inverse a) with constant, spectrally averaged parameters at various environmental temperatures and b) effective parameters, weighted to the signal and the instrument.

Figure 15. Shown are a) the spectral emissivity and spectral reflectivity of the measured surface, b) the averaged and effective emissivity as a function of the temperature of the measured object and c) the effective reflectivity as a function of the environmental temperature, assuming pure emission according to Planck’s law, e.g. when the environment has (a single) homogeneous temperature. Thermally non-homogenous environments are expected under real conditions, in which case, spectral radiance of the environment can be either measured or theoretically derived by summation of emission for this calculation method.

Figure 16. Sum of effective scalar emissivity and reflectivity with a) object and b) environmental temperature. Multiple plots show variation of a) environmental and b) object temperature.

Figure 17. The sum of effective atmospheric transmissivity and emissivity with a) object temperature and b) environmental temperature, assuming a thermally homogeneous environment. Multiple plots show the variation of a) environmental temperature and b) object temperature.

Figure 18. Measurement uncertainty intervals for grey body radiation thermometry of surfaces with different spectral emissivities and homogeneities. The uncertainty contributions are calculated at 25 °C environmental temperature and correspond to the probability of occurrence of the spectral emissivity within the specified uncertainty interval.

Figure 19. Relative measurement uncertainty intervals for grey body radiation thermometry of surfaces with different spectral emissivities and homogeneities, expressed relative to the temperature difference between the measured object and the 25 °C environment. The uncertainty contributions correspond to the probability of occurrence of the spectral emissivity within the specified uncertainty interval. The singularity of the relative error at temperature 25 °C due to the division of the absolute error with 0 °C thermal difference was omitted. If temperature of the object and the reflected radiance are equal, emissivity is irrelevant and the measurement uncertainty due to the uncertainty of the emissivity does not exist.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Traceable Spectral Radiation Model of Radiation Thermometry

Abstract

1. Introduction

1.1. Radiation thermometry of black bodies

1.2. Radiation thermometry of grey bodies

1.3. Radiation thermometry of real bodies

2. Defining the direct (physical) model

2.1. The process of radiation thermometry and the full system of measurement

2.2. Thermal radiation emission, transfer and absorption

2.3. Mathematical definition of the direct model

2.3.1. Object’s emission and environmental radiation reflection

2.3.2. Atmospheric transmission and self-emission

2.3.3. Transmission through the optical system of the measuring instrument

2.3.4. Sensor absorption and black body calibration

2.4. Final spectral interaction of the physical model

3. Defining the inverse of the physical model

3.1. Inverse model of measurement

3.1.1. Theoretically ideal spectral inverse of the direct model

3.1.2. Scalar inverse model

3.1.3. Hybrid model

3.1.4. Characteristic function of the sensor

3.2. Optimized hybrid model

3.3. Conversion of spectral emissivity to an effective scalar value

3.3.1. Averaging in the spectral range of the measuring instrument

3.3.2. Experimentally obtained signal- and sensitivity-weighted mean

3.3.3. Calculated signal-weighted mean

4. Results

4.1. Validation of the model of radiation thermometry with hybrid inverse

4.2. Effective scalarized parameters as instrumental settings

4.3. Measurement uncertainty due to uncertainty of emissivity

5. Discussion

5.1. State of the art in the field of radiation thermometry

5.2. Theoretically derived mathematical model and hybrid inverse, validated by simulation

5.3. The use of the equilibrium equation for instrumental settings in radiation thermometry under real conditions is theoretically incorrect

5.4. Uncertainty of radiation thermometry due to uncertainty of spectral emissivity

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe