Path Planning in Case of Swarm Unmanned Surface Vehicles for Visiting Multiple Targets

Preprint

Article

Path Planning in Case of Swarm Unmanned Surface Vehicles for Visiting Multiple Targets

Altmetrics

Downloads

161

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 February 2023

Posted:

16 February 2023

You are already at the latest version

Alerts

Abstract

In this study we present a hybrid approach of ACO with fuzzy logic and clustering methods to solve multi-objective path planning problems in case of swarm USVs. This study aims to enhance the performance of ACO algorithm by integrating fuzzy logic in order to cope with the multiple contradicting objectives and generate quality solutions by in parallel identifying the mission areas of each USV to reach the desired targets. The objectives that are taken into account are the minimization of traveled distance and energy consumption, and the maximization of path smoothness. A comparative evaluation is conducted among ACO and fuzzy inference systems, Mamdani (ACO-M) and Takagi–Sugeno–Kang (ACO-TSK). The results showed that depending on the needs of the application, each methodology can contribute respectively. ACO-M generates better paths but ACO-TSK presents higher computation efficiency.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

Robotic vehicles are integrated into modern style of life to undertake challenging tasks, such as monitoring or navigation assistance [1]. Unmanned Surface Vehicle (USV) is a type of autonomous robotic vehicle with various application including ocean monitoring [2,3], safety and rescuing [4] and swarm approaches combined with UAVs and/or UGVs for monitoring. The increase use and application of USVs impose the need for more autonomous functions/decisions in dynamic and complex environments without any human interference, such as the ability to find an optimal route and to avoid detected obstacles in real time [5].

Path planning problems can be found in various domains, such as Air Transportation and UAVs [6,7,8,9], robotic vehicles and USV [5] and even for smart assistive systems for individuals with disabilities [1,10]. To address the USV path planning problem in complex and dynamic environments, multiple factors/objectives should be considered for generating an optimal path. Traditional approaches for path planning are based on single objective metaheuristics for finding the shortest path, most energy efficient or safest path, among others. For instance A* [11,12], Dijkstra [13] and Ant Colony Optimization (ACO) [14,15] among others, have been used to address the aforementioned single objectives path planning problems.

In case of single objective USV path planning, ACO has been applied for obstacle avoidance [16], hybridized with artificial potential field for adaptive early warning [17]; for global path planning combined with quantum computing [18], with Bayesian network [19] and with immune algorithm [20]; for collision avoidance [15]. A* was used as a stand-alone or hybrid approach in maritime environments with dynamic obstacles and ocean currents [12]; and for path smoothing [11], [21]. Other studies propose the use of multilayer path planner for obstacle avoidance [22]; Voronoi diagram [23] or Particle Swarm Optimization algorithm [24] for finding energy efficient paths.

When it comes to path planning with multiple objectives of USVs, limited studies have been proposed. The majority of them are based on common approaches like scalarization and Pareto optimality [25]. On the other hand, few methodologies employ Fuzzy Logic (FL) or develop novel approaches to address efficiently in terms of computational effort the multi-objective path planning problem [26]. In the literature, the scalarization of the objective terms by using mostly the weighted sum has been proposed for multi-objective USV path planning to combine time, distance and energy consumption. To solve the aforementioned modeling a hybrid A* algorithm was developed [27]. In another study [28] the Pareto optimality was adopted with particle swarm optimization algorithm for path planning of USV with currents effects. In [29] FL has been integrated to Ant Colony Optimization (ACO) algorithm for finding an optimal path among multiple objectives, distance, energy consumption and path smoothness. A comparative study [26] among FL and Root Mean Square Error evaluation criterion was conducted for the novel swarm intelligence algorithm (SIGPA) [30].

This study takes advantage of the state-of-art ACO-FS algorithm proposed in [29] enhanced with fuzzy logic to address the multi-objective path planning problem. To overcome the limitations of [29] and expand the methodology to a swarm of USVs to cover a certain area and visit multiple targets, this study employs a clustering approach to group the targets based on their coordinates, current velocity and direction. For the clustering 3 popular clustering methods, such as the Mini Batch K-Means, Ward’s Hierarchical Agglomerative Clustering and Birch adopted, compared and evaluated based on the aggregation of three clustering evaluation methods. Then, a comparative evaluation of two popular Fuzzy Inference Systems (FIS) Mamdani and Takagi–Sugeno–Kang (TSK) follows. Therefore, through a comparative evaluation process, the best suitable FIS and clustering algorithm for this application will be identified (Figure 1).

2. Materials and Methods

2.1. Objective terms of the USV path planning problem

In this study the multi-objective path planning problem with multiple targets is addressed in case of a swarm of USVs. The formulation of the problem is based on [26,29]. The goal is to find optimal path to cover the specified areas by minimizing: (i) the distance (1); (ii) the brut turns along the route (2); and (iii) the energy consumption due to current velocity and direction (3).

-: Term 1 for the minimization of traveled distance.

m i n D = \sum_{i \in N} \sum_{\begin{matrix} j \in N : \\ (i, j) \in E \end{matrix}} d_{i j} = \sum_{i \in N} \sum_{\begin{matrix} j \in N : \\ (i, j) \in E \end{matrix}} (\sqrt{{(j_{x} - i_{x})}^{2} + {(j_{y} - i_{y})}^{2}})

(1)

where

N

and

E

are the sets of nodes and the edges of the graph, respectively;

d_{i j}

is the Euclidean distance metric between node

i

and node

j

i_{x}, j_{x}

and

i_{y}, j_{y}

are the geographical coordinates of nodes

i

and

j

on horizontal and vertical axes, respectively.

-: Term 2 for the minimization of brut changes along the path.

m i n θ = \sum_{i \in N} \sum_{\begin{matrix} j \in N : \\ (i, j) \in E \end{matrix}} \sum_{\begin{matrix} k \in N : \\ (j, k) \in E \end{matrix}} θ_{i j k}

(2)

-: Term 3 for the minimization of the fuel consumption of the USV.

where

θ_{i j k}

is the angle that is formed from the edges

(i, j)

and

(j, k)

m i n F C = \sum_{i \in N} \sum_{\begin{matrix} j \in N : \\ (i, j) \in E \end{matrix}} \frac{d_{i j}}{V + v_{c}} f

(3)

where

f

is the fuel consumption per unit time

(k g / h)

V

and

v_{c}

are the velocities of the USV and of the currents, respectively. The term is included in the model since if a USV is moving against the currents more energy is needed to retain a certain velocity during a route [18,28,31].

2.2. Ant Colony Optimization Algorithm with Fuzzy Logic

ACO algorithm is one of the most popular heuristic algorithms used to solve path planning problems formed as graphs for finding the shortest path [14]. To adapt ACO algorithm to solve the above defined multi-objective path planning problem for USVs, ACO is enhanced with fuzzy logic. This enables the ability to evaluate the impact of multiple objectives and identify the optimal solution. ACO is inspired by the operation of ants to trace their food by depositing pheromone along the path [32]. ACO operation consists of two main steps: In the first step the transition probability,

p_{i j}

, of each edge in the graph is calculated based on (4); and in the second step the equation (5) is used to update of the pheromones. This is achieved by recalculating the pheromone deposit,

τ_{i j}

, on each edge for the ant population

P

p_{i j} = \frac{{(τ_{i j})}^{γ} {(η_{i j})}^{β}}{\sum_{(k, l) \in E} τ_{k l}}

(4)

τ_{i j} = (1 - ρ) τ_{i j} + ρ \sum_{a \in P} \frac{Q}{L_{a}}

(5)

where

ρ \in [0,1]

is the evaporation coefficient,

η_{i j} = \frac{1}{d_{i j}}

where

d_{i j}

is α distance metric,

γ \geq 0

and

β \geq 1

are the parameters to control the influence of

τ_{i j} (t)

and

η_{i j}

, respectively.

L_{a}

is the cost of the path of ant

a

and

Q

is a constant that is associated with the remaining pheromone amount [32]. In the literature in case of single-objective optimization problems the

L_{a}

corresponds the objective cost/value. For example, in shortest distance problems, the cost is the length of the path found by the ant

a

. Bellow more details are given for the calculation of this cost in our study.

The pseudocode of ACO algorithm is shown bellow in Algorithm 1. In the initialization phase

I n i t i a l i z e P h e r o m o n e V a l u e s (τ)

the pheromone values (

τ_{i j}

) are all initialized to a constant value

c > 0

at the start of the algorithm. In the phase of the solution construction,

C o n s t r u c t S o l u t i o n (τ)

, the construction of a solution starts with an empty partial solution

s^{p} = 〈〉

. Then, at each construction step the current partial solution

s^{p}

is extended by adding a feasible solution component based on the transition probabilities and the heuristic information (4). Also, the pheromone update process follows,

A p p l y P h e r o m o n e U p d a t e (τ, G_{i t e r}, s^{*})

based on (

5

Algorithm 1: ACO pseudoalgorithm

Input: variables of ACO

I n i t i a l i z e P h e r o m o n e V a l u e s (τ)

s^{*} \leftarrow N U L L

// current best solution does not exist

while termination criteria are not met do

G_{i t e r} \leftarrow \emptyset

// the set of the path at the current iteration is empty

for

j = 1, \dots, n_{a}

s \leftarrow C o n s t r u c t S o l u t i o n (τ)

(f (s) < f (s^{*}))

s^{*} i s N U L L

then

s^{*} \leftarrow s

G_{i t e r} \leftarrow G_{i t e r} \cup \{s^{*}\}

end for

A p p l y P h e r o m o n e U p d a t e (τ, G_{i t e r}, s^{*})

end while

Output: current best solution

s^{*}

In this study, a path planning problem formulated as a multi-objective optimization problem is investigated. To this end, the cost of the path,

L_{a},

used in (5) is defined in a way to reflect the objective cost derived from all the objectives (1), (2), and (3) of the problem presented in section 2.1. Therefore, to calculate the

L_{a}

cost of the path of each ant two popular FIS systems are employed. The FISs are used to aggregate the impact of the objective terms into a single value derived from the defuzzification process. Hybridization of ACO with Mamdani or TSK FISs has been successfully implemented in our previous studies where more details on this process can be found [26,33].

2.2.1. FIS1 1: Mamdani Fuzzy Inference System (ACO-M)

In the hybridization of ACO with Mamdani FIS the defuzzification value of the Mamdani FIS is used as cost of the path (

L_{a}

). This is because the defuzzification value denotes the optimality of the generated path after the aggregation of the objective terms and the defined fuzzy sets and rules. For this study the following fuzzy membership functions (Figure 2) corresponding to each objective term and fuzzy rules (Table 1) are defined and used for the Mamdani FIS.

2.2.2. FIS 2: Takagi–Sugeno–Kang Fuzzy Inference System (ACO-TSK)

In the second approach where the ACO is hybridized with TSK FIS, as path cost (

L_{a}

) the value of the TSK FIS is used. Similarly, to Mamdani FIS, this value denotes the optimality of the generated path. TSK FIS calculates a crisp output value by using a weighted average of the fuzzy rules’ consequent [34]. This makes the TSK FIS a less computationally demanding approach compared to Mamdani. For the TSK FIS the same membership functions and rules (Figure 2, Table 1) are adopted.

2.3. Swarm approach of USV path planning problem

To solve the swarm USV path planning problem, various clustering methods, namely Mini Batch K-Means, Ward’s Hierarchical Agglomerative Clustering (Ward) and Birch, are tested and evaluated through a comparative evaluation process (described in Section 3) in order to identify the most effective one for this application. Mini Batch K-Means is an alternative clustering method to the K-Means algorithm. The advantages of this method include the reduction of the computational effort by using small random batches of a fixed size instead of all the dataset in each iteration [35]. Ward’s Hierarchical Agglomerative Clustering Method belongs to the family of the hierarchical agglomerative clustering. It is based on the criterion of sum of squares to produce groups that minimize within-group dispersion at each binary fusion [36]. Balanced Iterative Reducing and Clustering using Hierarchies (Birch) is an unsupervised data mining algorithm used to perform hierarchical clustering. It generates a compact summary that retains as much distribution information as possible, and then clusters the data summary instead of the original dataset [37,38].

The clustering of the targets that need to be visited in an area by the swarm of the USVs is performed based on the geospatial coordinates and the wind information (velocity and direction). To this end, targets with similar characteristics are grouped. The number of clusters is defined by the number of the USVs that form the swarm so that each USV will perform a mission.

3. Evaluation Methodology

Two case studies are performed to evaluate the presented methodology for a swarm of 3 USVs with the same characteristics by comparing the effectiveness of the clustering algorithms and the selected FISs in the specific application. To this end, a fully connected graph was randomly generated with 25 nodes. For each node the values of current velocity and direction were set based on Gaussian distribution. The current velocity was set from 1 and 3 m/s. Also, the direction was set from 0 to 360 degrees clockwise. Nodes with yellow correspond to lower values of current velocity (close to 1 m/s) while dark blue nodes correspond to higher values of current velocity (close to 3 m/s). It is assumed that all the USVs have the necessary fuel and energy to perform the tasks. Regarding the parameter settings of ACO, the iterations were set to 20 with 5 size population. The evaporation coefficient was set to 0.5,

Q

was set to 1. Regarding the USV characteristics,

F

was set to 2

k g / h

and

V

to 3 m/s. The experiments were implemented in Python using Microsoft Windows 10 Environment operational system, with AMD Ryzen 7 3800X 8-Core Processor at 3.89 GHz and 32GB RAM.

The evaluation of the clustering methods is performed based on the aggregation of 3 evaluation methods, adopted from [39]. The chosen clustering evaluation criteria are the Silhouette Coefficient, the Calinski–Harabasz Index (CHI), and the Davies–Bouldin Index. The normalized scores of the evaluation criteria are summed for calculating a cumulative evaluation score (Figure 3).

Silhouette Coefficient is an evaluation metric that calculates the goodness of a clustering technique and its value ranges from -1 to 1. The higher value 1 shows that the means clusters are well apart from each other and clearly distinguished. The lower value -1 shows that the means clusters are wrongly assigned while the value 0 shows that the distance between the means clusters is not significant. For each point i, the distance to its own cluster centroid

a_{i}

, and the distance to the nearest neighboring centroid

b_{i}

are calculated. The Silhouette score for the point

i

is calculated based on (6):

s i l h o u e t t e s c o r e = \frac{(b_{i} - a_{i})}{m a x (a_{i}, b_{i})}

(6)

The Calinski–Harabasz Index, also known as the Variance Ratio Criterion, measures the similarity of a point

i

with its own cluster (cohesion) compared to other clusters (separation). The cohesion is calculated based on the distances from the data points within the cluster to its cluster centroid while the separation is calculated based on the distance of the cluster centroids from the global centroid. A high score indicates better cluster compactness.

The cohesion or else instar-cluster dispersion or the within group sum of squares (WGSS) is calculated by the following expression (7), where

n_{i}

is the number of data points/elements in cluster i,

X_{j i}

the j-th element of the cluster i and

C_{i}

the centroid of cluster i and K the number of clusters:

W G S S = \sum_{i = 1}^{K} \sum_{j = 1}^{n_{i}} {‖X_{j i} - C_{i}‖}^{2}

(7)

The separation or else inter-cluster dispersion or the between group sum of squares (BGSS) is calculated by the following expression (8), where C is the centroid of the dataset (barycenter):

B G S S = \sum_{i = 1}^{K} n_{i} \times ‖C_{i} - C‖

(8)

Calinski–Harabasz Index is defined as shown in (9), where N is the total number of data points/elements in the dataset:

C H I = \frac{\frac{B G S S}{K - 1}}{\begin{matrix} W G S S \\ N - K \end{matrix}} = \frac{B G S S}{W G S S} \times \frac{N - K}{K - 1}

(9)

The Davies–Bouldin Index shows the average similarity of clusters, where similarity is a measure that relates cluster distance to cluster size. Comparing clustering algorithms, lower values of DBI means that a better separation between the clusters has been achieved. This reflects a function of intra-cluster dispersion and separation between the clusters.

The intra-cluster dispersion of cluster i is calculated by (10), where

T_{i}

is the number of elements in cluster i,

X_{j}

is the j-th element in the cluster i,

C_{i}

is the centroid of cluster i and q is a predefined value usually set to 2 to calculate the Euclidean distance:

S_{i} = {[\frac{1}{T_{i}} \sum_{j = 1}^{T_{i}} {|X_{j} - C_{i}|}^{q}]}^{\frac{1}{q}}

(10)

The separation measure is calculated based on (11), where K is the total number of clusters,

c_{k i}

and

c_{k j}

are the k-th component of n-dimensional centroid

C_{i}

of cluster i and

C_{j}

of cluster j, respectively, and p similarly to q in (10) is a predefined value usually set to 2 to calculate the Euclidean distance:

M_{i j} = {[\sum_{k = 1}^{K} {|c_{k i} - c_{k j}|}^{p}]}^{\frac{1}{p}}

(11)

The DBI is calculated based on the following Equation (12), where:

\bar{D} = \frac{1}{K} \sum_{i = 1}^{K} \sum_{\begin{matrix} j = 1 \\ j \neq i \end{matrix}}^{K} m a x \{\frac{S_{i} + S_{j}}{M_{i j}}\}

(12)

For the evaluation of the path planning of the swarm of USVs, the evaluation criteria are the objective terms:

The evaluation criteria among the solutions are:

The objective criteria: (i) distance; (ii) brut turns; and (iii) fuel consumption
Path quality based on the defuzzification value of Mamdani and TSK FISs
The computing time
The relative percentage deviation (RPD) adopted by [46,47]:

R P D = \frac{|{B e s t}_{s o l} - {A l g}_{s o l}|}{{B e s t}_{s o l}} 100 %

(13)

The relative deviation index (RDI) adopted by [46,47]:

R D I = \frac{|{B e s t}_{s o l} - {A l g}_{s o l}|}{|{B e s t}_{s o l} - {W o r s t}_{s o l}|} 100 %

(14)

where

{B e s t}_{s o l}

and

{W o r s t}_{s o l}

are the best and the worst solutions, respectively; and

{A l g o}_{s o l}

is the path quality value of the examined solution. Based on Equations (13) and (14), it is obvious that the lowest values of RPD and RDI indicate the preferable solution based on the satisfaction of objective criteria.

Each case study was run 20 times. For the proposed ACO variations the population size was set to 10 ants and the number of iterations to 20. Also, the evaporation coefficient ρ was set to 0.5 and Q was set to 1. The case studies were designed based on the evaluation methodology adopted in related works [15,24,44,45]. The experiments and the algorithms were implemented in Python, on Microsoft Windows 10 Environment operational system, with AMD Ryzen 7 3800X 8-Core Processor at 3.89 GHz and 32GB RAM.

4. Results and Discussion

The clustering results of the two case studies are illustrated bellow in Figure 4 and Figure 5. For better visualization the edges are not depicted, and each cluster is shown in different color and represents the operational area for each USV. In the CS1 all the clustering algorithms achieved the same result (Figure 4) since the nodes were scattered and the areas based on the clustering features were enough discrete. For this reason, clustering evaluation was not performed. On the other hand, for more complex areas, such as the one of case study 2, the Mini Batch K-Means and Ward’s Hierarchical Agglomerative Clustering generated the same clusters with better evaluation score compared to Birch (Figure 5, Table 2). It can be observed that the clusters constructed by Mini Batch K-Means and Ward are more balanced in terms of distance, current velocity and number of targets that each USV has to visit in their operational area, compared to Birch’s clusters.

For the presented case studies, we evaluated the proposed hybrid ACO – FIS schemes. The best clustering results were used to determine the operational area of each USV. Table 3 shows the multi-objective path planning mean results for the case studies after 20 runs solved with ACO-Mamdani and ACO-TSK approaches for the swarm of USVs and the selected operational areas for each USV. We should notice that all the USVs have the same characteristics and therefore, it is not important to identify which USV will perform a certain operation. The three operational areas are declared with different colors in the Figure 4 and Figure 5. The mean results showed that ACO-Mamdani is capable to generate more balanced paths (better overall path optimality in both cases, Table 3) with respect to the objective terms while on the other hand ACO-TSK due to the lack of the defuzzification step achieves lower computing times, an important factor in real time applications. Indeed, based on the evaluation criteria RPD and RDI for distance (Table 4), number of turns (Table 5) and consumption (Table 6) we observe that the paths derived from ACO-Mamdani are of better quality almost in all USVs and case studies, but the difference is not that much significant making the ACO TSK an adequate option when computing time is also important.

5. Conclusions

This study presents a methodology to address the swarm USV path planning problem for visiting multiple targets formulated as a multi-objective optimization problem. To this end, a comparative study among two popular FISs was conducted and 3 popular clustering algorithms. The results showed that in simple problems with highly discrete areas, in terms of weather conditions, all the clustering methods achieved similar results, however, in uniform weather data Mini Batch K-Means and Ward presented a slightly better performance based on the evaluation criteria. Regarding the performance of FISs for solving the USV path planning problem, the results were in accordance with the literature, where each FIS can be suitable depending on the need of the application. For instance, ACO enhanced with Mamdani FIS presents a better performance with respect to the quality of the solution, but on the other hand, ACO with TSK FIS decrease the computing time which is also important in real time applications.

Author Contributions

Conceptualization, C.N.; methodology, C.N.; software, C.N.; validation, C.N.; formal analysis, C.N.; writing—original draft preparation, C.N.; writing—review and editing, C.N. and D.L.; visualization, C.N.; supervision, C.N.; project administration, D.L.; funding acquisition, D.L. All authors have read and agreed to the published version of the manuscript.

Funding

This paper is based on the results of the successfully completed three-year research project OPTINET. OPTINET has been co-financed by the European Regional Development Fund of the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call “Research-Create-Innovate” (project code: Τ1ΕΔΚ-01907).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are strictly used within the project but could be available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ntakolia, C.; Iakovidis, D.K. A Route Planning Framework for Smart Wearable Assistive Navigation Systems. SN Appl. Sci. 2021, 3, 104. [Google Scholar] [CrossRef]
Vasilijević, A.; Nađ, Đ.; Mandić, F.; Mišković, N.; Vukić, Z. Coordinated Navigation of Surface and Underwater Marine Robotic Vehicles for Ocean Sampling and Environmental Monitoring. IEEE/ASME Transactions on Mechatronics 2017, 22, 1174–1184. [Google Scholar] [CrossRef]
Yang, T.H.; Hsiung, S.H.; Kuo, C.H.; Tsai, Y.D.; Peng, K.C.; Peng, K.C.; Hsieh, Y.C.; Shen, Z.J.; Feng, J.; Kuo, C. Development of Unmanned Surface Vehicle for Water Quality Monitoring and Measurement.; 2018; pp. 566–569.
Wilde, G.A.; Murphy, R.R. User Interface for Unmanned Surface Vehicles Used to Rescue Drowning Victims. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR); August 2018; pp. 1–8. [Google Scholar]
Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The Review Unmanned Surface Vehicle Path Planning: Based on Multi-Modality Constraint. Ocean Engineering 2020, 200, 107043. [Google Scholar] [CrossRef]
Ntakolia, C.; Caceres, H.; Coletsos, J. A Dynamic Integer Programming Approach for Free Flight Air Traffic Management (ATM) Scenario with 4D-Trajectories and Energy Efficiency Aspects. Optim Lett 2020, 14, 1659–1680. [Google Scholar] [CrossRef]
Aggarwal, S.; Kumar, N. Path Planning Techniques for Unmanned Aerial Vehicles: A Review, Solutions, and Challenges. Computer Communications 2020, 149, 270–299. [Google Scholar] [CrossRef]
Ntakolia, C.; Lyridis, D.V. A n − D Ant Colony Optimization with Fuzzy Logic for Air Traffic Flow Management. Oper Res Int J 2022. [Google Scholar] [CrossRef]
Ntakolia, C.; Kalimeri, A.; Coletsos, J. A Two-Level Hierarchical Framework for Air Traffic Flow Management. International Journal of Decision Support Systems 2021, 4, 271–292. [Google Scholar] [CrossRef]
Ntakolia, C.; Dimas, G.; Iakovidis, D.K. User-Centered System Design for Assisted Navigation of Visually Impaired Individuals in Outdoor Cultural Environments. Univ Access Inf Soc 2020. [Google Scholar] [CrossRef]
Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A Constrained A* Approach towards Optimal Path Planning for an Unmanned Surface Vehicle in a Maritime Environment Containing Dynamic Obstacles and Ocean Currents. Ocean Engineering 2018, 169, 187–201. [Google Scholar] [CrossRef]
Song, R.; Liu, Y.; Bucknall, R. Smoothed A* Algorithm for Practical Unmanned Surface Vehicle Path Planning. Applied Ocean Research 2019, 83, 9–20. [Google Scholar] [CrossRef]
Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D. Optimal Path Planning of an Unmanned Surface Vehicle in a Real- Time Marine Environment Using a Dijkstra Algorithm. In Marine Navigation; CRC Press, 2017 ISBN 978-1-315-09913-2.
Mirjalili, S.; Song Dong, J.; Lewis, A. Ant Colony Optimizer: Theory, Literature Review, and Application in AUV Path Planning. In Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Mirjalili, S., Song Dong, J., Lewis, A., Eds.; Studies in Computational Intelligence; Springer International Publishing: Cham, 2020; ISBN 978-3-030-12127-3. [Google Scholar]
Wang, H.; Guo, F.; Yao, H.; He, S.; Xu, X. Collision Avoidance Planning Method of USV Based on Improved Ant Colony Optimization Algorithm. IEEE Access 2019, 7, 52964–52975. [Google Scholar] [CrossRef]
Liu, X.; Li, Y.; Zhang, J.; Zheng, J.; Yang, C. Self-Adaptive Dynamic Obstacle Avoidance and Path Planning for USV Under Complex Maritime Environment. IEEE Access 2019, 7, 114945–114954. [Google Scholar] [CrossRef]
Chen, Y.; Bai, G.; Zhan, Y.; Hu, X.; Liu, J. Path Planning and Obstacle Avoiding of the USV Based on Improved ACO-APF Hybrid Algorithm With Adaptive Early-Warning. IEEE Access 2021, 9, 40728–40742. [Google Scholar] [CrossRef]
Xia, G.; Han, Z.; Zhao, B.; Liu, C.; Wang, X. Global Path Planning for Unmanned Surface Vehicle Based on Improved Quantum Ant Colony Algorithm. Mathematical Problems in Engineering 2019, 2019, e2902170. [Google Scholar] [CrossRef]
Zhongjing, L.; Junjie, F.; Zhaohui, L.; Jiahui, Y. Bayesian Network Based Ant Colony Optimization Algorithm for USV Path Planning in a Dynamic Environment. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS); August 2020; pp. 547–551. [Google Scholar]
Wang, H.; Zhang, J.; Dong, J. Application of Ant Colony and Immune Combined Optimization Algorithm in Path Planning of Unmanned Craft. AIP Advances 2022, 12, 025313. [Google Scholar] [CrossRef]
Zhang, J.; Zhang, F.; Liu, Z.; Li, Y. Efficient Path Planning Method of USV for Intelligent Target Search. J geovis spat anal 2019, 3, 13. [Google Scholar] [CrossRef]
Wang, N.; Jin, X.; Er, M.J. A Multilayer Path Planner for a USV under Complex Marine Environments. Ocean Engineering 2019, 184, 1–10. [Google Scholar] [CrossRef]
Niu, H.; Lu, Y.; Savvaris, A.; Tsourdos, A. An Energy-Efficient Path Planning Algorithm for Unmanned Surface Vehicles. Ocean Engineering 2018, 161, 308–321. [Google Scholar] [CrossRef]
Ding, F.; Zhang, Z.; Fu, M.; Wang, Y.; Wang, C. Energy-Efficient Path Planning and Control Approach of USV Based on Particle Swarm Optimization. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston; October 2018; pp. 1–6. [Google Scholar]
Folio, D.; Ferreira, A. Two-Dimensional Robust Magnetic Resonance Navigation of a Ferromagnetic Microrobot Using Pareto Optimality. IEEE Transactions on Robotics 2017, 33, 583–593. [Google Scholar] [CrossRef]
Ntakolia, C.; Lyridis, D.V. A Swarm Intelligence Graph-Based Pathfinding Algorithm Based on Fuzzy Logic (SIGPAF): A Case Study on Unmanned Surface Vehicle Multi-Objective Path Planning. Journal of Marine Science and Engineering 2021, 9, 1243. [Google Scholar] [CrossRef]
Yu, K.; Liang, X.; Li, M.; Chen, Z.; Yao, Y.; Li, X.; Zhao, Z.; Teng, Y. USV Path Planning Method with Velocity Variation and Global Optimisation Based on AIS Service Platform. Ocean Engineering 2021, 236, 109560. [Google Scholar] [CrossRef]
Ma, Y.; Hu, M.; Yan, X. Multi-Objective Path Planning for Unmanned Surface Vehicle with Currents Effects. ISA Transactions 2018, 75, 137–156. [Google Scholar] [CrossRef] [PubMed]
Lyridis, D.V. An Improved Ant Colony Optimization Algorithm for Unmanned Surface Vehicle Local Path Planning with Multi-Modality Constraints. Ocean Engineering 2021, 241, 109890. [Google Scholar] [CrossRef]
Ntakolia, C.; Iakovidis, D.K. A Swarm Intelligence Graph-Based Pathfinding Algorithm (SIGPA) for Multi-Objective Route Planning. Computers & Operations Research 2021, 133, 105358. [Google Scholar] [CrossRef]
Chen, Z.; Zhang, Y.; Zhang, Y.; Nie, Y.; Tang, J.; Zhu, S. A Hybrid Path Planning Algorithm for Unmanned Surface Vehicles in Complex Environment With Dynamic Obstacles. IEEE Access 2019, 7, 126439–126449. [Google Scholar] [CrossRef]
Dorigo, M.; Blum, C. Ant Colony Optimization Theory: A Survey. Theoretical Computer Science 2005, 344, 243–278. [Google Scholar] [CrossRef]
Ntakolia, C.; Lyridis, D.V. A Comparative Study on Ant Colony Optimization Algorithm Approaches for Solving Multi-Objective Path Planning Problems in Case of Unmanned Surface Vehicles. Ocean Engineering 2022, 255, 111418. [Google Scholar] [CrossRef]
Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing-A Computational Approach to Learning and Machine Intelligence [Book Review]. IEEE Transactions on Automatic Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
Ntakolia, C.; Kokkotis, C.; Moustakidis, S.; Tsaopoulos, D. A Machine Learning Pipeline for Predicting Joint Space Narrowing in Knee Osteoarthritis Patients. In Proceedings of the 2020 IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE); October 2020; pp. 934–941. [Google Scholar]
Murtagh, F.; Legendre, P. Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion? J Classif 2014, 31, 274–295. [Google Scholar] [CrossRef]
Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An Efficient Data Clustering Method for Very Large Databases. SIGMOD Rec. 1996, 25, 103–114. [Google Scholar] [CrossRef]
Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A New Data Clustering Algorithm and Its Applications. 1997, 42.
Ntakolia, C.; Priftis, D.; Charakopoulou-Travlou, M.; Rannou, I.; Magklara, K.; Giannopoulou, I.; Kotsis, K.; Serdari, A.; Tsalamanios, E.; Grigoriadou, A.; et al. An Explainable Machine Learning Approach for COVID-19’s Impact on Mood States of Children and Adolescents during the First Lockdown in Greece. Healthcare 2022, 10, 149. [Google Scholar] [CrossRef]

Figure 1. Concept of this study and methodological steps.

Figure 2. Membership functions of (a) path distance; (b) path turns; (c) fuel consumption; and (d) path optimality.

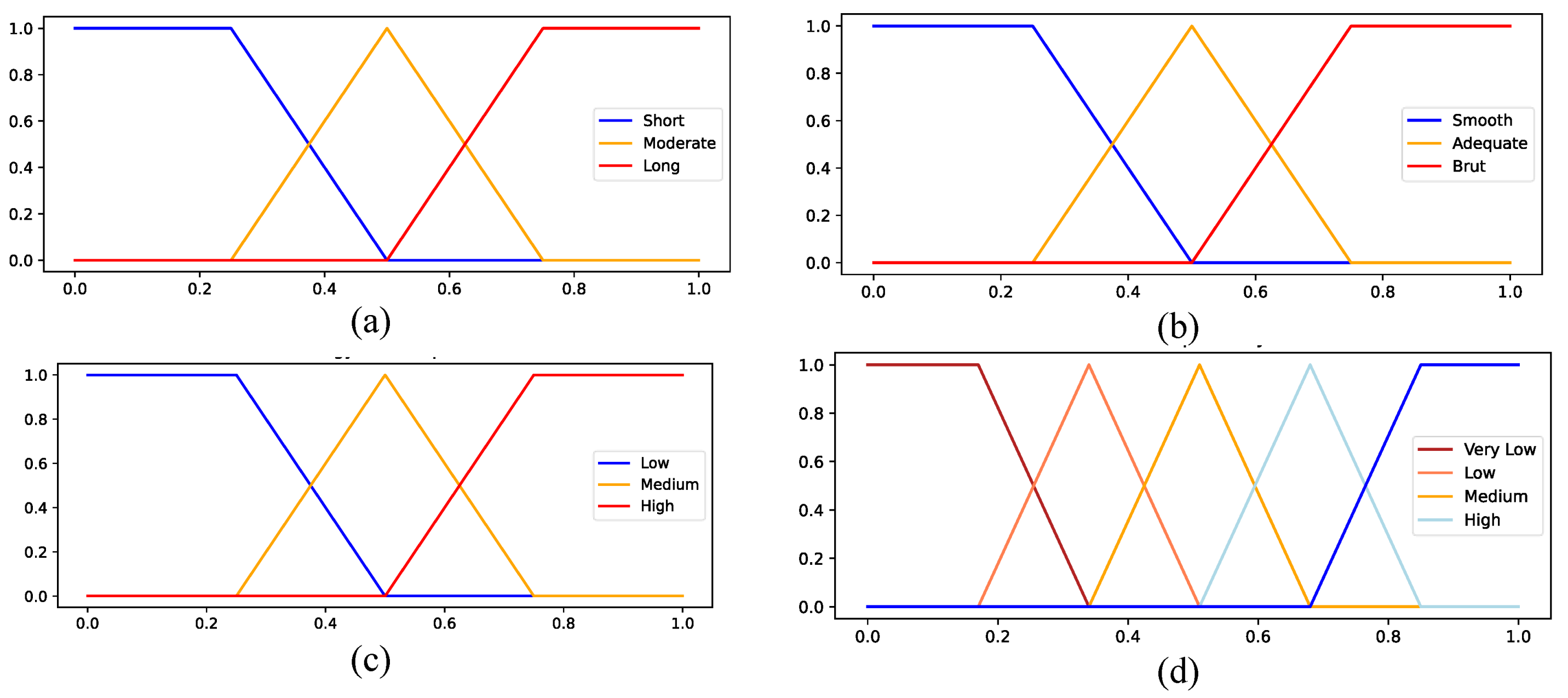
Figure 3. Clustering evaluation methodology.

Figure 4. Clustering results of case study 1 based on distance and current information.

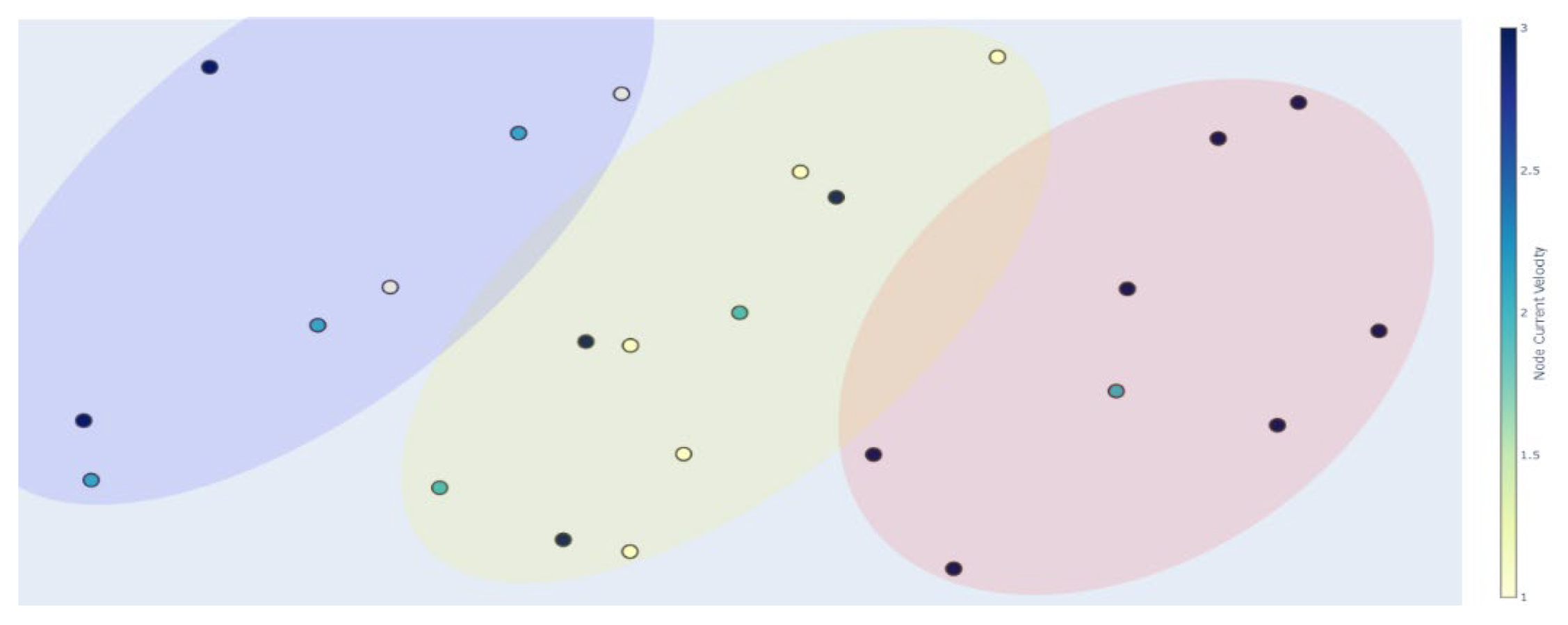
Figure 5. Clustering results of case study 2 with: Mini Batch K-Means and Ward Clustering (a); and Birch (b).

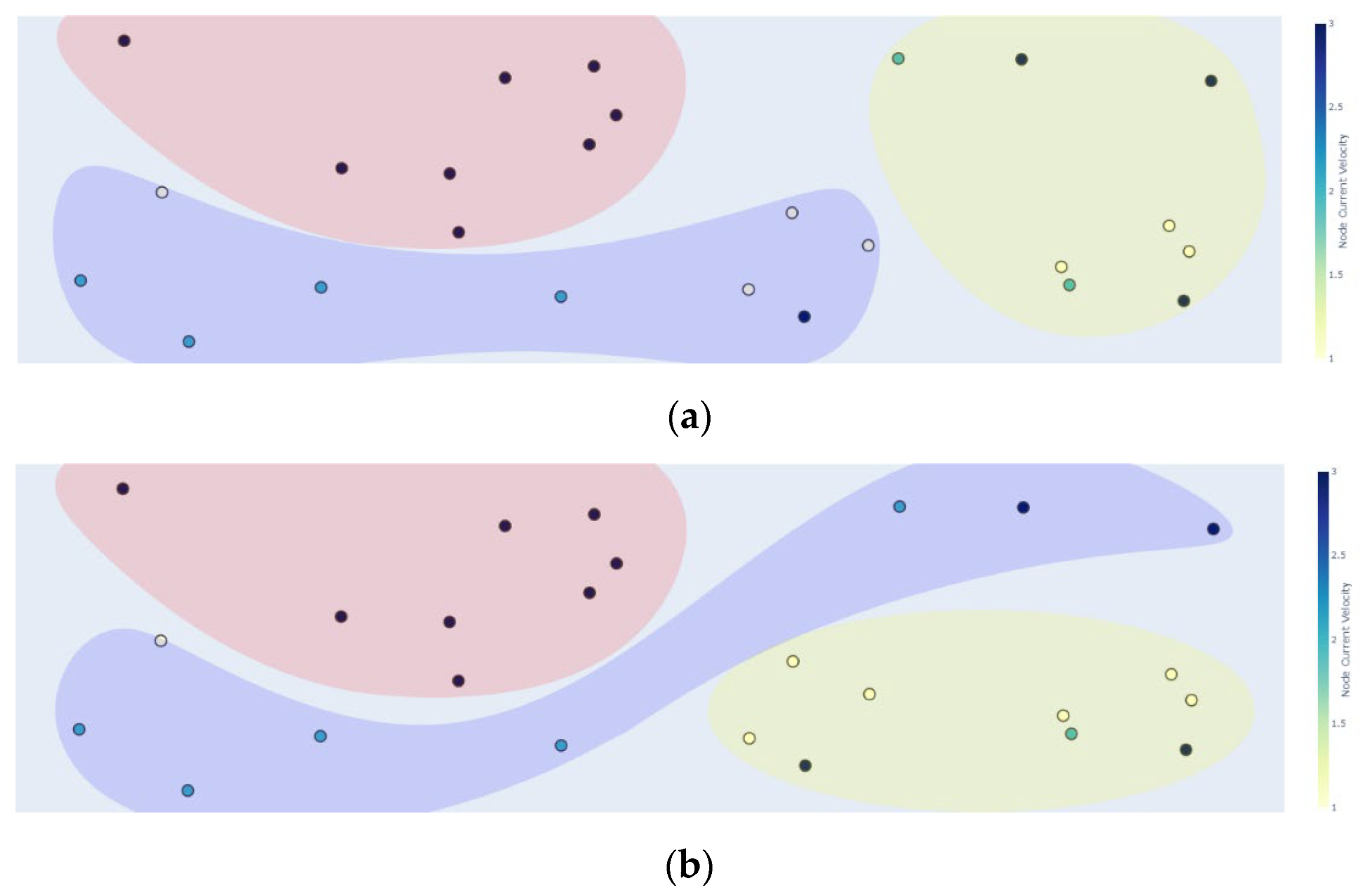
Table 1. Fuzzy rules.

Path length	Path deviations	Energy consumption	Path optimality
Short	Smooth	Low or Medium	High
Short	Moderate	Low	High
Moderate	Smooth	Low	High
Short	Moderate	Medium	Medium
Moderate	Smooth	Medium	Medium
Moderate	Moderate	Low or Medium	Medium
Moderate or Long	Moderate or Brut	Medium or High	Low

Table 2. Evaluation of clustering methods for CS2. The best evaluation score is shown in bold.

Clustering Algorithm	Silhouette Coefficient	Calinski-Harabasz Index	Davies-Bouldin Index	Cumulative Evaluation Score
Mini Batch K-Means	0.82	1301.34	0.36	3
Ward	0.82	1301.34	0.36	3
Birch	0.77	1205.45	0.42	0

Table 3. Path planning mean results after 20 runs of the case studies for each ACO-FIS approach for the swarm of USVs. The number of turns have been rounded. Best solutions are denoted with bold.

Case Study	ACO-FIS	Swarm USVs	Distance (km)	Number of Turns	Consumption (kg)	Optimality	Computing time (ms)
CS1	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	17.61 18.55 18.43 17.63 18.62 18.43	8 9 5 8 8 5	3.75 3.87 3.73 3.78 3.89 3.72	0.82 0.80	3.46 3.39
CS2	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	17.22 15.76 19.04 17.37 16.05 19.18	7 6 5 7 6 6	3.58 3.32 3.64 3.65 3.38 3.79	0.75 0.66	4.12 4.01

Table 4. Evaluation results of mean relative percentage deviation (RPD) and mean relative deviation index (RDI) for distance. Best solutions are denoted with bold.

Case Study	ACO-FIS	Swarm USVs	RPD	$\bar{R P D}$	RDI	$\bar{R D I}$
CS1	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	0,00% 5,34% 4,66% 0,11% 5,74% 4,66%	3.33% 3.50%	0,00% 93,07% 81,19% 1,98% 100,00% 81,19%	58,09% 61,06%
CS2	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	9,26% 0,00% 20,81% 10,22% 1,84% 21,70%	10.03% 11.25%	0,426900585 0 0,959064327 0,470760234 0,084795322 1	46,20% 51,85%

Table 5. Evaluation results of mean relative percentage deviation (RPD) and mean relative deviation index (RDI) for brut turns. Best solutions are denoted with bold.

Case Study	ACO-FIS	Swarm USVs	RPD	$\bar{R P D}$	RDI	$\bar{R D I}$
CS1	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	60,00% 80,00% 0,00% 60,00% 60,00% 0,00%	46,67% 40,00%	75,00% 100,00% 0,00% 75,00% 75,00% 0,00%	58,33% 50,00%
CS2	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	40,00% 20,00% 0,00% 40,00% 20,00% 20,00%	20,00% 26,67%	100,00% 50,00% 0,00% 100,00% 50,00% 50,00%	50,00% 66,67%

Table 6. Evaluation results of mean relative percentage deviation (RPD) and mean relative deviation index (RDI) for consumption. Best solutions are denoted with bold.

Case Study	ACO-FIS	Swarm USVs	RPD	$\bar{R P D}$	RDI	$\bar{R D I}$
CS1	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	0,81% 4,03% 0,27% 1,61% 4,57% 0,00%	1,70% 2,06%	17,65% 88,24% 5,88% 35,29% 100,00% 0,00%	37,25% 45,10%
CS2	ACO-Mamdani ACO-TSK	USV1 (red) USV2 (yellow) USV3 (blue) USV1 (red) USV2 (yellow) USV3 (blue)	7,83% 0,00% 9,64% 9,94% 1,81% 14,16%	5,82% 8,63%	55,32% 0,00% 68,09% 70,21% 12,77% 100,00%	41,13% 60,99%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Path Planning in Case of Swarm Unmanned Surface Vehicles for Visiting Multiple Targets

Abstract

1. Introduction

2. Materials and Methods

2.1. Objective terms of the USV path planning problem

2.2. Ant Colony Optimization Algorithm with Fuzzy Logic

2.2.1. FIS1 1: Mamdani Fuzzy Inference System (ACO-M)

2.2.2. FIS 2: Takagi–Sugeno–Kang Fuzzy Inference System (ACO-TSK)

2.3. Swarm approach of USV path planning problem

3. Evaluation Methodology

4. Results and Discussion

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe