Prerpints.org logo
Preprint
Article

Machine Learning to Predict the Adsorption Capacity for Microplastics

Altmetrics

Downloads

196

Views

121

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 February 2023

Posted:

17 February 2023

You are already at the latest version

Alerts
Abstract
Nowadays, there is extensive production and use of plastic materials for different industrial activities. These plastics, either from their primary production sources or through degradation processes of the plastics themselves, can contaminate the ecosystem with micro and nanoplastics. Once in the aquatic environment, these microplastics can be the basis for the adsorption of chemical pollutants, favoring that these chemical pollutants disperse more quickly in the environment and can affect living beings. Due to the lack of information on adsorption, three machine learning models (random forest, support vector machine, and artificial neural network) to predict different microplastic/water partition coefficients (log Kd) were developed using two different approximations (based on the number of input variables). The best-selected machine learning models present, in general, correlation coefficients upper than 0.92 in the query phase, which indicate that these type of models could be used for a rapid estimation of the absorption of organic contaminants on microplastics.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

Since the appearance of plastics, their production has grown exponentially in the last decades, and,due to their versatility, they are used in different fields, such as packaging, building, or electronic industries, among others [1]. Plastics, which by fragmentation become microplastics (MPs) and these become nanoplastics (NPs), which make the presence of micro- and nano-plastics (MNPs) in the water sources, or in the agroecosystems, of our planet a worldwide concern [2,3,4,5]. In this sense, and as reported by Matthews et al. (2021), microplastics are plastic fragments less than 5 mm and nanoplastics, the most common size accepted, is inside the range of 1 nm and 1000 nm [6].
The cycle from the production of plastics to their entry into the environment includes different stages, as reported by Woods et al. (2021) [7]: production for textile manufacturing and use, tires use or packaging production, among others [8]. Besides, there are different sources of pollution by MPs; due to this, they can be differentiated between primary and secondary sources [9]. The primary MPs are commonly generated during the manufacturing of different products, or during the fabrication of microbeads or microfibers; the secondary ones are formed from larger plastic litters due to degradation processes by external factors (chemical, physical or biological) [9].
Once released into the aquatic environment, it has been reported that microplastics, can play the role of vectors for persistent organic pollutants (POPs) [10,11]. Chemical contaminants can capture on the surface of microplastics and nanoplastics due to their surface charge, among other characteristics [12].
Currently, micro- and nano-plastics can be found in terrestrial and aquatic environments, being able to affect a large number of organisms [6] and can be considered, as reported by Hu et al. (2022) and Katsumiti et al. (2021) [13,14], Trojan horse.
The adsorption capacity between microplastics and water can be expressed as an equilibrium partitioning coefficient (Kd) [15]. According to Li et al. (2020) [15], due to absorption data are currently scarce, it would be very useful to have a tool that would be able to accurately predict the values of Kd in different conditions. In this sense, the use of Quantitative structure–property relationship (QSPR) supported by machine learning models could be an interesting combination.
Machine learning (ML) is one of the subsets that include artificial intelligence (AI) and consists of the attempt to train machines that are capable of imitating the ability of the human being to learn based on knowledge and experience [16]. Most existing machine-learning methods encompass supervised and unsupervised learning [17]. In the supervised learning method, each training case has input and output labels, and the machine attempts to predict the outputs using the provided inputs [17]. The three supervised learning models used in this research will be briefly presented below.

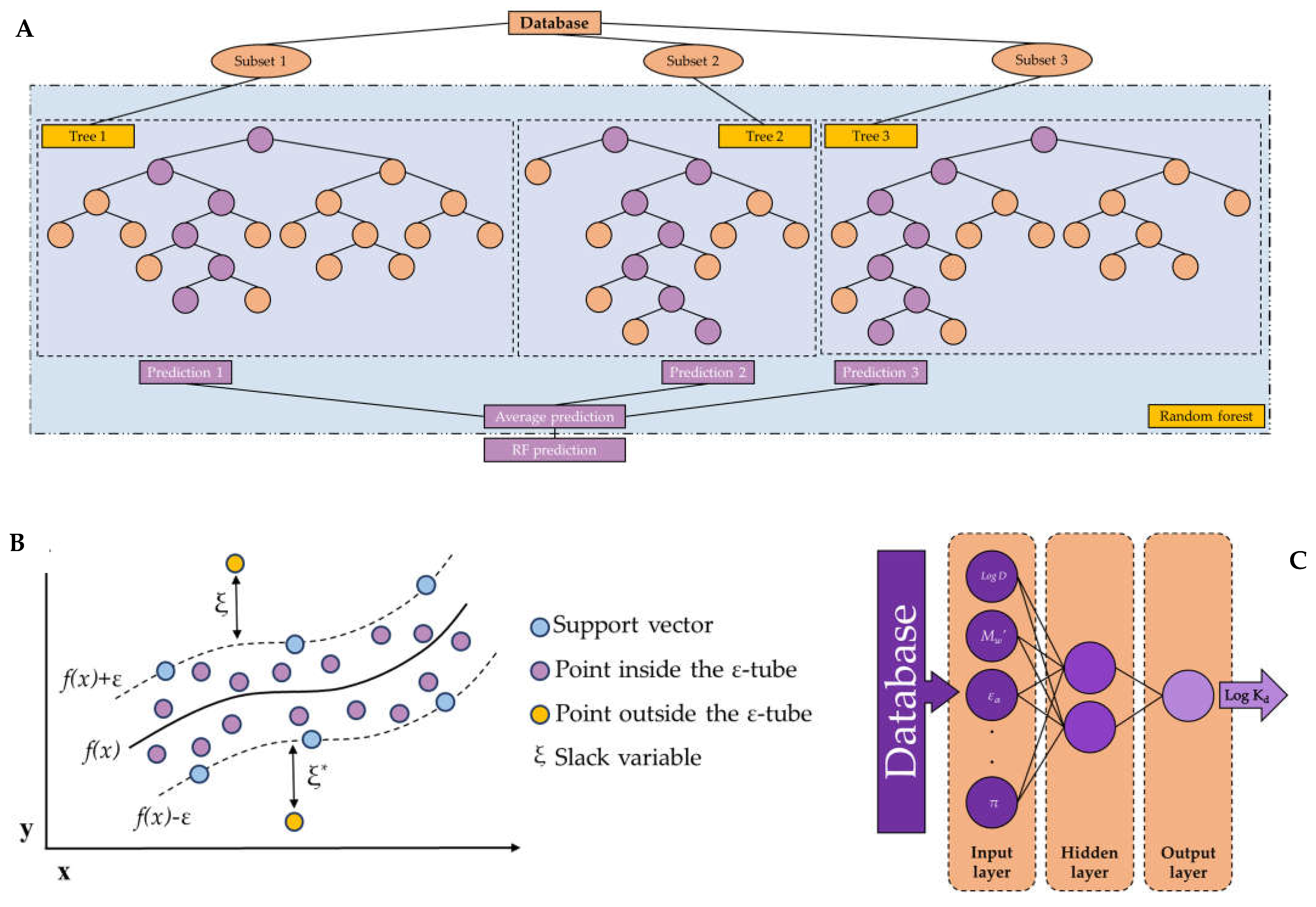
1.1. Random forest

The first of the selected ML models is a random forest (RF) model, which is composed of decision trees that can be used for regression and regression purposes [18]. These decision trees can be considered as one of the main methods for solving real problems [19]. Random forests are an ensemble machine learning method that has been proposed by Breiman (2001) [20], which can get over the instability and overfitting problems when only a single decision tree is used [21]. When working on regression and classification mode, the random forest generates more than one decision tree using bootstrap samples of the original training data to develop and train each decision tree [22]. Therefore, the random forest involves developing different decision trees using random subsets of the original training data [21].
Each decision tree starts in a called root node, and each node is divided into two new subnodes; each of these divisions is carried out to minimize the mean square error [23]. The predictions of each tree are used for the final prediction; that is, when working in regression mode (quantitative data), these are averaged, and when working in classification mode (qualitative data) a voting process is carried out [18,19,24]. RF is considered a robust method that can provide good results compared to different regression algorithms [25].
Random forest models can be used in different research fields, such as:
  • cloud computing to develop DDoS-attack-detection method [18],
  • chemistry to determine molecular electronic transitions [23], or in
  • farming to predict regional and local-scale wheat yield [26], among others.

1.2. Support vector machine

The second of the ML models developed in this research is the support vector machine (SVM). According to Geppert et al. (2010) [27], this method became popular during the 90s of the last century based on the work carried out by Cortes & Vapnik (1995) [28] and, as reported by Rodríguez-Pérez et al. (2017) [29] have become more and more popular. A support vector machine is based on statistical learning theory [30] and can be used for regression and classification purposes [30,31]. According to [31], the support vector machine can work with linear and nonlinear problems.
Working in classification mode, the support vector machine's main objective is to find a hyperplane in an N-dimensional space that classifies the data points [32]. As Sareminia (2022) reports [32], for two classes, different hyperplanes could be chosen, but the support vector machine aim is to locate the plane that has the largest margin, that is, the maximum gap between the data points of both classes. Whether the problem is linear or nonlinear, the support vector machine separates the data into two classes by mapping the information into spaces with dimensions greater than two [33]. On the other hand, as Rodríguez-Pérez et al. (2017) report [29], SVM can be used in the regression model (support vector regression, SVR) to predict numerical property values [34,35]. In this kind of SVM model, alternatively, to determine a hyperplane for class label prediction, a different function is derived according to the training data for predicting numerical values [29].
Support vector machines can be applied in different fields, such as:
  • Chemistry to identify polar liquids [36],
  • energy storage to self-discharge prediction in batteries of lithium-ion [37], or in
  • medicine to diagnose breast cancer [38], inter alia.

1.3. Artificial neural networks

The last ML models carried out in this research were models based on artificial neural networks (ANN). An artificial neural network is a well-documented/known artificial intelligence model [39] that can be defined as a mathematical model which is inspired in the behavior of biological neurons [19,39].
As reported by Paturi et al. (2022) [40], McCulloch & Pitts (1943) [41] were the first that can explain the logical relationship that exists between neural events of the nervous system. This imitation of biological neurons' behavior can be learned through a process of backpropagation [42].
ANN is a powerful tool to find relationships between data, in this case, input and output data [39], and can be used to solve complex problems in optimization, clustering, or prediction, among others [43]. ANN is formed by units (neurons) that are organized into different layers Khan et al. (2019). A neuron carries out two functions: collect the inputs and produce an output [43].
An ANN architecture is usually made up of three elements, a first layer (called the input layer), a second layer (known as the hidden layer), and a final layer (called the output layer) [44]. One of the existing neural network types, the multi-layer perceptron network (MLP), has one or more hidden layers [40,44], and, in principle, and according to Saikia et al. (2020) [45], it is possible to approximate any continuous function with only one hidden layer [46]. According to [45], an artificial neural network is a popular ML procedure due to its capacity to complex nonlinear function modelling. The number of neurons in the intermediate layer can be determined by trial and error procedure [44,47].
To find the relationship between the input and the output data it is necessary to subject the artificial neural network to a training process using the database containing both input and output data [39]. Following Niazkar & Niazkar (2020) [39], the first layer presents neurons associated with the input vector, hidden layer connects the input neurons and the output neuron/neurons and turns the input data into the corresponding output data. Finally, the output layer presents the neuron/neurons associated with the output vector.
In each processing neuron, the input is multiplied by the importance of the connection, also called weight, and the result and bias are added to be treated by the activation function and provide an output in the neuron [43]. There are different activation functions, such as sigmoid or Gaussian, among others [44].
Finally, artificial neural networks can be used in the following ways:
  • Engineering to predict the building construction time and cost [48],
  • water management to model and predict the amount of salt removed by the capacitive deionization method [49], or in
  • biotechnology to optimize the parameters in Ganoderma lucidum residue aerobic composting process [50].
Therefore, this research aimed to develop machine learning models (RF, SVM, and ANN) to predict the adsorption capacity for MPs ((polyethylene -PE-, polypropylene -PP-, polystyrene -PS-) in different waters using different configurations of input variables (n-octanol/water distribution coefficient at special pH condition -log D-, molecular mass -M'w- and six quantum chemical descriptors) obtained from the literature [15]. These computational models will allow a quick adsorption capacity prediction of organic pollutants onto these three types of microplastics in water environments.

2. Materials and Methods

2.1. Experimental data used

The data used for the developing of the different machine learning models were extracted from the work developed by Li et al. (2020) [15]. Li et al. (2020) [15] also used different articles reported in the literature to obtain data. These articles can be consulted in Table 2 of the research paper of Li et al. (2020).
Li et al. (2020) provide in their study and the accompanying supplementary material: i) the n-octanol/water distribution coefficient at special pH condition (log D), ii) the molecular mass (M'w) and iii) six different quantum chemical descriptors, that allow the modelling the microplastic/water partition coefficients (log Kd) for diverse organics between and polyethylene/seawater-freshwater-pure water, polystyrene/seawater and polypropylene/seawater [15]. The quantum chemical descriptors calculated by Li et al. (2020) were: i) molecular volume (V′), ii) the most negative atomic charge (q−), iii) the most positive atomic charge on H atom (qH+), iv) the ratio of average molecular polarizability and molecular volume (π) and the covalent, v) basicity (εβ) and vi) acidity (εα).
In the present research work, two approximations have been carried out. The first is using the same variables that the researchers used to develop their models [15]. On the other hand, due to the authors' data of 8 different input variables, models that included the maximum number of input variables were developed to improve the models developed with the variables selected by the authors. Table 1 shows the variables selected for each selected model.
The database was divided into three data sets. In this sense, the cases used by Li et al. (2020) to develop the models have been used to generate two groups, a training group, to develop de different ML models and another group, the validation group, to select the best model (according to the RMSE value in the validation phase). The query group (the same cases used by Li et al. (2020) as test cases) has been used to check the adjustments provided by the different ML models.

2.2. Models implemented

2.2.1. Random forest models

Random forest models have been successfully used in fields related to this research, for example, to identify and monitor different microplastics in environmental samples [51]. Hufnagl et al. (2019) [51] developed a methodology to discriminate five different polymers (polyethylene, poly(methyl methacrylate), polypropylene, polystyrene, and polyacrylonitrile) and determine their abundance and size distribution. Later, some of the previous authors extended the previous research to develop a model capable of differentiating more than 20 types of polymers [52].
In this research, the RF models (Figure 1-A) were carried out using different parameter combinations. The following parameters were studied: the number of trees (1 to 100 using 99 steps in linear scale), maximum depth (1 to 100 using 99 steps in linear scale-) and prepruning (false or true). All models were developed using the least square criterion.

2.2.2. Support vector machine models

Support vector machine models have also been used successfully in related fields. An example of this is the research carried out by Yan et al. (2022) [56]; the aim was to develop an ensemble machine learning method capable to classify and identify MPs by ATR-FTIR (attenuated total reflection Fourier transform infrared spectroscopy) data. On the other hand, Bifano et al. (2022) [57] developed a method based on a support vector machine to detect polypropylene and polyolefin in water using electrical impedance spectroscopy.
In the research presented in this article, the SVM models (Figure 1-B) were carried out using the LibSVM learner developed by [58,59]. The following parameters combination were studied: the SVM type (ε-SVR or ν-SVR), γ was studied between ≈ 2-20 and 28 using 28 steps in linear or logarithmic scale, and C between ≈ 2-10 and 220 using 30 steps in linear and logarithmic scale (SVM and SVMlog). These values were an extension of the proposed values of Hsu et al. (2016) [60]
In addition to using the database in their real-scale, they were also normalized in the interval [-1,1] (first just normalizing the input variables -SVMn and SVMn log- and then normalizing the input and the output variables -SVMn2 and SVMn2 log-). The normalization was applied to the training input data and later it was applied to the other phases. After the model selection, the output data were de-normalized to allow real-scale comparison between all developed models

2.2.3. Artificial neural network models

Artificial neural network models have been used to categorize microplastic contamination in the soil using infrared spectroscopy [61]. On the other hand, ANN has also been used successfully to determine the sorption capacity of heavy metal ions onto microplastics [62]. In this sense, Guo & Wang (2021) developed an ANN model using data from the literature, and were able to predict the sorption capacity of different heavy metal ions onto microplastics in global environments with correlation coefficients greater than 0.93.
In the research presented in this article, the ANNs (Figure 1-C) have been developed with one single hidden layer. The hidden neurons have been studied in a range between 1 and 2n+1, where n is the input neurons number. The training cycles were studied between 1 and 131072 using 17 steps in linear or logarithmic scale (ANNlin and ANNlog). In addition, decay was studied in mode, true or false. The neural net operator to develop the ANN models scaled the values between -1 and 1 [63].

2.2.4. Statistics used to analyze the models

Different statistical parameters have been used to evaluate the ML models implemented in this research. In this sense, were calculated (for training, validation, and query phase) the correlation coefficient (r), the root mean square error (RMSE), and the mean absolute percentage error (MAPE, expressed in %).
The best model for each ML approach was chosen considering the root mean square error for the validation phase. Once each best ML models were chosen, they were compared using the query data.

2.2.5. Equipment and software used for the development of the models

The ML models developed were implemented in two computers; the first, an Intel® Core™ i9-10900 at 2.80 GHz with 64GB RAM and Windows 10 Pro 21H1, and the second an AMD Ryzen 7 3700X 8-Core at 3.60 GHz with 32 GB RAM and Windows 11 Pro 21H2.
The data used in this research were collected from Li et al. (2020) [15] using Microsoft Excel 2016 from Microsoft Office Professional Plus 2016. The ML models (RF, SVM and ANN) were developed using an Educational and a free version of RapidMiner Studio 9.10.001 and 9.10.011 software. Figures were drawn with Microsoft PowerPoint 2016 from Microsoft Office Professional Plus 2016 and SigmaPlot v. 13.0 from Systat Software, Inc.

3. Results and Discussion

The following sections analyze the results obtained by the different machine learning methods for each of the analyzed assumptions.

3.1. ML models using input variables Type 1

Table 2 shows the adjustments obtained for the selected machine learning models to predict log Kd, developed with the same variable combination used by Li et al. (2020) [15].
Table 2. Adjustments for the different machine learning models developed using the input variables selection Type 1. Random forest (RF), support vector machine (SVM), and artificial neural network (ANN). T, V, and Q are training, validation, and query phases, respectively. Root mean square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (r). The best models (regarding RMSE for the validation phase) are in bold.
Table 2. Adjustments for the different machine learning models developed using the input variables selection Type 1. Random forest (RF), support vector machine (SVM), and artificial neural network (ANN). T, V, and Q are training, validation, and query phases, respectively. Root mean square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (r). The best models (regarding RMSE for the validation phase) are in bold.
T V Z
Model RMSE MAPE r RMSE MAPE r RMSE MAPE r
PE/seawater
RF 0.525 18.67 0.983 0.380 7.48 0.988 0.523 13.38 0.979
SVM 0.287 2.83 0.993 0.248 4.61 0.993 0.357 13.24 0.990
ANN 0.257 3.13 0.994 0.236 4.42 0.994 0.561 23.33 0.979
PE/freshwater
RF 0.549 8.08 0.973 0.744 13.67 0.944 0.565 7.23 0.963
SVM 0.536 8.93 0.976 0.770 11.14 0.945 0.475 10.46 0.978
ANN 0.489 6.79 0.978 0.865 13.20 0.932 0.464 8.59 0.974
PE/pure water - 1
RF 0.471 11.28 0.968 0.176 3.31 0.992 0.531 9.48 0.929
SVM 0.356 5.93 0.974 0.132 2.06 0.993 0.411 6.90 0.958
ANN 0.309 4.92 0.981 0.225 3.92 0.982 0.729 12.21 0.937
PE/pure water - 2
RF 0.410 7.79 0.967 0.132 2.25 0.993 0.526 8.59 0.936
SVM 0.466 9.51 0.955 0.205 3.47 0.983 0.439 8.10 0.953
ANN 0.409 6.45 0.965 0.231 4.23 0.981 0.431 7.72 0.955
PP/seawater
RF 0.255 9.95 0.990 0.199 6.69 0.994 0.298 4.97 0.968
SVM 0.260 5.12 0.989 0.244 6.92 0.988 0.779 7.32 0.817
ANN 0.160 3.19 0.996 0.270 8.94 0.988 0.307 4.21 0.956
PS/seawater
RF 0.221 5.28 0.996 0.794 14.61 0.883 1.003 15.11 0.820
SVM 0.554 23.10 0.969 0.524 21.69 0.965 0.436 12.85 0.988
ANN 0.337 9.21 0.988 0.643 15.69 0.972 0.773 15.07 0.956
The first models (PE/seawater) correspond with ML models to predict the adsorption capacity for polyethylene in seawater. In this case, the three best selected models (each according to their RMSE value for the validation phase) can be seen. The model with the best adjustments is the artificial neural network (ANNlog) model (0.236), followed by the support vector machine (SVMn2 log) model (0.248), and finally, the random forest model (0.380). As can be seen, the three models present very high correlation coefficients for the validation phase, equal to or greater than 0.988; in addition, the mean absolute percentage error remains low, between 4.42% and 7.48%.
The good adjustments shown in the validation phase can also be observed in the training phase, where the values of RMSE remain similar to those of the validation phase, except for the random forest model, where the RMSE value grows to 0.525 (MAPE of 18.67%. It can be seen how, for the query phase, the model that provided the best result in the validation and training phases, the ANN model, presents the worst results in terms of RMSE and MAPE (0.561 and 23.33%, respectively) despite that maintaining a high coefficient of correlation (0.979). The other two models, the support vector machine and the random forest model, present slightly higher errors, in terms of RMSE, than those presented in the validation phase (0.357 and 0.523, respectively).
Given these results (Table 2), it can be said that the three models show a good performance, although, for the query phase, the errors increase slightly. Despite this, the errors, in terms of RMSE, remain below the test error reported by Li et al. (2020) (0.752) for the model developed with these three input variables (log D, εα and εβ).
The second group of models (PE/freshwater) corresponds to machine learning models that predict the adsorption capacity for polyethylene in freshwater. In this case, it can be seen, for the validation phase, that the errors made in terms of RMSE are closer to each other, compared to the model´s behavior in the previous block. In this case, it can be seen that the worst model corresponds to the artificial neural network (ANNlin) model that presents an RMSE of 0.865, followed by the support vector machine (SVMn log) model with a value of 0.770, with the best model being the random forest, which has a root mean square error of 0.744. In this case, it can be seen that the mean absolute percentage errors exceed those obtained by the ML models of the first block, varying between 11.14% and 13.67%.
For the training phase, it can be seen that the validation phase adjustments are improved in a significant way, presenting RMSE values between 0.489 and 0.549. For the query phase, it can be seen that the root mean square error remain at acceptable levels, corresponding to mean absolute percentage errors between 7.23% y 10.46%. The best model for the validation phase (RF with RMSE of 0.744) presents the worst results for the query phase (RMSE of 0.565) and vice versa; the best model of the query phase (ANN with RMSE of 0.464) is the worst model in the validation phase (RMSE of 0.865).
Despite these behaviors, the three selected models have suitable adjustments for all phases (Table 2). If these models are compared with the model developed by Li et al. (2020), it can be seen that all of them improve the adjustments in terms of the RMSE value in the test phase (0.661 vs. 0.464, 0.475, and 0.565) for the model developed with this input variable (log D).
The following two groups (PE/pure water - 1 and PE/pure water - 2) correspond to the machine learning models developed to determine the adsorption capacity for polyethylene in pure water. In this case, two blocks have been developed because Li et al. (2020) present two different approaches, one using two input variables (PE/pure water - 1 with log D and M'w) and the other one using only one input variable (PE/pure water – 2 with log D).
In our research, for the model development with two input variables (PE/pure water - 1), the case of 17α-ethinyl estradiol was not considered because the authors did not report the experimental log Kd value, so this model lacks this case. As expected, the models offer different results depending on the input variables. When two input variables are used, the model that presents the best results for the validation phase is the support vector machine (SVMn log) model, while when only one input variable is used, the best model is the random forest. It can be seen that the use of two input variables improves the adjustments in the training and validation phases (except for the RF model). For the query phase, the adjustments remain practically unchanged, except for the case of the ANN (ANNlin) model where the error, in terms of RMSE, drops from 0.729 to 0.431. As can be seen, the models developed with two input variables present low mean absolute percentage errors between 2.06% and 3.92% for the validation phase. This behavior worsens slightly for the training phase, passing to 4.92% and 5.93% for the ANN and SVM models, respectively, and 11.28% for the RF model. On the other hand, in the query phase, the MAPE values are between 6.90% and 12.21%. Despite the increase in both the RMSE and the MAPE values, these models developed with two variables seem to behave adequately to predict log Kd.
The models developed to predict the adsorption capacity for polyethylene in pure water (PE/pure water - 2) present, in general, slightly lower adjustments than those obtained by PE/pure water - 1). In this case, the best model, considering the value of the root mean square error in the validation phase, is the random forest model, which presents an RMSE of 0.132. This model presents, in the query phase, an increase in its RMSE value (0.526). The other two models, the SVM (SVMn2 log) model and the ANN (ANNlin) model present an RMSE value of 0.439 and 0.431 for this phase, slightly improving the results of the RF model for this phase.
According to these results (Table 2), it can be said that the SVM and ANN models for PE/pure water - 2 show good performance in terms of RMSE, and improve the adjustment of RMSE value for the test phase (0.471) provided by the model developed by Li et al. (2020) using only one input variable (log D).
Before continuing, it is necessary to emphasize that all the machine learning models developed to predict the adsorption capacity for PE in the different water samples present, in terms of mean absolute percentage error for the query phase, adequate values, generally, below 10%. In other cases, the value is slightly higher (SVM for PE/freshwater and ANN for PE/pure water - 1), and in others, the difference is more significant, for example for the models intended to predict log Kd in seawater, which present errors between 13.24% and 23.33%.
The following models (PP/seawater) correspond to the models developed to predict the adsorption capacity of polypropylene in seawater. Based on the results provided in the validation phase, it can be said that the best model corresponds to the random forest model (0.199), followed by the SVM (SVMlog) model with an RMSE of 0.244 and, finally, the artificial neural network (ANNlin) model (0.270). The other statistics parameters of the validation phase show favorable behavior with MAPE values below 9% and with correlation coefficients above 0.980. For the training phase, the adjustments are similar to the validation phase, although an increase in the MAPE value of the random forest model is observed; even so, it remains below 10%.
For the query phase, it can be seen an inconsistent behavior. Thus, for the RF model and the ANN model is observed that the statistics remain close to the values of the training and the validation phase, while the SVM model suffers an increase in terms of RMSE that makes this statistic parameter reach a value of 0.779, lowering its correlation coefficient to 0.817.
Given these results (Table 2), it can be said that the RF and ANN models can perform prediction tasks correctly. These two models present lower RMSE values (0.298 and 0.307) than the model proposed by Li et al. (2020) in the test phase (0.369), which was developed with two input variables (log D and εβ). The SVM model presents high generalization errors, which imply that it should not be used for prediction tasks. It should be noted that this SVM model, which is the one with the lowest error for the validation phase among all the SVM models developed, is the one with the highest error for the query phase. Other SVM models with close RMSE values in the validation phase (0.255 and 0.262) subsequently showed a better result in the query phase (0.287 and 0.266, respectively).
Finally, the last group of models (PS/seawater) developed corresponds to the machine learning models aimed to predict the adsorption capacity for polystyrene in seawater. Based on the results shown in Table 2, and taking into account the value of RMSE for the validation phase, it can be stated that the model that presents the best behavior in this phase is the support vector machine (SVMn2 log) model (0.524), followed by the artificial neural (ANNlin) network (0.643) and the random forest model (0.794). Based on the results presented by the mean absolute percentage error, it can be affirmed that these models destined to predict the adsorption for PS in seawater are the models that present the worst adjustments for the validation phase, varying between 14.61% and 21.69%. Despite this, the correlation coefficients remain high, with values greater than 0.960, except for the random forest model, whose correlation coefficient falls to 0.883. For the query phase, the values in terms of RMSE remain close, except for the random forest model, keeping the MAPE values above 15.1%.
Taking into account the results shown in Table 2, it can be concluded that the models to predict the adsorption capacity for PS in seawater do not present, in general, good results, except for the SVM model, which improves the RMSE value for the test phase (0.714) of the model developed by Li et al. (2020) with two input variables (log D and π).
Taking into account the results obtained by the machine learning models that have used the same variables as Li et al. (2020), it can be said that, in general, the ML models improve the results obtained by Li et al. (2020). However, these types of ML models often need a large number of experimental cases and input variables to correlate the desired variable. Therefore, in this research, in addition to developing ML models with the variables used by Li et al. (2020), other ML models have been developed with more input variables. This is possible because Li et al. (2020) report eight different input variables; therefore, the results obtained by the models with the input variables selection Type 2 are shown below (Table 3).

3.2. ML models using input variables Type 2

Table 3 shows the adjustments obtained for the machine learning models developed with the input variables combination Type 2 using all the available input variables (except for the cases in which the variable qH+ is not possible).
The first models (PE/seawater) correspond with ML models to predict the adsorption for polyethylene in seawater. Unlike the Type 1 models for PE/seawater where three input variables, log D, εα and εβ were used, in this new PE/seawater model, seven input variables were used (Log D,M'w, εα, εβ, q-, V', π). It can be seen (Table 3), based on the RMSE value for the validation phase, that the best-developed machine learning model is the SVM (SVMn log) model, which has a value of 0.243, followed by the ANN (ANNlin) model (0.306), being the random forest model, the model with the highest RMSE value for this phase (0.373). It is clear that for this phase, the three selected models present suitable adjustments. In addition, these models also present high values of the correlation coefficient, all greater than 0.990. These promising results are also obtained for the training phase, although the random forest model presents a substantial increase regarding RMSE (from 0.373 to 0.824).
For the query phase, the RMSE values obtained by the model show an increase, in the same way that happened for the models with the input variables selection Type 1. In addition, looking at the data for the query phase of Table 2 and Table 3, it can be seen that the incorporation of the five variables concerning the input variables selection Type 1 destabilizes the models' prediction, causing in all of them an increase in the RMSE value for this phase.
Despite this, the random forest and support vector machine models improve the results of the three-variable model proposed by Li et al. (2020) (0.693, 0.443 vs. 0.752, respectively, in terms of RMSE values for the test phase). The artificial neural network model developed with seven input variables presents an RMSE value close to the value of the Li et al. (2020) model for the query phase (0.762 vs. 0.752). Only the SVM model developed using the input variables selection Type 2 has improved the ML models that used the input variables selection Type 1.
The second group of models (PE/freshwater) corresponds to machine learning models aimed at predicting the adsorption capacity of polyethylene in freshwater using eight input variables (Log D, M'w, εα, εβ, qH+, q-, V', π). In this case, the best model, based on the RMSE value for the validation phase, corresponds to the ANN (ANNlog) model (0.446), followed by the SVM (SVMn) model (0.473) and the RF model (0.697). These reasonable adjustments are reflected in the high correlation coefficients, all greater than 0.960. This behavior is improved in all statistical parameters for the training phase, except for the mean absolute percentage error of the random forest model. For the query phase, these new models present RMSE values between 0.210 and 0.392, maintaining high correlation coefficients, all higher than 0.980. Comparing the ML models developed using the input variables selection Type 2 with the previously developed models using the input variables selection Type 1, it can be said that the ML models developed with eight variables improve the models developed with only one variable; the improvement is appreciable in all the parameters except three MAPE values.
Because of the results reported in Table 3, it can be concluded that the RF, SVM, and ANN models developed using eight input variables improve the model developed by Li et al. (2020) (0.392, 0.210, and 0.272 vs. 0.661, respectively, in terms of RMSE values for test phase).
The next group of models (PE/pure water) corresponds with ML models to predict the adsorption for polyethylene in pure water. In this case, these models were developed using the eight input variables (Log D, M'w, εα, εβ, qH+, q-, V', π) instead of the two or one which were used by Li et al. (2020) and that was also used in the development of the previous ML models (Table 2). In this case, the optimization process carried out by the RF model involved the elimination of the variable V' in the trees of the forest.
It can be seen in Table 3 that the best-selected model, according to the RMSE value for the validation phase, is the SVM (SVMlog) model, which presents a value of 0.154, followed by the RF model (0.204) and the ANN (ANNlog) model (0.403). As in the previous models developed using the input variables selection Type 2, the correlation coefficients are high, all greater than 0.930. This good behavior for the validation phase is also observed in the training phase, although a small increase in the errors made by the models can be seen. For the query phase, the different models present RMSE values between 0.433 and 0.551, keeping the MAPE value around 10% and correlation coefficients greater than 0.920.
Comparing the ML models Type 2 with the previously developed models Type 1, it can be said that, for the query phase, the random forest and support vector machine models present similar adjustments, in terms of RMSE, to those presented by the Type 1 models. Despite this, only the support vector machine model improve the results of the best model proposed by Li et al. (2020) (0.433 vs. 0.471, respectively, in terms of RMSE values for the test phase).
The next models (PP/seawater) correspond to the models developed to predict the adsorption for polypropylene in seawater using seven input variables (Log D, M'w, εα, εβ, q-, V', π).
Based on the results provided by the root mean square error in the validation phase, it can be said that the best model is the support vector machine (SVMlog) model (0.229), followed by the random forest model (0.245) and finally, the artificial neural network (ANNlin) model, which presents a higher error than the other two models (0.419). The correlation coefficients of the three models are greater than 0.975. This good behavior in the validation phase is also observed in the training phase, both for the random forest model and the support vector machine model; however, it should be noted that the artificial neural network model presents in the training phase an error of 0.029. The three models present RMSEs for the query phase between 0.215 and 0.494, with the support vector machine model offering the best results, as was the case in the validation phase.
If the results obtained by the models developed using the input variables selection Type 2 are compared with Type 1, it can be said that the increase in the number of variables has led to a significant decrease in the RMSE values obtained in the query phase for the RF and the SVM model. This can be seen in the support vector machine model, which goes from an RMSE of 0.779 to 0.240.
Given the results reported in Table 3, it can be concluded that the RF and the SVM models developed using seven input variables improve the model developed by Li et al. (2020) with two variables (0.215 and 0.240 vs. 0.369, respectively, in terms of RMSE values for test phase). In addition, these models also improve the machine learning models developed using the input variables selection Type 1 except for the ANN model, which is slightly worse.
Finally, the last group of models (PS/seawater) corresponds to the ML models to predict the adsorption for polystyrene in seawater using seven input variables (Log D, M'w, εα, εβ, q-, V', π). In these new models, a significant improvement can be seen in the validation and query phase adjustment parameters. In fact, for the validation phase, the RMSE values are between 0.290 and 0.475 for the SVM (SVMn2 log) model and the RF model, respectively, while in the Type 1 models, the RMSE values were included between 0.524 and 0.794. Similar behavior is observed for the query phase, with the RMSE values between 0.385 and 0.873. As can be seen in Table 3, the best model on this occasion is the support vector machine model, which also offers the best adjustment parameters for the query phase (0.385).
Given the results, it can be said that the SVM and the ANN (ANNlog) models developed using seven input variables improve the model developed by Li et al. (2020) with two input variables (0.385 and 0.407 vs. 0.714, respectively, in terms of RMSE values for the test phase).
Figure 1 represents the experimental and predicted values of log Kd for the best machine learning models, according to RMSE in the validation phase) of each block shown in Table 3.
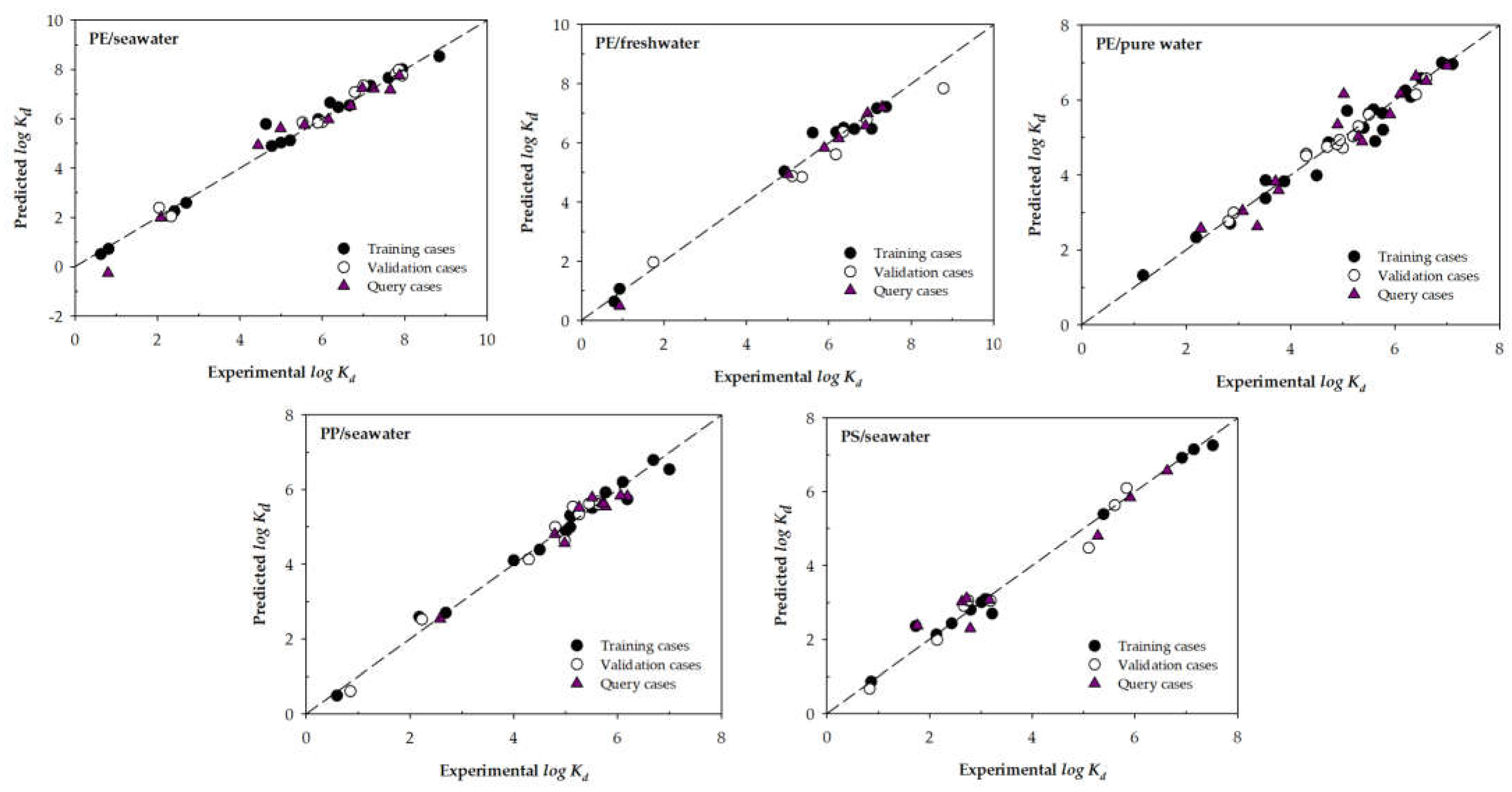
Preprints 68686 g002
Figure 1. Scatter plots for the experimental and predicted values of log Kd for the selected ML models developed using the input variables selection Type 2. The dashed line corresponds to the line with slope 1.
Figure 1. Scatter plots for the experimental and predicted values of log Kd for the selected ML models developed using the input variables selection Type 2. The dashed line corresponds to the line with slope 1.
Preprints 68686 g002
Each graph shows that the adjustments of the training, validation, and query cases are conveniently fitted to the line of slope 1, although some deviation can be observed as it happens in a query case for the PE/seawater model or the PE/pure water model. In general, it can be seen that all the best models consistently predict the log Kd values.
Given the results shown in Table 1 and Table 2, key points can be drawn about the results obtained for the different machine learning models developed.
  • Regardless of the input variables chosen, there is always some machine learning model that improves the adjustments of Li et al. (2020) (in terms of RMSE for the query phase).
  • Including additional variables to develop the ML models does not always improve the variable selection carried out by Li et al. (2020). This is especially evident in the ML models destined to predict PE/seawater, where no model developed using the input variables selection Type 2 improves the models Type 1.
  • To the best of the authors' knowledge, increasing the number of experimental cases for each microplastic/water group used to develop the models would be appropriate. Presumably, this increase would help the models present better adjustments.

4. Conclusions

In this research, various prediction models based on machine learning have been developed using different variables to determine the adsorption capacity for PE, PP, and PS towards organic pollutants in various specific water environments.
Given the results, it can be concluded, regardless of the variables chosen for the development of the model, that there is always some machine learning model that provides good results.
On the other hand, the increase in input variables does not necessarily mean an improvement in the results of the models. This can be seen in the models intended to be used in PE/seawater, where no model developed using the variables selection Type 2 improves the Type 1 models.
To the best of the authors' knowledge, it would be necessary to improve all models using: i) more experimental cases for each microplastic/water group, ii) different datasets for training, validation, and query, or means different configuration parameters, among others.

Author Contributions

Conceptualization, A.C-S., J.C.M. and G.A.; methodology, J.C.M. and G.A.; validation, G.A. and E.B.; formal analysis, G.A and E.B..; investigation, A.C-S., J.C.M. and G.A.; data curation, A.C-S., G.A. and A.S.; writing—original draft preparation, A.C-S., G.A. and A.S.; writing—review and editing, A. C-S., J.C.M. and G.A.; visualization, A.S, A.C-S. and G.A.; supervision, J.C.M. A.C-S. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used was taken from the research paper of Li et al. (2020).

Acknowledgments

The authors thank Li et al. (2020) [15] for publishing their experimental data in Scientific Reports under Attribution 4.0 International (CC BY 4.0), which has allowed to be carried out this study. The authors thank RapidMiner Inc. for the Educational and the free license of RapidMiner Studio 9.10.001 and 9.10.011 software. A. C-S. thanks to the University of Vigo the María Zambrano position. Belonging to the launch of a European Recovery Instrument (“Next Generation EU”), aimed at requalifying the Spanish university system, specifically for teachers and attracting international talent.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lee, H.; Shim, J.E.; Park, I.H.; Choo, K.S.; Yeo, M.-K. Physical and Biomimetic Treatment Methods to Reduce Microplastic Waste Accumulation. Mol. Cell. Toxicol. 2022. [Google Scholar] [CrossRef] [PubMed]
  2. Jaiswal, K.K.; Dutta, S.; Banerjee, I.; Pohrmen, C.B.; Singh, R.K.; Das, H.T.; Dubey, S.; Kumar, V. Impact of Aquatic Microplastics and Nanoplastics Pollution on Ecological Systems and Sustainable Remediation Strategies of Biodegradation and Photodegradation. Sci. Total Environ. 2022, 806, 151358. [Google Scholar] [CrossRef] [PubMed]
  3. Singh, S.; Kumar Naik, T.S.S.; Anil, A.G.; Dhiman, J.; Kumar, V.; Dhanjal, D.S.; Aguilar-Marcelino, L.; Singh, J.; Ramamurthy, P.C. Micro (Nano) Plastics in Wastewater: A Critical Review on Toxicity Risk Assessment, Behaviour, Environmental Impact and Challenges. Chemosphere 2022, 290, 133169. [Google Scholar] [CrossRef] [PubMed]
  4. Ng, E.-L.; Huerta Lwanga, E.; Eldridge, S.M.; Johnston, P.; Hu, H.-W.; Geissen, V.; Chen, D. An Overview of Microplastic and Nanoplastic Pollution in Agroecosystems. Sci. Total Environ. 2018, 627, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
  5. Vivekanand, A.C.; Mohapatra, S.; Tyagi, V.K. Microplastics in Aquatic Environment: Challenges and Perspectives. Chemosphere 2021, 282, 131151. [Google Scholar] [CrossRef] [PubMed]
  6. Matthews, S.; Mai, L.; Jeong, C.-B.; Lee, J.-S.; Zeng, E.Y.; Xu, E.G. Key Mechanisms of Micro- and Nanoplastic (MNP) Toxicity across Taxonomic Groups. Comp. Biochem. Physiol. Part C Toxicol. Pharmacol. 2021, 247, 109056. [Google Scholar] [CrossRef] [PubMed]
  7. Woods, J.S.; Verones, F.; Jolliet, O.; Vázquez-Rowe, I.; Boulay, A.-M. A Framework for the Assessment of Marine Litter Impacts in Life Cycle Impact Assessment. Ecol. Indic. 2021, 129, 107918. [Google Scholar] [CrossRef]
  8. Peano, L.; Kounina, A.; Magaud, V.; Chalumeau, S.; Zgola, M.; Boucher, J. Plastic Leak Project, Methodological Guidelines; 2020.
  9. Ramachandraiah, K.; Ameer, K.; Jiang, G.; Hong, G.-P. Micro- and Nanoplastic Contamination in Livestock Production: Entry Pathways, Potential Effects and Analytical Challenges. Sci. Total Environ. 2022, 844, 157234. [Google Scholar] [CrossRef] [PubMed]
  10. Abihssira-García, I.S.; Kögel, T.; Gomiero, A.; Kristensen, T.; Krogstad, M.; Olsvik, P.A. Distinct Polymer-Dependent Sorption of Persistent Pollutants Associated with Atlantic Salmon Farming to Microplastics. Mar. Pollut. Bull. 2022, 180, 113794. [Google Scholar] [CrossRef]
  11. Gouin, T. Addressing the Importance of Microplastic Particles as Vectors for Long-Range Transport of Chemical Contaminants: Perspective in Relation to Prioritizing Research and Regulatory Actions. Microplastics and Nanoplastics 2021, 1, 14. [Google Scholar] [CrossRef]
  12. Ali, I.; Tan, X.; Li, J.; Peng, C.; Naz, I.; Duan, Z.; Ruan, Y. Interaction of Microplastics and Nanoplastics with Natural Organic Matter (NOM) and the Impact of NOM on the Sorption Behavior of Anthropogenic Contaminants – A Critical Review. J. Clean. Prod. 2022, 376, 134314. [Google Scholar] [CrossRef]
  13. Katsumiti, A.; Losada-Carrillo, M.P.; Barros, M.; Cajaraville, M.P. Polystyrene Nanoplastics and Microplastics Can Act as Trojan Horse Carriers of Benzo(a)Pyrene to Mussel Hemocytes in Vitro. Sci. Rep. 2021, 11, 22396. [Google Scholar] [CrossRef] [PubMed]
  14. Hu, L.; Zhao, Y.; Xu, H. Trojan Horse in the Intestine: A Review on the Biotoxicity of Microplastics Combined Environmental Contaminants. J. Hazard. Mater. 2022, 439, 129652. [Google Scholar] [CrossRef]
  15. Li, M.; Yu, H.; Wang, Y.; Li, J.; Ma, G.; Wei, X. QSPR Models for Predicting the Adsorption Capacity for Microplastics of Polyethylene, Polypropylene and Polystyrene. Sci. Rep. 2020, 10, 14597. [Google Scholar] [CrossRef] [PubMed]
  16. Kathuria, C.; Mehrotra, D.; Misra, N.K. A Novel Random Forest Approach to Predict Phase Transition. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 494–503. [Google Scholar] [CrossRef]
  17. Varnek, A.; Baskin, I. Machine Learning Methods for Property Prediction in Chemoinformatics: Quo Vadis? J. Chem. Inf. Model. 2012, 52, 1413–1437. [Google Scholar] [CrossRef]
  18. Alduailij, M.; Khan, Q.W.; Tahir, M.; Sardaraz, M.; Alduailij, M.; Malik, F. Machine-Learning-Based DDoS Attack Detection Using Mutual Information and Random Forest Feature Importance Method. Symmetry (Basel). 2022, 14, 1095. [Google Scholar] [CrossRef]
  19. Taoufik, N.; Boumya, W.; Achak, M.; Chennouk, H.; Dewil, R.; Barka, N. The State of Art on the Prediction of Efficiency and Modeling of the Processes of Pollutants Removal Based on Machine Learning. Sci. Total Environ. 2022, 807, 150554. [Google Scholar] [CrossRef] [PubMed]
  20. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  21. He, S.; Wu, J.; Wang, D.; He, X. Predictive Modeling of Groundwater Nitrate Pollution and Evaluating Its Main Impact Factors Using Random Forest. Chemosphere 2022, 290, 133388. [Google Scholar] [CrossRef]
  22. Saglam, C.; Cetin, N. Prediction of Pistachio (Pistacia Vera L.) Mass Based on Shape and Size Attributes by Using Machine Learning Algorithms. Food Anal. Methods 2022, 15, 739–750. [Google Scholar] [CrossRef]
  23. Kang, B.; Seok, C.; Lee, J. Prediction of Molecular Electronic Transitions Using Random Forests. J. Chem. Inf. Model. 2020, 60, 5984–5994. [Google Scholar] [CrossRef]
  24. Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest:  A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
  25. Bienefeld, C.; Kirchner, E.; Vogt, A.; Kacmar, M. On the Importance of Temporal Information for Remaining Useful Life Prediction of Rolling Bearings Using a Random Forest Regressor. Lubricants 2022, 10, 67. [Google Scholar] [CrossRef]
  26. Pang, A.; Chang, M.W.L.; Chen, Y. Evaluation of Random Forests (RF) for Regional and Local-Scale Wheat Yield Prediction in Southeast Australia. Sensors 2022, 22, 717. [Google Scholar] [CrossRef] [PubMed]
  27. Geppert, H.; Vogt, M.; Bajorath, J. Current Trends in Ligand-Based Virtual Screening: Molecular Representations, Data Mining Methods, New Application Areas, and Performance Evaluation. J. Chem. Inf. Model. 2010, 50, 205–216. [Google Scholar] [CrossRef] [PubMed]
  28. Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  29. Rodríguez-Pérez, R.; Vogt, M.; Bajorath, J. Support Vector Machine Classification and Regression Prioritize Different Structural Features for Binary Compound Activity and Potency Value Prediction. ACS Omega 2017, 2, 6371–6379. [Google Scholar] [CrossRef] [PubMed]
  30. Liu, G.; Zhu, H. Displacement Estimation of Six-Pole Hybrid Magnetic Bearing Using Modified Particle Swarm Optimization Support Vector Machine. Energies 2022, 15, 1610. [Google Scholar] [CrossRef]
  31. Houssein, E.H.; Hosney, M.E.; Oliva, D. A Hybrid Seagull Optimization Algorithm for Chemical Descriptors Classification. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC); 2021; pp. 381–386.
  32. Sareminia, S. A Support Vector Based Hybrid Forecasting Model for Chaotic Time Series: Spare Part Consumption Prediction. Neural Process. Lett. 2022. [Google Scholar] [CrossRef]
  33. Orgeira-Crespo, P.; Míguez-Álvarez, C.; Cuevas-Alonso, M.; Doval-Ruiz, M.I. Decision Algorithm for the Automatic Determination of the Use of Non-Inclusive Terms in Academic Texts. Publications 2020, 8, 41. [Google Scholar] [CrossRef]
  34. Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Proceedings of the Advances in Neural Information Processing Systems; 1997; pp. 155–161. [Google Scholar]
  35. Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
  36. Prasanna, T.H.; Shantha, M.; Pradeep, A.; Mohanan, P. Identification of Polar Liquids Using Support Vector Machine Based Classification Model. IAES Int. J. Artif. Intell. 2022, 11, 1507–1516. [Google Scholar] [CrossRef]
  37. Liu, Z.; He, H.; Xie, J.; Wang, K.; Huang, W. Self-Discharge Prediction Method for Lithium-Ion Batteries Based on Improved Support Vector Machine. J. Energy Storage 2022, 55, 105571. [Google Scholar] [CrossRef]
  38. Elkorany, A.S.; Marey, M.; Almustafa, K.M.; Elsharkawy, Z.F. Breast Cancer Diagnosis Using Support Vector Machines Optimized by Whale Optimization and Dragonfly Algorithms. IEEE Access 2022, 10, 69688–69699. [Google Scholar] [CrossRef]
  39. Niazkar, H.R.; Niazkar, M. Application of Artificial Neural Networks to Predict the COVID-19 Outbreak. Glob. Heal. Res. Policy 2020, 5, 50. [Google Scholar] [CrossRef]
  40. Paturi, U.M.R.; Cheruku, S.; Reddy, N.S. The Role of Artificial Neural Networks in Prediction of Mechanical and Tribological Properties of Composites—A Comprehensive Review. Arch. Comput. Methods Eng. 2022, 29, 3109–3149. [Google Scholar] [CrossRef]
  41. McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
  42. Khan, M.T.; Kaushik, A.C.; Ji, L.; Malik, S.I.; Ali, S.; Wei, D.-Q. Artificial Neural Networks for Prediction of Tuberculosis Disease. Front. Microbiol. 2019, 10, 395. [Google Scholar] [CrossRef]
  43. Mohamed, Z.E. Using the Artificial Neural Networks for Prediction and Validating Solar Radiation. J. Egypt. Math. Soc. 2019, 27, 47. [Google Scholar] [CrossRef]
  44. Dikshit, A.; Pradhan, B.; Santosh, M. Artificial Neural Networks in Drought Prediction in the 21st Century–A Scientometric Analysis. Appl. Soft Comput. 2022, 114, 108080. [Google Scholar] [CrossRef]
  45. Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial Neural Networks in the Domain of Reservoir Characterization: A Review from Shallow to Deep Models. Comput. Geosci. 2020, 135, 104357. [Google Scholar] [CrossRef]
  46. Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Networks 1989, 2, 359–366. [Google Scholar] [CrossRef]
  47. Shin-ike, K. A Two Phase Method for Determining the Number of Neurons in the Hidden Layer of a 3-Layer Neural Network. In Proceedings of the Proceedings of SICE Annual Conference 2010; 2010; pp. 238–242.
  48. Ujong, J.A.; Mbadike, E.M.; Alaneme, G.U. Prediction of Cost and Duration of Building Construction Using Artificial Neural Network. Asian J. Civ. Eng. 2022, 23, 1117–1139. [Google Scholar] [CrossRef]
  49. Salari, K.; Zarafshan, P.; Khashehchi, M.; Pipelzadeh, E.; Chegini, G. Modeling and Predicting of Water Production by Capacitive Deionization Method Using Artificial Neural Networks. Desalination 2022, 540, 115992. [Google Scholar] [CrossRef]
  50. Shi, C.-F.; Yang, H.-T.; Chen, T.-T.; Guo, L.-P.; Leng, X.-Y.; Deng, P.-B.; Bi, J.; Pan, J.-G.; Wang, Y.-M. Artificial Neural Network-Genetic Algorithm-Based Optimization of Aerobic Composting Process Parameters of Ganoderma Lucidum Residue. Bioresour. Technol. 2022, 357, 127248. [Google Scholar] [CrossRef] [PubMed]
  51. Hufnagl, B.; Steiner, D.; Renner, E.; Löder, M.G.J.; Laforsch, C.; Lohninger, H. A Methodology for the Fast Identification and Monitoring of Microplastics in Environmental Samples Using Random Decision Forest Classifiers. Anal. Methods 2019, 11, 2277–2285. [Google Scholar] [CrossRef]
  52. Hufnagl, B.; Stibi, M.; Martirosyan, H.; Wilczek, U.; Möller, J.N.; Löder, M.G.J.; Laforsch, C.; Lohninger, H. Computer-Assisted Analysis of Microplastics in Environmental Samples Based on ΜFTIR Imaging in Combination with Machine Learning. Environ. Sci. Technol. Lett. 2022, 9, 90–95. [Google Scholar] [CrossRef]
  53. Zou, Z.-M.; Chang, D.-H.; Liu, H.; Xiao, Y.-D. Current Updates in Machine Learning in the Prediction of Therapeutic Outcome of Hepatocellular Carcinoma: What Should We Know? Insights Imaging 2021, 12, 31. [Google Scholar] [CrossRef]
  54. Sarraf Shirazi, A.; Frigaard, I. SlurryNet: Predicting Critical Velocities and Frictional Pressure Drops in Oilfield Suspension Flows. Energies 2021, 14, 1263. [Google Scholar] [CrossRef]
  55. Moldes, Ó.A.; Morales, J.; Cid, A.; Astray, G.; Montoya, I.A.; Mejuto, J.C. Electrical Percolation of AOT-Based Microemulsions with n-Alcohols. J. Mol. Liq. 2016, 215, 18–23. [Google Scholar] [CrossRef]
  56. Yan, X.; Cao, Z.; Murphy, A.; Qiao, Y. An Ensemble Machine Learning Method for Microplastics Identification with FTIR Spectrum. J. Environ. Chem. Eng. 2022, 10, 108130. [Google Scholar] [CrossRef]
  57. Bifano, L.; Meiler, V.; Peter, R.; Fischerauer, G. Detection of Microplastics in Water Using Electrical Impedance Spectroscopy and Support Vector Machines. In Proceedings of the Sensors and Measuring Systems; 21th ITG/GMA-Symposium; 2022; pp. 356–359.
  58. Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
  59. Chang, C.C.; Lin, C.J. LIBSVM -- A Library for Support Vector Machines. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 17 October 2022).
  60. Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 17 October 2022).
  61. Ng, W.; Minasny, B.; McBratney, A. Convolutional Neural Network for Soil Microplastic Contamination Screening Using Infrared Spectroscopy. Sci. Total Environ. 2020, 702, 134723. [Google Scholar] [CrossRef]
  62. Guo, X.; Wang, J. Projecting the Sorption Capacity of Heavy Metal Ions onto Microplastics in Global Aquatic Environments Using Artificial Neural Networks. J. Hazard. Mater. 2021, 402, 123709. [Google Scholar] [CrossRef]
  63. RapidMiner Documentation. Neural Net. Available online: https://docs.rapidminer.com/latest/studio/operators/modeling/predictive/neural_nets/neural_net.html (accessed on 17 October 2022).
Preprints 68686 g001
Figure 1. Schemes of the different ML models developed in this research, A- RF model -inspired in the figure of Zou et al. (2021) [53], B- SVM model - inspired in the figure of Sarraf Shirazi & Frigaard (2021) [54] and C- ANN model - inspired in the figure of Moldes et al. (2016) [55].
Figure 1. Schemes of the different ML models developed in this research, A- RF model -inspired in the figure of Zou et al. (2021) [53], B- SVM model - inspired in the figure of Sarraf Shirazi & Frigaard (2021) [54] and C- ANN model - inspired in the figure of Moldes et al. (2016) [55].
Preprints 68686 g001
Table 1. Input variables, marked in purple, are used according to input variable selection to predict log Kd. Type 1 and type 1* are the configurations used by Li et al. (2020) [15], and Type 2 is the configuration used in this research. Polyethylene -PE-, polypropylene -PP-, polystyrene -PS-, and the eight variables reported used by Li et al. (2020) [15]: i) n-octanol/water distribution coefficient at special pH condition -log D-, ii) molecular mass -M'w-, covalent, iii) acidity -εα- and iv) basicity -εβ-, v) most positive atomic charge on H atom -qH+-, vi) most negative atomic charge -q−-, vii) molecular volume -V′- and viii) molecular volume -π-.
Table 1. Input variables, marked in purple, are used according to input variable selection to predict log Kd. Type 1 and type 1* are the configurations used by Li et al. (2020) [15], and Type 2 is the configuration used in this research. Polyethylene -PE-, polypropylene -PP-, polystyrene -PS-, and the eight variables reported used by Li et al. (2020) [15]: i) n-octanol/water distribution coefficient at special pH condition -log D-, ii) molecular mass -M'w-, covalent, iii) acidity -εα- and iv) basicity -εβ-, v) most positive atomic charge on H atom -qH+-, vi) most negative atomic charge -q−-, vii) molecular volume -V′- and viii) molecular volume -π-.
Model Input variables Model Input variables
Log D M'w εα εβ qH+ q- V' π Log D M'w εα εβ qH+ q- V' π
PE/seawater PP/seawater
Type 1 Type 1
Type 2 Type 2
PE/freshwater PS/seawater
Type 1 Type 1
Type 2 Type 2
PE/pure water
Type 1
Type 1*
Type 2
Table 3. Adjustments for the different machine learning models developed using the input variables selection Type 2. Random forest (RF), support vector machine (SVM), and artificial neural network (ANN). T, V, and Q are training, validation, and query phases, respectively. Root mean square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (r). The best models (regarding RMSE for the validation phase) are in bold.
Table 3. Adjustments for the different machine learning models developed using the input variables selection Type 2. Random forest (RF), support vector machine (SVM), and artificial neural network (ANN). T, V, and Q are training, validation, and query phases, respectively. Root mean square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (r). The best models (regarding RMSE for the validation phase) are in bold.
T V Z
Model RMSE MAPE r RMSE MAPE r RMSE MAPE r
PE/seawater
RF 0.824 38.89 0.954 0.373 7.69 0.988 0.693 26.80 0.970
SVM 0.336 5.52 0.991 0.243 5.22 0.994 0.443 16.38 0.984
ANN 0.040 0.56 1.000 0.306 5.46 0.989 0.762 15.28 0.946
PE/freshwater
RF 0.424 16.78 0.991 0.697 8.78 0.962 0.392 11.86 0.986
SVM 0.320 6.87 0.991 0.473 7.05 0.990 0.210 8.18 0.999
ANN 0.289 4.94 0.992 0.446 7.10 0.991 0.272 10.40 0.997
PE/pure water
RF 0.473 10.77 0.955 0.204 3.31 0.983 0.542 10.37 0.929
SVM 0.306 5.34 0.981 0.154 2.56 0.990 0.433 7.25 0.956
ANN 0.634 14.70 0.916 0.403 7.90 0.937 0.551 11.57 0.926
PP/seawater
RF 0.295 6.44 0.988 0.245 9.42 0.994 0.215 3.36 0.983
SVM 0.222 4.74 0.992 0.229 6.98 0.990 0.240 3.66 0.974
ANN 0.029 0.54 1.000 0.419 12.20 0.979 0.494 8.20 0.938
PS/seawater
RF 0.486 11.07 0.980 0.475 15.16 0.970 0.873 23.01 0.882
SVM 0.248 4.72 0.994 0.290 8.50 0.986 0.385 12.05 0.976
ANN 0.309 7.01 0.990 0.445 9.74 0.984 0.407 12.43 0.973
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated