Preprint

Brief Report

G4v and the Correspondence Principle

Altmetrics

Downloads

351

Views

134

Comments

Daniel Piasecki^*

This version is not peer-reviewed

Submitted:

04 August 2023

Posted:

04 August 2023

You are already at the latest version

Alerts

Abstract

G4v is a four-vector theory of gravitation proposed by Mead (2015, 2023a,b) which reinterprets several major results commonly celebrated for the tensor-based approach of General Relativity (GR). Here, we show that G4v obeys the correspondence principle, an important test of any relativistic theory. We derive the non-relativistic Lagrangian and Energy expressions at the limit of low speeds and potentials, complete with the correct terms for potential energy (something traditional Special Relativity is incapable of achieving). G4v could represent a new interpretation of the gravitational field with essentially the same mathematics as electromagnetism (Mead 2023a). It is also possible to interpret G4v as a very interesting (and useful) approximation of the Einstein field equations (Mead 2023b).

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The idea of a changing speed of light has been the subject of controversy in Physics for decades. The concept has been used to solve various cosmological problems, such as inflation, but with mixed outcomes (Landau, Sisterna, and Vucetich 2001). It seems unlikely that the speed of light would change drastically over cosmological time due to charge conservation (Landau, Sisterna, and Vucetich 2001) but there is the question if the speed of light might vary over space. This was the initial proposal of an early Albert Einstein when first trying to formulate a theory of gravitation compatible with his Special Relativity (SR) theory.

In 1911 and 1912 Einstein articulated his belief that light has a constant value

c_{0}

in the presence of a constant gravitational potential. If the potential varied, however, Einstein proposed that light slows down in accordance to the classical Huygen principle:

“From the proposition which has just been proved, that the velocity of light in the gravitational field is a function of the location, we may easily infer, by means of Huygens’s principle, that light-rays propagated across a gravitational field undergo deflection."

(Einstein 1911)

“The principle of constancy of the speed of light can be upheld only when one restricts oneself to regions of constant gravitational potential." (Einstein 1912a)

Einstein (1911) reasoned that the relationship between the constant speed of light

c_{0}

and the slowed speed of light c1 was given by

\frac{c}{c_{0}} = 1 - \frac{G M}{r c_{0}^{2}}

(1)

For historical reasons Einstein’s first approach was eventually abandoned due to the successes of his metric tensor formulation of General Relativity (GR), including predicting the correct degree light was deflected by an astronomical mass. His original theory was believed to have given a value that is a factor of two too small. However, this common belief has recently come under question with the formulation of G4v.

G4v is a four-vector theory of gravitation developed by Mead (2015; 2023a,b) and Isi et al (2015). The four-vector Mead (2015; 2023a,b) proposes for gravitation is:

Z^{0} = - G \sum_{i} \frac{M_{i}}{r_{i}}

(2)

\vec{Z} = - \frac{G}{c_{0}^{2}} \sum_{i} \frac{{\vec{p}}_{i}}{r_{i}}

(3)

The above four-vector can be used to explain Einstein’s observations on the gravitational analog to electrodynamic induction (Einstein 1912b). Einstein (1912b) demonstrated that if a small object of mass

m_{0}

is inside a hollow shell of mass M, then the smaller mass will gain inertia when the shell is moved relative to it:

m = m_{0} (1 + \frac{G M}{r c_{0}^{2}})

(4)

where m is the induced mass and

m_{0}

is the mass of the object at infinity. The r here would represent the radius of the shell (Einstein 1912b). Just like in electrostatics, the force felt on the smaller mass cannot be due to the scalar coupling, as the uniform shell around it would cancel out any effect. Rather, Mead interprets this as being due to a vector coupling with the above vector potential. At these small speeds, we know

p \approx m v

and we expect the coupling to have the following form in general:

p = p_{0} (1 + \frac{G M}{r c_{0}^{2}})

(5)

Mead argues that while deBroglie showed us that

\vec{p} = ℏ \vec{k}

, Schrödinger showed us that the kinetic momentum is

\vec{p} = ℏ \vec{k} - q \vec{A}

. The momentum’s dependence on the magnetic potential

\vec{A}

is significant. There is a similar dependence here as indicated in Equation 5.

Mead argues that had Einstein taken into account both the slowing and the vector coupling of the light, he could have calculated the correct deflection angle back in 1911 (Mead 2015, 2023a; see Appendix I). Several other effects, such gravitational redshift/time dilation, perihelion advance of Mercury, and Shapiro time delay, can also be fully accounted for with simpler mathematics than the traditional tensor-based approach of GR (Mead 2023a; Appendix I).

The elegance of G4v lies in that it treats the electromagnetic and gravitational four-vectors on equal footing. In his classic work Collective Electrodynamics, Mead (2002) showed how one can derive Electrodynamics on the basis of collective quantum wavefunction behavior. G4v is based on the same principle and thus has an almost identical four-vector formulation to electrodynamics. Having a similar basis for both electrodynamics and gravitational physics might serve as insightful into the deeper nature of the universe, both connected to the quantum.

It is important to note that the proposed gravitational four-vector exists within the tensor-based approach of GR at the limit of weak gravity (Mead 2023b). One can show that Einstein’s field equations produce the gravitational four-vector when mainly the energy-momentum entries of the stress-energy tensor are dominant (Mead 2023b). This result suggests that G4v might not necessarily represent an affront to GR, but is a closely related reinterpretation of our understanding of gravity. These two theories might not be that different, but one provides a more straightforward `shortcut’ to carrying out otherwise very intricate calculations.

The purpose of this short letter is not to expound on the different interesting features of G4v in general (for that, see Mead 2023a,b), but to highlight one in particular. G4v nicely satisfies the correspondence principle. The correspondence principle was a famous guiding principle in the development of Quantum Mechanics that stated one must recover standard classical non-relativistic Physics at the appropriate limit. We can also apply this correspondence principle to relativistic theories, hoping to recover appropriate non-relativistic equations at low speeds. As we will see, G4v has a surprising non-relativistic limit where potential energies are included in the equations. Although this does not innately confirm G4v as a correct theory, it also means G4v passes a crucial test. Another famous variable lightspeed theory does not satisfy this requirement, as we will see.

2. Methods

We will take Einstein’s initial conviction (as part of G4v) and demonstrate that it fully satisfies the correspondence principle for the Lagrangian and Energy conservation. Many authors have noted that SR is conspicuously ill-adapted for handling the concepts of potential energy (e.g., Brillouin 1965, Hecht 2016, etc.) However, the G4v approach lets one naturally incorporate the concept of gravitational potential into SR. Although introductory textbooks of relativity will all note how you can derive non-relativistic kinetic energy by a simple binomial expansion, no one has shown how full non-relativistic Lagrangian and Energy conservation expressions can be derived through one simple assumption. Although Hilo (2011) and Hilo et al (2012) get close to this goal through their Generalized Special Relativity (GSR), their work starts with a construction based in GR, whereas here we justify their conclusions based on Einstein’s postulate of a variable speed of light.

To begin, let us see how Einstein’s concept of a variable speed of light (Eq. 1) would impact the Lorentz factor. The Lorentz factor is often derived in undergraduate textbooks from the spacetime interval. Assume that a coordinate frame is set up to measure the proper time

τ

of the object. If this system is set at infinity where the gravitational potential will be zero, this frame must measure a constant speed of light

c_{0}

by Eq. 1. However, if the object is in motion with respect to a different coordinate frame, and it finds itself in a gravitational potential, Einstein’s assumption shows that the speed of light c would slow down. We can therefore show that the spacetime interval gives us:

d s^{2} = c_{0}^{2} d τ^{2} = c^{2} d t^{2} - d {\vec{r}}^{2}

c_{0}^{2} \frac{d τ^{2}}{d t^{2}} = c^{2} - \frac{d {\vec{r}}^{2}}{d t^{2}} = c^{2} - v^{2}

\frac{d τ}{d t} = \sqrt{\frac{c^{2} - v^{2}}{c_{0}^{2}}}

(6)

where

τ

is measured in zero gravitational potential. Plugging in Eq. 1, we get the full inverse Lorentz factor as:

\frac{d τ}{d t} = \sqrt{{(1 - \frac{G M}{r c_{0}^{2}})}^{2} - \frac{v^{2}}{c_{0}^{2}}}

(7)

Note, the only assumption in deriving the above expression is Einstein’s postulate. No other assumptions were made in its derivation, so if c truly varies and Einstein was correct, the above must be the form of the inverse Lorentz factor. At the very least, if c varies, then Eq. 6 must be the proper form of the inverse Lorentz factor. Where

c = c_{0}

, Eq. 6 reduces to the standard inverse Lorentz factor of SR. G4v is Lorentz invariant under constant gravitational potential (Mead 2023a).

With the above derivation of the Lorentz factor, we can turn our attention to the relativistic Action, which will be crucial to developing the proper Lagrangian. The relativistic Action has the form of

S = - \int m c_{0} d s = - \int \sqrt{P^{μ} P_{μ} d x^{ν} d x_{ν}}

where

d s

is the spacetime interval once again. The relativistic Action utilizes the factor

c_{0}

instead of c as it emerges from the invariant four-momentum inner product. As Appendix II demonstrates, the four-momentum inner product will always be in terms of

c_{0}

, even if c slows in the presence of a gravitational mass. Plugging in for proper time and extracting the Lagrangian we get:

S = - \int m c_{0}^{2} d τ = - \int m c_{0}^{2} \frac{d τ}{d t} d t

(8)

L = - m c_{0}^{2} \frac{d τ}{d t}

(9)

The full relativistic Lagrangian is therefore:

L = - m c_{0}^{2} \sqrt{{(1 - \frac{G M}{r c_{0}^{2}})}^{2} - \frac{v^{2}}{c_{0}^{2}}}

(10)

From this, we can demonstrate the correspondence principle holds.

First, to do so let us assume a weak gravitational field. We can use a binomial approximation to show that:

L \approx - m c_{0}^{2} \sqrt{1 - \frac{2 G M}{r c_{0}^{2}} - \frac{v^{2}}{c_{0}^{2}}}

This corresponds to the weak gravitational metric (Weinberg 1972), with

g_{00} = 1 - \frac{2 G M}{r c_{0}^{2}}

and

g_{11} = g_{22} = g_{33} = - 1

. In fact, this is how Hilo (2011) and Hilo et al (2012) derived their approximate GSR. We will reproduce all major results of GSR.

Next, assuming that the terms

- \frac{2 G M}{r c_{0}^{2}} - \frac{v^{2}}{c_{0}^{2}}

under the radical are sufficiently small, we can binomial approximate again (in the spirit of Hilo 2011 and Zakaria et al 2014) to get:

L \approx - m c_{0}^{2} [1 + \frac{1}{2} (- \frac{2 G M}{r c_{0}^{2}} - \frac{v^{2}}{c_{0}^{2}})] =

= \frac{1}{2} m v^{2} - (- \frac{G M m}{r}) - m c_{0}^{2}

This is the standard non-relativistic Lagrangian

L = T - U

, with the gravitational and rest mass energies acting as potential energies. It is significant that the relativistic Lagrangian can be fully collapsed into the non-relativistic Lagrangian with the G4v postulate, complete with its potential energy terms (not merely the kinetic energy, as most treatments give).

We can also derive the full conservation of energy expression from Eq. 8. From Noether’s Theorem, we can show

E = - \frac{δ S}{δ t} = \frac{m c_{0}^{2}}{\sqrt{{(1 - \frac{G M}{r c_{0}^{2}})}^{2} - \frac{v^{2}}{c_{0}^{2}}}} {(1 - \frac{G M}{r c_{0}^{2}})}^{2}

(11)

Assuming a weak gravitational field as before:

E \approx \frac{m c_{0}^{2}}{\sqrt{1 - \frac{2 G M}{r c_{0}^{2}} - \frac{v^{2}}{c_{0}^{2}}}} (1 - \frac{2 G M}{r c_{0}^{2}})

And finally applying another binomial expansion as we did for the Lagrangian above:

E \approx (1 - \frac{2 G M}{r c_{0}^{2}}) m c_{0}^{2} [1 + (- \frac{1}{2}) (- \frac{2 G M}{r c_{0}^{2}} - \frac{v^{2}}{c_{0}^{2}})] =

= m c_{0}^{2} [1 - \frac{2 G M}{r c_{0}^{2}} + \frac{G M}{r c_{0}^{2}} + \frac{v^{2}}{2 c_{0}^{2}} - \frac{2 G^{2} M^{2}}{c_{0}^{4}} - \frac{G M v^{2}}{r c_{0}^{4}}]

Eliminating all terms with a value of

c_{0}^{4}

in the denominator (following Hilo 2011 and Zakaria et al 2014) gives us the nonrelativistic energy as:

E = - \frac{G M m}{r} + \frac{1}{2} m v^{2} + m c_{0}^{2}

We can see that G4v gives a means of deriving the full nonrelativistic Lagrangian and Energy expressions, complete with gravitational potential energies.

Furthermore, at the limit of small velocities (

v \to 0

), we recover Newtonian gravity if we treat the relativistic energy E as a type of potential energy:

\vec{F} = - \vec{\nabla} E \approx - \frac{\partial}{\partial r} m c_{0}^{2} (1 - \frac{G M}{r c_{0}^{2}}) \hat{r} = - \frac{G M m}{r^{2}} \hat{r}

3. Discussion

This basic result highlights that G4v passes an important test of any relativity theory. Both GR and G4v agree that the gravitational potential is encoded within

d τ / d t

, with the above elegant limit quickly giving us the correct form of the Lagrangian,

L = T - U

Other variable lightspeed theories fail in the above regard. For instance, Dicke (1957) famously proposed that the relationship for the slowing speed of light was

\frac{c}{c_{0}} = {(1 + \frac{G M}{r c_{0}^{2}})}^{- 2} \approx 1 - \frac{2 G M}{r c_{0}^{2}}

(See also Unzicker 2009 Appendix). This value was postulated in part to derive the correct deflection value for light around massive astronomical objects (see Appendix I). It is clear, however, that Dicke’s suggestion cannot be the case as it violates the correspondence principle:

∴ \frac{d τ}{d t} = \sqrt{{(1 - \frac{2 G M}{r c_{0}^{2}})}^{2} - \frac{v^{2}}{c_{0}^{2}}}

L = - m c_{0}^{2} \frac{d τ}{d t} ⟹ L \approx \frac{1}{2} m v^{2} - (- \frac{2 G M m}{r}) - m c_{0}^{2}

E = \frac{m c_{0}^{2}}{\sqrt{{(1 - \frac{2 G M}{r c_{0}^{2}})}^{2} - \frac{v^{2}}{c_{0}^{2}}}} {(1 - \frac{2 G M}{r c_{0}^{2}})}^{2} ⟹ E \approx - \frac{2 G M m}{r} + \frac{1}{2} m v^{2} + m c_{0}^{2}

Dicke’s deduction gives us gravitational potential energies double what we see in Nature. G4v is the only changing-speed-of-light model we are aware of that avoids this issue.

The results of this paper show another appealing feature of the G4v theory. We can reproduce all the major insights of GSR (Hilo 2011, Hilo et al 2012, and Zakaria et al 2014) with one simple assumption, whereas other variable speed of light theories (like that of Dicke) would fail. The results here also agree with a hypothesis put forward by Austin (2017) on a modified Lorentz factor. Using Eq. 1, G4v can reproduce the gravitational redshift, deflection of light, perihelion advance of Mercury, and Shapiro time delay through simple mathematics (Mead 2015, 2023a; Appendix I). Whether Einstein’s initial idea is correct or not remains to be seen through further gravitational experimentation (Mead 2015, 2023a,b; Isi et al 2015). At the very least, G4v represents a very interesting approximation to standard GR that reproduces all major experimental results credited to GR through simple mathematics.

Funding

This research received no external funding

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

I would like to thank Dr. Frank Tipler of Tulane University for providing insight into how the potential might be reduced from the spacetime metric. Dr. Carver Mead of CalTech for graciously providing permission for the reproduced figures in the Appendix.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. G4v Calculations

This section is based on a presentation that Carver Mead gave at CalTech entitled “G4v: An Engineering Approach to Gravitation" on 4/21/2015. The presentation is available online. We reproduce three major results of G4v that are normally accredited to GR. (For perihelion advance of mercury, refer to Mead 2023a). We utilize Figures 1 and 2 from Mead’s presentation to demonstrate these calculations.

Appendix A.1. Deflection of Light

Figure A1. The path of light bending around a massive object M. Reproduced from Mead’s presentation.

We first begin with Einstein’s erroneous calculation for the deflection of light (Einstein 1911). Einstein began by writing the wavenumber of the photon as

k = \frac{ω}{c}

and using his prediction for the slowing lightspeed (Eq. 1) he derived:

k = \frac{ω}{c_{0} (1 - \frac{G M}{r c_{0}^{2}})} \approx \frac{ω}{c_{0}} (1 + \frac{G M}{r c_{0}^{2}})

We can derive the phase

ϕ

to be:

ϕ = \int_{R_{1}}^{- R_{2}} k d Γ

where

Γ

is the path length taken by the photon in Figure 1. One derives:

ϕ \approx \frac{ω}{c_{0}} (R_{1} + R_{2} + \frac{d^{2}}{2 R_{1}} + \frac{d^{2}}{2 R_{2}} - \frac{G M}{c_{0}^{2}} log (\frac{d^{2}}{4 R_{1} R_{2}}))

If we take a partial with respect to

d^{2}

we will get:

\frac{\partial ϕ}{\partial d^{2}} = \frac{1}{2 R_{1}} + \frac{1}{2 R_{2}} - \frac{G M}{c_{0}^{2} d^{2}} = 0

Keeping in mind that the distance

R_{1}

light travels from distant stars is tremendously larger than the distance

R_{2}

between the Sun of mass M and the Earth. So we therefore get in the end:

d^{2} \approx 2 R_{2} \frac{G M}{c_{0}^{2}}

The angle of deflection

θ

(Figure 1) is therefore:

θ \approx \frac{d}{R_{2}} = \frac{2 G M}{c_{0}^{2} d}

This is Einstein’s 1911 result. It was shown by experiment to be off by a factor of 2.

G4v takes a slightly modified approach. Mead treats Einstein’s mass induction insight (Eq. 4; Einstein 1912b) as a way to understand the momentum increase of a photon (Eq. 5). Following the spirit of his work Collective Electrodynamics, all wavefunctions are given equal treatment, including photonic wavefunctions. Rewriting Equation 5 in terms of the wavenumber:

k = \frac{ω}{c} (1 + \frac{G M}{r c_{0}^{2}})

However, as the photon approaches the massive body, the speed of light c is also slowing down. Taking that into consideration we can write:

k = \frac{ω}{c_{0}} \frac{(1 + \frac{G M}{r c_{0}^{2}})}{(1 - \frac{G M}{r c_{0}^{2}})}

Just like with light entering a medium and slowing down, we do not expect

ω

to change. Completing a simple approximation:

k \approx \frac{ω}{c_{0}} (1 + \frac{G M}{r c_{0}^{2}}) (1 + \frac{G M}{r c_{0}^{2}}) \approx \frac{ω}{c_{0}} (1 + \frac{2 G M}{r c_{0}^{2}})

Both effects in tandem will give us the correct deflection of the light ray if we then follow the same procedure above once more:

θ = \frac{4 G M}{c_{0}^{2} d}

Both G4v and GR predict the same correct deflection. Einstein could have predicted the correct deflection if he used his discovery of both the vector and scalar couplings.

Appendix A.2. The Shapiro Time Delay

Figure A2. Graph for calculating the Shapiro time delay. Reproduced from Mead’s presentation.

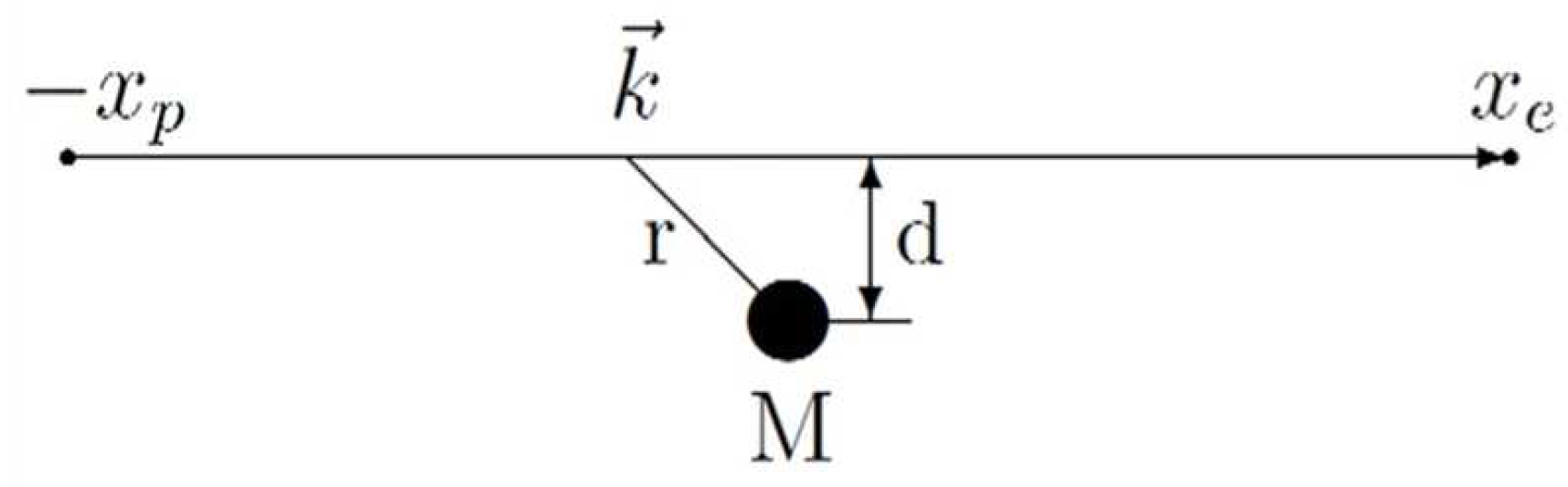
The Shapiro time delay can be predicted in much the same way as the correct deflection of light was. We will refer to Figure 2 for this demonstration. To predict the time delay T, we utilize

T = \frac{1}{ω} \int_{- x_{p}}^{x_{e}} k d x

If we utilize the k which takes into account both the slowing speed of light and change in the momentum of the photon we get:

T = \frac{x_{e} + x_{p}}{c_{0}} + \frac{2 G M}{c_{0}^{3}} log (\frac{\sqrt{d^{2} + x_{e}^{2}} + x_{e}}{\sqrt{d^{2} + x_{p}^{2}} - x_{p}})

The last term in the above expression is the Shapiro delay.

Appendix A.3. Gravitational Redshift/Time Dilation

Deeper derivations can be found in Hilo (2011) and Austin (2017). We can make a straightforward derivation by utilizing Eq. 7, however. Setting the speed of the light emitter equal to zero, we can approximate:

\frac{d τ}{d t} = \sqrt{{(1 - \frac{G M}{r c_{0}^{2}})}^{2}} \approx \sqrt{1 - \frac{2 G M}{r c_{0}^{2}}}

Since the

τ

is measured outside the influence of gravity, it acts as the time without gravity, and since t is within the gravitational potential, it is the time within gravity. The above is precisely the same equation that standard GR derives for gravitational time dilation (Austin, 2017).

Appendix B. Proof P μ P μ =m 2 c 0 2 in G4v

Proof that the dot product of four-momentum depends on the constant speed of light at infinity

c_{0}

instead of the changing value of the speed of light c. This is essential for making the correct derivation in Eq. 8. The proper time

τ

is measured infinitely far away from nearby masses. G4v assumes a flat spacetime metric.

d x^{μ} = (c d t, d \vec{r})

u^{μ} = \frac{d x^{μ}}{d τ} = (c \frac{d t}{d τ}, \frac{d \vec{r}}{d τ}) = (c \frac{d t}{d τ}, \frac{d \vec{r}}{d t} \frac{d t}{d τ}) = \frac{d t}{d τ} (c, \vec{v})

P^{μ} = m \frac{d x^{μ}}{d τ} = \frac{d t}{d τ} (m c, m \vec{v})

Because the derivative above is with respect to the proper time at infinity, the mass associated with the above equation is also the mass at infinity.

P^{μ} P_{μ} = m^{2} u^{μ} u_{μ} = m^{2} (\frac{c_{0}^{2}}{c^{2} - v^{2}}) (c^{2} - v^{2})

∴ P^{μ} P_{μ} = m^{2} c_{0}^{2}

References

Austin, R.W. Gravitational Time Dilation Derived from Special Relativity and Newtonian Gravitational Potential. European Scientific Journal 2017, 13(3), 447–454. [Google Scholar] [CrossRef]
Brillouin, L. The Actual Mass of Potential Energy, A Correction to Classical Relativity. PNAS 1965, 53(3), 475–482. [Google Scholar] [CrossRef] [PubMed]
Dicke, R. Gravitation without a principle of equivalence. Reviews of Modern Physics 1957, 29(3), 363–376. [Google Scholar] [CrossRef]
Einstein, A. Einfluss der Schwerkraft auf die Ausbreitung des Lichtes. (On the Influence of Gravitation on the Propagation of Light). Annalen der Physik 1911, 35, 898–908. [Google Scholar] [CrossRef]
Einstein, A. Relativitat und Gravitation. Erwiderung auf eine Bemerkung von M. Abraham. (Relativity and Gravitation. Reply to a Comment by M. Abraham). Annalen der Physik 1912, 38, 1059–1064. [Google Scholar] [CrossRef]
Einstein, A. Gibt es eine Gravitationswirkung die der elektromagnetischen Induktionswirkung analog ist? (Is There a Gravitational Effect Which Is Analogous to Electrodynamic Induction?). Vierteljahrschrift für gerichtliche Medizin 1912, 44, 37–40. [Google Scholar]
Hecht, E. Relativity, potential energy, and mass. European Journal of Physics 2016, 37(6), 065804. [Google Scholar] [CrossRef]
Hilo, M.H.M. Using of the generalized special relativity in deriving the equation of the gravitational red shift. Journal of Modern Physics 2011, 2, 370–373. [Google Scholar] [CrossRef]
Hilo, M.H.M. , et al. Generalized general and special relativity in the presence of the gravitation, related to the space-time curvature. Natural Science 2012, 4, 336–339. [Google Scholar] [CrossRef]
Isi, M. , Weinstein, A.J., Mead, C., and Pitkin, M. Detecting beyond-Einstein polarizations of continuous gravitational waves. Physical Review D 2015, 91, 082002. [Google Scholar] [CrossRef]
Landau, S.J. , Sisterna, P.D., and Vucetich, H. Charge conservation and time-varying speed of light. Physical Review D 2015, 63, 081303. [Google Scholar] [CrossRef]
Mead, C. Collective Electrodynamics 1st edition; The MIT Press, 2002. [Google Scholar]
Mead, C. Gravitational Waves in G4v. ArXiv 2015. [Google Scholar] [CrossRef]
Mead, C. Engineering View of Gravitation. Caltech.edu 2023a. [CrossRef]
Mead, C. A Simple Cosmology in G4v. Symmetry 15, 1309. [CrossRef]
Unzicker, U. A Look at the Abandoned Contributions to Cosmology of Dirac, Sciama and Dicke. Annalen der Physik 2009, 521(1), 57–70. [Google Scholar] [CrossRef]
Weinberg, S. Gravitation and Cosmology 1st edition; John Wiley and Sons, Inc., 1972. [Google Scholar]
Zakaria, A. , Abd allah, M.D., and Haroun, Kh.M. Expression of Mass in Einstein Generalized Special Relativity. International Journal of Science and Research 2014, 3(6), 594–596. [Google Scholar]

1	Throughout the text of this paper, we will strictly distinguish between $c_{0}$ and c in accordance with this equation.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.