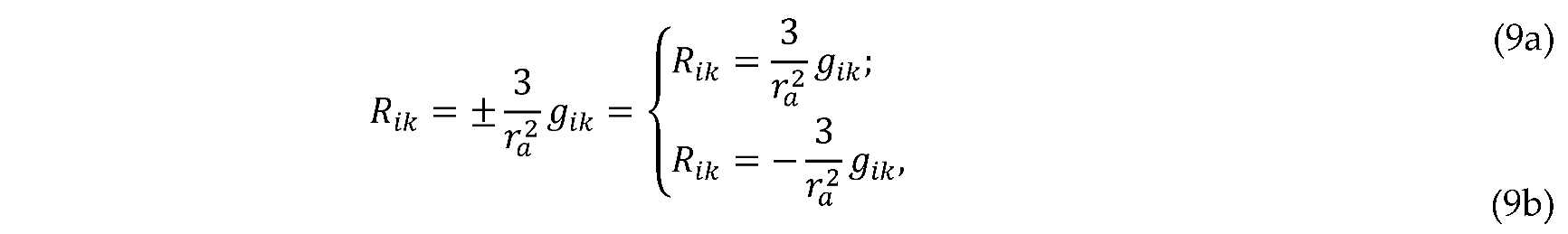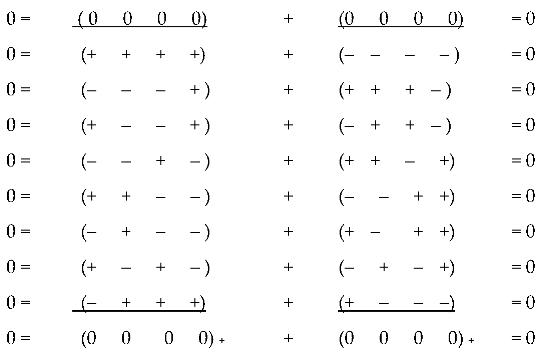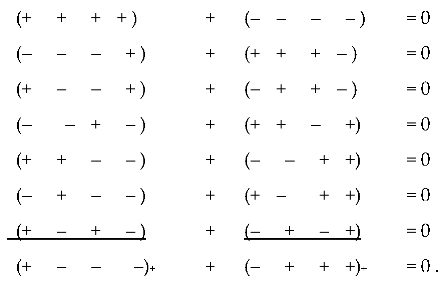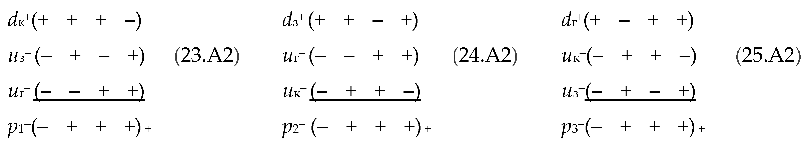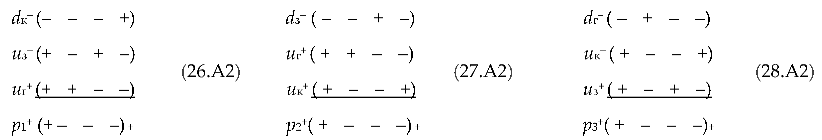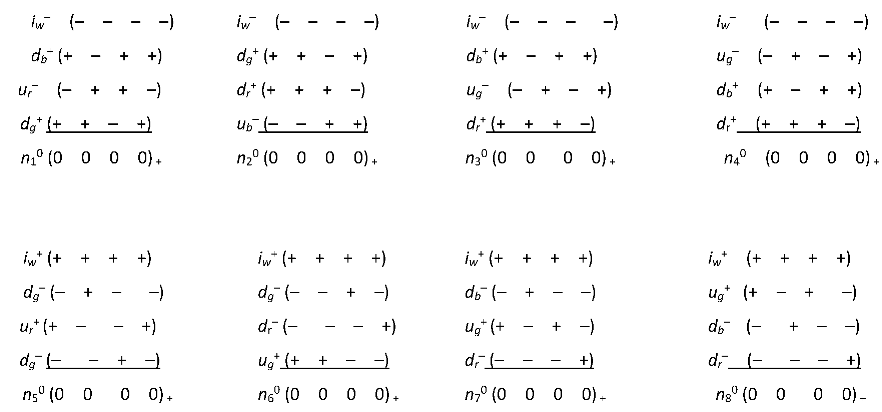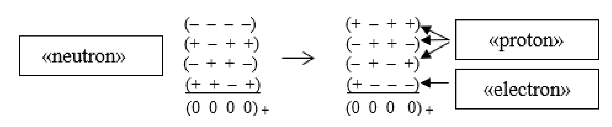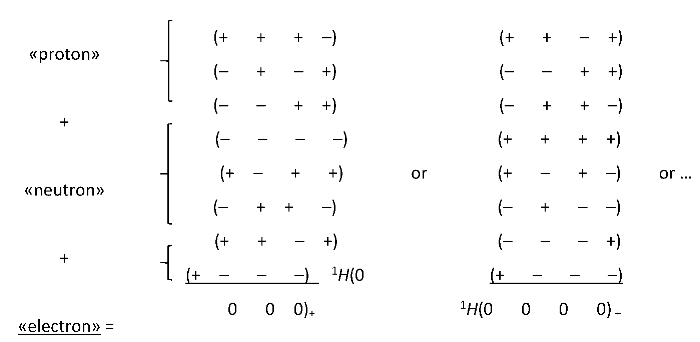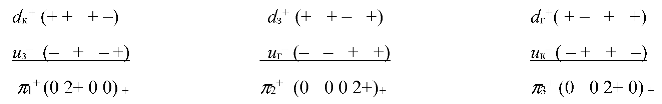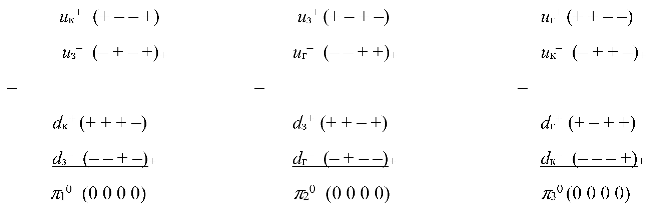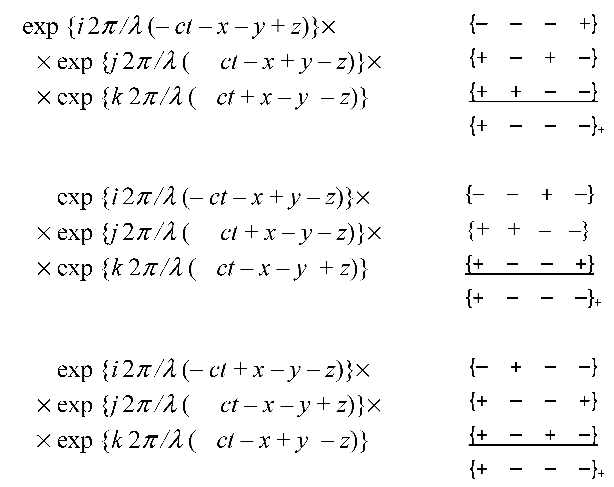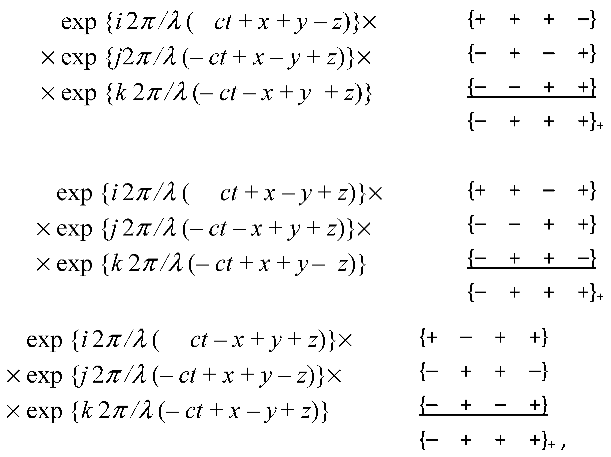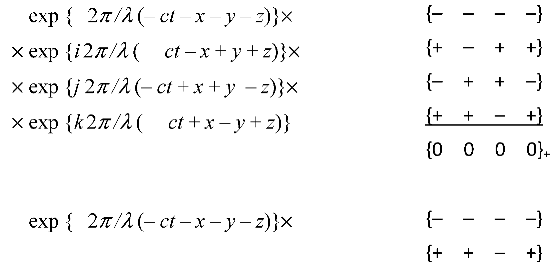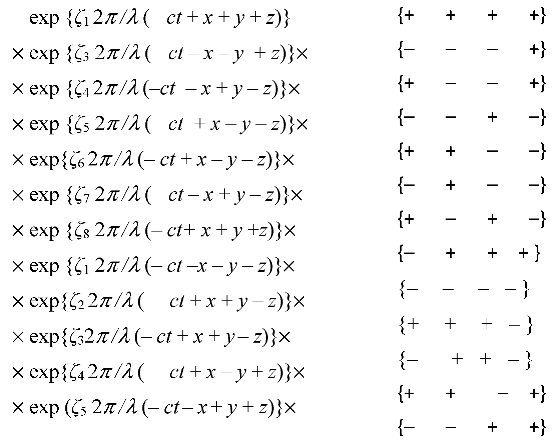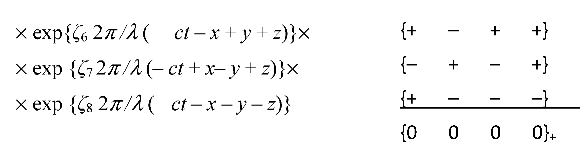Multilayer and Multilevel Cosmological Models Based on So-Lutions of the Extended Einstein Field Equations

Preprint

Article

Multilayer and Multilevel Cosmological Models Based on So-Lutions of the Extended Einstein Field Equations

Altmetrics

Downloads

205

Views

Comments

Mikhail Batanov-Gaukhman^*

This version is not peer-reviewed

This preprints belongs to the Topic

Covariance, Objectivity and Evolution Equations in Either Classical or Quantum Gravity and Quantum Mechanics

Submitted:

20 February 2023

Posted:

21 February 2023

Read the latest preprint version here

Alerts

Abstract

This article proposes the multilayer and multilevel cosmological model, on average, balanced with respect to the Einsteinian vacuum. This hierarchical model is based on 10 possible Kottler solutions of the extended Einstein's field equations. The extension of the Einstein field equations is associated with the addition of an infinite number of lambda_j-terms to these equations with the condition that the series (i.e., the total sum) of these terms converges to zero. A simplified ten-layer and ten-level case is considered, in which ten spherical formations are sequentially nested into each other like "nesting dolls", while the radii of these spherical formations correspond to the characteristic sizes of a discrete sequence of observed spherical objects: metagalaxy core, galactic cores, stellar (planet) core, biological cells and nuclei of atoms and elementary particles, etc. As an example, from the general ten-level (hierarchical) solution of extended Einstein's field equations, two antipodal spherical formations with a core radius commensurate with the classical electron radius are singled out. Therefore, the metric-dynamic models of these formations obtained in this way are called «electron» and «positron». The article is aimed at the development of differential geometry and the program for the complete geometrization of physics by Clifford-Einstein-Wheeler.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Background and introduction

In 1915, the efforts of Albert Einstein, with the assistance of Marcel Grossmann, and David Hilbert culminated in the derivation of the equations of general relativity [1]

R_{i k} - \frac{1}{2} R g_{i k} = \frac{8 π G}{c^{2}} T_{i k},

(1)

where

g_{i k}

are the components of the metric tensor;

T_{i k}

are the components of the matter energy-momentum tensor; c is the speed of light in vacuum; G is Newton's gravitational constant;

R = g^{i k} R_{i k}

is the scalar curvature;

R_{i k} = \frac{\partial Г_{i k}^{l}}{\partial x^{l}} - \frac{\partial Г_{i l}^{l}}{\partial x^{k}} + Г_{i k}^{l} Г_{l m}^{m} - Г_{i l}^{m} Г_{m k}^{l} is Ricci tensor;

(1a)

Г_{i k}^{λ} = \frac{1}{2} g^{λ μ} (\frac{\partial g_{μ k}}{\partial x^{i}} + \frac{\partial g_{i μ}}{\partial x^{k}} - \frac{\partial g_{i k}}{\partial x^{μ}}) is Christoffel symbols.

(1b)

However, Eq.s (1) did not allow the possibility of describing the static universe. Therefore, Einstein in 1917, used the property of covariant derivatives:

\nabla_{j} (R_{i k} - \frac{1}{2} R g_{i k}) = 0, \nabla_{j} T_{i k} = 0, \nabla_{j} g_{i k} = 0,

(2)

and as a result, in the article [2], he wrote down the Einstein's field equations (13a), which is transformed into the formula

R_{i k} - \frac{1}{2} R g_{i k} + Λ g_{i k} = \frac{8 π G}{c^{2}} T_{i k},

(3)

where Λ is a constant, called the "cosmological constant".

In various cosmological models, for example [4–6,8,10,11], it is often assumed

Λ = 3/r_a² or Λ = –3/r_a²,

(4)

where r_a is the radius of some sphere (in particular, the radius of the observable universe); For

T_{i k} = 0

, the case Λ > 0 corresponds to the de Sitter model, Λ < 0 corresponds to the anti-de Sitter model.

This article assumes the complete absence of matter (

T_{i k} = 0

), i.e. the vacuum version of the Einstein field equations (3) is considered

R_{i k} - \frac{1}{2} R g_{i k} + Λ g_{i k} = 0 .

(5)

Combining Eq.s (5) with the contravariant components of the metric tensor

g^{i k}

, we obtain

g^{i k} \{R_{i k} - \frac{1}{2} R g_{i k} + Λ g_{i k}\} = R - \frac{n}{2} R + n Λ = 0,

(6)

where

{n = g}^{i k} g_{i k}

is the number of space dimensions.

From Ex. (6) it follows

R = \frac{2 n}{n - 2} Λ,

(7)

in this case, Eq.s (5) takes the form

R_{i k} - \frac{n}{n - 2} Λ g_{i k} + Λ g_{i k} = R_{i k} - \frac{2}{n - 2} Λ g_{i k} = 0 .

For a 4-dimensional space: n = 4, R = 4Λ, and Eq.s (5) takes the simplest form [4]

R_{i k} - Λ g_{i k} = 0

(8)

or R_{i k} = Λ g_{i k}

(8a)

This equation, taking into account expressions (4), can be represented as a system

where r_a can also take both positive and negative values (

{\pm r}_{a})

Eq.s (8) are essentially conservation laws, since the condition (3b.A1) in Appendix 1 is satisfied, and the solutions of these equations describe the metric-dynamic state of stable deformations of local or global areas of vacuum.

The solution of Eq.s (9a) is written in the form of the Kottler metric, which is also called the de Sitter-Schwarzschild solution [4–6,12]

d s_{K o t t l e r}^{2} = (1 - \frac{r_{b}}{r} - \frac{r^{2}}{r_{a}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{b}}{r} - \frac{r^{2}}{r_{a}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(10)

where

r_{a}

and

r_{b}

are constant parameters of the metric with distance dimension.

In the case: r_a = ∞ and r_b ≠ 0, the Kottler metric (10) turns into the Schwarzschild metric

d s_{S c h w a r z s c h i l d}^{2} = (1 - \frac{r_{b}}{r}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{b}}{r})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(11)

In another case: r_a≠ ∞ and r_b = 0, the Kottler metric (10) becomes the de Sitter metric

d s_{d e S i t t e r}^{2} = (1 - \frac{r^{2}}{r_{a}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r^{2}}{r_{a}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(12)

In the third case: r_a= ∞ and r_b = 0, the metric (10) takes the form of the Minkowski metric

d s_{M i n k o w s k i}^{2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(13)

2. Generalized Kottler metrics

In fact, Friedrich Kottler wrote down in [3] not the metric (10), but the metric of the form

d s_{K o t}^{2} = - (1 + \frac{r_{b}}{r} - \frac{r^{2}}{r_{a}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{b}}{r} - \frac{r^{2}}{r_{a}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2})

this can be easily seen on page 443 of that article.

Article [3] was published in March 1918, that is, almost immediately after the publication of Einstein's GR, so the metrics given below will be called the generalized Kottler metrics.

Since the metric (10) is used in many cosmological models, for example, [4–12], in this article it is proposed to pay attention to the fact that the parameters 3/r_a² and

r_{b}

can take both positive and negative values (±3/r_a² and

{\pm r}_{b}

), so the system of Eq.s (9) generally has the following 10 mutually irreducible solutions:

- with signature (+ – – –)

d s_{1}^{(-) 2} = (1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(14)

d s_{2}^{(-) 2} = (1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(15)

d s_{3}^{(-) 2} = (1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(16)

d s_{4}^{(-) 2} = (1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(17)

d s_{5}^{(-) 2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(20)

- and with signature (– + + +)

d s_{1}^{(+) 2} = - (1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(2118)

d s_{2}^{(+) 2} = - (1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(22)

d s_{3}^{(+) 2} = - (1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(19)

d s_{4}^{(+) 2} = - (1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(20)

d s_{5}^{(+) 2} = - c^{2} d t^{2} + d r^{2} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(21)

where

r_{a 1}, r_{a 2}, r_{a 3}, r_{a 4}

and

r_{b 1}, r_{b 2}, r_{b 3}, r_{b 4}

are parameters of the cosmological model.

All ten metrics (14) – (25) are solutions of one system of Eq.s (9), which determines the metric-dynamic state of the same region of space. Therefore, we can assume that these solutions describe the metric-dynamic state of the ten "layers" of this area. In this case, the additive overlay (i.e. sum or average) of all ten metrics

\sum_{i = 1}^{5} s_{i}^{(-) 2} + \sum_{j = 1}^{5} s_{j}^{(+) 2} = 0

(22)

leads to two more trivial solutions of Eq.s (9) with mutually opposite signatures (+ – – –) and (– + + +)

0 = {0 \cdot c}^{2} d t^{2} - 0 \cdot d r^{2} - {0 \cdot r}^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(23)

0 = - {0 \cdot c}^{2} d t^{2} + 0 \cdot d r^{2} + 0 \cdot r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(24)

This can be easily seen if we substitute the zero components of the metric tensor

g_{i k} = 0

from metrics (27) and (28) into Eq.s (9) taking into account Ex.s (1a) and (1b).

All 12 solutions of the system Einstein's field equations (9) will be taken into account in the multilayer cosmological model.

Before discussing the possibility of additive superposition (i.e., summation or averaging) of metric layers on each other, we note the following important circumstance.

Addition of two quadratic forms

ds_a²+ ds_b² = ds_ab²,

(25)

or their averaging

\frac{1}{2} {ds}_{a} 2^{} + \frac{1}{2} {ds}_{b}^{2} = \frac{1}{2} d_{{Sab}^{2}}

(26)

resembles the Pythagorean theorem (see Figure 1a) a² + b² = c².

This means that the segments ds_a and ds_b of the corresponding lines s_a and s_b are always mutually perpendicular to each other (ds_a _⊥ds_b). This is possible only if the lines s_a and s_b form a double helix (see Figure 1b), which can be described by a system of two complex conjugate numbers

d s_{a b} = d s_{a} + i d s_{b},

(30)

d s_{a b}^{*} = d s_{a}^{'} - i d s_{b}^{'} .

(30a)

The product of complex numbers (30) and (30a), under the condition

{d s}_{a} = d s_{a}^{'}

s_{b} = d s_{b}^{'}

, is equal to the quadratic form (29).

Figure 1. Double helix of lines s_a and s_b.

Figure 2. Illustration of a 4 line

s_{a}, s_{b}, s_{a}^{'} s_{b}^{'}

spiral

Figure 2. Illustration of a 4 line

s_{a}, s_{b}, s_{a}^{'} s_{b}^{'}

spiral

Such a spiral will be called a 4-braid (i.e., a bundle consisting of 4 interlaced lines

s_{a}, s_{b},

s_{a}^{'},

s_{b}^{'}

), wherein:

-: the line $s_{a}$ belongs to the outer side of the a-th affine space;
-: the line $s_{a}^{'}$ belongs to the inner side of the a-th affine space;
-: the line $s_{b}$ belongs to the outside of the b-th affine space;
-: the line $s_{b}^{'}$ belongs to the inner side of the b-th affine space.

The addition of quadratic forms (29) or their averaging (29a) depends on the model representation. If we assume that two metric spaces are additively superimposed on each other, then the addition operation (29) should be used. If we assume that a metric space can be in a state with the metric s_a² or with the metric s_b² with equal probability, then this corresponds to the quantum mechanical approach, and the averaging operation (29a) should be used.

At this stage of the study, it is difficult to decide which operation "addition" (29) or "averaging" (29a) should be used. However, the quantum mechanical approach provides additional opportunities for probability theory and does not require an answer to the question: "Is the sum of solutions (for example, s_a² and s_b²) of Einstein's non-linear differential equations also a solution of this equations?". Therefore, the quantum mechanical approach looks much more preferable, especially when the sum of solutions is also a solution to a nonlinear equation. Arguments in favor of the second approach are presented in Appendix 1, see Ex.s (4.A1) – (32.A1).

Now, for example, consider the averaging of four metrics (14) – (20)

d_S1-4 = 1/4(ds₁^(–)2+ ds₂^(–)2 +ds₃^(–)2+ ds₄^(–)2).

(31)

As a result, we obtain the averaged metric

d s_{1 - 4}^{(-) 2} = f (r) c^{2} d t^{2} - k (r) d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(32)

where f (r) = \frac{1}{4} [(1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}}) + (1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}}) + (1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}}) + (1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}})],

(33)

k (r) = \frac{1}{4} [\frac{1}{(1 - \frac{r_{b 1}}{r} + \frac{r^{2}}{r_{a 1}^{2}})} + \frac{1}{(1 + \frac{r_{b 2}}{r} - \frac{r^{2}}{r_{a 2}^{2}})} + \frac{1}{(1 - \frac{r_{b 3}}{r} - \frac{r^{2}}{r_{a 3}^{2}})} + \frac{1}{(1 + \frac{r_{b 4}}{r} + \frac{r^{2}}{r_{a 4}^{2}})}] .

(34)

By analogy with (29) – (30), such a metric space is based on the interweaving of four affine extensions, which respectively belong to 8 linear forms ds_i^(–) and ds_i^(–)′, i.e. segments of 8 lines twisted into an 8-braid.

Such an 8-braid is described by a system of two complex conjugate quaternions:

d s_{1 - 4}^{(-)} = \frac{\sqrt{4}}{1} (d s_{1}^{(-)} + i d s_{2}^{(-)} + j d s_{3}^{(-)} + k d s_{4}^{(-)}),

(35)

d s_{1 - 4}^{(-) *} = \frac{\sqrt{4}}{1} (d {s_{1}^{(-)}}^{'} - i d {s_{2}^{(-)}}^{'} - j d {s_{3}^{(-)}}^{'} - k d {s_{4}^{(-)}}^{'}),

(35a)

whose product is equal to the metric (32).

On Figure 3 shows an illustration of the interweaving of several affine subspaces that form a multilayer metric space.

Properties of intertwined affine subspaces and multilayer metric spaces with signatures (+ – – –) and (– + + +) corresponding to the “vacuum balance” condition

(+ – – –) + (– + + +) = 0

(36)

detailed in the "Algebra of signatures" [16,17].

In the same papers [16,17], a more detailed analysis was carried out, considering metric spaces with all sixteen possible signatures:

\begin{matrix} (+ + + +) & (+ + + -) & (- + + -) & (+ + - +) \\ (- - - +) & (- + + +) & (- - + +) & (- + - +) \\ (+ - - +) & (+ + - -) & (+ - - -) & (+ - + +) \\ (- - + -) & (+ - + -) & (- + - -) & (- - - -) \end{matrix},

(27)

which in total correspond to the principle of "full vacuum (i.e., zero) balance", (37a)

In this expression, called in [16,17] ranking, the summation of the signs "+" and "–" is performed both in columns and in rows.

The simplified “vacuum balance” (36) follows from the ranking Ex. (37a) [16,17]

(37b)

That is, the additive superposition (in this case, the addition of signs of signatures by columns) of seven metric spaces with signatures in the denominator of the left column of the ranking Ex. (37b), form a Minkowski space with signature (+ – – –).

Whereas the additive superposition of seven metric spaces with signatures in the denominator of the right column of the ranking Ex. (37b), form an anti-Minkowski space with the opposite signature (– + + +).

Accounting for all sixteen metric spaces with signatures (37) can significantly enrich the cosmological models of the universe (see Appendix 2 and also [16,17]).

3. Extended Einstein's field equations

In the previous paragraphs of this article, we considered a set of solutions to the Einstein field equations (8), well known to specialists. In this paragraph, for the first time, it is proposed to consider an extended version of this equations.

Recall that Einstein, in order to write Eq.s (3), used the following property of the metric tensor

Λ \nabla_{j} g_{i k} = \nabla_{j} {Λ g}_{i k} = 0,

(28)

however, it is obvious that the covariant derivative of the infinite series

Λ_{l} \nabla_{j} g_{i k}

is also equal to zero

\nabla_{j} (Λ_{1} g_{i k} + Λ_{2} g_{i k} + Λ_{3} g_{i k} + . . . + Λ_{\infty} g_{i k}) = Λ_{1} \nabla_{j} g_{i k} + Λ_{2} \nabla_{j} g_{i k} + . . . + Λ_{\infty} \nabla_{j} g_{i k} = 0,

(39)

where Λ₁, Λ₂, … , Λ_∞ are constants that can take both positive (Λ_i > 0) and negative (Λ_i < 0) values.

Therefore, we use the same method that Einstein used to introduce the Λ-term into Eq.s (1) [2], and write the equations

R_{i k} - \frac{1}{2} R g_{i k} + Λ_{1} g_{i k} + Λ_{2} g_{i k} + Λ_{3} g_{i k} + . . . + Λ_{\infty} g_{i k} = 0,

or in a more compact form

R_{i k} - \frac{1}{2} R g_{i k} + g_{i k} \sum_{j = 1}^{\infty} Λ_{j} = 0,

(29)

where Λ_j = 3/r_аj² or – 3/r_аj², here r_aj is the radius of the j-th spherical formation.

If the sum of the series Λ₁ + Λ₂ + Λ₃ +…+ Λ_∞ converges to a constant number Λ₀, i.e., if

\sum_{j = 1}^{\infty} Λ_{j} = Λ_{0},

(41)

then Eq.s (40) takes the form of Eq.s (5)

R_{i k} - \frac{1}{2} R g_{i k} + Λ_{0} g_{i k} = 0,

(42)

which, like (6) – (7), is reduced to the form similar to Eq.s (8)

R_{i k} - g_{i k} Λ_{0} = 0 .

(43)

Therefore, the solutions of Eq.s (43) practically coincide with the solutions (14) – (25):

- with signature (+ – – –)

d s_{1}^{(-) 2} = (1 - \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(44)

d s_{2}^{(-) 2} = (1 + \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(45)

d s_{3}^{(-) 2} = (1 - \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(46)

d s_{4}^{(-) 2} = (1 + \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(47)

d s_{5}^{(-) 2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(48)

- and with signature (– + + +)

d s_{5}^{(+) 2} = - c^{2} d t^{2} + d r^{2} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(49)

d s_{4}^{(+) 2} = - (1 + \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(50)

d s_{3}^{(+) 2} = - (1 - \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(51)

d s_{2}^{(+) 2} = - (1 + \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{f}}{r} - \frac{Λ_{0} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(52)

d s_{1}^{(+) 2} = - (1 - \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{f}}{r} + \frac{Λ_{0} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(53)

where

Λ_{0}

and

r_{f}

are the zero results of the summation of alternating series

Λ_{0} = \sum_{j = 1}^{\infty} Λ_{j} = \sum_{j = 1}^{\infty} {(- 1)}^{j} \frac{3 N_{j}}{r_{a j}^{2}} = \sum_{n = 2 j}^{\infty} \frac{3 N_{n}}{r_{a n}^{2}} + \sum_{m = 2 j - 1}^{\infty} (- \frac{3 N_{m}}{r_{a m}^{2}}) = 0,

(54)

r_{f} = \sum_{j = 1}^{\infty} {{(- 1)}^{j} r}_{b j} = \sum_{n = 2 j}^{\infty} r_{b n} + \sum_{m = 2 j - 1}^{\infty} (- r_{b m}) = 0,

(55)

where N_j are the dimensionless corrective parameters of the considered cosmological model.

Such a cosmological model is the most optimal, since in the case of

Λ_{0} = 0

(54) the extended Einstein field equations as a whole take on the simplest form

R_{i k} = 0,

(55a)

with four Schwarzschild solutions

d s_{1}^{(-) 2} = (1 - \frac{r_{f}}{r}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{f}}{r})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{2}^{(-) 2} = (1 + \frac{r_{f}}{r}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{f}}{r})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{4}^{(+) 2} = - (1 + \frac{r_{f}}{r}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{f}}{r})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{3}^{(+) 2} = - (1 - \frac{r_{f}}{r}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{f}}{r})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

which, when condition (55) is met, turn into two Minkowski solutions (20) and (25), which is consistent with the principle of “maximum rationality” and the principle of “total average absence” (i.e., observance of the “vacuum balance”).

At the same time, it is possible that there is a slight imbalance between the positive and negative members of the series (54)

Λ_{0} = \sum_{n = 2 j}^{\infty} \frac{3 N_{n}}{r_{a n}^{2}} + \sum_{m = 2 j - 1}^{\infty} (- \frac{3 N_{m}}{r_{a m}^{2}}) \neq 0,

(55b)

r_{f} = \sum_{n = 2 j}^{\infty} r_{b n} + \sum_{m = 2 j - 1}^{\infty} (- r_{b m}) = 0,

(55c)

where j =1,2,3,…

For example, it is possible that the imbalance exists, but is extremely small.

{\lim_{n, m \to \infty} Λ}_{0} = Λ_{Σ} = 1.0905 \cdot 10^{- 52} m^{- 2},

i.e., tend to the value published by the Plank collaboration [14] for the Standard cosmological model Lambda-CDM; where

Λ_{Σ}

is the total cosmological constant (TCC).

Then Eq.s (43) takes the form

R_{i k} = Λ_{Σ} g_{i k},

(55d)

with four de Sitter solutions

d s_{1}^{(-) 2} = (1 + \frac{Λ_{Σ} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{Λ_{Σ} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{2}^{(-) 2} = (1 - \frac{Λ_{Σ} r^{2}}{3}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{Λ_{Σ} r^{2}}{3})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{4}^{(+) 2} = - (1 + \frac{Λ_{Σ} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{Λ_{Σ} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

d s_{3}^{(+) 2} = - (1 - \frac{Λ_{Σ} r^{2}}{3}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{Λ_{Σ} r^{2}}{3})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

In this case, according to Ex.s (7) and (4)

{4 Λ}_{Σ} = R, so R = \frac{12}{r_{a Σ}^{2}}, where r_{a Σ} = \sqrt{\frac{R}{12}} = \sqrt{\frac{Λ_{Σ}}{3}} \approx 1,6586 \cdot 10^{26} m .

(55e)

If there is a predominance of positive terms in Ex. (55b), then

Λ_{Σ}

> 0 (de Sitter universe); if negative terms predominate, then

Λ_{Σ}

< 0 (anti - de Sitter universe).

At the same time, in the author's opinion, the "vacuum balance" cannot be violated, since only mutually opposite entities can appear from the void (for example, convexity - concavity, wave - antiwave, particle-antiparticle, etc.). Therefore, if an imbalance (55b) of type

Λ_{Σ}

> 0 exists, then a counter-imbalance of type

Λ_{Σ}

< 0 must also coexist.

It is possible to restore the averaged “vacuum balance” in such a situation if we assume that the sign of the total cosmological constant (TCC) periodically changes with time. For example, it can be assumed that the value of the TCC fluctuates according to a sinusoidal law with an amplitude

Λ_{Σ} \approx 10^{- 52} m^{- 2}

. Then, on average, the “vacuum balance” is restored

R_{i k} = g_{i k} \bar{Λ_{Σ} \sin (2 π f_{u} t)} = 0,

(55f)

where

f_{u}

is the cosmological oscillation frequency.

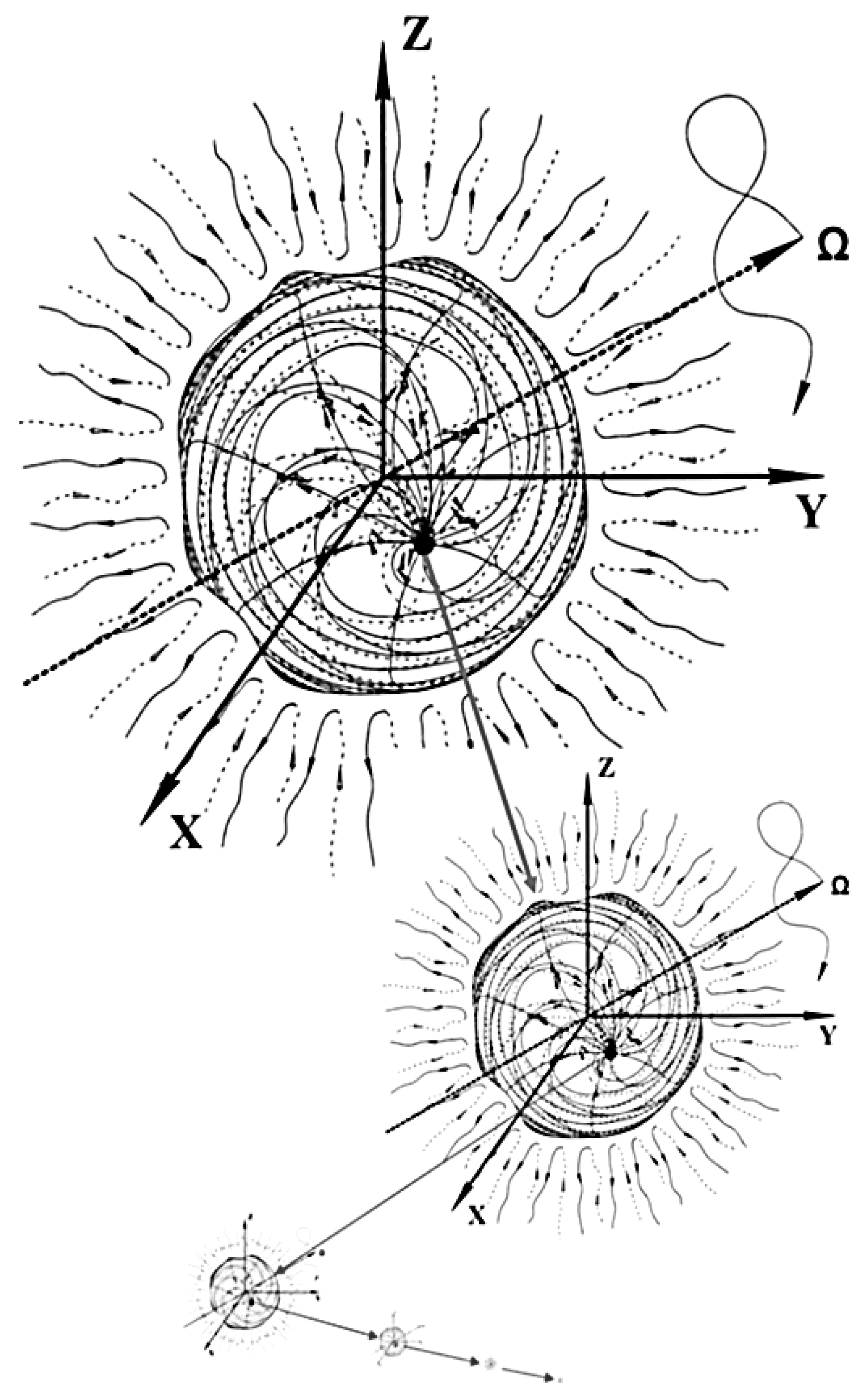
4. Closed ten-layer and ten-level cosmological model

In the previous section, it was shown that the extended Einstein field equations can contain an infinite number of

\pm Λ_{j}

-terms, provided that the sum of all these terms must tend to zero to maintain the “vacuum balance”.

Further, it will be shown that the cosmological model based on the extended Einstein field equations (43), taking into account Ex.s (54) and (55) [or (55b) and (55c)], can be a closed spherical space filled with an infinite number of spherical formations ("bubbles") and opposite anti-spherical formations ("anti-bubbles") with different radii

r_{а j}

, inside which there is an infinite number of smaller "bubbles" and "anti-bubbles" with different radii

r_{b j}

, and so it continues to infinity from level to level (see Figure 4).

At this point, for simplicity, we single out only ten levels with two mutually opposite spherical formations (i.e., a “bubble” and an “anti-bubble”) at each level.

In other words, to identify the main parameters of the multilevel cosmological model, we study a special case when, instead of infinite series (54) and (55), we use a simplified series limited by ten mutually opposite pairs of terms:

Λ_{0 (10)} = \sum_{j = 1}^{10} Λ_{j} = \sum_{j = 1}^{10} \frac{3}{r_{j}^{2}} + \sum_{j = 1}^{10} (- \frac{3}{r_{j}^{2}}) = 0,

(56)

r_{f (10)} = \sum_{k = 1}^{10} r_{j} + \sum_{j = 1}^{10} (- r_{j}) = 0 .

(57)

Consider separately the series with positive and negative terms

r_{f (10)} = \sum_{j = 1}^{10} r_{j}, Λ_{0 (10)} = 3 \sum_{j = 1}^{10} \frac{1}{r_{j}^{2}};

(58)

r_{f (- 10)} = \sum_{j = 1}^{10} (- r_{j}), Λ_{0 (- 10)} = 3 \sum_{k = 1}^{10} (- \frac{1}{r_{j}^{2}}) .

(59)

Let’s substitute series (58) into metrics (44) – (48) instead of series (56) and (57) and take into account that we can write:

1 - \frac{r_{f (10)}}{r} + \frac{Λ_{0 (10)} r^{2}}{3} = 1 - \frac{r_{1} + r_{2} + \dots + r_{10}}{r} + (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}} + \dots + \frac{1}{r_{10}^{2}}) r^{2} = = (1 - \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - (1 + \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + + (1 - \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}),

(60)

1 + \frac{r_{f (10)}}{r} - \frac{Λ_{0 (10)} r^{2}}{3} = 1 + \frac{r_{1} + r_{2} + . . . + r_{10}}{r} - (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}} + . . . + \frac{1}{r_{10}^{2}}) r^{2} = = (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - . . . + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}),

(61)

1 - \frac{r_{f (10)}}{r} - \frac{Λ_{0 (10)} r^{2}}{3} = 1 - \frac{r_{1} + r_{2} + . . . + r_{10}}{r} - (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}} + . . . + \frac{1}{r_{10}^{2}}) r^{2} = = (1 - \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - . . . + (1 - \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}),

(62)

1 + \frac{r_{f (10)}}{r} + \frac{Λ_{0 (10)} r^{2}}{3} = 1 + \frac{r_{1} + r_{2} + . . . + r_{10}}{r} + (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}} + . . . + \frac{1}{r_{10}^{2}}) r^{2} = = (1 + \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - . . . + (1 + \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) .

(63)

As a result, we obtain five metrics with signature (+ – – –):

d s_{1}^{(-) 2} = \{\begin{matrix} (1 - \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} - - {\{\begin{matrix} (1 - \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} - - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(64)

d s_{2}^{(-) 2} = \{\begin{matrix} (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} - - {\{\begin{matrix} (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} - - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(65)

d s_{3}^{(-) 2} = \{\begin{matrix} (1 - \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} - - {\{\begin{matrix} (1 - \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} - - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(66)

d s_{4}^{(-) 2} = \{\begin{matrix} (1 + \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} - - {\{\begin{matrix} (1 + \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} - - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(30)

d s_{5}^{(-) 2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(68)

Similarly, substitution of series (59) into metrics (49) – (53) leads to the following five similar metrics, but with the opposite signature (– + + +):

d s_{5}^{(+) 2} = - c^{2} d t^{2} + d r^{2} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(69)

d s_{4}^{(+) 2} = - \{\begin{matrix} (1 + \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} + + {\{\begin{matrix} (1 + \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} + + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(70)

d s_{3}^{(+) 2} = - \{\begin{matrix} (1 - \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} + + {\{\begin{matrix} (1 - \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} + + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(31)

d s_{2}^{(+) 2} = - \{\begin{matrix} (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} + + {\{\begin{matrix} (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} + + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(32)

d s_{1}^{(+) 2} = - \{\begin{matrix} (1 - \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\} c^{2} d t^{2} + + {\{\begin{matrix} (1 - \frac{r_{10}}{r} + \frac{r^{2}}{r_{9}^{2}}) - (1 + \frac{r_{9}}{r} - \frac{r^{2}}{r_{8}^{2}}) + (1 - \frac{r_{8}}{r} + \frac{r^{2}}{r_{7}^{2}}) - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) + (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 + \frac{r_{5}}{r} - \frac{r^{2}}{r_{4}^{2}}) + (1 - \frac{r_{4}}{r} + \frac{r^{2}}{r_{3}^{2}}) - (1 + \frac{r_{3}}{r} - \frac{r^{2}}{r_{2}^{2}}) + (1 - \frac{r_{2}}{r} + \frac{r^{2}}{r_{1}^{2}}) - (1 + \frac{r_{1}}{r} - \frac{r^{2}}{r_{10}^{2}}) \end{matrix}\}}^{- 1} d r^{2} + + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(33)

Let's try to connect the radii r_j, included in Ex.s (56) and (57), with the characteristic sizes of bodies in the world around us.

Let's assume that in the basis of a fully geometrized cosmological model there are only two geometric constants: R_v is the parametric radius of the universe, and l_с ≈ сΔt ≈ с·1sec ≈ 2.9·10¹⁰ cm is the distance that a light beam travels in vacuum in a time interval Δt = 1 sec.

Let’s assume that the radii r_j in the metrics (64) – (73) are estimated by the recursive formula consisting of the above two constants

r_j ~ R_v²/l_сj,

(34)

where

l_{с j} = {(2.9 \cdot 10^{10})}^{j}

cm is the distance obtained by raising the number 2.9·10¹⁰ to the power j (1, 2,…,10) with the dimension centimeter.

If we assume R_v ≈ 10²⁵ cm, then we obtain the following approximate recurrent formula

r_{j} ~ \frac{R_{v}^{2}}{l_{c j}} = \frac{10^{50}}{{(2.9 \cdot 10^{10})}^{j}} cm,

(35)

from which follows a hierarchical sequence of radii of ten spheres nested into each other (see Figure 5 and Figure 6):

(76)

Figure 5. Hierarchical sequence of nested spherical formations.

Figure 6. Three levels of a sequence of nested spherical formations.

The existence of spherical formations marked with an asterisk * has not been confirmed in practice due to the imperfection of modern technology. Therefore, it is proposed to consider the 10-level cosmological model as a speculative forecast of the author intended for the first working hypothesis. This forecast is based on the confessional intuition of the author, connected with the philosophical doctrine of the “Tree of Life” (i.e., “Tree of ten Sefirot”).

However, the radii r₂, r₃, r₄, r₅ and r₆ from the sequence (76), obtained using the recurrent formula (75), surprisingly turned out to be commensurate with the characteristic sizes of the cores (or nuclei) of the observed discrete hierarchical sequence of real spherical formations: metagalaxies, galaxies, stars (planets) and biological cells, while the radius r₆ practically coincided with the "classical radius of the electron" 2.8·10^–13 cm. Therefore, it is possible that compact formations with characteristic sizes r₁, r₇, r₈, r₉ and r₁₀ can also be detected over time.

Metrics (64) – (73) with a hierarchical sequence of radii r_j (76) describe the metric-dynamic state of a sequence of ten nested multilayer spherical formations (see Figure 5 and Figure 6), the proportions of which partially coincide with the sizes of a discrete sequence of cores (or nuclei) of real objects [17]. Therefore, such a ten-layer and ten-level cosmological model looks promising for further development and refinement.

However, this hierarchical model has one circumstance that does not lend itself to logical understanding. The fact is that from metrics (64) – (73) it follows that the 1-st sphere (whose radius is commensurate with the radius of the mega-universe r₁ ~ 10³⁹ cm) is located inside the 10-th sphere (with the instanton size r₁₀ ~ 10^–55 cm).

To verify this, follow, for example, the sequence of terms:

\begin{matrix} (1 + \frac{r_{10}}{r} - \frac{r^{2}}{r_{9}^{2}}) - (1 - \frac{r_{9}}{r} + \frac{r^{2}}{r_{8}^{2}}) + (1 + \frac{r_{8}}{r} - \frac{r^{2}}{r_{7}^{2}}) - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) + (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) - \\ - (1 - \frac{r_{5}}{r} + \frac{r^{2}}{r_{4}^{2}}) + (1 + \frac{r_{4}}{r} - \frac{r^{2}}{r_{3}^{2}}) - (1 - \frac{r_{3}}{r} + \frac{r^{2}}{r_{2}^{2}}) + (1 + \frac{r_{2}}{r} - \frac{r^{2}}{r_{1}^{2}}) - (1 - \frac{r_{1}}{r} + \frac{r^{2}}{r_{10}^{2}}) \end{matrix}

(77)

and pay attention to the last term, which contains r₁ and r₁₀. This means that the sphere with radius r₁ is inside the sphere with radius r₁₀ [17], as can be seen from the previous terms of the same expression. A similar situation takes place in all metrics (64) – (73).

Such isolation of the proposed 10-layer and 10-level cosmological model looks very extravagant and requires additional study and reflection. However, the history of science teaches that sometimes what looks impossible is disproved by experiment. For example, 100 years ago, Einstein and many of his contemporaries could not admit the idea that the part of the universe we observe is expanding with acceleration.

Note that today we do not see only the upper and lower "ends" of the proposed 10-layer and 10-level cosmological model, but in the interval from r₂ ~ 10²⁸ cm (scale of the observable universe) to r₆ ~ 10^–16 cm (intranuclear scale), this model can be useful for solving many problems.

5. Metric-dynamic models of «electron» and «positron»

For example, let’s select from a hierarchical discrete sequence of spheres nested into each other (see Figure 5 and Figure 6) two mutually opposite spherical formations with a radius r₆ ~ 10^–13 cm, which corresponds to the characteristic size of the "core" of an elementary particle (in particular core of the «electron» and "positron"). All other spherical formations from the considered hierarchical model (64) – (73) are arranged similarly.

In this work, the names of the particles are quoted, for example, «electron», since the metric-dynamic models of these spherical formations differ in many respects from the model ideas about these formations in modern physics.

In metrics (64) – (68), let’s leave for consideration only those terms that contain radii r₆. As a result, we obtain the following multilayer metric-dynamic model of a "convex" spherical formation, which we will call «electron»:

«ELECTRON»

(78)

"Convex" multilayer spherical formation with

a signature (+ – – –), consisting of:

The outer shell of the «electron»

in the interval [r₅, r₆] (Figure 7)

d s_{1}^{(+ - - -) 2} = (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(79)

d s_{2}^{(+ - - -) 2} = (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(80)

d s_{3}^{(+ - - -) 2} = (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(81)

d s_{4}^{(+ - - -) 2} = (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(82)

The сore of the «electron»

in the interval [r₅, r₆] (Figure 7)

d s_{1}^{(+ - - -) 2} = (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(83)

d s_{2}^{(+ - - -) 2} = (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(84)

d s_{3}^{(+ - - -) 2} = (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(85)

d s_{4}^{(+ - - -) 2} = (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(86)

The shelt of the «electron»

in the interval [0, ∞]

d s_{5}^{(+ - - -) 2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(36)

where r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~10^–24 cm.

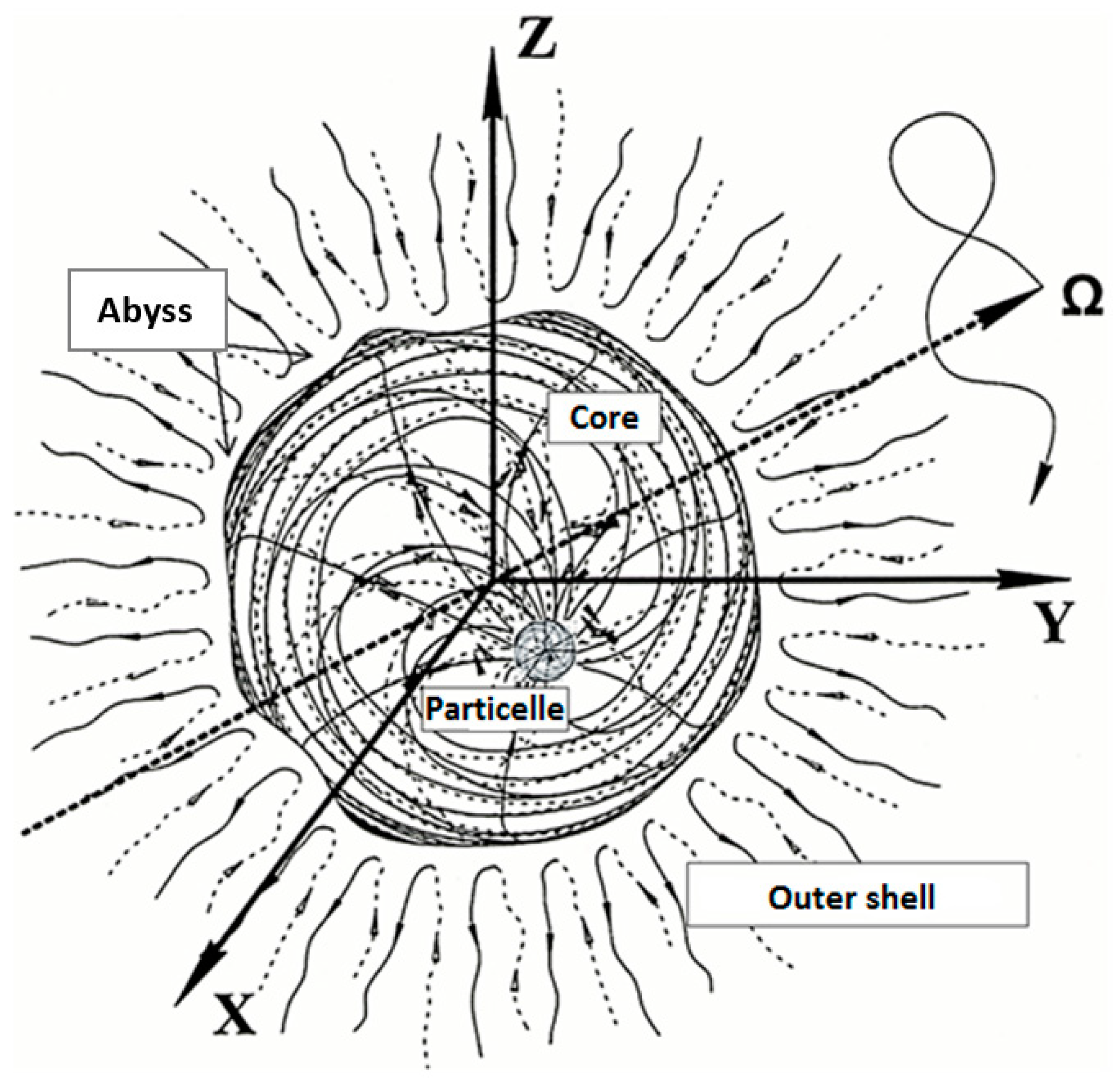
Figure 7. A model of a spherical formation (in particular, an «electron») with four clearly defined areas: "outer shell", "abyss" (or "rakia"), "core" and inner "nucleolus" (or “particelle”).

Similarly, in the metrics (69) – (73) we also leave only those terms that contain the radii r₆. As a result, we obtain the following multilayer metric-dynamic model of a "concave" spherical formation, which we will call «positron»:

«POSITRON»

(88)

"Concave" multilayer spherical formation with

a signature (– + + +), consisting of:

The outer shell of the «positron»

in the interval [r₅, r₆] (negative of the Figure 7)

d s_{1}^{(- + + +) 2} = - (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(89)

d s_{2}^{(- + + +) 2} = - (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(90)

d s_{3}^{(- + + +) 2} = - (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(91)

d s_{4}^{(- + + +) 2} = - (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(92)

The core of the «positron»

in the interval [r₅, r₆] (negative of the Figure 7)

d s_{1}^{(- + + +) 2} = - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(93)

d s_{2}^{(- + + +) 2} = - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(37)

d s_{3}^{(- + + +) 2} = - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(38)

d s_{4}^{(- + + +) 2} = - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(96)

The shelt of the «positron»

in the interval [0, ∞]

d s_{5}^{(- + + +) 2} = c^{2} d t^{2} - d r^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(97)

where r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~10^–24 cm.

The sets of metrics (78) and (88) differ only in their signature. That is, «electron» and «positron» are completely identical, but antipodal copies of each other. If an «electron» is conventionally called a "convex" spherical formation, then a «positron» is exactly the same conventionally "concave" spherical formation.

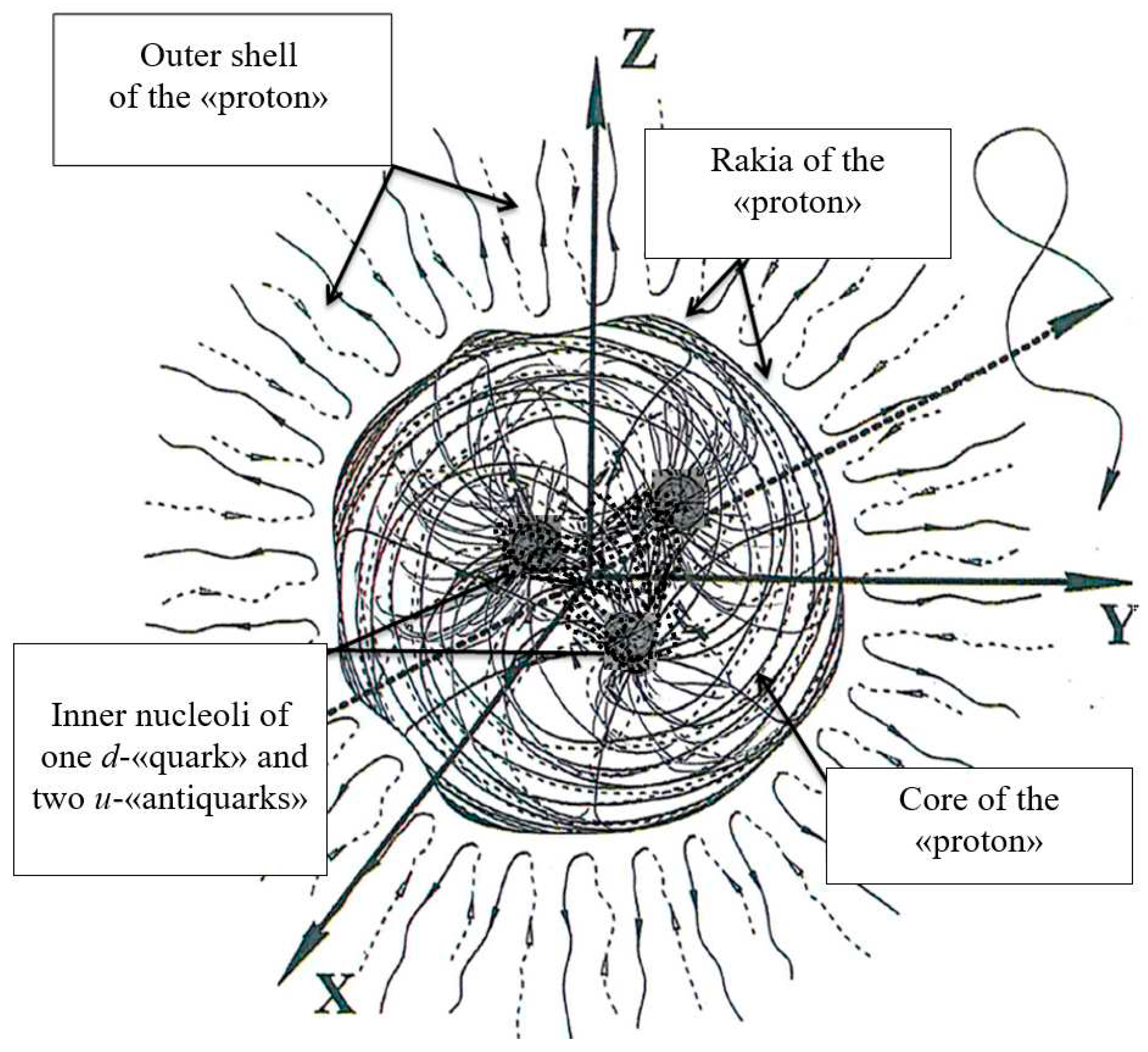
The Figure 7 shows a metric-dynamic (i.e., fully geometrized) model of a spherical formation with a radius from the hierarchical sequence (76). In a particular case, an «electron» (and/or its exact antipodal copy, a "positron") has (see Figure 7):

-: core with radius r₆ ~10^–13 cm;
-: inner “nucleolus” with radius r₇ ~10^–24 cm;
-: "outer shell", extending from r₆ ~10^–13 cm to r₅ ~ 10^–3 cm (or up to r₄ ~ 10⁸ cm, or up to

r₃ ~ 10¹⁸ cm and etc. depending on which spherical formation the given core of the «electron» is located inside).

In another case, for example, «planets» (or «anti-planets»): the "core" has a radius r₄ ~1,4·10⁸ cm; the inner "nucleolus" has a radius r₅ ~ 10^–3 cm (or r₆ ~ 10^-13 cm, etc., depending on which spherical formation is located inside the core of the «planet»), and "outer shell" extends from r₄ ~ 10⁸ cm to r₃ ~ 10¹⁸ cm (or up to r₂ ~ 10²⁹ cm, or up to r₁ ~ 10³⁹ cm and depending on, inside which sphere is the core of the "planet"). And so on.

The "shelt" (87) or (97) of a spherical formation begins at its center, and ends at infinity. The "shelt" is a kind of memory of the undeformed state of the considered area of space. The “shelt” does not seem to exist in the curved state of this area of space, but without the components of the metric tensor of the "shelt"

g_{i i}^{0 (-)}

g_{i i}^{0 (+)}

it is impossible to determine the deformation, relative elongation, speed and direction of movement of each local section of the object under study (see [16,17]).

The "abyss" (or "rakia") (see Figures 7) is a spherical boundary between the "core" and the "outer shell" of any spherical vacuum formation. The "rakia" is the most complex spherical area of the object under study, since it contains sub-layers associated with all higher spheres, inside which is the core of the «electron» (see Figures 5), as well as sub-layers associated with all the spheres that are inside the same core of the «electron».

A detailed study of the sets of metrics (79) – (87) describing the «electron» and (89) – (97) describing the «positron» is given in [17]. In the same place, taking into account all sixteen signatures (37), metric-dynamic models of almost all elementary particles included in the Standard Model are proposed: all types of «quarks», all types of «neutrinos», «mesons», etc., with the exception of Higgs boson (see Appendix 2 and also http://metraphysics.ru Contents, Chapter 2, sections 2.9 – 2.14).

6. Conclusion and discussion

The article proposes to take into account all 10 Kottler solutions (14) – (25) of the system of Einstein field (vacuum) equations (9) when constructing a multilayer and multilevel cosmological model, balanced on average with respect to the Einstein vacuum (i.e., "emptiness").

It is shown that the averaging of metric spaces represented by the quadratic forms

d s_{i}^{(-) 2}

and

d s_{i}^{(+) 2}

(14) – (25) is connected with the intertwining (i.e. twisting into bundles or braids) of the corresponding affine spaces, represented by linear forms

d s_{i}^{(-)}

and

d s_{i}^{(+)}

. Moreover, these affine bundles are described by Clifford algebras with the number of generators equal to the number of intertwined linear forms

d s_{i}^{(-)}

and

d s_{i}^{(+)}

(see [16,17]).

The second innovation proposed in this article is related to the increase to infinity of Λ_i-terms in Einstein's field equations (1).

The restrictions imposed on the sum of Λ_i-terms made it possible to propose a 10-layered and 10-level (hierarchical) cosmological model.

This model is a hierarchical sequence of nested spheres (see Figure 5) with the corresponding radii r_i (76), which are obtained using the recurrent formula (75) using only two dimensional parameters: R_v ≈ 10²⁵ cm is parametric the radius of the universe, and l_с ≈ 2,9·10¹⁰ cm is the distance that a light beam travels in vacuum in a single time interval Δt = 1sec.

Wherein, part of the radii r₂, r₃, r₄, r₅ and r₆ from the hierarchy (76) turned out to be commensurate with the characteristic sizes of the core (or nuclei) of the observed discrete sequence of real spherical formations (i.e., cores): metagalaxies, galaxies, stars (planets), biological cells (bacteria) and elementary particles.

At the end of the article, from the hierarchical solutions (64) – (73), the metric-dynamic models of the «electron» (78) and «positron» (88) are singled out, which are part of the proposed ten-layer and ten-level cosmological model.

Similarly, from solutions (64) – (73) can be singled out metric-dynamic models a «biological cell» with characteristic radius r₅ ~ 10^–3 cm, a «star» with characteristic core radius r₄ ~ 10⁸ cm and a «galaxy» with characteristic core radius r₃ ~ 10¹⁸ cm, etc.

Mathematical techniques that allow extracting various information about local spherical formations from a set of the solutions of extended Einstein's field equations, including a geometrized description of all particles that included in the Standard Model and all known force interactions: electrostatic, electromagnetic, weak and nuclear, are presented in the author's work [17] and on the website www.metraphysics.ru.

The advantages of the multilayer and multilevel cosmological model, proposed in this article, include:

- the complete absence of the need to introduce the concept of matter and its energy-momentum tensor as a source of curvature of 4-dimensional space. Here matter is replaced by an infinite number of spherical objects (see Figure 5 and Figure 6) with 10 types of characteristic sizes r_j (76) [17]. In this case, the right side of the Einstein-Hilbert equations (1) naturally vanishes. In this case, Einstein's field equations (8) and (43) are the general covariant expression of the conservation laws [16,17].

The disadvantages of the hierarchical 10-layer and 10-level cosmological model proposed in this article include:

- causal and logical inconsistency of this type of closedness of the universe, in which the largest sphere with the size r₁ ~ 10³⁹ cm is inside the smallest sphere with the size r₁₀ ~ 10^–55 cm, see, for example, Ex. (77a);

- unreasonable presence of the anthropic principle element in the recurrent formula (75), since the distance l_с ≈ с·1sec ≈ 2,9·10¹⁰ cm, which passes a light beam in vacuum in 1 sec (i.e., approximately during the period of oscillation of the human heart);

- an intuitive (i.e., scientifically unfounded) choice of 10 levels (nested spheres) of the cosmological model, despite the fact that today only five discrete levels out of ten are observed.

- the model does not answer the question why we observe a discrete (i.e., in fact, quantum) scale hierarchy of spherical formations (galaxies, stars, biological cells, elementary particles, etc.). The proposed model only "copies" such a discrete-hierarchical manifestation of reality. Obviously, Einstein's field equations (8) and (43) do not contain the possibility of explaining hierarchical discretization (i.e., scaling quantization). This means that Einstein's field equations are not complete. Perhaps, the Einstein-Cartan equations with torsion, or the equations of the geometry of absolute parallelism in a tetrad representation, have such properties. On the other hand, it can be assumed that hierarchical discreteness is not the result of the properties of differential equations, but is associated with boundary conditions. This is how Maxwell's equations for a waveguide or resonator lead to a discrete spectrum of electromagnetic waves.

At the same time, the multilayer and multilevel cosmological model proposed here is variable, that is, it can be refined as further analysis and accumulation of empirical data.

Acknowledgements

For assistance, I express my deep appreciation and gratitude to the mathematician David Reid (USA, Israel), Ph.D. Tatyana Levi, IT-specialist Alexander Maslov and Eliezer Reichman.

Appendix 1

The first Einstein field equation and its solutions

The Einstein-Hilbert equation for empty space (i.e., Einstein vacuum) has the form of equation (1) for

T_{i k} = 0

R_{i k} - \frac{1}{2} R g_{i k} = 0,

(1.A1)

where

R = g^{i k} R_{i k}

is the scalar curvature;

R_{i k} = \frac{\partial Г_{i k}^{l}}{\partial x^{l}} - \frac{\partial Г_{i l}^{l}}{\partial x^{k}} + Г_{i k}^{l} Г_{l m}^{m} - Г_{i l}^{m} Г_{m k}^{l}

is Ricci tensor;

Г_{i k}^{λ} = \frac{1}{2} g^{λ μ} (\frac{\partial g_{μ k}}{\partial x^{i}} + \frac{\partial g_{i μ}}{\partial x^{k}} - \frac{\partial g_{i k}}{\partial x^{μ}})

is Christoffel symbols.

Combining Eq.s (1.A1) with the contravariant components of the metric tensor

g^{i k}

, we obtain

g^{i k} (R_{i k} - \frac{1}{2} R g_{i k}) = R - \frac{n}{2} R = 0,

(2.A1)

where

n = g^{i k} g_{i k}

is the number of space dimensions.

For any n-dimensional space (except for n = 2), equality (2.A1) can be satisfied only for R = 0. Therefore, for n = 4, Eq. (1.A1) takes the simplest form

R_{i k} = 0

(3.A1)

We will call this equation the first Einstein vacuum equation, and it is an expression of the conservation laws, since

\nabla_{j} R_{i k} = \frac{\partial R_{i k}}{\partial x^{j}} = 0,

(3a.A1)

because \nabla_{j} 0 = \frac{\partial 0}{\partial x^{j}} - Г_{i j}^{l} 0 - Г_{k j}^{l} 0 = \frac{\partial 0}{\partial x^{j}} = 0.

(3b.A1)

In this case, the solutions of Eq.s (3.A1) describe the metric-dynamic state of stable vacuum formations.

Einstein wrote [19]: “The equation of gravity for empty space is the only rationally substantiated case of field theory that can claim to be rigorous.”

Solutions of the Eq.s (3.A1) are considered in many works on modern differential geometry and general relativity. However, none of the publications known to the author discusses the relationship between various solutions of this equations, so we will consider it in sufficient detail.

Solutions to Eq.s (3.A1) are sought in a spherical coordinate system in the form of metrics:

ds^(–)2 = е^νс²dt² – е^λdr² – r²dθ ² – r²sin²θ dϕ ² with signature (+ – – –),

(4.A1)

ds⁽⁺⁾² = –е^νс²dt² + е^λdr² + r²dθ ² + r² sin²θ dϕ ² with signature (– + + +),

(5.A1)

where ν and λ are the required functions of t and r.

As a result of substitution of the covariant and contravariant components of the metric tensor from the metric (4.A1) into Eq. (3.A1) for the stationary (i.e., time-independent) state of the "vacuum", a system of three equations is obtained [20]:

ν = – λ ,

(6.A1)

– е ^ν (ν′ /r + 1/r²) + 1/r² = 0,

(7.A1)

ν′′ + ν′ ² + 2ν′ /r = 0.

(8.A1)

The differential Eq. (7.A1) has three solutions:

ν₁ = ln(h₁+ h₂ /r), ν ₂ = ln(h₁ – h₂ /r), ν₃ = h₃,

(9.A1)

where h1, h2, h3 are integration constants.

Eq. (8.A1) also has three solutions:

ν₁ = ln(1+ r_b b/r), ν ₂ = ln(1 – r_b /r), ν ₃ = 0,

(10.A1)

where r_b is the integration constant (the radius of the spherical volume).

For h₁ = 1, h₂ = r_b and h₃ = 0, the solutions of Eq.s (7.A1) and (8.A1) coincide.

Substituting three possible solutions (10.A1) into the metric (4.A1) we get three metrics with the same signature (+ – – –):

ds₁^(–)2 = (1– r_b /r)с²dt² – (1– r_b /r) ^–1dr² – r²dθ ² – r²sin²θ dϕ ²,

(11.A1)

ds₂^(–)2 = (1+ r_b /r)с²dt² – (1+ r_b /r) ^–1dr² – r²dθ ² – r²sin²θ dϕ ²,

(12.A1)

ds₃^(–)2 = с²dt² – dr² – r²dθ ² – r²sin²θ dϕ ².

(13.A1)

Performing similar operations with the components of the metric tensor from the metric (5.A1), we obtain three more metrics that also satisfy Eq.s (3.A1), but with the opposite signature (– + + +):

ds₁⁽⁺⁾² = – (1– r_b /r)с²dt² + (1– r_b /r) ^–1dr² + r²dθ ² + r²sin²θ dϕ ²,

(14.A1)

ds₂⁽⁺⁾² = – (1+ r_b/r)с²dt² + (1+ r_b /r) ^–1dr² + r²dθ ² + r²sin²θ dϕ ²,

(15.A1)

ds₃⁽⁺⁾² = – с²dt² + dr² + r²dθ ² + r²sin²θ dϕ ².

(16.A1)

Irreducible into each other metrics (11.A1) – (16.A1) will be called generalized Schwarzschild metrics.

Metrics (11.A1) – (16.A1) describe the metric-dynamic state of the same vacuum region, therefore it is proposed to consider various options for averaging them, despite the fact that Eq.s (3.A1) is non-linear and, as a rule, in such cases, the sum of his decisions is not his own decision.

If the centers of the metrics (11.A1) – (13.A1) and (14.A1) – (16.A1) are aligned, then it is obvious that their sum is equal to zero

ds₁^(–)2+ds₂^(–)2+ds₃^(–)2+ds₁⁽⁺⁾²+ds₂⁽⁺⁾²+ds₃⁽⁺⁾² = 0∙с²dt² +0∙dr² + 0∙dθ ²+ 0∙sin²θ dϕ ²= 0.

(17.A1)

Received metric d_s⁽⁰⁾² = g_ij⁽⁰⁾ dxⁱ dx^j ,

(18.A1)

where g_{i j}^{(0)} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}),

(19.A1)

is also a trivial solution of the vacuum Eq.s (3.A1).

Thus, contrary to expectations, the addition of six metrics (11.A1) – (16.A1) led to an additional solution to Eq. (3.A1).

Consider now the arithmetic mean of two metrics (11.A1) and (12.A1)

d s_{12}^{(-) 2} = \frac{1}{2} (d s_{a}^{(-) 2} + d s_{b}^{(-) 2}) = c^{2} d t^{2} - \frac{r^{2}}{r^{2} - r_{b}^{2}} d r^{2} - r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2} .

(20.A1)

The distance between two points r₁ and r₂ along the length with the signature (+ – – –) in general relativity is determined by the expression

r_{2} - r_{1} = \int_{r_{1}}^{r_{2}} \sqrt{- g_{11}^{(-)}} d r .

(21.A1)

in the case of substitution

g_{11}^{(-)}

from the averaged metric (20.A1), we obtain

r_{2} - r_{1} = \int_{r_{1}}^{r_{2}} \sqrt{- (- \frac{r^{2}}{r^{2} - r_{b}^{2}})} d r = \int_{r_{1}}^{r_{2}} \frac{r d r}{\sqrt{r^{2} - r_{b}^{2}}} = \sqrt{r^{2} - r_{b}^{2}} |_{r_{1}}^{r_{2}} .

(22.A1)

Let’s first find the value of the segment between the points r₁= r_b and r₂ = ∞:

\sqrt{r^{2} - r_{b}^{2}} |_{0}^{r_{b}} = - \sqrt{- r_{b}^{2}} = - \sqrt{- 1} r_{b} = - i r_{b} .

(23.A1)

The length of this segment is equal to the radius of the cavity r_b, and the imaginary nature of this result indicates that there is no "vacuum" in the cavity. Outside this cavity from r₁= r_b to r₂ = ∞ we have

r_{2} - r_{1} = \sqrt{r^{2} - r_{b}^{2}} |_{r_{b}}^{\infty} = \sqrt{\infty^{2} - r_{b}^{2}} .

(24.A1)

In the absence of vacuum deformation, the distance between the points r₂ = ∞ and r₁ = r_b is equal ∞ – r_b, and in the case under consideration it is equal to (24.A1). The difference between these segments is approximately equal to

\sqrt{\infty^{2} - r_{b}^{2}} - (\infty - r_{b}) \approx r_{b} .

(25.A1)

This result shows that the average vacuum extension on the segment ]r_b, ∞[ is compressed by the value ~ r_b, in all radial directions due to the fact that it is displaced from the cavity with radius (25.A1). This result is similar to an air bubble in a liquid (Figure 2.A.1).

The difference between the initial (non-curved) state of a local area of vacuum and its actual (curved) state is determined by the difference [21]

{ds}^{(–) 2} – {ds}^{0 (–) 2} = (g_{i j}^{(-)} – g_{i j}^{0 (-)}) {dx}^{i} {dx}^{j}

(26.A1)

where

g_{i j}^{0 (-)}

are the components of the metric tensor of the non-curved vacuum from the metric (13.A1).

Figure 2.A1. Air bubble in liquid

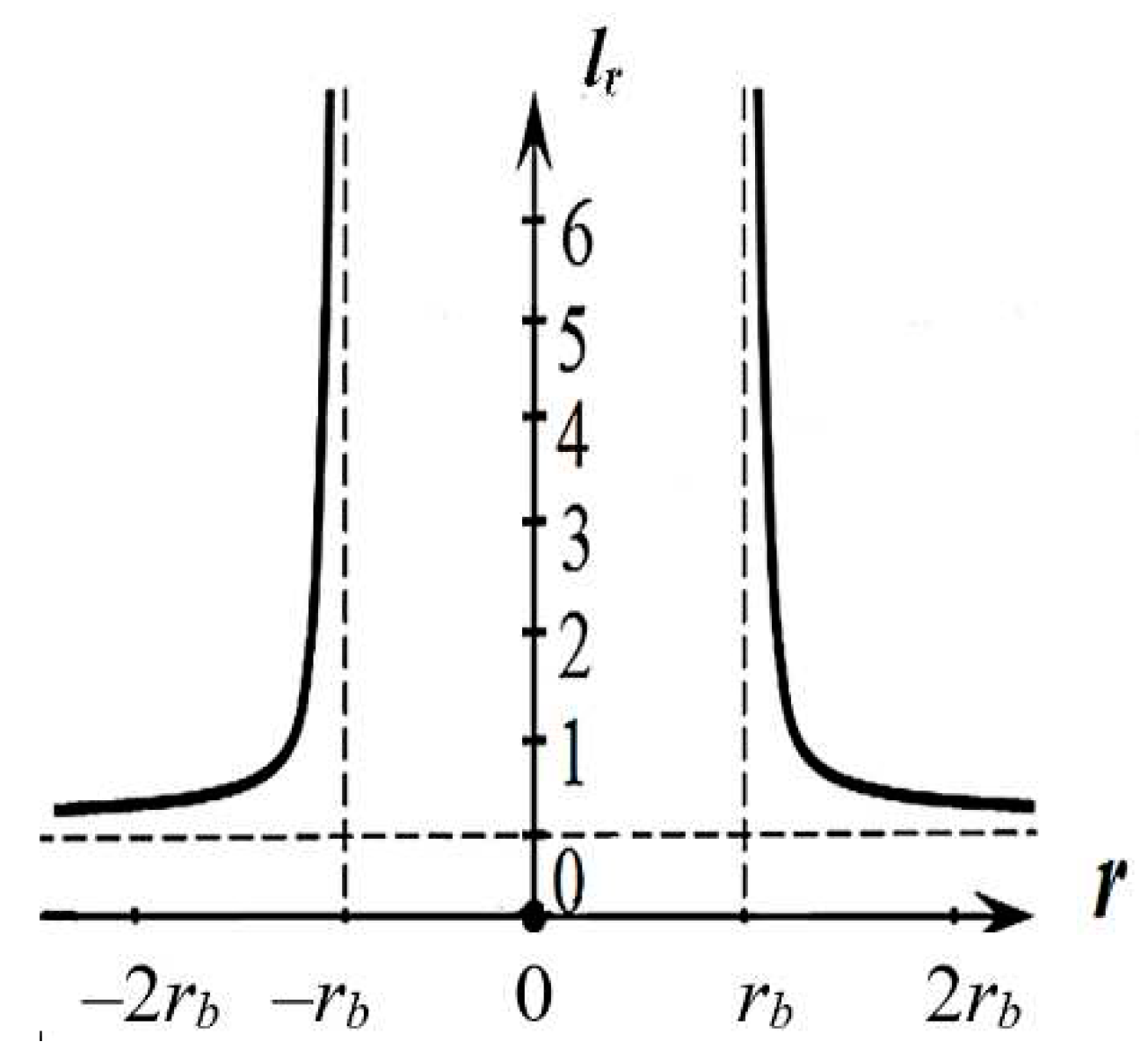
Figure 3.A1. Graph of the function l_r^(–) – the relative elongation of the vacuum in the outer shell surrounding the spherical cavity. The calculation was performed at r_b = 2, using the software MathCad 15

The relative elongation of the vacuum region in this case is [21]

l^{(-)} = \frac{d s^{(-)} - d s^{0 (-)}}{d s^{0 (-)}} = \frac{d s^{(-)}}{d s^{0 (-)}} - 1,

(27.A1)

whence it follows [21]

ds^(–)2 = (1 + l^(–))² ds^0(–)2,

(28.A1)

and

l_{i}^{(-)} = \sqrt{1 + \frac{g_{i i}^{(-)} - g_{i i}^{0 (-)}}{g_{i i}^{0 (-)}}} - 1 = \sqrt{\frac{g_{i i}^{(-)}}{g_{i i}^{0 (-)}}} - 1.

(29.A1)

The uncarved state of the vacuum section under consideration is given by the metric (13.A1), therefore, substituting the components g_ii^0(–) and g_ii^(–), respectively, from (13.A1) and (20.A1) into (29.A1), we obtain the relative elongation of the vacuum in each radial direction in the region from r_b to ∞ (30.A1)

l_{t}^{(-)} = 0, l_{r}^{(-)} = \sqrt{\frac{r^{2}}{r^{2} - r_{b}^{2}}} - 1, l_{θ}^{(-)} = 0, l_{ϕ}^{(-)} = 0 .

The graph of the function l_r^(–) (30.A1) is shown in Figure 3.A1. For r = r_b, this function tends to infinity, and for r < r_b it becomes imaginary.

Here we will not discuss the question: – What is inside the cavity with radius r_b, if the vacuum is displaced from there? When considering the second and third Einstein vacuum equations (8) and (43), this problem will be solved by itself.

Thus, averaging the metrics (11.A1) and (11.A1) leads to a metric-dynamic description of a stable vacuum formation of the "air bubble in liquid" (see Figure 3.A1) type, while these metrics alone do not lead to such results.

Averaging the metrics (14.A1) and (15.A1) allows you to get similar results, but with the opposite signature

d s_{12}^{(+) 2} = \frac{1}{2} (d s_{1}^{(+) 2} + d s_{2}^{(+) 2}) = - c^{2} d t^{2} + \frac{r^{2}}{r^{2} - r_{b}^{2}} d r^{2} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2} .

(31.A1)

l_{i}^{(+)} = \sqrt{1 + \frac{g_{i i}^{(+)} - g_{i i}^{0 (+)}}{g_{i i}^{0 (+)}}} - 1 = \sqrt{\frac{g_{i i}^{(+)}}{g_{i i}^{0 (+)}}} - 1 = \sqrt{\frac{r^{2}}{r^{2} - r_{b}^{2}}} - 1.

(32.A1)

Appendix 2

The Standard Model of Elementary Particles

from the Algebra of signatures

1.A2 Models of х_i⁺-«quark» and x_i^–-«antiquark» in the Algebra of signatures

The fundamentals of "Algebra of signatures" and "Stochastic Metraphysics" (that is, fully geometrized physics from the standpoint of Algebra of signatures) are described in [16,17].

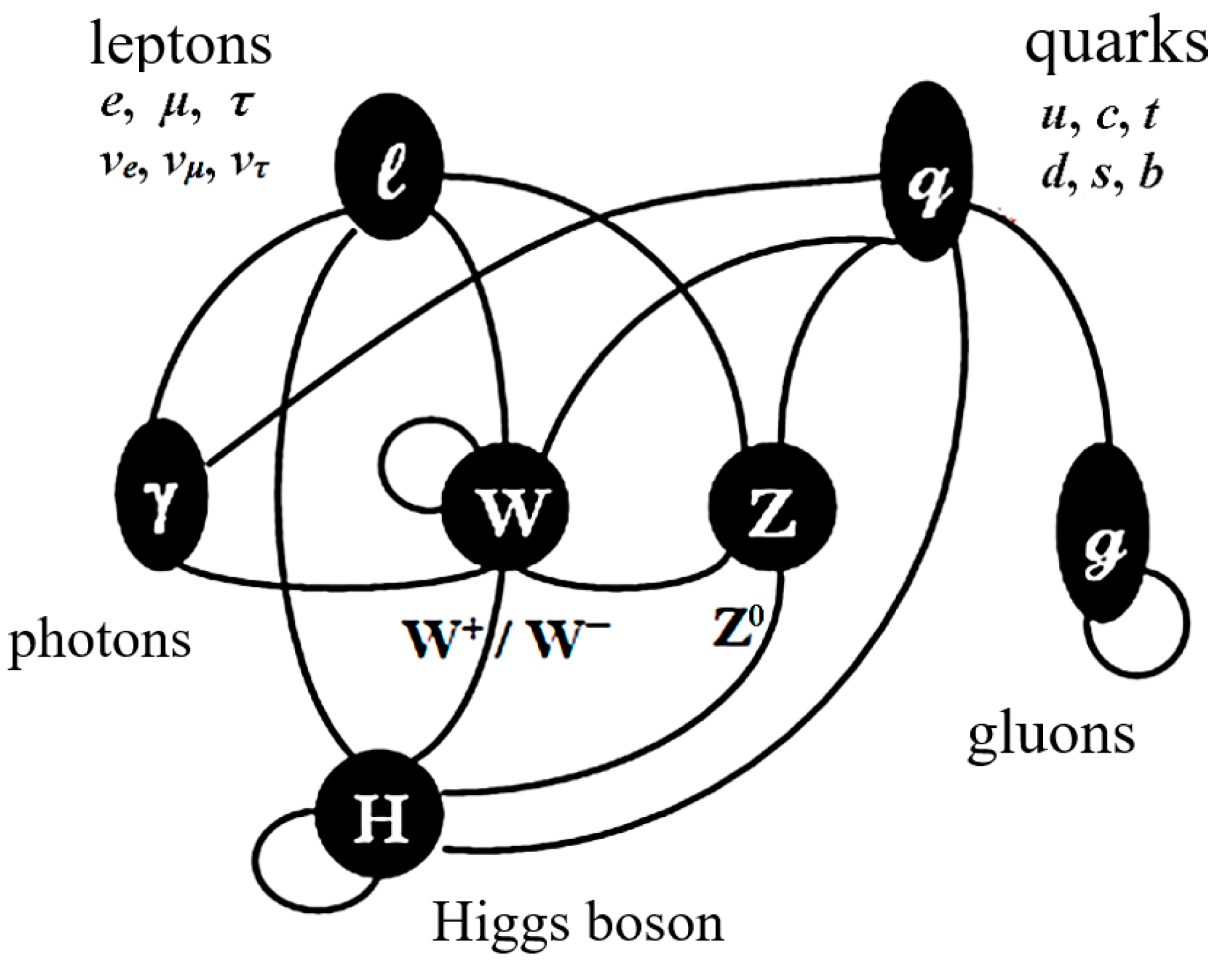
This Appendix contains only the main conclusions of the Algebra of signatures related to the Standard Model of elementary particles (Figure 1.A2).

Figure 1.A2. Elements of the Standard Model of elementary particles

In the above article, it was conditionally assumed that an «electron» is a spherical convexity in empty space (i.e., the Einstein vacuum), which is described by a set of metrics (79) – (87) with the signature (+ – – –); and a «positron» is the exact opposite copy of an «electron», i.e. spherical concavity in the Einstein vacuum, which is described by a set of metrics (89) – (97) with an inverted signature (– + + +).

The Algebra of signatures takes into account all 16 signatures (37), and the "building material" of the entire variety of observed objects are «quarks» and «antiquarks»:

Х_i^–-«QUARK» or Х_i⁺-«ANTIQUARK»

(1.A2)

"Convex-concave" multilayer spherical formation

with one of the following signatures:

\begin{matrix} (+ + + +) & (+ + + -) & (- + + -) & (+ + - +) \\ (- - - +) & (- + + +) & (- - + +) & (- + - +) \\ (+ - - +) & (+ + - -) & (+ - - -) & (+ - + +) \\ (- - + -) & (+ - + -) & (- + - -) & (- - - -) \end{matrix},

(2.A2)

consisting of:

The outer shell of thex_i⁺-«quark» orx_i^–-«antiquark»

in the interval [r₅, r₆] (Figure 8)

d s_{1}^{(\pm) 2} = \pm (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(3.A2)

d s_{2}^{(\pm) 2} = \pm (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(4.A2)

d s_{3}^{(\pm) 2} = \pm (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(5.A2)

d s_{4}^{(\pm) 2} = \pm (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(6.A2)

The core of thex_i⁺-«quark» orx_i^–-«antiquark»

in the interval [r₆, r₇] (Figure 8)

d s_{1}^{(\pm) 2} = \pm (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(7.A2)

d s_{2}^{(\pm) 2} = \pm (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(8.A2)

d s_{3}^{(\pm) 2} = \pm (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}),

(9.A2)

d s_{4}^{(\pm) 2} = \pm (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} \pm \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2});

(10.A2)

The shelt of thex_i⁺-«quark» orx_i^–-«antiquark»

in the interval [0, ∞]

d s_{5}^{(\pm) 2} = \pm c^{2} d t^{2} \pm d r^{2} \pm r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) .

(11.A2)

where r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~10^–24 cm.

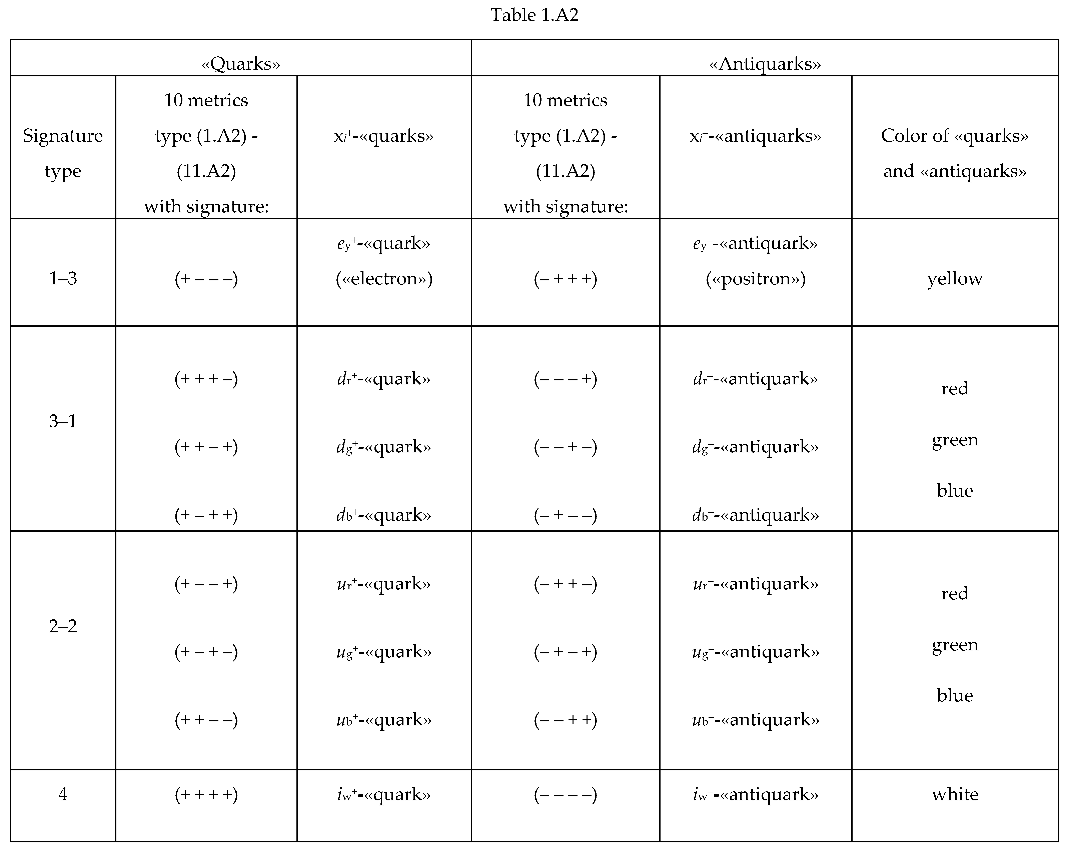
Signatures, colors and names of all 16 possible x_i⁺-«quarks» and x_i^–-«antiquarks» presented in Table. 1.A2.

Note that within the framework of the Algebra of signatures, these 16 x_i⁺-«quarks» and x_i^–-«antiquarks» refer not only to elementary particles, but also to any other spherical formations from the hierarchy (76). Only instead of radii r₅ , r₆ , r₇ in metrics (1.П2) – (11.П2) it is necessary to substitute accordingly: for bacteria r₄ , r₅ , r₆; for stars r₃ , r₄ , r₅; for galaxies r₂ , r₃ , r₄ etc.

For example, let's represent a u_r^–-«antiquark» in expanded form:

u_r^–-«ANTIQUARK»

(12.A2)

"Convex-concave" multilayer spherical formation

with the signatures (– + + –), consisting of:

The outer shell of theu_r^–-«antiquark»

in the interval [r₅, r₆] (Figure 8)

d s_{1}^{(- + + -) 2} = - (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

(13.A2)

d s_{2}^{(- + + -) 2} = - (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

(14.A2)

d s_{3}^{(- + + -) 2} = - (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

(15.A2)

d s_{4}^{(- + + -) 2} = - (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2};

(16.A2)

The core of the u_r^–-«antiquark»

in the interval [r₆, r₇] (Figure 8)

d s_{1}^{(- + + -) 2} = - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2}

(17.A2)

d s_{2}^{(- + + -) 2} = - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

(18.A2)

d s_{3}^{(- + + -) 2} = - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

(19.A2)

d s_{4}^{(- + + -) 2} = - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2};

(20.A2)

The shelt of the u_r^–-«antiquark»

in the interval [0, ∞]

d s_{5}^{(- + + -) 2} = - c^{2} d t^{2} + d r^{2} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2} .

(21.A2)

where r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~10^–24 cm.

Let's introduce the notation for 16 types of spherical formations: (22.A2)

10* metrics of the form (12.A2) with signature (+ – – –) – yellow e_y^–-«quark» («electron»);

10 metrics of the form (12.A2) with signature (– + + +) – yellow e_y⁺-«antiquark» («positron»);

10 metrics of the form (12.A2) with signature (+ + + –) – red d_r⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (+ + – +) – green d_g⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (+ – + +) – blue d_b⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (– – – +) – red d_r^–-«quark»;

10 metrics of the form (12.A2) with signature (– – + –) – green d_g^–-«quark»;

10 metrics of the form (12.A2) with signature (– + – –) – blue d_b^–-«quark»;

10 metrics of the form (12.A2) with signature (+ – – +) – red u_r⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (+ – + –) – green u_g⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (+ + – –) – blue u_b⁺-«antiquark»;

10 metrics of the form (12.A2) with signature (– + + –) – red u_r^–-«quark»;

10 metrics of the form (12.A2) with signature (– + – +) – green u_g^–-«quark»;

10 metrics of the form (12.A2) with signature (– – + +) – blue u_b^–-«quark»;

10 metrics of the form (12.A2) with signature (– – – –) – white i_w^–-«quark»;

10 metrics of the form (12.A2) with signature (+ + + +) – white i_w⁺-«antiquark».

*10 metrics (12.A2), because Shelt type (21.A2) refers to both the "core" and the "outer shell" of the corresponding x_i^–-«quark» or x_i⁺-«antiquark» (Figure 8). Thus, 5 metrics describe the "core", and 5 metrics describe the "outer shell" of each x_i^–-«quark» and x_i⁺-«antiquark».

Of the spherical formations (22.A2), only a convex formation are stable – «electron» (e_y^–-«quark») with the signature (+ – – –) and a concave formation is a “positron” (e_y⁺-«antiquark») with signature (– + + +), because they consist of solutions of Einstein's field equations (8), which is the stability condition. All other spherical formations from the list (22.A2) are unstable, because do not satisfy the conditions of stability (8). That is, when substituting the components of metric tensors from metrics (1.A2) – (11.A2) with any other signature except (+ – – –) and (– + + +) into Eq.s (8), equality will not work.

At the same time, out of 16 x_i⁺-«quark» and x_i^–-«antiquark» from the list (22.A2) it is possible to compose averaged stable spherical formations with signatures (+ – – –) or (– + + +). This will be shown in the following paragraphs.

2.A2 Models of «proton» and «antiproton» in the Algebra of signatures

On average, stable spherical formations with signatures (+ – – –) or (– + + +) can be composed of two different-colored u-«quarks» (or u-«antiquarks») and one d-«quark» (or d-«antiquark») from the list (22.A2):

where p_i^– are three possible states of p_i^–-«proton» (i = 1, 2, 3) with signature (– + + +)

where p_i⁺ are three possible states of p_i⁺-«antiproton» with signature (+ – – –).

In a more compact form, the states a p_i^–-«proton» and p_i⁺-«antiproton» can be represented as

p₁⁺ = u_з^–u_г^–d_к⁺, p₂ ⁺ = u_к^– u_г^– d_з⁺, p₃⁺ = u_з^– u_к^– d_г⁺,

(29.A2)

p₁^– = u_з^–u_г^–d_к⁺, p₂ ^– = u_к^– u_г^– d_з⁺, p₃^– = u_з^– u_к^– d_г⁺.

(30.A2)

This type of recording of the states of the «proton» and «antiproton» almost completely coincides with the recording of the states of the proton and antiproton in modern quantum chromodynamics, on which the Standard Model of elementary particles is based.

The difference, however, is that in the Standard Model, protons are made up of quarks and antiprotons are made up of antiquarks, while in the Algebra of signatures p_i^–-«proton» and p_i⁺-«antiproton» are made up of x_i⁺-«quarks» and x_i^–-«antiquarks». Therefore, in the Algebra of signatures, there is no problem associated with the baryon asymmetry of the Universe.

For example, let's imagine a multilayer metric-dynamic model of p_i^–-«proton» (23.A2)

d_к⁺(+ + + –)

u_з^– (– + – +)

u_г^–(– – + +)

р₁⁺(– + + +) ₊

in the expanded form:

p₁^–-«PROTON»

(31.A2)

On average, a "concave" multilayer vacuum formation

with a common signature (– + + +)

consisting of:

d_r⁺-«quark»

"Convex-concave" multilayer spherical formation

with the signatures (+ + + –), consisting of:

The outer shell of the d_r⁺-«quark» (+ + + –)

(32.A2)

in the interval [r₅, r₆] (Figure 1.A2)

d s_{1}^{(+ + + -) 2} = (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(+ + + -) 2} = (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(+ + + -) 2} = (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(+ + + -) 2} = (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

The core of the d_r⁺-«quark» (+ + + –)

(33.A2)

in the interval [r₆, r₇] (Figure 1.A2)

d s_{1}^{(+ + + -) 2} = (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(+ + + -) 2} = (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(+ + + -) 2} = (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(+ + + -) 2} = (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2},

The shelt of thed_r⁺-«quark» (+ + + –)

(34.A2)

in the interval [0, ∞]

d s_{5}^{(+ + + -) 2} = c^{2} d t^{2} + d r^{2} + r^{2} d θ^{2} - r^{2} \sin^{2} θ d ϕ^{2};

u_g^–-«antiquark»

"Convex-concave" multilayer spherical formation

with the signatures (– + – +), consisting of:

The outer shell of the u_g^–-«antiquark» (– + – +)

(35.A2)

in the interval [r₅, r₆] (Figure 1.A2)

d s_{1}^{(- + - +) 2} = - (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(- + - +) 2} = - (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(- + - +) 2} = - (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(- + - +) 2} = - (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

The core of the u_g^–-«antiquark» (– + – +)

(36.A2)

in the interval [r₆, r₇] (Figure 1.A2)

d s_{1}^{(- + - +) 2} = - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(- + - +) 2} = - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(- + - +) 2} = - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(- + - +) 2} = - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} + \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

The shelt of the u_g^–-«antiquark» (– + – +)

(37.A2)

in the interval [0, ∞]

d s_{5}^{(- + - +) 2} = - c^{2} d t^{2} + d r^{2} - r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2};

u_b^–-«antiquark»

"Convex-concave" multilayer spherical formation

with the signatures (– – + +), consisting of:

The outer shell of the u_b^–-«antiquark» (– – + +)

(38.A2)

in the interval [r₅, r₆] (Figure 1.A2)

d s_{1}^{(- - + +) 2} = - (1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(- - + +) 2} = - (1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(- - + +) 2} = - (1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{6}}{r} - \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(- - + +) 2} = - (1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{6}}{r} + \frac{r^{2}}{r_{5}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

The core of the u_b^–-«antiquark» (– – + +)

(39.A2)

in the interval [r₆, r₇] (Figure 1.A2)

d s_{1}^{(- - + +) 2} = - (1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{2}^{(- - + +) 2} = - (1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{3}^{(- - + +) 2} = - (1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 - \frac{r_{7}}{r} - \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

d s_{4}^{(- - + +) 2} = - (1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}}) c^{2} d t^{2} - \frac{d r^{2}}{(1 + \frac{r_{7}}{r} + \frac{r^{2}}{r_{6}^{2}})} + r^{2} d θ^{2} + \sin^{2} θ d ϕ^{2},

The shelt of the u_g^–-«antiquark» (– – + +)

(40.A2)

in the interval [0, ∞]

d s_{5}^{(- - + +) 2} = - c^{2} d t^{2} - d r^{2} + r^{2} d θ^{2} + r^{2} \sin^{2} θ d ϕ^{2},

where r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~10^–24 cm.

Figure 1.A2. Core of the «proton» consists of 3 practically superimposed cores: the core of one d-«quark» and of two cores u-«antiquarks». The inner nucleoli of these 3 "quarks" are in constant chaotic movement and interweaving with each other.

When averaging homogeneous terms in metrics (32.A2) – (40.A2), is obtained a set of metrics (89) – (97) describing the metric-dynamic state of the «positron». However, it should be expected that the radius of the core of the «protons», consisting of the cores of 1 «quark» and 2 «antiquarks», will be greater than the radius of the core of the «positron», because the inner nucleoli of the three «quarks» are difficult to interact, pushing each other away from the common center r = 0 (see Figure 1.A2).

The problem of the confinement of three convex-concave spherical formations: d_r⁺-«quark», u_g^–-«antiquark» and u_b^–-«antiquark» is solved by itself, since each x_i⁺-«quark» or x_i^–-«antiquark» from list (22.A2), except e_y^– and e_y⁺, are unstable deformed states of vacuum.

Separately d_r⁺-«quark», u_g^–-«antiquark» and u_b^–-«antiquark» cannot exist for a long time, because the metrics describing them (32.A2) – (40.A2) are not solutions of Einstein's vacuum equation (8). Only together, they form a stable on average "concave" vacuum formation «proton» (see Figure 1.A2), each averaged layer of which satisfies the stability condition (8).

The centers of the «quarks» d_r⁺, u_b^– and u_b^– should wander so chaotically about the common center r = 0 and relative to each other (see Figure 1.A2) so that only on average their centers coincide with the common center of the «proton» cores: <r_r> = r = 0, <r_g> = r = 0, <r_b> = r = 0. Therefore, we are forced to apply not only the metric-dynamic, but also the statistical description of intranuclear processes, which partly considered in [16,17].

The set of metrics (32.A2) – (40.A2) when using the mathematical techniques given in [16,17], allows to extract information about the set of processes and sub-processes occurring both inside the «proton» core and in its "outer shell".

A serious difference between the Algebra of signatures (AS) and the Standard Model of Elementary Particles (SMEP) is that the AS not only largely coincides with the quantum chromodynamics of SMEP, but also extends to spherical objects of any scale.

For example, if in the metrics (1.A2) – (40.A2) we substitute instead of radii:

r₅ ~ 10^–3 cm, r₆ ~10^–13 cm, r₇ ~ 10^–24 cm,

respectively, the radii from the hierarchical sequence (76):

r₃ ~ 10¹⁸ cm, r₄ ~ 10⁸ cm, r₅ ~ 10^–3 cm,

then we get stellar metric Chromodynamics.

Similarly, if from the same sequence (76) we substitute into metrics (32.A2) – (40.A2), respectively, the radii

r₂ ~ 10²⁹ cm, r₃ ~ 10¹⁸ cm, r₄ ~ 10⁸ cm,

then we get galactic metric Chromodynamics, and so on.

3.A2 The «neutron» model in the Algebra of signatures

In modern nuclear physics, it is believed that the neutron consists of two d-quarks with a charge of (–1/3)e and one u-quark with a charge of (2/3)e (where e is the electron charge)

n = ddu.

(41.A2)

As a result of this combination, the neutron turns out to be an electrically neutral particle with a zero total charge (–1/3)e + (–1/3)e + (2/3)e = 0.

In Algebra of signatures of a «particle» consisting of three «quarks» («antiquarks») with a zero “electric” environment are not obtained. Since there is not a single additive combination of three of the 16 signatures (37), leading to a zero signature (0 0 0 0), which actually means that all vacuum currents (flows) in the outer shell of such a «particle» are completely mutual compensated [17].

The desired result is achieved in the case of rankings consisting of four signatures. Therefore, an "electrically" neutral «particle» («neutron») can have the following topological (nodal) configurations:

(42.A2)

where (43.A2)

i_w⁺ – white i_w⁺-«quark», i.e. 10 metrics of the form (1.A2) with signature (+ + + +);

i_w^– –white i_w⁺-«antiquark», i.e. 10 metrics of the form (1.A2) with signature (– – – –),

(i from the word invisible). These «quarks» are called white because they are practically invisible inside the core of the «neutron», because in terms of topology, they are "point" and "anti-point" [16,17]. Apparently, therefore, their presence in the core of the neutron was not detected experimentally, and was not taken into account by the Standard Model.

Thus, within the framework of the Algebra of signatures, eight possible states of the «neutron» can be represented as:

n₁⁰ = i_б^–d_г⁺d_з⁺u_к^–, n₂⁰ = i_б^–d_к⁺d_з⁺u_г^–, n₃⁰ = i_б^–d_к⁺d_г⁺u_з^–, n₄⁰ = i_б^–d_к⁺d_г⁺u_з^–,

(44.A2)

n₅⁰ = i_б⁺d_г^–d_з^–u_к⁺, n₆⁰ = i_б⁺d_з^–d_к^–u_г⁺, n₇⁰ = i_б⁺d_г^–d_к^–u_з⁺, n₈⁰ = i_б⁺d_г^–d_к^–u_з⁺,

which differs from the neutron of the Standard Model (41.A2) by the presence of barely distinguishable i_w⁺-«quark» and i_w^–-«antiquark».

Due to the complex topological (or signature) metamorphoses inside the core of the «neutron», any permutation of the 4-«quarks-antiquarks» (44.A2) can be rearranged so that inside a given vacuum formation a combination will be obtained, consisting, for example, of a «proton» and an «electron»:

(45.A2)

Apparently, this restructuring ("decoupling") a topological node inside the core of a «neutron» and leads to a decay reaction

n → p⁺ + e^– + ν_e ,

(46.A2)

where ν_e is an electronic «neutrino».

4.A2 The model of the «atom» of hydrogen in the Algebra of signatures

Compared to the neutron, the atom of hydrogen is a much more stable formation.

A hydrogen atom (more precisely deuterium) consists of one proton, one neutron and one electron. Within the framework the Algebra of signature, it also turns out that the deuterium «atom» consists of a «proton», a «neutron» and an «electron». The ranking (topological) equivalent of the nodal configuration of such a spherical formation is:

(47.A2)

Recall that each signature in these rankings corresponds to 10 metrics of the form (1.A2) with a given signature.

The relationship between the metric extent signature and its topology is shown in §1.11 in [17].

It is possible to make many combinations of signatures similar to (47.A2), which reflects the possibilities of "colored" combinatorics of intranuclear metamorphoses. But the topological configuration of this "knot" always remains the same:

¹Н = 3u3die ,

(48.A2)

taking into account the topological properties of metrics with corresponding signatures (see §1.11 in [17]), we find that this "knot" consists of 3 intertwined "tori", 4 "oval surfaces" and one "point".

In a similar way, all known chemical elements of the Mendeleev periodic table of elements can be "designed" ("woven"). In this case, the average sizes of the core of «atoms» r_A must depend on the number of x_i⁺-«quarks» and x_i^–-«antiquarks» A that form these "topological nodes"

r_A ≈ ½ А^1/3r₆ ≈ ½ А^1/3·10^–13 cm.

(49.A2)

The Algebra of signatures extends the approach proposed here to the "construction" of multilayer metric-dynamical models of all «atoms» from the periodic table of elements using Fermi’s «quarks» and «antiquarks» (with characteristic sizes of core r₄ ~ 10⁸ cm), to "construction" of metric-dynamical models of "stars» and «planets» with the help of Newton’s «quarks» and «antiquarks» (with characteristic sizes of core r₄ ~ 10⁸ cm), as well as for the construction of «galaxies» with the help of Galileo’s «quarks» and «antiquarks» (with characteristic sizes of core r₃ ~ 10¹⁸ cm), as well as on the construction of «metagalaxies» with the help of Einstein’s «quarks» and «antiquarks» (with characteristic sizes of core r₃ ~ 10²⁹ cm), etc.

5.A2 Models of «mesons» and «baryons» in the Algebra of signatures

In quantum chromodynamics, mesons are composed of a quark and an antiquark, and are given by the formula

M = q^{-} q^{+} = q_{α}^{-} q_{α}^{+} = \frac{1}{\sqrt{3}} (q_{b}^{-} q_{b}^{+} + q_{r}^{-} q_{r}^{+} + q_{g}^{-} q_{g}^{+}) g,

(50.A2)

where

q^{-}

is the color quark triplet (α = b,

g

,r);

q^{+}

is the color triplet of the antiquark.

Baryons consist of 3 quarks, and are given by the formula

B = \frac{1}{\sqrt{6}} q_{α} q_{β} q_{γ} ε_{α β γ},

(51.A2)

where ε_αβγ is a completely antisymmetric tensor.

Almost exactly the same way «mesons» and «baryons» are composed within the Algebra of signatures. Consider a specific example: three varieties of π-mesons in the theory of strong interactions (quantum chromodynamics) have the following quark structure:

π^{+} = u^{-} d^{+}, π^{0} = \frac{1}{\sqrt{2}} (u^{-} u^{+} - d^{+} d^{-}), π^{-} = u^{+} d^{-} .

(52.A2)

In the Algebra of signatures, for example, three states of the meson π⁺ = u^– d ⁺ is represented as

(53.A2)

where each signature corresponds to a set of 10 metrics of type (1.A2) with a given signature.

In turn, the quark construction

π^{0} = \frac{1}{\sqrt{2}} (u^{-} u^{+} - d^{+} d^{-})

(54.A2)

may have the following signature (topological) analogues: (55.A2)

Similarly, within the framework of the Algebra of signatures, all known mesons and baryons of the Standard Model can be "constructed".

The construction of the Algebra of signatures (AS) differs from the constructions of the Standard Model of elementary particles, only by the presence of additional i_w⁺-«quark» and i_w^–-«antiquark», as well as by the fact that most of the studied AS of multilayer spherical formations consist of intertwining x_i⁺-«quarks» and x_i^–-«antiquarks», so there is no problem of baryon asymmetry in AS.

6.A2 Models of «bosons» in the Algebra of signatures

«Bosons» are various types of wave (more precisely, helical harmonic) perturbations in vacuum (see §§1.1 – 1.9 in [17]). In this section, we present the main mathematical models of the Algebra of signatures for these wave disturbances.

(a): "Photon" and "antiphoton"

Spiral harmonic perturbation [17]

cos{(2π/λ)(сt–x–y–z)} + i sin{(2π/λ)(сt–x–y–z)} = ехр{i (2π/λ)(сt–x–y–z)}= ехр{i(ω t – k⋅ r)}.

(56.A2)

we will conventionally call it a «photon» with signature {+ – – –}.

Then a spiral harmonic perturbation propagating in the opposite direction,

cos{(2π /λ)(–сt+x+y+z)}+ i sin{(2π/λ)(–сt+x+y+z)} = ехр{i (2π/λ)(–сt+x+y+z)}= ехр –{i(ω t – k⋅ r)}.

(57.A2)

we will conventionally call it an «antiphoton» with the stignature {– + + +}.

The notion of the stignature of an affine space was introduced in §1.8 in [17].

(b): W^±-«bosons»

The three color states of the W⁺-«boson» are given by the following expressions and their corresponding rankings [17] (58.A2)

The three color states of the W^–-«boson»: (59.A2)

where i, j, k are imaginary units, form the anticommutative algebra

i²= j²= k² = ijk = –1 и ij + ji = 0.

(60.A2)

(c): Z⁰-«bosons»

The six color states of the Z⁰-«boson» are given by the following expressions and the corresponding rankings [17] (61.A2)

(d): «Graviton» (or «landscapeton»)

In the Algebra of signatures, there is another «boson», which is called «graviton» (or «landscapeton») [17] (62.A2)

where the objects ζm satisfy the anticommutative relations of the Clifford algebra

ζ_m ζ_k + ζ_k ζ_m = 0 or m ≠ k , ζ_m ζ_m = 1, or ζ_m ζ_k + ζ_k ζ_m = 2δ_km,

(63.A2)

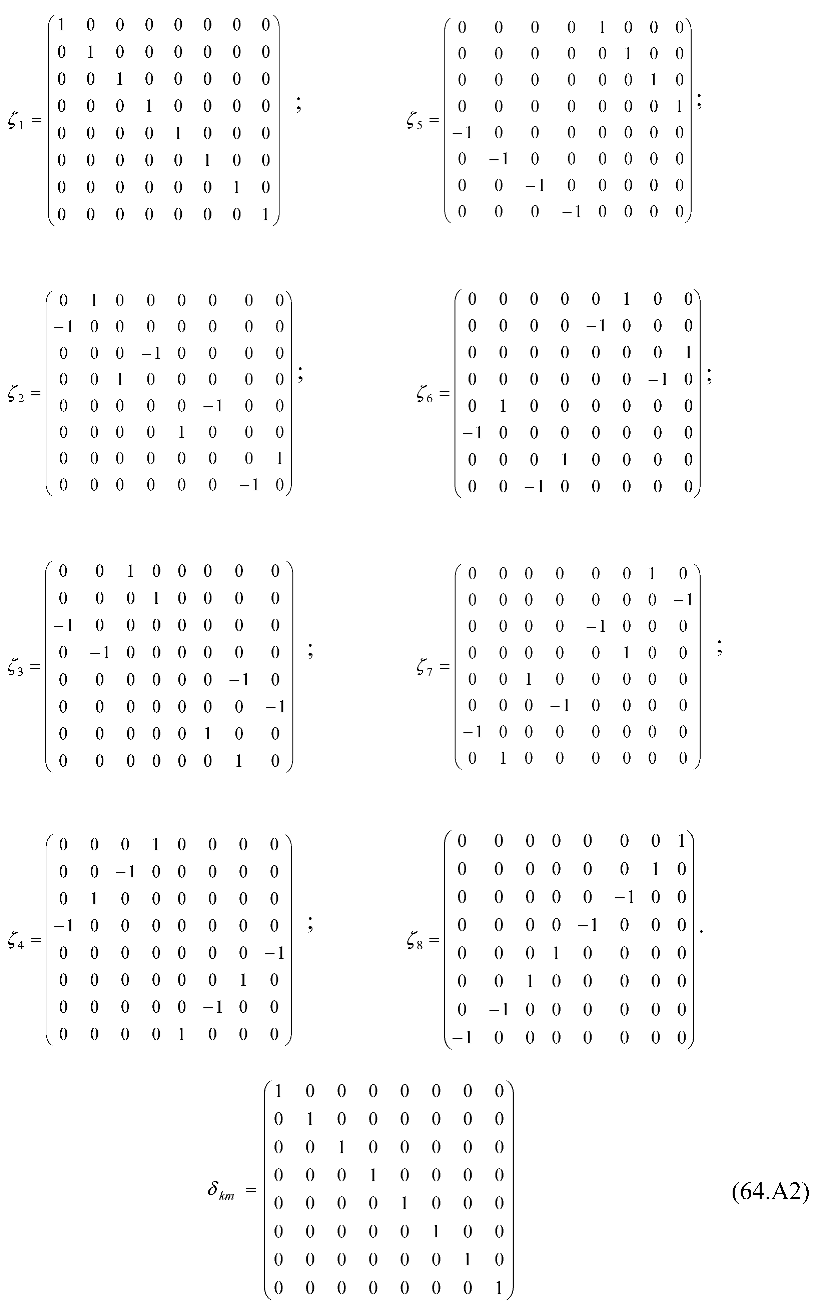
where δ_km is the Kronecker symbol (δ_km= 0 for m ≠ k and δ_km= 1 for m = k ). One of the possibilities for determining the objects ζ_m and the Kronecker symbol δ_km is presented below:

7.A2 Conclusions on Annex 2

Metric-dynamic models of all kinds of «neutrinos», «muons» and «antimuons», τ-«leptons», c⁺,s⁺,b⁺,t⁺-«quarks» and c^–,s^–,b^–,t^–-«antiquarks», as well as a geometrized description of the main force interactions: electrostatic, electromagnetic, weak and nuclear are given in chapters 3 – 10 [17].

Thus, taking into account the superposition of stably curved metric spaces with all 16 possible signatures (37)

\begin{matrix} (+ + + +) & (+ + + -) & (- + + -) & (+ + - +) \\ (- - - +) & (- + + +) & (- - + +) & (- + - +) \\ (+ - - +) & (+ + - -) & (+ - - -) & (+ - + +) \\ (- - + -) & (+ - + -) & (- + - -) & (- - - -) \end{matrix}

, allow metric-statistical description of almost all elements of the Standard Model of elementary particles, except for the Higgs boson.

In the massless Algebra of signatures (or stochastic metaphysics) proposed here, there is no concept of "mass", so there is no need to introduce the concept of a field that provides a mechanism for spontaneous breaking of electroweak symmetry, and, accordingly, about the quanta of this field - Higgs bosons. However, it is possible that in a fully geometrized theory, metric-dynamic models of vacuum formations with characteristics similar to those of these bosons will arise.

Note that if in the aggregate of metrics of the form (78), (88), (12.A2) and (31.A2) instead of:

r₅ ~ 10^–3 cm is the characteristic radius of the «biological cell»;

r₆ ~10^–13 cm is the characteristic radius of the «electron» core;

r₇ ~ 10^–24 cm is the characteristic radius of the «proto-quark» core,

substitute accordingly, for example,

r₃ ~ 10¹⁸ cm is the radius commensurate with the radius of the «galaxy» core;

r₄ ~ 10⁸ cm is the radius commensurate with the radius of the core of a «star» («planet»);

r₅ ~ 10^–3 cm is the radius commensurate with the size of a «biological cell»;

then we get a practically similar multilayer metric-dynamic description of spherical formations on a stellar-planetary scale.

Whereas, if we substitute

r₂ ~ 10²⁹ cm is the characteristic radius of the core of the «metagalaxy»;

r₃ ~ 10¹⁸ cm is the characteristic radius of the core of the «galaxy»;

r₄ ~ 10⁸ cm – characteristic radius, the core of a "star" or «planet»,

then we get a description of spherical formations of a galactic scale, etc.

Thus, in the opinion of the author, has been obtained a universal metric-dynamic model of a closed and, at the same time, Ricci-flat universe, inhabited by countless spherical formations of various scales,

The probabilistic formalism of the Standard Model also remains valid, since the cores and nucleoli of stable vacuum formations constantly move chaotically under the influence of neighboring stable spherical formations and many other vacuum fluctuations. The study of the chaotic motion of the core of a vacuum formation led to the derivation of the Schrödinger equation (see Chapters 3 and 4 in [17]).

References

Einstein, A. (1916) The Foundation of the General Theory of Relativity // Annalen der Physik. 354 (7): 769. Bibcode:1916AnP...354..769E.
Einstein, A. (1917) Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie // Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften. Berlin, DE. part 1: pp.142-152. https://web.archive.org/web/20200329142916/http://echo.mpiwg-berlin.mpg.de/ECHOdocuView?url=/permanent/echo/einstein/sitzungsberichte/S250UZ0K/index.meta.
Kottler, F. (1918) Uber die physikalischen Grundlagen der Einsteinschen Gravitationstheorie// Annalen der Physik, Vol. 56, pp. 401-462. [CrossRef]
Glass, E.N., Krisch, J.P. (2004) Kottler-Lambda-Kerr Spacetime, arXiv:gr-qc/0405143v1 , . [CrossRef]
Desai, S. (2022), Galaxy cluster hydrostatic bias in Kottler spacetime// Physics of the Dark Universe, Vol. 35, 100928, arXiv:2111.14105.
Bambi, С. (2007) Dark Energy and the mass of galaxy clusters. Phys. Rev. D 75, 083003 arXiv:astro-ph/0703645.
Nariai, H. (1951). "On a new cosmological solution of Einstein's field equations of gravitation". Sci. Rep. Tohoku Univ. 35: 62.
Solanki, R. (2021) Kottler Spacetime in Isotropic Static Coordinates // Classical and Quantum Gravity, Vol. 39, № 1, arXiv:2103.10002. [CrossRef]
Gibbons, G.W. , Warnickand, C.M., Werner, M.C. (2008) “Light-bending in Schwarzschild-de-Sitter: Projective Geometry of the Optical Metric// Class. Quant. Grav. 25, 245009.
Cohn, J.D. Cohn, J.D. (1998) Living with Lambda//Astrophysics and Space Science, Vol. 259, p. 213–234, arXiv:astro-ph/9807128v2.
Rindler, W., Ishak, M. (2007) The Contribution of the Cosmological Constant to the Relativistic Bending of Light Revisited// Phys. Rev. D 76, 043006, arXiv:0709.2948.
Sereno, M. (2007) On the influence of the cosmological constant on gravitational lensing in small systems// Phys. Rev. D 77, 043004, arXiv:0711.1802. [CrossRef]
Ishak, M., Rindler, W., Dossett, J., (2010) More on Lensing by a Cosmological Constant // Mon.Not. R. As- tron. Soc. 403, 2152, 0810.4956. arXiv:0810.4956 ,. [CrossRef]
Aghanim N. et al. (Planck Collaboration) (2020). Planck 2018 results. VI. Cosmological parameters (англ.) // Astronomy and Astrophysics. 2020. Vol. 641. P. A6. arXiv:1807.06209. [CrossRef]
Bachelot, A. (2008) The Dirac system on the Anti-de Sitter Universe//Communications in Mathematical Physics vol. 283, pp.127–167, arXiv:0706.1315,. [CrossRef]
Batanov-Gaukhman, M. (2021) The Geometrized Vacuum Physics Based Onthe Algebra of Signature. Preprints, 2021060658, doi: 10.20944/preprints202106.0658.v1 https://www.preprints.org/manuscript/202106.0658/v1. [CrossRef]
Batanov-Gaukhman, M. (2019) Fully geometrized physics from the standpoint of the Algebra of signature// Lambert, ISBN 978-613-9-45278-1, 2019, С. 415. Аvailable in English: http://metraphysics.ru/.
Gaukhman, M.Kh. (2007) Algebra of signatures "NAMES" (orange Alsigna)// ed. Rabbi Gavriel Davidov. - M.: LKI, ISBN-5203-027780-x, available on the Internet URL: http://alsigna.ru/, section "Orange Alsigna "NAMES"", [in Russian].
Einstein, A. (1966)// Collection of scientific papers. – M.: Nauka,. Vol.2, p.789.
Landau, L.D. , Lifshitz E.M. (1971) The Classical Theory of Fields / Course of theoretical physics, V. 2 Translated from the Russian by Hamermesh M. Uni-versity of Minnesota – Pergamon Press Ltd. Oxford, New York, Toronto, Sydney, Braunschwei, p. 387.
Sedov, L.I. (1994) Continuum mechanics. T.1. – M.: Nauka, [in Russian].
Novikov, S.P. , Taimanov I.A. (2014) Modern geometric structures and fields. - M.: MTSNMO, 2014. - P. 584 [in Russian].

Figure 3. Illustration of the interweaving of several affine subspaces forming a multilayer metric space.

Figure 4. Illustration of a sequence of “bubbles” within “bubbles” within “bubbles”….

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multilayer and Multilevel Cosmological Models Based on So-Lutions of the Extended Einstein Field Equations

Abstract

1. Background and introduction

2. Generalized Kottler metrics

3. Extended Einstein's field equations

4. Closed ten-layer and ten-level cosmological model

5. Metric-dynamic models of «electron» and «positron»

6. Conclusion and discussion

Acknowledgements

Appendix 1

Appendix 2

1.A2 Models of хi+-«quark» and xi–-«antiquark» in the Algebra of signatures

2.A2 Models of «proton» and «antiproton» in the Algebra of signatures

3.A2 The «neutron» model in the Algebra of signatures

4.A2 The model of the «atom» of hydrogen in the Algebra of signatures

5.A2 Models of «mesons» and «baryons» in the Algebra of signatures

6.A2 Models of «bosons» in the Algebra of signatures

7.A2 Conclusions on Annex 2

References

MDPI Initiatives

Important Links

Subscribe

1.A2 Models of х_i⁺-«quark» and x_i^–-«antiquark» in the Algebra of signatures