Defining the Most Generalized, Natural Extension of the Expected Value on Measurable Functions

Preprint

Concept Paper

Defining the Most Generalized, Natural Extension of the Expected Value on Measurable Functions

Altmetrics

Downloads

667

Views

272

Comments

Bharath Krishnan^*

This version is not peer-reviewed

Submitted:

25 April 2023

Posted:

26 April 2023

You are already at the latest version

Alerts

Abstract

In this paper, we will extend the expected value of the function w.r.t the uniform probability measure on sets measurable in the Caratheodory sense to be finite for a larger class of functions, since the set of all measurable functions with infinite or undefined expected values forms a prevalent subset of the set of all measurable functions, which means "almost all" measurable functions have infinite or undefined expected values. Before we define the specific problem in section 2, we will outline some preliminary definitions. We'll then define the specific problem (along with a partial solution in section 3) to visualize the complete solution. Along the way, we will ask a series of questions to clarify our understanding of the paper.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

0. Background

I am an undergraduate from Indiana University despite being the age of a grad student. I should have graduated by now, but my obsession with research prevents me from moving forward. There is a chance that I might have a learning disability since writing isn’t very easy for me.

As I’ve been in and out of college, I never got the chance to rigorously learn the subjects I’m researching. Most of what I learned was from Wikipedia, blogs and random research articles. I know little of what I read but learn what I can from asking questions on math stack exchange.

What I truly want, however; is for someone to take my ideas and publish them.

I warn that the definitions may not be rigorous so try to go easy on me. (I recommend using programming such as Mathematica, Python, JavaScript or Matlab to understand later sections).

1. Preliminaries

Suppose A is a set measurable in the Carathèodory sense [7], such for

n \in N

A \subseteq R^{n}

, and function

f : A \to R

1.1. Motivation

It seems the set of measurable functions with infinite or undefined expected values (def. 1), using the uniform measure ([17], pp. 32-37), may be a prevalent subset [11,14] of the set of all measurable functions, meaning "almost every" measurable function has infinite or undefined expected values. Furthermore, when the Lebesgue measure of A, measurable in the Caratheodory sense, has zero or infinite volume (or undefined measure), there may be multiple, conflicting ways of defining a "natural" uniform measure on A.

Below I will attempt to define a question regarding an extension of the expected value (when it’s undefined or infinite) which allows for finite values instead (def. 3).

Note the reason the question will be so long is there are plenty of “meaningless” extensions of the expected value (e.g. if the expected value is infinite or undefined we can just replace it with zero).

Therefore we must be more specific about what is meant by “meaningful” extension but there are some preliminary definitions we must clarify.

1.2. Preliminary Definitions

Definition 1

(Expected value w.r.t the Uniform Probability Measure). From an answer to a question in cross validated (a website for statistical questions) [10] , let

X \sim Uniform (A)

denote a uniform random variable on set

A \subseteq R^{n}

and

p_{X}

denote the probability density function from the radon-nikodym derivative ([2], pp. 419-427) of the uniform probability measure on A measurable in the Carathèodory sense. If

I (x \in A)

denotes the indicator function on

x \in A

I (x \in A) = \{\begin{matrix} 1 & x \in A \\ 0 & x \notin A \end{matrix}

then the radon-nikodym derivative of uniform probability measure must have the form

I (x \in A) / U^{'} (A)

. (Note

U^{'}

is not the derivative of U in the sense of calculus but rather the denominator of the probability density function derived from the uniform probability measure U.)

Therefore, by using the law of the unconscious statistician, we should get

\begin{matrix} E [f (X)] & = \int_{R^{n}} f (x) \cdot p_{X} (x) d x \\ = \int_{R^{n}} f (x) \cdot \frac{I (x \in A)}{U^{'} (A)} d x \\ = \frac{1}{U^{'} (A)} \int_{A} f (x) d x \\ = E_{U^{'}} [f (X)] \end{matrix}

(P1)

such the expected value is undefined when A does not have a uniform probability distribution or f is not integrable w.r.t the measure

U^{'}

Definition 2

(Defining the pre-structure). Since there’s a chance that

X \sim Uniform (A)

does not exist or f is not integrable w.r.t to

U^{'}

, using def. 1 we define a sequence of sets

{(F_{r})}_{r \in N}

where if:

(a): $\underset{r \to \infty}{lim inf} F_{r} = ⋃_{r \geq 1} ⋂_{q \geq r} F_{q}$
(b): $\underset{r \to \infty}{lim sup} F_{r} = ⋂_{r \geq 1} ⋃_{q \geq r} F_{q}$

then we have:

$\underset{r \to \infty}{lim inf} F_{r} = \underset{r \to \infty}{lim sup} F_{r} = A$
For all $r \in N$ , $X_{r} \sim Uniform (F_{r})$ exists (when A is countable infinite, then for every $r \in N$ , $F_{r}$ must be finite since $X_{r}$ would be a discrete uniform distribution of $F_{r}$ ; otherwise, when A is uncountable, $X_{r}$ is the normalized Lebesgue measure or some other uniform measure on $F_{r}$ (e.g. [8]) where for every $r \in N$ , either measure on $F_{r}$ exists and is finite.
For all $r \in N$ , $U^{'} (F_{r})$ is positive and finite such that $U^{'}$ is intrinsic. (For countably infinite A, $U^{'}$ would be the counting measure where $U^{'} (F_{r})$ is positive and finite since $F_{r}$ is finite. For uncountable A, $U^{'}$ would either be the Lebesgue measure or the radon-nikodym derivative of some other uniform measure on $F_{r}$ (e.g. [8]), where either of the measures on $F_{r}$ are positive and finite.)

where

{(F_{r})}_{r \in N}

is apre-structureof A, since for every

r \in N

the sequence does not equal A, but "converges" to A as r increases (see (a) & (b) of this definition).

Example 1.

Suppose

A = Q

. One pre-structure of

Q

{(F_{r})}_{r \in N} = {(\{c / r! : c \in Z, - r \cdot r! \leq c \leq r \cdot r!\})}_{r \in N}

since:

$\underset{r \to \infty}{lim inf} F_{r} = \underset{r \to \infty}{lim sup} F_{r} = A \Rightarrow$

$⋃_{r \geq 1} ⋂_{q \geq r} \{c / q! : c \in Z, - q \cdot q! \leq c \leq q \cdot q\} = ⋂_{r \geq 1} ⋃_{q \geq r} \{c / q! : c \in Z, - q \cdot q! \leq c \leq q \cdot q\} = Q$
For every $r \in N$ , set $F_{r} = \{c / r! : c \in Z, - r \cdot r! \leq c \leq r \cdot r!\}$ is finite, meaning each term of the pre-structure has a discrete uniform distribution. Therefore, $X_{r} \sim Uniform (F_{r})$ exists.
For every $r \in N$ , $F_{r}$ is finite; meaning $U^{'}$ is the counting measure. Furthermore, since $U^{'} (F_{r}) = 2 r \cdot r! + 1$ and for all $r \in N$ , $2 r \cdot r! + 1$ is positive and finite, criteria (3) of def. 2 is satisfied.

Example 2.

Suppose

A = Q

. Another pre-structure of

Q

{(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, - d r \leq c \leq d r\})}_{r \in N}

where we note the following:

$\underset{r \to \infty}{lim inf} F_{r} = \underset{r \to \infty}{lim sup} F_{r} = A \Rightarrow$

$⋃_{r \geq 1} ⋂_{q \geq r} \{c / d : c \in Z, d \in N, d \leq q, - d q \leq c \leq d q\} = ⋂_{r \geq 1} ⋃_{q \geq r} \{c / d : c \in Z, d \in N, d \leq q, - d q \leq c \leq d q\} = Q$
For every $r \in N$ , set $F_{r} = \{c / d : c \in Z, d \in N, d \leq r, - d r \leq c \leq d r\}$ is finite, meaning each term of the pre-structure has a discrete uniform distribution. Therefore, $X_{r} \sim Uniform (F_{r})$ exists.
For every $r \in N$ , $F_{r}$ is finite; meaning $U^{'}$ is the counting measure, since (when $ϕ (\cdot)$ is the Euler’s totient function [15], pp.239-249) we have $U^{'} (F_{r}) = |\{c / d : c \in Z, d \in N, d \leq r, - d r \leq c \leq d r\}| = \sum_{d = 1}^{r} 2 d ϕ (d)$ , and if correct, $\sum_{d = 1}^{r} 2 d ϕ (d)$ is greater than zero and positive for all $r \in N$ . Therefore, criteria (3) of def. 2 is satisfied.

There are plenty of pre-structures of

Q

. Infact, there may be countably infinite many of these pre-structures.

Example 3.

We need additional examples, where

U^{'}

is not the counting measure. Perhaps one example of

{(F_{r})}_{r \in N}

(where

A = R

) is:

{(F_{r})}_{r \in N} = {([- r, r])}_{r \in N}

(2)

It’s obvious that:

\underset{r \to \infty}{lim inf} F_{r} = \underset{r \to \infty}{lim sup} F_{r} = A \Rightarrow ⋃_{r \geq 1} ⋂_{q \geq r} [- q, q] = ⋂_{r \geq 1} ⋃_{q \geq r} [- q, q] = R

Note that the uniform random variable of

A = R

doesn’t exist but for every

r \in N

, the uniform density of

F_{r}

I (x \in [- r, r]) / (2 r)

Furthermore, for every

r \in N

U^{'}

is the 1-d Lebesgue measure where

U^{'} (F_{r}) = 2 r

, such where

2 r

is positive and finite (since

r > 0

Definition 3

(Expected value of f on Pre-Structure). If

{(F_{r})}_{r \in N}

is a pre-structure of A (def. 2), then for

r \in N

, if

E_{U^{'}} [f (X_{r})] = \frac{1}{U^{'} (F_{r})} \int_{F_{r}} f d x

(3)

we then have that the expected value of f on the pre-structure could be described as

E_{U^{'}} [f (X_{r})] \to E_{U^{'}}^{★} [f]

where:

\begin{matrix} \forall (ϵ > 0) \exists (N \in N) \forall (r \in N) (r \geq N \Rightarrow |E_{U^{'}} [f (X_{r})] - E_{U^{'}}^{★} [f]| < ϵ) \Rightarrow \end{matrix}

(4)

\begin{matrix} \forall (ϵ > 0) \exists (N \in N) \forall (r \in N) (r \geq N \Rightarrow |\frac{1}{U^{'} (F_{r})} \int_{F_{r}} f d x - E_{U^{'}}^{★} [f]| < ϵ) \end{matrix}

(5)

Example 4.

Suppose

A = Q

where

f : A \to R

such that:

f (x) = \{\begin{matrix} 1 & x \in \{(2 n + 1) / 2 m : n \in Z, m \in N\} \\ 0 & x \notin \{(2 n + 1) / 2 m : n \in Z, m \in N\} \end{matrix}

Using the pre-structure in example 1 or

{(F_{r})}_{r \in N} = {(\{c / r! : c \in Z, - r \cdot r! \leq c \leq r \cdot r!\})}_{r \in N}

, we presume (and prove)

E_{U^{'}}^{★} [f]

using def. 3 is 1.

And using the pre-structure in example 2 or

{(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, - d r \leq c \leq d r\})}_{r \in N}

we presume (but must prove)

E_{U^{'}}^{★} [f]

, using def. 3 is

1 / 3

This shows different pre-structures give different expected values; therefore, we must choose a unique set of equivelant pre-structures (def. 8) which gives the same & finite expected value.

Definition 4

(Uniform

ε

coverings of each term of the pre-structure). We define the uniform ε coverings of each term of the pre-structure

{(F_{r})}_{r \in N}

(i.e.,

F_{r}

) as a group of pair-wise disjoint sets that cover

F_{r}

for every

r \in N

, such the measure

U^{'}

of each of the sets that cover

F_{r}

have the same value of

ε \in range (U^{'})

, where

ε > 0

and the total sum of

U^{'}

of the coverings is minimized. In shorter notation, if

The element $t \in N$
The set $T \supset N$ is arbitrary and uncountable.

and set Ω is defined as:

Ω = \{\begin{matrix} \{1, \cdot \cdot \cdot, t\} & if there are t ways of writing uniform ε coverings of F_{r} \\ N & if there are countably infinite ways of writing uniform ε coverings of F_{r} \\ T & if there are uncountable ways of writing uniform ε coverings of F_{r} \end{matrix}

(6)

then for every

ω \in Ω

, the set of uniform ε coverings is defined using

U (ϵ, F_{r}, ω)

where ω “enumerates" all possible uniform ε coverings of

F_{r}

for every

r \in N

Example 5.

Suppose

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, 0 \leq c \leq d\})}_{r \in N}$

Inorder to calculate

U (2, F_{4}, 1)

, note that:

\begin{matrix} F_{4} & = \{0, 1\} \cup \{0, 1 / 2, 1\} \cup \{0, 1 / 3, 2 / 3, 1\} \cup \{0, 1 / 4, 2 / 4, 3 / 4, 1\} \cup \{0 / 5, 1 / 5, 2 / 5, 3 / 5, 4 / 5, 5 / 5\} \end{matrix}

(7)

\begin{matrix} = \{0, 1, 1 / 2, 1 / 3, 2 / 3, 1 / 4, 3 / 4, 1 / 5, 2 / 5, 3 / 5, 4 / 5\} \end{matrix}

(8)

and; since

ε = 2

and

U^{'}

is the counting measure, one example of

U (2, F_{4}, 1)

\{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

Note

U^{'}

(in this case the counting measure) of each set in the uniform ε covering is 2 where we’re "over-covering"

F_{4}

by one element (i.e.

6 / 5

) as we are minimizing the total sum of

U^{'}

of the coverings (which for

U (2, F_{4}, 1)

6 \cdot 2 = 12

U (2, F_{4}, 1) = \{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

, then

U (2, F_{4}, 2) = \{\{0, 1 / 2\}, \{1 / 3, 1\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

and e.g.

U (2, F_{4}, 3) = \{\{0, 1 / 3\}, \{1 / 2, 1\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

Also note, for counting measure

U^{'}

, where

ε > 0

and

ε \in range (U^{'})

(i.e.

ε \in N

), we have that

inf (ε) = 1

Definition 5

(Sample of the uniform

ε

coverings of each term of the pre-structure). The sample of uniform ε coverings of each term of the pre-structure

{(F_{r})}_{r \in N}

F_{r}

is the set of points, such for every

ε \in range (U^{'})

and

r \in N

, we take a point from each pair-wise disjoint set in the uniform ε coverings of

F_{r}

(def. 4). In shorter notation, if

The element $k \in N$
The set $K \supset N$ is arbitrary and uncountable.

and set

Ψ_{ω}

is defined as:

Ψ_{ω} = \{\begin{matrix} \{1, \cdot \cdot \cdot, k\} & if there are k ways of writing the sample of uniform ε coverings of F_{r} \\ N & if there are countably infinite ways of writing the sample of uniform ε coverings of F_{r} \\ K & if there are uncountable ways of writing the sample of uniform ε coverings of F_{r} \end{matrix}

(9)

then for every

ψ \in Ψ_{ω}

, the set of all samples of the set of uniform ε coverings is defined using

S (U (ϵ, F_{r}, ω), ψ)

, where ψ “enumerates" all possible samples of

U (ϵ, F_{r}, ω)

Example 6.

From example 5 where:

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, 0 \leq c \leq d\})}_{r \in N}$
$U (2, F_{4}, 1) = \{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}$

Then one sample of

U (2, F_{4}, 1) = \{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

is:

S (U (2, F_{r}, 1), 1) = \{0, 1 / 3, 1 / 4, 1 / 5, 3 / 5, 6 / 5\}

and another sample of

U (2, F_{4}, 1) = \{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}

is:

S (U (2, F_{r}, 1), 2) = \{0, 1 / 2, 1 / 4, 3 / 4, 2 / 5, 4 / 5\}

Definition 6

(Entropy on the sample of uniform coverings of each term of the pre-structure). Since there are finitely many points in the sample of the uniform ε coverings of each term of pre-structure

{\{F_{r}\}}_{r \in N}

(def. 5), we:

Arrange the x-value of the points in the sample of uniform ε coverings from least to greatest. This is defined as:

$Ord (S (U (ϵ, F_{r}, ω), ψ))$
Take the multi-set of the absolute differences between all consecutive pairs of elements in (1). This is defined as:

$\nabla Ord (S (U (ϵ, F_{r}, ω), ψ))$
Normalize (2) into a probability distribution. This is defined as:

$P (S (U (ϵ, F_{r}, ω), ψ)) = \{y / (\sum_{z \in \nabla Ord (S (U (ϵ, F_{r}, ω), ψ))} z) : y \in \nabla Ord (S (U (ϵ, F_{r}, ω), ψ))\}$

(10)
Take the entropy of (3), (for further reading, see [12]). This is defined as:

$E (S (U (ϵ, F_{r}, ω), ψ)) = - \sum_{x \in P (S (U (ϵ, F_{r}, ω), ψ))} x {log}_{2} x$

where (4) is the entropy on the sample of uniform coverings of

F_{r}

Example 7.

From example 6:

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, 0 \leq c \leq d\})}_{r \in N}$
$U (2, F_{4}, 1) = \{\{0, 1\}, \{1 / 2, 1 / 3\}, \{2 / 3, 1 / 4\}, \{3 / 4, 1 / 5\}, \{2 / 5, 3 / 5\}, \{4 / 5, 6 / 5\}\}$
$S (U (2, F_{4}, 1), 1) = \{0, 1 / 3, 1 / 4, 1 / 5, 3 / 5, 6 / 5\}$

Then

$Ord (S (U (2, F_{4}, 1), 1)) = \{0, 1 / 5, 1 / 4, 1 / 3, 3 / 5, 6 / 5\}$ which organizes elements in $S (U (2, F_{4}, 1), 1)$ from least to greatest.
$\nabla Ord (S (U (2, F_{4}, 1), 1)) = \{|0 - 1 / 5|, |1 / 5 - 1 / 4|, |1 / 4 - 1 / 3|, |1 / 3 - 3 / 5|, |3 / 5 - 6 / 5|\} = \{1 / 5, 1 / 20, 1 / 12, 4 / 15, 3 / 5\}$
Since $\sum_{z \in \nabla Ord (S (U (2, F_{4}, 1), 1))} z = 1 / 5 + 1 / 20 + 1 / 12 + 4 / 15 + 3 / 5 = 6 / 5$ we use this to normalize (2) into a probability distribution

$\begin{matrix} P (S (U (2, F_{4}, 1), 1)) = \{y / (6 / 5) : y \in \nabla Ord (S (U (2, F_{4}, 1), 1))\} = \{(5 / 6) y : y \in \{1 / 5, 1 / 20, 1 / 12, 4 / 15, 3 / 5\}\} = \\ \{1 / 6, 1 / 24, 5 / 72, 2 / 9, 1 / 2\} \end{matrix}$
Hence we take the entropy of $\{1 / 6, 1 / 24, 5 / 72, 2 / 9, 1 / 2\}$ or:

$\begin{matrix} E (S (U (ϵ, F_{r}, ω), ψ)) = - \sum_{x \in P (S (U (ϵ, F_{r}, ω), ψ))} x {log}_{2} x = \\ - ((1 / 6) {log}_{2} (1 / 6) + (1 / 24) {log}_{2} (1 / 24) + (5 / 72) {log}_{2} (5 / 72) + (2 / 9) {log}_{2} (2 / 9) + (1 / 2) {log}_{2} (1 / 2)) \approx 1.8713 \end{matrix}$

Definition 7

(Pre-Structure Converging Uniformly to A). For every

r \in N

(using def. 4, 5, and 6)if set A is finite and for

ε \in range (U^{'})

, we have

ε > 0

, we then want:

lim_{ε \to 0} sup_{r \in N} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} E (S (U (ϵ, F_{r}, ω), ψ)) \geq E (F_{r})

and if set A is non-finite:

lim_{ε \to 0} sup_{r \in N} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} E (S (U (ϵ, F_{r}, ω), ψ)) = + \infty

we say the pre-structure

{(F_{r})}_{r \in N}

converges uniformlyto A (or in shorter notation):

F_{r} \overset{r \in N}{⇉} A

(11)

(Note we wish to define a uniform convergence of a sequence of sets to A since the definition is analogous to a uniform measure.)

Theorem 1.

Show every pre-structure of A converges uniformly to A.

Example 8.

I assume, using example 5, if

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, 0 \leq c \leq d\})}_{r \in N}$

then

F_{r} \overset{r \in N}{⇉} A

. I need to prove this.

Definition 8

(Equivalent Pre-Structures). The pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

of A areequivalentif for all

f \in R^{A}

, where from def. 3,

E_{U^{'}} [f (X_{r})] \to E_{U^{'}}^{★} [f]

E_{U^{'}} [f (X_{j}^{'})] \to E_{U^{'}}^{★ ★} [f]

such that:

E_{U^{'}}^{★} [f] = E_{U^{'}}^{★ ★} [f]

Definition 9 (Equivelant Pre-Structures The pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

of A areequivalentif we have:

r_{j} = \underset{r \in N}{arg min} \{U^{'} (F_{r} ∖ F_{j}^{'}) : F_{r} \supseteq F_{j}^{'}\}

is the r-value (for every

j \in N

) where

U^{'} (F_{r} ∖ F_{j}^{'})

is minimized

r_{j}^{'} = \underset{r \in N}{arg min} \{U^{'} (F_{j}^{'} ∖ F_{r}) : F_{r} \subseteq F_{j}^{'}\}

is the r-value (for every

j \in N

) where

U^{'} (F_{j}^{'} ∖ F_{r})

is maximized

j_{r} = \underset{j \in N}{arg min} \{U^{'} (F_{j}^{'} ∖ F_{r}) : F_{j}^{'} \supseteq F_{r}\}

is the j-value (for every

r \in N

) where

U^{'} (F_{r} ∖ F_{j}^{'})

is minimized and:

j_{r}^{'} = \underset{j \in N}{arg min} \{U^{'} (F_{r} ∖ F_{j}^{'}) : F_{j}^{'} \subseteq F_{r}\}

is the j-value (for every

r \in N

) where

U^{'} (F_{j}^{'} ∖ F_{r})

is maximized such that:

sup \{inf \{U^{'} (⋃_{j = 1}^{\infty} F_{r_{j}} ∖ F_{j}^{'}), U^{'} (⋃_{j = 1}^{\infty} F_{j}^{'} ∖ F_{r_{j}^{'}})\}, inf \{U^{'} (⋃_{r = 1}^{\infty} F_{j_{r}} ∖ F_{r}), U^{'} (⋃_{r = 1}^{\infty} F_{r} ∖ F_{j_{r}^{'}})\}\} < + \infty

(12)

means the pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

are equivelant.

Example 9.

From example 3, if

A = R

where

{(F_{r})}_{r \in N} = {([- r, r])}_{r \in N}

, the cantor set is

C

and

{(F_{j}^{'})}_{j \in N} = {([- j, j] \cup \{x + j : x \in C\})}_{j \in N}

. Since with either pre-structure,

U^{'}

is the 1-d dimensional Lebesgue measure and (using equation 12) we get:

sup \{inf \{+ \infty, 0\}, inf \{0, + \infty\}\} = sup \{0, 0\} = 0 < + \infty

Definition 10

(Non-Equivalent Pre-Structures). The pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

of A arenon-equivalentif there exists an

f \in R^{A}

, where from def. 3,

E_{U^{'}} [f (X_{r})] \to E_{U^{'}}^{★} [f]

E_{U^{'}} [f (X_{j}^{'})] \to E_{U^{'}}^{★ ★} [f]

where:

E_{U^{'}}^{★} [f] \neq E_{U^{'}}^{★ ★} [f]

Definition 11 (Non-Equivelant Pre-Structures The pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

of A arenon-equivalentif we have:

r_{j} = \underset{r \in N}{arg min} \{U^{'} (F_{r} ∖ F_{j}^{'}) : F_{r} \supseteq F_{j}^{'}\}

is the r-value (for every

j \in N

) where

U^{'} (F_{r} ∖ F_{j}^{'})

is minimized

r_{j}^{'} = \underset{r \in N}{arg min} \{U^{'} (F_{j}^{'} ∖ F_{r}) : F_{r} \subseteq F_{j}^{'}\}

is the r-value (for every

j \in N

) where

U^{'} (F_{j}^{'} ∖ F_{r})

is maximized

j_{r} = \underset{j \in N}{arg min} \{U^{'} (F_{j}^{'} ∖ F_{r}) : F_{j}^{'} \supseteq F_{r}\}

is the j-value (for every

r \in N

) where

U^{'} (F_{r} ∖ F_{j}^{'})

is minimized and:

j_{r}^{'} = \underset{j \in N}{arg min} \{U^{'} (F_{r} ∖ F_{j}^{'}) : F_{j}^{'} \subseteq F_{r}\}

is the j-value (for every

r \in N

) where

U^{'} (F_{j}^{'} ∖ F_{r})

is maximized such that:

sup \{inf \{U^{'} (⋃_{j = 1}^{\infty} F_{r_{j}} ∖ F_{j}^{'}), U^{'} (⋃_{j = 1}^{\infty} F_{j}^{'} ∖ F_{r_{j}^{'}})\}, inf \{U^{'} (⋃_{r = 1}^{\infty} F_{j_{r}} ∖ F_{r}), U^{'} (⋃_{r = 1}^{\infty} F_{r} ∖ F_{j_{r}^{'}})\}\} = + \infty

means the pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

are non-equivelant.

Example 10.

From example 4, if

A = Q

, pre-structures

{(F_{r})}_{r \in N} = {(\{c / r! : c \in Z, - r \cdot r! \leq c \leq r \cdot r!\})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N} = {(\{c / d : c \in Z, d \in N, d \leq j, - d j \leq c \leq d j\})}_{j \in N}

are non-equivelant since for

f : Q \to R

where:

f (x) = \{\begin{matrix} 1 & x \in \{(2 n + 1) / 2 m : n \in Z, m \in N\} \\ 0 & x \notin \{(2 n + 1) / 2 m : n \in Z, m \in N\} \end{matrix}

we have

E_{U^{'}}^{★} [f] = 1

(i.e. the expected value of f on

F_{r}

) and

E_{U^{'}}^{★ ★} [f] = 1 / 3

(i.e. the expected value of f on

F_{j}^{'}

), which means

E_{U^{'}}^{★} [f] \neq E_{U^{'}}^{★ ★} [f]

hence from def. 10, the pre-structures

{\{F_{r}\}}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

are non-equivelant.

Example 11.

Suppose

A = Z

, where

{(F_{r})}_{r \in N} = {(\{s \in Z : - r \leq s \leq r\})}_{r \in N}

{(F_{j}^{'})}_{j \in N} = {(\{s \in Z : - 2 j \leq s \leq 2 j\})}_{j \in N}

and

f (x) = \{\begin{matrix} 2 x + 1 & x = r, r is odd, r < 0 \\ 0 & x = r, r is even, r < 0 \\ 2 x + 1 & x = r, r is even, r \geq 0 \\ 0 & x = r, r is odd, r \geq 0 \end{matrix}

(13)

E_{U^{'}}^{★} [f]

is undefined (i.e. the expected value of f on

F_{r}

) and

E_{U^{'}}^{★ ★} [f] = 1

(i.e. the expected value of f on

F_{j}^{'}

). Since at least one of the pre-structure i.e.

{(F_{j}^{'})}_{j \in N}

has a defined expected value and

E_{U^{'}}^{★} [f] \neq E_{U^{'}}^{★ ★} [f]

(i.e. undefined values do not equal 1), we can say that

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

are non-equivelant.

Definition 12

(Pre-Structures converging Sublinearly, Linearly, or Superlinearly to A compared to that of another Sequence).Suppose pre-structures

{(F_{r})}_{r \in N}

and

{(F_{j}^{'})}_{j \in N}

are non-equivalent and converge uniformly to A; and suppose for every

ε \in range (U^{'})

, where

ε > 0)

and

r \in N

(a): From def. 5 and 6, suppose we have:

$\begin{matrix} \bar{| S (U (ϵ, F_{r}, ω), ψ)} | = \\ inf \{| S (U (ϵ, F_{j}^{'}, ω^{'}), ψ^{'}) | : j \in N, ω^{'} \in Ω, ψ^{'} \in Ψ_{ω}, E (S (U (ϵ, F_{j}^{'}, ω^{'}), ψ^{'})) \geq E (S (U (ϵ, F_{r}, ω), ψ))\} \end{matrix}$

(14)

then (using 14) we have

$\bar{α} (ϵ, r, ω, ψ) = |S (U (ϵ, F_{r}, ω), ψ))| / \bar{|S (U (ϵ, F_{r}, ω), ψ)|}$

(15)
(b): From def. 5 and 6, suppose we have:

$\begin{matrix} \underset{̲}{| S (U (ϵ, F_{r}, ω), ψ)} | = \\ sup \{| S (U (ϵ, F_{j}^{'}, ω^{'}), ψ^{'}) | : j \in N, ω^{'} \in Ω, ψ^{'} \in Ψ_{ω}, E (S (U (ϵ, F_{j}^{'}, ω^{'}), ψ^{'})) \leq E (S (U (ϵ, F_{r}, ω), ψ))\} \end{matrix}$

(16)

then (using 16) we get

$\underset{̲}{α} (ϵ, r, ω, ψ) = |S (U (ϵ, F_{r}, ω), ψ))| / \underset{̲}{|S (U (ϵ, F_{r}, ω), ψ)|}$

(17)

If using equations 15 and 17 we have that:

$\underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) = \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) = 0$

we say ${(F_{r})}_{r \in N}$ converges uniformly to A at asuperlinear rateto that of ${(F_{j}^{'})}_{j \in N}$ .
If using equations 15 and 17 we have either:

(a)

$0 \leq \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) < + \infty$

$0 < \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) \leq + \infty$

(b)

$0 < \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) \leq + \infty$

$0 \leq \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) < + \infty$

(c)

$0 \leq \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) < + \infty$

$0 < \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) \leq + \infty$

(d)

$0 < \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) \leq + \infty$

$0 \leq \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) < + \infty$

we then say ${(F_{r})}_{r \in N}$ converges uniformly to A at alinear rateto that of ${(F_{j}^{'})}_{j \in N}$ .
If using equations 15 and 17 we have that:

$\underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) = \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) = + \infty$

we say ${(F_{r})}_{r \in N}$ converges uniformly to A at asublinear rateto that of ${(F_{j}^{'})}_{j \in N}$ .

Note 2. Since def. 12 is difficult to apply, we make assumptions (without proofs) for the examples below:

Example 12

(Example of pre-structure converging super-linearly to A compared to that of another pre-structure). From example 5:

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{s / r! : 0 \leq s \leq r!\})}_{r \in N}$
${(F_{j}^{'})}_{j \in N} = {(\{c / d : c \in Z, d \in N, d \leq j, 0 \leq c \leq d\})}_{j \in N}$

we assume that

{(F_{r})}_{r \in N}

converges uniformly to A, at asuperlinearrate, compared to that of

{(F_{j}^{'})}_{j \in N}

Example 13

(Obvious Example of pre-structure converging linearly to A compared to that of another pre-structure). Consider the following:

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{s / r! : 0 \leq s \leq r!\})}_{r \in N}$
${(F_{j}^{'})}_{j \in N} = {(\{w / (2 j)! : w \in Z, 0 \leq w \leq 2 j\})}_{j \in N}$

we assume that

{(F_{r})}_{r \in N}

converges uniformly to A, at alinearrate, compared to that of

{(F_{j}^{'})}_{j \in N}

, since using programming we assume:

0 < \underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) = \underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) < + \infty

Example 14

(Non-Obvious Example of pre-structure converging linearly to A compared to another pre-structure). If

[\cdot]

is the nearest integer function and

⌊ \cdot ⌋

is the floor function, consider the following:

$A = \{\sqrt{a} : a \in Q \cap [0, 1]\}$
${(F_{r})}_{r \in N} = {(\{\sqrt{s / r}! : 0 \leq s \leq r!\})}_{r \in N}$
${(F_{j}^{'})}_{j \in N} = {(\{\sqrt{[{(s / 2^{z})}^{2}]} / j! : 0 \leq s \leq {(j!)}^{{1 / (7}^{\land} z)}, 0 \leq z \leq ⌊{log}_{2} (\sqrt[3]{j + 1})⌋\} \cap [0, 1])}_{j \in N}$ (we choose this pre-structure since if ${log}_{2} (| F_{j}^{'} |)$ is the highest entropy (def. 6) that $E (F_{j}^{'})$ could be for every $j \in N$ , we say ${(F_{j}^{'})}_{j \in N}$ has ahigher entropy per elementthan that of ${(F_{r})}_{r \in N}$ if there exists a $k \in N$ , such for all $j \geq k$ , $E (F_{j}^{'}) / {log}_{2} (| F_{j}^{'} |) > E (F_{j}) / {log}_{2} (|F_{j}|)$ ).

despite

{(F_{j}^{'})}_{j \in N}

having a higher entropy per element,

{(F_{r})}_{r \in N}

converges uniformly to A at alinearrate, compared to that of

{(F_{j}^{'})}_{j \in N}

, since using programming we assume:

\underset{ε \to 0}{lim inf} \underset{r \to \infty}{lim inf} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{α} (ϵ, r, ω, ψ) = 0

\underset{ε \to 0}{lim sup} \underset{r \to \infty}{lim sup} sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{α} (ϵ, r, ω, ψ) = + \infty

which should satisfy criteria (2a) in def. 12.

Theorem 2.

{(F_{r})}_{r \in N}

converges super-linearly to A compared to that of

{(F_{j}^{'})}_{j \in N}

then

{(F_{j}^{'})}_{j \in N}

converges sub-linearly to A compared to that of

{(F_{r})}_{r \in N}

Example 15

(Example of pre-structure converging sub-linearly to A compared to another pre-structure). In example 12, if we swap

{(F_{r})}_{r \in N}

for

{(F_{j})}_{j \in N}

where:

$A = Q \cap [0, 1]$
${(F_{r})}_{r \in N} = {(\{c / d : c \in Z, d \in N, d \leq r, 0 \leq c \leq d\})}_{r \in N}$
${(F_{j}^{'})}_{j \in N} = {(\{s / j! : 0 \leq s \leq j!\})}_{j \in N}$

we assume that

{(F_{r})}_{r \in N}

converges to A at asublinearrate to that of

{(F_{j}^{'})}_{j \in N}

1.3. Question on Preliminary Definitions

Are there “simpler" alternatives to either of the preliminary definitions? (Keep this in mind as we continue reading).

2. Main Question

Does there exist a unique extension (or a method that constructively defines a unique extension) of the expected value of f when the value’s finite, using the uniform probability measure [17] on sets measurable in the Carathèodory sense, such we replace f with infinite or undefined expected values with f defined on a chosen pre-structure which depends on A where:

The expected value of f on each term of the pre-structure is finite
The pre-structure converges uniformly to A
The pre-structure converges uniformly to A at a linear or superlinear rate to that of other non-equivalent pre-structures of A which satisfies (1) and (2).
The generalized expected value of f on a pre-structure (i.e. an extension of def.3 to answer the full question) has a unique & finite value, such the pre-structure satisfies (1), (2), and (3).
A choice function is defined which chooses a pre-structure from A where the following satisfies (1), (2), (3), and (4) for the largest possible subset of $R^{A}$ .
If there is more than one choice function that satisfies (1), (2), (3), (4) and (5), we choose the choice function with the “simplest form", meaning for a general pre-structure of A, when each choice function is fully expanded, we take the choice function with the fewest variables/numbers (excluding those with quantifiers).

How do we answer this question? (See Section 3.1, Section 3.2 and Section 3.4 for a partial answer.)

3. Informal Attempt to Answer Main Question

(I advise using computer programmings such as Mathematica, Python, JavaScript, or Matlab to understand the definitions of the answer below.)

3.1. Generalized Expected Values

If the image of f under A is

f [A] : = \{f (x) : x \in A\}

, such from def. 2 and 7, we take the pre-structure of

f [A]

where:

F_{r} \overset{r \in N}{⇉} f [A]

and take the pre-image under f of

F_{r}

(defined as

f^{- 1} [F_{r}] : = \{x \in A : f (x) \in F_{r}\}

) such that:

f^{- 1} [F_{r}] \overset{r \in N}{⇉} A

However, note the expected value of

f^{- 1} [F_{r}]

(def. 3) may be infinite (e.g. unbounded f). Hence, for every

r \in N

, we take the pre-structure

{(F_{r, t_{r}})}_{t_{r} \in N}

f^{- 1} [F_{r}]

where:

\forall (r \in N) (F_{r, t_{r}} \overset{t_{r} \in N}{⇉} f^{- 1} [F_{r}])

Thus, the generalized expected value or

{\ddot{E}}_{U^{'}} [f]

is:

\begin{matrix} \forall (ϵ > 0) \exists (N \in N) \forall (r \in N) \exists (N^{'} \in N) \forall (t_{r} \in N) \\ (r \geq N, t_{r} \geq N^{'} \Rightarrow \frac{1}{U^{'} (F_{r, t_{r}})} \int_{F_{r, t_{r}}} f d x - {\ddot{E}}_{U^{'}} [f] < ϵ) \end{matrix}

(18)

and (similar to def. 2 & 3) if

E_{U^{'}} [f (X_{r, t_{r}})] = \frac{1}{U^{'} (F_{r, t_{r}})} \int_{F_{r, t_{r}}} f d x

(19)

we describe the process of the generalized expected value as

E_{U^{'}} [f (X_{r, t_{r}})] \to {\ddot{E}}_{U^{'}} [f]

3.2. Choice Function

Suppose

S^{'} (A)

is the set of all pre-structures of A which satisfies criteria (1) and (2) of the main question where the generalized expected value of the pre-structures, as they converge uniformly to A, is unique and finite such the pre-structure

{({(F_{r, t_{r}}^{″})}_{t_{r} \in N})}_{r \in N} \in S^{'} (A)

should be a sequence of sets that satisfies criteria (1), (2), (3) and (4) of the main question where (using the end of

§

E_{U^{'}} [f (X_{r, t_{r}}^{''})] \to {\ddot{E}}_{U^{'}}^{''} [f]

(20)

and pre-structure

{({(F_{j, t_{j}}^{'})}_{t_{j} \in N})}_{j \in N}

is an element of

S^{'} (A)

such (using the end of

§

E_{U^{'}} [f (X_{j, t_{j}}^{'})] \to {\ddot{E}}_{U^{'}}^{'} [f]

(21)

but is not an element of the set of equivelant pre-structures of

{({(F_{r, t_{r}}^{″})}_{t_{r} \in N})}_{r \in N}

(i.e. def. 8).

Further note from (a), with equation 14 in def. 12, if we take:

\begin{matrix} \bar{| S (U (ϵ, F_{r, t_{r}}^{''}, ω), ψ)} | = \\ inf \{| S (U (ϵ, F_{j, t_{j}}^{'}, ω^{'}), ψ^{'}) | : j \in N, t_{j} \in N, ω^{'} \in Ω, ψ^{'} \in Ψ_{ω}, E (S (U (ϵ, F_{j, t_{j}}^{'}, ω^{'}), ψ^{'})) \geq E (S (U (ϵ, F_{r, t_{r}}^{''}, ω), ψ))\} \end{matrix}

(22)

and from (b), with equation 16 in def. 12, we take:

\begin{matrix} \underset{̲}{| S (U (ϵ, F_{r, t_{r}}^{''}, ω), ψ)} | = \\ sup \{| S (U (ϵ, F_{j, t_{j}}^{'}, ω^{'}), ψ^{'}) | : j \in N, t_{j} \in N, ω^{'} \in Ω, ψ^{'} \in Ψ_{ω}, E (S (U (ϵ, F_{j, t_{j}}^{'}, ω^{'}), ψ^{'})) \leq E (S (U (ϵ, F_{r, t_{r}}^{''}, ω), ψ))\} \end{matrix}

(23)

Then, using def. 5 with equations 22 and 23, if:

sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} S (U (ϵ, F_{r, t_{r}}^{''}, ω), ψ) = S^{'} (ε, F_{r, t_{r}}^{''}) = S^{'}

(24)

sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \bar{| S (U (ϵ, F_{r, t_{r}}^{″}, ω), ψ)} | = \bar{| S^{'} (ε, F_{r, t_{r}}^{″})} | = \bar{| S^{'}} |

(25)

sup_{ω \in Ω} sup_{ψ \in Ψ_{ω}} \underset{̲}{| S (U (ϵ, F_{r, t_{r}}^{″}, ω), ψ)} | = \underset{̲}{| S^{'} (ε, F_{r, t_{r}}^{″})} | = \underset{̲}{| S^{'}} |

(26)

where, using absolute value function

| | \cdot

, we have:

\begin{matrix} S (r) = \\ (sup (F_{r, t_{r} + 1}^{''}) - sup (F_{r, t_{r}}^{''})) (inf (F_{r, t_{r}}^{''}) - inf (F_{r, t_{r} + 1}^{''})) | | (inf (F_{r, t_{r}}^{''}) - inf (F_{r, t_{r} + 1}^{''})) (sup (F_{r, t_{r} + 1}^{''}) - sup (F_{r, t_{r}}^{''}) - 1) | | \end{matrix}

(27)

such that

\begin{matrix} T (r) = \\ (sup (F_{r, t_{r}}^{''}) inf (F_{r, t_{r}}^{''}) - sup (F_{r, t_{r}}^{''}) inf (F_{r, t_{r} + 1}^{''})) ((inf (F_{r, t_{r}}^{''}) - inf (F_{r, t_{r} + 1}^{''})) - (sup (F_{r, t_{r} + 1}^{''}) - sup (F_{r, t_{r}}^{''})) - 1) \\ (inf (F_{r, t_{r}}^{''}) - inf (F_{r, t_{r} + 1}^{''})) (sup (F_{r, t_{r} + 1}^{''}) - sup (F_{r, t_{r}}^{''})) \end{matrix}

(28)

and, using equations 24, 25, 26, 27, 28 with the nearest integer function

[\cdot]

, we want:

(29)

such, using equation 29, if set

S^{''} (A) \subseteq S^{'} (A)

and

P (\cdot)

is the power-set, then set

C (A)

is the largest element of:

\begin{matrix} {S^{″} (A) \subseteq S^{'} (A) : \forall (ϵ_{1} > 0) \exists (M \in N) \forall (ε \in range (U^{'})) \exists (k \in N) \forall (r \in N) \exists (k^{'} \in N) \forall (t_{r} \in N) \forall (\{F_{r, t_{r}}^{″}\} \in S^{″} (A)) \\ (0 < ε \leq M, r \geq k, t_{r} \geq k^{'} \Rightarrow | S^{'} (ε, F_{r, t_{r}}^{''}) - K (ε, F_{r, t_{r}}^{''}) - inf_{\{F_{g, t_{g}}\} \in S^{'} (A)} (S^{'} (ε, F_{g, t_{g}}) - K (ε, F_{g, t_{g}})) | < ϵ_{1})} \subseteq P (S^{'} (A)) \end{matrix}

(30)

w.r.t to inclusion, such the choice function is

C (A)

if the following contains just one element.

Otherwise, for

k \in N

, suppose we say

C^{k} (A)

represents the k-th iteration of the choice function of A, e.g.

C^{3} (A) = C (C (C (A)))

, where the infinite iteration of

C (A)

(if it exists) is

lim_{k \to \infty} C^{k} (A) = C^{\infty} (A)

. Therefore, when taking the following:

C^{'} (A) = \{\begin{matrix} C (A) & if C (A) contains one element \\ C^{j} (A) & if j \in N, such for all k \geq j, C^{k} (A) contains one element \\ C^{\infty} (A) & if it exists, and C^{\infty} (A) contains one element \end{matrix}

(31)

we say

C^{'} (A)

is the choice function and the expected value, using def. 20, is

{\ddot{E}}_{U^{'}}^{″} [f]

3.3. Questions on Choice Function

Suppose we define function $f : A \to R$ . What unique pre-structure would $C^{'} (A)$ contain (if it exists) for:
- $A = Z$ where if ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} \in C^{'} (Z)$ and $f = {id}_{Z}$ , we want
  
  ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} = {({(\{m \in Z : - r \leq - t_{r} \leq m \leq t_{r} \leq r\})}_{t_{r} \in N})}_{r \in N}$
- $A = Q$ where if ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} \in C^{'} (Q)$ and $f = {id}_{Q}$ , we want
  
  ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} = {({(\{s / r! : s \in Z, - r \cdot r! \leq - t_{r} \leq s \leq t_{r} \leq r \cdot r!\})}_{t_{r} \in N})}_{r \in N}$
- $A = R$ where we’re not sure what ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} \in C^{'} (R)$ would be if $f = {id}_{R}$ . What would ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N}$ be if it’s unique?

3.4. Increasing Chances of an Unique and Finite Expected Value

In case

C^{'} (A)

, in equation 31, does not exist; if there exists a unique and finite

{\ddot{E}}_{U^{'}}^{″} [f]

(see

§

) where:

(32)

Then

{\ddot{E}}_{U^{'}}^{″} [f]

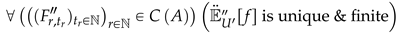
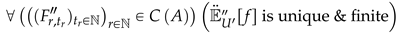
is the generalized expected value w.r.t choice function C, which answers criteria (1), (2), (3), (4), (perhaps (5)) of the question in

§

; however, there is still a chance that the equation 32 fails to give an unique

{\ddot{E}}_{U^{'}}^{″} [f]

. Hence; if

k \in N

, we take the k-th iteration of the choice function C in 30, such there exists a

j \in N

, where for all

k \geq j

, if

{\ddot{E}}_{U^{'}}^{″} [f]

is unique and finite then the following is the generalized expected value w.r.t finitely iterated C.

In other words, if the k-th iteration of C is represented as

C^{[k]}

(where e.g.

C^{3} (A) = C (C (C (A)))

), we want a unique and finite

{\ddot{E}}_{U^{'}}^{″} [f]

where:

(33)

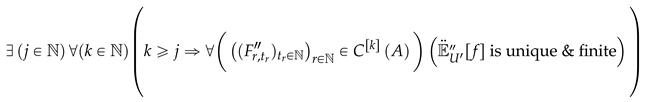
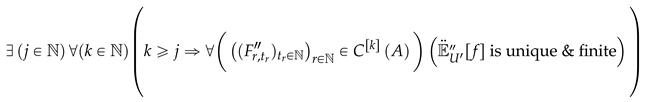
If this still does not give a unique and finite expected value, we then take the most generalized expected value w.r.t an infinitely iterated C where if the infinite iteration of C is stated as

lim_{k \to \infty} C^{[k]} (f [A]) = C^{\infty} (f [A])

, we then want a unique

{\ddot{E}}_{U^{'}}^{″} [f]

where:

(34)

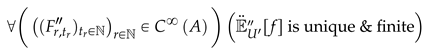
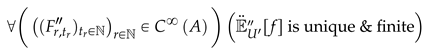
However, in such cases,

{\ddot{E}}_{U^{'}}^{″} [f]

should only be used for functions where the expected value is infinite or undefined or for worst-case functions—badly behaved

f : A \to R

(where for

n \in N

A \subseteq R^{n}

, and f is a function) defined on infinite points covering an infinite expanse of space. For example:

For a worst-case f defined on countably infinite A (e.g. countably infinite "pseudo-random points" non-uniformly scattered across the real plane), one may need just one iteration of C (since most function on countable sets need just one iteration of C for ${\ddot{E}}_{U^{'}}^{″} [f]$ to be unique); otherwise, one may use equation 33 for finite iterations of C.
For a worst-case f defined on uncountable A, we might have to use equation 34 as averaging such a function might be nearly impossible. We can imagine this function as an uncountable number of "pseudo-random" points non-uniformly generated on a subset of the real plane (see Section 4.1 for a visualization.)

Note, however, that no matter how generalized and “meaningful" the extension of an expected value is, there will always be an f where the expected value does not exist.

3.5. Questions Regarding The Answer

Using prevalence and shyness [11,14], can we say the set of f where either equations 32, 33 and 34 have an unique and finite ${\ddot{E}}_{U^{'}}^{″} [f]$ which forms either a prevalent or neither prevalent nor shy subset of $R^{A}$ ? (If the subset is prevalent, this implies either one of the generalized expected values can be unique and finite for a “large" subset of $R^{A}$ ; however, if the subset is neither prevalent nor shy we need more precise definitions of “size" which takes “an exact probability that the expected values are unique & finite"—some examples (which are shown in this answer [9]) being:

(a)

Fractal Dimension notions

(b)

Kolmogorov Entropy

(c)

Baire Category and Porosity
There may be a total of 292 variables in the choice function C (excluding quantifiers). Is there a choice function (ignoring quantifiers) which answers criteria (1), (2), (3) & (4) of the main question in Section 2 for a "larger" subset of $R^{A}$ ? (This might be impossible to answer since such a solution cannot be shown with prevalence or shyness [11,14])—therefore, we need a more precise version of “size" with some examples, again, shown in [9].
If question (2) is correct, what is the choice function C using either equations 32, 33 and 34 fully answers the question in Section 2?
Can either equations 32, 33 and 34 (when A is the set of all Liouville numbers [6] and $f = {id}_{A}$ ) give a finite value? What would the value be?
Similar to how definition 13 in §4 approximates the expected value in definition 1, how do approximate equations 32, 33 and 34?
Can programming be used to estimate equations 32, 33 and 34 respectively (if an unique/finite result of either of the expected values exist)?

3.6. Applications

In Quanta magazine [3], Wood writes on Feynman Path Integrals: “No known mathematical procedure can meaningfully average1 an infinite number of objects covering an infinite expanse of space in general. The path integral is more of a physics philosophy than an exact mathematical recipe."—despite Wood’s statement, mathematicians Bottazzi E. and Eskew M. [5] found a constructive solution to the statement using integrals defined on filters over families of finite sets; however, the solution was not unique as one has to choose a value in a partially ordered ring of infinite and infinitesimal elements.

(a)

Perhaps, if Botazzi’s and Eskew’s Filter integral [5] is not enough to solve Wood’s statement, could we replace the path integral with expected values from equations 32, 33 and 34 respectively (or a complete solution to Section 2)? (See, again, Section 4.1 for a visualization of Wood’s statement.)
As stated in Section 1.1, “when the Lebesgue measure of A, measurable in the Caratheodory sense, has zero or infinite volume (or undefined measure), there may be multiple, conflicting ways of defining a "natural" uniform measure on A." This is an example of Bertand’s Paradox which shows, "the principle of indifference (that allows equal probability among all possible outcomes when no other information is given) may not produce definite, well-defined results for probabilities if applied uncritically, when the domain of possibilities is infinite [16].

Using $§$ , perhaps if we take (from def. 31):

$C^{'} (A) = \{\begin{matrix} C (A) & if C (A) contains one element \\ C^{j} (A) & if j \in N, such for all k \geq j, C^{k} (A) contains one element \\ C^{\infty} (A) & if it exists, and C^{\infty} (A) contains one element \end{matrix}$

then for ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} \in C^{'} (A)$ , if we want $S \subseteq A$ and we get the following:

$\begin{matrix} \exists (U (S) \in R) \forall (ϵ > 0) \exists (N \in N) \forall (r \in N) \exists (N^{'} \in N) \forall (t_{r} \in N) \\ (r \geq N, t_{r} \geq N^{'} \Rightarrow |\frac{U^{'} (S \cap F_{r, t_{r}}^{''})}{U^{'} (F_{r, t_{r}}^{''})} - U (S)| < ϵ) \end{matrix}$

(35)

Then $U (S)$ might serve as a solution to Bertand’s Paradox (unless there’s a better $C^{'} (A)$ and ${({(F_{r, t_{r}}^{''})}_{t_{r} \in N})}_{r \in N} \in C^{'} (A)$ which completely solves the main question in $§$ ).

Now consider the following:
(a)
How do we apply $U (S)$ (or a better solution) to the usual example which demonstrates the Bertand’s Paradox as follows: for an equilateral triangle (inscribed in a circle), suppose a chord of the circle is chosen at random—what is the probability that the chord is longer than a side of the triangle? [4] (According to Bertand’s Paradox there are three arguments which correctly use the principle of indifference yet give different solutions to this problem [4]:
- The “random endpoints" method: Choose two random points on the circumference of the circle and draw the chord joining them. To calculate the probability in question imagine the triangle rotated so its vertex coincides with one of the chord endpoints. Observe that if the other chord endpoint lies on the arc between the endpoints of the triangle side opposite the first point, the chord is longer than a side of the triangle. The length of the arc is one-third of the circumference of the circle, therefore the probability that a random chord is longer than a side of the inscribed triangle is $1 / 3$ .
- The "random radial point" method: Choose a radius of the circle, choose a point on the radius, and construct the chord through this point and perpendicular to the radius. To calculate the probability in question imagine the triangle rotated so a side is perpendicular to the radius. The chord is longer than a side of the triangle if the chosen point is nearer the center of the circle than the point where the side of the triangle intersects the radius. The side of the triangle bisects the radius, therefore the probability a random chord is longer than a side of the inscribed triangle is $1 / 2$ .
- The "random midpoint" method: Choose a point anywhere within the circle and construct a chord with the chosen point as its midpoint. The chord is longer than a side of the inscribed triangle if the chosen point falls within a concentric circle of radius $1 / 2$ the radius of the larger circle. The area of the smaller circle is one-fourth the area of the larger circle, therefore the probability a random chord is longer than a side of the inscribed triangle is $1 / 4$ .

4. Glossary

4.1. Example of Case (2) of Worst Case Functions

(If the explanation below is difficult to understand, see the code in [1] to accompany the explanation.)

We wish to create a function that has uncountable points which are non-uniform (i.e. without complete spatial randomness [13]) in the sub-space of

R^{2}

, , such a countable collection of non pseudo-randomy-values in the range of the function "almost surely" or never "almost unsurely" has corresponding pseudo-random x-values, where the expected value or integral of the function w.r.t uniform probability measure [17][ p.32-37] is non-obvious (i.e. not equivalent to the arithmetic mean of the output of the function on the uniform sample of domain). For the sake of simplicity, I shall say the function is made of uncountable "nearly" pseudo-random points, even though that’s technically impossible.

Suppose for real numbers

x_{1}, x_{2}, y_{1}

and

y_{2}

, we generate an uncountable number of "nearly pseudo-random" points that are non-uniform in the subspace

[x_{1}, x_{2}] \times [y_{1}, y_{2}] \subseteq R^{2}

We therefore define the function as

f : [x_{1}, x_{2}] \to [y_{1}, y_{2}]

Now suppose

b \in \{2, 3, \cdot \cdot \cdot, 10\}

where the base-b expansion of real numbers, in interval

[x_{1}, x_{2}]

, have infinite decimals that approach x from the right side so when

x_{1} = x_{2}

we get

f (x_{1}) = f (x_{2})

Furthermore, for

N \cup \{0\} = N_{0}

, if

r \in N_{0}

and

{digit}_{b} : R \times Z \to \{0, 1, \cdot \cdot \cdot, b - 1\}

is a function where

{digit}_{b} (x, r)

takes the digit in the

b^{r}

-th decimal fraction of the base-b expansion of x (e.g.

{digit}_{10} (1.789, 2) = 8

), then

{\{{g_{r}}^{'}\}}_{r \in N_{0}}

is a sequence of functions such that

{g_{r}}^{'} : N_{0} \to N_{0}

is defined to be:

g_{r}^{'} (x) = [\frac{10}{b} sin (r x) + \frac{10}{b}]

(36)

then for some large

k \in N

and

x_{1}, x_{2} \in R

, the intermediate function (before f) or

f_{1} : [x_{1}, x_{2}] \to R

is defined to be

\begin{matrix} f_{1} (x) = & |(\sum_{r = 0}^{\infty} g_{r + 1}^{'} (\sum_{p = r}^{r + k} {digit}_{b} (x, p)) / b^{r}) - 10| = \\ |((\sum_{r = 0}^{\infty} [\frac{10}{b} sin ((r + 1) (\sum_{p = r}^{r + k} {digit}_{b} (x, p))) + \frac{10}{b}]) / b^{r}) - 10| \end{matrix}

(37)

where the points in

f_{1}

are "almost pseudo-randomly" and non-uniformly distributed on

[x_{1}, x_{2}] \times [0, 10]

. What we did was convert every digit of the base-b expansion of x to a pseudo-random number that is non-equally likely to be an integer, including and in-between, 0 and

(10 \cdot 10^{s}) / b

. Furthermore, we also make the function appear truly “pseudo-random", by adding the

b^{r}

-th decimal fraction with the next k decimal fractions; however, we want to control the end-points of

[0, 10^{s + 1}]

such if

y_{1}, y_{2} \in R

, we convert

[x_{1}, x_{2}] \times [0, 10]

[x_{1}, x_{2}] \times [y_{1}, y_{2}]

by manipulating equation 37 to get:

\begin{matrix} f (x) = & y_{2} - \frac{y_{2} - y_{1}}{10} f_{1} (x) \\ y_{2} - (\frac{y_{2} - y_{1}}{10}) |((\sum_{r = 0}^{\infty} [\frac{10}{b} sin ((r + 1) (\sum_{p = r}^{r + k} {digit}_{b} (x, p))) + \frac{10}{b}]) / b^{r}) - 10| \end{matrix}

(38)

such the larger k is, the more pseudo-random the distribution of points in f in the space

[x_{1}, x_{2}] \times [y_{1}, y_{2}]

, but unlike most distributions of such points, f is uncountable.

4.2. Question Regarding Section 4.1

Let us give a specific example, suppose for the function in equation 38 of Section 4.1, we have:

$b = 3$
$[x_{1}, x_{2}] \times [y_{1}, y_{2}] = [0, 1] \times [0, 1]$
$k = 100$

(one can try simpler parameters); what is the expected value using either equations 33 and 34 (or a more complete solution to Section 2) if the answer is finite and unique?

What about for f in general (i.e. in terms of b,

x_{1}

x_{2}

y_{1}

y_{2}

and k)?

(Note if

x_{1}, y_{1} \to - \infty

and

x_{2}, y_{2} \to \infty

, then the function is an explicit example of the function that Wood2 describes in Quanta Magazine)

4.3. Approximating the Expected Value

Definition 13

(Approximating the Expected Value). In practice, the computation of this expected value may be complicated if the set A is complicated. If analytic integration does not give a closed-form solution then a general and relatively simple way to compute the expected value (up to high accuracy) is with importance sampling. To do this, we produce values

X_{1}, X_{2}, . . ., X_{M} \sim IID g

for some density function g with support

A \subseteq support (g) \subseteq R^{n}

(hopefully with support fairly close to A) and we use the estimator:

\begin{matrix} {\hat{μ}}_{M} & \equiv \frac{\sum_{i = 1}^{M} I (X_{i} \in A) \cdot f (X_{i}) / g (X_{i})}{\sum_{i = 1}^{M} I (X_{i} \in A) / g (X_{i})} \end{matrix}

(39)

From the law of large numbers, we can establish that

E [f (X)] = {lim}_{M \to \infty} {\hat{μ}}_{M}

so if we take M to be large then we should get a reasonably good computation of the expected value of interest.

Note importance sampling requires three things:

We need to know when point x is in set A or not
We need to be able to generate points from a density g that is on a support that covers A but is not too much bigger than A
We have to be able to compute $f (x)$ and $g (x)$ for each point $x \in A$

References

Krishnan B. Finding expected value over uncountable number of pseudo-random points, non-uniformly distributed over the sub-space of R², 2023. https://mathematica.stackexchange.com/questions/283525/finding-expected-value-over-uncountable-number-of-pseudo-random-points-non-unif.
Patrick B. John Wiley & Sons, New York, 3 edition, 1995. https://www.colorado.edu/amath/sites/default/files/attached-files/billingsley.pdf.
Wood C. Mathematicians prove 2d version of quantum gravity really works. Quanta Magazine. https://www.quantamagazine.org/mathematicians-prove-2d-version-of-quantum-gravity-really-works-20210617.
Alon Drory. Failure and uses of jaynes’ principle of transformation groups. Foundations of Physics, 45(4):439–460, feb 2015. https://arxiv.org/pdf/1503.09072.pdf.
Bottazi E. and Eskew M. Integration with filters. https://arxiv.org/pdf/2004.09103.pdf.
Adam Grabowski and Artur Kornilowicz. Introduction to liouville numbers. Formalized Mathematics, 25, 01 2017. https://sciendo.com/article/10.1515/forma-2017-0003.
Michael Greinecker (https://mathoverflow.net/users/35357/michael greinecker). Demystifying the caratheodory approach to measurability. MathOverflow. https://mathoverflow.net/q/34007.
Mark McClure (https://mathoverflow.net/users/46214/mark mcclure). Integral over the cantor set hausdorff dimension. MathOverflow. https://mathoverflow.net/q/235609 (version: 2016-04-07).
Dave L. Renfro (https://math.stackexchange.com/users/13130/dave-l renfro). Proof that neither “almost none” nor “almost all” functions which are lebesgue measurable are non-integrable. Mathematics Stack Exchange. https://math.stackexchange.com/q/4623168 (version: 2023-01-21).
Ben (https://stats.stackexchange.com/users/173082/ben). In statistics how does one find the mean of a function w.r.t the uniform probability measure? Cross Validated. https://stats.stackexchange.com/q/602939 (version: 2023-01-24).
Brian R. Hunt. Prevalence: a translation-invariant “almost every” on infinite-dimensional spaces. 1992. https://arxiv.org/abs/math/9210220.
Gray M. Springer New York, New York [America];, 2 edition, 2011. https://ee.stanford.edu/~gray/it.pdf.
Rokach L. Maimon O. Springer New York, New York [America];, 2 edition, 2010. [CrossRef]
William Ott and James A. Yorke. Prevelance. Bulletin of the American Mathematical Society, 42(3):263–290, 2005. https://www.ams.org/journals/bull/2005-42-03/S0273-0979-05-01060-8/S0273-0979-05-01060-8.pdf.
Kenneth H. Rosen. Elementary number theory and its applications (6. ed.). Addison-Wesley, 1993. https://www.bibsonomy.org/bibtex/2bdf609bd9cb49ba96ef69ca99540db82/dblp.
Nicholas Shackel. Bertrand’s paradox and the principle of indifference. Philosophy of Science, 74(2):150–175, 2007. https://orca.cardiff.ac.uk/id/eprint/3803/1/Shackel%20Bertrand’s%20paradox%205.pdf.
Leinster T. and Roff E. The maximum entropy of a metric space. https://arxiv.org/pdf/1908.11184.pdf.

1	Meaningful Average—The average answers the main question in §2.
2	Wood wrote on Feynman Path Integrals: “No known mathematical procedure can meaningfully average 1 an infinite number of objects covering an infinite expanse of space in general."

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Defining the Most Generalized, Natural Extension of the Expected Value on Measurable Functions

Abstract

0. Background

1. Preliminaries

1.1. Motivation

1.2. Preliminary Definitions

1.3. Question on Preliminary Definitions

2. Main Question

3. Informal Attempt to Answer Main Question

3.1. Generalized Expected Values

3.2. Choice Function

3.3. Questions on Choice Function

3.4. Increasing Chances of an Unique and Finite Expected Value

3.5. Questions Regarding The Answer

3.6. Applications

4. Glossary

4.1. Example of Case (2) of Worst Case Functions

4.2. Question Regarding Section 4.1

4.3. Approximating the Expected Value

References

MDPI Initiatives

Important Links

Subscribe