Approximate Numerical Procedures for the Navier-Stokes System Through the Generalized Method of Lines

Preprint

Article

Approximate Numerical Procedures for the Navier-Stokes System Through the Generalized Method of Lines

Altmetrics

Downloads

261

Views

706

Comments

A peer-reviewed article of this preprint also exists.

Fabio Botelho^*

This version is not peer-reviewed

This preprints belongs to the Topic

Numerical Methods for Partial Differential Equations

Submitted:

23 February 2023

Posted:

24 February 2023

Read the latest preprint version here

Alerts

Abstract

This article develops applications of the generalized method of lines to numerical solutions of the time-independent, incompressible Navier-Stokes system in fluid mechanics. We recall that for such a method, the domain of the partial differential equation in question is discretized in lines (or more generally in curves), and the concerning solutions are written on these lines as functions of the boundary conditions and the domain boundary shape.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

In this article, we develop approximate solutions for the time independent incompressible Navier-Stokes system, through the generalized method of lines. We recall again, for such a method, the domain of the partial differential equation in question is discretized in lines and the concerning solution is written on these lines as functions of the boundary conditions and boundary shape. We emphasize these last main results are established through applications of the Banach fixed point theorem.

Remark 1.1.

We also highlight the first two paragraphs in this article ( a relatively small part) overlaps with the Chapter 27, starting page 512, in the book F.S. Botelho, [2], published in 2020, by CRC Taylor and Francis. However, we emphasize the present article includes substantial new parts, including a concerning software not included in the previous version of 2020. Another novelty in the present version is the establishment of appropriate boundary conditions for an elliptic system equivalent to original Navier-Stokes one. Such new boundary conditions and concerning results are indicated in Section 2.

At this point we describe the system in question.

Consider

Ω \subset R^{2}

an open, bounded and connected set, whose the regular (Lipschitzian) internal boundary is denoted by

Γ_{0}

and the regular external one is denoted by

Γ_{1}

. For a two-dimensional motion of a fluid on

Ω

, we denote by

u : Ω \to R

the velocity field in the direction x of the Cartesian system

(x, y)

, by

v : Ω \to R

, the velocity field in the direction y and by

p : Ω \to R

, the pressure one. We define

P = p / ρ

, where

ρ

is the constant fluid density. Finally,

ν

denotes the viscosity coefficient and g denotes the gravity field. Under such notation and statements, the time-independent incompressible Navier-Stokes system of partial differential equations stands for,

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u \partial_{x} u - v \partial_{y} u - \partial_{x} P + g_{x} = 0, & in Ω, \\ ν \nabla^{2} v - u \partial_{x} v - v \partial_{y} v - \partial_{y} P + g_{y} = 0, & in Ω, \\ \partial_{x} u + \partial_{y} v = 0, & in Ω, \end{matrix} \end{matrix}

(1)

\begin{matrix} \{\begin{matrix} u = v = 0, & on Γ_{0}, \\ u = u_{\infty}, v = 0, P = P_{\infty}, & on Γ_{1} \end{matrix} \end{matrix}

(2)

At first we look for solutions

(u, v, P) \in W^{2, 2} (Ω) \times W^{2, 2} (Ω) \times W^{1, 2} (Ω)

. We emphasize details about such Sobolev spaces may be found in [1]. Finally, standard results on finite differences and existence theory and other results for similar systems may be found in [6,7,8,9,10] and [11], respectively.

2. Details about an equivalence of a concerning elliptic system

Consider again the Navier-Stokes system

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u \partial_{x} u - v \partial_{y} u - \partial_{x} P + g_{x} = 0, & in Ω, \\ ν \nabla^{2} v - u \partial_{x} v - v \partial_{y} v - \partial_{y} P + g_{y} = 0, & in Ω, \\ \partial_{x} u + \partial_{y} v = 0, & in Ω, \end{matrix} \end{matrix}

(3)

\begin{matrix} \{\begin{matrix} u = v = 0, & on Γ_{0}, \\ u = u_{\infty}, v = 0, P = P_{\infty}, & on Γ_{1} \end{matrix} \end{matrix}

(4)

As previously mentioned, at first we look for solutions

(u, v, P) \in W^{2, 2} (Ω) \times W^{2, 2} (Ω) \times W^{1, 2} (Ω)

We are going to obtain an equivalent Elliptic system with appropriate boundary conditions.

Our main result is summarized by the following theorem.

Theorem 2.1.

Let

Ω \subset R^{2}

be an open, bounded, connected set a regular (Lipschitzian) boundary.

Assume

u, v, P \in W^{2, 2} (Ω)

are such that

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u u_{x} - v u_{y} - P_{x} + g_{x} = 0, & in Ω, \\ ν \nabla^{2} v - u v_{x} - v v_{y} - P_{y} + g_{y} = 0, & in Ω, \\ \nabla^{2} P + u_{x}^{2} + v_{y}^{2} + 2 u_{y} v_{x} - \nabla^{2} g = 0, & in Ω, \end{matrix} \end{matrix}

(5)

\begin{matrix} \{\begin{matrix} u = u_{0}, v = v_{0}, & on \partial Ω, \\ u_{x} + v_{y} = 0, & on \partial Ω . \end{matrix} \end{matrix}

(6)

Suppose also the unique solution of equation in w

ν \nabla^{2} w - u w_{x} - v w_{y} = 0, in Ω

with the boundary conditions

w = 0 on \partial Ω,

w = 0, in Ω .

Under such hypotheses,

u, v, P

solve the following Navier-Stokes system

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u u_{x} - v u_{y} - P_{x} + g_{x} = 0, & in Ω, \\ ν \nabla^{2} v - u v_{x} - v v_{y} - P_{y} + g_{y} = 0, & in Ω, \\ u_{x} + v_{y} = 0, & in Ω, \end{matrix} \end{matrix}

(7)

\begin{matrix} \{\begin{matrix} u = u_{0}, v = v_{0}, & on \partial Ω, \\ u_{x} + v_{y} = 0, & on \partial Ω . \end{matrix} \end{matrix}

(8)

Proof.

In (1), taking the derivative in x of the first equation and adding with the derivative in y of the second equation, we obtain

\begin{matrix} ν \nabla^{2} (u_{x} + v_{y}) - u {(u_{x} + v_{y})}_{x} - v {(u_{x} + v_{y})}_{y} \\ - \nabla^{2} P - u_{x}^{2} - v_{y}^{2} - 2 u_{y} v_{x} + \nabla^{2} g = 0, in Ω \end{matrix}

(9)

Assume now

u, v, P

are such that

\nabla^{2} P + u_{x}^{2} + v_{y}^{2} + 2 u_{y} v_{x} - \nabla^{2} g = 0, in Ω,

From this and (9), we get

ν \nabla^{2} (u_{x} + v_{y}) - u {(u_{x} + v_{y})}_{x} - v {(u_{x} + v_{y})}_{y} = 0, in Ω .

(10)

Denoting

w = u_{x} + v_{y}

, from this last equation we obtain

ν \nabla^{2} w - u w_{x} - v w_{y} = 0, in Ω .

From the hypothesis, the unique solution of this last equation with the boundary conditions

w = 0, on \partial Ω,

w = 0

From this and (10) we have

u_{x} + v_{y} = 0,

Ω

with the boundary conditions

u_{x} + v_{y} = 0, on \partial Ω .

The proof is complete. □

3. An approximate proximal approach

In this section we develop an approximate proximal numerical procedure for the model in question.

Such results are extensions of previous ones published in F.S. Botelho, [3] now for the Navier-Stokes system context.

More specifically, we solve the equation

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u \partial_{x} u - v \partial_{y} u - \partial_{x} P = 0, & in Ω, \\ ν \nabla^{2} v - u \partial_{x} v - v \partial_{y} v - \partial_{y} P = 0, & in Ω, \\ \nabla^{2} P + {(\partial_{x} u)}^{2} + {(\partial_{y} v)}^{2} + 2 (\partial_{y} u) (\partial_{x} v) = 0, & in Ω, \end{matrix} \end{matrix}

(11)

We present a software similar to those presented in [3], with

ν = 0.0177

, and with

Ω = [0, 1] \times [0, 1]

with the boundary conditions

u = u_{0} = 0.65 y (1 - y), v = v_{0} = 0, P = p_{0} = 0.15 on [0, y], \forall y \in [0, 1],

u = v = P_{y} = 0, on [x, 0] and [x, 1], \forall x \in [0, 1],

u_{x} = v_{x} = 0, and P = p_{f} = 0.12 on [1, y], \forall y \in [0, 1] .

The equation (11), in partial finite differences, stands for

\begin{matrix} ν (\frac{u_{n + 1} - 2 u_{n} + u_{n - 1}}{d^{2}} + \frac{\partial^{2} u_{n}}{\partial y^{2}}) - u_{n} \frac{(u_{n} - u_{n - 1})}{d} - v_{n} \frac{\partial u_{n}}{\partial y} \\ - \frac{P_{n} - P_{n - 1}}{d} = 0, \end{matrix}

(12)

\begin{matrix} ν (\frac{v_{n + 1} - 2 v_{n} + v_{n - 1}}{d^{2}} + \frac{\partial^{2} v_{n}}{\partial y^{2}}) - u_{n} \frac{(v_{n} - v_{n - 1})}{d} - v_{n} \frac{\partial v_{n}}{\partial y} \\ - \frac{\partial P_{n}}{\partial y} = 0, \end{matrix}

(13)

\begin{matrix} (\frac{P_{n + 1} - 2 P_{n} + P_{n - 1}}{d^{2}} + \frac{\partial^{2} P_{n}}{\partial y^{2}}) + (u_{n} - u_{n - 1}) \frac{(u_{n} - u_{n - 1})}{d^{2}} + {(\frac{\partial v_{n}}{\partial y})}^{2} \\ + 2 \frac{\partial u_{n}}{\partial y} (\frac{v_{n} - v_{n - 1}}{d}) = 0 . \end{matrix}

(14)

After linearizing such a system about

U_{0}, V_{0}, P_{0}

and introducing the proximal formulation, for an appropriate non-negative real constant K,we get

\begin{matrix} ν (\frac{u_{n + 1} - 2 u_{n} + u_{n - 1}}{d^{2}} + \frac{\partial^{2} u_{n}}{\partial y^{2}}) - {(U_{0})}_{n} \frac{(u_{n} - {(U_{0})}_{n - 1})}{d} - {(V_{0})}_{n} \frac{\partial u_{n}}{\partial y} \\ - \frac{{(P_{0})}_{n} - {(P_{0})}_{n - 1}}{d} - K u_{n} + K {(U_{0})}_{n} = 0, \end{matrix}

(15)

\begin{matrix} ν (\frac{v_{n + 1} - 2 v_{n} + v_{n - 1}}{d^{2}} + \frac{\partial^{2} v_{n}}{\partial y^{2}}) - {(U_{0})}_{n} \frac{(v_{n} - {(V_{0})}_{n - 1})}{d} - {(V_{0})}_{n} \frac{\partial v_{n}}{\partial y} \\ - \frac{\partial {(P_{0})}_{n}}{\partial y} - K v_{n} + K {(V_{0})}_{n} = 0, \end{matrix}

(16)

\begin{matrix} (\frac{P_{n + 1} - 2 P_{n} + P_{n - 1}}{d^{2}} + \frac{\partial^{2} P_{n}}{\partial y^{2}}) + (u_{n + 1} - {(U_{0})}_{n}) \frac{({(u)}_{n + 1} - {(U_{0})}_{n})}{d^{2}} + {(\frac{\partial {(V_{0})}_{n}}{\partial y})}^{2} \\ + 2 \frac{\partial {(U_{0})}_{n}}{\partial y} (\frac{v_{n + 1} - {(V_{0})}_{n}}{d}) - K P_{n} + K {(P_{0})}_{n} = 0 . \end{matrix}

(17)

At this point denoting

ν = e_{1},

we define

{(T_{1})}_{n} = (- {(U_{0})}_{n} \frac{(u_{n} - {(U_{0})}_{n - 1})}{d} - {(V_{0})}_{n} \frac{\partial u_{n}}{\partial y} - \frac{{(P_{0})}_{n} - {(P_{0})}_{n - 1}}{d}) \frac{d^{2}}{e_{1}} + \frac{\partial^{2} u_{n}}{\partial y^{2}} d^{2},

{(T_{2})}_{n} = (- {(U_{0})}_{n} \frac{(v_{n} - {(V_{0})}_{n - 1})}{d} - {(V_{0})}_{n} \frac{\partial v_{n}}{\partial y} - \frac{\partial {(P_{0})}_{n}}{\partial y}) \frac{d^{2}}{e_{1}} + \frac{\partial^{2} v_{n}}{\partial y^{2}} d^{2},

and

\begin{matrix} {(T_{3})}_{n} & = & (u_{n + 1} - {(U_{0})}_{n}) \frac{({(u)}_{n + 1} - {(U_{0})}_{n})}{d^{2}} d^{2} + {(\frac{\partial {(V_{0})}_{n}}{\partial y})}^{2} d^{2} \\ + 2 \frac{\partial {(U_{0})}_{n}}{\partial y} (\frac{v_{n + 1} - {(V_{0})}_{n}}{d}) d^{2} + \frac{\partial^{2} P_{n}}{\partial y^{2}} d^{2} . \end{matrix}

(18)

Therefore, we may write

u_{n + 1} - 2 u_{n} + u_{n - 1} + K u_{n} \frac{d^{2}}{e_{1}} + {(T_{1})}_{n} + {(f_{1})}_{n} = 0,

where

{(f_{1})}_{n} = - K {(U_{0})}_{n} \frac{d^{2}}{e_{1}},

\forall n \in {1, \dots, N - 1} .

In particular for

n = 1

, we obtain

u_{2} - 2 u_{1} + u_{0} + {(T_{1})}_{1} + {(f_{1})}_{1} = 0,

so that

u_{1} = a_{1} u_{2} + b_{1} u_{0} + c_{1} {(T_{1})}_{1} + {(h_{1})}_{1} + {(E_{r})}_{1},

where

a_{1} = {(2 + K \frac{d^{2}}{e_{1}})}^{- 1},

b_{1} = a_{1}

c_{1} = a_{1}

{(h_{1})}_{1} = a_{1} {(f_{1})}_{1},

{(E_{r})}_{1} = 0 .

Similarly, for

n = 2

we get

u_{3} - 2 u_{2} + u_{1} + {(T_{1})}_{2} + {(f_{1})}_{2} = 0,

so that

u_{2} = a_{2} u_{3} + b_{2} u_{0} + c_{2} {(T_{1})}_{2} + {(h_{1})}_{2} + {(E_{r})}_{2},

where

a_{2} = {(2 + K \frac{d^{2}}{e_{1}} - a_{1})}^{- 1},

b_{2} = a_{2} b_{1}

c_{2} = a_{2} (c_{1} + 1)

{(h_{1})}_{2} = a_{2} ({(h_{1})}_{1} + {(f_{1})}_{2}),

{(E_{1})}_{2} = a_{2} (c_{1} ({(T_{1})}_{1} - {(T_{1})}_{2})) .

Reasoning inductively, having

u_{n - 1} = a_{n - 1} u_{n} + b_{n - 1} u_{0} + c_{n - 1} {(T_{1})}_{n - 1} + {(h_{1})}_{n - 1} + {(E_{r})}_{n - 1},

we obtain

u_{n} = a_{n} u_{n + 1} + b_{n} u_{0} + c_{n} {(T_{1})}_{n} + {(h_{1})}_{n} + {(E_{r})}_{n},

(19)

where

a_{n} = {(2 + K \frac{d^{2}}{e_{1}} - a_{n - 1})}^{- 1},

b_{n} = a_{n} b_{n - 1}

c_{n} = a_{n} (c_{n - 1} + 1)

{(h_{1})}_{n} = a_{n} ({(h_{1})}_{n - 1} + {(f_{1})}_{n}),

(E_{r}) = a_{n} ({(E_{r})}_{n - 1} + c_{n - 1} ({(T_{1})}_{n - 1} - {(T_{1})}_{n})),

\forall n \in {1, \dots, N - 1} .

Observe now that

n = N - 1

we have

u_{N - 1} = u_{N},

so that

\begin{matrix} u_{N - 1} & \approx & a_{N - 1} u_{N - 1} + b_{N - 1} u_{0} + c_{N - 1} {(T_{1})}_{N - 1} + {(h_{1})}_{N - 1} \\ a_{N - 1} u_{N - 1} + b_{N - 1} u_{0} \\ + c_{N - 1} \frac{\partial^{2} u_{N - 1}}{\partial y^{2}} d^{2} \\ + c_{N - 1} (- {(U_{0})}_{n} \frac{(u_{n} - {(U_{0})}_{n - 1})}{d} - {(V_{0})}_{n} \frac{\partial u_{n}}{\partial y} - \frac{{(P_{0})}_{n} - {(P_{0})}_{n - 1}}{d}) \frac{d^{2}}{e_{1}} \\ + {(h_{1})}_{N - 1} \end{matrix}

(20)

This last equation is a second order ODE in

u_{N - 1}

which must be solved with the boundary conditions

u_{N - 1} (0) = u_{N - 1} (1) = 0 .

Summarizing we have obtained

u_{N - 1} .

Similarly, we may obtain

v_{N - 1}

and

P_{N - 1} .

Having

u_{N - 1}

we may obtain

u_{N - 2}

with

n = N - 2

in equation (19) (neglecting

{(E_{r})}_{N - 2} .

)

Similarly, we may obtain

v_{N - 2}

and

P_{N - 2} .

Having

u_{N - 2}

we may obtain

u_{N - 3}

with

n = N - 3

in equation (19) (neglecting

{(E_{r})}_{N - 3} .

)

Similarly, we may obtain

v_{N - 3}

and

P_{N - 3} .

And so on up to obtaining

u_{1}, v_{1}

and

P_{1}

The next step is to replace

{{(U_{0})}_{n}, {(V_{0})}_{n}, {(P_{0})}_{n}}

{u_{n}, v_{n}, P_{n}}

and repeat the process until an appropriate convergence criterion is satisfied.

Here we present a concerning software in MATLAB based in this last algorithm (with small changes and differences where we have set

K = 0

)

******************************

$c l e a r a l l$

$m_{8} = 3000;$

$d = 1 / m 8;$

$m_{9} = 120;$

$d_{1} = 1 / m_{9};$

$e_{1} = 0.1;$

$K = 0.0;$

$m_{2} = z e r o s (m 9 - 1, m 9 - 1);$
$f o r i = 2 : m_{9} - 2$

$m 2 (i, i) = - 2.0;$

$m_{2} (i, i + 1) = 1.0;$

$m_{2} (i, i - 1) = 1.0;$

$e n d;$

$m_{2} (1, 1) = - 1.0;$

$m_{2} (1, 2) = 1.0;$

$m_{2} (m 9 - 1, m 9 - 1) = - 1.0;$

$m 2 (m 9 - 1, m 9 - 2) = 1.0;$

$m_{22} = z e r o s (m_{9} - 1, m_{9} - 1);$
$f o r i = 2 : m_{9} - 2$

$m_{22} (i, i) = - 2.0;$

$m_{22} (i, i + 1) = 1.0;$

$m_{22} (i, i - 1) = 1.0;$

$e n d;$

$m_{22} (1, 1) = - 2.0;$

$m_{22} (1, 2) = 1.0;$

$m_{22} (m_{9} - 1, m_{9} - 1) = - 2.0;$

$m_{22} (m_{9} - 1, m_{9} - 2) = 1.0;$

$m 1 a = z e r o s (m_{9} - 1, m_{9} - 1);$

$m 1 b = z e r o s (m_{9} - 1, m_{9} - 1);$
$f o r i = 1 : m_{9} - 2$

$m 1 a (i, i) = - 1.0;$

$m 1 a (i, i + 1) = 1.0;$

$e n d;$

$m 1 a (m_{9} - 1, m_{9} - 1) = - 1.0;$
$f o r i = 2 : m_{9} - 1$

$m 1 b (i, i) = 1.0;$

$m 1 b (i, i - 1) = - 1.0;$

$e n d;$

$m 1 b (1, 1) = 1.0;$

$m 1 = (m 1 a + m 1 b) / 2;$

$I d = e y e (m 9 - 1);$

$a (1) = 1 / (2 + K * d^{2} / e 1);$

$b (1) = 1 / (2 + K * d^{2} / e 1);$

$c (1) = 1 / (2 + K * d^{2} / e 1);$
$f o r i = 2 : m 8 - 1$

$a (i) = 1 / (2 - a (i - 1) + K * d^{2} / e 1);$

$b (i) = a (i) * b (i - 1);$

$c (i) = (c (i - 1) + 1) * a (i);$

$e n d;$
$f o r i = 1 : m_{9} - 1$

$u 5 (i, 1) = 0.65 * i * d 1 * (1 - i * d 1);$

$e n d;$

$P f = 0.12 * o n e s (m_{9} - 1, 1);$

$u o = u 5;$

$v o = z e r o s (m_{9} - 1, 1);$

$p o = 0.15 * o n e s (m_{9} - 1, 1);$

$U o = 0.25 * o n e s (m_{9} - 1, 1);$

$V o = 0.05 * o n e s (m_{9} - 1, 1);$

$P o = 0.05 * o n e s (m_{9} - 1, 1);$
$f o r i = 1 : m 8 - 1$

$U 1 (:, i) = U o;$

$V 1 (:, i) = V o;$

$P 1 (:, i) = P o;$

$e n d;$
$f o r k 7 = 1 : 28$

$e 1 = e 1 * . 94;$

$b 14 = 1.0;$

$k 1 = 1;$

$k 1 m a x = 500;$

$w h i l e (b 14 > 10^{- 4})$ and $(k 1 < 1000)$

$k 1 = k 1 + 1;$

$b 12 = 1.0;$

$k m a x = 100;$

$k = 1; i = 1;$

$w h i l e (b 12 > 10^{- 4})$ and $(k < k m a x)$

$k = k + 1;$

$M 50 = (I d - a (m 8 - 1) * I d - c (m 8 - 1) * m 22 / d 1^{2} * d^{2})$

$M 50 = M 50 + c (m 8 - 1) * d i a g (V o) * m 1 / d 1 * d^{2} / e 1;$

$z 1 = b (m 8 - 1) * u o + K * U 1 (:, m 8 - 1) * d^{2} * c (m 8 - i) / e 1;$

$M 60 = (I d - a (m 8 - 1) * I d - c (m 8 - 1) * m 22 / d 1^{2} * d^{2})$

$M 60 = M 60 + c (m 8 - 1) * d i a g (V o) * m 1 / d 1 * d^{2} / e 1;$

$z 2 = b (m 8 - 1) * v o + K * V 1 (:, m 8 - 1) * d^{2} * c (m 8 - i) / e 1;$

$M 70 = (I d - c (m 8 - 1) * m 2 / d 1^{2} * d^{2});$

$z 3 = a (m 8 - 1) * P f + b (m 8 - 1) * p o + c (m 8 - 1) * ((m 1 / d 1 * V o) . * (m 1 / d 1 * V o) * d^{2})$

$z 3 = z 3 + K * P 1 (:, m 8 - 1) * d^{2} * c (m 8 - i) / e 1;$

$U (:, m 8 - 1) = i n v (M 50) * z 1;$

$V (:, m 8 - 1) = i n v (M 60) * z 2;$

$P (:, m 8 - 1) = i n v (M 70) * z 3;$

$b 12 = m a x (a b s (U (:, m 8 - 1) - U o));$

$U o = U (:, m 8 - 1);$

$V o = V (:, m 8 - 1);$

$P o = P (:, m 8 - 1);$

$e n d;$
$f o r i = 2 : m 8 - 1$

$b 12 = 1.0;$

$k m a x 2 = 100; k = 1;$

$w h i l e (b 12 > 10^{- 4})$ and $(k < k m a x 2)$

$k = k + 1;$

$M 50 = (I d - c (m 8 - i) * m 22 / d 1^{2} * d^{2})$

$M 50 = M 50 + c (m 8 - i) * (- d i a g (U o) * d + d i a g (V o) * m 1 / d 1 * d^{2}) / e 1;$

$z 1 = b (m 8 - i) * u o + a (m 8 - i) * U (:, m 8 - i + 1)$

$z 1 = z 1 + c (m 8 - i) * (- U o . * U (:, m 8 - i + 1) * d + (P (:, m 8 - i + 1) - P o) * d) / e 1;$

$z 1 = z 1 + K * U 1 (:, m 8 - i) * d^{2} * c (m 8 - i) / e 1;$

$M 60 = (I d - c (m 8 - i) * m 22 / d 1^{2} * d^{2})$

$M 60 = M 60 + c (m 8 - i) * (- d i a g (U o) * d + d i a g (V o) * m 1 / d 1 * d^{2}) / e 1;$

$z 2 = b (m 8 - i) * v o + a (m 8 - i) * V (:, m 8 - i + 1)$

$z 2 = z 2 + c (m 8 - i) * (- U o . * V (:, m 8 - i + 1) * d + m 1 * P o / d 1 * d^{2}) / e 1;$

$z 2 = z 2 + K * V 1 (:, m 8 - i) * d^{2} * c (m 8 - i) / e 1;$

$M 70 = (I d - c (m 8 - i) * m 2 / d 1^{2} * d^{2});$

$z 3 = b (m 8 - i) * p o + a (m 8 - i) * P (:, m 8 - i + 1)$

$z 3 = z 3 + c (m 8 - i) * ((U (:, m 8 - i + 1) - U o) . * (U (:, m 8 - i + 1) - U o)$

$z 3 = z 3 + (m 1 / d 1 * V o) . * (m 1 / d 1 * V o) * d^{2});$

$z 3 = z 3 + 2 * (m 1 / d 1 * U o) . * (V (:, m 8 - i + 1) - V o) * d$

$z 3 = z 3 + K * P 1 (:, m 8 - i) * d^{2} * c (m 8 - i) / e 1;$

$U (:, m 8 - i) = i n v (M 50) * z 1;$

$V (:, m 8 - i) = i n v (M 60) * z 2;$

$P (:, m 8 - i) = i n v (M 70) * z 3;$

$b 12 = m a x (a b s (U (:, m 8 - i) - U o));$

$U o = U (:, m 8 - i);$

$V o = V (:, m 8 - i);$

$P o = P (:, m 8 - i);$

$e n d;$ $e n d;$

$b 14 = m a x (m a x (a b s (U - U 1)));$

$U 1 = U;$

$V 1 = V;$

$P 1 = P;$

$k 1$

$U (m 9 / 2, 10)$

$e n d;$

$k 7$

$e n d$ ;

$f o r i = 1 : m_{9} - 1$

$y (i) = i * d 1;$

$e n d;$

$f o r i = 1 : m 8 - 1$

$x (i) = i * d;$

$e n d;$

$m e s h (x, y, U)$

**********************************

For the field of velocities U, V and the pressure field P, please see Figure 1, Figure 2 and Figure 3, respectively.

4. The generalized method of lines for the Navier-Stokes system

In this section we develop the solution for the Navier-Stokes system through the generalized method of lines, which was originally introduced in [4], with further developments in [5].

We present a software in MATHEMATICA for

N = 10

lines for the case in which

\begin{matrix} \{\begin{matrix} ν \nabla^{2} u - u \partial_{x} u - v \partial_{y} u - \partial_{x} P = 0, & in Ω, \\ ν \nabla^{2} v - u \partial_{x} v - v \partial_{y} v - \partial_{y} P = 0, & in Ω, \\ \nabla^{2} P + {(\partial_{x} u)}^{2} + {(\partial_{y} v)}^{2} + 2 (\partial_{y} u) (\partial_{x} v) = 0, & in Ω, \end{matrix} \end{matrix}

(21)

Such a software refers to the algorithm presented in Chapter 27, in [2], in polar coordinates, with

ν = 1.0

, and with

Ω = {(r, θ) \in R^{2} : 1 \leq r \leq 2, 0 \leq θ \leq 2 π},

\partial Ω_{1} = {(1, θ) \in R^{2} : 0 \leq θ \leq 2 π},

and

\partial Ω_{2} = {(2, θ) \in R^{2} : 0 \leq θ \leq 2 π} .

The boundary conditions are

u = v = 0, P = 0.15 on \partial Ω_{1},

u = - 1.0 sin (θ), v = 1.0 cos (θ), P = 0.10 on \partial Ω_{2} .

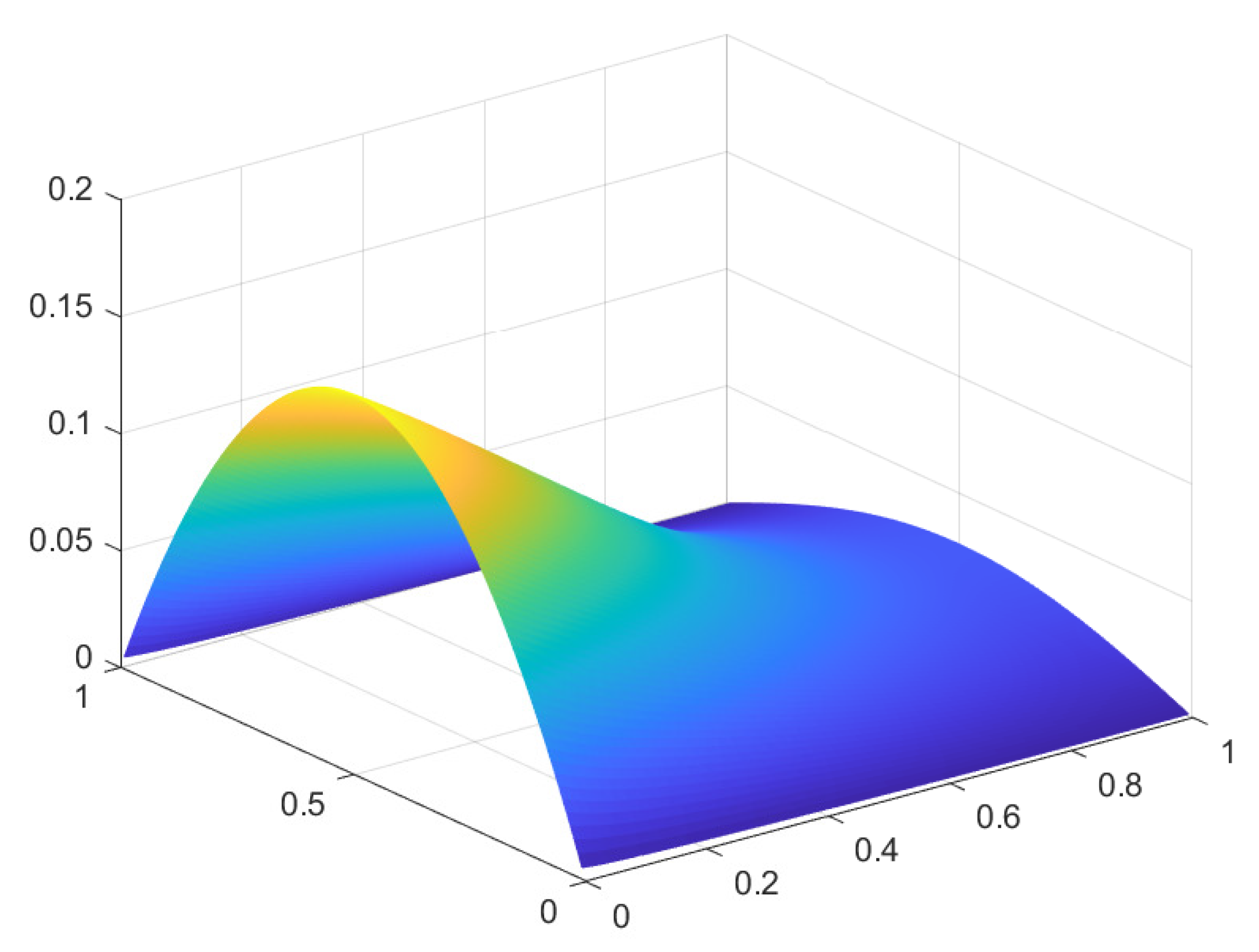
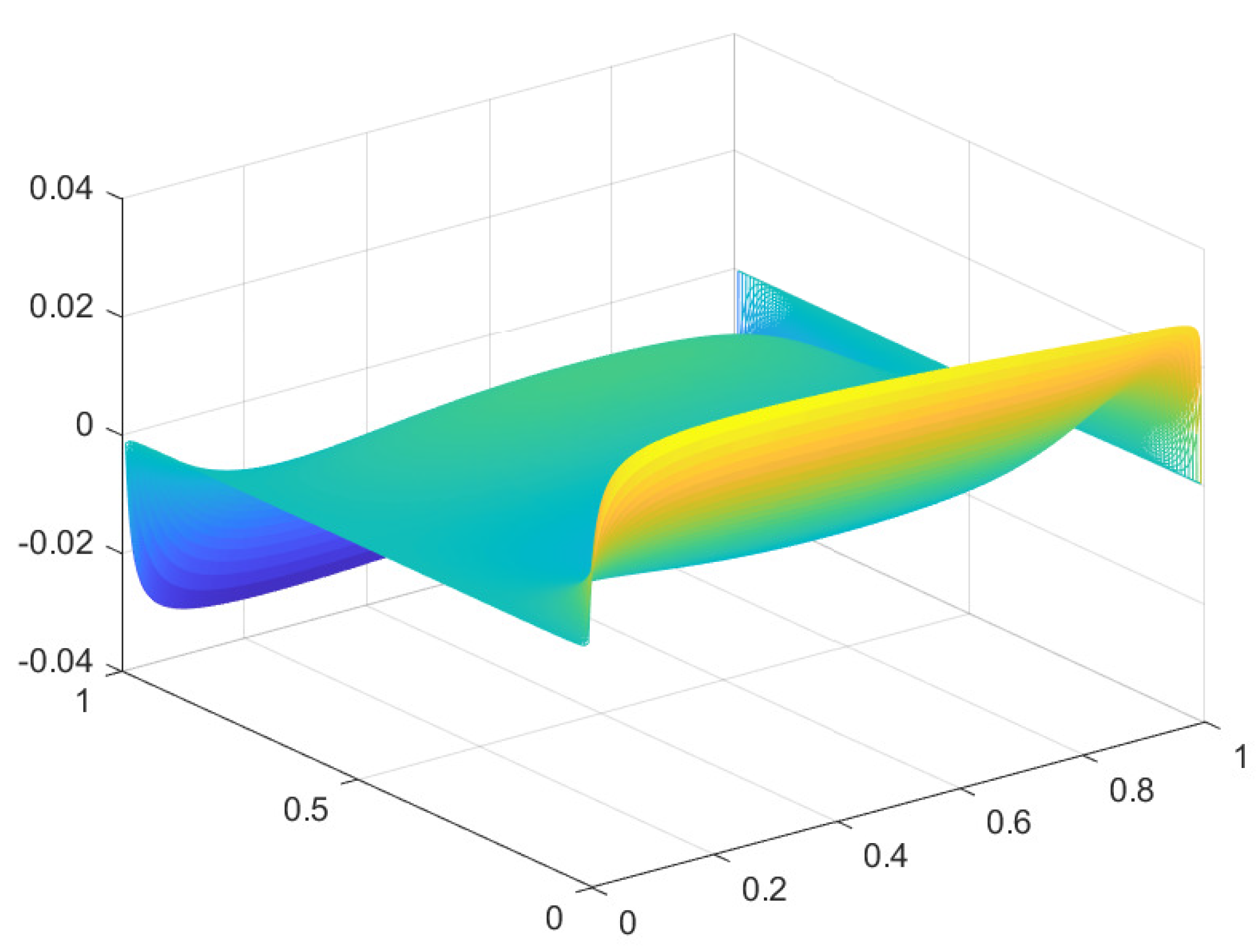
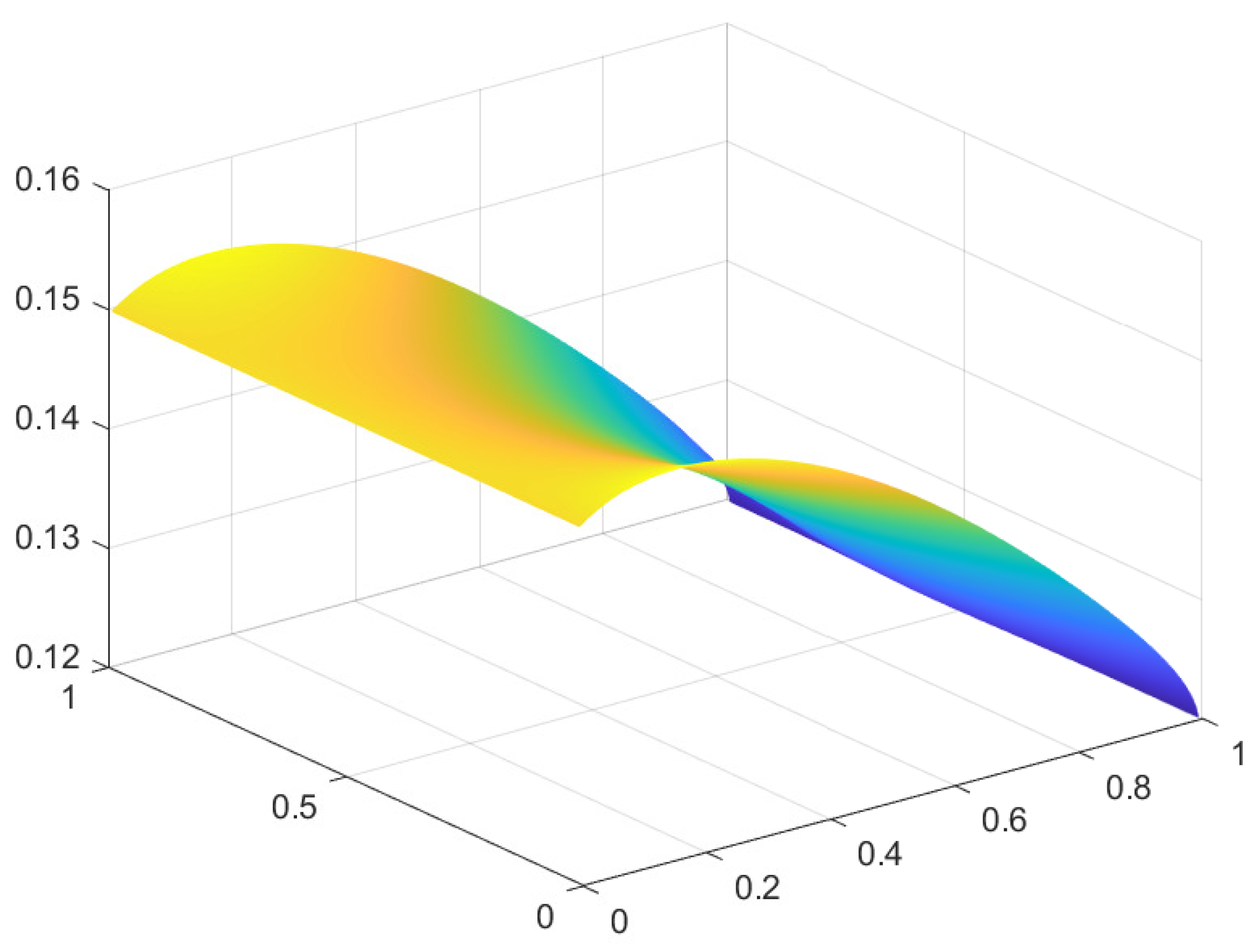
We remark some changes have been made, concerning the original conception, in order to make it suitable through the software MATHEMATICA for such a Navier-Stokes system.

We highlight the nature of this approximation is qualitative.

*****************************************

$m_{8} = 10;$
$C l e a r [z_{1}, z_{2}, z_{3}, u_{1}, u_{2}, P, b_{1}, b_{2}, b_{3}, a_{1}, a_{2}, a_{3}];$
$C l e a r [P_{f}, t, a_{11}, a_{12}, a_{13}, b_{11}, b_{12}, b_{13}, t_{3}]$ ;
$d = 1.0 / m 8;$
$e_{1} = 1.0;$
$a_{1} = 0.0;$
$a_{2} = 0.0;$
$a_{3} = 0.15;$
$F o r [i = 1, i < m 8, i + +,$

$P r i n t [i];$

$C l e a r [b_{1}, b_{2}, b_{3}, u_{1}, u_{2}, P];$

$b_{1} [x_{-}] = u_{1} [i + 1] [x];$

$b_{2} [x_{-}] = u_{2} [i + 1] [x];$

$b_{3} [x_{-}] = P [i + 1] [x];$

$t [i] = 1 + i * d;$

$d u 1 x = C o s [x] * (b_{1} [x] - a_{1}) / d * t_{3} - 1 / t [i] * S i n [x] * D [b_{1} [x], x] * t_{3};$

$d u 1 y = S i n [x] * (b_{1} [x] - a_{1}) / d * t_{3} + 1 / t [i] * C o s [x] * D [b_{1} [x], x] * t_{3};$

$d u 2 x = C o s [x] * (b_{2} [x] - a_{2}) / d * t_{3} - 1 / t [i] * S i n [x] * D [b_{2} [x], x] * t_{3};$

$d u 2 y = S i n [x] * (b_{2} [x] - a_{2}) / d * t_{3} + 1 / t [i] * C o s [x] * D [b_{2} [x], x] * t_{3};$

$d P x = C o s [x] * (b_{3} [x] - a_{3}) / d * t 3 - 1 / t [i] * S i n [x] * D [b_{3} [x], x] * t_{3};$

$d P y = S i n [x] * (b_{3} [x] - a_{3}) / d * t 3 + 1 / t [i] * C o s [x] * D [b_{3} [x], x] * t_{3};$
$F o r [k = 1, k < 6, k + +,$ (in this example, we have fixed a relatively small number of iterations )

$P r i n t [k];$

$z_{1} = (u_{1} [i + 1] [x] + b_{1} [x] + a_{1} + 1 / t [i] * (b_{1} [x] - a_{1}) * d + 1 / t {[i]}^{2} * D [b_{1} [x], x, 2] * d^{2}$

$- (b_{1} [x] * d u 1 x + b_{2} [x] * d u 1 y) * d^{2} / e 1 - d P x * d^{2} / e_{1}) / 3.0;$

$z_{2} = (u_{2} [i + 1] [x] + b_{2} [x] + a_{2} + 1 / t [i] * (b_{2} [x] - a_{2}) * d + 1 / t {[i]}^{2} * D [b_{2} [x], x, 2] * d^{2}$

$- (b_{1} [x] * d u 2 x + b_{2} [x] * d u 2 y) * d^{2} / e 1 - d P y * d^{2} / e_{1}) / 3.0;$

$z_{3} = (P [i + 1] [x] + b_{3} [x] + a_{3} + 1 / t [i] * (b_{3} [x] - a_{3}) * d + 1 / t {[i]}^{2} * D [b_{3} [x], x, 2] * d^{2}$

$+ (d u 1 x * d u 1 x + d u 2 y * d u 2 y + 2.0 * d u 1 y * d u 2 x) * d^{2}) / 3.0;$
$z_{1} = S e r i e s [z_{1}, {u_{1} [i + 1] [x], 0, 2}, {u_{1} {[i + 1]}^{'} [x], 0, 1}, {u_{1} {[i + 1]}^{''} [x], 0, 1},$

${u_{1} {[i + 1]}^{'''} [x], 0, 0}, {u_{1} {[i + 1]}^{''''} [x], 0, 0}, {u_{2} [i + 1] [x], 0, 1},$

${u_{2} {[i + 1]}^{'} [x], 0, 0}, {u_{2} {[i + 1]}^{''} [x], 0, 0}, {u_{2} {[i + 1]}^{'''} [x], 0, 0},$

${u_{2} {[i + 1]}^{''''} [x], 0, 0}, {P [i + 1] [x], 0, 1}, {P {[i + 1]}^{'} [x], 0, 0},$

${P {[i + 1]}^{''} [x], 0, 0}, {P {[i + 1]}^{'''} [x], 0, 0}, {P {[i + 1]}^{''''} [x], 0, 0},$

${S i n [x], 0, 1}, {C o s [x], 0, 1}];$

$z_{1} = N o r m a l [z_{1}];$

$z_{1} = E x p a n d [z_{1}];$

$P r i n t [z_{1}];$
$z_{2} = S e r i e s [z_{2}, {u_{1} [i + 1] [x], 0, 1}, {u_{1} {[i + 1]}^{'} [x], 0, 1}, {u_{1} {[i + 1]}^{''} [x], 0, 1},$

${u_{1} {[i + 1]}^{'''} [x], 0, 0}, {u_{1} {[i + 1]}^{''''} [x], 0, 0}, {u_{2} [i + 1] [x], 0, 2},$

${u_{2} {[i + 1]}^{'} [x], 0, 0}, {u_{2} {[i + 1]}^{''} [x], 0, 0}, {u_{2} {[i + 1]}^{'''} [x], 0, 0},$

${u_{2} {[i + 1]}^{''''} [x], 0, 0}, {P [i + 1] [x], 0, 1}, {P {[i + 1]}^{'} [x], 0, 0},$

${P {[i + 1]}^{''} [x], 0, 0}, {P {[i + 1]}^{'''} [x], 0, 0}, {P {[i + 1]}^{''''} [x], 0, 0},$

${S i n [x], 0, 1}, {C o s [x], 0, 1}];$

$z_{2} = N o r m a l [z_{2}];$

$z_{2} = E x p a n d [z_{2}];$

$P r i n t [z_{2}];$
$z_{3} = S e r i e s [z_{3}, {u_{1} [i + 1] [x], 0, 2}, {u_{1} {[i + 1]}^{'} [x], 0, 1}, {u_{1} {[i + 1]}^{''} [x], 0, 1},$

${u_{1} {[i + 1]}^{'''} [x], 0, 0}, {u_{1} {[i + 1]}^{''''} [x], 0, 0}, {u_{2} [i + 1] [x], 0, 2},$

${u_{2} {[i + 1]}^{'} [x], 0, 1}, {u_{2} {[i + 1]}^{''} [x], 0, 0}, {u_{2} {[i + 1]}^{'''} [x], 0, 0},$

${u_{2} {[i + 1]}^{''''} [x], 0, 0}, {P [i + 1] [x], 0, 1}, {P {[i + 1]}^{'} [x], 0, 1},$

${P {[i + 1]}^{''} [x], 0, 0}, {P {[i + 1]}^{'''} [x], 0, 0}, {P {[i + 1]}^{''''} [x], 0, 0},$

${S i n [x], 0, 1}, {C o s [x], 0, 1}];$

$z_{3} = N o r m a l [z_{3}];$

$z_{3} = E x p a n d [z_{3}];$

$P r i n t [z_{3}];$
$b_{1} [x_{]} = z_{1};$

$b_{2} [x_{]} = z_{2};$

$b_{3} [x_{]} = z_{3};$

$b_{11} = z_{1};$

$b_{12} = z_{2};$

$b_{13} = z_{3};];$
$a_{11} [i] = b_{11};$

$a_{12} [i] = b_{12};$

$a_{13} [i] = b_{13};$

$P r i n t [a_{11} [i]];$

$C l e a r [b_{1}, b_{2}, b_{3}];$

$u_{1} [i + 1] [x_{]} = b_{1} [x];$

$u_{2} [i + 1] [x_{]} = b_{2} [x];$

$P [i + 1] [x_{]} = b_{3} [x];$

$a_{1} = S e r i e s [b_{11}, {t_{3}, 0, 1}; {b_{1} [x], 0, 1}, {b_{2} [x], 0, 1}, {b_{3} [x], 0, 1},$

${b_{1}^{'} [x], 0, 0}, {b_{2}^{'} [x], 0, 0}, {b_{3}^{'} [x], 0, 0}, {b_{1}^{''} [x], 0, 0}, {b_{2}^{''} [x], 0, 0}, {b_{3}^{''} [x], 0, 0}];$

$a_{1} = N o r m a l [a_{1}];$

$a_{1} = E x p a n d [a_{1}];$

$a_{2} = S e r i e s [b_{12}, {t_{3}, 0, 1}; {b_{1} [x], 0, 1}, {b_{2} [x], 0, 1}, {b_{3} [x], 0, 1},$

${b_{1}^{'} [x], 0, 0}, {b_{2}^{'} [x], 0, 0}, {b_{3}^{'} [x], 0, 0}, {b_{1}^{''} [x], 0, 0}, {b_{2}^{''} [x], 0, 0}, {b_{3}^{''} [x], 0, 0}];$

$a_{2} = N o r m a l [a_{2}];$

$a_{2} = E x p a n d [a_{2}];$

$a_{3} = S e r i e s [b_{13}, {t_{3}, 0, 1}; {b_{1} [x], 0, 1}, {b_{2} [x], 0, 1}, {b_{3} [x], 0, 1},$

${b_{1}^{'} [x], 0, 0}, {b_{2}^{'} [x], 0, 0}, {b_{3}^{'} [x], 0, 0}, {b_{1}^{''} [x], 0, 0}, {b_{2}^{''} [x], 0, 0}, {b_{3}^{''} [x], 0, 0}];$

$a_{3} = N o r m a l [a_{3}];$

$a_{3} = E x p a n d [a_{3}];$
$b_{1} [x_{]} = - 1.0 * S i n [x];$

$b_{2} [x_{]} = 1.0 * C o s [x];$

$b_{3} [x_{]} = 0.10;$
$F o r [i = 1, i < m 8, i + +,$

$A_{11} = a_{11} [m 8 - i];$

$A_{11} = S e r i e s [A_{11}, {S i n [x], 0, 2}, {C o s [x], 0, 2}];$

$A_{11} = N o r m a l [A_{11}];$

$A_{11} = E x p a n d [A_{11}];$

$A_{12} = a_{12} [m_{8} - i];$

$A_{12} = S e r i e s [A_{12}, {S i n [x], 0, 2}, {C o s [x], 0, 2}];$

$A_{12} = N o r m a l [A_{12}];$

$A_{12} = E x p a n d [A_{12}];$

$A_{13} = a_{13} [m_{8} - i];$

$A_{13} = S e r i e s [A_{13}, {S i n [x], 0, 2}, {C o s [x], 0, 2}];$

$A_{13} = N o r m a l [A_{13}];$

$A_{13} = E x p a n d [A_{13}];$
$u_{1} [m 8 - i] [x_{-}] = A_{11};$

$u_{2} [m 8 - i] [x_{-}] = A_{12};$

$P [m 8 - i] [x_{-}] = E x p a n d [A_{13}];$
$t_{3} = 1.0;$
$P r i n t [" u_{1} [", m_{8} - i, "] = ", A_{11}];$

$C l e a r [t_{3}];$

$b_{1} [x_{]} = A_{11};$

$b_{2} [x_{]} = A_{12};$

$b_{3} [x_{]} = A_{13};];$
$t_{3} = 1.0;$
$F o r [i = 1, i < m_{8}, i + +,$

$P r i n t [" u_{1} [", i, "] = ", u_{1} [i] [x]]]$

***************************************************

Here the line expressions for the field of velocity

u = {u_{1} [n] (x)}

, where gain we emphasize

N = 10

lines:

$\begin{matrix} u_{1} [1] (x) & = & 0.0044548 C o s [x] - 0.174091 S i n [x] + 0.00041254 C o s {[x]}^{2} S i n [x] \\ + 0.0260471 C o s [x] S i n {[x]}^{2} - 0.000188598 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(22)
$\begin{matrix} u_{1} [2] (x) & = & 0.00680614 C o s [x] - 0.331937 S i n [x] + 0.000676383 C o s {[x]}^{2} S i n [x] \\ + 0.0501544 C o s [x] S i n {[x]}^{2} - 0.000176433 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(23)
$\begin{matrix} u_{1} [3] (x) & = & 0.00775103 C o s [x] - 0.470361 S i n [x] + 0.000863068 C o s {[x]}^{2} S i n [x] \\ + 0.0682792 C o s [x] S i n {[x]}^{2} - 0.000121656 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(24)
$\begin{matrix} u_{1} [4] (x) & = & 0.00771379 C o s [x] - 0.589227 S i n [x] + 0.000994973 C o s {[x]}^{2} S i n [x] \\ + 0.0781784 C o s [x] S i n {[x]}^{2} - 0.00006958 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(25)
$\begin{matrix} u_{1} [5] (x) & = & 0.00701567 C o s [x] - 0.690152 S i n [x] + 0.00106158 C o s {[x]}^{2} S i n [x] \\ + 0.0796091 C o s [x] S i n {[x]}^{2} - 0.0000330485 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(26)
$\begin{matrix} u_{1} [6] (x) & = & 0.00589597 C o s [x] - 0.775316 S i n [x] + 0.00104499 C o s {[x]}^{2} S i n [x] \\ + 0.0734277 C o s [x] S i n {[x]}^{2} - 0.0000121648 C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(27)
$\begin{matrix} u_{1} [7] (x) & = & 0.00452865 C o s [x] - 0.846947 S i n [x] + 0.000931782 C o s {[x]}^{2} S i n [x] \\ + 0.0609739 C o s [x] S i n {[x]}^{2} - 2.74137 * 10^{- 6} C o s {[x]}^{2} S i n {[x]}^{2} \end{matrix}$

(28)
$\begin{matrix} u_{1} [8] (x) & = & 0.00303746 C o s [x] - 0.907103 S i n [x] + 0.000716865 C o s {[x]}^{2} S i n [x] \\ + 0.0437018 C o s [x] S i n {[x]}^{2} \end{matrix}$

(29)
$\begin{matrix} u_{1} [9] (x) & = & 0.00150848 C o s [x] - 0.957599 S i n [x] + 0.000403216 C o s {[x]}^{2} S i n [x] \\ + 0.0229802 C o s [x] S i n {[x]}^{2} \end{matrix}$

(30)

5. Conclusion

In this article, we develop solutions for two-dimensional examples also for the time-independent incompressible Navier-Stokes system, through the generalized method of lines. We also obtain the appropriate boundary conditions for a equivalent elliptic system. Finally, the extension of such results to

R^{3}

, compressible and time dependent cases is planned for a future work.

References

R.A. Adams and J.F. Fournier, Sobolev Spaces, 2nd edn. (Elsevier, New York, 2003).
F.S. Botelho, Functional Analysis, Calculus of Variations and Numerical Methods in Physics and Engineering, CRC Taylor and Francis, Florida, 2020.
Botelho, F.S. An Approximate Proximal Numerical Procedure Concerning the Generalized Method of Lines. Mathematics 2022, 10, 2950. [Google Scholar] [CrossRef]
F. Botelho, Topics on Functional Analysis, Calculus of Variations and Duality, Academic Publications, Sofia, (2011).
F. Botelho, Existence of solution for the Ginzburg-Landau system, a related optimal control problem and its computation by the generalized method of lines, Applied Mathematics and Computation, 218, 11976-11989, (2012).
P. Constantin and C. Foias, Navier-Stokes Equation, University of Chicago Press, Chicago, 1989.
Makram Hamouda, Daozhi Han, Chang-Yeol Jung and Roger Temam, Boundary layers for the 3D primitive equations in a cube: the zero-mode. Journal of Applied Analysis and Computation 2018, 8, 873–889. [CrossRef]
Andrea Giorgini, Alain Miranville and Roger Temam, Uniqueness and regularity for the Navier-Stokes-Cahn-Hilliard system. SIAM J. of Mathematical Analysis (SIMA) 2019, 51, 2535–2574. [CrossRef]
Ciprian Foias, Ricard M.S. Rosa and Roger M. Temam, Properties of stationary statistical solutions of the three-dimensional Navier-Stokes equations, J. of Dynamics and Differential Equations. J. of Dynamics and Differential Equations, Special issue in memory of George Sell, 2019; 31, 1689–1741. [CrossRef]
J.C. Strikwerda, Finite Difference Schemes and Partial Differential Equations, SIAM, second edition (Philadelphia, 2004).
R. Temam, Navier-Stokes Equations, AMS Chelsea, reprint (2001).

Figure 1. solution

U (x, y)

for the case

ν = 0.0177

Figure 1. solution

U (x, y)

for the case

ν = 0.0177

Figure 2. solution

V (x, y)

for the case

ν = 0.0177

Figure 2. solution

V (x, y)

for the case

ν = 0.0177

Figure 3. solution

P (x, y)

for the case

ν = 0.0177

Figure 3. solution

P (x, y)

for the case

ν = 0.0177

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Approximate Numerical Procedures for the Navier-Stokes System Through the Generalized Method of Lines

Abstract

1. Introduction

2. Details about an equivalence of a concerning elliptic system

3. An approximate proximal approach

4. The generalized method of lines for the Navier-Stokes system

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe