Prerpints.org logo
Preprint
Article

Gravity, Information and Accelerated Expansion

Altmetrics

Downloads

295

Views

154

Comments

1

This version is not peer-reviewed

Submitted:

07 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts
Abstract
The holographic principle states that the information about the volume of space is stored on its boundary. Assuming this holds, we can explain the aspects of gravity. The spacetime needs to be extended to 5D to explain gravity in this context. This naturally explains the four classical tests of gravity namely the gravitational redshift, the perihelion precession, the bending of light, and the gravitational time delay. We also show a novel way in which the universe expands in an accelerated manner at late times without the need for any form of dark energy.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Our first encounter with gravity came from the realization of Newton of gravity as an attractive force between every two objects in the universe, mathematically described by the universal law of gravitation. Despite being experienced by us in daily life, gravity remains the most mysterious force of all. Einstein realized gravity not as a fundamental force but as a very abstract phenomenon arising from the curvature of spacetime induced by matter and encoded in the famous Einstein’s field equation. General Relativity(GR) as we call Einstein’s theory is a metric theory that beautifully explains every phenomenon observed at large scales to date. However, the theory is incompatible with another cornerstone and highly successful theory of Quantum Mechanics. Moreover being a metric theory, it admits certain unphysical solutions such as closed timelike curves and spacetime singularity. It also remains difficult to explain dark matter and dark energy within the framework of GR. The first link between thermodynamics and gravity came from black hole physics where there is an apparent connection between horizon area and the entropy of the black hole. Hawking[1] first showed that the area of the horizon(A) of a black hole is a non-decreasing function of time.
d A d t ≥ 0
Bekenstein[2,3,4] took this further and asserted the equivalence of the horizon area with the thermodynamic parameter, entropy(S) as
S = γ A
where γ is a constant. The claim got a robust description when Hawking[5] derived the temperature of the black hole, thus making the relation between the area and entropy clear. Later, in 1995, Jacobson[6] derived Einstein’s equation from the proportionality of entropy and horizon area together with the relation d Q = T d S connecting heat, entropy, and temperature. There are also closely related follow-up articles[7,8,9,10,11]. Another work relating thermodynamics and gravity is due to Padmanabhan (see [12] for a review) and his collaborators[13,14,15,16,17]. These results suggest that gravity may be explained as an emergent phenomenon and have a thermodynamic or entropic origin. Recently, Verlinde[18] proposed Newtonian gravity as a physical entropic force, caused by changes in the information associated with the positions of material bodies, although, this description of Newtonian gravity as a physical entropic force has been technically questioned too[19,20,21,22]. Our goal here is different, we are making no connection with the background spacetime metric g μ ν and are thus not set to derive Einstein’s gravity as Jacobson and Padmanabhan did because we do not think that Einstein’s approach of describing gravity as background spacetime curvature is the only and ultimate reality. We are also not justifying or falsifying the claim of Verlinde of Newtonian gravity as a physical entropic force. Since we are not using Einstein’s approach of gravity as spacetime curvature, we explicitly show then, how can we explain the gravitational redshift, the modified equation of motion for both massive and massless particles, and the accelerated expansion of the universe. This way of describing gravity as a non-metric theory naturally does away with the inherent unphysical problems of a metric theory such as closed timelike curves and spacetime singularity. The study of type Ia supernova in 1998 by two independent projects, the Supernova Cosmology Project and the High-Z Supernova Search Team revealed an astonishing result that the universe is not only expanding but it is expanding at an accelerating rate [23]. The accelerated expansion of the universe is thought to have begun since the universe entered its dark-energy-dominated era roughly 5 billion years ago. The currently accepted theory of gravity, General Relativity, accounts for this accelerated expansion by introducing a small and positive value of the cosmological constant Λ . Alternative explanations such as phantom energy, quintessence are also hypothesized as the explanation of late time cosmic acceleration. Some explanations beyond four dimensions also exist such as the Dvali-Gabadadze-Porrati (DGP) model[24] which argues that gravity behaves as 5 D at large distances while reducing to that of usual 4 D gravity at short distances. However the precise nature of dark energy remains unknown. Alternative explanations are promising but have their own shortcomings, as was argued in[25] that the self-accelerating solution of DGP model[26] contains a ghost mode. Very intiguing arguments are presented in [27,28,29,30] that the universe should exist in pairs with their time oppositely related.
The paper is organized as follows: we begin our discussion by understanding this new connection between gravity and "information" in the system. In section 3 we explain how the thermodynamic nature of our system changes the total energy and this leads to the extension of the spacetime to 5 D . In section 4 we find the solution for a point mass in our theory. In section 5 we review the Quantum Focusing Conjecture(QFC)[31]. We briefly recall Casini’s work on relative entropy and Bekenstein bound in section 6 and conclude the paper by putting forth a novel way in which the accelerated expansion of the universe happens at late times.

2. Some Terminology

Let us first define some quantities relevant to our discussion and approach. Consider the system consisting of a source mass M and a boundary. The "boundary" here is a data-storing surface such as a holographic screen. Motivated by the Bekenstein bound[32], let us define a quantity C D as the maximum degrees of freedom associated with the mass M at a distance R from the boundary as1
C D = 2 π R M ℏ
Another quantity C I is defined as the maximum degrees of freedom available. This is assumed to follow the holographic principle[33,34] which has strong pieces of evidence from the AdS/CFT correspondence[35] and black hole physics[3,5], such that the information about the volume of space is stored on the boundary. Thus we assume that the total degrees of freedom is given by
N = A l p 2
where A is the surface area of the boundary and l p is the Planck length. Therefore
C I = N = A l p 2
The "disorder" D in the system which gives the ratio of the maximum degrees of freedom of the mass M to the maximum available degrees of freedom is therefore given by2
D = C D C I
Now that we have defined some important quantities needed to present our approach, we turn toward a specific and important property of the boundary which is the temperature T. This can be found by invoking the use of the boundary as a holographic screen that can store data, thus as an object comes near this holographic screen, its total energy( p 0 ) is stored on the boundary as evenly bits of information N. Since the distribution is even, we can use our good old equipartition rule of thermodynamics to find the temperature of the boundary as
p 0 = 1 2 N T
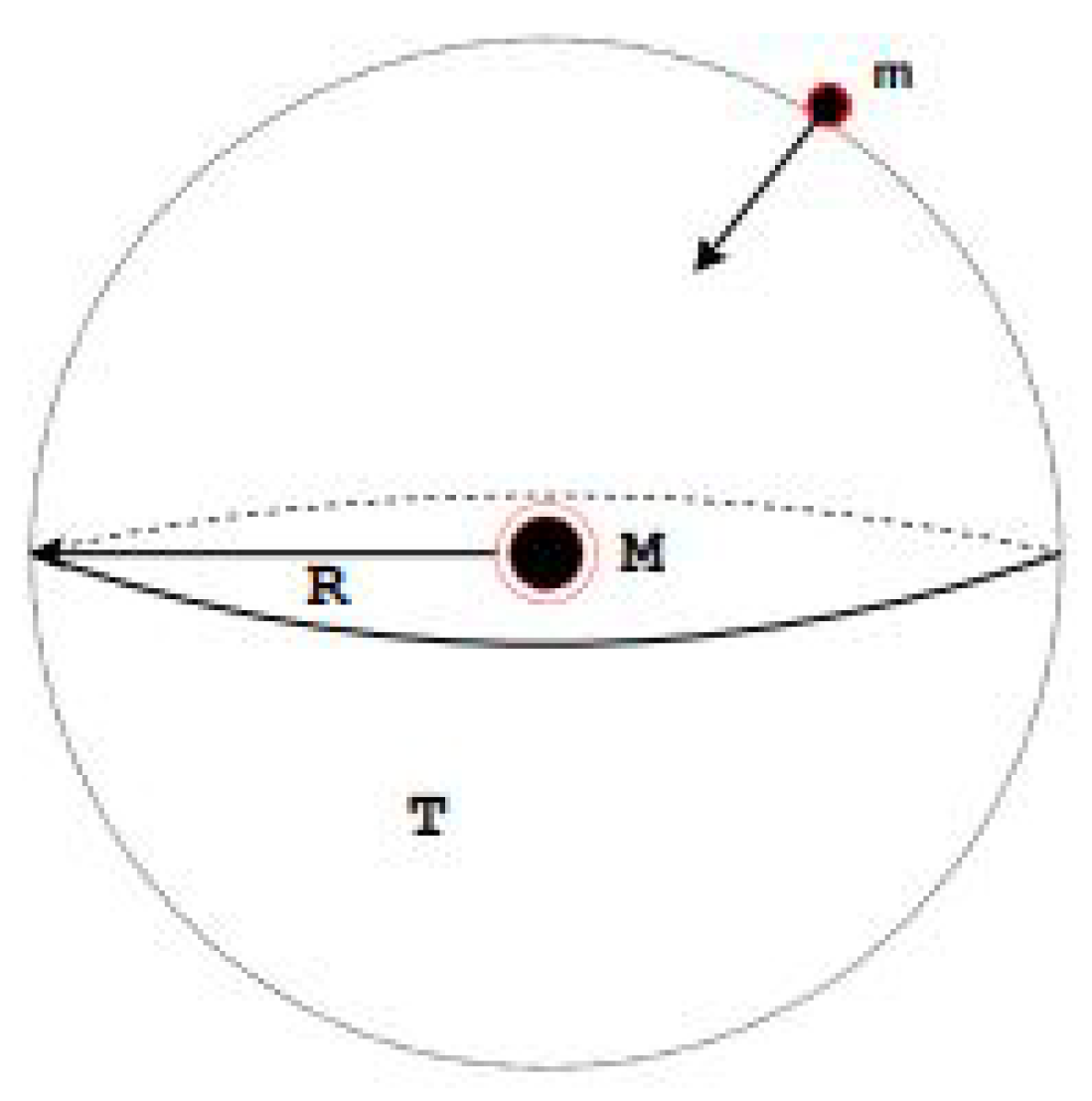
Preprints 84530 g001
Figure 1. Our system consists of a source mass M and a "boundary" which is a data storing surface such as a holographic screen. T is the temperature of the bounding surface arising from the even distribution of the total energy E of the mass m as N bits of information as it approaches the holographic boundary.
Figure 1. Our system consists of a source mass M and a "boundary" which is a data storing surface such as a holographic screen. T is the temperature of the bounding surface arising from the even distribution of the total energy E of the mass m as N bits of information as it approaches the holographic boundary.
Preprints 84530 g001

3. Effect on Total Energy

Due to the thermodynamic nature of our system, the total energy changes by the internal energy(U) and the fluctuation energy as we show now. The internal energy is given by
U = T S
where T is the temperature of the boundary and S is given by C D . To find the degree of fluctuation in our system we expand the disorder D about its equilibrium position x 0 μ
D = D 0 + ∂ D ∂ x μ | 0 d x μ + 1 2 ∂ 2 D ∂ x μ ∂ x ν | 0 d x μ d x ν + . . . . .
Note that here μ varies from 0 to 3 on 4 D spacetime. Since x 0 μ is the equilibrium point for D, we have
∂ D ∂ x μ | 0 = 0
Thus, in second order we have:
Δ D = D − D 0 = 1 2 ∂ 2 D ∂ x μ ∂ x ν | 0 d x μ d x ν
The hessian h μ ν which captures the degree of "fluctuation" in our thermodynamic system is given as
h μ ν = ∂ μ ∂ ν D
Another important dimensionless quantity(which can be used to define the "length" of fluctuation) is defined as
h ˜ μ ν = A π h μ ν
where A is the surface area of the boundary. d l 2 is the length squared of fluctuation given by
d l 2 = 1 2 h ˜ μ ν d x μ d x ν
We thus define the fluctuation energy as
d l d τ 2 = 1 2 h ˜ μ ν d x μ ˙ d x ν ˙
This thermodynamic expansion of the total energy comes at the expense of extending the 4 D spacetime to 5 D spacetime such that the non-zero metric elements are given by
g 00 = 1 , g 11 = g 22 = g 33 = g 04 = g 40 = − 1
The fifth element of the "five-momentum" p μ is defined as
p 4 = U + d l d τ

4. Static Mass and Spherically Symmetric Solution

The total degrees of freedom on the boundary is
N = A l p 2 = 4 π r 2 l p 2
Thus
U = M p 0 r
for h ˜ μ ν , only 11 component survives. Thus
h ˜ 11 = 4 M r
Hence the fluctuation energy in our thermodynamic system is
d l d τ 2 = 2 M r r ˙ 2
Thus
d l d τ = 2 M r r ˙
So we get
d x 4 = M r d t + 2 M r d r
The spacetime interval is given as
d s 2 = g μ ν d x μ d x ν
where g μ ν is the fixed 5 D background spacetime. Hence in the spherical coordinates, we get the spacetime interval as
d s 2 = d t 2 − d r 2 − r 2 ( d θ 2 + s i n 2 θ ϕ 2 ) − 2 M r d t 2 − 2 2 M r d t d r
Eq.(25) is the Gullstrand-Painleve metric and a coordinate transformation converts it to the well-known Schwarzschild metric given as
d s 2 = 1 − 2 M r d t 2 − 1 − 2 M r − 1 d r 2 − r 2 ( d θ 2 + s i n 2 θ d ϕ 2 )

5. Quantum Focusing Conjecture

Using the Quantum Focusing Conjecture(QFC)[31], we can show that the second derivative of the radius of a null boundary which respects the null energy condition(NEC) is non-negative. In this section, we first review the formulation of QFC.

5.1. Generalised Entropy for Cauchy-splitting surfaces

Generalized entropy was originally defined in [37] in asymptotically flat space as the area A of all black hole horizons, plus the entropy of matter outside the black holes
S g e n = S o u t + A 4 G ℏ
A rigorous definition of S o u t can be given as the von Neumann entropy of the quantum state of the exterior of the horizon
S o u t = − t r ρ o u t l n ρ o u t
The GSL was introduced to keep the second law of thermodynamics intact when matter entropy is lost in a black hole. Bekenstein conjectured that GSL [37] holds: that the area increase of the black hole compensates for the lost matter entropy so that the generalized entropy does not decrease. The notion of generalized entropy can be extended beyond the context of causal horizons [31]. Let E be a spacelike codimension-2 surface that splits a Cauchy surface C into two portions. By choosing any one of the two sides arbitrarily, we can define an entropy restricted to one side of C as S o u t .
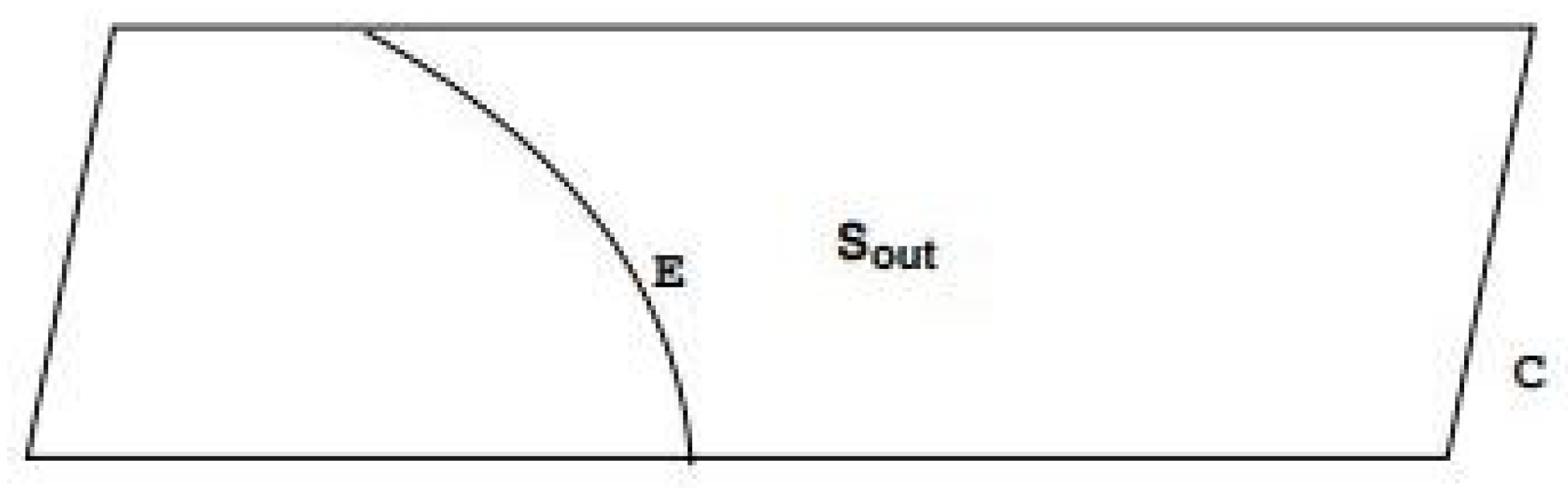
Preprints 84530 g002
Figure 2. A Cauchy surface C is divided into two parts by a surface E. S o u t is defined as entropy restricted to one side of splitting surface E
Figure 2. A Cauchy surface C is divided into two parts by a surface E. S o u t is defined as entropy restricted to one side of splitting surface E
Preprints 84530 g002

5.2. Quantum Focusing Conjecture

It conjectures [31] that the quantum expansion Θ , where Θ is given by
Θ = θ + 4 G ℏ A S o u t ′
( θ is the classical expansion and A is the width of null congruence along its generator), cannot increase along any congruence, which is valid for quantum states too
d Θ d λ ≤ 0
where λ is an affine parameter. The evolution of the expansion θ along congruence is determined by the Raychaudhuri equation:
d θ d λ = − θ 2 2 − σ a b σ a b − R a b k a k b :
where R a b is the Ricci tensor, σ a b is the shear and k a is the (null) tangent vector to the congruence. This gives QFC as
0 ≥ Θ ′ = θ ′ + 4 G ℏ A ( S o u t ′ ′ − S o u t ′ θ ) = − 1 2 θ 2 − ζ 2 − 8 π G 〈 T k k 〉 + 4 G ℏ A ( S o u t ′ ′ − S o u t ′ θ )
ζ is shear. The special choice of congruence for θ = ζ = 0 , gives the Quantum Null Energy Condition (QNEC)
〈 T k k 〉 ≥ ℏ 2 π A S o u t ′ ′
The entropy S o u t which refers to the entropy on a spacelike Cauchy surface can also be alternatively seen as the entropy of the state restricted to the part of null surface N [31]. The stress tensor T a b and entanglement entropy S o u t is related to relative entropy S ( ρ | | ρ o ) on a null surface by
2 π A ℏ T k k − S o u t ′ ′ = S ′ ′ ( ρ | | ρ o )
where T k k = T a b k a k b , k a is a null vector, i.e, it satisfies g μ ν k μ k ν = 0 . ρ is an arbitrary state and ρ o is the vacuum state.

6. Relative Entropy and Bekenstein Bound

The Bekenstein bound is given as
S ≤ λ E R
where λ is a constant, R is the size of the system, E is the total energy. Casini[38] showed that the above bound can be written in the form
S V ≤ K V
where S V is a localized entropy and K V is a localized energy. Using K = − l o g ρ V 0 − l o g ( t r e − K ) and t r ρ V = t r ρ V 0 = 1 , this can be written as
t r ( ρ V l o g ρ V ) − t r ( ρ V l o g ρ V 0 )
This is simply the statement of the positivity of the relative entropy S ( ρ V | ρ V 0 ) between the state ρ V and the vacuum state ρ V 0 and thus the bound holds. Suppose the size of a system is L and the radius of the boundary R, in the limit when the system is far enough from the boundary such as at the center, R ⪆ L then Eq.(36) reduces to Eq.(35). We will use this limit in the next section.

7. Towards Accelerated Expansion

Consider a surface Σ on a stationary null surface N (a Rindler horizon) and its deformation along N toward the future, so that the deformation vector k a is future-directed and the outside is chosen to be the side towards which k a points (see Fig.1). A measure of distinguishability between any two states of an arbitrary quantum system is relative entropy. It is a quantity of particular significance in quantum information theory. Its illuminating use in the gravitational context was put by Casini[38]. On the states restricted to this causal horizon, the relative entropy is given by
S ′ ′ ( ρ | | ρ ( 0 ) ) = 2 π A ℏ 〈 T k k 〉 − S o u t ′ ′
At late times on this causal horizon, we take the matter entropy S o u t to stop evolving such that S o u t ′ = 0 . This essentially requires the quantum expansion Θ → 0 on the causal horizon since for the stationary causal horizon, the classical expansion vanishes, θ = 0 . Using the QNEC, we can now write Eq.(38) as an inequality given by
S ′ ′ ( ρ | | ρ ( 0 ) ) > 0
The relative entropy can be written as the statement of the Bekenstein Bound as
S ( ρ | | ρ ( 0 ) ) = K v − S v
where K v is a localized energy and S v = S o u t − S o u t ( 0 ) , S o u t ( 0 ) being vacuum entropy. Since S o u t ′ = 0 and the vacuum entropy is independent of the affine parameter λ (the vacuum state on the pencil is invariant under translations in the affine parameter), Eq.(39) takes the form
K v ′ ′ > 0
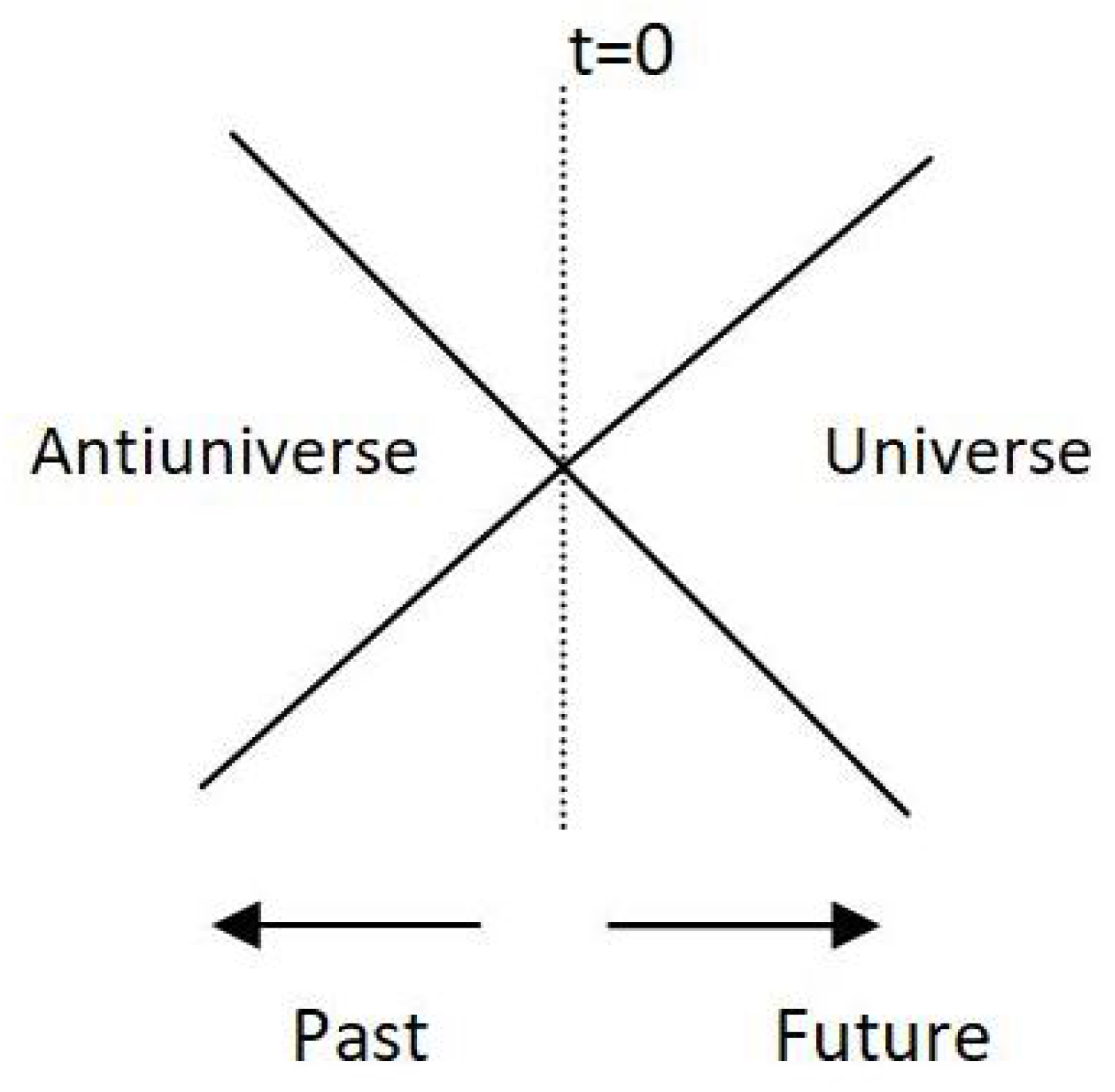
Since, in the local neighborhood of any point p, we can define a Rindler horizon, this result holds for the entire spacetime points. We now apply this result to the universe as a whole. Since the arguments presented hold locally, the extension to the entire universe requires a global existence of a causal horizon. This can be circumvented by considering a universe-antiuniverse pair, in which case, the junction ( t = 0 ) of the universe-antiuniverse pair which causally disconnects the pair (see Fig.2) naturally serves as the stationary causal horizon and the result of Eq.(41) can be extended globally. This is similar to the existence of the Unruh effect for a local Rindler horizon to that of the Hawking effect for a global event horizon of a black hole. The affine parameter λ can now be taken to be the cosmic time t and the total energy E of the universe is constant. Take the radius of the boundary of the universe to be R (with R possibly infinity), such that the bulk of size L always satisfies L < < R . In this limit, K v ≡ 2 π E R and we can finally write Eq.(41) as
R ¨ > 0
Thus, the boundary of the universe expands in an accelerated manner. It should be noted that the sign of S o u t ′ ′ can be anything, including negative, but at late times, the matter entropy stops evolving such that the quantum expansion tends to zero, Θ → 0 , and in this case, the expansion of the universe is accelerating without need of any external agent, all by itself!
Preprints 84530 g003
Figure 3. A Rindler horizon shown by a bold line of a 2-surface element P. To the right Rindler wedge in the region z > | t | with Cauchy surface the spatial half-plane V defined by z > 0 at t = 0 , we can apply Casini’s idea.
Figure 3. A Rindler horizon shown by a bold line of a 2-surface element P. To the right Rindler wedge in the region z > | t | with Cauchy surface the spatial half-plane V defined by z > 0 at t = 0 , we can apply Casini’s idea.
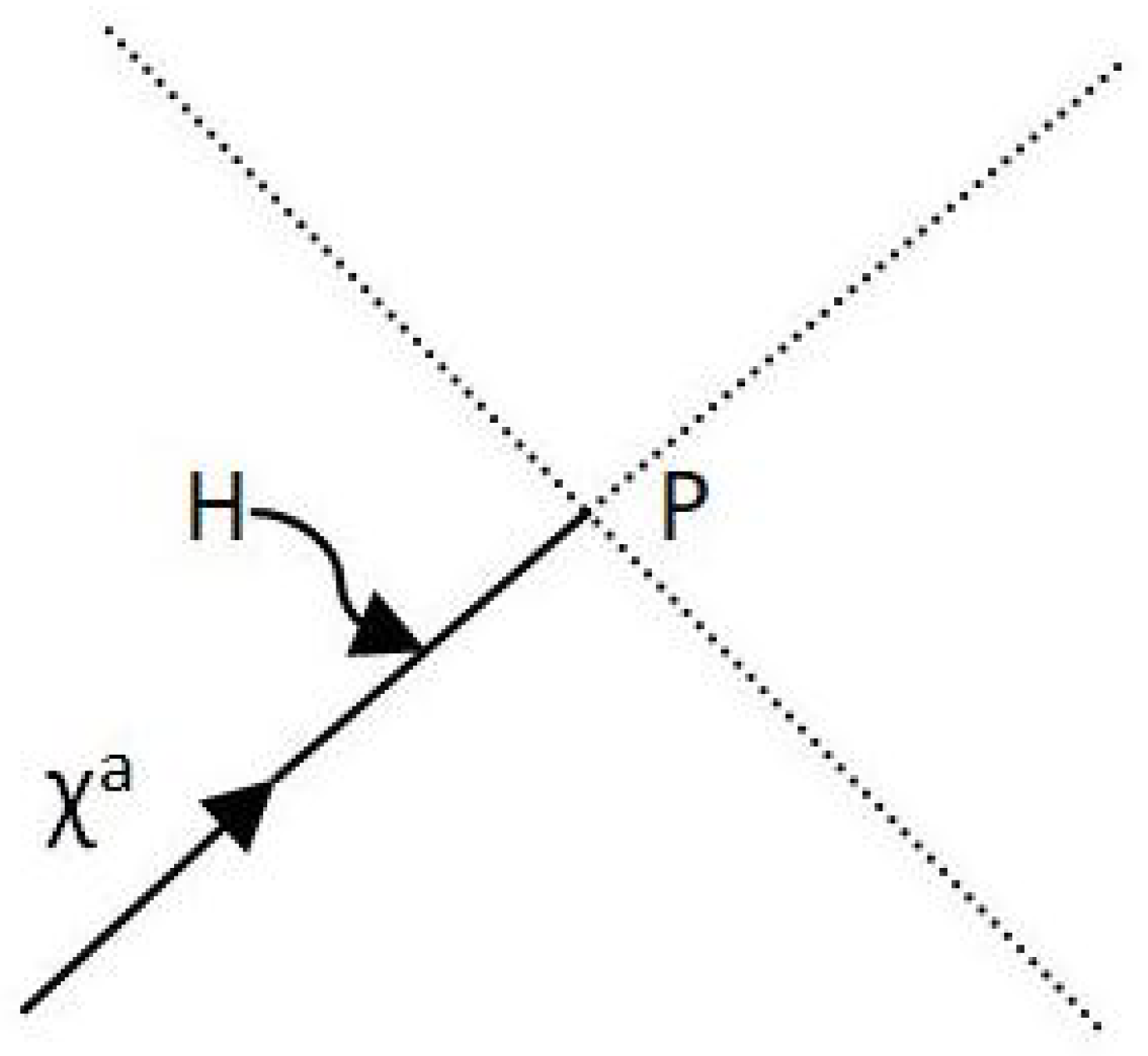
Preprints 84530 g003
Preprints 84530 g004
Figure 4. A universe-antiuniverse pair. The surface at t = 0 acts as a causal horizon.
Figure 4. A universe-antiuniverse pair. The surface at t = 0 acts as a causal horizon.
Preprints 84530 g004

8. Conclusion

This approach of describing gravity as information leads to a very important question of whether or not gravity is a fundamental force as popularly seen. We think the way gravity affects time strongly suggests that gravity can not be a force in the usual sense. Of course, we have to make an additional assumption that the degrees of freedom follow the holographic principle and scales as the area rather than the volume of space but this assumption is very robust in itself looking at black hole physics and gauge/gravity duality. The other important result we argued is: if we look at from a quantum perspective, the most natural way in which the universe can be created is in pairs whose time flow is oppositely related. This suggests the idea of the creation of a universe-antiuniverse pair. Assuming the validity of this hypothesis, in this paper, we showed that the universe at late times expand in an accelerated manner. This does not require any form of dark energy as used in the standard cosmological model of Λ C D M .

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Hawking, S.W. Gravitational radiation from colliding black holes. Physical Review Letters 1971, 26, 1344. [Google Scholar] [CrossRef]
  2. Bekenstein, J.D. Black holes and the second law. Lett. Nuovo Cim. 1972, 4, 737–740. [Google Scholar] [CrossRef]
  3. Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
  4. Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Physical Review D 1974, 9, 3292. [Google Scholar] [CrossRef]
  5. Hawking, S.W. Particle creation by black holes. Communications in Mathematical Physics 1975, 43, 199–220. [Google Scholar] [CrossRef]
  6. Jacobson. Thermodynamics of spacetime: The Einstein equation of state. Physical review letters 1995, 75, 1260–1263. [CrossRef] [PubMed]
  7. Jacobson, T.; Parentani, R. Horizon entropy. Foundations of Physics 2003, 33, 323–348. [Google Scholar] [CrossRef]
  8. Jacobson, T. On the nature of black hole entropy. AIP Conference Proceedings. American Institute of Physics 1999, 493, 85–97. [Google Scholar]
  9. Eling, C.; Guedens, R.; Jacobson, T. Nonequilibrium thermodynamics of spacetime. Physical Review Letters 2006, 96, 121301. [Google Scholar] [CrossRef]
  10. Eling, C. Hydrodynamics of spacetime and vacuum viscosity. Journal of High Energy Physics 2008, 2008, 048. [Google Scholar] [CrossRef]
  11. Chirco, G.; Liberati, S. Nonequilibrium thermodynamics of spacetime: The role of gravitational dissipation. Physical Review D 2010, 81, 024016. [Google Scholar] [CrossRef]
  12. Padmanabhan, T. Lessons from classical gravity about the quantum structure of spacetime. Journal of Physics: Conference Series. IOP Publishing 2011, 306, 012001. [Google Scholar] [CrossRef]
  13. Paranjape, A.; Sarkar, S.; Padmanabhan, T. Thermodynamic route to field equations in Lanczos-Lovelock gravity. Physical Review D 2006, 74, 104015. [Google Scholar] [CrossRef]
  14. Mukhopadhyay, A.; Padmanabhan, T. Holography of gravitational action functionals. Physical Review D 2006, 74, 124023. [Google Scholar] [CrossRef]
  15. Kothawala, D.; Sarkar, S.; Padmanabhan, T. Einstein’s equations as a thermodynamic identity: The cases of stationary axisymmetric horizons and evolving spherically symmetric horizons. Physics Letters B 2007, 652, 338–342. [Google Scholar] [CrossRef]
  16. Kothawala, D.; Padmanabhan, T. Thermodynamic structure of Lanczos-Lovelock field equations from near-horizon symmetries. Physical Review D 2009, 79, 104020. [Google Scholar] [CrossRef]
  17. Kolekar, S.; Padmanabhan, T. Holography in action. Physical Review D 2010, 82, 024036. [Google Scholar] [CrossRef]
  18. Verlinde, E. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 2011, 1–27. [Google Scholar] [CrossRef]
  19. Chaichian, M.; Oksanen, M.; Tureanu, A. On gravity as an entropic force. Physics Letters B 2011, 702, 419–421. [Google Scholar] [CrossRef]
  20. Gao, S. Is gravity an entropic force? Entropy 2011, 13, 936–948. [Google Scholar] [CrossRef]
  21. Kobakhidze, A. Gravity is not an entropic force. Physical Review D 2011, 83, 021502. [Google Scholar] [CrossRef]
  22. Kobakhidze, A. Once more: gravity is not an entropic force. arXiv 2011, arXiv:1108.4161 2011. [Google Scholar]
  23. et al., A.; et al. G.R. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal 1998, 116, 1009–1038. [Google Scholar]
  24. Dvali, G.; Gabadadze, G.; Porrati, M. 4D gravity on a brane in 5D Minkowski space. Physics Letters B 2000, 485, 208–214. [Google Scholar] [CrossRef]
  25. Gorbunov, D.; Koyama, K.; Sibiryakov, S. More on ghosts in the Dvali-Gabadaze-Porrati model. Physical Review D 2006, 73, 044016. [Google Scholar] [CrossRef]
  26. Deffayet, C.; Dvali, G.; Gabadadze, G. Accelerated universe from gravity leaking to extra dimensions. Physical Review D 2002, 65, 044023. [Google Scholar] [CrossRef]
  27. Boyle, L.; Finn, K.; Turok, N. C p t-symmetric universe. Physical review letters 2018, 121, 251301. [Google Scholar] [CrossRef] [PubMed]
  28. Boyle, L.; Finn, K.; Turok, N. The Big Bang, CPT, and neutrino dark matter. Annals of Physics 2022, 438, 168767. [Google Scholar] [CrossRef]
  29. Robles-Pérez, S.J. Time reversal symmetry in cosmology and the creation of a universe–antiuniverse pair. Universe 2019, 5, 150. [Google Scholar] [CrossRef]
  30. Robles-Pérez, S. Quantum creation of a universe-antiuniverse pair. arXiv preprint arXiv:2002.09863, arXiv:2002.09863 2020.
  31. Bousso, R.; Fisher, Z.; Leichenauer, S.; Wall, A.C. Quantum focusing conjecture. Physical Review D 2016, 93, 064044. [Google Scholar] [CrossRef]
  32. Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 23, 287–298. [Google Scholar] [CrossRef]
  33. Hooft, G. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
  34. Susskind, L. The world as a hologram. Journal of Mathematical Physics 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
  35. Maldacena, J. The large-N limit of superconformal field theories and supergravity. International journal of theoretical physics 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
  36. Landsberg, P. Can entropy and “order” increase together? Physics Letters A 1984, 102, 171–173. [Google Scholar] [CrossRef]
  37. Bekenstein, J.D. Black holes and the second law. Lettere al Nuovo Cimento (1971-1985) 2019, 4, 737–740. [Google Scholar] [CrossRef]
  38. Casini, H. Relative entropy and the Bekenstein bound. Classical and Quantum Gravity 2008, 25, 205021. [Google Scholar] [CrossRef]
1
We set k B = c = 1
2
see [36]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated