Preprint
Article
MHD Simulation in the Solar Corona to Obtain Conditions for the Acceleration of Cosmic Rays during Solar Flares
Altmetrics
Downloads
139
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 February 2023
Posted:
28 February 2023
You are already at the latest version
Alerts
Abstract
Solar cosmic rays (SCR) are generated during the primordial energy release in solar flares. This explosive process takes place in the solar corona above the active region. It represents fast release of the magnetic field energy of the current sheet, which is formed near a singular magnetic field line. Solar cosmic rays appear as a result of acceleration of charged particles, mainly protons, by an inductive electric field in the current sheet, equal to the field E=V´B/c near the current sheet. To study the mechanism of solar flares and obtain conditions for stydy SCR acceleration it is necessary to carry out magnetohydrodynamic (MHD) simulation of a flare situation in the solar corona above a real active region. The methods of stabilization were developed which made it possible to solve partially the problem of numerical instabilities. MHD simulations showed complicated configuration near the singular line. Comparison of the results of MHD simulations with observations showed a general agreement of the positions of the current sheets with regions of intense flare radiation. However, there are some problems with the details of such coincidences. The results show the possibility of improving the methods of MHD simulation in order to solve the arisen problems.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Solar cosmic rays are generated during the primordial energy release in solar flares. This explosive process takes place in the solar corona above the active region at altitudes of 15 000 to 70 000 km (~1/40–1/10 of the solar radius). This has been proven by direct measurements of the thermal X-ray emission of flares on the limb [1]. There is a number of other evidence for the energy release of a flare in the corona, based on an analysis of observations (see, for example, [2,3]). The possible positions of the flares found from the results of numerical simulations in the corona above the active region confirm the appearance of flares at these altitudes.
The slow accumulation of magnetic energy that occurs in the solar corona, and then its fast release during a flare, is explained by the mechanism according to which, during a flare, the energy accumulated in the magnetic field of the current sheet is released [4,5]. The current sheet, which is formed in the vicinity of a singular line of the X-type magnetic field as a result of the accumulation of disturbances, is first in a stable state. Further, in the process of quasi-stationary evolution, during which the plasma flows fast out of the sheet under the action of the magnetic tension force, the current sheet transfers into an unstable state. The instability in the current sheet causes a flare release of energy with all the observed manifestations, which are explained by the electrodynamic model of the flare proposed by I.M. Podgorny [6]. The model was developed based on the results of observations and numerical MHD simulation and uses analogies with the substorm electrodynamic model proposed earlier by its author [7].
Solar cosmic rays appear as a result of acceleration of charged particles, mainly protons, by an inductive electric field in the current sheet, equal to the field E=-V×B/c near the current sheet [8]. This inductive electric field is caused by a rapid change in the magnetic field during the current sheet instability. I. M. Podgorny noted an important property of this electric field for a wider class of physical phenomena: it is equal to E=-V×B/c in the field B of the powerful current formed near its location and in the plasma accelerated by magnetic pressure towards the location of the current. Besides the current sheet such an electric field arises in the pinch [9] created in an installation for solving the problem of controlled thermonuclear fusion. In both processes, charged particles are accelerated by an inductive electric field. For solar flares, they (mainly protons) under favorable conditions can leave the magnetic field above the active region, which will lead to the appearance of solar cosmic rays (SCR).
This mechanism can accelerate galactic cosmic rays during superflares on stars to energies five orders of magnitude higher than the SCR energy [10].
To study the mechanism of solar flares, the process of formation of a current sheet and the accumulation of energy in its magnetic field for each specific flare, and to obtain the possibility of improving the prognosis of solar flares based on an understanding of their physical mechanism, it is necessary to carry out magnetohydrodynamic (MHD) simulation of a flare situation in the solar corona above a real active region. The electric and magnetic fields obtained by MHD simulation above a real active region at the site of the primordial flare energy release and near it are necessary for studying the generation of solar cosmic rays. The acceleration of charged particles and the possibility of their exit from the acceleration region must be studied by calculating the trajectories of charged particles in electric and magnetic fields obtained by MHD simulation. The first results of studying the acceleration of charged particles were obtained by calculating trajectories in electric and magnetic fields, found by MHD simulation above the active region under simplified conditions [11].
Here, MHD simulation is continued above the real active region in order to more accurately determine the configurations of the magnetic and electric fields for studying SCR generation by calculating the trajectories of charged particles. More complex field configurations are obtained and analyzed near singular lines at the places where current sheets appear. A more detailed comparison of the MHD simulation results with observations has led to some problems, the solution of which requires further development of the numerical simulation technique.
When setting the conditions for MHD simulation, no assumptions were made about the physical mechanism of the solar flare; the boundary conditions were taken from observations. For MHD simulation in the real scale of time, a significant computational speed is required, which is achieved only through the use of parallel computing on supercomputers. Parallelization of calculations was carried out by computational threads on graphic cards (GPU). Experience has shown that the physical mechanism of a solar flare can be studied by MHD simulation only if the calculation starts a few days before the appearance of flares, when magnetic energy for the flare has not yet accumulated in the corona. Simulation in this setting of the problem showed the appearance of a current sheet above the active region [12]. Also, the appearance of a current sheet in such a setting of the problem was demonstrated by MHD simulations carried out by C. Jiang, S.T. Wu et al [13,14]. MHD simulations in the solar corona in other problem settings were performed in [15,16,17,18].
2. Methods of MHD Simulation
MHD simulation is carried out above the active region of AR 10365. The computational domain in the corona is a rectangular parallelepiped (0≤х≤1, 0≤y≤0.3, 0≤z≤1) (the length unit was chosen L0=4×1010 cm). The lower boundary of the computational domain y=0 (XZ) is located on the surface of the Sun (photosphere) and contains the active region; the Y axis is directed from the Sun perpendicular to the photosphere. The three-dimensional system of MHD equations is solved numerically in a dimensionless form:
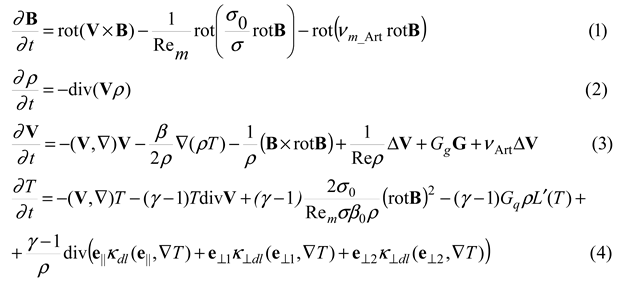
A typical magnetic-field strength in the active region, B0 = 300 G, was used as the unit of the magnetic field. The units of the plasma density and temperature were taken to be their typical values in the corona above the active region, n0=ρ0/mi=108 cm-3, T0=106 oK, which were assumed to be initially constant (mi = 1.67×10-24 g – ion mass). The units of plasma velocity and time are, respectively, the Alfvén velocity and Alfvén time = 0.65×1010 cm/s, t0=L0/V0= 6.1 s. In equations (1) - (4) γ=5/3 is adiabatic constant, Rem=V0L0/νm0 is the magnetic Reynolds number, νm0=с2/4πσ0 is the magnetic viscosity for the conductivity σ0 at the temperature T0, σ is conductivity, σ/σ0=T3/2, β=8πn0kT0/B02 (n0=ρ0/mi, mi is the ion mass). Re=ρ0L0V0/η is the Reynolds number, η is the viscosity. Gq=L(T0)ρ0t0/T0, L'(T)=L(T0T)/L(T0) is the dimensionless radiation function. κdl=κ/(Πκ0) is the dimensionless thermal conductivity along the magnetic field lines, Π=ρ0L0V0/κ0 is the Peclet number, κ0 is the thermal conductivity for the temperature T0, κ is the thermal conductivity, κ/κ0=T5/2.
κ⊥dl=[(κκ0-1Π-1)(κBκ0B-1ΠB-1)]/[(κκ0-1Π-1)+(κBκ0B-1ΠB-1)] is the dimensionless thermal conductivity perpendicular to the magnetic field lines, ΠB=ρ0L0V0/κ0B is the Peclet number for the thermal conductivity across the strong magnetic field (when the cyclotron radius is much smaller than the free path length). This thermal conductivity is denoted as κB, and κ0B is its value for the temperature T0, plasma density ρ0, and field B0; κB/κ0B=ρ2B-2T -1/2.
To select the parameters, the principle of limited simulation [19] was used, according to which, much larger and much smaller units of dimensionless parameters are set in calculations much larger and much smaller than unity without accurately preserving their values. The main parameters are the magnetic and ordinary Reynolds numbers Rem and Re. Dimensionless values of artificial viscosities (νm_Art_Ph и νArt_Ph) were set to stabilize the numerical instabilities.
For the numerical solution, an upwind absolutely implicit finite-difference scheme was developed, which is conservative with respect to the magnetic flux [20]. The scheme is solved by the method of iterations. The methods were applied with the aim of constructing a scheme that remains stable for the maximum possible time step. The scheme is realized in the computer program PERESVET.
A stable finite difference scheme (high stability is achieved if this scheme is implicit) should approximate the magnetic induction equation (1), in which the diffusion term is taken as νmΔB rather than -rot(νmrotB). For this purpose, it is necessary to preserve the magnetic flux through the boundary of each cell of the difference scheme, which means that the finite-difference analog [divB] is equal to zero with high accuracy, if the values are correctly specified on the grid elements of the difference scheme. For a difference scheme conservative with respect to the magnetic flux, the finite-difference analogs of [νmΔB] and [-rot(νmrotB)] coincide. If in the finite difference scheme the magnetic flux is conserved with high accuracy, then the scheme with finite difference approximation of the diffusion term in the form [-rot(νmrotB)] is also stable, since this diffusion term is equal to [νmΔB] with high accuracy. In addition, when solving a finite difference scheme by iteration method, the values at the central point of the template can be taken both at the current iteration and at the next iteration. It becomes possible to use various variants of the difference scheme. The above considerations for the constant magnetic viscosity νm extend to the case where νm depends on spatial coordinates. To do this, it is necessary to add finite-difference analogs of the products of the spatial derivatives of νm and the spatial derivatives of the B components to the scheme, which do not cause instability of the difference scheme.
For the numerical solution of the MHD equations, several versions of the scheme were proposed, in which the magnetic flux is conserved with high accuracy. A more accurate visual representation of the arrangement of quantities on a three-dimensional grid of a finite-difference scheme, conservative with respect to the magnetic flux, is done. Images of the location of the values on the grid are shown in Figure 1 and Figure 2. The finite-difference analogue of the magnetic field divergence [divB] for such a scheme should be equal to zero with high accuracy, for our calculations the dimensionless value |[divB]| ~ 10-4. In connection with the appearance of numerical instabilities near the boundary of the region, additional test calculations were carried out for possible corrections in the choice of the scheme variant with the conservation of the magnetic flux. As a result, taking into account the influence of instabilities near the boundary, the variant in which the iterations converge the fastest remains the most efficient. In this version, the diffusion term in the equation for the magnetic field was taken in the form of a finite-difference analog ΔB ([ΔB]), rather than rot(rotB) ([rot(rotB)]), and the values at the central point of the grid template of the finite-difference scheme were taken on the next iteration.
In the finite-difference scheme, which is conservative with respect to the magnetic flux, the magnetic field is specified not by the field vectors at the grid points, but by the magnetic fluxes through the boundaries of the grid cells, averaged per unit area (Figure 1). Used to specify the magnetic field components, the magnetic fluxes through the cell faces, averaged per unit area, approximate the components of the magnetic field vector perpendicular to the given face, taken at the central point of the given face. The values of plasma density ρ, velocity V, and temperature T were set at the grid points of the finite-difference scheme, i.e., at the vertices of the cubes, which are grid cells.
The dimensionless electric field E= -V×B + νm j (here νm = Rm-1 (σ0/σ) = Rm-1 T-3/2 is the dimensionless magnetic viscosity) and the dimensionless electric current density j=rotB is clearly are not included in the equations of magnetic hydrodynamics, but are expressed in terms of the quantities included in these equations. It is convenient to use the values E and j for constructing a difference scheme; they are determined on the edges of the grid cells. The edges of the grid cells, which can be parallel to one of the coordinate axes X, Y or Z, are numbered by the three-dimensional number i, j, k of the end of this face with the minimum value of the corresponding coordinate.
The equation for the magnetic field (1) in the introduced notation has the form . The flux of the magnetic field B through the surface of a small area S, perpendicular to the vector B is equal to ΦB= B S, (if there is an arbitrary surface of a large area, then the magnetic flux through it can no longer be expressed through the field vector at any one point, the magnetic flux will be equal to the integral over the surface , where B is the magnetic field vector defined at each point of the surface, ds is the vector perpendicular to the surface, the value of which is equal to the small area ds on the surface under consideration, and (B,ds) is the scalar product of these vectors).
The flux of the vector rot(-E) through the surface of a small area S, perpendicular to the vector rot(-E) is equal to Φrot(-E) = rot(-E) S. According to the induction equation , this flow Φrot(-E) represents is a change in time of the magnetic flux ΦB. Since the divergence of the magnetic field must always be zero divB=0, the magnetic flux through a surface bounding any region in space will be zero. This confirms the induction equation, from which it follows that if for an initial magnetic field its flux through the surface bounding any region in space is zero, it will remain zero for any moment in time, since the flux of the vector field rotor (in this case rot(-E) ), representing the change in time of the magnetic flux, is always zero.
To improve stability, a scheme is constructed in which the flow through the grid cell boundary remains equal to zero with very high accuracy (with the accuracy of iteration convergence if this is an implicit scheme solved by the iteration method, or with the accuracy of representing numbers in a computer if an explicit scheme is used, which less stable). This is a scheme that is conservative with respect to magnetic flux.
The magnetic flux through a face perpendicular to the X axis is equal to the product of the magnetic field component Bx, defined on this face, by the area of this face
Φx, i, j, k = Bx, i, j, k Sx = Bx, i, j, k hy hz (hy, hz - grid steps along the Y and Z axes, Figure 1. bottom row).
Similarly, magnetic fluxes are determined through faces perpendicular to the Y and Z axes. The total flux of the magnetic field emerging through the surface limiting the volume of the computational grid cell with numbers i+1, j+1, k+1 (the cell shown in Figure 1 with the limits of coordinate change (xi≤x≤xi+1, yj≤y≤yj+1, zk≤z≤zk+1) ) can be found knowing the flows through the faces of this cell; for a scheme that is conservative with respect to the magnetic flux, this value should be equal to zero (with high accuracy):
Φx, i+1, j+1, k+1 - Φx,i, j+1, k+1 + Φy,i+1, j+1, k+1 - Φy, i+1, j, k+1 + Φz,i+1, j+1, k+1 - Φz,i+1, j+1, k = 0
or, substituting the values of magnetic fluxes:
Bx, i+1, j+1, k+1 Sx - Bx,i, j+1, k+1 Sx + By,i+1, j+1, k+1 Sy - By, i+1, j, k+1 Sy + Bz,i+1, j+1, k+1 Sz - Bz,i+1, j+1, k Sz =0
Where Sx Sy Sz are the areas of cell faces perpendicular to the vectors of the selected coordinate system ex ey ez : Sx= hyhz ; Sy=hxhz ; Sz=hxhy
The density of the magnetic flux source in a grid cell is the value of the total magnetic flux divided by the volume of the cell. Dividing the total magnetic flux by the volume of the grid cell V=hxhyhz we get
(Bx, i+1, j+1, k+1 - Bx,i, j+1, k+1 )/hx + (By,i+1, j+1, k+1 - By, i+1, j, k+1)/hy + (Bz,i+1, j+1, k+1 - Bz,i+1, j+1, k)/hz = 0
i.e. finite-difference analog of the magnetic field divergence divB ([divB]) vanishes, as expected
Equality to zero of the total flux of the magnetic field through the cell boundary in a scheme that is conservative with respect to the magnetic flux is achieved by setting the initial magnetic field on the faces of the grid cells with zero total magnetic flux and zero change in the flux with time. The change in the magnetic flux, representing the flux of the vector rot(-E), which goes through the boundary of the grid cell, will be zero if, in the scheme of the components of the vector rot(-E), the finite-difference analogs of the derivatives are expressed in terms of the components of the vectors, the electric field E, specified on the edges of the cells grids, as illustrated in Figure 2.
Despite the use of special methods, simulation in the real scale of time is possible only with the help of parallel computing. They were carried out by parallel computing threads on graphics cards using CUDA technology.
The main problem of MHD simulation above a real active region is the numerical instabilities that arise near the boundary of the computational region. The developed methods for stabilizing the instability made it possible to solve partially the problem for calculations with relatively low viscosities (Rem= 109, Re= 107), which practically do not suppress the perturbation propagating from the photosphere. The results obtained make it possible to determine ways to further improve the technique for stabilizing numerical instabilities.
3. Results
The configuration of the magnetic field obtained by MHD simulation is so complex that it is often impossible to determine from this configuration the positions of singular lines and the current sheets appearing near them from it. For this purpose, a graphical search system of flare positions has been developed [12] and then modernized. The system is based on the search for current density maxima, which are reached in the middle of the current sheets, and further analysis of the magnetic field configuration near the points of the found maxima.
Figure 3, Figure 4 and Figure 5 present a comparison of the results of MHD simulations with observations of radio emission at a frequency of 17 GHz obtained with the Nobeyama radioheliograph (NoRH) before the M 1.9 flare on May 26, 2003 above the active region of AR 10365 and during this flare (2003- 05-26 04:47:05, 05:32:05 and 05:41:05). The positions of the current density maxima are marked with numbers 1, 2, 3, 4, 5, 11, 13, 14, 15, 16, 62, 64, 97, and 115, the remaining maxima are indicated by green dots (the current density maxima are renumbered in decreasing order of density current). A divergent magnetic field is superimposed on the X-type magnetic field at many current density maxima. However, due to the presence of the X-type configuration, current sheets are formed at such locations even if the divergent field dominates and a deformed divergent magnetic field is obtained as a result of the superposition.
4. Discussion
Comparison of the results of MHD simulations with observations before and during flares showed a general agreement between the positions of the current sheets found by our graphical search system and the regions of intense flare radiation. A significant number of points at which current density maxima are reached are located in the region of strong radiation. Also, a significant part of the points of maxima is located at a relatively small distance from the region of strong radiation (~10 Mm and less), which can be explained by the error of the numerical method and physical processes during the flare. These results confirm the mechanism according to which the energy accumulated in the magnetic field of the current sheet is released during the flare.
There are some problems with the details of such coincidences. Especially if you choose current sheets in which the current directions are almost parallel to the solar surface and they are located at the tops of magnetic loops (or at least near the tops of magnetic loops) at a fairly high altitude of 25,000 km - 45,000 km. These heights are lower than 60,000 - 70,000 km, where it is difficult to expect the accumulation of large magnetic energy due to low magnetic fields, but at the same time, these are not heights of 15,000 - 20,000 km, where, apparently, a current sheet may not appear with a sufficiently small longitudinal field so that explosive instability can occur in it. In the magnetic field of current sheets at the tops of magnetic loops at altitudes of 25,000–45,000 km, apparently, energy for a flare can accumulate best of all, and after a quasi-stationary evolution, such current sheets can go into an unstable state.
The results obtained indicate the need for work to solve the problems that have arisen. It may be necessary to carry out more accurate calculations. This can be helped by a more efficient stabilization of the instability near the boundary of the computational domain, as well as a more accurate setting of the boundary conditions, for which there are also some possibilities.
5. Conclusions
- The methods of MHD simulation in the solar corona above a real active region have been improved. The application made it possible to perform calculations above the active region of AR 10365 during a time interval of about three days, but showed the need for further modernization. For the upwind, absolutely implicit finite-difference scheme, which is conservative with respect to the magnetic flux, developed and implemented in the PERESVET program, a variant of magnetic flux conservation was chosen, for which the stabilization of the numerical instability that occurs near the boundary of the computational domain is best performed. The parallel computing algorithm implemented by computational threads on graphics cards using CUDA technology has been modernized over the past few years, after its first version was developed. The stabilization of the numerical instability that occurs near the boundary of the computational domain has been improved by more accurate selection of artificial viscosity values and by using other methods.
- An analysis of the new results of MHD simulation before solar flares and during solar flares confirmed the formation of singular X-type lines in the magnetic field configuration and the appearance of current sheets in them, in the magnetic field of which energy for solar flares is accumulated.
- The results obtained confirmed the existence of a large number of singular magnetic field lines, in the vicinity of which a divergent magnetic field is superimposed on the X-type field configuration. Even if the divergent magnetic field dominates such that a deformed divergent magnetic field results from the superposition, the presence of an X-type field can produce a sufficiently strong current sheet to explain the appearance of a medium-power flare.
- The results of the analysis of MHD simulation data for the time moments before and during flares confirmed that a large number of current density maxima (more than a hundred), located on a singular magnetic field line in the vicinity of which the current sheet is formed, are in the region of intense flare radio emission at a frequency of 17 GHz, or at a distance from the region of intense radiation not exceeding 10 Mm. This arrangement of current density maxima confirms the solar flare mechanism based on the release of energy stored in the magnetic field of the current sheet. The details of the location of the current density maxima did not always correspond to the observational data, which indicates the need to develop more accurate methods for solving the equations of magnetohydrodynamics and setting the boundary conditions on the solar surface.
Acknowledgments
The authors are grateful to the SOHO/MDI team and Nobeyama radioheliograph for the scientific data provided, as well as to the many professional cloud service specialists, which made it relatively easy for us to configure rented remote computers for GPU computing
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lin, R.P. , Krucker S., Hurford G.J., Smith D.M., Hudson H.S. Holman G.D., Schwartz R.A., Dennis B.R., Share G.H., Murphy R.J., Emslie A.G., Johns-Krul C., Vilmer N. RHESSI observations of particle acceleration and energy release in an intense solar gamma-ray line flare. Astrophys. J. 2003, 595, L69–L76. [Google Scholar] [CrossRef]
- Podgorny AI, Podgorny IM, Meshalkina NS. Dynamics of magnetic fields of active regions in pre-flare states and during solar flares. Astron Rep. 2015, 59, 795–805. [Google Scholar] [CrossRef]
- Podgorny I., M. and Podgorny A. I.. Diagnostic of a solar flare via analyses of emission in spectral lines of highly ionized iron. Astron Rep. 2018, 62, 696–704. [Google Scholar] [CrossRef]
- Syrovatskii, S.I. . Dynamic dissipation of energy in the vicinity of the magnetic field neutral line. Zh. Eksp. Teor. Fiz. 1966, 50, 1133–1147. [Google Scholar]
- Bratenahl, A. , Hirsch, W. An experimental study of a neutral point in a plasma ball. Am. Phys. Soc. 1966, 11, 580. [Google Scholar]
- Podgorny, I.M. , Balabin Yu.V., Vashenyuk E.V., Podgorny A.I. The generation of hard X-rays and relativistic protons observed during solar flares. Astron. Rep. 2010, 54, 645–656. [Google Scholar] [CrossRef]
- Podgorny I., M. , Dubinin E. M., Israilevich P. L. Nicolaeva N. S.. Large-scale structure of the electric field and field-aligned currents in the auroral oval from the Intercosmos-Bulgaria satellite data. GRL. 1988, 15, 1538–1540. [Google Scholar] [CrossRef]
- Podgorny, I.M. , Podgorny A.I.. Solar cosmic ray acceleration and propagation. Sun and Geosphere. 2016, 11, 85–90. [Google Scholar]
- Podgorny, I.M. , Kovalsky N.G, Palchikov V.E. 1958. Reports of Academy of Sciences. 123, 825-828. In Russian. (Пoдгoрный И.М., Кoвальский Н.Г., Пальчикoв В.Е. ДАН. 1958. 123. 825-828.
- Podgorny, I.M. , Podgorny A. I. 2019. The single mechanism of solar and galactic cosmic rays acceleration arising during the flare process. J. Phys.: Conf. Ser., 2019, 1390, 012064–1. [Google Scholar] [CrossRef]
- Podgorny I., M. , Balabin Yu.V., Podgorny A.I., Vashenyuk E.V. Spectrum of solar flare protons. Journ. Atm. Solar-Ter. Phys. 2010, 72, 988–991. [Google Scholar] [CrossRef]
- Podgorny, A.I. and Podgorny I. M. MHD simulation of solar flare current sheet position and comparison with X-ray observations in active region NOAA 10365. Sun Geosph. 2013, 8, 71–76. [Google Scholar]
- Jiang, C. , Wu S.T., Feng X., Hu, Q. Nature Communications. 2016, 7, 11522. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C. , Wu S.T., Yurchyshyn V., Wang H., Feng X., Hu Q. Astrophys. J. V. 2016, 828, 62. [Google Scholar] [CrossRef]
- Aulanier, G. Torok T., Demoulin P., DeLuca, E. E. Astrophysical Journal. 2010, 708, 314–333. [Google Scholar] [CrossRef]
- Zuccarello, F.P. , Aulanier G., Dudik J., Demoulin P., Schmieder B., Gilchrist S.A.. Astrophys. J. V. 2017, 837, 115. [Google Scholar] [CrossRef]
- Jiang, C. , Zou P., Xueshang X., Hu Q. et al. . Astrophys. J. 2018, 869, 13. [Google Scholar] [CrossRef]
- Bian, X. , Jiang C., Feng X., Zuo P., Wang Yi., Wang, X.. Astronomy and Astrophysics. V. 2002, 658, A174. [Google Scholar] [CrossRef]
- Podgorny I., M. Simulation studies of Space. Fundamentals of Cosmic Phys. 1978, 4, 1–72. [Google Scholar]
- Podgorny, A.I. and Podgorny I.M.. MHD simulation of phenomena in the solar Corona by using an absolutely implicit scheme . Comput Math Mathemat Phys. 2004, 44, 1784–1806. [Google Scholar]
Figure 1.
Numeration of grid elements of a finite-difference scheme that is conservative with respect to magnetic flux and setting values on the grid elements.
Figure 1.
Numeration of grid elements of a finite-difference scheme that is conservative with respect to magnetic flux and setting values on the grid elements.
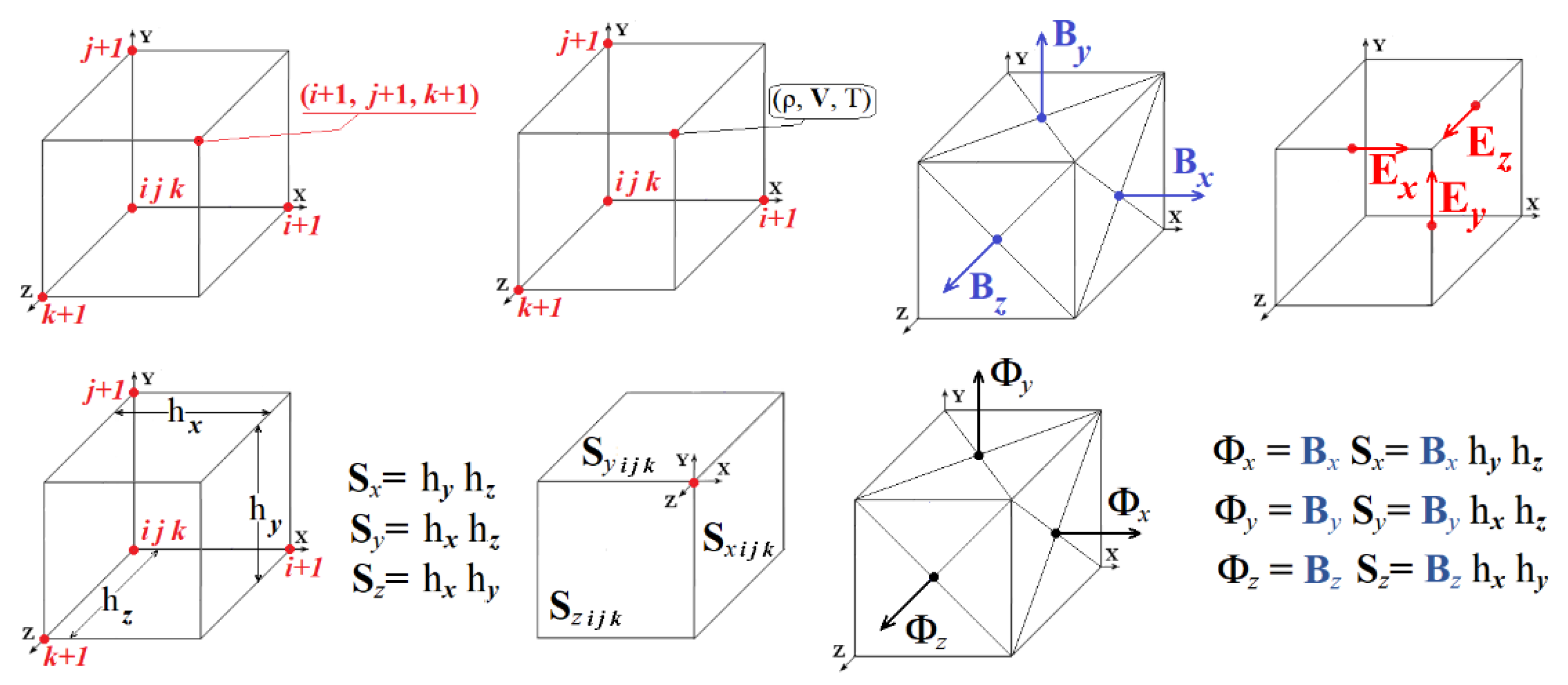
Figure 2.
Compensation for changes in the magnetic flux through the faces of the grid cells of the finite-difference scheme adjacent to the same edge. The contributions of the electric field on a common edge to the change in the magnetic flux through the faces are equal in absolute value and opposite in sign.
Figure 2.
Compensation for changes in the magnetic flux through the faces of the grid cells of the finite-difference scheme adjacent to the same edge. The contributions of the electric field on a common edge to the change in the magnetic flux through the faces are equal in absolute value and opposite in sign.
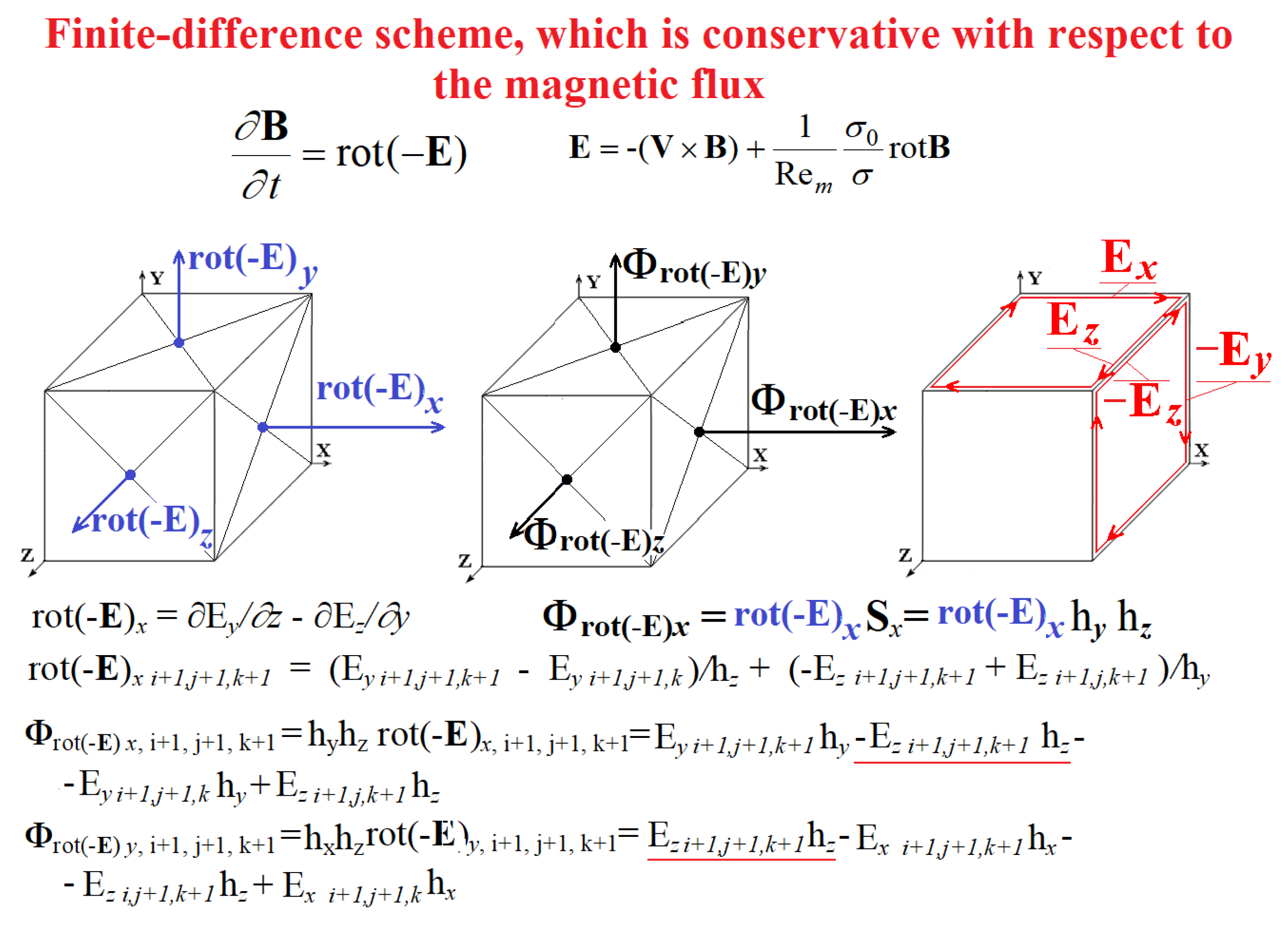
Figure 3.
Comparison of the magnetic field configuration and the position of the current density maxima with the distribution of radio emission intensity at a frequency of 17 GHz before the M1.9 flare on May 26, 2003 at 04:47:05. The configurations of the magnetic field in the region of the 3rd, 4th, 13th, 14th, 62nd, and 63rd current density maximums are presented, which are numbered in descending order of current density.
Figure 3.
Comparison of the magnetic field configuration and the position of the current density maxima with the distribution of radio emission intensity at a frequency of 17 GHz before the M1.9 flare on May 26, 2003 at 04:47:05. The configurations of the magnetic field in the region of the 3rd, 4th, 13th, 14th, 62nd, and 63rd current density maximums are presented, which are numbered in descending order of current density.
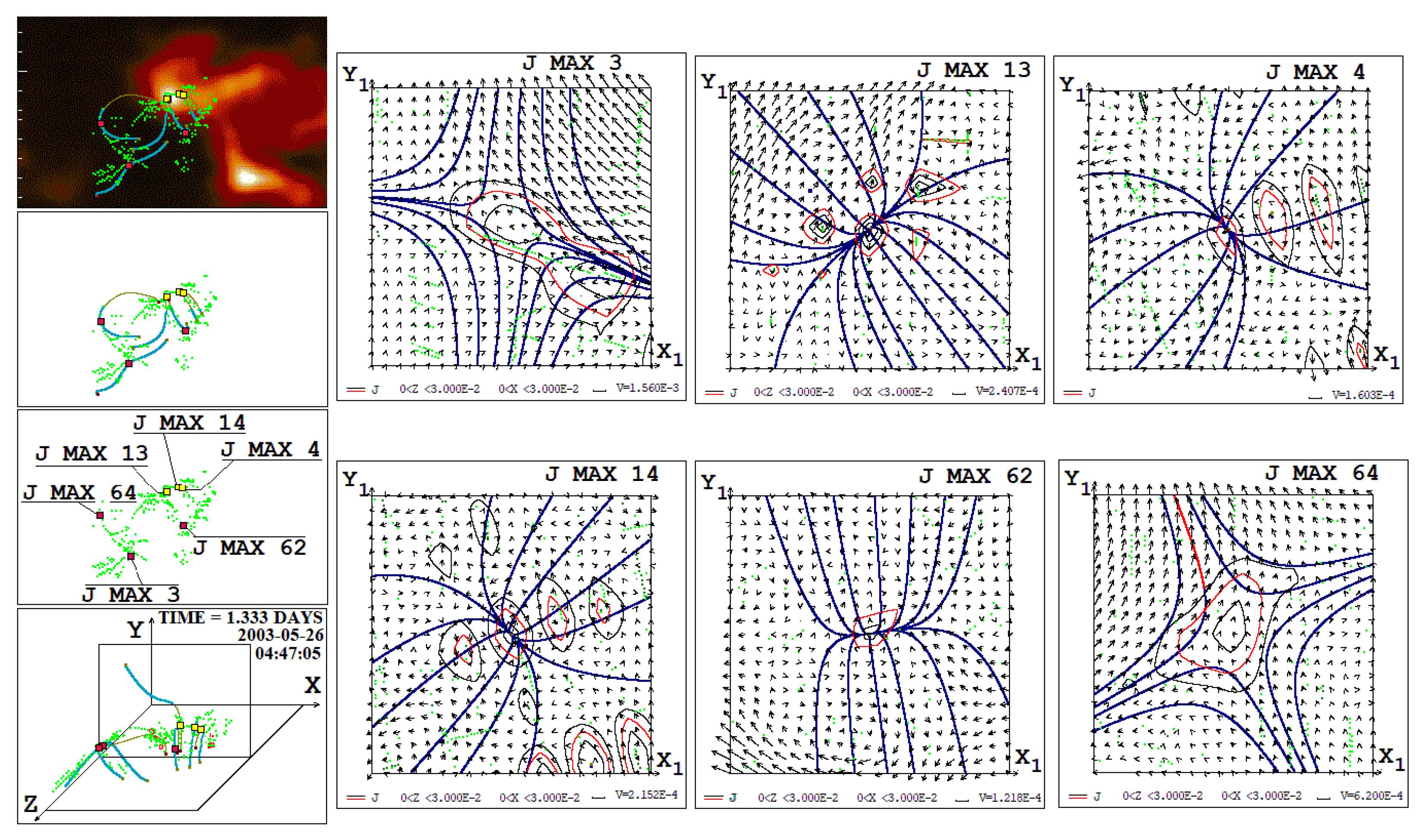
Figure 4.
Comparison of the magnetic field configuration and the positions of the current density maxima with the distribution of radio emission power at a frequency of 17 GHz during an M1.9 flare on May 26, 2003 at 05:32:05. The configurations of the magnetic field in the vicinity of the 2nd, 5th, 15th, and 115th current density maximums are presented.
Figure 4.
Comparison of the magnetic field configuration and the positions of the current density maxima with the distribution of radio emission power at a frequency of 17 GHz during an M1.9 flare on May 26, 2003 at 05:32:05. The configurations of the magnetic field in the vicinity of the 2nd, 5th, 15th, and 115th current density maximums are presented.
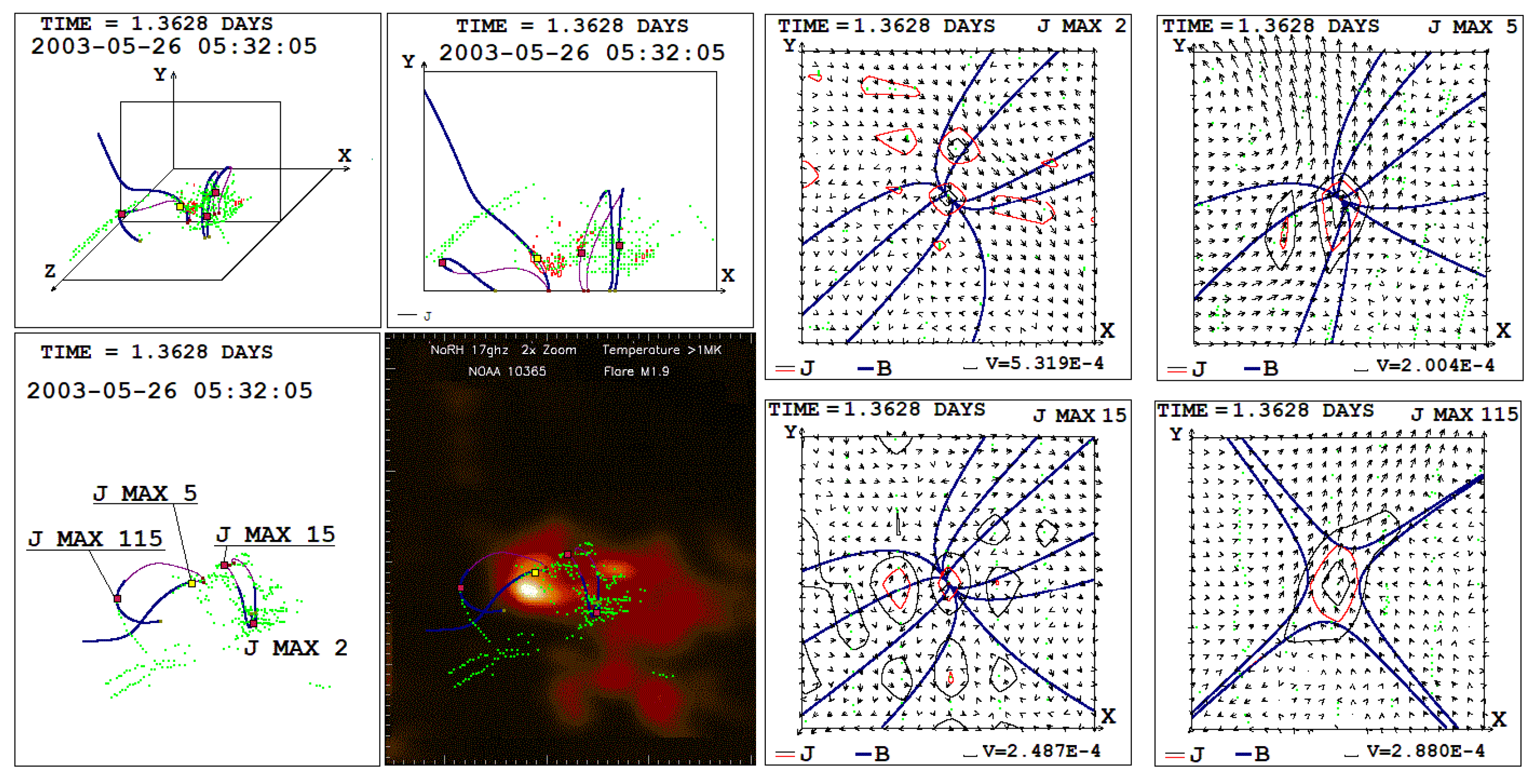
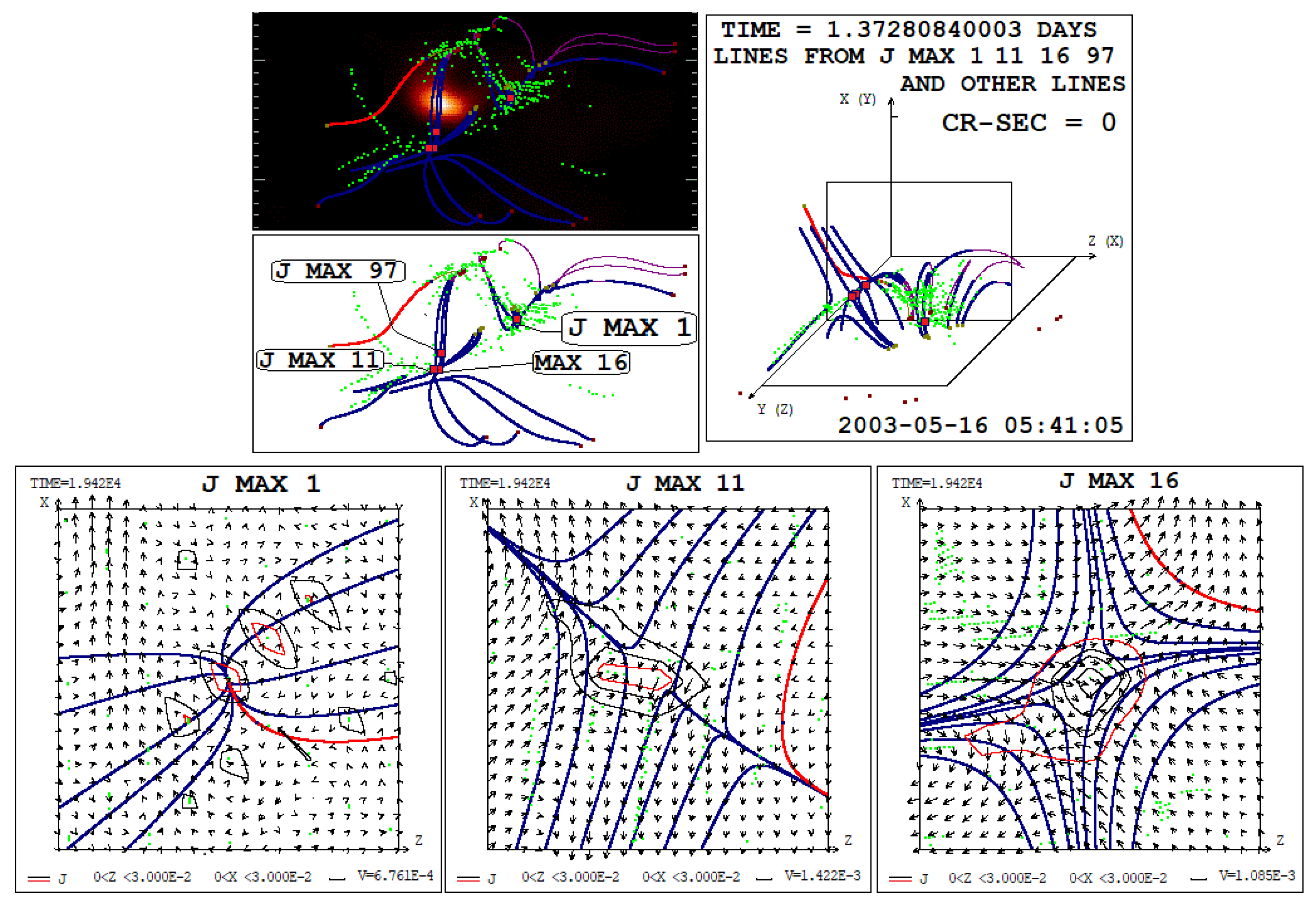
Figure 5.
Comparison of the magnetic field configuration and positions of current density maxima with the distribution of radio emission power at a frequency of 17 GHz at a later stage of the M1.9 flare on May 26, 2003 at 05:41:05. The configurations of the magnetic field in the vicinity of the 1st, 11th, and 16th current density maximums are presented.
Figure 5.
Comparison of the magnetic field configuration and positions of current density maxima with the distribution of radio emission power at a frequency of 17 GHz at a later stage of the M1.9 flare on May 26, 2003 at 05:41:05. The configurations of the magnetic field in the vicinity of the 1st, 11th, and 16th current density maximums are presented.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




