Prerpints.org logo
Preprint
Technical Note

Supplemental Analyses for Comment on “Impacts of Sugarcane Fires on Air Quality and Public Health in South Florida”

Altmetrics

Downloads

175

Views

221

Comments

0

Submitted:

28 February 2023

Posted:

28 February 2023

You are already at the latest version

Alerts
Abstract
This document serves as supplemental information to Shapero et al. (2023), which is itself a comment on Nowell et al. (2022). Environmental Health Perspective’s publishing standards for article comments have strict word counts and do not allow the addition of new primary data analyses; therefore, this document provides an additional level of detail and supporting analyses that serve as an important backup to and expansion of Shapero et al. (2023) and that also respond to some comments within the author’s reply to our comments (Holmes and Nowell, 2023). Nowell et al. (2022) evaluated potential PM2.5 community impacts from sugarcane harvesting. However, their analysis is flawed by erroneous assumptions and misapplied technical approaches, as discussed in Shapero et al. (2023) and as detailed in this supplemental information document. Additionally, the authors ended their analysis with 2018 data, but later data shows no marginal increase in PM2.5 during sugarcane harvest following 2019 even using the authors’ approach (Holmes and Nowell, 2023). Therefore, the authors’ evaluations have no relevance to current conditions. Nonetheless, even their evaluation and conclusions regarding PM2.5 concentrations purportedly attributable to sugarcane harvesting prior to 2019 are unsupported and technically unsound as detailed below.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1.Introduction

This document serves as supplemental information to Shapero et al. (2023), [1] which is itself a comment on Nowell et al. (2022). [2] Environmental Health Perspective’s publishing standards for article comments have strict word counts and do not allow the addition of new primary data analyses; therefore, this document provides an additional level of detail and supporting analyses that serve as an important backup to and expansion of Shapero et al. (2023) and that also respond to some comments within the author’s reply to our comments (Holmes and Nowell, 2023). [3]
Nowell et al. (2022) evaluated potential PM2.5 community impacts from sugarcane harvesting. However, their analysis is flawed by erroneous assumptions and misapplied technical approaches, as discussed in Shapero et al. (2023) and as detailed in this supplemental information document. Additionally, the authors ended their analysis with 2018 data, but later data shows no marginal increase in PM2.5 during sugarcane harvest following 2019 even using the authors’ approach (Holmes and Nowell, 2023). Therefore, the authors’ evaluations have no relevance to current conditions. Nonetheless, even their evaluation and conclusions regarding PM2.5 concentrations purportedly attributable to sugarcane harvesting prior to 2019 are unsupported and technically unsound as detailed below.

2. Air Data Evaluation

2.1 Background

In Nowell et al. (2022), surface PM2.5 observations serve as the impetus to use the HYSPLIT model to calculate PM2.5 emissions during sugarcane harvest. However, the authors’ analysis of the surface observations data was faulty, and the subsequent model was developed to simply reinforce the authors’ erroneous a priori assumptions about PM2.5 during sugarcane harvest and not to corroborate their findings. The authors’ main conclusion from the surface PM2.5 observations is the following: “At Belle Glade, the only monitoring site within the SGR, PM2.5 was 0.7 µg/m3 higher during the sugarcane harvest season than the rest of the year (95% CI: −0.4, 1.8 µg/m3, p= 0.19).” This conclusion is not supported by the data or the authors’ own analysis.

2.2. Purpose

Using the same data source as Nowell et al. (2022), we re-calculated and re-analyzed the PM2.5 data.

2.2.1. Data Download and Cleaning

  • Data for 2009-2022 were obtained from EPA’s outdoor air quality data download page. [4]
  • Data from the sites analyzed in Nowell et al. (2022) was selected.
  • Data was categorized into “Harvest” (October through March, inclusive) and “Non-Harvest” (April through September, inclusive).
  • In cases where the POC code [5] was greater than 1, data points for a given day were averaged.
  • For days in which there was data with both AQS Parameter [6] “PM2.5 – Local Conditions” and AQS Parameter “Acceptable PM2.5 AQI & Speciation Mass,” the data with AQS Parameter “PM2.5 – Local Conditions” was selected.

2.2.2. Data Analysis

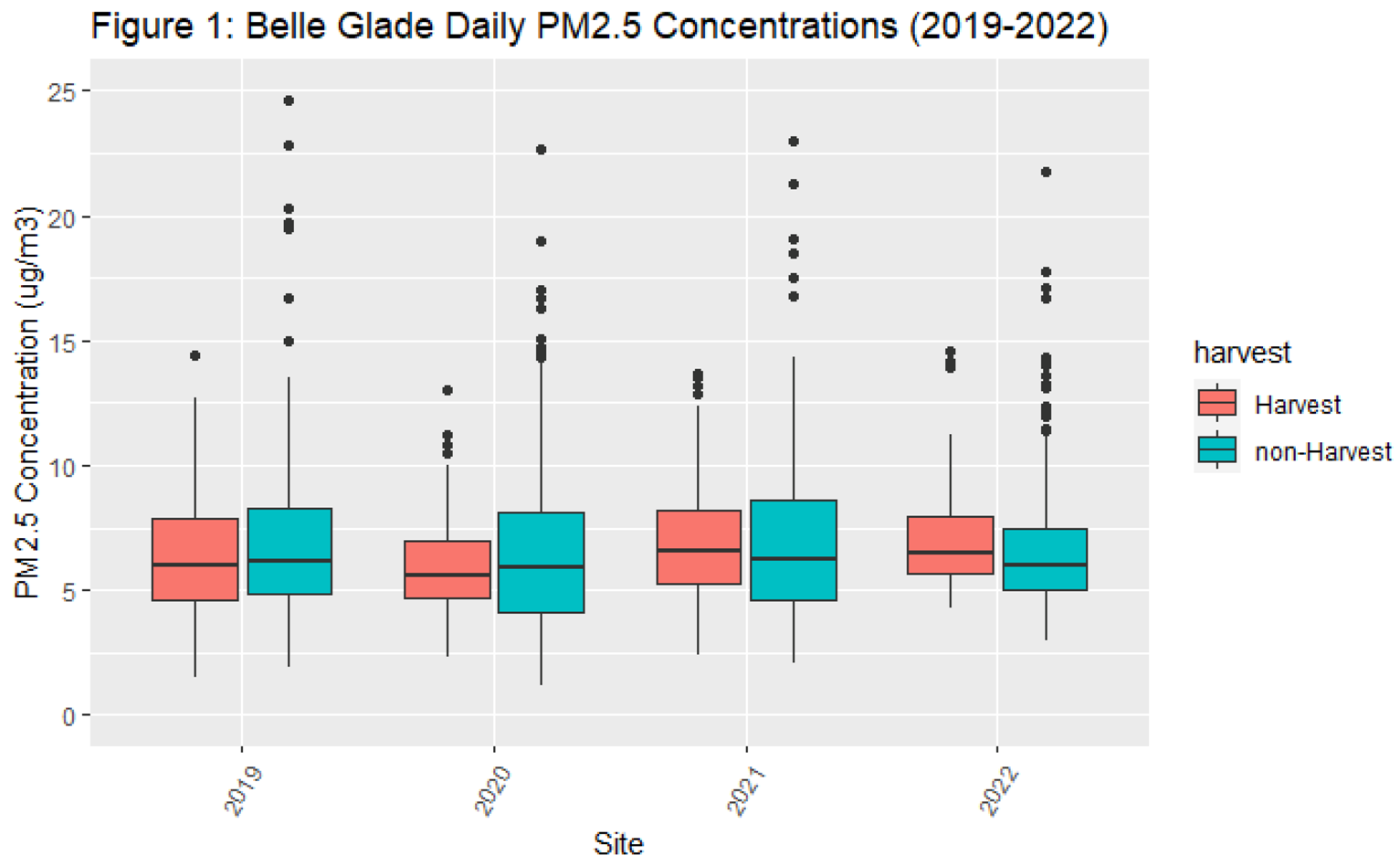
  • While the authors’ publication was submitted in 2022, the dataset they relied upon only spanned from 2009 to 2018. According to the authors, their analysis did not extend beyond 2018 because the satellite-derived PM2.5 data was not available (Holmes and Nowell, 2023). Figure 1 presents the data the authors excluded from 2019-2022 that shows some years’ PM2.5 concentrations are lower during harvest compared to non-harvest season, contradicting their conclusion.
  • The authors’ use of an unpaired t-test was inappropriate to compare harvest versus non-harvest PM2.5 concentrations since the data used in the t-test are not independent—a requirement for conducting a t-test. At a minimum, such an evaluation requires use of a regression that accounts for yearly fixed effects and clustered standard errors. When using the full dataset from 2009-2022 and clustering standard errors at the month level, there was a statistically insignificant difference at Belle Glade (95% CI: -0.99, 0.25; p = 0.24). Further, adding a fixed effect for the year variable did not substantially change the results (95% CI: -0.99, 0.25; p = 0.25).
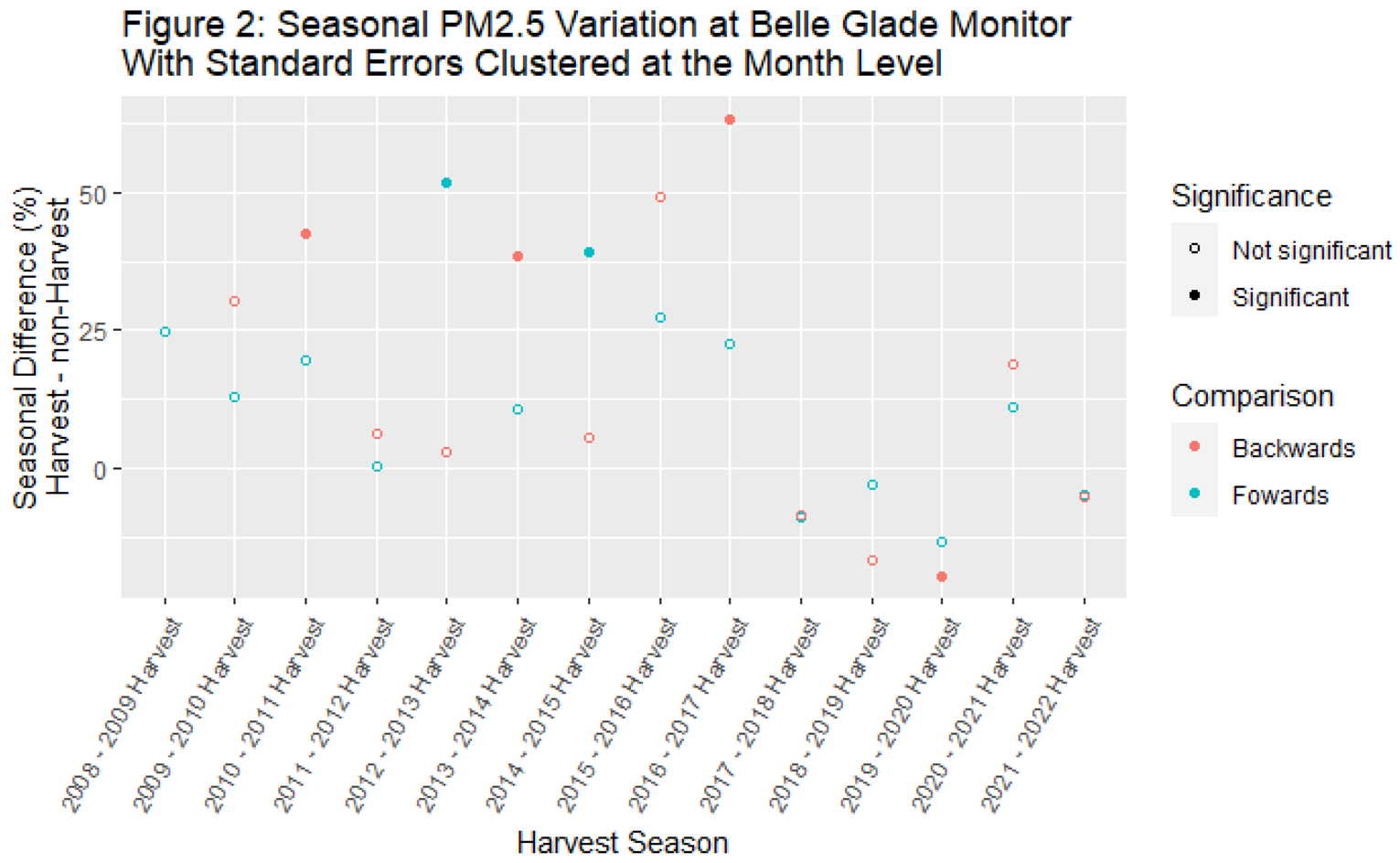
  • We further evaluated the data by evaluating concentrations in neighboring seasons on a year-by-year basis. We compared the mean concentration in each harvest season with the mean concentration in the previous non-harvest season (“backwards” analysis) and the following non-harvest season (“forwards” analysis). We conducted this analysis clustering standard errors at the month level. We log-transformed the concentration data for these analyses. Regression coefficients were transformed to be interpreted as percent increases and are shown in Figure 2.
  • When clustering standard errors, no harvest season had PM2.5 concentrations that were significantly greater than both the preceding non-harvest season and the following non-harvest season. For example, during the 2012-2013 harvest season, mean PM2.5 concentration was greater than the 2013 non-harvest season. But the 2012-2013 harvest season mean PM2.5 concentration was no different from the 2012 non-harvest season mean PM2.5 concentration. Since the 2017-2018 harvest season, mean concentrations during the harvest season have more often than not been lower than mean concentrations during the preceding and following harvest seasons.
Preprints 69228 i001
Preprints 69228 i002

2.3. Discussion:

The authors state “Only two sites in South Florida—Belle Glade and Royal Palm Beach— measured higher mean PM2.5 in winter, which is the sugarcane harvest and prescribed fire season.” In fact, other cities in the region have marginally increased PM2.5 concentrations during harvest season: Winter Park (seasonal difference 0.04 µg/m3) and Sydney (seasonal difference 0.25 µg/m3). Also worth noting is that the absolute concentration of PM2.5 during harvest for 2009-2022 in Belle Glade (7.49 µg/m3) and Royal Palm Beach (6.25 µg/m3) is lower than the annual average PM2.5 concentration in other cities throughout the region: Naples (8.17 µg/m3), Sydney (7.76 µg/m3), Tampa (9.13 µg/m3).
There is no consistent pattern of elevated PM2.5 concentrations during harvest compared with the previous and subsequent non-harvest time periods. Therefore, there is no way to group data into harvest vs. non-harvest season and conclude that any systematic PM2.5 concentration differences are a result of sugarcane harvesting. Holmes and Nowell (2023) point out that the lack of consistent pattern comparing harvest and non-harvest seasons is due to summer wildfires, which further underscores that attributing any marginal PM2.5 difference between seasons to sugarcane harvest is not appropriate or scientifically supported. There are multiple potential unaccounted for factors and sources that confound the alleged relationship between harvest season and PM2.5 concentrations.
The comparison of harvest seasons and neighboring non-harvest seasons does not adjust the threshold for statistical significance (p=0.05), despite consisting of about two dozen statistical tests. Conducting such a number of tests means there is likely to be at least one false positive. However, the lack of consistent directional effects, whether they are significant or not, contradicts the authors’ harvest vs. non-harvest season analysis and conclusions.

3. Air Modeling Critique

3.1. Nowell et al. (2022) Background

The authors used the Hybrid Single Particle Lagrangian Integrated Trajectory model (HYSPLIT) to estimate the contribution of sugar cane fires to annual mean PM2.5 concentrations for selected cities in South Florida. The authors report that the model results suggest that sugarcane fires contribute an additional 0.65 µg/m3 (95% CI: 0.57, 0.73) of PM2.5 to the annual mean concentration in Belle Glade. It is important to understand though that the authors’ model results of 0.65 µg/m3 were inappropriately calibrated to match the authors’ reported seasonal difference in PM2.5 observed from 2009-2018 – which was not statistically significant.
Additionally, the authors’ application of the HYSPLIT model for PM2.5 has a spectrum of technical issues associated with the use of fire data, plume rise models, sugarcane emission factors, sugarcane loading factors, and secondary particle formation factors. These technical issues result in biased results and overly confident confidence intervals.

3.2. Fire Data

Fire area uncertainty:
The article acknowledges uncertainty in fire area in two ways, but ultimately does not quantitatively build this uncertainty into the model.
  • The authors cite Nowell et al. (2018) [7] in a discussion of uncertainty of fire area inputs and indicate that open burn authorization (OBA) data and actual observations differ by <10% overall and by up to 20-40% for individual fires. Nowell et al. (2018) was not an analysis of sugarcane fires; therefore, its relevance to the matter at hand is questionable, and at a minimum increases the uncertainty associated with extrapolation of the data from that study. However, the authors do not quantitatively incorporate any uncertainty in fire area into its analysis: the OBA fire area data is utilized at face value.
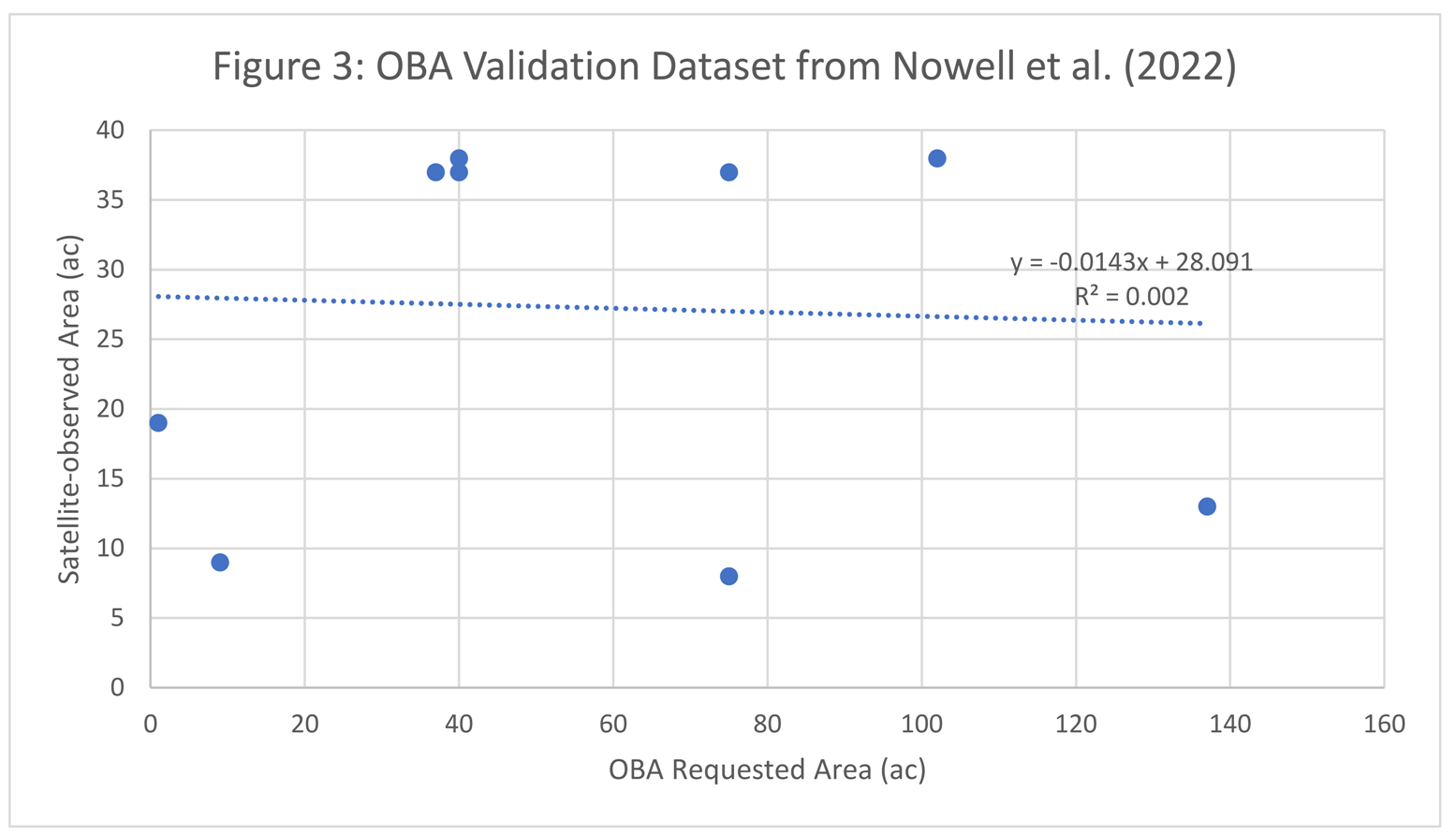
  • The authors compare a random sample of 10 sugarcane OBAs with satellite imagery. It is unclear why the authors relied on satellite imagery for this check, given that, “satellites detect only 25% of open biomass fire area” (Nowell et al., 2018). Nevertheless, the authors imply that there is adequate agreement between the OBA data and the satellite data by stating that they, “found a median area discrepancy of just [emphasis added] 2.5 acres (ac) or 6%.” Roux has confirmed this median calculation. However, the average discrepancy was 28 acres or 77%. Roux also found no statistical relationship between the OBA data and the satellite data (as seen in Figure 3).
Fire area point estimates:
In its discussion of fire area uncertainty, the authors state there is good agreement between OBA areas and actual observations, citing Nowell et al. (2018), but in fact Nowell et al. (2018) found that “fires are typically a little smaller than requested.” Therefore, reliance on OBA data is expected to bias the fire area data high.
Fire location uncertainty:
The article makes no attempt to characterize uncertainty in the location of each fire. Nowell et al. (2018) found that actual fires were typically about 0.7-0.8 km away from the requested OBA fire and that 50-98% of OBA fire point locations were outside the actual fire perimeter.
Preprints 69228 i003

3.3. Plume Rise Models

Estimating the release height or plume rise is an important aspect of HYSPLIT modeling. [8,9]
In general, HYSPLIT model results are very sensitive to smoke release height (i.e., plume rise), and the final outputs are therefore dependent on how plume rise is characterized (Stein et al., 2009).
However, accurately estimating plume rise “depends on many factors that may never be known with sufficient accuracy to estimate the smoke plume heights using only numerical modeling techniques. Further methods may need to rely more heavily on satellite observations” (Stein et al., 2009).
The authors rely on numerical methods to generate point estimates, and they then rely on a range of correction factors to adjust those estimates.
The correction factors are derived from a comparison of empirical data from seven smoke plumes identified via MISR satellite from 2005 to 2009 and three numerical methods (i.e., the Surface, Uniform, and Briggs methods) based on a January 2012 simulation.
The authors use seven plumes to characterize approximately 70,000 plumes over a seven-year period (i.e., 10,000 fires/year from 2012-2018). The article does not indicate how the seven smoke plumes identified via MISR satellite were selected for analysis, the extent to which they are representative, or the weather conditions during which they occurred.
These plumes were not selected randomly, and any data generated from these data are therefore subject to sampling bias.
Given that plume rise depends on many factors (such as fire heat release rate, atmospheric stability, wind speed, size of the burn, shape of the burn area, moisture, loading, distribution of the fire on the landscape, and amount of fire on the landscape), [10,11,12,13] data from seven observed plumes could not adequately characterize uncertainty and variability across an expected range of conditions.
Thus, uncertainty in the plume rise portion of the modeling is significant.

3.4. Sugarcane Emission Factors

The article cites the following emission factors from McCarty (2011): 4.35 g/kg (range 3.9–4.99 g/kg). [14] These emission factors reflect the values in Table 2 from McCarty (2011) and represent central estimates that McCarty (2011) obtained from the literature.
McCarty (2011) presents as its conclusion the emission factors reflected in Table 1 from McCarty (2011). These emission factors reflect the full extent of uncertainty in the emission factors and are 4.35 g/kg with a standard error 0.57. Using the appropriate McCarty (2011) emissions factor conclusion would instead result in a 95% confidence interval range of 3.23-5.47 g/kg.
The use of incorrect confidence interval from McCarty’s (2011) emission factors also results in the authors overestimating the confidence intervals in the model outputs.
The authors’ model uses a uniform distribution of emission factors. The use of the uniform distribution from 3.9-4.99 g/kg results in the authors overriding the given central estimate of 4.35 g/kg (inflating it to about 4.46 g/kg), thereby biasing the central estimate model outputs high by about 3%.

3.5. Sugarcane Loading Factors

The article cites the following emission factors from McCarty (2011) and Pouliot et al. (2017): 10,648 kg/ha (range 8,967–15,692 kg/ha). [15] Roux verified the central estimate in Pouliot et al. (2017) but was unable to verify the range.
A range of sugarcane loading factors are used to generate a range of model uncertainty in the PM2.5 concentrations resulting from harvesting. Even if the authors’ range were correct, their application of that range as a uniform distribution is inappropriate because it overrides the given central estimate (10,648 kg/ha) and inflates it to about 12,330 kg/ha, thereby biasing the central estimate of the model outputs by about 15%.

3.6. Secondary particle formation factors

HYSPLIT model outputs are multiplied by a factor with a uniform distribution of 1 (i.e., no secondary particle formation) to 2 as a representation of secondary particle formation. Therefore, on average, the secondary particle formation factor is equal to 1.5.
This range is supposedly obtained from peer-reviewed literature; however, the article’s interpretation of the literature is incorrect. The authors cite seven articles to justify their PM2.5 secondary particle formation factor. [16,17,18,19,20,21,22] However, only one of these articles (Yokelson, et al, 2017) provides a PM2.5 secondary particle formation factor. The site conditions from Yokelson et al. (2017) do not reflect sugarcane harvest nor Florida air quality conditions, but instead only the condition of crop residue biomass burning in the Yucatan. Given that secondary particle formation is an atmospheric chemistry process, expected differences in source emissions chemistry and atmospheric conditions contributes significant uncertainty into the authors’ evaluation.
The authors also selected these particle formation factors because they “resulted in dispersion modeling data commensurate with surface monitor observations” (Nowell et al., 2022). From a modeling perspective, it is inappropriate to use secondary particle formation as a knob to turn in order to scale up the model outputs to match an erroneous a priori assumptions about PM2.5 during sugarcane harvest.

References

  1. Shapero, A.; Keck, S.; Goswami, E.; Love, A.H. Comment on “Impacts of Sugarcane Fires on Air Quality and Public Health in South Florida”. Environ. Health Perspect. 2022, 131, 028001. [Google Scholar] [CrossRef] [PubMed]
  2. Nowell, H.K.; et al. Impacts of sugarcane fires on air quality and public health in south Florida. Environ. Health Perspect. 2022, 130, 087004. [Google Scholar] [CrossRef] [PubMed]
  3. Holmes, C.D.; Nowell, H.K. Response to “Comment on ‘Impacts of Sugarcane Fires on Air Quality and Public Health in South Florida’”. Environ. Health Perspect. 2023, 131, 028002. [Google Scholar] [CrossRef] [PubMed]
  4. EPA. AirNow.gov - Home of the U.S. Air Quality Index. Year 2009 through September 2022. Available online: https://www.epa.gov/outdoor-air-quality-data/download-daily-data.
  5. EPA. What does the POC number refer to? Available online: https://www.epa.gov/outdoor-air-quality-data/what-does-poc-number-refer#:~:text=POC%20is%20the%20Parameter%20Occurrence%20Code%20and%20is,and%20monitor%20type%20are%20independent%20of%20each%20other.
  6. EPA. AQS Memos–Technical Note on Reporting PM2.5 Continuous Monitoring and Speciation Data to the Air Quality System (AQS). Available online: https://www.epa.gov/aqs/aqs-memos-technical-note-reporting-pm25-continuous-monitoring-and-speciation-data-air-quality.
  7. Nowell, H.K.; Holmes, C.D.; Robertson, K.; Teske, C.; Hiers, J.K. A new picture of fire extent, variability, and drought interaction in prescribed fire landscapes: insights from Florida government records. Geophys. Res. Lett. 2018, 45, 7874–7884. [Google Scholar] [CrossRef] [PubMed]
  8. Draxler, R.R.; Hess, G.D. An overview of the HYSPLIT_4 modelling system for trajectories, dispersion and deposition. Aust. Meteorol. Mag. 1998, 47, 295–308. [Google Scholar]
  9. Stein, A.F.; et al. Verification of the NOAA Smoke Forecasting System: Model Sensitivity to the Injection Height. Weather Forecast. 2009, 24, 379–394. [Google Scholar] [CrossRef]
  10. Stein, A.F.; et al. Verification of the NOAA Smoke Forecasting System: Model Sensitivity to the Injection Height. Weather Forecast. 2009, 24, 379–394. [Google Scholar] [CrossRef]
  11. Achtemeier, G.L.; Goodrick, S.A.; Liu, Y.; Garcia-Menendez, F.; Hu, Y.; Odman, M.T. Modeling smoke plume-rise and dispersion from Southern United States prescribed burns with Daysmoke. Atmosphere 2011, 2, 358–388. [Google Scholar] [CrossRef]
  12. Liu, Y.; Achtemeier, G.L.; Goodrick, S.L.; Jackson, W.A. Important parameters for smoke plume rise simulation with Daysmoke. Atmos. Pollut. Res. 2010, 1, 250–259. [Google Scholar] [CrossRef]
  13. Val Martin, M.; Logan, J.A.; Kahn, R.A.; Leung, F.-Y.Y.; Nelson, D.L.; Diner, D.J. Smoke injection heights from fires in North America: analysis of 5 years of satellite observations. Atmos. Chem. Phys. 2010, 10, 1491–1510. [Google Scholar] [CrossRef]
  14. McCarty, J.L. Remote sensing-based estimates of annual and seasonal emissions from crop residue burning in the contiguous United States. J. Air Waste Manag. Assoc. 2011, 61, 22–34. [Google Scholar] [CrossRef] [PubMed]
  15. Pouliot, G.; Rao, V.; McCarty, J.L.; Soja, A.J. Development of the crop residue and rangeland burning in the 2014 national emissions inventory using information from multiple sources. J. Air Waste Manag. Assoc. 2017, 67, 613–622. [Google Scholar] [CrossRef] [PubMed]
  16. Fang, Z.; Deng, W.; Zhang, Y.; Ding, X.; Tang, M.; Liu, T.; et al. Open burning of rice, corn and wheat straws: primary emissions, photochemical aging, and secondary organic aerosol formation. Atmos. Chem. Phys. 2017, 17, 14821–14839. [Google Scholar] [CrossRef]
  17. Liu, X.; Zhang, Y.; Huey, L.G.; Yokelson, R.J.; Wang, Y.; Jimenez, J.L.; et al. Agricultural fires in the southeastern U.S. during SEAC4RS. J. Geophys. Res. Atmos. 2016, 121, 7383–7414. [Google Scholar] [CrossRef]
  18. Vakkari, V.; Kerminen, V.; Beukes, J.P.; Tiitta, P.; Zyl, P.G.; Josipovic, M.; et al. Rapid changes in biomass burning aerosols by atmospheric oxidation. Geophys. Res. Lett. 2014, 41, 2644–2651. [Google Scholar] [CrossRef]
  19. Ahern, A.T.; Robinson, E.S.; Tkacik, D.S.; Saleh, R.; Hatch, L.E.; Barsanti, K.C.; et al. Production of secondary organic aerosol during aging of biomass burning smoke from fresh fuels and its relationship to VOC precursors. J. Geophys. Res. Atmos. 2019, 124, 3583–3606. [Google Scholar] [CrossRef]
  20. Cubison, M.J.; Ortega, A.M.; Hayes, P.L.; Farmer, D.K.; Day, D.; Lechner, M.J.; et al. Effects of aging on organic aerosol from open biomass burning smoke in aircraft and laboratory studies. Atmos. Chem. Phys. 2011, 11, 12049–12064. [Google Scholar] [CrossRef]
  21. Yokelson, R.J.; Crounse, J.D.; DeCarlo, P.F.; Karl, T.; Urbanski, S.; Atlas, E.; et al. Emissions from biomass burning in the Yucatan. Atmos. Chem. Phys. 2009, 9, 5785–5812. [Google Scholar] [CrossRef]
  22. Vakkari, V.; Beukes, J.P.; Dal Maso, M.; Aurela, M.; Josipovic, M.; van Zyl, P.G. Major secondary aerosol formation in Southern African open biomass burning plumes. Nature Geosci. 2019, 11, 580–583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated