Prerpints.org logo
Preprint
Article

Improving the Fatigue Design of Mechanical Products Such as Bearings Based on a (Generalized) Life-Stress Prototype and Sample Size

Altmetrics

Downloads

155

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 February 2023

Posted:

28 February 2023

You are already at the latest version

Alerts
Abstract
To prolong the fatigue life of a product handled by machine, parametric accelerated life testing (ALT) is mentioned as an organized technique to pinpoint design flaws and minimize fatigue-connected failures. It requires (1) an ALT procedure, (2) fatigue model, (3) parametric ALTs with adjustment, and (4) an approximate of whether present product complete the BX life. The use of a quantum-transported time-to-failure archetype and a sample size are advised. The improvements in the reliability of a refrigerator ice-maker, comprising an auger motor with bearing, were utilized as a case investigation. In the 1st ALT, a steel rolling bearing cracked due to repeated loads under cold circumstances (below −20 C) in the freezer compartment. The bearing was altered by adjusting the matter from AISI 52100 alloy steel with 1.30-1.60% chromium to lubricated sliding bearing with sintered and hardened steel (FLC 4608-110HT) because of its high fatigue strength at lower temperatures. In the 2nd ALT, a helix made of polycarbonates (PCs) fractured. As an adjustment, a reinforced rib of the helix was thickened. As no troubles in the 3rd ALT occur, the lifetime of an ice-maker was proved to be B1 life 10 years.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

To have good qualities competitive with rival companies in the market, mechanical systems such as refrigerators shall be enhanced with new scientific knowledge and performance to satisfy the desires of purchaser. If these new attributes are supplied to the field with insufficient testing, there is the possibility for early failure of these new properties. These untimely failures undesirably influence the recognition of the aspect of the products. To avoid discovering unanticipated design defects in the market, the new attributes for a product should be judged in the development process before being launched into the end-user. Assessing the reliability of a new mechanical system should include a systematic method with reliability quantitative (RQ) specifications [1].
Achieving decreasing speed through several gears engaged with a driving gear mounted in the shaft, an ice-maker including auger motor with bearing is designed to attain a sufficient torque that can squash the through a large torque. Under the low temperature condition (-20°C↓) in the freezing compartment, the auger motor is subjected to repeated stresses supported by bearings. A common material utilized in ball bearing rings is the alloy steel AISI 52100 because it is effortlessly forged, heat treated, and machined. To stop the cancellations of mechanical systems from the market which have structural imperfections [2-5], it might be designed to outlast the normal functioning circumstances executed by customers who acquire and utilize the product.
For example, after 346 passengers died in a crash, the Boeing 737 MAX airline from March, 2019 to December, 2020 was prohibited from flying. The airplane used the CFM International LEAP-1B engines adopting the most effective 68-inch fan design. They were 12% more fuel efficient and 7% lightweight than previous engine [6]. Inspectors had conjectured that the accident was produced by the engine in the aircraft. As a result, the whole economy experiences the elimination of lots of parts (or wastes) due to improper design. Possible troublesome components thus need to be confirmed by laboratory testing that shall cause reliability quantitative (RQ) expression [7-9].
Fatigue is the main origin of metallic failure in structural elements, elucidating more or less 80–95% of all failures [10]. It displays itself in the form of cracks which usually start from stress raisers, such as holes, edges, slender surfaces, grooves, etc., on the structure of systems. Fatigue is the withering of a matter that is frequently produced by cyclic loading. Notable concern concentrates on the (low-cycle) fatigue of components, specifically in the area of turbine–engine that is nickel-built polycrystalline matter [11,12]. It is also measured as a quantity element, such as the stress proportion, R (=σmin/σmax), which shall be explained as the correlation of the greatest cyclic stress to the least cyclic stress [13]. Utilizing a stress proportion, R, which shall be presented in an ALT, shall identify the design defects in the mechanical system.
Designers have frequently recognized design imperfections and have fixed them by utilizing technique such as Taguchi’s method [14]. Especially, design of experiments (DOE) [15] is an organized method to decide the connection between the factor affecting a procedure and its production. The aim is to secure that the factors are placed in the most successful manner for functioning (or environmental) situations. DOE is executed for related factors which influence the product designs. Their functionality is revealed by analysis of variance (ANOVA). Because a person who operates DOE may not know which factors are the most influential in a failure, there is no fatigue failure in the process to be followed in calculations. Thus, DOE may require a large number of mathematical calculations and may not identify a potential source of failure.
Designers have frequently utilized the strength of materials as a solution to conventional design [16-18]. A crucial element in fracture mechanics [19] is the toughness as a material attribute of strength. With the implementation of quantum mechanics, engineers have pinpointed that structural failures occur from nanoscale or microscale voids, which may occur in metallic alloys or engineering plastics. As finite samples and limited testing periods are utilized [20,21,22,23,24], this method cannot reproduce the design flaws in a complex form or identify the fatigue problem which occurs to the elements by consumer in the market. To identify the fatigue phenomena in a system functioned by machine, a life-stress type [25,26] can be integrated with a (quantum) mechanics way to distinguish a prevailing defect or crack form in matter because unsuccessfulness stochastically happens in the region of particularly big stress.
The finite element method (FEM) [27] is utilize as different way. Designers think that failures may be determined by (1) an appropriate mathematical (Lagrangian or Newtonian) formulation; (2) deriving the time response for (dynamic) loads, which generates the stress/strain on the part structure; (3) employing the generally accepted way of rain-flow counts with von Mises stress [28]; and (4) evaluating system effectiveness by Palmgren–Miner’s principle [29]. Deploying this methodology shall give closed-formation answers. However, this method cannot pinpoint fatigue failures in a complex system produced by structural defects such as micro-voids, sharp edges, slender surfaces, contacts, etc.
This investigation proposes parametric ALT as a straightforward way that can be employed to identify structural flaws of a new product and improve them. It involves the following: (1) a parametric ALT plan developed on BX life, (2) load study, (3) ALTs with the structure modifications, and (4) an appraisal of whether the system structure fulfills the objective BX life. This procedure for recognizing the root causes and enhancing design examines properness in the mechanical system such as appliance, automobile, airplane, etc. The quantum-transported failure type and sample size also are advocated. A new refrigerator ice-maker involving an auger motor with a bearing is deployed to explain it.

2. Parametric ALT for a System functioned by machine

2.1. Meaning of BX life

Product operated by machine utilizes (generated) power to achieve a desired motion by adapting an appropriate mechanism [30]. Forces are utilized to supply movement of mechanisms in the system. This movement signifies that the system shall be subjected to repeated loads. In a mechanical product, fatigue falls when there are structural imperfections such as notches, sharp-edged, grooves, slender surfaces, etc., in a component.
For instance, a refrigerator uses the heat pump cycle that consists of condenser, capillary tube, evaporator, and compressor. In a heat exchanger, chilled air is generated so that it keeps not having decayed for the food in the refrigerator and freezer sections. Figure 1 manifests that a refrigerator covers some complete subsystems (or modules) – the cupboard and door, shelves and boxes, compressor or (electric) motor, evaporator and condenser, water supplying and ice-maker apparatus, controller, and diverse parts. A domestic refrigerator includes the same number of 2000 elements. It can be divided into up to 20 units (or 8~10 modules) possessing roughly 100 elements.
As the objective of system life is presumed to have B20 life 10 years, the lifetime objective of all units should have B1 life 10 years. As a new subsystem, named Module #3 in Figure 2, has a design flaw, it resolves the lifetime of the total refrigerator.
BX lifetime, LB, could be explained as a quantity of lifetime that X percent of the population has been unsuccessful. ‘BX life Y years’ therefore is a further reasonable clause. That is, as the life of a mechanical part is B20 life 10 years, 20% of the concern parts shall have been failed for ten-year. Otherwise, as the reverse of the failure rate, the B60 life, denoting the mean time to failure (MTTF), might not be utilized for system lifetime as it is too lengthy for 60% of system to be unsuccessful. BX lifetime shall assign an acceptable indicator for system life.

2.2. Posing an Entire ALT procedure

Reliability might be defined as the potential to function under a set of prescribed operational/environmental circumstances for a required period of time [31]. It is mainly demonstrated as bathtub curve, having three divisions. They may be expressed in accordance with the shape parameter in the Weibull chart. In the 1st division, there is a declining rate of failure in the premature section of the system’s life (β < 1). In the 2nd division, there is a uniform rate of failure (β = 1) in the medium lifetime of the system, pursuing an exponential distribution. Finally, there is a growing rate of failure to the ending of the product life (β > 1), which pursuits a Weibull distribution (Figure 3).
The reliability function, R ( t ) , is R ( t ) = 1 − F ( t ) ( o r   X ) . The unreliability or accumulative distribution function (CDF), F ( t ) ( o r   X ) = 1 − R ( t ) , is expressed by
F ( t ) = P ( T < t )
On the (slanted) bathtub in Figure 3, the failure rate, λ, shall be defined as:
λ ( t ) = f ( t ) / R ( t ) = d F ( t ) / d t R ( t ) = ( 1 − R ( t ) ) ' R ( t ) = − R ′ ( t ) R ( t )
where f is the failure density function.
If Equation (2) takes the integral, the life of X% cumulative failure, F(LB), at t = LB may be assessed. F(LB) shall be expressed:
F ( t ) = ∫ ​ λ ( t ) d t = − ln R ( t )
Or   A ( o r   X ) = λ ⋅ L B = ∫ 0 L B λ ( t ) ⋅ d t = − ln R ( L B ) = − ln ( 1 − F ) ≅ F ( L B )
As T1 is presumed to have the period of the 1st failure in the 2nd division of the (slanted) bathtub, reliability, R(t), shall be expressed:
R ( t ) = P ( T 1 > t ) = P ( no   failure   in   ( 0 , t ] ) = ( m ) 0 e − m 0 ! = e − m = e − λ t
As the failure rate of a system mimics the features on the (slanted) bathtub curve (Stage Ⅰ or Ⅱ), it shall be unsuccessful in the marketplace. Due to design flaws, the huge number of premature failures in the early part of the curve could spoil the brand name of the company with the product release. High failure rates in the initial product lifetime require warranty costs on the manufacturer, and market share would be anticipated to be negatively affected. The company would be required to enhance the system by (1) abolishing unpredicted premature failures, (2) lessening (random) failures for its function time, and (3) growing the product life.
As a structural design is enhanced, the system lifetime from the market should increase, and its failure rate should decrease. In a situation, the (slanted) bathtub might be altered to a curve with low failure rates and a long lifetime. Eventually, if the system is competently made, the accumulative failure rate, F(t), is improved till the useful life is fulfilled. The product’s bathtub shall be similar to the straight line categorized the “Hockey stick line” (stageⅠ→ Ⅲ) in Figure 3.
In Equation (5), the product reliability is simply expressed as the failure rate,   λ , and lifetime, L B . Namely,
R ( L B ) = 1 − F ( L B ) = e − λ L B ≅ 1 − λ L B
This correlation is adequate and less than just about 20% of the cumulative failure rate [32].
As an instance, an ice maker repetitively demands a straightforward mechanical operation: (1) water is provided to the flat and shallow container; (2) it then solidifies into ice by cooled air being blown over it; and (3) it is then harvested till the ice container is filled. Ice is retrieved by the consumer when the end-user applies force on a lever that allows the cubed (or crushed) ice to dispense. During the process, an ice-maker shall be subjected to repeated stresses. Failed parts from the field are decisive for comprehending and pinpointing the repetitive usage methods of end-users and picking out structural imperfections in the structure. From the marketplace statistics, the real cause(s) of the troublesome auger motor, including the bearing, was recognized. As setting the objective life, LB, by employing an ALT, the part functioned by machine shall be altered by pinpointing the controversial component and improving it (Figure 4).
From the market statistics – present lifetime and failure rate – the real cause(s) of the troublesome ice-maker failed from the end-user had been plainly recognized. To fulfill the desirable reliability from the objective life, LB, and failure rate, λ, the possible design flaws of the component might be found and altered by utilizing an ALT.
To reach the target of a product life by ALT, three subsystems (or modules) were classified: (1) a modified system, (2) a newly designed system, and (3) the same system. The subsystem such as ice-maker in a household refrigerator utilized as a test investigation here was a system which had design flaws to be corrected. End-users had been demanding for substitutions which had been failing too soon before the anticipated life of the system. System D (Table 1) from the field statistics had a failure rate of 0.20% per year and a B1 life 5.0 years. To reply to end-user appeal, an objective life for the ice maker was specified to be B1 life 10 years.

2.3. Deduction of Life-Stress Model

As a customer has a desire to have (cubed or crushed) ice, new function such as an ice-maker is included in a household refrigerator. The major components are the geared auger motor, helix support, bucket case, helix upper dispenser, blade, etc. An auger motor has two or more gears working together by interlocking their teeth and revolving each other to produce torque and speed. As motors are employed, the geared trains lessen the speed of the augers and grow torque. Namely, the auger motor operated by alternating current (AC) grows the torque by gearbox to crush it at the end of an ice-maker. As a consumer pushes the lever with a cup on the dispenser, (cubed/crushed) ice flows to fill the cup. Consequently, the ice maker shall be subjected to repeated stresses due to loading/unloading in the process of crushing ice. If there are structural flaws, such as an inadequate strength to withstand repeated loads, the ice-maker can be successful before satisfying its targeted life. That is, failure happens when the materials in the system parts are too fragile to withstand the exerted stress under environmental circumstance [33].
As reproducing the field failures by ALT, an engineer must understand and quantify the loading that is encountered by the ice maker in the field before designing the system shape and materials to achieve the objective reliability of the system. Once optimally redesigned, the product might be anticipated to endure the minimum repeated loading in its expected life so that it may extend the targeted life. From the relation between load and lifetime, the (generalized) life-stress prototype that will integrate with geometry and material as design solution should be derived, which can be described by the phenomena of void generation/transport from the level of quantum mechanics. Eventually, cracks and their propagation might be described by a sample size formulation (Figure 5).
The motivation for ALT is to resolve how premature the anticipated failure mode might be pinpointed by mathematically employing the work for parametric modeling. That is why elevated tests need to be carried out. To depict the elevated testing time into actual usage time, it is requisite to arrange a straightforward failure expression and resolve the correct numerical method for the life type. The life-stress (LS) type, which requires quantifiable stresses and reaction factors, should be developed. Thus, it will express mechanical failure, such as structural fatigue. Fatigue on the surface of a structure can occur not only due to component stresses but also due to defects such as cracks.
It is presumed that fatigue shall arise from structural defects—electron/void—which appear in a Nano-range or microscopic. Think about a particle which is restrained to move only in the x orientation from x = 0 to x = a. The (potential) energy,   V ( x ) , shall be expressed:
V ( x ) = { 0   ( 0 ≤ x ≤ a ) ∞   ( x 〈 0   o r   x 〉 a )
The Schrodinger governing equation shall be defined:
H ^ ψ = E ψ
where H ^ is the Hamiltonian operator, ψ is the wave function, and E is the (electron) energy.
If H ^ = − h 2 8 π 2 m d 2 d x 2 + V in Equation (8), it shall be set as follows,
d 2 ψ d x 2 + 8 π 2 m h 2 ( E − V ) ψ = 0
where h is the Planck constant and m is the electron mass.
As V = ∞ at the wall exteriors, it is feasible when ψ = 0 . Electron is not at the wall exteriors. As V = 0 at the wall interiors, Equation (9) shall be expressed:
d 2 ψ d x 2 + K 2 ψ = 0
where K 2 = 8 π 2 m E h 2
The answer in Equation (10) shall be presumed:
ψ ( x ) = A s i n K x + B c o s K x
where A and B are constant
As x = 0 or x = a at the barriers, ψ(0) = ψ ( a ) = 0 , B = 0, K = n π a , and E = n 2 h 2 8 m a 2 , n = 1,2,3,4
Thus, Equation (11) shall be expressed:
ψ ( x ) = A s i n ( n π a ) x
The chance of discovering the electron in a limited room between x and x + dx is expressed:
∫ 0 a ψ 2 ( x ) d x = 1   or   ∫ 0 a ( A s i n ( n π a ) x ) 2 d x = 1
Thus, the answer of Equation (12) shall be attained:
ψ ( x ) = 2 a s i n ( n π a ) x
where ψ ( x + a ) = ψ ( x ) , a is the (periodic) interval, and n is the main quantum number.
The transport diffusion procedure can be expressed (Table 2) [34,35]:
J = L D
where J is the diffusion flux, D is the driving force, and L is the transport quantity.
In particular, as an electromagnetic force, ξ, is exerted, the metal impurities, caused by electronic motion, easily float to the right-hand as the magnitude of the junction energy is lowered. Expressing solid-state diffusion of impurities of silicon in a semiconductor can be shortened: (1) electro-migration-induced voiding; (2) build-up of chloride ions; and (3) trapping of electrons or holes. The transport diffusion process, J, might be defined as [36]:
J = [ a C ( x − a ) ] ⋅ exp [ − q k T ( W − 1 2 a ξ ) ] ⋅ v
= − [ a 2 ve − qw / kT ] ⋅ cosh qa ξ 2 kT ∂ C ∂ x + [ 2 ave − qw / kT ] C sinh qa ξ 2 kT
where A is constant, C is the concentration quantity, q is the amount of accumulated electrical energy, ν is the jump frequency, a is the atomic interval, ξ is the applied field, k is Boltzmann’s quantity, Q is the energy quantity, and T is the (absolute) temperature.
Unless the electric field is relatively small, i.e., ξ ≪ q a 2 k T , Equation (16) might be redefined as follows:
J = Φ ( x , t , T ) sinh ( a ξ ) exp ( − Q k T ) = B sinh ( a ξ ) exp ( − Q k T )
where Q is the energy, Φ() & B are constant.
On the other hand, the chemical process which relies on speed shall be expressed as
K = K + − K − = a k T h e − Δ E − a S k T − a k T h e − Δ E + a S k T = A sinh ( a S ) exp ( − Δ E k T )
where K is the reaction speed, S is the (chemical) field result, E is the (activation) energy, Δ is the difference, and A is constant.
Equations (17) and (18) could be shortened as
K = B s i n h ( a S ) exp ( − Q k T )
If Equation (19) captures a reverted formulation, the life-stress (LS) type shall be clarified as:
T F = A [ sinh ( a S ) ] − 1 exp ( E a k T )
As a life-stress (LS) prototype, Equation (20) is clarified as a general expression because the sine hyperbolic expression [ sinh ( a S ) ] − 1 designating stress shall be exchanged into a power (or exponential) formulation. It then may outline most of the LS prototypes about some failure, such as fatigue in the system. It can be conveyed: (1) first, ( S ) − 1 has a nearly straight line, (2) second, ( S ) − n has what is viewed, and (3) third, ( e a S ) − 1 is largely developed (Figure 6).
Because ALT is frequently carried out in the span of midst stress, Equation (20) shall be expressed as:
T F = A ( S ) − n exp ( E a k T )
where n = − [ ∂ l n ( T F ) ∂ l n ( S ) ] T
For an expressed crack and structural form, Equation (21) can be redefined as
T F = B ( Δ K ) − n exp ( Q k T )
where B is constant, Δ K = Y S ( o r   Δ σ ) π a
As stress intensity factor, ∆K, is exerted on a material, the crack will produce to a specific amount ∆a, which relies on the crack growth speed, ∆a/∆N, in component shapes such as crack tip such as grooves, sharp-edged, slender areas, holes, etc. It therefore propagates to a risky magnitude. As loads are exerted till the targeted lifetime, LB or mission time, the stress raisers (or material) in a component can be discovered.
The stress of a product functioned by machinery is a complex quantity to formulate in a raised testing. Because the energy is clarified as the product of flow and effort, the stress comes from effort in an energy transport system [37]. Thus, Equation (21) or (22) can be stated as follows:
T F = A ( S ) − n exp ( E a k T ) = C ( e ) − λ exp ( E a k T )
where C is constant.
The acceleration factor (AF) is defined as the proportion between the raised stress and typical functioning situation. AF from Equation (23) shall be modified to merge the effort idea:
A F = ( S 1 S 0 ) n [ E a k ( 1 T 0 − 1 T 1 ) ] = ( e 1 e 0 ) λ [ E a k ( 1 T 0 − 1 T 1 ) ]

2.4. Obtaining of sample size formulation for ALT

To attain the desired mission time of ALT from the targeted BX lifetime on the testing plan, expressed in sections 2.1 and 2.2, the sample size formulation integrated with AF in section 2.3 might be derived.
Each testing time Bernoulli test has one of the pair yields, such as failure or success. The cumulative probability, which pursuits a binomial distribution, shall be defined:
L ( p ) = ∑ r = 0 c ( n r ) p r ⋅ ( 1 − p ) n − r ≤ α
where n is the sample amount and c is the presumed unsuccessful amount.
If chance p is minute and n is big enough, Equation (25), which pursues a Poisson distribution, will be redefined:
L ( n Δ p ) = ∑ r = 0 c 1 r ! ( n Δ p ) r ⋅ e − ( n p ) = ∑ r = 0 c 1 r ! m r ⋅ e − m ≤ α
where m = parameter = n Δ p .
As the p amount is α from Equation (26), parameter m pursuits the chi-square distribution, χ α 2 (). That is,
m = n Δ p ~ χ α 2 ( 2 r + 2 ) 2
The Weibull distribution for system lifetime is extensively employed because it is defined as an expression of the characteristic life, η, and shape parameter, β. Therefore, if the system pursuits the Weibull distribution, the accumulative failure rate, F(t), in Equation (1) is defined as
F ( t ) = 1 − e − ( t η ) β
where t is the (elapsed) time.
In the occasion of unreliability, p = F ( t ) , and reliability, 1 − p = R ( t ) , Equation (28) shall be placed into Equation (25). That is,
L ( p ) = ∑ r = 0 c ( n r ) ( 1 − e − ( t η ) β ) r ⋅ ( e − ( t η ) β ) n − r ≤ α
Because e − ( t η ) β ≅ 1 − ( t η ) β , Equation (29) can be closed as follows:
L ( p ) ≅ ∑ r = 0 c 1 r ! ( t η ) β r ⋅ ( 1 − ( t η ) β ) n − r ≤ α
As Equations (26) & (30) have a close shape, the characteristic life with a confidence level of 100 (1–α) may be clarified:
m = n · p = n · ( t η ) β ~ χ α 2 ( 2 r + 2 ) 2   o r   η α β = 2 χ α 2 ( 2 r + 2 ) ⋅ n ⋅ t β
At BX life, LB, in Equation (28), testing time, t, becomes h.
L B β ≅ x ⋅ η α β = x ⋅ 2 χ α 2 ( 2 r + 2 ) ⋅ n ⋅ t β = x ⋅ 2 χ α 2 ( 2 r + 2 ) ⋅ n ⋅ h β ≥ L B * β   for   x     0.2
where x = 0.01F(t)
If Equation (32) is reordered, the sample size expression is found as:
n ≥ χ α 2 ( 2 r + 2 ) 2 × 1 x × ( L B * h ) β
As the 1st term χ α 2 ( 2 r + 2 ) 2 in a 60% confidence level is approximated to (r + 1), Equation (33) shall be redefined as:
n ≥ ( r + 1 ) × 1 x × ( L B * h ) β
As AF in Equation (24) is replaced into the testing time, h, Equation (34) shall be redefined as:
n ≥ ( r + 1 ) × 1 x × ( L B * A F · h a ) β
where Equation (35) will be clarified as n ~ (failed samples + 1)·(1/cumulative failure rate)·((objective life/(test time)) ^ β.
Equation (35) shall be affirmed as [1,38]. Namely, for n ≫ r , the sample size shall be expressed as:
n = χ α 2 ( 2 r + 2 ) 2 m β l n R L − 1 = χ α 2 ( 2 r + 2 ) 2 × 1 l n ( l − F L ) − 1 × ( L B h ) β
where m ≅ h / L B
If the life objective of a system such as ice maker is presumed to have B1 life 10 years, the allocated test shall be computed for the assigned parts under raised circumstances. In performing parametric ALTs, the structural imperfections of a mechanical product will be found and altered to obtain the intended system life.

2.5. Case Investigation—Magnifying Lifetime of an Ice-Maker Incorporating Auger Motor with a Bearing in a Household Refrigerator

Because customers want to be the convenience of (cubed or crushed) ice being dispensed from a domestic refrigerator, an ice-making system was designed in a refrigerator. As a consumer utilizes a cup to apply force on the dispenser lever, (crushed or cubed) ice is distributed. The major parts are composed of an auger motor, incorporating a geared system and bearing, helix support, helix upper dispenser, etc. They are required to have high-strength fatigue because of the repetitive stresses under the consumer’s operation environment (Figure 7).
In ice-making, the parts undergo repeated mechanical loads and need to be strong enough to not fracture due to fatigue before the expected life. A household refrigerator in the United States is equipped to harvest ice at a rate of 10 cubes per usage and 200 cubes per day. Ice harvest may also be affected by individual end-user usage patterns, such as ice usage, (tap) water pressure, notch positions in refrigerators, and the cycles of doors opening. When set to the crushed mode, the ice-maker is repetitively subjected to (impact) loads in crushing ice. In the market, icemakers, including auger motors, were unsuccessful under unidentified consumer usage in a refrigerator. Field statistics also manifested that the ice makers returned from the market had structural defects such as material problems (high carbon alloy steel with 1.30-1.65% chromium) under the typical freezing temperatures (below –20 °C) found in the refrigerator. For the customer, the ice-maker system experienced a sudden failure and no longer functioned. Engineer was required to discover the basic causes by failure analysis (or laboratory test) and then modify the ice maker (Figure 8).
By utilizing failure analysis (and laboratory tests) for failed market parts, under typical freezer temperatures (below –20 °C), a crack began in the outer ring of the bearing and propagated to the end. To work it for its expected life, company should redesign the failed product such as bearing fractures in an auger motor. Namely, if there are structural defects — improper bearing material in the auger motor—where repeated loads are exerted in the freezer section, it will fail in its expected life. To reproduce the troublesome component(s) and modify them, a designer was required to perform ALT for a new product. It was made up of (1) a load inspection for the troublesome product (section 2.5), (2) the measures of taking the feasible and actual usage of ALTs with modifications (section 3), and (3) the appraisal of whether the life target of current structures (section 3) had been accomplished.
To attain the differential equations which is made up to state variables for the parametric prototype, the bond graph in Figure 9b shall be settled at each node:
d f × E 2 / d t = 1 / L a × e E 2
d f M 2 / d t = 1 / J × e M 2
where La is the electromagnetic inductance.
The junction from Equation (25) is
e E 2 = e a − e E 3
e E 3 = R a × f E 3
where ea is the exerted voltage and Ra is the (electromagnetic) resistance.
The junction from Equation (26) is
e M 2 = e M 1 − e M 3
e M 1 = ( K a × i ) − T P u l s e
e M 3 = B × f M 3
where B is the viscous friction constant and ka is the constant of the counterelectromotive force.
Because f M 1 = f M 2 = f M 3 = ω and i = f E 1 = f E 2 = f E 3 = i a from Equations (27) and (28),
e E 2 = e a − R a × f E 3
f E 2 = f E 3 = i a
If Equations (32) and (33) are substituted into Equation (25), then
d i a / d t = 1 / L a × ( e a − R a × i a )
From Equations (29)–(31), we can attain
e M 2 = [ ( K a × i ) − T L ] − B × f M 3
i = i a
f M 3 = f M 2 = ω
If Equations (35)–(37) are substituted into (26), then
d ω / d t = 1 / J × [ ( K a × i ) − T L ] − B × ω
From Equations (34) and (38), the state equations can be attained as follows:
[ d i a / d t d ω / d t ] = [ − R a / L a 0 m k a − B / J ] [ i a ω ] + [ 1 / L a 0 ] e a + [ 1 − 1 / J ] T L
As the differential equation in Equation (39) find the integral, the output harvested by the ice-maker is obtained as follows:
y p = [ 0    1 ] [ i a ω ]
From Equation (39), the lifetime of ice-maker depends on the required torque to harvest the crushed ice. By altering the torque, the ALT can be performed. The life-stress prototype in Equation (19) shall be adjusted as
T F = A ( S ) − n = A T L − λ = A ( F c × R ) − λ = B ( F c ) − λ
where A and B are constants
Therefore, the AF in Equations (20) & (21) shall be defined as
A F = ( S 1 S 0 ) n = ( T 1 T 0 ) λ = ( F 1 × R F 0 × R ) λ = ( F 1 F 0 ) λ
ALT from Equation (22) can be carried out till the mission time which satisfies the life objective—B1 life 10 years—are attained.
The surrounding situations of an ice-maker in a household refrigerator can change from almost −15 to −30 °C with a relative humidity altering from 0% to 20%. Relying on end-user use circumstances, an ice-maker is expected to operate from three to eighteen cycles per day. Under the largest utilization for ten years, 65,700 life cycles may occur.
To settle the stress amount for ALT, established on the permitted utilization span of the Auger motor manufacturer in bench-marked statistics, achieved from different main companies, the step-stress lifetime testing was applied, which shall judge the life under a constant usage circumstance for some accelerated loads, such as 0.8 kN-cm, 1.0 kN-cm, and 1.47 kN-cm [39]. As the different stress quantity was changed because the common torque is 0.69 kN-cm, the failure time of an auger motor at specific stress quantities might be noticed.
Engineering statistics from the company of auger motor showed that the common torque was 0.69 kN-cm and the maximum torque was 1.47 kN-cm. If the cumulative damage factor, λ, is 2, AF in Equation (42) was almost five.
For lifetime target – a B1 life 10 years, the number of mission time for ten components (attained by employing Equation (22)) was 42,000 cycles if the shape parameter was supposed to be 2.0. The ALT was set to assure a life objective—B1 life 10 years—if it shall be unsuccessful less than once for 42,000 cycles. Figure 10 manifests the test equipment of an ALT for reproducing the failed ice-maker, involving the auger motor in the field. Figure 11 shows the duty cycles applied by the crushing torque TL.
The evaluated life LB in every ALT stage is expressed as
L B β ≅ x ⋅ n ⋅ ( h a ⋅ A F ) β r + 1
where ha is the real testing time
Let x = λ ⋅ LB. The approximated failure rate λ of the selected parts shall be expressed as
λ ≅ 1 L B ⋅ ( r + 1 ) ⋅ L B β n ⋅ ( h a ⋅ A F ) β
In every ALT stage, by measuring the approximated LB life and failure rate λ, the reliability of the design for a system operated by machinery can be secured.

3. Results and Discussion

From Equation (41), the life of an ice-maker relies on the exerted impact torque TL. To rapidly identify the failure time of an ice maker, the torque was enhanced from Equation (42). Putting a scale of stress quantity due to applied load through the step-stress life testing, the failure cycles was investigated at the successive stress levels: 0.8 kN-cm, 1.0 kN-cm, and 1.47 kN-cm (torque for ALT). For 0.8 kN-cm, the ice maker stopped at approximately 11,000 cycles. For 1.0 kN-cm, the ice-maker stopped at approximately 9,000 cycles and 13,000 cycles. And, for 1.47 kN-cm, the ice-maker stopped at approximately 5000 cycles and 8000 cycles. Therefore, the stress level as 1.47 kN-cm was set for ALT as it had a comparatively excellent linearity in the Weibull chart, compared to the dissimilar stress quantities.
In the 1st ALT, the fractured bearings of auger motor were occurred at approximately 6500 cycles and 6900 cycles as failed ice-makers were disassembled. Figure 12 illustrates a photograph compared with the product failed from the field and that from the 1st ALT. By employing scanning electron microscopy (SEM), fractured image was carried out on the outer ring. The fracture surface on the cross-section had an intergranular (IG) crack and fatigue due to repeated impact under severe environmental conditions.
Because failed samples were indistinguishable in shape through ALT, we might reproduce the fractured outer ring of a bearing in the market. There was material design defect—AISI 52100 Alloy Steel with 1.30 – 1.60% chromium, which cannot endure stress due to repetitive torque at the freezing temperatures (−20 °C below) in the refrigerator. As the bearing and shaft in an ice maker repetitively struck together, they began to crack and ultimately fractured because the material (AISI 52100 Alloy Steel) was too brittle under these circumstances – repeated impacts and severe cold temperature (-20°C↓). Figure 13 shows the visual inspection of the parametric ALT outcomes and field data on a Weibull chart. The shape parameter in the 1st ALT which relied on loading circumstances was estimated to be 2.0. For the test, the shape parameter was affirmed to be 4.38 in the Weibull chart (Figure 14).
To withstand the repetitive impact torque, the material of the troublesome bearing in an auger motor was modified from AISI 52100 Alloy Steel with 1.30-1.65% chromium to lubricated sliding bearing with sintered and hardened steel (FLC 4608-110HT).
In the 2nd ALT, about 10,000 cycles and 12,000 cycles, the helix upper dispenser (polycarbonates (PC)) fractured in the exposure area of the blade dispenser (Figure 14). To understand the basic cause of the failed system, it was examined. It was discovered that there was a constructional flaw—the weld line between the helix upper dispenser and the blade dispenser—that had countless micro-voids generated in the plastic injection procedure. As the blade dispenser (stainless-steel) stroke the helix upper dispenser (PC) under extreme freezing circumstances, it started to crack and finally fractured at the weld line (Figure 14b). As an alternative, a strengthened rib of the helix was thickened after the plastic injection procedure was altered. Then, finite element analysis (FEA), integrated with ALT, was carried out. As the helix upper dispenser was fastened against the barrier, a simple impact torque (1.47 kN-cm), as shown in Figure 9, was applied. Utilizing materials and processing circumstances close to those of the helix upper dispenser, the constitutive material properties such as PC (helix upper dispenser) were decided. As a consequence, the stress of the parts by FEA inspection was lessened from 45.0 kPa to 20.0 kPa (Figure 15) [40,41].
As the matter of the bearing in an auger motor was modified and the strengthened rib of the helix upper dispenser was thickened, the lifetime of an ice-maker was expanded. However, as 42,000 mission time in the 2nd ALT was not yet achieved, the 3rd ALT was performed to assure the structural alternation of an ice-maker.
There was no problem in the 3rd ALT till 60,000 cycles. Over the route of three ALTs with alternations, the ice-maker was assured to be B1 life 10 years with an accumulated failure rate of 1% from Equations (43) and (44) when the real cycles,   h a = 60 , 000   c y c l e s , in inserting in lifetime target, x = 0.01, sample size, n = 10, accelerated factor, AF = 5.0, shape parameter, β = 4.38 , and failure number, r = 0.0. Table 3 shows a curtailed outcome of the parametric ALTs.

4. Summary and Conclusions

To strengthen the lifetime of a system operated by machinery such as an ice-maker, incorporating an auger motor with a bearing, utilized in a domestic refrigerator and failed from the field, a reliability structured way was employed, which involved a (generalized) life-stress prototype by a transport process and a sample size formulation. It covered as follows: (1) the system BX lifetime formed the ALT scheme, (2) ALTs with design modifications, and (3) resolve if the product design obtained the targeted cycles. The ice-maker was examined as a case investigation.
  • In the 1st ALT, the auger motor in an ice maker stopped near 6600 cycles and 6900 cycles as exerted for torque − 1.47 kN-cm under the freezing temperatures (−20 °C below) in the refrigerator. After disassembling the troublesome samples, we found the fractured outer ring of the bearing in an auger motor. As an action plan, the bearing matter in an ice-maker was altered from AISI 52100 Alloy Steel with 1.30-1.60% chromium to lubricated sliding bearing with sintered and hardened steel (FLC 4608-110HT).
  • In the 2nd ALT, the helix (polycarbonates) at 10,000 cycles and 12,000 cycles was fractured because the ice-maker had insufficient fatigue strength for repetitive stress in the freezer department. As an alternative, a reinforced rib of the helix was thickened after plastic injection procedure was modified.
  • In the 3rd ALT, no problems were found. The ice-maker, involving an auger motor, will satisfy the life objective—B1 life 10 years. Inspecting controversial field parts and carrying out ALTs with modifications could grow the life of an ice maker, involving an auger motor with a bearing.
  • By comprehending the design problems of products failed from the market, we might carry out parametric ALTs with system modifications. As reproducing the market failures, the design defects could be recognized and alter them. Ultimately, we approximated whether the system reached the life targets. In the process, the (generalized) time-to-failure type and sample size also were utilized.
This structured method has been relevant to different products operated by machinery. Engineer is required to grasp why multimodule system fails in their life. Namely, if there are structural defects where it is subjected to repeated loads in its working, the system shall be unsuccessful during its expected life. Designer might be required to know the (dynamic) loads of a mechanical product so that testing shall be carried out till the mission time. Therefore, this ALT will be deployed to pinpoint the structural imperfection and adjust it.

Author Contributions

S.W. carried out the idea development, method, investigation, and experiment and wrote the manuscript. D.L.O. edited the original documents and provided comments on the methods. Y.M.H. and G.M. altered the draft. All authors have understood and consented to the ready and published version of the manuscript.

Funding

This study received without outside funding.

Institutional Review Board Statement

Not relevant.

Informed Consent Statement

Not relevant.

Data Availability Statement

The data utilized in this study may be acquired on demand from the corresponding author.

Conflicts of Interest

The authors proclaim no conflict of interest.

Abbreviations

BX Time which is a cumulated failure rate of X%
Ea Activation energy, eV
e Effort
eb Counterelectromotive force
ef Field voltage, V
f Flow
Fc Ice crushing force, kN
F(t) Unreliability
h Testing time
h* Nondimensional testing time, h * = h / L B ≥ 1
if Field current, A
J Momentum of inertia, kg m2
k Boltzmann’s numerical quantity, 8.62 × 10−5 eV/deg
LB Objective BX lifetime and x = 0.01 X, on the conditions that x ≤ 0.2
m Gear ratio
MGY Gyrator in causal forms for basic 2-ports and 3-ports
n Sample number
Q Entire number of dopants per unit area
R Ratio for minimum stress to greatest stress in stress cycle, σmin/σmax
r Failed numbers
r Coefficient of gyrator
S Stress
T Temperature, K
ti Test time for each sample
TF Time to failure
TL Ice-crushing torque in bucket, kN cm
X Cumulated failure rate, %
x x = 0.01 X, on condition that x ≤ 0.2.
Greek symbols
ξ Electrical field exerted
η Characteristic life
λ Cumulative damage quantity in Palmgren–Miner’s rule
χ2 Chi-square distribution
α Confidence level
ω Angular velocity in ice bucket, rad/s
Superscripts
β Shape parameter on the Weibull chart
n Stress dependence, n = − [ ∂ ln ( T f ) ∂ ln ( S ) ] T
Subscripts
0 Usual stress conditions
1 Accelerated stress conditions

References

  1. Woo, S.; Pecht, M.; O’Neal, D. Reliability design and case study of the domestic compressor subjected to repetitive internal stresses. Reliab. Eng. Syst. Saf. 2019, 193, 106604. [Google Scholar] [CrossRef]
  2. Magaziner, I.C.; Patinkin, M. Cold competition: GE wages the refrigerator war. Harv. Bus. Rev. 1989, 89, 114–124. [Google Scholar]
  3. Bigg, G.; Billings, S. The iceberg risk in the Titanic year of 1912: Was it exceptional? Significance 2014, 11, 6–10. [Google Scholar] [CrossRef]
  4. Rogers, W.P.; Armstrong, N.A.; Acheson, D.C.; Covert, E.E.; Feynman, R.P.; Hotz, R.B.; Kutyna, D.J.; Ride, S.K.; Rummel, R.W.; Sutter, J.F.; et al. Report of the Presidential Commission on the Space Shuttle Challenger Accident; NASA: Washington, DC, 1986. [Google Scholar]
  5. ASTM International. Failures of Rolling-Element Bearings. Volume 11 Failure Analysis and Prevention. Metals Handbook, 9th ed.; ASTM International: West Conshohocken, 1990; p. 508. [Google Scholar]
  6. DVB Bank SE Aviation Research (AR). An Overview of Commercial Jet Aircraft 2013; DVB Bank SE Aviation Research (AR): Schiphol, The Netherlands, 2014; p. 20. [Google Scholar]
  7. Woo, S.; O’Neal, D.L. Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses. Metals 2021, 11, 1261. [Google Scholar] [CrossRef]
  8. Woo, S.; O’Neal, D.L.; Matvienko, Y.G.; Mebrahtu, G. Enhancing the Fatigue of Mechanical Systems Such as Dispensers Entrenched on Generalized Life-Stress Models and Sample Sizes. Appl. Sci. 2023, 13, 1358. [Google Scholar] [CrossRef]
  9. Wang, L.; Li, Y. Boundary for aviation bearing accelerated life test based on quasi-dynamic analysis. Tribol. Int. 2017, 116, 414–421. [Google Scholar] [CrossRef]
  10. Duga, J.J.; Fisher, W.H.; Buxaum, R.W.; Rosenfield, A.R.; Buhr, A.R.; Honton, E.J.; McMillan, S.C. The Economic Effects of Fracture in the United States; Final Report; Available as NBS Special Publication 647-2; Battelle Laboratories: Columbus, OH, USA, 1982. [Google Scholar]
  11. Gope, P.C.; Mahar, C.S. Evaluation of fatigue damage parameters for Ni-based super alloys Inconel 825 steel notched specimen using stochastic approach. Fatigue Fract. Eng. Mater. Struct. 2020, 44, 427–443. [Google Scholar] [CrossRef]
  12. Sola, J.F.; Kelton, R.; Meletis, E.I.; Huang, H. Predicting crack initiation site in polycrystalline nickel through surface topography changes. Int. J. Fatigue 2019, 124, 70–81. [Google Scholar] [CrossRef]
  13. Campbell, F.C. (Ed.) Fatigue. In Elements of Metallurgy and Engineering Alloys; ASM International: Materials Park, OH, USA, 2008. [Google Scholar]
  14. Chowdhury, S.; Taguchi, S. Robust Optimization: World's Best Practices for Developing Winning Vehicles, 1st ed.; John Wiley and Son: Hoboken, NJ, USA, 2016. [Google Scholar]
  15. Montgomery, D. Design and Analysis of Experiments, 10th ed.; John Wiley and Son: Hoboken, NJ, USA, 2020. [Google Scholar]
  16. Elishakoff, I. Stepan Prokofievich Timoshenko, in Encyclopedia of Continuum Mechanics; Altenbach, H., Öchsner, A., Eds.; Springer: Berlin, Germany, 2020; pp. 2552–2555. [Google Scholar]
  17. Weingart, R.G.; Stephen, P. Timoshenko: Father of Engineering Mechanics in the U.S. Structure Magazine, 20 August.
  18. Goodno, B.J.; Gere, J.M. Mechanics of Materials, 9th ed.; Cengage Learning, Inc.: Boston, MA, USA, 2017. [Google Scholar]
  19. Anderson, T.L. Fracture Mechanics—Fundamentals and Applications, 3rd ed.; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
  20. Standard Test Method for Strain-Controlled Fatigue Testing. ASTM E606/E606 M, ASTM International: West Conshohocken, PA, USA, 2019.
  21. Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials. ASTM E399, ASTM International: West Conshohocken, PA, USA, 2020.
  22. Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM E647, ASTM International: West Conshohocken, PA, USA, 2015.
  23. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S‒N) and Strain-Life (ε-N) Fatigue Data. ASTM E739-10, ASTM International: West Conshohocken, PA, USA, 2015.
  24. Braco, R.; Prates, P.; Costa, J.D.M.; Berto, F. New methodology of fatigue life evaluation for multiaxially loaded notched components based on two uniaxial strain-controlled tests. Int. J. Fatigue 2018, 111, 308–320. [Google Scholar] [CrossRef]
  25. McPherson, J. Accelerated Testing, Electronic Materials Handbook Volume 1: Packaging; ASM International Publishing: Materials Park Campus, OH, USA, 1989. [Google Scholar]
  26. McPherson, J. Reliability Physics and Engineering: Time-to-Failure Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
  27. Reddy, J.N. An Introduction to the Finite Element Method, 4th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
  28. Matsuishi, M.; Endo, T. Fatigue of metals subjected to varying stress. Jpn. Soc. Mech. Eng. 1968. [Google Scholar]
  29. Palmgren, A.G. Die Lebensdauer von Kugellagern. Z. Ver. Dtsch. Ing. 1924, 68, 339–341. [Google Scholar]
  30. Cengel, Y.; Boles, M.; Kanoglu, M. Thermodynamics: An Engineering Approach, 9th, ed.; McGraw—Hill: New York, NY, USA, 2018. [Google Scholar]
  31. IEEE Standard Glossary of Software Engineering Terminology. IEEE STD 610.12-1990. Standards Coordinating Committee of the Computer Society of IEEE. (REAFFIRMED SEPTEMBER 2002). Available online: https://ieeexplore.ieee.org/document/159342 (accessed on 31 December 2020).
  32. Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley and Son: Hoboken, NJ, USA, 2011; p. 683. [Google Scholar]
  33. Evans, J.W.; Evans, J.Y. Product Integrity and Reliability in Design; Springer: New York, NY, USA, 2001; p. 7. [Google Scholar]
  34. Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley and Son: Hoboken, NJ, USA, 2006. [Google Scholar]
  35. Plawsky, J.L. Transport Phenomena Fundamentals, 4th ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
  36. Grove, A. Physics and Technology of Semiconductor Device, 1st ed.; Wiley International Edition: New York, NY, USA, 1967; p. 37. [Google Scholar]
  37. Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems, 6th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
  38. Wasserman, G. Reliability Verification, Testing, and Analysis in Engineering Design; Marcel Dekker: New York, NY, USA, 2003; p. 228. [Google Scholar]
  39. Tang, L.C. Multiple-steps step-stress accelerated life tests: A model and its spreadsheet analysis. Int. J. Mater. Prod. Technol. 2004, 21, 423–434. [Google Scholar] [CrossRef]
  40. El-Azeem, S.O.A.; Abu-Moussa, M.H.; El-Din, M.M.M.; et al. On Step-Stress Partially Accelerated Life Testing with Competing Risks Under Progressive Type-II Censoring. Ann. Data. Sci. 2022. [Google Scholar] [CrossRef]
  41. Samanta, D.; Mondal, S.; Kundu, D. Optimal plan for ordered step-stress stage life testing. Statistics 2022, 56, 1–26. [Google Scholar] [CrossRef]
Preprints 69201 g001
Figure 1. Classification of a domestic refrigerator with multiple subsystems.
Figure 1. Classification of a domestic refrigerator with multiple subsystems.
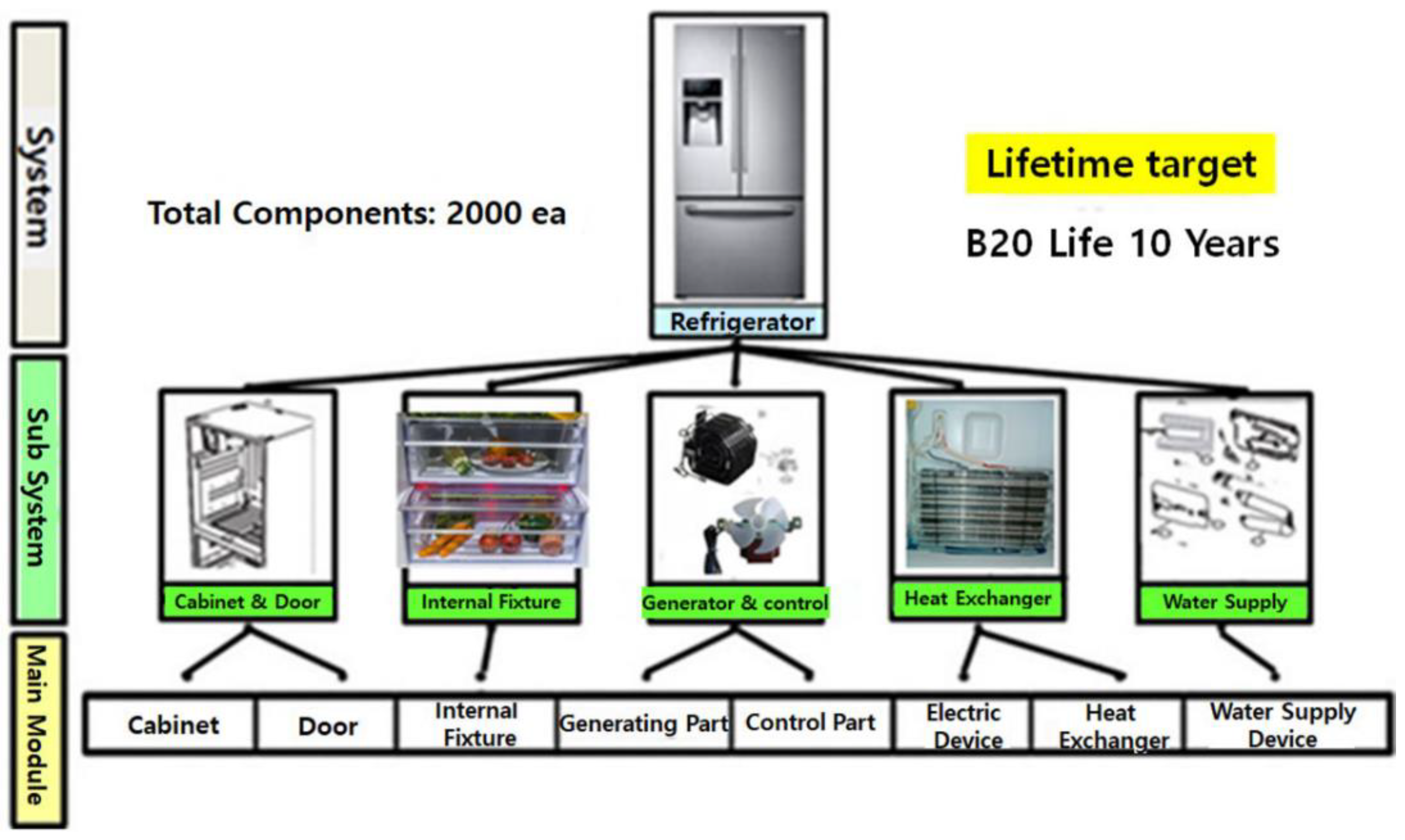
Preprints 69201 g001
Preprints 69201 g002
Figure 2. Complex product lifetime determined by the new module.
Figure 2. Complex product lifetime determined by the new module.
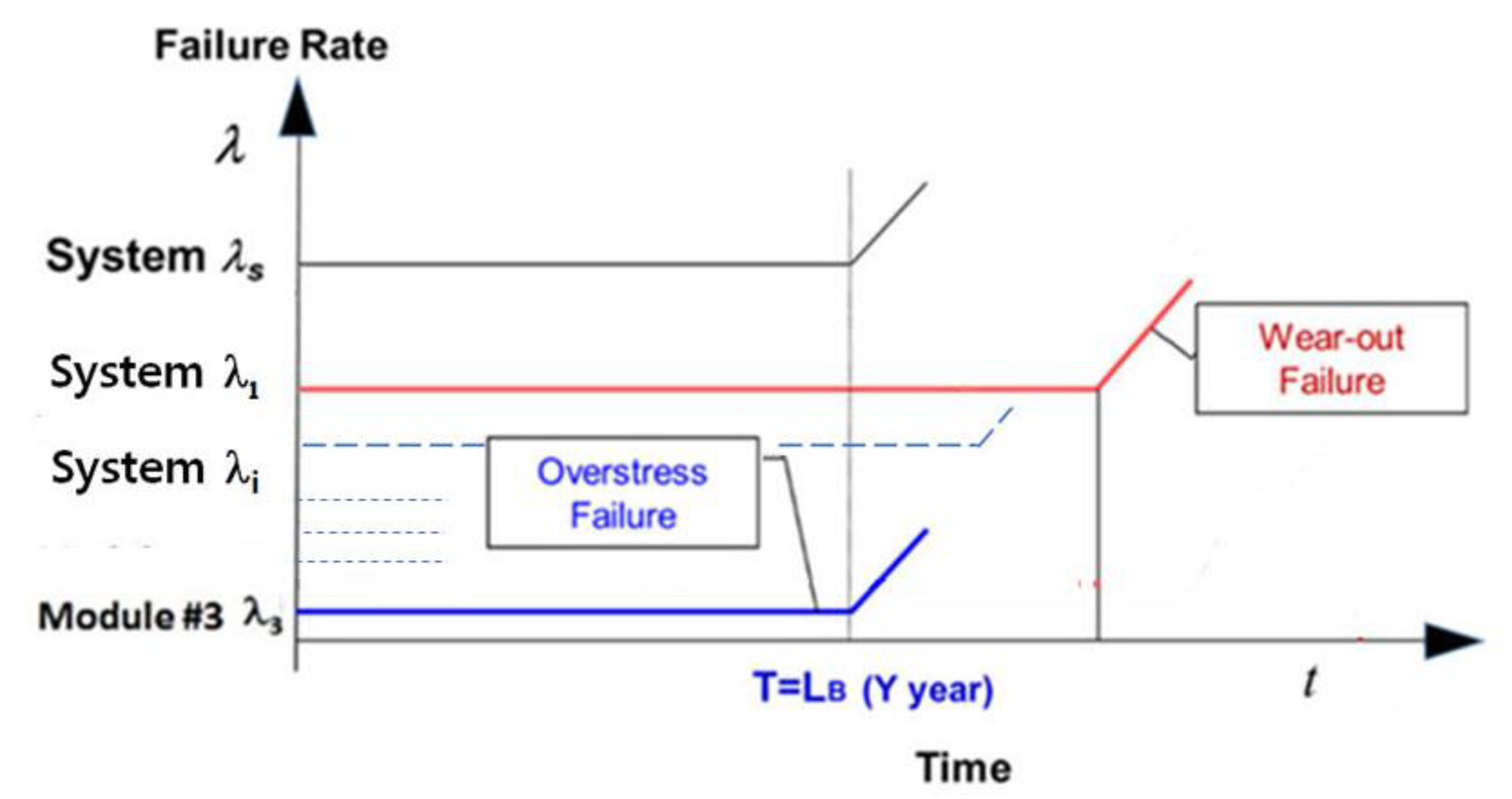
Preprints 69201 g002
Preprints 69201 g003
Figure 3. BX lifetime (LB) on the (slanted) bathtub.
Figure 3. BX lifetime (LB) on the (slanted) bathtub.
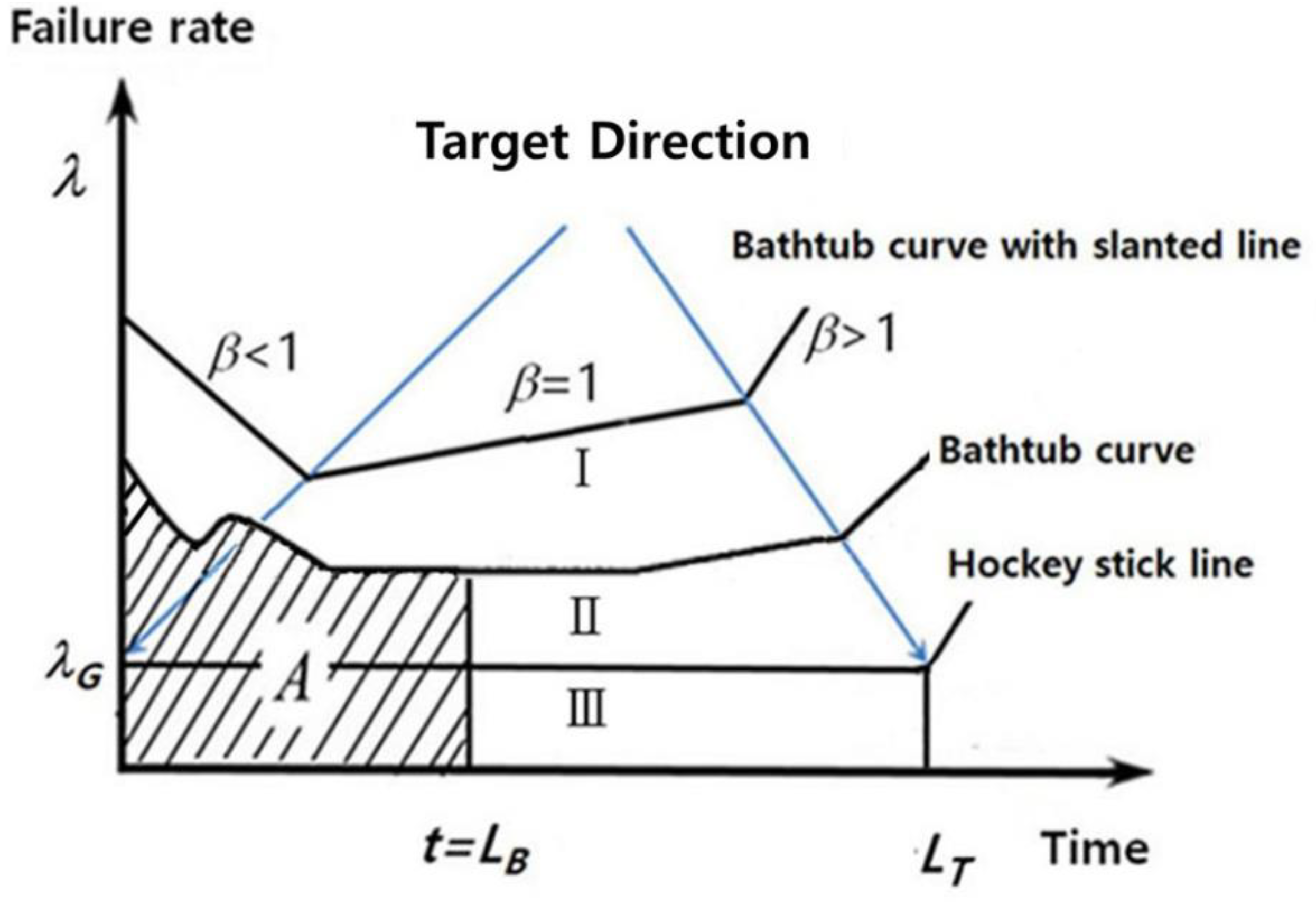
Preprints 69201 g003
Preprints 69201 g004
Figure 4. Parameter description of the ice maker (example).
Figure 4. Parameter description of the ice maker (example).
Preprints 69201 g004
Preprints 69201 g005
Figure 5. Fatigue produced by repeated loads and design deficiencies.
Figure 5. Fatigue produced by repeated loads and design deficiencies.
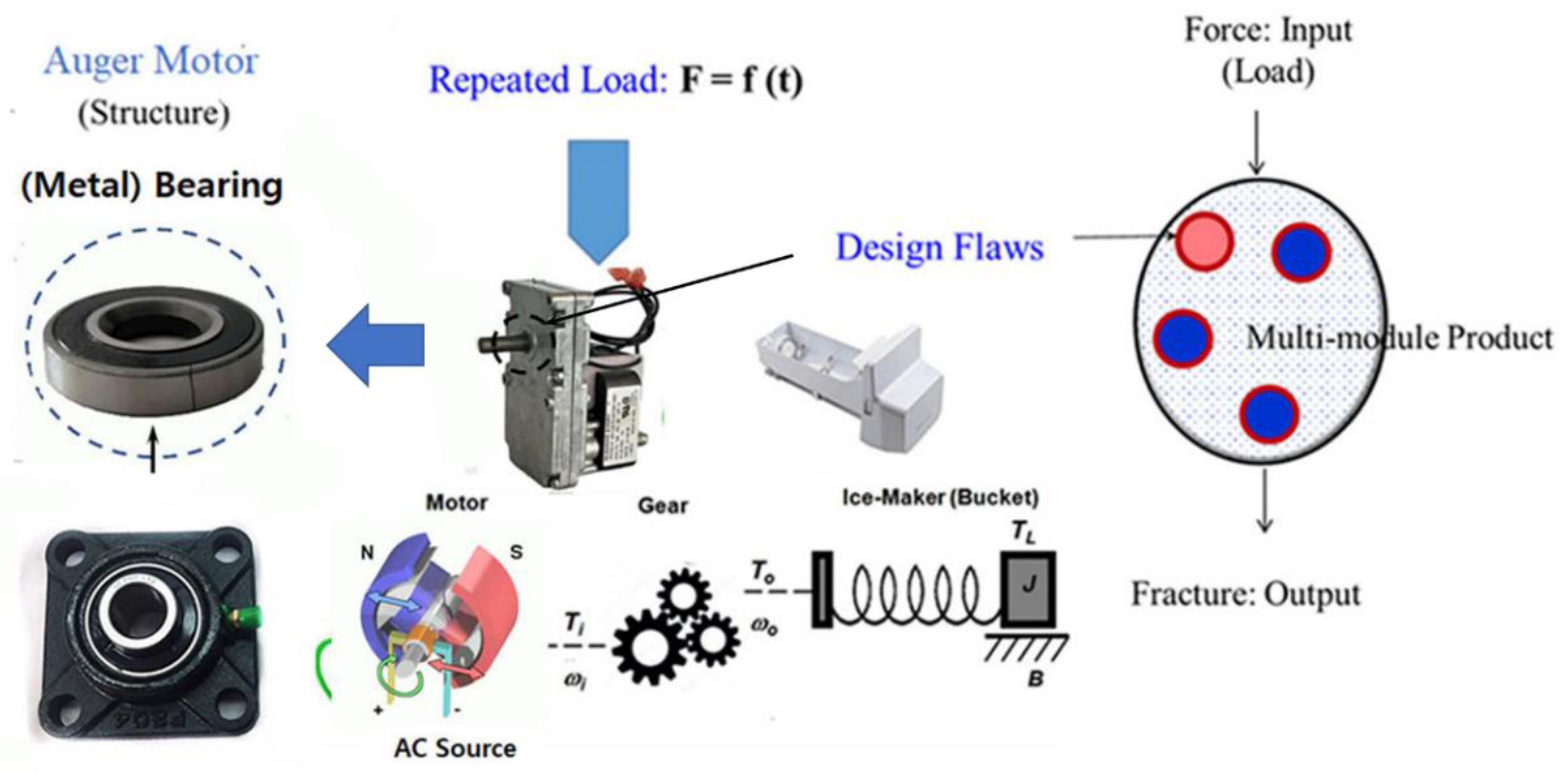
Preprints 69201 g005
Preprints 69201 g006
Figure 6. Meaning of the hyperbolic sine stress in the S‒N curve and Paris law.
Figure 6. Meaning of the hyperbolic sine stress in the S‒N curve and Paris law.
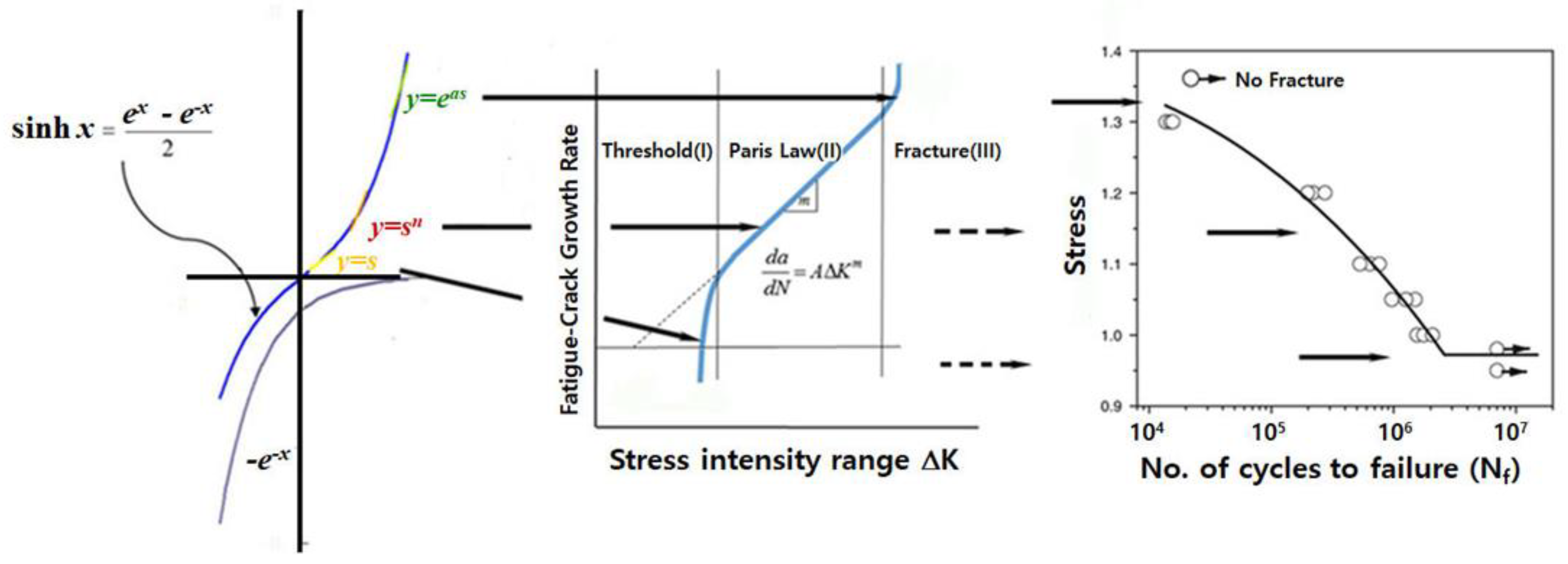
Preprints 69201 g006
Preprints 69201 g007
Figure 7. A household refrigerator equipped with ice-maker. (a) Household refrigerator; (b) parts of a domestic ice-maker: helix support ①, blade dispenser ②, helix upper dispenser ③, blade ④, and auger motor ⑤.
Figure 7. A household refrigerator equipped with ice-maker. (a) Household refrigerator; (b) parts of a domestic ice-maker: helix support ①, blade dispenser ②, helix upper dispenser ③, blade ④, and auger motor ⑤.
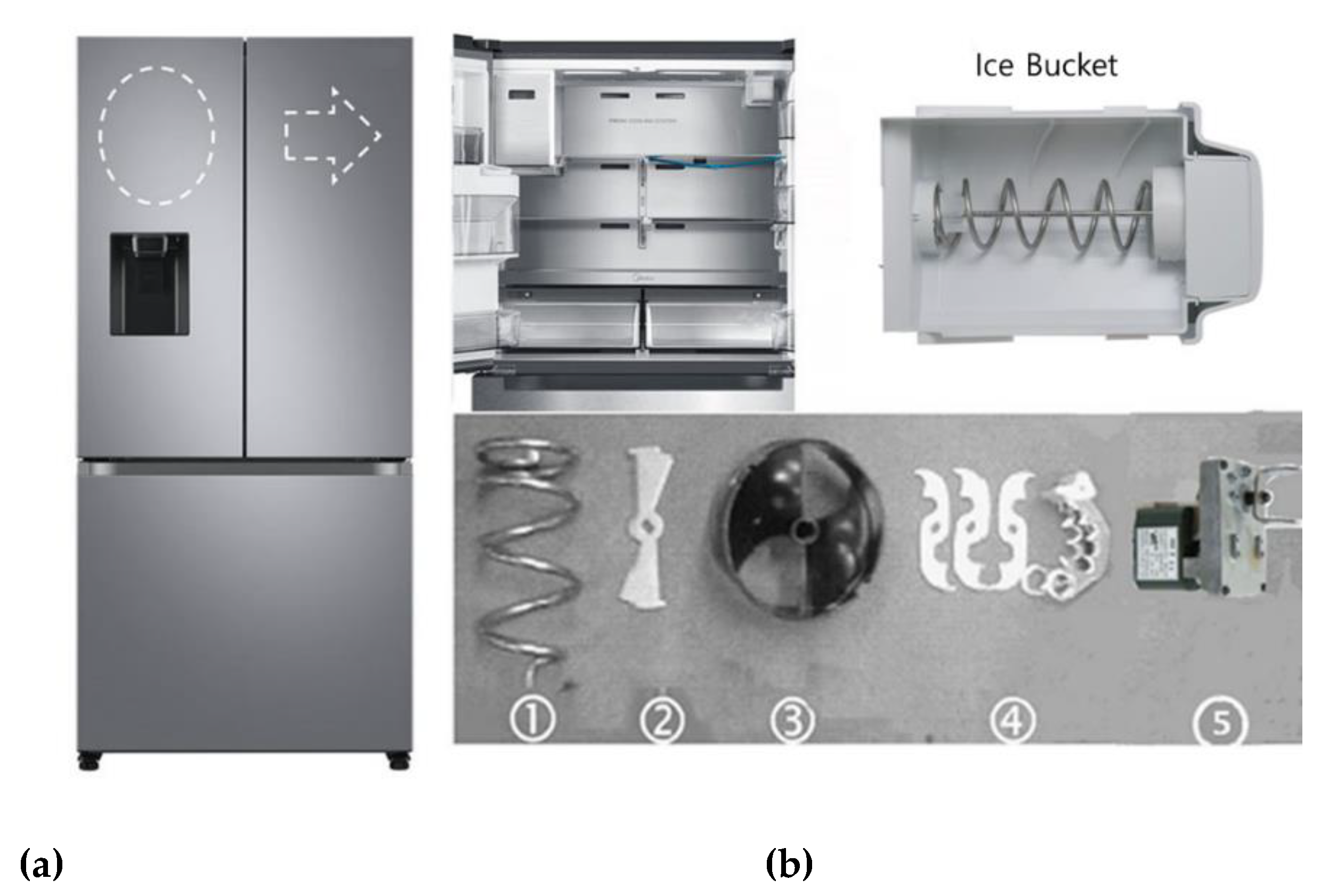
Preprints 69201 g007
Preprints 69201 g008
Figure 8. Failed auger motor in the market.
Figure 8. Failed auger motor in the market.
Preprints 69201 g008
Preprints 69201 g009
Figure 9. Design concepts of an ice-maker. (a) Exemplifying drawing of the auger motor, ice crusher, ice bucket, blade, etc. (b) Bond graph of an ice-maker.
Figure 9. Design concepts of an ice-maker. (a) Exemplifying drawing of the auger motor, ice crusher, ice bucket, blade, etc. (b) Bond graph of an ice-maker.
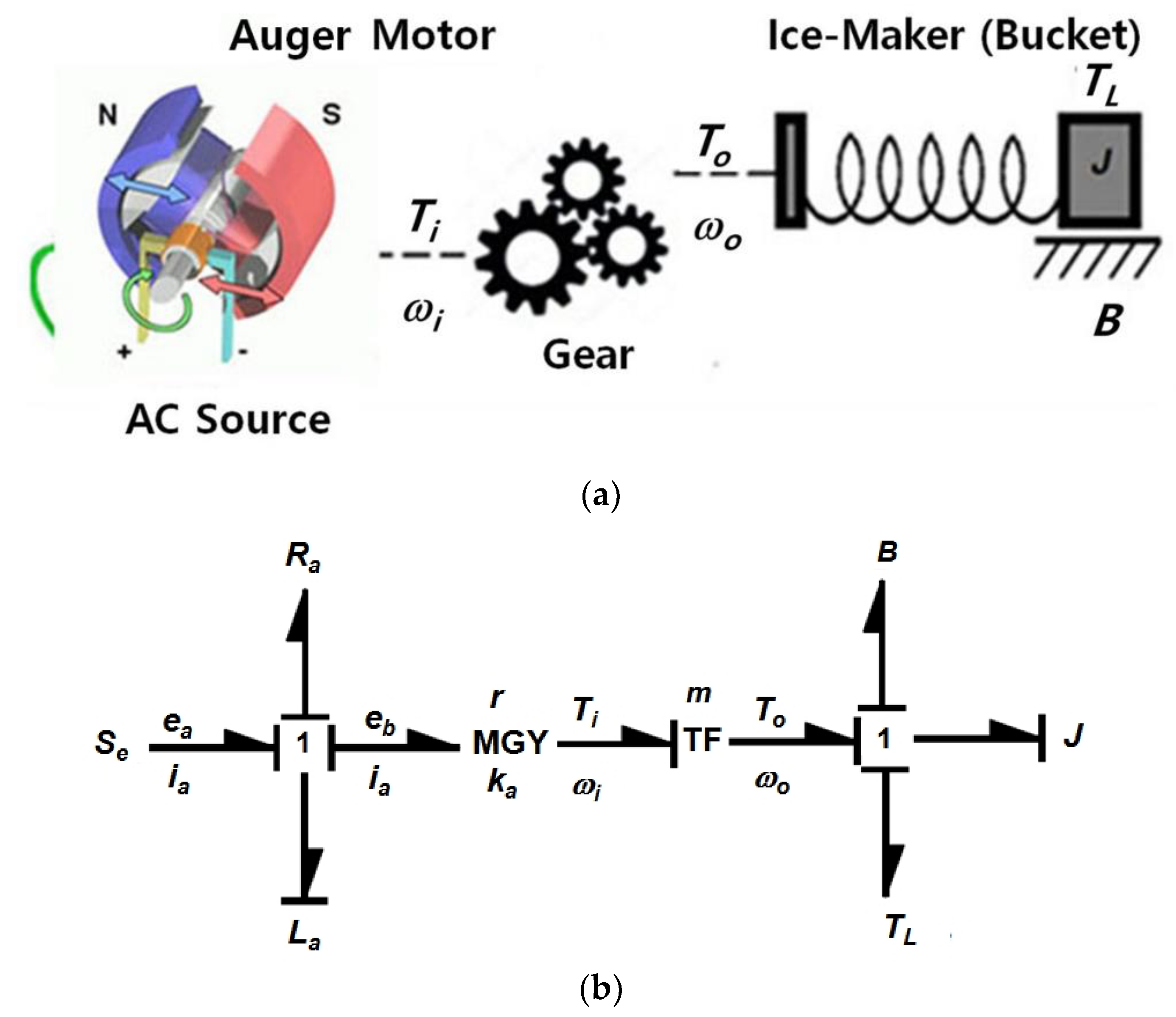
Preprints 69201 g009
Preprints 69201 g010
Figure 10. ALT system; (a) Equipment, (b) Controller.
Figure 10. ALT system; (a) Equipment, (b) Controller.
Preprints 69201 g010
Preprints 69201 g011
Figure 11. Duty cycles applied by ice-squashing torque TL exerted in the band clamper.
Figure 11. Duty cycles applied by ice-squashing torque TL exerted in the band clamper.
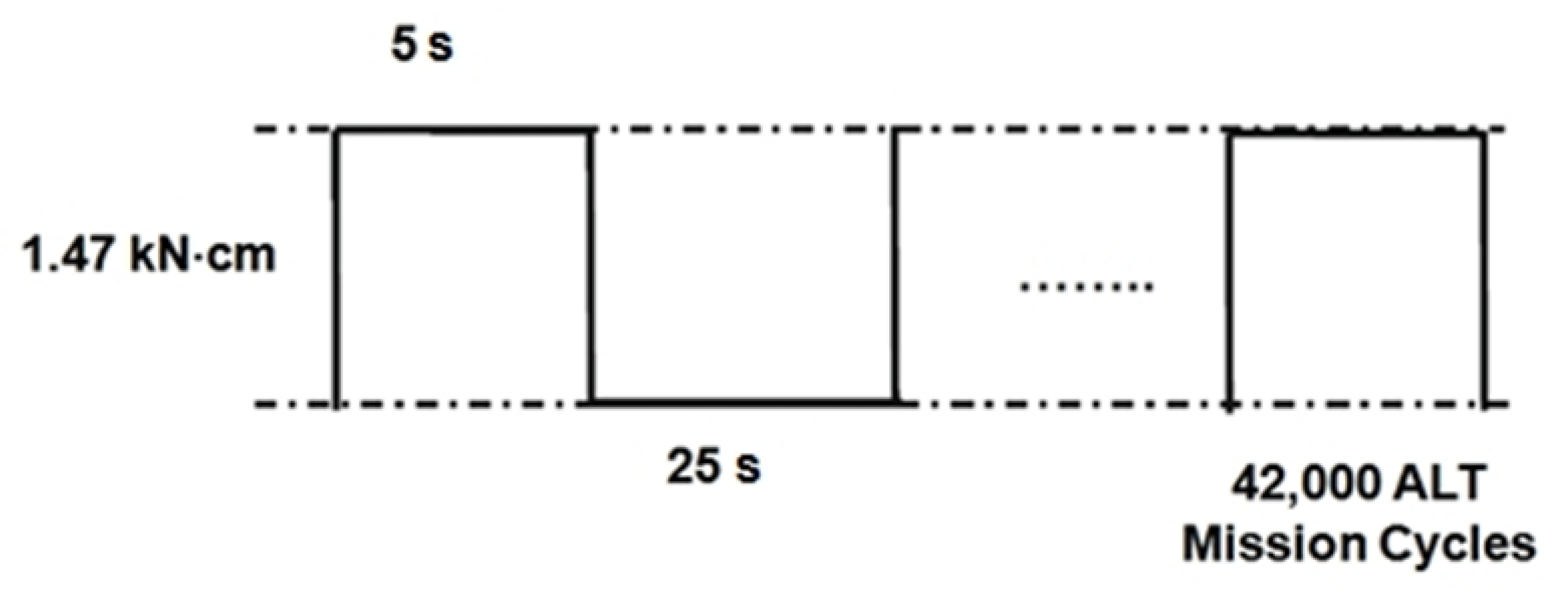
Preprints 69201 g011
Preprints 69201 g012
Figure 12. Failed bearing in auger motor from the marketplace and in the 1st ALT; (a) Unsuccessful part from the marketplace, (b) Failed bearing with in 1st ALT – crack origin at outer ring.
Figure 12. Failed bearing in auger motor from the marketplace and in the 1st ALT; (a) Unsuccessful part from the marketplace, (b) Failed bearing with in 1st ALT – crack origin at outer ring.
Preprints 69201 g012
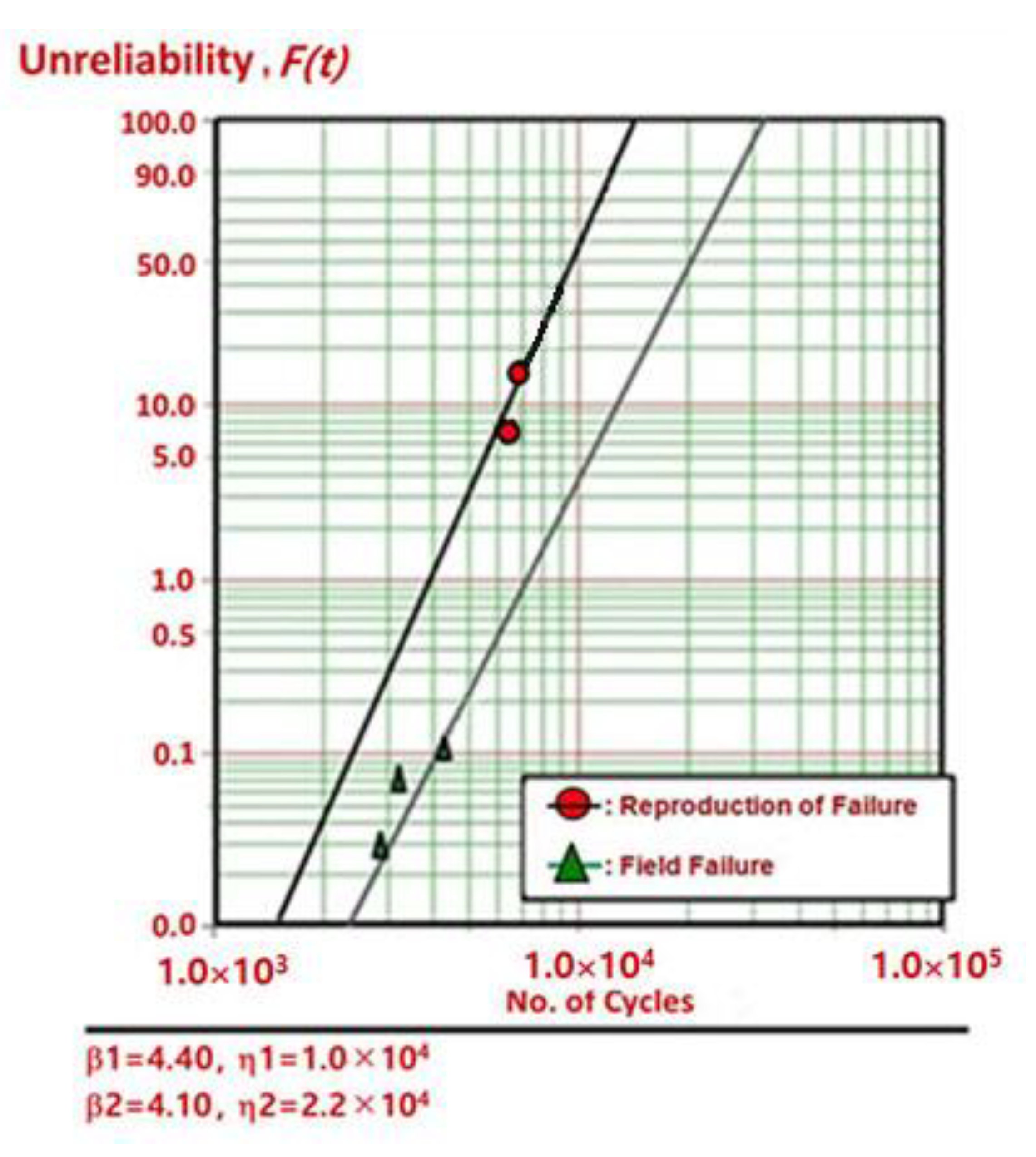
Preprints 69201 g013
Figure 13. Failed products on the Weibull chart.
Figure 13. Failed products on the Weibull chart.
Preprints 69201 g013
Preprints 69201 g014
Figure 14. Failed parts in the 2nd ALT: (a) failed parts, (b) the basic cause of fractured parts.
Figure 14. Failed parts in the 2nd ALT: (a) failed parts, (b) the basic cause of fractured parts.
Preprints 69201 g014
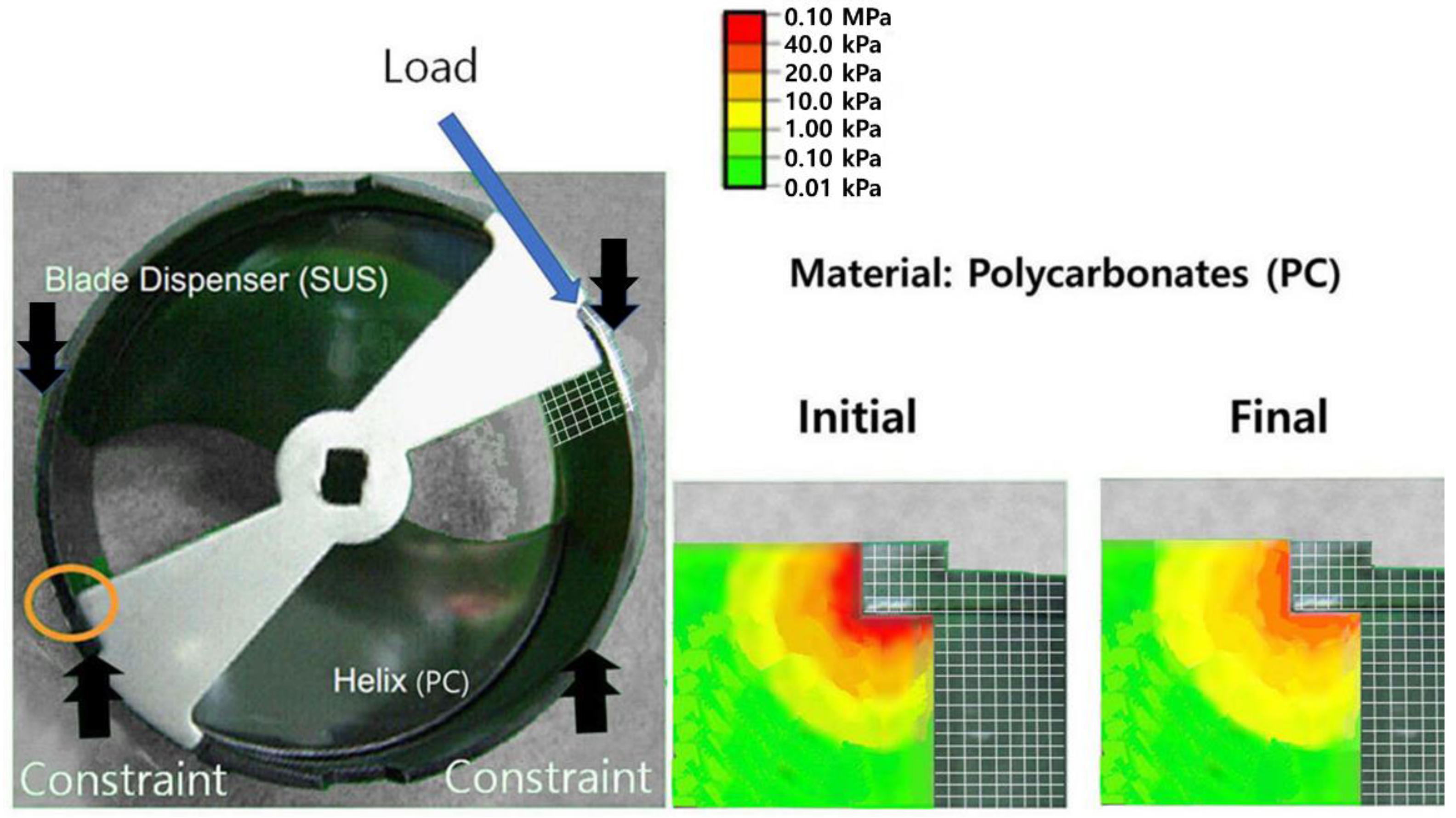
Preprints 69201 g015
Figure 15. Outcome of stress by employing finite element analysis (FEA).
Figure 15. Outcome of stress by employing finite element analysis (FEA).
Preprints 69201 g015
Table 1. Complete ALT idea of subsystems in a household refrigerator
Table 1. Complete ALT idea of subsystems in a household refrigerator
Modules Market Reliability Predicted Reliability Goal Reliability
Failure Rate Per Year, %/Year BX Life, Year Failure Rate Per Year, %/Year BX Life,
LB (Year)		 Failure Rate Per Year, %/Year BX Life, Year
A 0.34 5.3 New ×5 1.70 1.1 0.15 12(BX = 1.8)
B 0.35 5.1 Same ×1 0.35 5.1 0.15 12(BX = 1.8)
C 0.25 4.8 Modified ×2 0.50 2.4 0.10 12(BX = 1.2)
D 0.20 6.0 Modified ×2 0.40 3.0 0.10 12(BX = 1.2)
E 0.15 8.0 Same ×1 0.15 8.0 0.10 12(BX = 1.2)
Miscellaneous 0.50 12.0 Same ×1 0.50 12.0 0.50 12(BX = 6.0)
System 1.79 7.4 - - 3.60 3.7 1.10 12(BX = 13.2)
Table 2. Linear transport phenomena.
Table 2. Linear transport phenomena.
Ohm’s Law: j = − σ   V
J = current density, j (quantity: A/cm2) D = electric field, −∇ V
(quantity: V/cm, V = potential)		 L = conductivity, σ = 1/ρ
(quantity: ρ = resistivity (Ω cm))
Fourier’s Law: q = −κ∇T
J = heat flux, q (quantity: W/cm2) D = thermal force, −∇ T
(quantity: °K/cm, T = temperature)		 L = thermal conductivity, κ
(quantity : W/°K cm)
Fick’s Law: F = −D∇ C
J = material flux, F (quantity:/sec cm2) D = diffusion force, −∇ C
(quantity:/cm4, C = concentration)		 L = diffusivity, D
(quantity: cm2/sec)
Newton’s Law: Fu = −μ∇ u
J = fluid velocity flux, Fu (quantity:/sec2 cm) D = viscous force, −∇ u
(quantity:/sec, u = fluid velocity)		 L = viscosity, μ
(quantity:/sec cm)
Table 3. ALT results for ice-makers.
Table 3. ALT results for ice-makers.
Parametric ALT 1st ALT 2nd ALT 3rd ALT
Draft Design - Final Design
Over the route of 42,000 cycles, the ice maker system has no issues 6500 cycles: 1/10 fail
6900 cycles: 1/10 fail
(Unsuccessful bearing samples)		 10,000 cycles: 1/10 fail
12,000 cycles: 1/10 fail
(Unsuccessful helix samples)		 42,000 cycles: 10/10
60,000 cycles: 10/10
OK
Structure Preprints 69201 i001
Action plans C1: from AISI 52100 Alloy Steel to lubricated sliding bearing with sintered and hardened steel (FLC 4608-110HT) C2: thickened reinforced rib on the side of helix
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated