Preprint

Article

Multilevel Functional Principal Components Analysis Presents a Viable Method of Modelling Dynamical Shape Changes

Altmetrics

Downloads

183

Views

Comments

A peer-reviewed article of this preprint also exists.

Damian Joseph John Farnell1^*

,Peter Claes

Damian Joseph John Farnell1^*

,Peter Claes

This version is not peer-reviewed

Submitted:

21 February 2023

Posted:

28 February 2023

You are already at the latest version

Alerts

Abstract

Multilevel functional principal components analysis (mFPCA) is used to treat dynamical changes in shape in this article. Results of standard (single-level) FPCA are presented here also as a comparison. Monte Carlo (MC) simulation is used to create univariate data (i.e., a single “outcome” variable) that contains two distinct classes of trajectory with time. MC simulation is also used to create multivariate data of sixteen 2D points that represent (broadly) an eye; this data also has two distinct classes of trajectory (an eye blinking and an eye widening in surprise). This is followed-up by an application of mFPCA and single-level FPCA to “real” data consisting of twelve 3D landmark outlining the mouth that are tracked over all phases of a smile. By consideration of eigenvalues, results for the MC datasets find correctly that variation due to differences in groups between the two classes of trajectories variation are larger than variation within each group. In both cases, differences in standardized component scores between the two groups are observed, as expected. Modes of variation are shown to model the univariate MC data correctly, and good model fits are found for both the “blinking” and “surprised” trajectories for the MC “eye” data. Results for the “smile” data show that the smile trajectory is modelled correctly, namely: the corners of the mouth are drawn backwards and wider during a smile. Furthermore, the first mode of variation at level 1 of the mFPCA model show only subtle and minor changes in mouth shape due to sex, whereas the first mode of variation at level 2 of the mFPCA model govern whether the mouth is upturned or downturned. These results are all an excellent test of mFPCA, which show that mFPCA presents a viable method of modelling dynamical changes in shape.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

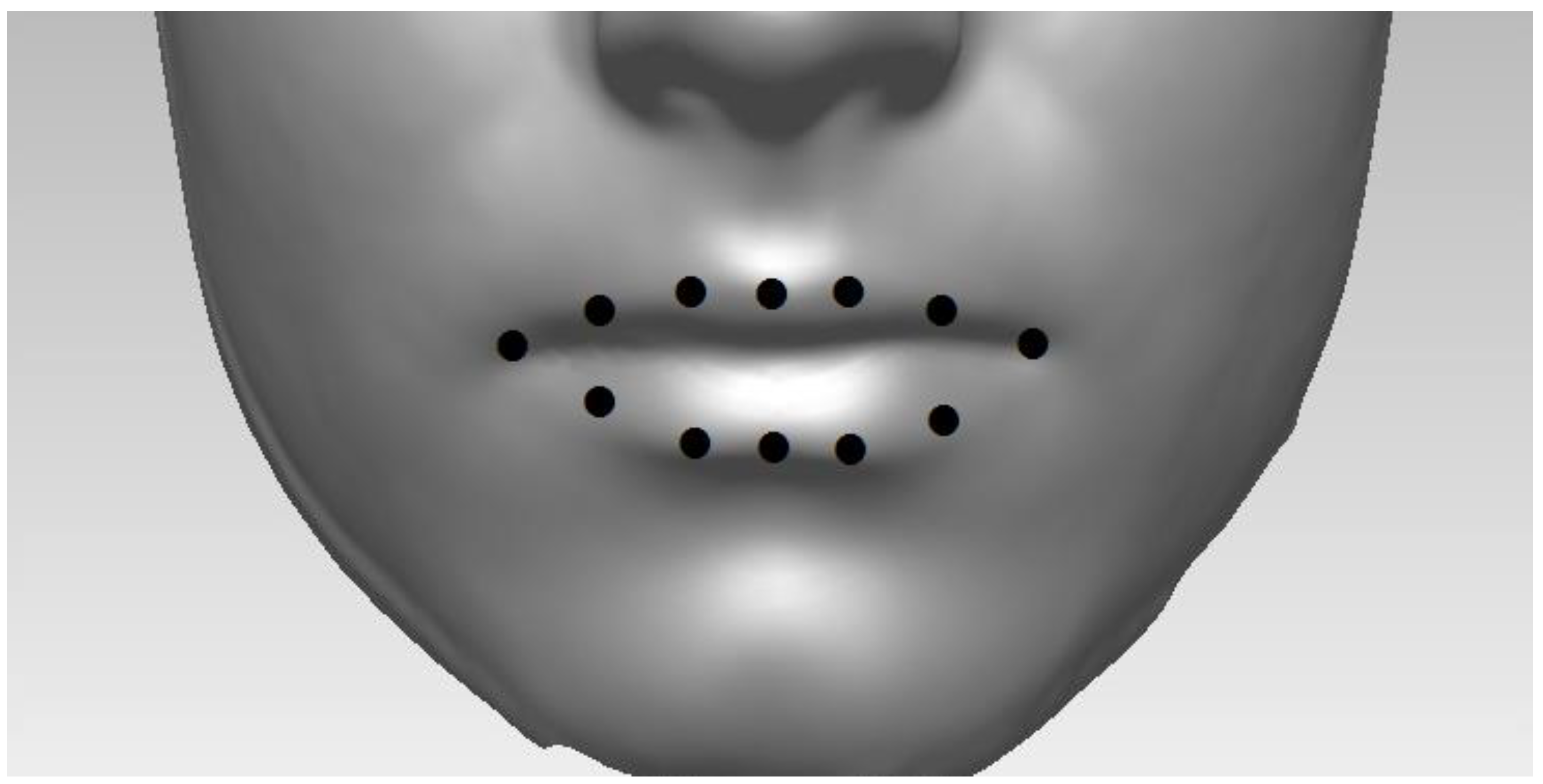
Figure 1. Illustration of lip shape, which is represented here by 12 landmark points placed on the 3D facial scans here.

Multivariate data occurs when we have more than one “outcome” in our data set. Biological shapes can be viewed as a form of multivariate data because the shapes can be represented by (e.g.) manual placement of key landmark points (e.g., see Figure 1) or by semi-landmark methods, which also position landmark points regularly on an (often parametric) topological surface [1,2]. One may use methods such as principal components analysis (PCA) [1] to analyze such data. Between-group (bgPCA) [3,4] is an extension of standard PCA that carries out separate PCAs on (between-group) covariance matrices based on “group means” and (within group) covariance matrices based on individual shapes around these means. Multilevel PCA (mPCA) has been used by us [5–12] to analyze 3D facial shapes obtained from 3D facial scans; note that two-level multilevel PCA (mPCA) is equivalent to bgPCA. mPCA has been used previously to investigate changes by ethnicity and sex [5,6], facial shape changes in adolescents due to age [7,8], and the effects of maternal smoking and alcohol consumption on the facial shape of English adolescents [9]. Previous work also employed mPCA to treat time-related changes in facial shape during the act of smiling [10,11].

However, standard mPCA does not recognize that time is a continuous variable. A functional PCA (FPCA) approach is therefore more appropriate for such dynamical data [13–15]. FPCA is very similar to PCA, albeit with a preceding step where time-series are represented via some basis expansion (e.g., B-splines, wavelets, or Fourier series) and smoothing occurs [13]. (Here, cubic splines are used to represent time series in these initial “proof-of-principle” calculations.) However, the standard FPCA approach (like single-level PCA) does not recognize clusters or multilevel structure within the subject population. Relatively few articles [16,17] have considered multilevel forms of FPCA (i.e., mFPCA) and certainly none have considered this in the context of facial shape.

Here we wish to apply mFPCA to study facial dynamics, where results of standard FPCA provide a comparison. Monte Carlo simulated datasets are used to test these methods in the first instance, although we also apply them to the “smile” data of Refs. [10,11] captured using a 3D dynamical scanner. We describe both datasets and methods in more detail in the methods section. We then discuss our results, before going on to consider the implications of this work.

2. Materials and Methods

2.1. Monte Carlo Data Generation

Two Monte Carlo simulated data sets are used here. Firstly, a very simple case is presented with just one outcome (such as a signal or simple time series) with two groups. Trajectories for each subject follow a sine wave. We will refer to this as the “Sine Wave” dataset. The period of the first group is set to 2 (with respect to abritrary units of time) and has an amplitude of 0.5 (with respect to abritrary units of distance), whereas the period of the second group is set to 1.5 and the amplitude of 0.4. Small normally distributed random errors are added to the amplitude (magnitude = 0.03) for each subject in order to provide variation between “within-subject” variation for the two groups. The magnitude of within-subject variation is therefore approximately two orders of magnitude smaller than that of between-groups variation (as variance scales with the amplitude squared). The second Monte Carlo dataset has 16 points in 2D (thus, 2 × 16 = 32 components) that delineate the boundary (roughly) of an eye during: (group 1) an entire blink; (group 2) an eye opening slightly, as if in surprise. We shall refer to this as the “Blink” dataset. Again, small normally distributed random errors are added to the amplitude (magnitude = 0.03) for each subject in order to provide variation between “within-subject” variation for the two groups. A two-level mFPCA model (presented below) is used to analyse this data. In both cases, between-groups variation has a much larger magnitude than within-groups variation.

2.2. Smile Dataset

This dataset consisted of 3D video shape data during all phases of a smile, where 12 points placed (and tracked) along the outer boundary of mouth, as shown in Figure 1. A 3DMD scanner was used to capture this 3D surface dynamical data. Sixty adult staff and students at Cardiff University, consisting of thirty one males and twenty nine females, were recruited for this study. There were between approximately 100 and 250 frames in total for each subject. All 3D shapes were centred to have a common origin. As described in Ref. [10,11], different phases of the smile were found for each subject separately by considering the normalized smile amplitudes. Including rest phases, these seven phases were found to be [10,11]: rest pre-smile, onset acceleration, onset deceleration, apex, offset acceleration, offset deceleration, and rest post-smile. Ethical approval for this project was granted by the School of Dentistry Ethics Committee at Cardiff University, UK.

2.3. Functional Principal Components Analysis (FPCA)

The covariance function for (single-level) FPCA with respect to time

t

(a continuous variable) is presented generally by

K (s, t) = E [\{X (s) - η (s)\} \{X (t) - η (t)\}]

(1)

η (t)

is the mean shape function (e.g., in practice with respect to all subjects in the dataset). Note that we may write

K (s, t)

K (s, t) = \sum_{l}^{\infty} θ_{l} ψ_{l} (s) ψ_{l} (t)

(2)

where

θ_{l}

are non-negative eigenvalues and

ψ_{l} (t)

are the associated eigenfunctions. Finally, the expansion of any (new) dynamic shape function

X (t)

is approximated by

X (t) = η (t) + \sum_{l}^{m} a_{l} ψ_{l} (t)

(3)

where

a_{l}

are scalar coefficients and

m

is often set to be finite. Component scores are standardized readily by finding,

a_{l} / \sqrt{θ_{l}}

In order to solve this problem practically, simple cubic spline fits are carried of

X

with respect to time for each subject separately at

T

regular time intervals for each subject in these initial calculations. Spline fits using the “spasp2” command in MATLAB were found to provide reliable trajectories (i.e., cubic splines fitted to data via a least-squares approach). Note that five “knots” gave reliable results without overfitting for these curves (assessed visually – this is adequate for these initial proof-of-principle calculations).

When the outcome is a scalar variable sampled at

T

regular time intervals (e.g., a signal or single point in 1D), we denote the outcome variable for each subject

i

as a vector

X^{i}

(of size

T

), where each component of this vector for subject

i

is denoted

X_{t}^{i}

, where the index

t

denotes each of the regularly sampled time points. The total number of subjects (i.e., the sample size) is given by

n

. The covariance matrix is therefore of size

T \times T

and is given by

K_{t_{1}, t_{2}} = \frac{1}{n - 1} \sum_{i}^{n} (X_{t_{1}}^{i} - η_{t_{1}}) (X_{t_{2}}^{i} - η_{t_{2}})

(4)

where each component of this matrix is denoted

K_{t_{1}, t_{2}}

and

η

is the mean trajectory vector, where

η = \frac{1}{n} \sum_{i}^{n} X^{i}

(5)

Eigenvalues of Eq. (4) are denoted

θ_{l}

and eigenvectors are denoted

ψ_{l}

. The expansion of any (new) trajectory vector

X^{n e w}

is given by

X^{n e w} = η + \sum_{l}^{m} a_{l} ψ_{l}

(6)

where again

a_{l}

are scalar coefficients and

m

is often set to be a finite number. The components

a_{l}

(referred to as “component scores” here) are found via:

a_{l} = (X^{n e w} - η) {\cdot ψ}_{l}

For multivariate shape data, shapes at each time point are themselves a vector rather than a scalar. Spline fits are carried out for each subject and for each 3D point component separately with respect to time. Again, this multivariate data may then be sampled regularly at

T

time points for each spline fit for each component. The simplest method is now to let

X^{i}

be an element of a concatenated vector of each of the

D i m \times M

components of the shape of dimension

D i m

(

D i m = 2,3

here for 2D and 3D point data, respectively) and at all

T

time points for each subject

i

. The size of the vector

X^{i}

is therefore given by

D i m \times M \times T

for each subject

i

. We denote the index of each element of this vector as

{k, t}

; components of this vector are therefore given by

X_{{k, t}}^{i}

. Elements of the covariance matrix is now written as

K_{{k_{1}, t_{1}}, {k_{2}, t_{2}}} = \frac{1}{n - 1} \sum_{i}^{n} (X_{{k_{1}, t_{1}}}^{i} - η_{{k_{1}, t_{1}}}) (X_{{k_{2}, t_{2}}}^{i} - η_{{k_{2}, t_{2}}})

(7)

η

is again the mean vector. The diagonalization of this covariance matrix can become an intensive computational problem and so direct iteration or the Lanczos method can be used (as appropriate) to find the eigenvalues

θ_{l}

and the eigenvectors

ψ_{l}

. The expansion of any (new) trajectory vector

X^{n e w}

may again be found via Eq. (6).

This approach assumes that all components of all landmark points are correlated potentially with all other components and at all time points. Clearly, this is an inefficient approach, although it is simple and straightforward to implement. It is therefore used in these initial calculations.

2.4. Multilevel Functional Principal Components Analysis (mFPCA)

Multilevel / hierarchical models allow clustering to be addressed by including between- and within-group variations at different levels of the model. For a simple two-level model (initially), we write our feature vector as

X^{i, j}

where

i

indicates a specific instance or subject in group or cluster

j

(of

p

such groups). Again, we assume initially that the outcome is a scalar and that the trajectory data has been sampled regularly at

T

time points. We write elements of the level 2 (within-group variation) covariance matrix

K^{2, j}

for each group

j

K_{t_{1}, t_{2}}^{2, j} = \frac{1}{n_{j} - 1} \sum_{i}^{n_{j}} (X_{t_{1}}^{i, j} - η_{t_{1}}^{j}) (X_{t_{2}}^{i, j} - η_{t_{2}}^{j})

(8)

η^{j}

is the mean for each group

j

, given by

η^{j} = \frac{1}{n_{j}} \sum_{i}^{n_{j}} X^{i, j}

(9)

However, a “common” covariance matrix is often assumed for mPCA (and so also mFPCA) at level 2. For

p

such groups in total, we note that

K^{2} = \frac{1}{p} \sum_{j}^{p} K^{2, j}

(10)

The “grand mean” is now given by

η = \frac{1}{p} \sum_{j}^{p} η^{j}

(11)

K^{2}

can now be diagonalized, where

θ_{l}^{2}

are non-negative eigenvalues at level 2 and

ψ_{l}^{2}

are the associated eigenvectors. By contrast, we now write elements of the covariance matrix at level 1 (between-group variation) as

K_{t_{1}, t_{2}}^{1} = \frac{1}{p - 1} \sum_{j}^{p} (η_{t_{1}}^{j} - η_{t_{1}}) (η_{t_{2}}^{j} - η_{t_{2}})

(12)

where

θ_{l}^{1}

are non-negative eigenvalues at level 1 and

ψ_{l}^{1}

are the associated eigenvectors. Note that the number of non-zero eigenvalues will be limited to

p - 1

due to the finite number of groups

p

. The expansion of any (new) dynamic shape

X^{n e w}

is given by

X^{n e w} = η + \sum_{l}^{m_{1}} a_{l}^{1} ψ_{l}^{1} + \sum_{l}^{m_{2}} a_{l}^{2} ψ_{l}^{2}

(13)

Again,

a_{l}^{1}

and

a_{l}^{2}

are scalar coefficients and

m_{1}

and

m_{2}

are set to be finite numbers. The coefficients

{a_{l}^{1}}

and

{a_{l}^{2}}

(again referred to as “component scores” here) are determined for mFPCA by using a global optimization procedure in MATLAB. Component scores are again standardized readily by finding,

a_{l}^{1} / \sqrt{θ_{l}^{1}}

and

a_{l}^{2} / \sqrt{θ_{l}^{2}}

This approach will work for cases where the outcome is a scalar (i.e.,

X

is a vector of size

T

) or for multivariate dynamic shape data (i.e.,

X

is a vector of size

D i m \times M \times T

). We write elements of the of the level 2 (within-group variation) covariance matrix

K^{2, j}

for each group

j

K_{{k_{1}, t_{1}}, {k_{2}, t_{2}}}^{2, j} = \frac{1}{n_{j} - 1} \sum_{i}^{n_{j}} (X_{{k_{1}, t_{1}}}^{i, j} - η_{{k_{1}, t_{1}}}^{j}) (X_{{k_{2}, t_{2}}}^{i, j} - η_{{k_{2}, t_{2}}}^{j})

(14)

This is a matrix of size:

D i m \times M \times T

D i m \times M \times T

. The common level 2 covariance matrix is again given by Eq. (10) and the “grand mean” by Eq. (11). Elements of the covariance matrix at level 1 (between-group variation) are

K_{{k_{1}, t_{1}}, {k_{2}, t_{2}}}^{1} = \frac{1}{p - 1} \sum_{j}^{p} (η_{{k_{1}, t_{1}}}^{j} - η_{{k_{1}, t_{1}}}) (η_{{k_{2}, t_{2}}}^{j} - η_{{k_{2}, t_{2}}})

(15)

The expansion of any (new) dynamic shape

X^{n e w}

is again given by Eq. (13). The extension to three or more levels is presented in the Appendix. We also note that if each subject is treated as a separate group then this approach models the “nested” nature of this dynamical shape data in an efficient manner (i.e., analogous to a mixed model in which repeated measurements of shape over time are made for each subject). Indeed, it is likely that this approach is probably very similar to that presented in Ref. [16], albeit now also for multivariate data.

A rough rule of thumb [12] is that the sample size per group in the training set must be larger than the overall size of the feature vector in order to avoid “pathologies” of mPCA based methods. For the “Sine Wave” dataset,

T = 101

(thus the feature vector is of size 101 also) and so we set the sample size for all groups to be

n_{j} = 1000

. Sample sizes per group in the test set are also set to be

n_{j} = 1000

. For the “Blink” dataset,

T = 101

thus the feature vector is of size

32 \times 101 = 3201

and so we set the sample size for all groups to be

n_{j} = 10000

. Sample sizes per group in the test set are also set to be

n_{j} = 10000

. For the “Smile” dataset, we note that

T = 60

and so the feature vector is of size

60 \times 12 \times 3 = 2160

. Unfortunately, data is limited in this case to 60 subjects in total only. However, this is adequate here as we wish to present a “proof-of-principle” calculation only for “real” data. Again, all calculations presented here were carried out in MATLAB R2021a.

3. Results

3.1. Sine Wave Dataset

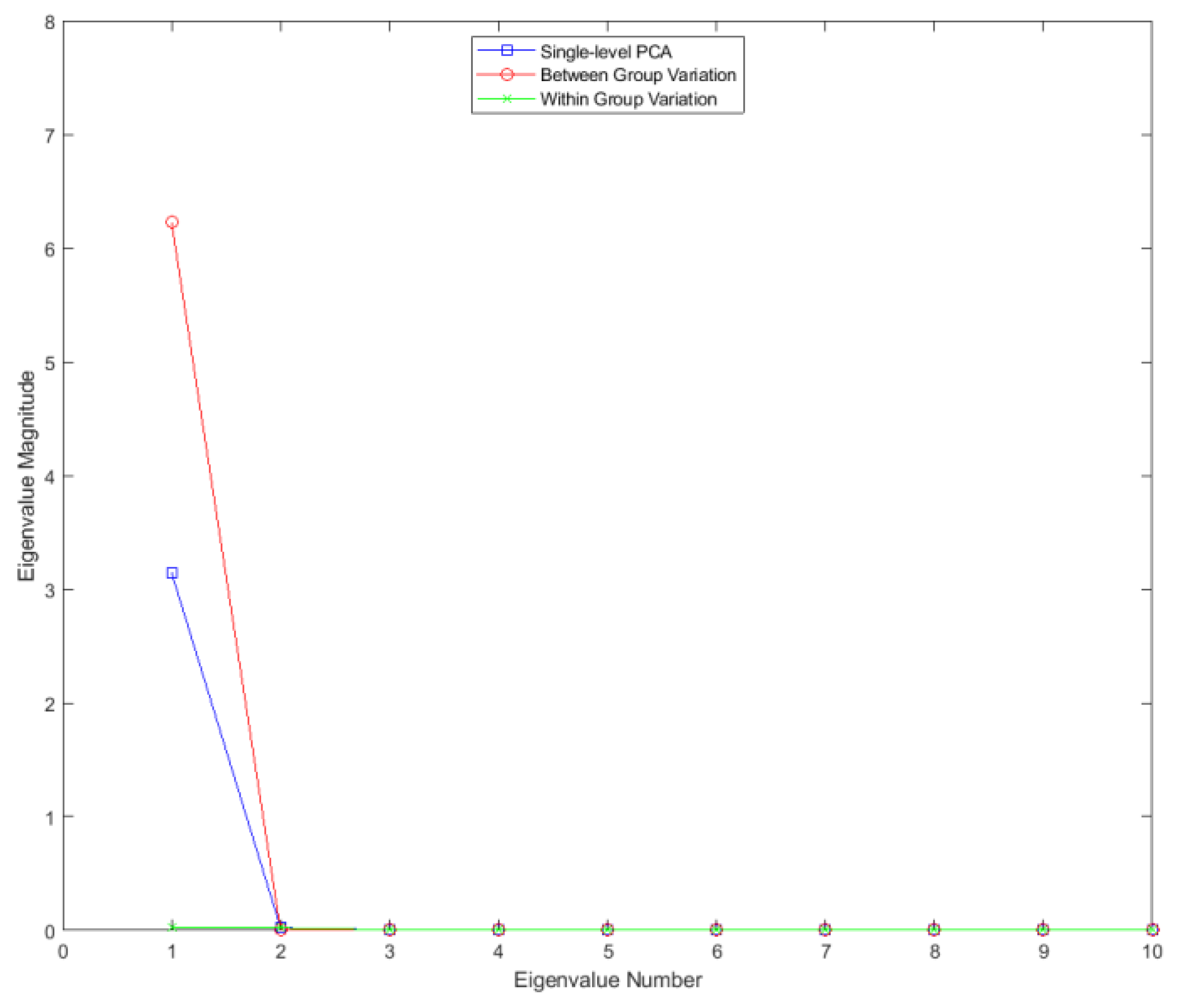
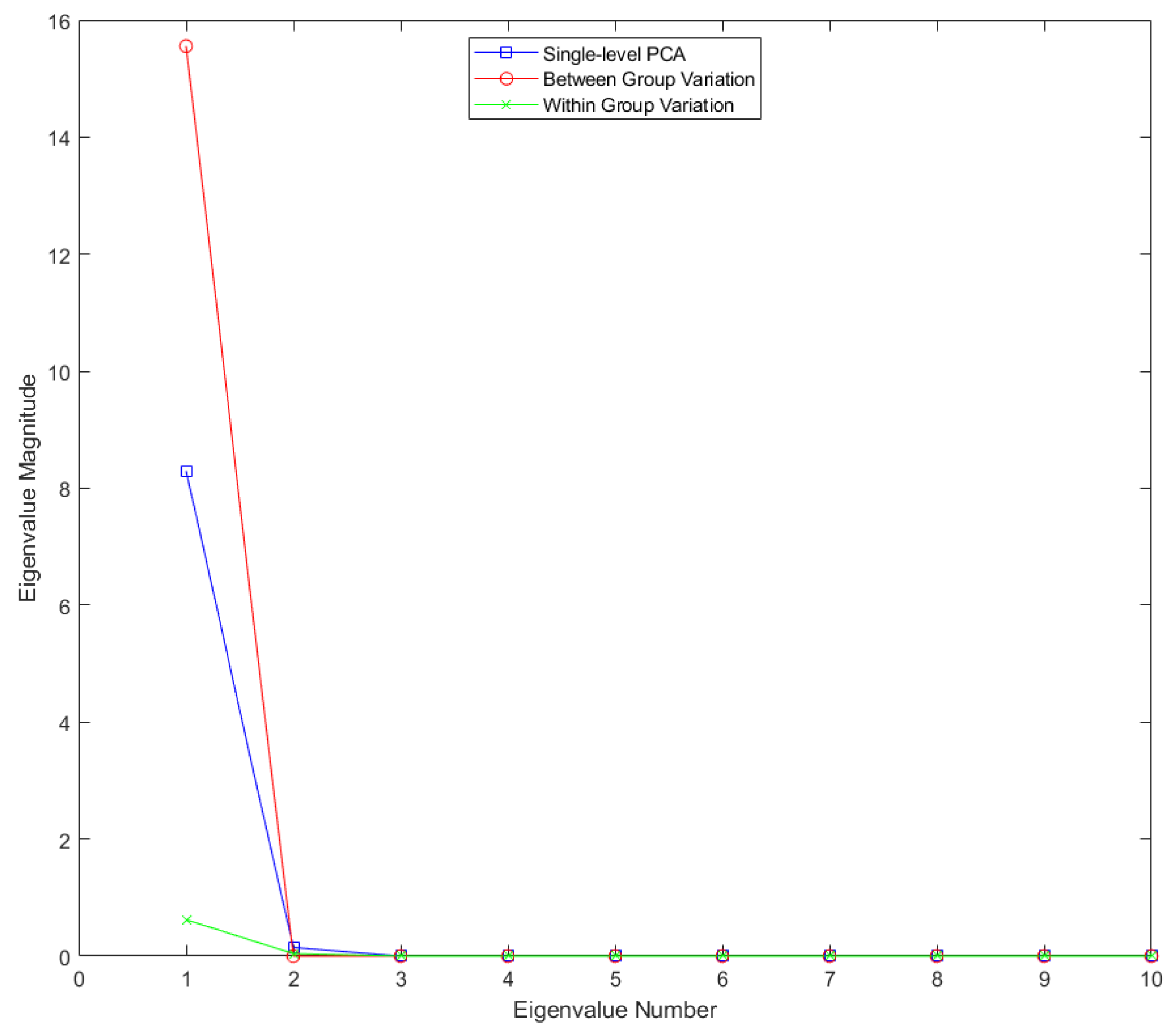
Figure 2. Eigenvalues for single-level FPCA and mFPCA for between-groups variation (level 1) and within-groups variation (level 2) for the Sine Wave dataset.

Results for the eigenvalues from mFPCA and single-level FPCA for the Sine Wave dataset are shown in Figure 2. There is only a single non-zero eigenvalue at level 1 (between-groups variation) via mFPCA, which is what we expect as the number of groups in this simple simulation is two. By contrast, there are three non-zero eigenvalues at level 2 (within-groups variation) via mFPCA, albeit with magnitudes less than approximately 0.03; this is to be expected as the between-group variation was set to be much larger than other (random) sources of variation. Three non-zero eigenvalues are found also for single-level FPCA, which agrees well with results at level 2 (within-groups variation) via mFPCA. The single large eigenvalue at level 1 via mFPCA is also clearly echoed in the first eigenvalue for single-level FPCA, as expected. Interestingly, the magnitude of this first eigenvalue is much lower for single-level FPCA compared to level 1, mFPCA; we speculate that this is because single-level FPCA is not capturing all of the variation of the data. The other two eigenvalues for single-level FPCA also have magnitude less than approximately 0.03.

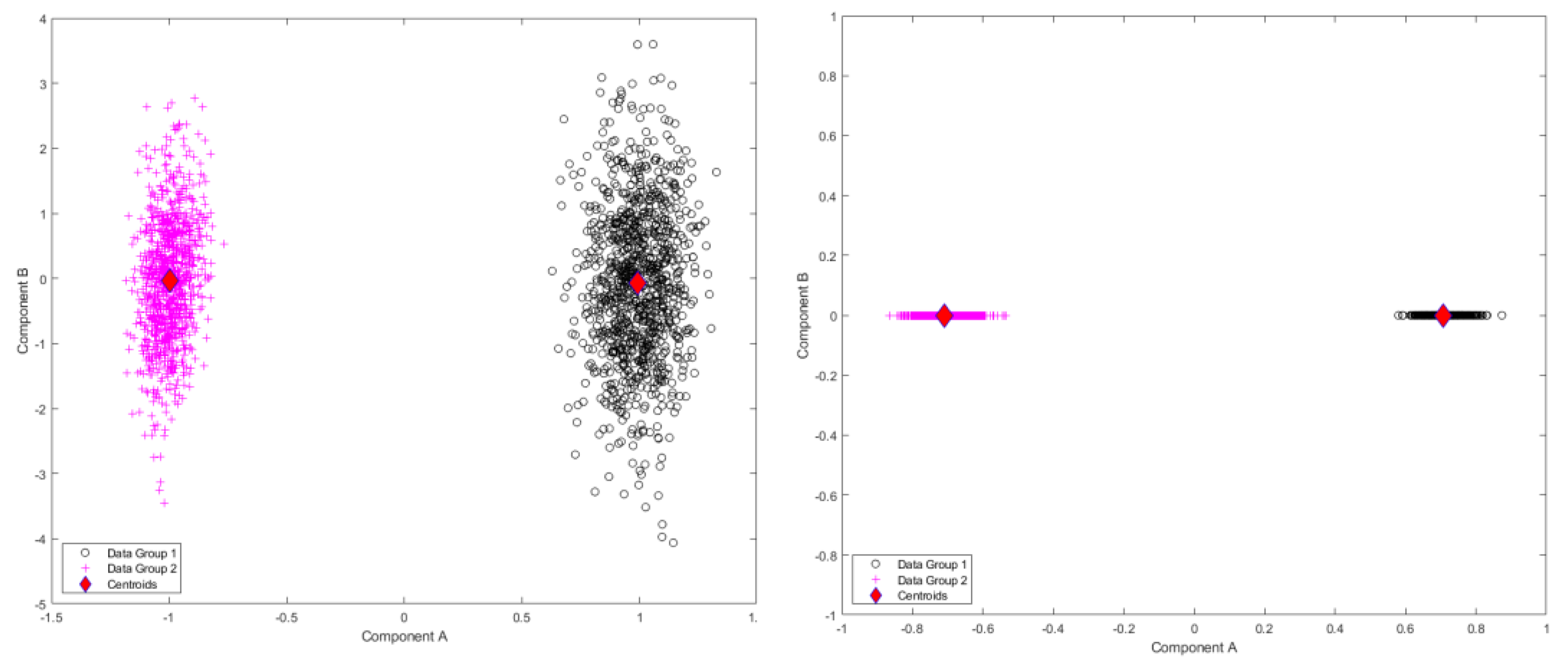
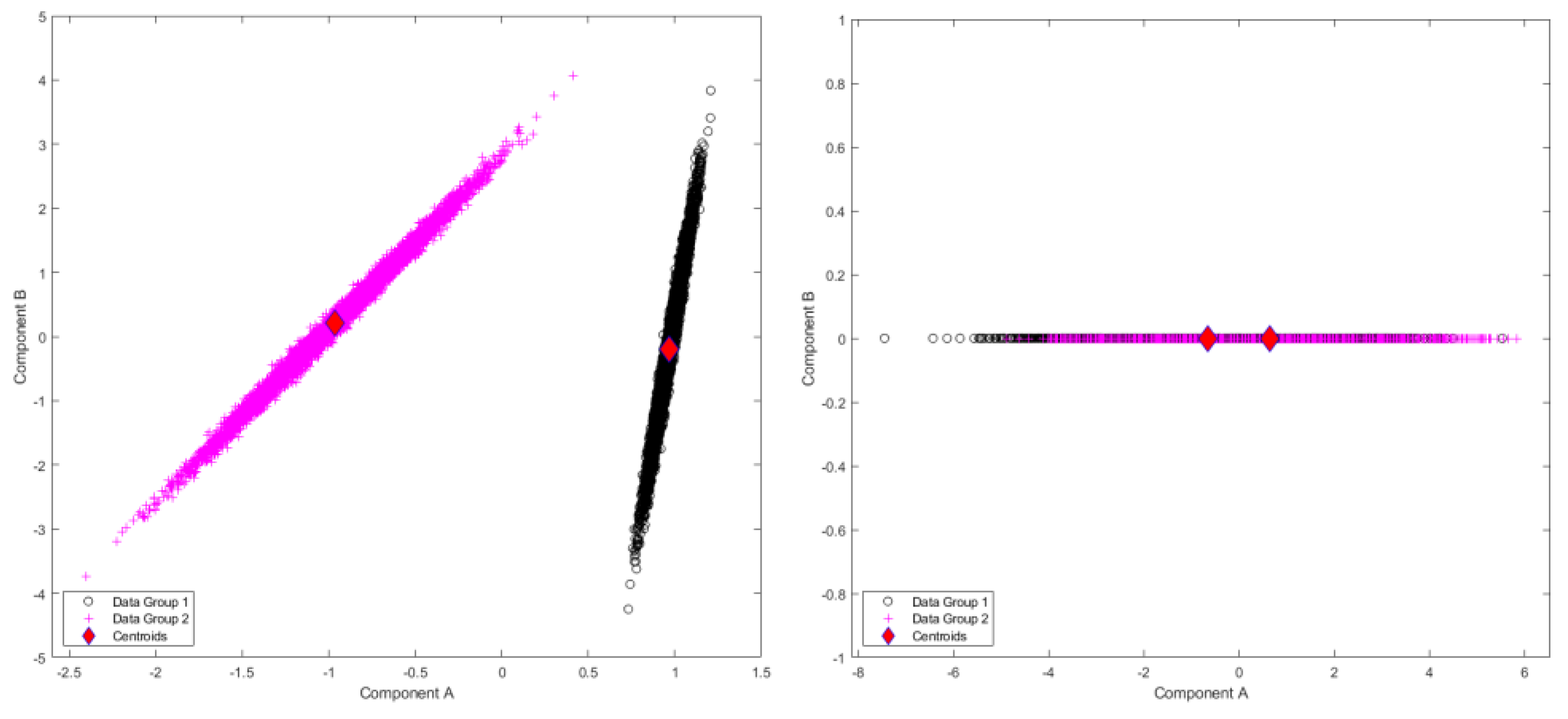
Figure 3. Results of standardized component scores for the test set of 1000 different trajectories per group in the test set for the Sine Wave dataset: (left) single-level FPCA; (right) level 1, mFPCA. These results show a strong clustering into the two groups.

Results for standardized component scores via single-level FPCA and mFPCA are shown in Figure 3. We see that strong differentiation between groups is seen for mode 1 in single-level FPCA. Strong differences between groups are also observed in Figure 3 at level 1 via mFPCA. No strong difference in component scores between groups is seen at level 2 for mFPCA and centroids for these group are congruent (not showed here).

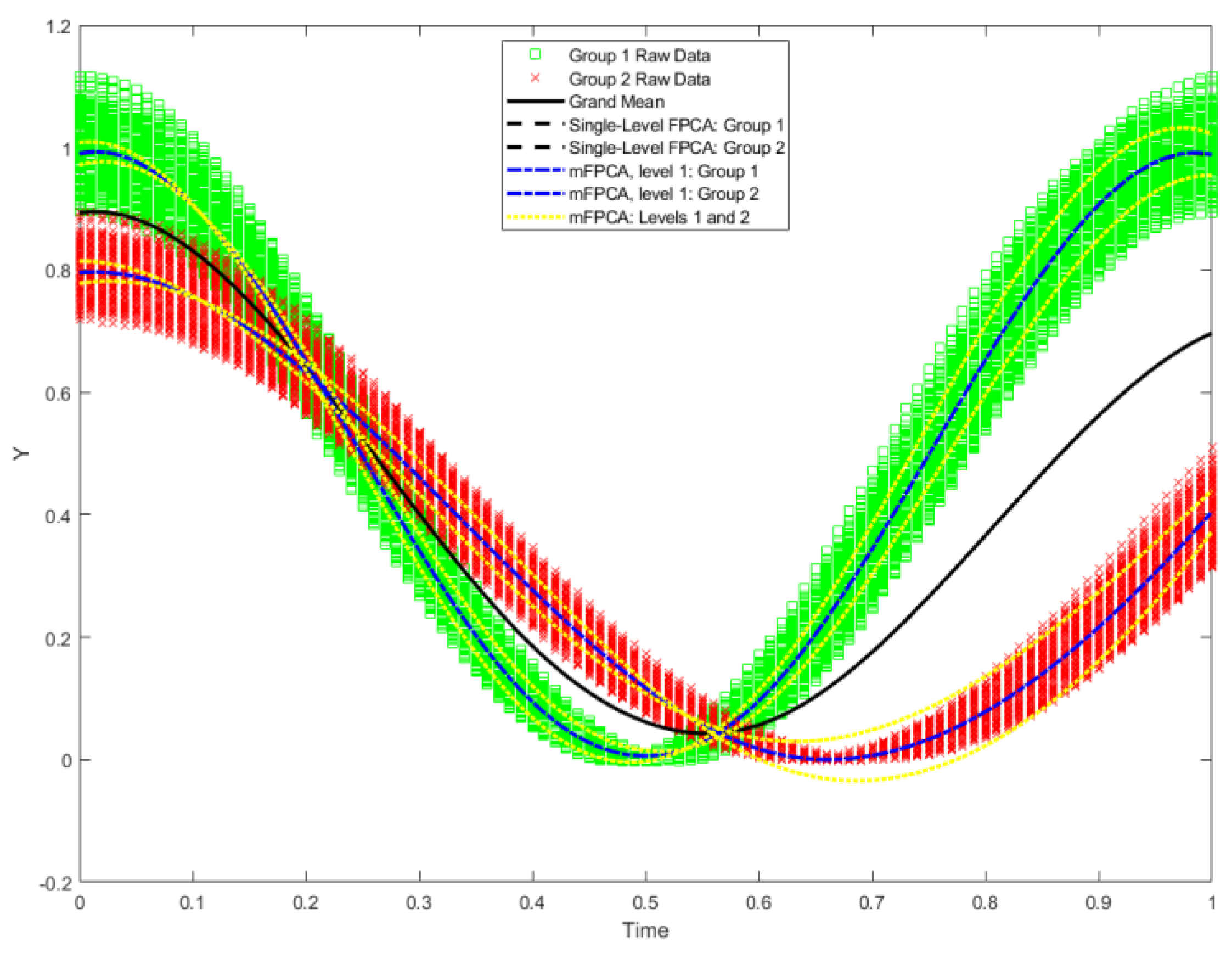
By using the centroids of standardized component scores shown in Figure 3, we may fit the single-level FPCA model and mFPCA at level 1 (between-group variation) only to the raw data in the test set and results are shown in Figure 4. Results for model fits via single-level FPCA model and mFPCA clearly capture mean trajectories with time for the two groups. These results for the two groups are also almost congruent at all time points. We also add in an additional source of variation at level 2, namely, model fit for mFPCA for each group plus/minus the first model at level 2, i.e., ±

1.96 \times \sqrt{θ_{1}^{2}} \times ψ_{1}^{2}

, which is essentially a 95% prediction interval with respect to this mode. We see that within-group variation around these two curves are being captured correctly (broadly). Presumably even better correspondence would be obtained by adding in more modes at level 2. All in all, the Sine Wave dataset has been a successful test of the mFPCA method.

Figure 4. Data for the two groups in the test set of the Sine Wave dataset are shown by the green squares and red crosses (1000 trajectories per group). The overall “grand mean” is shown also. Model fits of single-level FPCA (first mode only denoted “Single-level FPCA: Group 1 / 2”) and mFPCA (first mode at level 1 only denoted “mFPCA, Level 1: Group 1 / 2”) based on the centroids in Figure 3 are shown also. Within-group (level 2) variation is added the model fit for mFPCA for each group (i.e., ±

1.96 \times \sqrt{θ_{1}^{2}} \times ψ_{1}^{2}

, denoted “mFPCA: Levels 1 and 2”).

1.96 \times \sqrt{θ_{1}^{2}} \times ψ_{1}^{2}

, denoted “mFPCA: Levels 1 and 2”).

3.2. Blink Dataset

Figure 5. Eigenvalues for single-level FPCA and mFPCA for between-groups variation (level 1) and within-groups variation (level 2) for the Blink dataset.

Results for the eigenvalues from mFPCA and single-level FPCA for the Blink dataset are shown in Figure 5. Again, there is only a single non-zero eigenvalues at level 1 (between-groups variation) via mFPCA, which again is what we expect as the number of groups in this simple simulation is just two (i.e. for “blinking” and “surprise” type trajectories). By contrast, there are 2 non-zero eigenvalues at level 2 (with-groups variation) via mFPCA, although the magnitude of these eigenvalues are much smaller than the single eigenvalue at level 1, which again is as expected. Three non-zero eigenvalues are found also for single-level FPCA, which also agrees well with results at level 2 (within-groups variation) via mFPCA. The single large eigenvalue at level 1 via mFPCA again also clearly reflected in the first eigenvalue for single-level FPCA. Interestingly again, the magnitude of this eigenvalue is much lower for single-level FPCA.

Figure 6. Results of standardized component scores for the test set of 10000 different trajectories per group in the test set for the Blink dataset: (left) single-level FPCA; (right) level 1, mFPCA. These results again show a strong clustering into the two groups (i.e., “surprised” in group 1 and “blinking” in group 2.).

Results for standardized component scores via single-level FPCA and mFPCA are shown in Figure 6. We see that strong differentiation between groups is again seen just for mode 1 for single-level FPCA. The magnitude of differences in centroids of standardized component scores for the two groups are of order two for single-level FPCA and of order one at level 1 via mFPCA, as shown in Figure 6. This suggests that strong differences occur between groups, although clearly Figure 6 also shows that there is much overlap between individual scores at level 1 via mFPCA. We note that this level has a single non-zero eigenvalue only because the rank of the covariance matrix, and so the maximum number of eigenvalues, is constrained to be no larger than the number of groups minus one. (Here there are just two groups). Again, no strong difference in component scores between groups is seen at level 2 for mFPCA and centroids for these group as congruent (not showed here).

Two specific cases from the test dataset (randomly chosen) may be explored via mFPCA by using exactly the same two-level model for both cases. Here we use just the single mode at level 1 only and no level 2 variation and results are shown in Figure 7. We see that FPCA correctly models the trajectories of all points delineating the boundary of the “eye” and at all stages of either the “surprised” expression or the “blinking” dynamic shape changes using the same model. Better model fits might be obtained by including additional modes from level 2, although we need to be careful not to overfit to the data. However, this is another excellent test of the viability of this method – now also for multivariate data.

Figure 7. mFPCA model fits (full lines) to entire trajectories (going from left to right in the images above) of the 16 2D landmark points of two specific examples chosen randomly from the test set: (upper row of images) from group 1: an eye “showing surprise,” i.e., the eye opens wider before returning to normal; (upper row of images) from group 2: an eye “blinking,” i.e., the eye closes before returning to normal. (The iris is added as an illustration only.).

3.3. Smile Dataset

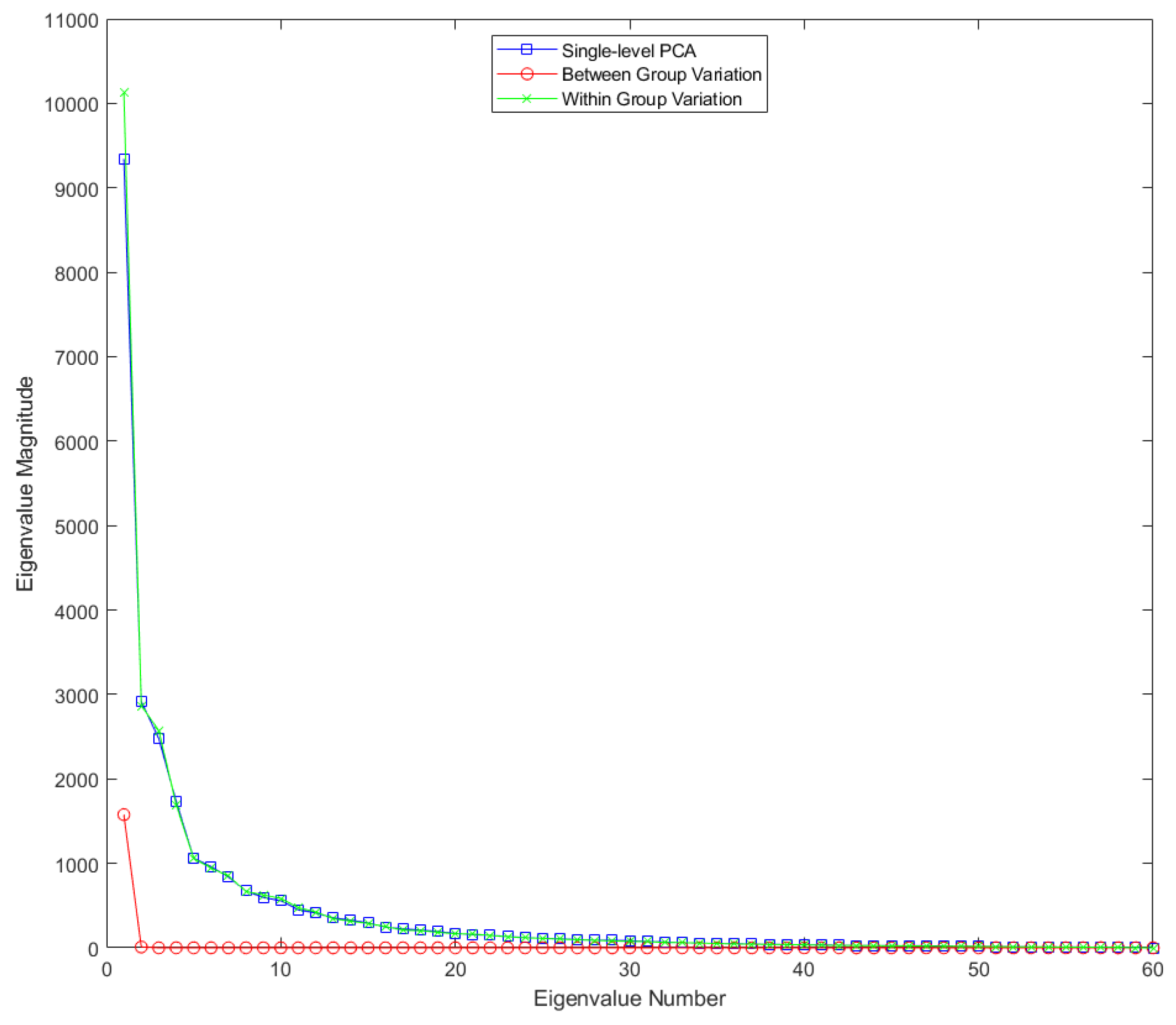
Figure 8. Eigenvalues for single-level FPCA and mFPCA for between-groups variation (level 1) and within-groups variation (level 2) for the Smile dataset.

Results for the eigenvalues from mFPCA and single-level FPCA for the Smile dataset are shown in Figure 8. Results of level 2 via mFPCA are almost congruent with single-level FPCA. The single eigenvalue at level 1 via mFPCA is of much smaller magnitude than those eigenvalues at level 2. This is the first evidence that the magnitude of the difference in smile dynamics between males and females is small.

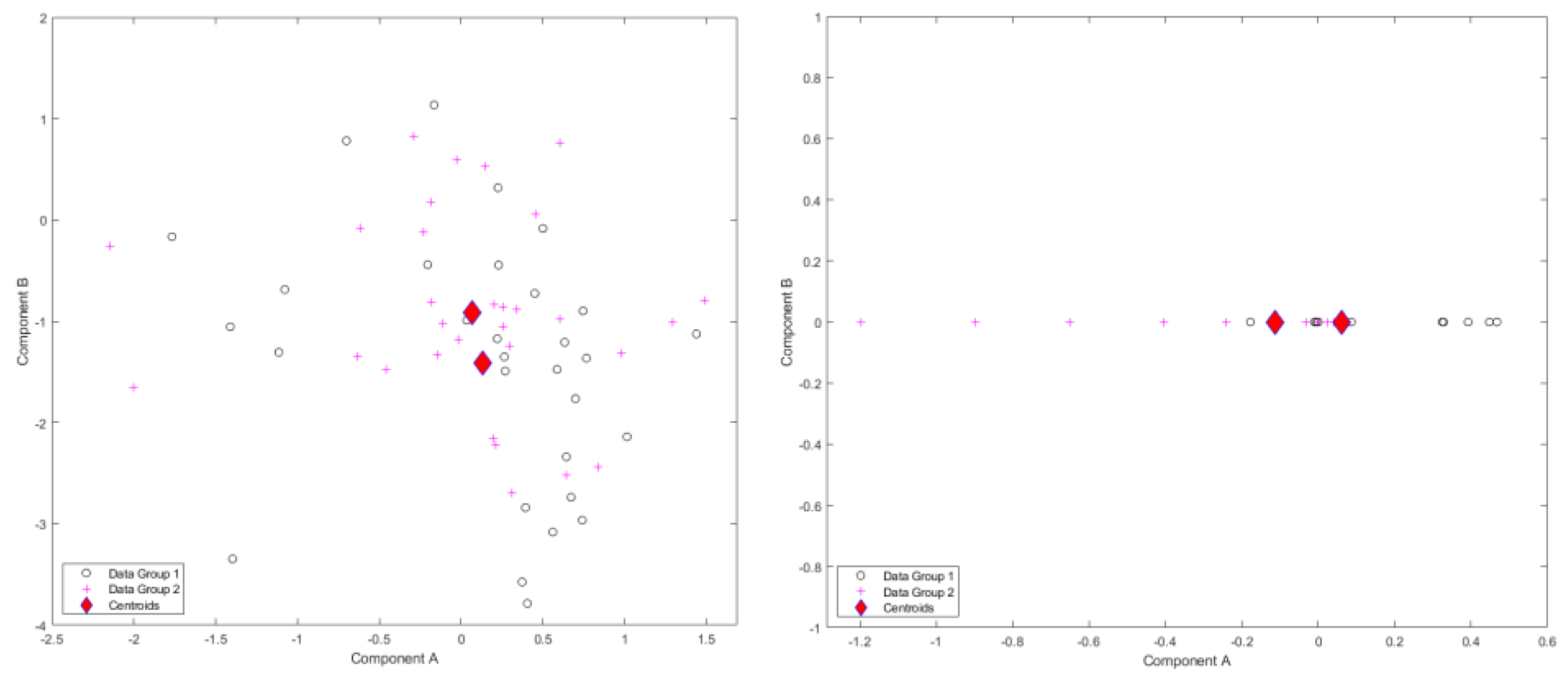
Figure 9. Results of standardized component scores for the Smile dataset: (left) single-level FPCA; (right) level 1, mFPCA. These results show only minor differences in dynamic 3D trajectories between males and females as the centroids for the two groups are quite close together.

Results for standardized component scores via single-level FPCA and mFPCA for the Smile dataset are shown in Figure 9. By contrast to the earlier simulated dataset, differences between groups (males and females) appears quite small for both single-level FPCA and mFPCA at level 1. This is yet more evidence that no strong differences in the 3D dynamics of smiles occur between men and women. Again, no strong difference in component scores between groups is seen at level 2 for mFPCA and centroids for males and females are congruent (not showed here).

Figure 10. Visualization of the first mode of variation via mFPCA at level 1 in the frontal / coronal plane (left) and horizontal plane (right) in each image. (Left Column) start of the smile; (Middle Column) mid-point (apex or plateau) of the smile; (Right Column) end of the smile. (Top row) mean shape trajectory; (Middle Row) mean shape trajectory minus

\sqrt{θ_{1}^{1}}

× first mode of variation via mFPCA at level 1; (Bottom Row) mean shape trajectory plus

\sqrt{θ_{1}^{1}}

× first mode of variation via mFPCA at level 1.

\sqrt{θ_{1}^{1}}

× first mode of variation via mFPCA at level 1; (Bottom Row) mean shape trajectory plus

\sqrt{θ_{1}^{1}}

× first mode of variation via mFPCA at level 1.

Results for the mean smile trajectory and also the first mode of variation at level 1 via mFPCA are shown in Figure 10. The results shown in Figure 10 with respect to time are subtle to interpret. However, it is possible to see from a “movie” of shape changes with respect to time for the mean that the corners of the mouth are pulled outwards and backwards slightly as time evolves, before returning somewhat close to the original shape at the end of the smile. The first mode of variation at level 1 (between sexes) is definitely subtle; this mode is quite weak in magnitude and appears to govern the width of the lips and relative positions of upper and lower lips. A “movie” of shape changes with respect to time of the trajectory for the mean plus or minus this mode indicates again that the corners of the mouth are pulled outwards and backwards slightly as time evolves, before returning somewhat close to the original shape at the end of the smile (with some increased noise right at the end).

Figure 11. Visualization of the first mode of variation via mFPCA at level 2 in the frontal / coronal plane (left) and horizontal plane (right) in each image. (Left Column) start of the smile; (Middle Column) mid-point (apex or plateau) of the smile; (Right Column) end of the smile. (Top row) mean shape trajectory; (Middle Row) mean shape trajectory minus

\sqrt{θ_{1}^{2}}

× first mode of variation via mFPCA at level 2; (Bottom Row) mean shape trajectory plus

\sqrt{θ_{1}^{2}}

× first mode of variation via mFPCA at level 2.

\sqrt{θ_{1}^{2}}

× first mode of variation via mFPCA at level 2; (Bottom Row) mean shape trajectory plus

\sqrt{θ_{1}^{2}}

× first mode of variation via mFPCA at level 2.

Results for the mean smile trajectory and also the first mode of variation at level 2 are shown in Figure 11. The results are much easier to interpret than those in Figure 10. We see that this mode is clearly governing whether the natural “resting” mouth shape is either up-turned or down-turned. A “movie” of shape changes with respect to time of the trajectory for the mean plus or minus this mode indicates again that the corners of the mouth are pulled outwards and backwards slightly as time evolves, before again returning somewhat close to the original shape at the end of the smile (again with some increased noise right at the end). Note that this pattern with time is superimposed on upturned (mean minus this mode) or downturned (mean plus this mode) mouth shape appropriately for the entire trajectory, as illustrated in Figure 11.

Figure 12. Example of model fits at five time points during specific trajectory for a single subject via mFPCA for the frontal / coronal plane. (Increasing time is shown from left to right.) Points for the raw data are shown by the filled circles and the model fits are given by the curved lines.

Results in the frontal / coronal plane of the model fit to the twelve points for a specific person’s trajectory are shown in Figure 12. We see that excellent fits are obtained at all time points shown. Again, the time evolution is somewhat subtle for this case, although a “movie” of points and model fits indicates that the width of the mouth increases very slightly with time and then starts to reduce at the end. These results for the Smile dataset have been another excellent test of the mFPCA method for “real” data.

4. Discussion

A form of multilevel functional PCA (mFPCA) was presented here and it was applied to model dynamical changes in biological shapes. Results for simulated data for a single variable with two groups and for “blink” data with 32 variables (16 2D points) and two groups were shown to be modelled correctly, i.e., trajectories appeared correct, and magnitude of eigenvalues made sense given the data generation model. The two dynamic trajectories of “surprise” and “blinking” were modelled adequately using the same multilevel model and strong differences between these trajectories was evident in both single-level FPCA and also at level 1 of mFPCA model, as expected (and required). This is an encouraging first step.

However, this is exactly what one would expect for such simple simulated datasets. It is therefore important to test the method also for “real” data. This was provided here via the “smile” dataset of Refs. [10,11] consisting of 12 points placed on the outer boundary of the lips during entire smile trajectories for 29 females and 31 males. Again, dynamic smiles appeared to be modelled correctly when compared to the original data. Interestingly, differences between males and females appeared small in terms of magnitude of variation and also differences between groups for standardized component scores. Indeed, there is no reason to suppose that males and females smile in fundamental different ways (i.e., a smile is just a smile) and so this is an excellent test of “no effect” in terms of differences between groups. Broadly, we take all of these results as an excellent test of method – both single-level FPCA and mFPCA can be applied to model shapes dynamically.

A limitation of mFPCA (as in bgPCA / mPCA) are that small numbers of groups can limit the number of non-zero eigenvalues (the rank of covariance matrices are reduced) at higher levels of the model. Another well-known “pathology” of bgPCA and multilevel PCA is that small sample sizes can lead to spurious differences between groups [3,12,18] because small differences between groups in terms of the positions of all points can become concentrated by dimensionality reduced. Although this can occur for standard PCA, this effect is more pronounced for bgPCA and mPCA because both are essentially a form of “guided” dimensionality reduction where differences between groups are concentrated at one specific level of the model. However, various techniques [18–20] have been proposed to address such effects, including cross validation [19]. Monte Carlo simulations in Ref. [12] suggest that the number of subjects per group should be at least equal to the number of parameters (here the number of points multiplied by spatial dimensionality). It is likely that similar “pathologies” occur also for mFPCA. This is particularly true for the implementation presented here where the number of parameters depends on the number of time points and the number of points.

Clearly also, the functional approaches considered here rely on spline fits with respect to time to produce trajectories for subsequent estimation of shapes at specific time points (here, time points that are sampled regularly over some overall period). Indeed, many of the practical aspects of implanting FPCA appear to depend on the choice of method of curve fitting / smoothing procedures [13]. Here we wished only to carry out a proof-of-principle of method and so we used a simple (cubic) spline fit (in MATLAB) to the data for each point component separately. This appeared to work well for both the simulated and real data, established by visual inspection of model fits to the (test) data.

There are many advantages to using a multilevel approach, especially for trajectories of dynamical shapes where paths for different groups (e.g., facial expressions for subjects with and without facial paralysis and / or for different types of expression) are likely to be radically different. In these cases, a multilevel approach should provide a more efficient and effective model because average trajectories for each group are found explicitly. Furthermore, mFPCA allows us to quantify and explore differences between groups. For example, it was shown in this article that differences in shape between phases of a smile are likely to be large, whereas overall differences in how people smile dynamically is likely to be small between males and females (as expected). Finally, we believe that models that take into account differences between groups explicitly (e.g., images or shapes from different types of scanners), as well as differences within groups, might generalize more effectively than those that do not.

Future work will concentrate on validating this new approach to study other types of dynamical objects. The issues of “pathologies” of mFPCA and choice of optimal curve fitting and smoothing algorithms will also be explored in future also. Finally, ideas of clustering and hierarchies in the image or subject set will be explored also in the context of Deep Learning.

Author Contributions

Conceptualization, D.J.J.F. and P.C.; methodology, D.J.J.F.; software, D.J.J.F.; validation, D.J.J.F. and P.C.; formal analysis, D.J.J.F.; investigation, D.J.J.F. and P.C; writing—original draft preparation, D.J.J.F.; writing—review and editing, D.J.J.F. and P.C.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This project was reviewed and approved by the School of Dentistry Ethics Committee at Cardiff University, UK.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We thanks Profs. David Marshall and Paul Rosin at Cardiff University for allowing use landmark points for the “Smile” dataset.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix

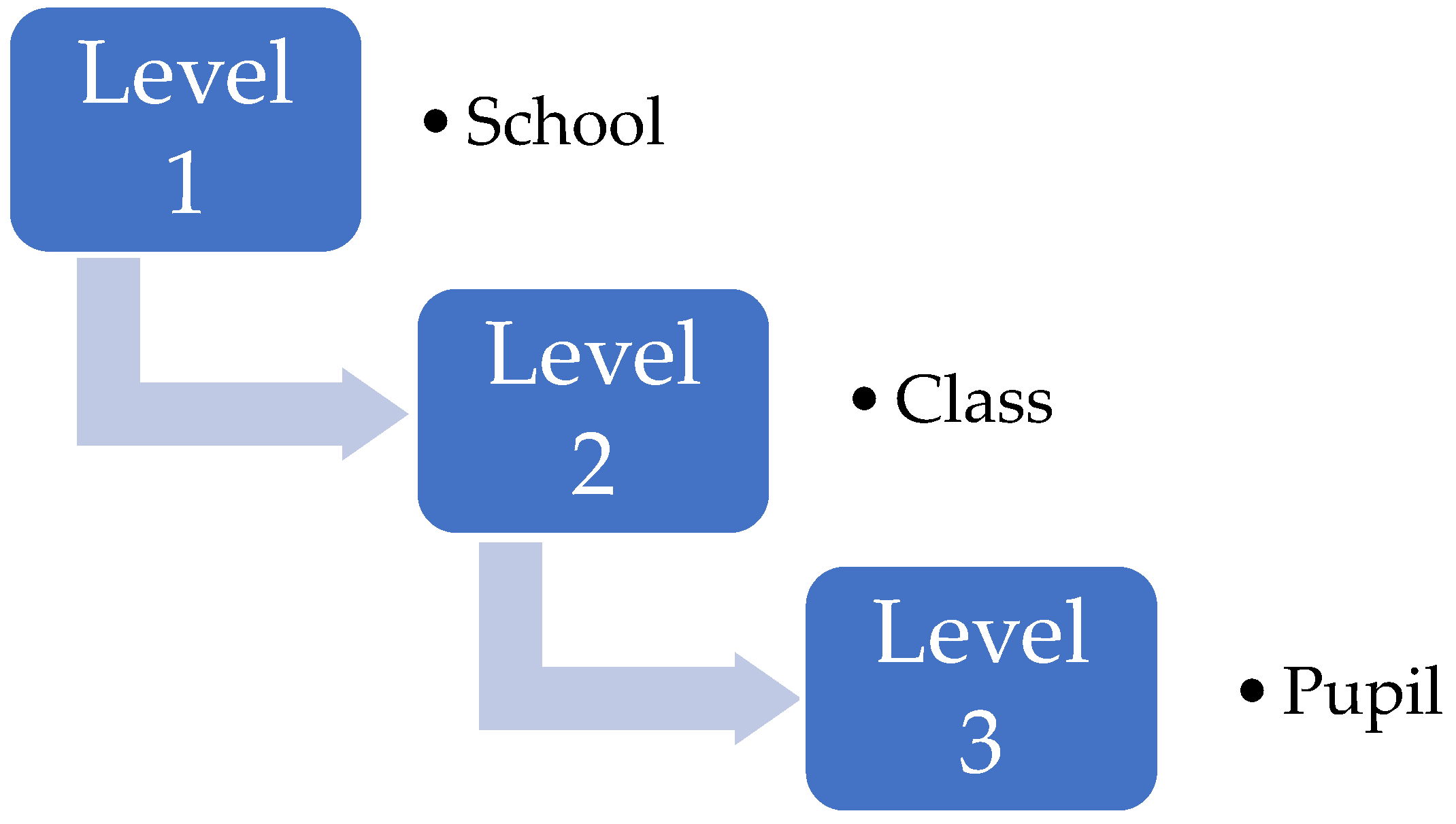
Figure A1. Example of a nested model, here for (say) marks in a test for pupils in a school. Individual pupils are at the lowest level (level 3), where each pupil belongs to just one class in level 2. Furthermore, each class belongs to just one school. Variation can occur at all levels of the models: between pupils in each class; between classes in each school; and between schools.

Again, we assume initially that the outcome is a scalar and that trajectory data has been sampled regularly at

T

time points. For three-level mFPCA, elements of the covariance matrix at level 3 for each group

j

K_{s, t}^{3, j} = \frac{1}{n_{j} - 1} \sum_{i}^{n_{j}} (X_{s}^{i, j} - η_{t}^{3, j}) (X_{t}^{i, j} - η_{t}^{3, j})

(A1)

η^{3, j}

is the mean for each group

j

at level 3, given by

η^{3, j} = \frac{1}{n_{j}} \sum_{i}^{n_{j}} X^{i, j}

(A2)

The “common” covariance matrix at level 3 is defined by

K^{3, j} = \frac{1}{p_{3}} \sum_{j}^{p_{3}} K^{3, j}

(A3)

Note that there are

p_{3}

groups in total at level 3. The analysis has, thus far, followed that of the 2-level model. For nested mFPCA, we now notice that means themselves may belong to specific groups in the level above them (e.g., classes in specific schools as shown in Figure B1). The means at level two are

η^{2, k} = \frac{1}{n_{k}} \sum_{j}^{n_{k}} η^{3, j}

(A4)

n_{k}

is the number of groups at level three that belong to the specific group

k

in level 2. Elements of the the covariance matrix at level 2 for each group

k

are given by

K_{s, t}^{2, k} = \frac{1}{m_{k} - 1} \sum_{i j}^{m_{k}} (η_{s}^{3, j} - η_{s}^{2, k}) (η_{t}^{3, j} - η_{t}^{2, k})

(A5)

The “common” covariance matrix at level 2 is defined by

K^{2} = \frac{1}{p_{2}} \sum_{k}^{p_{2}} K^{2, k}

(A6)

Note that there are

p_{2}

groups at level 2. The “grand mean” at level 1 is now given by

K^{2} = \frac{1}{p_{2}} \sum_{k}^{p_{2}} K^{2, k}

(A7)

Elements of the covariance matrix at level 1 are written finally as

K_{s, t}^{1} = \frac{1}{p_{2} - 1} \sum_{k}^{p_{2}} (η_{s}^{2, k} - η_{s}^{1}) (η_{t}^{2, k} - η_{t}^{1})

(A8)

θ_{l}^{1}

θ_{l}^{2}

, and

θ_{l}^{3}

are non-negative eigenvalues at levels 1, 2 and 3, and

ψ_{l, t}^{1}

ψ_{l, t}^{2}

, and

ψ_{l, t}^{3}

are the associated eigenfunctions at these levels. Again, the number of non-zero eigenvalues at levels 1 and 2 will be limited to the finite numbers of groups at these levels. The expansion of any (new) dynamic shape

X_{t}^{n e w}

is given by

X^{n e w} = η^{1} + \sum_{l}^{m_{1}} a_{l}^{1} ψ_{l}^{1} + \sum_{l}^{m_{2}} a_{l}^{2} ψ_{l}^{2} + \sum_{l}^{m_{3}} a_{l}^{3} ψ_{l}^{3}

(A9)

Again,

a_{l}^{1}

a_{l}^{2}

, and

a_{l}^{3}

are scalar coefficients and

m_{1}

m_{2}

, and

m_{3}

are set to be finite numbers. The coefficients

{a_{l}^{1}}

{a_{l}^{2}}

and

{a_{l}^{3}}

may again be obtained by using a global optimization procedure in MATLAB. The extension to 4 or more levels for a fully nested model (reflecting the data) follows the pattern as that established above. Similarly, multivariate data can be tackled readily also by concatenating shape vectors at all time points. Non-nested cases (where there is no natural “nested” order to the data) may be carried out as for mPCA as described in an Appendix in Ref. [8]. An example of a non-nested cases might be marks in a test for groupings by both school and sex; there is no natural order to either sex or school, though one might posit that clustering might be possible via both variables.

References

Zelditch, M.L.; Swiderski D.L.; Sheets H.D. Geometric morphometrics for biologists: a primer. (Academic Press 2012).
Botton-Divet, L.; Houssaye, A.; Herrel, A.; Fabre, A.C.; Cornette, R. Tools for quantitative form description; an evaluation of different software packages for semi-landmark analysis. PeerJ 2015, 3, e1417. [Google Scholar] [CrossRef] [PubMed]
Bookstein, F.L. Pathologies of between-groups principal components analysis in geometric morphometrics. Evol. Biol. 2019, 46, 271–302. [Google Scholar] [CrossRef]
Cardini, A.; O’Higgins, P.; Rohlf, F.J. Seeing distinct groups where there are none: spurious patterns from between-group PCA. Evol. Biol. 2019, 46, 303–316. [Google Scholar] [CrossRef]
Farnell, D.J.J.; Popat, H.; Richmond, S. Multilevel principal component analysis (mPCA) in shape analysis: A feasibility study in medical and dental imaging. Comput. Methods Programs Biomed. 2016, 129, 149–159. [Google Scholar] [CrossRef] [PubMed]
Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Perttiniemi, P.; Katic, V. Initial Results of Multilevel Principal Components Analysis of Facial Shape. Commun. Comput. Inf. Sci. 2017, 723, 674–685. [Google Scholar]
Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S. Multilevel Models of Age-Related Changes in Facial Shape in Adolescents. Commun. Comput. Inf. Sci. 2020, 1065, 101–113. [Google Scholar]
Farnell, D.J.J.; Richmond, S.; Galloway, J.; Zhurov, A.I.; Pirttiniemi, P.; Heikkinen, T.; Harila, V.; Matthews, H.; Claes, P. Multilevel Principal Components Analysis of Three-Dimensional Facial Growth in Adolescents. Comput. Methods Programs Biomed. 2019, 188, 105272. [Google Scholar] [CrossRef] [PubMed]
Galloway, J.; Farnell, D.J.J.; Richmond, S.; Zhurov, A.I. Multilevel Analysis of the Influence of Maternal Smoking and Alcohol Consumption on the Facial Shape of English Adolescents. J. Imaging 2020, 6, 34. [Google Scholar] [CrossRef] [PubMed]
Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Perttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Results of Multilevel Principal Components Analysis of Facial Shape and Image Texture. Commun. Comput. Inf. Sci. 2018, 894, 177–188. [Google Scholar]
Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Marshall, D.; Rosin, P.L.; Al-Meyah, K.; Perttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance. J. Imaging 2019, 5, 2. [Google Scholar] [CrossRef] [PubMed]
Farnell, D.J.J. An exploration of pathologies of multilevel principal components analysis in statistical models of shape. J. Imaging 2022, 8, 63. [Google Scholar] [CrossRef] [PubMed]
Warmenhoven, J.; Bargary, N.; Liebl, D.; Harrison, A.; Robinson, M.A.; Gunning, E.; Hooker, G. PCA of waveforms and functional PCA: a primer for biomechanics. J. Biomech. 2021, 116, 110106. [Google Scholar] [CrossRef] [PubMed]
Hall, P.; Hosseini-Nasab, M. On properties of functional principal components analysis. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 109–126. [Google Scholar] [CrossRef]
Shang, H.L. A survey of functional principal component analysis. AStA Adv. Stat. Anal. 2014, 98, 121–142. [Google Scholar] [CrossRef]
Di, C.Z.; Crainiceanu, C.M.; Caffo, B.S.; Punjabi, N.M. Multilevel functional principal component analysis. Ann. Appl. Stat. 2009, 3, 458. [Google Scholar] [CrossRef] [PubMed]
Zipunnikov, V.; Caffo, B.; Yousem, D.M.; Davatzikos, C.; Schwartz, B.S.; Crainiceanu, C. Multilevel functional principal component analysis for high-dimensional data. J. Comput. Graph. Stat. 2011, 20, 852–873. [Google Scholar] [CrossRef] [PubMed]
Rohlf, F.J. Why Clusters and Other Patterns Can Seem to be Found in Analyses of High-Dimensional Data. Evol. Biol. 2021, 48, 1–16. [Google Scholar] [CrossRef]
Cardini, A.; Polly, P.D. Cross-validated Between Group PCA Scatterplots: A Solution to Spurious Group Separation? Evol. Biol. 2020, 47, 85–95. [Google Scholar] [CrossRef]
Thioulouse, J.; Renaud, S.; Dufour, A.B.; Dray, S. Overcoming the Spurious Groups Problem in Between-Group PCA. Evol. Biol. 2021, 48, 458–471. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multilevel Functional Principal Components Analysis Presents a Viable Method of Modelling Dynamical Shape Changes

Abstract

1. Introduction

2. Materials and Methods

2.1. Monte Carlo Data Generation

2.2. Smile Dataset

2.3. Functional Principal Components Analysis (FPCA)

2.4. Multilevel Functional Principal Components Analysis (mFPCA)

3. Results

3.1. Sine Wave Dataset

3.2. Blink Dataset

3.3. Smile Dataset

4. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix

References

MDPI Initiatives

Important Links

Subscribe