Prerpints.org logo
Preprint
Article

Experimental-AI Investigation of the Effect of Particle Shape on the Damping Ratio of Dry Sand under Simple Shear Test Loading

Altmetrics

Downloads

268

Views

116

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 February 2023

Posted:

01 March 2023

You are already at the latest version

Alerts
Abstract
This paper reports on a series of dynamic simple shear tests conducted to investigate the influence of particle shape on the damping ratio of dry sand. The tests were conducted on sand samples subjected to simple cyclic shear tests to evaluate their cyclic behavior. The particle shape was quantified using three shape parameters: roundness, sphericity, and regularity. The sand samples were subjected to twelve different scenarios with varying vertical stresses and cyclic stress ratios (CSR), in both constant and controlled stress states. Each scenario involved five cyclic tests, using the same sand that was reconstructed from its previous cyclic test. After each cyclic test, hysteresis loops were created to determine the damping ratio. The results showed that the shape of the sand particles changed during cyclic loading, becoming more rounded and spherical, which resulted in an increase in damping ratio. Moreover, the paper presents two artificial intelligence models, an artificial neural network (ANN) and a support vector machine (SVM), which were developed to predict the effect of grain shape on the damping ratio. The models were found to be effective in predicting the damping ratio based on the shape of the grain, vertical stress, CSR, and number of loading cycles. Furthermore, a parameter analysis was conducted to identify the most important shape parameter, which was found to be vertical stress and regularity, while parameter CSR was the least important. Overall, this study contributes to a better understanding of the relationship between particle shape and damping ratio, which could have practical implications for geotechnical engineering applications.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Soil damping ratio is one of the fundamental properties of soil that determines its response to various dynamic loads, such as earthquakes, vibrations, and machine operations [1,2,3,4]. The damping ratio is influenced by a number of factors, including the type of soil, particle size, particle shape, and confining pressure. Many researchers are interested in the effect of particle shape on the damping ratio of sand [5,6,7,8,9,10].
Studies have shown that the damping ratio of sand tends to decrease with increasing strain amplitude [7,11,12]. As the amplitude of cyclic loading increases, the soil particles undergo more severe deformations, which results in the energy dissipation through damping being more ineffective. Therefore, it is important to consider the effect of strain amplitude when evaluating the damping ratio of sand [7,11,12].
The stress history of the soil can also affect its damping properties [13,14]. For example, cyclic loading can lead to a buildup of excess pore pressure, which can affect the damping behavior of the soil [15]. The buildup of pore pressure can cause changes in the effective stress, which in turn affects the soil stiffness and damping behavior. Moreover, the magnitude and duration of the cyclic loading can also affect the stress history of the soil, which has an impact on the damping ratio [16].
The degree of saturation of the sand can also affect its damping properties [17,18,19,20]. In general, the damping ratio tends to increase with increasing saturation. The reason for this is that the presence of water in the soil provides a pathway for energy dissipation through viscous damping. As the degree of saturation increases, the viscous damping effect becomes more prominent, which results in a higher damping ratio. However, it should be noted that the effect of saturation on damping is not always consistent and depends on other factors such as the type of soil and the loading conditions [17,18,19,20].
The confining pressure is another parameter that can have an impact on the damping ratio of sand. According to Bayat et al. [21], the damping ratio of sand decreases as confining pressure increases. Similarly, the moisture content of sand has also been investigated with regard to its effect on damping ratios. Ling et al. [22] found that the damping ratio of sand increased with an increase in moisture content. The loading frequency of sand is another factor that can influence its damping ratio. According to Chen et al. [23], sand's damping ratio decreases with increasing loading frequency. Additionally, the particle distribution, or uniformity coefficient, of the sand has been investigated for its influence on damping ratios. According to Wichtmann et al. [24], the damping ratio of sand decreases with increasing uniformity ratio. In general, several factors can affect the damping ratio of sands, including particle shape, grain size, confining pressure, moisture content, loading frequency, and particle distribution [25,26,27,28,29,30]. The complex relationship between these parameters and the damping ratio of sand requires further research.
The present study contributes significantly to the literature by being the first to systematically investigate the impact of particle shape and size on the damping ratio of dry sand, where the minerals are identical, and the only different variable is the shape and size of the particles. The study's unique approach is the use of cyclic loading type to examine the effect of cyclic stress ratio (CSR) loading on the impact of particle shape and size and damping ratio of sands. This type of cyclic loading is particularly useful as it can simulate the effect of earthquakes, which may be important in geotechnical engineering applications. The study aims to demonstrate how particle shape can impact other factors such as void ratios, ultimately leading to changes in damping ratio. The primary objective is to investigate the effect of particle shape on damping ratio of dry sands experimentally. To achieve this, a series of samples of sands with different particle shapes and sizes are tested in a cyclic simple shear apparatus in both constant-stress and controlled-stress modes to determine their damping ratio. The analysis of the results is then incorporated into different correlations in the form of curves. Overall, the study provides novel insights into the relationship between particle shape and damping ratio, which could inform future geotechnical engineering applications.
The study conducted a pioneering investigation into the use of artificial intelligence (AI) models for predicting the damping ratio based on the shape of the grain, vertical stress, CSR, and number of loading cycles. Artificial intelligence methods were used successfully in different areas of geotechnical engineering [31,32,33,34,35,36]. This is the first time that AI models have been applied to this problem. The novelty of this approach lies in its potential to improve the accuracy and efficiency of predicting the damping ratio. Moreover, this study represents an important step towards expanding the use of AI models in the field of geotechnical engineering. After developing the models, the study focused on analyzing the importance of input parameters to gain a deeper understanding of the factors that affect the damping ratio prediction.

2. Materials and Methods

2.1. Sand

The objective of this study is to assess the characteristics of sand gathered from a coastal area. The results provided in Figure 1 are from a particle size analysis and other related tests that were conducted on the used sand sample based on standards [37,38,39]. A particle size analysis is important because it provides valuable information about the properties of the sample, such as its permeability, compressibility, and shear strength, which are essential for various engineering and construction applications. The results of the sieving process were used to draw and determine the particle size distribution, which is expressed in Figure 1 and also in terms of the D10, D30, D50, and D60 values. These values represent the particle size at which 10%, 30%, 50%, and 60% of the sand sample is finer by weight, respectively. The particle size analysis shows that the sand has a D10 of 0.19 mm, a D30 of 0.245 mm, a D50 of 0.265 mm, and a D60 of 0.275 mm. Moreover, the uniformity coefficient (Cu) and curvature coefficient (Cc) values of 1.447 and 1.149 respectively indicate that according to the Unified Soil Classification System (UCSC) the sand is poorly graded.
In addition to the particle size analysis, the sand sample was also tested for its specific gravity (Gs), minimum and maximum void ratios (emin and emax). The specific gravity is a measure of the density of the sand particles, while the minimum and maximum void ratios provide information about the compaction characteristics of the sand. The specific gravity of sand was 2.65, and the minimum and maximum void ratios (emin and emax) of 0.76 and 1.07 respectively show that the sand has a relatively low maximum compactness.
To better understand the nature of the sand, several mineralogical studies were conducted. The results indicate that the main mineral present in the sand is quartz, followed by minor minerals such as magnesium silicate and aluminum silicate.

2.2. Simple Shear Apparatus and Test Plan

The study employed a 2D simple shear test to assess the properties of sand samples under cyclic loading conditions. The test involved applying forces in two directions, a vertical force along the sample's axis and a shear force parallel to its horizontal surface. To generate cyclic shear stresses, a dynamic simple shear test was used with a frequency of 0.5 Hz. The samples, with a diameter of 70 mm and a height of 20 mm, were prepared using dry sand and wet tamping method with a moisture content of 7%, as per Ladd [40].
Figure 2 illustrates a schematic diagram of the dynamic simple shear test, wherein the samples were subjected to sinusoidal shear stress. The test is useful in determining the shear strength, deformation characteristics, and stress-strain behavior of the sand samples. The data obtained from this test is crucial in understanding the response of soil and sand materials to cyclic loading, which is relevant to various applications such as the design of foundations, retaining walls, and embankments.
The methodology of this study involved investigating the behavior of sand through a series of cyclic tests. Prior to this, a monotonic test was performed on the sand, which demonstrated dilative behavior, as noted by Baghbani et al. [41]. The cyclic tests were carried out on samples with a relative density of approximately 45%, and vertical stresses of 50, 150, and 250 kPa were applied. Different cyclic stress ratios (CSR) were employed for each test. The cyclic loading involved applying a vertical load at a rate of 5 N/sec, followed by sinusoidal shear loading. Constant-stress and stress-control modes were utilized during the cyclic tests, with the same sample being used for five repetitions under identical conditions.
CSR loading is commonly used to evaluate the resistance of soil to cyclic loading and its ability to withstand repeated cycles of stress and strain. This method directly applies cyclic stress to the soil, and the soil's response is measured in terms of strain. CSR loading is particularly useful in simulating the loading conditions experienced by soils during an earthquake, especially for soils with a low plasticity index.
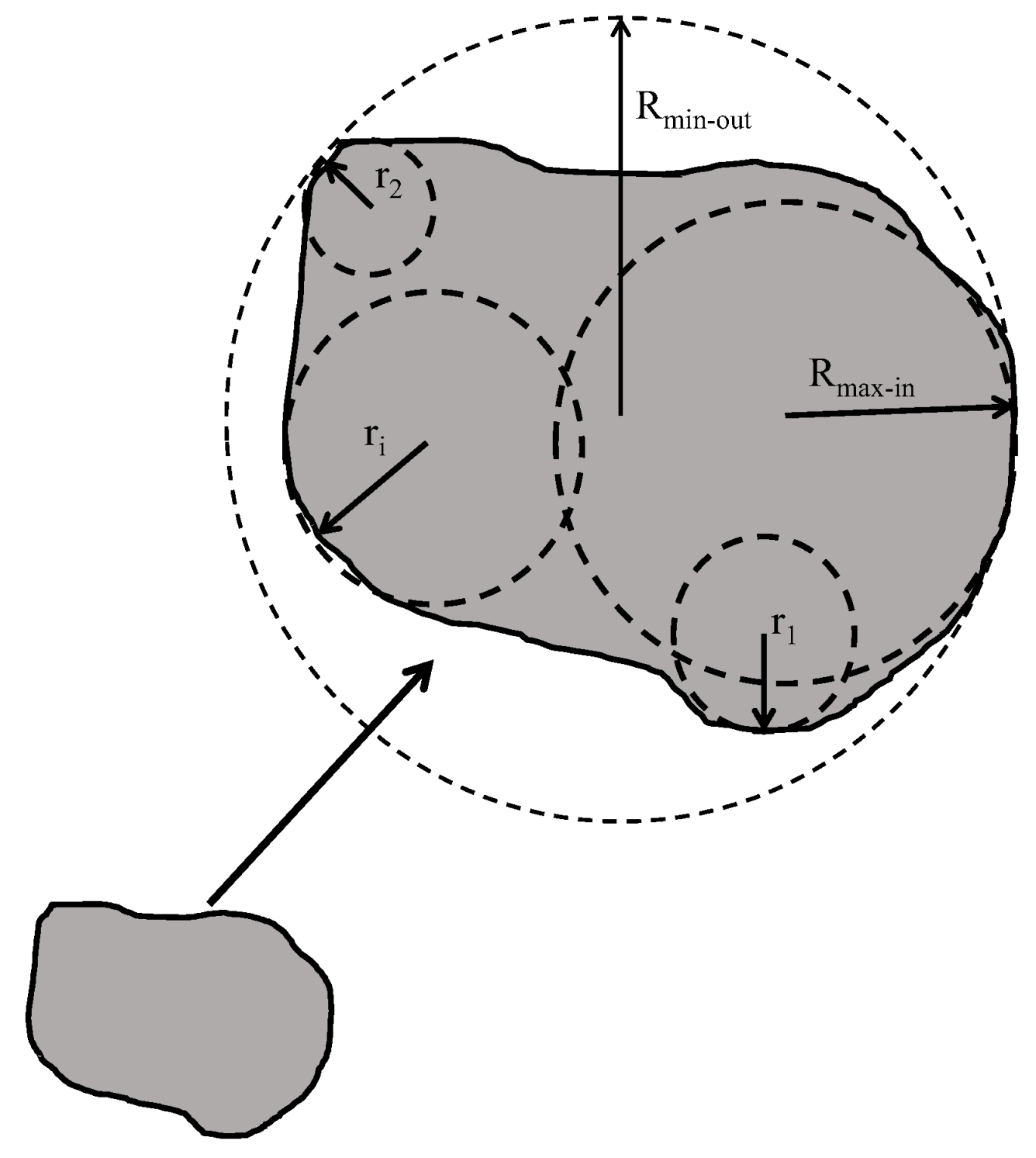
To quantify the shape characteristics of sand grains, the Krumbein and Sloss [42] empirical chart was utilized in this study. This chart uses an optical microscope to express grain shape in various ways. Roundness R, sphericity S, and regularity ρ were the three shape descriptors quantified in this study using Equations 1, 2, and 3. Figure 3 and Figure 4 defines the parameters in these equations and was adapted from Krumbein and Sloss [42] and Cho et al. [43].
R = ∑ i = 1 N r i R m a x − i n
S = R m a x − i n R m i n − c i r
ρ = 0.5 [ R + S ]
where r = the radius of the sand particle corners; Rmax-in = the largest inner radius of the sand particle corners; Rmin-cir = the smallest outer radius of the sand particle; i = index of summation; and N = number of inscribed spheres.
This study conducted a comprehensive investigation on the effect of particle shape changes on damping ratio. To achieve this, 25 sand particles were randomly selected at three stages: before testing, before the second test, and before the fifth test. The three shape descriptors R, S, and ρ were quantified for each selected particle, and the average of the three descriptors for the 25 particles was considered as R, S, and ρ for each stage. This method was used to isolate the effect of particle shape changes on damping ratio, as other physical characteristics remained nearly constant.
To determine the optimal number of grains for this study, a test group was conducted first. Initially, 10 particles were selected, but the standard deviation for the three parameters S, R, and ρ was not adequate. In the second step, 20 particles were considered, and the standard deviation was acceptable. Finally, 25 particles were selected to ensure accuracy.
The particles were removed in five layers during the particle selection procedure as shown in Figure 5, with five particles randomly selected from each layer. This method ensured that 25 grains were selected almost perfectly with a uniform distribution in height and horizontal surface.

2.3. Artificial Neural Network (ANN)

Artificial Neural Networks (ANNs) have a rich and fascinating history that spans several decades. The roots of ANNs can be traced back to the late 1940s and the work of Warren McCulloch and Walter Pitts, who proposed a mathematical model of a neuron, known as the McCulloch-Pitts neuron [44]. They suggested that neurons in the brain could be modeled as binary on-off switches, which laid the foundation for ANNs. In the 1950s and 1960s, several researchers began to develop neural network models, such as the perceptron, which was proposed by Frank Rosenblatt in 1958 [45]. The perceptron is a type of single-layer neural network that can learn to classify patterns by adjusting its weights. In the 1970s and 1980s, the development of backpropagation algorithm by Paul Werbos and others revolutionized the field of ANNs [46]. This algorithm allowed for the training of multi-layer neural networks, which could learn to perform more complex tasks than single layer perceptron’s.
ANNs can be used for a variety of tasks, including classification, regression, and time-series prediction. They have been successfully applied in various fields, such as finance, healthcare, and image recognition. However, the accuracy of the ANN model heavily relies on the quality and quantity of the training data, and the model may suffer from the problem of vanishing gradients, where the gradients become too small to update the weights during backpropagation.
To implement the ANN methodology, first, the data is divided into training and testing sets. The ANN model is then trained on the training set using backpropagation algorithm to minimize the error between the predicted and actual outputs. The number of hidden layers and the number of neurons in each layer are determined using trial and error or using a validation set. The performance of the ANN model is evaluated on the testing set using various metrics such as mean squared error (MSE) and mean absolute error (MAE). The hyperparameters of the ANN model, such as learning rate and momentum, are optimized using techniques such as grid search or randomized search.
Additionally, before training the ANN model, the input data need to be preprocessed by normalizing the data to ensure that all features have equal importance. The activation function for each neuron is chosen based on the problem being addressed, such as sigmoid, tanh, or ReLU. Regularization techniques such as dropout or weight decay may also be applied to prevent overfitting during the training process.

2.4. Support Vector Machine (SVM)

Support Vector Machine (SVM) is a supervised learning algorithm used for classification and regression analysis. It was first proposed by Vapnik and colleagues in the 1990s and has since been widely used in various fields such as finance, biology, and image recognition [47,48]. The idea behind SVM is to find a hyperplane that separates the data into different classes in the highest possible margin. The margin is defined as the distance between the hyperplane and the closest data points from each class. The SVM algorithm then tries to maximize this margin by finding the optimal hyperplane.
Initially, SVM was developed for linearly separable data only, where a single hyperplane could separate the data perfectly. Later, it was extended to non-linearly separable data by using kernel functions to map the data to a higher dimensional space, where it could be linearly separated.
SVM has several advantages over other classification algorithms, such as its ability to handle high dimensional data and its robustness to outliers. However, its performance can be affected by the choice of kernel function and hyperparameters. Over the years, several variants of SVM have been proposed, such as the support vector regression (SVR) for regression analysis, and the multiple kernel learning (MKL) for combining multiple kernel functions. SVM remains an active area of research, with ongoing efforts to improve its performance and scalability for large datasets.
To implement the SVM methodology, first, the data is divided into training and testing sets. The SVM model is then trained on the training set using a kernel function such as linear, polynomial, or radial basis function (RBF). The optimal values of the hyperparameters, such as C (penalty parameter) and gamma (kernel coefficient), are determined using techniques such as grid search or randomized search. The performance of the SVM model is evaluated on the testing set using various metrics such as accuracy, precision, recall, and F1-score. The SVM model can also be used for regression tasks by modifying the objective function and using the epsilon-insensitive loss function. The performance of the SVM regression model can be evaluated using metrics such as mean squared error (MSE) and mean absolute error (MAE).

3. Results

After conducting the simple shear test, the collected data comprised of displacements and forces. These raw values were then transformed into horizontal and vertical stress and strain values by utilizing the displacement-strain and stress-force relationships. The damping ratio (D) was then calculated using Equations 4 and 5, and Figure 6.
D = ∆ W 2 π W = A L o o p 2 π W
W = ( γ m a x − γ m i n ) ( τ γ m a x − τ γ m i n ) 2

3.1. Cyclic Tests

The results of the experiment show the effect of particle shape changes on the damping ratio of sand. The hysteresis loops of shear stress-strain were plotted after each cyclic test, and the damping ratio was estimated using Equation 3. Figure 7 illustrates an example of the results obtained during cyclic tests, where CSR and vertical stresses were 0.3 and 150 kPa, respectively. In addition, the results demonstrate that the volumetric strain exhibits a negative trend with an increasing number of cycles. This indicates that the sample experienced settlement and its density increased after cycling. The constant vertical pressure loading in the cyclic tests is the reason for this phenomenon.
The impact of the number of cycles on the damping ratio under different CSR conditions and vertical stresses was demonstrated by Figure 8, Figure 9 and Figure 10 for the reconstruction of the first, second, and fifth samples, respectively. As shown in the figures, the damping ratio decreased with an increase in the number of cycles in all tests.
Table 1, Table 2 and Table 3, and Figure 11 present the results of tests conducted on samples before cycling (Table 1), after 30 cycles (Table 2), and after 120 cycles (Table 3). The tables report the minimum, maximum, mean, and standard deviation for three shape descriptors: sphericity (S), roundness (R), and regularity (ρ), as well as the damping ratio (D). Comparing the values across the three tables allows us to draw some conclusions about how these shape descriptors and the damping ratio are affected by cycling.
Looking at Table 1, it can be seen that the mean values for S, R and ρ, and D are 0.713, 0.518, 0.616, and 16.050, respectively, before cycling. The standard deviations for S, R and ρ are relatively small (0.014 and 0.011, respectively), indicating that the samples are relatively consistent in terms of their shape descriptors. The standard deviation for D is larger (5.903), suggesting more variability in the damping ratio.
Moving to Table 2, it can be seen that after 30 cycles, the mean values for S, R and ρ, and D are 0.760, 0.557, 0.658, and 13.392, respectively. Compared to Table 1, the mean values for all three shape descriptors have increased, suggesting that the samples have become more spherical, rounder, and more regular after 30 cycles. Additionally, the damping ratio has decreased, indicating that the samples have become less stiff and more flexible over the course of cycling.
Finally, in Table 3, after 120 cycles, it can be seen that the mean values for S, R and ρ, and D are 0.774, 0.570, 0.672, and 12.425, respectively. Compared to Table 2, we can see that the mean values for all three shape descriptors have continued to increase, suggesting that the samples have become even more spherical, rounder, and more regular after 120 cycles. Additionally, the damping ratio has continued to decrease, indicating that the samples have become even less stiff and more flexible over the course of additional cycling.
This section investigated the effect of loading cycles on three parameters of grain shape and damping ratio. The experimental results are presented in Figure 12 and Figure 13, where the diameter of the circles represents the magnitude of the damping ratio. It was observed that an increase in the number of loading cycles led to an increase in the three shape parameters (S, R and ρ) of the grains, indicating that the grains had become more spherical, rounder, and regular. Moreover, an increase in the number of cycles and the three parameters of the grain shape resulted in an increase in the diameter of the circles and damping ratio in the shapes. These findings demonstrate the relationship between the number of loading cycles, grain shape, and damping ratio, and highlight the importance of considering these factors in the design and optimization of granular materials for various applications.
The results are presented in Figure 4, where the size of the diameter of the circle represents the magnitude of the damping ratio. The findings indicate that the damping ratio increased with an increase in vertical stress, as evidenced by the increase in the diameter of the circle. These results provide insight into the influence of normal and loading stresses on the damping behavior of sand, which has significant implications for the design and construction of various geotechnical structures.

3.2. Artificial Neural Network (ANN)

Equations 6-11 provide definitions for various performance parameters that can be used to evaluate a network's performance. These parameters include Mean Absolute Error (MAE), Mean Square Error (MSE), Root Mean Square Error (RMSE), Mean Squared Logarithmic Error (MSLE), Root Mean Squared Logarithmic Error (RMSLE), and Coefficient of Determination (R2).
M A E = ∑ N X m − X p N
M S E = ∑ N X m − X p 2 N
R M S E = ∑ N X m − X p 2 N
M S L E = ∑ N log ⁡ ( X m + 1 ) − log ⁡ X p + 1 2 N
R M S L E = ∑ N log ⁡ ( X m + 1 ) − log ⁡ X p + 1 2 N
R 2 = ∑ i = 1 N ( X m − X m ¯ ) ( X p − X p ¯ ) ∑ i = 1 N ( X m − X m ¯ ) 2 ∑ i = 1 n ( X p − X p ¯ ) 2 2
Where N is the number of datasets, Xm and Xp are actual and predicted values, and X m ¯ , X p ¯ are the average of actual and predicted values, respectively. Ideally, the model should have a R2 value of 1 and a MAE, MSEM RMSE, MSLE, RMSLE value of 0.
To implement mathematical models, two types of databases are necessary, namely training databases and testing databases. Both types of databases were randomly divided for two mathematical models. 80% of the main database was assigned to the training dataset and the remaining 20% to the testing dataset.
Several parameters, including the number of hidden layers and neurons, can impact the accuracy of ANN models. To obtain the most optimal and accurate ANN model, multiple models were generated and assessed to determine the best one. The performance of the selected model was evaluated by comparing the predicted damping ratio values against those obtained from the test dataset, as illustrated in Figure 14. The results demonstrate the high accuracy of the ANN model in predicting the damping ratio of sand.
To elaborate further on the results of the ANN model, it should be noted that the model had one hidden layer, and the number of neurons in the input layer was 5, corresponding to the five independent variables of particle shape (R, S and ρ) of sand, vertical stress, number of cycles, and CSR. The number of neurons in the hidden layer was initially set to 50, but through an iterative process of trial and error, the optimum number of neurons was determined to be 28. This process is essential for optimizing the model's performance and ensuring that it is not overfitting the training data.
The results presented in Table 4 show the performance of an Artificial Neural Network (ANN) model trained using a Levenberg-Marquardt (LM) algorithm to predict damping ratio based on the particle shape of sand, vertical stress, number of cycles, and CSR. The model's performance was evaluated using several metrics, including Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Squared Log Error (MSLE), Root Mean Squared Log Error (RMSLE), and R-squared (R²). The results indicate that the ANN model performs well in predicting damping ratio, as evidenced by the high R² value of 0.962 for both the training and testing datasets. R² is a statistical measure that represents the proportion of the variance in the dependent variable (damping ratio, in this case) that is explained by the independent variables (particle shape of sand, vertical stress, number of cycles, and CSR). Therefore, R² value close to 1 indicates that the model fits the data well. The MAE, MSE, and RMSE values for the training dataset are higher than those for the testing dataset, indicating that the model performs better on the testing dataset. This could be due to overfitting, which occurs when the model fits the training data too closely, resulting in poor performance on new, unseen data. The MSLE and RMSLE values are low for both the training and testing datasets, indicating that the model's predictions are accurate and have low error. In conclusion, the results suggest that the ANN model trained using ML algorithm is a promising approach for predicting damping ratio based on the particle shape of sand, vertical stress, number of cycles and CSR. However, further research is needed to validate the model's performance on a larger dataset.

3.3. Support Vector Machine (SVM)

The performance and accuracy of SVM models can be significantly impacted by various parameters such as kernel function, C parameter, and Gamma parameter. To obtain the optimal and accurate SVM model, several models were trained and evaluated, and the best one was selected. The evaluation of the selected model was carried out by comparing the predicted damping ratio values against the actual values obtained from the test dataset, as illustrated in Figure 15. The results indicate that the SVM model exhibits high accuracy in predicting the damping ratio of sand.
The results of the SVM model to predict damping ratio based on the shape of sand particles, vertical stress, number of cycles, and CSR are presented in Table 5. The model's performance was evaluated using various metrics such as MAE, MSE, RMSE, MSLE, RMSLE, and R² for both training and testing datasets. The SVM model achieved an MAE of 0.716 and 0.831 for training and testing datasets, respectively. The corresponding MSE values were 0.761 and 1.302, and the RMSE values were 0.872 and 1.141. Moreover, the model's MSLE and RMSLE values were 0.006 and 0.079 for the training dataset and 0.003 and 0.057 for the testing dataset. Furthermore, the model's coefficient of determination (R²) values was 0.973 for the training dataset and 0.892 for the testing dataset. These results suggest that the SVM model performs well in predicting the damping ratio based on the input parameters, with a high R² value indicating a good fit to the data. Overall, these findings demonstrate the potential of the SVM model as a useful tool for predicting the damping ratio of sand samples based on their particle shape, vertical stress, number of cycles, and CSR conditions.

4. Discussion

4.1. Effect of void ratio changes on damping ratio

An investigation was conducted to examine the impact of cyclic loading on the void ratio of the samples. Results from tests based on parameters R, S, and ρ are illustrated in Figure 16, Figure 17 and Figure 18, respectively. The diameter of the circles in these figures represents void ratio in the sample, while the shapes are constructed based on two minimum and maximum void ratios. The findings demonstrate that with an increase in the number of cycles and a consequent rounding of sand grains, the void ratio between the grains reduces.
This is due to the fact that more rounded and spherical particles have a higher packing density, which results in a reduction in the volume of voids and an increase in the contact area between particles. This, in turn, leads to an increase in the number of contact points between particles, resulting in higher energy dissipation during cyclic loading, which is reflected in the higher damping ratio.

4.2. Importance of input parameters

In this study, a sensitivity analysis was conducted on the input parameters of several models, namely ANN and SVM, to investigate their impact on the accuracy of the AI models. For this purpose, each input parameter was increased and decreased individually by 100% and measured the resulting error to determine the sensitivity of the model to that parameter. The results of the sensitivity analysis were plotted in Figure 19, which shows the mean increase in error as the parameter was increased or decreased. The higher the error, the more sensitive the model is to that parameter.
Table 6 presents the ranking results of variable importance for all models. The models considered in this study are Artificial Neural Network (ANN) and Support Vector Machine (SVM). The input parameters for each model are number of cycles, S, R, ρ, normal stress, and CSR. The ranking results are based on the total score obtained by each input parameter in both models. The total score for each input parameter is the sum of the scores obtained in ANN and SVM models. The ranking is then determined based on the total score of each input parameter.
From Table 6, it can be observed that the most important input parameter is vertical stress, with a total score of 2 and a ranking of 1. The significance of the vertical stress in regulating the contact forces between particles and, consequently, the dissipation of energy during cyclic loading is the reason behind this phenomenon. The second most important input parameter is R, with a total score of 5 and a ranking of 2. The third most important input parameter is ρ, with a total score of 6 and a ranking of 3. The fourth and fifth most important input parameters are number of cycles and S, with total scores of 7 and 10, respectively, and rankings of 4 and 5, respectively. Finally, CSR has the lowest total score of 12 and is ranked sixth. These rankings provide valuable insight into the relative importance of the input parameters in predicting the output variable in the models considered in this study. This information can be useful in optimizing the models and selecting the most important input parameters for a particular application.

5. Conclusions

This paper presents a comprehensive investigation into the effect of particle shape on the damping ratio of dry sand. The study uses a unique approach of cyclic loading to evaluate the impact of particle shape and size on the damping ratio, which has practical implications for geotechnical engineering applications. In order to investigate the impact of particle shape and size on the damping ratio of dry sand, a series of simple shear tests were performed. Three parameters, namely roundness (R), sphericity (S), and regularity (ρ), were employed to characterize the shape and size of particles. Additionally, the study develops two artificial intelligence models, an artificial neural network and a support vector machine, which effectively predict the effect of grain shape on the damping ratio. The following is a summary of the findings:
-
The results show that the shape of sand particles changes during cyclic loading, becoming more rounded and spherical, resulting in an increase in damping ratio.
-
The results of the study also showed that the damping ratio of sand decreases as the number of loading cycles increases. This is due to the fact that cyclic loading causes a rearrangement of the sand particles, resulting in an increase in the packing density and a decrease in the volume of voids, which increase the number of contact points between particles and, therefore, the energy dissipation during cyclic loading.
-
The results indicate that the ANN model performs well in predicting damping ratio, as evidenced by the high R² value of 0.962 for both the training and testing datasets. The results indicate that the ANN model performs well in predicting damping ratio, as evidenced by the high R² value of 0.962 for both the training and testing datasets. To conclude, the study suggests that utilizing an ANN model trained through ML algorithms holds promise for predicting the damping ratio of sand based on particle shape, vertical stress, number of cycles, and CSR.
-
The results showed that vertical stress is the most important parameter affecting the damping coefficient, while the effect of CSR is relatively small. This is because the vertical stress plays a major role in controlling the contact forces between particles and, therefore, the energy dissipation during cyclic loading. The study found that increasing the vertical stress resulted in an increase in the damping coefficient, while increasing the CSR had a relatively small effect on the damping coefficient.
This study provides novel insights into the relationship between particle shape and damping ratio, which could inform future geotechnical engineering applications. Further research is needed to validate the results of the AI model and to investigate the impact of other factors on the damping ratio, such as particle size, particle sorting, and loading rate. In addition, the study could be expanded to include other types of soils and rocks, as well as to investigate the effect of particle shape on other geotechnical properties such as shear strength and compressibility. Overall, the study provides a strong foundation for future research on the impact of particle shape on geotechnical engineering applications.

Acknowledgments

This research as a part of first author’s PhD research.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Ashmawy AK, Salgado R, Guha S, Drnevich VP. Soil damping and its use in dynamic analyses. InInternational conferences on recent advances in geotechnical earthquake engineering and soil dynamics 1995 Apr (Vol. 9).
  2. Luna R, Jadi H. Determination of dynamic soil properties using geophysical methods. InProceedings of the first international conference on the application of geophysical and NDT methodologies to transportation facilities and infrastructure, St. Louis, MO 2000 Dec (pp. 1-15).
  3. Ventura CE, Finn WL, Lord JF, Fujita N. Dynamic characteristics of a base isolated building from ambient vibration measurements and low level earthquake shaking. Soil dynamics and earthquake engineering. 2003 Jun 1;23(4):313-22.
  4. Sahebzadeh S, Heidari A, Kamelnia H, Baghbani A. Sustainability features of Iran’s vernacular architecture: A comparative study between the architecture of hot–arid and hot–arid–windy regions. Sustainability. 2017 May 4;9(5):749.
  5. Seed HB, Wong RT, Idriss IM, Tokimatsu K. Moduli and damping factors for dynamic analyses of cohesionless soils. Journal of geotechnical engineering. 1986 Nov;112(11):1016-32.
  6. Senetakis K, Payan M. Small strain damping ratio of sands and silty sands subjected to flexural and torsional resonant column excitation. Soil Dynamics and Earthquake Engineering. 2018 Nov 1;114:448-59.
  7. Senetakis K, Anastasiadis A, Pitilakis K. Normalized shear modulus reduction and damping ratio curves of quartz sand and rhyolitic crushed rock. Soils and Foundations. 2013 Dec 1;53(6):879-93.
  8. Edinçliler A, Yildiz O. Effects of processing type on shear modulus and damping ratio of waste tire-sand mixtures. Geosynthetics International. 2022 Aug;29(4):389-408.
  9. Akbarimehr D, Fakharian K. Dynamic shear modulus and damping ratio of clay mixed with waste rubber using cyclic triaxial apparatus. Soil Dynamics and Earthquake Engineering. 2021 Jan 1;140:106435.
  10. Bayat M, Ghalandarzadeh A. Stiffness degradation and damping ratio of sand-gravel mixtures under saturated state. International Journal of Civil Engineering. 2018 Oct;16:1261-77.
  11. Li W, Lang L, Wang D, Wu Y, Li F. Investigation on the dynamic shear modulus and damping ratio of steel slag sand mixtures. Construction and Building Materials. 2018 Feb 20;162:170-80.
  12. Wichtmann T, Triantafyllidis T. Effect of uniformity coefficient on G/G max and damping ratio of uniform to well-graded quartz sands. Journal of geotechnical and geoenvironmental engineering. 2013 Jan 1;139(1):59-72.
  13. Hardin BO, Drnevich VP. Shear modulus and damping in soils: measurement and parameter effects (terzaghi leture). Journal of the soil mechanics and foundations division. 1972 Jun;98(6):603-24.
  14. Kumar SS, Krishna AM, Dey A. Parameters influencing dynamic soil properties: a review treatise. InNational conference on recent advances in civil engineering 2013 (pp. 1-10).
  15. Okur DV, Ansal A. Stiffness degradation of natural fine grained soils during cyclic loading. Soil Dynamics and Earthquake Engineering. 2007 Sep 1;27(9):843-54.
  16. Ling XZ, Zhang F, Li QL, An LS, Wang JH. Dynamic shear modulus and damping ratio of frozen compacted sand subjected to freeze–thaw cycle under multi-stage cyclic loading. Soil Dynamics and Earthquake Engineering. 2015 Sep 1;76:111-21.
  17. Jafarzadeh F, Sadeghi H. Experimental study on dynamic properties of sand with emphasis on the degree of saturation. Soil Dynamics and Earthquake Engineering. 2012 Jan 1;32(1):26-41.
  18. Wu S, Gray DH, Richart Jr FE. Capillary effects on dynamic modulus of sands and silts. Journal of Geotechnical Engineering. 1984 Sep;110(9):1188-203.
  19. Clayton CR, Priest JA, Best AI. The effects of disseminated methane hydrate on the dynamic stiffness and damping of a sand. Geotechnique. 2005 Aug;55(6):423-34.
  20. Baghbani A, Choudhury T, Costa S, Reiner J. Application of artificial intelligence in geotechnical engineering: A state-of-the-art review. Earth-Science Reviews. 2022 May 1;228:103991.
  21. Bayat M, Ghalandarzadeh A. Stiffness degradation and damping ratio of sand-gravel mixtures under saturated state. International Journal of Civil Engineering. 2018 Oct;16:1261-77.
  22. Ling XZ, Zhang F, Li QL, An LS, Wang JH. Dynamic shear modulus and damping ratio of frozen compacted sand subjected to freeze–thaw cycle under multi-stage cyclic loading. Soil Dynamics and Earthquake Engineering. 2015 Sep 1;76:111-21.
  23. Chen G, Zhou Z, Sun T, Wu Q, Xu L, Khoshnevisan S, Ling D. Shear modulus and damping ratio of sand–gravel mixtures over a wide strain range. Journal of Earthquake Engineering. 2019 Sep 14;23(8):1407-40.
  24. Wichtmann T, Hernández MN, Triantafyllidis T. On the influence of a non-cohesive fines content on small strain stiffness, modulus degradation and damping of quartz sand. Soil Dynamics and Earthquake Engineering. 2015 Feb 1;69:103-14.
  25. Tong L, Wang YH. DEM simulations of shear modulus and damping ratio of sand with emphasis on the effects of particle number, particle shape, and aging. Acta Geotechnica. 2015 Feb;10:117-30.
  26. Jafarian Y, Javdanian H, Haddad A. Dynamic properties of calcareous and siliceous sands under isotropic and anisotropic stress conditions. Soils and foundations. 2018 Feb 1;58(1):172-84.
  27. Baghbani A, Costa S, O’Kelly BC, Soltani A, Barzegar M. Experimental study on cyclic simple shear behaviour of predominantly dilative silica sand. International Journal of Geotechnical Engineering. 2022 Oct 23:1-5.
  28. Baghbani A, Choudhury T, Samui P, Costa S. Prediction of secant shear modulus and damping ratio for an extremely dilative silica sand based on machine learning techniques. Soil Dynamics and Earthquake Engineering. 2023 Feb 1;165:107708.
  29. Nguyen MD, Baghbani A, Alnedawi A, Ullah S, Kafle B, Thomas M, Moon EM, Milne NA. Experimental Study on the Suitability of Aluminium-Based Water Treatment Sludge as a Next Generation Sustainable Soil Replacement for Road Construction. Available at SSRN 4331275.
  30. Baghbani A, Baumgartl T, Filipovic V. Effects of Wetting and Drying Cycles on Strength of Latrobe Valley Brown Coal. Copernicus Meetings; 2023 Feb 22.
  31. Baghbani A, Daghistani F, Baghbani H, Kiany K. Predicting the Strength of Recycled Glass Powder-Based Geopolymers for Improving Mechanical Behavior of Clay Soils Using Artificial Intelligence. EasyChair; 2023 Feb 19.
  32. Baghbani A, Daghistani F, Baghbani H, Kiany K, Bazaz JB. Artificial Intelligence-Based Prediction of Geotechnical Impacts of Polyethylene Bottles and Polypropylene on Clayey Soil. EasyChair; 2023 Feb 19.
  33. Baghbani A, Daghistani F, Kiany K, Shalchiyan MM. AI-Based Prediction of Strength and Tensile Properties of Expansive Soil Stabilized with Recycled Ash and Natural Fibers. EasyChair; 2023 Feb 19.
  34. Baghbani A, Daghistani F, Naga HA, Costa S. Development of a Support Vector Machine (SVM) and a Classification and Regression Tree (CART) to Predict the Shear Strength of Sand Rubber Mixtures. InProceedings of the 8th International Symposium on Geotechnical Safety and Risk (ISGSR), Newcastle, Australia 2022.
  35. Baghbani A, Costa S, Choundhury T, Faradonbeh RS. Prediction of Parallel Desiccation Cracks of Clays Using a Classification and Regression Tree (CART) Technique. InProceedings of the 8th International Symposium on Geotechnical Safety and Risk (ISGSR), Newcastle, Australia 2022.
  36. Baghbani A, Baghbani H, Shalchiyan MM, Kiany K. Utilizing artificial intelligence and finite element method to simulate the effects of new tunnels on existing tunnel deformation. Journal of Computational and Cognitive Engineering. 2022 Aug 15.
  37. ASTM D854–14. Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. 2014.
  38. ASTM D4253 A. Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. In.; 2006.
  39. ASTM D4254, A. Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. In.; 2006.
  40. Ladd, RS. Specimen preparation and liquefaction of sands. Journal of the Geotechnical Engineering Division. 1974 Oct;100(10):1180-4.
  41. Baghbani A, Costa S, Lu Y, Soltani A, Abuel-Naga H, Samui P. Effects of Particle Shape on Shear Modulus of Sand Using Dynamic Simple Shear Testing. Arabian journal of geosciences. 2023.
  42. Krumbein WC, Sloss LL. Stratigraphy and sedimentation (Vol. 71, No. 5, p. 401).
  43. Cho GC, Dodds J, Santamarina JC. Closure to “particle shape effects on packing density, stiffness, and strength: natural and crushed sands” by Gye-Chun Cho, Jake Dodds, and J. Carlos Santamarina. Journal of geotechnical and geoenvironmental engineering. 2007 Nov;133(11):1474.
  44. Kay, LE. From logical neurons to poetic embodiments of mind: Warren S. McCulloch’s project in neuroscience. Science in Context. 2001 Dec;14(4):591-614.
  45. Yadav N, Yadav A, Kumar M, Yadav N, Yadav A, Kumar M. History of neural networks. An Introduction to Neural Network Methods for Differential Equations. 2015:13-5.
  46. Werbos, PJ. The roots of backpropagation: from ordered derivatives to neural networks and political forecasting. John Wiley & Sons; 1994 Mar 31.
  47. Kecman, V. Learning and soft computing: support vector machines, neural networks, and fuzzy logic models. MIT press; 2001.
  48. Vapnik V, Chapelle O. Bounds on error expectation for support vector machines. Neural computation. 2000 Sep 1;12(9):2013-36.
Preprints 69240 g001
Figure 1. Particle size distribution curve of sand.
Figure 1. Particle size distribution curve of sand.
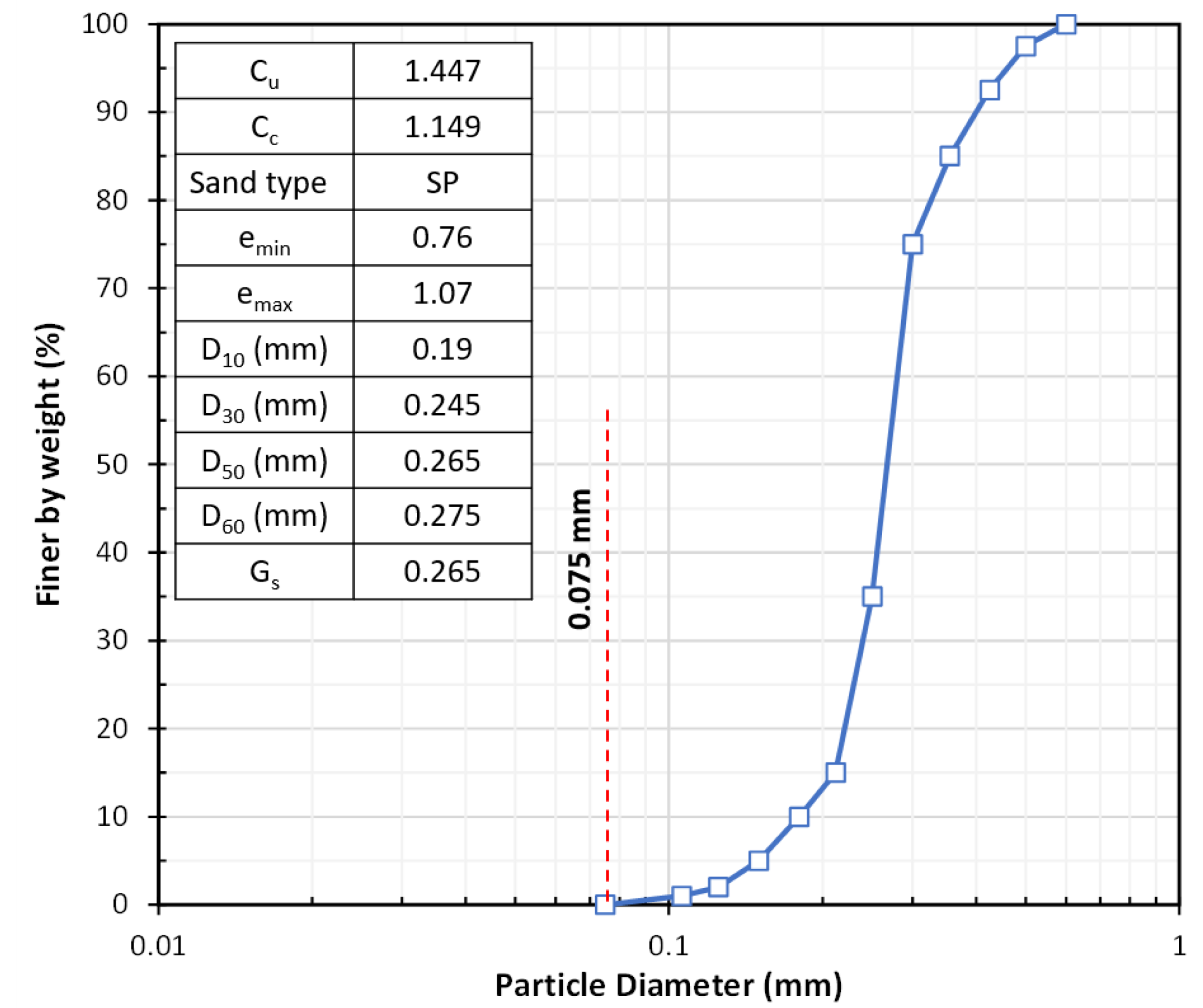
Preprints 69240 g001
Preprints 69240 g002
Figure 2. Schematic diagram of a cyclic simple shear test apparatus.
Figure 2. Schematic diagram of a cyclic simple shear test apparatus.
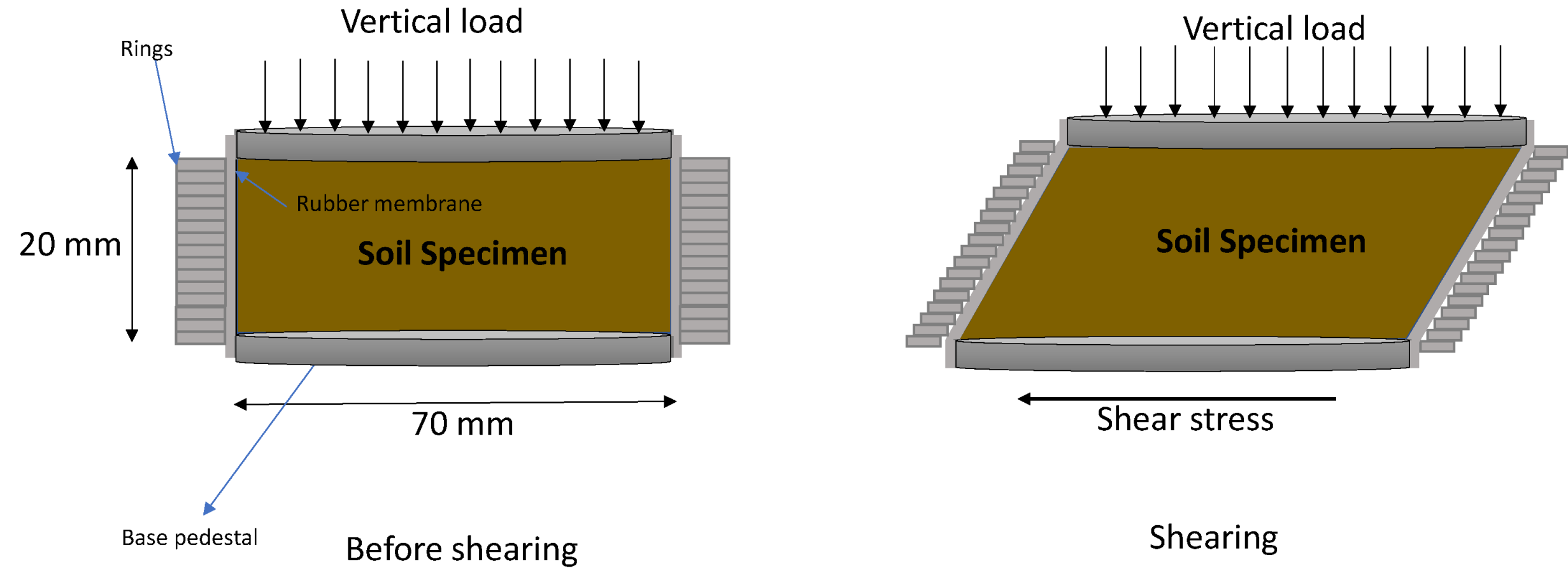
Preprints 69240 g002
Preprints 69240 g003
Figure 3. Particle shape of one sample [41,42].
Figure 3. Particle shape of one sample [41,42].
Preprints 69240 g003
Preprints 69240 g004
Figure 4. Particle shape characterization chart [42,43].
Figure 4. Particle shape characterization chart [42,43].
Preprints 69240 g004
Preprints 69240 g005
Figure 5. Schematic image of the selection location of 25 particles for each sample (no scale).
Figure 5. Schematic image of the selection location of 25 particles for each sample (no scale).
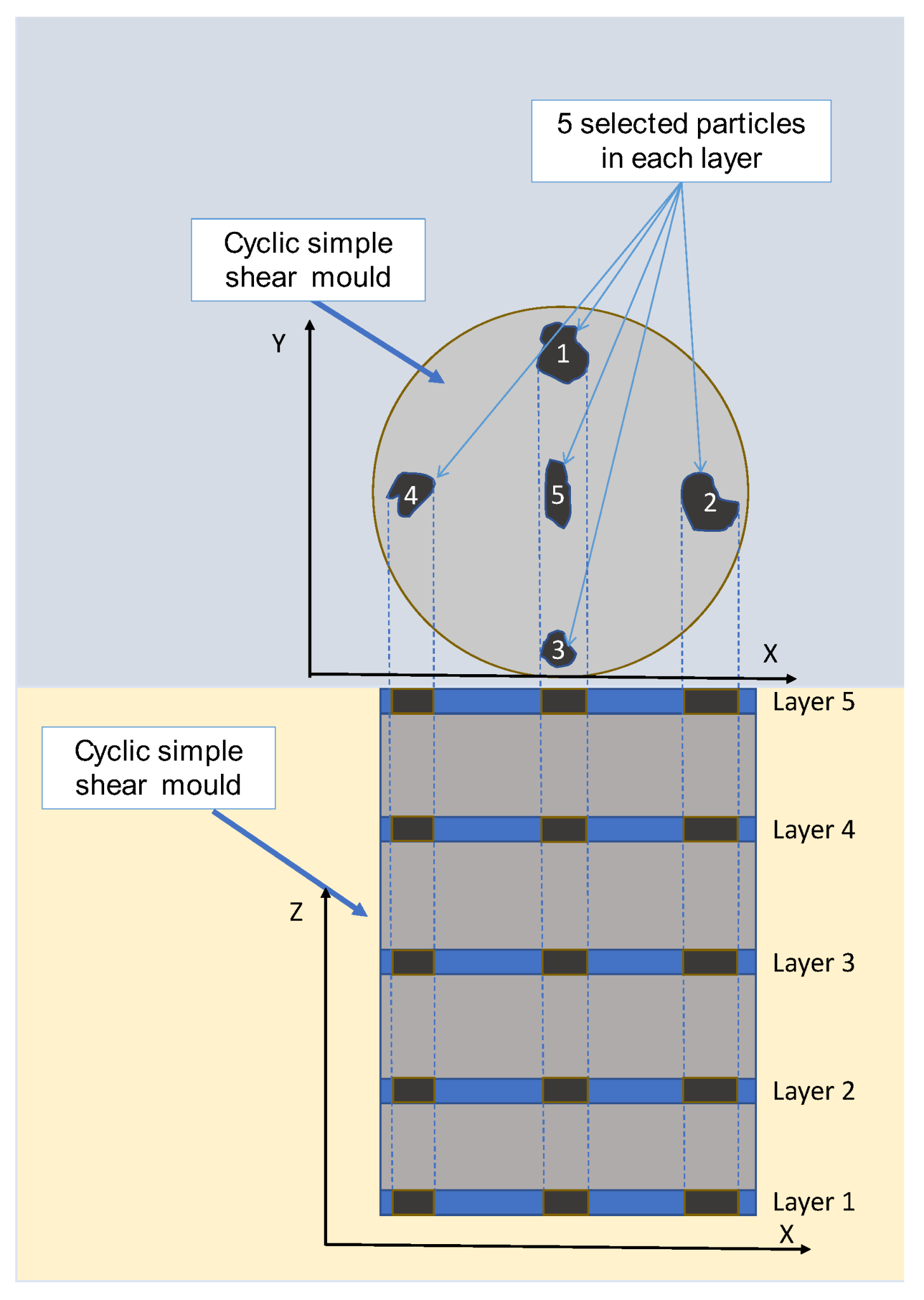
Preprints 69240 g005
Preprints 69240 g006
Figure 6. Schematic hysteresis loop in cyclic tests.
Figure 6. Schematic hysteresis loop in cyclic tests.
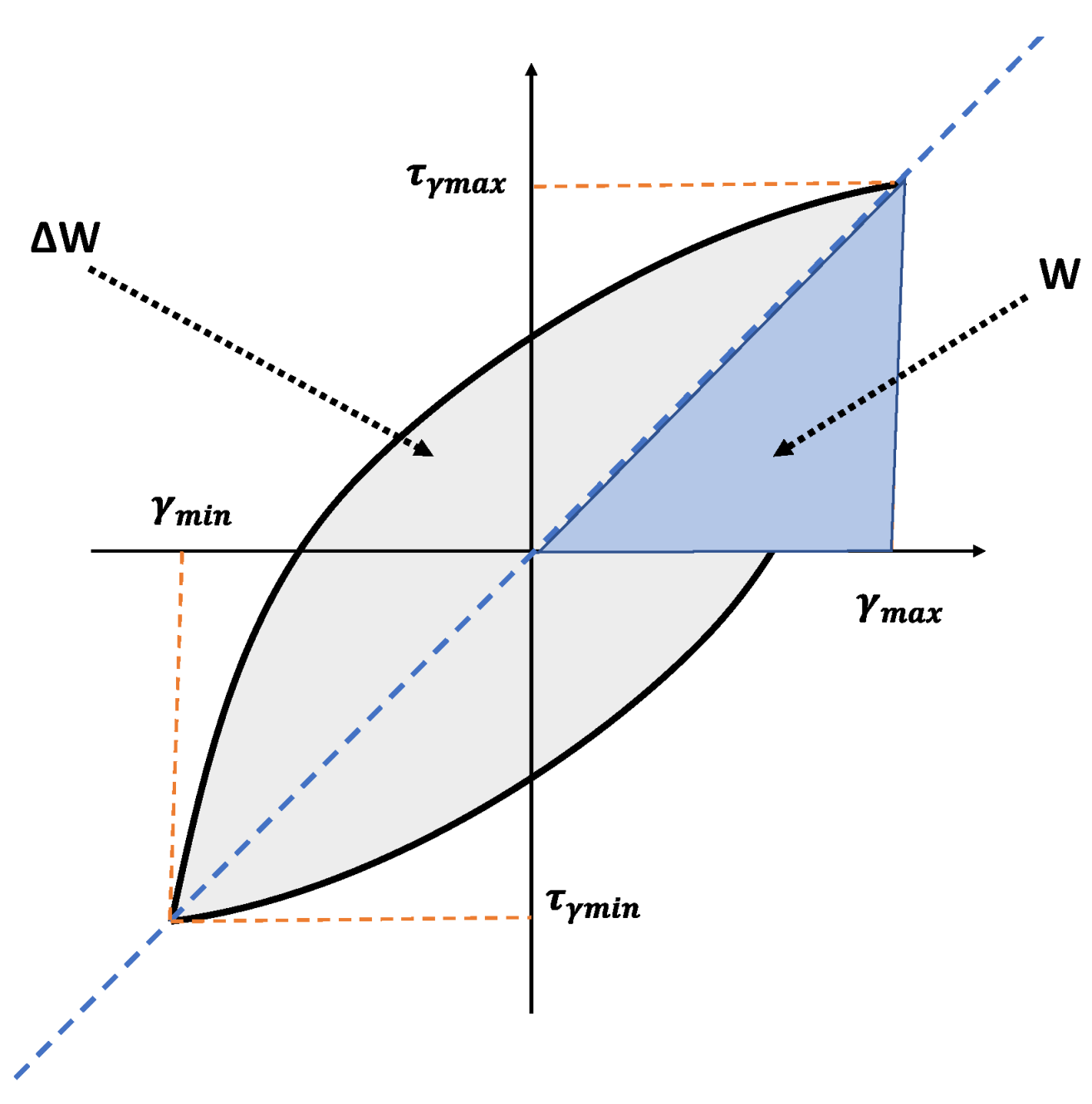
Preprints 69240 g006
Preprints 69240 g007
Figure 7. Results of cyclic tests under condition of CSR = 0.3 and vertical stress= 150 kPa as the curves of (a) shear stress-strain hysteresis loop, (b) volumetric strain-cyclic numbers.
Figure 7. Results of cyclic tests under condition of CSR = 0.3 and vertical stress= 150 kPa as the curves of (a) shear stress-strain hysteresis loop, (b) volumetric strain-cyclic numbers.
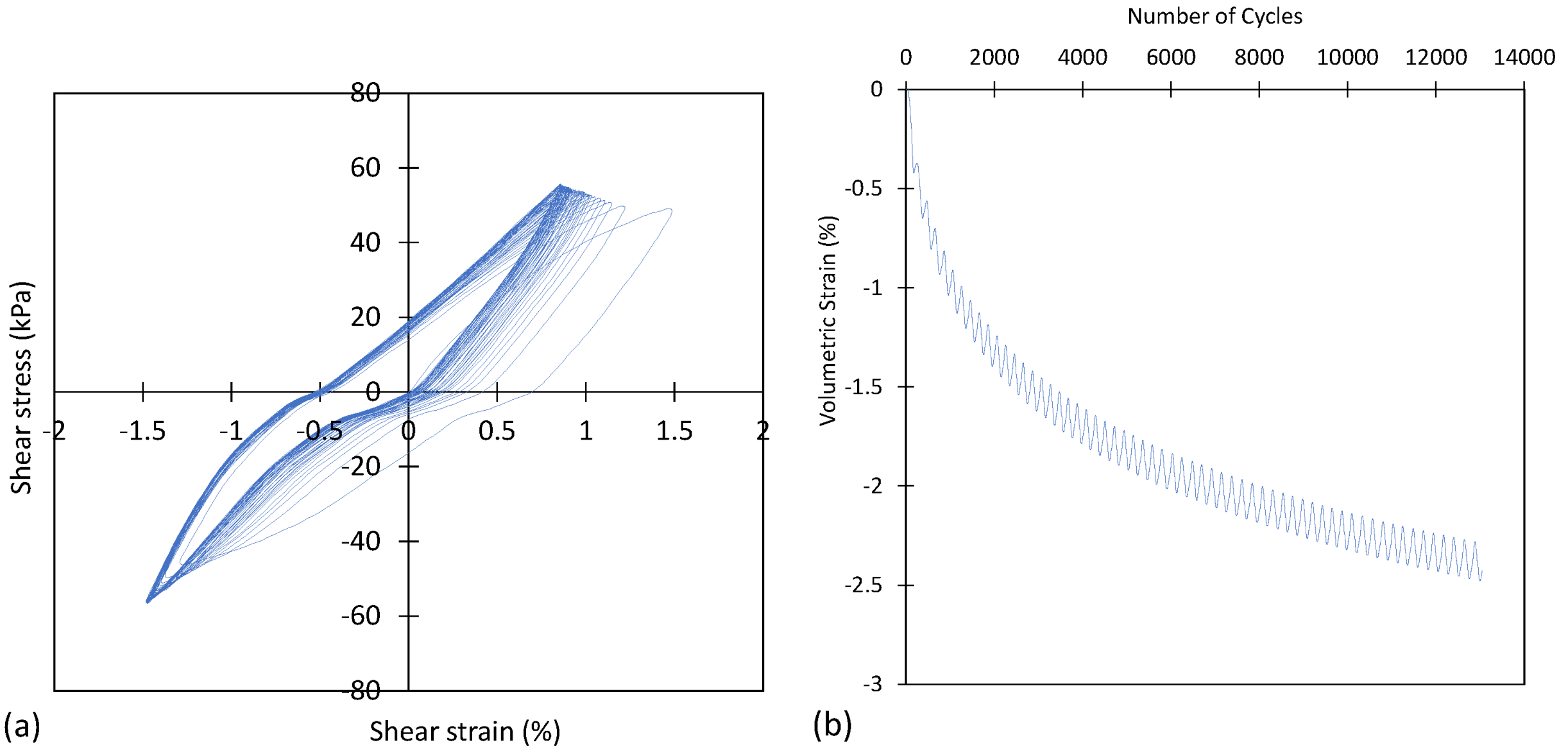
Preprints 69240 g007
Preprints 69240 g008
Figure 8. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 1 reconstruction.
Figure 8. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 1 reconstruction.
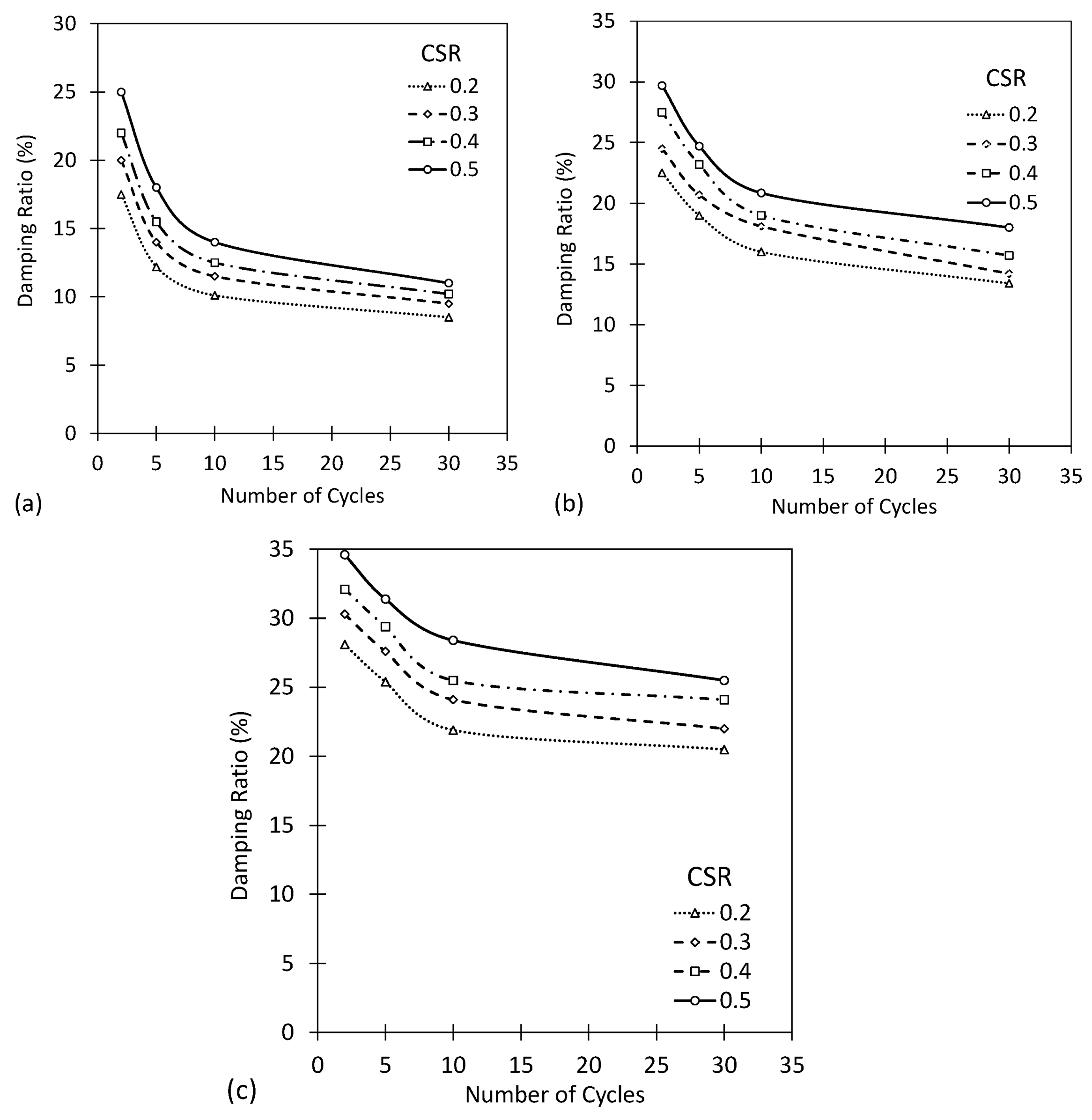
Preprints 69240 g008
Preprints 69240 g009
Figure 9. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 2 reconstructions.
Figure 9. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 2 reconstructions.
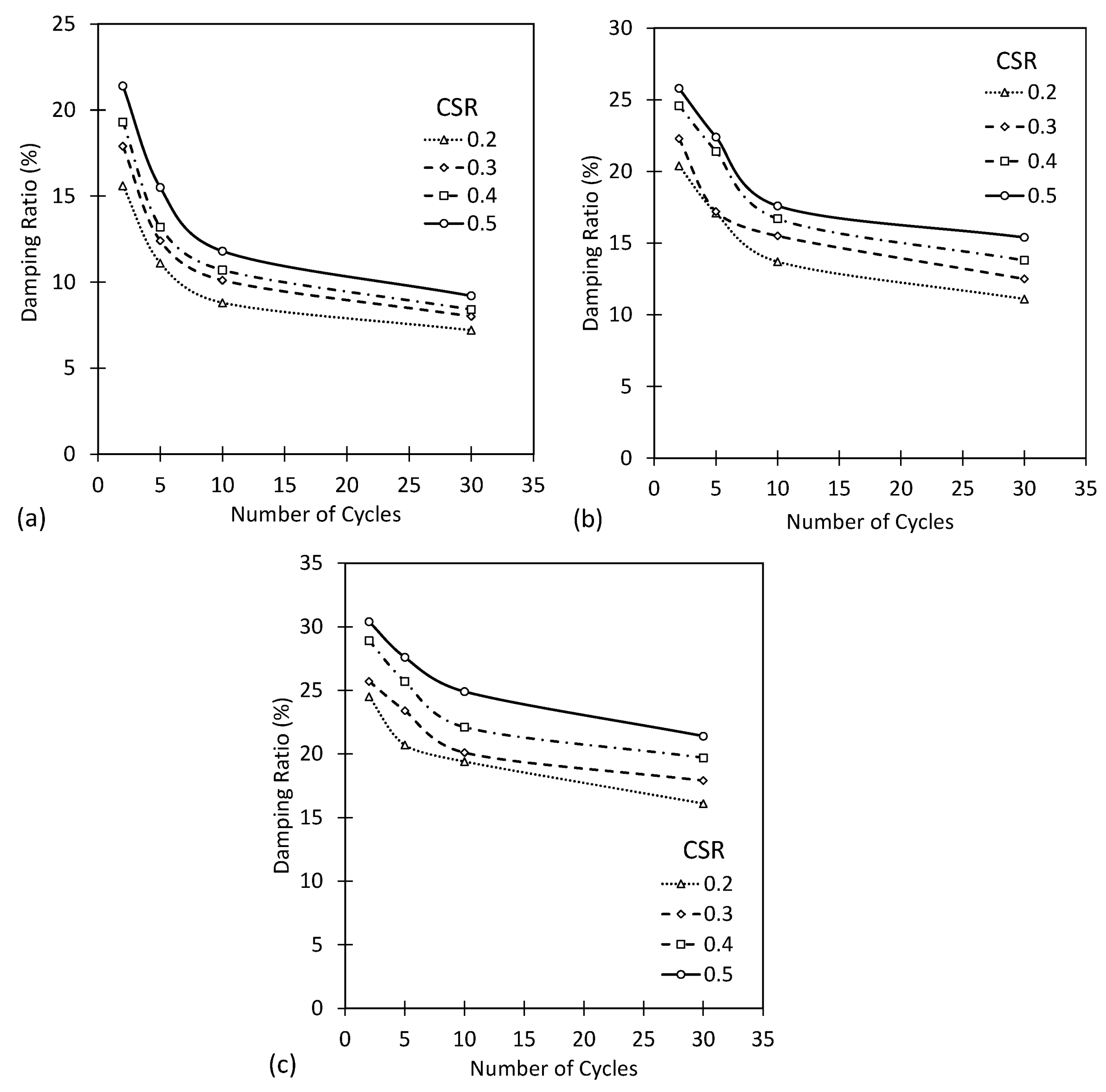
Preprints 69240 g009
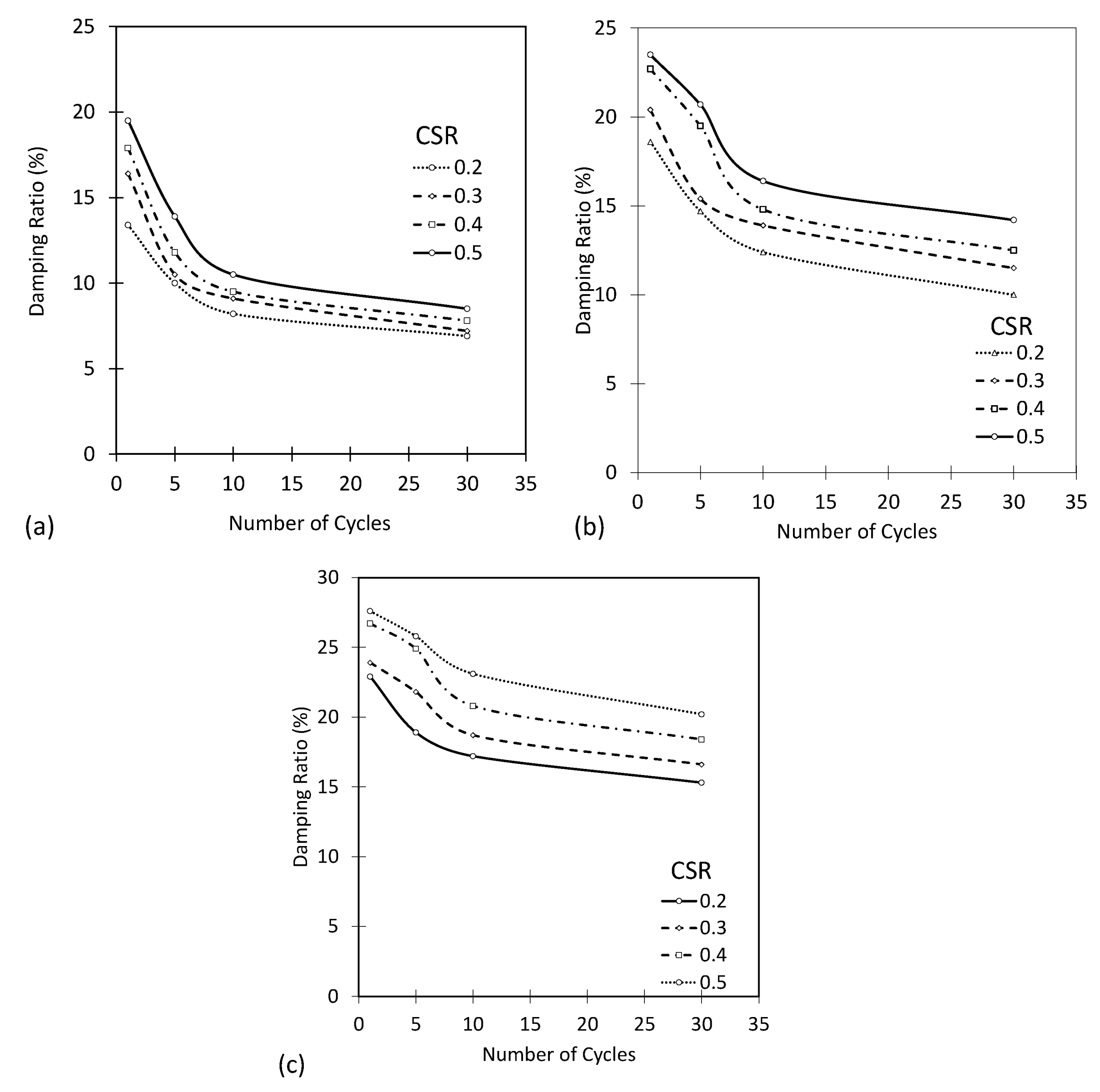
Preprints 69240 g010
Figure 10. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 5 reconstructions.
Figure 10. Effect of the number of loading cycles on the damping ratio for different CSR and the vertical stress of (a) 50 kPa, (b) 150 kPa, (c) 250 kPa for 5 reconstructions.
Preprints 69240 g010
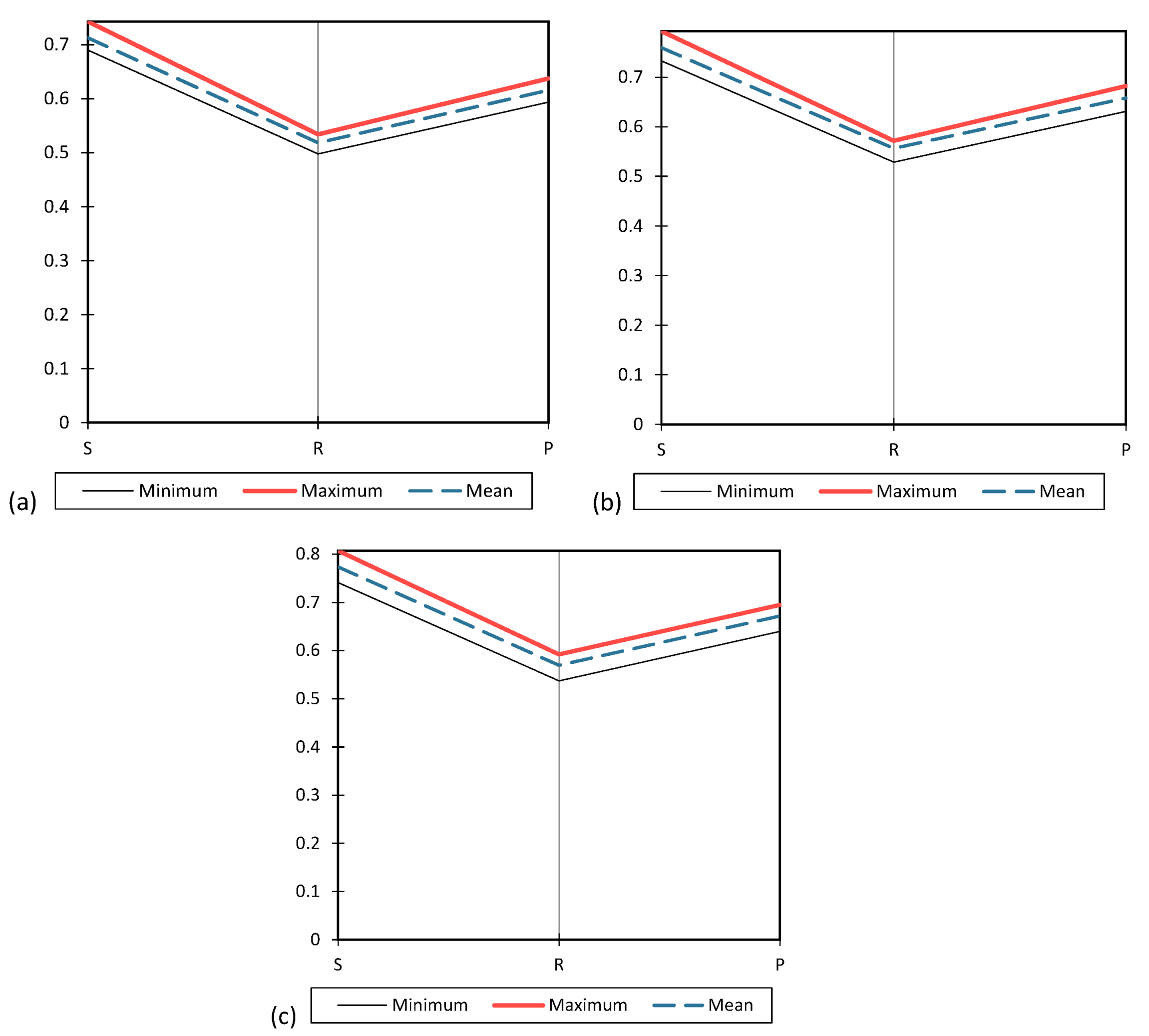
Preprints 69240 g011
Figure 11. The results of three shape descriptors (a) before cycling tests, (b) after 30 cycles and (c) after 120 cycles.
Figure 11. The results of three shape descriptors (a) before cycling tests, (b) after 30 cycles and (c) after 120 cycles.
Preprints 69240 g011
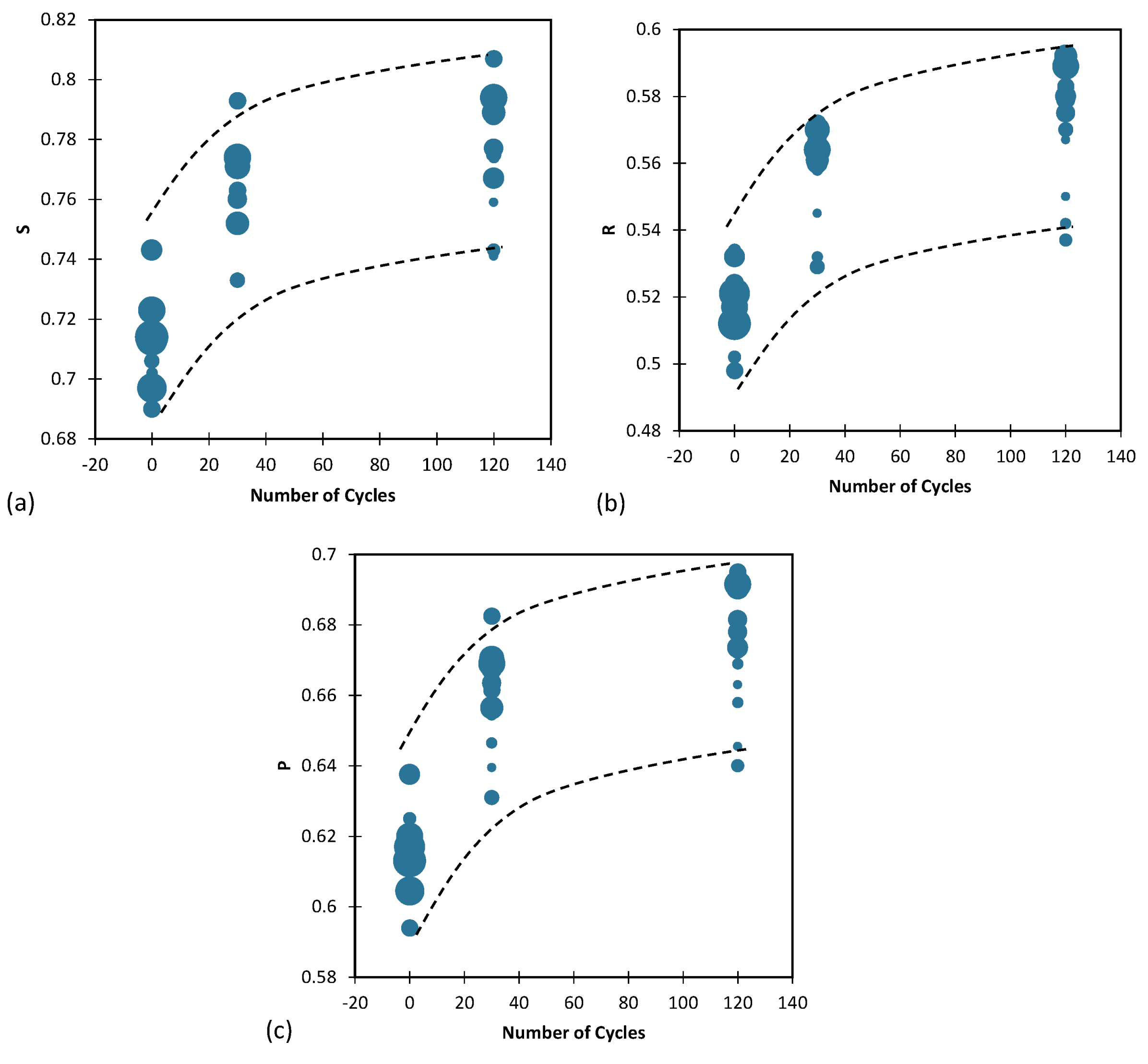
Preprints 69240 g012
Figure 12. Effect of number of cycles and (a) S, (b) R and (c) ρ on the damping ratio.
Figure 12. Effect of number of cycles and (a) S, (b) R and (c) ρ on the damping ratio.
Preprints 69240 g012
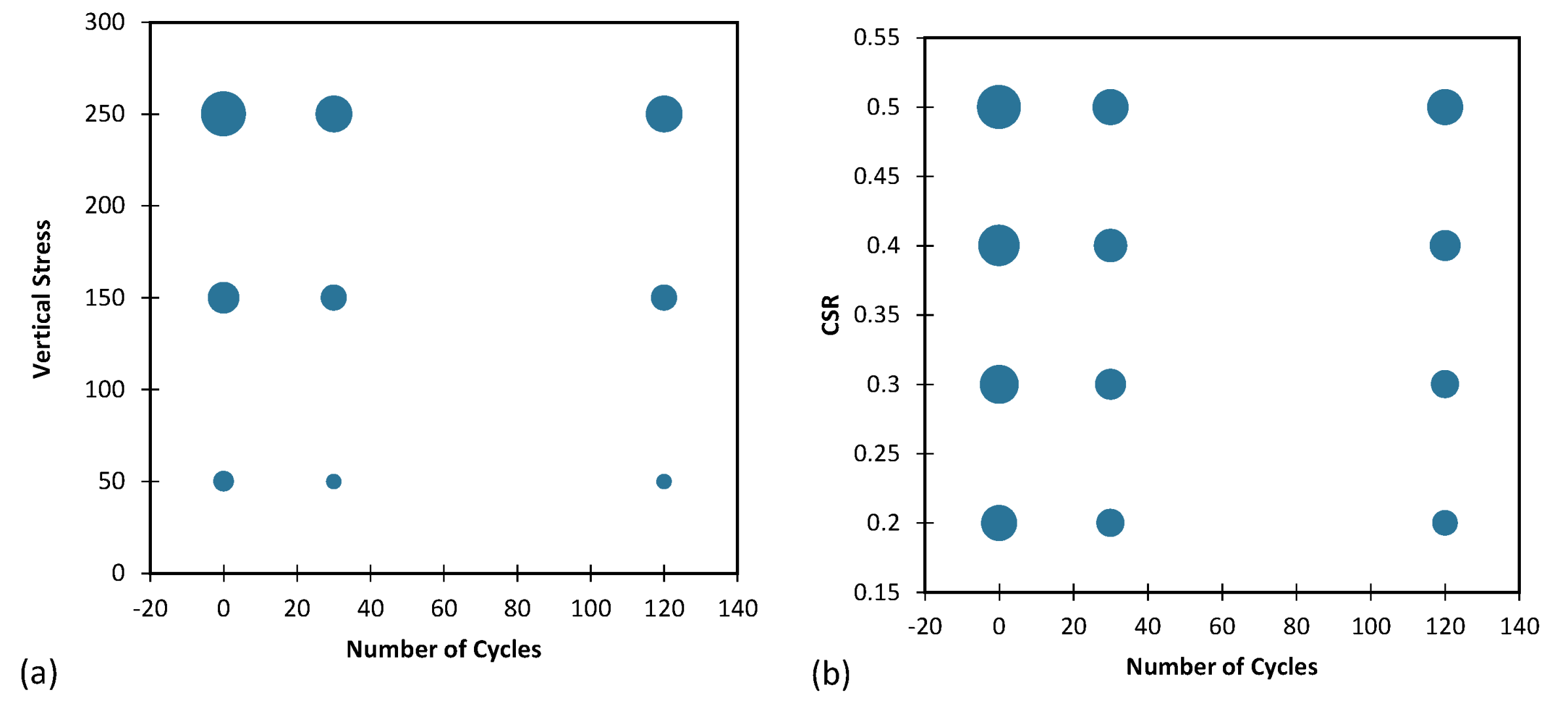
Preprints 69240 g013
Figure 13. Effect of number of cycles and (a) vertical stress and (b) CSR on the damping ratio.
Figure 13. Effect of number of cycles and (a) vertical stress and (b) CSR on the damping ratio.
Preprints 69240 g013
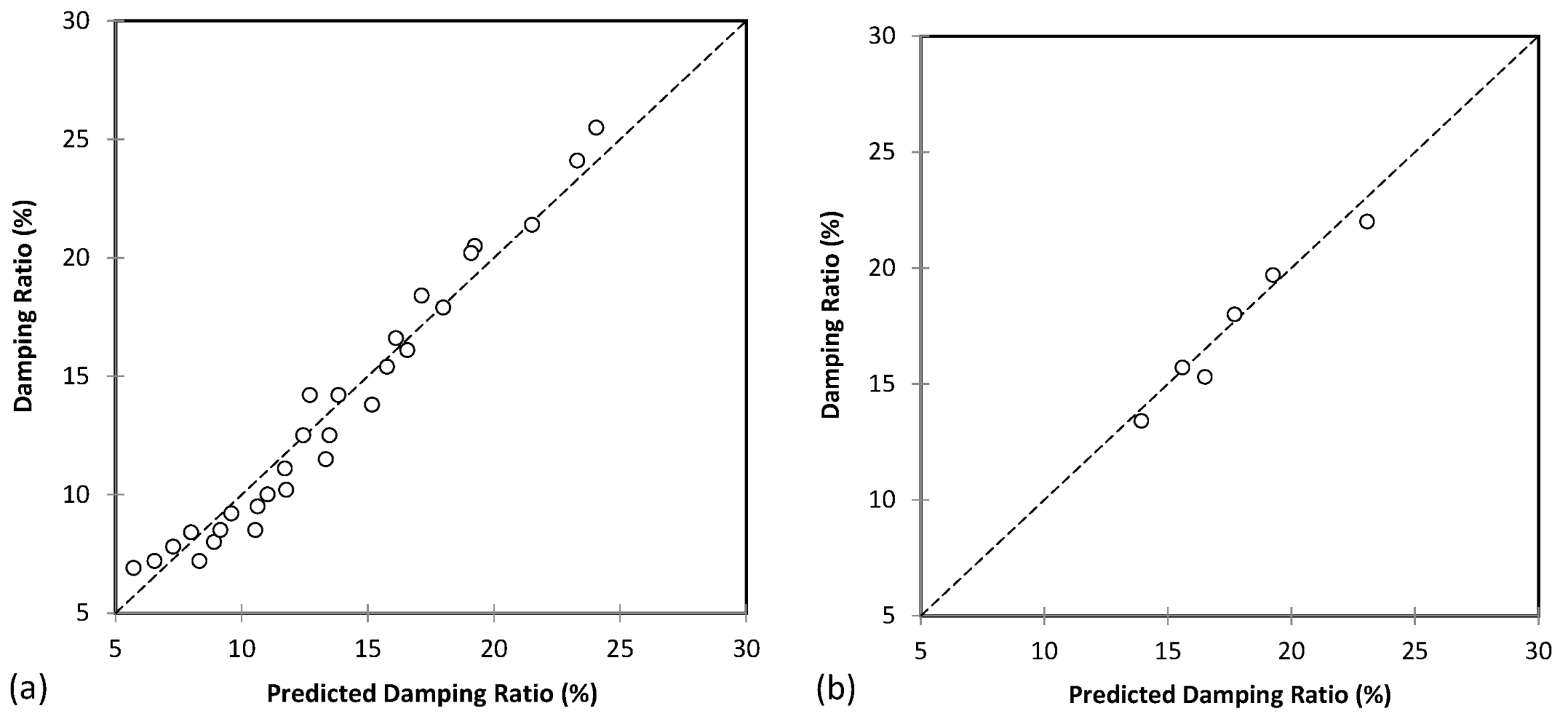
Preprints 69240 g014
Figure 14. Results of best ANN-ML model to predict damping ratio for (a) training and (b) testing databases.
Figure 14. Results of best ANN-ML model to predict damping ratio for (a) training and (b) testing databases.
Preprints 69240 g014
Preprints 69240 g015
Figure 15. Results of best SVM model to predict damping ratio for (a) training and (b) testing databases.
Figure 15. Results of best SVM model to predict damping ratio for (a) training and (b) testing databases.
Preprints 69240 g015
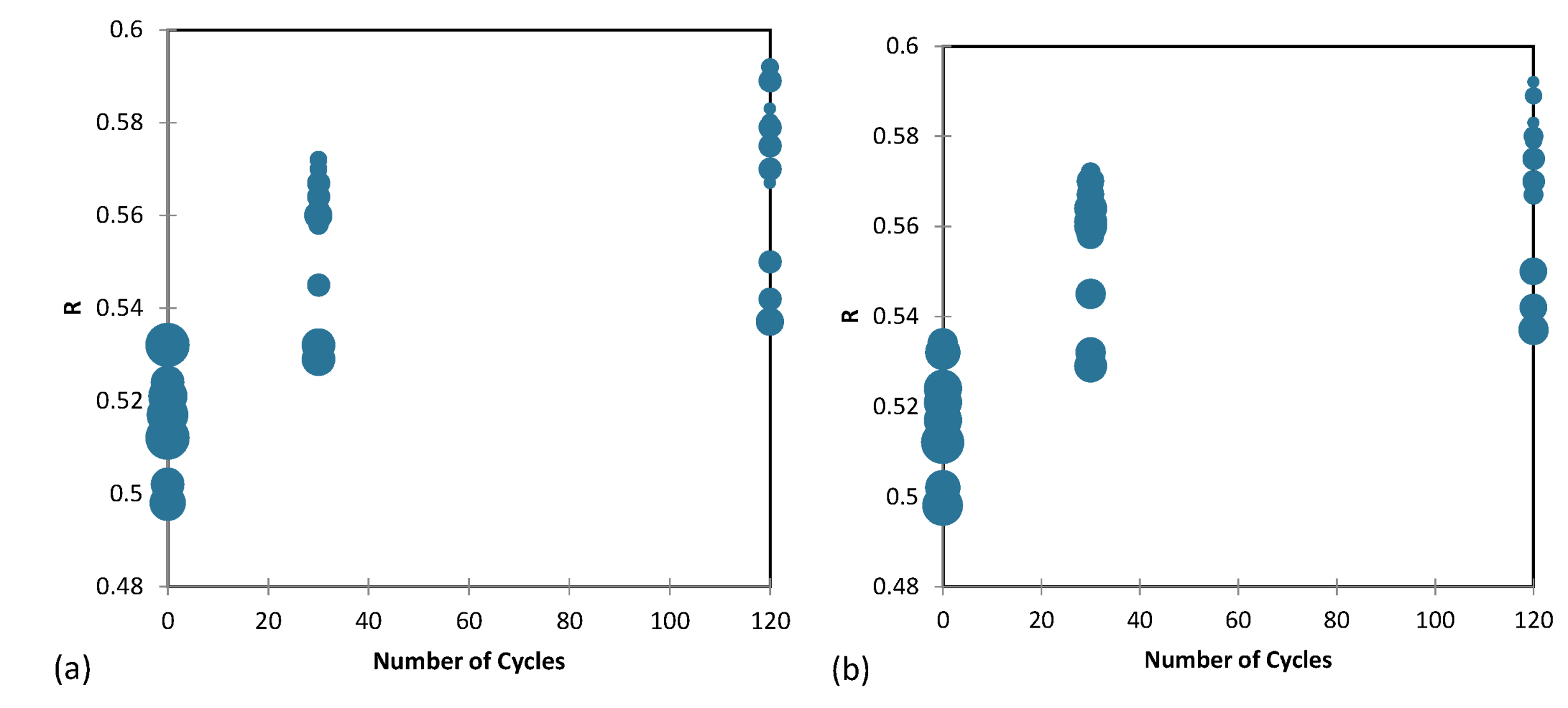
Preprints 69240 g016
Figure 16. The effect of cycling loading on (a) emin and (b) emax based on the R parameter.
Figure 16. The effect of cycling loading on (a) emin and (b) emax based on the R parameter.
Preprints 69240 g016
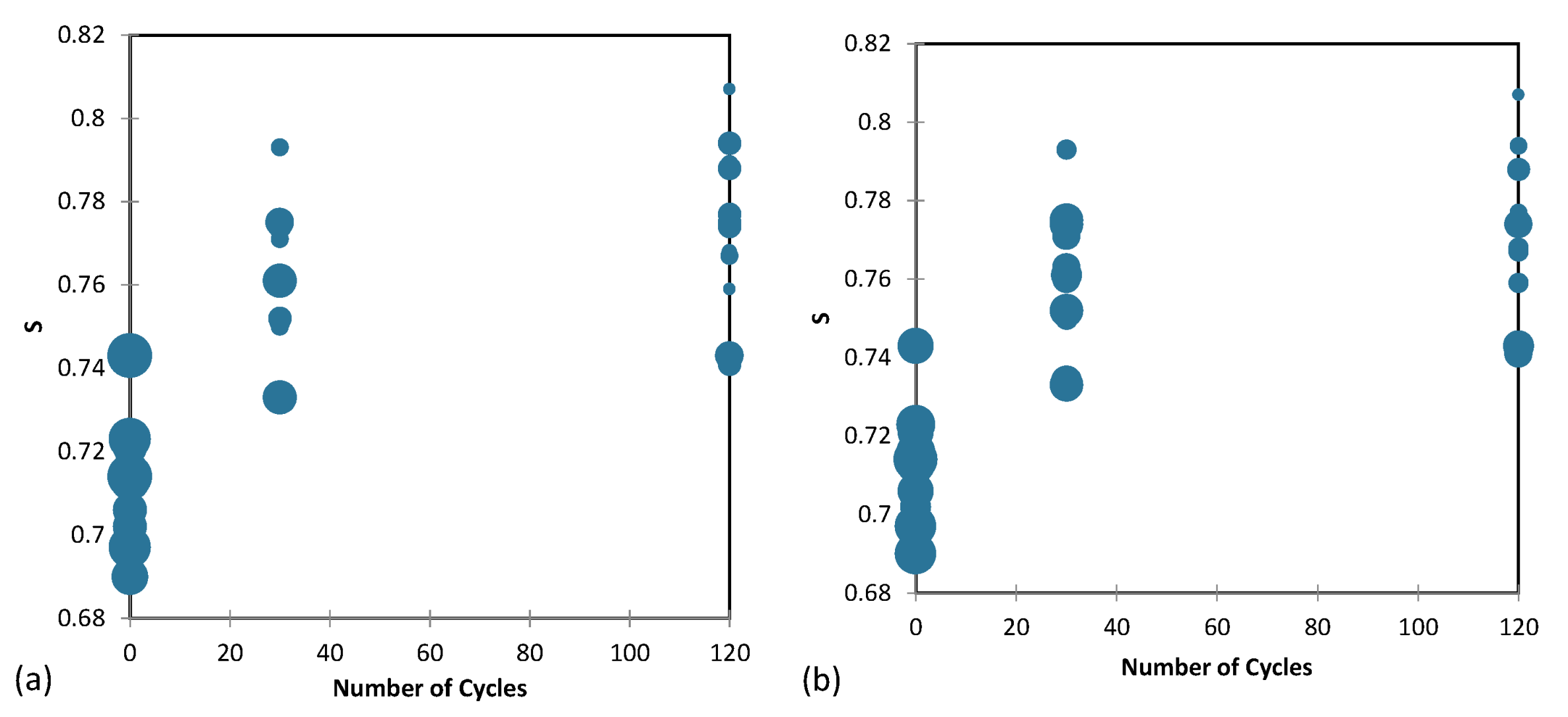
Preprints 69240 g017
Figure 17. The effect of cycling loading on (a) emin and (b) emax based on the S parameter.
Figure 17. The effect of cycling loading on (a) emin and (b) emax based on the S parameter.
Preprints 69240 g017
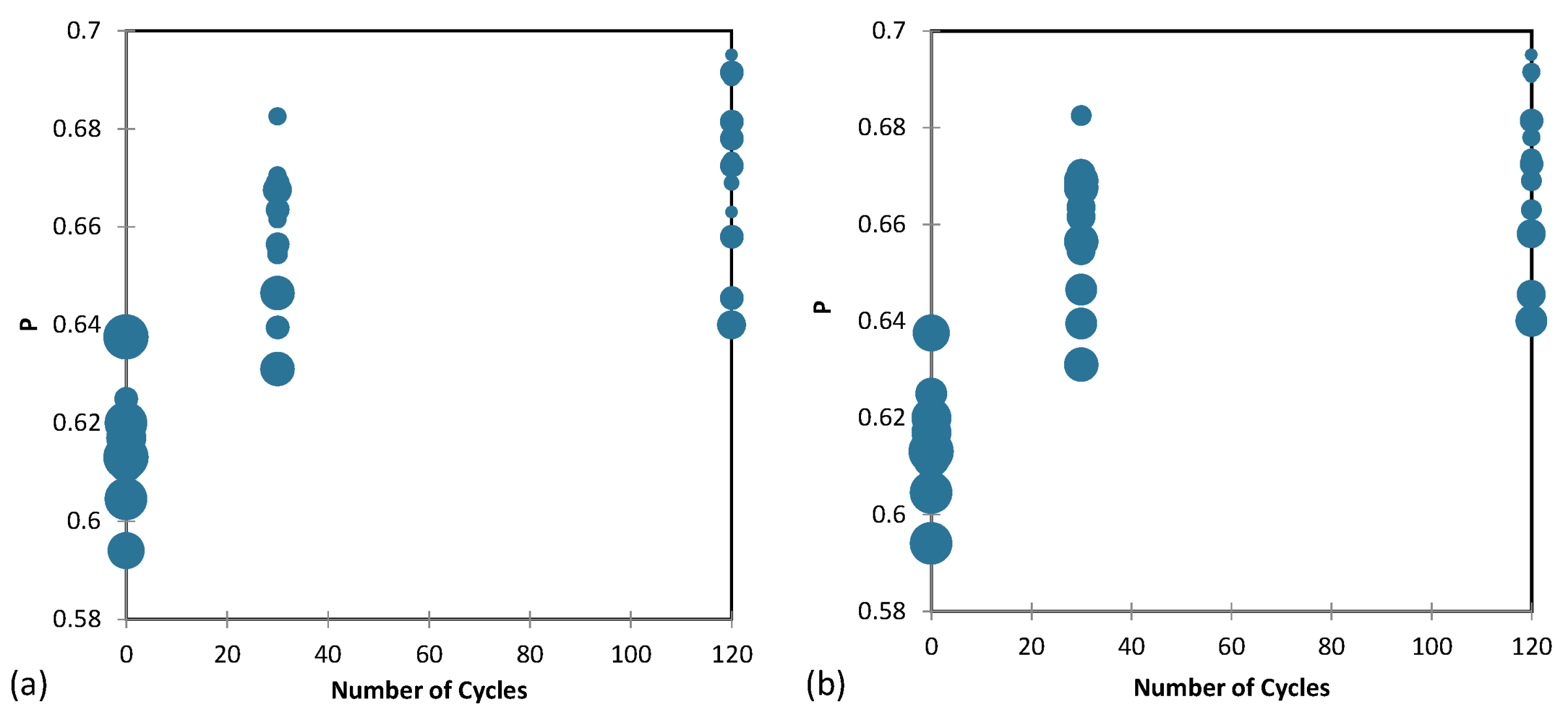
Preprints 69240 g018
Figure 18. The effect of cycling loading on (a) emin and (b) emax based on the ρ parameter.
Figure 18. The effect of cycling loading on (a) emin and (b) emax based on the ρ parameter.
Preprints 69240 g018
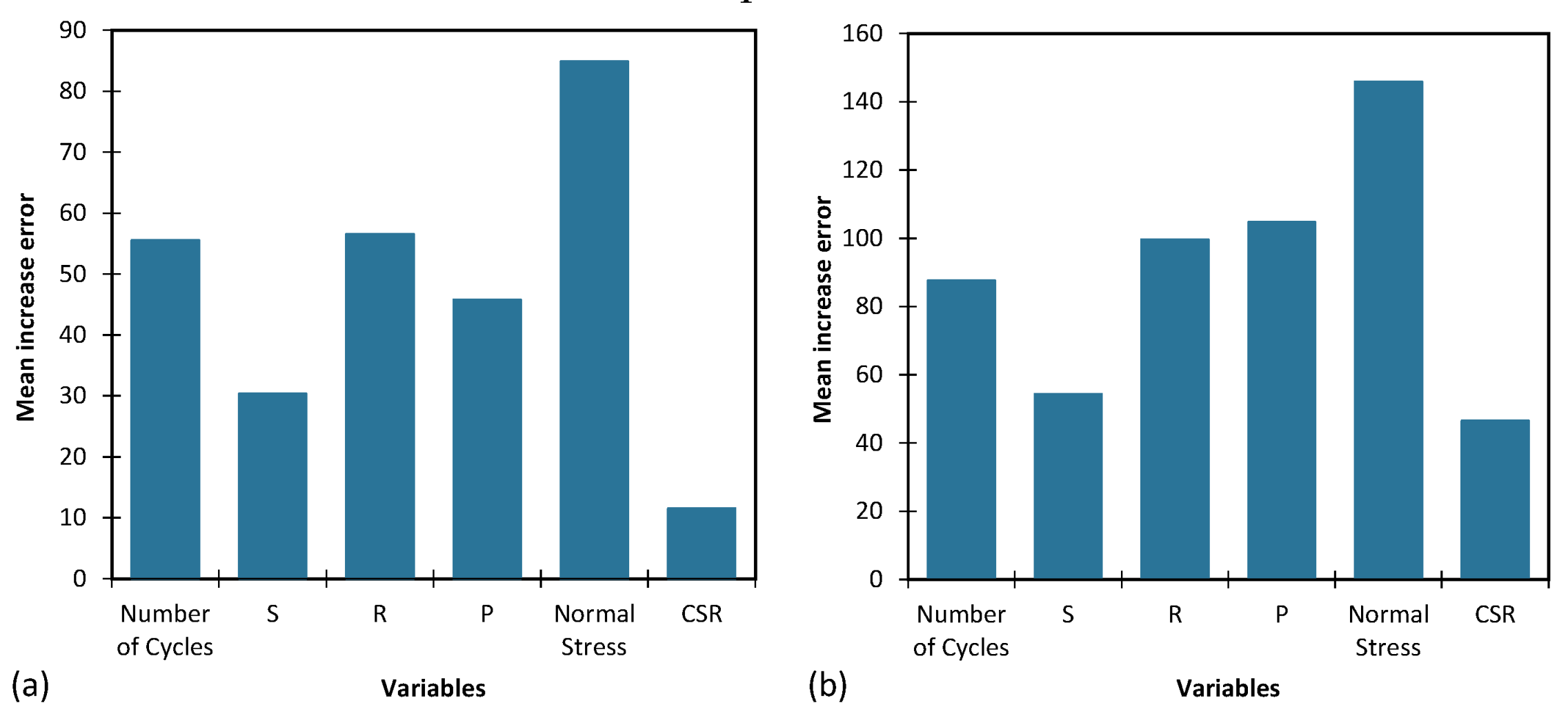
Preprints 69240 g019
Figure 19. The importance of input parameters on the MAE of the best (a) ANN, and (b) SVM model.
Figure 19. The importance of input parameters on the MAE of the best (a) ANN, and (b) SVM model.
Preprints 69240 g019
Table 1. Three shape descriptors before cycling tests.
Table 1. Three shape descriptors before cycling tests.
Variable Minimum Maximum Mean Std. deviation
S 0.690 0.743 0.713 0.014
R 0.498 0.534 0.518 0.011
ρ 0.594 0.638 0.616 0.011
D 8.500 25.500 16.050 5.903
Table 2. Three shape descriptors after 30 cycling tests.
Table 2. Three shape descriptors after 30 cycling tests.
Variable Minimum Maximum Mean Std. deviation
S 0.733 0.793 0.760 0.017
R 0.529 0.572 0.557 0.014
ρ 0.631 0.683 0.658 0.014
D 7.200 21.400 13.392 4.784
Table 3. Three shape descriptors after 120 cycling tests.
Table 3. Three shape descriptors after 120 cycling tests.
Variable Minimum Maximum Mean Std. deviation
S 0.741 0.807 0.774 0.020
R 0.537 0.592 0.570 0.018
ρ 0.640 0.695 0.672 0.018
D 6.900 20.200 12.425 4.536
Table 4. Results of best ANN-ML model to predict damping ratio for both training and testing databases.
Table 4. Results of best ANN-ML model to predict damping ratio for both training and testing databases.
Metrics Training Database Testing Database
MAE 0.887 0.551
MSE 1.056 0.460
RMSE 1.027 0.679
MSLE 0.007 0.001
RMSLE 0.084 0.037
R² 0.962 0.962
Table 5. Results of best SVM model to predict damping ratio for both training and testing databases.
Table 5. Results of best SVM model to predict damping ratio for both training and testing databases.
Metrics Training Database Testing Database
MAE 0.716 0.831
MSE 0.761 1.302
RMSE 0.872 1.141
MSLE 0.006 0.003
RMSLE 0.079 0.057
R² 0.973 0.892
Table 6. The ranking results of variable importance for all models.
Table 6. The ranking results of variable importance for all models.
Models Input parameters
Numbre of cycles S R ρ Vertical Stress CSR
ANN 3 5 2 4 1 6
SVM 4 5 3 2 1 6
Total score 7 10 5 6 2 12
Ranking 4 5 2 3 1 6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated