TAN: A Transferable Adversarial Network for DNN-based UAV SAR Automatic Target Recognition Models

In recent years, the unmanned aerial vehicle (UAV) synthetic aperture radar (SAR) has become a highly sought-after topic for its wide applications in the field of target recognition, detection, and tracking. However, SAR automatic target recognition (ATR) models based on deep neural networks (DNN) are suffering from adversarial examples. Generally, non-cooperators rarely disclose any information about SAR-ATR models, making adversarial attacks challenging. In this situation, we propose Transferable Adversarial Network (TAN) to attack these models with highly transferable adversarial examples. The proposed method improves the transferability via a two-player game, in which we simultaneously train two encoder-decoder models: a generator that crafts malicious samples through a one-step forward mapping from original data, and an attenuator that weakens the effectiveness of malicious samples by capturing the most harmful deformations. In particular, compared to traditional iterative methods, our approach is able to one-step map original samples to adversarial examples, thus enabling real-time attacks. Experimental results indicate that the proposed approach achieves state-of-the-art transferability with acceptable adversarial perturbations and minimum time costs compared to existing attack methods, i.e., it excellently realizes real-time transferable adversarial attacks.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The ongoing advances in unmanned aerial vehicle (UAV) and synthetic aperture radar (SAR) technologies have enabled the acquisition of high-resolution SAR images through UAVs. However, unlike visible light imaging, SAR images reflect the reflection intensity of imaging targets to radar signals, making it difficult for humans to extract effective semantic information from SAR images without the aid of interpretation tools. Currently, deep learning has achieved excellent performance in various scenarios [1,2,3], and SAR automatic target recognition (SAR-ATR) models based on deep neural networks (DNN) [4,5,6,7,8] have become one of the most popular interpretation methods. With their powerful representation capabilities, DNNs outperform traditional approaches in image classification tasks. Yet, recent studies have shown that DNN-based SAR-ATR models are susceptible to adversarial examples [9].

The concept of adversarial examples was first proposed by Szegedy et al. [10], which suggests that a carefully designed tiny perturbation can cause a well-trained DNN model to misclassify. This finding has made adversarial attacks one of the most serious threats to artificial intelligence (AI) security. To date, researchers have proposed a variety of adversarial attack methods, which can be mainly divided into two categories from the perspective of prior knowledge: the white-box and black-box attacks. In the first case, attackers can utilize a large amount of prior knowledge, such as the model structure and gradient information, etc., to craft adversarial examples for victim models. Examples of white-box methods include gradient-based attacks [11,12], boundary-based attacks [13], and saliency map-based attacks [14], etc. While in the second case, attackers can only access the output information or even less, making adversarial attacks much more difficult. Examples of black-box methods include probability label-based attacks [15,16] and decision-based attacks [17], etc. We now consider an extreme situation, where attackers have no access to any feedback from victim models, such that existing attack methods are unable to craft adversarial examples until researchers discover that adversarial examples can transfer among DNN models. Liu et al. [18] proposed an ensemble-based approach to generating transferable adversarial examples for the non-targeted and targeted attacks. Subsequent studies focused on improving the basic FGSM [11] method to enhance the transferability of adversarial examples, such as gradient-based methods [19,20], transformation-based methods [20,21], and variance-based methods [22], etc. However, the transferability and real-time performance of the above approaches are still insufficient to meet realistic attack requirements. Consequently, further improvements in the adversarial attack are pending to be solved in the future.

With the wide application of DNNs in the field of remote sensing, researchers have embarked on investigating the adversarial examples of remote sensing images. Xu et al. [23] first investigated the adversarial attack and defense in safety-critical remote sensing tasks, and proposed the mixup attack [24] to generate universal adversarial examples for remote sensing images. However, the research on the adversarial example of SAR images is still in its infancy. Li et al. [25] generated abundant adversarial examples for CNN-based SAR image classifiers through the basic FGSM method and systematically evaluated critical factors affecting the attack performance. Du et al. [26] designed a Fast C&W algorithm to improve the efficiency of generating adversarial examples by introducing an encoder-decoder model. To enhance the universality and feasibility of adversarial perturbations, the work in [27] presented a universal local adversarial network to generate universal adversarial perturbations for the target region of SAR images. Furthermore, the latest research [28] has broken through the limitations of the digital domain and implemented the adversarial example of SAR images in the signal domain by transmitting a two-dimensional jamming signal. Despite the high attack success rates achieved by the above methods, the problem of transferable adversarial examples in the field of SAR-ATR has yet to be addressed.

In this paper, a transferable adversarial network (TAN) is proposed to improve the transferability and real-time performance of adversarial examples in SAR images. Specifically, during the training phase of TAN, we simultaneously train two encoder-decoder models: a generator that crafts malicious samples through a one-step forward mapping from original data, and an attenuator that weakens the effectiveness of malicious samples by capturing the most harmful deformations. We argue that if the adversarial examples crafted by the generator are robust to the deformations produced by the attenuator, i.e., the attenuated adversarial examples remain effective to DNN models, then they are capable of transferring to other victim models. Moreover, unlike traditional iterative methods, our approach can one-step map original samples to adversarial examples, thus enabling real-time attacks. In other words, we realize real-time transferable adversarial attacks through a two-player game between the generator and attenuator.

The main contributions of this paper are summarized as follows.

(1): For the first time, this paper systematically evaluates the transferability of adversarial examples among DNN-based SAR-ATR models. Meanwhile, our research reveals that there may be potential common vulnerabilities among DNN models performing the same task.
(2): We propose a novel network to enable real-time transferable adversarial attacks. Once the proposed network is well-trained, it can real-time craft adversarial examples with high transferability, thus attacking black-box victim models without resorting to any prior knowledge. As such, our approach possesses promising applications in AI security.
(3): The proposed method is evaluated on the most authoritative SAR-ATR dataset. Experimental results indicate that our approach achieves state-of-the-art transferability with acceptable adversarial perturbations and minimum time costs compared to existing attack methods, i.e., it excellently realizes real-time transferable adversarial attacks.

The rest parts of this paper are arranged as follows. Section 2 introduces the relevant preparation knowledge, and Section 3 describes the proposed method in detail. The experimental results and conclusions are given in Section 4 and Section 5, respectively.

2. Preliminaries

2.1. Adversarial Attacks for DNN-Based SAR-ATR Models

Suppose

x_{n} \in {[0, 255]}^{W \times H}

is a single channel SAR image from the dataset

X

and

f (\cdot)

is a DNN-based K-class SAR-ATR model. Given a sample

x_{n}

as input to

f (\cdot)

, the output is a K-dimensional vector

f (x_{n}) = [f {(x_{n})}_{1}, f {(x_{n})}_{2}, \dots, f {(x_{n})}_{K}]

, where

f {(x_{n})}_{i} \in R

denotes the score of

x_{n}

belonging to class i. Let

C_{p} = {arg max}_{i} (f {(x_{n})}_{i})

represent the predicted class of

f (\cdot)

for

x_{n}

. The adversarial attack is to fool

f (\cdot)

with an adversarial example

{\tilde{x}}_{n}

that only has a minor perturbation on

x_{n}

. The detail process can be expressed as follows:

\underset{i}{arg max} f {({\tilde{x}}_{n})}_{i} \neq C_{p}, s . t . {∥{\tilde{x}}_{n} - x_{n}∥}_{p} \leq ξ

(1)

where the

L_{p}

-norm is defined as

{∥v∥}_{p} = {(\sum_{i} {|v_{i}|}^{p})}^{\frac{1}{p}}

, and

ξ

controls the magnitude of adversarial perturbations.

Meanwhile, adversarial attacks can be mainly divided into two modes. The first basic mode is called the non-targeted attack, making DNN models misclassify. The second one is more stringent, called the targeted attack, which induces models to output specified results. There is no doubt that the latter poses a higher level of threat to AI security. In other words, the non-targeted attack is to minimize the probability of models correctly recognize samples; conversely, the targeted attack maximizes the probability of models identifying samples as target classes. Thus, (1) can be transformed into the following optimization problems:

For the non-targeted attack:

$m i n i m i z e (\frac{1}{N} \sum_{n = 1}^{N} D (\underset{i}{arg max} f {({\tilde{x}}_{n})}_{i} = = C_{t r})), s . t . {∥{\tilde{x}}_{n} - x_{n}∥}_{p} \leq ξ$

(2)
For the targeted attack:

$m a x i m i z e (\frac{1}{N} \sum_{n = 1}^{N} D (\underset{i}{arg max} f {({\tilde{x}}_{n})}_{i} = = C_{t a})), s . t . {∥{\tilde{x}}_{n} - x_{n}∥}_{p} \leq ξ$

(3)

where the discriminant function

D (\cdot)

equals one if the equation holds; otherwise, it equals zero.

C_{t r}

and

C_{t a}

represent the true and target classes of the input. N is the number of samples in the dataset. Obviously, the above optimization problems are exactly the opposite of a DNN’s training process, and the corresponding loss functions will be given in the next chapter.

2.2. Transferability of Adversarial Examples

We consider an extreme situation where attackers have no access to any feedback from victim models, such that existing white-box and black-box attacks are unable to craft adversarial examples. In this case, attackers can utilize the transferability of adversarial examples to attack models. Specifically, due to the similarity between models, adversarial examples generated for a certain model can also successfully attack other models performing the same task [18]. Details are shown in Figure 1.

As shown in Figure 1, for an image classification task, we have trained three recognition models. Suppose that only the surrogate model

f_{s} (\cdot)

is a white-box model, and victim models

f_{v 1} (\cdot)

f_{v 2} (\cdot)

are black-box models. Undoubtedly, given an sample x, attackers can craft an adversarial example

\tilde{x}

to fool

f_{s} (\cdot)

through attack algorithms. Meanwhile, since the transferability of adversarial examples,

\tilde{x}

can also fool

f_{v 1} (\cdot)

and

f_{v 2} (\cdot)

successfully. However, the transferability generated by existing algorithms is very weak, so this paper is dedicated to crafting highly transferable adversarial examples.

3. The Proposed Transferable Adversarial Network (TAN)

In this paper, the proposed Transferable Adversarial Network (TAN) utilizes the encoder-decoder model and data augmentation technology to improve the transferability and real-time performance of adversarial examples. The framework of our network is shown in Figure 2. As we can see, compared to traditional iterative methods, TAN introduces a generator

G (\cdot)

to learn the one-step forward mapping from the clean sample x to the adversarial example

\tilde{x}

, thus enabling real-time attacks. Meanwhile, to improve the transferability of

\tilde{x}

, we simultaneously train an attenuator

A (\cdot)

to capture the most harmful deformations, which are supposed to weaken the effectiveness of

\tilde{x}

while still preserving the semantic meaning of x. We argue that if

\tilde{x}

is robust to the deformations produced by

A (\cdot)

, i.e.,

{\tilde{x}}^{*}

remains effective to DNN models, then

\tilde{x}

is capable of transferring to the black-box victim model

f_{v} (\cdot)

. In other words, we achieve real-time transferable adversarial attacks through a two-player game between

G (\cdot)

and

A (\cdot)

. This chapter will introduce our method in detail.

3.1. Training Process of the Generator

For easy understanding, Figure 3 shows the detailed training process of the generator. Note that a white-box model is selected as the surrogate model

f_{s} (\cdot)

during the training phase.

As we can see, given a clean sample x, the generator

G (\cdot)

crafts the adversarial example

\tilde{x}

through a one-step forward mapping, as follows:

\tilde{x} = G (x)

(4)

Meanwhile, the attenuator

A (\cdot)

takes

\tilde{x}

as input and outputs the attenuated adversarial example

{\tilde{x}}^{*}

{\tilde{x}}^{*} = A (\tilde{x})

(5)

Since

\tilde{x}

has to fool

f_{s} (\cdot)

with a minor perturbation, and

{\tilde{x}}^{*}

needs to remain effective against

f_{s} (\cdot)

, the loss function of

G (\cdot)

consists of three parts. Next, we will give the generator loss

L_{G}

of non-targeted and targeted attacks, respectively.

For the non-targeted attack: First, according to (2),

\tilde{x}

is to minimize the classification accuracy of

f_{s} (\cdot)

, which means that it has to decrease the confidence of being recognized as the true class

C_{t r}

, i.e., to increase the confidence of being identified as others. Thus, the first part of

L_{G}

can be expressed as:

\begin{matrix} L_{G 1} (f_{s} (\tilde{x}), C_{t r}) & = - log (\frac{\sum_{i \neq C_{t r}} exp (f_{s} {(\tilde{x})}_{i})}{\sum_{i} exp (f_{s} {(\tilde{x})}_{i})}) \\ = - log (1 - \frac{exp (f_{s} {(\tilde{x})}_{C_{t r}})}{\sum_{i} exp (f_{s} {(\tilde{x})}_{i})}) \end{matrix}

(6)

Second, to improve the transferability of

\tilde{x}

, we expect that

{\tilde{x}}^{*}

remains effective to

f_{s} (\cdot)

, so the second part of

L_{G}

can be derived as:

\begin{matrix} L_{G 2} (f_{s} ({\tilde{x}}^{*}), C_{t r}) & = - log (\frac{\sum_{i \neq C_{t r}} exp (f_{s} {({\tilde{x}}^{*})}_{i})}{\sum_{i} exp (f_{s} {({\tilde{x}}^{*})}_{i})}) \\ = - log (1 - \frac{exp (f_{s} {({\tilde{x}}^{*})}_{C_{t r}})}{\sum_{i} exp (f_{s} {({\tilde{x}}^{*})}_{i})}) \end{matrix}

(7)

Finally, the last part of

L_{G}

is used to limit the perturbation magnitude. We introduce the traditional

L_{p}

-norm to measure the degree of image distortion as follows:

\begin{matrix} L_{G 3} (x, \tilde{x}) & = {∥\tilde{x} - x∥}_{p} \\ = {(\sum_{i} {|Δ x_{i}|}^{p})}^{\frac{1}{p}} \end{matrix}

(8)

In summary, we apply the linear weighted sum method to balance the relationship between

L_{G 1}

L_{G 2}

, and

L_{G 3}

. As such, the complete generator loss for the non-targeted attack can be represented as:

\begin{matrix} L_{G} & = ω_{G 1} \cdot L_{G 1} (f_{s} (\tilde{x}), C_{t r}) + ω_{G 2} \cdot L_{G 2} (f_{s} ({\tilde{x}}^{*}), C_{t r}) + ω_{G 3} \cdot L_{G 3} (x, \tilde{x}) \end{matrix}

(9)

where

ω_{G 1} + ω_{G 2} + ω_{G 3} = 1

ω_{G 1}, ω_{G 2}, ω_{G 3} \in [0, 1]

are the weight coefficients of

L_{G 1}

L_{G 2}

, and

L_{G 3}

, respectively.

For the targeted attack: According to (3),

\tilde{x}

is to maximize the probability of being recognized as the target class

C_{t a}

, i.e., to increase the confidence of

C_{t a}

. Thus,

L_{G 1}

here can be expressed as:

L_{G 1} (f_{s} (\tilde{x}), C_{t a}) = - log (\frac{exp (f_{s} {(\tilde{x})}_{C_{t a}})}{\sum_{i} exp (f_{s} {(\tilde{x})}_{i})})

(10)

To maintain the effectiveness of

{\tilde{x}}^{*}

against

f_{s} (\cdot)

L_{G 2}

here is derived as:

L_{G 2} (f_{s} ({\tilde{x}}^{*}), C_{t a}) = - log (\frac{exp (f_{s} {({\tilde{x}}^{*})}_{C_{t a}})}{\sum_{i} exp (f_{s} {({\tilde{x}}^{*})}_{i})})

(11)

The perturbation magnitude is still limited by the

L_{G 3}

shown in (8). Therefore, the complete generator loss for the targeted attack can be represented as:

\begin{matrix} L_{G} & = ω_{G 1} \cdot L_{G 1} (f_{s} (\tilde{x}), C_{t a}) + ω_{G 2} \cdot L_{G 2} (f_{s} ({\tilde{x}}^{*}), C_{t a}) + ω_{G 3} \cdot L_{G 3} (x, \tilde{x}) \end{matrix}

(12)

3.2. Training Process of the Attenuator

According to Figure 2, during the training phase of TAN, an attenuator

A (\cdot)

is introduced to weaken the effectiveness of

\tilde{x}

while still preserving the semantic meaning of x. We show the detailed training process of

A (\cdot)

in Figure 4.

As we can see, the attenuator loss

L_{A}

also consists of three parts. First, to preserve the semantic meaning of x,

f_{s} (\cdot)

has to keep a basic classification accuracy on the following attenuated sample

x^{*}

x^{*} = A (x)

(13)

It means that the first part of

L_{A}

should increase the confidence of

x^{*}

being recognized as the true class

C_{t r}

, as follows:

L_{A 1} (f_{s} (x^{*}), C_{t r}) = - log (\frac{exp (f_{s} {(x^{*})}_{C_{t r}})}{\sum_{i} exp (f_{s} {(x^{*})}_{i})})

(14)

Meanwhile, to weaken the effectiveness of

\tilde{x}

A (\cdot)

also need to improve the confidence of the attenuated adversarial example

{\tilde{x}}^{*}

being identified as

C_{t r}

, so the second part of

L_{A}

can be expressed as:

L_{A 2} (f_{s} ({\tilde{x}}^{*}), C_{t r}) = - log (\frac{exp (f_{s} {({\tilde{x}}^{*})}_{C_{t r}})}{\sum_{i} exp (f_{s} {({\tilde{x}}^{*})}_{i})})

(15)

Finally, to avoid excessive image distortion caused by

A (\cdot)

, the third part of

L_{A}

is used to limit the deformation magnitude, which can be expressed by the traditional

L_{p}

-norm, as follows:

\begin{matrix} L_{A 3} (x, x^{*}) & = {∥x^{*} - x∥}_{p} \\ = {(\sum_{i} {|Δ x_{i}|}^{p})}^{\frac{1}{p}} \end{matrix}

(16)

As with the generator loss, we utilize the linear weighted sum method to derive the complete attenuator loss as follows:

\begin{matrix} L_{A} & = ω_{A 1} \cdot L_{A 1} (f_{s} (x^{*}), C_{t r}) + ω_{A 2} \cdot L_{A 2} (f_{s} ({\tilde{x}}^{*}), C_{t r}) + ω_{A 3} \cdot L_{A 3} (x, x^{*}) \end{matrix}

(17)

where

ω_{A 1} + ω_{A 2} + ω_{A 3} = 1

ω_{A 1}, ω_{A 2}, ω_{A 3} \in [0, 1]

are the weight coefficients of

L_{A 1}

L_{A 2}

, and

L_{A 3}

, respectively.

3.3. Network Structure of the Generator and Attenuator

According to Section 3.1 and Section 3.2, the generator and attenuator are essentially two encoder-decoder models, so the choice of a suitable model structure is necessary. We mainly consider two factors. First, as the size of original samples and adversarial examples should be the same, the model has to keep the input and output sizes identical. Second, to prevent our network from overfitting while saving computational resources, a lightweight model will be a better choice. In summary, we apply ResNet Generator proposed in [29] as the encoder-decoder model of TAN. The structure of ResNet Generator is shown in Figure 5.

As we can see, ResNet Generator mainly consists of downsampling, residual, and upsampling modules. For a visual understanding, given an input data of size

1 \times 128 \times 128

, the input and output sizes of each module are listed in Table 1.

Obviously, the input and output sizes of ResNet Generator are the same. Meanwhile, to ensure the validity of the generated data, we add a

t a n h

function after the output module, which restricts the generated data to the interval

[0, 1]

. The total number of parameters in ResNet Generator has been calculated to be approximately

7.83 M

, which is a fairly lightweight network. For more details, please refer to literature [29].

3.4. Complete Training Process of TAN

As we described earlier, TAN improves the transferability of adversarial examples through a two-player game between the generator and attenuator, which is quite similar to the working principle of generative adversarial networks (GAN) [30]. Therefore, we also adopt an alternating training scheme to train our network. Specifically, given the dataset

X

and batch size S, we first randomly divide

X

into M batches

{b_{1}, b_{2}, \dots, b_{M}}

at the beginning of each training iteration. Second, we set a training ratio

R \in N^{*}

, which means that TAN trains the generator R times and then trains the attenuator once, i.e., once per batch for the former and only once per R batches for the latter. In this way, we can prevent the attenuator from being so strong that the generator cannot be optimized. Meanwhile, to shorten training time, we set an early stop condition

E S C

so that training can be ended early when certain indicators meet the condition. Note that the generator and attenuator are trained alternately, i.e., the attenuator’s parameters are fixed when the generator is trained, and vice versa. More details of the complete training process for TAN are shown in Algorithm 1.

Algorithm 1 Transferable Adversarial Network Training.

Input:: Dataset $X$ ; batch size S; surrogate model $f_{s}$ ; target class $C_{t a}$ ; training loss function of the generator $L_{G}$ ; training loss function of the attenuator $L_{A}$ ; number of training iterations T; learning rate $η$ ; training ratio of the generator and attenuator R; early stop condition $E S C$ .
Output:: The parameter $θ_{G}$ of the well-trained generator.
1:: Randomly initialize $θ_{G}$ and $θ_{A}$
2:: for $t = 1$ to T do
3:: According to S, randomly divide $X$ into M batches ${b_{1}, b_{2}, \dots, b_{M}}$
4:: for $m = 1$ to M do
5:: Calculate $L_{G} (θ_{G}, θ_{A}, f_{s}, b_{m}, C_{t a})$
6:: Update $θ_{G} = θ_{G} - η \cdot \frac{\partial}{\partial θ_{G}} L_{G}$
7:: if $m % R = = 0$ then
8:: Calculate $L_{A} (θ_{G}, θ_{A}, f_{s}, b_{m})$
9:: Update $θ_{A} = θ_{A} - η \cdot \frac{\partial}{\partial θ_{A}} L_{A}$
10:: else
11:: $θ_{A} = θ_{A}$
12:: end if
13:: end for
14:: if $E S C = = T r u e$ then
15:: Break
16:: else
17:: Continue
18:: end if
19:: end for

4. Experiments

4.1. Data Descriptions

To date, there is no publicly available dataset for UAV SAR-ATR, thus this paper experiments on the most authoritative SAR-ATR dataset, i.e., the moving and stationary target acquisition and recognition (MSTAR) dataset [31]. MSTAR is collected by a high-resolution spotlight SAR and published by the U.S. Defense Advanced Research Projects Agency (DARPA) in 1996, which contains SAR images of Soviet military vehicle targets at different azimuth and depression angles. In standard operating conditions (SOC), MSTAR includes ten classes of targets, such as self-propelled howitzers (2S1); infantry fighting vehicles (BMP2); armored reconnaissance vehicles (BRDM2); wheeled armored transport vehicles (BTR60, BTR70); bulldozers (D7); main battle tanks (T62, T72); cargo trucks (ZIL131); and self-propelled artillery (ZSU234). The training dataset contains 2747 images collected at a depression angle of

17^{\circ}

, and the testing dataset contains 2426 images captured at a depression angle of

15^{\circ}

. More details about the dataset are given in Table 2, and Figure 6 shows the optical images and corresponding SAR images of each class.

4.2. Implementation Details

We evaluate the attack performance of our approach on the following six common DNN models: DenseNet121 [32], GoogLeNet [33], InceptionV3 [34], Mobilenet [35], ResNet50 [36], and Shufflenet [37]. To uniform image sizes, we resize all the images in MSTAR to

128 \times 128

. As for the dataset processing, we uniformly sample

10 %

of data from the training dataset to form the validation dataset. During the training phase of recognition models, we set the training epoch and batch size to 100 and 32, respectively. For the training parameters of TAN, we set the generator loss weights

[ω_{G 1}, ω_{G 2}, ω_{G 3}]

[0.25, 0.25, 0.5]

, the attenuator loss weights

[ω_{A 1}, ω_{A 2}, ω_{A 3}]

[0.25, 0.25, 0.5]

, the training ratio to 3, the training epoch to 50, the batch size to 8, and the norm type to the

L_{2}

-norm. For above models, we optimize them through an Adam optimizer [38] with the learning rate of

0.001

. When evaluating the transferability of adversarial examples, we first take each network as the surrogate model in turn and craft adversarial examples for them, respectively. Then, we assess the transferability by testing the recognition results of victim models on corresponding adversarial examples. Detailed experimental results will be given later.

For baseline methods, we adopt the following six attack algorithms from the Torchattacks [39] toolbox to compare with TAN: MIFGSM [19], DIFGSM [21], NIFGSM [20], SINIFGSM [20], VMIFGSM [22], and VNIFGSM [22]. All codes were written in Pytorch, and the experimental environment consisted of Windows 10 with an NVIDIA GeForce RTX 2080 Ti GPU and a

3.6

GHz Intel Core i9-9900K CPU).

4.3. Evaluation Metrics

We mainly consider two factors to comprehensively evaluate the performance of adversarial attacks: the effectiveness and stealthiness, which are directly related to the classification accuracy

\tilde{A c c}

of victim models on adversarial examples and the norm value

{\tilde{L}}_{p}

of adversarial perturbations, respectively. For the

\tilde{A c c}

metric, the formula is as follows:

\tilde{A c c} = \{\begin{matrix} \frac{1}{N} \sum_{n = 1}^{N} D (\underset{i}{arg max} (f_{v} {({\tilde{x}}_{n})}_{i}) = = C_{t r}) & for the non - targeted attack \\ \frac{1}{K \times N} \sum_{C_{t a} = 1}^{K} \sum_{n = 1}^{N} D (\underset{i}{arg max} (f_{v} {({\tilde{x}}_{n})}_{i}) = = C_{t a}) & for the targeted attack \end{matrix}

(18)

where

C_{t r}

and

C_{t a}

represent the true and target classes of the input data, K is the number of target classes, and

D (\cdot)

is a discriminant function. In the non-targeted attack, the

\tilde{A c c}

metric reflects the probability that the victim model

f_{v} (\cdot)

identifies the adversarial example

{\tilde{x}}_{n}

C_{t r}

, while in the targeted attack it indicates the probability that

f_{v} (\cdot)

recognizes

{\tilde{x}}_{n}

C_{t a}

. Obviously, in the non-targeted attack, the lower the

\tilde{A c c}

metric, the better the attack. Conversely, in the targeted attack, a higher

\tilde{A c c}

metric represents

f_{v} (\cdot)

is more likely to recognize

{\tilde{x}}_{n}

C_{t a}

, and thus the attack is more effective. In conclusion, the effectiveness of non-targeted attacks is inversely proportional to the

\tilde{A c c}

metric, and the effectiveness of targeted attacks is proportional to this metric. Additionally, there are other three similar indicators

A c c

A c c^{*}

, and

{\tilde{A c c}}^{*}

that represent the classification accuracy of

f_{v} (\cdot)

for the original sample

x_{n}

, the attenuated sample

x_{n}^{*}

, and the attenuated adversarial example

{\tilde{x}}_{n}^{*}

, respectively. Note that whether it is a non-targeted or targeted attack,

A c c^{*}

always represents the accuracy with which

f_{v} (\cdot)

identifies

x_{n}^{*}

C_{t r}

, while the other three accuracy indicators need to be calculated via (18) based on the attack mode. In particular,

{\tilde{A c c}}^{*}

represents the recognition result of

f_{v} (\cdot)

{\tilde{x}}_{n}^{*}

, which indirectly reflects the strength of the transferability possessed by

{\tilde{x}}_{n}

Meanwhile, we apply the following

L_{p}

-norm values to measure the attack stealthiness:

\{\begin{matrix} {\tilde{L}}_{p} = \frac{1}{N} \sum_{n = 1}^{N} {∥{\tilde{x}}_{n} - x_{n}∥}_{p} & for the generator \\ L_{p}^{*} = \frac{1}{N} \sum_{n = 1}^{N} {∥x_{n}^{*} - x_{n}∥}_{p} & for the attenuator \end{matrix}

(19)

where

{\tilde{L}}_{p}

and

L_{p}^{*}

represent the image distortion caused by the generator and attenuator, respectively. In our experiments, the

L_{p}

-norm defaults to

L_{2}

-norm. In summary, we can set the early stop condition

E S C

mentioned in Section 3.4 with the above indicators, as follows:

E S C = \{\begin{matrix} \tilde{A c c} \leq 0.05, A c c^{*} \geq 0.9, {\tilde{A c c}}^{*} \leq 0.1, {\tilde{L}}_{p} \leq 4, L_{p}^{*} \leq 4 & for the non - targeted attack \\ \tilde{A c c} \geq 0.95, A c c^{*} \geq 0.9, {\tilde{A c c}}^{*} \geq 0.9, {\tilde{L}}_{p} \leq 4, L_{p}^{*} \leq 4 & for the targeted attack \end{matrix}

(20)

Furthermore, to evaluate the real-time performance of adversarial attacks, we introduce the

T c

metric to denote the time cost of generating a single adversarial example, as follows:

T c = \frac{T i m e}{N}

(21)

where

T i m e

is the total time consumed to generate N adversarial examples.

4.4. DNN-Based SAR-ATR Models

A well-trained recognition model is a prerequisite for effective adversarial attacks, so we have trained six SAR-ATR models on the MSTAR dataset: DenseNet121, GoogLeNet, InceptionV3, Mobilenet, ResNet50, Shufflenet. All of them achieve outstanding recognition performance, with the classification accuracy of

98.72 %

98.06 %

96.17 %

96.91 %

97.98 %

, and

96.66 %

on the testing dataset, respectively. In addition, we show the confusion matrix of each model in Figure 7.

4.5. Comparison of Attack Performance

In this section, we first evaluated the attack performance of the proposed method against DNN-based SAR-ATR models on the MSTAR dataset. Specifically, during the training phase of TAN, we took each network as the surrogate model in turn and assessed the recognition results of corresponding models on the outputs of TAN at each stage. The results of non-targeted and targeted attacks are detailed in Table 3 and Table 4, respectively.

In non-targeted attacks, the

A c c

metric of each model on the MSTAR dataset exceeds

95 %

. However, after the non-targeted attack, the classification accuracy of all models on the generated adversarial examples, i.e., the

\tilde{A c c}

metric, is below

5 %

, and the

{\tilde{L}}_{2}

indicator is less than

3.7

. It means that adversarial examples deteriorate the recognition performance of models rapidly through minor adversarial perturbations. Meanwhile, during the training phase of TAN, we evaluate the performance of the attenuator. According to the

{\tilde{A c c}}^{*}

metric, the attenuator leads to an average improvement of about

25 %

in the classification accuracy of models on adversarial examples, that is, it indeed weakens the effectiveness of adversarial examples. We also should pay attention to the metrics

A c c^{*}

and

L_{2}^{*}

, i.e., the recognition accuracy of models on the attenuated samples, and the deformation distortion caused by the attenuator. The fact is that the

A c c^{*}

indicator of each model exceeds

80 %

, and the average value of the

L_{2}^{*}

metric is about 4. It means that the attenuator retains most semantic information of original samples without causing excessive deformation distortion, which is in line with our requirements.

In targeted attacks, the

A c c

metric represents the probability that models identify original samples as target classes, so it can reflect the dataset distribution, i.e., each category accounts for about

10 %

of the total dataset. While after the targeted attack, the probability of each model recognizing adversarial examples as target classes, i.e., the

\tilde{A c c}

metric, is over

97 %

, and the

{\tilde{L}}_{2}

indicator shows that the image distortion caused by adversarial perturbations is less than

3.5

. It means that the adversarial examples crafted by the generator can induce models to output specified results with high probability through minor perturbations. As with the non-targeted attack, we evaluate the performance of the attenuator. The

{\tilde{A c c}}^{*}

metric shows that the attenuator results in an average decrease of about

17 %

in the probability of adversarial examples being identified as target classes. Meanwhile, the

A c c^{*}

metric of each model exceeds

85 %

, and the average value of the

L_{2}^{*}

indicator is about

3.7

. That is, the attenuator weakens the effectiveness of adversarial examples through slight deformations, while preserving the semantic meaning of original samples well.

In summary, for both non-targeted and targeted attacks, the adversarial examples crafted by the generator can fool models with high success rates, and the attenuator is able to weaken the effectiveness of adversarial examples with slight deformations while retaining the semantic meaning of original samples. Moreover, we ensure that the generator always outperforms the attenuator by adjusting the training ratio between the two models. To visualize the attack results of TAN, we take ResNet50 as the surrogate model and display the outputs of TAN at each stage in Figure 8.

Finally, we compared the non-targeted and targeted attack performance of different methods against DNN-based SAR-ATR models on the MSTAR dataset, as detailed in Table 5. Obviously, for the same image distortion, the attack effectiveness of the proposed method against a single model may not be the best. Nevertheless, we focus more on the transferability of adversarial examples, which will be the main topic of the following section.

4.6. Comparison of Transferability

In this section, we evaluated the transferability of adversarial examples among DNN-based SAR-ATR models on the MSTAR dataset. Specifically, we first took each network as the surrogate model in turn and crafted adversarial examples for them, respectively. Then, we assessed the transferability by testing the recognition results of victim models on corresponding adversarial examples. The transferability in non-targeted and targeted attacks are shown in Table 6 and Table 7, respectively.

In non-targeted attacks, when the proposed method sequentially takes DenseNet121, GoogLeNet, InceptionV3, Mobilenet, ResNet50, and Shufflenet as the surrogate model, the highest recognition accuracy of victim models on the generated adversarial examples are

12.90 %

26.88 %

23.45 %

18.59 %

11.01 %

, and

23.54 %

, respectively. Equivalently, the highest recognition accuracy of victim models on the adversarial examples produced by baseline methods are

36.11 %

44.44 %

56.06 %

65.99 %

33.84 %

, and

68.51 %

, respectively. Meanwhile, for each surrogate model, victim models always have the lowest recognition accuracy on the adversarial examples crafted by our approach. Obviously, compared with baseline methods, the proposed method slightly sacrifices the performance on attacking surrogate models, but achieves state-of-the-art transferability among victim models in non-targeted attacks. Detailed results are shown in Table 6.

In targeted attacks, the proposed method still takes DenseNet121, GoogLeNet, InceptionV3, Mobilenet, ResNet50, and Shufflenet as the surrogate model in turn, and the minimum probability that victim models identify the generated adversarial examples as target classes are

52.39 %

55.02 %

54.57 %

57.66 %

66.26 %

, and

47.78 %

, respectively. Correspondingly, the minimum probability that victim models recognize the adversarial examples produced by baseline methods as target classes are

22.18 %

19.63 %

19.49 %

15.52 %

19.36 %

, and

13.06 %

, respectively. Moreover, for each surrogate model, victim models always identify the adversarial examples crafted by our approach as target classes with the maximum probability. Thus, the proposed method also achieves state-of-the-art transferability among victim models in targeted attacks. Detailed results are shown in Table 7.

In conclusion, for both non-targeted and targeted attacks, our approach generates adversarial examples with the strongest transferability. In other words, it performs better on exploring the common vulnerability of DNN models. We attribute this to the adversarial training between the generator and attenuator. Figuratively speaking, it is because the attenuator constantly creating obstacles for the generator that the attack capability of the generator is continuously enhanced and completed.

4.7. Comparison of Real-Time Performance

To evaluate the real-time performance of adversarial attacks, we calculated the time cost of generating a single adversarial example through different attack algorithms. We show the time consumption of non-targeted and targeted attacks in Table 8 and Table 9, respectively.

As we can see, there is almost no difference in the time cost of crafting a single adversarial example in non-targeted and targeted attacks. Meanwhile, for all the victim models, the time cost of generating a single adversarial example through the proposed method is stable around

2 m s

. As for baseline methods, it depends on the complexity of victim models, the more complex the model, the longer the time cost. However, even for the simplest victim model, the minimum time cost of baseline methods is about

4.5 m s

, consuming twice as much time as our approach. Thus, there is no doubt that the proposed method achieves the most superior and stable real-time performance.

4.8. Visualization of Adversarial Examples

In this section, we take ResNet50 as the surrogate model and visualize the adversarial examples crafted by different methods in Figure 9. Obviously, the adversarial perturbations generated by our method are continuous, and mainly focus on the target region of SAR images. In contrast, the perturbations produced by baseline methods are quite discrete, and almost cover the global area of SAR images. First, from the perspective of feature extraction, since the features that have a greater impact on recognition results are mainly concentrated in the target region rather than the background clutter area, a focused disruption of key features is certainly a more efficient attack strategy. Second, from the perspective of physical feasibility, the fewer pixels modified in adversarial examples, the smaller range perturbed in reality, so localized perturbations are more feasible than global ones. In summary, the proposed method improves the efficiency and feasibility of adversarial attacks by focusing perturbations on the target region of SAR images.

5. Conclusions

This paper proposed a transferable adversarial network (TAN) to generate adversarial examples for DNN-based SAR-ATR models, with the benefit that not only the transferability but also the real-time performance of adversarial examples is significantly improved. In the proposed method, a generator was designed to craft malicious samples through a one-step forward mapping from original data, and an attenuator was introduced to weaken the effectiveness of malicious samples by capturing the most harmful deformations. Our motivation is to enable real-time attacks by one-step mapping original samples to adversarial examples, and enhance the transferability through a two-player game between the generator and attenuator. Experimental results demonstrated that our approach achieves state-of-the-art transferability with acceptable adversarial perturbations and minimum time costs compared to existing attack methods, i.e., it excellently realizes real-time transferable adversarial attacks. Potential future work could consider attacking DNN-based SAR-ATR models under small sample conditions. It is also of great interest to real-world achieve the adversarial example of SAR images in addition to improving the performance of attack algorithms.

Author Contributions

Conceptualization, M.D. (Meng Du) and D.B.; methodology, M.D. (Meng Du); software, M.D. (Meng Du); validation, D.B., Y.S., B.S. and Z.W.; formal analysis, D.B. and M.D. (Mingyang Du); investigation, M.D. (Mingyang Du); resources, D.B.; data curation, M.D. (Meng Du); writing—original draft preparation, M.D. (Meng Du); writing—review and editing, M.D. (Meng Du), L.L. and D.B.; visualization, M.D. (Meng Du); supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant 62071476.

Institutional Review Board Statement

The study does not involve humans or animals.

Informed Consent Statement

The study does not involve humans.

Data Availability Statement

The experiments in this paper use public datasets, so no data are reported in this work.

Conflicts of Interest

The authors declare that they have no conflict of interest to report regarding the present study.

References

Li, D.; Kuai, Y.; Wen, G.; Liu, L. Robust Visual Tracking via Collaborative and Reinforced Convolutional Feature Learning. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 2019, pp. 0–0. [CrossRef]
Kuai, Y.; Wen, G.; Li, D. Masked and dynamic Siamese network for robust visual tracking. Information Sciences 2019, 503, 169–182. [CrossRef]
Cong, R.; Yang, N.; Li, C.; Fu, H.; Zhao, Y.; Huang, Q.; Kwong, S. Global-and-local collaborative learning for co-salient object detection. IEEE transactions on cybernetics 2022. [CrossRef]
Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [CrossRef]
Chen, S.; Wang, H.; Xu, F.; Jin, Y.Q. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [CrossRef]
Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [CrossRef]
Du, C.; Chen, B.; Xu, B.; Guo, D.; Liu, H. Factorized discriminative conditional variational auto-encoder for radar HRRP target recognition. Signal Process. 2019, 158, 176–189. [CrossRef]
Vint, D.; Anderson, M.; Yang, Y.; Ilioudis, C.; Di Caterina, G.; Clemente, C. Automatic Target Recognition for Low Resolution Foliage Penetrating SAR Images Using CNNs and GANs. Remote Sens. 2021, 13, 596. [CrossRef]
Huang, T.; Zhang, Q.; Liu, J.; Hou, R.; Wang, X.; Li, Y. Adversarial attacks on deep-learning-based SAR image target recognition. J. Netw. Comput. Appl. 2020, 162, 102632. [CrossRef]
Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [CrossRef]
Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [CrossRef]
Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: London, UK, 2018; pp. 99–112.
Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2574–2582. [CrossRef]
Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrücken, Germany, 21–24 March 2016; pp. 372–387. [CrossRef]
Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [CrossRef]
Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 15–26. [CrossRef]
Chen, J.; Jordan, M.I.; Wainwright, M.J. Hopskipjumpattack: A query-efficient decision-based attack. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (sp), San Francisco, CA, USA, 18–21 May 2020; pp. 1277–1294. [CrossRef]
Liu, Y.; Chen, X.; Liu, C.; Song, D. Delving into transferable adversarial examples and black-box attacks. arXiv preprint arXiv:1611.02770 2016. [CrossRef]
Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 9185–9193. [CrossRef]
Lin, J.; Song, C.; He, K.; Wang, L.; Hopcroft, J.E. Nesterov accelerated gradient and scale invariance for adversarial attacks. arXiv preprint arXiv:1908.06281 2019. [CrossRef]
Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving transferability of adversarial examples with input diversity. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 2730–2739. [CrossRef]
Wang, X.; He, K. Enhancing the transferability of adversarial attacks through variance tuning. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 1924–1933. [CrossRef]
Xu, Y.; Du, B.; Zhang, L. Assessing the threat of adversarial examples on deep neural networks for remote sensing scene classification: Attacks and defenses. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1604–1617. [CrossRef]
Xu, Y.; Ghamisi, P. Universal Adversarial Examples in Remote Sensing: Methodology and Benchmark. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [CrossRef]
Li, H.; Huang, H.; Chen, L.; Peng, J.; Huang, H.; Cui, Z.; Mei, X.; Wu, G. Adversarial examples for CNN-based SAR image classification: An experience study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1333–1347. [CrossRef]
Du, C.; Huo, C.; Zhang, L.; Chen, B.; Yuan, Y. Fast C&W: A Fast Adversarial Attack Algorithm to Fool SAR Target Recognition with Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [CrossRef]
Du, M.; Bi, D.; Du, M.; Xu, X.; Wu, Z. ULAN: A Universal Local Adversarial Network for SAR Target Recognition Based on Layer-Wise Relevance Propagation. Remote Sensing 2022, 15, 21. [CrossRef]
Xia, W.; Liu, Z.; Li, Y. SAR-PeGA: A Generation Method of Adversarial Examples for SAR Image Target Recognition Network. IEEE Transactions on Aerospace and Electronic Systems 2022, pp. 1–11. [CrossRef]
Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part II 14. Springer, 2016, pp. 694–711. [CrossRef]
Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Communications of the ACM 2020, 63, 139–144. [CrossRef]
Keydel, E.R.; Lee, S.W.; Moore, J.T. MSTAR extended operating conditions: A tutorial. Algorithms Synth. Aperture Radar Imag. III 1996, 2757, 228–242. [CrossRef]
Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4700–4708. [CrossRef]
Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [CrossRef]
Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 June 2016; pp. 2818–2826. [CrossRef]
Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861 2017. [CrossRef]
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [CrossRef]
Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 6848–6856. [CrossRef]
Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [CrossRef]
Kim, H. Torchattacks: A pytorch repository for adversarial attacks. arXiv preprint arXiv:2010.01950 2020. [CrossRef]

Figure 1. Transferability of adversarial examples.

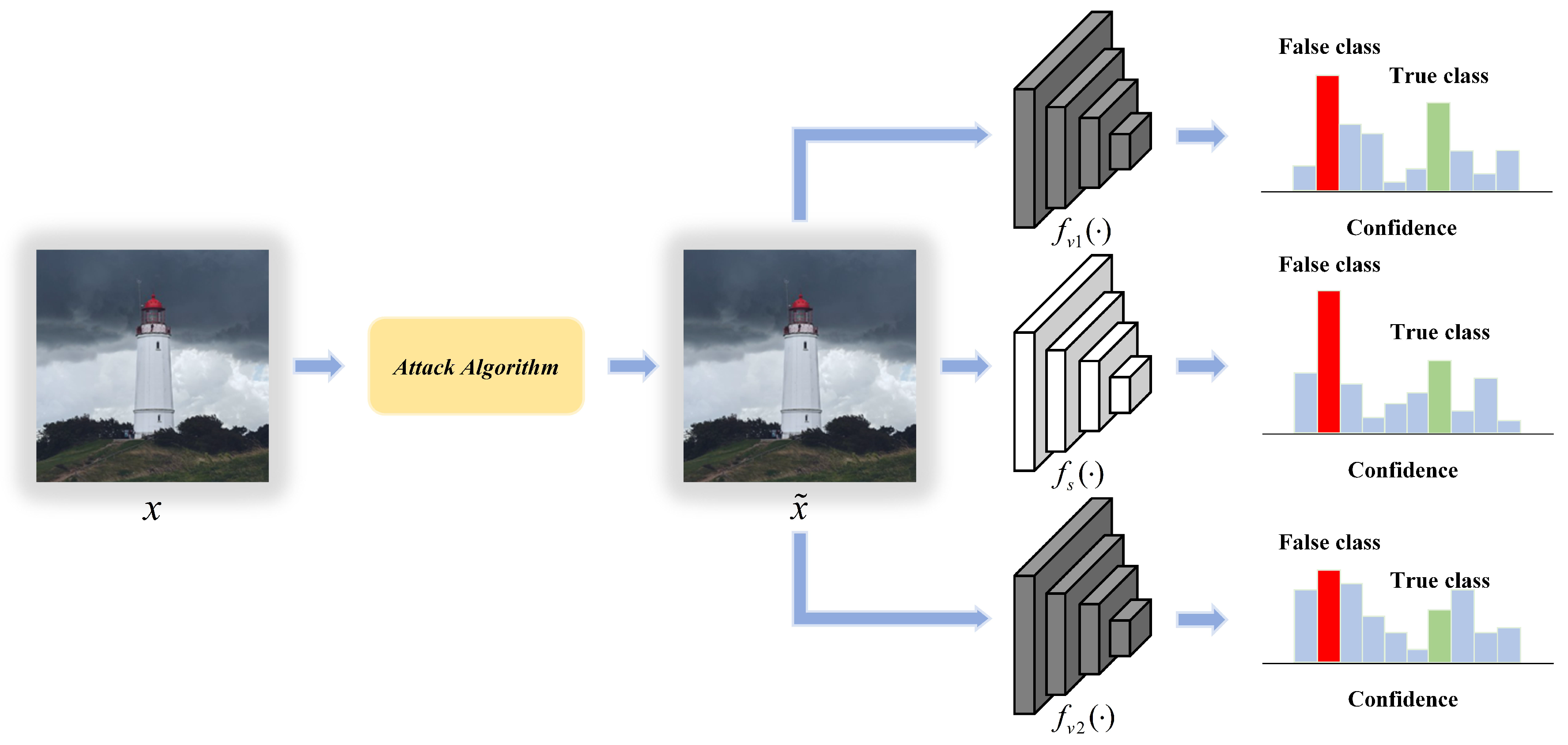
Figure 2. Framework of TAN.

Figure 3. Training process of the generator.

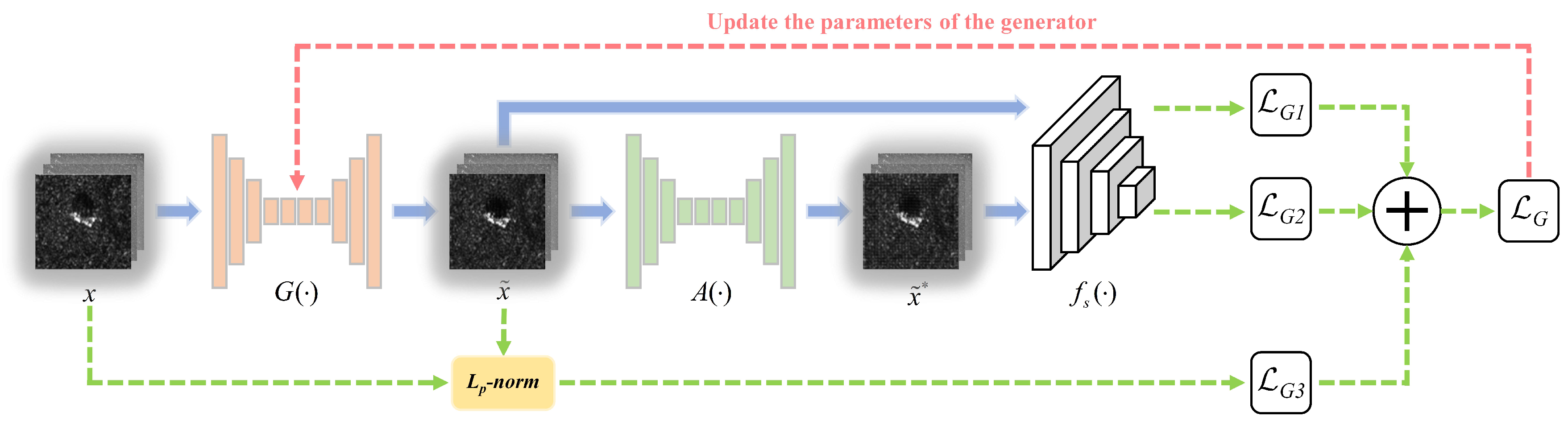
Figure 4. Training process of the attenuator.

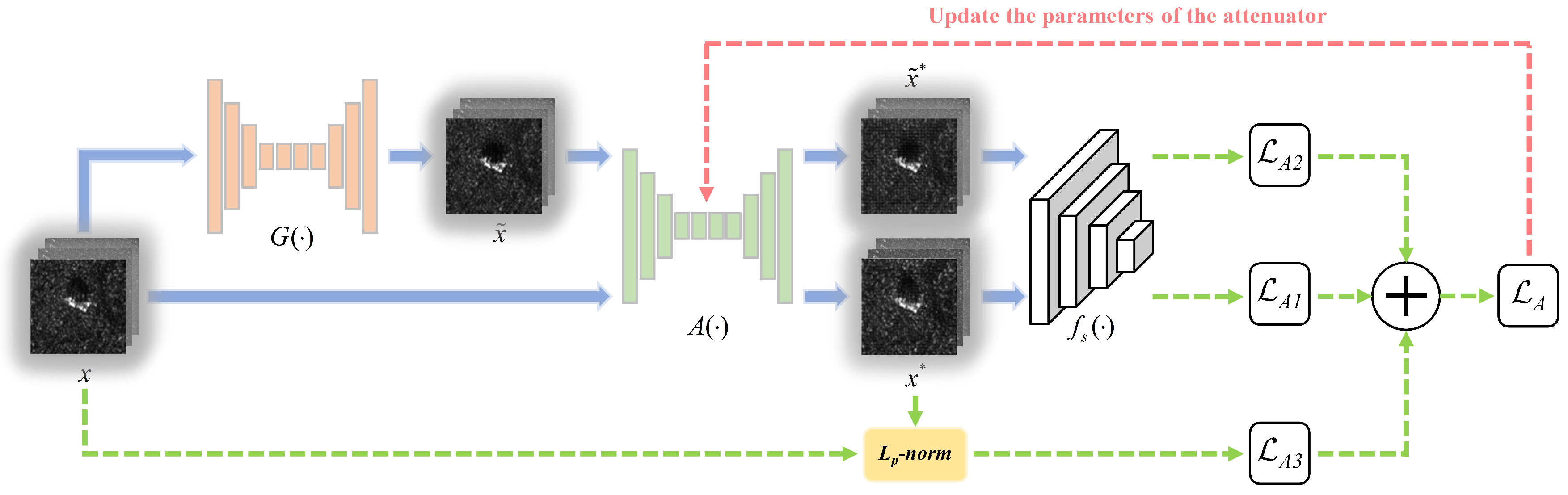
Figure 5. Structure of ResNet Generator.

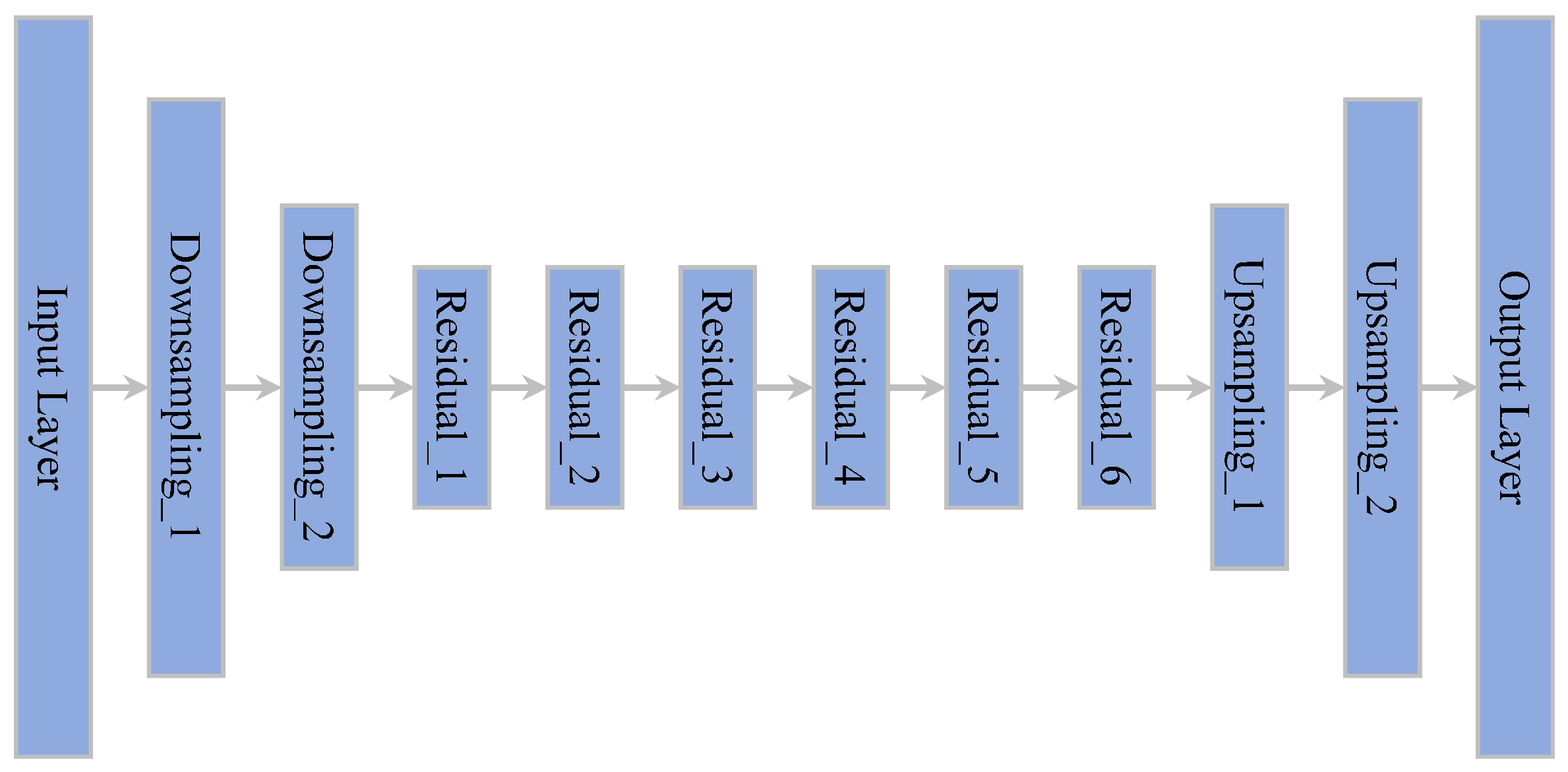
Figure 6. Optical images (top) and SAR images (bottom) of the MSTAR dataset.

Figure 7. Confusion matrixes of DNN-based SAR-ATR models on the MSTAR dataset. (a) DenseNet121. (b) GoogLeNet. (c) InceptionV3. (d) Mobilenet. (e) ResNet50. (f) Shufflenet.

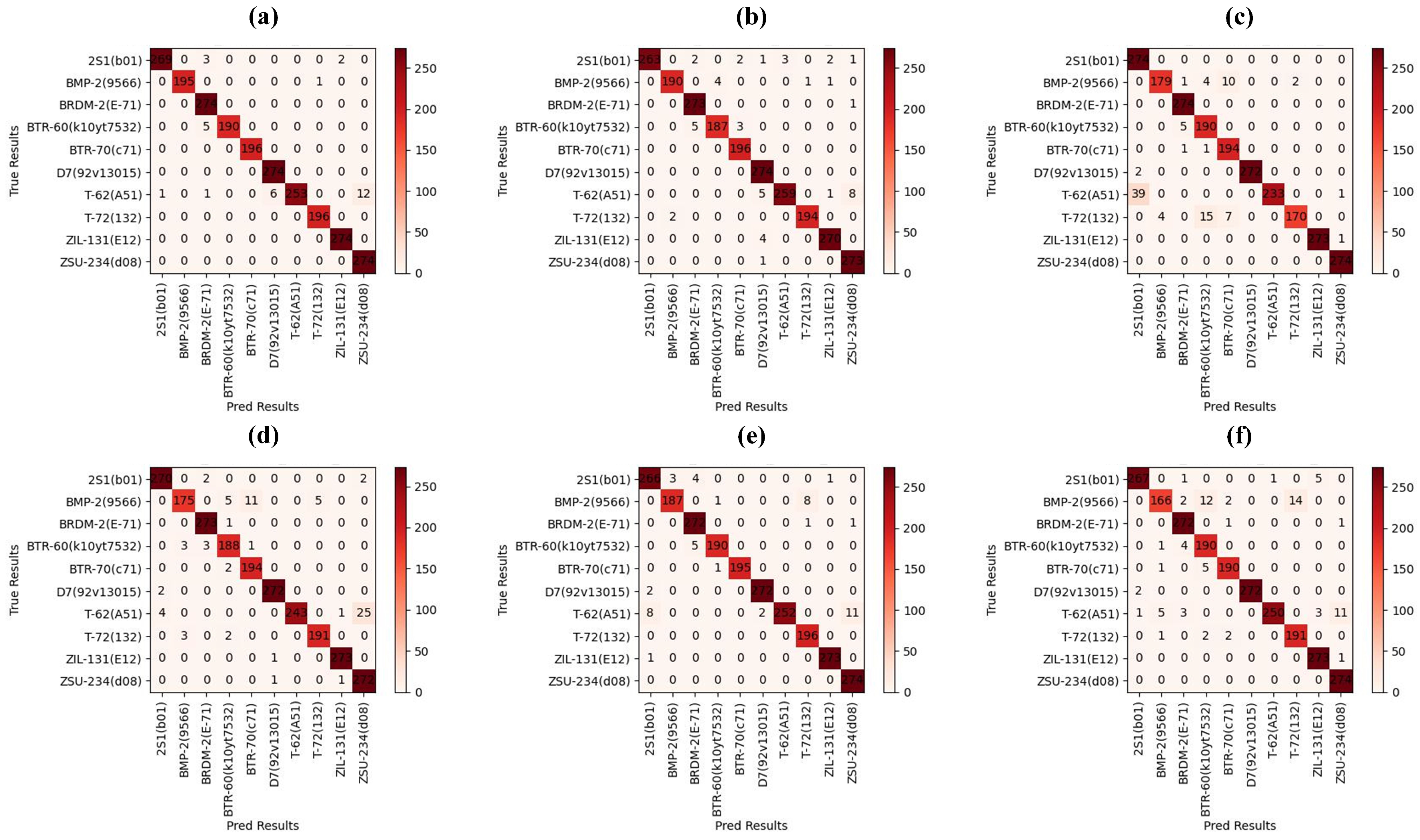
Figure 8. Visualization of attack results against ResNet50. (a) Original samples. (b) Adversarial examples. (c) Adversarial perturbations. (d) Attenuated samples. (e) Deformation distortion. (f) Attenuated adversarial examples. From top to bottom, the corresponding target classes are None, 2S1, and D7, respectively.

Figure 9. Visualization of adversarial examples against ResNet50. (a) TAN. (b) MIFGSM. (c) DIFGSM. (d) NIFGSM. (e) SINIFGSM. (f) VMIFGSM. (g) VNIFGSM. From top to bottom, the corresponding target classes are None, BMP2, BTR60, D7, T72, and ZSU234, respectively. For each attack, the first row shows adversarial examples, and the second row shows corresponding adversarial perturbations.

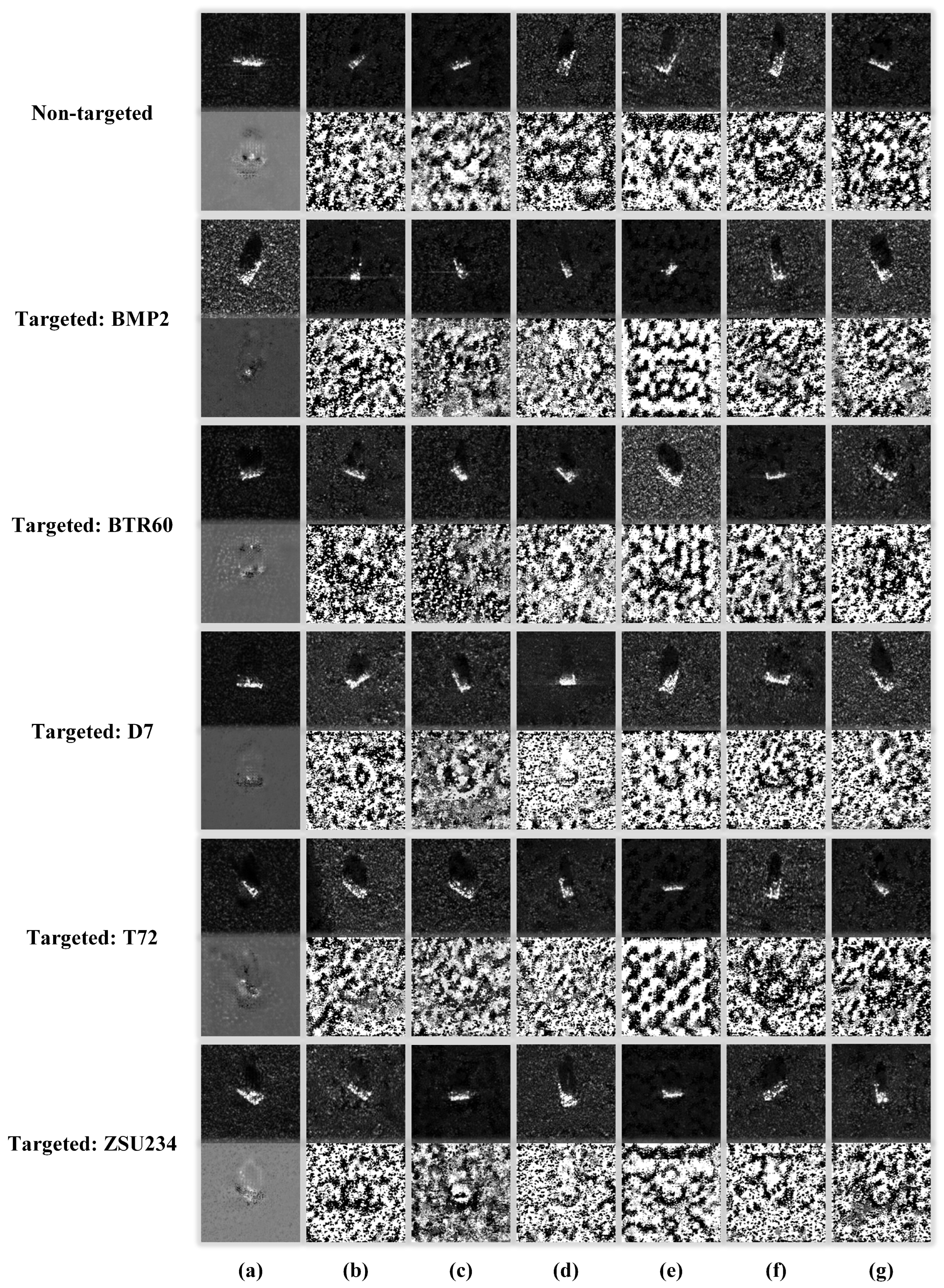
Table 1. Input-output relationships for each module of ResNet Generator.

Module	Input size	Output Size
Input	$1 \times 128 \times 128$	$64 \times 128 \times 128$
Downsampling_1	$64 \times 128 \times 128$	$128 \times 64 \times 64$
Downsampling_2	$128 \times 64 \times 64$	$256 \times 32 \times 32$
Residual_1 ∼ 6	$256 \times 32 \times 32$	$256 \times 32 \times 32$
Upsampling_1	$256 \times 32 \times 32$	$128 \times 64 \times 64$
Upsampling_2	$128 \times 64 \times 64$	$64 \times 128 \times 128$
Output	$64 \times 128 \times 128$	$1 \times 128 \times 128$

Table 2. Details of the MSTAR dataset under SOC, including target class, serial, depression angle, and sample numbers.

Target Class	Serial	Training Data		Testing Data
Target Class	Serial	Depression Angle	Number	Depression Angle	Number
2S1	b01	$17^{\circ}$	299	$15^{\circ}$	274
BMP2	9566	$17^{\circ}$	233	$15^{\circ}$	196
BRDM2	E-71	$17^{\circ}$	298	$15^{\circ}$	274
BTR60	k10yt7532	$17^{\circ}$	256	$15^{\circ}$	195
BTR70	c71	$17^{\circ}$	233	$15^{\circ}$	196
D7	92v13015	$17^{\circ}$	299	$15^{\circ}$	274
T62	A51	$17^{\circ}$	299	$15^{\circ}$	273
T72	132	$17^{\circ}$	232	$15^{\circ}$	196
ZIL131	E12	$17^{\circ}$	299	$15^{\circ}$	274
ZSU234	d08	$17^{\circ}$	299	$15^{\circ}$	274

Table 3. Non-targeted attack results of our method against DNN-based SAR-ATR models on the MSTAR dataset.

Surrogate	$Acc$	$\tilde{Acc}$	${Acc}^{*}$	${\tilde{Acc}}^{*}$	${\tilde{L}}_{2}$	$L_{2}^{*}$
DenseNet121	98.72%	1.90%	81.53%	24.03%	3.595	4.959
GoogLeNet	98.06%	3.83%	89.78%	36.11%	2.884	3.305
InceptionV3	96.17%	0.82%	89.41%	19.62%	3.552	4.181
Mobilenet	96.91%	2.72%	87.88%	36.81%	3.218	4.083
ResNet50	97.98%	3.34%	83.80%	28.65%	3.684	4.568
Shufflenet	96.66%	3.46%	84.30%	23.66%	3.331	3.286
Mean	97.42%	2.68%	86.12%	28.15%	3.377	4.064

Table 4. Targeted attack results of our method against DNN-based SAR-ATR models on the MSTAR dataset.

Surrogate	$Acc$	$\tilde{Acc}$	${Acc}^{*}$	${\tilde{Acc}}^{*}$	${\tilde{L}}_{2}$	$L_{2}^{*}$
DenseNet121	10.00%	98.08%	88.47%	78.09%	3.086	3.587
GoogLeNet	10.00%	99.09%	89.25%	85.90%	3.377	4.289
InceptionV3	10.00%	98.81%	86.87%	78.97%	3.453	3.495
Mobilenet	10.00%	97.40%	88.38%	81.37%	3.257	3.553
ResNet50	10.00%	97.69%	87.29%	82.10%	3.408	3.490
Shufflenet	10.00%	98.36%	86.85%	83.11%	3.345	3.874
Mean	10.00%	98.24%	87.85%	81.59%	3.321	3.714

Table 5. Attack performance of different methods against DNN-based SAR-ATR models on the MSTAR dataset.

Surrogate	Method	Non-targeted		Targeted
Surrogate	Method	$\tilde{Acc}$	${\tilde{L}}_{2}$	$\tilde{Acc}$	${\tilde{L}}_{2}$
DenseNet121	TAN	1.90%	3.595	98.08%	3.086
	MIFGSM	0.00%	3.555	98.61%	3.613
	DIFGSM	0.00%	3.116	95.39%	2.816
	NIFGSM	0.21%	3.719	68.72%	3.550
	SINIFGSM	1.15%	3.676	82.32%	3.648
	VMIFGSM	0.00%	3.665	98.14%	3.602
	VNIFGSM	0.08%	3.691	96.89%	3.635
GoogLeNet	TAN	3.83%	2.884	99.09%	3.377
	MIFGSM	0.04%	3.615	98.36%	3.601
	DIFGSM	0.04%	3.090	94.47%	2.830
	NIFGSM	0.41%	3.674	64.32%	3.520
	SINIFGSM	4.04%	3.647	69.79%	3.615
	VMIFGSM	0.04%	3.587	97.84%	3.601
	VNIFGSM	0.37%	3.588	95.74%	3.636
InceptionV3	TAN	0.82%	3.552	98.81%	3.453
	MIFGSM	0.00%	3.599	96.00%	3.563
	DIFGSM	0.04%	3.010	86.72%	2.811
	NIFGSM	0.21%	3.671	51.66%	3.397
	SINIFGSM	2.93%	3.689	62.46%	3.593
	VMIFGSM	0.00%	3.614	91.54%	3.577
	VNIFGSM	0.00%	3.632	84.02%	3.605
Mobilenet	TAN	2.72%	3.218	97.40%	3.257
	MIFGSM	8.29%	3.557	99.86%	3.538
	DIFGSM	6.64%	2.821	91.64%	2.610
	NIFGSM	6.88%	3.575	80.05%	3.519
	SINIFGSM	1.77%	3.664	85.14%	3.662
	VMIFGSM	2.35%	3.572	99.40%	3.499
	VNIFGSM	1.32%	3.635	95.58%	3.582
ResNet50	TAN	3.34%	3.684	97.69%	3.408
	MIFGSM	0.95%	3.659	97.08%	3.613
	DIFGSM	0.33%	3.141	90.35%	2.824
	NIFGSM	0.33%	3.710	45.34%	3.501
	SINIFGSM	3.96%	3.720	71.64%	3.652
	VMIFGSM	0.87%	3.644	96.17%	3.618
	VNIFGSM	0.25%	3.692	94.17%	3.632
Shufflenet	TAN	3.46%	3.331	98.36%	3.345
	MIFGSM	0.00%	3.567	100.00%	3.518
	DIFGSM	0.00%	2.790	97.54%	2.599
	NIFGSM	0.16%	3.632	91.77%	3.455
	SINIFGSM	0.00%	3.660	95.79%	3.568
	VMIFGSM	0.00%	3.617	100.00%	3.511
	VNIFGSM	0.04%	3.654	99.73%	3.568

Table 6. Transferability of adversarial examples generated by different attack algorithms in non-targeted attacks.

Surrogate	Method	DenseNet121	GoogLeNet	InceptionV3	Mobilenet	ResNet50	Shufflenet
DenseNet121	TAN	1.90%	4.25%	7.46%	9.93%	9.11%	12.90%
	MIFGSM	0.00%	10.10%	12.82%	26.46%	16.32%	28.65%
	DIFGSM	0.00%	8.16%	11.46%	26.01%	19.17%	30.83%
	NIFGSM	0.21%	14.67%	14.67%	26.75%	20.07%	30.67%
	SINIFGSM	1.15%	16.69%	19.29%	35.66%	17.64%	36.11%
	VMIFGSM	0.00%	8.86%	11.62%	24.40%	15.13%	25.89%
	VNIFGSM	0.08%	8.04%	11.62%	22.38%	13.60%	23.54%
GoogLeNet	TAN	6.88%	3.83%	8.16%	23.62%	10.51%	26.88%
	MIFGSM	10.18%	0.04%	17.72%	32.36%	27.66%	42.13%
	DIFGSM	8.33%	0.04%	14.47%	32.52%	24.73%	38.66%
	NIFGSM	22.88%	0.41%	24.28%	32.32%	35.16%	44.44%
	SINIFGSM	7.96%	4.04%	13.15%	33.22%	15.09%	28.07%
	VMIFGSM	8.57%	0.04%	16.32%	29.72%	25.64%	38.58%
	VNIFGSM	10.02%	0.37%	15.50%	27.99%	26.30%	36.93%
InceptionV3	TAN	8.20%	9.60%	0.82%	21.43%	14.67%	23.45%
	MIFGSM	19.25%	35.00%	0.00%	39.45%	33.14%	42.54%
	DIFGSM	16.86%	33.22%	0.04%	43.69%	33.76%	47.07%
	NIFGSM	32.11%	34.46%	0.21%	42.09%	43.08%	44.89%
	SINIFGSM	27.37%	38.05%	2.93%	49.22%	41.18%	56.06%
	VMIFGSM	18.51%	26.92%	0.00%	34.46%	31.04%	37.18%
	VNIFGSM	21.68%	26.38%	0.00%	33.80%	34.50%	37.63%
Mobilenet	TAN	14.34%	15.83%	13.56%	2.72%	14.18%	18.59%
	MIFGSM	65.99%	59.32%	53.59%	8.29%	55.56%	59.77%
	DIFGSM	51.28%	53.34%	49.34%	6.64%	49.34%	52.18%
	NIFGSM	65.75%	58.66%	51.85%	6.88%	52.31%	55.56%
	SINIFGSM	64.67%	45.14%	49.01%	1.77%	51.81%	58.37%
	VMIFGSM	62.49%	52.10%	50.45%	2.35%	49.63%	52.84%
	VNIFGSM	56.27%	50.04%	43.61%	1.32%	43.82%	48.19%
ResNet50	TAN	5.94%	9.27%	10.14%	12.94%	3.34%	11.01%
	MIFGSM	14.59%	24.15%	17.72%	16.90%	0.95%	26.42%
	DIFGSM	11.13%	17.07%	15.09%	20.45%	0.33%	26.59%
	NIFGSM	21.72%	28.19%	20.28%	19.74%	0.33%	29.43%
	SINIFGSM	26.50%	24.15%	22.59%	30.50%	3.96%	33.84%
	VMIFGSM	13.31%	22.42%	16.36%	15.95%	0.87%	23.33%
	VNIFGSM	15.00%	22.67%	16.45%	14.47%	0.25%	22.63%
Shufflenet	TAN	17.72%	23.54%	16.49%	22.22%	17.85%	3.46%
	MIFGSM	66.69%	70.03%	65.00%	55.81%	65.00%	0.00%
	DIFGSM	53.46%	57.58%	55.32%	51.44%	55.44%	0.00%
	NIFGSM	67.23%	61.58%	58.62%	48.35%	61.62%	0.16%
	SINIFGSM	68.51%	58.33%	60.92%	50.41%	56.64%	0.00%
	VMIFGSM	57.25%	55.32%	54.29%	40.23%	53.34%	0.00%
	VNIFGSM	56.68%	54.25%	51.57%	37.30%	52.14%	0.04%

Table 7. Transferability of adversarial examples generated by different attack algorithms in targeted attacks.

Surrogate	Method	DenseNet121	GoogLeNet	InceptionV3	Mobilenet	ResNet50	Shufflenet
DenseNet121	TAN	98.08%	79.12%	70.71%	59.03%	62.31%	52.39%
	MIFGSM	98.61%	52.47%	49.05%	39.47%	43.78%	37.62%
	DIFGSM	95.39%	51.08%	46.62%	35.02%	39.51%	32.29%
	NIFGSM	68.72%	33.06%	27.61%	22.18%	25.78%	22.92%
	SINIFGSM	82.32%	40.62%	33.17%	29.95%	31.93%	30.59%
	VMIFGSM	98.14%	48.94%	44.10%	33.56%	39.29%	34.06%
	VNIFGSM	96.89%	48.78%	46.03%	34.70%	39.80%	35.52%
GoogLeNet	TAN	81.04%	99.09%	66.59%	56.72%	63.86%	55.02%
	MIFGSM	61.56%	98.36%	47.57%	34.16%	37.57%	29.75%
	DIFGSM	58.81%	94.47%	47.91%	32.17%	36.20%	26.88%
	NIFGSM	31.46%	64.32%	25.34%	19.85%	23.14%	19.63%
	SINIFGSM	41.97%	69.79%	34.39%	28.21%	29.77%	25.48%
	VMIFGSM	53.37%	97.84%	42.19%	30.67%	34.94%	26.36%
	VNIFGSM	56.26%	95.74%	43.96%	32.31%	36.11%	29.49%
InceptionV3	TAN	75.11%	71.56%	98.81%	67.23%	63.62%	54.57%
	MIFGSM	42.64%	35.92%	96.00%	32.49%	35.00%	29.51%
	DIFGSM	42.99%	33.70%	86.72%	31.16%	34.13%	28.20%
	NIFGSM	27.12%	24.67%	51.66%	19.49%	23.76%	22.45%
	SINIFGSM	26.76%	25.23%	62.46%	21.90%	24.36%	22.59%
	VMIFGSM	36.38%	34.05%	91.54%	30.15%	31.43%	28.52%
	VNIFGSM	37.82%	33.55%	84.02%	31.44%	32.28%	28.58%
Mobilenet	TAN	61.30%	57.66%	61.53%	97.40%	60.97%	63.11%
	MIFGSM	19.98%	18.66%	22.87%	99.86%	23.55%	20.31%
	DIFGSM	23.96%	21.92%	23.79%	91.64%	24.51%	22.65%
	NIFGSM	15.76%	15.58%	16.85%	80.05%	18.06%	15.91%
	SINIFGSM	16.81%	15.52%	18.96%	85.14%	21.20%	16.63%
	VMIFGSM	18.46%	17.84%	18.70%	99.40%	21.49%	19.61%
	VNIFGSM	21.60%	18.41%	22.34%	95.58%	24.67%	21.96%
ResNet50	TAN	71.39%	71.54%	71.02%	73.68%	97.69%	66.26%
	MIFGSM	43.23%	30.51%	41.57%	42.41%	97.08%	36.29%
	DIFGSM	45.18%	34.25%	42.37%	39.40%	90.35%	34.36%
	NIFGSM	22.07%	20.45%	20.33%	19.36%	45.34%	19.75%
	SINIFGSM	25.81%	21.38%	27.15%	31.01%	71.64%	26.02%
	VMIFGSM	36.44%	26.33%	35.75%	38.61%	96.17%	32.79%
	VNIFGSM	40.80%	27.10%	38.26%	38.87%	94.17%	36.49%
Shufflenet	TAN	53.91%	47.78%	51.69%	60.35%	58.78%	98.36%
	MIFGSM	18.29%	16.43%	17.06%	19.46%	17.20%	100.00%
	DIFGSM	23.55%	20.36%	20.80%	22.55%	21.35%	97.54%
	NIFGSM	13.96%	13.06%	13.14%	14.47%	13.66%	91.77%
	SINIFGSM	15.83%	15.23%	15.34%	19.42%	16.05%	95.79%
	VMIFGSM	17.58%	16.34%	17.09%	21.65%	18.46%	99.94%
	VNIFGSM	19.43%	17.97%	18.68%	22.87%	19.98%	99.73%

Table 8. Time cost of generating a single adversarial example through different attack algorithms in non-targeted attacks.

Method	DenseNet121	GoogLeNet	InceptionV3	Mobilenet	ResNet50	Shufflenet	Mean
TAN	0.002029	0.002201	0.002039	0.002218	0.002031	0.002045	0.002094
MIFGSM	0.018285	0.006351	0.012636	0.005093	0.013445	0.004451	0.010044
DIFGSM	0.018276	0.006363	0.012653	0.005103	0.013468	0.004488	0.010059
NIFGSM	0.018312	0.006354	0.012646	0.005111	0.013477	0.004456	0.010059
SINIFGSM	0.091032	0.031499	0.063015	0.024865	0.067202	0.021676	0.049882
VMIFGSM	0.109252	0.037827	0.075580	0.029803	0.080479	0.025968	0.059818
VNIFGSM	0.109184	0.037804	0.075483	0.029776	0.080560	0.025907	0.059786

Table 9. Time cost of generating a single adversarial example through different attack algorithms in targeted attacks.

Method	DenseNet121	GoogLeNet	InceptionV3	Mobilenet	ResNet50	Shufflenet	Mean
TAN	0.002070	0.002069	0.002036	0.002055	0.002087	0.002097	0.002069
MIFGSM	0.018281	0.006353	0.012634	0.005088	0.013451	0.004446	0.010042
DIFGSM	0.018291	0.006369	0.012652	0.005104	0.013490	0.004488	0.010065
NIFGSM	0.018306	0.006358	0.012661	0.005105	0.013486	0.004460	0.010063
SINIFGSM	0.091064	0.031539	0.063066	0.024871	0.067216	0.021664	0.049903
VMIFGSM	0.109262	0.037860	0.075579	0.029776	0.080481	0.025984	0.059823
VNIFGSM	0.109176	0.037819	0.075502	0.029798	0.080546	0.025923	0.059794

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

TAN: A Transferable Adversarial Network for DNN-based UAV SAR Automatic Target Recognition Models

Abstract

1. Introduction

2. Preliminaries

2.1. Adversarial Attacks for DNN-Based SAR-ATR Models

2.2. Transferability of Adversarial Examples

3. The Proposed Transferable Adversarial Network (TAN)

3.1. Training Process of the Generator

3.2. Training Process of the Attenuator

3.3. Network Structure of the Generator and Attenuator

3.4. Complete Training Process of TAN

4. Experiments

4.1. Data Descriptions

4.2. Implementation Details

4.3. Evaluation Metrics

4.4. DNN-Based SAR-ATR Models

4.5. Comparison of Attack Performance

4.6. Comparison of Transferability

4.7. Comparison of Real-Time Performance

4.8. Visualization of Adversarial Examples

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe