Prerpints.org logo
Preprint
Article

A Deep Learning Method for Predicting the Minimum Inhibitory Concentration of Antimicrobial Peptides against Escherichia coli using Multi-Branch-CNN and Attention

Altmetrics

Downloads

256

Views

196

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 March 2023

Posted:

03 March 2023

You are already at the latest version

Alerts
Abstract
Antimicrobial peptides (AMPs) are a promising alternative to antibiotics to combat drug resistance in pathogenic bacteria. However, the development of AMPs with high potency and specificity remains a challenge, and new tools to evaluate antimicrobial activity are needed to accelerate the discovery process. As a step toward direct prediction of the experimental minimum inhibitory concentration (MIC) of AMPs, we proposed MBC-Attention, a combination of a multi-branch CNN architecture and attention mechanism. Using a curated dataset of 3929 AMP against Escherichia coli, the optimal MBC-Attention model achieved an average Pearson correlation coefficient of 0.775 and an RMSE of 0.533 (log μM) in three independent tests of 393 sequences each. This results in a 5–12% improvement in PCC and 7–13% improvement in RMSE compared with RF and SVM models. Ablation studies confirmed that both attention mechanisms contributed to performance improvement.
Keywords: 
Subject: Biology and Life Sciences  -   Immunology and Microbiology

1. Introduction

To counteract the rapid global spread of antibiotic-resistant pathogenic bacteria, some solutions have been proposed including the prudent use of conventional antibiotics, the consistent application of infection control procedures, and the development of new antibiotics [1,2]. However, the current pace of development of new antibacterial therapeutics is slow due to economic and regulatory barriers. Most recently found candidate antibiotics are merely derivatives of antibiotics already in clinical use [3,4,5], which makes the emergence of bacterial resistance almost inevitable. Therefore, antimicrobials with novel structural properties exploiting different mechanisms of action are the hope for a way out of this conundrum.
Antimicrobial peptides (AMPs) are a class of molecules found in the innate immune system of living organisms [6,7]. Many of them have shown broad-spectrum activity, rapid killing action, and remarkable potency against bacteria, yeasts, fungi, viruses and parasites. Some AMPs also exhibited promising in vivo activity against multidrug-resistant pathogens [8]. Because their mechanism of action differs from that of general antibiotics, they are thought to lead to bacterial resistance only to a limited extent and thus represent an option for the next generation of antibiotics [9].
Key Points:
  • We propose MBC-Attention to regress the experimental MIC values of AMPs against the Gram-negative bacteria Escherichia coli.
  • MBC-Attention is based on an ensemble of CNNs via multiple input branches, integrated with a local attention module within each CNN branch and a global attention module between CNN branches.
  • MBC-Attention performs with higher accuracy and more stable than traditional machine learning methods on a test set of 393 peptides.
  • Data, scripts to reproduce experiments, and the final production models are available at https://github.com/jieluyan/MBC-Attention (the link will be activated upon paper publication).
Biological experiments have been the mainstream method to discover new AMPs from isolates of living organisms. However, these wet-lab procedures are both labor-intensive and cost-intensive. With recent advances in the field of artificial intelligence and the availability of public AMP databases, the scientific community has made intense efforts to develop more accurate prediction tools to aid in the detection and design of AMP sequences. Based on our recent review of the computational studies on machine learning and deep learning of AMPs [10], we found that most of the prediction methods only focused on the binary classification of AMPs. Since the fundamental goal in early-stage drug discovery is to identify lead molecules with high potency and specificity, predictive tools that can provide the experimental biological activity value of molecules are critical for the selection of the most promising (and successful) candidates.
Toward the de novo sequence design of AMPs, Nagarajan et al. [11] trained a Bi-LSTM regression model on 501 sequences from the YADAMP database against E. coli. They normalized the MIC values to the range of 0 and 1 so that the predictions also fell within this range. The regression model was used to sort the predicted sequences generated by an LSTM model previously trained with 1011 known AMP sequences. The paper did not include an evaluation of the regression model, but using the data reported in this study for the 17 synthesized peptides, we calculated a correlation of 0.56 between the predicted and experimental MIC values. Along the same line of thought, Dean et al. [12] developed another peptide generation framework, PepVAE, based on a variational autoencoder to sample new sequences from different regions of the learned latent space and on a gradient boosting regressor to predict the MIC of the new sequences. The regressor model was constructed from E. coli data, obtained by comparing eight different models (CNN, Elastic Net [13], Gradient Boosting [14], Kernel Ridge [15], Lasso [16], RF [17], Light Gradient Boosting Machine [18], and Extreme Gradient Boosting [19]). The best model was achieved by the Gradient Boosting algorithm with an R2 value of 0.73 and an RMSE of 0.5.
Instead of predicting MIC values, some works exploited the MIC values to create positive and negative datasets for AMP classification. For example, in the studies of Vishnepolsky et al.[20] and Soylemez et al.[21], they partitioned AMPs with experimentally known MIC values against a bacterial target into the positive sets (with low MIC values of <25 µg/mL) and the negative sets (with high MIC values of >100 µg/mL). Subsequently, Vishnepolsky et al. constructed a semi-supervised machine learning method with density-based clustering algorithm (DBSCAN) using Physical-Chemical features as input. Their E. coli classification model achieved an accuracy of 80% on the validation set. On the other hand, Soylemez et al. [21] utilized RF with Physico-Chemical features as input and finally achieved an accuracy of 98% and 95% for the Gram-negative and Gram-positive datasets respectively.
Predicting the activity of AMPs in relation to other medically important properties, such as anticancer activity, is also critical, and the techniques could be applicable to AMP prediction. Chen et al. [22] developed xDeep-AcPEP, a powerful regression model that predicts the anticancer activity of six tumor cells (including breast, cervix, colon, lung, skin, and prostate cancers). They used Multitask Learning strategy to supplement the shortage of small datasets of cancer-specific peptides. The best models with the applicability domain defined obtained an average Pearson correlation coefficient of 0.8086.
Accurate prediction of the MIC of AMPs therefore remains challenging due to limited data, the wide range of activity measurements using different experimental methods and under different experimental conditions, and the presence of noise in the data. Nevertheless, as a step toward accurate quantitative prediction of the activity of AMPs, we present MBC-Attention, a regressive model for predicting the MIC value of AMPs against E. coli, the Gram-negative bacterium with the most data available in databases. MBC-Attention exploits the Multi-Branch-CNN (MBC) architecture [23], a deep learning architecture with multiple parallel CNN branches at the input level and single prediction at the output level concatenated from independent predictions of CNNs to classify biological activity of peptides. In this work, two attention mechanisms were introduced into MBC to improve its regressive power: one that localizes within each CNN branch (attention-local) and another that links the different CNN branches (attention-global). The MBC-Attention model was developed based on MBC that performed well in classifying ion channel interacting peptides. Here, we modified MBC to handle a regression task by adding the attention mechanisms mentioned above and showed that it also performed well in regression.
For model construction, optimization, and error estimation, we divided the dataset into train, validation, and test sets. The test set was used for final testing, while the train and validation sets were used for model building and optimization. To obtain a more reliable estimate of model performance, the data splitting procedure was repeated to generate three sets of train, validation, and test sets. Finally, the proposed model was compared to two traditional machine learning methods, namely RF [17] and SVM [24], which showed to have best performance in our preliminary tests (data not shown). To show that the proposed MBC-Attention method also performs better than MBC in classification tasks, we compare MBC-Attention and the MBC method with all the datasets in our previous MBC work [23]. A series of ablation tests were performed to confirm the necessity of the designed components in MBC attention, including MBC alone, MBC with attention-global, and MBC with attention-local.

2. Results

2.1. Single feature selection

Prior to training a machine learning model, the peptide sequences in the dataset were converted into numerical values called features, which represent different properties of the sequence at the peptide level or at the amino-acid level. To select the most informative feature types for encoding AMP sequences, a total of 4481 different feature types was examined. These include the ’OneHot’ feature type, 53 feature types that were generated by different feature encoding methods (e.g., ’AAC’, ’CKSAAP’ [25], ’KSCTRiad’ [26], etc.), and 4427 feature types generated by the Pseudo K-tuple Reduced Amino Acids Composition (PseKRAAC) encoding method [27]. For each feature type, we constructed an RF using 400 trees and computed its predictive performance in terms of the Pearson Correlation Coefficient (PCC). Each experiment was repeated 3 times and the average of PCC values in the three validation sets was computed for each feature type.
As shown in Figure 1, about half of the features achieved average PCC values between 0.55 and 0.75, while for about 200 of the feature types (i.e., about 4.5%), their average model performance in the validation sets was within one standard deviation of the best model. For training a MBC model with this large number of features is still a formidable task with limited computational resources. Hence, we kept the top 30 feature types to proceed with the Best-K feature combination selection.

2.2. Best-K features combination selection

To obtain the best possible predictive performance, it is necessary to determine the combination of feature types for the multiple branch inputs of MBC. For this purpose, we evaluated the feature combinations best-1, best-2, and so on, up to best-26 using the MBC-Attention architecture to predict the experimental MIC values of AMPs against E. coli. Best-K features combination means the combination of the top-1, top-2, …, top-K feature types obtained in the single feature selection. In the best-K features combination selection, MBC-Attention was run using the parameters identified for MBC for sodium ion channel binding peptides prediction in the previous work [23]. Training an MBC-Attention model was feasible up to best-26, larger architectures with more CNN branches failed to train due to insufficient computational resources.
Figure 2 showed the performance of the best-1 to best-26 MBC-Attention models; the results were presented in descending order of the average PCC value in validation. The PCC values of models in the test sets were also recorded to confirm the appropriateness of the model selection, which was primarily based on the validation performance. According to the results, the best-1 to best-15 models showed stable performance in the train, validation, and test experiments consistently. Conversely, best-16 to best-26 models showed poor performance with substantially reduced PCC values and exhibited large standard deviation. Although the best-16 and best-17 models produced reasonable results in validation, they showed exceptionally poor predictions in the test sets for unknown reasons. With the exception of the best-16 and best-17 models, all models in the test showed a similar performance trend as in the validation, indicating that model selection based on the validation result is reliable.
As a result, the best-14 features combination was selected for final model optimization where the included feature types were listed in Table 1. It is worth noting that most of the best feature types are from the PseKRAAC and QSOrder features, differing by the sequence encoding parameters such as the number of reduced amino acid clusters, and the λ value (the positional distance between two amino acids along the sequence).

2.3. Traditional machine learning model selection

To establish the baseline performance for MIC regression of AMPs, we set out to identify the optimal traditional machine learning model based on RF and SVM. For this purpose, we evaluated a range of RF and SVM models with different model parameters. All experiments were repeated three times using the best-14 features combination (refer to Table 1) selected in the Best-K features combination selection work, and the average PCC value of each model on the three validation datasets was computed. Figure 3 shows the average PCC of the validation and training datasets, and all algorithms are sorted by the average PCC of the validation datasets.
RF models with different numbers of trees (from 100 to 2000 with an interval of 100) and different functions for the maximum features ("log2" or "sqrt") were searched by the grid search algorithm. As can be seen in Figure 3(a), all RF models performed similarly showing high stability of the algorithm for this regressive task, with the small trees (< 700) and "log2" performing better than the other selections. We found that RF performed best with 200 trees and the maximum feature function of "log2". Meanwhile, SVM models with different kernels ("rbf", "linear", "poly") and regularization parameters (C=0.01, 0.1, 1, 10, 100) were searched by the grid search algorithm. The result in Figure 3(b) shows that SVM performed best with the kernel "rbf" and C of 10 on validation datasets. Overall, for validation datasets, the kernel "rbf" performed better than "linear" and most "poly" performed worst. For the training datasets, average PCCs change only slightly when RF parameters change, and conversely, average PCCs change greatly when SVM parameters change.
To evaluate the best-14 features combination as the optimal choice, we also searched all the above parameters of RF and SVM based on the best-1 features combination and obtained the best average PCCs of RF and SVM of 0.738 and 0.715, respectively, on validation datasets. They are worse than the average PCCs of RF and SVM based on the best-14 features combination. Finally, the best RF model and the best SVM model were selected as the baseline models for deep learning model comparison.

2.4. Comparison between MBC-Attention and traditional machine learning methods

Once the best 14 features were identified, we tuned the MBC-Attention model using grid search to find the optimal hyperparameters for the CNN including the number of filters, dropout rate, number of layers, and loss function. Based on the best hyperparameters, we then manually tuned the early stopping parameters, including learning rate, decay rate, decay steps, patience, monitoring, and so on.
To confirm the effectiveness of MBC-Attention in learning AMP data for MIC regression, the optimized model was compared to the two most widely used traditional machine learning methods, RF and SVM. The two selected models - RF with 1800 trees and max features of "log2" and SVM with the "rbf" kernel – were utilized. All models used the best-14 features combination as input features.
As shown in Table 2, six criteria were used to evaluate the proposed models. Here, the higher the average PCC, CCC and R2 are, the better the models perform (↑). Conversely, the lower the average MAE, MSE, and RMSE, the better the models perform (↓). Also, mean stands for average, and std denotes standard deviation. Differences in model performance in the triplicate test experiments were indicated by the standard deviation (sd) in the Table. The results showed that our proposed MBC-Attention performed best on all criteria compared to RF and SVM. Furthermore, MBC-Attention achieved an average PCC of 0.775, which is 5.4% and 12.2% better than the RF and SVM models, respectively.
To test the influence of duplicated features in the best-14 feature combination, we performed an experiment in which all duplicated features were removed, using the same procedure described in Yan et al. [23] before constructing the MBC-Attention model. As shown in Table 2, MBC-Attention with reduced features performed slightly worse (average PCC 1.4% lower) than MBC-Attention, but still provided an improved PCC measure, 3.9% and 10.6% higher than those of RF and SVM, respectively.
It is noteworthy that MBC-Attention showed higher stability than the other three models compared. The standard deviation values obtained for MBC-Attention in all the measures are relatively low (e.g., for PCC, it is 66.7% lower; for RMSE, it is 93.8% to 94.3%) than those for RF and SVM. Reducing input features to MBC-Attention also weakened the stability of the model suggesting that some information was missed if certain features were discarded.

2.5. Ablation study

An ablation study was performed to understand the importance of each component, namely MBC, global attention, and local attention, in the MBC-Attention architecture. As shown in Table 3, MBC alone performed the worst among all four models. The use of local attention increased PCC by 2.97%, meanwhile the use of global attention produced 3.37% improvement. Together, the two attention schemes increased the performance of MBC by 4.59%, suggesting the importance of attention in learning AMP sequences. Furthermore, MBC-Attention has the highest stability among all four models given the lower standard deviation results in triplicate test experiments.

2.6. Comparison between MBC-Attention and MBC on ion channel datasets

To evaluate the ability of the attention modules on classification problems, we compared MBC-Attention to MBC in predicting ion channel binding of peptides. In [23], we proposed the MBC method for ion channel binding peptides classification for the sodium (Na-pep), potassium (K-pep), and calcium (Ca-pep) ion channels. For each channel, two different test sets were developed: The ’test set’ consisted of peptides with moderate similarity to those in the training set, whereas the ’novel-test’ set contained peptides that were dissimilar or with low similarity to the training peptides. We added the attention-local module in the middle of the 2D convolutional layer and the max-pooling layer for each CNN layer of all CNN branches and the attention-global module at the end of each CNN branch. MBC-Attention has the same hyperparameters as the MBC method used in the work of MBC for Na-pep, K-pep, and Ca-pep. As shown in Figure 4, It can be observed that the MBC-Attention performed better than the MBC method for all the three channels (Na-pep, K-pep, and Ca-pep) on both test and novel-test data sets.

3. Conclusion

We proposed an MBC-Attention model to regress the experimental MIC values of AMPs against E. coli. The MBC-Attention model was developed based on our previous MBC model [23], which is a multiple CNN branch architecture that performs well in classifying ion channel interacting peptides. We used the MBC architecture for regression tasks and improved its predictive power by adding two attention mechanisms. To evaluate the regressive performance of MBC-Attention, we divided the entire dataset into the train, validation, and test sets. The validation set was used for model tuning and the test set was used to evaluate the generalizability of the final model and for model comparision with the best traditional machine learning models.
Overall, the optimal MBC-Attention model achieved an average PCC of 0.775, R2 of 0.588, and RMSE of 0.533 (log µM) in three repeated tests using 393 sequences randomly selected from the dataset. The optimal MBC-Attention model achieved on average 5.4% and 12.2% higher PCCs and the best stability compared to RF and SVM, respectively. While MBC performed slightly better than RF, the use of attention, particularly local attention, increased the performance of the MBC model by more than 2.9%, resulting in a better quantitative model for AMP activity prediction for E. coli. Moreover, we showed that the performance of MBC-Attention on classification tasks was improved compared to MBC evaluated on ion channel peptide classification test datasets [23]. In future work, we will apply MBC-Attention for antibacterial activity prediction of peptides for other pathogenic bacterial species.

4. Materials and Methods

4.1. Dataset Preparation

We downloaded a total of 7861 data entries of AMP monomers from the DBAASP v3 database [34] with antibacterial activity against E. coli. To prepare for ML, the data entries with unnatural amino acids (’B’, ’J’, ’O’, ’U’, ’Z’, ’X’) in the sequence or entries without experimental MIC values were removed; sequences that are too long (> 60 aa) and too short (< 5 aa) were discarded. For the remaining entries, their MIC values were converted into the same measurement unit (µM) and then converted to pMIC by Eq.1. For a sequence that has multiple MIC values, these values were averaged to obtain the mean activity measure for the peptide. Finally, the processed dataset of AMP sequence and MIC for E. coli contains 3929 entries. As shown in Figure 5, these sequences have a median length of 20 residues and antibacterial activity of 14.8 µM (equivalent to pMIC of -1.17).
For model construction and evaluation, the dataset was randomly split into a train, validation, and test sets. The test set consisted of 10% of the entire dataset, while the validation set consisted of 10% of the remaining set after removal of the test data. To ensure reliable error estimation, the dataset splitting procedure was repeated three times. All experiments were performed on each of the three replicates and the average performance values were reported.
Table 4. Summary of the AMP data against the Gram-negative bacteria E. coli and data partition for predictive modeling.
Table 4. Summary of the AMP data against the Gram-negative bacteria E. coli and data partition for predictive modeling.
Name Description No. of entries
EC of all subtypes Downloaded from DBAASP (as of August 2021) 7861
Whole After removing incomplete and duplicate entries 3929
Test Randomly select 10% from the Whole set 393
Validation Randomly select 10% from the Whole set after removing Test 354
Train Data not included in Test and Validation 3182

4.2. Regressive predictive target

In this work, the negative logarithmic MIC (pMIC) against the bacteria is the regressive predictive target. The pMIC can be represented as follows:
pMIC = − log 10 MIC .

4.3. Performance Metrics

We used Pearson Correlation Coefficient (PCC), Concordance Correlation Coefficient (CCC), mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), and coefficient of determination ( R 2 ) as metrics to measure the performance of the regressive models. Note that the lower the value of MAE, MSE, or RMSE, the better the regression models. Conversely, the higher the value of PCC, CCC, and R 2 , the better the regressive models.
The formula of PCC or ρ is shown as follows:
P C C = ρ = ∑ i = 1 N ( y i − μ y ) ( y ^ i − μ y ^ ) ∑ i = 1 N ( y i − μ y ) 2 ∑ i = 1 N ( y ^ i − μ y ^ ) 2 , μ y = ∑ i = 1 N y i N , μ y ^ = ∑ i = 1 N y ^ i N .
where i denotes the i t h sample and N is the sample number; y represents a true target value and y ^ the predicted target value by the regressive model; μ y , and μ y ^ represent the average of the true and predicted regressive target values, respectively.
The formula of CCC or ρ c is shown as follows:
C C C = ρ c = 2 ρ σ y σ y ^ σ y 2 + σ y ^ 2 + ( μ y − μ y ^ ) 2 , σ y = ∑ i = 1 N ( μ y − y i ) 2 N , σ y ^ = ∑ i = 1 N ( μ y ^ − y ^ i ) 2 N , i ∈ { 1 , 2 , . . . , N } .
where σ y 2 and σ y ^ 2 denote the corresponding variances of true and predicted regressive target value, respectively.
The formula of MAE is shown as follows:
M A E = 1 N ∑ i = 1 N | y ^ i − y i | , i ∈ { 1 , 2 , . . . , N } ,
where i denotes the i t h sample of prediction target value of regressive models ( y ^ ); y represents true target value of regressive models; N is the sample number.
The formula of MSE is presented as follows:
M S E = 1 N ∑ i = 1 N ( y ^ i − y i ) 2 , i ∈ { 1 , 2 , . . . , N } .
The formula of RMSE is defined as follows:
M S E = 1 N ∑ i = 1 N ( y ^ i − y i ) 2 , i ∈ { 1 , 2 , . . . , N } .
The formula of R 2 is shown as follows:
R 2 = 1 − ∑ i = 1 N ( y i ^ − y i ) 2 ∑ i = 1 N ( y ¯ − y i ) 2 , i ∈ { 1 , 2 , . . . , N } .

4.4. Feature encoding of peptide sequences

We examined a total of 4481 different features to find the optimal combination of AMP sequence encoding methods. The encoding for 4480 features was generated using the iFeature package [35] while the oneHot feature encoding was implemented ourselves. oneHot produces a L m a x × 20 feature matrix ( L m a x is the maximum length of all given peptides) which represents the position of each amino acid in the sequence. Among the different features from iFeature, 53 of them were generated by 21 feature types (such as AAC, CKSAAP, KSCTriad, SOCNumber, etc.) using different parameters. But a majority of features (totally 4427) were from PseKRAAC, which generates encodings based on a set of user-defined parameters including ktuple, g-gap and λ -correlation. Table 5 shows all feature types and corresponding parameters used in sequence encoding.

4.5. MBC-Attention

MBC is short for Multi-Branch-CNN, which is a deep learning architecture for peptide activity prediction based on amino acid sequences. It was proposed in our previous study of machine learning for ion channel interacting peptides prediction [23]. MBC accepts multiple square matrices as input in a parallel fashion to multiple CNNs via independent branches. Each CNN branch contains 2 CNN blocks. Each block in turn consists of a batch normalization layer, a 2D convolutional layer with 64 filters, and a max pooling layer. Subsequently, outputs from all CNN branches are flattened, concatenated, and passed to a dense, fully connected layer with 64 nodes. The output layer contains 2 nodes to generate classification outcomes. All nodes use relu as the activation function except for the last output nodes which use the sigmoid function.
MBC was designed to solve classification tasks for peptide sequences. Here, modifications were required to accommodate the more challenging regression modeling and to improve predictive performance. The final architecture of MBC-Attention is shown in Figure 6. Unlike MBC, MBC-Attention contains only one output node that generates the regressive target (pMIC). Each CNN branch contains a batch normalization layer, a 2D convolutional layer, an attention-local layer, the max-pooling layer, and a dense layer. Then, all 1D outputs of the dense layer were concatenated into a 2D matrix and passed to the global attention layer. Then, the output of the attention-global layer was flattened and another dense layer was run. Finally, a dense layer with a node was created as the final regressive output. The network was updated by back-propagation. After the tuning procedure (as detailed below), the optimal MBC-Attention was determined with the following hyperparameters: 14 CNN branches, 1 convolutional layer with 32 filters in each CNN branch, a dense network with 32 nodes, the relu activation function for the internal nodes, and the sigmoid function for the output node.
For extracting the whole information in each branch and the correlation between the different branches, we proposed two modules: attention-local and attention-global. Attention has three elements – key, query, and value. It aims to use the similarity of a query and a key to weigh and adjust the value accordingly. As shown in Figure 6, the attention-local module is introduced in each CNN branch to improve the regressive performance. In the attention-local-i layer ( i ∈ { 1 , 2 , . . . , K } ), the local-i input is a H × W × C matrix, where H, W, and C stand for height, width, and channel, respectively, where C corresponds to the filter number of the previous convolution layer (Figure 6(b)). Furthermore, ⨂ denotes matrix multiplication and ⨁ denotes matrix addition. First, three convolutional layers with the same blocks of 50 filters whose size is 1 × 1 were utilized to generate three equal 3D matrices and reshape them into three 2D matrices ( ( H × W ) × C ) to mimic the key, query, and value terms. We then used the transposed query and key by matrix multiplication to compute their similarity, and the output was processed by a softmax function for each row to obtain the local weights. Then, the local weights were multiplied by the value and transformed into the same dimension of the input of the attention-local-i module. Finally, matrix addition of the local-i weighted input and the local-i input was performed to adjust the original inputs. As can be seen in Figure 6(c), the attention-global module aims to adjust the information of the global/branches by transposing its input and then multiplying it by the global-input. After that, softmax was used to generate the global/branch weights, and the global weights were then multiplied by the global inputs. Finally, matrix addition of the global-input and the previous output was used to obtain the fitted information of the branches.
In summary, the main change in MBC-Attention compared to the previous MBC is the introduction of attention mechanisms. Within each CNN branch, an attention-local module was added to compute the importance of local features, and in addition, an attention-global module was integrated to extract the relationship between different CNN branches.

4.6. Feature selection

Inherited from the MBC architecture, MBC-Attention can accept multiple feature types as input and learn each of the feature types independently via multiple branch CNN. To determine a set of informative feature types for the regressive task at hand, a two-step feature selection was performed similarly to the previous study [23]. In the first step, each feature type had a quick evaluation for regressive performance using RF with 400 trees. The top-performing feature types were identified based on the average PCC value of the model. In the second step, all the best-K feature combinations were evaluated using MBC-Attention, where best-K is the top K feature types from the sorted list returned in the first step. Due to limited computational resources, the largest K features combination examined was 26.

4.7. MBC-Attention parameter tuning

To find the best CNN architecture in MBC-Attention, we tested the model performance using 1, 2, or 3 convolutional layers and setting the dropout rate to 0, 0.1, 0.2, 0.3, 0.4, or 0.5; the number of filters in each layer to 16, 32, 48, 64, 80, 96, 112, or 128; and the loss functions to MSE (mean square error) or MSLE (mean square logarithmic error). Note that all the training stopped at 200 epochs for reducing the time for tuning. Furthermore, each experiment was repeated 3 times. The parameter search was performed by grid search and the results were sorted by average PCC values in validation. In total, there were 3 × 3 × 6 × 8 experiments to find the best hyperparameters of the final MBC-Attention model. The final hyperparameters are as follows: CNN layer = 1, filter = 32, dropout = 0.4. To obtain a stable performance in the prediction model, we manually tested the use of an early stopping criterion over different settings of the parameters ’patience’ and ’monitor’, as well as training using different learning rates, decay rates and numbers of decay steps. Finally, we found that early stopping monitored with ’loss’, via a learning rate of 0.0005 and patience of 15, decay rate of 0.92, and decay steps of 25 were the best combination.

Author Contributions

SWIS and FXCV conceived the study. JLY designed the methods, conducted the experiments, analyzed the results, and drafted the manuscript. SWIS, MZ, and BZ supervised the work. SWIS, FXCV, MZ, and BZ finalized the manuscript. All the authors read and approved the final manuscript. SWIS, FXCV and BZ acquired project funding.

Data and Software Availability

All peptide data used in this study were downloaded from DBAASP v3 [34]. The data and script files for reproducing the experiments can be downloaded from https://github.com/jieluyan/MBC-Attention (the link will be activated upon paper publication). The final predictive models are also available at the above link. The implementation was done using Python 3.6.13, pycaret 2.3.1 [45], and pytorch 1.7.1 [46].

Acknowledgments

We acknowledge the support of the Government of Canada’s New Frontiers in Research Fund (NFRF), [NFRFE-2021-00913]. JLY was supported by University of Macau (grant no. MYRG2019-00098-FST) and the Science and Technology Department Fund of Macau SAR (File no. 0010/2021/AFJ). We also thank Pratiti Bhadra for her help in reviewing the paper.

Conflicts of Interest

None declared.

References

  1. Ventola, C.L. The Antibiotic Resistance Crisis, Part 1: Causes and Threats. Pharmacy and Therapeutics 2015, 40, 277–283. [Google Scholar] [PubMed]
  2. Ventola, C.L. The Antibiotic Resistance Crisis, Part 1: Management Strategies and New Agents. Pharmacy and Therapeutics 2015, 40, 344–352. [Google Scholar] [PubMed]
  3. Butler, M.S.; Paterson, D.L. Antibiotics in the clinical pipeline in October 2019. The Journal of Antibiotics 2020, 73, 329–364. [Google Scholar] [CrossRef] [PubMed]
  4. Beyer, P.; Paulin, S. The Antibacterial Research and Development Pipeline Needs Urgent Solutions. ACS Infectious Diseases 2020, 6, 1289–1291. [Google Scholar] [CrossRef]
  5. Miethke, M.; Pieroni, M.; Weber, T.; Brönstrup, M.; Hammann, P.; Halby, L.; Arimondo, P.B.; Glaser, P.; Aigle, B.; Bode, H.B.; Moreira, R.; Li, Y.; Luzhetskyy, A.; Medema, M.H.; Pernodet, J.L.; Stadler, M.; Tormo, J.R.; Genilloud, O.; Truman, A.W.; Weissman, K.J.; Takano, E.; Sabatini, S.; Stegmann, E.; Brötz-Oesterhelt, H.; Wohlleben, W.; Seemann, M.; Empting, M.; Hirsch, A.K.H.; Loretz, B.; Lehr, C.M.; Titz, A.; Herrmann, J.; Jaeger, T.; Alt, S.; Hesterkamp, T.; Winterhalter, M.; Schiefer, A.; Pfarr, K.; Hoerauf, A.; Graz, H.; Graz, M.; Lindvall, M.; Ramurthy, S.; Karlén, A.; van Dongen, M.; Petkovic, H.; Keller, A.; Peyrane, F.; Donadio, S.; Fraisse, L.; Piddock, L.J.V.; Gilbert, I.H.; Moser, H.E.; Müller, R. Towards the sustainable discovery and development of new antibiotics. Nature Reviews Chemistry 2021, 5, 726–749. [Google Scholar] [CrossRef]
  6. Haney, E.F.; Mansour, S.C.; Hancock, R.E.W. Antimicrobial Peptides: An Introduction. In Antimicrobial Peptides: Methods and Protocols; Springer New York: New York, NY, 2017; pp. 3–22. [Google Scholar] [CrossRef]
  7. Huan, Y.; Kong, Q.; Mou, H.; Yi, H. Antimicrobial peptides: classification, design, application and research progress in multiple fields. Frontiers in microbiology 2020, 2559. [Google Scholar]
  8. Mwangi, J.; Hao, X.; Lai, R.; Zhang, Z.Y. Antimicrobial peptides: new hope in the war against multidrug resistance. Zoological research 2019, 40, 488. [Google Scholar] [CrossRef] [PubMed]
  9. Bechinger, B.; Gorr, S.U. Antimicrobial peptides: mechanisms of action and resistance. Journal of dental research 2017, 96, 254–260. [Google Scholar] [CrossRef] [PubMed]
  10. Yan, J.; Cai, J.; Zhang, B.; Wang, Y.; Wong, D.F.; Siu, S.W. Recent Progress in the Discovery and Design of Antimicrobial Peptides Using Traditional Machine Learning and Deep Learning. Antibiotics 2022, 11, 1451. [Google Scholar] [CrossRef] [PubMed]
  11. Nagarajan, D.; Nagarajan, T.; Roy, N.; Kulkarni, O.; Ravichandran, S.; Mishra, M.; Chakravortty, D.; Chandra, N. Computational antimicrobial peptide design and evaluation against multidrug-resistant clinical isolates of bacteria. Journal of Biological Chemistry 2018, 293, 3492–3509. [Google Scholar] [CrossRef]
  12. Dean, S.N.; Alvarez, J.A.E.; Zabetakis, D.; Walper, S.A.; Malanoski, A.P. PepVAE: variational autoencoder framework for antimicrobial peptide generation and activity prediction. Frontiers in microbiology 2021, 12, 725727. [Google Scholar] [CrossRef]
  13. Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. Journal of the royal statistical society: series B (statistical methodology) 2005, 67, 301–320. [Google Scholar] [CrossRef]
  14. Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Frontiers in neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
  15. Vovk, V. Kernel ridge regression. In Empirical inference; Springer, 2013; pp. 105–116.
  16. Ranstam, J.; Cook, J. LASSO regression. Journal of British Surgery 2018, 105, 1348–1348. [Google Scholar] [CrossRef]
  17. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  18. Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light Gradient Boosting Machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agricultural water management 2019, 225, 105758. [Google Scholar] [CrossRef]
  19. Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; others. Xgboost: extreme gradient boosting. R package version 0.4-2 2015, 1, 1–4. [Google Scholar]
  20. Vishnepolsky, B.; Gabrielian, A.; Rosenthal, A.; Hurt, D.E.; Tartakovsky, M.; Managadze, G.; Grigolava, M.; Makhatadze, G.I.; Pirtskhalava, M. Predictive model of linear antimicrobial peptides active against gram-negative bacteria. Journal of chemical information and modeling 2018, 58, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
  21. Söylemez, Ü.G.; Yousef, M.; Kesmen, Z.; Büyükkiraz, M.E.; Bakir-Gungor, B. Prediction of Linear Cationic Antimicrobial Peptides Active against Gram-Negative and Gram-Positive Bacteria Based on Machine Learning Models. Applied Sciences 2022, 12, 3631. [Google Scholar] [CrossRef]
  22. Chen, J.; Cheong, H.H.; Siu, S.W.I. xDeep-AcPEP: Deep Learning Method for Anticancer Peptide Activity Prediction Based on Convolutional Neural Network and Multitask Learning. Journal of Chemical Information and Modeling 2021, 61, 3789–3803. [Google Scholar] [CrossRef] [PubMed]
  23. Yan, J.; Zhang, B.; Zhou, M.; Kwok, H.F.; Siu, S.W. Multi-Branch-CNN: Classification of ion channel interacting peptides using multi-branch convolutional neural network. Computers in Biology and Medicine 2022, 105717. [Google Scholar] [CrossRef]
  24. Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intelligent Systems and their applications 1998, 13, 18–28. [Google Scholar] [CrossRef]
  25. Chen, Z.; Chen, Y.Z.; Wang, X.F.; Wang, C.; Yan, R.X.; Zhang, Z. Prediction of ubiquitination sites by using the composition of k-spaced amino acid pairs. PloS one 2011, 6, e22930. [Google Scholar] [CrossRef] [PubMed]
  26. Shen, J.; Zhang, J.; Luo, X.; Zhu, W.; Yu, K.; Chen, K.; Li, Y.; Jiang, H. Predicting protein–protein interactions based only on sequences information. Proceedings of the National Academy of Sciences 2007, 104, 4337–4341. [Google Scholar] [CrossRef] [PubMed]
  27. Zuo, Y.; Li, Y.; Chen, Y.; Li, G.; Yan, Z.; Yang, L. PseKRAAC: a flexible web server for generating pseudo K-tuple reduced amino acids composition. Bioinformatics 2017, 33 1, 122–124. [Google Scholar] [CrossRef]
  28. Susko, E.; Roger, A.J. On reduced amino acid alphabets for phylogenetic inference. Molecular biology and evolution 2007, 24, 2139–2150. [Google Scholar] [CrossRef] [PubMed]
  29. Chou, K.C. Prediction of protein subcellular locations by incorporating quasi-sequence-order effect. Biochemical and biophysical research communications 2000, 278, 477–483. [Google Scholar] [CrossRef] [PubMed]
  30. Zuo, Y.C.; Li, Q.Z. Using K-minimum increment of diversity to predict secretory proteins of malaria parasite based on groupings of amino acids. Amino acids 2010, 38, 859–867. [Google Scholar] [CrossRef]
  31. Rakshit, S.; Ananthasuresh, G. An amino acid map of inter-residue contact energies using metric multi-dimensional scaling. Journal of theoretical biology 2008, 250, 291–297. [Google Scholar] [CrossRef] [PubMed]
  32. Kosiol, C.; Goldman, N.; Buttimore, N.H. A new criterion and method for amino acid classification. Journal of Theoretical biology 2004, 228, 97–106. [Google Scholar] [CrossRef]
  33. Oğul, H.; Mumcuoğlu, E.Ü. A discriminative method for remote homology detection based on n-peptide compositions with reduced amino acid alphabets. BioSystems 2007, 87, 75–81. [Google Scholar] [CrossRef]
  34. Pirtskhalava, M.; Amstrong, A.A.; Grigolava, M.; Chubinidze, M.; Alimbarashvili, E.; Vishnepolsky, B.; Gabrielian, A.; Rosenthal, A.; Hurt, D.E.; Tartakovsky, M. DBAASP v3: database of antimicrobial/cytotoxic activity and structure of peptides as a resource for development of new therapeutics. Nucleic Acids Research 2020, 49, D288–D297. [Google Scholar] [CrossRef]
  35. Chen, Z.; Zhao, P.; Li, F.; Leier, A.; Marquez-Lago, T.; Wang, Y.; Webb, G.I.; Smith, A.; Daly, R.; Chou, K.; Song, J. iFeature: a Python package and web server for features extraction and selection from protein and peptide sequences. Bioinformatics 2018, 34, 2499–2502. [Google Scholar] [CrossRef] [PubMed]
  36. Ding, Y.; Cai, Y.; Zhang, G.; Xu, W. The influence of dipeptide composition on protein thermostability. FEBS letters 2004, 569, 284–288. [Google Scholar] [CrossRef] [PubMed]
  37. Bhasin, M.; Raghava, G.P. Classification of nuclear receptors based on amino acid composition and dipeptide composition. Journal of Biological Chemistry 2004, 279, 23262–23266. [Google Scholar] [CrossRef] [PubMed]
  38. Saravanan, V.; Gautham, N. Harnessing computational biology for exact linear B-cell epitope prediction: a novel amino acid composition-based feature descriptor. Omics: a journal of integrative biology 2015, 19, 648–658. [Google Scholar] [CrossRef] [PubMed]
  39. Cai, C.; Han, L.; Ji, Z.L.; Chen, X.; Chen, Y.Z. SVM-Prot: web-based support vector machine software for functional classification of a protein from its primary sequence. Nucleic acids research 2003, 31, 3692–3697. [Google Scholar] [CrossRef] [PubMed]
  40. Chen, Z.; Zhou, Y.; Song, J.; Zhang, Z. hCKSAAP_UbSite: improved prediction of human ubiquitination sites by exploiting amino acid pattern and properties. Biochimica et Biophysica Acta (BBA)-Proteins and Proteomics 2013, 1834, 1461–1467. [Google Scholar] [CrossRef] [PubMed]
  41. Chou, K.C.; Cai, Y.D. Prediction of protein subcellular locations by GO–FunD–PseAA predictor. Biochemical and Biophysical Research Communications 2004, 320, 1236–1239. [Google Scholar] [CrossRef] [PubMed]
  42. Chou, K.C. Prediction of protein cellular attributes using pseudo-amino acid composition. Proteins: Structure, Function, and Bioinformatics 2001, 43, 246–255. [Google Scholar] [CrossRef]
  43. Chou, K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics 2005, 21, 10–19. [Google Scholar] [CrossRef]
  44. Sokal, R.R.; Thomson, B.A. Population structure inferred by local spatial autocorrelation: an example from an Amerindian tribal population. American Journal of Physical Anthropology: The Official Publication of the American Association of Physical Anthropologists 2006, 129, 121–131. [Google Scholar] [CrossRef] [PubMed]
  45. Ali, M. PyCaret: An open source, low-code machine learning library in Python, 2020. PyCaret version 2.3.1.
  46. Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; Desmaison, A.; Kopf, A.; Yang, E.; DeVito, Z.; Raison, M.; Tejani, A.; Chilamkurthy, S.; Steiner, B.; Fang, L.; Bai, J.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc., 2019; pp. 8024–8035. [Google Scholar]
Preprints 69345 g001
Figure 1. Regressive performance of 4481 single-feature models in validation set using RF with 400 trees. To have a closer look at the most informative features, the top 50 feature types are displayed on the left.
Figure 1. Regressive performance of 4481 single-feature models in validation set using RF with 400 trees. To have a closer look at the most informative features, the top 50 feature types are displayed on the left.
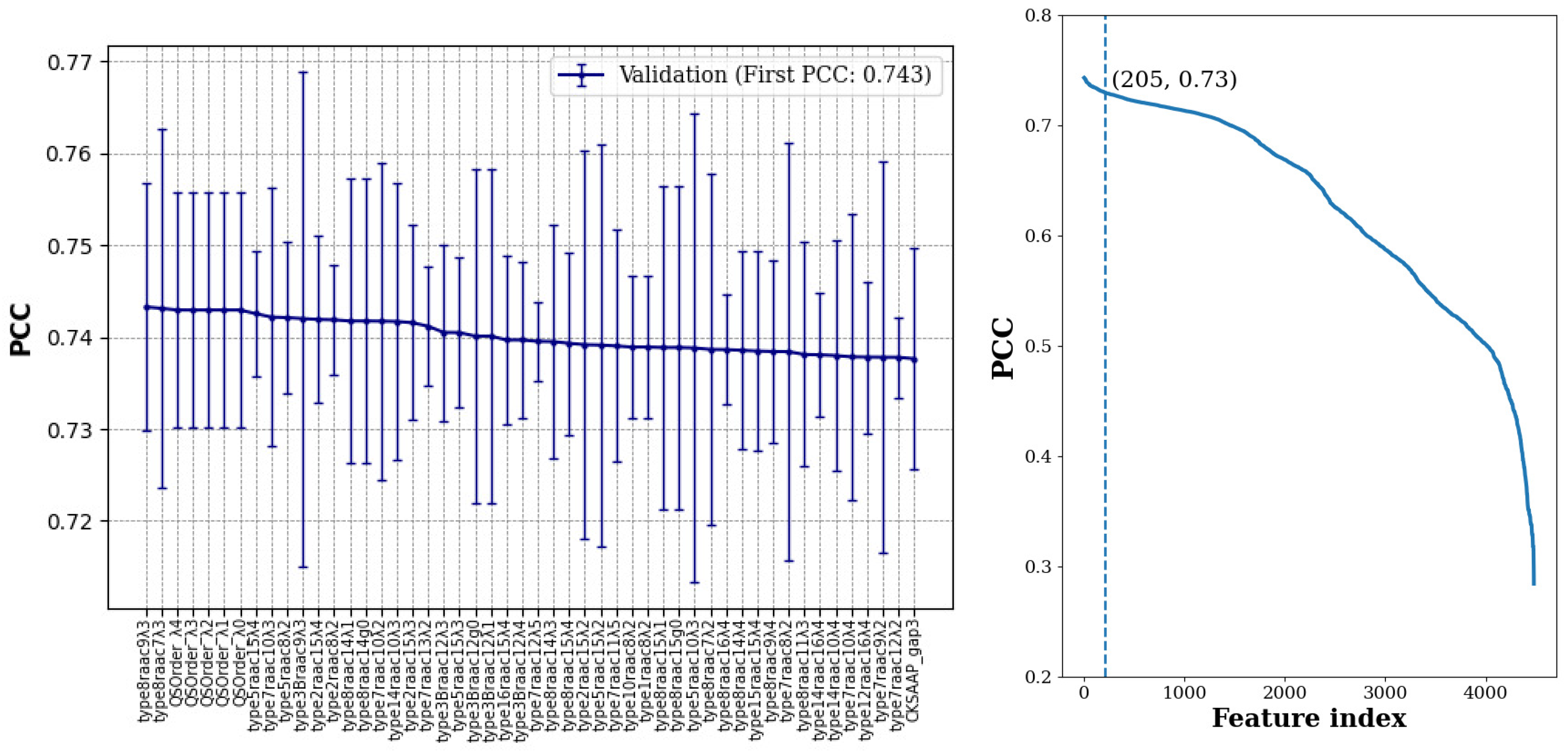
Preprints 69345 g001
Preprints 69345 g002
Figure 2. Train, validation, and test performances of the best-1 to best-26 models using MBC-Attention in feature combination selection. Experiments were repeated three times, and average PCC values were reported along with one standard deviation as error bars.
Figure 2. Train, validation, and test performances of the best-1 to best-26 models using MBC-Attention in feature combination selection. Experiments were repeated three times, and average PCC values were reported along with one standard deviation as error bars.
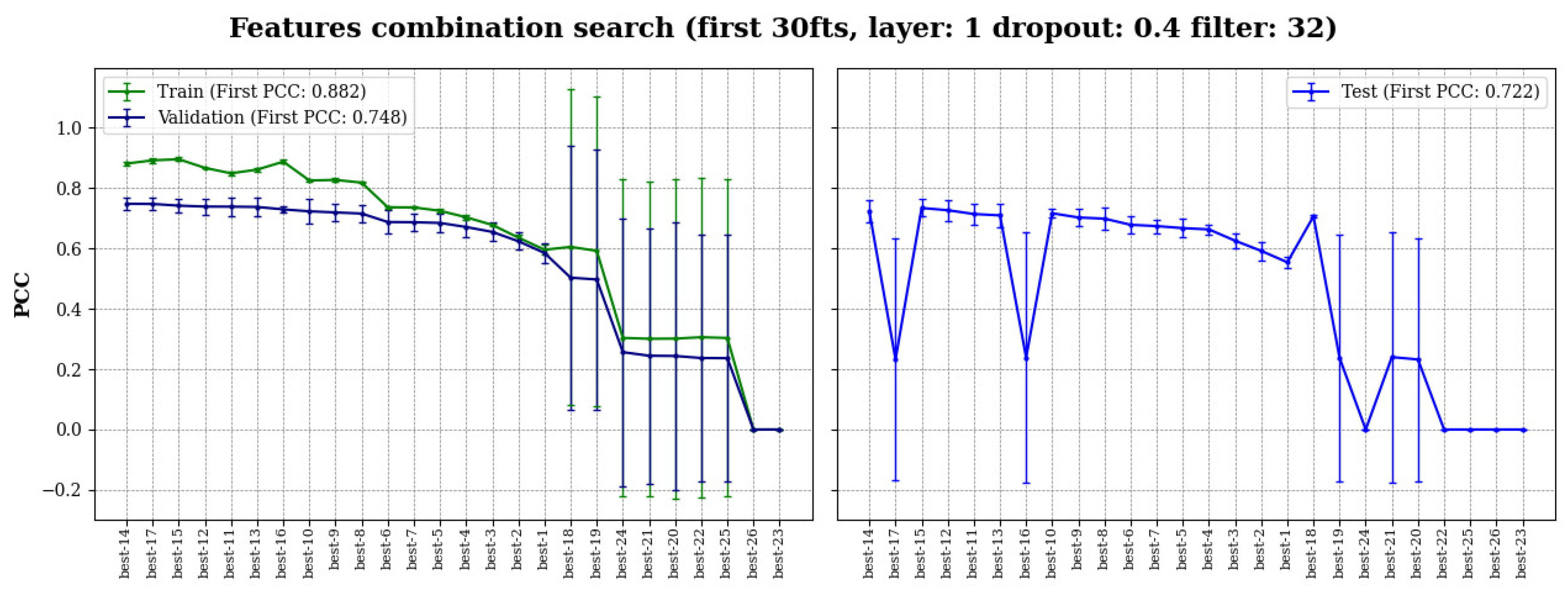
Preprints 69345 g002
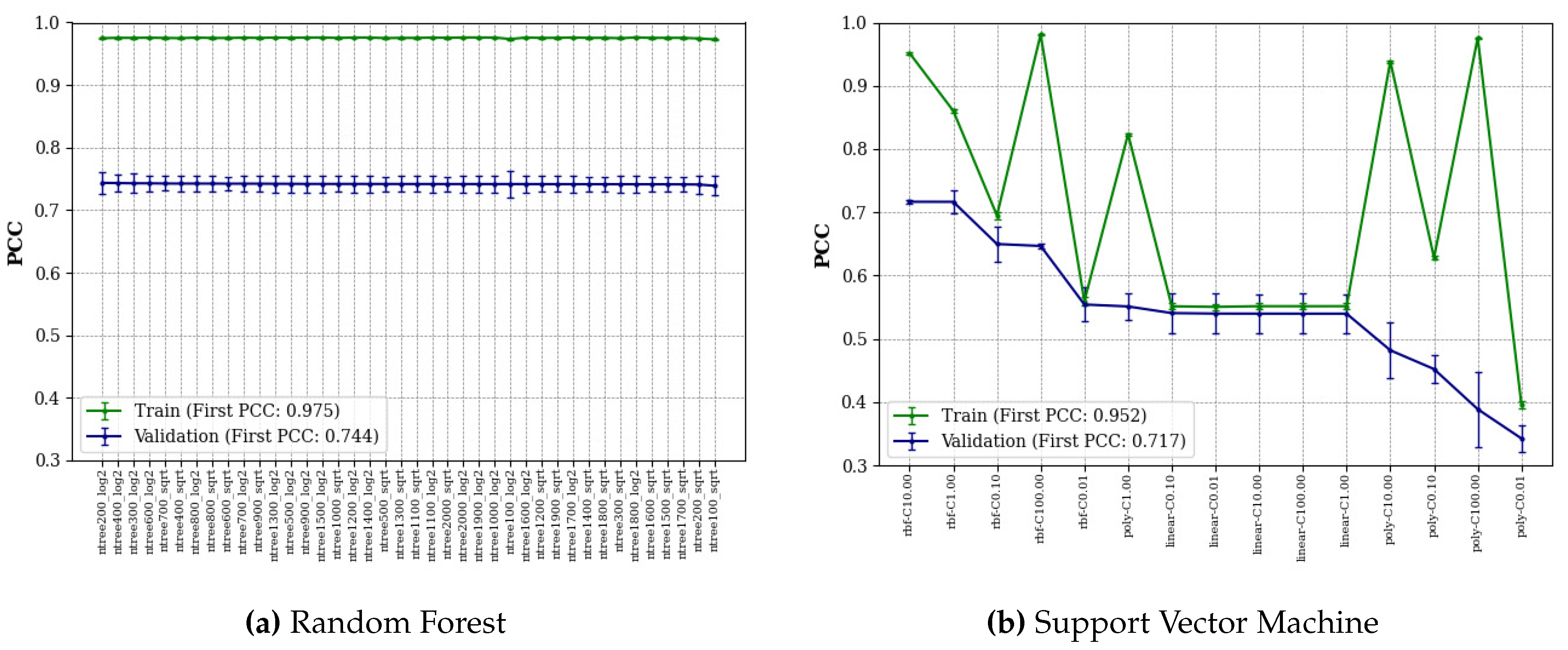
Preprints 69345 g003
Figure 3. Regressive performance of RF (a) and SVM (b) models in the validation set with different parameters
Figure 3. Regressive performance of RF (a) and SVM (b) models in the validation set with different parameters
Preprints 69345 g003
Preprints 69345 g004
Figure 4. Comparative accuracy of Multi-Branch-CNN (MBC) and MBC-Attention on test (left) and novel-test (right) sets of Na-pep, K-pep, and Ca-pep predictions.
Figure 4. Comparative accuracy of Multi-Branch-CNN (MBC) and MBC-Attention on test (left) and novel-test (right) sets of Na-pep, K-pep, and Ca-pep predictions.
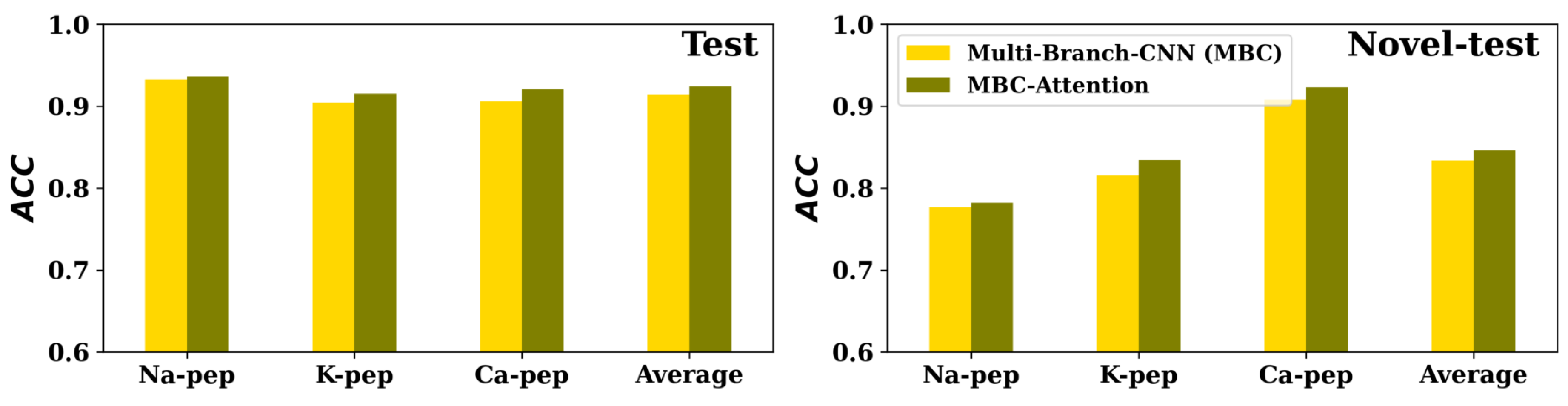
Preprints 69345 g004
Preprints 69345 g005
Figure 5. (Left) The histogram of sequence lengths and (right) pMIC values of the curated AMP dataset of 3929 entries for E. coli.
Figure 5. (Left) The histogram of sequence lengths and (right) pMIC values of the curated AMP dataset of 3929 entries for E. coli.
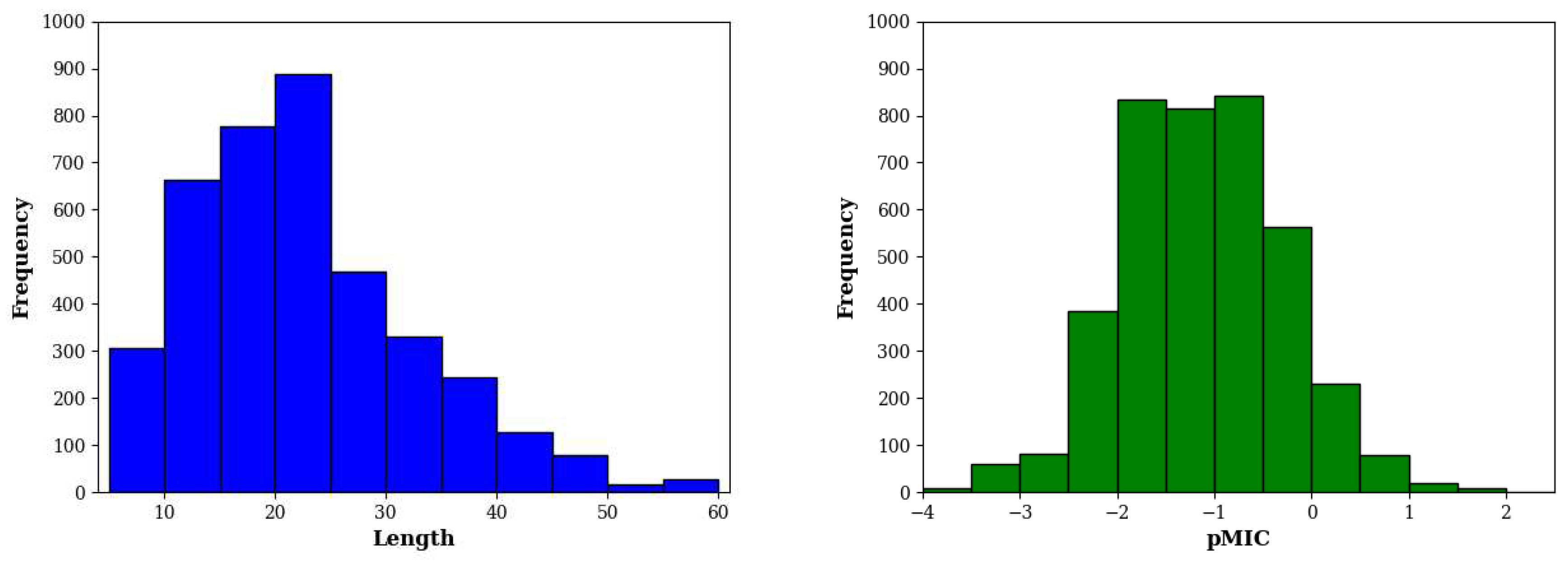
Preprints 69345 g005
Preprints 69345 g006aPreprints 69345 g006b
Figure 6. The proposed MBC-Attention method based on (a) the Multi-Branch CNN architecture and enhanced with (b) a local attention and (c) the global attention mechanism.
Figure 6. The proposed MBC-Attention method based on (a) the Multi-Branch CNN architecture and enhanced with (b) a local attention and (c) the global attention mechanism.
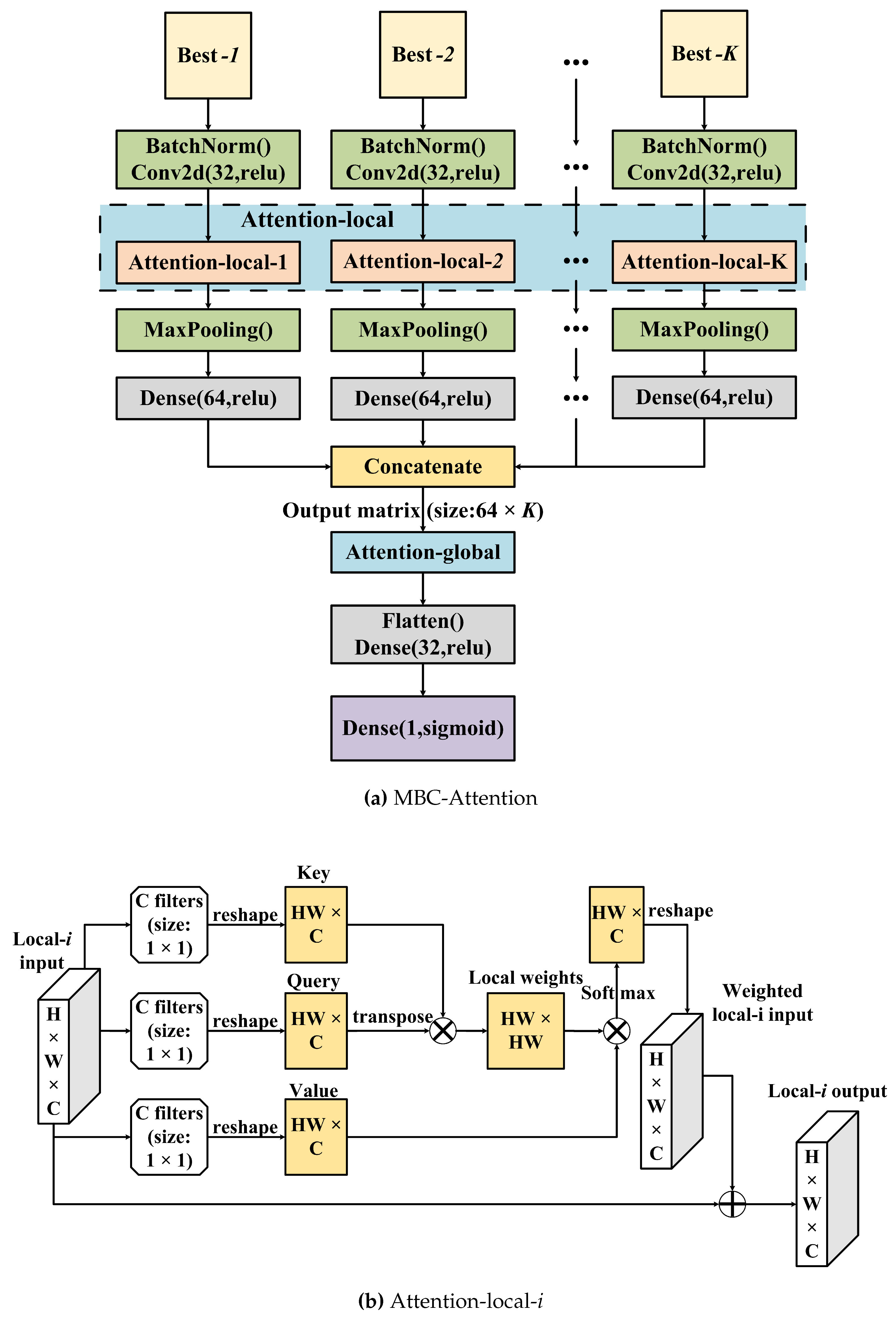
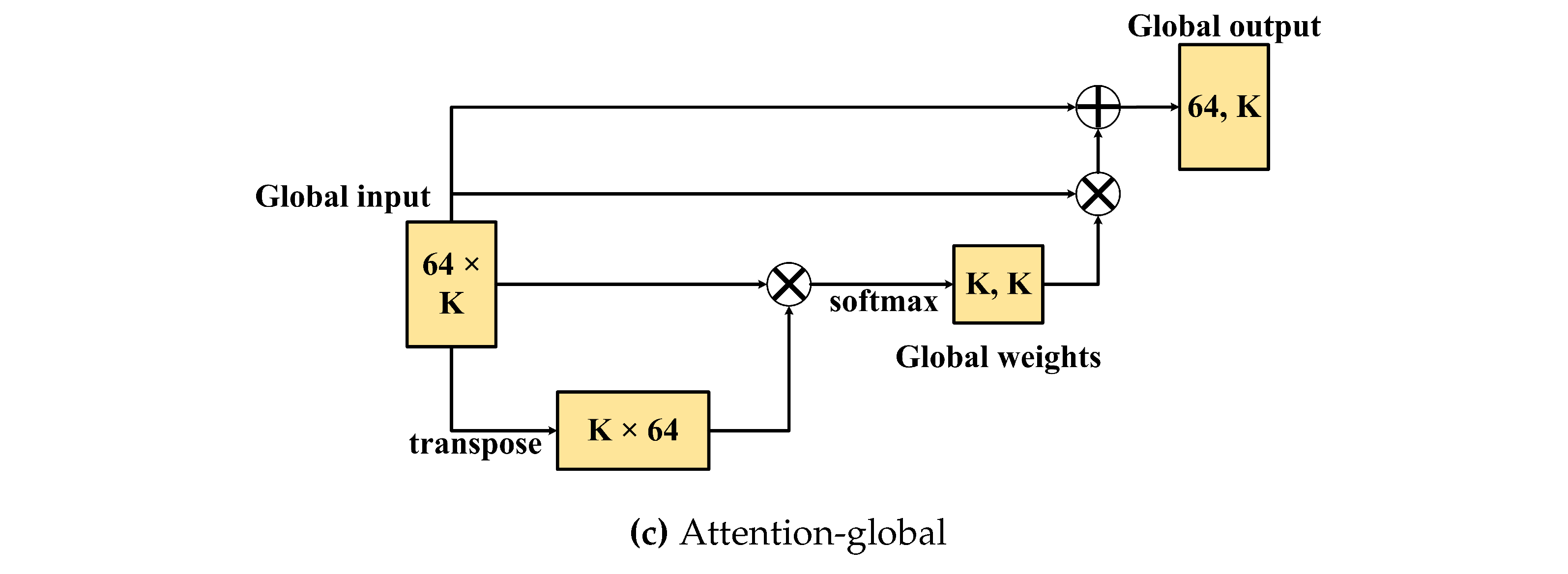
Preprints 69345 g006aPreprints 69345 g006b
Table 1. The best-14 feature types selected using Random Forest
Table 1. The best-14 feature types selected using Random Forest
Feautre Groups Type Type Description RAAC Type λ No. of Features
PseKRAAC 8 Grantham Distance Matrix (Saturation) [28] 9 3 81
PseKRAAC 8 Grantham Distance Matrix (Saturation) 7 3 49
QSOrder - Quasi-sequence-order [29] - 4 343
QSOrder - Quasi-sequence-order - 3 343
QSOrder - Quasi-sequence-order - 2 343
QSOrder - Quasi-sequence-order - 1 343
QSOrder - Quasi-sequence-order - 0 343
PseKRAAC 5 BLOSUM50 matrix [30] 15 4 225
PseKRAAC 7 Metric multi-dimensional scaling (MMDS) [31] 10 3 100
PseKRAAC 5 BLOSUM50 matrix 8 2 64
PseKRAAC 3B Whelan and Goldman (WAG) matrix [32] 9 3 81
PseKRAAC 2 BLOSUM 62 matrix [33] 15 4 225
PseKRAAC 2 BLOSUM 62 matrix 8 2 64
PseKRAAC 8 Grantham Distance Matrix (Saturation) 14 1 196
Table 2. Comparative performance of RF, SVM, MBC-Attention, and MBC-Attention with reduced features.
Table 2. Comparative performance of RF, SVM, MBC-Attention, and MBC-Attention with reduced features.
Algorithm PCC ↑ CCC ↑ R2 ↑ MAE ↓ MSE ↓ RMSE ↓
RF (200 trees and max features of "log2") mean 0.735 0.666 0.531 0.441 0.327 0.571
std 0.042 0.049 0.059 0.027 0.037 0.032
SVM ("rbf" kernel and C of 10) mean 0.691 0.675 0.466 0.461 0.375 0.612
std 0.042 0.045 0.070 0.030 0.043 0.035
MBC-Attention mean 0.775 0.738 0.588 0.402 0.284 0.533
std 0.014 0.015 0.005 0.006 0.003 0.002
MBC-Attention with reduced features mean 0.764 0.735 0.582 0.419 0.298 0.545
std 0.019 0.030 0.026 0.021 0.020 0.014
Table 3. Comparative performance of MBC, MBC with global attention, MBC with local attention, MBC-Attention methods.
Table 3. Comparative performance of MBC, MBC with global attention, MBC with local attention, MBC-Attention methods.
Algorithm PCC ↑ (std) % increase ↑ CCC ↑ R2 ↑ MAE ↓ MSE ↓ RMSE ↓
MBC 0.741(0.019) – 0.692 0.528 0.451 0.336 0.580
MBC with global attention 0.766(0.017) 3.37 0.743 0.587 0.411 0.293 0.542
MBC with local attention 0.763(0.016) 2.97 0.735 0.581 0.419 0.298 0.546
MBC-Attention 0.775(0.014) 4.59 0.738 0.588 0.402 0.284 0.533
Table 5. The feature types and parameters used to encode peptide sequences.
Table 5. The feature types and parameters used to encode peptide sequences.
Feature
Name		 Description Parameters
OneHot One Hot Encoding -
AAC Amino Acid Composition -
DPC Di-Peptide Composition [36] -
TPC Tri-Peptide Composition [37] -
DDE Dipeptide Deviation from Expected Mean [38] -
GAAC Grouped Amino Acid Composition -
GDPC Grouped Di-Peptide Composition -
GTPC Grouped Tri-Peptide Composition -
CTDC Composition of Composition/Transition/Distribution [39] -
CTDT Transition of Composition/Transition/Distribution -
CTDD Distribution of Composition/Transition/Distribution -
CSKAAP Composition of k-spaced Amino Acid Pairs [40] g a p ∈ { 0 , 1 , 2 , 3 }
CKSAAGP Composition of k-Spaced Amino Acid Group Pairs [25] g a p ∈ { 0 , 1 , 2 , 3 }
CTriad Conjoint Triad [26] g a p ∈ { 0 , 1 , 2 , 3 }
KSCTriad k-Spaced Conjoint Triad [26] g a p ∈ { 0 , 1 }
SOCNumber equence-Order-Coupling Number [41] λ ∈ { 0 , 1 , . . . , 4 }
QSOrder Quasi-sequence-order [29] λ ∈ { 0 , 1 , . . . , 4 }
PAAC seudo-Amino Acid Composition [42] λ ∈ { 0 , 1 , . . . , 4 }
APAAC Amphiphilic Pseudo-Amino Acid Composition [43] λ ∈ { 0 , 1 , . . . , 4 }
NMBroto Normalized Moreau-Broto Autocorrelation n l a g ∈ { 2 , 3 , 4 }
Moran Moran correlation [44] n l a g ∈ { 2 , 3 , 4 }
Geary Geary correlation [44] n l a g ∈ { 2 , 3 , 4 }
PseKRAAC Pseudo K-tuple Reduced Amino Acid Composition [27] k t u p l e = 2
s u b t y p e ∈ { ′ g − g a p ′ , ′ λ − c o r r e l a t i o n ′ }
g − g a p ∈ { 0 , 1 , . . . , 9 }
λ − c o r r e l a t i o n ∈ { 0 , 1 , . . . , 9 }
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated