Prerpints.org logo
Preprint
Article

High Accuracy Remote Data Detection Method for Underground Space Information Based on Fractional-order Differential Algorithm

Altmetrics

Downloads

129

Views

48

Comments

0

This version is not peer-reviewed

Submitted:

03 March 2023

Posted:

03 March 2023

You are already at the latest version

Alerts
Abstract
The quality of underground space information has become a major problem that endangers the safety of underground spaces. Currently, the main methods for the high-precision and long-distance transmission of detection information are radar and optical methods. However, in practical applications, we found that the radar method has the shortcomings of large energy loss and poor anti-jamming ability, which limit the accuracy of information data transmission and distance. The optical method has the shortcomings that the weather has a great impact on its accuracy and can only be applied to static objects above ground; therefore, it has the limitation of application objects and use environment. More importantly, the current high-precision information remote detection methods are limited to the detection of overground space objects and are not applicable to the detection of various information data in underground space. In this study, we analyze the spectral properties of the fractional differential operator and find that it is suitable for studying non-linear, non-causal, and non-stationary signals. The theory of fractional calculus is applied to the field of data processing, and a mathematical model of remote transmission and high-precision detection of information based on fractional difference is established, which realizes the functions of high-precision and remote detection of information. By fusing the information data to detect the mathematical model over a long distance and with high accuracy, a mathematical model for stratum data processing used to provide long-distance and high-accuracy data was established. Through application in engineering practice, the effectiveness of this method for underground space information data detection was verified.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Currently, the development of larger and more complex underground spaces has become a trend for future underground space development [1]. Underground space has the characteristics of "deep, large, clustered, and hidden". Once an accident occurs, it can easily cause a catastrophic impact [2,3]. However, the existing safety perception and prediction technology for underground space structures cannot guarantee the safety of underground space structure construction and operation. In particular, urgent problems still need to be solved in terms of state perception, disease identification, and mechanistic analysis [4]. In addition, the working environment of underground space detection equipment is complex, spatio-temporal monitoring data are unusually diverse, and the quality is uneven, which often causes problems such as "unclear detection, inaccurate measurement, and inaccurate judgment" of the underground space, thus leading to an incorrect estimation of the safety status of the underground space, which may endanger the safety of the underground space [5]. Therefore, improving the global awareness of underground spaces and the quality of data detection has become an urgent problem to be solved in the construction of underground spaces.
The detection objects of underground space information include the detection of underground tangible objects and intangible material parameters; however, the essence of realizing their information data detection quality lies in improving the detection accuracy of information data and the strength of signal transmission. The tangible objects in the underground space include the underground space structure, object contour shape, production equipment position, and moving object trajectory. At present, the detection methods of underground space are mainly based on ground-penetrating radar [6], and the portability and high-resolution characteristics of GPR [7,8] make GPR widely used in subgrade surveys and underground space pipeline detection [9]. However, the penetration depth of ground-penetrating radar is limited, and the effective detection depth generally does not exceed 10m [10,11], it can only detect shallow urban facilities and has no detection capability for underground targets below 30m. The existing shallow surface wave method [12,13,14] has difficulty meeting the detection requirements of urban geophysical exploration owing to its weak anti-jamming capability. Reference [15,16] proposed a load differential radiation pulse on a transient electromagnetic high-performance radiation source for pulse scanning detection to solve the problems of urban electromagnetic interference and insufficient harmonic components emitted by radiation sources. However, the detection method of pulse scanning alone is incomplete and a corresponding imaging method is required. More importantly, the above methods can only be applied to the detection of information tens of meters below the ground, and they cannot be applied to underground spaces hundreds of meters deep.
The objects of detection of intangible substances in underground spaces include gas, pressure, temperature, humidity, noise, and stress. At present, the detection methods for the parameters of underground intangible substances are still the same as those for intangible substances in above-ground space. Reference [17,18,19] designed a hardware system based on radar and realized the real-time detection function of underground space related information by enlarging the detection information. However, the measurement error cannot be eliminated and applied to underground spaces with tortuous paths. Reference [20] proposed a three-frequency resonance transmission scheme to solve the problems of low efficiency in the conventional single-frequency transmission method and high voltage stress in the multifrequency pseudorandom transmission method. However, the scheme only solves the problem of signal transmission efficiency and does not improve the quality of information data. Reference [21,22]The self-developed rotary drilling system and three-dimensional flexible boundary loading device were developed to carry out the rotary drilling model and realize the detection technology of stress betteen rocks in underground space. However, they have limitations in the application space and cannot be used for remote detection of information data. ZhengXuezhao et al.[23] studied a multi-information drilling detection device based on key technologies, such as multimedia information collection, synchronous transmission, and underground explosion-proof facilities, and realized the collection function of key information data of underground space. However, this method is based on drilling from the ground to the underground space and placing the equipment in the underground space for later detection, so there are shortcomings of low efficiency and information lag. Bin Sun et al. [24] proposed a bionic artificial intelligence algorithm driven by temperature data to detect a fire source in the three-dimensional space of an underground pipe gallery. However, this method can be used only for fire prevention in underground pipelines.
More importantly, the above methods have the following shortcomings in the information collection of underground spaces:
  • They are mainly used to detect the position and shape of tangible objects, and there are shortcomings in the field of high-precision remote detection that cannot be applied to object performance parameters. Therefore, there are limitations in the application field.
  • Their essence is to highlight the difference between information data to improve the detection accuracy of the difference data, It fails to eliminate the detection error caused by various factors in the process of long-distance transmission of in-formation data fundamentally.
  • In the detection process, because the detection object is in a random transformation state, the above information detection system does not have the ability to adjust the technical parameters with the changes in the tested object in a timely manner. Therefore, it affects the accuracy and real-time detection of the information.
  • In the detection of underground space information data, the above methods have the disadvantage of large energy loss in application, which restricts the depth and data accuracy of detection information; therefore, there are limitations in the application space.
Therefore, to date, no detection method that can be applied to various types of detection objects in underground spaces with high precision over long distances has been found. To solve these problems, our team has engaged in research on methods using fractional-order calculus theory in data processing for many years and found that the fractional-order differential operator has the dual function of improving the signal strength and reducing the variability between information data. Therefore, it can effectively improve the transmission distance and detection accuracy of information [25,26,27,28,29,30,31]. Based on previous research, in this study, we applied fractional calculus theory to the detection of underground space information data.

2. Fractional Calculus Theory

The concept of fractional differentiation was mentioned in 1812; however, after hundreds of years of research, fractional derivatives do not have a unified definition. At present, the most commonly used definitions are those of Grunwald–Letnikov (G-L), Caputo, and Riemann–Liouville (R-L) [32,33]. Because the G-L definition has the advantage of fast calculation speed, it is widely used in the engineering field. Therefore, the G-L definition was used in this study to study the application of fractional calculus theory for detection data processing.

2.1. Fractional-Order Calculus Definition

Suppose there is a real number v, and its part of v is denoted as [v]. If the function f t has (n + 1) continuous derivatives within the interval [a, b], when v > 0 and n ≥ [v], the G-L definition of a fractional v-order derivative is defined as
D a ​ ​ t v f t = lim h → 0 f h v t = lim h → 0 ​ h − v ∑ j = 0 b − a h − 1 j v j f t − j h .
In (1), 0 ≤ n − 1 < v < n , and v j is a binomial coefficient, defined as
v j = v v − 1 v − 2 .... v − j + 1 j ! .
where h = (b –a )/n, and n = [(b - a)/h]. When h → 0, n →∞.

2.2. Spectral Characteristics of Fractional Calculus Operators

For an arbitrary square productable energy signal f(t)∈L2(R), it is assumed that its Fourier transform is F ( ω ) , and the Fourier transform of the v-order fractional differential Dvf(t) can be obtained as follows:
d v f ( t ) d t v ⇔ ( i ω ) v F ( ω )
The characteristic function of the signal v-order fractional order differential operator Dv is
D ( ω ) = α ( ω ) θ ( ω ) = ( i ω ) v
where α ( ω ) = ω v and θ ( ω ) = π v 2 sgn ( ω )
Based on the filter function, we can draw spectral characteristic curves of the fractional-order differential operator in signal processing, as shown in Figure 1. After analyzing the spectral characteristic curves, we can obtain the following characteristics of fractional-order calculus for signal processing:
  • It has the function of nonlinearly retaining the very low-frequency components of various signals while boosting the high-frequency components of the signal. This can effectively enhance the middle and high-frequency parts of the signal, and the amplitude tends to increase nonlinearly and rapidly with an increase in the frequency and fractional order of the derivative.
  • When ω > 1, with an increase in the fractional order v and signal frequency ω, the variability between the signal enhancement coefficients of the fractional-order differential operators at different orders tends to decrease, and with an increase in frequency, the enhancement effect of the differential operators of the same order on the signal intensity at different frequencies is basically the same.

2.3. Application of Fractional Calculus

In the expression of the fractional-order calculus under the G-L definition, the time t in the signal f(t) is the influence factor of the signal amplitude, where t∈[t1, t2]. If t i = x i and t 1 , t 2 ⇔ a , b , reference (1), then the following equation can be obtained:
D a G ​ t v f t ⇔ D a G ​ x v f x = lim h → 0 ​ h − v ∑ i = 0 b − a h − 1 i v i f x − i h .
In (5), 0 < n – 1 < n, and v i is a binomial coefficient defined as:
v i = v v − 1 v − 2 .... v − i + 1 i ! .
In (5), where h → 0 , n → ∞ , and h = b − a / n .
In recent years, many experts and scholars have studied the theory of fractional-order calculus and found that it is suitable for the study of signals with undesirable characteristics, such as nonlinearity, non-causality, and non-stationarity, and for various data applications. Various research results have been used to solve technical problems in the study of temperature field distributions, image processing, mechanical analysis, and detection technology [34,35,36,37,38]. For example, WANG Bao et al. [39] applied fractional partial derivatives to the thickness design of high-temperature protective clothing under limited conditions. Zhou et al. [40] applied fractional derivatives to demonstrate their advantages in image denoising and reducing the step effect, as well as in signal denoising and super-resolution reconstruction. SHEN Tianlong [41] applied fractional partial derivatives to fluid mechanics. The working environment of an underground space is complex and changeable, so all types of signals have poor characteristics such as nonlinearity, non causality, and non stationarity. Therefore, fractional differential operators can be used to process various underground signals. This solves the problem of application field limitations in current underground space information detection methodssuccessfully.

3. High Precision Detection Method of Underground Space Information Based on Fractional Differential Algorithm

3.1. Fundamental Principle

The essence of fractional-order calculus processing of the signal under the G-L definition is to apply a linear fit to the spectral characteristic curve obtained via fractional-order calculus, where the system detects an energy signal F(t), where t∈ (t1, t2). During information detection, the detection data in the transmission process will inevitably be affected by a variety of factors, such as equipment performance, working environment, and signal interference, thus causing a large data detection error. Referring to Equation (5), considering x as a detection value for the influence factor, we can obtain the corresponding equation F(x), x∈ (a, b), h is the step value of the variation of x between (a, b), and the number of fitting steps is n = [b − a]/h. According to (2) and Figure 1, the spectral curve of the fractional-order calculus under the definition of G-L when the value of h is different is shown in Figure 3. According to Figure 2, the fitting error between the fitted line and actual spectral curve increases gradually when the step values are h, 2h, 3h and 4h. Therefore, the accuracy of the data can be adjusted by gradually adjusting the step value h until the requirements of the detection system are satisfied. However, in the value range [a, b] of x, as step h decreases, the system efficiency decreases because of the increase in the number of fitting steps n. Therefore, the best step h should be chosen to achieve high-precision detection of the data based on full consideration of the detection accuracy and efficiency.

3.2. Mathematical Model

The optimal fractional order v for fractional-order differential processing of the data was selected according to the signal characteristics and spectral properties of the fractional-order differential operator. Referring to (5), the system obtains the functional equation F(x) that relates the data value F(xi) and the influence factor xi, where x ∈ (a, b). According to (4), the derivative processing equation of F(x) at fractional-order v can be obtained as follows:
D a ​ ​ x v F x = lim h → 0 F h v x = h − v ∑ i = 0 n − 1 i v i F x i − i h ,
where v i = v v − 1 v ​ − 2 .... v − i + 1 i ! , and n = [ b − a ] / h
According to the above analysis of the spectral characteristics of the fractional-order differential operator, the fractional order differential operator has the effect of enhancing the signal intensity. Suppose that when x takes the value interval [a, b], the amplification factor of the data value of the function F(x) after differentiation of order v is K. For comparison, the data value after v-order differentiation is divided by the amplification coefficient K. The result is combined with the formula for the standard deviation S of the data as follows:
S = F a v − F ¯ v 2 + F ​ a + h ​ v − F ¯ v 2 + F a + 2 h v ​ − F ¯ v 2 .... + F F b v − F ¯ v 2 n K 0.5       = ∑ i = 0 n 1 （ F a + i h v − F ¯ v ） 2 n K 0.5 ,
where
F a + i h ​ v = lim h ​ → 0 F h ​ v ​ a + i h = h − v ∑ i = 0 n − 1 i v i F x i ,
F ¯ v = F a v + F a + h ​ v + F a + 2 h v + ⋯ + F b ​ v ​ n = ∑ i = 0 n F a + i h v / n ,
K = F a v + F a + h ​ v + F a + 2 h v + ⋯ + F b ​ v F a ​ + F a + h ​ ​ + F a ​ + 2 h ​ ​ + ⋯ + F b ​ = ∑ i = 0 n F a ​ + i h ​ v / ∑ i = 0 n F a ​ + i h ​ ​ ​ .
By substituting (8) and (9) into (7), we obtain
S = ∑ i = 0 n （ F a + i h v − F ¯ v ） 2 n ∑ i = 0 n F a + i h v ​ / ∑ i = 0 n F a + i h ​ ​ 0.5 .
If the accuracy of the data is set based on Sg, S should satisfy:
S ≤ S g S g − S ≈ 0 .
Initially, step value h is chosen. Combined with the known parameter values a and b, we can calculate the inter-data accuracy for step value h.
S = ∑ i = 0 [ b − a ] / h （ F a + i h v − F ¯ v ） / n K 0.5 .
The error between the standard deviations S and Sg was compared, and the step value h was gradually adjusted until the conditions shown in (12) were met. The corresponding step value, h is the best step value for meeting the set accuracy of the detection system.

3.3. Implementation Steps

Based on the above fundamental principle and mathematical model, the implementation steps of the high-precision data detection method for underground spaces are as follows:
  • Based on the characteristics of the detected signal and the spectral characteristics of the fractional-order differential operator, the optimal fractional derivative order v was selected for data F(x).
  • Referring to (1) and (7), the derivative-processed model Fv(x) of the corresponding data function F(x) is established at fractional order v.
  • The functional equation S(h) relating the standard deviation S of the data and step size h is established based on the calculated value of Fv (x).
  • The initial step value h was set, and the standard deviation S(h) of the detection data when the step value was h was calculated based on the functional equation S(h).
  • The error between the standard deviation S(h) and the specified standard deviation Sg threshold of the underground space information detection system was compared, and the step value h was continuously adjusted based on the error value between them.
  • If the standard deviation S(hk) is slightly less than the specified standard deviation Sg threshold, hk is selected as the best step value to satisfy the accuracy requirement of the underground space information detection system.
If the standard deviation S(h) is slightly less than the specified standard deviation Sg threshold, h is selected as the best step value to satisfy the accuracy requirement of the information detection system.

4. Long-Distance Transmission Method of Under-Ground Space Information Based on Frac-Tional Differential Algorithm

4.1. Fundamental Principle

By combining the amplitude–frequency characteristics of the fractional-order differential operator shown in Figure 1 and the fractional-order differential processing equation under the G-L definition shown in (1), suppose that the system detects an energy signal G(t), where t∈ (t1, t2). Referring to (5), we can obtain the corresponding equations G(x), x∈ (a, b). The local enlargement of the spectral characteristics of the function G(x) in the interval x ∈ (a, b) after differential processing of different orders is shown in Figure 3. When the fractional order vi and influence factor xi are the same, the amplification coefficient Ki of the fractional-order differential operator is a fixed value. If the energy data G(t) are processed by the differential operator of fractional order vi, and the amplification coefficient of the data is ki, then the amplification coefficient of the signal after m cycles of applying the differential operator of fractional order v is denoted as K=kim, and the data after processing are denoted as G n ( x ) = k i m G ¯ h v x . Therefore, the detection system can realize the long-distance detection function of data by adjusting the number of cycles of fractional-order differential processing of the detection data to m.

4.2. Mathematical Model

The interval of values of x in the function G(x) is [a, b], where h is the step value, that is, xi = xi−1 + h, and the corresponding step number n =(b - a)/h]. Thus, the average value of function G(x) in this interval can be obtained as follows:
G ¯ x = ∑ i = 0 n G a + i h / n .
The functional equation of function G(x) after differentiation of order v is Gv (x). From the fractional-order derivative in (1) and (2), the derivative of the order v for G(x) can be obtained as follows:
D a ​ ​ x v G x = lim h → 0 G h v x = h − v ∑ i = 0 n − 1 i v i G x − i h ,
where v i = v v − 1 v − 2 .... v − i + 1 i ! .
Therefore, the average value of the function G(x) processed by the differentiation operator of order v is.
G ¯ v x = ∑ i = 1 n G v x i / n = h − v n ∑ i = 0 n ∑ i = 0 n − 1 i v i G x − i h ,
According to the formula for the amplification coefficient K, the amplification coefficient k of the function G(x) in the interval [a, b] after the function value is processed by the differentiation operator of order v asfollows:
K = G ¯ v x / G ¯ ( x ) = h − v n ∑ i = 0 n ∑ i = 0 n − 1 i v i G x i / ∑ i = 0 n G a + i h .
According to the working principle of long-distance transmission of the data above, it is known that the signal strength will be amplified k times each time the data function G(t) is processed by the v-order differential operator. Therefore, if the detection system needs to achieve the required amplification factor Kg for the set long-distance transmission targets under the existing conditions, it must satisfy Kg ≤ km, where m is the number of fractional-order derivatives required to achieve the set detection target. Thus, the required number of v-order differential operator processes m should satisfy
K ​ m = G ¯ v ​ x / G ¯ ( x ) m ≥ K g .
The increase in the number of iterations increases the computational workload and decreases the efficiency of the system. Therefore, in the process of increasing the data intensity, the number of fractional-order differentiations is set to
K g ≤ K ​ m ＜ K ​ ​ m + 1 .
where m is the number of cycles in the differential operator for the data.

4.3. Implementation Steps

The premise of realizing remote detection of underground space information data is to obtain the detection value G (xi) of detection data G (t) at different time points in real time and then analyze the main influence factor x and its range of values [a, b] based on the data. This lays the foundation for the long-distance transmission of detection data. The specific implementation process of the long-distance detection method for underground space information data is as follows.
  • The detection values G(xi) of the signal G(t) of underground space information at different time points were acquired, and the influence factor x and its value interval [a. b] were analyzed.
  • The acquired detection values G(xi) and the values of their corresponding influence factor xi were used to fit a function G(x).
  • Considering the signal characteristics of G(t) and the spectral characteristics of the fractional-order differential operator, a suitable fractional order v was selected.
  • The amplification factor k of the fractional-order differential operator is calculated based on the fractional order v and the data function G(x).
  • The energy loss of the signal transmitted under the existing conditions was calculated by formulating a transmission method based on the characteristics of the signal G(t).
  • The amplification factor Kg required for the effective transmission of signal G(t) is calculated using the detection system based on the transmission distance L of the system.
  • The required amplification factors Kg and K are combined, and the number of differential processing cycles m required by the system is calculated to realize the remote transmission target of the information dataset by the underground space detection system.

5. High-Precision and Long-Distance Detection Method for Under-Ground Space Information Based on Fractional Differential Algorithm

5.1. Fundamental Principle

The remote and high-precision detection of data by a detection system is essentially a dual function achieved through the processing of the detection data. As mentioned previously, the transmission of data over a desired distance can be achieved by setting the number of iterations j of the differential operator for data processing based on the amplification factor K of the fractional-order differential operator and the established amplification factor KG of the detection system. The detection accuracy of the data can be achieved by comparing the established accuracy SG of the system and the accuracy S of the fractional-order differential operator, and gradually adjusting the step value h of the fractional-order differential operator so that SG can be approximately achieved. Therefore, obtaining the step value h and amplification factor K required by the fractional-order differential operator in data processing under the established conditions is a prerequisite for achieving the research objectives. From the results of the above study, it is known that the accuracy of data detection at the same fractional order depends on the step value h of the fractional-order differential operator, which is independent of the amplification factor K. The calculation of the amplification factor k of the fractional-order differential operator must be based on the fact that step value h is known. Therefore, in the implementation of the long-range, high-precision acquisition method for detecting data, the method of calculating the step value h required to satisfy the established target and then applying it to calculate the amplification coefficient K of the fractional-order differential operator can be sequentially used.

5.2. Mathematical Model

The analysis system is intended to transmit an energy signal H(t) to a location at distance L, and the accuracy of the acquired data must not be lower than SG. To ensure the reliability of the data detection system, the detection signal must be amplified, and the enhancement factor must not be lower than KG. The data H(xi) of signal H(t) at different time points ti are collected. The main influencing factor of the obtained data is x and its value interval [a, b]. A function H(x) relating the detection data value H(xi) to xi is fitted. According to the signal characteristics of the signal H(t) and the spectral characteristics of the fractional-order differential operator, the proposed method of applying the differential operator at fractional order v for the long-range, high-precision detection of data was used. With reference (1), the fractional-order differential processing equation of data under known conditions is
D a ​ ​ x v H x = lim h → 0 H h v x = h − v ∑ i = 0 n − 1 i v i H x − i h .
In (21), v i is a binomial coefficient, defined as
v ​ i = v ​ v ​ − 1 v ​ − 2 .... v ​ − i + 1 i ! .
According to the above theory for long-distance and high-precision transmission of data, the standard deviation of the data is calculated after the fractional-order differential operator is applied as follows:
S = ∑ i = 0 n （ H a + i h v − H ¯ v ） / K       0.5 .
If the detection accuracy target set by the system is to be achieved, the following conditions must be satisfied:
S ≤ S G S G − S ≈ 0 .
As mentioned above, if the step value of the fractional-order differential operator is h, the system can be calculated using a stepwise approximation method to meet the system accuracy target SG. Then, h is introduced into (23) to obtain the amplification factor of the detection data after processing by the v-order differential operator, as follows:
K = H ¯ v x / H ¯ ( x ) = h − v ∑ i = 0 n ∑ i = 0 n − 1 i v i H x − i h / ∑ i = 0 n H a + i h .
By combining the required data enhancement factor KG of the detection system and referring to (19), the number of fractional-order differentiations m required to detect the data is.
m = K G / K = K G H ¯ ( x ) / H ¯ v x = K G h v ∑ i = 0 n H a + i h / ∑ i = 0 n ∑ i = 0 n − 1 i v i H x − i h .
The number of fractional order differentiation processes for the detection data is m.

5.3. Implementation Steps

Suppose the underground space information detection system detects an energy signal H(t), where t∈ (t1, t2). Referring to (7), we can get the corresponding equation G(x), x∈ (a, b). The signal characteristics of the data to be detected and its usage requirements are analyzed. The data accuracy SG and the amplification factor KG required to achieve the data detection target are set. According to the above fundamental principle, The remote and high-precision detection methods of underground space information data are as follows:
  • A data processing scheme is developed for underground space information data based on fractional calculus theory, according to the set data accuracy SG and signal amplification coefficient KG.
  • The collected data H(xi) of underground space information is applied to analyze the important influence factor x, and the functional relationship between the data and the influence factor H(x) is obtained by fitting.
  • The appropriate fractional order v for the processing of data is selected based on the characteristics of the detection data signal and the amplitude and frequency characteristics of the fractional-order differential operator.
  • The step value h required to achieve the required accuracy SG of the system is calculated based on the mathematical model shown in (12) and (14).
  • The amplification factor K of the fractional-order differential operator is calculated based on the data, and the number of iterative cycles j required to achieve the data amplification factor KG is determined.
Through the integration of high-precision detection method and long-distance transmission method of underground space information data, the high-precision remote transmission function of a signal in underground space is realized. It not only successfully solves the problem that the two functions of the current method cannot be considered, but also realizes the detection technology of information data under the established detection target.

6. Application Examples

6.1. Experimental Environment

Therefore, controlling the gas concentration at the working face is a key issue, and it is difficult to ensure safe mine production. To realize the effective control of the gas concentration at the working surface, we first need to accurately measure the gas concentration at the working surface and transmit the detection data in real time. However, the transmission distance and accuracy of the detection data are limited by the performance of the detection instruments, working environment, signal interference, and other factors. Therefore, achieving accurate measurement and long-distance transmission of gas concentration at the working surface has always been a technical problem in the safety management of high-gas coal mines.
To test the application of fractional-order calculus theory in data detection, the 151302 working surface of a mine in Huainan City was considered, which is located approximately 100 m from the surface and 2 km from the main shaft. The test required real-time accurate detection of the gas concentration at the working site under existing conditions. The experiment required a real-time accurate gas concentration detection function for the operation site under existing conditions. Owing to the long distances and dynamic changes in the operation site at the coal mine working face, the experiment required a wireless network to realize the real-time long-distance transmission of the collected data. To ensure the normal production of the working surface and the safety of the experiment site, after considering various factors, we designed a structural diagram of the gas concentration detection system, which is shown in Figure 5, and developed the corresponding data detection scheme. The data sensed by the gas concentration sensor were first transmitted to the gas concentration detection system near the working face by Wi-Fi wireless network transmission, and then the data processed by fractional-order differentiation were transmitted to the underground data center by an optical fiber transmission method. Finally, the data collected by the underground data center were transmitted to the surface data management center using a Controller Area Network (CAN). Owing to the complex structure of underground space, there are many interference sources in the process of data detection.
Owing to the complex spatial environment of the underground structure and the twists and turns of the fiber arrangement path, the traditional calculation of the fiber energy attenuation coefficient is not suitable for this case. To ensure the accuracy of the experimental results, this study adopted an experimental method to calculate the energy attenuation coefficient during signal transmission under existing working conditions. In the experiment, we chose an information transmission distance of 100 m and found its energy attenuation coefficient to be 0.63 after testing. Therefore, the data management center needs to amplify the signal strength by more than 6.25 times to achieve effective sensing and high-precision collection of data on the operating surface 2 km away. To ensure the detection quality of the collected data, the standard deviation should not exceed 0.005.
To improve the accuracy of the data, six working 3-2.3V LEL combustible gas sensors were used to measure the gas concentration at the working site of the working face. The six sensors worked simultaneously and were measured once every 5 s, and the data collection center collected five gas concentration measurements from the six sensors. Therefore, we can extract 30 data points at the same location in real time as the experimental samples, as shown in Table 1.

6.2. Pre-processing of Data

6.2.1. Analysis of Data

In the experiment, the average value of five measurements of each sensor, E ¯ i , was considered to be the true value, and the average value of all measurements, E ¯ , was considered to be the true value, E. A summary of gas concentration detection data for the working face is presented in Table 2. The detection data exhibited an irregular distribution around the measured true values. Therefore, influenced by multiple factors, such as the performance of the detection equipment and the working environment, the initial detection value of the gas concentration at the coal mine working surface had a large detection error, which created difficulties in providing accurate detection values for the safety management of the coal mine and significantly affected the decision-making of the safety management system.

6.2.2. Influence Factor of Data

Owing to the harsh environment and complex working conditions of the underground structural space, the detection data in the transmission process will inevitably be affected by a variety of factors, which results in a large data detection error. Six sensors were applied in the same working environment, and they operated at the same time and frequency to detect the gas concentration at the location. Thus, the effects of the environment and energy losses on the transmission of data are essentially the same. The variability of the detection data between the sensors was mainly due to differences in the performance of the detection equipment. Because the standard deviation is the best parameter for measuring the performance of the testing equipment, it was used as the influencing factor of the measured values of the sensor to analyze the correlation between the performance of the testing equipment and the measured value.

6.2.3. Equation Relating Concentration Data and Impact Factor

Because the least squares method has the advantage of not requiring a priori data in the data processing, it is widely used to fit polynomials to relate data and its influencing factors, and it can achieve ideal data processing accuracy. Thus, the least-squares method was used in this case to fit the function E(x) between the measured value Ei of each sensor and its influence factor xi. According to the parameter values of each sensor's measured value Ei and its influence factor xi (standard deviation) shown in Table 2, the mathematical expression of the function E(x) is assumed to be:
E ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n .
To obtain the function E(x), the polynomial order n and the coefficients ai (i = 0, 1, … n).
For least-squares fitting, the order of the fitted polynomial should be smaller than the number of data samples. Thus, the order of the function E(x) is sought when n < 6. Because the fitting accuracy of the function E(x) does not necessarily improve with an increase in the order n, the best order value was found between 0 < n < 6 to minimize the error between the function E(x) and the measured true value. The Polyfit function in the MATLAB software was applied, and the total errors of the fitted values of (27) at different orders are shown in Table 3. Based on these results, we can conclude that, when n=3, the total error between the fitted and measured true values of each sensor is 0.012, which is the smallest. The equation for the E(x) function is:
E ( x ) = 0.035 x − 10.727 .

6.3. High-precision Detection of Data Based on Stepwise Approximation Method

According to the working principle of the stepwise approximation method and the characteristics of the data in this case, the implementation process of the method is as follows:
  • The corresponding mathematical treatment under fractional-order differentiation was modeled based on the available experimental conditions and data.
  • The appropriate differential order v is selected based on the detection data characteristics and fractional-order differential operator properties.
  • The established mathematical model was applied to set the initial step value h and the initial standard deviation Ss was calculated under known conditions.
  • The step value h was continuously adjusted by comparing it with the set system threshold SG until the accuracy met the set system accuracy threshold SG.
Based on the properties of the fractional-order differential operator shown in Figure 1, the fractional-order differential operator has a certain enhancement effect on the signal when the differential order is 0 < v < 1. The enhancement effect becomes more significant as the order decreases, and it has the effect of nonlinear retention of the low-frequency components of the signal. Thus, the middle value of v= 0.5 was selected in this case to explore the application of the stepwise approximation method for improving the accuracy of the gas concentration detection.

6.3.1. Mathematical Model of Data accuracy Calculation Based on Fractional-order Differential Operator

According to (7), the formula for the standard deviation of the data in this case can be obtained as follows:.
S = ∑ i = 0 b − a / h E ​ ​ 0.5 ( x + i h ) − E ¯ 0.5 x 2 n K 0.5 ,
where
E 0.5 x + i h = lim h 4 → 0 E h ​ 0.5 x + i h = h ​ ​ − 0.5 ∑ i = 0 b − a / h − 1 i 0.5 i E x − i h .
Combined with (28), the data shown in the table were processed by the 0.5-order differential operator, and the result was:
E 0.5 x i = h − 0.5 E x i − 0.5 E x i − h − 0.5 1 − 0.5 2 ! E x i − 2 h − ⋯ − Γ 1 − 0.5 n ! Γ n + 1 − 0.5 E x i − n h ,
where b = 0.26 ； a = 0.07 ； n = b − a / h = 0.26 − 0.07 / h = 0.19 .

6.3.2. Calculation of Ttep Size h Based on Step-by-Step Approach Method

To improve the efficiency of the system, a step-by-step method was used to adjust the step value h to achieve a continuous improvement in the accuracy of the system data and select the best step value in terms of data accuracy and efficiency. The detection accuracy of the system was calculated by initially selecting h= 0.01. The data processing model for the detection data with step h = 0.01 and order v= 0.5, was obtained according to (29) and (31):
E 0.01 0.5 x = 10 ∑ i = 0 19 − 1 i 0.5 i E 0.01 x − 0.19 .
According to the data shown in Table 2 and (32), the experimental data shown in Table 4 were obtained for the fractional order v= 0.5, and step size h=0.01.
To facilitate a comparison of the standard deviation between the data before and after data processing, the processing results shown in Table 4 were divided by the amplification factor K0.01, and the results are shown in Table 5.
When h = 0.01, the accuracy of the fused data was significantly lower than the threshold value of 0.005. Based on the error between the two values, the step value was adjusted to h= 0.005. From (31), we determined that the data-processing model at this time is
E 0.005 0.5 x = 14 . 144 ∑ i = 0 38 − 1 i 0.5 i E 0.005 x − 0.19 .
The processing results shown in Table 6 can be obtained based on the data presented in Tables 2 and (33).
To compare the standard deviations of the data before and after data processing, the data processing results shown in Table 6 were divided by the amplification factor k0.005 to obtain the data values shown in Table 7.
When h= 0.005, the accuracy of the fused data was slightly lower than the threshold value, which was selected to improve the efficiency. Next, h= 0.003 was selected, and we obtained the following processing model of the data:
E 0.003 0.5 x = 18 . 257 ∑ i = 0 63 − 1 i 0.5 i E 0.003 x − 0.19 .
To compare the standard deviations of the data before and after data processing, the data processing results shown in Table 4 were divided by the amplification factor k0.003 to obtain the values shown in Table 8.
The data obtained by this process met the system accuracy requirement after being processed by the differential operator with fractional order v= 0.5 and step value h= 0.003.

6.4. Long-distance Data Transmission Based on Cyclic Iteration Method

6.4.1. Value of Parameter h and Amplification Factor k

Because the strength of the signal depends on its step value h and the number of fractional differential processing iterations, the original data were processed for the first iteration using the differential results with h= 0.003, v=0.5, and x ∈ [0.27, 0.42]. Before and after the iterations, the applied parameters were the same as those in the mathematical model. The various data points before the iterations are presented in Table 4.
By combining the fractional-order differential operator shown in Eq.(35) with the data processing model, the data shown in Table 9 were processed by the first fractional-order differential operator iteration to obtain the values shown in Table 10. The amplification coefficient and data accuracy before the iterations were essentially equal between the data after iterative processing by the fractional-order differential operator, thus verifying the correctness of the above assertion regarding the relationship between the accuracy and amplification coefficient in the data processing and the fractional-order differential parameters. When v = 0.5 and h= 0.003, the amplification factor K≈ 1.47 for the data before and after the iteration of the fractional-order differential operator.

6.4.2. Values of Amplification Factor K and Number of Iterations m

From the above discussion on fractional-order calculus theory, data processing accuracy, and amplification coefficient, combined with the results for this exam ple, the amplification coefficient k of the fractional-order differential operator on the data was obtained based on the relationship between the data accuracy S and the number of iterations. The relationships are as follows:
k = 1.47 S = 0.0019 ,
q is the number of fractional-order differential processing iterations of the data.
For the detection system given in and (19), to meet the amplification factor set for the detection system, it was necessary to satisfy the following equations:
K = 1.47 q 6.25 ≤ 1.47 q < 1.47 q + 1
By solving for q in (36), we can see that under the above detection conditions, when the fractional-order differential operator step h = 0.003, the number of fractional-order differential processing cycles q = 5. The amplification coefficient of the detection signal K = 6.86, which satisfies the set system requirements.

6.5. Experimental results and their analysis

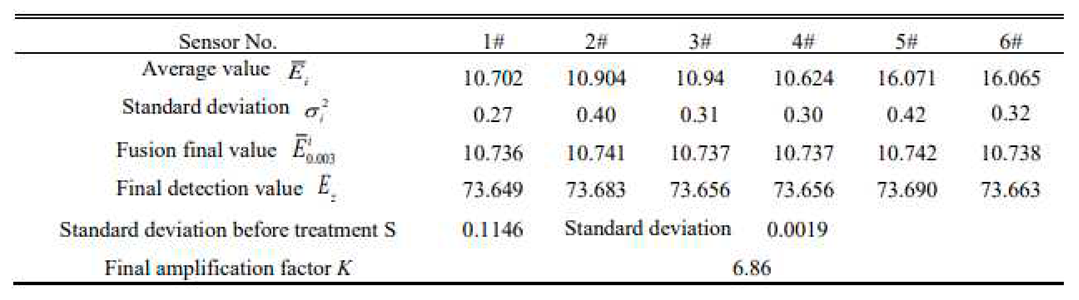
According to the above research results, it can be concluded that when the fractional order v=0.5 and the step size h=0.003, the detection accuracy of the information data in Table 1 is 0.0019 after the experimental data are processed by fractional order differentiation, as shown in Table 9. After processing five times by the fractional-order differentiation operator, the amplification coefficient of the information data was 6.86 after 5 times processing by fractional order differentiation operator. The final information data processing results are shown in Table 11, from which it can be seen that the detected information data can completely satisfy the detection target set by the system.
Because the experimental site in this study was located in a structural space more than 500 m underground, it was a harsh experimental environment. The experiments were conducted by simplifying the calculation steps and selecting typical parameter values to analyze and process the experimental data. In practical applications, the corresponding fractional order v can be selected based on the data characteristics, and the detection system can arbitrarily achieve the detection distances and data accuracies by adjusting the step value h and processing number n of the fractional-order differential operator.

7. Conclusion

Fractional-order calculus theory was applied to detect underground space information. by analyzing the characteristics of the generated information in complex environments and the signal amplitude and frequency characteristics after fractional differentiation algorithm processing to satisfy the current demand for long-distance and high-precision data detection. The fractional differentiation algorithm was applied to the detection of information data. The application experiments proved that the method described in this study has the following characteristics.
(1)
According to the characteristics of the fractional differential operator, the real-time detection function of various types of information data in an underground space can be realized.
(2)
By adjusting the step value h, the high-precision detection technology of information data in the complex environment of underground space is realized.
(3)
The remote detection technology of underground space information data is realized by adjusting the number n of fractional differential processing.
(4)
Through the integration of high-precision detection and long-distance transmission methods, a high-precision remote transmission function of a signal in an underground space is realized.
(5)
Using the integration of high-precision detection methods and long-distance transmission methods, an underground space information detection system can realize information data detection technology for setting performance goals.
(6)
Therefore, the algorithm used in this study can successfully solve the problems existing in current underground space information detection methods.

Acknowlelgments

This project was supported by national natural science fundation of china [grant numbers 51878005 and 51778004] and the Anhui Provincial Education Commission Foundation, China [grant number KJ2020A0488]

References

  1. Makana, L.O.; Metje, N.; Jefferson, I.; Sackey, M.; Rogers, C.D. Cost estimation of utility strikes: Towards proactive management of street works. Infrastruct. Asset Manage 2018, 7, 64–76. [Google Scholar] [CrossRef]
  2. Cheon, D.S.; Jin, K.; Kim, C.O. Analysis of microseismic parameters for the safety of underground structures [C]．14th International Congress on Rock Mechanics and Rock Engineering, ISRM 2019, September 13, 2019.
  3. Huang, Q.; Peng, J.; Wang, F.; et al. Issues and challengs in the deveopment of urban undergound space in advaerses geological environment. Earth science Frontiers 2019, 26, 85–94. [Google Scholar] [CrossRef]
  4. Xie, H.; Zhang, Y.; Chen, Y.; et al. A case study of development and the Guang-Hong Kong-Macao Greater Bay Area. Tunnelling undergound space Technology 2021, 107, 103651. [Google Scholar] [CrossRef]
  5. Li, S.L.; Cheng, Y.Z.; et al. Opportunities and challenges of construction safety in underground engineering projects. Journal of Shandong University of Science and Technology (Natural Science). 2020, 39, 1–13. [Google Scholar]
  6. Hao, L.; Xu, X.; Peng, S.; et al. 2016.Development and application of a novel combined low-frequency antenna for ultradeep advance detection in mine. //proceeding of 16th interntional conference on ground penetrating radar. Hongkong, Chiina: IEEE.
  7. Hong, W.; Kang, S.; Lee, S. Analyses of GPR signals for characterization of ground conditions in nrban areas. Journal of applied Geophysics 2018, 152, 65–76. [Google Scholar] [CrossRef]
  8. Hunt, D.V.L.; Makana, L.O.; Jefferson, I. Liveable cities and urban underground space technolgy 2016, 55, 8–20. [CrossRef]
  9. Li, W.; Li, K.; et al. A new method for space-based detection small-scale space debrise with high-resllution using transient electromagnetsm. Chinese Journal of Geophysics 2018, 61, 5066–5076. (in Chinese). [Google Scholar] [CrossRef]
  10. Li, W.; Lu, H.; Lu, K.; et al. New multi-resolution and multi-scale electromagnetic detection methods for urban uunderground spaces. Journal of Applied Geophysics 2018, 159, 742–753. [Google Scholar] [CrossRef]
  11. Li, W.; Lu, H.; Lu, K. multi-scale target detection for urban uunderground spaces with teasient electromagnetics based on diffrential pulse scanning. New multi-resolution and electromagnetic methods. Journal of Applied Geophysics, 159:742-753. Journal of of Environmental and Engineering Geophysics (In Chinese). 2019, 48, 1185–1190. [Google Scholar] [CrossRef]
  12. Persico, R.; Dei, D.; Parrinei, F.; et al. Mitigation of narrowband interferences by means of a Reconfigurable stepped frequency GPR sytem. Radio Science 2016, 51, 1322–1331. [Google Scholar] [CrossRef]
  13. Sefried, D.; Schoebel, J. Stepped-frequency radar signal processing. Journal of Applied Geophysiss 2015, 112, 42–51. [Google Scholar] [CrossRef]
  14. Engborg, P.; Sturk, R. Development of use of underground space in Sweden. Tunnelling and Underground Space Technology 2016, 55, 339–341. [Google Scholar] [CrossRef]
  15. Li, W.; Li, B.; Shu, C.; et al. New muti-resolotion and muti-scale electromagnetic detection methods for urban underground spaces. Journal of Applied Geophysics 2018, 159, 742–753. [Google Scholar] [CrossRef]
  16. Li, W.; Li, B.; Shu, C.; et al. Study on muti-resolotion imaging of urban underground spaces based on high performnce transient electromagnetic source. Chinese Lournal of Applied Geophysics 2020, 63, 4553–4564. [Google Scholar] [CrossRef]
  17. Ahmed, N.; Radchenko, A.; Pommerenke, D.; Zheng, Y.R. Design and evaluation of low-cost and energy-efficient magnetoinductive sensor nodes for wireless sensor networks. IEEE Syst. J. 2019, 13, 1135–1144. [Google Scholar] [CrossRef]
  18. Pal, A.; Kant, K. NFMI: Near field magnetic induction based communication. Comput. Netw. 2020, 181, 107548. [Google Scholar] [CrossRef]
  19. Guo, H.; Sun, Z.; Zhou, C. Practical design and implementation of metamaterial-enhanced magnetic induction communication. IEEE Access 2017, 1, 17213–17229. [Google Scholar] [CrossRef]
  20. Zheng, Z.; Fu, Y.; Liu, K.; Xiao, R.; Wang, X.; Shi, H. Three-stage vertical distribution of seawater conductivity. Sci. Rep. 2018, 8, 9916. [Google Scholar] [CrossRef] [PubMed]
  21. Wang, C.; Wang, Y.; Han, Z.; et al. An in-situ stress measurement method based on borehole shape analysis. Rock and Soil Mechanics 2019, 40, 549–556. [Google Scholar] [CrossRef]
  22. Lv, X.; Zhou, H. Quantitative Detection of In-Service Strength of Underground Space Strata considering Soil-Water Interaction. Advances in Civil Engineering, Volume 2020.
  23. Zheng, X.; Wang, H.; Guo, J.; et al. Method for multi-information drilling detection after mining disasters. OMPUTERS & ELECTRICAL ENGINEERING 2020, 86, 106726. [Google Scholar] [CrossRef]
  24. Sun, B.; Liu, X.; Xu, Z.; et al. Temperature data-driven fire source estimation algorithm of the underground pipe gallery. International Journal of Thermal Sciences 2022, 171, 107247. [Google Scholar] [CrossRef]
  25. Zuo, Y.; Zhang, K. Discrete Data Fusion with Integral Discrete Guidance in Internet of Things. Computer Science 2014, 41, 149–152. [Google Scholar]
  26. Zuo, Y.; Cheng, H.; Zhang, K. Fusion algorithm of discrete manufacturing system detection data based on fractional partial differential. Computer Integrated Manufacturing Systems 2015, 21, 3256–3262. [Google Scholar]
  27. Zuo, Y.; Cheng, H.; Zhu, Y. The Algorithm for Multi-sensors Detection Data Fusion Based on Fractional Differential. Science Technology and Engineering 2019, 19, 189–194. [Google Scholar]
  28. Zuo, Y. “Research on discrete manufacturing inspection data fusion technology based on fractional calculus,” Ph.D. dissertation, Dept. Mechanics Eng., Hefei University of technology, HeFei, China, 2019.
  29. Zuo, Y.; Cheng, H.; Cheng, T. Application of fractional differential operator in coal mine detection data fusion processing. Journal of China Coal Society 2020, 45, 819–826. [Google Scholar]
  30. Zuo, Y.; Cheng, H.; Cheng, T. On-Line Detection Data Fusion Algorithm of Underground Mobile Equipment Based on Fractional Order Partial Differential. Chin. J. Sens. Actuators 2021, 34, 237–243. [Google Scholar]
  31. Zuo, Y.; Zuo, C.; Fang, J. Engine On-line Detection Data Fusion Technology Based on Fractional Integral. Science Technology and Engineering 2021, 21, 644–650. [Google Scholar] [CrossRef]
  32. Podlubny, i. Fractional differential equations//Mathem- atics in Science and Engineering [S.l.].: Academic Press, 1999.
  33. PU, Y.-f.; Zhou, J.-l.; Yuan, X. Fractional differential mask: a fractional differential-based approach for multiscale texture enhancement. IEEE Trans on Image Processing. 2010, 19, 491–511. [Google Scholar] [CrossRef]
  34. Dal, F. Application of variational iteration method to fractional hyperbolic partial differential equation, Math. Probl. Eng. (2009). [CrossRef]
  35. Akinlar, M.A.; Kurulay, M. A novel method for analytical solutions of fractional partial differential equations, Math. Probl. Eng. (2013). [CrossRef]
  36. Eslami, M.; Vajargah, B.F.; Mirzazadeh, M.; Biswas, A. Application of first integral method to fractional partial differential equations. Indian J. Phys. 2014, 8, 177–184. [Google Scholar] [CrossRef]
  37. Gua, B.; Pu, X.; Haung, F. Fractional Partial Differential Equations and their Numerical Solutions. World Scientific. 2015. [CrossRef]
  38. Hassan, S.Z.; Abdelrahman, M.A. Solitary wave solutions for some nonlinear time fractional partial differential equation. Pramana. 2018, 91, 67. [Google Scholar] [CrossRef]
  39. WANG, B.; ZHU, J. Quantitative Analysis of High Temperature Protective Clothing Design Based on Fractional Partial Differential Equation Solution and Optimization Model. Journal of Sichuan University of Science & Engineering(Natural Sicence Edition). 2019, 32, 86–93. [Google Scholar]
  40. ZHOU, S.; WANG, L.; YIN, X. Applications of fractional partial differential equations in image processing. Journal of Computer Applications. 2017, 37, 546–552. [Google Scholar] [CrossRef]
  41. SHEN, T. “Dynamics of stochastic Fractional Partial Differential Equations,” Ph.D. dissertation, Dept. Mathematical Theory., National Defense University of science and technology, ChangSha, China, 2017.
Preprints 69368 i011 ZUO Yanhong (1973.11—) An associate professor of Chinese Anhui University of architecture and vice director of vocational skills appraisal institute of Anhui University, subordinate member of professional skills appraisal expert committee of Chinese Anhui Province, senior welder assessor, vice chairman of Chinese Anhui Construction Machinery Management Association and subordinate member of non road mobile machinery pollution prevention and control expert group. He has been engaged in teaching and research work in mechanical equipment fault diagnosis and advanced manufacturing technology for a long time He has published more than 20 related papers in national core journals.
Preprints 69368 i012 CHENG Hua (1956.10—), Male, Han nationality, from Chaohu, Anhui Province, doctoral advisor, professor and advanced worker in Anhui Province. Enjoying the special allowance of the State Council, he is a top-notch professional and technical talent in the national coal system, the first batch of discipline and technology leaders in Colleges and universities in Anhui Province, the leader of scientific and technological innovation academic team in Anhui Province, and a famous teaching teacher in Anhui Province. Vice president of Anhui society of rock mechanics and engineering.
Preprints 69368 i013 FANG Jigen (1989.12—) He presided over 2 projects in Anhui Province and participated in and completed 3 projects funded by the (National Natural Science Foundation of 3 hina; Presided over and completed 3 horizontal scientific research projects, with a total of 1.2 million yuan of scientific research funds in recent three years; 14 national invention patents were authorized; He participated in the formulation of 2 national industry standards, participated in the compilation of Made in China 2025 series books, and published more than 10 academic papers.
Preprints 69368 g001
Figure 1. Amplitude–frequency characteristic curves of fractional differential operator.
Figure 1. Amplitude–frequency characteristic curves of fractional differential operator.
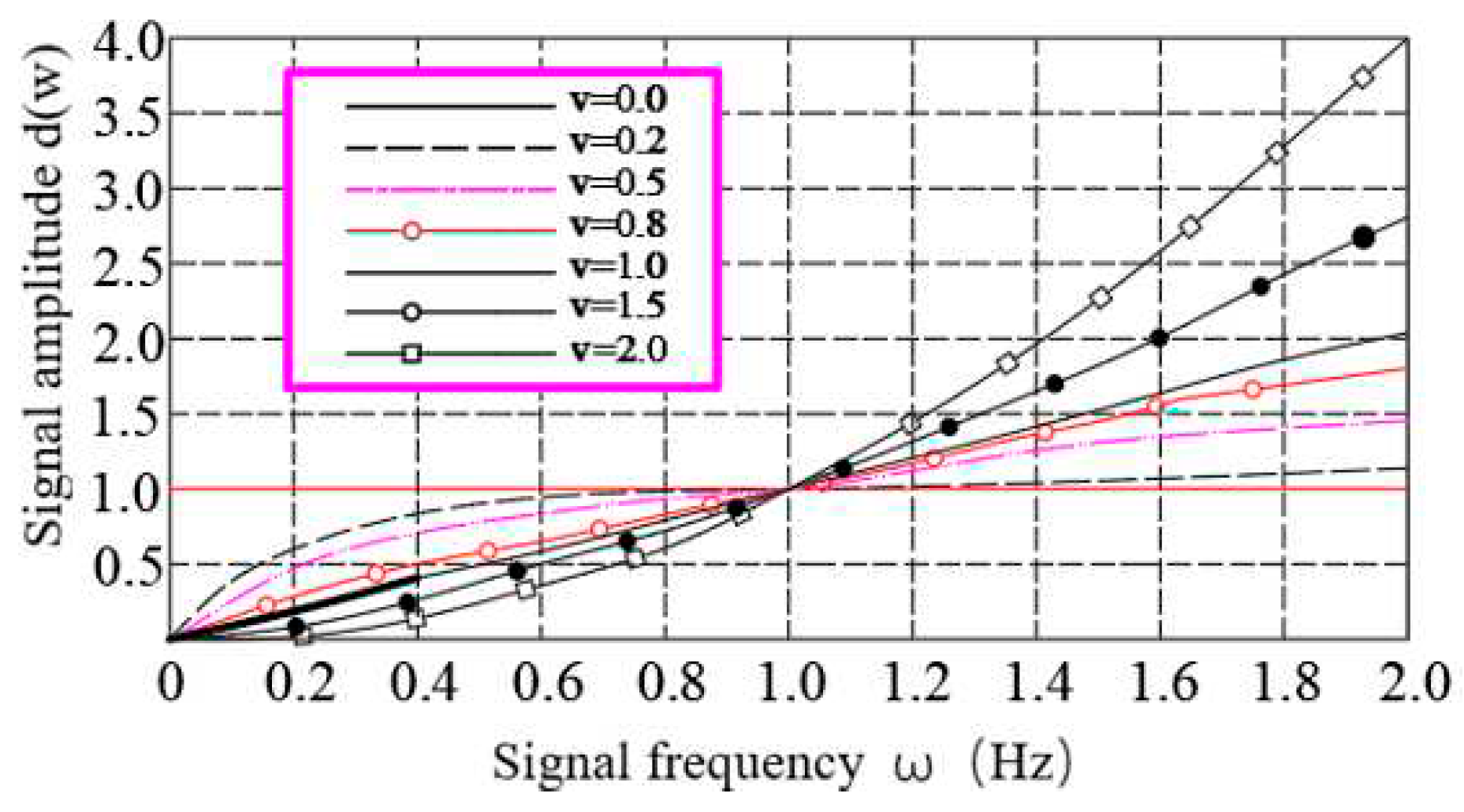
Preprints 69368 g001
Preprints 69368 g002
Figure 2. Data fitting accuracy for differential operators of the same order.
Figure 2. Data fitting accuracy for differential operators of the same order.
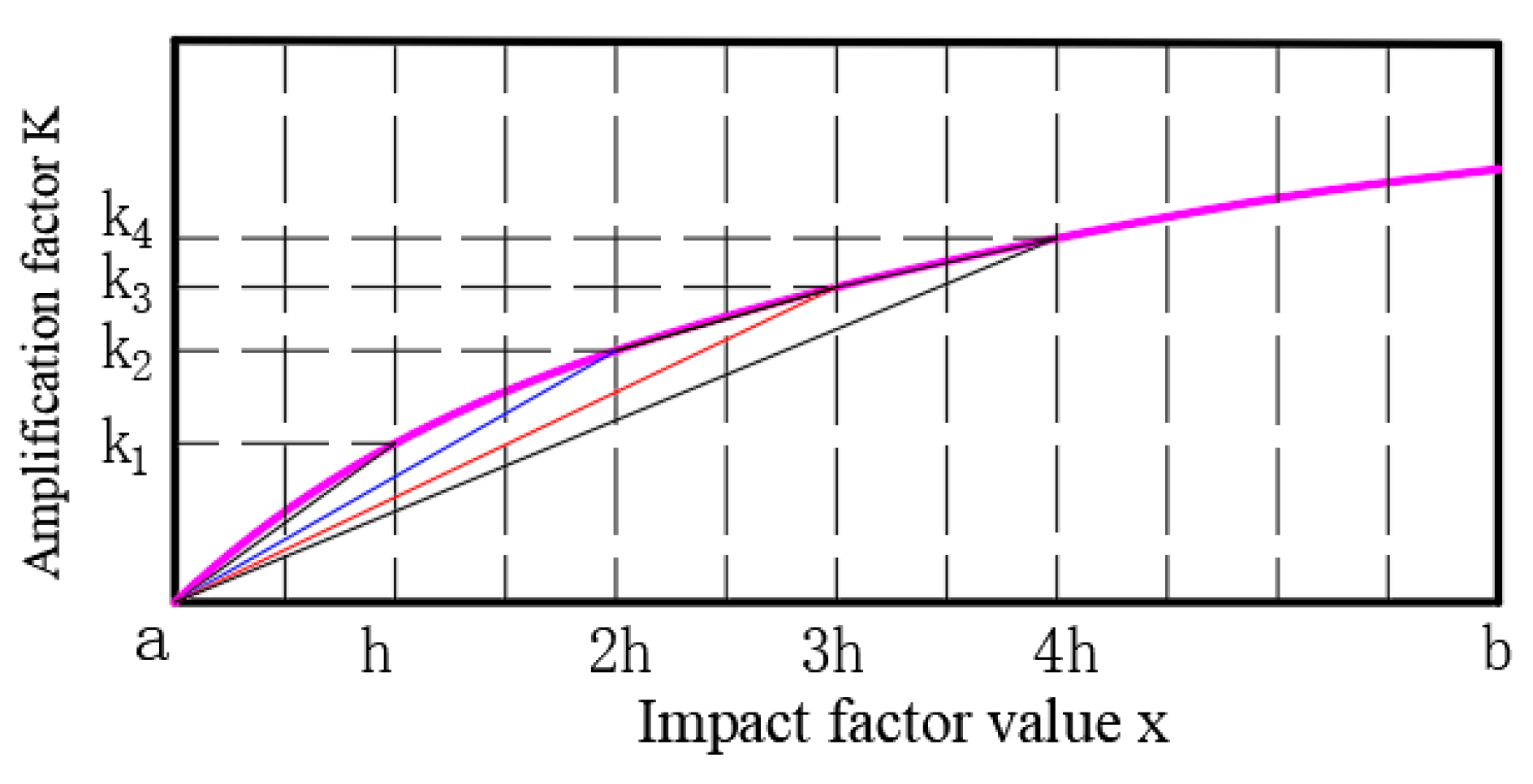
Preprints 69368 g002
Preprints 69368 g003
Figure 3. Differential operator signal characteristics under different orders.
Figure 3. Differential operator signal characteristics under different orders.
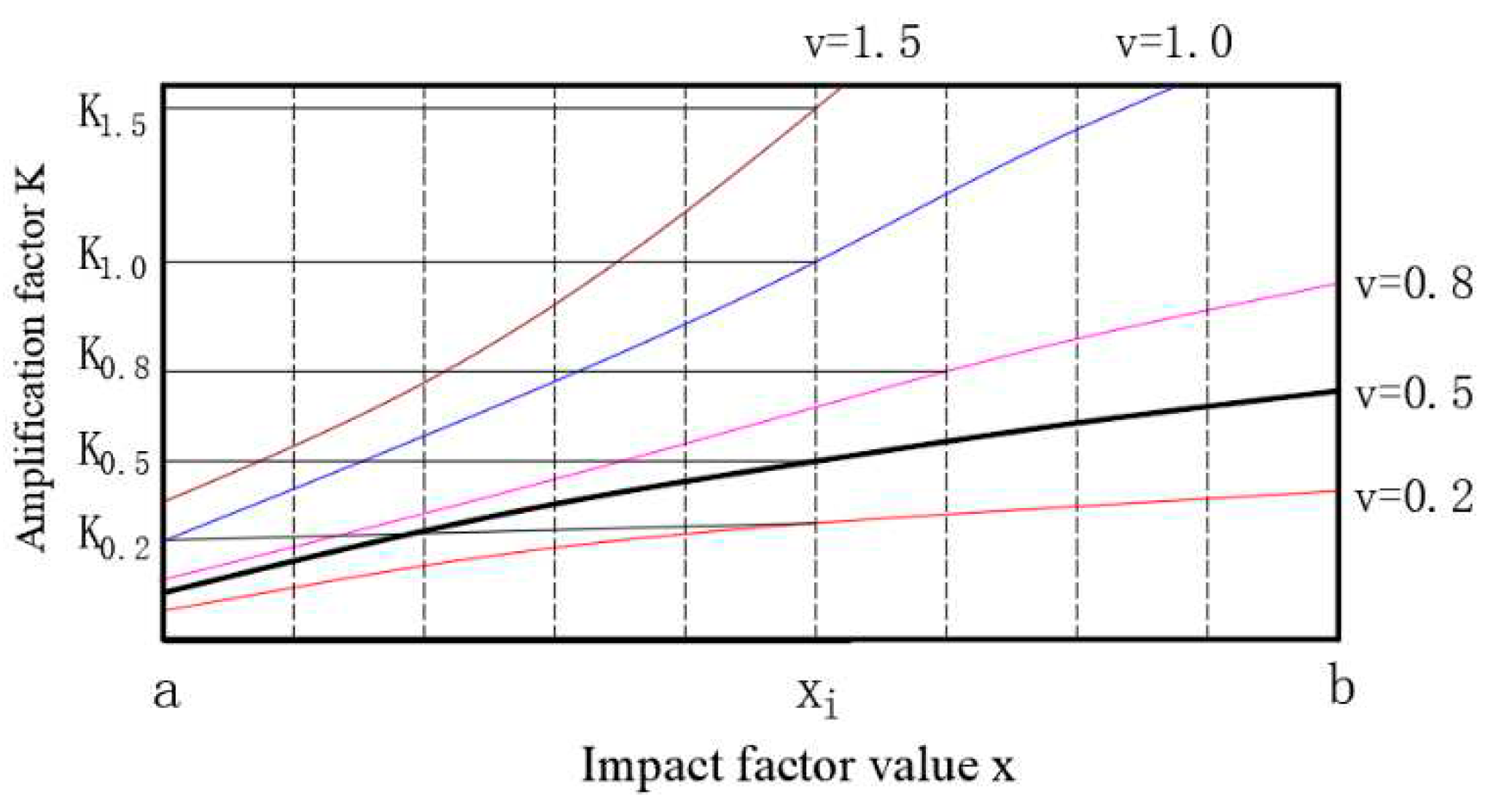
Preprints 69368 g003
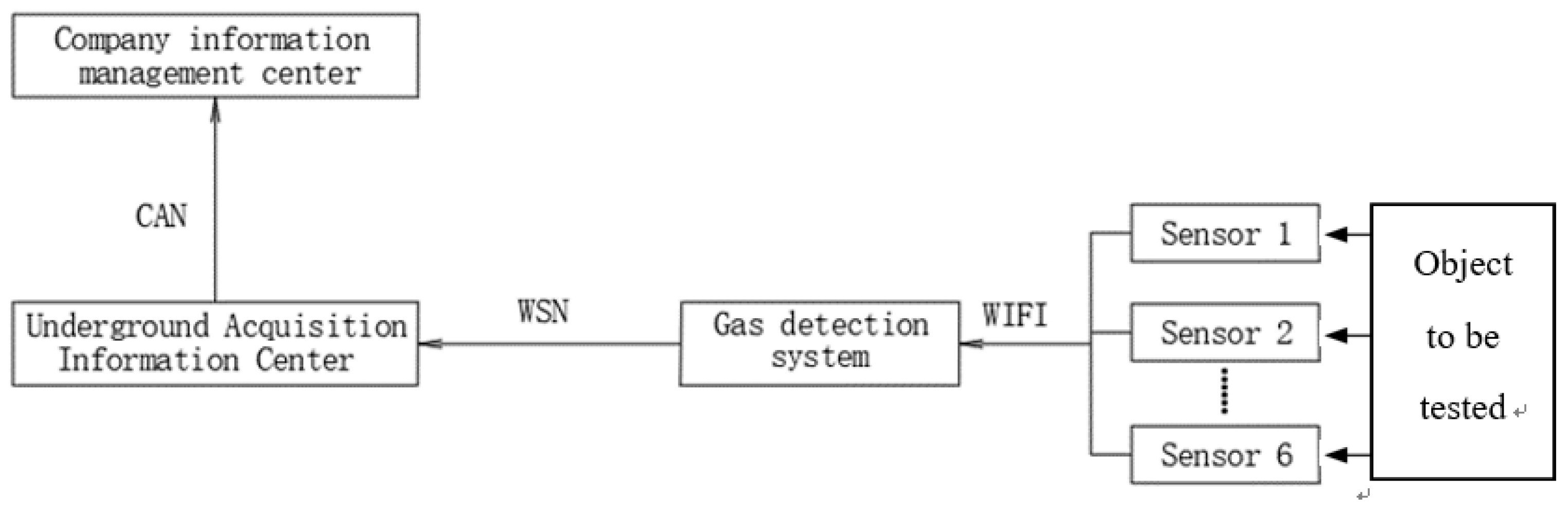
Preprints 69368 g004
Figure 4. Structure diagram of gas concentration detection system.
Figure 4. Structure diagram of gas concentration detection system.
Preprints 69368 g004
Table 1. EXPERIMENTAL DATA TABLE (%).
Table 1. EXPERIMENTAL DATA TABLE (%).
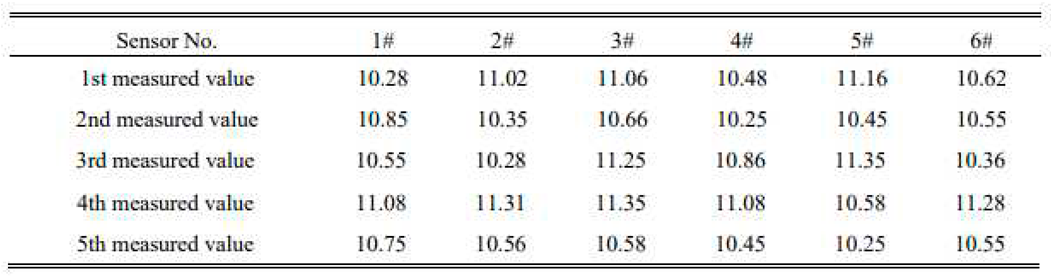Preprints 69368 i001
Table 2. SUMMARY OF EXPERIMENTAL DATA (%).
Table 2. SUMMARY OF EXPERIMENTAL DATA (%).
Preprints 69368 i002
Table 3. SUMMARY OF EXPERIMENTAL DATA (%).
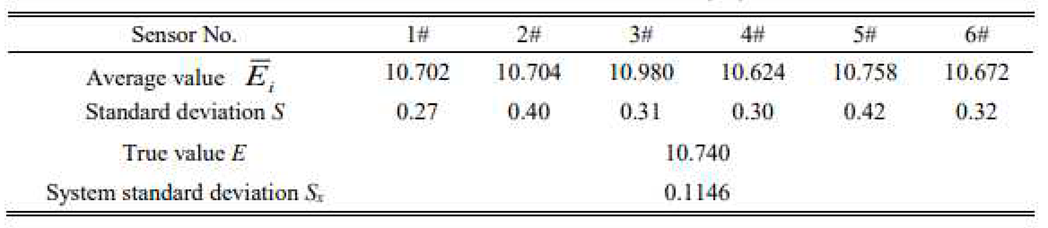Table 3. SUMMARY OF EXPERIMENTAL DATA (%).
Preprints 69368 i003
Table 4. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
Table 4. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
Preprints 69368 i004
Table 5. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
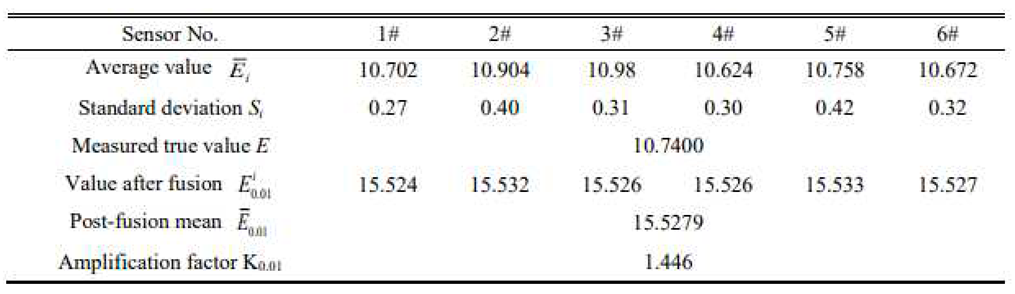Table 5. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
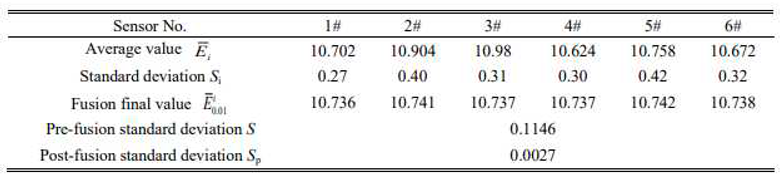Preprints 69368 i005
Table 6. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.005 (%).
Table 6. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.005 (%).
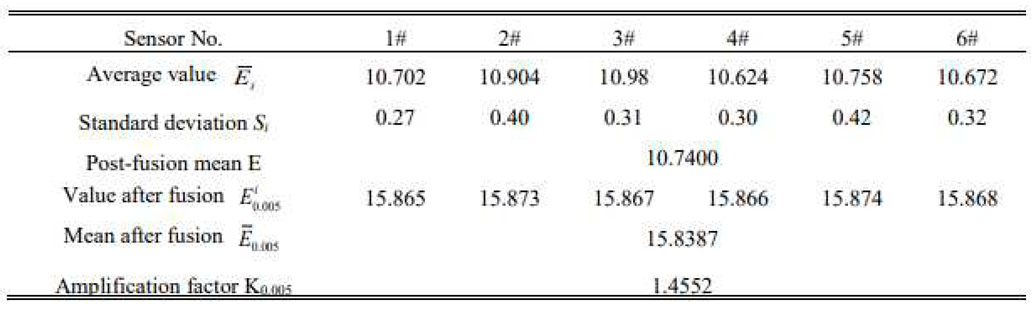Preprints 69368 i006
Table 7. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
Table 7. EXPERIMENTAL DATA SUMMARY TABLE WHEN H = 0.01 (%).
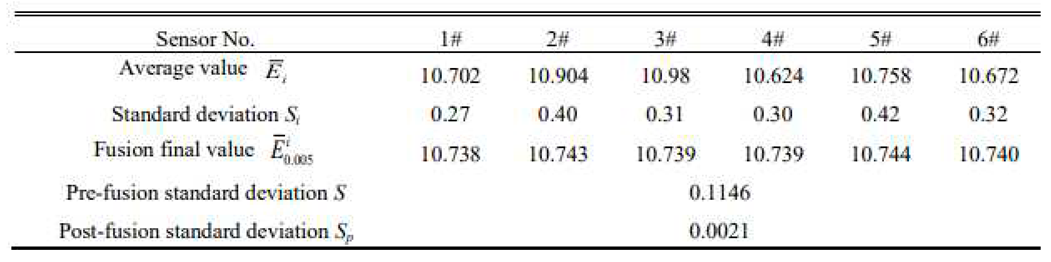Preprints 69368 i007
Table 8. EXPERIMENTAL DATA TABLE WHEN H= 0.003 (%).
Table 8. EXPERIMENTAL DATA TABLE WHEN H= 0.003 (%).
Preprints 69368 i008
Table 9. EXPERIMENTAL DATA TABLE WHEN H = 0.003 (%).
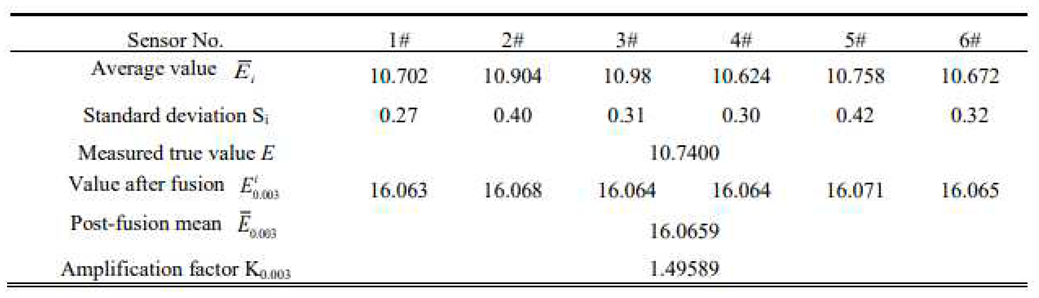Table 9. EXPERIMENTAL DATA TABLE WHEN H = 0.003 (%).
Sensor No. 1# 2# 3# 4# 5# 6#
Average value E ¯ i 10.702 10.904 10.940 10.624 16.071 16.065
Standard deviation Si 0.27 0.40 0.31 0.30 0.42 0.32
Fusion final value E ¯ 0.003 i 10.738 10.741 10.739 10.739 10.744 10.739
Pre-fusion standard deviation S 0.1146
Post-fusion standard deviation S0.003 0.0019
Table 10. SUMMARY OF EXPERIMENTAL DATA (%).
Table 10. SUMMARY OF EXPERIMENTAL DATA (%).
Preprints 69368 i009
Table 11. SUMMARY OF FINAL PROCESSING RESULTS OF EXPERIMENTAL DATA (%).
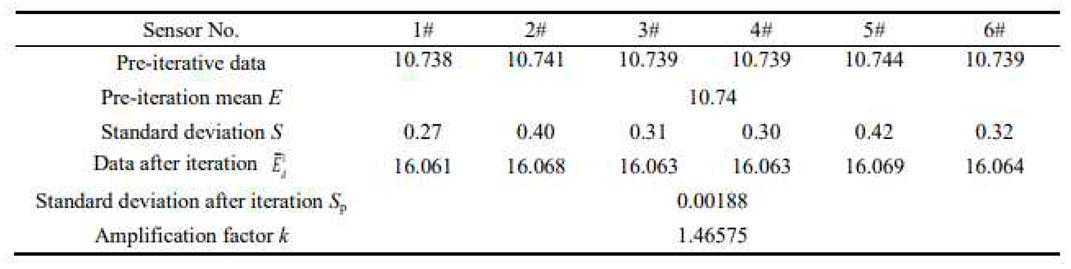Table 11. SUMMARY OF FINAL PROCESSING RESULTS OF EXPERIMENTAL DATA (%).
Preprints 69368 i010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated